Abstract

The OpenPathSampling (OPS) package provides an easy-to-use framework to apply transition path sampling methodologies to complex molecular systems with a minimum of effort. Yet, the extensibility of OPS allows for the exploration of new path sampling algorithms by building on a variety of basic operations. In a companion paper [Swenson et al. J. Chem. Theory Comput. 2018, 10.1021/acs.jctc.8b00626] we introduced the basic concepts and the structure of the OPS package, and how it can be employed to perform standard transition path sampling and (replica exchange) transition interface sampling. In this paper, we elaborate on two theoretical developments that went into the design of OPS. The first development relates to the construction of path ensembles, the what is being sampled. We introduce a novel set-based notation for the path ensemble, which provides an alternative paradigm for constructing path ensembles and allows building arbitrarily complex path ensembles from fundamental ones. The second fundamental development is the structure for the customization of Monte Carlo procedures; how path ensembles are being sampled. We describe in detail the OPS objects that implement this approach to customization, the MoveScheme and the PathMover, and provide tools to create and manipulate these objects. We illustrate both the path ensemble building and sampling scheme customization with several examples. OPS thus facilitates both standard path sampling application in complex systems as well as the development of new path sampling methodology, beyond the default.
1. Introduction
Many dynamical processes, including nucleated phase transitions, chemical reactions, and complex conformational changes in biomolecular systems, such as proteins and nucleic acids, occur on long time scales,1−4 primarily due to large kinetic barriers between metastable states.5−7 Straightforward molecular dynamics simulations are then highly inefficient due to the long waiting times within metastable basins, while the rare events of interest occur over a short time.8 Methods such as umbrella sampling,9 blue moon sampling,10 local elevation sampling,11 conformational flooding,12 hyperdynamics,13 metadynamics,14 adaptive biasing force methods,15 replica exchange,16 simulated tempering,17 integrated sampling,18 orthogonal space sampling,19 and numerous others enhance the occurrence of the rare event by biasing the potential energy surface or the density of sampled conformations. To be effective, bias potentials require (a set of) collective variables that approximate the reaction coordinate. However, a poor choice will lead to poor sampling of reactive pathways and hence poor estimates of the dynamical bottlenecks and the related barrier heights and rates.
The transition path sampling (TPS) methodology20−23 can enhance the sampling of complex dynamical transitions in complex (bio)molecular systems, avoiding the exponentially long time scales that the system spends in metastable states and, most importantly, bypassing the need for a reaction coordinate. Notwithstanding the efficiency of path sampling, the complexity of implementation and lack of standard tools have hampered widespread application.
The OpenPathSampling (OPS) framework aims at providing a toolbox to make complex transition path sampling simulation easily accessible for users. In Paper 1, we introduced the basic concepts and structure of the OPS framework, discussed its ingredients, and gave a tutorial on how to conduct some standard simulations using the OPS framework.24 The current work builds heavily on this companion paper, and we refer the reader to ref (24) for full details. The OPS framework facilitates implementation of the three stages in any path sampling study: initialization, sampling, and analysis. In the initialization step the user defines the (network of) transitions that needs to be sampled. This requires definition of stable states and path and/or interface ensembles to be used in (replica exchange) transition interface sampling (TIS) schemes. These definitions are based on phase space volumes defined as a function of a priori chosen collective variables. Since path sampling is basically a Monte Carlo (MC) approach, the user also has to decide on the specific details of how each type of move is implemented, which OPS facilitates with the MoveStrategy objects, and the user has to create the overall (and sometimes complex) decision tree for the MC procedure, which OPS implements in a MoveScheme. The transition network and the MoveScheme, together with the Molecular Dynamics Engine, a Storage file, and an initial path sample set, are used by the PathSimulator, which performs the sampling. Analysis of the sampled paths is subsequently performed using information obtained from the Storage object. OPS provides tools for the initialization step and for the analysis. For more details we refer to Paper 124 and to the online documentation at http://openpathsampling.org.
This paper is mainly aimed at method developers and researchers interested in devising their own path sampling methods using the OPS framework. This requires an extensive treatment of the more fundamental ideas that went into the design of OPS. The paper focuses on two of those fundamental aspects. One is the construction of path ensembles, which can be viewed as what is being sampled. The other is the customization of the Monte Carlo procedures, which relates to how the path ensembles are being sampled. This paper provides novel conceptional frameworks for dealing with these two aspects.
In the first part, we focus on the path ensembles. While the definition of path ensembles in the original TPS and TIS papers is perfectly usable for many applications, these definitions can become quite cumbersome when multiple states or multiple collective variables come into play. This also holds for the more complex path moves, such as the minus interface move(25,26) used in replica exchange TIS (RETIS), which exchanges a trajectory in the first interface ensemble with a trajectory exploring the stable state (the minus interface ensemble) in order to decorrelate the (usually short) pathways in the first interface and to provide a direct estimate for the flux out of the stable state.25−27 Here, we present a framework allowing one to build arbitrarily complex path ensembles from fundamental path ensembles. To facilitate this, we first introduce a novel set-based notation for the path ensembles. For completeness, we also provide connections to the original TPS and TIS notation. This novel notation provides an alternative paradigm for constructing path ensembles with several major advantages: (1) It allows one to easily create complex ensembles as combinations of simpler ensembles, e.g., using set logic. (2) It creates a systematic connection between the ensemble indicator function and the stopping criteria used when generating a trajectory for the ensemble, e.g., with a shooting move. Previously, the stopping criteria were identified separately for every ensemble/path generating move. (3) It facilitates analysis, as many analysis procedures can be framed as searching for subtrajectories that satisfy some ensemble indicator function. Examples of this are provided in Section 4. Of particular importance herein is the sequential path ensemble, which is directly related to the way that OPS implements path sampling and testing. We explain in detail how different ensembles are being built in terms of these sequential path ensembles. We end the first part with a set of general guidelines and simple rules on how arbitrary path ensembles could be built in OPS.
In the second part of the paper, we describe the framework that creates the Monte Carlo process used by OPS. This framework is designed to be extremely flexible, which enables one to customize the Monte Carlo move scheme and to build nonstandard path sampling schemes with little effort. This ability to customize the move scheme is one of the major advantages of the OPS framework. It allows experienced users to design a sampling method tailored to a specific system. Here the two central concepts are (1) the move scheme, which encodes the entire Monte Carlo procedure as a decision tree, and (2) the path movers, which perform the moves. We describe both concepts in detail, as well as the tools in OPS that facilitate customization of the move scheme.
The paper is organized as follows. In Section 2.1 we briefly review the original standard notation for TPS path ensembles. Subsequently, we introduce the novel path ensemble set notation, including the sequential ensemble. We then describe in Section 2.5 how OPS implements these ensembles and give some guidelines and rules on how new ensembles could be built. In Section 3 we discuss customizing the Monte Carlo moves in detail. We give illustrations of these concepts in Section 4, where we discuss the application of generating and splitting trajectories, as well as customizing the move schemes for alternative replica exchange simulations. Finally, we end with conclusions and an outlook.
2. Building Blocks for Path Ensembles and Volumes
2.1. Standard TPS and TIS Notation
In this section, we briefly recapitulate the standard notation for the path ensemble and distribution functions used in TPS and TIS before introducing the novel set based notation that is more commensurate with the way OPS implements path sampling. This section is not meant as an introduction to path sampling but rather to describe the connection between the novel set-based notation and the standard notation found in the literature. For a review of path sampling methodology we refer the reader to refs (20−23 and 28). In the next sections we follow the notation that was introduced in refs (26) and (28).
2.1.1. The TPS Path Ensemble
A path is
a discretized, time-ordered sequence of states in phase space x ≡ {x0, x1, x2, ..., xL}, in which consecutive states, or frames,
are separated by a small time increment Δτ. Each frame x = {r, p} consists of the positions and momenta of all particles in the entire
system. The path-length L can be chosen fixed or
variable, depending on the type of path ensemble. The path probability
for a trajectory of duration 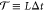 is
is
| 1 |
where p(xi → xi+1) denotes the Markovian transition probability to go from xi to xi+1 in one time step, which depends on the underlying dynamics.22 Further, ρ(x0) is the distribution of initial conditions, in many cases the equilibrium distribution. TPS constrains pathways between two stable states A and B. Such states are defined using a collective variable or order parameter λ, for example
| 2 |
and likewise for B. Here, λ(x) returns the order parameter λ for frame x, and λA defines the boundary of state A. [Note that the terms “order parameter” and “collective variable” are used interchangeably in this work. As explained in Paper 1,24 the term collective variable refers to any function of the system’s coordinates.]
The standard TPS path ensemble distribution with a fixed length L constrains the path to begin in A and end in B
| 3 |
where 1A(x0) and 1B(xL) are indicator functions that are, respectively, unity if the trajectory starts with x0 ∈ A and ends with xL ∈ B and zero otherwise. The formal definition of 1A(x0) is
| 4 |
and 1B(xL) is defined likewise.
The normalization factor 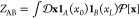 is akin to a partition function, where
the integral over
is akin to a partition function, where
the integral over 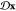 takes into account paths of length L starting at all possible initial conditions x0.
takes into account paths of length L starting at all possible initial conditions x0.
For variable path length TPS a similar path ensemble distribution can be written
| 5 |
where the indicator function h[x] now selects the paths that immediately leave A and just enter B
 |
6 |
Note that this path
ensemble indicator function
already shows some complexity. The normalization factor is now  where
the integral over
where
the integral over 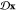 takes now into account paths of all length
starting at all possible initial conditions x0.
takes now into account paths of all length
starting at all possible initial conditions x0.
2.1.2. The TIS Path Ensemble
Transition interface sampling (TIS) defines a series of successive nonintersecting interfaces λ0, λ1, ..., λn, based on an order parameter λ and samples the TIS path ensemble for each interface. Paths in the interface ensemble i start in A (at λ0), cross the interface λi at least once, and finally either return to A or end in B. Defining adjacent phase space regions separated by interface λi as Λi+ ≡ {x: λ(x) > λi} the path probability for an interface ensemble i is given by
| 7 |
where the subscripts AΛi+ denote the phase phase regions connected by the paths and the TIS indicator function
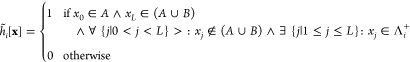 |
8 |
where the first and second lines ensure that only the initial and end points are in A and B, respectively, whereas the third line requires that the path cross the interface. The normalization factor ZAΛi+ is defined by
| 9 |
where the path integral runs again over all possible paths of all lengths. The ensembles for the reverse reaction B → A are defined in an analogous fashion.26,28
The path ensemble indicator functions become rather complex even for the basic TPS and TIS ensembles. Moreover, the indicator functions as described above are not directly implementable in a path sampling code such as OPS, as they only apply to entire paths. During a shooting move, which is at the heart of TPS and TIS, OPS has to monitor a newly generated path and apply a stopping criterion. Such a criterion requires a notation that is better suited to the way that OPS implements both the monitor function and the path ensembles themselves.
2.2. Volumes as Sets
As the novel notation is based on set logic, it is only natural to also treat the stable states as sets. In OPS, stable states, and in fact any region in phase space, are described as “volumes”. Additionally, TIS interfaces are treated as volumes. This has several advantages, among which is the fact that it is then easy to combine volumes using set logic.
Volumes are defined by collective variable functions. As mentioned above, a state consists of the (usually infinite) set of all configurations that obey the state definition. For instance, using one order parameter λ(x) state A can be defined as in eq 2
| 10 |
More general definitions are possible, e.g. by using an arbitrary number of order parameters. TIS interface volumes for an interface i connected to state A can be defined as
| 11 |
which is the part of phase space complementary to ΛAi+ defined in the previous section. Crossing an interface now amounts to leaving ΛAi, putting it conceptually on the same level as leaving A or entering B.
Volumes (e.g., states) can be combined using set logic. For two states A and B
| 12 |
denotes the union of sets, while
| 13 |
denotes the intersection. In this way volumes obeying an arbitrary number of conditions can be constructed.
In OPS this set logic is implemented by several functions. We can take unions and intersections of volumes and negations of volumes using the objects UnionVolume, IntersectionVolume, and NegatedVolume. From these operations any logical operation can be constructed. Take as an example the SymmetricDifference, which for two volumes A and B would amount to all points that are either in A or in B but not in both. This is logically equivalent to
| 14 |
where the overbar denotes the complement or negation of the volume. Other logical operations can be constructed at will.
2.3. Path Ensembles as Sets
2.3.1. Unifying Two Basic Tasks in OPS
As discussed in Section 2.1, path ensembles are the
set of all trajectories that satisfy
the ensemble indicator function hE[x] of the ensemble E, weighted
by the natural path probability 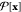 . In OPS, the ensemble indicator
function
is part of the Ensemble object. Paths are sampled
with the correct relative weights by using Monte Carlo moves that
preserve the distribution. Trajectories with nonzero weight form a
set of paths that satisfy the constraints imposed by the ensemble
indicator function. Indeed, these constraints define the ensemble
indicator function. For instance, a TPS ensemble requires the constraints
that the first snapshot be in the initial state, that the last snapshot
be in the final state, and that no other frames of the trajectory
visit a stable state. An important task in OPS is to test whether
a trajectory fits a certain ensemble. The Ensemble object takes a trajectory as input and returns whether or not it
belongs to that ensemble. Take, for instance, the simple ensemble
for which all frames should be in a certain state A. The predefined ensemble class AllInXEnsemble(state) tests exactly that, returning True only if
all frames are in the given state. One of the
most productive ways to define useful path ensembles in OPS is the SequentialEnsemble object. SequentialEnsemble comprises a list of path ensembles that the trajectory needs to
fulfill in the correct order. This is crucial when performing path
sampling, identifying whether a path fulfills the right conditions
for a move, e.g. an exchange move. Moreover, they can be useful for
analysis of pathways.
. In OPS, the ensemble indicator
function
is part of the Ensemble object. Paths are sampled
with the correct relative weights by using Monte Carlo moves that
preserve the distribution. Trajectories with nonzero weight form a
set of paths that satisfy the constraints imposed by the ensemble
indicator function. Indeed, these constraints define the ensemble
indicator function. For instance, a TPS ensemble requires the constraints
that the first snapshot be in the initial state, that the last snapshot
be in the final state, and that no other frames of the trajectory
visit a stable state. An important task in OPS is to test whether
a trajectory fits a certain ensemble. The Ensemble object takes a trajectory as input and returns whether or not it
belongs to that ensemble. Take, for instance, the simple ensemble
for which all frames should be in a certain state A. The predefined ensemble class AllInXEnsemble(state) tests exactly that, returning True only if
all frames are in the given state. One of the
most productive ways to define useful path ensembles in OPS is the SequentialEnsemble object. SequentialEnsemble comprises a list of path ensembles that the trajectory needs to
fulfill in the correct order. This is crucial when performing path
sampling, identifying whether a path fulfills the right conditions
for a move, e.g. an exchange move. Moreover, they can be useful for
analysis of pathways.
When performing path sampling, and in particular during a shooting move, another important task in OPS is to monitor whether a trajectory is finished, i.e., fulfills the conditions for stopping. At first sight, one might think that such a test is simply applying the same Ensemble object as above. However, this is not the case, since there are obviously many paths that do not obey the desired path ensemble but still are clearly to be rejected. For instance, a path that leaves A and returns to A, without having visited B, is clearly to be rejected. Hence, a halting criterion is needed or, rather, a continuing criterion that tells OPS to keep integrating the molecular dynamics trajectory, until it is clear that the trajectory can no longer ever satisfy the path ensemble. The can_append method provides the test for whether the path can be extended or not. Moreover, the can_append method is the building block from which the SequentialEnsemble is constructed.
In the following sections, we present a general set-based approach, which connects the ensemble to its halting criteria and which allows one to build arbitrarily complex ensembles from simple building blocks. As we build up to more complicated ensembles, we will, at each stage, first describe the set-based approach, introducing a new notation for describing path ensembles. Then we will show how that new notation maps directly onto objects in OPS.
2.3.2. The Basic Building Blocks
As above we denote a (sub)trajectory as a discretized time-ordered sequence of phase space points x ≡ {xb, xb+1, ..., xe} where b and e denote the beginning and end of the (sub)trajectory, respectively. For e < b we define the trajectory of zero length x = {}. Note that a time-reversed path also has positive time-order {y0, y1, ..., yL} and can be constructed from the trajectory {x0, x1, ..., xL} by setting yi = xL–i.
A path ensemble is an (infinite) set of trajectories obeying a certain criterion, encoded by indicator functions. A basic example is the ensemble of trajectories for which all frames are within volume A. In OPS, indicator functions determine whether a trajectory belongs a particular ensemble. For instance, the (formal) function InA(x) returns unity only when the entire trajectory belongs to volume A
| 15 |
and zero otherwise. Likewise the indicator for the set of trajectories entirely outside of A requires an indicator function OutA(x) that determines that no element belongs to A
| 16 |
As can be seen directly from these definitions
| 17 |
Just as volumes can can be seen as sets allowing set-based logic, path ensembles can be combined or intersected using set logic. An ensemble can be combined, e.g. using a union (indicated by ∪) or an intersection (indicated by ∩). A union of ensembles means that the trajectory has to belong to any one of the ensembles; an intersection means that the trajectory has to belong to all ensembles. Combinations of these logical operations are likewise defined.
Suppose that we are interested in the ensemble OutS, with S = A ∪ B the union of states A and B. The ensemble logic gives
| 18 |
Note that here, the notation InA and OutA refers to the ensemble, i.e., the entire set of trajectories, whereas when we talk about the associated indicator function we use InA(x) and OutA(x).
To construct all possible logical statements, we need the complement or (negation) of ensembles. We can take complements of ensembles, e.g.
| 19 |
where the overbar indicates the complement
of the set. The  refers to the complement of the union of
the set of trajectories entirely inside A and the
set of trajectories entirely inside B. Indeed, a
trajectory that is not entirely inside A or entirely
inside B has to be partly outside A and partly outside B.
refers to the complement of the union of
the set of trajectories entirely inside A and the
set of trajectories entirely inside B. Indeed, a
trajectory that is not entirely inside A or entirely
inside B has to be partly outside A and partly outside B.
The complement of the OutA ensemble is the PartInA ensemble, defined by the indicator function
| 20 |
likewise, the complement of the InA ensemble, called PartOutA, is defined by the indicator function where part of the trajectory is outside A.
| 21 |
From these definitions it is clear that
| 22 |
| 23 |
In addition, analogously to eq 17, we have
| 24 |
One might expect that InS would obey logic analogous to OutS. However, it turns out
| 25 |
because this would state that either all frames are in A or all frames are in B. Instead, it is possible that some frames are in A and some frames are in B, but no frames are outside of S. Thus, the connection is
| 26 |
In OPS the four basic functions InX, OutX, PartInx, and PartOutX (illustrated in Figure 1) have their own predefined objects AllInXEnsemble, AllOutXEnsemble, PartInXEnsemble, and PartOutXEnsemble, which act as building blocks from which ensembles can be constructed. Indeed, as the names suggest, these ensembles only return True if, respectively all frames are in X, all frames are out of X, at least one frame is in X, and at least one frame is out of X (see Table 1).
Figure 1.

“Building block” ensembles in OPS, with example trajectories. Sequences of logical combinations of these ensembles are used to create path ensembles used in OPS. Note that several example trajectories could satisfy the PartInX and PartOutX ensembles. Either of the trajectories shown for one would satisfy the other. In addition, the trajectory for the InX would also satisfy PartInX, and the trajectory for OutX would also satisfy PartOutX.
Table 1. Basic Building Block Ensemblesa.
| notation | OPS object | returns True if | complement |
|---|---|---|---|
| InX | AllInXEnsemble | all frames are in volume X | PartOutX |
| OutX | AllOutXEnsemble | all frames are in volume X | PartInX |
| PartInX | PartInXEnsemble | at least one frame is in volume X | OutX |
| PartOutX | PartOutXEnsemble | at least one frame is in volume X | InX |
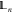 |
LengthEnsemble | trajectory consists of n frames | any length but n |
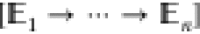 |
SequentialEnsemble | subtrajectories are in subensembles | failing any subensemble |
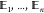 in the
correct order in the
correct order |
While PartInXEnsemble and PartOutXEnsemble at first sight seem to be identical ensembles, they are in fact different since PartInXEnsemble also yields True for a trajectory that is all in X, whereas PartOutXEnsemble does not. Also, contrary to what one might naively think, the complement of AllInXEnsemble is not the AllOutXEnsemble. As discussed above, the complement of the InX implementation AllInXEnsemble is the PartOutX implementation PartOutXEnsemble. Indeed, PartOutXEnsemble gives True always if one frame is out of X, and only returns False if all frames are in X, the very definition of AllInXEnsemble. In Table 1 the complements of the basic building block ensembles are given.
2.3.3. The Length Ensemble
The length ensemble consists of all paths of a specific length n. Formally, it can be defined by the indicator function
| 27 |
where  can take any positive integer number n > 0.
An additional definition is needed for the zero length n = 0 ensemble
can take any positive integer number n > 0.
An additional definition is needed for the zero length n = 0 ensemble
| 28 |
which is the case for e < b. The indicator function  thus
returns unity only if the trajectory
consists of n frames. To test whether a trajectory
is entirely in state A with a length n = 7 thus becomes
thus
returns unity only if the trajectory
consists of n frames. To test whether a trajectory
is entirely in state A with a length n = 7 thus becomes
| 29 |
OPS implements this ensemble with the object LengthEnsemble(n) which, as one might expect, requires the (sub)trajectory to be of a specified length n.
2.4. The Can-Append Criterion
In practice, path sampling uses methods like the shooting move to generate new trajectories by running dynamics. The shooting move must have some criterion to determine when to stop the trajectories it generates. In early versions of path sampling, this was based only on trajectory length, but more advanced variants gain efficiency by stopping the simulation based on information from the coordinates/momenta of snapshots in the trajectory; for example, stopping upon entering a stable state. As such, each path ensemble must be associated with a halting criterion.
In the formalism presented here, the halting condition (or more
correctly, the not-yet-halt condition) is called the can-append criterion.
The can-append criterion is associated with and determined by a specific
ensemble  and
denoted
and
denoted  . It takes a trajectory x as
input and answers the question, “Is the trajectory x a subtrajectory of any trajectory
. It takes a trajectory x as
input and answers the question, “Is the trajectory x a subtrajectory of any trajectory  ?”.
More formally, it is defined
as an indicator function on the set of all trajectories for which
an additional slice in the forward time direction would not immediately
fail the specified criterion for ensemble
?”.
More formally, it is defined
as an indicator function on the set of all trajectories for which
an additional slice in the forward time direction would not immediately
fail the specified criterion for ensemble 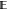 . For each ensemble object in OPS, there
is a method called can_append that returns True for trajectories that satisfy the can-append criterion
and False for trajectories that do not. For
the negative time direction, there is an analogous criterion
. For each ensemble object in OPS, there
is a method called can_append that returns True for trajectories that satisfy the can-append criterion
and False for trajectories that do not. For
the negative time direction, there is an analogous criterion 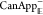 and a can_prepend method, which tests the addition of an extra frame at the beginning
of the trajectory. The discussion that follows is framed in terms
of the forward-time can_append method. However,
similar arguments apply to the backward-time can_prepend.
and a can_prepend method, which tests the addition of an extra frame at the beginning
of the trajectory. The discussion that follows is framed in terms
of the forward-time can_append method. However,
similar arguments apply to the backward-time can_prepend.
The indicator function for these ensembles acts on a (sub)trajectory x. Perhaps the simplest example is the can-append criterion for a length ensemble:
| 30 |
As long as the length of the trajectory is less that n, the can-append criterion is satisfied, and LengthEnsemble.can_append returns True.
Another example is the InA ensemble. The indicator function for CanAppInA+ is given by
| 31 |
because adding an additional frame that is not in A will immediately fail the ensemble. The additional logical or with the zero-length trajectory signifies that for an empty trajectory CanApp should return True, as adding a frame to an empty trajectory is always possible. An analogous formula can be written for CanAppOutA+.
In contrast, for the ensembles CanAppPartInA+ and CanAppPartOutA, the indicator functions always return True since there is no reason to stop if the additional frame is not in (or out) the state. If a frame of the trajectory is already outside the volume, there is still no reason to stop the trajectory: all extensions will then lead to trajectories that still satisfy the ensemble.
More complex can-append criteria can be constructed
using set logic
involving intersections and unions,29 or
using sequential ensembles, as described below. One important, but
somewhat subtle, point is that the logical negation of the result
of can_append for an ensemble 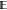 is not necessarily equal to the result
of can_append for the complement of ensemble
is not necessarily equal to the result
of can_append for the complement of ensemble  . For example, the can_append method for AllInXEnsemble returns True if
and only if all frames of the input trajectory
are in the volume associated with the ensemble. However, as discussed
above, the complement of an AllInXEnsemble is
a PartOutXEnsemble, for which the can_append method always returns True. Taking the complement applies to the ensemble; determining the
result of the can_append for the complement
depends on the complement ensemble, not on the result of can_append in the original ensemble.
. For example, the can_append method for AllInXEnsemble returns True if
and only if all frames of the input trajectory
are in the volume associated with the ensemble. However, as discussed
above, the complement of an AllInXEnsemble is
a PartOutXEnsemble, for which the can_append method always returns True. Taking the complement applies to the ensemble; determining the
result of the can_append for the complement
depends on the complement ensemble, not on the result of can_append in the original ensemble.
OPS also implements two other related methods for each ensemble: strict_can_append and strict_can_prepend. Whereas the normal can_append (respectively can_prepend) returns True for any subtrajectory of a trajectory in the ensemble, the strict variant only returns True if the input trajectory is the beginning (respectively end) of a trajectory in the ensemble. This is useful when looking for a trajectory that satisfies the ensemble, such as when identifying subtrajectories of a long trajectory that satisfy the ensemble. For the basic ensembles above, there is no distinction between these (in fact, there is also no distinction between can_append and can_prepend, since any trajectory that satisfies one must satisfy the other). However, for sequential ensembles, described in Section 2.5, there are significant differences, both for can_append vs can_prepend and for their strict and normal variants.
We stress that the basic formalism introduced here, connecting each path ensemble to a can-append criterion, is general and applicable beyond the ensembles implemented by OPS. For example, one could imagine an ensemble of all trajectories with an even number of frames, for which the corresponding can_append method would always returns True. OPS does not try to implement all possible ensembles; while the ensemble of all even-length trajectories could be implemented, it is not part of OPS due to its limited practical scientific use.
Note that the can-append criterion, as used by the shooting move (and similar trajectory generation approaches), results in what are called candidate trajectories. A candidate trajectory comes from the first trajectory that fails the can-append criterion. For some can-append criteria, such as that of the InX ensemble, the can-append test ‘overshoots’ and only fails after the input trajectory could not possibly be in the desired ensemble. For others, such as that of the LengthEnsemble, can-append failure can be predicted before overshooting. To maximize efficiency, OPS trims the overshot frame to make candidate trajectories for ensembles where necessary, while not overshooting if not necessary.
2.5. The Sequential Ensemble
2.5.1. Definition of the Sequential Ensemble
One of the most productive ways to define useful ensembles in OPS is the SequentialEnsemble, which comprises a list of path ensembles that the trajectory must fulfill in the correct order. To understand this, consider a simple situation with a single state X. Suppose we are interested in a path ensemble defined by a trajectory that begins in the state, then exits the state, and then again returns to the state X. This ensemble can be summarized by the sequence [InX, OutX, InX]. Trajectories in this sequential ensemble can be split into subtrajectories that fulfill these three subensembles in the correct order.
Conceptually, a sequential ensemble consists of an ordered list of subensembles and an assignment algorithm to assign frames of a candidate trajectory to those subensembles. A trajectory satisfies the sequential ensemble if the assignment algorithm decomposes the trajectory into subtrajectories that satisfy each subensemble in the correct order. The can-append criterion for the sequential ensemble can be defined based on the can-append criterion of the subensembles (and the assignment algorithm). While no unique choice for assignment algorithm exists, here we describe the approach used in OpenPathSampling.
A sequential ensemble is defined as an ordered set of (e.g., three)
ensembles  for which the indicator
function is
for which the indicator
function is
| 32 |
with frame indices e1 and e2 given by the assignment algorithm. For the assignment algorithm used in OPS, they are, respectively
| 33 |
and
| 34 |
where the first equation (eq 33) selects the maximum index e1 which still could fulfill the 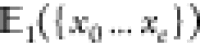 condition and the second equation
(eq 34) likewise for e2. Note that here we make use of the fact that
CanAppend returns True for an empty (zero-length) trajectory to ensure
that the index ei always
has a value. Naturally, the number of ensembles in the sequential
ensemble can be arbitrarily large:
condition and the second equation
(eq 34) likewise for e2. Note that here we make use of the fact that
CanAppend returns True for an empty (zero-length) trajectory to ensure
that the index ei always
has a value. Naturally, the number of ensembles in the sequential
ensemble can be arbitrarily large:
| 35 |
with bi = ei–1 + 1, e0 = −1, and
| 36 |
Note that if the first condition in eq 32 or eq 35 fails, all next conditions are not computed. The sequential ensemble thus is the set of trajectories that sequentially fulfill a set of ensembles.
The can-append criterion for the sequential ensemble is to use the frame assignment algorithm (the can-append of the subensembles) to assign all frames of the input trajectory to a subsequence of the subensembles. If all frames can be assigned to a subensemble, and if either (1) the subtrajectory assigned to the last subensemble satisfies the can-append criterion for that subensemble or (2) there are more subensembles later in the sequence, then the sequential ensemble’s can-append criterion is satisfied.
As an example of a sequential ensemble, consider the situation with just two states A and B defined, and their union S = A ∪B. The TPS ensemble connecting A and B can then be written as the sequential ensemble
| 37 |
The indicator function for this ensemble SeqEnsTPS(x) returns True only if the first frame is in A, the last frame is in B, and no snapshot is in A nor B during the rest of the trajectory. Note that this function is identical to the h[x] in eq 5. A very similar expression is used for the fixed length TPS
| 38 |
where the criterion is that the first and last slice are in A and B, respectively, and the L – 1 slices are allowed to go anywhere.
The sequential ensemble for the TIS ensemble is defined as
| 39 |
The corresponding indicator function SeqEnsTIS(x) returns 1 only if the first slice is in A, the last one ends in A or B, and there is no slice in A nor B during the rest of the trajectory, but there is at least one slice that is not in the interface i volume. Note that this indicator function is identical to h̃i[x] in eq 7.
As a final example, the minus interface ensemble25,30 is
| 40 |
The indicator function for this ensemble SeqEnsMinA(x) returns unity if the first and last slice is in A and the trajectory leaves A at least once. Note that this definition allows multiple (n) entries into A. Here, we assumed that the boundary of A and the first interface are identical. Below, we discuss the OPS implementation of the minus ensemble for the more general case.
2.5.2. Use of Sequential Ensembles for Path Sampling in OPS
The sequential ensemble is implemented in OPS by the SequentialEnsemble object. The test for whether a given trajectory satisfies the SequentialEnsemble uses the strict_can_append method of the underlying subensembles. It starts by making a candidate subtrajectory for the first subensemble, using that subensemble’s strict_can_append method until it returns False. The “strict” version is used because the subtrajectory that is assigned to the subensemble must satisfy the subensemble. If the resulting subtrajectory satisfies the first subensemble, then the process is continued with the next subensemble. This continues until no more frames can be assigned, either because all have been assigned or because there are no more subensembles. If all frames are assigned and all subensembles have been assigned a subtrajectory, then the given trajectory is in the SequentialEnsemble.
For most TPS/TIS purposes,
one would like to stop integrating trajectories as soon as they enter
the state. This is done by combining a volume ensemble, such as AllInXEnsemble(state), with a LengthEnsemble(1), requiring an ensemble of length 1. This results in exactly one
frame in the desired state. Hence, the SeqEnsTPS ensemble, eq 37, for
which the initial and the final trajectory frames are in the initial
and final states, respectively, but all other frames (at least one)
are outside both states, is given by where we have made use of the set logic of the ensembles
(see eq 29). The path
should start with one frame in the initial state, then an arbitrary
number outside either state, followed by precisely one frame inside
the final state.
where we have made use of the set logic of the ensembles
(see eq 29). The path
should start with one frame in the initial state, then an arbitrary
number outside either state, followed by precisely one frame inside
the final state.
The slightly more complex sequential TIS ensemble
SeqEnsTIS, eq 39, can
be defined as where A, B, and I are the volume-based definitions of states A and B and interface I, respectively.
Note that we have used set logic to define the union of A and B as a final state. Moreover, we require the
middle part of the path to be outside of this union. Finally, the
TIS ensemble requires at least a part of the entire trajectory to
be outside the interface volume.
where A, B, and I are the volume-based definitions of states A and B and interface I, respectively.
Note that we have used set logic to define the union of A and B as a final state. Moreover, we require the
middle part of the path to be outside of this union. Finally, the
TIS ensemble requires at least a part of the entire trajectory to
be outside the interface volume.
Figure 2 provides
an example, based on the TIS ensemble, of how frame assignment works
for a sequential ensemble. For simplicity we left out the interface
crossing requirement. Two trajectories are shown, both of which fulfill
the ensemble conditions. Each trajectory starts in A, which assigns the first frame in the (blue)  subensemble. Then there
are a number of
frames which are outside of the union of A and B and which are assigned to the (black) OutA∪B subensemble. The first
frame that does not satisfy that criterion is also the last frame
of each trajectory. For the top trajectory, the last frame is in B. For the bottom trajectory, the last frame is in A. In both cases, the last frame satisfies the subensemble
InA∪B.
subensemble. Then there
are a number of
frames which are outside of the union of A and B and which are assigned to the (black) OutA∪B subensemble. The first
frame that does not satisfy that criterion is also the last frame
of each trajectory. For the top trajectory, the last frame is in B. For the bottom trajectory, the last frame is in A. In both cases, the last frame satisfies the subensemble
InA∪B.
Figure 2.
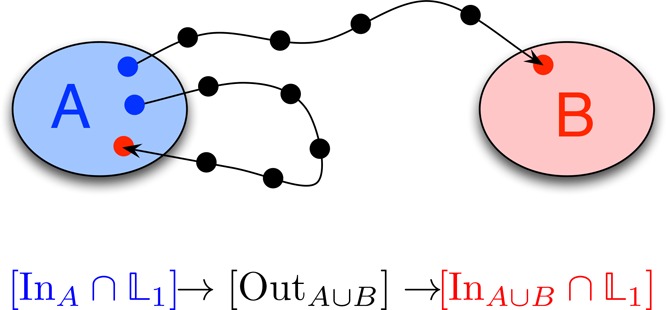
Frame assignment in an ensemble based on the TIS ensemble, for two trajectories. The points, which indicate individual frames in the trajectories, are colored to match the subensembles of the sequential ensemble, as given below the illustration. This ensemble differs from a real TIS ensemble because there is no interface.
In some cases, there is a need for an ”optional”
step in the sequence, which uses the so-called OptionalEnsemble. This means that a subtrajectory of a path can be in that ensemble
but does not have to be. In OPS this is implemented by forming the
union of the ensemble  with
a zero-length ensemble
with
a zero-length ensemble
| 41 |
If no subtrajectory fits the OptionalEnsemble, a zero-length trajectory still allows the Sequential Ensemble to continue, thus effectively skipping the OptionalEnsemble.
One example where we need to use the OptionalEnsemble class is when there is an interstitial space between the edge of the state and the innermost interface.31 In simple cases, the innermost TIS interface λ1 is usually set to be exactly the boundary of the state λ0, but this is not required. A trajectory therefore can leave a state, visit the interstitial space, and then cross the first interface, or it can skip this interstitial space in one frame and go directly from the state to the cross the interface. Both situations should be dealt with. The above TIS ensemble definition as already given works in this case. However, the minus interface ensemble needs special care. This ensemble is one of the more complicated ensembles in the TIS framework. As explained in Paper 1,24 the minus interface ensemble is used (as part of the minus move) in RETIS to perform dynamics within the stable state and return a new trajectory to one of the innermost TIS ensembles. This can be used to calculate the flux, to connect different interface sets in MISTIS, or to enhance decorrelation of trajectories.25,30 The code for the minus ensemble in eq 40 with n = 1 entries into A is given in Chart 1. Note the use of the OptionalEnsemble for the interstitial regions. This code will also be discussed in more detail in the following subsections.
Chart 1. Implementation of the Minus Interface Ensemble, Assuming Existing Definitions of the State Volume A and the Innermost Interface Volume Ia.
a This implements the minus interface ensemble with n = 1 re-entries into the state between the end points (i.e., with 2 interface crossings).
2.5.3. The Reverse Check and can_prepend for Sequential Ensembles
Up to this point, we have focused on sequential ensembles where the volumes associated with successive ensembles cannot overlap. That is, there can be no ambiguity as to which subensemble a given frame of a trajectory is assigned to, regardless of the assignment algorithm used for the sequential ensemble. However, it is possible to define sequential ensembles where such overlaps are allowed, but these will become much more complicated and more subtle. In particular, special attention needs to be paid to whether one can sample the same ensemble using the can_append and can_prepend methods.
OPS implements
two main assignment rules. The normal OPS assignment algorithm is
based on dynamics propagating forward in time (using 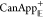 ) and, for clarity, can be called “forward
assignment”. In the code, the forward assignment can be tested
using ensemble(trajectory). The alternative
approach is based on dynamics propagating backward in time (using
) and, for clarity, can be called “forward
assignment”. In the code, the forward assignment can be tested
using ensemble(trajectory). The alternative
approach is based on dynamics propagating backward in time (using 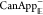 ) and will be called “reverse assignment”.
The code to use it in OPS is ensemble.check_reverse(trajectory).
) and will be called “reverse assignment”.
The code to use it in OPS is ensemble.check_reverse(trajectory).
The reverse assignment algorithm is used to simplify the can_prepend ( ) approach as implemented in OPS. The can_prepend algorithm for the OPS SequentialEnsemble is implemented analogously to the can_append algorithm. Both are “greedy” algorithms, in the sense
that they try to assign the largest subtrajectory possible to the
current subensemble. Since the forward assignment is greedy starting
with the first subensemble of the sequential ensemble, and the reverse
assignment is greedy starting with the last subensemble, the two algorithms
might not yield equivalent results. Any ensemble that will be sampled
with both forward and backward dynamics (as is done in the standard
shooting moves in path sampling) must result in identical ensembles
for both the forward assignment and the reverse assignment. Note that
there are many cases in which the reverse assignment will not matter.
For instance, generating initial trajectories (illustrated in Section 4.1) or analyzing
existing trajectories (see Section 4.2) only requires forward assignment. Moreover, many
rare events methods (e.g., forward flux sampling32) involve propagating forward in time only.
) approach as implemented in OPS. The can_prepend algorithm for the OPS SequentialEnsemble is implemented analogously to the can_append algorithm. Both are “greedy” algorithms, in the sense
that they try to assign the largest subtrajectory possible to the
current subensemble. Since the forward assignment is greedy starting
with the first subensemble of the sequential ensemble, and the reverse
assignment is greedy starting with the last subensemble, the two algorithms
might not yield equivalent results. Any ensemble that will be sampled
with both forward and backward dynamics (as is done in the standard
shooting moves in path sampling) must result in identical ensembles
for both the forward assignment and the reverse assignment. Note that
there are many cases in which the reverse assignment will not matter.
For instance, generating initial trajectories (illustrated in Section 4.1) or analyzing
existing trajectories (see Section 4.2) only requires forward assignment. Moreover, many
rare events methods (e.g., forward flux sampling32) involve propagating forward in time only.
Since
the forward and reverse assignment algorithms are not equivalent,
certain sequential ensembles could accept a trajectory when checked
with the forward propagation but not when checked with backward propagation
(or vice versa). For example, imagine volumes A, I1, and I2 as illustrated
in Figure 3, where I1 ⊂ I2, and A ∩ I2 = ⌀. Consider
the ensemble 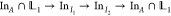 . As shown in the top panel of Figure 3, for the illustrated
trajectory, the forward assignment starts by assigning the first frame
to the first ensemble InA (shaded blue
in the figure). Then the frame assignment algorithm will look for
a subtrajectory that satisfies the InI1 ensemble. In the example trajectory shown, it finds a two-frame
subtrajectory that satisfies the InI1 ensemble. The next frame is the first one that can be assigned
to the InI2 ensemble. Since
frames that are in the volume I1 are also
in the volume I2, the trajectory continues
to assign frames to InI2 until
it exits that volume and enters A. The last frame,
in A, is assigned to the final
. As shown in the top panel of Figure 3, for the illustrated
trajectory, the forward assignment starts by assigning the first frame
to the first ensemble InA (shaded blue
in the figure). Then the frame assignment algorithm will look for
a subtrajectory that satisfies the InI1 ensemble. In the example trajectory shown, it finds a two-frame
subtrajectory that satisfies the InI1 ensemble. The next frame is the first one that can be assigned
to the InI2 ensemble. Since
frames that are in the volume I1 are also
in the volume I2, the trajectory continues
to assign frames to InI2 until
it exits that volume and enters A. The last frame,
in A, is assigned to the final 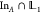 ensemble, shaded purple
in the figure.
Frames have been assigned to all ensembles, in the correct order,
and no frames are unassigned. Therefore, this trajectory satisfies
the ensemble.
ensemble, shaded purple
in the figure.
Frames have been assigned to all ensembles, in the correct order,
and no frames are unassigned. Therefore, this trajectory satisfies
the ensemble.
Figure 3.
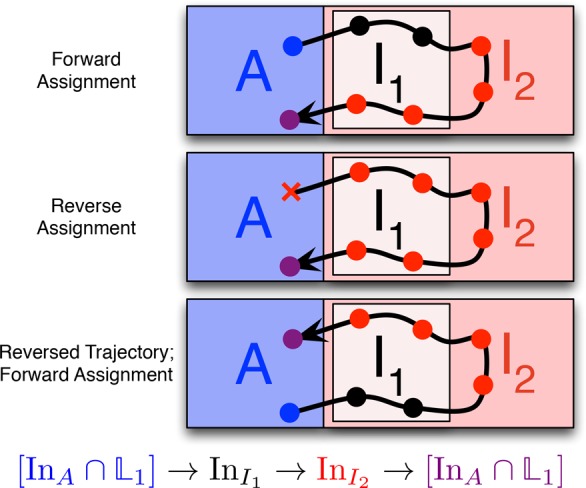
Applying different assignment approaches to a given trajectory. Points represent frames in the trajectory and are colored to show assignment, as with Figure 2. The forward assignment algorithm (top) assigns frames in forward time order of the trajectory, with the forward order of the subensembles of the sequential ensemble. The reverse assignment algorithm (middle) assigns frames in the reverse order of the subensembles in the sequential ensemble, in reverse time order of the trajectory. Finally, the forward assignment of the reversed trajectory (bottom) is shown to illustrate that this is distinct from the reverse assignment. Note that a trajectory may be accepted by one assignment algorithm and rejected by the other (as shown here by the red x for an unassigned frame in the reverse assignment).
Next consider the reverse assignment algorithm, as illustrated
in the middle panel of Figure 3. Assignment starts at the last frame of the trajectory and
at the final subensemble in the sequential ensemble. This frame is
assigned to the final subensemble  (shaded purple), as would
also happen in
the case of forward assignment. Stepping backward along the trajectory,
the assignment algorithm is looking for frames in the volume I2, following the penultimate subensemble. Since I1 ⊂ I2, it
finds such frames, and it continues to find frames in I2 until the last frame to be assigned (the first frame
of the trajectory), which is in A. Reaching that
frame, the algorithm first checks whether it can be assigned to the
InI2 ensemble, as with the
frame before. As this is not the case, the algorithm checks whether
the frame can be assigned to the InI1 ensemble, the next subensemble in the reverse order. Since
this is also not the case, the reverse check algorithm deems this
trajectory to fail the sequential ensemble, as it does not contain
subtrajectories assigned to all the correct ensembles in the correct
order. In the figure, we signify this with the red x.
(shaded purple), as would
also happen in
the case of forward assignment. Stepping backward along the trajectory,
the assignment algorithm is looking for frames in the volume I2, following the penultimate subensemble. Since I1 ⊂ I2, it
finds such frames, and it continues to find frames in I2 until the last frame to be assigned (the first frame
of the trajectory), which is in A. Reaching that
frame, the algorithm first checks whether it can be assigned to the
InI2 ensemble, as with the
frame before. As this is not the case, the algorithm checks whether
the frame can be assigned to the InI1 ensemble, the next subensemble in the reverse order. Since
this is also not the case, the reverse check algorithm deems this
trajectory to fail the sequential ensemble, as it does not contain
subtrajectories assigned to all the correct ensembles in the correct
order. In the figure, we signify this with the red x.
Note that the reverse assignment is not the same as using the forward assignment algorithm to assign frames from the time-reversed trajectory, as is shown in the bottom panel in Figure 3. For this trajectory, the process of first reversing the trajectory and then assigning in the forward order leads to an assignment analogous to the forward assignment of the nonreversed trajectory. The trial trajectory will be accepted in this case.
The requirement for a trajectory to be sampled correctly with both forward and backward dynamics is that the forward and reverse assignment algorithms accept the same trajectories. For some sequential ensembles, such as the TPS and TIS ensembles, this means that the frame assignment is identical in both directions. However, this does not need to be the case, as can be seen from the minus ensemble listed in Chart 1 and the trajectory assignments illustrated in Figure 4.
Figure 4.

Frame assignment for an example trajectory in the minus ensemble. Points represent frames in the trajectory and are colored to show assignment, as with Figure 2. The solid line represents the boundary of the state volume A, and the dashed line represents the boundary of the interface volume I, with everything below the lines in the respective volume. The forward assignment algorithm (top) and reverse assignment algorithm (bottom) give the same result (the trajectory satisfies the ensemble), although the specific assignment of frames differs.
The minus ensemble includes trajectories that start with one frame in the state, go on to cross the interface, then return to the state, then cross the interface again, and finally end with one frame in the state. When the interface and state are not equivalent, there is an interstitial volume between them. This means that there could be recrossings of the interface or of the state boundary, as illustrated by the trajectory in Figure 4, which also shows how this is handled by the careful implementation of the minus ensemble in Listing 1 in Chart 1.
Recrossings are handled by using the fact that the criterion for failing a subensemble is to enter the next volume X. The not-yet-halt criterion for the subensemble is then the requirement to be in the complement volume X, thus InX = OutX. For instance, the green OutA subensemble handles the condition that the trajectory should re-enter state A, while allowing many crossings of the I interface. Likewise, the red InI = OutI subensemble handles the second first exit of I, allowing many recrossings of the A boundary.
Note that some successive subensembles involve volumes that have overlap. For example, consider part of the minus ensemble OutA → InI → OutA. Because the associated volumes are not disjoint (i.e., I ∩ A≠ ⌀), frames in that intersection can be assigned to either ensemble and will be assigned differently for the forward and reverse assignment algorithms. Additionally, the assignment of the optional ensembles depends on the assignment algorithm, again because of this volume overlap. The difference in the two assignment algorithms is shown for an example trajectory in Figure 4.
Unlike the example in Figure 3, any trajectory that satisfies the forward assignment for the minus ensemble will also satisfy the reverse assignment. Specific frames may be assigned to different subensembles, but the overall trajectory will either satisfy both assignment criteria or fail both.
In addition, because the minus move is one of the most computationally expensive moves in path sampling, we want to design the ensemble so that candidate trajectories are almost certain to be accepted. Without that requirement, the optional ensembles could be removed from the sequence, and the OutA ensembles in the sequence would become OutA ∩ PartOutI. Here still, the forward and reverse frame assignments would differ. However, this would have the disadvantage that candidate trajectories could return to A immediately after the first frame in the interstitial, without crossing the interface. Such trajectories would be expensive to generate and would not be accepted. The sampling would be correct but inefficient.
Because of the possible difference between frame assignment in the forward and reverse directions, it is important to know that the code defaults to forward propagation to check whether a trajectory is in an ensemble. We emphasize that an ensemble which does not give the same results in both directions can still be suitable for situations where only forward dynamics will be used (e.g., generating an initial trajectory) but will not be suitable for approaches such as the shooting move in path sampling, which involves both forward and backward dynamics.
2.6. Performance Considerations
The previous
sections provide a mathematically complete description of a new, set-based
approach to describing path ensembles and their halting criteria in
a consistent and unified manner. However, this approach, naively implemented,
is not always computationally efficient. The functions described (such
as the can-append criterion) take an entire trajectory as input and
therefore must iterate over all previously visited frames after each
new frame is added. This leads to algorithms that scale as 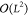 instead of
instead of 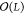 in L, the number of frames.
In OPS, this scaling problem is managed by using caches for the sequential
ensemble, combined with a Boolean parameter trusted that can be passed to the can_append and can_prepend functions (as well as their strict variants). The trusted parameter for can_append indicates that, as of the previous frame,
the trajectory satisfied the can_append criterion
(and similarly for can_prepend and the strict variants). Additionally, the ensemble indicator
function, given by ensemble(trajectory), takes
an optional Boolean parameter called candidate. If candidate = True, then the code assumes
that the trajectory was generated by the can_append or can_prepend method, and therefore only
certain parts of the trajectory need to be tested.
in L, the number of frames.
In OPS, this scaling problem is managed by using caches for the sequential
ensemble, combined with a Boolean parameter trusted that can be passed to the can_append and can_prepend functions (as well as their strict variants). The trusted parameter for can_append indicates that, as of the previous frame,
the trajectory satisfied the can_append criterion
(and similarly for can_prepend and the strict variants). Additionally, the ensemble indicator
function, given by ensemble(trajectory), takes
an optional Boolean parameter called candidate. If candidate = True, then the code assumes
that the trajectory was generated by the can_append or can_prepend method, and therefore only
certain parts of the trajectory need to be tested.
For example, consider a flexible-length TPS ensemble as in eq 37 and a trajectory (x0, ..., xi). If (x0, ..., xi–1) satisfied the can-append criteria, then we know that the last trajectory with frames assigned was OutS, and we should first check whether xi ∉ S, which would allow us to assign it to that subensemble as well. The trusted parameter tells us that we can trust that the previous frame passed can-append, enabling a faster path for checking the can-append criterion. In addition, the SequentialEnsemble keeps a cache of the frame assignment, so the algorithm knows immediately to which ensemble the frame should be assigned (with safety checks that this frame is still part of the same trajectory.)
As an example of the use of the candidate parameter, again consider the flexible-length TPS ensemble, with some trajectory (x0, ..., xL) . If that trajectory was generated using the can_append or can_prepend rules, no frames except for the first and last can be in any state. In this case, we can check whether the trajectory satisfies the ensemble just by checking if the first and last frames are in the appropriate states. The methods built into OPS for arbitrary ensembles are general but might not be the most efficient. Customized ensembles can make use of the trusted and candidate parameters to provide faster calculations for trajectories known to be generated by dynamics, while still benefiting from the general approaches for trajectories of unknown origin.
2.7. Guidelines for Designing Custom Ensembles
The above sections introduced the set-based notation for path ensembles, illustrated the connection between this notation and the inner workings of OPS, and showed how OPS uses this conceptual framework to implement ensembles used in path sampling simulations. In Section 4, we will provide several more examples of useful path ensembles. However, defining new ensembles might not seem completely straightforward. To help bridge the gap between understanding the ensembles we present and creating new ensembles, in this section we provide some general guidelines and tricks that could be seen as rules of thumb for ensemble building.
Use anchors. In many path ensembles, trajectories start and end with a frame in a specific volume (or union of volumes). It can be useful to think of these as anchors to start designing the ensemble. Typically, the building block is a single frame in some volume A, i.e., the ensemble
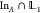 .
.Use complement ensembles and volumes. If we want a trajectory to end with the first frame in some volume A, we might think of this as a PartInA ensemble; but, as discussed in Section 2.4, the PartInA ensemble never halts. However, the first trajectory that will satisfy it can come from the first trajectory that does not satisfy its complementary ensemble, OutA. This can, of course, also be written as InA̅. In some cases, the complement volume may be the one that is more naturally defined. For example, if part of a sequential ensemble is supposed to lead to a first frame in A, we can use the OutA ensemble, as is done in the minus ensemble, which also uses this to create a first frame outside of the interface I using InI (where it is more natural to refer to a frame outside the interface volume than a frame inside the complement of the interface volume). A more elaborate example using this reasoning is given in Section 4 for the ensemble used to get the initial trajectory that visits all states.
Think in terms of halting criteria. First, it is important to make sure that every ensemble (and every subensemble of a sequential ensemble) will eventually halt. Second, the halting criteria can be useful when designing sequential ensembles. Because the sequential ensemble uses a greedy algorithm, it is important to think in terms of the stopping criteria of the previous ensemble and where that leaves you. The previous guideline explained how to get a crossing out of some volume (call it I), but typically we speak of crossing from starting in one volume (call it A) and then exiting the volume I. To know which volume the subensemble will start in, look at the previous subensemble and apply the rules in the guideline about complement ensembles and volumes.
Prefer set logic on volumes, not ensembles. When creating ensembles, set logic on ensembles and on volumes might seem very similar. For instance, one might be tempted to code the ensemble OutA∪B as OutA ∪ OutB. However, this is incorrect, as explained in Section 2.3. Also, the logical complement of ensembles in general is not what one naively would expect. The set logic for volumes is usually more familiar and, therefore, whenever possible, should be used.
Beware of unions with PartIn or PartOut. This relates to both the suggestion of thinking in terms of halting criteria and preferring set logic on volumes. The danger here is that, while an ensemble such as InI ∪ PartOutA may seem reasonable, the stopping criterion of PartOutA is to never stop, and therefore a union with it leads to infinite trajectories.
Check the reverse assignment. If using path sampling, or any other algorithm that requires generating dynamics in the backward time direction, check that the reverse assignment gives the same results as the forward assignment. The ideas behind this are described in Section 2.5.3. Developing a symmetric sequence for the sequential ensemble can help with the reverse assignment. Not all methods require that the reverse assignment be used, only those that involve propagating backward in time.
Use optional ensembles for flexibility. The optional ensemble allows a particular subensemble of a sequential ensemble to be skipped. This is useful when the ensemble will be employed in many variants, and when it is uncertain whether the subensemble will always be satisfied (as with the minus ensemble). Including optional ensemble can also ensure that both the forward and reverse assignments work properly.
Use unions of complex ensembles. Sometime a union of complex ensembles, such as sequential ensembles, is the best way to achieve a desired ensemble. For example, consider sampling A → B transitions and B → A transitions in one ensemble. A TPS ensemble from A ∪ B to A ∪ B will not work, since it will allow A → A and B → B transitions. Instead use a union of sequential ensembles, SeqEnsTPSA→B ∪ SeqEnsTPSB→A.
Finally, there is often more than one way to implement a given path ensemble. These guidelines should provide tools both for the design of new ensembles, as well as to understand ensembles we have provided as examples in Section 4.
3. General Framework for Custom Monte Carlo Approaches
Transition path sampling amounts to Monte Carlo of trajectory space. In standard TPS, the Monte Carlo procedure samples trajectories from a single path ensemble. In TIS, and particularly in RETIS, the Monte Carlo procedure simultaneously samples trajectories from an expanded ensemble, combining multiple interface ensembles. Standard TPS can be seen as a special case of this expanded ensemble, where only a single path ensemble is sampled. The expanded ensemble gives rise to the SampleSet object in OPS, as described in Paper 1.24
Monte Carlo moves in OPS, based on this expanded ensemble, are performed by the PathMover object. PathMovers can change trajectories within the ensemble being sampled (as with the shooting move), or they can alter the ensembles associated with trajectories without changing the trajectories (as with path replica exchange), or they can alter both the trajectory and its associated ensemble (as with the minus move).
The PathMovers are organized in an overall move decision tree. This tree includes, besides the movers that perform the Monte Carlo steps, several so-called structural movers, e.g., the RandomChoiceMover that randomly selects one of several submovers (these structural movers are described in Section 3.1). In principle, a manually assembled move decision tree is all that is necessary for a path sampling simulation. However, for complicated move decision trees, this becomes tedious and difficult. The PathMovers, including the structural movers, constitute a low-level interface that is sufficient but not particularly user-friendly. Therefore, we have developed a higher-level layer, using the MoveStrategy and MoveScheme objects, which automates the repetitive lower-level operations and enables the user to customize the move decision tree easily.
The MoveScheme is an overall container that builds the move decision tree, while each MoveStrategy deals with a part of that tree: providing, for example, details on how the shooting move will be performed or which pairs of ensembles are involved in replica exchange. A path sampling simulation will have one MoveScheme, and that MoveScheme will include multiple MoveStrategy objects.
The following subsections describe how the structural path movers allow combining existing movers into a more complicated move and how to use the MoveStrategy and MoveScheme. Subclassing existing objects can create more complicated path movers; details are available in the online documentation for OpenPathSampling at http://openpathsampling.org.
3.1. Structural Movers
PathMover objects such as the OneWayShootingMover and ReplicaExchangeMover generate new trial paths. However, they need to be organized into the overall move decision tree. This organization is done by other subclasses of PathMover, which we call structural movers. Important structural movers include the following:
A RandomChoiceMover, one of the main structural elements in most move decision trees, randomly selects one of its submovers. For example, a first RandomChoiceMover selects the type of move (shooting, replica exchange, etc.), followed by a second RandomChoiceMover that selects a mover for the specific ensemble(s) involved in the move. The RandomChoiceMover is also an important element in many PathMovers. For example, the OneWayShootingMover consists of a RandomChoiceMover that selects between a ForwardShootingMover and a BackwardShootingMover. By default, the submovers within a RandomChoiceMover have identical probability of being selected; this can be changed with the weights parameter at initialization.
A SequentialMover employs several submovers in a specific order, where each submover is accepted independently. This mover is not a combined trial move but a bundle of several moves together in a specific order.
The ConditionalSequentialMover is similar to a SequentialMover but provides an early rejection scheme, which is important for moves where a failure in an early step can guarantee that the whole move fails, especially if later steps are very expensive. Below we will discuss how this plays a role in the MinusMover.
An EnsembleFilterMover removes resulting Samples associated with intermediate ensembles from the results. In complicated movers, extra, internally defined Ensemble objects can create intermediate steps in the mover, which would end up in the results. The EnsembleFilterMover filters those (often uninformative data) out of the results.
The move decision tree can take many forms. To obtain information about the path mover most likely of interest (e.g., ReplicaExchangeMover or ForwardShootingMover) regardless of the specific structure of the move decision tree, we implemented a property canonical in the MoveChange. As discussed in Paper 1,24 a PathMover takes a SampleSet as input and returns a MoveChange object. This MoveChange can contain other MoveChanges from submovers; in this way the whole path taken through the move decision tree is preserved. However, the nested structure of MoveChanges can make it cumbersome to access attributes from the MoveChange of the specific submover of interest (e.g., shooting point from the MoveChange associated with the shooting mover). Therefore, the MoveChange.canonical property directly accesses the first nested MoveChange associated with a mover that identifies itself as “canonical”. Subclasses of PathMover can declare themselves canonical by setting the class attribute _is_canonical to True. Examples using the canonical property can be found in Paper 1, Section 6.1.6.24
The MinusMover provides a useful example of how several structural movers can be put together to generate a new Monte Carlo move. As described in Paper 1,24 the OPS MinusMover is, in a way, a combination of replica exchange and shooting moves. In MSTIS, each state typically has one MinusMover, which takes trajectories from two ensembles as input: the TIS innermost interface ensemble and the minus ensemble. In the discussion that follows, the state is denoted A, and the innermost interface volume is denoted X. In many cases the state definition A will be identical to X, but this is not required.
Both the TIS ensemble and the minus interface ensemble
are described
in Section 2.5. In
the minus move, both use the same interface volume, X. In addition, there is an ensemble which is used internally in the
minus move. This ensemble is nearly the same as the TIS ensemble used
as input, except that instead of allowing paths to end in either A or make a transition to another state B, all paths in this internal ensemble must start in A, cross the interface, and also end in A, i.e.,
this is the ensemble 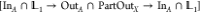 . In the
context of the minus move, we refer
to this as the “segment ensemble”. Trajectories in the
minus interface ensemble begin and end with subtrajectories that also
satisfy the segment ensemble and therefore satisfy the innermost interface
ensemble.
. In the
context of the minus move, we refer
to this as the “segment ensemble”. Trajectories in the
minus interface ensemble begin and end with subtrajectories that also
satisfy the segment ensemble and therefore satisfy the innermost interface
ensemble.
The minus move consists of three steps: (1) randomly selecting one of the subtrajectories that satisfies the segment ensemble from the minus ensemble trajectory; (2) performing a replica exchange move between the selected segment and the path in the innermost interface; and (3) extending that path in a random time direction until it satisfies the minus interface ensemble.
The first step is performed by a RandomChoiceMover that selects between either a FirstSubtrajectorySelectMover or a FinalSubtrajectorySelectMover, where in both cases the subtrajectory satisfies the segment ensemble. This step should always be accepted as the initial path satisfies the minus ensemble.
When there is only one innermost ensemble, the second step is just a replica exchange. This replica exchange can only fail if the innermost interface path happens to cross to another stable state. In the case of multiple interface sets (as in MISTIS), however, there are multiple innermost interfaces.30 The interface to exchange with is selected with a RandomChoiceMover that includes ReplicaExchangeMovers for each innermost interface. The segment might not overlap with the selected interface, and therefore this step very well might fail for MISTIS.
In the final step, the trajectory that was initially in the innermost interface ensemble is extended until it satisfies the minus ensemble, using a RandomChoiceMover to choose either a ForwardExtendMover or a BackwardExtendMover.
No part of the move can be accepted unless all parts succeed. Therefore, we use a ConditionalSequentialMover for this. In addition, we used the intermediate “segment” ensemble. To remove this from the results, we wrap the mover in a EnsembleFilterMover.
Figure 5 shows the internal structure of this mover. Normally, this structure is not shown in the move decision tree visualization because the MinusMover is marked as a canonical mover, and the visualizer does not show internal structure of canonical movers. This setting can be overridden by changing the options.analysis dictionary of the visualizer.
Figure 5.
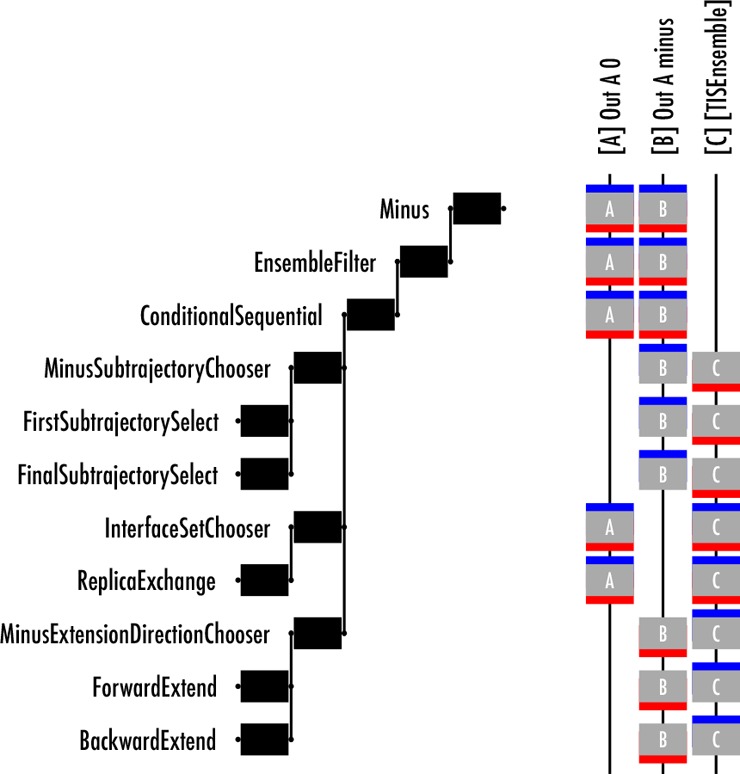
Internal structure of a MinusMover. At the left, the hierarchical structure of mover. Each layer (moving left) is encapsulated in the objects to the right. During a minus move, submovers are visited from top to bottom (but not all submovers are visited). The MinusMover, labeled “Minus”, is the outermost container. Inside it is the EnsembleFilterMover that filters out results in the internally used segment ensemble. The primary sequence of the minus move is in the ConditionalSequentialMover, each of which involves a RandomChoiceMover, which select the specific movers to do at each stage. On the right are the three ensembles involved in the minus move, labeled with A, B, and C. Ensemble A is the innermost TIS ensemble, ensemble B is the minus ensemble, and ensemble C is the segment ensemble. The input and output ensembles for each mover are shown in blue and red (respectively). Movers like replica exchange have the same input and output ensembles (even if the replicas have changed), whereas movers like the subtrajectory selectors move a replica from one ensemble to another.
3.2. MoveScheme and MoveStrategy Objects
The MoveScheme contains multiple MoveStrategy objects, used to automatically build the (often elaborate) move decision tree. It also is possible to build move decision trees manually. To make these manually built trees compatible with other parts of OPS, the root mover needs to be wrapped in a LockedMoveScheme. However, many of the tools for MoveSchemes are not available for LockedMoveSchemes, and much of what is discussed in the remainder of this section is not applicable to LockedMoveSchemes.
In addition to containing the move decision tree, a MoveScheme organizes information about the sampling process and provides access to tools for analyzing the sampling procedure after the simulation. In particular, the MoveScheme organizes the movers into labeled or named groups. For the default TIS scheme, the group names are ’shooting’ (shooting movers), ’repex’ (replica exchange), ’pathreversal’ (path reversal), and ’minus’ (minus move). These can be accessed with scheme.movers[group_name]. Each group consists of multiple PathMovers. Each PathMover in turn has specific input and output ensembles. For shooting, a single ensemble is used for both input and output. For EnsembleHopMovers (the single-replica version of replica exchange, which moves a single replica from one ensemble to a different ensemble), the input mover is different from the output mover. ReplicaExchangeMovers have two input and two output ensembles (the same pair for both). We refer to this set of input and output ensembles as the mover’s ensemble signature.
To build the move decision tree, one must decide (1) which ensemble signatures will be part of each type of move (e.g., which ensembles to shoot from), (2) how the movers will be implemented (e.g., what kind of shooting move to use), and (3) how all movers are organized into the overall decision tree (e.g., select type of mover first and then specific ensembles to include). MoveScheme builds the move decision tree by applying multiple MoveStrategy objects. Each MoveStrategy is associated with a specific priority level. When building the move decision tree, the strategies are applied in order of priority level, and within a priority level, in order of addition to the MoveScheme. The default priority levels are in openpathsampling.strategies.levels.LEVELNAME, where LEVELNAME can be, in order of ascending priority, SIGNATURE, MOVER, GROUP, or GLOBAL. Internally, these priority levels are represented by integers between 0 and 100, but these specific levels are named for convenience. The recommended use for these levels is as follows:
Strategies at the SIGNATURE level modify the set of ensemble signatures to be used; for example, the default NearestNeighborRepExStrategy, which executes replica swaps among neighboring interfaces, versus the AllSetRepExStrategy, which implements replica swaps among all interfaces within the same Transition (interface set).
Strategies at the MOVER level customize the behavior of the created path movers; for example, the OneWayShootingStrategy provides the ability to choose a shooting point selector for the shooting group.
Strategies at the GROUP level can take the already-built movers and rearrange them or convert them to a different approach. For example, the single-replica EnsembleHop movers can be converted to normal replica exchange using the ReplicaExchangeStrategy, which is a GROUP-level strategy. In Section 4, we show another GROUP-level strategy, which will take the already-created shooting and replica exchange movers and reorganize them into a single sequential move.
Strategies at the GLOBAL level organize the overall move decision tree. The two GLOBAL-level strategies in OPS are the OrganizeByMoveGroupStrategy, which first selects a move type and then selects which specific mover (which signature, i.e., which ensembles), and the OrganizeByEnsembleStrategy, which starts with the selection of the ensemble to move (as necessary with single-replica approaches) and then selects which type of move to do.
By using this priority-level system, the move decision tree can be built correctly, regardless of the order in which the specific move strategies are added to the scheme. Parts that must be built later are built later because of the priority levels. In addition, the details of what has already been built (e.g., specific choices of parameters for movers, such as the shooting point selection in a shooting move) can be retained by later moves that reorganize the entire move decision tree.
MoveStrategy objects deal with the details
of the implementation, when building the move decision tree. For example,
two-way shooting could be used instead of one-way shooting by starting
with the default scheme applying a TwoWayShootingStrategy to the scheme: where engine and network were already appropriately defined (see Paper
1 for details24). This implements a two-way
shooting move decision
tree where the shooting point is not modified, and the decorrelation
depends on the stochastic dynamics. Alternatively, for NVT dynamics,
one could choose the momenta randomly from a Maxwell–Boltzmann
distribution, as is, for instance, done in the aimless shooting33 approach. The scheme then becomes
where engine and network were already appropriately defined (see Paper
1 for details24). This implements a two-way
shooting move decision
tree where the shooting point is not modified, and the decorrelation
depends on the stochastic dynamics. Alternatively, for NVT dynamics,
one could choose the momenta randomly from a Maxwell–Boltzmann
distribution, as is, for instance, done in the aimless shooting33 approach. The scheme then becomes where temperature, engine, and network were already appropriately defined.
This implements a two-way shooting move decision tree where the shooting
point obtains random velocities taken from a Maxwell–Boltzmann
distribution at the desired temperature. If the engine supports constraints,
the RandomVelocities modifier will project
that distribution into the space of constraints.
where temperature, engine, and network were already appropriately defined.
This implements a two-way shooting move decision tree where the shooting
point obtains random velocities taken from a Maxwell–Boltzmann
distribution at the desired temperature. If the engine supports constraints,
the RandomVelocities modifier will project
that distribution into the space of constraints.
As another
example, a modified shooting point selector could be
used, instead of the default (uniform selector). For instance, the GaussianBiasSelector selects the shooting point according
to a Gaussian probability in a specified collective variable.34 After setting up the scheme as above and creating a collective variable cv, the following code will implement this selector where the Gaussian bias is defined by exp(−α(cv(x) – l0)2)
with x representing a snapshot, and l0 and α, respectively, controlling the position
and width of the Gaussian.
where the Gaussian bias is defined by exp(−α(cv(x) – l0)2)
with x representing a snapshot, and l0 and α, respectively, controlling the position
and width of the Gaussian.
A third example of a MoveStrategy is to
add a specific ensemble pair to the list of possible replica exchange
moves. To do this, one would first select the ensembles (call them ens1 and ens2). Then, after creating
the scheme as before, the new replica exchange
pairs can be added with Note that this last example was a signature-level
strategy,
whereas the other examples were mover-level. The priority-level system
used in OPS means that the user does not have to consider the order
in which the strategies are built when appending them to a custom
move scheme. For example, the signature-level strategy that changes
the ensembles used in replica exchange can be appended after the mover-level
strategy that provides details of how to perform the shooting move,
even though the order they are used in is the opposite order when
building the move decision tree.
Note that this last example was a signature-level
strategy,
whereas the other examples were mover-level. The priority-level system
used in OPS means that the user does not have to consider the order
in which the strategies are built when appending them to a custom
move scheme. For example, the signature-level strategy that changes
the ensembles used in replica exchange can be appended after the mover-level
strategy that provides details of how to perform the shooting move,
even though the order they are used in is the opposite order when
building the move decision tree.
4. Illustrative Examples
4.1. Creating New Ensembles
One of the significant features of OpenPathSampling is the ability to generate valid paths for arbitrary path ensembles. This capability facilitates the development of new methodologies, which often require the creation of new path ensembles. In addition, this feature has practical advantages for users as well. In the Appendix of Paper 1, we briefly mentioned one such practical use.24 To obtain the initial conditions for a path sampling simulation, we can use a high temperature trajectory. For multiple state TIS simulations, we also need initial trajectories that satisfy all the ensembles in the MSTIS network: there must be trajectories that begin in each state and which exit each interface volume. For most MSTIS simulation setups, a path that undergoes a transition to another state will cross all the interfaces associated with the initial state. Therefore, we can use such a transition path as an initial path for all interfaces; and since we can reverse paths, a long trajectory that visits all states will contain, for each of the defined MSTIS ensemble in the network, a (possibly reversed) subtrajectory that satisfies that ensemble.
Thus, our high temperature target trajectory is one that has visited all states. To define an ensemble that will generate such a trajectory, we use complement ensembles and think in terms of halting criteria, as suggested in the guidelines in Section 2.7. We need a condition that remains true until the trajectory has visited all states — in other words, the opposite of the condition that the trajectory has visited all states. This means that we should continue as long as the trajectory has not visited at least one state. We can express this idea as a path ensemble
| 42 |
which is only true if none of the M Out conditions are fulfilled. The continuation condition is now the negation of this ensemble
| 43 |
This condition translates
in OPS to the Python code where states is a list of the state
volumes. We can then create the goal trajectory using the engine.generate method by
where states is a list of the state
volumes. We can then create the goal trajectory using the engine.generate method by The resulting trajectory will have
visited every state, and the last frame will be in the last state
visited. Since it visits every state, then it has, for every state,
a subtrajectory that starts in that state and ends in another (in
some cases requiring time reversal). This means that subtrajectories
of this long trajectory can be found to satisfy all the ensembles
in the MSTIS network. Note that we use the ensemble itself as a condition,
not its CanApp function. In this case, because these are In/OutA-type ensembles, the CanApp is equivalent
to the ensemble check (this is not necessarily the case for other
ensembles). Conceptually, we are after the first trajectory that does
not satisfy the ensemble, so we use the ensemble check itself.
The resulting trajectory will have
visited every state, and the last frame will be in the last state
visited. Since it visits every state, then it has, for every state,
a subtrajectory that starts in that state and ends in another (in
some cases requiring time reversal). This means that subtrajectories
of this long trajectory can be found to satisfy all the ensembles
in the MSTIS network. Note that we use the ensemble itself as a condition,
not its CanApp function. In this case, because these are In/OutA-type ensembles, the CanApp is equivalent
to the ensemble check (this is not necessarily the case for other
ensembles). Conceptually, we are after the first trajectory that does
not satisfy the ensemble, so we use the ensemble check itself.
We can also define another (arbitrary) ensemble to obtain a first trajectory suitable for the TIS bootstrapping procedure. This procedure takes a trajectory satisfying the innermost interface ensemble of a TIS transition and performs shooting moves until the resulting paths satisfy the ensemble(s) for the subsequent interface(s). To get that initial trajectory, we want to start from any arbitrary frame, then have at least one frame in state A, then have at least one frame that crosses the interface, and end with exactly one frame in either state A or state B (where state B can be generalized to the union of multiple other states). The sequential ensemble to do this is
| 44 |
Following Section 2.7, this ensemble uses an anchor that combines
the optional ensemble outside of A with a required
ensemble inside A. As also suggested in the guidelines,
the OptionalEnsembles in this ensemble are
designed to ensure that any possible trajectory that satisfies the
overall goal will still be accepted. This ensemble translates into
OPS code as A similar ensemble is part of the FullBootstrapping calculation, which fills TIS ensembles
starting from a single snapshot.
A similar ensemble is part of the FullBootstrapping calculation, which fills TIS ensembles
starting from a single snapshot.
4.2. Using Ensemble.split for Trajectory Analysis
The Ensemble object in OpenPathSampling provides a convenient way of analyzing trajectories in terms of subtrajectories. The ensemble.split(trajectory, overlap) method takes a long trajectory and returns a list of subtrajectories that satisfy the ensemble. Successive subtrajectories will have at most overlap frames in common (with a default of 1 shared frame). For example, we can check whether any trajectories in a fixed-length TPS simulation included recrossings. Given state volumes A and B, we first create the B → A transition ensemble
| 45 |
which in OPS
code translates to  Making frames outside of both A and B optional captures trajectories
where the transition
occurs without any intermediate frames (this is unlikely in our examples
but could be common in long paths with (too) infrequent saving of
frames). We can apply B_to_A.split(trajectory) to every trajectory accepted by the fixed-length TPS ensemble. If
the resulting list is not empty, a recrossing in the B → A direction took place. Since the first
frame of every accepted trajectory has to be in A and the last frame of every trajectory is necessarily in B, the existence of a B → A transition guarantees a recrossing. For the fixed path
length alanine dipeptide example from Paper 1,24 Section 6.6, we find 109 accepted trials with recrossings,
including 5 with 2 recrossing events. For accepted paths with a single
recrossing, there are two α → β transitions in
the path — one before recrossing and one after. With two recrossings,
there would be three transitions. An example of an accepted recrossing
trajectory is shown in Figure 6.
Making frames outside of both A and B optional captures trajectories
where the transition
occurs without any intermediate frames (this is unlikely in our examples
but could be common in long paths with (too) infrequent saving of
frames). We can apply B_to_A.split(trajectory) to every trajectory accepted by the fixed-length TPS ensemble. If
the resulting list is not empty, a recrossing in the B → A direction took place. Since the first
frame of every accepted trajectory has to be in A and the last frame of every trajectory is necessarily in B, the existence of a B → A transition guarantees a recrossing. For the fixed path
length alanine dipeptide example from Paper 1,24 Section 6.6, we find 109 accepted trials with recrossings,
including 5 with 2 recrossing events. For accepted paths with a single
recrossing, there are two α → β transitions in
the path — one before recrossing and one after. With two recrossings,
there would be three transitions. An example of an accepted recrossing
trajectory is shown in Figure 6.
Figure 6.
Accepted TPS trajectory with recrossing taken from the fixed-length TPS simulation of alanine dipeptide in Paper 1.24 The angle ψ is plotted as a function of time. Frames in C7eq are marked in red; frames in αR are marked in blue.
This approach also allows distinguishing between multiple channels for a given reaction. For instance, we can compare the behavior of fixed path length TPS and flexible path length TPS for alanine dipeptide. By taking ensemble as the flexible path length TPS ensemble, application of the split function identifies subtrajectories of the fixed path length TPS that match the flexible path length ensemble.
The top panel of Figure 7 shows path-length histograms for the transitions in the flexible path length TPS ensemble and in the fixed path length ensemble (selected using the split function), from our TPS simulations of alanine dipeptide reported in Paper 1.24 These histograms differ because the fixed length ensemble in fact sampled two different transition mechanisms. To show this, we can define custom path ensembles that distinguish between the two mechanisms. First, we define additional volumes, based on the ψ collective variable: an A volume for 100 < ψ < 200 (where the CVPeriodicRangeVolume automatically wraps into the correct bounds) and a B volume for −100 < ψ < 200. These two volumes are based on the original states but have no restrictions in ϕ. Two additional volumes account for the “no-man’s land” region outside the states: nml_increasing for −160 < ψ < −100 and nml_decreasing for 0 < ψ < 100. Next, we identify a transition as “increasing” if the trajectory crosses the nml_increasing volume (i.e., the value of ψ increases while going from one state to the next) and “decreasing” if it crosses the nml_decreasing volume. The sequential ensemble for the increasing transitions can be defined by
| 46 |
which is in OPS code The ensemble for decreasing transitions is defined similarly
but using nml_decreasing in place of nml_increasing. Trajectories that satisfy the original
TPS ensemble will have subtrajectories that satisfy one of these ensembles.
By using the ensemble.split() method, we can
identify which mechanism each trajectory represents.
The ensemble for decreasing transitions is defined similarly
but using nml_decreasing in place of nml_increasing. Trajectories that satisfy the original
TPS ensemble will have subtrajectories that satisfy one of these ensembles.
By using the ensemble.split() method, we can
identify which mechanism each trajectory represents.
Figure 7.
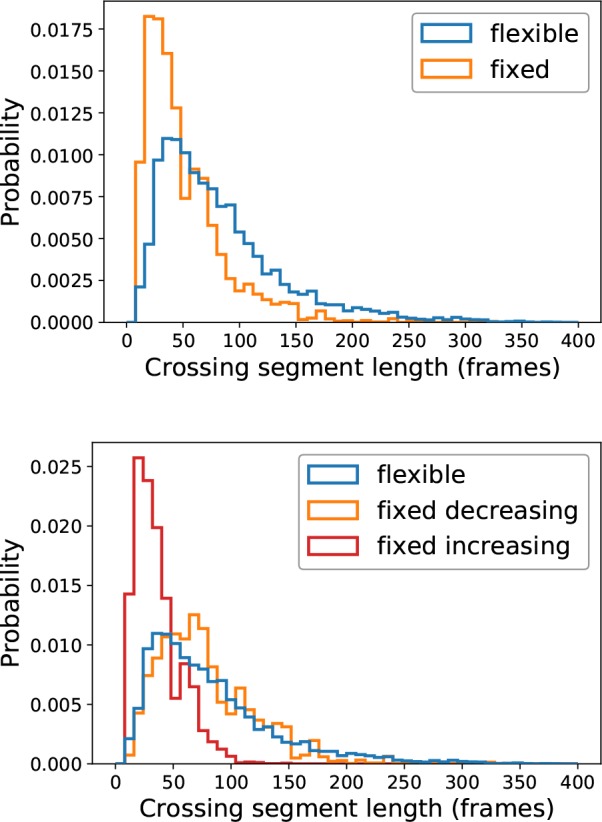
Transition path length distributions. Top: Without distinguishing between increasing and decreasing transition types from the fixed length TPS. Bottom: Distinguishing the increasing and decreasing transitions. The difference in the path length distributions can be attributed to the fixed-length simulation sampling both increasing and decreasing transitions.
Figure 8 shows several trajectories (blue and purple) connecting the original two stable states (dark red). The states are defined in terms of periodic variables and can wrap around the periodic boundary. The “extended” versions of the states that were defined above are shown in light red, and the two different “no man’s land” volumes are labeled nml_decreasing and nml_increasing. Several hypothetical trajectories are shown, all of which would count as a decreasing transition. Trajectory (a) would be easy to analyze by a volume-based approach (and is also a realistic trajectory for this system). Trajectories (b) and (c) would count as decreasing transitions, but an analysis based only on volumes (without consideration of ordering) might miss them. Trajectory (d) includes both an increasing and a decreasing transition (and would be extraordinarily unlikely in this system).
Figure 8.

Volumes and example trajectories for the different ways a “decreasing” transition can occur. The shaded areas represent the extended state definitions used in the analysis of the transitions, while the darker shaded areas are the actual states of the system. (a) A typical decreasing path. (b) and (c) Paths which visit the “increasing” no man’s land but only transition across the decreasing. (d) Path with both increasing and decreasing transitions.
The fixed length alanine dipeptide example shows 3570 trajectories in the decreasing channel and 6670 trajectories in the increasing channel (weighted by the Monte Carlo weights from the TPS simulation). All transition trajectories satisfy exactly one of the two channels, although some TPS trajectories, due to recrossings, have more than one transition trajectory. The flexible length example has all its trajectories in the decreasing channel. The existence of recrossings in the fixed length TPS ensemble demonstrates that these transitions in alanine dipeptide are not that rare, so it is not surprising that we would also observe switching between the two mechanisms. The bottom panel of Figure 7 shows the path length histograms when the increasing and decreasing transitions are distinguished. The decreasing subtrajectories from the fixed-length sampling and the trajectories from the flexible-length sampling (which are all decreasing) show much closer agreement, and the increasing transition shows a very different distribution.
We can also replace other common analyses with versions based on Ensemble.split. For example, consider the lifetime in a given state, which is defined by the time from when a trajectory first enters the state (having previously been in another state) until it enters another state. We refer to the desired state as A and the combination of all other states as B.
To think of this in terms of path ensembles, we describe it in two stages. First, we need to find the path ensemble which goes from another state, enters the desired state, and then enters another state. We denote this as the “BAB” ensemble. The trajectories which are relevant to the lifetime calculation are subtrajectories of trajectories in the BAB ensemble. These go from the first entrance in A to the first entrance in B. We will call this the “AB” ensemble. We obtain trajectories in the AB ensemble by first getting all the segments that satisfy the BAB ensemble and then selecting the relevant subtrajectories. Defining the BAB ensemble as
| 47 |
the corresponding OPS code is given by  The AB ensemble is defined as
The AB ensemble is defined as
| 48 |
with the
OPS code given by Both ensembles make use of the guideline
on thinking about
the halting criteria (from Section 2.7) by using OutB as part
of the middle subensemble. This guarantees that the middle subensemble
stops, and the first frame afterward must be the first frame in state B (thus satisfying the final subsensemble). Additionally
both of these ensembles use anchors requiring one frame in a state.
Formally, the intersection with
Both ensembles make use of the guideline
on thinking about
the halting criteria (from Section 2.7) by using OutB as part
of the middle subensemble. This guarantees that the middle subensemble
stops, and the first frame afterward must be the first frame in state B (thus satisfying the final subsensemble). Additionally
both of these ensembles use anchors requiring one frame in a state.
Formally, the intersection with  is not necessary, as we might as well have
selected the last subtrajectory of frames in B/the
first subtrajectory of frames in A, instead of the
last frame in B/first frame in A.
is not necessary, as we might as well have
selected the last subtrajectory of frames in B/the
first subtrajectory of frames in A, instead of the
last frame in B/first frame in A.
To use these, we just run In Figure 9, we visualize
the trajectory segments associated with each of these
ensembles for a sample trajectory from a toy model.
In Figure 9, we visualize
the trajectory segments associated with each of these
ensembles for a sample trajectory from a toy model.
Figure 9.
Trajectory segments for lifetimes. A trajectory for a toy model is shown with a light gray line. The red area represents state B, and the blue area represents state A. The segment that satisfies the BAB ensemble is shown by the dark gray line, and the segment that satisfies the AB ensemble is shown in blue (and overlaps the BAB segment).
In the above example, the average time of the resulting trajectories gives the average lifetime in a state. In a two-state system, the reciprocal of the average lifetime is the rate. This could be modified to get the transition rate constants for a multiple state system by replacing the AllInXEnsemble(B) in the BAB sequential ensemble with an ensemble that would allow any state other than A, while the last one allows a specific state B. This would give the lifetime associated with the rate of A → B.
A similar procedure can be used to obtain the flux from a state through a given interface in TIS. In that case, we do two lifetime analyses: the lifetime outside the interface (where A is everything outside the interface, and B is the state) and the lifetime inside the state (where A is the state, and B is everything outside the interface). The reciprocal of the sum of the average lifetimes from these gives us the flux.25
Since this example involves two loops over the snapshots, it may not be as fast as code custom-designed to this purpose. (Although, in fact, the caching of OPS collective variables renders the vast majority of the total computational effort done in the first pass.) However, our primary intent here is to highlight how simple it is to prototype a trajectory analysis based on using the Ensemble.split method. It may be possible to write faster code, but it is hard to write code faster.
The specific implementations of flux and lifetime discussed here are included in the SingleTrajectoryAnalysis object.
4.3. Custom PathMovers
The default RETIS move scheme selects a type of move at random (shooting, replica exchange, etc.) and then attempts one move of that type (shooting in a single ensemble, replica exchange for a specific pair, etc.); but perhaps a move which does all the replica exchanges in sequential order, then does shooting moves on all the ensembles, and then does the replica exchange in the reverse order would be more efficient. This move will satisfy detailed balance — the question is whether it is more efficient.
For the most part, this simulation is set up as in the examples in Paper 1.24 The specific potential energy surface is given by
| 49 |
States are defined such that state A is x < −0.5 and state B is x > 0.5. Only the A → B transition is studied, with interface volumes from xmin = −∞ to xmax,i = {−0.4, −0.3, −0.2, −0.1}. The potential energy surface, with states and interface boundaries, is shown in Figure 10.
Figure 10.
Model system for the custom move scheme example. Potential energy surface with states in blue and interface boundaries in red.
The main difference with the examples in Paper 124 is that here we define a custom MoveStrategy object, which creates a custom sequential mover. The code for this mover and a move strategy to manage it is given in Chart 2.
Chart 2. Custom Path Mover and Move Strategy for Repex-Shoot-Repex Movea.

a The make_movers method is the primary point: first, the replica exchange movers and shooting movers are extracted from the existing move scheme, removing them if replace is true. Then these movers are combined into a sequence in the mover_list, representing the sequential order in which they should run doing the combined move. That list is then input to create the sequential mover.
To use this strategy, we first create
a default scheme and then
append the new strategy
The visualization of this move scheme is in Figure 11. There is still a random choice of type of move, but the types available are now minus move, path reversal, and the sequential mover, which is the only choice under the “Repex_shoot_repexChooser” in the illustration of the move decision tree. The relative probabilities for each move type are determined as ratios. By default, a new move type has the same (relative) probability as a shooting move, which is twice that of a replica exchange or path reversal and five times that of a minus move. This means that when the repex-shoot-repex move replaces shooting and replica exchange in the move scheme, the ratio of per-ensemble shooting attempts to path reversals or to minus moves stays the same.
Figure 11.

Move scheme including the repex-shoot-repex mover.
On the other hand, the number
of total MC steps per ensemble shooting
attempts will, of course, be very different between the custom and
default schemes. To compare these fairly, we use the function scheme.n_steps_for_trials, which takes a mover
and the number of desired attempts of that mover as arguments. We
can ensure the two simulations do about the same amount of work by
aiming for the same number of per-ensemble shooting moves. For the
default scheme, this is and for the custom scheme, it is
and for the custom scheme, it is  We arbitrarily select the first shooting mover in the default
scheme, since all have the same probability. We take the total probability
of selecting the ’repex_shoot_repex’ group, because there is one mover in that group, and every time
it occurs, it creates one shooting attempt for each ensemble.
We arbitrarily select the first shooting mover in the default
scheme, since all have the same probability. We take the total probability
of selecting the ’repex_shoot_repex’ group, because there is one mover in that group, and every time
it occurs, it creates one shooting attempt for each ensemble.
To ensure that this is a fair comparison, there are a few comparisons that should be made. First, we use the scheme.move_summary function (described in Paper 124) to show that we have the same number of path reversal and minus moves in each scheme. We can also use the move summary to see that we have the same number of shooting moves per ensemble, by comparing the per-ensemble shooting count obtained by adding ’shooting’ as a second argument to default_scheme.move_summary with the number of repex-shoot-repex moves in the custom_scheme. Since both schemes are sampling the same number of shooting moves in the same ensembles, they should create roughly the same number of total snapshots. We can check this with len(storage.snapshots) for each storage.
To analyze these results, we consider replica round trip times and replica flow,35 concepts that monitor the presence of bottlenecks during the replica exchange. Both concepts require defining ensembles as “top” and “bottom”. We put the minus ensemble as the bottom ensemble and the outermost TIS ensemble as the top ensemble. A round trip can start from either the first entry to the “top” ensemble or the first entry to the “bottom” ensemble and will use whichever the given replica visits first. If the replica visits the “top” ensemble first, the round trip duration is the number of Monte Carlo steps from the first entry into “top” until the replica returns to “top” after visiting “bottom”, with the case starting in “bottom” defined analogously.
Replica flow is defined by labeling each replica as either traveling “up” or “down”, depending on whether it more recently visited the “bottom” or “top” ensemble, respectively. For each ensemble i, the count of visits by “up” replicas is given by ni↑, with the number of visits by “down” replicas given by ni. The flow for a given ensemble is defined as fi = ni↑/(ni + ni↓). Formally, flow is 1 at the “bottom” ensemble and 0 at the “top” ensemble. The ideal flow is linear with the replica index.35
Round trip times and flow are both calculated as part of the ReplicaNetwork analysis tool. The code to analyze the
default scheme is Then default_trips[’round’] returns a list of the duration (in Monte Carlo steps) of each round
trip that occurred. Analysis for the custom scheme is analogous.
Then default_trips[’round’] returns a list of the duration (in Monte Carlo steps) of each round
trip that occurred. Analysis for the custom scheme is analogous.
For this simple example, we find the custom move scheme does not yield significant improvement. The default scheme generates 345 round trips, whereas the custom scheme generates 311. There may be a small difference in the distribution of the round trip times (see Figure 12). The distribution of round trip times is skewed toward slightly longer round trips for the custom scheme. The replica flow, shown in Figure 13, is very similar for both approaches. Overall, the default scheme is probably a slightly better choice.
Figure 12.
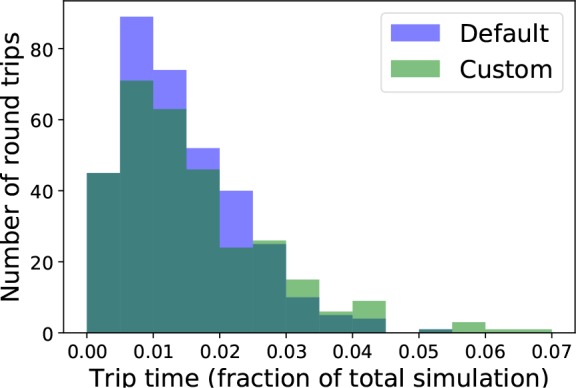
Histogram of round trip times for the default RETIS scheme and the custom scheme with the “repex-shoot-repex” move, with duration normalized to the total number of MC steps. Although both give about the same number of round trips, the distributions may differ somewhat.
Figure 13.
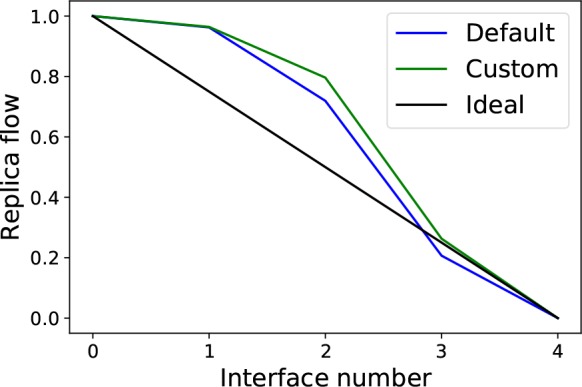
Replica flow for the default TIS scheme and the custom scheme with the “repex-shoot-repex” move. This example shows little difference, with the suggestion that the default scheme may be slightly better.
5. Conclusion
In this paper we have described some advanced topics relevant to the OpenPathSampling framework.24 We have introduced a novel set-based approach to constructing path ensembles, along with a new notation suitable to this approach. This allows the application of set logic to path ensembles and fits seamlessly with the way that OPS is written. Another advantage of this new notation is that it unifies the description of the monitor function of OPS with the path ensemble indicator function. Of particular importance herein is the sequential path ensemble, which is directly related to the way that OPS implements the path sampling monitoring and testing. Using this new notation it is remarkably simple to create new path ensembles and immediately implement these in OPS.
In addition, we provided insight in how one can customize the path sampling Monte Carlo movers within OPS in order to build nonstandard sampling schemes. These customizations are required if one wants to develop new path sampling schemes or adapt existing ones.
In short, in this paper we have illustrated the power and flexibility of the OPS package. Users can now develop their own advanced sampling protocol entirely in OPS and apply it to compute kinetic and thermodynamic observables.
In future work we will further elaborate on the foundation of the ensemble set-logic. Another direction is to parallelize the OPS code. While running multiple simulations in parallel is already possible, true parallelization requires the load balancing of multiple ensembles, where trajectories can have different and unpredictable path lengths, over the available computational resources.
Acknowledgments
The authors are grateful for feedback from many people who helped beta-test the software, whose names are listed at http://openpathsampling.org/latest/acknowledgments.html. The authors are particularly grateful to Sander Roet (University of Amsterdam) for his feedback and to Jocelyne Vreede (University of Amsterdam) for the feedback obtained by using OPS as a teaching tool in courses on biomolecular simulation.
Author Contributions
∞ D.W.H.S. and J.H.P. contributed equally to this work.
D.W.H.S. and P.G.B. acknowledge support from the European Union’s Horizon 2020 research and innovation program, under grant agreement No. 676531 (project E-CAM). J.D.C. acknowledges support from Cycle for Survival, NIH grant P30CA008748, and NIH grant R01GM121505. J.D.C., J.H.P., and D.W.H.S. gratefully acknowledge support from the Sloan Kettering Institute. F.N. acknowledges ERC consolidator grant 772230 “ScaleCell”, DFG NO 825/2-2, and SFB1114, project A04. The Chodera laboratory receives or has received funding from multiple sources, including the National Institutes of Health, the National Science Foundation, the Parker Institute for Cancer Immunotherapy, Relay Therapeutics, Entasis Therapeutics, Silicon Therapeutics, EMD Serono (Merck KGaA), AstraZeneca, the Molecular Sciences Software Institute, the Starr Cancer Consortium, Cycle for Survival, a Louis V. Gerstner Young Investigator Award, and the Sloan Kettering Institute. A complete funding history for the Chodera lab can be found at http://choderalab.org/funding. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
The authors declare the following competing financial interest(s): J.D.C. was a member of the Scientific Advisory Board for Schrodinger, LLC during part of this study, and is a current member of the Scientific Advisory Board of OpenEye Scientific Software.
References
- Lindorff-Larsen K.; Piana S.; Dror R. O.; Shaw D. E. How Fast-Folding Proteins Fold. Science 2011, 334, 517–520. 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- Buch I.; Giorgino T.; De Fabritiis G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 10184–10189. 10.1073/pnas.1103547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plattner N.; Noe F. Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 2015, 6, 7653. 10.1038/ncomms8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva D.-A.; Bowman G. R.; Sosa-Peinado A.; Huang X. A Role for Both Conformational Selection and Induced Fit in Ligand Binding by the LAO Protein. PLoS Comput. Biol. 2011, 7, e1002054. 10.1371/journal.pcbi.1002054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütte C.; Huisinga W. In Handbook of Numerical Analysis; Ciaret P. G., Lions J.-L., Eds.; Elsevier: 2003; Vol. X, pp 699–744. [Google Scholar]
- Noé F.; Horenko I.; Schütte C.; Smith J. C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126, 155102. 10.1063/1.2714539. [DOI] [PubMed] [Google Scholar]
- Chodera J. D.; Singhal N.; Pande V. S.; Dill K. A.; Swope W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 2007, 126, 155101. 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- Chandler D. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne B. J.; Ciccotti G.; Coker D. F., Eds.; World Scientific: 1998; Chapter Barrier crossings: classical theory of rare but important events, pp 3–23. [Google Scholar]
- Torrie G. M.; Valleau J. P. Monte Carlo Free Energy Estimates Using Non-Boltzmann Sampling: Application to the Sub-Critical Lennard-Jones Fluid. Chem. Phys. Lett. 1974, 28, 578. 10.1016/0009-2614(74)80109-0. [DOI] [Google Scholar]
- Carter E.; Ciccotti G.; Hynes J. T.; Kapral R. Constrained Reaction Coordinate Dynamics for the Simulation of Rare Events. Chem. Phys. Lett. 1989, 156, 472. 10.1016/S0009-2614(89)87314-2. [DOI] [Google Scholar]
- Huber T.; Torda A.; van Gunsteren W. J. Comput.-Aided Mol. Des. 1994, 8, 695. 10.1007/BF00124016. [DOI] [PubMed] [Google Scholar]
- Grubmüller H. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1995, 52, 2893–2906. 10.1103/PhysRevE.52.2893. [DOI] [PubMed] [Google Scholar]
- Voter A. F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 1997, 106, 4665. 10.1063/1.473503. [DOI] [Google Scholar]
- Laio A.; Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 12562. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darve E.; Pohorille A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169. 10.1063/1.1410978. [DOI] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Marinari E.; Parisi G. Simulated Tempering - A new monte-carlo scheme. Europhys. Lett. 1992, 19, 451–458. 10.1209/0295-5075/19/6/002. [DOI] [Google Scholar]
- Zheng L.; Chen M.; Yang W. Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 20227–20232. 10.1073/pnas.0810631106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y. Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. 10.1063/1.2825614. [DOI] [PubMed] [Google Scholar]
- Dellago C.; Bolhuis P. G.; Csajka F. S.; Chandler D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 1998, 108, 1964–1977. 10.1063/1.475562. [DOI] [Google Scholar]
- Bolhuis P. G.; Chandler D.; Dellago C.; Geissler P. Transition path sampling: Throwing ropes over mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- Dellago C.; Bolhuis P. G.; Geissler P. L. Transition path sampling. Adv. Chem. Phys. 2003, 123, 1–78. 10.1002/0471231509.ch1. [DOI] [Google Scholar]
- Dellago C.; Bolhuis P. G. Transition Path Sampling and Other Advanced Simulation Techniques for Rare Events. Adv. Polym. Sci. 2009, 221, 167–233. 10.1007/978-3-540-87706-6_3. [DOI] [Google Scholar]
- Swenson D. W. H.; Prinz J.-H.; Noé F.; Chodera J. D.; Bolhuis P. G. J. Chem. Theory Comput. 2018, 10.1021/acs.jctc.8b00626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Erp T. Reaction Rate Calculation by Parallel Path Swapping. Phys. Rev. Lett. 2007, 98, 268301. 10.1103/PhysRevLett.98.268301. [DOI] [PubMed] [Google Scholar]
- Bolhuis P. G. Rare events via multiple reaction channels sampled by path replica exchange. J. Chem. Phys. 2008, 129, 114108. 10.1063/1.2976011. [DOI] [PubMed] [Google Scholar]
- van Erp T. S. Dynamical rare event simulation techniques for equilibrium and nonequilibrium systems. Adv. Chem. Phys. 2012, 151, 27–60. 10.1002/9781118309513.ch2. [DOI] [Google Scholar]
- Bolhuis P. G.; Dellago C.. Reviews of Computational Chemistry; Wiley-VCH: Hoboken, 2009; 10.1002/SERIES6143. [DOI] [Google Scholar]
- Swenson D. W. H. to be published 2018.
- Swenson D. W. H.; Bolhuis P. G. A replica exchange transition interface sampling method with multiple interface sets for investigating networks of rare events. J. Chem. Phys. 2014, 141, 044101. 10.1063/1.4890037. [DOI] [PubMed] [Google Scholar]
- van Erp T. S.; Moroni D.; Bolhuis P. G. A novel path sampling method for the calculation of rate constants. J. Chem. Phys. 2003, 118, 7762. 10.1063/1.1562614. [DOI] [Google Scholar]
- Allen R.; Frenkel D.; ten Wolde P. Simulating rare events in equilibrium or nonequilibrium stochastic systems. J. Chem. Phys. 2006, 124, 024102. 10.1063/1.2140273. [DOI] [PubMed] [Google Scholar]
- Peters B.; Trout B. L. Obtaining reaction coordinates by likelihood maximization. J. Chem. Phys. 2006, 125, 054108. 10.1063/1.2234477. [DOI] [PubMed] [Google Scholar]
- Juraszek J.; Bolhuis P. G. Rate Constant and Reaction Coordinate of Trp-Cage Folding in Explicit Water. Biophys. J. 2008, 95, 4246–4257. 10.1529/biophysj.108.136267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzgraber H. G.; Trebst S.; Huse D. A.; Troyer M. Feedback-optimized parallel tempering Monte Carlo. J. Stat. Mech.: Theory Exp. 2006, 2006, P03018–P03018. 10.1088/1742-5468/2006/03/P03018. [DOI] [Google Scholar]



