Abstract

Transition path sampling techniques allow molecular dynamics simulations of complex systems to focus on rare dynamical events, providing insight into mechanisms and the ability to calculate rates inaccessible by ordinary dynamics simulations. While path sampling algorithms are conceptually as simple as importance sampling Monte Carlo, the technical complexity of their implementation has kept these techniques out of reach of the broad community. Here, we introduce an easy-to-use Python framework called OpenPathSampling (OPS) that facilitates path sampling for (bio)molecular systems with minimal effort and yet is still extensible. Interfaces to OpenMM and an internal dynamics engine for simple models are provided in the initial release, but new molecular simulation packages can easily be added. Multiple ready-to-use transition path sampling methodologies are implemented, including standard transition path sampling (TPS) between reactant and product states and transition interface sampling (TIS) and its replica exchange variant (RETIS), as well as recent multistate and multiset extensions of transition interface sampling (MSTIS, MISTIS). In addition, tools are provided to facilitate the implementation of new path sampling schemes built on basic path sampling components. In this paper, we give an overview of the design of this framework and illustrate the simplicity of applying the available path sampling algorithms to a variety of benchmark problems.
1. Introduction
Biomolecular systems, such as proteins and nucleic acids, can undergo complex conformational changes on long time scales that are challenging for atomistic molecular simulations to reach. For example, atomistic molecular dynamics (MD) must employ timesteps on the scale of femtoseconds to faithfully reproduce the fastest vibrational modes to maintain simulation stability and fidelity, while the kinetic time scales (e.g., of protein folding or binding) can often range from microseconds to seconds or more. In protein–ligand binding, mean residence times for bound druglike molecules are often several hours, presenting an enormous challenge to studying dissociation mechanisms or predicting unbinding rates by straightforward MD.1−3 In these and other situations, simulating a sufficient number of these rare events (folding/unfolding or binding/unbinding) to produce a statistically meaningful description of the dominant mechanism or estimate of rate constants is often so challenging as to be untenable by straightforward means. Slow kinetic time scales primarily arise from large kinetic barriers between metastable states.4−7 The observed dynamics is dominated by long waiting times within metastable basins, punctuated by rare events of interest occurring over a short time.8,9 Straightforward molecular simulation is highly inefficient as most effort will be wasted simulating uninteresting dynamics as the system remains trapped within metastable states.10
One approach to overcoming the rare event problem is to bias the potential energy surface or alter the probability density of sampled conformations to enhance the occurrence of the rare event. A priori knowledge of a suitable reaction coordinate allows the use of biasing potentials or higher effective temperatures, reducing effective free energy barriers. Many such enhanced sampling methods have been developed (e.g., see refs (11−21)). Useful bias potentials capable of enhancing the frequency of rare events require (a set of) collective variables that approximate the reaction coordinate; poor choices will lead to poor sampling of the reactive pathways and hence poor estimates of the dynamical bottlenecks and the related barrier heights and rates. Even worse, some methods are sensitive to the omission of slow degrees of freedom and may lead to incorrect models of the reactive pathways. In general, removing the effect of the bias potential to yield correct dynamics is difficult.
Path sampling techniques, in particular transition path sampling,10,22−24 provide a solution to the rare event problem without requiring the same degree of knowledge of reactive pathways. Instead of biasing the potential—which leads to heavily perturbed dynamics—these techniques bias the probability with which a given transition path is sampled, without perturbing these paths themselves. This property allows the unbiased equilibrium dynamics to be recovered. For the simple case of a two-state system separated by a single barrier, the straightforward MD simulation time to observe a number of transitions scales exponentially in the barrier height. In contrast, transition path sampling only focuses on short parts of the MD trajectory that traverse the barrier, providing exponential acceleration in the sampling of rare events.10,23 Other methods based on trajectory sampling include forward flux sampling (FFS),25 adaptive multilevel splitting,26 milestoning,27 partial path transition interface sampling,28 the RESTART methodology,29 SPRESS,30 NEUS,31 Weighted Ensemble,32,33 and many others.
In addition to studying rare events directly, path sampling methods can be combined with other approaches for describing statistical conformational dynamics. For example, Markov state models (MSMs) have emerged as a popular way to represent the long time statistical dynamics of complex processes involving many distinct metastable conformational states.34 By discretizing conformation space and describing stochastic transitions between regions with a transition or rate matrix, MSMs can describe the long-time statistical dynamics of complex systems with bounded approximation error.34 While standard MSM construction approaches utilize large quantities of unbiased simulation data, path sampling techniques can be utilized to rapidly construct or improve MSM transition matrices by focusing on harvesting trajectories for poorly sampled transitions.2,35−39 More recently, techniques have emerged for combining both biased and unbiased dynamics to construct multiensemble Markov Models (MEMMs),40−43 enabling even richer combinations of multiple efficient sampling techniques for rapid construction of statistical models of dynamics.
While transition path sampling techniques are very flexible, the complexity of their implementation and lack of a standard tool for applying them have slowed their adoption. In particular, many path sampling techniques require monitoring of dynamics to detect when stopping conditions are reached, and the control of and integration with standard simulation packages has been a practical obstacle for widespread use. As a solution to this, we have developed a new framework called OpenPathSampling (OPS) that enables path sampling techniques to be employed in a flexible, general manner. This framework is “batteries included”, with a number of different path sampling algorithms and worked examples available that can help users to apply path sampling techniques on their own system. Both low-dimensional toy model systems and complex molecular systems are supported, with complex systems supported using interfaces to external simulation codes. Currently, OPS supports the GPU-accelerated molecular simulation code OpenMM,44,45 although support for other codes can be added. The framework is flexible and extensible, allowing users to easily explore implementation of new path sampling algorithms in addition to applying or extending existing algorithms or connecting new simulation codes. Many other methods, such as FFS or milestoning, could also be implemented within the framework of OPS. For the sake of clarity, however, we will limit ourselves here to the transition path sampling based methods. [Note that in this work we often use ’transition path sampling’ and ’path sampling’ interchangeably. The reason is that the concept of path sampling is more inclusive and also covers algorithms that do not immediately aim to cross (single) barriers. However, it is understood that all path sampling methods in this work fall into the larger ’transition path sampling’ family of algorithms.] OPS differs in scope and versatility from the PyRETIS package,46 a recently developed package to conduct advanced transition path sampling simulations. In particular, the novel approaches to path ensembles and Monte Carlo moves, detailed in the companion paper,47 differ significantly from the approaches taken in PyRETIS and facilitate the implementation of new methods within the OPS framework.
In this paper, we first give a brief overview of a variety of path sampling techniques that are implemented in the OPS framework (Section 2); explain how the basic path sampling concepts relate to OPS object classes (Section 4); review the general workflow associated with setting up, running, and analyzing a path sampling calculation (Section 5); and then provide a number of detailed examples that illustrate the flexibility and simplicity of applying various path sampling techniques using this framework (Section 6). In the process of developing a framework capable of easily implementing a multitude of path sampling techniques, we have significantly generalized the manner in which path ensembles can be constructed and used within the path sampling mathematical framework. While this expressive path ensemble specification language is briefly introduced (Section 3) and utilized in the examples described here, this approach is described in detail in a companion paper in this issue.47
2. Background
2.1. The Concept of Path Ensembles
Here, we presume the reader is somewhat familiar with the transition path sampling literature.10,22−24,48 While we give a brief overview of the main concepts in this section, readers not familiar with this topic are encouraged to start with a basic review such as ref (48).
The types of path sampling considered in this paper—and implemented and supported by OpenPathSampling—deal with equilibrium dynamics, obeying microscopic reversibility, so that a stationary distribution is preserved during the dynamics. This distribution is generally a thermodynamic distribution such as the Boltzmann distribution or distributions associated with NVE or NPT ensembles. Moreover, ergodicity is assumed; that is, an infinitely long trajectory has a nonzero probability to visit every point in phase space. This guarantees that (dynamical) averages computed in the path ensemble, such as rate constants, are identical to those of an infinitely long trajectory.
A path or trajectory consists of a sequence of L +
1 points in configuration or phase space x ≡ {x0, x1, ..., xL} generated by some dynamical
model (such as Hamiltonian, Langevin, Brownian, or even Monte Carlo
dynamics), with the initial configuration x0 drawn from an initial (equilibrium) distribution ρ(x0). The path ensemble is defined
by the probability distribution 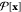 of such paths (with the length L either fixed or varying) and can be sampled using a Markov
Chain Monte Carlo (MCMC) algorithm. Path sampling algorithms consist
of a few main ingredients: (1) a scheme for initializing the sampler
with an initial path; (2) one or more schemes for proposing new trial
paths from the current path; and (3) acceptance criteria (e.g.,
based on Metropolis-Hastings) used to accept or reject the proposed
trial path to generate a new sample from the path probability density
(ensemble) of interest.
of such paths (with the length L either fixed or varying) and can be sampled using a Markov
Chain Monte Carlo (MCMC) algorithm. Path sampling algorithms consist
of a few main ingredients: (1) a scheme for initializing the sampler
with an initial path; (2) one or more schemes for proposing new trial
paths from the current path; and (3) acceptance criteria (e.g.,
based on Metropolis-Hastings) used to accept or reject the proposed
trial path to generate a new sample from the path probability density
(ensemble) of interest.
The idea of path sampling is to enhance the probability sampling of certain paths, either by biasing the path probability or by constraining the path ensemble. Analogous to how standard Monte Carlo importance sampling techniques can enhance sampling of rare configurations by multiplying the probability density by a biasing factor wbias(x) based on the instantaneous conformation x
| 1 |
and subsequently using this bias to unbias the sampled ensemble and recover equilibrium expectations, path sampling techniques can enhance the sampling of rare trajectories by multiplying by a biasing weight wbias[x], based on the trajectory x
| 2 |
Many types of path sampling, notably standard transition path sampling (TPS),10,22 define constrained path ensembles which select trajectories that begin in one region of configuration space A and end in another region B. OPS supports a simple but powerful way of defining path ensembles, described briefly in Section 5.2 and expanded upon in detail in a companion paper.47 Below, we give a brief overview of common kinds of transition path sampling simulations supported by OPS.
2.2. Transition Path Sampling
The transition path sampling (TPS)10,22 method attempts to harvest trajectories connecting two specific regions of configuration space, such as a reactant and product separated by a single free energy barrier. The constrained path ensemble for a fixed length L is thus
| 3 |
Here, x ≡ {x0, x1, ..., xL} is a discrete-time trajectory of snapshots, 1A(x0) and 1B(xL) are indicator functions that are unity if the trajectory
starts with x0 ∈ A and ends with xL ∈ B and zero otherwise, and 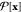 is the equilibrium path probability
density. In a TPS simulation, new trial trajectories are proposed
from the current sampled trajectory by selecting a phase space point
along the trajectory, applying a perturbation (usually of the momenta),
and “shooting” forward and backward by integrating the
equations of motion until a trajectory of the original length is generated.
The trial trajectory is then accepted or rejected with a Metropolis-Hastings
criterion. For the simplest case of drawing the shooting point uniformly from the current trajectory, assigning a new velocity
from the Maxwell–Boltzmann distribution, and imposing the trajectory
of fixed length to begin in state A and end in B, this acceptance criteria amounts to accepting the new
trajectory when it satisfies the defined ensemble of interest by terminating
in regions A and B; the old path
is otherwise retained if the proposed trajectory is rejected. Depending
on the details of the shooting move, the exact acceptance criteria
will take on different forms.10,22−24,48
is the equilibrium path probability
density. In a TPS simulation, new trial trajectories are proposed
from the current sampled trajectory by selecting a phase space point
along the trajectory, applying a perturbation (usually of the momenta),
and “shooting” forward and backward by integrating the
equations of motion until a trajectory of the original length is generated.
The trial trajectory is then accepted or rejected with a Metropolis-Hastings
criterion. For the simplest case of drawing the shooting point uniformly from the current trajectory, assigning a new velocity
from the Maxwell–Boltzmann distribution, and imposing the trajectory
of fixed length to begin in state A and end in B, this acceptance criteria amounts to accepting the new
trajectory when it satisfies the defined ensemble of interest by terminating
in regions A and B; the old path
is otherwise retained if the proposed trajectory is rejected. Depending
on the details of the shooting move, the exact acceptance criteria
will take on different forms.10,22−24,48
Transition path sampling is immensely powerful, as the difficult problem of describing reaction mechanisms is reduced to the much easier problem of defining stable states A and B. Reactive trajectories are efficiently harvested because the trial trajectory quickly decorrelates from the original trajectory yet is still likely to meet the same path ensemble constraints, such as connecting the reactant and product regions of configuration space A and B.
In order for the reactive trajectories connecting metastable sets A and B to be useful for computing transition rates and physical interpretation of mechanisms, the system must commit to and remain in the metastable states for a long time after encountering them, i.e., transitions between A and B are rare events on the molecular time scale. The states A and B are generally defined as configurational space regions within the basin of attraction of the distinct metastable states. Trajectories initiated from configurations in these regions, called core sets, should have a high probability (close to unity) to remain in or quickly return to the core set rather than escape to other states, even at the boundary of these sets.34,49
TPS can also be used with flexible-length trajectories that are constrained to terminate when they encounter the boundary of core sets A and B. This can be encoded in the path ensemble definition by demanding that frames 1 to L – 1 are neither in A nor in B. This approach is more efficient at sampling reactive trajectories by avoiding sampling long dwell times in each state at either end of the trajectory.50 To maintain detailed balance, the acceptance criterion then contains the ratio of the previous and trial path length, i.e., the number of frames from which the shooting point is randomly chosen. TPS can also easily be extended to multiple states by allowing more states in the path ensemble definition.36 A variety of other path proposal moves have been described to attempt to increase acceptance probabilities in certain regimes, including shifting moves,22 small velocity perturbations,22 precision shooting,51 permutation shooting,52 aimless shooting,52 and spring shooting.53 In addition, path proposal moves such as the web-throwing and stone-skipping moves54 have been developed to enhance the decorrelation of successive trajectories.
2.3. Transition Interface Sampling (TIS)
While TPS yields information about the mechanism of the rare events, important quantities such as the kinetic rate constant require an additional scaling factor that quantifies how frequent transition paths are relative to nontransition paths. Therefore, one has to relate the constrained TPS ensemble with the unconstrained path ensemble, as given by an infinitely long ergodic unbiased MD trajectory.10 This unconstrained total (or complete) path ensemble comprises the set of path ensembles starting from each stable state, consisting of all (properly weighted) paths that leave that state and either return to it or go on to any other stable state. Even when restricting the path ensemble to start in a particular state A, straightforward path sampling of an otherwise unconstrained ensemble is naturally very inefficient, as the important transitions to other states are exceedingly rare. However, one can construct the total path ensemble (for each state) by a staging procedure. In such a procedure one can constrain the paths to reach further and further out of the state (while of course still starting in the stable state). This constraining can be done using the transition interface sampling method (TIS),55 an extension of TPS that is explained below. Reweighting of the resulting paths then yields (an estimate of) the total path ensemble.56
Transition interface sampling (TIS)55 provides a more efficient evaluation of the rates compared to the original TPS rate constant calculation57 by sampling each constrained interface ensemble. TIS defines a set of N nonintersecting hypersurfaces (the ’interfaces’) around the stable state, parametrized by a collective variable λ, and foliating, in principle, the entire configuration space (or even phase phase55). The rate constant from A to B is expressed as
| 4 |
where ϕ0A denotes the flux out of A through λ0, and PA(λB|λ0) is the crossing probability, the probability that a trajectory originating from A reaches interface λB before returning to A, provided that the path already crosses λ0 at least once. This probability is generally low, as the transition is a rare event, but can be computed through the product of all crossing probabilities for the individual interfaces, as indicated in eq 4, with λN ≡ λB.55 Interfaces should be optimally placed such that each crossing probability in the product is roughly PA(λi+1|λi) ≈ 0.2.58 The total number of required interfaces is thus of the order N ≈ |log5P(λB|λA)|. As an example, for a barrier of 30 kBT, this roughly translates into N = 30/ln(5) ≈ 18 interfaces. The staging approach thus avoids the problem of the exponentially low rate in a way analogous to umbrella sampling.59 An iterative approach to optimize the location of the interfaces, based on restrictions such as targeting a successive crossing probability of 0.2, has been developed.60
Note that the product is not simply a product of Markovian transition probabilities, as for each interface the entire trajectory starting from A is taken into account. Evaluation of the crossing probabilities requires sampling the path ensemble for each interface with the constraint that the path needs to cross that interface. While trajectories could in principle be stopped when they reach the next interface, it turns out to be beneficial to continue the trajectory integration until a stable state (A or B) has been reached. This also allows the application of the so-called reversal move of A-to-A trajectories, where the time direction of the path is reversed, which can be done with no additional cost, but assists in decorrelating paths. The flux ϕ0A can be easily obtained using straightforward MD inside state A.55,61
The reverse rate can be computed by repeating the TIS simulation from state B: define a set of interfaces, sample the interface ensembles, and compute the crossing probability PB(λB|λA) .
Similar to TPS, the TIS algorithm can be extended to multiple states.36 To estimate kinetic rates between multiple states, each state I gets its own set of interfaces λiI, and the rate constant from state I to state J is given by
| 5 |
where ϕ0I is again the flux from I through λ0I. The second factor is the crossing probability to an outermost interface m, which is typically very small and expressed as P(λmI|λ0I) = ∏i=0m–1PI(λ(i+1)I|λiI). The last factor in eq 5 is the conditional probability that a trajectory crossing the outermost interface also reaches state J. The location of the outermost interfaces should be chosen such that the probability to escape from A is sufficiently large. Note that while interfaces belonging to state I constitute a foliation of nonoverlapping hypersurfaces, they are completely independent from the interfaces of state J and in fact are allowed to overlap.62,63
We introduce the concept of a transition network(64) that, in its simplest form, represents the ensembles of paths connecting pairs of defined states. For each state in the transition network (multiple state) TIS results in a set of interface path ensembles and a straightforward MD ensemble of that stable state, which can be combined to yield the total path ensemble by reweighting. Repeating this for all states, and (again) properly reweighting,56,65,66 leads to an accurate description of the kinetic rate matrix, the free energy landscape, the mechanisms, and reaction coordinates of all transitions between the metastable states. This data can be further analyzed using theory of Markovian stochastic processes, e.g., the Chapman-Kolgomorov equation67 or transition path theory.68
2.4. Considerations in Transition Path Sampling
The reader should be aware of a number of challenges they may encounter in setting up transition path sampling based simulations. While an exhaustive list is beyond the scope of this paper, we list some important issues below. (See also ref (69).)
2.4.1. Definition of the States
Transition path sampling requires knowledge of the stable states. Usually the stable states are easier to characterize and identify than the transition region. Analyzing straightforward MD can provide information on how to describe the states in terms of (several) collective variables. Such heuristic approaches have been used in previous applications.50,70,71 In addition, tools such as clustering can be used to define the states.63 Ideally, one would like to use automatic state recognition, and recently attempts have been made in that direction.49 In OPS we assume that the reader has an idea about how to capture stable states by defining a range in (several) collective variables. OPS provides the user with tools to facilitate identification of these ranges and hence definition of the states. The choice of the stable state definitions still requires careful attention, as an erroneous definition can easily lead to improper or failed path sampling. For a detailed discussion on the stable state definitions, see refs (23, 48, and 69).
2.4.2. Intermediate Metastable States
Even if the process of interest exhibits two-state kinetics, suggesting only two highly stable states are involved, it is possible that the presence of one or more intermediate states with lifetimes short on the overall time scale but long on the molecular time scale will cause reactive trajectories connecting the stable states to be quite long. A solution to this problem is to identify the intermediate state(s), define their core sets, and to use multistate transition interface sampling (MSTIS).36,62 Alternatively, one can choose to simply sample long pathways,72 which can still be quite fast given the speed of modern GPU-accelerated molecular simulation engines like OpenMM.44,45
2.4.3. Ergodicity of Path Space
While the TPS and TIS algorithms are “exact” in the sense that they should lead to the asymptotically unbiased estimates of path averages in the limit of infinite sampling, they suffer from the same problems that all Monte Carlo methods encounter, the problem of slowly mixing Markov chains, which in severe cases may result in broken ergodicity for practical computer times. As TIS samples path space by perturbing an existing path to generate new proposals, decorrelation from the initial path to generate many effectively uncorrelated paths is essential for producing useful unbiased estimates. However, since there might be (possibly high) barriers in path space orthogonal to the interfaces between different allowed reaction channels, this is far from guaranteed. One way of solving this problem is by using replica exchange among path ensembles in transition interface sampling (RETIS).73,74
2.5. Replica Exchange Transition Interface Sampling (RETIS)
The RETIS algorithm simultaneously samples all TIS ensembles while allowing for swapping of paths between interface ensembles when possible.73,74 A transition path that follows one particular mechanism can then slowly morph into a completely different transition path by exchanging it back and forth among all interfaces to state B. Including an exchange between pathways belonging to different states further enhances sampling convergence.74
Further sampling improvement can be achieved by including van Erp’s minus interface ensemble.73,74 The minus interface move exchanges a trajectory in the first interface ensemble with a trajectory exploring the stable state (the minus interface ensemble). This serves two aims: (1) to decorrelate pathways in the first interface which tend to be short and (2) to provide a direct estimate for the flux out of the stable state.73−75 OPS includes an implementation of multiple state RETIS, which we will refer to as MSTIS.
The default MSTIS approach employs a single set of interfaces for each state, based on one order parameter. Multiple interface set TIS (MISTIS), also implemented in OPS, generalizes this approach to include multiple interface sets for states or transitions.76 Although TIS is much less sensitive to the choice of order parameter than other enhanced sampling methods,58 in practice, the efficiency is affected by this choice. Using different order parameters to describe (sets of) interfaces for different transitions and/or states, with the help of replica exchange, might alleviate such efficiency problems.
A drawback of the (multiple state) RETIS approach
is that it requires one replica to be simulated for each interface;
for systems with multiple stable cores and associated interface sets
defined, this can quickly get out of hand, as each core might possess 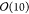 interfaces. This large number of interface ensembles prevents efficient
implementation of the method for systems more complex than toy models.
A parallel implementation of all interfaces might seem a simple solution
but will be complicated by the fact that the duration of the paths
in the different interface ensembles varies wildly. Single replica
TIS (SRTIS), based on the method of expanded ensembles,77 can alleviate this problem.66 Instead of exchanging paths between interface
ensembles, only one replica is sampled, and transitions between ensembles
are proposed. To avoid the replica remaining close to the stable state
interface ensemble, one needs a biasing function that pushes the replica
to higher interfaces. Selecting the (unknown) crossing probability
as the biasing function would ensure equal sampling
of all interfaces, which is close to optimal. While the crossing probabilities
are initially unknown, an iterative procedure can be used to adapt
the bias during the simulation, as each interface ensemble naturally
gives an estimate for the crossing probability.66,78 SRTIS can easily be extended to include multiple states66 or utilize multiple independent walkers.63,79
interfaces. This large number of interface ensembles prevents efficient
implementation of the method for systems more complex than toy models.
A parallel implementation of all interfaces might seem a simple solution
but will be complicated by the fact that the duration of the paths
in the different interface ensembles varies wildly. Single replica
TIS (SRTIS), based on the method of expanded ensembles,77 can alleviate this problem.66 Instead of exchanging paths between interface
ensembles, only one replica is sampled, and transitions between ensembles
are proposed. To avoid the replica remaining close to the stable state
interface ensemble, one needs a biasing function that pushes the replica
to higher interfaces. Selecting the (unknown) crossing probability
as the biasing function would ensure equal sampling
of all interfaces, which is close to optimal. While the crossing probabilities
are initially unknown, an iterative procedure can be used to adapt
the bias during the simulation, as each interface ensemble naturally
gives an estimate for the crossing probability.66,78 SRTIS can easily be extended to include multiple states66 or utilize multiple independent walkers.63,79
3. Novel Concepts in OPS
OpenPathSampling contains many new approaches to implementing transition path sampling simulations, but there are two points that we would particularly like to draw attention to: (1) the use of volume-based interface definitions in TIS and (2) the general treatment of path ensembles.
3.1. Volume-Based Interface Definitions
In the original TIS algorithm and most path sampling algorithms based on TIS, interfaces are defined as hypersurfaces in configuration space. To belong to the interface ensemble, a path needs to cross this interface, meaning that at a certain time it is at one side of the interface, while a time step later it is on the other side. We consider a novel interface definition in OPS which relies on hypervolumes in configuration or phase space rather than hypersurfaces. We use the convention that the initial state is inside the hypervolume. In this definition, a path belongs to an interface ensemble defined by a hypervolume if it starts in the initial state, leaves the hypervolume at some point along the path, and terminates in any stable state. The advantage of using volumes instead of surfaces is that set logic (e.g., a union or intersection) can be applied to generate new volume definitions from existing volumes. For a more extensive discussion see the companion paper.47
3.2. General Treatment of Ensembles
One of the novel approaches in OPS is the generalization of path ensembles. Previously, each path ensemble had to be treated with a specialized code. However, as the number of path ensembles types has grown, the need to treat them in a general fashion arose. In this paper, we make use of a range of path ensembles, including the following, which are illustrated in Figure 1:
Flexible length TPS ensemble (Figure 1a): The standard TPS ensemble is a path ensemble between two states. Only the initial and final frames are inside the states.
Fixed length TPS ensemble (Figure 1b): As with the flexible length TPS ensemble, the initial and final frames must be in the initial and final states. However, the fixed length ensemble has a predefined length and also allows frames other than the first and final to be in the state.
TIS ensemble (Figure 1c): The elementary path ensembles in TIS have an interface associated with them. They must begin in a given state, exit the interface hypervolume, and end in any stable state.
Minus (interface) ensemble (Figure 1d): Paths in the minus ensemble can be described in terms of three segments: the first and last segments are similar to TIS ensemble paths. They start in the state, exit the interface hypervolume, and return to the state (where TIS ensemble paths can go to another state, these segments cannot). These two segments are connected by another segment that never exits the interface. Note that this implementation of the minus interface ensemble is based on ref (76), as opposed to the original minus interface ensemble introduced in ref (73). The two versions differ slightly (with the original being subtrajectories of the version used here). Both versions serve the purpose of enhancing decorrelation by running dynamics inside the state, but the version used here is also useful for replica exchange in multiple interface set TIS.
Figure 1.
Common path ensembles in TPS and TIS with representative trajectories. Shaded areas represent states, and dashed lines represent interface boundaries.
All of these common ensembles can be generalized for more complicated reaction networks. The TPS ensembles become multiple state TPS ensembles if they allow any state to be the initial or final state, as long as the initial and final states are different. The TIS ensemble becomes a multiple state TIS ensemble by allowing any state as the final state. The minus ensemble becomes the multiple interface set minus ensemble by taking its interface as the union of innermost interfaces.
This list of ensembles is by no means exhaustive. OPS allows complicated ensembles to be built from simpler ones. It generalizes both the procedure for testing whether a given trajectory satisfies the ensemble and the procedure for generating new trajectories. This allows one to easily construct other ensembles, such as the fixed-length ensemble where trajectories start in initial state A and must visit (but necessarily end in) final state B, as described in ref (57). Details of the implementation of this generalization, as well as novel approaches to analysis that this implementation enables, will be discussed in the companion paper.47
4. The Ingredients of OPS
Before explaining the OpenPathSampling framework and workflow in more detail, we first explain the frequently used basic objects of OPS that are related to path sampling concepts described in the previous sections. The objects in OPS are divided into two main categories: (1) data objects that contain the sampled paths and information about the sampling process and (2) simulation objects that perform the sampling. All objects generated in OPS, both data and simulation objects, are stored in a single Storage file and can be accessed from it. For example, the MCStep objects saved during the simulation can be accessed with storage.steps once a file is loaded into storage.
4.1. Data Objects
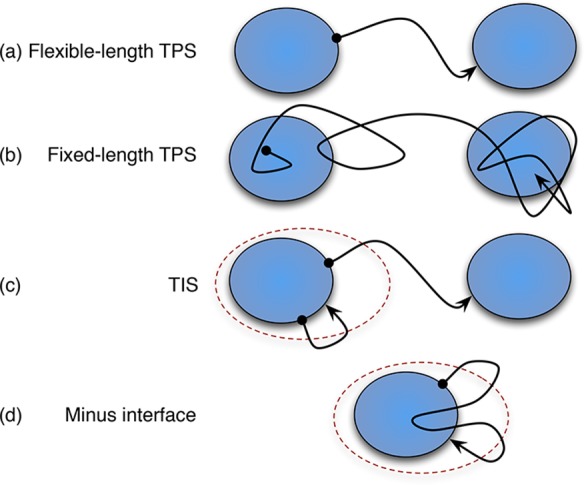
The main data objects of OPS fit into a hierarchy as shown in Figure 2. The data structure can be divided into what is being sampled (i.e., which trajectories from which ensembles) and how it is being sampled (i.e., the nature of the path moves performed.) All of this is unified in the MCStep object, which describes a step of the path sampling simulation and which has two important attributes: a SampleSet object called active, which records the state of all replicas in the simulation at the end of a given simulation step (the “what”); and a MoveChange object called change, which describes what happened during the simulation step (the “how”). Below we describe these attributes in more detail.
Figure 2.

Hierarchical data structure of the MCStep data object. The attribute names are shown, and the type is provided in parentheses.
4.1.1. Data Structures for What Is Being Sampled
Snapshots, sometimes called “frames” or “time slices,” are at the core of any simulation technique. They describe the state of the physical system at a point in time and, in molecular dynamics, typically consist of coordinates, velocities, and periodic cell vectors. The Snapshot object in OPS can be easily extended to carry additional data, such as wave function information or variables from an extended phase space.
A Trajectory, also called a “path,” is essentially a list of Snapshots in temporal order. In addition, it provides several convenience methods, for example, to identify which Snapshots are shared by two trajectories.
The Sample object is a data structure that links a Trajectory with the Ensemble object (described in Section 4.2) from which it was sampled, and with an integer replica ID. The Sample is needed because methods such as TIS, and especially RETIS, sample multiple ensembles simultaneously. Correct analysis requires knowing the ensemble from which the Trajectory was sampled.
Since methods like TIS have several active Samples during a path simulation step, OPS collects them into one SampleSet. The SampleSet contains a list of Samples and also has convenience methods to access a sample either by replica ID or by ensemble, using the same syntax as a Python dict.
4.1.2. Data Structures for How the Sampling Occurs
The MoveChange contains a record of what happened during the simulation step. Because the simulation move itself generally consists of several nested decisions (type of move, which ensemble to sample, etc.), the MoveChange object can contain subchanges, which record this entire sequence of decisions. In addition, it includes a pointer to its PathMover (described in section 4.2), a list of the trial Samples generated during the step, and a boolean as to whether the trial move was accepted.
The MoveChange also contains a Details object, which is essentially a dictionary to store additional metadata about a move. This metadata will vary depending on the type of move. For example, with a shooting move, it would include the shooting point. In principle, all the additional information that might be of interest for analysis should be stored in the Details.
4.2. Simulation Objects
The simulation objects actually perform the simulation and can be assembled in different ways to perform many types of simulations. In addition, simulation objects in OPS can be stored. This facilitates restarts to continue a simulation and enables reuse for other types of simulations, e.g., using the same state definitions for committor analysis as well as path sampling. The PathSimulator class contains all the information to run the simulation. The PathSampling subclass of PathSimulator is used for path sampling simulations. Figure 3 shows the relation between path sampling concepts and the associated objects in OPS. Each of the components is described in more detail below.
A DynamicsEngine performs the actual molecular dynamics: that is, it generates a trajectory from an initial frame. OPS has built-in support for an internal toy dynamics engine (primarily intended for 2D models) and for OpenMM.80 Support for Gromacs81,82 and LAMMPS83 will be added in future releases.
A CollectiveVariable is a function of a Snapshot and in many cases is just a function of the coordinates. It is also sometimes called the “order parameter”, “progress variable”, “reaction coordinate”, or “feature”. In line with the rare event terminology (e.g., refs (84 and 85)) the neutral term CV (for Collective Variable) can both be used to define interfaces and states (via Volumes), as well as to construct order parameters. The CollectiveVariable in OPS is a wrapper class around an arbitrary function. For example, the CoordinateFunctionCV will wrap any user-defined function that only depends on the snapshot’s coordinates. In addition, specific classes enable the use of functions from other packages, e.g, the MDTrajFunctionCV provides a wrapper class for function from the MDTraj86 analysis package. Other wrappers exist for MSMBuilder87,88 and PyEMMA.89
The Volume class in OPS represents a hypervolume in phase space. This can be used to define a state, also called a “core set.” In addition, interfaces are also defined by volumes, rather than by hypersurfaces as in the traditional TIS literature (see section 3.1). A volume is typically defined based on allowed ranges of CVs; in OPS the CVDefinedVolume object creates such a volume based on a minimum and maximum value of the CV.
-
The Ensemble class in OPS defines the paths that are allowed within a given path ensemble. It is more accurately thought of as the indicator function for a restricted path ensemble (cf. eq 3). The indicator function alone reduces the set of all possible paths to the trajectories with nonzero probability in the path ensemble, but with no distinction in their relative statistical probabilities. Sampling according to the correct statistical weights is the role of the PathMover, described below.
In addition to the indicator function, Ensemble objects contain two methods, can_append and can_prepend, which check whether a given trajectory could be appended or prepended into a trajectory in the ensemble. This allows us to create a rich toolkit to create custom ensembles. For instance, a path that connects states A and B is defined as a trajectory that follows the sequence of events that it is first in A, then not in (A ∪ B), and finally in B. In OPS, this sequence is described with a SequentialEnsemble object, which provides a flexible way to implement arbitrarily complex path ensembles (see ref (47)).
Despite this powerful toolkit and the fundamental role of the Ensemble, under most circumstances the user does not need to instantiate Ensemble objects. Instead, they are automatically created by the Transition and Network objects, described below.
Figure 3.
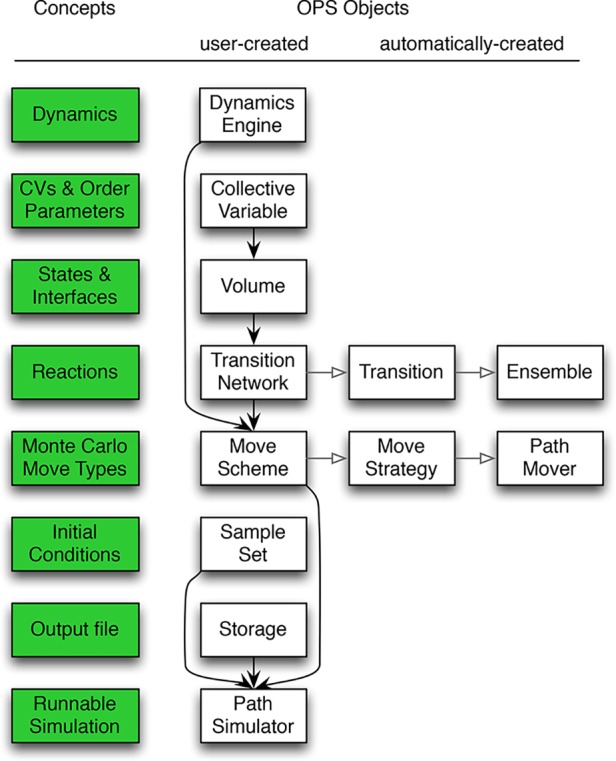
Schematic representation of the connection between the path sampling concepts and their related OPS objects. The concepts are listed in the leftmost column, shaded green. The next column shows the objects which must be created by a user to run a simulation. The filled arrows indicate when one object is the input to create another object. The objects in the right two columns are automatically created. The open arrows point from an object to the objects it automatically creates. In this way a TransitionNetwork creates a Transition object that creates in turn Ensemble objects.
A Transition object contains all information for studying a single-direction reaction connecting a specific initial state and a specific final state, such as A → B, and serves as an organizational structure for systems with many states, where the number of possible transitions grows as N(N – 1) for N states. For TPS, this object consists just of one ensemble, while for TIS it usually consists of several interface path ensembles, as well as the minus ensemble (used in RETIS). Note that A → B and B → A are two different transitions, each with their own sets of ensembles, thus requiring two Transition objects. A single rate k would be associated with each Transition and kA→B ≠ kB→A.
A TransitionNetwork object (which we will frequently refer to as simply the “network”) consists of a set of Transitions. Since OPS is designed to handle the systems with many states, the network gathers all the transitions into one object. It is a network in the graph theory sense: states are nodes; reactions (transitions) are directed edges. Subclasses of TransitionNetwork, such as TPSNetwork or MSTISNetwork, deal with specific approaches to sample the network. All the ensembles to be sampled are contained in the TransitionNetwork. Section 5.4 provides more details.
PathMovers, or “movers,” perform Monte Carlo moves in path space, such as shooting, reversal, minus, or replica exchange. They are organized into a move decision tree, which selects the specific move to use (the move type and the ensemble). An example of a move decision tree is given in Figure 6. The Ensemble associated with a given mover determines whether a trajectory is in the path harvest for that mover, but the mover itself can reject paths such that the correct statistics for the path ensemble are obeyed (i.e., to preserve detailed balance.) PathMovers are discussed in more detail in section 5.5.1.
The MoveScheme contains and builds the move decision tree, which in turn contains all the PathMovers available to a simulation. The MoveScheme is created by associating several MoveStrategy objects with it. Each MoveStrategy builds several related PathMovers. For example, a NearestNeighborReplicaExchangeStrategy will create a ReplicaExchangeMover for each pair of nearest-neighbor ensembles in each Transition from the TransitionNetwork. Options for creating the strategy can control which ensembles are used, and whether this adds to or replaces existing strategies. This provides the user a great deal of flexibility when customizing the move decision tree using the MoveScheme and MoveStrategy objects. For simplicity, OPS provides a DefaultScheme with reasonable defaults for TIS (one-way shooting, nearest-neighbor replica exchange, path reversal, and minus move) and a OneWayShootingMoveScheme with a reasonable default for TPS. The MoveScheme and MoveStrategy objects will be discussed in more detail in section 5.5.2.
Figure 6.
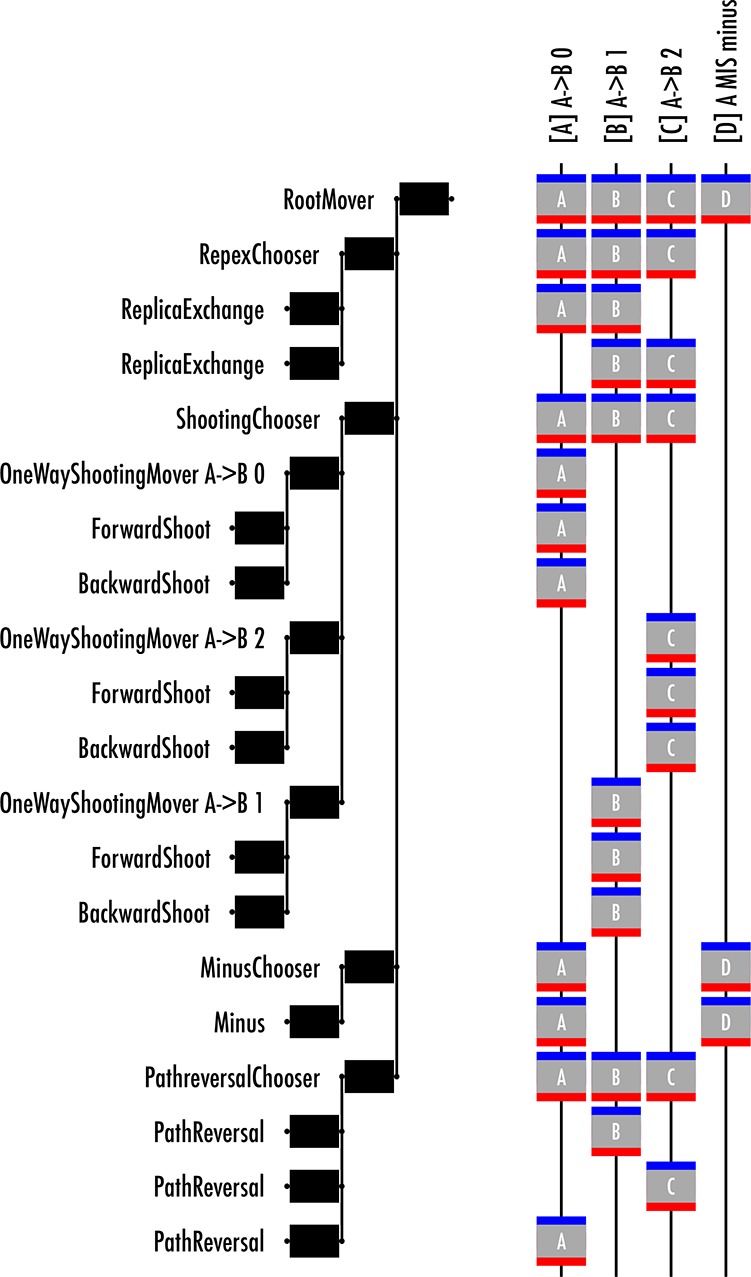
Schematic representation of the decision tree as constructed by the MoveScheme object. Shown is an example for RETIS. The MoveScheme points to the root of this tree (left). The branches are the different move levels. The first level is the decision about what type of move: shooting, replica, reversal. The next level is the decision about what ensemble needs to be moved. For the shooting, the next level is about which direction the shot is. For other moves the choice is slightly different. The right part of the picture shows which ensembles are affected. Each vertical line denotes an ensemble. At the root of the tree each ensemble can be chosen. Going down the tree, the ensembles affected reduce in number. The letters are arbitrary labels for each ensemble. The gray box around each letter shows the input (red) and the output (blue). This sort of schematic can be generated using the paths.visualize.MoveTreeBuilder object.
4.3. Layers of Abstraction in OPS
OPS is structured as a set of Python modules, organized according to major classes. As a library, users can interact with different levels of abstraction. Figure 3 and the previous section have already indicated how TransitionNetwork objects act as a more user-friendly layer for Ensembles and how MoveScheme and MoveStrategy objects create a simpler layer for working with PathMovers, but these lower-level objects can also be accessed by users, as will be discussed in the companion paper.47
Objects like Ensembles and PathMovers are specific to path sampling and related topics. These are built on even more generic objects, which might be useful beyond the scope of path sampling. Many PathMovers use the generic DynamicsEngine wrapper to run the molecular dynamics. Volumes are defined in terms of CollectiveVariables, which have many uses beyond path sampling. The specific OPS Storage class is based on the more generic NetCDFPlus subpackage, built for OPS. This is shown in Figure 4, where lower levels are more generic, while higher levels are more specific to path sampling. Higher levels also tend to be more user-friendly.
Figure 4.
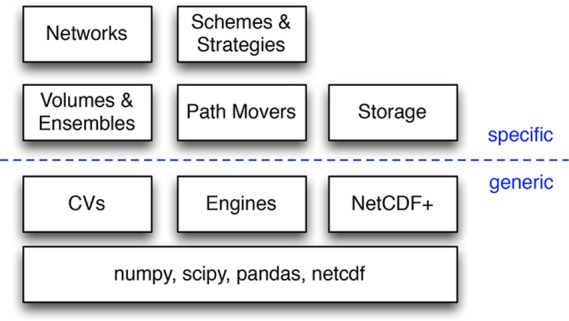
The modules of OPS can be separated into different layers of abstraction. The layers can be considered as both increasing specificity of purpose (from bottom to top) as well as increasing ease of use or ease of implementation of new subclasses. Underneath the OPS modules are the external packages upon which OPS is built. Above that are OPS modules which have potential for use outside the context of reaction dynamics and path sampling. Above that the code becomes more specific to path sampling and to the OpenPathSampling project. At the top layer, some of the more powerful OPS libraries are abstracted into a more simple user interface. The level of user that is likely to spend significant time working at each level is indicated on the left.
5. OPS Workflow
In this section we give an overview of the process for setting up and running a path sampling simulation with OpenPathSampling, including some general discussion on practical aspects of path sampling simulations. In general, every path sampling simulation can be split into the following steps:
-
1.
Setting up the molecular dynamics engine
-
2.
Defining states and interfaces
-
3.
Setting up the transition network and move scheme
-
4.
Obtaining initial pathways
-
5.
Equilibration and running the simulation
-
6.
Analyzing the results
In practice, the human effort in path sampling using OPS will focus on defining the states and interfaces, obtaining trajectories for initial conditions, and analyzing the simulation results. OPS aims to facilitate those steps and automate what it can, such as setting up the TransitionNetworks and MoveSchemes and running the simulation. In addition, OPS provides many tools for the analysis of the simulation results.
In the first setup steps (1–3), the user chooses the dynamics of interest and decides on the DynamicsEngine, the CollectiveVariables, defines the Volumes for the states and interfaces, as well as the topology of the reaction network, and decides on the sampling MoveScheme. Figure 3 renders these steps from the top down. The selection of relevant collective variables and their use to define state volumes are of critical importance. However, they are also dependent on the system being studied. We assume that a user is already familiar enough with the system to make reasonable choices for these.
The specific definition of the transition network is handled in OPS by a TransitionNetwork object, which automates the creation of Transitions and Ensembles for common variants of TPS (including multiple state) and TIS (including multiple state and multiple interface set variants). These objects take as input the Volume based states and interfaces definitions.
The MoveScheme is created based on the TransitionNetwork and a DynamicsEngine. It can be customized by adding additional MoveStrategy objects, but OPS provides default schemes for convenience. The MoveScheme and its accompanying MoveStrategy objects create all the PathMovers. Each PathMover knows on which ensemble(s) it acts and is organized into a total move decision tree.
The final initialization step is to create an initial SampleSet by loading valid pre-existing initial trajectories into each of the ensembles. See Appendix A for several approaches to obtain initial conditions.
The simulation is performed by a PathSimulator object. Path sampling simulations use a subclass called PathSampling. Other subclasses of the PathSimulator include CommittorSimulation for calculating committors and DirectSimulation for calculating rates and fluxes via direct MD. All PathSimulator objects take a Storage object as input, to determine where to save data. In addition, PathSampling takes the MoveScheme and the initial SampleSet as input.
Analysis is done independently from the sampling and requires only the Storage and TransitionNetwork for the computing observables and additionally the MoveScheme for the sampling statistics. Everything that is needed for analysis is stored in the output file, including the TransitionNetwork and MoveScheme.
In the next subsections we discuss these six steps in more detail.
5.1. Step 1: Setting up the Molecular Dynamics
Of course, before embarking on a path sampling simulation, one must decide on the system to simulate and the nature of the underlying dynamics (i.e., the thermodynamic ensemble represented, the integrator used for the dynamics, the force field to define interactions, etc.). OPS is designed to wrap around other engines to take advantage of the flexibility already built into other software. Currently, OPS supports OpenMM80 as well as its own internal dynamics engine intended mostly for 2D toy models.
The basic Engine takes general OPS specific options defining, e.g., handling of failing simulations, maximal trajectory length, etc., as well as dimensions used in snapshots that the engine generates (e.g., number of atoms). Each specific engine also carries information necessary for it to set up a simulation. In case of OpenMM this includes a description of the Integrator, the System object (force field, etc.), the system's Topology, and some OpenMM specific options (e.g., hardware platform and numerical precision).
5.2. Step 2: Defining States and Interfaces
The ensembles used in path sampling methods require definitions of (meta)stable states and, in the case of transition interface sampling, interfaces connecting these states. OPS implements both states and interfaces in terms of Volume objects.
The main types of volume objects are the CVDefinedVolume and its periodic version, PeriodicCVDefinedVolume. Each of these defines a volume in phase space based on some CollectiveVariable. This could include such quantities as atom–atom distances, dihedral angles, RMSD from a given reference frame, number of contacts, etc. The user must first define a CollectiveVariable object, either as a wrapper around functions from other software packages (some examples below use MDTrajFunctionCV, which wraps MDTraj analysis function) or around a user-written function (other examples will show the use of the more general CoordinateFunctionCV).
Using the CollectiveVariable we have a clear separation between the full simulation data and what we consider relevant for state definitions and later analysis. This separation allows us to later run analysis without the need to load a single frame and to store a reduced set without the actual coordinates.
To define a volume, the user must also specify minimum and maximum values for the CV. The volumes can then be created with, e.g., CVDefinedVolume(cv, minimum, maximum), which defines a frame as being inside the volume if minimum ≤ cv(frame) < maximum. Volumes can be combined using the same set operation as Python sets: & (intersection), | (union), - (relative complement), ^ (symmetric difference), and ∼ (complement). Volume combinations of the same collective variable are automatically simplified when they can be recognized [e.g., (0 ≤ x < 5)&(3 ≤ x < 8) becomes 3 ≤ x < 5]. The ability to arbitrarily combine volumes allows one to define arbitrary states, e.g., “this hydrogen bond is formed and this dihedral is near a certain value.” This provides OPS with powerful flexibility.
5.3. Step 3: Setting up the Transition Network and Move scheme
The transition network (path ensembles) and the move scheme (Monte Carlo moves) can be thought of as what to sample and how to sample, respectively.
For complex TIS simulations, the number of path ensembles to be sampled can grow into the hundreds. TransitionNetwork objects efficiently create those ensembles according to standard ways of organizing and facilitate later analysis. The examples in Section 6 will demonstrate the four main kinds of network objects: TPSNetwork for flexible-length TPS, FixedLengthTPSNetwork for fixed-length TPS, MSTISNetwork for multiple-state TIS, and MISTISNetwork for TIS and multiple interface set TIS.
The MoveScheme creates and organizes the possible Monte Carlo moves, as appropriate for a given transition network. As with the transition networks, the MoveScheme object also facilitates later analysis. The examples in section 6 will go over the simplest default move schemes (OneWayShootingMoveScheme for TPS; DefaultScheme for TIS). However, the move scheme is very customizable, as will be elaborated on in the companion paper.47
As both the TransitionNetwork and MoveScheme are crucial in OPS, we devote extra attention to these objects below.
5.4. Step 3a: Transition Networks
The TransitionNetwork object contains all the path ensembles to be sampled for the reaction network of interest. To simplify analysis, most ensembles are grouped into Transition objects, which describe a single transition within the network. There are also special ensembles (e.g., ensembles associated with multiple state interfaces or with minus interfaces) which may not be specific to a single transition and are only associated with the network as a whole. In general, the user only needs to create the TransitionNetwork object, which will automatically create the relevant Transitions and Ensembles. The simplest transition network contains a single transition, the one-way A → B. A bidirectional network A ↔ B is thus characterized by two transitions, each associated with its own set of ensembles.
Each network involves two groupings of transitions: the sampling transitions and the physical transitions. MSTIS shows a clear example of the distinction between these: while sampling, the transitions studied are A → (B ∪ C), B → (A ∪ C), and C → (A ∪ B) . However, in analysis we obtain the rates for all the individual physical transitions A → B, A → C, B → A, B → C, C → A, and C → B. For a network with N states, up to N(N – 1) unique physical transitions are possible. The sampling transitions are found in a list, accessed as network.sampling_transitions, and the physical transitions are in a dict, with state pairs (initial, final) as keys and the associated Transition object as value.
The Transition and the TransitionNetwork objects depend on the type of simulation that is intended, just as the Ensemble does. Table 1 shows how different input parameters create different numbers of physical and sampling transitions for the built-in network objects in OPS. The network for a TPS simulation is made with either the TPSNetwork or FixedLengthTPSNetwork objects. The TPSNetwork is initialized with a list of initial states and a list of final states; all pairs of (nonself) transitions are generated internally. A TPSNetwork has only one sampling TPSTransition, which has only one ensemble. However, for analysis the network includes ensembles for every possible physical transition. If A is the only initial state and B is the only final state, then A → B is the only physical transition. When multiple initial and final states are given, then all the nonself physical transitions are allowed: in the second line of Table 1, that would be A → B, A → C, and B → C. When all N states are given as both initial and final states, all N(N – 1) nonself transitions are included. The FixedLengthTPSNetwork is exactly like the TPSNetwork, except that its initialization also requires the length of the path (in snapshots).
Table 1. Predefined Network Types and the Number of (Physical) Transitions, Sampling Transitions, and Sampling Ensembles Arising from Different Initialization Parametersa.
| network and initialization | transitions | sampling transitions | sampling ensembles |
|---|---|---|---|
| TPSNetwork: | |||
| A, B | 1 | 1 | 1 |
| [A, B], [B, C] | 3 | 1 | 1 |
| [A, B,..., N], [A, B,..., N] | N(N – 1) | 1 | 1 |
| MSTISNetwork: | |||
| [(A, mA), (B, mB)] | 2 | 2 | mA + mB |
| [(A, mA), (B, mB),..., (N, mN)] | N(N – 1) | N | ∑ImI |
| MISTISNetwork: | |||
| [(A, mAB, B)] | 1 | 1 | mAB |
| [(A, mAB, B) (A, mAC, C), ..., (A, mAN, N)] | N–1 | N–1 | ∑J≠AmAJ |
| [(A, mAB, B), ..., (A, mAN, N), ... | |||
| ..., (N, mNA, A)] | N(N – 1) | N(N – 1) | ∑I ∑J≠ImIJ |
Volumes are represented with capital letters (e.g., A or B), and interface sets are represented as mA for the interfaces leaving A in MSTIS or mAB for interfaces leaving A toward B in MISTIS. The number of interfaces in an interface set is given by mA or mAB, respectively. The total number of states is assumed to be N (with the final state represented by N). Under each network type, different potential initialization arguments are given. TPSNetwork can be initialized with two states or two lists of states (with lists in square brackets). MSTISNetwork and MISTISNetwork are initialized with lists of tuples, with square brackets indicating the list and parentheses indicating the tuple.
Within standard TPS approaches, there is a one-to-one correspondence of (sampling) ensemble to network. That makes these networks relatively simple. The situation becomes more complicated with TIS. In TIS, each transition involves a set of interface ensembles. In addition, there are the minus ensembles, which (in MISTIS) can be associated with more than one transition, and there are the multiple state outer ensembles (in MSTIS and MISTIS), which are also associated with more than one transition.
The MSTISNetwork and MISTISNetwork are initialized with specific data about the transitions. In MSTIS, this includes the initial states and the interface sets associated with them, provided as a list of tuples. The MSTISNetwork creates sampling ensembles that allow paths that end in any state and always samples all transitions between all states. As shown in Table 1, it therefore always has N(N – 1) physical transitions and N sampling transitions for N input states. The number of ensembles depends on the number of ensembles per interface set but scales linearly with the number of states. (See Figure 5 for a visualization of an example transition network.)
Figure 5.
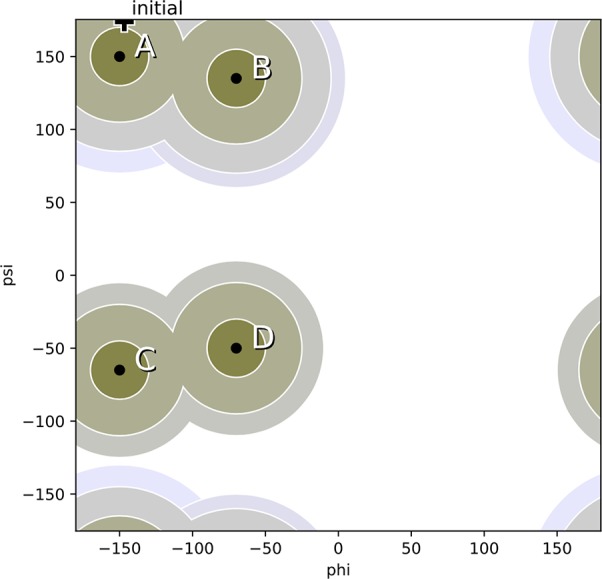
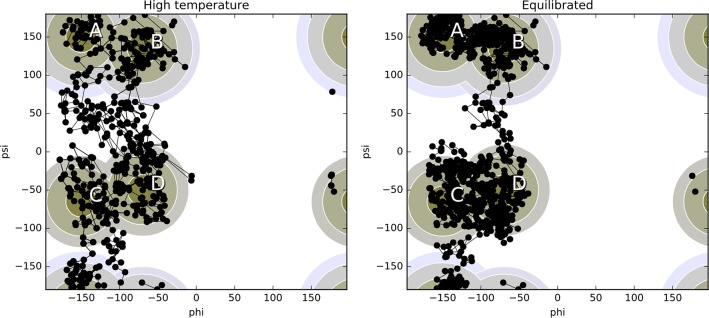
Example of a transition network used in the MSTIS alanine dipeptide examples (see Section 6). Multiple states A–D are defined according to the dihedral angles ψ and ϕ. The core sets for A–D are defined as being within 10 degrees of the core center (indicated by black dot). Each state has its own set of interfaces using the geometric distance in ψ – ϕ space to the core center, indicated by shaded circles. The MSTISNetwork object creates for each state the collection of path ensembles for each interface plus the minus interface. In addition there is a multiple state union interface for the outermost interfaces. The plus marks the location of the initial conformation used in the example.
In addition to the initial states and the interface sets, MISTISNetwork also requires the ending state for each transition, provided as a third item in each tuple. The number of physical transitions for the MISTISNetwork is always equal to the number of sampling transitions, and the number of ensembles grows with the number of sampling transitions. This means that, in the worst case of sampling all possible transitions, the number of ensembles scales quadratically with the number of states. However, MISTIS has the advantage that it allows one to select only specific transitions of interest or to use different interface sets for transitions beginning in the same initial state, allowing each transition to be sampled more efficiently.
Both of these TIS networks automatically create appropriate minus interface ensembles, and they can optionally take an MSOuterTISInterface for the multiple state (MS) outer interface ensemble. The MS-outer ensemble is the union of several TIS ensembles starting from different initial states.36,76 Whereas a TIS ensemble only allows trajectories that begin in a single given initial state, the MS-outer ensemble allows trajectories that begin in any of multiple initial states. This ensemble, combined with replica exchange, facilitates decorrelation of trajectories.
MSTIS and MISTIS are two different ways to create ensembles to study a reaction network. The MSTIS approach is more efficient when all transitions from the same state are described by the same order parameter. The MISTIS approach allows more flexibility in sampling, by allowing different transitions from an initial state to use different order parameters or selection of specific transitions of interest.
The simplest network, A → B, can be studied using the MISTISNetwork object. The bidirectional A ↔ B network can be studied using either a MISTISNetwork or a MSTISNetwork: the ensembles which are created would be indistinguishable.
These networks are not exhaustive, and other possibilities might be implemented by users. For example, it might be interesting to sample transitions from one state to all other states in an MSTIS simulation. This cannot be done with the built-in MSTISNetwork, but it would be relatively straightforward to create another subclass of TransitionNetwork that allows this.
5.5. Step 3b: The Monte Carlo Move Scheme
5.5.1. Path Movers
In OPS, each PathMover instance is connected to specific ensembles. For example, there is a separate shooting mover for each ensemble and a separate replica exchange mover for each pair of ensembles that are allowed to swap in replica exchange. The move method of the PathMover object actually performs the Monte Carlo move. It takes a SampleSet as input and returns a MoveChange, which the PathSimulator applies to the original SampleSet in order to create the updated SampleSet.
OPS includes a rich toolkit so that developers of new methods can create custom methods. Those toolkits are discussed in detail in the companion paper.47 Here, we will introduce some of the built-in path movers.
Shooting movers: OPS has support for both one-way (stochastic) shooting50,70 as well as the two-way shooting algorithm. These are implemented as OneWayShootingMover and TwoWayShootingMover. In addition to a specific ensemble, the shooting movers require a ShootingPointSelector to choose the shooting point. The most commonly used selector is the UniformSelector, which, by default, selects any point except the end points of the trajectory (which are in the defined states) with equal probability. Other possibilities could also be implemented, such as using a Gaussian distribution24 or a distribution constrained to the interface.74 The TwoWayShootingMover also requires a SnapshotModifier to change the snapshot in some way (e.g., modifying the velocities). Several possibilities exist, including either changing the direction of the velocity for some atoms or completely randomizing velocities according to the Boltzmann distribution.
Path reversal mover: Another standard mover is the PathReversal mover, which takes the current path in the ensemble and tries to reverse its time direction. For a path that leaves and returns to the same stable state this move is always accepted. As stated in Section 2.3, this move helps to decorrelate the sampled trajectories.
Replica Exchange mover: A ReplicaExchangeMover involves two ensembles (see Figure 6). When a move is attempted, the mover takes the paths associated with these ensembles in the current sample set and tries to exchange them. This trial move will be accepted if both paths are valid paths in their respective ensembles.
Minus mover: The MinusMover is a more complicated PathMover. In essence, it combines replica exchange with extension of the trajectory. OPS has a toolkit to simplify the creation of more complicated moves from simpler ones, which is to be discussed in more detail in the companion paper.47 The MinusMover uses both the minus interface ensemble and the innermost normal TIS ensemble. It extends the trajectory from the innermost ensemble until it again recrosses the interface and returns to the stable state, resulting in a trajectory with two subtrajectories that satisfy the innermost TIS ensemble. This trajectory satisfies the minus ensemble. The trajectory that had previously been associated with the minus ensemble also has two subtrajectories that satisfy the innermost TIS ensemble, and one of them is selected. After the move, the newly extended trajectory is associated with the minus ensemble, and the selected subtrajectory is associated with the innermost TIS ensemble.
5.5.2. The MoveScheme and MoveStrategy
The MoveScheme creates and contains the move decision tree, which is essentially the protocol for the simulation. Figure 6shows a graphical representation of the decision tree created by a simple MoveScheme. The decision tree contains the different choices of move type (e.g., shooting, reversal, replica exchange) and assigns specified weights to them. At the leaves of the tree are path movers. Each path mover acts on a certain ensemble (shown on the right of Figure 6).
The MoveScheme object organizes the path movers in several mover groups, held in a dictionary called movers, with strings as keys, and a list of PathMovers are values. Each group corresponds to a related set of movers (which are used on different ensembles). For example, the default shooting movers are in the group ’shooting’ and the default replica exchange movers are in the group ’repex’.
The most common MoveScheme objects are the DefaultScheme (for TIS) and the OneWayShootingMoveScheme (for TPS). All move schemes require a network; DefaultScheme and OneWayShootingMoveScheme also require an engine. The move decision tree can also be generated by hand and then given as input to a LockedMoveScheme, although some additional information (such as the choice_probability, a dictionary mapping each path mover to its relative probability of being selected) must be manually added to a LockedMoveScheme for some analysis to work. Furthermore, a LockedMoveScheme cannot by modified using MoveStrategy objects.
In general, the easiest way to customize the move scheme is to start with a DefaultScheme or a OneWayShootingMoveScheme and then append strategies that give the desired behavior. The whole scheme is built by applying the MoveStrategy objects in sequence. Each subclass of MoveStrategy has a priority level associated with it, and the strategies are built in an order sorted first by that priority level and second by the order in which they were appended to the scheme (so later additions can override earlier versions). Several aspects of the way a MoveStrategy contributes to the move decision tree can be set in its initialization: which ensembles the strategy applies to, which mover group the strategy is for, and whether to replace the effects of previous strategies. Additionally, mover-specific parameters (such as shooting point selector for shooting moves) are passed along to the movers that are constructed by the strategy.
This allows one to, for example, add a shooting move of a different type (e.g., two-way instead of one-way or using a different shooting point selection algorithm) for a specific ensemble — either overriding the original mover or adding a second “group” of shooting movers (with a different name, e.g., ’shooting2’ so as not to conflict with the existing ’shooting’). One might do this so that there are two kinds of shooting moves: one which causes large decorrelations in path space (but might have lower acceptance) and one that has a better acceptance probability.
5.6. Step 4: Obtaining Initial Conditions
The initial conditions for a path sampling simulation consist of a SampleSet with at least one Sample for any possible initial move. As discussed above, each Sample consists of a trajectory, the ensemble for that trajectory, and a replica ID. Preparing the initial sample set thus breaks down into two parts: (1) creating the initial trajectories and (2) assigning them to appropriate ensembles and giving them individual replica IDs.
The first part, obtaining initial trajectory from the path ensemble, is in general nontrivial since the events we are interested in are rare, and the best approach is likely to be system specific. We discuss several possible approaches in detail in Appendix A.
The second part is much easier. Once we have trajectories, scheme.initial_conditions_from_trajectories will take those trajectories and create appropriate initial conditions for the move scheme called scheme. This method attempts to create a sample for every ensemble required by the move scheme by checking if the given trajectories (or subtrajectories of them) or their time-reversed versions satisfy the ensemble. Internally, this uses the ability of the Ensemble object to test whether a trajectory (or subtrajectory thereof) satisfies the ensemble.
For some ensembles, such as the minus interface ensemble, the method extend_sample_from_trajectories has been implemented, which runs dynamics to create a trajectory that satisfies the ensemble, starting from input subtrajectories.
Last, the move scheme method MoveScheme. assert_initial_conditions can be used to check if a given set of initial conditions contains all Samples needed to run the simulation and raises an AssertionError if not.
5.7. Step 5: Equilibration and Running the Simulation
As with other simulation techniques, such as molecular dynamics and configurational Monte Carlo, the equilibration process for path sampling is often just a shorter version of the production run. Both equilibration and production require creating a PathSimulator object, which creates the runnable simulation. The examples here focus on PathSampling, but other subclasses of PathSimulator include CommittorSimulation and DirectSimulation (for rates and fluxes). The PathSampling simulator is initialized with a storage file, a move scheme, and initial conditions. It has a run method which takes the number of MC trial steps to run. All the simulation and storage to disk is done automatically.
5.8. Step 6: Analyzing the Results
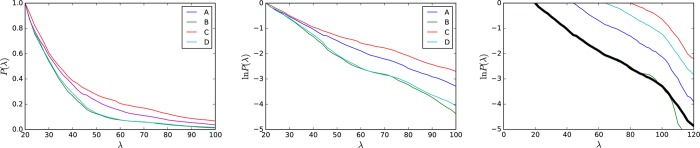
OPS has many built-in analysis tools, and users could create a wide variety of custom analyses: the companion paper includes several examples.47 However, nearly all analysis of path sampling falls into two categories: either the analysis provides information about the ensemble that is sampled (often tied to observables such as the rate) or the analysis provides information about the sampling process itself. Both analysis types are extremely important — poor behavior of the sampling process would indicate low confidence in the calculated observable, and, of course, combining insights from both can yield understanding of the physical process under study. The basic use of OPS analysis tools to calculate rates from MSTIS and MISTIS simulations and mechanistic information (path densities) from TPS simulations, as well as properties of the sampling process such as the replica history tree (a generalization of the “TPS move tree” in the existing literature), measures of mover acceptance ratios, and measures of the replica exchange network and its efficiency, will be illustrated in the following examples.
6. Illustrative Examples
In this section, we give and discuss
several examples. These examples are meant to show the user how to
set up, run, and analyze several basic applications of TPS, MSTIS, and MISTIS. In the examples,
the following set of initial imports is assumed:
These imports load not only the required modules, notably the OPS modules, but also modules such as MDTraj,86 OpenMM,80 the toy dynamics, and the Python plotting modules. We note that the explicit code given in this section is for illustrative purposes only and refers to the 1.0 release. Up-to-date versions of the examples are available as interactive Jupyter notebooks on the Web site http://openpathsampling.org.
6.1. TPS on Alanine Dipeptide
This example illustrates details about setting up transition path sampling calculations, both with fixed and flexible path length ensembles. This example and the next consider alanine dipeptide (AD) in explicit TIP3P90 water, using the AMBER9691 force field to enable comparison to some previous work.92,93 This model has been widely used as a biomolecular test system for rare events methods. We use a VVVR-Langevin integrator at 300 K,94 with a 2 fs time step and a collision rate of 1 ps–1. The long ranged interactions were treated with PME with a cutoff of 1 nm. The AD molecule was solvated with 543 water molecular in a cubic box and equilibrated at constant pressure of 1 atm using a Monte Carlo barostat. Afterward the box size was set to the average value of 25.58 Å, as obtained in the NPT run. All subsequent simulations were done in the NVT ensemble.
While the example is based on the explicit solvent calculations by Bolhuis, Dellago, and Chandler,95 we differ in several details, including our choice of force field and the details of our ensembles: ref (95) used a shorter fixed-length TPS ensemble, whereas we use both a flexible-length TPS ensemble and an 8 ps fixed-length TPS ensemble.
6.1.1. Setting up the Molecular Dynamics
We use OpenMM to set up an MD engine for the AD system. The OpenMM-based OPS engine is essentially a wrapper for the OpenMM Simulation object. As with the OpenMM Simulation, it requires an OpenMM System, and an OpenMM Integrator. The interactive OpenMM simulation builder tool [http://builder.openmm.org/] allows us construct an appropriate System and Integrator. In addition, the OpenMM Simulation takes a openmm_properties dictionary, which we must define.
To build the OPS engine,
we also need to fill an engine_options dictionary
with some OPS-specific and OpenMM-specific entries. All OPS engines
should define n_steps_per_frame, the number
of time steps per saved trajectory frame, and n_frames_max, an absolute maximum trajectory length. For the alanine dipeptide
examples, we save every 20 fs (10 steps) and abort the trajectory
if it reaches 40 ps:
After creating the OpenMM system,
the OpenMM integrator, the OpenMM properties dictionary, and the OPS
engine options dictionary, all of these can be combined to create
on OpenMM-based OPS engine:![]()
where the template is a snapshot loaded from a PDB file with omm.snapshot_from_pdb(ˈˈfile.pdbˈˈ). The template snapshot will be used again to provide the storage file with a template to automatically identify the sizes of various arrays to be saved. The above engine-creation command also associates a name with the engine, which makes it easier to reload from storage for reuse.
6.1.2. Defining States and Interfaces
The collective variables of interest
for alanine dipeptide are the backbone ϕ and ψ dihedrals.
To create a collective variable for these angles, we use our wrapper
around MDTraj’s compute_dihedrals function: ![]()
The ϕ angle is defined similarly, consisting of the atoms with indices 4, 6, 8, and 14.
MDTraj reports dihedral angles in radians. The MDTrajFunctionCV wrapper can wrap any function that uses MDTraj; we use the simplest example here for illustrative purposes. It would be straightforward to write a Python function that converts this to degrees and to use that in place of md.compute_dihedrals; the AD MSTIS example in section 6.2 uses a more complicated approach to wrapping CVs.
In this example, we define two states, C7eq and αR, similarly
to ref (95). Since
we are using a different force field, we use slightly different values
for the ψ angles. Our state C7eq is defined (in degrees) by 180 ≤ ϕ
< 0 and 100 ≤ ψ < 200 (wrapped periodically), whereas
αR is given by 180 ≤ ϕ
< 0 and −100 ≤ ψ < 0. To convert between
degrees and radians, we define deg = np.pi/180. The code to define C7eq is:
and state αR can be coded accordingly.
For nonperiodic CVs, the equivalent form is CVDefinedVolume, and it does not include the period_min and period_max arguments. The periodic version allows the C7eq state to wrap across the periodic boundary in the ψ variable: We define the state from 100 degrees to 200 degrees, even though the function reports values between −180 deg and 180 deg. We would get the exact same behavior by setting lambda_max to −160 degrees. For a TPS simulation, we only need to define the states — there are no interfaces to define.
6.1.3. Setting up the Transition Network and Move Scheme
The
transition network creates and contains all the ensembles to be sampled.
In this case, there is only one ensemble. Later examples will deal
with sets of ensembles. The fixed and flexible path length examples
diverge here: the fixed path length TPS simulation uses a fixed path
length network with path length 400 frames (8 ps), created with: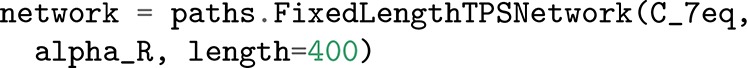
For the flexible path length, which is better in practice, we use![]()
This one line of code selects between the two approaches. Multiple
state TPS can be set up similarly. For instance, a multiple state
TPS with states A, B, and C (allowing all transitions) can be
created by![]()
Next, we set up the move scheme.
For the TPS simulations, we only need a shooting move. This move scheme
is created with  The selector defines
how to choose the shooting points, e.g., UniformSelector selects the points uniformly. Another option would be to use the GaussianBiasSelector(lambda, alpha, l_0), which takes
the collective variable lambda and biases the
shooting point selection according to exp(–α(λ–l0)2), where l0 is the position of the maximum,
and α determines the width of the distribution.96
The selector defines
how to choose the shooting points, e.g., UniformSelector selects the points uniformly. Another option would be to use the GaussianBiasSelector(lambda, alpha, l_0), which takes
the collective variable lambda and biases the
shooting point selection according to exp(–α(λ–l0)2), where l0 is the position of the maximum,
and α determines the width of the distribution.96
6.1.4. Obtaining Initial Conditions
We obtained an initial trajectory by running at high temperature (T = 500 K) until both states had been visited. Appendix A provides details on this and other possible methods to obtain initial trajectories.
We generate the trajectory for fixed length TPS by taking the appropriate trajectory for flexible length TPS, adding frames to either side, and using the fixed-length ensemble’s ensemble.split to select a segment of the appropriate length that satisfies the requirements.
To assign this first trajectory to the ensemble we will be sampling, we use the move scheme’s scheme.initial_conditions_from_trajectories method.
6.1.5. Equilibration and Running the Simulation
All OPS simulation details and simulation
results are stored in a single NetCDF storage file. The storage requires
a template snapshot to determine sizes of arrays
to save per snapshot. Before running the simulations, we need to create
a file to store our results in. A new file named tps_AD.nc can be created with
The PathSampling simulator object is created with 
We can run the OPS simulation using
with n_steps trial moves. We use 10,000 steps for the TPS examples.
In all molecular simulation approaches initial conditions are unlikely to be representative for the equilibrium distribution (e.g., one could start with the solvent molecules on a grid, or with a high temperature snapshot), and equilibration is usually required before one can take averages of observables. Likewise, we need to equilibrate the path sampling before we can take statistics, when the initial trajectories are not from the real dynamics (e.g., generated with metadynamics or high-temperature simulation). As with MD and MC approaches, the equilibration phase can be just a short version of the production run.
6.1.6. Analyzing the Results
Analysis of a simulation is usually done separately
from running the simulation. The first step is to open the storage
file with the simulation results. ![]()
will open a file for reading.
The tables of stored data objects are attributes of the storage. To see the number of items stored, the standard Python len function can be used. For example, len(storage.steps) gives the number of Monte Carlo steps run (plus 1 for the initial conditions).
The move scheme serves as the starting point for much of the analysis.
Since there is only one in storage, we obtain the correct move scheme
with scheme = storage.schemes[0]. The command![]()
returns a quick overview of the moves performed and information on the acceptance ratios. Since our TPS move scheme contained only one PathMover, all performed moves were shooting moves. In this example, we find a 56% acceptance ratio for flexible length TPS and a 50% acceptance rate for fixed length TPS.
As discussed in Section 4, every Monte Carlo step in the storage consists of two main parts: the SampleSet of active samples, given by step.active, and the PathMoveChange with details about
the move, given by step.change. Typically,
analysis begins with a loop over steps and then extracts the relevant
information. The first step (step 0) corresponds to the initial conditions.
For example, a list of all the path lengths (in frames) can be obtained
with
which loops over each MC step in storage.steps and takes the length of the trajectory associated with replica ID 0 in the active sample set. For TPS, this is the only replica, so this gives us the length of every accepted trajectory, weighted correctly for the ensemble. From here, we can use standard Python libraries to analyze the list, obtaining, for example, the maximum (max(path_lengths)), the mean (np.mean(path_lengths)), and the standard deviation (np.std(path_lengths)), or to plot a histogram (plt.hist(path_lengths)). In this specific example, we are often interested not in the exact number of frames but in the time associated with that number of frames. This can be accessed by multiplying the path length by engine.snapshot_time step, which gives the time between saved snapshots. In the case of the OpenMM engine, this result even includes correct units, and we find that the average path length for the flexible path length simulation is 1.6 ps, with a maximum path length of 10.1 ps.
One of the
tools for checking the behavior of path sampling simulations, particularly
of one-way flexible length path sampling, is the visualization known
as the “path tree”. This has several uses, including
checking for path decorrelation and that there is sufficient alternation
between accepted forward shots and accepted backward shots.97 In OPS, we generate this object with![]()
which works with any list of steps, although the visualizations get unwieldy for large numbers of steps. The generator describes how to generate the list of samples to be displayed from steps. In TPS, there is only one replica (replica = 0), but trees can also be used to track the move history of a specific replica in TIS, where there are multiple replicas.
This PathTree object only consists of the data and data structures to create and analyze the visualization. The actual image can be generated (in SVG format) using path_tree.svg() for visualization in a Jupyter notebook or written to file. The resulting image, shown in Figure 7, shows the original trajectory in gray, the forward shots in red, and the backward shots in blue. However, these colors are customizable using CSS options that can be modified by the user. The top uses an additional CSS-based customization to show the individual snapshots. Additional information is shown to the left of the tree. At the far left, a number indicates the MC trial step index. Next to that, a vertical bar contains horizontal lines to indicate groups of correlated paths (paths which share at least one configuration in common).
Figure 7.
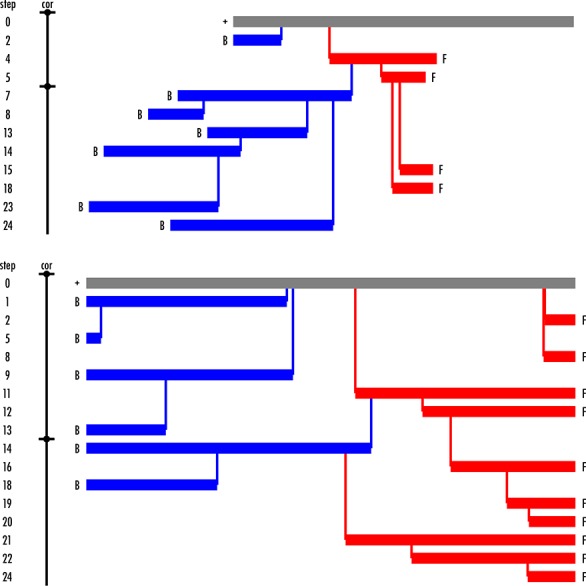
Path sampling history tree for alanine dipeptide TPS simulations from Section 6.1. Top: The path tree for first 25 trial MC moves using flexible path length TPS. Here the initial path is represented by a gray horizontal line of a length equal to the path length. Going downward, the sequential MC shooting moves are indicated. The vertical line indicates the shooting point. Red and blue horizontal lines indicate forward and backward shots, respectively. Note that these are partial paths, replacing the old path from the shooting point forward (or backward). The remainder of the path is retained from the previous paths. To the left is indicated the MC step (trial) index. Only accepted paths are shown. The bars to the left indicate complete decorrelation of the previous decorrelated path. Bottom: the path tree for fixed path length TPS. Note that the width is scaled differently; paths in the bottom tree are much longer than the top tree.
The list of first-decorrelated paths (the first member of each such group) can be obtained with replica_history.decorrelated_trajectories. This number is a good estimate of the number of uncorrelated samples drawn from an ensemble. For the flexible path length simulation, we have 893 decorrelated trajectories, decorrelating on average every 11.2 MC steps. For the fixed path length simulation, there are only 409 decorrelated trajectories, decorrelating every 24.4 MC steps. Note that this set itself has no special relevance but rather gives an indication of the sampling efficiency.
Besides analyzing the sampling statistics,
we can, of course, perform normal MD trajectory analysis on trajectories
generated by OPS. For example, suppose we wanted the active trajectory
after the 10th MC step. We can obtain this with![]()
where, again, TPS only has one replica, with replica ID 0. We can directly analyze this trajectory with the tools in OPS. For example, taking phi(trajectory) will give us the list of values of ϕ for each frame in the trajectory. Any other OPS collective variable will work similarly, whether it was used in sampling or not.
The path density gives
the number
of paths in the ensemble that visit a particular region in the projected
collective variable space. The appropriate histogram requires defining
the (inclusive) lower bound of a bin and the width of the bin in each
collective variable. In OPS, we can calculate the path density with
utilizing a bin width of 2 degrees.
In principle, an OPS path density can be in any number of collective variables. However, in practice, path densities are almost always shown as 2D projections. Figure 8 gives the path density for the flexible path length ensemble in the (ϕ, ψ) plane, along with two representative trajectories.
Figure 8.
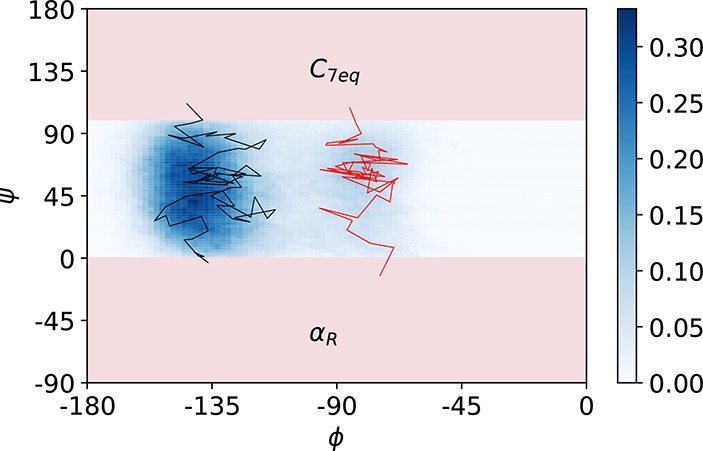
Path density histogram for flexible path TPS of the C7eq → αR transition in alanine dipeptide from Section 6.1. The path density is a 2D histogram of the number of paths that traverse a (discrete) ψ – ϕ value.71 On top of the path density we plot two individual trajectories, one for each of the two observed channels. Note that the left channel between C7eq and αR around ϕ ≈ –135 is much more frequently sampled.
If one would rather
use other tools, it is possible to convert an OPS trajectory generated
by OpenMM to an MDTraj86 trajectory with ![]()
From there, we can analyze the trajectory with MDTraj or export it to any of the file formats supported by MDTraj, to be read in by other analysis programs. In addition, MDTraj can be used as a gateway to other libraries, such as NGLView.98
The step.change starts from the root of the move decision tree and therefore also contains information about what kind of move was decided. This is very simple in TPS but can be much more complicated for the move schemes used in TIS. The details that are probably of greatest interest can be accessed with step.change.canonical. The nature of a given step.change.canonical depends on the type of Monte Carlo move. However, as discussed in Section 4 and shown in Figure 2, all changes have a few properties: a Boolean as to whether the trial was accepted, a link to the actual mover that created the change, and a list of attempted samples in trials.
Sometimes we might want to study the rejected trajectories,
for example, to determine whether they continued to the maximum possible
time in flexible length TPS. This could indicate a metastable state
that was not considered. The list of rejected samples (which contain
the trajectories, as well as the associated ensembles) can be created
with
Since each step.change.canonical.trials is a list, we use Python’s sum function
to add (extend) the lists with each other. For more
complicated move schemes, we might want to add a restriction such
as step.change.mover = = desired_mover with
an and in the if statement.
The code above results in a list of Sample objects.
The trajectories can be extracted with![]()
These rejected trajectories can be analyzed in the same way as above.
6.2. Multiple State Replica Exchange TIS on Alanine Dipeptide
6.2.1. Setting up the Molecular Dynamics
In this example we use the same system as in the previous example,
with the same MD engine. In the online Jupyter notebook — which
contains additional details not presented here — we set up
the engines from scratch. However, as OPS saves all the details of
the engine, we can reload a usable engine from the output file of
the previous example. In fact, we can even use that file to reload
the collective variables that we defined:
6.2.2. Defining States and Interfaces
In contrast to the above example we take the MSTIS state definitions
for alanine dipeptide from ref (62) to make the results comparable with that work. The states
are defined by a circular region around a center in ϕ –
ψ space, while interfaces are defined by circular regions with
increasing diameter λ. For instance, for state A we can define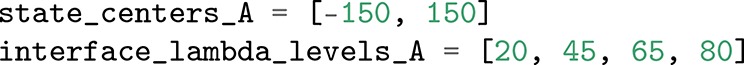
For convenience, Python dict objects can be used to contain the centers and interface levels for all states (e.g., state_centers[″A″]), although in this example we will use separate objects for each.
In MSTIS, each state is associated with an order parameter (CV). In simple cases like this one, a single functional can be used for all the order parameters. In OPS, this can be accomplished by creating a single Python function which takes a Snapshot as its first argument and parameters for the functional as the remaining arguments. This was also done implicitly in the previous example, where the md.compute_dihedrals Python function is actually a functional with indices as parameters. In this case, we need to explicitly create a Python function with the signature circle_degree(snapshot, center, cv_1, cv_2), where snapshot is an OPS Snapshot, center is a two-member list like state_centers_A, and cv_1 and cv_2 are OPS collective variable objects (in all cases, we will use our phi and psi variables).
In this example, we could redefine the phi and psi variables inside the function, but using them as parameters has an additional advantage: they will only be calculated once, and then the values will be cached in memory (and optionally saved to disk). This is extremely useful for expensive CVs that are likely to be reused as part of other CVs.
Once
the functional has been defined, we can wrap it in an OPS FunctionCV for each state. For state A:
We can now use this CV to define the volume associated
with the state:
All of this is analogous to the TPS example;
however, TIS also requires defining interfaces. These can be created
with:![]()
In many cases, the innermost interface volume is identical
to the state. For those examples, one could first create the interfaces
and then select the innermost using![]()
The state definition used here is illustrated in Figure 5. In this example we restrict the states to {A, B, C, D}. The transitions to the E and F states are extremely rare and require additional restricted path sampling.62
6.2.3. Setting up the Transition Network
MSTIS can make use of the optional multistate outer
interface, in which all state-to-state paths are allowed, as long
as they cross the outer interface MSOuterInterface. This special interface allows switching paths from one associated
state to another when reversing a transition path. Note that in all
other interface ensembles/replicas such reversal trials are rejected
by construction. We create this multistate outer interface with ![]()
where the lambdas are the interface levels as defined above, and
the dots indicate a short hand for all other state volumes and interfaces. We now construct the Network that contains
the structure of states and interfaces.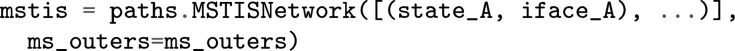
We finally construct the DefaultScheme with ![]()
This scheme includes minus moves, moves for the multistate outer interface ensemble, as well as the standard shooting, path reversal, and nearest neighbor replica exchange moves.
6.2.4. Obtaining Initial Conditions
Initial conditions for the MSTIS simulation can be obtained with an approach similar to the one used in the TPS example in Section 6.1. The initial conditions must include a trajectory that satisfies each (interface) ensemble. However, the same trajectory can be reused for multiple ensembles, and a trajectory that transitions from a given state to another must exit all interfaces associated with the initial state. A trajectory that visits all states has (when considering both the trajectory and its time-reversed version) at least one subtrajectory that represents a transition out of every state.
As with the TPS example, we therefore use the approach described in Appendix A, using a temperature of T = 1000 K. Again, the scheme.initial_conditions_from_trajectories method is used to identify the specific subtrajectories and associate them with the correct ensembles.
When the initial paths for the minus ensembles are not directly found, we use the innermost TIS ensemble trajectories and extend them until they match the required (minus) ensemble (or fail in doing so) using the .extend_sample_from_trajectories method and associating them with the correct ensembles using scheme.initial_conditions_from_trajectories.
6.2.5. Equilibrating and Running the Simulation
As in the TPS examples, the path replicas first need to be equilibrated since the initial trajectories are not from the real dynamics (e.g., generated with metadynamics, high temperature, etc.) and/or because the initial trajectories are not likely representatives of the path ensemble (e.g., if state-to-state transition trajectories are used for all interfaces).
As with
straightforward MD simulations, running equilibration can be the same
process as running the total simulation. However, in path sampling
we could equilibrate without replica exchange moves or path reversal
moves, for instance. In the example below, we create a new move scheme
that only includes shooting movers, to achieve equilibration of the
interface ensemble replicas,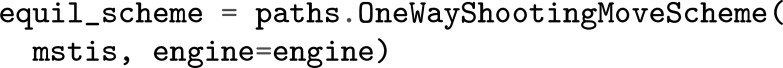
and run this scheme for 500
steps the way we run any other scheme, using the PathSampling object.
Figure 9 shows the set of initial and final samples. Note that the large coverage of phase space at high temperature narrows after cooling down, as expected.
Figure 9.
Comparison between initial sample after generation at high temperature and room temperature equilibration for alanine dipeptide in the psi–phi plane from Section 6.2. The trajectories are plotted as connect dots, where each dot represents a snapshot. The stable state and interface definitions for A, B, C, and D are plotted in the background. Note that after cooling to room temperature the trajectories are sampling a more narrow path samples, as expected.
Finally, we run the simulation
for 100,000 steps using the PathSampling object as in a previous example,
with the default scheme as defined above, a Storage object, and the initial conditions from the equilibration.
6.2.6. Analyzing the Results
To do analysis
on the path simulation results we first have to load the production
file for analysis: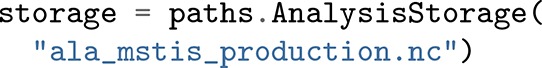
Then we can run analysis on this storage.
One of the main objectives for doing multiple state replica exchange
TIS is to compute the rate constant matrix. To obtain the rate constant
matrix, we run![]()
which gives as an output the full rate constant matrix kIJ, obtained from a computation of the fluxes ϕ0I, the crossing probabilities PI(λmI|λ0I), and the conditional transition matrix PI(λ0J|λmI) (see eq 5).
An example of such a rate constant matrix computation is shown in Table 2, which agrees well with the results in ref (62). For comparison, the computed fluxes ϕ0I and crossing probabilities PI(λmI|λ0I) are presented in Table 3, while Table 4 reports the conditional state-to-state transition matrix PI(λ0J|λmI), which represents the probabilities to reach a state provided that the trajectories have passed the outermost interface of a state.
Table 2. Rate Constant Matrix for Alanine Dipeptidea.
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 0.06512 | 0.003514 | 0.0009725 |
| B | 0.07606 | 0 | 0.001202 | 0.001107 |
| C | 0.05311 | 0.01103 | 0 | 0.1202 |
| D | 0.01102 | 0.005624 | 0.06909 | 0 |
The average rate constant matrix, in units of ps–1, for the four-state Markov model based on several independent runs. Rows denote leaving, and columns denote arriving states. Subscript denotes error in the last 2 digits.
Table 3. Fluxes and Outer Interface Crossing Probabilities for TIS Simulation of Alanine Dipeptidea.
| ϕ0I [ps–1] | PI(λmI |λ0I) | ϕmI [ps–1] | |
|---|---|---|---|
| A | 1.56 | 0.06609 | 0.10313 |
| B | 1.85 | 0.05909 | 0.11017 |
| C | 1.67 | 0.19313 | 0.32321 |
| D | 2.29 | 0.07109 | 0.16220 |
Flux at the first interface (second column), the crossing probability from the first to the outermost interface (third column), and the flux at the outermost interface (last column).
Table 4. Conditional Transition Probability Matrix between Alanine Dipeptide Statesa.
| A | B | C | D | |
|---|---|---|---|---|
| A | 0.3506 | 0.6106 | 0.03208 | 0.009012 |
| B | 0.7203 | 0.2603 | 0.01102 | 0.01108 |
| C | 0.1702 | 0.03307 | 0.4003 | 0.4001 |
| D | 0.06605 | 0.03413 | 0.4203 | 0.4804 |
These probabilities follow directly from the path sampling in the multistate outer ensemble. Rows denote leaving, and columns arriving states.
OPS also includes other analysis tools such as the crossing probabilities and the sampling statistics. Both are important for purposes of checking the validity of the simulations results. The crossing probability graphs in Figure 10 can be helpful in interpreting the rate matrix. The sampling statistics provides the Monte Carlo acceptance ratio for the different movers. Of course, each trajectory in the ensemble can be accessed and scrutinized individually, as in previous sections.
Figure 10.
TIS crossing probabilities for alanine dipeptide, from section 6.2. Left: Total crossing probability as a function of the order parameter (CV) λ for each individual state (A–D). Center: Natural logarithm of the total crossing probability per state. Right: Per interface crossing probabilities for state A. The master curve (black) is obtained by reweighting.65,74
6.3. MISTIS on a Three-State 2D Model System
This example deals with a three-state 2D model system, which we also refer to as a toy model. OPS includes simple code to simulate the dynamics of small toy models like the one considered here. This is intended for use for either educational purposes or for rapid prototyping of new methodologies. Since the overall path sampling code is independent of the underlying engine, many types of new methods could be developed and tested on the toy models and would be immediately usable for more complicated systems, simply by changing the engine.
6.3.1. Setting up the Molecular Dynamics
We create a simple 2D model with a potential consisting of a sum of Gaussian wells
| 6 |
with (x0, y0) = (−0.5, 0.5), (x1, y1) = (−0.5,
– 0.5), and (x2, y2) = (0.5, – 0.5) using
This results in a potential energy surface with three stable states, caused by the Gaussian wells at (−0.5, – 0.5), (0.5, – 0.5), and (−0.5, 0.5) . We call those states A, B, and C, respectively. This potential interface surface, along with the state and interface definitions described below, is illustrated in Figure 11.
Figure 11.
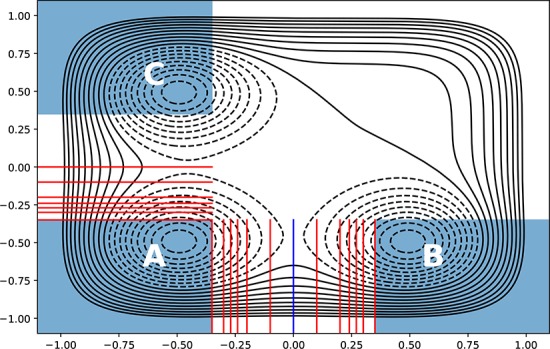
Potential energy surface, states, and interfaces for the 2D toy model. States are light blue, boundaries of normal interfaces are red, and the boundary of the multiple state outer interface is dark blue. For clarity when showing multiple interface sets, the interface bondaries are only drawn part of the way. They continue in an infinite straight line.
To integrate
the equations of motion, we use the BAOAB Langevin integrator of Leimkuhler
and Matthews,99 which we initialize with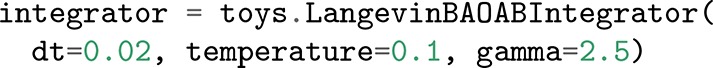
The toy engine employs units where kB = 1. The “topology” for the toy engine stores
the number of spatial degrees of freedom, as well as a mass for each
degree of freedom and the potential energy surface. We also create
an options dictionary for the engine.
We then instantiate an engine with toy_eng = toys.Engine(options, topology).
6.3.2. Defining States and Interfaces
In this calculation, we will set up multiple interface set transition interface sampling (MISTIS).76 This involves defining different interface sets for each transition. To simplify and to highlight some of the flexibility of MISTIS, we will only focus on the A → B, B → A, and A → C transitions.
First, we define simple collective
variables. We use the Cartesian x and y directions for both our state definitions and for our interfaces.
We define these as standard Python functions, for example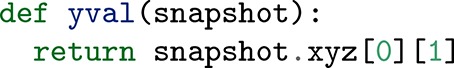
and xval is similar but returns the [0][0] element, where the first index refers to the atom
number and the second to the spatial dimension. We wrap these functions in OPS collective variables with, for example, cvX
= FunctionCV(ˈˈxˈˈ, xval). We define
a volume called x_lower for x < – 0.35 with CVDefinedVolume(cvX, float(ˈˈ-infˈˈ),
−0.35). Similarly we define x_upper for x ≥ 0.35 and use the same bounds for y with y_lower and y_upper. With these, we define our states as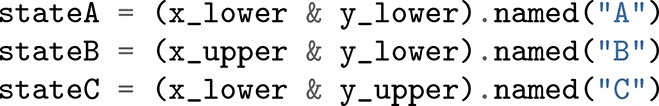
For our TIS analysis, the order parameter must increase with the
interface. So for the B → A transition we create another collective variable, cvNegX, based on a function that returns -snapshot[0][0]. For all of these, we will set interfaces at −0.35, −0.3,
−0.27, −0.24, −0.2, and −0.1. The A → C transition has an additional
interface at 0.0. The A → B and B → A transitions will
share a multiple state outer interface at 0.0. Note that, for the B → A transition, the interface
associated with cvNegX = −0.35 is actually
at x = 0.35, since cvNegX returns
−x. These interfaces are created by, for example
with similar lines for interfacesAC and interfacesBA. The multiple state outer interface, which
connects the A → B and B → A transitions, can be created
at x = 0.0 with
6.3.3. Setting up the Transition Network and Move Scheme
Like the MSTISNetwork, the syntax for setting up a MISTISNetwork requires a list of tuples. However, since
MISTIS requires a final state as well an initial
state, it also requires that the final state be included as an extra
piece of information in that tuple. So we set up our desired MISTIS
network with
The strict_sampling argument means that an A → C path will be rejected if sampling the A → B transition. Note that A is the initial state for transitions to two states, whereas B is the initial state for transitions to one state, and C is not an initial state at all. The flexibility to define arbitrary reaction networks is an important aspect of the MISTIS approach.
The move scheme is set up in exactly the same way as for MSTIS: scheme = DefaultScheme(network, toy_eng). One could also use a single replica move scheme with a MISTIS network, just as was done in the MSTIS example.
6.3.4. Obtaining Initial Conditions
Here, we will use the bootstrapping approach to obtain initial
trajectories. This approach is most effective with simple systems
like this, where the collective variables we have chosen as order
parameters are good representations of the actual reaction coordinate.
The bootstrapping runs separately on each transition A → B, A → C, and B → A. Given
an initial snapshot snapA in state A, the initial samples for the A → B transition can be obtained with This will create a trajectory for each of the normal interface ensembles,
as well as the multiple state outer interface ensembles. The other
transitions can be prepared similarly, although they can omit the extra_ensembles option, since there is only one multiple
state outer ensemble to fill. Whereas snapshots for the OpenMM engine
used in the previous examples came from PDBs or other files, for the
toy engine, the initial snapshot can be manually created:
This will create a trajectory for each of the normal interface ensembles,
as well as the multiple state outer interface ensembles. The other
transitions can be prepared similarly, although they can omit the extra_ensembles option, since there is only one multiple
state outer ensemble to fill. Whereas snapshots for the OpenMM engine
used in the previous examples came from PDBs or other files, for the
toy engine, the initial snapshot can be manually created:
The individual sample sets created by the FullBootstrapping approach can be combined into one using![]()
From here, the setup follows that of the MSTIS example: the trajectories can be assigned to ensembles using scheme.initial_conditions_from_trajectories, and the minus ensembles, of which there is one for each state, can be filled using minus.extend_sample_from_trajectories.
6.3.5. Running the Simulation and Analyzing the Results
The path sampling follows exactly as with the previous examples. The PathSampling object is created with a storage file, the move scheme, and the initial conditions. We use the .run(n_steps) method to run the simulation.
One difference with the MSTIS approach is that trajectories from the multiple set minus interface cannot be used to calculate the flux. To obtain the flux, we do a separate calculation, which we call DirectSimulation and which runs a molecular dynamics trajectory and calculates the flux and the rates from the direct MD.
Setting up the DirectSimulation requires the same toy_engine object. The
set of all states is given by![]()
To determine the flux out of
a given state and through a given interface, it needs the pairs of
(state, interface) for each transition. We can create this with![]()
The simulation is then created with
where we choose not to store the output, and where we can use any snapshot as our initial snapshot. The method sim.run(n_steps) runs the simulation for the given number of MD steps. Note that, although the direct simulation here is for the MISTIS network, it would work equally well for any other network. However, the flux calculation based on the minus interface is more convenient for the MSTIS case.
Once the direct simulation has been run, we can obtain the flux from it using sim.fluxes. This returns a Python dictionary with the (state, interface) pairs as keys and the calculated flux as value. Prior to the rate matrix calculation, we can set the fluxes for the network by using network.set_fluxes(sim.fluxes).
Aside from setting the flux, the analysis for the MISTIS network is exactly as it is for other path sampling methods. The rate matrix for this model is presented in Table 5. Note that the rate matrix only includes the specific transitions we selected for study by MISTIS; others are not listed. The MISTIS rates represent the average of 10 runs of 105 MC steps each, with the standard deviation as the reported error. To demonstrate correctness, we compare these rates to those from a direct MD simulation (also performed using OPS), with a length of 8 × 108 frames. The cumulative MD time for the 10 MISTIS simulations was less than 1.8 × 107 frames. Errors for the direct MD rate were determined by splitting the total simulation into 10 sequential blocks and calculating the standard deviation of the rate in each block. Rates and error bars from the two methods compare favorably, even though the MD simulation took more than 40 times more CPU time.
Table 5. Rates Constants for the Toy Model, Multiplied by 104a.
| A | B | C | |
|---|---|---|---|
| A | 1.9814 | 1.9517 | |
| B | 2.0016 |
| A | B | C | |
|---|---|---|---|
| A | 1.9443 | 2.2065 | |
| B | 2.1037 |
Subscripts indicate error in the last two digits. Top: Rate constant calculated from a very long direct molecular dynamics simulation. Bottom: Rate constant calculated using MISTIS. By symmetry, all three rate constants in each table should be nearly the same.
7. Conclusion
In this paper we have presented a new easy-to-use Python framework for performing transition path sampling simulations of (bio)molecular systems. The OpenPathSampling framework is extensible and allows for the exploration of new path sampling algorithms by building on a variety of basic operations. As the framework provides a simple abstraction layer to isolate path sampling from the underlying molecular simulation engine, new molecular simulation packages can easily be added. Besides being able to execute existing complex path sampling simulations schemes, tools are provided to facilitate the implementation of new path sampling schemes built on basic path sampling components. In addition, tools for analysis of, e.g., rate constants are also provided. Modules that provide additional functionality are continuously added to be used by the community (see, e.g., the repositories at https://gitlab.e-cam2020.eu/Classical-MD_openpathsampling).
In summary, the OpenPathSampling package can assist in making the transition path sampling approach easier to use for the (bio)molecular simulation community.
Acknowledgments
The authors are grateful for feedback from many people who helped beta-test the software, whose names are listed at http://openpathsampling.org/latest/acknowledgments.html. The authors are particularly grateful to Sander Roet (University of Amsterdam) for his feedback and to Jocelyne Vreede (University of Amsterdam) for the feedback obtained by using OPS as a teaching tool in courses on biomolecular simulation.
Appendix A: Obtaining an Initial Trajectory
Just as configurational Monte Carlo requires a valid initial configuration for input, path sampling Monte Carlo requires a valid initial trajectory for input; and just as with configurational Monte Carlo, an unrealistic initial state can equilibrate into a realistic state, but more realistic starting conditions are preferred. Unrealistic starting conditions can take longer to equilibrate and can get trapped in unrealistic metastable basins. In the case of path sampling, this can mean sampling a transition with a much higher energy barrier than is realistic.
Obtaining a good first trajectory is thus of paramount importance. However, there is no single best method to do so. Here we review a few options and explain how OPS can facilitate first trajectory generation. In all of these, the key OPS functions that simplify the process are the Ensemble.split function, which can identify subtrajectories that satisfy the desired ensemble, and the MoveScheme.initial_conditions_from_trajectories function, which attempts to create initial conditions for the desired move scheme based on given trajectories. The fundamental trade-off for these approaches is between how “realistic” the initial trajectory is and how computationally expensive it is to obtain the first trajectory.
A.1. Long-Time MD
While a transition from an unbiased MD trajectory will provide a realistic initial trajectory, these are difficult to obtain for rare events. Nevertheless, distributed computing projects like Folding@Home100 and special-purpose computers for MD such as Anton101 might yield trajectories that include a transition. The Ensemble.split function can then select subtrajectories that satisfy a desired ensemble.
In these trajectories frames are often saved very infrequently, leading to transitions with only one or two (or even zero) frames in the “no-man’s land” between the states. Path sampling requires at least a few to a few tens of frames. A CommittorSimulation using the desired states as end points and any frames between the two states as input could generate an initial trajectoriy by joining two path segments ending in different states, provided the committor for at least one of the intermediate frames is reasonable.
A.2. High Temperature MD
In the alanine dipeptide example, we use MD at high temperature to increase the probability of getting a transition. This method could cause problems in larger systems, by allowing transitions that are not accessible at the relevant low temperature. However, it works well on simple systems such as AD and is very easy to set up.
First, we create an engine with a higher temperature. For the AD example, we use OPS’s OpenMM engine. For the 2-state system, we used a high temperature of 500 K. For the 4-state system, we used a high temperature of 1000 K in order to easily reach the higher-lying states.
To ensure that we visit all states,
we generate a trajectory using the ensemble![]()
which creates the union of AllOutXEnsembles for each state. Running with this ensemble as the continue condition means that the trajectory will stop with the first trajectory that does not satisfy it, i.e. the first trajectory with at least one frame in each state. For MSTIS, this guarantees that a subtrajectory (or its reversed version) will exist for every path ensemble.
We
obtain the relevant trajectories by using the ensemble.split method with the outermost ensemble for each sampling transition
(see also ref (47)).![]()
These trajectories can then be given to the MoveScheme.initial_conditions_from_trajectories method.
Relaxing the high temperature initial trajectories down to ambient conditions might be difficult, requiring many shooting attempts before a valid room temperature path is created. Again, a CommittorSimulation can alleviate this problem, by joining forward and backward committor segments from a snapshot with a finite committor value.
A.3. Bootstrapping/Ratcheting
In the toy model example in Section 6.3.4, we use a “bootstrapping” approach, which is specifically useful for TIS. In this approach, we initialize a trajectory in a stable state, e.g. A, and perform MD until the first interface is crossed, which allows the first interface ensemble to be populated. Subsequently, TIS is performed until the second interface is crossed, allowing the second interface to be populated, etc. In this way one can ratchet oneself up the barrier and populate each TIS interface. All this is taken care of by the FullBootstrapping method. Note that this path ensemble needs to be equilibrated subsequently.
A.4. Using Biased Trajectories
The use of unbiased dynamics is not necessary, as the goal is to obtain an initial trajectory that is just “reasonably close” to the unbiased dynamics. Subsequent path sampling will then equilibrate the trajectories with the unbiased dynamics.
Recent work53 has employed metadynamics16 to obtain an initial trajectory. Although metadynamics biases the underlying dynamics, the first transition in a metadynamics simulation will not have added much bias to the barrier region. Therefore, further path sampling can equilibrate the first metadynamics trajectories into the unbiased dynamics path ensemble. This initial metadynamics trajectory could be generated with PLUMED84 and then read into OPS.
The same basic approach could be employed for other approaches to generate a nonphysical initial transition trajectory, including steered MD,102 nudged elastic band,103 or the string method.104
D.W.H.S. and P.G.B. acknowledge support from the European Union’s Horizon 2020 research and innovation program, under grant agreement No. 676531 (project E-CAM). J.D.C. acknowledges support from Cycle for Survival, NIH grant P30CA008748, and NIH grant R01GM121505. J.D.C., J.H.P., and D.W.H.S. gratefully acknowledge support from the Sloan Kettering Institute. F.N. acknowledges ERC consolidator grant 772230 “ScaleCell”, DFG NO 825/2-2, and SFB1114, project A04. The Chodera laboratory receives or has received funding from multiple sources, including the National Institutes of Health, the National Science Foundation, the Parker Institute for Cancer Immunotherapy, Relay Therapeutics, Entasis Therapeutics, Silicon Therapeutics, EMD Serono (Merck KGaA), AstraZeneca, the Molecular Sciences Software Institute, the Starr Cancer Consortium, Cycle for Survival, a Louis V. Gerstner Young Investigator Award, and the Sloan Kettering Institute. A complete funding history for the Chodera lab can be found at http://choderalab.org/funding. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
The authors declare the following competing financial interest(s): J.D.C. was a member of the Scientific Advisory Board for Schrodinger, LLC during part of this study, and is a current member of the Scientific Advisory Board of OpenEye Scientific Software.
Author Contributions
∞ D.W.H.S. and J.H.P. contributed equally to this work.
References
- Buch I.; Giorgino T.; De Fabritiis G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 10184–10189. 10.1073/pnas.1103547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plattner N.; Doerr S.; Fabritiis G. D.; Noé F. Complete protein-protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 2017, 9, 1005–1011. 10.1038/nchem.2785. [DOI] [PubMed] [Google Scholar]
- Silva D.-A.; Bowman G. R.; Sosa-Peinado A.; Huang X. A Role for Both Conformational Selection and Induced Fit in Ligand Binding by the LAO Protein. PLoS Comput. Biol. 2011, 7, e1002054. 10.1371/journal.pcbi.1002054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schütte C.; Fischer A.; Huisinga W.; Deuflhard P. A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. 10.1006/jcph.1999.6231. [DOI] [Google Scholar]
- Schütte C.; Huisinga W. In Handbook of Numerical Analysis; Ciaret P. G., Lions J.-L., Eds.; Elsevier: 2003; Vol. X, pp 699–744, 10.1016/S1570-8659(03)10013-0. [DOI] [Google Scholar]
- Noé F.; Horenko I.; Schütte C.; Smith J. C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126, 155102. 10.1063/1.2714539. [DOI] [PubMed] [Google Scholar]
- Chodera J. D.; Singhal N.; Pande V. S.; Dill K. A.; Swope W. C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 2007, 126, 155101. 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- Chandler D. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne B. J., Ciccotti G., Coker D. F., Eds.; World Scientific: 1998; Chapter Barrier crossings: classical theory of rare but important events, pp 3–23. [Google Scholar]
- Peters B.Reaction Rate Theory and Rare Events; Elsevier Science: Amsterdam, 2017. [Google Scholar]
- Bolhuis P. G.; Chandler D.; Dellago C.; Geissler P. Transition path sampling: Throwing ropes over mountain passes, in the dark. Annu. Rev. Phys. Chem. 2002, 53, 291–318. 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- Torrie G. M.; Valleau J. P. Monte Carlo Free Energy Estimates Using Non-Boltzmann Sampling: Application to the Sub-Critical Lennard-Jones Fluid. Chem. Phys. Lett. 1974, 28, 578. 10.1016/0009-2614(74)80109-0. [DOI] [Google Scholar]
- Carter E.; Ciccotti G.; Hynes J. T.; Kapral R. Constrained Reaction Coordinate Dynamics for the Simulation of Rare Events. Chem. Phys. Lett. 1989, 156, 472. 10.1016/S0009-2614(89)87314-2. [DOI] [Google Scholar]
- Huber T.; Torda A.; van Gunsteren W. J. Comput.-Aided Mol. Des. 1994, 8, 695. 10.1007/BF00124016. [DOI] [PubMed] [Google Scholar]
- Grubmüller H. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1995, 52, 2893–2906. 10.1103/PhysRevE.52.2893. [DOI] [PubMed] [Google Scholar]
- Voter A. F. A method for accelerating the molecular dynamics simulation of infrequent events. J. Chem. Phys. 1997, 106, 4665. 10.1063/1.473503. [DOI] [Google Scholar]
- Laio A.; Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 12562. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darve E.; Pohorille A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169. 10.1063/1.1410978. [DOI] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Marinari E.; Parisi G. Simulated Tempering - A new monte-carlo scheme. Europhys. Lett. 1992, 19, 451–458. 10.1209/0295-5075/19/6/002. [DOI] [Google Scholar]
- Zheng L.; Chen M.; Yang W. Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 20227–20232. 10.1073/pnas.0810631106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y. Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. 10.1063/1.2825614. [DOI] [PubMed] [Google Scholar]
- Dellago C.; Bolhuis P. G.; Csajka F. S.; Chandler D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 1998, 108, 1964–1977. 10.1063/1.475562. [DOI] [Google Scholar]
- Dellago C.; Bolhuis P. G.; Geissler P. L. Transition path sampling. Adv. Chem. Phys. 2003, 123, 1–78. 10.1002/0471231509.ch1. [DOI] [Google Scholar]
- Dellago C.; Bolhuis P. G. Transition Path Sampling and Other Advanced Simulation Techniques for Rare Events. Adv. Polym. Sci. 2009, 221, 167–233. 10.1007/978-3-540-87706-6_3. [DOI] [Google Scholar]
- Allen R.; Frenkel D.; ten Wolde P. Simulating rare events in equilibrium or nonequilibrium stochastic systems. J. Chem. Phys. 2006, 124, 024102. 10.1063/1.2140273. [DOI] [PubMed] [Google Scholar]
- Cerou F.; Guyader A.; Lelievre T.; Pommier D. A multiple replica approach to simulate reactive trajectories. J. Chem. Phys. 2011, 134, 054108. 10.1063/1.3518708. [DOI] [PubMed] [Google Scholar]
- Faradjian A. K.; Elber R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys. 2004, 120, 10880–10889. 10.1063/1.1738640. [DOI] [PubMed] [Google Scholar]
- Moroni D.; Bolhuis P. G.; van Erp T. S. Rate constants for diffusive processes by partial path sampling. J. Chem. Phys. 2004, 120, 4055–4065. 10.1063/1.1644537. [DOI] [PubMed] [Google Scholar]
- Villen-Altamirano M.; Villen-Altamirano J. Analysis of RESTART simulation: Theoretical basis and sensitivity study. Eur. Trans. Telecom. 2002, 13, 373–385. 10.1002/ett.4460130409. [DOI] [Google Scholar]
- Berryman J. T.; Schilling T. Sampling rare events in nonequilibrium and nonstationary systems. J. Chem. Phys. 2010, 133, 244101. 10.1063/1.3525099. [DOI] [PubMed] [Google Scholar]
- Dickson A.; Warmflash A.; Dinner A. R. Separating forward and backward pathways in nonequilibrium umbrella sampling. J. Chem. Phys. 2009, 131, 154104. 10.1063/1.3244561. [DOI] [PubMed] [Google Scholar]
- Huber G.; Kim S. Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophys. J. 1996, 70, 97–110. 10.1016/S0006-3495(96)79552-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B. W.; Jasnow D.; Zuckerman D. M. The “weighted ensemble” path sampling method is statistically exact for a broad class of stochastic processes and binning procedures. J. Chem. Phys. 2010, 132, 054107. 10.1063/1.3306345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz J.-H.; Wu H.; Sarich M.; Keller B.; Senne M.; Held M.; Chodera J. D.; Schütte C.; Noé F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- Singhal N.; Snow C. D.; Pande V. S. Using path sampling to build better Markovian state models: Predicting the folding rate and mechanism of a tryptophan zipper beta hairpin. J. Chem. Phys. 2004, 121, 415–425. 10.1063/1.1738647. [DOI] [PubMed] [Google Scholar]
- Rogal J.; Bolhuis P. G. Multiple state transition path sampling. J. Chem. Phys. 2008, 129, 224107. 10.1063/1.3029696. [DOI] [PubMed] [Google Scholar]
- Pronk S.; Bowman G. R.; Hess B.; Larsson P.; Haque I. S.; Pande V. S.; Pouya I.; Beauchamp K.; Kasson P. M.; Lindahl E.. Copernicus: A new paradigm for parallel adaptive molecular dynamics. 2011 International Conference for High Performance Computing, Networking, Storage and Analysis (SC); 2011; pp 1–10, 10.1145/2063384.2063465. [DOI]
- Preto J.; Clementi C. Fast recovery of free energy landscapes via diffusion-map-directed molecular dynamics. Phys. Chem. Chem. Phys. 2014, 16, 19181–19191. 10.1039/C3CP54520B. [DOI] [PubMed] [Google Scholar]
- Balasubramanian V.; Bethune I.; Shkurti A.; Breitmoser E.; Hruska E.; Clementi C.; Laughton C.; Jha S.. ExTASY: Scalable and flexible coupling of MD simulations and advanced sampling techniques. 2016 IEEE 12th International Conference on e-Science (e-Science); 2016; pp 361–370, 10.1109/eScience.2016.7870921. [DOI]
- Wu H.; Mey A. S. J. S.; Rosta E.; Noé F. Statistically optimal analysis of state-discretized trajectory data from multiple thermodynamic states. J. Chem. Phys. 2014, 141, 214106. 10.1063/1.4902240. [DOI] [PubMed] [Google Scholar]
- Wu H.; Paul F.; Wehmeyer C.; Noé F. Multiensemble Markov models of molecular thermodynamics and kinetics. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, E3221–E3230. 10.1073/pnas.1525092113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mey A. S. J. S.; Wu H.; Noe F. xTRAM: Estimating Equilibrium Expectations from Time-Correlated Simulation Data at Multiple Thermodynamic States. Phys. Rev. X 2014, 4, 041018. 10.1103/PhysRevX.4.041018. [DOI] [Google Scholar]
- Rosta E.; Hummer G. Free Energies from Dynamic Weighted Histogram Analysis Using Unbiased Markov State Model. J. Chem. Theory Comput. 2015, 11, 276–285. 10.1021/ct500719p. [DOI] [PubMed] [Google Scholar]
- Eastman P.; Pande V. S. OpenMM: A hardware-independent framework for molecular simulations. Comput. Sci. Eng. 2010, 12, 34–39. 10.1109/MCSE.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eastman P.; Friedrichs M.; Chodera J. D.; Radmer R.; Bruns C.; Ku J.; Beauchamp K.; Lane T. J.; Wang L.-P.; Shukla D.; Tye T.; Houston M.; Stitch T.; Klein C. OpenMM 4: A reusable, extensible, hardware independent library for high performance molecular simulation. J. Chem. Theory Comput. 2013, 9, 461. 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lervik A.; Riccardi E.; van Erp T. S. PyRETIS: A well-done, medium-sized python library for rare events. J. Comput. Chem. 2017, 38, 2439–2451. 10.1002/jcc.24900. [DOI] [PubMed] [Google Scholar]
- Swenson D. W. H.; Prinz J.-H.; Noé F.; Chodera J. D.; Bolhuis P. G. J. Chem. Theory Comput. 2018, 10.1021/acs.jctc.8b00627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolhuis P. G.; Dellago C.. Reviews of Computational Chemistry; Wiley-VCH: Hoboken, 2009. [Google Scholar]
- Guarnera E.; Vanden-Eijnden E. Optimized Markov state models for metastable systems. J. Chem. Phys. 2016, 145, 024102. 10.1063/1.4954769. [DOI] [PubMed] [Google Scholar]
- Juraszek J.; Bolhuis P. G. Sampling the multiple folding mechanisms of Trp-cage in explicit solvent. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 15859–15864. 10.1073/pnas.0606692103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grünwald M.; Dellago C.; Geissler P. L. Precision shooting: Sampling long transition pathways. J. Chem. Phys. 2008, 129, 194101. 10.1063/1.2978000. [DOI] [PubMed] [Google Scholar]
- Mullen R. G.; Shea J.-E.; Peters B. Easy transition path sampling methods: Flexible-length aimless shooting and permutation shooting. J. Chem. Theory Comput. 2015, 11, 2421–2428. 10.1021/acs.jctc.5b00032. [DOI] [PubMed] [Google Scholar]
- Brotzakis Z. F.; Bolhuis P. G. A one-way shooting algorithm for transition path sampling of asymmetric barriers. J. Chem. Phys. 2016, 145, 164112. 10.1063/1.4965882. [DOI] [PubMed] [Google Scholar]
- Riccardi E.; Dahlen O.; van Erp T. S. Fast Decorrelating Monte Carlo Moves for Efficient Path Sampling. J. Phys. Chem. Lett. 2017, 8, 4456–4460. 10.1021/acs.jpclett.7b01617. [DOI] [PubMed] [Google Scholar]
- van Erp T. S.; Moroni D.; Bolhuis P. G. A novel path sampling method for the calculation of rate constants. J. Chem. Phys. 2003, 118, 7762. 10.1063/1.1562614. [DOI] [Google Scholar]
- Rogal J.; Lechner W.; Juraszek J.; Ensing B.; Bolhuis P. G. The reweighted path ensemble. J. Chem. Phys. 2010, 133, 174109. 10.1063/1.3491817. [DOI] [PubMed] [Google Scholar]
- Dellago C.; Bolhuis P. G.; Chandler D. On the calculation of reaction rate constants in the transition path ensemble. J. Chem. Phys. 1999, 110, 6617–6625. 10.1063/1.478569. [DOI] [Google Scholar]
- Cabriolu R.; Refsnes K. M. S.; Bolhuis P. G.; van Erp T. S. Foundations and latest advances in replica exchange transition interface sampling. J. Chem. Phys. 2017, 147, 152722. 10.1063/1.4989844. [DOI] [PubMed] [Google Scholar]
- Torrie G. M.; Valleau J. P. Monte Carlo Free Energy Estimates Using Non-Boltzmann Sampling: Application to the Sub-Critical Lennard-Jones Fluid. Chem. Phys. Lett. 1974, 28, 578. 10.1016/0009-2614(74)80109-0. [DOI] [Google Scholar]
- Borrero E. E.; Weinwurm M.; Dellago C. Optimizing transition interface sampling simulations. J. Chem. Phys. 2011, 134, 244118. 10.1063/1.3601919. [DOI] [PubMed] [Google Scholar]
- van Erp T. S.; Bolhuis P. G. Elaborating transition interface sampling methods. J. Comput. Phys. 2005, 205, 157–181. 10.1016/j.jcp.2004.11.003. [DOI] [Google Scholar]
- Du W.-N.; Marino K. A.; Bolhuis P. G. Multiple state transition interface sampling of alanine dipeptide in explicit solvent. J. Chem. Phys. 2011, 135, 145102. 10.1063/1.3644344. [DOI] [PubMed] [Google Scholar]
- Du W.; Bolhuis P. G. Sampling the equilibrium kinetic network of Trp-cage in explicit solvent. J. Chem. Phys. 2014, 140, 195102. 10.1063/1.4874299. [DOI] [PubMed] [Google Scholar]
- Noe F.; Krachtus D.; Smith J.; Fischer S. Transition networks for the comprehensive characterization of complex conformational change in proteins. J. Chem. Theory Comput. 2006, 2, 840–857. 10.1021/ct050162r. [DOI] [PubMed] [Google Scholar]
- Minh D.; Chodera J. Optimal estimators and sysmptotic variances for nonequilibrium path-ensemble averages. J. Chem. Phys. 2009, 131, 134110. 10.1063/1.3242285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du W.-N.; Bolhuis P. G. Adaptive single replica multiple state transition interface sampling. J. Chem. Phys. 2013, 139, 044105. 10.1063/1.4813777. [DOI] [PubMed] [Google Scholar]
- van Kampen N. G.Stochastic processes in physics and chemistry, 2nd ed.; Elsevier: 1997. [Google Scholar]
- Noé F.; Schütte C.; Vanden-Eijnden E.; Reich L.; Weikl T. R. Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 19011–19016. 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolhuis P. G.; Dellago C. Practical and conceptual path sampling issues. Eur. Phys. J.: Spec. Top. 2015, 224, 2409–2427. 10.1140/epjst/e2015-02419-6. [DOI] [Google Scholar]
- Bolhuis P. Transition-path sampling of beta-hairpin folding. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 12129–12134. 10.1073/pnas.1534924100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vreede J.; Juraszek J.; Bolhuis P. G. Predicting the reaction coordinates of millisecond light-induced conformational changes in photoactive yellow protein. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 2397–2402. 10.1073/pnas.0908754107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brotzakis Z. F.; Bolhuis P. G. to be published.
- van Erp T. Reaction Rate Calculation by Parallel Path Swapping. Phys. Rev. Lett. 2007, 98, 268301. 10.1103/PhysRevLett.98.268301. [DOI] [PubMed] [Google Scholar]
- Bolhuis P. G. Rare events via multiple reaction channels sampled by path replica exchange. J. Chem. Phys. 2008, 129, 114108. 10.1063/1.2976011. [DOI] [PubMed] [Google Scholar]
- van Erp T. S. Dynamical rare event simulation techniques for equilibrium and nonequilibrium systems. Adv. Chem. Phys. 2012, 151, 27–60. 10.1002/9781118309513.ch2. [DOI] [Google Scholar]
- Swenson D. W. H.; Bolhuis P. G. A replica exchange transition interface sampling method with multiple interface sets for investigating networks of rare events. J. Chem. Phys. 2014, 141, 044101. 10.1063/1.4890037. [DOI] [PubMed] [Google Scholar]
- Lyubartsev A. P.; Martsinovski A. A.; Shevkunov S. V.; Vorontsov-Velyaminov P. N. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J. Chem. Phys. 1992, 96, 1776–1783. 10.1063/1.462133. [DOI] [Google Scholar]
- Tan Z. Optimally Adjusted Mixture Sampling and Locally Weighted Histogram Analysis. J. Comput. Graph. Stat. 2017, 26, 54–65. 10.1080/10618600.2015.1113975. [DOI] [Google Scholar]
- Newton A. C.; Groenewold J.; Kegel W. K.; Bolhuis P. G. Rotational diffusion affects the dynamical self-assembly pathways of patchy particles. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 15308–15313. 10.1073/pnas.1513210112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eastman P.; et al. OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J. Chem. Theory Comput. 2013, 9, 461–469. 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
- Tribello G. A.; Bonomi M.; Branduardi D.; Camilloni C.; Bussi G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
- Noé F.; Clementi C. Collective variables for the study of long-time kinetics from molecular trajectories: Theory and methods. Curr. Opin. Struct. Biol. 2017, 43, 141–147. 10.1016/j.sbi.2017.02.006. [DOI] [PubMed] [Google Scholar]
- McGibbon R. T.; Beauchamp K. A.; Harrigan M. P.; Klein C.; Swails J. M.; Hernández C. X.; Schwantes C. R.; Wang L.-P.; Lane T. J.; Pande V. S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchamp K. A.; Bowman G. R.; Lane T. J.; Maibaum L.; Haque I. S.; Pande V. S. MSMBuilder2: Modeling Conformational Dynamics on the Picosecond to Millisecond Scale. J. Chem. Theory Comput. 2011, 7, 3412–3419. 10.1021/ct200463m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrigan M. P.; Sultan M. M.; Hernández C. X.; Husic B. E.; Eastman P.; Schwantes C. R.; Beauchamp K. A.; McGibbon R. T.; Pande V. S. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophys. J. 2017, 112, 10–15. 10.1016/j.bpj.2016.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherer M. K.; Trendelkamp-Schroer B.; Paul F.; Pérez-Hernández G.; Hoffmann M.; Plattner N.; Wehmeyer C.; Prinz J.-H.; Noé F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Kollman P. A. Advances and Continuing Challenges in Achieving Realistic and Predictive Simulations of the Properties of Organic and Biological Molecules. Acc. Chem. Res. 1996, 29, 461–469. 10.1021/ar9500675. [DOI] [Google Scholar]
- Chodera J. D.; Swope W. C.; Pitera J. W.; Dill K. A. Long-Time Protein Folding Dynamics from Short-Time Molecular Dynamics Simulations. Multiscale Model. Simul. 2006, 5, 1214–1226. 10.1137/06065146X. [DOI] [Google Scholar]
- Prinz J.-H.; Chodera J. D.; Pande V. S.; Swope W. C.; Smith J. C.; Noé F. Optimal use of data in parallel tempering simulations for the construction of discrete-state Markov models of biomolecular dynamics. J. Chem. Phys. 2011, 134, 244108. 10.1063/1.3592153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivak D. A.; Chodera J. D.; Crooks G. E. Time Step Rescaling Recovers Continuous-Time Dynamical Properties for Discrete-Time Langevin Integration of Nonequilibrium Systems. J. Phys. Chem. B 2014, 118, 6466–6474. 10.1021/jp411770f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolhuis P. G.; Dellago C.; Chandler D. Reaction coordinates of biomolecular isomerization. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 5877–5882. 10.1073/pnas.100127697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juraszek J.; Bolhuis P. G. Rate Constant and Reaction Coordinate of Trp-Cage Folding in Explicit Water. Biophys. J. 2008, 95, 4246–4257. 10.1529/biophysj.108.136267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolhuis P. G.; Dellago C. Practical and conceptual path sampling issues. Eur. Phys. J.: Spec. Top. 2015, 224, 2409–2427. 10.1140/epjst/e2015-02419-6. [DOI] [Google Scholar]
- Nguyen H.; Case D. A.; Rose A. S. NGLview - interactive molecular graphics for Jupyter notebooks. Bioinformatics 2018, 34, 1241. 10.1093/bioinformatics/btx789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leimkuhler B.; Matthews C. Robust and efficient configurational molecular sampling via Langevin dynamics. J. Chem. Phys. 2013, 138, 174102. 10.1063/1.4802990. [DOI] [PubMed] [Google Scholar]
- Shirts M. COMPUTING: Screen Savers of the World Unite!. Science 2000, 290, 1903–1904. 10.1126/science.290.5498.1903. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Piana S.; Dror R. O.; Shaw D. E. How Fast-Folding Proteins Fold. Science 2011, 334, 517–520. 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- Isralewitz B.; Gao M.; Schulten K. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 2001, 11, 224–230. 10.1016/S0959-440X(00)00194-9. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. 10.1063/1.1323224. [DOI] [Google Scholar]
- E W.; Ren W.; Vanden-Eijnden E. Finite Temperature String Method for the Study of Rare Events. J. Phys. Chem. B 2005, 109, 6688–6693. 10.1021/jp0455430. [DOI] [PubMed] [Google Scholar]