The Influence of Molecular Structure on the Adsorption of PFAS to Fluid-Fluid Interfaces: Using QSPR to Predict Interfacial Adsorption Coefficients

Abstract

Per- and poly-fluoroalkyl substances (PFAS) are emerging contaminants of critical concern for human health risk. Assessing exposure risk requires a thorough understanding of the transport and fate behavior of PFAS in the environment. Adsorption to fluid-fluid interfaces, which include air-water, OIL-water, and air-OIL interfaces (where OIL represents organic immiscible liquid), is a potentially significant retention process for PFAS transport. Fluid-fluid interfacial adsorption coefficients (K_i) are required for use in transport modeling and risk characterization, yet these data are currently not available for the vast majority of PFAS. Surface-tension and interfacial-tension data sets collected from the literature were used to determine interfacial adsorption coefficients for 42 individual PFAS. The PFAS evaluated comprise homologous series of perfluorocarboxylates and perfluorosulfonates, branched perfluoroalkyls, polyfluoroalkyls, alcohol PFAS, and nonionic PFAS. The K_i values vary across eight orders of magnitude, and are a function of molecular structure. The results of quantitative-structure/property-relationship (QSPR) analysis demonstrate that a model employing molar volume (V_m) as a descriptor provides robust predictions of log K_i values for air-water interfacial adsorption of the wide range of PFAS. The model also produced good predictions for a limited set of data for OIL-water interfacial adsorption. The predictive capability of the QSPR model for a wide range of PFAS with greatly varying structures reflects the fact that molar volume provides a reasonable representation of the influence of molecular size on cavity formation/destruction in solution, and thus the hydrophobic-interaction driving force for interfacial adsorption. The QSPR model presented herein provides a means to incorporate the fluid-fluid interfacial adsorption process into transport characterization and risk assessment of PFAS in the environment. This will be particularly relevant for determining PFAS mass flux in the atmosphere, in the vadose zone, in source zones containing organic immiscible liquids, and in water/wastewater treatment systems.

Graphical Abstract

Introduction

Numerous research reports have demonstrated that per- and poly-fluoroalkyl substances (PFAS) are widespread in the environment, occurring in the atmosphere, surface water, sediment, soil, groundwater, treated wastewater, biosolids, landfill leachate, and drinking water (e.g., Moody and Field, 1999; Higgins et al., 2005; Schultz et al., 2006; Quiñones and Snyder, 2009; Rayne and Forest, 2009; Ahrens, 2011; Ahrens et al., 2011; Krafft and Riess, 2015; Cousins et al., 2016; Hu et al., 2016; Xiao, 2017; Hamid et al., 2018). This ubiquitous distribution, in conjunction with toxicity concerns for humans and other organisms, has resulted in PFAS becoming primary emerging contaminants of concern. Assessing exposure risk requires a thorough understanding of the transport and fate behavior of PFAS in the environment. Phase-transfer processes are a primary factor affecting the transport and fate of PFAS. To date, research has focused primarily on two such processes, the sorption of PFAS to solids such as soil, sediment, and activated carbon, and air-water partitioning. However, given the molecular properties of PFAS, it is critical to also consider adsorption at fluid-fluid interfaces as a potential retention process for environmental systems (Brusseau, 2018).

There are four scenarios for which fluid-fluid interfacial adsorption may be particularly relevant for PFAS in environmental systems. First, it is recognized that certain PFAS undergo extensive atmospheric transport (e.g., Simcik, 2005; Prevedouros et al., 2006; Ahrens, 2011; Rauert et al., 2018). Water droplets and hydrated aerosols in the atmosphere provide air-water interface that can serve as significant retention domains for contaminants (e.g., Donaldson and Valsaraj, 2010). Extensive research has demonstrated that a wide range of organic compounds undergo adsorption at air-water interfaces (e.g., Karger et al., 1971; Valsaraj, 1988; Hoff et al., 1993; Brusseau et al., 1997; Costanza and Brusseau, 2000; Roth et al., 2002). Given the surface-active nature of PFAS, it is likely that air-water interfacial adsorption is an important factor in the atmospheric transport of PFAS. This was hypothesized in a study wherein enrichment of select PFAS at the air-water interface was measured for microdroplets produced by pneumatic nebulization of aqueous solutions (Psillakis et al., 2009).

A second scenario involves PFAS transport in vadose-zone systems. Detailed evaluations of PFAS occurrence at field sites have shown that vadose-zone sources are a primary subsurface reservoir of PFAS, serving as long-term sources to groundwater (Shin et al., 2011; Xiao et al., 2015; Weber et al., 2017). The air-water interface is a primary potential retention domain for constituents in the vadose zone. Transport studies have shown that air-water interfacial adsorption significantly influences the transport of both surfactants and non-surfactants in water-unsaturated porous media (e.g., Brusseau et al., 1997, 2007, 2015; Kim et al., 1997, 1998, 2001; Anwar et al., 2000; Anwar, 2001; Costanza and Brusseau, 2002; Peng and Brusseau, 2005; Costanza-Robinson et al., 2013). Thus, it is likely to be relevant for PFAS transport in the vadose zone. Adsorption at the air-water interface was shown to be a significant source of retention for PFOS and PFOA transport in unsaturated porous media in recent theoretical and experimental studies (Brusseau, 2018; Lyu et al., 2018; Brusseau et al., 2019).

The transport of PFAS in source zones containing immiscible organic liquids comprises a third scenario. PFAS co-occur with organic liquids such as fuels and chlorinated solvents at certain types of sites, such as fire training areas (e.g., Moody et al., 2003; McGuire et al., 2014). Prior research has demonstrated that the transport of hydrocarbon surfactants in organic-liquid contaminated porous media is greatly influenced by adsorption at the OIL-water interface (e.g., Saripalli et al., 1997, 1998; Cho and Annable, 2005; Dobson et al., 2006; Brusseau et al., 2008, 2010; Narter and Brusseau, 2010; McDonald et al., 2016; Zhong et al., 2016). The potential impact of OIL-water interfacial adsorption was noted but not quantified in a recent study investigating PFAS transport in a trichloroethene-contaminated soil (McKenzie et al., 2016). The impact of OIL-water interfacial adsorption on PFAS transport was quantitatively characterized in recent studies (Brusseau, 2018; Brusseau et al., 2019).

A fourth scenario involves the fate of PFAS in water and wastewater treatment systems. Air-water interfaces are created in several widely used treatment processes. Hence, it is possible that air-water interfacial adsorption may be significant in such systems. For example, it was recently hypothesized that adsorption to the interfaces of air bubbles trapped on the surfaces of carbonaceous water-treatment sorbents is a primary source of the retention they provide for treatment (Meng et al., 2014).

These four scenarios illustrate the likely importance of fluid-fluid interfacial adsorption to the transport and fate of PFAS in environmental systems. Measured fluid-fluid interfacial adsorption coefficients are required for transport modeling and risk assessment of PFAS. However, PFAS comprise hundreds of compounds and it is impractical to conduct measurements for all of them. In such cases, quantitative-structure/property-relationship (QSPR) analysis methods can be used to provide empirical-based estimates. This approach is widely used for the estimation of many phase-transfer (partition) coefficients, and it has been applied to PFAS (e.g., Gabriel et al., 1996; Bhhatarai and Gramatica, 2011; Kim et al., 2015; Lyu et al., 2018). For example, Bhhatarai and Gramatica conducted an extensive QSPR analysis for PFAS, and showed that aqueous solubility, vapor pressure, and critical micelle concentration (CMC) were all well described by simple QSPR models. Similarly, Kim et al. (2015) demonstrated the effectiveness of simple QSPR models for estimating vapor pressures, aqueous solubilities, octanol/water partition coefficients, air/water partition coefficients, and octanol/air partition coefficients of PFAS. Lyu et al. (2018) successfully applied QSPR analysis to air-water interfacial adsorption coefficients for a homologous series of perfluoroalkyl carboxylates.

The development of a QSPR model for estimation of interfacial adsorption coefficients would be a significant first step in enabling consideration of fluid-fluid interfacial adsorption in transport modeling and risk assessment of PFAS in the environment. The objective of this study is to develop and evaluate the efficacy of QSPR-based models for predicting fluid-fluid interfacial adsorption coefficients for PFAS. First, an extensive literature search is conducted to collect published measured surface-tension and interfacial-tension data sets for a broad range of PFAS. A meta-analysis is then conducted to generate the largest data set for one consistent set of conditions. These data are used to determine air-water and OIL-water interfacial adsorption coefficients. Finally, QSPR models are developed using simple, whole-molecule descriptors, and tested for performance.

Materials and Methods

Literature Data

Approximately 65 journal articles were retrieved that reported measured surface-tension or interfacial-tension data sets for PFAS. Some studies reported data for multiple compounds or conditions. Hence, a total of ∼160 individual data sets for PFAS were obtained from the literature search. In addition, data sets were obtained for four common hydrocarbon surfactants, sodium dodecyl sulfate (SDS), sodium dodecylbenzene sulfonate (SDBS), hexadecyltrimethylammonium bromide (CTAB), and octylphenol ethoxylate (Triton 45) for use in comparative analysis. Different methods were used in the studies to measure surface/interfacial tension, including Du Nouy ring, Wilhelmy plate, pendant drop, and drop-weight methods.

It is well known that surface/interfacial tension is influenced by solution properties such as ionic strength and by surfactant form (acid versus salt). Therefore, the data sets were collated to generate the largest data set for one consistent set of conditions. The great majority of the reported surface-tension measurements were conducted using deionized water as the aqueous phase. Also, salt forms of PFAS rather than acid forms comprised the majority of the data sets. Specifically, Na-salts were predominant for perfluorocarboxylates (PFCAs) and K-salts were predominant for perfluorosulfonates (PFSAs). Eight interfacial-tension data sets were analyzed for OIL-water systems, six for PFAS and two for hydrocarbon surfactants. The final set of data used for this work is presented in Tables 1 and S1. These tables include the acronyms employed for each compound as well as molecular formulas. The open-source Engauge program (Mitchell et al., 2017) was used to digitize the reported surface- and interfacial-tension data sets.

Table 1.

Names, Acronyms, and K_i values for data used in this study.

Acronym	Perfluorocarboxylates	Ki (cm)
PFAA	Na-Perfluoroacetoate	1.52E-07
PFPrA	Na-Perfluoropropanoate	7.14E-07
PFBA	Na-Perfluorobutanoate	1.72E-06
PFPeA	Na-Perfluoropentanoate	5.84E-06
PFHxA	Na-Perfluorohexanoate	2.20E-05
PFHpA	Na-Perfluoroheptanoate	5.76E-05
PFOA	Na-Perfluorooctanoate	2.32E-04
PFNA	Na-Perfluorononanoate	9.34E-04
PFDA	Na-Perfluorodecanoate	3.72E-03
PFUnA	Na-Perfluoroundecanoate	1.90E-02
	Branched PFCAs
Iso-PFOA	Na perfluoro-methyl-heptanoate	2.39E-04
Iso-PFDA	Na-perfluoro-methyl-nonanoate	6.94E-03
	Perfluorosulfonates
PFBS	K-Perfluorobutanesulfonate	1.78E-05
PFHxS	K-Perfluorohexanesulfonate	9.72E-05
PFHpS	Na-Perfluoroheptanesulfonate	5.14E-04
PFOS	K-Perfluorooctanesulfonate	2.30E-03
PFNS	K-Perfluorononanesulfonate	3.70E-02
	Polyfluoroalkyls
9H-PFNA	Na-9H Hexadecafluorononanoate	2.00E-04
7H-PFHpA	NH4-7H-dodecafluoroheptanoate	4.84E-05
SPBS	Na-p-perfluorononenyloxy benzene sulfonate	6.69E-01
FC-53	K-3-oxa-perfluorononane-sulfonate	1.67E-03
TDFHD	Na-tridecafluorohexadecanoate	8.00E-01
F9-CTAB	Nonafluoropentadecyl-CTAB	4.93E-03
F12-CTAB	Dodecafluoropentadecyl-CTAB	7.40E-03
F17-CTAB	Heptadecafluorotetradecyl-CTAB	1.60E-02
UDFOS	Na-undecafluorooctanesulfonate	1.00E-04
NFHES	Na-nonafluorohexylethersulfonate	6.64E-05
UDFHES	Na-undecafluoroheptylethersulfonate	2.94E-04
TDFP	Na-tridecafluoropentanoate	3.16E-04
TDHP	Na-tridecafluorohexanoate	4.26E-04
HDFPEC	Na-heptadecafluoropolyether carboxylate	1.24E-03
TDFPBP	Li-tridecafluoropentylbenzene phosphonate	3.43E-03
	Nonionic PFAS
TDFTDE	Tridecafluoro thiodiethoxylate	1.10E+00
TDFTTE	Tridecafluoro thiotriethoxylate	1.80E+00
TDFTPE	Tridecafluoro thiopentaethoxylate	6.50E+00
PFOA-amide	N-(2-hydroxypropyl)perfluorooctane amide	5.35E-02
NFTME	Nonafluoro triethyleneoxide methyl ether	5.58E-02
TDFTME	Tridecafluro triethyleneoxide methyl ether	7.50E-01
HOFTME	H-octafluoro triethyleneoxide methyl ether	2.00E-02
HDDFTME	H-dodecafluoro triethyleneoxide methyl ether	2.31E-01
	Alcohols
8:1 FTOH	8:1 Fluorotelomer alcohol	1.66E-02
FC8diol	Perfluorooctane-1,8-diol	4.12E-03
	Hydrocarbons
SDBS	Na-dodecylbenzene sulfonate	1.10E-01
SDS	Na-dodecyl sulfate	2.36E-04
CTAB	Hexadecyltrimethylammonium bromide	1.30E-03
Triton 45	Octylphenol Ethoxylate	6.46E-01
	OIL-Water
PFOA	Cs-PFOA Decane-Water	1.26E-04
PFOA	Cs-PFOA Benzene-Water	5.60E-05
PFOA	Na-PFOA Heptane-Water	1.67E-04
PFNA	Na-PFNA Heptane-Water	6.57E-04
TDFP	Na-TDFP Heptane-Water	8.47E-05
TDHP	Na-TDHP Heptane-Water	1.31E-04
SDBS	SDBS Tetrachloroethene-Water	7.35E-02
SDBS	SDBS Decane-Water	4.69E-02

Determining Fluid-Fluid Interfacial Adsorption Coefficients

Fluid-fluid interfacial adsorption coefficients can be determined from the surface/interfacial tension function. The surface excess Γ (mol/cm²) of a compound at the interface is related to the aqueous-phase concentration (C) using the Gibbs equation:

$$\Gamma =\frac{-1}{\text{xRT}}\frac{\partial \gamma }{\partial \mathit{lnC}}$$ (1)

where γ is the interfacial tension (dyn/cm or mN/m), C represents the aqueous phase concentration (mol/cm³), T is temperature (°K), R is the universal gas constant (dyne-cm/mol °K), and x is a coefficient equal to 1 for systems with nonionic surfactants (or ionic surfactants with excess electrolyte in solution), and equal to 2 for systems with ionic surfactants without excess electrolyte (e.g., deionized water). The Gibbs equation has been shown in innumerable studies to provide accurate representation of surfactant behavior at fluid-fluid interfaces (e.g., Adamson, 1982; Hiemenz, 1986; Pashley and Karaman, 2004; Barnes and Gentle, 2005; Berg, 2010; Rosen and Kunjappu, 2012; Kronberg et al., 2014). The amount adsorbed at the interface as a function of aqueous concentration (adsorption isotherm) can be determined as (e.g., Fridrikhsberg, 1986; Hiemenz, 1986; Barnes and Gentle, 2005; Berg, 2010):

$$K_i=\frac{\Gamma }{C}=\frac{-1}{\text{xRT}\mathrm{C}}\frac{\partial \gamma }{\partial \mathit{lnC}}$$ (2)

where K_i is the interfacial adsorption coefficient (cm). K_i can be determined for any given aqueous concentration by calculating the slope of surface tension versus 1n C (i.e., Γ in equation 1) through use of a tangent taken at the concentration of interest (e.g., Fridrikhsberg, 1986; Hiemenz, 1986), and dividing by the relevant C (equation 2).

Surfactant adsorption at the fluid-fluid interface is nonlinear. For industrial applications, Γ_max is typically the value of interest, which is calculated using the constant slope determined for solution concentrations approaching the critical micelle concentration. For environmental systems wherein lower concentrations are of interest, Γ and K_i are calculated using the local slope of the surface-tension function for the given concentration of interest (e.g., Kim et al., 1997; Brusseau et al., 2007; Zhong et al., 2016). This approach accounts for the nonlinearity of fluid-fluid interfacial adsorption. This is illustrated in Figure S1, which presents the full range of K_i values determined for three selected PFAS. These values were determined using the best-fit of the Szyszkowski equation (see below) to the measured surface-tension data sets, with K_i values calculated using local slopes for each discrete C. It is relevant to note that the results of recent studies have demonstrated that K_i values determined from surface-tension data in this manner are consistent with values determined from miscible-displacement transport experiments for PFOA (Lyu et al., 2018) and PFOS (Brusseau et al., 2019).

A target concentration of 0.1 mg/L was used to calculate K_i values for this work. The selected value is within the range of groundwater concentrations reported for PFAS at contaminated sites (e.g., Moody and Field, 1999; Ahrens, 2011; Schultz et al., 2004; McGuire et al., 2014; Cousins et al., 2016; Baduel et al., 2017). The representativeness of K_i values obtained for this target concentration will be evaluated in the Results section, with the outcome revealing that the so-determined K_i values are essentially maximum values.

The resolution of the data sets (concentration range and density of measurements) varied among the studies. Thus, the Szyszkowski equation was applied to all of the measured data sets to provide a uniform means of data analysis. Numerous authors have demonstrated that the Szyszkowski equation provides accurate representation of surfactant surface-tension and interfacial-tension data (e.g., Adamson, 1982; Schick, 1987; Fainerman et al, 2001; Barnes and Gentle, 2005; Berg, 2010; Rosen and Kunjappu, 2012; Zhong et al., 2016), including for PFAS (e.g., Vecitis et al., 2008; Lunkenheimer et al., 2015). One form of the equation is given as (e.g., Adamson, 1982; Barnes and Gentle, 2005):

$$\gamma ={\gamma }_0[1-B\text{ln}\left(1+\frac{C}{A}\right)]$$ (3)

where γ₀ is the interfacial tension at [PFAS] = 0 (e.g., the surface tension of pure water), and A and B are variables related to properties of the specific compound and of the homologous series, respectively. The best-fit functions were used to obtain the slope factors required for equation 1 for all data sets.

QSPR Analysis

A wide variety of molecular descriptors are available for QSPR analysis, ranging from simple size-based descriptors such as molecular weight (MW) and molar volume (V_m), simple constitutional descriptors based on numbers of a specific type of atom or bond (e.g., carbon number, CN), descriptors characterizing molecular structure (such as the molecular connectivity index, X), to complex 3-D geometrical descriptors (e.g., Todeschini and Consonni, 2009). The work herein will focus on simple descriptors that can be readily calculated for even the most complex PFAS structures.

QSPR analysis can be conducted using models based on the application of a single descriptor (one-descriptor models), or using multiple descriptors. The approach used herein employs the single-descriptor approach to maintain simplicity. The four primary descriptors to be tested are MW, V_m, CN, and number of fluorine atoms (FN). A variation of CN will also be tested, based on the number of carbon atoms associated specifically with the surfactant tail (CN_t). Focusing on these whole-molecule descriptors is consistent with the single-descriptor approach and facilitates ease of use.

As reviewed by Costanza and Brusseau (2000), several single-descriptor QSPR models have been reported for predicting K_i values for non-surfactant organic compounds, including ones based on V_m and X. These descriptors have also been shown to be effective for predicting distribution coefficients for sorption of organic compounds by soils and sediments (Brusseau, 1993; Hu and Brusseau, 1995). Furthermore, molar volume in particular is widely used for environmental chemical fate estimation applications (e.g., Mackay et al., 2006). The rationale for testing CN, CN_t, and FN is based on the widely observed phenomenon that the surface activity of surfactants increases as a function of chain length of the tail, referred to as Traube’s rule.

Molar volumes can be determined in three ways, measured by experiment, calculated using molecular-analysis approaches, and calculated as the quotient of MW and compound density (ρ_c). Measured V_m values are readily available for many common hydrocarbon surfactants. Conversely, there are minimal reported values for PFAS. In keeping with the theme of simplicity, V_ms for this analysis were calculated as MW/ρ_c (e.g., Kaliszan, 1987; Baum, 1998; Reinhard and Drefahl, 1999). Densities were obtained from ChemSpider, PubChem, and product manufacturer’s websites. For the ionic compounds, the molecular weight of the base (ionized) PFAS molecule was used for the analysis, excluding the contribution of the counterion. A standard group-contribution analysis approach, employing the Schroeder method (e.g., Baum, 1998; Reinhard and Drefahl, 1999; Poling et al., 2000), was used to calculate V_m values for those compounds for which densities were unavailable.

The V_m values calculated from MW/ρ_c compare well to reported independently determined values. For example, Zhao et al. (2006) employed atomic force microscopy to measure precisely the single-molecule volume of CTAB. The reported value of 0.469 nm³ translates to a molar volume of 282.4 cm³/mol, which is very similar to the value (∼280) obtained using the standard solution-density measurement method (Bhattarai et al., 2015). The V_m calculated from MW/ρ_c is 282, which is essentially identical to the measured values. Similarly, the calculated V_m of 241 for SDS compares very well to the mean of three measured values reported in the literature (245 ±3). V_m values for several PFAS, calculated using molecular-analysis software from ACD/Labs, are reported in the ChemSpider website. The mean difference between V_m values calculated from MW/ρ_c and the ChemSpider-reported values is 1.3%, with the largest difference being 4%, for the 21 PFAS used in this study for which values are reported in ChemSpider. These results indicate that calculating V_m from MW/ρ_c is a reasonable approach for this study.

The QSPR analysis was conducted following recommended best-practice guidelines (e.g., Dearden et al., 2009). The data were split into a training set and an independent external validation set. The training set consists of the homologous series of PFCAs and PFSAs, which represent the “standard” linear anionic PFAS. Prior research has shown that the surface activity of these PFAS is a function of chain length (e.g., Hendricks, 1953; Shinoda et al., 1972; Tamaki et al., 1989; Kissa, 2001; Lunkenheimer et al., 2015). The PFCAs and PFSAs comprise 10 and 5 compounds, respectively, for a total of 15 data points for the training set. The ratio of number of training-set compounds to the number of descriptors is 15:1, much greater than the recommended minimum of 5:1 (Dearden et al., 2009). The training set spans a majority of the range of values exhibited by the dependent and independent variables, and is uniformly distributed across the span. The data for the 10 PFCAs were obtained from two primary sources (Table S1), which enhances internal consistency for the training set. A comparison of K_i values determined from the surface-tension data reported by the two sources for the one compound in common (PFHpA) shows excellent agreement-- 5.5 ·10⁻⁵ cm versus 6.0 ·10⁻⁵ cm.

Inspection of Table 1 reveals that the compounds comprising the training set represent the simplest molecular structures among the data set. Conversely, the validation set comprises much greater molecular-structure complexity, including 2 branched PFAS, 15 poly-PFAS (of which three are cationic rather than anionic, and another three are branched), 8 nonionic PFAS, and 2 alcohols. In addition, data are included for four common hydrocarbon surfactants, SDS, SDBS, CTAB, and Triton. Finally, eight data points for OIL-water interfacial adsorption are included, comprising PFOA for benzene-water, decane-water, and heptane-water systems, PFNA, TDFP, and TDHP for heptane-water, and SDBS for tetrachloroethene-water and decane-water. This sums to a total of 39 data points for the validation set, which is more than double the number of data comprising the training set, and 54 for the combined total. The data sources for the validation set are different from the sources for the training set, and thus the validation set comprises an independent external test set. Statistical analyses were conducted using Microsoft excel.

Results and Discussion

Surface tension data

A critical factor to consider when integrating data collected from a large number of studies is consistency among the individual data sets. This is especially true for QSPR analyses, where it is important to determine that observed variations in the target property are actually due to associated variations in molecular structure and not to inter-study inconsistencies. Data consistency was evaluated for this study by examining the variation among measured surface-tension data sets reported for Na-perfluorooctanoate, the most commonly reported compound.

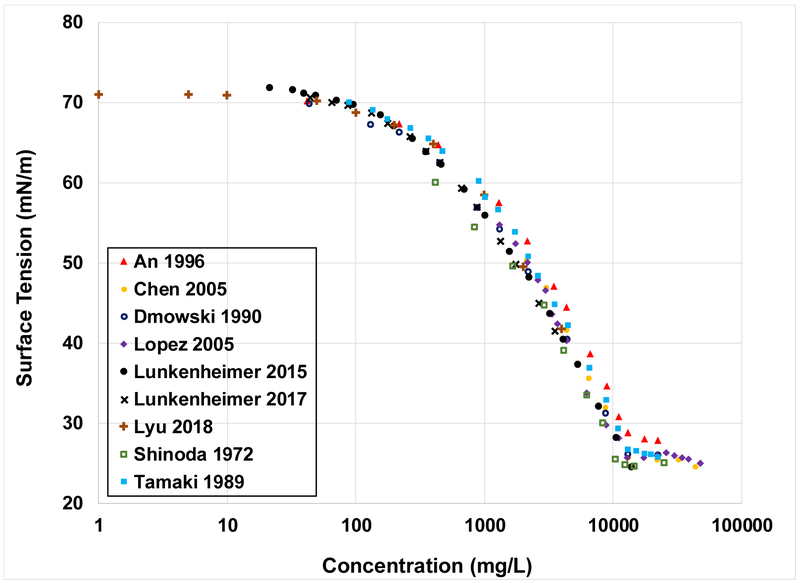
A plot of Na-PFOA surface-tension data reported in nine separate studies is presented in Figure 1. Inspection of the data reveals remarkable consistency of measured surface tensions across the nine studies. This is especially noteworthy considering that the studies span 46 years and include different measurement methods. Given these results, it is concluded that the compiled surface-tension data sets are sufficiently consistent to support QSPR analysis.

Figure 1.

Surface-tension data reported from 9 sources for Na-PFOA. The legend is referenced to Table S1.

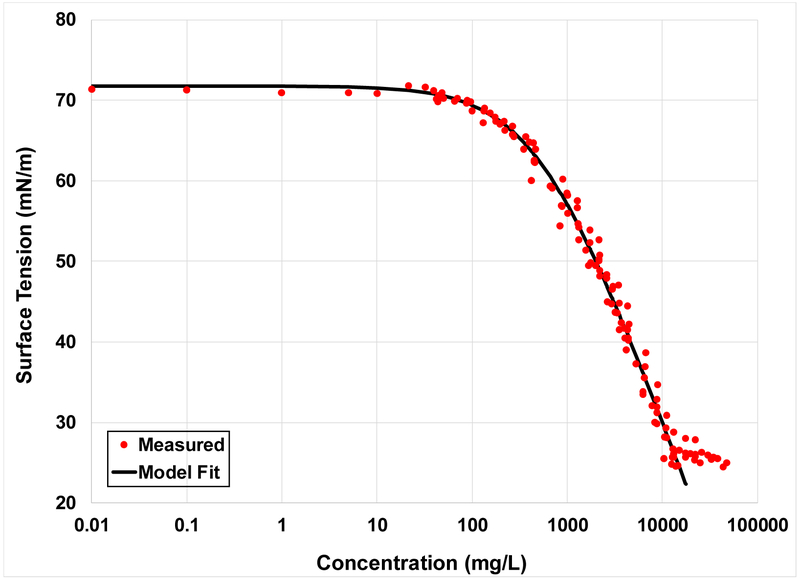
The fit of the Szyszkowski equation to the aggregated Na-PFOA data set is shown in Figure 2. The equation provides a very good match to the measured data presented in Figure 2, and for all of the data sets used in this study. This indicates that it is reasonable to use the equation for application to the surface/interfacial-tension data. This is consistent with the results of prior research.

Figure 2.

The fit of the Szyszkowski equation to the aggregated Na-PFOA data presented in Figure 1. Values for B and A are 0.2 and 542, respectively. RMSE = 1.5.

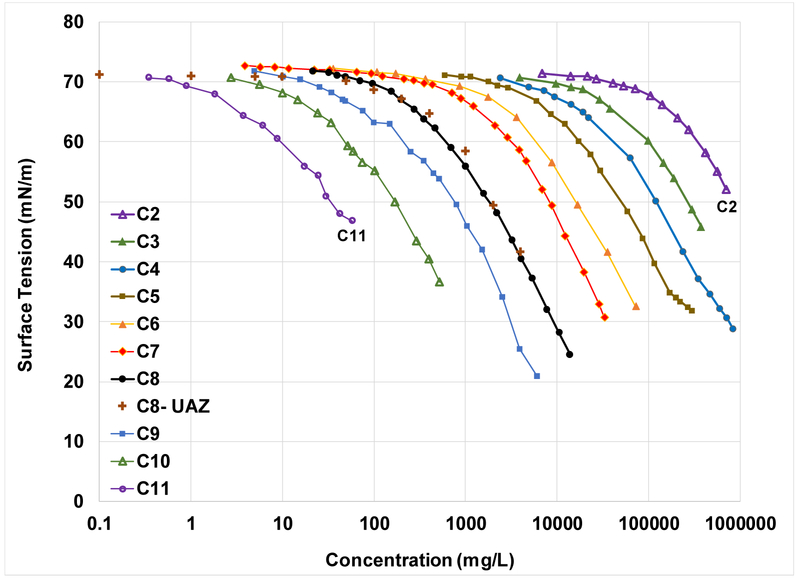
Examples of the measured surface-tension data are presented in Figure 3 for the homologous series of Na-perfluorocarboxylates. It is clearly observed that surface activity is a function of chain length, with much greater activity for C11 compared to C2 for example. This is consistent with Traube’s rule, and such behavior has long been observed for PFAS as noted previously. The strong dependence of surface activity on molecular structure, in this case chain length (CNt), indicates high probability for developing effective QSPR models for predicting fluid-fluid interfacial adsorption coefficients.

Figure 3.

Measured surface-tension data for the homologous Na-perfluorocarboxylate series. Data reproduced from Lunkenheimer et al. (2015) and Tamaki et al. (1989), except for C8-UAZ, which is from Lyu et al. (2018).

Interfacial Adsorption Coefficients

The K_i values determined from the surface/interfacial tension data are reported in Table 1. The magnitudes range from 10⁻⁷ to 10¹ cm, spanning 8 logs. It is evident that values are larger for longer-chain PFAS compared to those with shorter chains. There are also distinct differences among values for different classes. For example, the perfluorosulfonates have larger K_i values than the corresponding perfluorocarboxylates of the same chain length. For another example, replacing a single fluorine with a hydrogen results in a ∼4-times smaller K_i value for Na-9H hexadecafluorononanoate versus Na-PFNA. This latter phenomenon relates to the well-known significant difference in free energies of adsorption from solution between CF and CH groups (e.g., Shinoda et al., 1972; Mukerjee and Handa, 1981; Lunkenheimer et al., 2015).

As noted previously, interfacial adsorption of surfactants is nonlinear, and hence K_i is a function of solution concentration. The change in K_i versus solution concentration is shown in Figure S1 for three PFAS that span a wide range in magnitudes of K_i The K_i values vary by more than a factor of 10 over the full concentration range, reflecting the nonlinearity of adsorption. However, the K_is asymptotically approach a limiting maximum value, and thus exhibit minimal change below a certain solution concentration. This critical concentration corresponds to the inflection point of the surface-tension curve, beyond which the slope begins to increase greatly. Inspection of Figures 2 and 3 reveals that the inflection points occur at approximately 10,000, 100, and 1 mg/L for PFBA, PFOA, and PFUnA, respectively. These inflection-point concentrations are roughly two logs lower than the CMC. They are one log lower than the concentrations at which the slopes of the surface-tension functions approach a constant value (i.e., Γ is constant), corresponding to saturation of the interface. At this point, K_i becomes a linear inverse function of C, as reflected in Figure S1. It is noteworthy that the inflection-point concentrations are generally significantly higher than groundwater concentrations typically observed for PFAS.

Inspection of the data sets revealed that K_i values determined for a solution concentration of 0.1 mg/L are essentially identical to values that would be determined at any given lower concentration for all but 9 compounds. The compounds for which their greater surface activities resulted in K_i(C=0.1) values not corresponding to maximum values are SPBS, TDFHD, TDFTDE, TDFTTE, TDFTPE, TDFTME, HDDFTME, SDBS, and Triton. Maximum K_i values were determined for these using a concentration of 0.01 mg/L. Therefore, the K_i values determined for this study reflect maximum potential values. Given that the vast majority of soil and groundwater concentrations reported for PFAS are in the sub-mg/L range, the K_i values reported herein are likely to be representative for the broad range of PFAS concentrations observed at field sites.

The greatest number of surface-tension data sets was reported for Na-PFOA as discussed above. The mean K_i value for the 9 data sets is 2.3 ·10⁻⁴ cm, with a 95% confidence interval of 1.9 ·10⁻⁴ to 2.7 ·10⁻⁴. The confidence interval is quite narrow, especially considering the disparate data sources. The K_i value is 5.8 ·10⁻⁵ cm for Na-PFHpA, the adjacent perfluorocarboxylate in the homologous series with one less carbon than PFOA. The K_i value is 9.3 ·10⁻⁴ cm for Na-PFNA, the adjacent perfluorocarboxylate in the homologous series with one more carbon than PFOA. Comparison of these values shows that the K_i values for Na-PFHpA and Na-PFNA are significantly different from the 95% confidence interval for Na-PFOA. This illustrates that the differences in K_i values among a set of similar PFAS is much greater than the K_i measurement variance.

QSPR Analysis

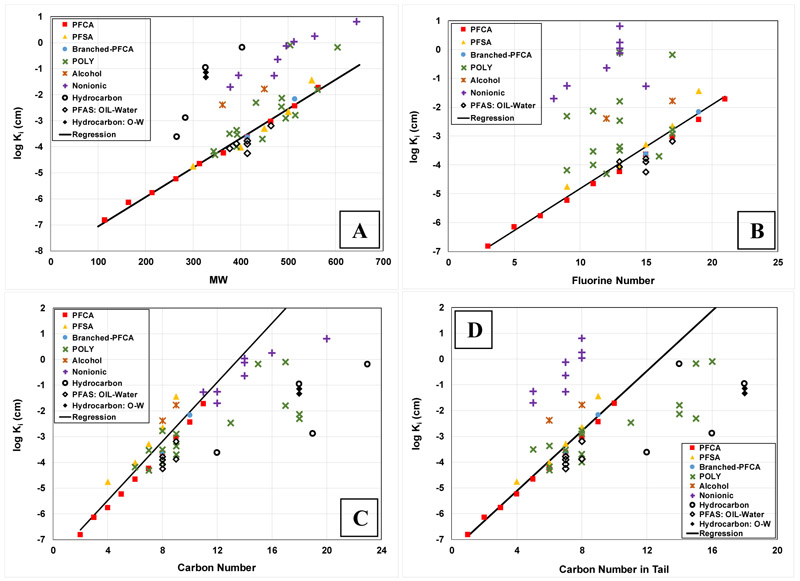
The QSPR models applied to the training data set produced r² values of 0.98 for molar volume, 0.98 for molecular weight, 0.97 for F-number, 0.90 for C-number, and 0.97 for number of carbons in the tail. It is observed that all descriptors provided very good predictions, with r² values ≥0.90. The models will now be tested with the validation data set to evaluate their predictive capabilities.

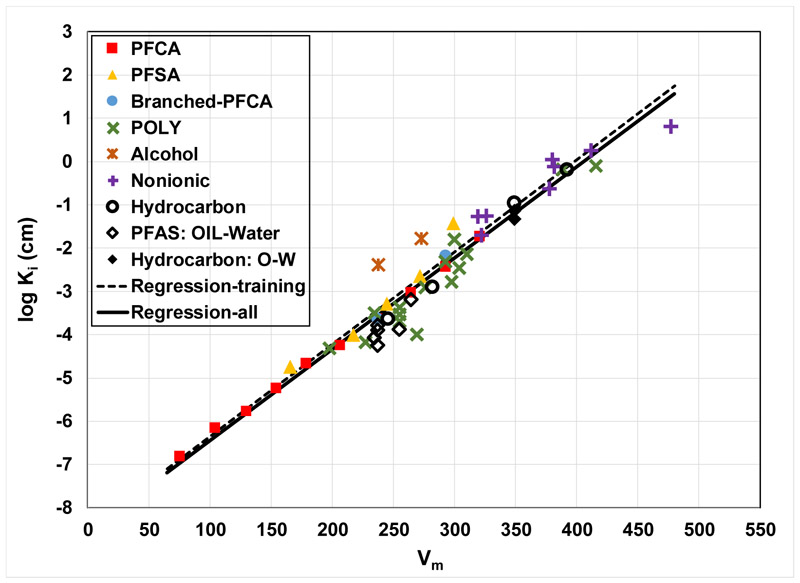
The validation data set is included with the training data set in Figure 4 for the V_m model and in Figure 5 for the other descriptors. It is observed that molar volume is the only descriptor that provides very good representation of the validation data set. These results are consistent with those of Kim et al. (2015), who tested three descriptors, V_m, FN, and total molecular surface area, for predicting several bulk-phase partition coefficients for PFAS. Molar volume was determined to be the best performing of the three. The forthcoming discussion will therefore focus on the V_m model.

Figure 4.

QSPR model for log K_i versus molar volume for all data. Regression equation for all data: log K_i = 0.021(±0.002)V_m − 8.56(±0.42), r² = 0.94 and MSE = 0.17. Legend acronyms are referenced to Table 1.

Figure 5.

QSPR models for all data with the descriptors A) molecular weight, B) number of fluorine atoms, C) number of carbons, and D) number of carbons in the tail. The regressions are based only on the training data set. The acronyms in the legend are referenced to Table 1.

The V_m-model correlation based on the combined data set is essentially identical to the correlation produced for the training set alone (compare the two regression lines in Figure 4). The r² is 0.94 for the entire data set, with a mean-square prediction error (MSE) of 0.17. The results demonstrate that the molar-volume based QSPR model can provide robust predictions of air-water interfacial adsorption coefficients for a wide variety of PFAS with greatly varying structures. The model also provides good predictions of air-water interfacial adsorption coefficients for the four tested hydrocarbon surfactants. It is noteworthy that these four include two anionic (SDS, SDBS), a cationic (CTAB), and a nonionic surfactant (Triton X-45).

The log K_i values for the six PFAS OIL-water data and the two hydrocarbon-surfactant OIL-water data are also well predicted by the V_m-model (Figure 4). The similarity of K_i values for air-water and OIL-water systems is highlighted by the observation that the values are very similar for all three SDBS data points, which comprise one for air-water and two for OIL-water (the V_m = 349 data points in Figure 4). This limited data set suggests that the model can produce reasonable predictions of OIL-water interfacial adsorption coefficients for both PFAS and hydrocarbon surfactants.

It is well established that hydrophobic interactions in solution drive the interfacial adsorption of surfactants (e.g., Kissa, 2001; Goodwin, 2004; Berg, 2010; Kronberg et al., 2014). The predictive capability of the V_m model for a wide range of PFAS with greatly varying structures reflects the fact that molar volume provides a reasonable representation of the influence of molecular size on cavity formation/destruction in solution (e.g., Kaliszan, 1987; Reinhard and Drefahl, 1999; Todeschini and Consonni, 2009), and thus the hydrophobic-interaction driving force for adsorption. The capability of the model to successfully predict the OIL-water data sets similarly reflects the importance of the hydrophobic-interaction driving force for interfacial adsorption in these systems.

Significant prediction errors are observed for 3 of the 54 data, specifically FTOH, FC8diol, and UDFOS, all with MSEs >1. The large errors observed for FTOH and FC8diol may be related to the differing behavior of alcohols, wherein the OH group confers significant hydrogen-bonding potential, and the resultant impact on interactions in solution and at the interface. This is especially true for FC8diol, which has a terminal OH at both ends of the molecule. There is no readily discernable explanation for the greater error observed for UDFOS, as the other polyfluoroalkyl data are well predicted.

Inspection of Figure 4 shows that the V_m model performed well for all 8 of the nonionic PFAS. Seven of the 8 nonionics contain hydrophilic polyethoxylate head groups comprised of 2-5 ethylene-oxide units. Application of the model to three other fluoropolyethoxylate compounds that have longer head groups, ranging from 7, 9, and ∼14 ethylene-oxide units (with V_ms >>500), produced predicted log K_i values that are progressively much larger than the measured values (data not shown). As noted previously, the V_m model performed well for the four tested hydrocarbon surfactants, including the nonionic Triton X-45. Similar to the fluoropolyethoxylates, Triton X-45 contains a hydrophilic polyethoxylate head group comprised of 4-5 ethylene-oxide units. Application of the model to another Triton surfactant, X-100 (V_m>550), produced a predicted log K_i that is approximately two log units larger than the measured value. The Triton X-100 head group contains 9-10 ethylene-oxide units compared to the 4-5 of Triton X-45. Conversely, they both contain the same hydrophobic tail, which means that the head group comprises a much greater proportion of the total molar volume for Triton X-100. This is also the case for the fluoropolyethoxylates, wherein the head group comprises an increasingly greater relative proportion of the total molar volume as the number of ethylene-oxide units increase. It is likely that the simple model does not adequately represent the relatively greater impact of the proportionally larger head groups on solution behavior compared to the hydrophobic-interaction driven behavior of the tails.

Improved prediction capability in such cases would require a fragment-based multiple-descriptor QSPR model that characterizes separately the solution behavior of the hydrophobic and hydrophilic components. An example is the model developed by Huibers et al. (1996) to predict critical micelle concentrations for a large set of nonionic surfactants comprising a diverse array of head-group structures, including both hydrocarbon polyethoxylates and fluoropolyethoxylates. However, employing a more complex model defeats the simplicity-based focus of the current effort. In any event, it may be anticipated that the long head groups of the larger fluoropolyethoxylates, Triton X-100, and similar surfactants would be degraded relatively quickly in many environmental systems (e.g., Soares et al., 2008; Fromel and Knepper, 2010), and therefore that long head-group surfactants would be much less prevalent than their shorter head-group counterparts.

Inspection of Figure 5 shows that the QSPR models using the other descriptors perform very poorly for the validation data set. They are not robust in particular for the nonionics and some of the polyfluoroalkyls, nor for the hydrocarbon surfactants. The ineffectiveness of the other descriptors reflects their inability to adequately represent the influence of molecular properties on hydrophobic interactions for a wide range of structures.

For molecular weight (Figure 5A), it is observed that data points for all 8 nonionic PFAS and for all 6 hydrocarbon surfactants reside far above the regression line. Data for a few poly-PFAS, those with the greatest number of CH₂ groups, also reside above the regression. For the hydrocarbons and poly-PFAS in particular, this disparity is a function of the significant difference in molecular weights of CF₂ versus CH₂ groups, wherein one of the former is equivalent to almost four of the latter. Thus, surfactants containing CH₂ groups have longer tails than do compounds of comparable molecular weight whose tails contain only CF₂ groups. For example, PFPeA has a CN_t of 4 for a MW of 264, whereas SDS has a CN_t of 12 for a MW of 266. The K_i for SDS is approximately 1.5 logs larger than for PFPeA due to the much greater surface activity conferred by SDS’s much longer tail. The effect of the significantly longer tail outweighs the greater free energy of adsorption associated with an individual CF₂ unit. It is observed that the MW-based model works well for most of the poly-PFAS, specifically those with few or no CH₂ groups in the tails. The behavior of the nonionic PFAS is influenced also by the presence of large numbers of CH₂ units in the head groups.

The FN descriptor works well for the PFCAs, PFSAs, branched-PFCAs, and several of the poly-PFAS (Figure 5B). It does not work well for the nonionic PFAS and some of the other poly-PFAS. This relates to the fact that these latter compounds have significant numbers of CH₂ groups that are contributing to surface activity. All of the poly-PFAS for which the FN-model provides a reasonable prediction of log K_i are those with relatively few or no CH₂ groups.

The CN-based model provides good representation for almost all of the data, with the exceptions comprising several poly-PFAS, specifically those with the greatest number of CH₂ groups, and all of the hydrocarbon surfactants (Figure 5C). The much smaller K_i values observed for these latter compounds compared to those well-represented by the regression for a comparable CN is due to the significant difference in free energies of adsorption from solution between CF₂ and CH₂ groups. It is widely observed that fluorinated surfactants have greater surface activities compared to their hydrocarbon-surfactant counterparts of similar chain length. Inspection of Figure 5D shows that the CN_t-model performs poorly for the nonionic PFAS in addition to several of the poly-PFAS and the hydrocarbon surfactants. The poor performance of the CNt-model for the nonionics reflects that their head groups contain significant numbers of carbons.

Conclusions

The results of recent research have indicated that adsorption to air-water and OIL-water interfaces can be a significant retention process for PFAS transport in environmental systems. Fluid-fluid interfacial adsorption coefficients are required for use in transport modeling and risk characterization, yet these data are currently not available for the vast majority of PFAS. Surface-tension and interfacial-tension data sets collected from the literature were used in this study to determine interfacial adsorption coefficients for 42 individual PFAS.

The K_i values vary across eight orders of magnitude, and are a function of molecular structure. The results of QSPR analysis demonstrate that a model employing molar volume as a descriptor provides robust predictions of log K_i for a wide range of PFAS, including homologous series of perfluorocarboxylates and perfluorosulfonates, branched perfluoroalkyls, polyfluoroalkyls, and nonionic PFAS, with molar volumes ranging from 75 to 477. The model also produced good predictions for a limited set of data for OIL-water interfacial adsorption of PFAS.

Data sets for deionized water were used to develop the QSPR model due to greater data availability. It is widely observed that the presence of salts generally increases the surface activity of surfactants. Thus, the K_i values determined herein should be considered as conservative in that values for many environmental systems may be somewhat larger due to the presence of salts in solution. In addition, the data sets represent single-solute systems, and therefore do not account for potential effects of PFAS mixtures or the presence of cocontaminants. Hence, the values produced with the QSPR model should be viewed as first-order estimates subject to uncertainties associated with the natural conditions of subsurface systems.

As discussed by Brusseau (2018), fluid-fluid interfacial adsorption of PFAS is influenced by numerous factors, many of which may be spatially and temporally variable. The potential influence of solution-chemistry related factors on K_i was noted above. Quantifying the magnitude of fluid-fluid interfacial adsorption also requires quantification of the magnitude of fluid-fluid interfacial area present in the system of interest. Multiple approaches are available for the measurement and estimation of interfacial areas (Costanza and Brusseau, 2000; Brusseau et al., 2015; 2019). It is important to note that the magnitude of fluid-fluid interface is a function of the dynamic conditions of the system. For example, water saturation in some portions of a vadose zone may change rapidly in conjunction with an infiltration event. Changes in water saturation will cause changes in the magnitudes of air-water interfacial area, which will result in changes in the magnitude of air-water interfacial adsorption. In addition, water saturation may vary spatially within the vadose zone due to physical and geochemical heterogeneity of the media. Finally, these dynamic conditions may influence mass-transfer processes and the establishment of local equilibrium, and thereby affect magnitudes of observed retention.

The ability to produce representative K_i values with the QSPR model presented herein provides a means to investigate the influence of fluid-fluid interfacial adsorption on the transport of PFAS, which will lead to an improved understanding of their fate in the environment. This in turn is anticipated to enhance the accuracy of risk assessments and the effectiveness of remediation and site-management efforts. The results of this work will be particularly relevant for characterizing PFAS mass flux and transport in the atmosphere, in the vadose zone, in source zones containing immiscible organic liquids, and in water/wastewater treatment systems.

Highlights.

Air-water and OIL-water interfacial adsorption coefficients are determined for many PFAS QSPR analysis results demonstrate that adsorption coefficients are a function of molecular structure Interfacial adsorption coefficients can be successfully predicted using the selected QSPR model