Spatio-Temporal Patterning in Primary Motor Cortex at Movement Onset

Abstract

Voluntary movement initiation involves the engagement of large populations of motor cortical neurons around movement onset. Despite knowledge of the temporal dynamics that lead to movement, the spatial structure of these dynamics across the cortical surface remains unknown. In data from 4 rhesus macaques, we show that the timing of attenuation of beta frequency local field potential oscillations, a correlate of locally activated cortex, forms a spatial gradient across primary motor cortex (MI). We show that these spatio-temporal dynamics are recapitulated in the engagement order of ensembles of MI neurons. We demonstrate that these patterns are unique to movement onset and suggest that movement initiation requires a precise spatio-temporal sequential activation of neurons in MI.

Introduction

Large ensembles of neurons in primary motor cortex (MI) are used to initiate movements. Even the simplest, single joint movement of the arm or hand recruits neurons distributed across the entire upper limb region of MI ( Sanes and Donoghue 1993 ; Schieber and Hibbard 1993 ); however, it remains unknown if the order in which these units are engaged is related to their spatial position on the cortical sheet.

At the same time, the amplitude of oscillations in the beta band (15–30 Hz) of the local field potential (LFP) attenuates sharply around movement onset ( Jasper and Penfield 1949 ; Sanes and Donoghue 1993 ; Murthy and Fetz 1996a ; Rubino et al. 2006 ). It is thought that this attenuation is a mesoscopic reflection of activated motor cortex and coincides with an epoch of enhanced corticospinal excitability ( Pfurtscheller and Lopes da Silva 1999 ). Although the spatio-temporal dynamics of beta attenuation are poorly understood, beta oscillations have been shown to propagate along the rostro-caudal dimension during motor preparation ( Rubino et al. 2006 ). These planar waves may be determined by the underlying pattern of horizontal connectivity within MI which exhibits a preponderance of long range connections distributed along the rostro-caudal dimension ( Gatter and Powell 1978 ; Huntley and Jones 1991 ). Using a Granger causality analysis, a recent study found that pairs of neurons are preferentially connected along this dimension and that sequential spiking between these pairs of neurons contains more information about movement direction ( Takahashi et al. 2015 ).

We reasoned that if spatial patterning in MI is related to its horizontal connectivity, spatial patterns may also emerge during movement initiation. Thus, we hypothesized that movement initiation is characterized by a specific spatio-temporal sequence of neural activity structured along the rostro-caudal axis. Furthermore, if such a pattern is indeed a unique signature of movement initiation, we would expect it to be absent during preparation, another epoch in which motor cortex is known to be transiently activated.

Materials and Methods

Behavioral Task

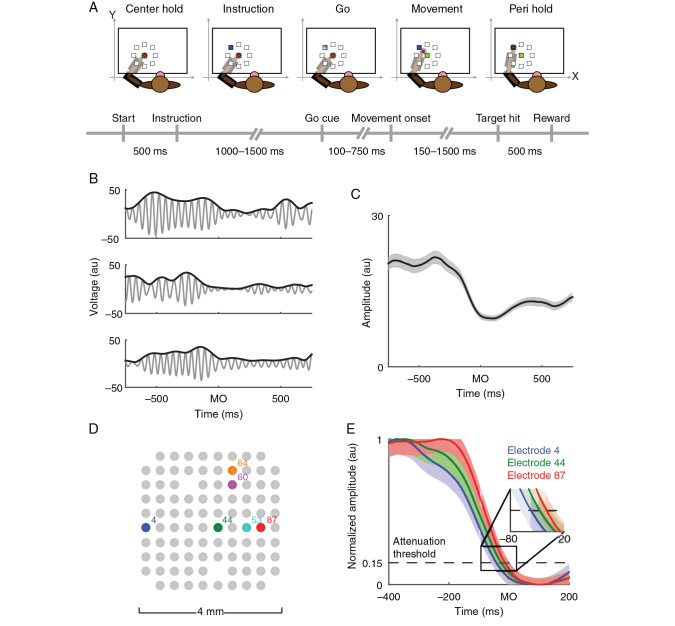
Four macaque monkeys (Macaca mulatta) of either sex were operantly trained to perform an instructed-delay center-out reaching task (for a complete description of the task, see Rubino et al. 2006 ). Briefly, each animal used an exoskeletal robot (BKIN Technologies) to make planar reaching movements that controlled the position of a cursor on a horizontal screen above the animal's arm. The animal had to hold the cursor on a center target for 500 ms before an instruction cue appeared. The instruction cue signaled the location of a peripheral target to which the animal had to ultimately move. Peripheral targets were located at 8 evenly spaced radial intervals around the center target with a distance of 5–7 cm between the center and peripheral targets. After receiving the instruction cue, the animal had to hold the cursor in the center target for a random amount of time (uniformly distributed between 1000 and 1500 ms) until a go cue appeared. Upon presentation of the go cue, the animal could move towards the peripheral target, and, if it held the cursor at the cued peripheral target for 500 ms, it received a juice reward (Fig.  1A ).

Figure 1.

Experimental setup and beta attenuation analysis. ( A ). Animals were trained to perform an instructed-delay center-out reaching task. The animals used a 2-link robotic exoskeleton to control the position of a cursor on a screen projected above their arm. ( B ). LFPs were filtered into the beta frequency range and aligned to movement onset (MO) for every trial. The beta oscillation of one electrode's LFP (gray trace) and its amplitude (black trace) in arbitrary units (au) are shown for 3 different example trials from animal Rs. ( C ). Beta amplitudes from the electrode in B were averaged across all trials including all movement directions to estimate the trial-averaged beta amplitude aligned to movement onset (black trace indicates average amplitude, gray area indicates ±2 standard errors of the mean [SEM]). ( D ). LFPs were simultaneously recorded across multiple sites in MI during the experiment. ( E ). Trial-averaged beta amplitude profiles for 3 different electrodes (color corresponding to the sites highlighted in ( D ) are shown [mean ± 2 SEM]). The time at which the beta amplitude passed an attenuation threshold (horizontal black dashed line) was estimated for every electrode. Note that beta activity on each electrode does not simultaneously pass the attenuation threshold ( E inset). Data are from animal Rs.

Behavioral Data Selection

We computed the reaction time and movement duration of each trial. We defined reaction time as the difference between the moment the cursor left the center target (i.e., movement onset) and go cue appearance. We excluded trials with reaction times of <100 ms and >750 ms. Movement duration was defined as the time between movement onset and acquisition of the peripheral target. We imposed a threshold on movement durations such that they had to be at least 150 ms, but no more than 1500 ms. Additionally, we observed a small percentage of trials that were considerably slower than the median, so we excluded the slowest 25% of trials from each movement direction to minimize variability arising from the behavior.

Neurophysiology

All surgical and experimental procedures were approved by the University of Chicago Animal Care and Use Committee and conform to the principles outlined in the Guide for the Care and Use of Laboratory Animals (NIH publication no 86–23, revised 1985). All monkeys were implanted with 96-electrode Utah arrays (1.0 mm length, 10 × 10 grid with 400 µm interelectrode spacing, Blackrock Microsystems) in MI contralateral to their working hand. During a recording session, signals from up to 96 electrodes were amplified with a gain of 5000, band-pass-filtered between 0.3 Hz and 7.5 kHz, and recorded digitally (14-bit) at 30 kHz using a Cerebus acquisition system (Blackrock Microsystems). Local field potentials were sampled at 1 kHz and digitally band-pass filtered between 0.3 and 500 Hz or 0.3 to 250 Hz using the Cerebus. Single units were sorted offline using a semimanual procedure (Offline Sorter, Plexon, Inc.).

Beta Attenuation Analysis

We performed a number of preprocessing steps on the LFPs to estimate beta attenuation. To begin, we found the frequency of peak power in the beta range (15–30 Hz) for each dataset, averaged over all electrodes and time. LFPs from each electrode were then filtered bidirectionally with a band-pass filter (Butterworth, fourth order) whose passband was 3 Hz on either side (i.e., a total bandwidth of 6 Hz) of the peak beta frequency power (animal Rs, 18 Hz; Rj, 18 Hz; Rx, 27 Hz; V, 21 Hz rounded to the nearest Hertz). We found that rounding the center of the filter to the nearest integer frequency had no effect on subsequent results. Power spectra from each animal were computed using the chronux ( http://chronux.org ) function mtspectrumc, log transformed into decibels, and then averaged over electrodes.

The Hilbert transform was applied to the band-pass filtered data to estimate the instantaneous beta amplitude of each LFP. For each electrode, the instantaneous amplitudes were trial aligned to movement onset and then averaged across trials, thereby estimating beta attenuation.

We found the maximum and minimum values of each electrode's beta profile in a window spanning ± 500 ms around movement onset. Beta profiles were normalized so that they ranged from 0 to 1. The time at which the normalized profile crossed an attenuation threshold (0.15) was computed for each electrode. This time, referred as the beta attenuation time (BAT), is one of the primary summary statistics of this paper. Early analysis experimented with several values of the attenuation threshold, and we found comparable results over a moderate range of attenuation thresholds. For some electrodes, visual inspection of their power spectrum revealed no significant bump in the beta frequency band; these electrodes were discarded from future analysis (2 from V and Rs, 4 from Rj, and 7 from Rx).

Computing the Beta Attenuation Orientation

We characterized the spatio-temporal progression of beta attenuation across the Utah array by using linear regression to estimate a vector that described the spatial orientation of BATs from earliest to latest. This vector will henceforth be referred to as the beta attenuation orientation (BAO). For each electrode, we predicted the BAT, denoted y_rc , from the spatial location of that electrode. The subscripts r and c are used to indicate the row and column coordinates of the electrode on the array. Mathematically, this relationship can be expressed as follows:

$$y_{\mathrm{rc}}={\beta }_{\mathrm{r}}r+{\beta }_{\mathrm{c}}c+\alpha ,$$

where β_r and β_c are the coefficients of the rows and columns, and α is a constant time offset. The arctangent of the ratio of β_r and β_c indicates the orientation of beta attenuation, that is, the BAO.

Goodness of fit was quantified using the coefficient of determination, R ² , defined as follows:

$$R^2=1-\frac{{\sum }_{\mathrm{rc}}{(y_{\mathrm{rc}}-{\hat{y}}_{\mathrm{rc}})}^2}{{\sum }_{\mathrm{rc}}{(y_{\mathrm{rc}}-\overline{y})}^2},$$

where y_rc and ${\hat{y}}_{\mathrm{rc}}$ denote the observed and fitted BATs for electrode rc , and $\overline{y}$ corresponds to the average BAT across all electrodes.

We used 2 fundamentally different procedures to test for the significance of the BAO. The first involved performing an F -test for the significance of our regression model by comparing it with a model that contained only the offset term α . The second test for significance of the BAO was based on a spatial shuffling of our data ( Riehle et al. 2013 ). After computing BATs for each electrode, we shuffled the spatial location of the BATs on the Utah array. We then estimated the BAO and corresponding R ² of the shuffled data. This procedure was repeated one million times to estimate a null distribution of R ² values in a population where spatial information had been explicitly destroyed. We additionally tested the consistency of the BAO. We repeatedly (1000 times) randomly divided each dataset into 2 equal sized halves and estimated a BAO for each half. We then computed the angle between the 2 BAOs and compared it with a null distribution of BAOs based on spatially shuffled data (using the preceding shuffling procedure).

Circular Dissimilarity Test

To statistically quantify the similarity between 2 directional vectors (e.g., the BAOs estimated from 2 discrete subsets of trials), the angle between them was measured and compared with the distribution of angles if 2 uniform random vectors were drawn independently of one another. This null distribution is uniform between 0° and 180°. To compare multiple angles simultaneously, their sum was computed and compared with the sum of n uniformly distributed random variables (on the interval [0, 180]), which is given by the Irwin–Hall distribution (rescaled to the interval [0 180]). For large values of n , the Irwin–Hall distribution is approximately normal with mean n/2 and variance n/12 .

Unit Spiking Analysis

For every dataset, each unit's spiking activity was binned into 1-ms bins and convolved with a Gaussian kernel (25 ms s.d. for monkeys Rs and V, and 50 ms s.d. for Rj due to lower trial counts) to smooth firing rate estimates. We trial aligned the smoothed firing rates to either the instruction cue, or movement onset, and then performed an analysis to identify the time at which each cell was most informative about movement. On every trial, we predicted the instantaneous probability that the animal was moving to each of the targets. We used the entropy of these probabilities to quantify the uncertainty about movement direction in that neuron. These probabilities were estimated from each neuron individually using a multinomial logistic regression model that will be subsequently described in greater mathematical detail.

We represented the firing rate of a given neuron, i , in a matrix, X , where each row corresponded to the j th of J trials, and each column corresponded to a time, t , relative to movement onset. At every moment in time and on every trial, that is, for each t and j , we used the firing rate of neuron i as the input of our multinomial logistic regression model. This model may be expressed as follows:

$${\hat{p}}_{\mathrm{kjt}}=\frac{\exp [{\alpha }_{\mathrm{kt}}+{\beta }_{\mathrm{kt}}\times X_{\mathrm{jt}}^i]}{{\sum }_{k=1}^8\exp [{\alpha }_{\mathrm{kt}}+{\beta }_{\mathrm{kt}}\times X_{\mathrm{jt}}^i]},$$

where ${\hat{p}}_{\mathrm{kjt}}$ represents the estimated probability that the animal moved to target k on trial j at time t , and ${\alpha }_{\mathrm{kt}},{\beta }_{\mathrm{kt}}$ represents the regression coefficients associated with target k at time t . Due to low trial counts in monkey Rj, we pooled adjacent movement directions as a single target location (e.g., targets at 0° and 45° were pooled). These 8 (4 for Rj) probabilities comprise a probability distribution, Z_jt , and we estimated the entropy of that distribution, H ( Z_jt ), as follows:

$$H(Z_{\mathrm{jt}})=-\sum _{k=1}^K{\hat{p}}_{\mathrm{kjt}}{\log }_2{\hat{p}}_{\mathrm{kjt}}.$$

To disambiguate chance fluctuations in entropy due to stochastic spiking from behaviorally significant modulation, we performed a bootstrap analysis. We repeatedly shuffled target locations (200 times) and recomputed the entropy, H ( Z_jt ), for each neuron. For each moment in time, we subtracted the fifth percentile of bootstrapped entropy values (corresponding to reductions in entropy due to stochastic spiking) from the unshuffled entropy values and added back 3 bits so that the corrected data were on approximately the same scale as uncorrected data. After performing this correction, only entropy values of <3 bits (2 for Rj) were considered significantly task modulated.

We manually identified local minima in the entropy profiles during the instruction (50–350 ms after the instruction) and execution epochs (175 ms before to 50 ms after movement onset for Rs and V, 325 to 25 before movement onset for Rj because its beta attenuation range was earlier, and longer). The time of the local entropy minimum defined that unit's modulation time, that is, its UMT. In additional analyses, we defined UMTs based on the timing of threshold crossings in the entropy profiles and observed no qualitative difference between minima and threshold crossings. The same linear regression procedure that was used to find the BAO was also used to find the unit modulation orientation (UMO). The UMO represents the spatial orientation along which motor cortical neurons are sequentially engaged from early to late.

Results

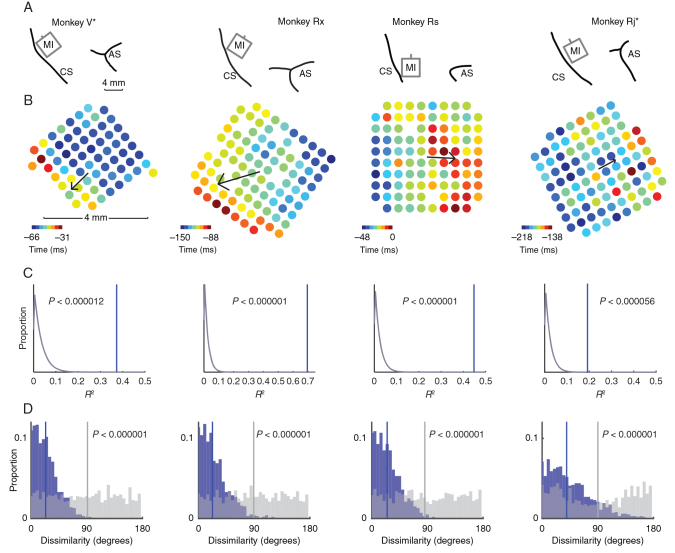
We recorded single unit spiking activity and LFPs from multielectrode arrays implanted in the primary motor cortex (MI) of 4 rhesus macaques while they engaged in an instructed-delay, center-out reaching task (Fig.  1A ). The amplitude of beta oscillations attenuated around movement onset (Fig.  1B–C ) as has been shown in many previous studies ( Sanes and Donoghue 1993 ; Murthy and Fetz 1996a ). This phenomenon is considered to be a mesoscopic reflection of local motor cortical activation and is often measured using macroscopic EEG electrodes in humans or intracortical electrodes in animals without reference to their spatial position within MI under the assumption that the entire cortical area is activated simultaneously. Instead, we considered whether MI is activated in a spatio-temporally organized fashion at movement onset by measuring the time at which the amplitude of beta band activity crossed an attenuation threshold across different sites in MI (Fig.  1D–E , see Materials and Methods for details). These trial-averaged BATs varied systematically along a rostro-caudal axis and were characterized using a linear regression model that predicted the BAT of an electrode from its spatial location on the array (Fig.  2A–B ). BATs were well predicted by this model ( R ² , Monkey V: 0.37, Rx: 0.70, Rs: 0.45, Rj: 0.30), and it was highly significant compared with a null model without spatial information ( F -test, P < 0.00001 for all monkeys). The resultant vector of our regression model defined a BAO corresponding to the gradient from earliest to latest BAT (arrows in Fig.  2B ). As a further independent test for the significance of the BAO, we performed a shuffle analysis where we randomly shuffled the spatial position of each BAT and fit a planar regression model to the shuffled BATs. We repeated this shuffling procedure one million times and compared the model goodness of fit to the unshuffled data with that of the shuffled data (Fig.  2C ).

Figure 2.

Array placement and beta attenuation maps. ( A ). Line drawings depicting placement of the multielectrode arrays in the upper limb area of MI in 4 monkeys. The central and arcuate sulci are indicated (CS and AS, respectively). Data from monkeys V and Rj have been flipped vertically to normalize the location of the CS and AS across animals. ( B ). Heat maps depicting the timings of attenuation in beta amplitude across all electrodes on each array relative to movement onset (time = 0). We fit a linear model to describe the spatial progression of BATs from earlier to later. This BAO is indicated by a black arrow whose magnitude is proportional to the model's goodness of fit. ( C ). We performed a spatial shuffle analysis to test for the significance of the BAO. The spatial location of BATs was shuffled one million times. For each shuffle, we computed the BAO of the shuffled data and its goodness of fit, R ² . The distribution of R ² values for each monkey from shuffled data (gray curve) is shown, as well as the R ² statistic observed in actual data (blue vertical line). The BAO was highly significant in all animals. ( D ). The consistency of the BAO was assessed with a bootstrap analysis. For each iteration of the bootstrap (1000 total), we randomly partitioned each dataset into halves. A BAO was estimated from the data in each half, and the angle between them was measured. The distribution of angular differences (blue bars) was compared with a null distribution of angular differences estimated from spatially shuffled data (gray bars) using the same shuffling procedure as ( C ). We found strong evidence that the angular differences we observed between BAOs estimated on subsets of trials were significantly less than what would be expected under chance (Kolmogorov–Smirnov test, P indicated on figure).

The consistency of the BAO was established in 3 ways: across trials, across attenuation thresholds, and across frequencies. We assessed the consistency of the BAO across trials by randomly partitioning the data into 2 subsets and comparing the BAOs across the 2 halves (Fig.  2D ). As a further test of the consistency of the BAO across trials, we computed movement direction-specific BAOs and found that they were oriented similarly ( Supplementary Fig. 1 ). We assessed the consistency of the BAO at different values of the attenuation threshold (ranging from 0.1 to 0.4 in steps of 0.05) using a circular dissimilarity test. In each animal, we found strong evidence that the BAOs were not significantly different across threshold values (V: h₂₁ = 0.10; Rx: h₂₁ = 4.21; Rs: h₂₁ = 0.23; Rj: h₂₁ = 2.53; all P < 0.000001). To address the consistency of the BAO across frequencies, we analyzed wide-band-filtered beta band activity (15–30 Hz). We computed the sample correlation, ρ , between BATs and wide-band BATs (wBATs). In each dataset, a significant correlation was observed ( V : ρ = 0.55, P < 0.000003; Rx: ρ = 0.42, P < 0.00004; Rs: ρ = 0.74, P < 1e-17; Rj: ρ = 0.44, P < 0.000007). As a further test, we compared the BAO with the wide-band BAO (wBAO). We found that there was a significant correspondence between the BAO and wBAO using a circular dissimilarity test ( h₄ = 160.0, P < 0.026).

In all animals, the BAO was organized along the rostro-caudal axis, although its precise directionality varied across animals. The BAO was rostro-caudal for Monkeys V and Rx and caudo-rostral for Monkeys Rs and Rj. One potential explanation for this difference in BAO is that the electrode arrays were placed at different positions medio-laterally along MI. For animals V and Rx, the array centers were 3 and 4 mm, respectively, medial to the genu of the arcuate sulcus, whereas for animals Rs and Rj, the array centers were exactly at the genu of the arcuate sulcus. Therefore, the BAO was oriented in the caudal direction for the arrays in a more medial position, whereas the BAO was in the rostral direction for the arrays situated more laterally. As it would be expected if attenuation reflects local activation of MI, BATs occurred before movement onset, and, their temporal range was ∼50 ms from earliest to latest across the 4 mm extent of the array, which we term the beta attenuation epoch.

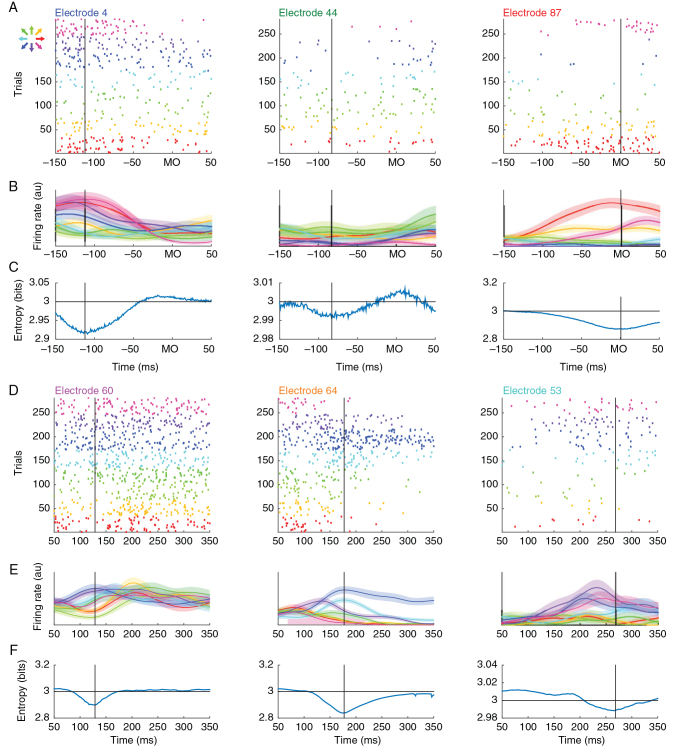
If beta attenuation is truly a reflection of local network activation, then the spatial patterning in beta activity should also be present in the engagement order of single units across MI. The temporal dynamics of individual neurons, in MI, however, are quite heterogeneous across neurons prior to movement onset and firing rate modulation times vary with different movement directions ( Murphy et al. 1985 ; Lecas et al. 1986 ; Scott 1997 ; Churchland and Shenoy 2007 ), so directly measuring activation times from firing rates is challenging ( Supplementary Fig. 2 ). Instead, we inferred modulation times of individual neurons by measuring when they were most informative about the upcoming movement direction (Fig.  3 , see Materials and Methods for computational details). Of the 82, 113, and 51 neurons with firing rates greater than 2 Hz in monkeys Rs, Rj, and V (no unit spiking data were available from animal Rx), we found that 63 (77%), 71 (63%), and 40 (78%) of neurons, respectively, exhibited significant direction-specific modulation during movement execution (Fig.  3A–C shows 3 exemplar neurons recorded on the red, green, and blue electrodes from Fig.  1D–E ), consistent with the previous observation that ∼75% of MI neurons are directionally tuned ( Georgopoulos et al. 1982 ). Significant direction-specific modulation was also observed during motor preparation (i.e., during the instructed-delay epoch); however, fewer cells were modulated (46 [56%], 38 [34%], and 13 [25%] for Rs, Rj, and V, respectively; Fig.  3D–F shows 3 different exemplar neurons whose spatial position is indicated in Fig.  1D ). Neurons were generally less informative about movement direction during motor preparation (KS test on entropy values, P < 0.00005 for all animals).

Figure 3.

Unit spiking analysis. ( A ). Raster plot of unit spiking activity on 3 electrodes corresponding to those in Figure  1 D. Each row in the raster indicates spiking activity on one trial aligned to movement onset. Color indicates the direction of movement. ( B ). Unit spiking activity was convolved with a Gaussian kernel and averaged across trials. Trial-averaged firing rates ± 1 SEM are shown for each movement direction. ( C ). Time-resolved entropy of the target direction probability distribution conditioned on the firing rates in ( B ). The dip in entropy reflects the directionally selective modulation of the neuron and is used to estimate its modulation time (vertical black line). Note that UMT follows the same pattern as BATs in Figure  1 E. ( D–F ). Three additional units that show significant modulation during movement preparation following the same conventions as ( A–C ) except data are aligned to the instruction cue. In both epochs, we have attempted to show units that are modulated early (left column), intermediately (center), or late (right) in their respective task epochs. During execution, the spatio-temporal sequence of unit modulation is consistent with the spatio-temporal sequence of beta attenuation; however, this consistency is absent during motor preparation.

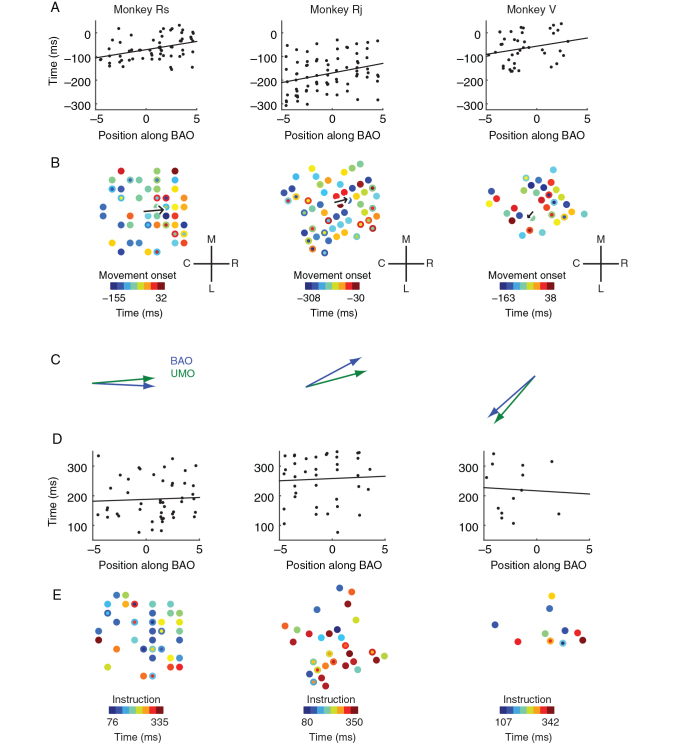
As a preliminary analysis to relate unit engagement order with mesoscopic patterning of beta activity, we computed the scalar projection of each unit's spatial location onto the BAO and compared that unit's position along the BAO with its modulation time (Fig.  4A ). Here, a unit's modulation time was operationally defined to be the moment when that cell was most informative about movement direction. We found that position along the BAO predicted unit modulation times (UMT) during movement execution when data were pooled across animals ( F -test on regression slope, F_1,175 = 18.6, P < 0.00003). A similar result was found in 2 of the 3 animals individually, whereas the third showed a consistent, but insignificant trend (Rs: F_1,61 = 10.5 P < 0.002; Rj: F_1,74 = 7.64, P < 0.007; V: F_1,38 = 2.34, P < 0.13). We also examined the relative timing of BATs and UMTs and found that UMTs significantly precede BATs ( Supplementary Fig. 3 ).

Figure 4.

Relationship of beta attenuation to unit modulation. ( A ). We performed an analysis to test whether units were sequentially engaged along the BAO. We compared the UMT of each cell to its position on the BAO and found a significant linear relationship across animals (see main text for statistics). Here, UMTs are relative to movement onset, that is, movement onset occurs at t = 0. ( B ). Raw heat maps of UMT relative to movement onset as a function of their spatial location on the electrode array. The black arrow indicates the UMO for each dataset (length proportional to goodness of fit as in Fig.  2 ). Concentric circles indicate UMTs for multiple units on a given electrode. Anatomical coordinates are the same as Figure  2 . ( C ). We compared the similarity of the BAO and UMO in each animal and found that they were closely aligned during movement execution. ( D–E ). Same as ( A–B ) except all unit activity is relative to the instruction cue. During preparation, there is no significant relationship between the BAO and unit modulation ( D ), and UMT exhibit no significant spatial gradient ( E ).

We then examined UMT for direct evidence of spatial patterning and used the same regression procedure that was used to find the BAO to identify an UMO. We found a spatial progression of UMT across the cortical sheet along the rostro-caudal axis (Fig.  4B ; UMO model statistics: Monkey Rs: R² = 0.15, F_2,60 = 5.27, P < 0.008; Rj: R² = 0.10, F_2,73 = 3.94, P < 0.024; V: R² = 0.06, F_2,37 = 1.16, P < 0.32; additional controls, see Supplementary Fig. 4 ).

There appeared to be a close correspondence between the BAO and UMO during movement onset (Fig.  4C ), so we developed a statistical test to quantitatively assess the similarity between these 2 vectors based on the angular difference between them. To apply a test to the group of animals as a whole, the angular differences between the BAO and UMO were added across animals to generate a test statistic, h . We found strong evidence that the BAO and UMO were similarly oriented in the 3 animals ( h = 28.62, P < 0.0007).

Directional modulation of single MI neurons is present not only during movement initiation but also during motor preparation, an epoch where overt movement does not occur. We compared these 2 task epochs to verify whether the spatio-temporal patterning of unit modulation was a unique feature of movement initiation. During preparation, modulation timing was not linearly related to position along the BAO (Fig.  4D , F_1,94 = 0.13, P < 0.72) and exhibited no significant spatial gradient (Fig.  4E , Rs: F_2,44 = 1.07, P < 0.35; Rj: F_2,35 = 1.02, P < 0.37; V: F_2,10 = 0.23, P < 0.80), in contrast to the UMO that was identified at movement onset.

Discussion

Relationship of Beta LFP to Unit Spiking Activity

Beta attenuation has often been interpreted as a reflection of activated motor cortex ( Pfurtscheller and Lopes da Silva 1999 ). Here, we have provided further support for this perspective by showing that the sequential engagement of unit spiking activity is aligned with the spatio-temporal progression of beta attenuation during movement onset. We determined the engagement order of cells by measuring when they were most informative about movement direction. Our findings do not, however, imply that directionally selective unit modulation is sufficient to cause beta attenuation. We found that cells in MI also exhibited significant directional modulation during motor preparation, and yet no beta attenuation occurred during this interval. In fact, beta oscillations are highest in amplitude and propagate as traveling waves during motor planning ( Rubino et al. 2006 ).

How, then, might directional modulation in cells give rise to beta attenuation during execution, but not during preparation? One possibility is that directional modulation is sufficiently gated during preparation to prevent beta attenuation, though recent studies have demonstrated this explanation is unlikely ( Kaufman et al. 2014 ). An alternative explanation is that the behavior of MI neurons during preparation and execution is fundamentally different. In particular, it has been previously noted that a majority of MI neurons become entrained to high amplitude beta oscillations ( Murthy and Fetz 1996b ), that is, during preparation. Yet, at movement onset (when beta attenuates), the temporal firing rate profiles ( Churchland and Shenoy 2007 ) and tuning properties ( Suminski et al. 2015 ) of these cells change, becoming heterogeneous and no longer phase locked to beta oscillations. Thus, beta attenuation represents the desynchronization of these cells around movement onset.

We observed that the temporal range of UMT is substantially longer than the range of BATs. This finding is not necessarily inconsistent with our interpretation of beta attenuation. In previous studies, it has been shown that modulation times of MI neurons span several hundred milliseconds in reaching tasks ( Murphy et al. 1985 ; Lecas et al. 1986 ), and more generally, firing rate profiles are extremely heterogeneous ( Churchland and Shenoy 2007 ). We have shown that the spatial location of a unit is one important factor for determining when that unit will become modulated, however, other factors are also involved. We speculate that at least some of these other factors are intrinsic to the neuron and not shared amongst neighboring cells. The beta LFP, being an aggregate signal, then, will average away this intrinsic component. Thus, we might expect that if we could record from tens to hundreds of cells on an electrode the average of their UMTs would converge to the BAT for that electrode. In this view, the temporal range of UMTs is larger than the range of BATs because the UMTs are inherently more variable. Nevertheless, the relationship between BATs and UMTs remains tentative and represents an opportunity for further inquiry. Specifically, a better understanding of the mechanistic link between beta attenuation and unit modulation may explain why the duration of UMTs is longer than BATs.

Several of the unit spiking results that were significant in animals Rj and Rs were weaker in animal V. However, all of animal V's results were, at minimum, qualitatively consistent with the other 2 animals. In this animal, we recorded from only 64 electrodes on the Utah array distributed over a smaller spatial area than the other 2 animals. Accordingly, we speculate that unit spiking results in animal V were weaker because we sampled fewer units over a smaller area than the other 2 animals.

Spatio-Temporal Patterning of Motor Cortical Activity

Considering the motor cortex is a physical neural substrate with intrinsic connectivity, it is perhaps not surprising that the regular temporal dynamics within neural state space ( Churchland et al. 2012 ) are manifested in specific spatio-temporal patterns on the cortical surface. And yet, any functional spatial structure within MI has remained elusive. Unlike most primary sensory cortical areas that exhibit clear topographic organization, the motor cortex reveals highly distributed responses over a large area ( Schieber and Hibbard 1993 ; Sanes et al. 1995 ; Rubino et al. 2006 ; Mollazadeh et al. 2011 ; Riehle et al. 2013 ; Peters et al. 2014 ). For example, whereas the somatosensory cortex possesses distinct representations of the segments of the upper limb, the somatotopic organization of upper limb MI is rather crude with highly overlapping representations, particularly between the elbow and shoulder ( Kwan et al. 1978 ; Park et al. 2004 ). And yet, we have shown that a regular, spatio-temporal pattern of neural activity accompanies movement onset.

Previously, spatio-temporal patterning in MI was interpreted as a cortical correlate of the proximal-to-distal sequence of muscle activation during prehension ( Murphy et al. 1985 ; Riehle et al. 2013 ). Such an interpretation, however, is unlikely to explain the spatio-temporal phenomena we observed in this study. The planar reaching movements used in this study only involved arm movements of the shoulder and elbow, which have been shown to evoke a diversity of muscle activation patterns including proximal-to-distal and distal-to-proximal patterns ( Karst and Hasan 1991 ; Scott 1997 ). And yet, we observed that the BAO was relatively consistent across all movement directions. Moreover, there is no clear delineation between shoulder and elbow representations on the cortical surface, although the extent to which they overlap remains the subject of some debate ( Schieber 2001 ). This does not, however, imply that the spatio-temporal patterning we have documented here is independent of any putative somatotopic map. Indeed, we speculate that the precise orientation of the BAO may be influenced by the local somatotopy underneath the Utah array. The BAO was oriented in the caudal direction for the arrays placed in a more medial position (monkeys V and Rx), whereas the BAO was in the rostral direction for the arrays placed more laterally (monkeys Rs and Rj). Several papers have suggested a horseshoe somatotopic organization where the proximal sites in MI form a horseshoe pattern surrounding a central distal core ( Park et al. 2001 , 2004 ). We speculate that the arrays in V and Rx may be situated in the medial arm of the horseshoe whereas the arrays in Rs and Rj are located in the lateral arm, and this differential positioning with respect to the underlying somatotopic representation drives the different orientations of the BAO. Further research will be needed to explain why different BAOs were observed across animals.

Rather than interpreting spatio-temporal activity patterns on the motor cortical surface as correlates of sequential muscle activation, we suggest that these patterns around movement onset reveal that MI performs a spatially distributed computation to initiate a movement. Inputs to MI from other cortical areas and subcortical structures, such as the cerebellum and basal ganglia, are presumably responsible for activating the motor cortex during movement initiation ( Donoghue and Sanes 1994 ); yet, how these inputs interact with the intrinsic spatio-temporal activity patterns in MI is unknown ( Khanna and Carmena 2015 ). We speculate that inputs to motor cortex are spatially distributed across large regions of MI and integrated via the dense network of horizontal connectivity ( Gatter and Powell 1978 ; Huntley and Jones 1991 ). Using an information theoretic analysis, it has been previously shown that single units exhibit a preponderance of directed, functional connections along the rostro-caudal axis after the onset of a visual cue to initiate movement ( Quinn et al. 2011 ). Moreover, it has recently been demonstrated that the sequential spiking activity of pairs of functionally connected neurons distributed along this axis contains more information about movement direction ( Takahashi et al. 2015 ). Thus, the spatio-temporal dynamics documented here may be supported, in part, by these functional connections aligned along the rostro-caudal axis.

The spatio-temporal patterning that we observed during movement initiation could serve to optimally drive downstream targets of MI, and specifically, muscles. Transcranial magnetic stimulation (TMS) experiments in humans have documented that motor evoked potentials (MEPs) in the muscles are differentially affected depending on the direction of current delivered across the motor cortex. In particular, the MEP amplitude is larger when the induced cortical currents occur along the anterior–posterior axis ( Brasil-Neto et al. 1992 ). Moreover, studies have observed differential MEP thresholds, latencies, and amplitudes when current flows in the anterior–posterior direction versus posterior–anterior direction ( Brasil-Neto et al. 1992 ; Kammer et al. 2001 ; Sommer et al. 2006 ; Jung et al. 2012 ). Thus, the natural rostro-caudal patterns we observed in motor cortical activity may explain why particular TMS current orientations are more effective to drive the motor periphery.

In summary, we found that movement initiation is characterized by a unique spatio-temporal sequence of neural activity and that this sequence is evident in both LFPs and unit spiking. From these findings, we introduced a new hypothesis about the nature of the motor cortical activity required to initiate movements. Future experiments using either electrical or optogenetic stimulation to perturb both the spatial and temporal dynamics of MI activity will be required to further test this hypothesis.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/online.

Funding

This work was supported by grant R01 NS045853 from the NINDS.

Notes

The authors are grateful for the support of the University of Chicago Research Computing Center for assistance with the calculations carried out in this work. The authors would like to thank D. Paulsen, W. Wu, J. Reimer, and Z. Haga for collection of the data. The authors would also like to thank F. Arce-McShane, D. Margoliash, and J. Maclean for useful commentary on this work. Conflict of Interest : None declared.