Abstract
Motivated by the great potential of deep learning in medical imaging, we propose an iterative positron emission tomography (PET) reconstruction framework using a deep learning-based prior. We utilized the denoising convolutional neural network (DnCNN) method and trained the network using full-dose images as the ground truth and low dose images reconstructed from downsampled data by Poisson thinning as input. Since most published deep networks are trained at a predetermined noise level, the noise level disparity of training and testing data is a major problem for their applicability as a generalized prior. In particular, the noise level significantly changes in each iteration, which can potentially degrade the overall performance of iterative reconstruction. Due to insufficient existing studies, we conducted simulations and evaluated the degradation of performance at various noise conditions. Our findings indicated that DnCNN produces additional bias induced by the disparity of noise levels. To address this issue, we propose a local linear fitting (LLF) function incorporated with the DnCNN prior to improve the image quality by preventing unwanted bias. We demonstrate that the resultant method is robust against noise level disparities despite the network being trained at a predetermined noise level. By means of bias and standard deviation studies via both simulations and clinical experiments, we show that the proposed method outperforms conventional methods based on total variation (TV) and non-local means (NLM) penalties. We thereby confirm that the proposed method improves the reconstruction result both quantitatively and qualitatively.
Keywords: PET, reconstruction, convolutional neural network, DnCNN, local linear fitting
I. Introduction
With high performance levels and a striking pace of innovation, the field of machine learning, in particular deep learning, has witnessed surging popularity in many research and industrial fields in recent years. In the domain of medical imaging, the potential deep learning target areas fall into one of two categories [1]. The first category consists of image analysis tasks, such as lesion detection, image segmentation, and diagnostics. The second category spans tasks aimed at image quality improvement including artifact correction, denoising, and reconstruction. In the fields of computed tomography (CT) and positron emission tomography (PET), where it is crucial to limit the radiation dose on patients, dose reduction is usually accompanied by elevated noise levels. Image denoising is of particular significance in these fields, motivated by the need for preserving image quality in low-dose images. A number of deep learning approaches, all employing convolutional neural networks, have been applied to low dose CT (LDCT) [2], [3], [4]. All of these approaches have been designed to work for a pre-defined noise level for both training and testing. Accordingly, the noise level of training data was preset in way of maximizing the denoising performance for that particular level of noise. A preset noise level is a reasonable assumption in CT imaging because radiation dose can be partially controlled via scanner X-source settings. Kang et al. [2] developed a wavelet-based CNN denoising method in which images at two dose levels (e.g. full-dose and quarter-dose) are processing via wavelet decomposition both in the training and application phases for the model. This promissing technique was awarded the second place of 2016 AAPM Low Dose CT Grand challenge [5]. Wu et al. [4] developed a cascaded deep learning method for denoising of LDCT images. The cascaded networks capture multiple features under different noise levels, which lead to higher image quality than single-network denoising. Chen et al. [6] proposed another CNN-based CT denoising approach that exhibited better performance than total variation (TV), k-clustering singular value decomposition (K-SVD), and patch-based block matching 3D (BM3D). However, since these methods also use a fixed noise level in the low-dose image during training, they are not suited in the context of iterative reconstruction, where the noise level of input image changes at each iteration. Recently, Wu et al. [7] proposed a k-sparse autoencoder for unsupervised feature learning in iterative CT reconstruction, and Gong et al. [8] proposed an optimization transfer based iterative PET reconstruction, in which the surrogate function is based on a deep learning model.
The potential of denoising methods based on deep learning in PET imaging has not been widely explored. Unlike CT scans, PET images do not have a consistent noise level making the training phase design challenging. Even with a fixed tracer injection dose, the uptake and bio-distribution can greatly vary across individuals. Furthermore, image noise in PET is spatially variant in a signal-dependent fashion. The tracer distribution may depend on tracer type, tracer dose, scan duration, subject weight and more, resulting in a high degree of variation in the noise level. To compensate for the noise variation in PET reconstruction, an iterative reconstruction approach that combines the Poisson likelihood with a deep learning prior is a more effective strategy for improving PET image quality while reducing artifacts at various noise conditions than a standalone deep learning-based denoising scheme.
In this paper, we propose an iterative PET reconstruction approach using a deep learning prior and demonstrate its ability to exploit the full potential of deep learning under variable noise conditions. As shown in Fig. 1(a), we utilized and modified the denoising convolutional neural network (DnCNN) method [9] trained using patient datasets with a preset noise level. Note that the development of a new network architecture is beyond the scope of this paper. To generate a low-dose image for training, the Poisson thinning process was used for downsampling regular dose data in which coincidence events can be randomly discarded with a predetermined sampling factor. The reconstructed image from 6× downsampled low-dose data was used as input for the DnCNN and the full-dose image was used as the ground truth. Several important issues that arise from combining iterative PET reconstruction and deep learning are demonstrated by simulations in this pioneering study. When using the DnCNN in an iterative reconstruction setting, the noise level disparity of datasets across training and testing setups poses a key challenge. The performance of a neural network trained at a certain noise level can decrease significantly when the noise level exceeds that in the training datasets (see Sec. III). Furthermore, unwanted bias can be accumulated if the DnCNN prior is updated at every iteration in response to noise level changes. Thus, to use the trained network in iterative reconstruction, an additional function or network may be required to control bias. Recent methods [10], [11] have been developed to adaptively estimate noise levels of test samples using additional networks combined with the trained network. In this paper, instead of using additional networks, we propose a novel local linear fitting (LLF) function to correct the unwanted bias by combining both the input image and the deep learning prior as shown in Fig. 1(b), which is incorporated into the cost function. The LLF function is inspired by the nature of CNN that computes networks locally based on small image patches. Thus, the LLF calculates a 3D patch-based linear transform which can locally adjust the bias of the DnCNN image while preserving the features and edges of the DnCNN image.
Fig. 1.
(a) Training of DnCNN with full dose image as the groud truth and low dose image as input. Low dose data is generated by Poisson thining process at a pre-defined noise level ϵ, and multislices along axial direction are used. (b) The trained DnCNN and local linear fitting are combined in iterative PET reconstruction.
For optimization, we utilize the ordered subsets separable quadratic surrogate (OS-SQS) method to maximize the Poisson log-likelihood [12] and use the alternating direction method of multipliers (ADMM) [13] and enforce convex inequality to split sub-optimization steps for DnCNN function and LLF. While convergence is not guaranteed due to nonlinearity of DnCNN, we demonstrate empirically that the cost function can converge with the DnCNN prior under various noise conditions.
For validation of the proposed method, we use both simulated and experimental data, the latter being a clinical dataset acquired using a High-Resolution Research Tomograph (HRRT) PET scanner. The noise level is controlled by a Poisson thinning process using prompt measurements. A down-sampling factor of 6 is used for training in both simulation and experiments. In the simulation study, we demonstrate that the performance of DnCNN can degrade when the noise level changes, and the bias significantly increases after a certain number of iterations. Bias and standard deviation studies via both simulation and experiments demonstrate that the DnCNN prior with LLF can improve the image quality in iterative PET reconstruction. By means of the clinical studies, we confirm that the proposed method outperforms TV-based [14] and NLM-based [15], [16] penalties both quantitatively and qualitatively.
This paper is organized as follows. Section II presents the problem formulation and optimization setup of the proposed method using the LLF with a DnCNN prior. Section III evaluates the performance of LLF for bias control in DnCNN. Section IV describes the details of DnCNN training. Section V presents results from the clinical experiment. Section VI discusses several technical issues, while Section VII presents our concluding remarks.
II. Method
A. Denoising convolutional neural network
DnCNN [9] was originally developed to handle blind Gaussian noise and has two key attributes: residual learning [17] and batch normalization [18]. Residual learning in DnCNN, ensures that the model needs to learn only the noise features. However, unlike the conventional DnCNN approach, we did not use residual learning to ensure flexibility under varying noise levels. Noise in PET raw data is Poisson distributed, and there is substantial variation in the noise level from voxel to voxel in the reconstructed image. It is therefore critical to incorporate the intensity information of PET image during training. DnCNN has 6 layers and a typical layer consists of convolution, rectified linear unit (ReLU) [19] and batch normalization (BN) [18] steps. More specifically, the convolution filter size is 3×3 with 64 feature maps are generated in the convolutional layers. ReLU [19] is an activation function defined as the positive part of its value (f(x) = max(x, 0)), which allows for effective and faster training of deep neural networks compared to other activation functions such as sigmoid function. BN [18] is used to enable for higher learning rates by normalizing each sub-sample set (sub-sample sets are also commonly referred to as mini-batches). The cost function l(w) for our training phase is as follows:
| (1) |
where the network parameters w are learned iteratively. x and x* are the noisy (low dose) and clean (high dose) image pairs for training, reconstructed via ordinary Poisson ordered subsets expectation maximization (OPOSEM) [20]. λ is a weight decay parameter for the L2 regularization to stabilize the training and is set to a value of 0.0005. N is the number of image pairs.
B. Local linear fitting
Due to the disparity of noise levels between traning and testing datasets, the unwanted artifacts can be produced. Specifically, we observed several accumulation of bias when using the DnCNN multiple times in iterations, as will be demonstrated in Sec. III. To address this issue, we propose a novel 3-D local linear fitting (LLF) step to reduce unknown bias as shown in Fig. 1(b), which is inspired by the fundamental nature of CNNs that operate on localized image patches while its implementation is motivated by conventional guided filtering [21]. Thus, the LLF calculates a 3D patch-based linear transform so that we can locally adjust the bias of the DnCNN image while preserving features and edges.
Let x and xD be a noisy input image and an output image, respectively. The main assumption underlying the LLF is that and xD in Fig. 1(b) have a local linear relationship, and their linear transfer function is calculated from the input image x. More specifically, we assume that the is a linear transform of in a local patch pi at a center voxel i.
| (2) |
where qi and bi denote the linear coefficients of a patch pi. To calculate qi and bi, the noisy input image x is used. The LLF cost function in a local patch pi is as follows:
| (3) |
where ϵ is a regularizing parameter meant to prevent large value of qi. However, ϵ also can introduce additional bias, thus, we set it close to zero. By minimizing the cost function, the solutions of qi and bi are calculated iteratively as follows:
| (4) |
| (5) |
where and are the mean values of noisy image x and DnCNN image xD in patch pi at center voxel i. n is the iteration number and Np is the number of voxels in a 3-D patch. Note that the qi and bi have closed-form solutions [21], being mainly affected by pixel variations of patches from two images. With PET images having many zeros and large noise variations, variations of qi and bi tend to be large, which, in turn, can potentially degrade the performance (see Sec. VI). Thus, Eq. (4) firstly updates qi as a local scaling factor that is robust to noise variations and then Eq. (5) corrects small margins, which can be easily updated in iterative PET reconstruction. q(0) and b(0) are set to 1 and 0, respectively.
Now, the fitting output image is
| (6) |
C. Formulation
We denote the reconstructed non-negative image as and the PET measurement . Nυ and Nm denote the numbers of voxels and sinogram bins, respectively. y is the number of photon counts that contain true, scatter and random coincidence events, which follows a Poisson statistical model:
| (7) |
where yi is the number of counts in the ith sinogram bin. ri is the mean value of scatter and random events [22] with the ith sinogram bin. is the system matrix. Specifically, represents the line integral along an LOR and aij denotes the probability that a pair of annihilation photons emitted from the jth voxel of image x is detected at the ith sinogram bin.
We minimize the following cost function Ψo(x):
| (8) |
where denotes the negative log-likelihood function from the Poisson statistics, and hi(k) = k + ri − yi log(k + ri). . and β > 0 is a hyper-parameter. fw(x) is the DnCNN function and all network weights w are already computed and fixed in training phase. Here, ⊙ is the Hadamard product. q and b are the LLF coefficients in Eq. (6).
D. Optimization
R(x) in Eq. (8) is hard to differentiate with respect to x because fw(x), q and b are functions of x. For simplifying our optimization and implementation, we first use the alternating direction method of multipliers (ADMM) to split the DnCNN function by setting xD = fw(x). The cost function becomes
| (9) |
where and . γ > 0 is a hyper-parameter.
To minimize the cost function, we use a majorizer of L(x) using separable quadratic surrogates (SQS) [12]:
| (10) |
and
| (11) |
where is a non-negative real value (gij = 0 only if aij = 0 for all I, j), and
| (12) |
where at nth iteration, and is the curvature of , in which we used the precompute curvature 1/max(yi, ϵ) for the computational efficiency. ϵ = 10−9 is a small positive constant.
Differentiation of R(x, xD) with respect to x is still difficult because both q and b are functions of x. By additionally setting z(n) = q(n) ⊙ xD + b(n) + x(n), we can obtain a separable surrogate of R(x, xD):
| (13) |
| (14) |
| (15) |
| (16) |
Here, we use the convex inequality in Eq. (14) to split q and b from x. In sub-optimizations, q and b become functions of xD and z(n). Thus we can directly calculate their solutions as done in Eqs. (4) and (5).
Now, a majorizer of the cost function is
| (17) |
Algorithm 1.
Proposed method with ordered subsets
| 1: Initialize x(0) using OPOSEM. |
| 2: Initialize q(0) = 1 and b(0) = 0. |
| 3: for n = 0, 1, … do |
| 4: for s = 0, 1, …, Ns − 1 do |
| 5: m = n × Ns + s |
| 6: for j = 1, 2, …, Nv do |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: end for |
| 14: end for |
| 15: end for |
Therefore, we update x, xD, q, b and η alternatingly:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
where and j is a voxel index in an image. This voxel-wise computation makes the optimization parallelizable in our implementation. When updating x, we solve the hybrid gradient surrogates [23], [24] including the Lipschitz surrogates of SQS , second-order surrogates of and D(x), which computes the gradient descent method with the pre-computed step size tj = . The second derivative of DnCNN function is hard to compute, thus, we used a constant α(> 0) in Eq. (22) to control the speed of gradient, where α = 1 and γ = 0.1 were used. β is selected based on the bias and standard deviation study as shown in Sec. V-A. Note that although we do not claim convergence due to the non-linearity of fw(x), we show that the proposed method can converge empirically, as presented in Sec. V.
To further accelerate the convergence speed, ordered subsets (OS) are exploited. We can set Ns equally distributed with angular bins. The system matrix A can be decomposed by subsets, , and the computational cost per sub-iteration decreases almost linearly with respect to the number of subsets Ns. Details of the proposed method is described in Algorithm 1.
E. Implementation
Graphics processing unit (GPU) based 3-D PET reconstruction has been widely used in our previous work [16], [25], [26], [27]. To efficiently use memory and threads in a GPU kernel, main functions were separately parallelized: LLF function, forward and backward projectors, which are implemented in MATLAB (Mathworks, Inc. version 2016a) using MEX (C/C++ compiler) and CUDA (computed unified device architecture, NVIDIA). To incorporate the DnCNN into our existing GPU frameworks in MATLAB, we installed Caffe (deep learning platform) version 1 with GPU and MATLAB options [28].
III. Performance study of LLF for bias control in DnCNN
We performed a simulation study to evaluate the performance of DnCNN and LLF for bias control. Nineteen 3D brain phantoms from the Brainweb database [29] were utilized in the simulation study. We used eighteen images for training and one image for testing, with 50 mid-axial slices were extracted from each image. The image size was 128×128×50 with 2 mm3 resolution. The intensity of each pixel was simulated based on a one-hour FDG scan following which each image was projected to generate the noise-free sinogram. The sinograms were subsequently corrupted by Poisson noise based on emission counts over the one-hour scan duration. Attenuation and uniform random effects were also simulated. However, scatter was not included in our simulation. The EM algorithm with 100 iterations was used to generate the reconstructed images. During training, the reconstructed images using full counts and 6× downsampled counts were used as the ground truth and input respectively. For evaluation, we generated 20 Poisson random measurements from one noise-free sinogram, and then calculated the following normalized terms: 1) noise reduction ratio , 2) bias and 3) standard deviation . Here x*is the ground truth image, x is the noisy input image and xD is the DnCNN image. For purposes of bias and standard deviation computation, x can represent either the DnCNN image or the image obtained using the DnCNN with LLF. is an average image calculated from reconstructed images of 20 randomly generated datasets.
We observed the noise reduction ratios for different inputs of various noise levels using the same pretrained DnCNN. Noise reduction for images reconstructed from 2×, 4×, 6×, 8× and 10× downsampled datasets was compared as shown in Fig. 2(a). The maximum performance is achieved at the same noise level of the training process, which demonstrated that the noise level disparity between training and testing datasets degrades the performance. In Fig. 2(b), we tested the bias increase when using DnCNN multiple times as the input of DnCNN. We observed severe accumulation of bias for EM with DnCNN after a certain number of iterations. However, the LLF function successfully prevented this bias accumulation. In addition, a bias and standard deviation study was conducted as shown in Fig. 2(c) in which the DnCNN with LLF outperformed the performance of DnCNN. Fig. 3 shows the reconstructed images using EM and DnCNN with and without LLF at different iterations. We confirmed that the LLF significantly reduces the bias induced by the disparity of noise levels.
Fig. 2.
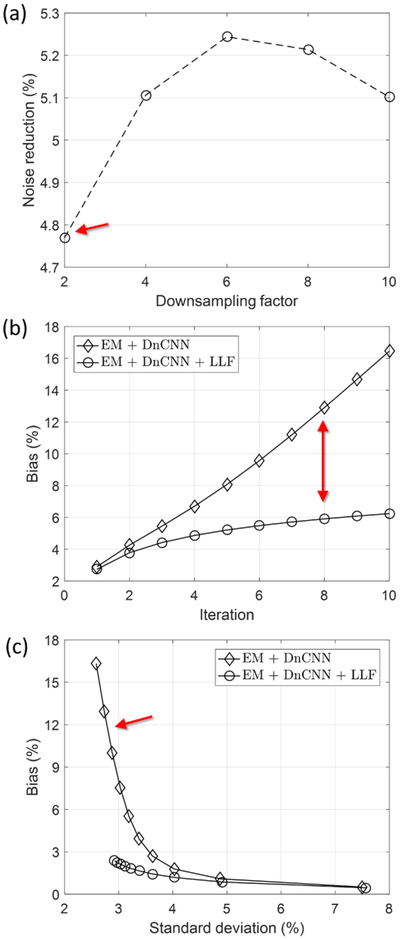
(a) The performance of noise reduction for different downsampling datasets. Because we trained the network using 6× downsampled data, the performace was highest with the 6× downsampled data. (b) Comparison of bias increase by iteration. We iterated DnCNN and DnCNN with LLF by setting the output image as input of next iteration. (c) Comparison of bias and standard deviation.
Fig. 3.
Reconstructed images using EM and DnCNN (a) without LLF and (b) with LLF at iterations (i) 2, (ii) 5 and (iii) 8.
IV. Network training
A. Training datasets
For the network training, we used the existing data acquired for a schizophrenia dynamic study [30], providing high-quality full-dose reference images. The protocol of this study was approved by the Institutional Review Board (IRB) of the Gachon University of Medicine and Science. The High Resolution Research Tomograph (HRRT, Siemens, Konxville, TN, USA) PET scanner with 11C-3-amino-4 benzonitrile ([11C]DASB) was used. The HRRT is an ultra-high resolution brain-dedicated PET scanner that has a transaxial in-plane resolution of 2.5 mm full-width-half-maximum (FWHM) with a voxel size of 1.25×1.25×1.25 mm3 [31]. It has a trans-axial diameter of 46.9 cm with an axial field of view of 25.2 cm, which is sufficient to cover the whole brain. A bolus injection of 577.6 MBq of [11C]DASB was administered and dynamic scan data over 90 mins was acquired. Transmission scans using a 137Cs point source equipped in the HRRT scanner were also obtained for attenuation correction. Random events were acquired in rebinning process, and 3D single scatter simulation [25] was used for scatter estimation. Datasets consisting of a total of 27 control subjects and clinical patients were used for the network training. Although the data were acquired for the dynamic study, we directly rebinned a full-dose prompt sinogram from list-mode data. The reconstructed images using full and downsampled data were used as ground truth and noisy images, respectively, during training. The training input image was reconstructed from a 6× downsampled prompt sinogram based on the Poisson thinning process, which discards coincidence events randomly by the downsampling factor. For example, if the downsampling factor is 6, we can assign uniform ([0,1]) random numbers to all coincidence events and then discard events over 0.167 (1/downsampling factor). Note that the Poisson thinning process should be applied to initial prompt data (listmode or sinogram) without normalization, random, scatter and attenuation corrections. Here, we assumed that the scatter and random fractions remain the same for low count data. After Poisson thinning, the downsampled prompt data was scaled up by downsampling factor to match the intensity level of the ground truth and to facilitate comparison. The ordinary Poisson ordered subsets expectation maximization (OPOSEM) method [20] was used for reconstruction with 6 outer iterations and 16 subsets.
B. Training details
We first generated 80000 pairs of patches with a size of 32×32×5 from 27 reconstructed images using full data and 6× downsampled data. Here, we used 5 axial slices. Overlap of patches was allowed using a 8×8×3 sliding window. In reconstructed images, we discarded patches with mean value less than 10−5 due to the prevalence of near-zero patches otherwise. After patch extraction, 80000 patches were randomly shuffled to avoid similar patches being assigned to the same mini-batch. The DnCNN was trained with mini-batch size of 50 using adaptive learning rate optimization based on the “Adam” approach [32]. The initial learning rate was set to 0.001, and the two momentum factors were set to 0.9. We obtained the trained weights acquired after 100000 epochs.
C. Validation results
For validation of the proposed method, we used a volunteer dataset with a different radiotracer type and dosage compared to the training datasets. A bolus injection of 18F-FDG with 185 MBq was administered to the subject via intra-venously and data was acquired for 75 mins. For the bias and standard deviation study, we generated 20 datasets with 10× downsampling factor based on the Poisson thinning random process. We also generated datasets with downsampling factors of 4, 6 and 8 to observe the robustness of the proposed method. For comparison, the proposed method was compared with state-ofthe-art methods such as OS-SQS with TV [14] and OS-SQS with NLM [15], [16].
V. Results
A. Hyper-parameter selection
For performance evaluation, we first conducted the bias and standard deviation trade-off study. The ground truth image was the OPOSEM image reconstructed from the fully sampled HRRT FDG data. We randomly generated 20 datasets with a 10× downsampling factor based on Poisson thinning. Bias and standard deviation studies were performed to compare reconstructed images generated using OPOSEM with Gaussian filtering, OS-SQS with TV, OS-SQS with NLM, OS-SQS with DnCNN and the proposed method. Here, the intensities of the reconstructed images were scaled up 10 times to calculate bias and standard deviation relative to the ground truth. The same initial image, such as the OPOSEM image from the 10× downsampled dataset with 6 outer iterations and 16 subsets, was used for all methods. Then, the reconstructed images from the penalized methods were obtained by various hyper-parameters after convergence, i.e. 64 sub-iterations (4 outer iterations and 16 subsets). Since OS-SQS with TV and NLM have additional inner hyper-parameters, such as shrinkage factor in TV and patch size, searching window size and smoothing factor (σ) in NLM, we empirically selected the inner hyper-parameters and then changed the β-parameters for the bias and standard deviation study to ensure a fair comparison involving best case scenarios for each method. In Fig. 4, the standard deviation of OPOSEM image with Gaussian filtering was the highest at the same bias. The standard deviation of OSSQS with DnCNN was smaller than the standard deviation of OS-SQS with TV penalty, and higher than the standard deviation of OS-SQS with NLM at the same bias. We also compared the normalized root mean square errors (NRMSEs, ) for the accuracy of quantification. We observed that, when the DnCNN and NLM were used as image filters on the initial OPOSEM image, the NRMSE of DnCNN (0.29) was smaller than the NRMSE of NLM (0.327), and the bias of DnCNN (0.081) was also smaller than the bias of NLM (0.085). However, we observed that the performance of OSSQS with DnCNN suddenly decreases after a certain number of iterations. The proposed method using DnCNN with LLF demonstrated the smallest bias and standard deviation, which confirmed that the LLF function reduced bias and standard deviation significantly. To perform fair comparisons, proper hyper-parameters were selected for OPOSEM with Gaussian filtering, OS-SQS with TV, OS-SQS with NLM, OS-SQS with DnCNN and the proposed method as pointed (i) in Fig. 4. We used the same hyper-parameters for the image quality comparisons reported below.
Fig. 4.
Bias and standard deviation studies for OPOSEM image with Gaussian filtering, OS-SQS with TV, OS-SQS with NLM, OS-SQS with DnCNN and the proposed method, calculated from 20 random datasets with 10× downsampling factor. By selecting similar biases, the hyper-parameters of (i) were used for image quality comparison throughout our experiments. The OPOSEM image using full data was used as the ground truth.
B. Image comparison
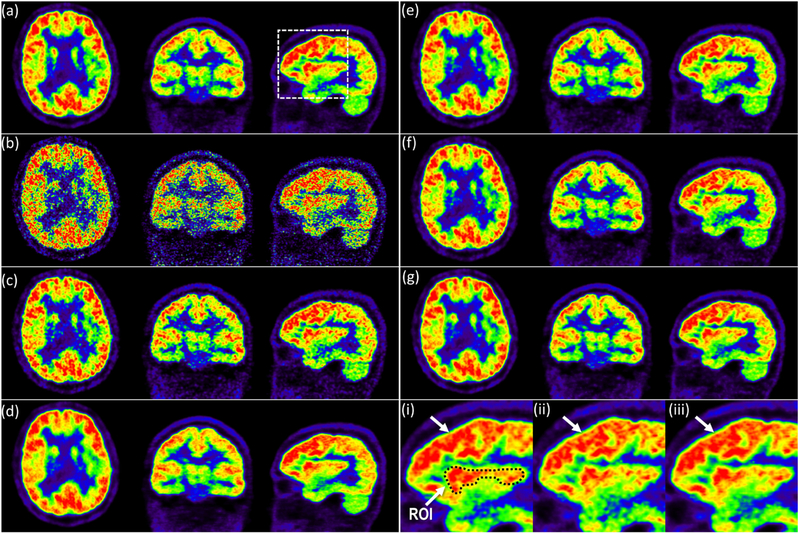
Fig. 5 compares the full dose OPOSEM image, 10× dose OPOSEM image with Gaussian filtering of FWHM 2.4 mm, 10× dose OPOSEM image with DnCNN, OS-SQS with TV, OS-SQS with NLM, OS-SQS with DnCNN and the proposed method; all based on the selected hyper-parameters in the bias and standard deviation study, and all iterative methods used 10× downsampled data. NRMSEs of OS-SQS with TV, OS-SQS with NLM, OS-SQS with DnCNN and the proposed method were 0.29, 0.294, 0.286 and 0.266, respectively. As revealed by magnified views of the full dose OPOSEM image, OS-SQS with NLM and the proposed method, overall structure and shape for the proposed method is visually more similar to the ground truth than the result from OS-SQS with NLM. Furthermore, we selected a region of interest (ROI) in Fig. 5(i) and compared structural similarity (SSIM) index. SSIM is defined by , where r* and r are the ROIs of the ground truth the and the reconstructed image, respectively. μ is the average, σ2 is the variance and σr*r is the covariance of r* and r. c1 = 2.5×10−5 and c2 = 2.25×10−4 were used. SSIMs of OPOSEM image with Gaussian filtering, OS-SQS with TV, OS-SQS with NLM and the proposed method were 0.461, 0.466, 0.487 and 0.496, respectively. We confirmed that the local structures of the proposed method were also quantitatively more similar to the ground truth compared to other methods.
Fig. 5.
Image comparison of (a) full dose OPOSEM image, (b) 10× low dose OPOSEM image, (c) 10× low dose OPOSEM image with Gaussian filtering of FWHM 2.4 mm and (d) 10× low dose OPOSEM image with DnCNN. Iterative reconstrution images using (e) OS-SQS with TV, (f) OS-SQS with NLM and (g) the proposed method. The initial image of (e)–(g) is 10× low dose OPOSEM image. Magnified views of (i) full dose OPOSEM image, (ii) OS-SQS with NLM and (iii) the proposed method; and ROI in (i) is used for SSIM comparison.
To demonstrate the robustness of the proposed method, we performed a convergence study using various downsampling factors: 4, 6, 8 and 10 as shown in Fig. 6. The OPOSEM image using each downsampled dataset was used as the initializer. Convergence was ensured, and images were compared at 100 iterations. The NRMSEs of reconstructed images using 4×, 6×, 8× and 10× downsampled data were 0.224, 0.244, 0.260 and 0.266, respectively. The image qualities corresponding to different downsampling factors were visually similar. We confirmed that the performance of the proposed method for different downsampling factors was consistent. It should be noted that the DnCNN was trained using [11C]DASB datasets and tested using [18F]FDG dataset. Although the noise levels (injection dose) and the intensity distributions of the two datasets were different, the proposed method provided the robust image quality. In addition, although we are not able to guarantee convergence, Fig. 6 demonstrated that the proposed method converged empirically at various noise conditions.
Fig. 6.
Convergence study using various downsampling factors: (a) 4, (b) 6, (c) 8 and (d) 10. The initial image was OPOSEM image using each downsampled data. The converged images were compared at 100 iterations.
C. Execution time
We used NVIDIA’s Titan GPU and CUDA in MATLAB. Main functions, such as forward and backward projectors, were implemented in Mex function of MATLAB with CUDA. DnCNN was implemented with Caffe v1 in MATLAB, which was easily incorporated with main functions. We implemented the 3D version of LLF function using a MATLAB script, which was partially parallelized exploiting gpuArray function. In HRRT geometry of the sinogram with 256 × 288 × 1281 (radial, azimuthal, planes for 3 segments) and the image 256 × 256 × 207 (x, y, z), the projection, back-projection, DnCNN, LLF functions took 3 sec, 3 sec, 2 sec and 2 sec, respectively. Here, the execution time of DnCNN was similar to that of GPU-based TV, and much less than GPU-based NLM.
VI. Discussion
Since the Caffe v1 platform does not support 3D convolution, this can potentially degrade the performance of DnCNN using 3D PET images. In Fig. 7, when the DnCNN was trained using only 2D transaxial slices, we observed axial artifacts in the coronal view. To solve this issue, we used five adjacent slices in DnCNN to promote axial relationships in the network. In our implementation, five channels corresponding to five slices were used in the Caffe script. To compute a fully 3D DnCNN image, the five channels with a sliding window with respect to one axial slice were used. By using overlapping adjacent slices in the DnCNN, axial artifacts were significantly removed.
Fig. 7.
Coronal views of reconstructed images using DnCNNs trained with (a) single slice and (b) five slices.
A conventional DnCNN model was based on a residual image calculated by subtracting a high dose image from a noisy low dose image for training image pairs. To evaluate the relationship of the noise level and the intensity of the PET image, we compared reconstructed images of the proposed method and the DnCNN trained by the residual image. All hyper-parameters and settings were the same. In our observation, the NRMSEs of the DnCNN using residual image and the proposed method were 0.278 and 0.266, respectively. Thus, we directly used the full dose image as groundtruth for training.
LLF function has the same cost function of the conventional guided filter. The cost function leads to the following closed-form solution:
| (24) |
| (25) |
where σi is the standard deviation of at the ith-patch. Unlike natural images corrupted by Gaussian noise (the original design target for the guided filter), the PET image has large variations in noise levels. In PET reconstruction, we found that qi in Eq. (24) is not stable due to large variations in ˙i, which degrades the overall performance as shown in Fig. 8. Therefore, we updated qi by means of a scaling operation and then corrected the margin by bi iteratively. This approach outperforms the closed-form solution and is robust against noise variations.
Fig. 8.
Comparison of NRMSEs using the guided filter and the LLF.
In our implementation, the numerical differentiation method was implemented for fw(x) with respect to x. Recent platforms, such as Tensorflow, support the automatic differentiation method [33], which is more computationally efficient and accurate compared to symbolic and numerical gradient methods, respectively. In future, we will utilize the another platform supporting the automatic differentiation method and the 3D convolution operation, and will extend the proposed method using 3D CNN-based dynamic PET reconstruction for parametric imaging. In addition, further improvements in image quality is still required for the clinical use. To this end, we will explore other deep learning networks for our framework.
VII. Conclusion
We proposed an iterative PET reconstruction framework using the ordered subsets separable quadratic surrogates (OSSQS) approach with a denoising convolutional neural network (DnCNN) and a local linear fitting (LLF) function. The optimization utilized the alternating direction method of multipliers (ADMM) and convex inequality to split suboptimizations, which variables were updated alternatingly. For training of the DnCNN, the full-dose image was used as the ground truth and a low-dose image with 6× downsampled data was used as the input. Our computer simulations demonstrated that the LLF function reduced the unwanted bias generated by DnCNN due to the disparity in noise levels between the training and testing datasets. In clinical experiments, the bias and standard deviation of the proposed method outperformed those of OS-SQS with TV and OS-SQS with NLM. The image quality of the proposed method was visually improved compared to that of other methods. In addition, the proposed method was proven robust against noise variations for a range of different downsampling factors. In future, we will extend this method to incorporate 3D CNNs applied to dynamic PET reconstruction for parametric imaging.
Acknowledgments
This work was supported in part by the Korean Health Technology R& D Project, Ministry of Health & Welfare, Republic of Korea (HI14C2750).
Footnotes
Accompanying codes are available: https://github.com/kssigari/LLF
Contributor Information
Joyita Dutta, Gordon Center for Medical Imaging, Massachusetts General Hospital and Harvard Medical School, US.; Department of Electrical and Computer Engineering, University of Massachusetts Lowell, US.
Jong Hoon Kim, Neuroscience Research Institute, Gachon University of Medicine and Science, Republic of Korea; Department of Psychiatry, Gil Medical Center, Gachon University, Republic of Korea..
References
- [1].Wang G, “A perspective on deep imaging,” IEEE Access, vol. 4, pp. 8914–8924, 2016. [Google Scholar]
- [2].Kang E, Min J, and Ye JC, “A deep convolutional neural network using directional wavelets for low-dose X-ray CT reconstruction,” Medical Physics, vol. 44, no. 10, 2017. [DOI] [PubMed] [Google Scholar]
- [3].Yang Q, Yan P, Kalra MK, and Wang G, “CT Image Denoising with Perceptive Deep Neural Networks,” arXiv preprint arXiv:1702.07019, 2017. [Google Scholar]
- [4].Wu D, Kim K, Fakhri GE, and Li Q, “A Cascaded Convolutional Nerual Network for X-ray Low-dose CT Image Denoising,” arXiv preprint arXiv:1705.04267, 2017. [Google Scholar]
- [5].McCollough C, “TU-FG-207A-04: Overview of the Low Dose CT Grand Challenge (http://www.aapm.org/GrandChallenge/LowDoseCT/),” Medical Physics, vol. 43, no. 6, pp. 3759–3760, 2016. [Google Scholar]
- [6].Chen H, Zhang Y, Zhang W, Liao P, Li K, Zhou J, and Wang G, “Low-dose CT via convolutional neural network,” Biomedical Optics Express, vol. 8, no. 2, pp. 679–694, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Wu D, Kim K, El Fakhri G, and Li Q, “Iterative Low-dose CT Reconstruction with Priors Trained by Artificial Neural Network,” IEEE Transactions on Medical Imaging, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Gong K, Guan J, Kim K, Zhang X, Fakhri GE, Qi J, and Li Q, “Iterative PET Image Reconstruction Using Convolutional Neural Network Representation,” arXiv preprint arXiv:1710.03344, 2017. [Google Scholar]
- [9].Zhang K, Zuo W, Chen Y, Meng D, and Zhang L, “Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising,” IEEE Transactions on Image Processing, vol. 26, no. 7, pp. 3142–3155, 2017. [DOI] [PubMed] [Google Scholar]
- [10].Sukhbaatar S, Bruna J, Paluri M, Bourdev L, and Fergus R, “Training convolutional networks with noisy labels,” arXiv preprint arXiv:1406.2080, 2014. [Google Scholar]
- [11].Patrini G, Rozza A, Menon AK, Nock R, and Qu L, “Making Deep Neural Networks Robust to Label Noise: a Loss Correction Approach,” Stat, vol. 1050, p. 22, 2017. [Google Scholar]
- [12].Erdogan H and Fessler JA, “Ordered subsets algorithms for transmission tomography,” Physics in Medicine and Biology, vol. 44, no. 11, pp. 2835–2851, 1999. [DOI] [PubMed] [Google Scholar]
- [13].Boyd S, Parikh N, Chu E, Peleato B, and Eckstein J, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Foundations and Trends in Machine Learning, vol. 3, no. 1, pp. 1–122, 2011. [Google Scholar]
- [14].Kim K, Dutta J, Groll A, Fakhri GE, Meng L-J, and Li Q, “Penalized maximum likelihood reconstruction of ultrahigh resolution PET with depth of interaction,” in The 13th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine, 2015, pp. 296–299. [Google Scholar]
- [15].Wang G and Qi J, “Penalized likelihood PET image reconstruction using patch-based edge-preserving regularization,” IEEE Transactions on Medical Imaging, vol. 31, no. 12, pp. 2194–2204, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Kim K, Son YD, Bresler Y, Cho ZH, Ra JB, and Ye JC, “Dynamic PET reconstruction using temporal patch-based low rank penalty for ROI-based brain kinetic analysis,” Physics in Medicine and Biology, vol. 60, no. 5, pp. 2019–2046, 2015. [DOI] [PubMed] [Google Scholar]
- [17].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]
- [18].Ioffe S and Szegedy C, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in International Conference on Machine Learning, 2015, pp. 448–456. [Google Scholar]
- [19].Krizhevsky A, Sutskever I, and Hinton GE, “Imagenet classification with deep convolutional neural networks,” in Advances in neural information processing systems, 2012, pp. 1097–1105. [Google Scholar]
- [20].Politte DG and Snyder DL, “Corrections for accidental coincidences and attenuation in maximum-likelihood image reconstruction for positron-emission tomography,” IEEE Transactions on Medical Imaging, vol. 10, no. 1, pp. 82–89, 1991. [DOI] [PubMed] [Google Scholar]
- [21].He K, Sun J, and Tang X, “Guided image filtering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 6, pp. 1397–1409, 2013. [DOI] [PubMed] [Google Scholar]
- [22].Humm JL, Rosenfeld A, and Del Guerra A, “From PET detectors to PET scanners,” European Journal of Nuclear Medicine and Molecular Imaging, vol. 30, no. 11, pp. 1574–1597, 2003. [DOI] [PubMed] [Google Scholar]
- [23].Beck A and Teboulle M, “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183–202, 2009. [Google Scholar]
- [24].Mairal J, “Optimization with first-order surrogate functions,” in International Conference on Machine Learning, 2013, pp. 783–791. [Google Scholar]
- [25].Kim K and Ye J, “Fully 3D iterative scatter-corrected OSEM for HRRT PET using a GPU,” Physics in Medicine and Biology, vol. 56, pp. 4991–5009, 2011. [DOI] [PubMed] [Google Scholar]
- [26].Kim KS, Son YD, Cho ZH, Ra JB, and Ye JC, “Ultra-fast hybrid CPU-GPU multiple scatter simulation for 3D PET,” IEEE Journal of Biomedical and Health Informatics, vol. 18, no. 1, pp. 148–156, 2014. [DOI] [PubMed] [Google Scholar]
- [27].Kim K, Ye JC, Worstell W, Ouyang J, Rakvongthai Y, El Fakhri G, and Li Q, “Sparse-view spectral CT reconstruction using spectral patch-based low-rank penalty,” IEEE transactions on Medical Imaging, vol. 34, no. 3, pp. 748–760, 2015. [DOI] [PubMed] [Google Scholar]
- [28].Jia Y, Shelhamer E, Donahue J, Karayev S, Long J, Girshick R, Guadarrama S, and Darrell T, “Caffe: Convolutional architecture for fast feature embedding,” in Proceedings of the 22nd ACM International Conference on Multimedia. ACM, 2014, pp. 675–678. [Google Scholar]
- [29].Cocosco CA, Kollokian V, Kwan RK-S, Pike GB, and Evans AC, “Brainweb: Online interface to a 3D MRI simulated brain database,” in NeuroImage, vol. 5 Citeseer, 1997, p. 425. [Google Scholar]
- [30].Kim J-H, Son Y-D, Kim J-H, Choi E-J, Lee S-Y, Lee JE, Cho Z-H, and Kim Y-B, “Serotonin transporter availability in thalamic subregions in schizophrenia: A study using 7.0-T MRI with [11 C] DASB high-resolution PET,” Psychiatry Research: Neuroimaging, vol. 231, no. 1, pp. 50–57, 2015. [DOI] [PubMed] [Google Scholar]
- [31].Wienhard K, Schmand M, Casey M, Baker K, Bao J, Eriksson L, Jones W, Knoess C, Lenox M, Lercher M et al. , “The ECAT HRRT: performance and first clinical application of the new high resolution research tomograph,” IEEE Transactions on Nuclear Science, vol. 49, no. 1, pp. 104–110, 2002. [Google Scholar]
- [32].Kingma D and Ba J, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
- [33].Bartholomew-Biggs M, Brown S, Christianson B, and Dixon L, “Automatic differentiation of algorithms,” Journal of Computational and Applied Mathematics, vol. 124, no. 1–2, pp. 171–190, 2000. [Google Scholar]