Effects of biological tissue structural anisotropy and anisotropy of magnetic susceptibility on the gradient echo MRI signal phase: theoretical background

Abstract

Quantitative susceptibility mapping is a potentially powerful technique for mapping tissue magnetic susceptibility from gradient recalled echo (GRE) MRI signal phase. In this review, we present up-to-date theoretical developments in analyzing the relationships between GRE signal phase and the underlying tissue microstructure and magnetic susceptibility at the cellular level. Two important phenomena contributing to the GRE signal phase are at the focus of this review – tissue structural anisotropy (e.g. cylindrical axonal bundles in white matter) and magnetic susceptibility anisotropy. One of the most intriguing and challenging problems in this field is calculating the so-called Lorentzian contribution to the phase shift induced by the local environment – magnetized tissue structures that have dimensions smaller than the imaging voxel (e.g. cells, cellular components, blood capillaries). In this review, we briefly discuss a “standard” approach to this problem, based on introduction of an imaginary Lorentzian cavity, as well as a more recent method – the generalized Lorentzian tensor approach (GLTA) – that is based on a statistical approach and a direct solution of the magnetostatic Maxwell equations. The latter adequately accounts for both types of anisotropy: the anisotropy of magnetic susceptibility and the structural tissue anisotropy. In the GLTA the frequency shift due to the local environment is characterized by the Lorentzian tensor $\widehat{L}$, which has a substantially different structure than the susceptibility tensor $\widehat{\chi }$. While the components of $\widehat{\chi }$ are compartmental susceptibilities “weighted” by their volume fractions, the components of $\widehat{L}$ are weighted by specific numerical factors depending on tissue geometrical microsymmetry. In multi-compartment structures, the components of the Lorentzian tensor also depend on the compartmental relaxation properties, hence the MR pulse sequence settings.

INTRODUCTION

Phase MR images obtained by gradient-recalled echo protocols provide greatly enhanced contrast between gray matter (GM) and white matter (WM) in the brain at high magnetic fields (1–5). Several mechanisms have been proposed over the years to provide the biophysical origin(s) of the phase (frequency) contrast: magnetic susceptibility effects induced by differing tissue chemical composition, specifically including differences in iron (6–10), deoxyhemoglobin (11,12), protein (2,13), and myelin (14–16) content; and magnetization exchange effects between “free” water and macromolecules (2,13,17).

One of the most curious phenomena seen in phase images is the very small contrast between WM and cerebrospinal fluid (CSF) (1,18) – the WM darkness effect (19). An example of a phase image demonstrating this paradox obtained from a human brain is shown in Figure 1. This effect is highly counterintuitive, because WM is a cellular structure containing a high concentration of cell-building materials – proteins, lipids, etc. As a result, a very strong contrast between WM and CSF is usually seen on practically all standard MRI images based on T₁, T₂, magnetization transfer (MT), and diffusion mechanisms.

Figure 1.

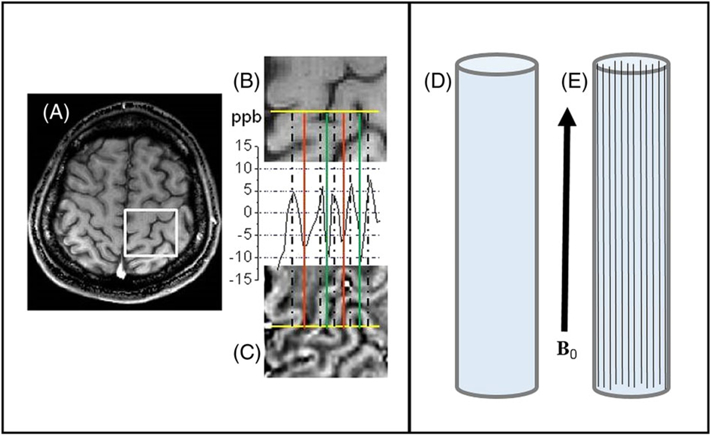
Left (courtesy of Jie Luo): example of the frequency distribution in human cortical brain tissue – data obtained with 3 T MRI scanner from a normal 25 year old male volunteer. (A) T1w image; (B) magnified view of a selected ROI (white rectangle); (C) frequency map of the same ROI as in B. The plot between B and C represents the frequency profile through the selected yellow line. Peaks match up with GM, deep troughs correspond to CSF, and intermediate troughs are WM tracts. The frequency difference between WM and CSF in this plot is very small, about 3 ppb. Right: a schematic diagram explaining the WM darkness effect. It shows two cylindrical containers: D filled with water, and E filled with water and long water-impermeable bars with arbitrary magnetic susceptibility. Since water containers and long bars are parallel to the magnetic field B₀, they do not add to the B₀ magnetic field outside themselves (assuming that the lengths of the main cylinders are much longer than their transverse sizes). Hence, there is no difference between water MR signal frequencies in these two objects in spite of the difference in their bulk (average) magnetic susceptibilities.

To explain these curious phenomena, He and Yablonskiy (18) (see also References (20–22)) introduced a new theoretical concept called the generalized Lorentzian approach (GLA). An important insight from this conceptual framework is that the contribution from the local environment in the neighborhood of a hydrogen nucleus to the MRI signal phase depends not on the bulk magnetic susceptibility of the tissue, but on the “magnetic micro-architecture” of the tissue – i.e. the geometrical distribution of magnetic susceptibility inclusions (lipids, proteins, iron, etc. that become magnetized in the external magnetic field B₀) at the cellular and sub-cellular levels. This theory provided an explanation of why the structural anisotropy of WM (comprised mostly of longitudinally arranged cylindrical myelinated fibers) leads to a very low WM/CSF phase contrast, independent of the sign and value of the WM magnetic susceptibility. The theory also provided a conceptual platform for the quantitative interpretation of data from MR phase imaging of WM diseases (19).

The concept of the GLA is illustrated in the right-hand panel of Figure 1. The two cylinders in D and E are filled with water. The cylinder in E contains long bars with arbitrary (in value and in sign) magnetic susceptibility; however, as is well known, such structures do not create any magnetic field outside of themselves when the external field B₀ is parallel to their axes. Thus, the frequency shift of the water signal in E is exactly the same as in D: it is independent of the value (and sign) of magnetic susceptibility of the bars and the bars’ cross-sectional shape. This example illustrates that, in the presence of longitudinal structures, the water MR signal frequency shift depends not on the bulk magnetic susceptibility, but rather on the details of the structure.

In the cortex area shown in the left-hand panel of Figure 1, the global geometrical orientation of the tissue boundaries and interfaces between GM, WM, and CSF can be approximated as parallel structures along the axis of the main static field B₀ and thus similar to the example shown in the right panel of Figure 1. Like the idealized cylinder example, the inter-tissue boundaries do not contribute to the susceptibility-induced magnetic field or frequency shifts. This explains the very small WM–CSF phase contrast independent of the sign and magnitude of the WM magnetic susceptibility.

The GLA approach was further advanced in Reference (23), where the concept of the structural anisotropy in the formation of phase contrast was combined with the concept of the magnetic susceptibility anisotropy of WM introduced by Liu (24) and Lee et al. (25). This resulted in the development of the generalized Lorentzian tensor approach (GLTA) (23) – the mathematical background for describing the relationship between the gradient recalled echo (GRE) signal phase/frequency and underlying tissue microstructure in biological tissues with anisotropic arrangements of cellular components, e.g. WM fibers. The GLTA makes it possible to bridge the microscopic and phenomenological considerations. Thus, it provides a new and more adequate theoretical basis for quantitative susceptibility mapping (QSM)– a potentially powerful technique for evaluating the magnetic susceptibility distribution in a tissue from GRE MRI phase images (see recent review papers (26–28) and references therein).

An important aspect of the GRE signal phase behavior in WM is related to its multi-component structure – the water molecules reside in the intracellular and extracellular spaces, as well as between lipid bilayers in the myelin sheath. It was demonstrated by Wharton and Bowtell (29) that the radial arrangement of long molecules forming lipid bilayer membranes leads to a very interesting phenomenon – an orientation-dependent frequency shift of the intra-axonal MR signal. Analogous analytical (30) and numerical (31) results have been also obtained. In Reference (32), an important discrepancy between the results of References (29–31) for the myelin signal frequency shift was pointed out. This discrepancy was successfully resolved in Reference (21) by introducing the “hop-in, hop-out” mechanism.

In this review we present the main biophysical ideas behind the anisotropic behavior of GRE signal phase and provide major equations describing the relationships between the underlying biological tissue microstructure and GRE MRI signal. In the following section we set the problem. In the next section, we show the main GLTA equations derived based on a combination of statistical approach and Maxwell equations. A generalization of the GLTA for multi-compartment structures is presented in the fourth section. The last three sections are devoted to discussion of the phase contrast in WM and its changes in multiple sclerosis (MS).

SUSCEPTIBILITY-INDUCED FREQUENCY SHIFT IN THE GRE SIGNAL

Let us consider tissue as comprised of water and spatially distributed magnetic susceptibility inclusions – biological structures of cellular or sub-cellular size with magnetic susceptibility different from that of water – cellular membranes, myelin layers, iron stores, neurofilaments, red blood cells, etc. In the external magnetic field B₀, the system (water + inclusions) becomes magnetized, forming “tissue magnetic architecture” (18–20).

We first consider the case when a biological system can be described in terms of a single water compartment with water-impermeable magnetic susceptibility inclusions. The case of multi-compartment tissue structures will be discussed later. An MR signal from a single-water-compartment system at time t after RF pulse can be presented as

$$S\left(t\right)\hspace{0.33em}=\hspace{0.33em}{S}_0\hspace{0.33em}\exp \left(-2\pi \text{i}\hspace{0.33em}\hspace{0.33em}\overline{f}\hspace{0.17em}t\right)\hspace{0.33em}\exp \left[-\Gamma \left(t\right)\right]$$ [1]

where S₀ is the signal amplitude, $\overline{f}$ is a net frequency and $\Gamma \left(t\right)$ is the attenuation function. This approximation is valid in two limiting cases – the static dephasing regime (33) and the motional narrowing regime when each molecule samples all possible positions in the voxel. The main topic of the present review is the analysis of the contribution of the tissue magnetic architecture on the GRE signal frequency $\overline{f}$.

For the inclusions characterized by the intrinsic volume magnetic susceptibility tensor ${\widehat{\chi }}_{\text{inclusions}}^{\left(0\right)}$ (the symbol ^ denotes a tensor), the distribution of magnetization induced by the external magnetic field B₀ is

$$\mathbf{\text{m}}\left(\mathbf{\text{r}}\right)={\widehat{\mathbf{\chi }}}_u^{\left(0\right)}\left(\mathbf{\text{r}}\right)\cdot {\mathbf{\text{H}}}_0,\hspace{1em}{\mathbf{\text{H}}}_0=\frac{1}{{\mu }_0}\cdot {\mathbf{\text{B}}}_0$$ [2]

where μ₀ is the permeability of vacuum, ${\widehat{\mathbf{\chi }}}_u^{\left(0\right)}\left(\mathit{\text{r}}\right)$ is the position-dependent volume magnetic susceptibility tensor, referenced to water with the volume magnetic susceptibility ${\chi }_{\text{water}}^{\left(0\right)}$,

$${\widehat{\mathbf{\chi }}}_u^{\left(0\right)}\left(\mathbf{\text{r}}\right)={\widehat{\mathbf{\chi }}}^{\left(0\right)}\cdot u\left(\mathbf{\text{r}}\right),\hspace{1em}{\widehat{\mathbf{\chi }}}^{\left(0\right)}=\left({\widehat{\mathbf{\chi }}}_{\text{inclusions}}^{\left(0\right)}-\widehat{\mathbf{I}}\cdot {\chi }_{\text{water}}^{\left(0\right)}\right),$$ [3]

where $\widehat{\mathit{I}}$ is the 3 × 3 unit matrix (I_ii = 1, I_{i ≠ j} = 0), and the function u(r) = 1 inside the inclusions and u(r) = 0 otherwise. The term “intrinsic volume magnetic susceptibility” means magnetic susceptibility of the substance (water or inclusions) and is denoted with superscript⁽⁰⁾ to distinguish it from an average (bulk) volume magnetic susceptibility (without superscript ⁽⁰⁾), i.e., the susceptibility “weighted” by its volume fraction $\zeta :\widehat{\mathbf{\chi }}=\zeta {\widehat{\mathbf{\chi }}}^{\left(0\right)}$.

The magnetization m(r) induces a secondary inhomogeneous magnetic field h(r), resulting in the magnetic-susceptibilityinduced water MR signal frequency shift. This frequency shift (with respect to the pure water MR signal frequency) at any given point r outside the inclusions is

$$\delta f\left(\mathbf{\text{r}}\right)=\frac{\gamma }{2\pi }\cdot \mathbf{\text{h}}\left(\mathbf{\text{r}}\right)\cdot \mathbf{\text{n}}$$ [4]

where n is the unit vector along B₀, and γ is the gyromagnetic ratio (magnetic fields created by external currents are not taken into consideration herein).

Given the distribution of m(r), the secondary magnetic field h(r) can be found from the magnetostatic Maxwell equations:

$$\text{div}\mathbf{\text{h}}=\hspace{0.33em}-\text{div}\mathbf{\text{m}},\hspace{1em}\text{curl}\mathbf{\text{h}}\hspace{0.33em}=\hspace{0.33em}0$$ [5]

A convenient way to solve them for a given distribution of m (r) and to calculate the magnetic field h(r) is to use the Fourier transform of the Maxwell equations (see, e.g., References (34– 36)). The frequency shift δf(r) can then be presented in the form

$$\delta f\left(\mathbf{\text{r}}\right)=-f_0\cdot \text{IFT}\left\{\frac{\left(\mathbf{\text{k}}\cdot \mathbf{\text{n}}\right)\hspace{0.33em}\left(\mathbf{\text{k}}\cdot {\widehat{\mathbf{\chi }}}_u^{\left(0\right)}{\hspace{0.17em}}_{\mathbf{\text{k}}}\cdot \mathbf{\text{n}}\right)}{k^2}\right\},\hspace{1em}{\widehat{\mathbf{\chi }}}_u^{\left(0\right)}{\hspace{0.17em}}_{\mathbf{\text{k}}}=\text{FT}\left\{{\widehat{\mathbf{\chi }}}_u^{\left(0\right)}\left(\mathbf{\text{r}}\right)\right\}$$ [6]

where f₀ = γH₀/2π, FT denotes a standard 3D Fourier transform applied to each component of the tensor ${\widehat{\mathbf{\chi }}}_u^{\left(0\right)}\left(r\right)$, and IFT is an inverse Fourier transform (k is a vector in the Fourier domain).

Of course, if the microscopic distribution and angular dependence of frequency shifts δf(r) could be measured, we would potentially be able to solve the inverse problem in Equation [[6]] and find the spatial and orientation dependences of the magnetic susceptibility tensor ${\widehat{\mathbf{\chi }}}^{\left(0\right)}\left(\mathbf{\text{r}}\right)$, Unfortunately, this problem cannot be solved by means of MRI, because the typical scale of magnetic susceptibility inclusions is of the order of micrometers (cellular and microvascular structures), while the typical resolution of MRI is on the millimeter scale.

Hence, the fundamental question is what the relationship is between an MR signal that measures an average phase/frequency across the imaging voxel and the underlying tissue microstructure at the cellular and sub-cellular levels. In other words, how should one properly define/quantify the influence of numerous magnetic susceptibility inclusions inside an imaging voxel on the MR signal phase measured from a whole voxel? To answer this question, Lorentz (37) formulated the idea of separating the magnetic fields induced by the susceptibility inclusions located far away from a given water molecule and those in the near environment. The former depends on the average (bulk) magnetic susceptibility $\widehat{\mathbf{\chi }}\left(\mathit{R}\right)$, which is a microscopic magnetic susceptibility, ${\widehat{\mathbf{\chi }}}_u^{\left(0\right)}\left(\mathbf{\text{r}}\right)$, averaged across the voxel (hereafter the capital R labels MRI voxels, while r in Eq. [5] and earlier stands for the microscopic coordinates on the sub-voxel level). The latter depends on the distribution of the magnetic susceptibility inclusions in the nearest environment (within a so-called Lorentzian cavity).

In most QSM papers the contribution of the local microscopic environment to the frequency shift is accounted for (i) by choosing the Lorentzian cavity of a spherical shape, and (ii) assuming that the susceptibility inclusions inside the sphere do not contribute to the frequency shift due to the phase averaging effect. In this case, the contribution of the near environment to the average magnetic field inside the cavity is equal to $\frac{1}{3}\widehat{\mathbf{\chi }}\left(\mathit{R}\right)\cdot {\mathit{\text{H}}}_0$, creating a frequency shift δf_L, which is identical to the shift that would exist for water molecules in an empty sphere. For isotropic magnetic susceptibility, $\widehat{\mathbf{\chi }}=\chi \cdot \widehat{\mathit{I}},\delta f_{\text{L}}$ is given by the well-known and broadly used expression

$$\frac{\delta f_{\text{L}}}{f_0}=\frac{1}{3}\cdot \chi .$$ [7]

However, it was demonstrated in Reference (18) (see also References (19,20,22,23,30) and further discussion in (20,21,32,38) and (39)) that the relationship in Equation [7] is incorrect when susceptibility inclusions form longitudinal structures with their lengths much larger than their transverse dimensions and the average distance between them (examples of longitudinal structures in the brain tissue are neurofilaments inside the axons and myelin layers covering the axons).

The most important shortcoming of the approach leading to Equation [7] is that it does not take into account the spatial distribution of the susceptibility inclusions (see detailed discussion in Reference (20)). An example in Figure 2 demonstrates how the spatial distribution of the susceptibility inclusions affects the frequency shift (19). In this example, the magnetic field was calculated based on the numerical solution of Maxwell equations for a given geometry of susceptibility inclusions and their distribution in space. The signal frequency shift δf(R) was calculated by averaging the frequencies δf(r) over space occupied by water molecules outside the susceptibility inclusions (no signal comes from within the susceptibility inclusions). Figure 2 demonstrates how a process of ideal cylindrical structure “randomization” (with a preservation of the total volume of magnetic susceptibility inclusions, hence the bulk volume magnetic susceptibility χ) affects the frequency shift. The structure changes from an ideal long cylinder (solid bold line in the center of the outer cylinder in Figure 2a) to a random distribution of spherical susceptibility inclusions in the same space (Figure 2c).

Figure 2.

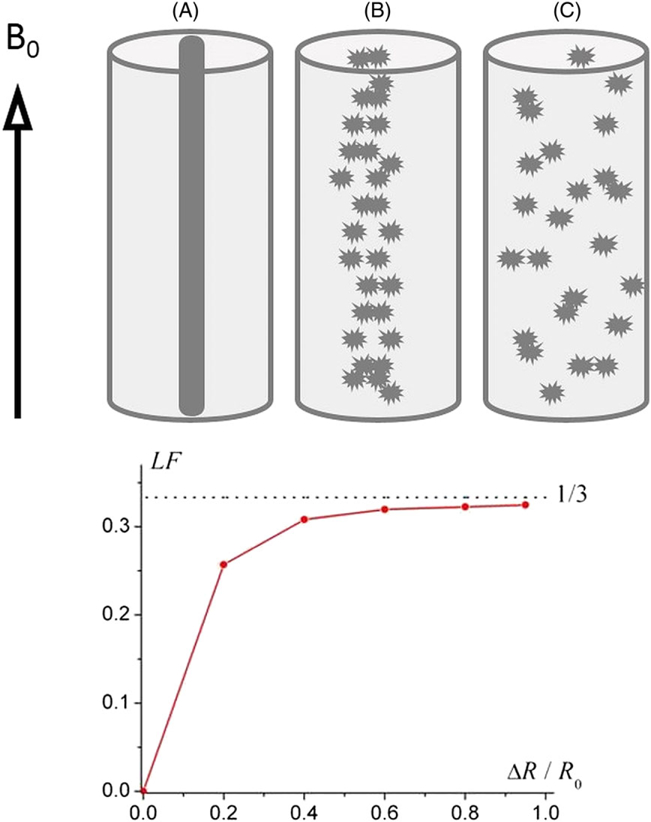
(adopted from Reference (19)). (a) An “ideal” cylindrical structure (black cylinder); (b) “mildly” randomized structure – fragments of the cylinder are slightly scattered; (c) “severely” randomized structure – fragments of the cylinder are scattered randomly. Lower panel – the dependence of the Lorentzian Factor (LF) on the “level of disorder” ΔR/R₀ (ΔR – an average fragment’s displacement, R₀ – the outer cylinder radius). The external magnetic field B₀ is parallel to the cylinder axis.

The simulations reveal that, for all “disorder levels”, the frequency shift can be presented as a product of the bulk volume magnetic susceptibility of the inclusions χ and a numerical coefficient LF (“Lorentzian factor”) depending on the disorder level:

$$\frac{\delta f}{f_0}=\text{LF}\cdot \chi \text{.}$$ [8]

An increase in the “disorder” parameter ΔR (horizontal axis) from zero (intact longitudinally organized structure) to unity (fully disordered structure) changes the LF from zero to the “spherical” value of 1/3, as in Equation [7].

It is important to note that the result illustrated in Figure 2 cannot be explained based on Equation [7], which corresponds to LF = 1/3 for any “disorder level” and, therefore, is not valid in the general case. It should be emphasized that Lorentz himself (37) never suggested that the cavity should have a spherical shape.

It should also be noted that Lorentz (37) discussed the problem of an electric field affecting a point dipole induced by other point dipoles in the system. In biological systems, this is an analog of a magnetic field at a water molecule induced by other water molecules playing the role of susceptibility inclusions. When susceptibility effects are referenced to water, the effect of water on water is implicitly included in the reference frequency.

GENERALIZED LORENTZIAN TENSOR APPROACH (GLTA)

As we can see from the example in Figure 2, even though Equation [7] represents a reasonable approximation for the case when magnetic susceptibility inclusions are randomly distributed in the tissue, it cannot be applied to the case of anisotropic structures (e.g. WM comprising myelinated axons) (18–20).

In Reference (18) (see also (20)), the GLA was proposed. The GLA adequately takes into account the structural anisotropy of susceptibility inclusions and predicts anisotropic behavior of GRE signal phase resulting from the structural anisotropy of WM (18). However, the contribution to the anisotropic behavior of the GRE signal phase could also be due to the anisotropy of magnetic susceptibility (24,25).

In Reference (23), the GLA was generalized to account for both types of anisotropy: the anisotropy of magnetic susceptibility and the structural tissue anisotropy. It is valid for arbitrary magnetic susceptibility anisotropy and arbitrary shape of the inclusions (hence the term generalized Lorentzian tensor approach – GLTA) including multi-compartment tissue structure.

The theoretical consideration based on the concept of a Lorentzian cavity (37) is an intuitive approach for calculating the effective magnetic field created by the local environment. However, similar results can also be obtained by employing another method that is based on a general consideration of Max-well’s equations and a statistical approach without enlisting the concept of the Lorentzian cavity (23). The following derivation of the frequency shift in the framework of the GLTA is based on that provided in the original paper 23.

Initially we assume that the inclusions do not contain water molecules. In this case, the frequency shift δf = f̄‒f₀ in a given voxel R is determined by the induced magnetic field averaged over the volume V_e(R) outside the inclusions (in what follows, for brevity, we omit the argument R labeling the voxels):

$$\delta f=\frac{\gamma }{2\pi }\left({\mathbf{\text{H}}}_{\text{e}}\cdot \mathbf{\text{n}}\right),\hspace{1em}{\mathbf{\text{H}}}_{\text{e}}={〈\mathbf{\text{h}}\left(\mathbf{\text{r}}\right)〉}_{\text{outside}}=\frac{1}{V_{\text{e}}}\underset{V_{\text{e}}}{\int }\text{d}\mathit{r}\hspace{0.33em}\mathbf{\text{h}}\left(\mathbf{\text{r}}\right).$$ [9]

The field H_e should be distinguished from the macroscopic magnetic field

$$\mathbf{\text{H}}=\frac{1}{V}\underset{V}{\int }\text{d}\mathbf{\text{r}}\hspace{0.33em}\mathbf{\text{h}}\left(\mathbf{\text{r}}\right)$$ [10]

obtained by averaging h(r) over the total voxel volume V. It is important to emphasize that just the magnetic field H (not H_e!) satisfies the macroscopic magnetostatic Maxwell equations

$$\text{div}\mathit{\text{H}}=-\text{div}\mathit{\text{M}},\hspace{1em}\text{curl}\hspace{0.33em}\mathit{\text{H}}=0$$ [11]

where

$$\mathbf{\text{M}}=\frac{1}{V}\underset{V}{\int }\text{d}\mathbf{\text{r}}\hspace{0.33em}\mathbf{\text{m}}\left(\mathbf{\text{r}}\right)$$ [12]

is the average magnetization in the voxel, and m(r) is given by Equation [2]. Equation [11] can be solved similarly to Equation [5], and the result can be presented in a form similar to Equation [6].

The quantities H and H_e are related:

$$\mathbf{\text{H}}=\left(1-\zeta \right){\mathbf{\text{H}}}_{\text{e}}{+\zeta \mathbf{\text{H}}}_{\text{i}}$$ [13]

where

$${\mathbf{\text{H}}}_{\text{i}}={〈\mathbf{\text{h}}\left(\mathbf{\text{r}}\right)〉}_{\text{inside}}=\frac{1}{V_{\text{i}}}\underset{V_{\text{i}}}{\int }\text{d}\mathit{r}\hspace{0.33em}\mathbf{\text{h}}\left(\mathbf{\text{r}}\right)$$ [14]

is the magnetic field h(r) averaged over the volume V_i inside the inclusions and ζ is the volume fraction occupied by the inclusions in the voxel.

Consider first the case when in a given voxel there is a single type of identical susceptibility inclusions of the same shape and orientation, occupying the volume fraction ζ and being described by the volume magnetic susceptibility tensor ${\widehat{\mathbf{\chi }}}^{\left(0\right)}$. In this case, the magnetization is also the same within all the inclusions, ${\mathbf{\text{m}}=\mathbf{\text{m}}}_{\text{0}}={\widehat{\mathbf{\chi }}}^{\left(0\right)}\cdot {\mathbf{\text{H}}}_{\text{0}}$, and $\mathbf{\text{M}}=\zeta {\mathbf{\text{m}}}_0$. In addition to B₀, each inclusion “feels” the position-dependent induced magnetic field h_e(r) created by all other inclusions and the field induced by the inclusion itself. In what follows, we assume that the shape of the inclusions can be approximated by an ellipsoid (spheres, long cylinders, in particular). In this case, the induced magnetic field within a given inclusion, h_i(r), is related to h_e(r) by a well-known expression for a shift of the magnetic field within a homogeneously magnetized ellipsoid: ${\mathit{h}}_{\text{i}}\left(\mathit{r}\right)={\mathit{h}}_e\left(\mathit{r}\right)-\widehat{\mathit{N}}{\mathit{m}}_0$, where $\widehat{\mathit{N}}$ is the so called demagnetization tensor determined by the inclusion’s shape (analytical expressions and tables for this tensor can be found, e.g., in References (40) and (41). By averaging this equation over all the positions (but not orientations) of the inclusions (similar to the statistical approach used in Reference (33)), we find that the average fields H_i and H_e are related as follows:

$${\mathbf{\text{H}}}_{\text{i}}={\mathbf{\text{H}}}_{\text{e}}-\widehat{\mathbf{N}}{\mathbf{\text{m}}}_0$$ [15]

Combining Equations [[13]] and [[15]], we obtain

$${\mathbf{\text{H}}}_{\text{e}}=\mathbf{\text{H}}+{\mathbf{\text{H}}}_{\text{L}};\hspace{1em}{\mathbf{\text{H}}}_{\text{L}}=\widehat{\mathbf{N}}\widehat{\mathbf{\chi }}{\mathbf{\text{H}}}_0$$ [16]

where $\widehat{\chi }=\varsigma \cdot {\widehat{\chi }}^{(0)}$ is the average volume magnetic susceptibility, often called the bulk volume magnetic susceptibility. As already mentioned, the average volume susceptibility is designated $\widehat{\mathbf{\chi }}$ to distinguish it from ${\widehat{\mathbf{\chi }}}^{\left(0\right)}$ ‒ the intrinsic volume magnetic susceptibility of the inclusions themselves.

Thus, the magnetic field H_e determining the frequency shift δf in Equation [9] comprises two parts: the field H satisfying the Maxwell equations, [11], and the Lorentzian field H_L:

$${\mathbf{\text{H}}}_{\mathbf{\text{L}}}=\widehat{\mathbf{L}}{\mathbf{\text{H}}}_0,\hspace{1em}\widehat{\mathbf{L}}=\widehat{\mathbf{N}}\widehat{\mathbf{\chi }}$$ [17]

Correspondingly, the frequency shift can be represented as

$$\delta f=\delta f_H+\delta f_L,\delta f_H=\frac{\gamma }{2\pi }\left(\mathbf{\text{H}}\cdot \mathbf{\text{n}}\right),\hspace{1em}\delta f_L=f_0\left(\mathit{\text{n}}\cdot \widehat{\mathit{L}}\cdot \mathit{\text{n}}\right)$$ [18]

The frequency shift δf_H in a given voxel is determined by the average magnetic field H in the voxel, which depends on the spatial distribution of the bulk magnetic susceptibility in the system, $\widehat{\mathbf{\chi }}\left(R\right)$, whereas the Lorentzian frequency shift δf_L describes the contribution of the local environment.

Hence, the frequency shift δf_L (defined by the Lorentzian tensor $\widehat{\mathit{L}}$ in Eq. [17]) is determined by the two types of anisotropy: the structural anisotropy of inclusions (spheres, cylinders, etc.), described by the demagnetization tensor $\widehat{\mathbf{N}}$, and the anisotropy of susceptibility, described by the susceptibility tensor $\widehat{\mathbf{\chi }}$.

Equations [17] and [18] can be readily generalized for the case when the voxel contains the susceptibility inclusions of several types, each of them characterized by its own volume fraction ζ_j demagnetization tensor ${\widehat{\mathbf{N}}}_j$, and intrinsic susceptibility tensor ${\widehat{\mathbf{\chi }}}_j^{\left(0\right)}$. In this case, the volume susceptibility tensor $\widehat{\mathbf{\chi }}$ and the Lorentzian tensor $\widehat{\mathit{L}}$ are simply the sums of the contributions of all the types of susceptibility inclusion:

$$\widehat{\mathbf{\chi }}=\sum _j{\widehat{\mathbf{\chi }}}_j,\hspace{1em}\widehat{\mathbf{L}}=\sum _n{\widehat{\mathbf{N}}}_j{\widehat{\mathbf{\chi }}}_j,\hspace{1em}{\widehat{\mathbf{\chi }}}_j={\zeta }_j\cdot {\widehat{\mathbf{\chi }}}_j^{\left(0\right)}.$$ [19]

The frequency shift δf, Equation [18], can also be presented in a form similar to Equation [6]:

$$\delta f=f_0\hspace{0.33em}\text{IFT}\left\{\left[\mathbf{\text{n}}\cdot {\widehat{\mathbf{L}}}_{\mathbf{\text{k}}}\cdot \mathbf{\text{n}}-\frac{\left(\mathbf{\text{k}}\cdot \mathbf{\text{n}}\right)\cdot \left(\mathbf{\text{k}}\cdot {\widehat{\mathbf{\chi }}}_{\mathbf{\text{k}}}\cdot \mathbf{\text{n}}\right)}{{\mathbf{\text{k}}}^2}\right]\right\}.$$ [20]

Two types of susceptibility inclusions are important in biological tissue.

(A) Randomly distributed spherical-like inclusions (e.g. small sub-cellular structures, iron stores) with isotropic susceptibility described by a single scalar χ_iso; in this case, the tensors $\widehat{\mathbf{\chi }}$, $\widehat{\mathit{N}}$ and $\widehat{\mathit{L}}$ are simply proportional to the unit tensor $\widehat{\mathit{I}}$:

$${\widehat{\mathit{N}}}_{\text{iso}}=\frac{1}{3}\cdot \widehat{\mathit{I}},\hspace{1em}{\widehat{\mathbf{\chi }}}_{\text{iso}}={\chi }_{\text{iso}}\cdot \mathit{I},\hspace{1em}{\widehat{\mathit{L}}}_{\text{iso}}=\frac{{\chi }_{\text{iso}}}{3}\cdot \widehat{\mathit{I}}.$$ [21]

It can be easily demonstrated that, due to the orientation averaging, the same result is reached when the inclusions with isotropic susceptibility χ_iso are not spheres but their orientations are random. Indeed, using the identity ${〈n_{\alpha }{n}_{\beta }〉}_{\text{orient}}={\Delta }_{\alpha \beta }/3$ (${\Delta }_{\alpha \beta }$ is the Kronecker delta) and Tr ($\widehat{\mathbf{N}}$) = 1, the orientation averaging of the quantity δf_L, Equation [18], leads to

$$\delta f_{\text{L}}=f_0\cdot {\chi }_{\text{iso}}{〈n_{\alpha }{\mathit{N}}_{\alpha \beta }{n}_{\beta }〉}_{\text{orient}}=f_0\cdot {\chi }_{\text{iso}}/3.$$ [22]

(B) Longitudinally arranged inclusions (neurons), which can be considered as long parallel cylinders with the anisotropic susceptibility described by two different components: axial χ_a and radial χ_r. In this case the tensors $\widehat{\mathbf{\chi }}$, $\widehat{\mathbf{N}}$, and $\widehat{\mathbf{L}}$ (with the Z-axis oriented along the inclusions) are

$${\widehat{\mathbf{N}}}_{\text{cyl}}=\frac{1}{2}\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right),{\widehat{\mathbf{\chi }}}_{\text{cyl}}=\left(\begin{array}{ccc}{\chi }_{\mathbf{\text{r}}}& 0& 0\\ 0& {\chi }_{\mathbf{\text{r}}}& 0\\ 0& 0& {\chi }_{\text{a}}\end{array}\right),{\widehat{\mathbf{L}}}_{\text{cyl}}=\frac{1}{2}\left(\begin{array}{ccc}{\chi }_{\mathbf{\text{r}}}& 0& 0\\ 0& {\chi }_{\mathbf{\text{r}}}& 0\\ 0& 0& 0\end{array}\right)$$ [23]

Importantly, the axial component of the susceptibility tensor is not present in the Lorentzian tensor $\widehat{\mathit{L}}$_cyl or, consequently, in the Lorentzian part of the frequency shift δf_L. Note that if the longitudinal inclusions are not parallel to each other (as in WM) but isotropically oriented (as in GM), the averaged Lorentzian tensor takes the form in Equation [22] with the substitution χ_iso → χ_r. It should be emphasized however that, despite this resemblance, the result is still different from that obtained by using the Lorentzian spherical cavity approach: the axial component χ_a does not contribute to the averaged Lorentzian tensor.

If both types (A) and (B) are present in a voxel, the average magnetic field H_e defining the resonance frequency (similar to Eq. [16]) is

$${\mathit{\text{H}}}_{\text{e}}=\mathbf{\text{H}}+\left({\widehat{\mathbf{N}}}_{\text{cyl}}\cdot {\widehat{\mathbf{\chi }}}_{\text{cyl}}+{\widehat{\mathbf{N}}}_{\text{iso}}\cdot {\widehat{\mathbf{\chi }}}_{\text{iso}}\right)\cdot {\mathbf{\text{H}}}_0$$ [24]

The tensors $\widehat{\mathbf{\chi }}$ and $\widehat{\mathit{L}}$ in Equation [20] in this case are

$$\widehat{\mathbf{\chi }}={\widehat{\mathbf{\chi }}}_{\text{iso}}+{\widehat{\mathbf{\chi }}}_{\text{cyl}}=\left(\begin{array}{ccc}{\chi }_{\text{iso}}& 0& 0\\ 0& {\chi }_{\text{iso}}& 0\\ 0& 0& {\chi }_{\text{iso}}\end{array}\right)+\left(\begin{array}{ccc}{\chi }_{\mathbf{\text{r}}}& 0& 0\\ 0& {\chi }_{\mathbf{\text{r}}}& 0\\ 0& 0& {\chi }_{\text{a}}\end{array}\right)$$ [25]

$$\widehat{\mathbf{L}}={\widehat{\mathbf{L}}}_{\text{iso}}+{\widehat{\mathbf{L}}}_{\text{cyl}}=\frac{1}{3}\cdot \left(\begin{array}{ccc}{\chi }_{\text{iso}}& 0& 0\\ 0& {\chi }_{\text{iso}}& 0\\ 0& 0& {\chi }_{\text{iso}}\end{array}\right)+\frac{1}{2}\cdot \left(\begin{array}{ccc}{\chi }_{\mathbf{\text{r}}}& 0& 0\\ 0& {\chi }_{\mathbf{\text{r}}}& 0\\ 0& 0& 0\end{array}\right)$$ [26]

and the frequency shift is given by Equations [18] and [20]. In this case, the Lorentzian part of the frequency shift, δf_L, can be presented as

$$\frac{\delta f_{\text{L}}}{f_0}=\frac{1}{3}\cdot {\chi }_{\text{iso}}+\frac{1}{2}\cdot {\chi }_{\mathbf{\text{r}}}{\sin }^2\alpha$$ [27]

THE ROLE OF THE MULTI-COMPARTMENT TISSUE STRUCTURE

It was assumed in the above consideration that there are no water molecules inside the susceptibility inclusions and the signal originates only from the space outside the inclusions. This is not the case, for example, in WM, where neuronal fibers comprise the axons surrounded by the myelin sheath, which in its turn is surrounded by the extracellular space. These compartments (axon, myelin sheath, extracellular space) contain water molecules contributing to the GRE MR signal (21,29–31), leading to a substantial non-linear dependence of the GRE signal phase on the gradient echo time T_E (29,31). Experimentally observed T_E dependences of the frequency shift in WM are illustrated in Figure 3 (adapted from References (29,31)). The different lines correspond to different orientation of axonal fibers with respect to the external field B₀.

Figure 3.

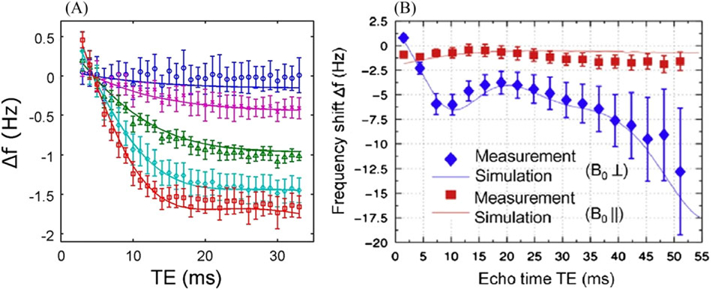
Experimentally observed T_E dependences of the frequency shifts in WM (A – adapted from Reference (29); B – adapted from (31)). The lines correspond to axonal fibers with different orientations with respect to the external field B₀. The frequency is practically independent of T_E for fibers parallel to B₀ and strongly depends on T_E for the perpendicular orientation.

Kim et al. (42) reported changes in the T_E dependences of the phase in WM for the standard GRE and the VISTa experiment (see Figure 4), in which the contributions to the signal from the long-T₁ compartments (intra-and extracellular water) are suppressed.

Figure 4.

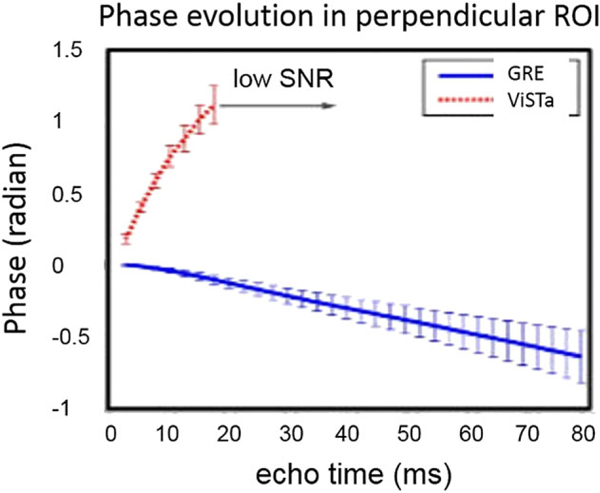
(adapted from Reference (42)). Phase evolution of the GRE and VISTa signals. The signals are from the fibers that are nearly perpendicular to the external field B₀.

Interestingly, the GRE curve shows a negative slope, suggesting that the total frequency shift of a WM sample is negative, whereas the VISTa curve, contributed mostly by the short-T₁ (myelin water) compartment, demonstrates a positive slope, suggesting a positive frequency shift in this compartment.

Below we demonstrate how this multi-compartment structure of WM can be incorporated in the GLTA. In a multi-compartment system, the MR signal is a sum of signals from the compartments:

$$S\left(T_{\text{E}}\right)=\sum _n{\epsilon }_n{S}_n\left(T_{\text{E}}\right)\exp \left(-\text{i2}\pi \delta f_n{T}_{\text{E}}\right)$$ [28]

where S_n(T_E)= S_n(0) exp (−Γ_n(T_E)) are the signal amplitudes at echo time T_E, and Γ_n(T_E), δf_n, and ε_n are the attenuation functions describing the signal decay, the average frequency shifts, and the volume fractions in the nth compartment, respectively. It is convenient to re-write Equation [28] in the form

$$S={\overline{S}}_0\left(T_{\text{E}}\right)\exp \left(-2\pi \text{i}\overline{\delta f\cdot }{T}_{\text{E}}\right)\sum _n{\epsilon }_n{c}_n\left(T_{\text{E}}\right)\exp \left(-2\pi \text{i}\cdot \Delta f_n{T}_{\text{E}}\right)$$ [29]

$${\overline{S}}_0\left(T_{\text{E}}\right)=\sum _n{\epsilon }_n{S}_n\left(T_{\text{E}}\right),\hspace{1em}{c}_n\left(T_E\right)=\frac{S_n\left(T_{\text{E}}\right)}{{\overline{S}}_0\left(T_{\text{E}}\right)}$$ [30]

$$\overline{\delta f}=\sum _n{\epsilon }_n{c}_n\left(T_{\text{E}}\right)\delta f_n,\hspace{1em}\Delta f_n=\delta f_n-\overline{\delta f}.$$ [31]

The total signal phase, in general, has a non-linear dependence on the gradient echo time T_E due to (i) the exponential factors with different ⊿f_n in the sum in Equation [29], and (ii) the “weighting factors” c_n, which depend on MRI pulse sequence parameters and the compartments’ relaxation properties.

The instant frequency shift of the signal can be obtained at arbitrary T_E by differentiating the signal phase. In what follows, we consider the case of sufficiently short times when, for all the compartments, 2πΔf_nT_E < 1. In this case, the sum in Equation [29] is close to unity and can be omitted. As a result, the signal phase can be characterized by a single (though T_E-dependent) average frequency $\overline{\delta f}$, Equation [31]. This approximation is also valid in the regime when the signal contribution from one of the compartments becomes negligible (e.g., Γ_n(T_E) > 1), even if the condition 2πΔf_nT_E < 1 for this compartment fails. An example of such a compartment is myelin water, which has a large frequency shift and a very short T₂* (29,31).

In what follows, we exemplify our general consideration of a multi-compartment structure by a model of neuronal fiber developed in References (21,30) and presented in Figure 5. The axon contains two types of magnetic susceptibility inclusion: randomly distributed and oriented inclusions with the isotropic susceptibility ${\chi }_{\text{iso}}^{\left(\text{A}\right)}$ (not shown in Figure 5) and longitudinally arranged inclusions (neurofilaments) with anisotropic susceptibility characterized by the susceptibility tensor ${\widehat{\mathbf{\chi }}}^{\left(\text{A}\right)}$ of cylindrical symmetry (as in Eq. [23]). The magnetic susceptibility of the lipoprotein layers is characterized by the parameters ${\chi }_{\parallel }^{\left(\text{ml}\right)}$ and ${\chi }_{\perp }^{\left(\text{ml}\right)}$, which are the susceptibilities parallel and perpendicular to the local radial direction in the myelin rings. For generality, we assume that the aqueous layers in myelin and extracellular space also contain randomly distributed and randomly oriented inclusions with isotropic susceptibilities ${\chi }_{\text{iso}}^{\left(\text{mw}\right)}$ and ${\chi }_{\text{iso}}^{\left(\text{e}\right)}$, respectively. All these susceptibilities represent contributions of corresponding inclusions to the bulk volume magnetic susceptibilities of a given compartment of a neuronal fiber (as there is no water in lipoprotein layers, the bulk susceptibilities ${\chi }_{\parallel }^{\left(\text{ml}\right)}$ and ${\chi }_{\perp }^{\left(\text{ml}\right)}$ coincide with their intrinsic values).

Figure 5.

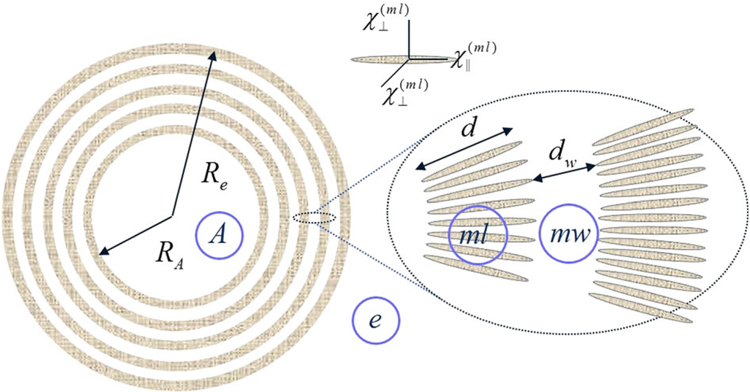
(modified from (30). A schematic structure of an axon (A) with radius R_A surrounded by a myelin sheath with external radius R_e consisting of interleaved lipoprotein layers (ml) of thickness d marked in grey, separated by aqueous layers (mw) of thickness d_w. Each lipoprotein layer is formed by highly organized, radially oriented long molecules (shown as ellipsoids in the inset) with presumed anisotropic magnetic susceptibility.

The volume fractions ε_n (n = A, ml, mw, e) of the four compartments in Figure 5: axon (A), myelin lipoprotein layers (ml), myelin aqueous layers (mw), and extracellular space (e) are

$$\begin{gathered} \hspace{0.33em}\hspace{0.17em}{\epsilon }_{\text{A}}=\zeta \cdot g^2,\hspace{1em}{\epsilon }_{\text{ml}}=\zeta \cdot \left(1-g^2\right).\frac{d}{d+d_{\text{w}}} \\ {\epsilon }_{\text{mw}}=\zeta \cdot \left(1-g^2\right)\cdot \frac{d_{\text{w}}}{d+d_{\text{w}}},\hspace{1em}{\epsilon }_e=1-\zeta \end{gathered}$$ [32]

where ζ is the volume fraction of the neurons (axons + myelin sheaths); g = R_A/R_e is the g-ratio. The components of the net (bulk) volume magnetic susceptibility of the object (neurons + extracellular space), determining the macroscopic magnetic field H, can be presented in the form of Equation [25] with

$${\chi }_{\text{iso}}={\epsilon }_{\text{A}}\cdot {\chi }_{\text{iso}}^{\left(\text{A}\right)}+{\epsilon }_{\text{mw}}\cdot {\chi }_{\text{iso}}^{\left(\text{mw}\right)}+{\epsilon }_{\text{e}}\cdot {\chi }_{\text{iso}}^{\left(\text{e}\right)}$$ [33]

$${\chi }_{\mathbf{\text{r}}}={\epsilon }_{\text{A}}\cdot {\chi }_{\mathbf{\text{r}}}^{\left(\text{A}\right)}+{\epsilon }_{\text{ml}}\cdot {\overline{\chi }}^{\left(\text{ml}\right)},\hspace{1em}{\overline{\chi }}^{\left(\text{ml}\right)}=\frac{1}{2}\left({\chi }_{\parallel }^{\left(\text{ml}\right)}+{\chi }_{\perp }^{\left(\text{ml}\right)}\right)$$ [34]

$${\chi }_{\text{a}}={\epsilon }_{\text{A}}\cdot {\chi }_{\text{a}}^{\left(\text{A}\right)}+{\epsilon }_{\text{ml}}\cdot {\chi }_{\perp }^{\left(\text{ml}\right)}$$ [35]

(the structure of ${\overline{\chi }}^{\left(\text{ml}\right)}$ is due to angular averaging of the angledependent local susceptibility of the lipoprotein layers (21,30)).

In the model proposed in References (21,30), the compartmental frequency shifts δf_n (n = A,mw, e) are

$$\frac{\delta f_{\text{A}}}{f_0}=\frac{1}{2}{\sin }^2\alpha \frac{d}{d+d_{\text{w}}}\Delta {\chi }^{\left(\text{ml}\right)}\text{In}\left(\frac{1}{g}\right)+\left(-\frac{1}{2}{\sin }^2\alpha +\frac{1}{3}\right){\chi }_{\text{iso}}^{\left(\text{A}\right)}$$ [36]

$$\begin{gathered} \frac{\delta f_{\text{mw}}}{f_0}=\frac{1}{2}{\sin }^2\alpha \frac{d}{d+d_{\text{w}}}\left\{\Delta {\chi }^{\left(\text{ml}\right)}\left[\frac{1}{2}+\frac{g^2\text{In}g}{\left(1-g^2\right)}\right]-\lambda \cdot {\chi }_{\parallel }^{\left(\text{ml}\right)}\right\} \\ \hspace{1em}\hspace{1em}\hspace{1em}+\left(-\frac{1}{2}{\sin }^2\alpha +\frac{1}{3}\right)\cdot {\chi }_{\text{iso}}^{\left(\text{mw}\right)} \end{gathered}$$ [37]

$$\frac{\Delta f_{\text{e}}}{f_0}=\left(-\frac{1}{2}{\sin }^2\alpha +\frac{1}{3}\right)\cdot {\chi }_{\text{iso}}^{\left(\text{e}\right)}$$ [38]

where $\Delta {\chi }^{\left(\text{ml}\right)}={\chi }_{\parallel }^{\left(\text{ml}\right)}-{\chi }_{\perp }^{\left(\text{ml}\right)}$ and α is the angle between the axonal and external magnetic field B₀ directions (as in Equation [8]). Equation [38] and the last terms in Equations [36] and [37] are due to the presence of randomly distributed and randomly oriented structures forming cellular matrix (neurofilaments, etc.) in a circular cylindrical shape of a neuronal fiber (and pure water outside the fiber). The longitudinally oriented parts of these structures are “invisible” in (do not contribute to) the frequency shift inside the fibers (18), though they affect the frequency shift outside the fibers due to their contribution to the bulk magnetic susceptibility, Equation [18]. The first term in Equation [36] is similar to that first derived by Wharton and Bowtell in the framework of the “hollow cylinder” model (29). Equation [37] for the myelin water signal is different from the corresponding expression in Reference (29) and computer simulations in 31. This difference is due to the fact that References (29,31) use Equation [7] to calculate the Lorentzian frequency shift in the myelin water signal, which is incompatible with the cylindrical symmetry of axonal bundles. This approximation predicts a substantial frequency shift even for the fibers parallel to B₀. Equation [37], on the other hand, predicts zero myelin-induced frequency shift for parallel fibers.

The term $\left(-\lambda \cdot {\chi }_{\parallel }^{\left(\text{ml}\right)}\right)$ in Equation [37], corresponding to the “hop-in hop-out” mechanism proposed in Reference (21), makes it possible to explain a positive frequency shift of myelin water despite negative susceptibility of lipoprotein layers. The essence of this mechanism is as follows. In the presence of the external magnetic field B₀, the lipoprotein layers become magnetized and create an additional magnetic field δh. This field can be described as a result of magnetostatic charges formed on the layers’ surfaces (surface charges) and inside the lipoprotein layers (volume charges). The volume charges are solely due to the anisotropy of magnetic susceptibility (30), whereas the surface charges exist even in the case of isotropic susceptibility. The surface magnetostatic charges (which are of interest for the hop-in hop-out mechanism and shown as + and – signs in Figure 6) are given by ${\rho }_S=\pm {\chi }_{\parallel }^{\left(\text{ml}\right)}{H}_0\sin \alpha \cos \varphi$ where ϕ is the azimuthal angle. The signs of the surface charges in Figure 6 and the direction of the field δh within the lipoprotein layers correspond to ${\chi }_{\parallel }^{\left(\text{ml}\right)}<0$. The projection of this field on B₀, averaged over the azimuthal angle ϕ, is equal to $\delta h=-{\chi }_{\parallel }^{\left(\text{ml}\right)}{H}_0{\sin }^2\alpha /2$.

Figure 6.

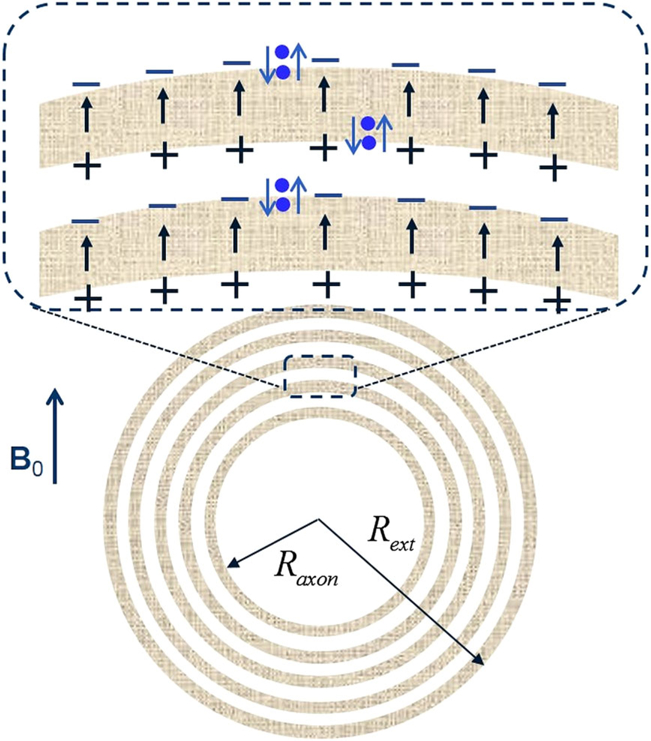
A schematic structure describing the “hop-in-hop-out” mechanism. All the parameters are the same as in Figure 5. Blue dots represent water molecules performing a “hokey pokey dance” from aqueous to lipoprotein layers. When a water molecule jumps from water layer to lipoprotein layer, it experiences an additional field δh (shown as arrows) induced by the surface charges.

The magnetic field induced by these charges is similar to the electric field of a capacitor. To experience this induced magnetic field, the water molecules do not need to get deep into the lipoprotein layer, because magnetostatic charges are located right on the layer’s surface; they (water molecules) just need to “hokey pokey dance” from aqueous phase to just beyond the lipoprotein surface. A typical width of the aqueous phase between lipoprotein layers is about 2.5nm (43). Given that the water diffusion coefficient in the tissue is about 1 μm²/ms, it takes only about 3 ns to diffuse across this width. Hence, it is reasonable to assume that all water molecules in the aqueous space can rapidly hop in and out of the superficial areas of the lipoprotein layers. Such rapid exchange would lead to an additional term in the myelin-associated water frequency shift described by the λ-term in Equation [[37]], in which the parameter λ defines the apparent fraction of time for which a water molecule resides in the lipoprotein layer (in Reference (21) this parameter was denoted as ζ ).

The total frequency shift $\overline{\delta f}$ is given by Equation [31] with ε_n and δf_ndefined by Equations [32] and [31]–[31]:

$$\overline{\delta f}={\epsilon }_{\text{A}}{c}_{\text{A}}\left(T_{\text{E}}\right)\delta f_{\text{A}}+{\epsilon }_{\text{mw}}{c}_{\text{mw}}\left(T_{\text{E}}\right)\delta f_{\text{mw}}+{\epsilon }_{\text{e}}{c}_{\text{e}}\left(T_{\text{E}}\right)\delta f_{\text{e}}.$$ [39]

The expression for $\overline{\delta f}$ in Equation [39] should satisfy the general Equation [[18]]: $\overline{\delta f}=\delta f_H+\delta f_{\text{L}}$. For the circular cylindrical axonal fiber considered above, δf_H is the same as that of a homogeneously magnetized circular cylinder forming an angle α with B₀. Using the demagnetization tensor for a long cylinder, Equation [23], we obtain

$$\delta f_H=-f_0\cdot \frac{1}{2}{\chi }_{\perp }{\sin }^2\alpha ,\hspace{1em}{\chi }_{\perp }={\chi }_{\text{iso}}+{\chi }_{\mathbf{\text{r}}}$$ [40]

where χ_⊥ is the total transverse volume magnetic susceptibility of the system; χ_iso and χ_r are given in Equations [33] and [34].

The Lorentzian tensor $\widehat{\mathit{L}}$ for a multi-compartment structure is substantially affected by the details of theMRI experiment (T_E, T_R, flip angles, etc.). For the model of the neuronal fiber discussed above, this tensor can be presented in a form similar to Equation [26]:

$$\widehat{\mathit{L}}=\frac{1}{3}\cdot \left(\begin{array}{ccc}{\chi }_{\text{iso}}^{\left(\text{app}\right)}& 0& 0\\ 0& {\chi }_{\text{iso}}^{\left(\text{app}\right)}& 0\\ 0& 0& {\chi }_{\text{iso}}^{\left(\text{app}\right)}\end{array}\right)\hspace{0.33em}+\frac{1}{2}\cdot \left(\begin{array}{ccc}{\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}& 0& 0\\ 0& {\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}& 0\\ 0& 0& 0\end{array}\right)$$ [41]

where ${\chi }_{\text{iso}}^{\left(\text{app}\right)}$ and ${\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}$ are apparent magnetic susceptibilities. The Lorentzian frequency shift corresponding to Equation [41] is determined by

$$\delta f_{{}_{\text{L}}}=f_0\cdot \left(\frac{1}{3}\cdot {\chi }_{\text{iso}}^{\left(\text{app}\right)}+\frac{1}{2}\cdot {\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}{\sin }^2\alpha \right).$$ [42]

The susceptibility tensor $\widehat{\chi }$, determining the quantity δf_H, depends mainly on the tissue electron structure and is still determined by Equation [25] (with “true” magnetic susceptibilities). Hence, the total frequency shift is

$$\delta f=\delta f_H+\delta f_{\text{L}}=f_0\left[\frac{1}{3}{\chi }_{\text{iso}}^{\left(\text{app}\right)}+\frac{1}{2}\left({\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}-{\chi }_{\mathbf{\text{r}}}-{\chi }_{\text{iso}}\right){\sin }^2\alpha \right].$$ [43]

Comparing this expression with $\overline{\delta f}$ in Equation [39], we obtain the relationships between the “true” and apparent susceptibilities:

$${\chi }_{\text{iso}}^{\left(\text{app}\right)}={\epsilon }_{\text{A}}{c}_{\text{A}}\left(T_{\text{E}}\right)\cdot {\chi }_{\text{iso}}^{\left(\text{A}\right)}+{\epsilon }_{\text{mw}}{c}_{\text{mw}}\left(T_{\text{E}}\right)\cdot {\chi }_{\text{iso}}^{\left(\text{mw}\right)}+{\epsilon }_{\text{e}}\cdot c_{\text{e}}\left(T_{\text{E}}\right)\cdot {\chi }_{\text{iso}}^{\left(\text{e}\right)}$$ [44]

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}{\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}={\chi }_{\mathbf{\text{r}}}+{\chi }_{\text{iso}}-{\chi }_{\text{iso}}^{\left(\text{app}\right)}+ \\ +\frac{d}{\left(d+d_{\text{w}}\right)}\left\{{\epsilon }_{\text{A}}{c}_{\text{A}}\left(T_{\text{E}}\right)\cdot \Delta {\chi }^{\left(\text{ml}\right)}\text{In}\left(\frac{1}{g}\right)+{\epsilon }_{\text{mw}}{c}_{\text{mw}}\left(T_{\text{E}}\right)\left[\Delta {\chi }^{\left(\text{ml}\right)}\left(\frac{1}{2}+\frac{g^2\text{In}g}{\left(1-g^2\right)}\right)-\lambda \cdot {\chi }_{\parallel }^{\left(\text{ml}\right)}\right]\right\} \end{gathered}$$ [45]

It is important to emphasize that Equations [44] and [45] describe the Lorentzian contribution to the frequency shift and are valid not only for a single neuronal fiber but also for an arbitrarily shaped neuronal bundle of parallel fibers (the shape of the bundle and surrounding medium affect only the term δf_H). These expressions (derived in the framework of the model of the neuronal fiber (21,30)) along with Equations [20] and [41] provide the basis for analyzing the phase images obtained by means of gradient echo MRI.

PHASE CONTRAST IN WM – THE “WM DARKNESS” EFFECT

The results described in the previous sections make it possible to shed light on the effect of “WM darkness” – the very small frequency shift between WM and CSF in some brain regions (1,18) – as well as to explain important features of phase contrast in MS lesions (19). To understand the latter, we first need to understand phase contrast in a normal brain.

As described in the previous sections, the intact myelinated axon is comprised of longitudinal structures with volume magnetic susceptibility χ_long (myelin and neurofilaments) aligned along the axonal axis, and isotropic components (free-floating organelles, proteins, lipids, etc.) with magnetic susceptibility χ_iso. As follows from Equation [26], the axial component of the magnetic susceptibility tensor of the longitudinal structures does not contribute to the Lorentzian tensor $\widehat{\mathit{L}}$. To confirm this result, the magnetic field was numerically calculated based on the solution of Maxwell equations for the simple cylindrical structure analogous to that described earlier, but with an arbitrary angle α between the external magnetic field B₀ and the cylinder’s axis. Figure 7 illustrates the dependence of the frequency shift on α for the ideal cylinder (green dots) and for the fully disordered structure (red dots). In both the cases, the frequency shift is a combination of the frequency shift caused by the magnetic field induced by the external surface of the cylinder,

$$\frac{\delta f_{\text{surface}}}{f_0}=-\frac{1}{2}\cdot \chi {\sin }^2\alpha ,$$ [46]

and the corresponding Lorentzian shift, δf_L/f₀ = χ/2 ·χsin²α for the ideal cylinder and δf_L/f₀ = χ/3 for the fully disordered structure. The surface contribution and the Lorentzian term compensate each other in the cylindrical case, leading to zero frequency shift for all angles α.

Figure 7.

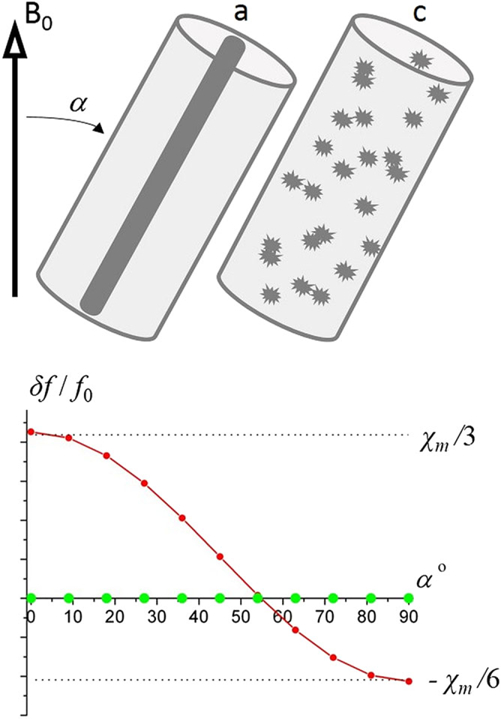
The relative frequency shift as a function of the angle α between the external magnetic field B₀ and the cylinder’s axis. Green dots – “ideal” structure (black cylinder) shows zero frequency shift for all angles α; red dots – fully disordered structure.

This important result means that, for a circular cylindrical myelinated axonal bundle (tract), the longitudinal structures do not contribute to the frequency shift within this bundle. Therefore, in the regions of the brain, such as the cortex, where gyri and sulci abut one another, the intact cylindrical axons in gyri should have very small frequency shifts relative to CSF in the sulci. This effect, first predicted by He and Yablonskiy (18) is counterintuitive, because there is a substantial difference between the structures of WM and CSF, presumably leading to a substantial difference between their magnetic susceptibilities – χ_WM and χ_e. One could, therefore, expect a substantial phase contrast between WM and CSF. However, the susceptibility of longitudinal structures, being one of the major components of χ_WM, does not contribute to the frequency shift, leading to very little contrast between WM and CSF in the brain regions where WM bundles are nearly parallel to B₀ (motor cortex and other areas at the top of the brain) (18). Importantly, this result does not depend on the value or the sign of the WM susceptibility χ_WM.

It is also important to note that, if WM contained only such longitudinal structures, there would be no angle dependence of the frequency shift in WM. However, a real situation is more complicated for several reasons: (a) WM is a multi-compartment tissue and it comprises not only the longitudinal structures but isotropic susceptibility inclusions as well, (b) the cross-section of the WM bundles is not always circular, (c) the difference in the bulk magnetic susceptibilities of WM and surrounding tissue can contribute to the non-local part of the frequency shift, and (d) WM has anisotropic magnetic susceptibility not accounted for in Figure 7. A more adequate description of the frequency shift in WM is given by the GLTA, Equation [[43]], which predicts the sin²α dependence of the frequency shift. Such a dependence was experimentally observed in rat (22) and pig (39) optic nerves (see also Figure 9 later). An angular dependence of the phase/frequency shift in WM was also reported in several experimental studies (e.g. References (31,44) – marmoset brain; (29,39,45) – human brain; (46) – rat brain). Figure 8 illustrates the orientation dependence of the frequency shift in WM in human (45) and rat (46) brains.

Figure 9.

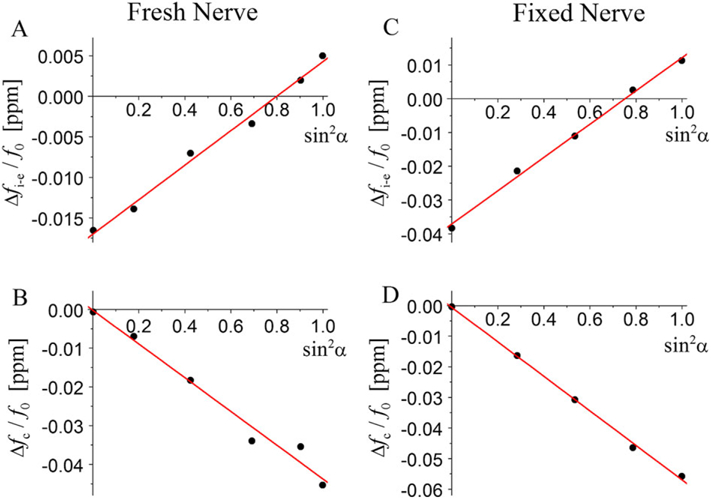
(adopted from (22)). Example of experimental data for fresh and fixed nerves. Filled circles – experimental data; lines – linear fits against sin² α. (A, C) Frequency shifts inside nerve versus surrounding medium; (B, D) characteristic function Δf_c(α) determining the frequency shifts outside the nerve.

Figure 8.

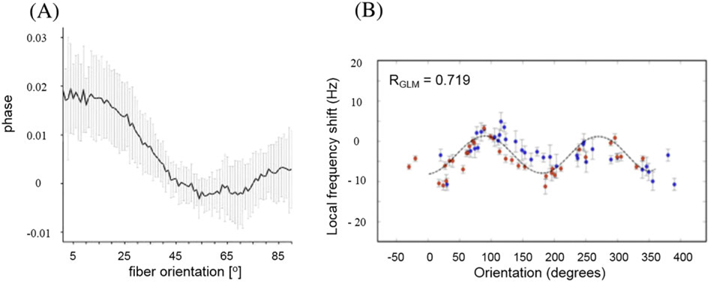
The orientation dependence of the frequency shift in WM in the human (A; adapted from Reference (45)) and rat (B; adapted from Reference (46)) brain. (A) Measurements for a single direction of the external field B₀ but for different fibers forming variable angles with B₀, evaluated by means of DTI. (B) The actually measured angular dependence of the frequency shift in fibers in a rat brain that was rotated within a static B₀.

It is also worth noting that a slight deviation from the circularity of individual axons should not have much effect on phase signal, because it is counteracted by a distribution of axonal shapes in WM bundles that, on average, can be considered as circular cylinders. For WM structures that are not circular cylinders (e.g. corpus callosum), frequency shift does depend on the structure global shape, the total magnetic susceptibility of WM, and the surrounding environment (18).

A negative WM–GM contrast usually observed in a human brain (18,47) (see also example in Figure 1) can also be explained by the WM darkness effect. As most of the magnetic susceptibility of the longitudinal structures does not contribute to the frequency shift in WM, the phase/frequency contrast between WM and GM is determined essentially by the positive magnetic susceptibility of GM (18).

WHAT DO WE ACTUALLY KNOW ABOUT WM SUSCEPTIBILITY?

Lounila et al. (48) used NMR spectroscopy to analyze magnetic properties of lipoprotein particles. The particles have a spherical structure with a core of hydrophobic lipids surrounded by an amphipathic surface comprising long, radially oriented molecules of apolipoproteins, phospholipids, and cholesterol. Despite the obvious difference between the particle and the myelin sheath – spherical structure of the particles versus cylindrical structure in myelin sheath – the systems have an important common feature: anisotropic susceptibility of the macromolecules. Using the theoretical model of anisotropic susceptibility of the surface and NMR spectroscopy experimental data, the authors inferred the susceptibility anisotropy – the difference between the susceptibilities parallel and perpendicular to the local radial direction: ~‒ 0.2 ppm (in our notations, this difference is similar to the ⊿χ^(ml) used in Equations [36] and [37] for describing the susceptibility anisotropy in the myelin sheath).

van Gelderen et al. (49) performed the most direct measurements of the magnetic susceptibility anisotropy of excised human spinal cord by using a torque balance method. The authors found that, on average, the susceptibility anisotropy ⊿χ = χ_||‒χ_⊥ was 16 ppb, where χ_|| and χ_⊥ are volume susceptibilities parallel and perpendicular to the axis of symmetry. While this result provides the most direct confirmation available to date of WM anisotropic susceptibility, one should bear in mind that the spinal cord has both WM and GM. Hence, further studies are needed to separate their relative contributions to the measured anisotropic effect.

Assuming the volume susceptibility anisotropy of a sample to be attributable only to the myelin sheath with the volume susceptibility anisotropy ⊿χ^(ml) (see Eq. [32]) and occupying the volume fraction ζ_ml, the quantities ⊿χ^(ml) and ⊿χ can be related (49):

$$\Delta \chi =-\frac{1}{2}\cdot \Delta {\chi }^{\left(\text{ml}\right)}{\zeta }_{\text{ml}}.$$ [47]

As follows from Equation [47], for the above-mentioned values of ⊿χ = 16 ppband ⊿χ^(ml) = − 0.2 ppm, the volume fraction of myelin sheath in the spinal cord should be given by ζ_ml = 0.15.

Luo et al. (22) performed experimental MRI-based measurements of the frequency shift of the MR signal from an isolated optic nerve and applied the GLA for post-processing analysis. A well-defined shape (circular cylinder) was used as a model system of WM. Such a simple geometry minimizes distortions from global magnetic field inhomogeneity and contamination from neighboring tissues. In Reference (22), experiments were performed with a fresh nerve (suspended in 1% PBS solution) and with fixed nerves (suspended in formalin). The magnetic susceptibilities of the solutions were measured independently. A nerve was positioned in a liquid-filled cylindrical NMR tube and the MR experiments were conducted at different angles α between the nerve’s axis and the external field B₀. Given the simple structure of the optic nerve, consisting of a bundle of nearly parallel myelinated axonal fibers, it is straightforward to apply the GLTA to this system.

According to the GLTA, the frequency shift inside the nerve versus the surrounding medium is determined by the combination of the “true” and apparent susceptibilities, Equation [[43]]. Outside the nerve, the frequency shift is inhomogeneous and is defined by the total transverse volume magnetic susceptibility of the nerve ${\chi }_{\perp }={\chi }_r+{\chi }_{\text{iso}}$:

$${\left(\Delta f\right)}_{r>r_0}=\Delta f_c\left(\alpha \right){\left(\frac{r_0}{r}\right)}^2\cos 2\theta ,\hspace{1em}\frac{\Delta f_c\left(\alpha \right)}{f_0}=\frac{1}{2}{\chi }_{\perp }{\sin }^2\alpha$$ [48]

where r = |r|, with r the radial vector extending from the center of the nerve to the in-plane coordinate of interest; r₀ is the radius of the nerve, α is the angle between the nerve’s axis and the external field B₀, and θ is the angle between r and the projection of B₀ onto the slice plane. Figure 9(A, C) presents the frequency shifts inside the nerve (versus the surrounding medium) as a function of sin²α, and the slope of the lines can be used for determining a combination of the susceptibilities entering Equation [43], namely, ${\chi }_r^{\left(\text{app}\right)}-{\chi }_r-{\chi }_{\text{iso}}$. B and D illustrate the sin² α dependence of the characteristic frequency ⊿f_c(α) defining the behavior of the frequency shift outside the nerve, and the slope of the lines can be used to determine the total transverse volume magnetic susceptibility of the nerve χ_⊥.

In Reference (23), the experimental data obtained in Reference (22) were re-analyzed according to the GLTA, Equations [25] and [43] (note that notations used in References (22,23) are different). The results are presented in Table 1.

Table 1.

True and apparent parameters obtained by re-analyzing the data for optic nerve (72). The third row is a linear combination of the first two. All the susceptibilities are with respect to water (ppm)

	Fresh nerve	Fixed nerve
${\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}-{\chi }_{\mathbf{\text{r}}}-{\chi }_{\text{iso}}$	0.044 ± 0.004	0.090 ± 0.018
${\chi }_{\perp }={\chi }_{\mathbf{\text{r}}}-{\chi }_{\text{iso}}$	−0.100 ± 0.010	−0.106 ± 0.028
${\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}$	−0.056 ± 0.011	−0.016 ± 0.033

The difference between the “apparent” parameters for fresh and fixed nerves can be explained by their different relaxation properties, whereas the “true” transverse volume magnetic susceptibility of the nerve, χ_⊥ = χ_r + χ_iso, does not depend on the re-laxation properties and therefore is the same for the fresh and fixed nerves.

It is important to emphasize that in the case of the “standard” (Lorentzian sphere) approach, in which the frequency shift inside the nerve would be given by Equation [[43]] with ${\chi }_r={\chi }_r^{\left(\text{app}\right)}=0$ and ${\chi }_{\text{iso}}^{\left(\text{app}\right)}={\chi }_{\text{iso}}$, the slopes of the lines inside and outside the nerve would be equal in magnitude. Obviously, this is not in agreement with experimental data.

Another experiment with the rat optic nerve performed by Wharton and Bowtell (39) also demonstrated the presence of structural magnetic anisotropy of the nerve. The images pro-vided in this study for different orientations of the nerve with respect to B₀ result in a conclusion that the total magnetic susceptibility of the nerve is negative with respect to the surrounding medium (though no information on the media magnetic susceptibility was provided).

Most of the QSM studies aiming at estimating susceptibility of WM rely on Equation [[7]] (or its generalization for anisotropic susceptibility (50)) for the Lorentzian frequency shift. Although these studies contribute to our understanding of QSM in WM, their results for specific values of susceptibility (or components of the susceptibility tensor) cannot be considered as quantitative since structural anisotropy of WM is not taken into account.

Another approach for the estimation of magnetic susceptibility of WM is based on theoretical estimations of the susceptibilities and the volume fractions of its constituents (lipids, proteins, non-heme iron, deoxyhemoglobin, etc.). Table 2 (adapted from Reference (18)) provides the volume magnetic susceptibilities of different constituents in the human brain frontal lobe. According to Table 2, the magnetic susceptibility of this part of WM is positive (less diamagnetic) with respect to water (+70 ppb). One can see that proteins are more diamagnetic than water. At the same time, lipids are less diamagnetic than water, generating a positive (“quasi-paramagnetic”) contribution. It should be noted, however, that in highly myelinated areas such as corpus callosum (51), or optic radiation (52), iron concentration is believed to be significantly lower. This would lead to a conclusion that the volume susceptibility of WM could approach or surpass (become more negative than) that of the water. Data on susceptibilities of phospholipids and stearic acid, provided in Reference (26), would also suggest a negative susceptibility of myelin sheath (if the iron contribution is not included).

Table 2.

(adapted from Reference (18)). The volume magnetic susceptibilities (relative to water) of “average, normal” brain tissue in the frontal lobe

	WM (ppb)	GM (ppb)	CSF (ppb)
Proteins	−57.3	−52.4	0.0
Lipids	69.4	29.8	0.0
Non-heme iron	55.3	55.3	4.1
Deoxyhemoglobin	2.6	11.3	0.0
Total	70.0	44.0	4.1

It should be mentioned, however, that magnetic susceptibilities of WM constituents are usually known from independent studies of lipids, proteins etc. in experimental environments, which can be substantially different from those in the brain. Theoretical estimations of WM susceptibility require a knowledge of density of the constituents, which are rarely known and might be different in the brain structures from those obtained from ex vivo studies. Besides, the densities vary with temperature and other experimental conditions. As the difference between the susceptibilities of WM and water (or CSF) is very small as compared with the susceptibilities themselves, even slight variations of experimental conditions may lead to substantial errors in estimates, even to an opposite sign of this difference. This is why the actual magnetic susceptibility of myelin sheath (and WM as a whole) remains debatable, and its direct measurement is extremely desirable.

PHASE CONTRAST CHANGES IN MS LESIONS

As mentioned above, MS lesions typically have a positive phase contrast as compared with the surrounding healthy tissue (19). Interestingly, this contrast appears in mild lesions and disappears in severe lesions (19). Several mechanisms have been proposed in the literature to explain the positive phase contrast. One of these is the structural disordering mechanism (19) attributing lesions’ features to a known MS pathology – destruction of myelin sheath. Several papers have attributed positive phase contrast to accumulation of iron in MS lesions (e.g. (10), (53–59)).

In what follows, we describe a structural disordering mechanism as it is directly related to structural anisotropy and magnetic susceptibility anisotropy of WM. In Reference (19), two scenarios of phase contrast changes in MS tissue, depending on the type of injury to tissue, were proposed. One of them takes place due to damage to the myelin sheath and is based on the assumption of the positive susceptibility of myelin; the second one occurs due to destruction of intra-axonal neurofilaments. The case of minor damage to the myelin sheath leads to positive changes in MR signal phase because the longitudinal structures in the sheath (being “invisible” before) partly break and these “broken” parts become “visible”, resulting in a positive phase/frequency change (see Figure 2). In advanced stages of tissue damage, due to removal of the “broken” parts of myelin sheath from the damaged area, the volume magnetic susceptibility of the myelin sheath decreases, which may lead to reduction of phase/frequency changes for severely damaged tissue. This scenario is depicted in Figure 10, left.

Figure 10.

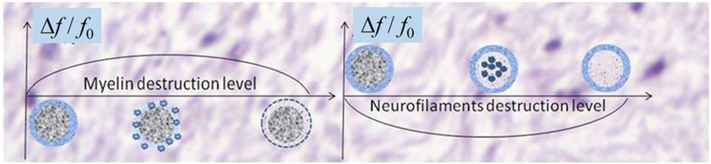
(adapted from (19)). Schematic structure of the MR signal phase/frequency change with MS lesion severity for two types of tissue destruction. Left, myelin injury (assuming positive magnetic susceptibility of myelin); right, neurofilament injury. Minor myelin injury corresponds to the initial ascending portion of the plot in the left-hand panel; i.e., phase/frequency increases. Neurofilament injury corresponds to the initial descending portion of the plot in the right-hand panel; i.e., phase/frequency decreases. Severe lesions with significant destruction of both myelin and axons might disappear from phase images.

A similar scenario (Figure 10, right) takes place in the case of neurofilament destruction, but with one important difference – phase/frequency experiences negative changes. This is due to the fact that the volume magnetic susceptibility of neurofilaments, mostly formed by proteins, is negative with respect to water (see, e.g., (60,61)). It should be mentioned, however, that when axons degenerate the surrounding myelin is also subsequently lost due to Wallerian degeneration. Thus, one would expect negative phase contrast to be relatively uncommon. This is consistent with our and others’ (62) observation of negative phase changes in MS lesions being very rare. Note, however, that the described scenarios can explain the reports of phase changes being detected only for a subset of MS lesions (e.g. (53,63)).

Examples of phase images obtained by means of the GEPCI technique (64,65) from a subject with secondary progressive MS (female, 49 years old) as well as several other images are shown in Figure 11.

Figure 11.

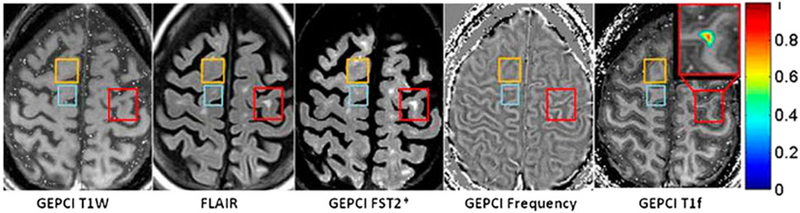
(adopted from (19)). T1w (T₁-weighted), FLAIR (flow attenuated inversion recovery), GEPCI FST2* (CSF-suppressed T₂*), frequency, and GEPCI T1f (a combination of T1w and frequency) maps from a subject with secondary progressive MS. Rectangles outline abnormalities observed on FLAIR and/or frequency (phase) maps. Lesion severity is determined by the TDS, which ranges from zero for healthy tissue to unity for fully destroyed tissue (64). Orange rectangles denote an alteration seen in phase images (bright contrast) but not T1w FLAIR, or GEPCI FST2*. This alteration may rep-resent a very mild lesion with damaged myelin, and it is also seen on the GEPCI T1f image as negative (dark) contrast. Blue rectangles outline a small MS lesion that is barely seen on FLAIR and GEPCI FST2*; this lesion is also visible on the phase image. Red rectangles outline a severe MS lesions (very high TDS score) that is seen in T1w, FLAIR, and GEPCI FST2* but does not have a footprint on the phase image. A magnified view of this lesion is shown in the inset with overlaid GEPCI TDS score in color according to the color bar.

The orange and blue rectangles mark MS lesions with no or very small values of tissue damage score (TDS) – a quantitative parameter characterizing severity of tissue damage (64); TDS around zero corresponds to normal tissue, TDS = 1 corresponds to severely injured tissue. These examples might represent changes in tissue microstructure that are not observed with conventional imaging techniques. The positive phase contrast indicates myelin damage. According to Figure 10, the phase contrast in severe lesions (red rectangles, high TDS score) can disappear, although these lesions would have substantially different magnetic susceptibility from the surrounding normal WM. The absence of phase contrast, together with high TDS in this case, suggests that myelin and axonal debris are mostly removed from the lesion area.

It should be mentioned that the structural disordering mechanism (19) of phase/frequency changes in MS lesions relies on the assumption that myelin susceptibility is positive (with respect to water). However, as mentioned in the previous section, this assumption is debatable and other sources of positive frequency change in MS lesions are quite possible. For example, in Reference (56) positive susceptibility values in some MS lesions are associated with iron presence in histology. To be clear, the structural disordering mechanism and the iron-based source of positive phase changes in MS lesions do not contradict each other. Indeed, according to Table 2, non-heme iron contributes substantially to the total magnetic susceptibility of WM, though, when this iron is located in longitudinally organized healthy nerve fibers, it does not contribute to the frequency shift; it is “MRI invisible” (see discussions above). However, when the myelin sheath is broken, this iron becomes “visible” and can contribute to the positive changes of the MR signal phase.

Images of active MS lesion pathology often reveal the entire width of the myelin sheath to be disrupted (66), but a small phase contrast could also be expected if demyelination were to proceed by gradual loss, layer by layer, of the myelin sheath. This mechanism could also explain positive phase contrast of MS lesions, due to the presence of magnetic susceptibility anisotropy of the myelin sheath ⊿χ^(ml) (see Eqs [[36]] and [[37]]). Indeed, if the susceptibility anisotropy of the myelin sheath ⊿χ^(ml) is negative, the frequency shift inside the axons δf_A is also negative (29–31) (see Eq. [[36]]). This frequency shift also depends on the g-ratio g = R_A/R_e. During gradual demyelination, the external radius R_e decreases, the g-ratio increases, and the negative contribution of the axon to the total frequency shift δf decreases, leading to a positive change in δf with respect to “healthy” surrounding tissue.

The sensitivity of phase contrast to initial stages of tissue destruction in MS was demonstrated by Wiggermann et al. (54), who found the increase in MR frequency of MS lesions before the lesions appeared on contrast enhanced MRI, hence before the MS pathology related to the disruption of blood–brain barrier. Heterogeneity of tissue in MS lesions was also demonstrated in Reference (59) by combining $R_2^{*}$ and QSM data. Several papers (e.g. 26,56,57,60) reported interesting features of QSM measurements in MS lesions. However, since anisotropic effects were not accounted for in this “traditional” QSM approach, their results can only be considered as qualitative.

CONCLUSION

Magnetic field inhomogeneities existing in biological systems placed in the external magnetic field play a significant role in the formation of MRI signal. According to their relative size scale, these inhomogeneities can be roughly divided into three categories (67): macroscopic, mesoscopic, and microscopic. Microscopic scale refers to changes in the magnetic field over distances that are comparable to the atomic or molecular size, i.e. over distances many orders of magnitude smaller than the imaging voxel size. Mesoscopic scale refers to the distances that are much smaller than the imaging voxel size but much larger than the atomic and molecular scale. Macroscopic scale refers to magnetic field changes over the distances that are larger than the imaging voxel. All three categories of magnetic field inhomogeneities affect GRE MRI signal phase. At the microscopic scale, these effects are related to the interaction of a water molecule with its nearest environment comprising other water molecules (water-on-water effect), and, due to the isotropic properties of water, can be described in terms of the Lorentzian sphere – Equation [7]. At the macroscopic scale, these effects are described by the average magnetic field H(R) satisfying the magnetostatic Maxwell equations (Eq. [11]) and contribute to the MRI signal frequency shift described by the term δf_H in Equation [[18]]. In this review, we mostly focus on the effects at the mesoscopic scale described by the Lorentzian term δf_L in Equation [18].

We emphasize that the expression for the Lorentzian frequency shift δf_L in Equation [7], frequently used in QSM literature, is not valid in the presence of long cells (e.g. axons). The inadequacy of Equation [7] in this case is obvious from the simple example illustrated in Figure 1, right.

In the presence of longitudinal structures, the frequency shift is determined by two different tensors, the susceptibility tensor $\widehat{\chi }$ and the Lorentzian tensor $\widehat{\mathit{L}}$. The structure of the Lorentzian tensor $\widehat{\mathit{L}}$ (especially, in multi-compartment structures), Equation [41], is substantially different from the structure of the susceptibility tensor $\widehat{\chi }$, Equation [25], in several ways:

1. magnetic susceptibility contributions from isotropic and longitudinal structures are “weighted” in $\widehat{\mathit{L}}$ by different numerical coefficients;

2. the axial component χ_a of the magnetic susceptibility tensor does not contribute to $\widehat{\mathit{L}}$;

3. if water also resides inside the susceptibility inclusions (e.g. in axons) and contributes to the MR signal, the cylindrical symmetry of the Lorentzian term $\widehat{\mathit{L}}$ is preserved but the components of $\widehat{\mathit{L}}$ become dependent not only on the original components of $\widehat{\chi }$ but also on tissue relaxation properties (e.g. T₁, T₂*) and pulse sequence parameters (e.g. T_E, T_R, flip angle).

Equations [44] and [45] provide specific relationships for the parameters of $\widehat{\mathit{L}}$, derived using the modeling results (21,30). The dependence of these parameters on the pulse sequence can be established for each particular case. Using Equations [44] and [45], one can obtain a set of data with different sequence parameters, which makes it potentially possible to determine “true” magnetic susceptibilities. Also, different techniques can be used to selectively suppress or enhance specific compartments. One should keep in mind the conditions under which Equations [44] and [45] were derived.

The anisotropic behavior of GRE signal phase predicted in Reference (18) has been confirmed in a number of publications (e.g. (39,45,46,68,69)). A rather strong similarity between signal phase anisotropy and diffusion anisotropy determined by DTI (50,70) suggests that some features of DTI and GRE phase signals are defined by common mechanisms. Equations [44] and [45] can provide further insights into this interesting phenomenon and obtain complementary information on the effects of tissue micro-structure that are common and/or different for DTI and GRE.

Equations [44] and [45] can also provide an explanation for the tissue-dependent frequency differences between NAA, Cho, Cr, and water signals reported in Reference (71). Indeed, due to a different localization of metabolites and water, their contributions to these equations are quite different. In the spectroscopy experiment (71), the water signal is generated mostly by intracellular and extracellular compartments (the contribution of myelin water signal is negligible because a very long echo time, 144 ms, was used), while NAA is known to be located mostly intracellularly.

In this review, we provide the theoretical background of the anisotropic (structural and magnetic susceptibility) phenomena affecting QSM, and discuss the “standard” Lorentzian surface approach as well as the advanced GLTA – a phenomenological method describing magnetic-susceptibility-induced gradient echo MRI signal frequency shifts in the presence of magnetic susceptibility inclusions of arbitrary shape and characterized by an arbitrary magnetic susceptibility tensor. The latter is based on direct solution of the magnetostatic Maxwell equations and does not require introduction of an imaginary Lorentzian surface. The GLTA is an essential tool to decipher information on tissue structural and magnetic anisotropy in WM comprising longitudinal structures (axons).

Abbreviations used:

GM

gray matter

WM

white matter

CSF

cerebrospinal fluid

GLA

generalized Lorentzian approach

GLTA

generalized Lorentzian tensor approach

GRE

gradient recalled echo

QSM

quantitative susceptibility mapping

MS

multiple sclerosis

TDS

tissue damage score

APPENDIX A: LIST OF NOTATIONS FOR SUSCEPTIBILITIES USED IN THE TEXT

All magnetic susceptibilities used in this paper are volume magnetic susceptibilities.

χ – generic scalar susceptibility

$\widehat{\chi }$ – generic susceptibility tensor

${\widehat{\chi }}_{\text{u}}^{\left(0\right)}$ – generic intrinsic susceptibility tensor of the inclusions

${\widehat{\chi }}_{water}^{\left(0\right)}$ – susceptibility of water

${\widehat{\chi }}^{\left(0\right)}$ – generic susceptibility tensor of the inclusions with respect to water

$\widehat{\chi }$ – generic average (bulk) susceptibility tensor of inclusions

χ_iso – scalar susceptibility of isotropically distributed inclusions

${\widehat{\chi }}_{cyl}$ – susceptibility tensor of longitudinally arranged cylindrical inclusions

χ_r and χ_a – radial and axial components of ${\widehat{\chi }}_{cyl}$

${\chi }_{\parallel }^{\left(\text{ml}\right)}\text{and}\hspace{0.33em}{\chi }_{\perp }^{\left(\text{ml}\right)}$ – components of susceptibility tensor of lipoprotein layers, parallel and perpendicular to the local radial direction

${\widehat{\chi }}^{\left(\text{A}\right)}$ – susceptibility tensor of longitudinally arranged inclusions (neurofilaments) in axons

${\chi }_{\mathbf{\text{r}}}^{\left(\text{A}\right)}\hspace{0.33em}\text{and}\hspace{0.33em}{\chi }_{\text{a}}^{\left(\text{A}\right)}$ – radial and axial components of ${\widehat{\chi }}^{\left(\text{A}\right)}$${\chi }_{\text{iso}}^{\left(\text{A,mw,e}\right)}$ – scalar susceptibilities of isotropically distributed inclusions in axons, myelin water layers, and extracellular space, respectively

${\chi }_{\text{iso}}^{\left(\text{app}\right)}$ – apparent isotropic magnetic susceptibility

${\chi }_{\mathbf{\text{r}}}^{\left(\text{app}\right)}$ – radial component of the apparent magnetic susceptibility tensor.