Evaluation and Optimization of Pharmacokinetic Models for in Vitro to in Vivo Extrapolation of Estrogenic Activity for Environmental Chemicals

Abstract

Background:

To effectively incorporate in vitro data into regulatory use, confidence must be established in the quantitative extrapolation of in vitro activity to relevant end points in animals or humans.

Objective:

Our goal was to evaluate and optimize in vitro to in vivo extrapolation (IVIVE) approaches using in vitro estrogen receptor (ER) activity to predict estrogenic effects measured in rodent uterotrophic studies.

Methods:

We evaluated three pharmacokinetic (PK) models with varying complexities to extrapolate in vitro to in vivo dosimetry for a group of 29 ER agonists, using data from validated in vitro [U.S. Environmental Protection Agency (U.S. EPA) ToxCast™ ER model] and in vivo (uterotrophic) methods. In vitro activity values were adjusted using mass-balance equations to estimate intracellular exposure via an enrichment factor (EF), and steady-state model calculations were adjusted using fraction of unbound chemical in the plasma (${\mathrm{f}}_{\mathrm{u}}$) to approximate bioavailability. Accuracy of each model-adjustment combination was assessed by comparing model predictions with lowest effect levels (LELs) from guideline uterotrophic studies.

Results:

We found little difference in model predictive performance based on complexity or route-specific modifications. Simple adjustments, applied to account for in vitro intracellular exposure (EF) or chemical bioavailability (${\mathrm{f}}_{\mathrm{u}}$), resulted in significant improvements in the predictive performance of all models.

Conclusion:

Computational IVIVE approaches accurately estimate chemical exposure levels that elicit positive responses in the rodent uterotrophic bioassay. The simplest model had the best overall performance for predicting both oral (PPK_EF) and injection (PPK_${\mathrm{f}}_{\mathrm{u}}$) LELs from guideline uterotrophic studies, is freely available, and can be parameterized entirely using freely available in silico tools. https://doi.org/10.1289/EHP1655

Introduction

In vitro assays are routinely used to provide mechanistic insight on the bioactivity of xenobiotics and offer the potential for more human-relevant, humane, and efficient alternatives to toxicity testing in animals. Over the past decade, significant effort has been devoted to overcoming the many challenges associated with implementing high-throughput screening (HTS) programs for environmental chemicals (e.g., establishing and managing chemical libraries, chemical dispensing, analytical quality control (QC), data processing and management, analytical precision, etc.) (Filer et al. 2017; Kavlock et al. 2012; Tice et al. 2013). These efforts have been successful to the point where screening $\sim \mathrm{10,000}$ chemicals in a few weeks is now routine in some facilities (Shukla et al. 2010). However, the utility of these approaches to quantitatively inform biological responses in vivo needs to be evaluated before the data can be effectively used for risk assessment and regulatory decision-making.

In vitro to in vivo extrapolation (IVIVE) uses in silico and computational approaches to translate bioactive chemical concentrations obtained from in vitro assays to corresponding exposures likely to induce bioactivity in vivo. Establishing confidence in IVIVE methods requires comparison of computationally predicted effects with those observed in humans or animal models. In previous work, we used a simple one-compartment population model and data from a single in vitro assay, the BG1Luc transactivation assay [Organization for Economic Cooperation and Development (OECD) TG455], for IVIVE analyses of two estrogen receptor (ER) reference chemicals, $17\mathrm{beta}\text{-estradiol}$ (E2) and bisphenol A (BPA), with mixed results (Chang et al. 2015). Other efforts have used heterologous in vitro data from largely uncharacterized assays (i.e., activity values from any of $\sim 600$ assays, without consideration of mechanism) paired with any effect from any in vivo end point reported in ToxRefDB (Martin et al. 2009; Wetmore et al. 2013), a U.S. Environmental Protection Agency (U.S. EPA) database that contains information on thousands of studies on hundreds of chemicals (Martin and Judson 2010). Although potentially useful in the context of prioritization, this methodology does not assess the ability of IVIVE approaches to inform mechanism-specific end points, nor does it expressly account for data quality. Here, we used highly curated data obtained from validated in vitro [U.S. EPA ToxCast™ ER model (Judson et al. 2015)] and in vivo (OECD rodent uterotrophic) methods that assess the same mechanism of action (ER agonist activity) (Kleinstreuer et al. 2016). This approach allowed us to evaluate, compare, and optimize the quantitative performance of IVIVE approaches used to predict exposures (mg/kg/day) likely to result in ER agonist pathway activation in vivo, with potential applicability to other mechanisms of action as well.

Several important factors need to be considered when conducting IVIVE analyses: biological relevance of the in vitro system, chemical-specific data to inform estimates of distribution and metabolism (e.g., metabolic clearance capacity, plasma protein binding, physicochemical properties, etc.), variability of the in vivo data (e.g., due to study design, genetic heterogeneity), and suitability of the computational model being used to make predictions. Biological relevance refers to how well the in vitro system represents the in vivo mechanism or pathway of interest. Our work looks at the U.S. EPA ToxCast™ ER model, a well-characterized signal transduction pathway of great relevance to human and ecological health (U.S. EPA 1998). On the in vitro side of the equation, the U.S. EPA ToxCast™ program screened 1,886 environmental chemicals in 16 in vitro assays that measure discrete biological processes along the ER agonist pathway: ligand binding, receptor dimerization, transcription factor–chromatin binding, transcription, protein production and cell proliferation. Data from these experiments were used to develop an integrated pathway activity model for predicting ER agonist activity (ER model) (Browne et al. 2015; Judson et al. 2015). ER model scores [the Area Under Curve (AUC)] range from 0 (no activity) to 1 (bioactivity of $17\text{beta}\text{-estradiol}$) and are used to parse chemicals into three categories: active, inactive, or inconclusive. A total of 266 chemicals classified as either active or inconclusive ($\text{AUC}>0.01$) were used in the present study. The ToxCast™ ER model, chemical classifications, and all supporting data underwent peer review sponsored by U.S. EPA and were found to be relevant and reliable tools for assessing the estrogenic potential of environmental chemicals (U.S. EPA 2014). On the in vivo side, the uterotrophic assay is a rodent test validated by the OECD and accepted by the U.S. EPA for measuring uterine hypertrophy caused by activation of the ER agonist pathway (U.S. EPA 2009). We previously published a curated database of uterotrophic assay results used to validate the ER model described above (Kleinstreuer et al. 2016), demonstrating a qualitative predictive relationship (active, inactive, inconclusive) between ER model activity and bioactivity in the uterotrophic assay. Here we use results from guideline uterotrophic studies to evaluate and optimize quantitative IVIVE approaches that incorporate in vitro ER model data to calculate chemical exposures predicted to cause estrogenic responses in the rodent model.

The accuracy of IVIVE approaches relies extensively on the accuracy of in vitro potency measurements, which are typically proportional to the in vivo exposures predicted to elicit the response of interest (e.g., lowering the in vitro activity twofold will lower the estimated in vivo exposure dose twofold). Traditionally, in vitro concentration–activity relationships (e.g., ${\mathrm{EC}}_{10}$, ${\mathrm{AC}}_{50}$, etc.) are described using the nominal concentration of the test article: the quantity of chemical added divided by the volume of the exposure medium. However, many experimental elements are known to affect chemical partitioning in the medium: vessel plastic, media lipids, media proteins, cell membranes, cell density, etc. These factors can alter the true exposure concentration of active chemical, potentially by many orders of magnitude, and thus introduce significant error into any dose-based measure of chemical activity (Gülden and Seibert 2003; Kramer et al. 2012; Teeguarden and Barton 2004; Truisi et al. 2015). Armitage et al. published a mass-balance model that considers critical assay components (e.g., percent serum in media, media volume, cell number, etc.) along with the physicochemical properties of the test article to calculate mass distribution of a chemical within the system (Armitage et al. 2014). Other, more complex, approaches have been published (Fischer et al. 2017), but require input parameters that are more difficult to obtain and in our experience, do not offer a significant improvement in performance (data not shown).

PK models used for IVIVE approaches vary in structure and complexity, from simple one-compartment models that rely on assumptions of linear dose–response curves and steady-state kinetics, to highly complex multicompartment ($15+$) models using tissue-specific partition coefficients to calculate time-dependent chemical concentrations (e.g., ${\mathrm{C}}_{\text{max}}$). Here, we evaluated the performance of three PK models of different structure and complexity in an attempt to identify the least complex (most accessible) model with the best accuracy. We then improved the accuracy of these models with incorporation of adjustments to chemical potency and bioavailability that are readily calculated using open-source in silico tools. This work facilitates comparison of chemical potency between in vitro and in vivo data mapped to a common biological pathway, with the aim of providing sufficient confidence in these approaches to warrant their routine use in chemical prioritization, hazard assessment, and regulatory decision-making.

Methods

In Vitro ${\mathit{\text{ACC}}}_{\mathit{\text{ER}}}$

ER in vitro bioactivity of 1,886 chemicals was measured in 16 in vitro assays run in U.S. EPA ToxCast™ and NIH National Center for Advancing Translational Sciences (NCATS) high-throughput screening programs (Browne et al. 2015; Judson et al. 2015). The assays measure five discrete aspects of ER model activation: ER binding, formation of $\text{ER}\mathrm{\alpha }$ and $\text{ER}\mathrm{\beta }$ hetero- and homodimers, interaction of the mature transcription factor with DNA, transactivation, and cell proliferation. Details of each assay have been previously published (Dix et al. 2007; Judson et al. 2010) and are described on U.S. EPA’s ToxCast™ website (http://www.epa.gov/ncct/toxcast/). Concentration–response curves for each chemical-assay pair were used to develop a computational ER model for bioactivity (ER model) (Browne et al. 2015; Judson et al. 2015). A detailed description of the model, including freely available source code, is provided in (Judson et al. 2015) and on the following EPA webpage (ftp://newftp.epa.gov/COMPTOX/STAFF/rjudson/publications/Judson%20ER%20Model%20ToxSci%202016/). Briefly, the ER model integrates data from each of the 16 assays in an unweighted manner, while subtracting background and other nonspecific assay interference, including cytotoxicity. The model outputs AUC ranging from 0 (no activity) to 1 (bioactivity of $17\text{beta}\text{-estradiol}$) used to classify chemicals as active, inactive, or inconclusive with regard to ER agonist activity. We selected all chemicals with an $\text{AUC}>0.01$ (all active and inconclusive) for further analysis. For these 266 chemicals, we used the ER model’s quantitative chemical activity output, the activity concentration at statistically significant cutoff (${\text{ACC}}_{\text{ER}}$), as a measure of chemical potency. The ${\text{ACC}}_{\text{ER}}$ is the median ACC from the ER model based on the integrated synthetic concentration–response curve and represents the concentration ($\mathrm{\mu }\mathrm{M}$) at which significant activity was observed against the ER model overall, providing an in vitro lowest effect level. ${\text{ACC}}_{\text{ER}}$ values have been published previously (Judson et al. 2015) and are available through the U.S. EPA ToxCast™ webpage (U.S. EPA 2015). The ${\text{ACC}}_{\text{ER}}$ values used in our analyses can be found in Table 1.

Table 1.

In vitro activity (${\text{ACC}}_{\text{ER}}$) and model parameters with source: experimental or predicted (E/Q).

Chemical Name	CASRN	${\text{ACC}}_{\text{ER}}$ (uM)	${\text{ACC}}_{\text{ER}\_}\text{EF}$ (uM)	${\text{log}}_{10}{\mathrm{K}}_{\text{OW}}$	${\mathrm{K}}_{\text{OW}}$ Source	${\text{log}}_{10}{\mathrm{K}}_{\mathrm{A}\mathrm{W}}$	${\mathrm{K}}_{\mathrm{A}\mathrm{W}}$ Source	${\text{CL}}_{\text{int}}$ ($\mathrm{L}/\mathrm{h}$)	${\text{CL}}_{\text{int}}$ Source	${\mathrm{f}}_{\mathrm{u}}$	${\mathrm{f}}_{\mathrm{u}}$ Source	pKa#	EF
4-Nonylphenol	104-40-5	$7.65\mathrm{E}+00$	$1.22\mathrm{E}+03$	5.76	Ea	$-5.06$	Q	2.61	Q	0.005	Q	10.49	159
4-Dodecylphenol	104-43-8	$6.20\mathrm{E}-01$	$1.30\mathrm{E}+02$	7.91	Ea	$-5.06$	Q	1.15	Q	0.005	Q	10.6	210
Tamoxifen	10540-29-1	$1.65\mathrm{E}-02$	$2.88\mathrm{E}+00$	6.24	Q	$-6.84$	Q	0.57	Eb	0.005	Eb	8.48#	174
2,2',4,4'-Tetrahydroxybenzophenone	131-55-5	$9.42\mathrm{E}-01$	$1.38\mathrm{E}+01$	2.58	Q	$-10.62$	Q	2.64	Q	0.225	Q	11.26; 9.98; 7.88; 7.14	15
2,4-Dihydroxybenzophenone	131-56-6	$1.91\mathrm{E}+00$	$4.40\mathrm{E}+01$	2.85	Q	$-9.76$	Q	3.33	Q	0.123	Q	11.68; 7.55	23
4-(1,1,3,3-Tetramethylbutyl)phenol	140-66-9	$7.63\mathrm{E}-01$	$9.29\mathrm{E}+01$	4.83	Q	$-4.68$	Q	1.80	Eb	0.019	Eb	10.42	122
Bisphenol AF	1478-61-1	$3.02\mathrm{E}-02$	$1.81\mathrm{E}+00$	3.62	Q	$-8.14$	Q	3.95	Q	0.037	Q	10.09; 9.39	60
Zearalenone	17924-92-4	$3.71\mathrm{E}-02$	$1.95\mathrm{E}+00$	3.49	Q	$-13.39$	Q	2.12	Q	0.489	Q	10.87; 7.78	53
Genistein	446-72-0	$6.16\mathrm{E}-02$	$9.87\mathrm{E}-01$	2.63	Q	$-12.93$	Q	1.25	Eb	0.300	Ec	11.28; 9.30; 7.68	16
Equilin	474-86-2	$1.62\mathrm{E}-03$	$6.95\mathrm{E}-02$	3.30	Q	$-9.61$	Q	3.47	Q	0.322	Q	10.03	43
17beta-Estradiold	50-28-2	$1.08\mathrm{E}-06$	$8.75\mathrm{E}-05$	4.01	Ea	$-8.99$	Q	1.00	Ee	0.053	Ee	10.31	81
Clomiphene citrate	50-41-9	$5.56\mathrm{E}-04$	$9.77\mathrm{E}-02$	6.29	Q	$-6.39$	Q	1.68	Q	0.005	Q	8.83#	176
2-Ethylhexylparaben	5153-25-3	$1.02\mathrm{E}+00$	$1.30\mathrm{E}+02$	4.94	Q	$-6.36$	Q	2.98	Q	0.097	Q	9.09	127
5alpha-Dihydrotestosterone	521-18-6	$1.90\mathrm{E}+00$	$1.06\mathrm{E}+02$	3.55	Ea	$-8.86$	Q	3.64	Q	0.354	Q	Neutral	56
Estrone	53-16-7	$3.61\mathrm{E}-03$	$1.25\mathrm{E}-01$	3.13	Ea	$-9.49$	Q	3.58	Q	0.037	Ef	10.21	35
Diethylstilbestrold	56-53-1	$7.36\mathrm{E}-06$	$9.74\mathrm{E}-04$	5.07	Ea	$-7.44$	Q	2.75	Eb	0.005	Eb	10.38; 9.74	132
17alpha-Ethinylestradiold	57-63-6	$1.39\mathrm{E}-06$	$8.68\mathrm{E}-05$	3.67	Ea	$-8.83$	Q	3.52	Q	0.470	Eg	10.32	62
17-Methyltestosterone	58-18-4	$3.82\mathrm{E}+00$	$1.75\mathrm{E}+02$	3.36	Ea	$-9.12$	Q	3.68	Q	0.058	Q	Neutral	46
4-Cumylphenol	599-64-4	$7.02\mathrm{E}-01$	$5.38\mathrm{E}+01$	3.93	Q	$-6.17$	Q	4.78	Q	0.005	Q	10.19	77
Norethindrone	68-22-4	$7.46\mathrm{E}-01$	$2.06\mathrm{E}+01$	2.97	Ea	$-9.56$	Q	3.50	Q	0.151	Q	Neutral	28
Mestranol	72-33-3	$2.65\mathrm{E}-02$	$2.67\mathrm{E}+00$	4.39	Q	$-8.48$	Q	2.76	Q	0.137	Q	Neutral	101
Methoxychlor	72-43-5	$2.53\mathrm{E}+00$	$3.35\mathrm{E}+02$	5.08	Ea	$-6.69$	Ea	1.95	Eh	0.005	Eh	Neutral	133
Bisphenol B	77-40-7	$7.35\mathrm{E}-02$	$5.00\mathrm{E}+00$	3.77	Q	$-7.57$	Q	2.38	Eb	0.018	Eb	10.50; 9.82	68
o,p'-DDT	789-02-6	$1.29\mathrm{E}+00$	$2.28\mathrm{E}+02$	6.31	Q	$-4.56$	Q	1.01	Eb	0.005	Eb	Neutral	176
Bisphenol A	80-05-7	$2.28\mathrm{E}-01$	$1.00\mathrm{E}+01$	3.32	Ea	$-8.03$	Q	0.16	Ei	0.060	Ej	10.47; 9.80	44
4,4'-Sulfonyldiphenol	80-09-1	$1.16\mathrm{E}+01$	$9.84\mathrm{E}+00$	1.21	Q	$-13.35$	Q	0.44	Q	0.404	Q	9.18; 8.37	1
4-(2-Methylbutan-2-yl)phenol	80-46-6	$1.82\mathrm{E}+00$	$1.12\mathrm{E}+02$	3.66	Q	$-4.92$	Q	1.40	Eb	0.005	Eb	10.26	62
Butylparaben	94-26-8	$1.99\mathrm{E}+00$	$1.13\mathrm{E}+02$	3.57	Ea	$-6.79$	Q	2.62	Eb	0.042	Eb	8.78	57
4-tert-Butylphenol	98-54-4	$9.66\mathrm{E}+00$	$4.18\mathrm{E}+02$	3.31	Ea	$-5.92$	Ea	1.29	Eb	0.105	Eb	10.25	43

Note: ${\text{ACC}}_{\text{ER}}$, median ACC based on the integrated synthetic concentration-response curve predicted from ER model in Judson et al. 2015; CASRN, chemical abstracts service registry number; ${\text{CL}}_{\text{int}}$, intrinsic clearance; E, experimental values; EF, intracellular enrichment factor; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein; ${\mathrm{K}}_{\mathrm{A}\mathrm{W}}$, air-water partition coefficient; ${\mathrm{K}}_{\mathrm{O}\mathrm{W}}$, octanol-water partition coefficient; Q refers to QSAR model for ${\mathrm{K}}_{\mathrm{A}\mathrm{W}}$, ${\mathrm{K}}_{\mathrm{O}\mathrm{W}}$ or ${\mathrm{f}}_{\mathrm{u}}$ prediction, whereas Q refers to QPPR model when predicting ${\text{CL}}_{\text{int}}$; pKa, multiprotic ionization constants of mainly acidic nature except for those indicated by #, which is the ionization constant of basic function groups. Table is sorted by CASRN.

^aData from EPA Chemistry Dashboard (https://comptox.epa.gov/dashboard/, accessed 12 June 2018).

^bData from Wetmore et al. 2015.

^cData from Schlosser et al. 2006.

^dEC10 from the manual luciferase-based assay in the VM7Luc4E2 cell line (Ceger et al. 2015) was used in IVIVE analysis.

^eData from Plowchalk and Teeguarden 2002.

^fData from Speight et al. 1979.

^gData from Grabowski and Park 1984.

^hData from Wetmore et al. 2012.

ⁱData from Wetmore et al. 2013.

^jData from Teeguarden et al. 2005.

${\text{ACC}}_{\text{ER}}$ values could not be calculated for three high-potency steroid estrogens that achieved maximum responses at the lowest tested concentration ($\sim 1\text{nM}$) in the HTS assays: (17alpha-ethinylestradiol, diethylstilbestrol, and 17beta-estradiol). For these chemicals, the ${\text{ACC}}_{\text{ER}}$ was replaced with ${\text{EC}}_{10}$ values (concentration at which 10% of maximum activity is observed, $\mathrm{\mu }\mathrm{M}$) from the manual luciferase-based assay in the VM7Luc4E2 cell line (Ceger et al. 2015), which included testing concentrations sufficiently low to produce a full dose–response curve (the HTS version of this assay was used in the ToxCast™ ER model). The ${\text{EC}}_{10}$ values are also reported in Table 1.

In Vivo Uterotrophic Assay Data

The uterotrophic bioassay is a short-term in vivo test designed to detect the estrogenic potential of chemicals by quantifying uterine weight changes after administration of the test article via either injection or oral dosing. The assay was validated by the OECD, incorporated into the OECD test guidelines program (OECD TG 440), and adopted by the U.S. EPA as an EDSP Tier 1 bioassay to screen for chemicals with estrogenic properties (EPA OPPTS 890.1600). The National Toxicology Program Interagency Center for the Evaluation of Alternative Toxicological Methods (NICEATM) conducted a comprehensive literature search to identify uterotrophic studies using $\sim 2000$ environmental chemicals identified by the U.S. EPA as relevant to EDSP efforts (Kleinstreuer et al. 2016). For each uterotrophic study, the experimental protocol was evaluated for fulfillment of a set of minimum criteria to assess compliance with the uterotrophic study protocol design requirements set forth in EPA OCSPP 890.1600 (U.S. EPA 2009) and OECD TG 440 (OECD 2007). The minimum criteria were based on protocol elements specific to these test guidelines, such as animal model, animal age, exposure/dosing regimen, administration route, group size, and necropsy timing. To minimize the impact of in vivo variability, only studies meeting all minimum criteria (guideline-like) were included in the current analysis, and only chemicals with at least two independent guideline studies were considered. The lowest effect level (LEL) associated with uterine weight gain (i.e., estrogenic effect) was recorded for each chemical–study combination and served as the reference value for judging the performance of the PK models evaluated herein. All uterotrophic data are available via NICEATM’s website at https://ntp.niehs.nih.gov/go/40658 (Kleinstreuer et al. 2016).

Chemical Selection

Our initial analysis was limited to those chemicals with both positive (active) ${\text{ACC}}_{\text{ER}}$ values in the ToxCast™ ER model and at least two positive (guideline-like) uterotrophic studies from the NICEATM uterotrophic database (Kleinstreuer et al. 2016). Of the 29 chemicals that fulfilled those criteria, all had uterotrophic LELs from studies using injection as the route of administration, and 8 chemicals (inclusive) also had LELs available from two or more oral uterotrophic studies (Table 2). The median potency of these chemicals in uterotrophic studies ranged from $2.5\times {10}^{-4}\mathrm{mg}/\mathrm{kg}/\text{day}$ (diethylstilbestrol) to $300\mathrm{mg}/\mathrm{kg}/\text{day}$ (butylparaben) for injection dosing and $1\times {10}^{-3}\mathrm{mg}/\mathrm{kg}/\text{day}$ (17alpha-ethinylestradiol) to $387\mathrm{mg}/\mathrm{kg}/\text{day}$ (BPA) for oral studies. The list included three chemicals known to require metabolic transformation for estrogenic activity, mestranol (Schmider et al. 1997), 17-methyltestosterone (Hornung et al. 2004; Pawlowski et al. 2004), and methoxychlor (Hu and Kupfer 2002), as well as two chemicals known to be ER agonists rendered largely inert or unavailable by metabolic processes in vivo, BPA (Kuester and Sipes 2007; Partosch et al. 2013) and genistein (Pritchett et al. 2008; Shelnutt et al. 2002). Subsequent analysis was performed using all 266 chemicals with significant activity in the ToxCast™ ER model (AUC-agonist score $>0.01$).

Table 2.

Uterotrophic data for 29 ER reference chemicals.

Chemical Name		Injection Uterotrophic Studies				Oral Uterotrophic Studies
	CASRN	${\text{Log}}_{10}$ (Median ${\text{LEL}}_{\text{inj}}$)	${\text{Log}}_{10}$ (Lowest ${\text{LEL}}_{\text{inj}}$)	${\text{Log}}_{10}$ (Highest ${\text{LEL}}_{\text{inj}}$)	# Inj. studies	${\text{Log}}_{10}$ (Median ${\text{LEL}}_{\text{oral}}$)	${\text{Log}}_{10}$ (Lowest ${\text{LEL}}_{\text{oral}}$)	${\text{Log}}_{10}$ (Highest ${\text{LEL}}_{\text{oral}}$)	# Oral Studies
17alpha-Ethinylestradiol	57-63-6	$-3.52$	$-4.00$	$-2.70$	35	$-3.00$	$-3.70$	$-2.20$	21
17beta-Estradiol	50-28-2	$-3.00$	$-4.00$	0.30	19	$-1.78$	$-2.30$	$-0.40$	5
Tamoxifen	10540-29-1	$-1.70$	$-2.00$	0.00	8	$-1.63$	$-2.30$	$-0.49$	4
Methoxychlor	72-43-5	2.00	1.70	2.00	12	1.33	1.30	1.70	6
o,p'-DDT	789-02-6	2.00	0.00	2.30	9	1.70	1.00	1.70	6
Genistein	446-72-0	1.18	0.00	1.54	19	1.78	1.30	2.30	8
4-Nonylphenol	104-40-5	2.30	2.00	2.30	3	1.92	1.88	1.95	2
Bisphenol A	80-05-7	2.00	0.30	2.90	29	2.59	2.30	3.00	8
4-Dodecylphenol	104-43-8	1.60	1.60	1.60	3
2,2',4,4'-Tetrahydroxybenzophenone	131-55-5	2.30	2.30	2.48	5
2,4-Dihydroxybenzophenone	131-56-6	2.30	2.00	2.48	2
4-(1,1,3,3-Tetramethylbutyl)phenol	140-66-9	2.30	2.30	2.30	2
Bisphenol AF	1478-61-1	0.78	0.60	0.90	4
Zearalenone	17924-92-4	0.30	0.30	1.30	3
Equilin	474-86-2	0.30	0.30	0.30	2
Clomiphene citrate (1:1)	50-41-9	0.30	0.30	0.30	2
2-Ethylhexylparaben	5153-25-3	2.30	2.30	2.30	2
5alpha-Dihydrotestosterone	521-18-6	1.30	0.60	2.30	3
Estrone	53-16-7	$-0.99$	$-2.74$	0.30	6
Diethylstilbestrol	56-53-1	$-3.60$	$-4.30$	$-2.70$	5
17-Methyltestosterone	58-18-4	1.00	1.00	1.00	3
4-Cumylphenol	599-64-4	2.04	1.30	2.30	2
Norethindrone	68-22-4	1.04	0.30	1.30	2
Mestranol	72-33-3	$-2.42$	$-2.80$	$-2.22$	2
Bisphenol B	77-40-7	2.04	1.30	2.30	2
4,4'-Sulfonyldiphenol	80-09-1	1.30	1.30	1.30	2
4-(2-Methylbutan-2-yl)phenol	80-46-6	2.30	2.30	2.31	4
Butylparaben	94-26-8	2.48	1.70	3.00	8
4-tert-Butylphenol	98-54-4	2.00	2.00	2.00	2

Note: CASRN, chemical abstracts service registry number; $\text{LE}{\text{L}}_{\text{inj}}$, lowest effect level in injection uterotrophic assay; $\text{LE}{\text{L}}_{\text{oral}}$, lowest effect level in oral uterotrophic assay; Inj., injection; #, number.

PK Modeling

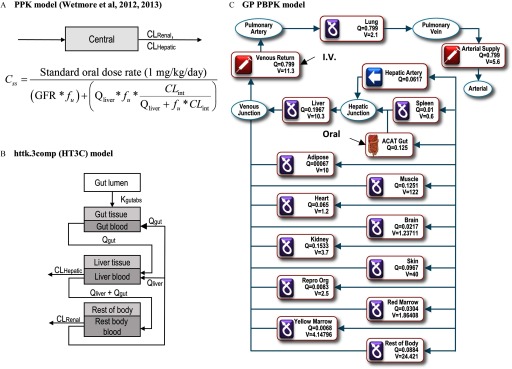
Three PK modeling approaches of differing complexity were used to estimate the daily equivalent administered dose (EAD; mg/kg BW/day) from a given route or exposure (oral or injection) that would result in a plasma concentration corresponding to the in vitro ${\text{ACC}}_{\text{ER}}$, the “lowest effect level” for ER-mediated bioactivity. First, we evaluated the standard one-compartment population-based PK (PPK) model described by Wetmore et al. (Wetmore et al. 2012, 2013), implemented using a publicly available R script (version 3.1.2) (Chang et al. 2015; R Core Team) (Figure 1A). This model combines physiologic and metabolic differences to quantitate subpopulation pharmacokinetic variability and produce chemical-specific steady-state plasma concentration (${\mathrm{C}}_{\text{ss}}$, in units of $\mathrm{\mu }\mathrm{M}$) equivalent to the in vitro ${\text{ACC}}_{\text{ER}}$. The PPK model does not account for tissue-partitioning of chemicals nor does it differentiate route of exposure but assumes a fixed dose rate and 100% absorption. Chemical elimination is calculated by the summation of liver metabolism, represented by hepatic intrinsic clearance (${\text{CL}}_{\text{int}}$, $\mathrm{L}/\mathrm{h}$), and renal clearance by passive glomerular filtration ($\mathrm{L}/\mathrm{h}$). These values are determined using Equations 1 and 2 (Wetmore et al. 2012), where ${\mathrm{Q}}_{\mathrm{H}}$ is hepatic blood flow rate, ${\mathrm{f}}_{\mathrm{u}}$ is the fraction of unbound chemical in plasma, ${\text{CL}}_{\text{int}}$ is hepatic intrinsic clearance, and GFR is glomerular filtration rate.

$$\text{Hepatic Clearance}\left(\mathrm{L}/\mathrm{h}\right)={\mathrm{Q}}_H(\mathrm{L}/\mathrm{h})\times \frac{{\mathrm{f}}_u{\times \text{CL}}_{int}}{{\mathrm{Q}}_H+{\mathrm{f}}_u{\times \text{CL}}_{int}}$$ (1)

$$\text{Renal Clearance}\left(\mathrm{L}/\mathrm{h}\right)=\text{GFR}\left(\mathrm{L}/\mathrm{h}\right){\times \mathrm{f}}_u$$ (2)

Figure 1.

Structures of models used for analyses. (A) The PPK model is a one-compartment model assuming 100% absorption and total clearance as the sum of hepatic and renal clearance. (B) The httk.3comp model (HT3C) includes compartments for gut lumen, gut, liver, and one compartment including all remaining tissues (figure adapted from Pearce et al. 2017). (C) The GP PBPK model consists of 14 tissue compartments as shown in the figure [figure adapted from the PBPK Model Editor window in the GastroPlus™ software (Simulations Plus, Inc.)]. To simulate absorption through the gastrointestinal tract, the model incorporates the ACAT model consisting of nine compartments (stomach, duodenum, jejunum 1, jejunum 2, ileum 1, ileum 2, ileum 3, caecum, and ascending colon). ACAT, advanced compartmental absorption and transit; ${\text{CL}}_{\text{Hepatic}}$, hepatic clearance ($\mathrm{L}/\mathrm{h}$); ${\text{CL}}_{\text{int}}$, intrinsic clearance ($\mathrm{L}/\mathrm{h}$); ${\text{CL}}_{\text{Renal}}$, renal clearance ($\mathrm{L}/\mathrm{h}$); ${\mathrm{C}}_{\text{ss}}$, steady state plasma concentration; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein; GFR, glomerular filtration rate ($\mathrm{L}/\mathrm{h}$); PBPK, physiologically based pharmacokinetic; PPK, one-compartment population-based pharmacokinetic model; ${\mathrm{Q}}_{\text{liver}}$, liver blood flow ($\mathrm{L}/\mathrm{h}$); Q, Tissue blood flow (mL/s); V, Tissue Volume (mL).

The second approach implemented the use of a three-compartment model available in “httk,” a published R package for high-throughput toxicokinetics (Pearce et al. 2017; Wambaugh et al. 2016). The httk “3compartment” model (HT3C), includes gut and liver compartments consisting of separate blood and tissue sections with constant partitioning along with a “$\text{rest-of-body}+\text{body blood}$” compartment without partitioning (Figure 1B). Like the PPK model, elimination of chemicals is by hepatic metabolism and passive glomerular filtration. Values for ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$ were the same as those used for the PPK model and determined as described below. Chemical-specific physicochemical data and species-specific in vitro and physiological data were used in calculating the partition coefficients, clearance, tissue volumes, and blood flows. Absorption from the gut lumen into gut tissue was modeled for determining oral EADs, using default setting of the physiological parameters, partition coefficients, and gut absorption kinetics. We used the HT3C model to calculate chemical-specific EADs that result in a maximum plasma concentration (${\mathrm{C}}_{\text{max}}$, in units of $\mathrm{\mu }\mathrm{M}$) corresponding to the in vitro ${\text{ACC}}_{\text{ER}}$ following once-daily oral or injection administration of chemical for three consecutive days (the protocol used in guideline uterotrophic studies).

In the third approach, PBPK models for oral and injection dosing were built using GastroPlus™ (GP) software (Simulations Plus, Inc.), which has compartments representing lung, liver, gastrointestinal tract, spleen, heart, brain, kidney, skin, bone marrow, muscle, adipose tissue, and reproductive tissues. Specifically, to simulate chemical absorption through the gastrointestinal tract, the GP PBPK model includes an advanced compartmental absorption and transit (ACAT) module consisting of nine compartments (stomach, duodenum, jejunum 1, jejunum 2, ileum 1, ileum 2, ileum 3, caecum, and ascending colon) (Figure 1C). The chemical-specific partition coefficients for each tissue were predicted using ADMET Predictor (Simulations Plus, Inc.). The GP injection model simulated subcutaneous injection exposure by modeling the ${\mathrm{C}}_{\text{max}}$ following a daily 3-h intravenous infusion, which was based on a literature report stating that the ${\mathrm{C}}_{\text{max}}$ for a well-dissolved drug is achieved 3 h after subcutaneous injection exposure (Hirano and Yamada 1983). The GP oral model simulated the ${\mathrm{C}}_{\text{max}}$ following a daily oral dosing in solution form for 3 days. We used the default settings for physiological parameters, partition coefficients, and gut absorption kinetics. Values for ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$ were the same as used for all the other models and determined as described below. The PBPK models were used to calculate chemical-specific EADs that result in a maximum plasma concentration (${\mathrm{C}}_{\text{max}}$, in units of $\mathrm{\mu }\mathrm{M}$) corresponding to the in vitro ${\text{ACC}}_{\text{ER}}$ following once-daily oral or injection administration of chemical for three consecutive days (the protocol used in guideline uterotrophic studies).

Source of PK Model Parameters ${\mathit{\text{CL}}}_{\mathit{\text{int}}}$ and ${\mathit{f}}_{\mathit{u}}$

Rat ${\text{CL}}_{\text{int}}$ values were obtained either directly from the literature (Plowchalk and Teeguarden 2002) or calculated by scaling in vitro metabolic clearance measurements from primary hepatocyte suspensions. Data from experiments using primary rat hepatocytes (Wetmore et al. 2013, 2015) were used if available; otherwise, we used data from experiments using human primary hepatocytes (Wetmore et al. 2012). If no experimental data were available from either species, we used values predicted from a published quantitative property–property relationship (QPPR) model (Kirman et al. 2015). The QPPR model predicts ${\text{CL}}_{\text{int}}$ for each chemical using octanol-water (${\mathrm{K}}_{\text{OW}}$) and air-water (${\mathrm{K}}_{\text{AW}}$) partition coefficients. ${\mathrm{K}}_{\text{OW}}$ values were obtained from the EPA Chemistry Dashboard (https://comptox.epa.gov/dashboard/), which provided experimentally determined (mean) values for 13 chemicals and consensus model predictions for the remaining 16 chemicals. All ${\mathrm{K}}_{\text{AW}}$ values were determined using a quantitative structure–activity relationship (QSAR) model developed in house using published data (http://esc.syrres.com/interkow/EPiSuiteData.htm). The same approach was applied to ${\mathrm{f}}_{\mathrm{u}}$, where all available experimental data were used, and predicted values were obtained via a QSAR model developed in house using published data (Ingle et al., 2016). Both ${\mathrm{K}}_{\text{AW}}$ and ${\mathrm{f}}_{\mathrm{u}}$ models were developed using multiple linear regression approach and are accessible through github (https://github.com/zang1123/PBPK-Parameter-Prediction). Of the 29 chemicals evaluated, 12 have experimental values for both ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ reported in the literature (Wetmore et al. 2012, 2013, 2015), and in silico predictions (QSAR/QPPR) were used to estimate both values for 15 chemicals (two chemicals had an experimental ${\mathrm{f}}_{\mathrm{u}}$ and QPPR-predicted ${\text{CL}}_{\text{int}}$) (Table 1).

ACC Adjustment Using a Mass-Balance Derived Enrichment Factor (EF)

The ${\text{ACC}}_{\text{ER}}$ represents the nominal concentration at which significant in vitro activity was observed in the ER model. To estimate in vitro partitioning of test chemicals and adjust ${\text{ACC}}_{\text{ER}}$ values used in the PK models, we applied the mass-balance model described by Armitage et al. (Armitage et al. 2014). The mass-balance model was applied using the macro-enabled Excel workbook provided as supplemental material by Armitage et al. The model applies to neutral organic chemicals and ionogenic organic chemicals that are predominantly neutral at the test system pH ($\text{pH}=7.4$), which was the case for 23 of the chemicals evaluated (Table 1). The remaining four chemicals (genistein, 2,2',4,4'-tetrahydroxybenzophenone, 2,4-dihydroxybenzophenone, and zearalenone) have one or two functional groups with acidic pKa of 7.14–7.88, and the other two chemicals (tamoxifen and clomiphere citrate) have basic pKa of 8.48 and 8.83. For chemical characterization, two physicochemical properties for each chemical are required: the octanol-water partition coefficient (${\mathrm{K}}_{\text{OW}}$) and air-water partition coefficient (${\mathrm{K}}_{\text{AW}}$) (Table 1). To characterize the assay system, the model requires user input for key in vitro assay parameters, such as cell number, system temperature, percentage fetal bovine serum (% FBS), well-volume, and head space. For the work described here, we used values that represented a consensus from across the 16 assays in the ER model, where most assays were conducted under similar conditions. The most critical parameter, % FBS, was identical in all assays (10%) with the exception of the Tox21 ER_BLA, which had 2% FBS (Gülden and Seibert 1997). The most relevant output parameter to estimate in vitro “exposure” is the cell enrichment factor (EF), which scales the nominal concentration to reflect the intracellular concentration at equilibrium (Armitage et al. 2014; Fischer et al. 2017). We applied chemical-specific EF adjustments to the ${\text{ACC}}_{\text{ER}}$ values used in all three models (Equation 3), thereby converting nominal ${\text{ACC}}_{\text{ER}}$ concentrations to “internal” cellular concentrations.

$${\text{ACC}}_{\text{ER}}\_\text{EF}\left(\mathrm{\mu }\mathrm{M}\right)={\text{ACC}}_{\text{ER}}\left(\mathrm{\mu }\mathrm{M}\right)\times \text{EF}$$ (3)

Steady-State EAD Adjustment Using Fraction of Unbound Chemical (${\mathit{f}}_{\mathit{u}}$)

The standard one-compartment PPK model described by Wetmore et al. (Wetmore et al. 2012, 2013) uses the fraction of unbound chemical (${\mathrm{f}}_{\mathrm{u}}$) to calculate both renal and hepatic clearance, as only the free chemical fraction is assumed available for glomerular filtration or uptake by hepatocytes. However, the model does not incorporate the fraction of unbound (freely available) chemical into calculations involving chemical potency. That is, the determination of chemical activity (i.e., EAD) is based on 100% chemical bioavailability for uptake into tissues and subsequent interactions with molecular targets. We assessed the impact of applying a simple correction to the estimated in vivo dose (EAD) to account for only freely available chemical being bioactive (Equation 4). This approach assumes a linear relationship between free and bound chemical and external-dose and steady-state concentration (${\mathrm{C}}_{\text{ss}}$). The value for ${\mathrm{f}}_{\mathrm{u}}$ is unitless (%) and is therefore assumed to be applicable to any concentration of chemical distributed in whole serum, an appropriate assumption given the context of our model. Likewise, the assumption of a linear relationship between dose and ${\mathrm{C}}_{\text{ss}}$ serves as the basis for much previously published work in the field, including the standard one-compartment model used here (Wetmore et al. 2012, 2013). We therefore used ${\mathrm{f}}_{\mathrm{u}}$ as a multiplicative factor to derive the unbound concentration at steady state from the total concentration at steady state. Accordingly, the relationship between the EAD adjusted using ${\mathrm{f}}_{\mathrm{u}}$ (${\text{EAD}}_{\text{fu}}$) and total EAD was represented as:

$$\text{PPK}{\text{EAD}}_{\text{fu}}=\text{PPK}\text{EAD}\times 1/{\mathrm{f}}_u$$ (4)

We did not apply the free fraction correction to the other more complex models (HT3C, GP), as the assumption of linearity may not hold for models that do not yield steady-state predictions.

EADs (mg/kg/day) were calculated from the chemical-specific ${\text{ACC}}_{\text{ER}}$ (Table 1) values using the three PK models described above: standard one-compartment (PPK), HTTK 3 Compartment (HT3C), and GastroPlus™ PBPK (GP). Both the HT3C and GP apply route-specific dosing models, which were used to estimate uterotrophic LELs from oral or injection exposure studies, respectively. The PPK model does not differentiate dosing routes but assumes instantaneous and uniform distribution of chemical in the serum. All models were also run using in vitro potency values derived from the mass-balance enrichment factor (EF), which converts the nominal active concentration (${\text{ACC}}_{\text{ER}}$) to an intracellular concentration at equilibrium (${\text{ACC}}_{\text{ER}\_}\text{EF}$) by multiplying ${\text{ACC}}_{\text{ER}}$ by EF (Table 1) (Armitage et al. 2014). EADs from the PPK model were additionally adjusted using ${\mathrm{f}}_{\mathrm{u}}$ to represent the predicted concentration of free chemical available to act on the molecular target. An overview of each of the eight model-adjustment combinations is provided in Table 3, with corresponding EADs for injection and oral dosing given in Excel Table S1.

Table 3.

Comparison of models and adjustment factors.

PK Model Name	Plasma Conc. Modeled		Adjustment Applied
	${\mathrm{C}}_{\text{ss}}$	${\mathrm{C}}_{\text{max}}$	None	EF	${\mathrm{f}}_{\mathrm{u}}$
Standard One-compartment
PPKa	X		X
$\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$a	X				X
PPK_EFa	X			X
$\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}\_\text{EF}$a	X			X	X
HTTK 3 Compartment
HT3Cb		X	X
HT3C_EFb		X		X
GastroPlus™ Multi-compartment
GPb		X	X
GP_EFb		X		X

Note: Model types are the standard one-compartment population-based pharmacokinetic model (PPK), the three-compartment model from the HTTK R package (HT3C), and the multicompartment model from the commercial GastroPlus™ software (GP). Models provide steady state (${\mathrm{C}}_{\text{ss}}$) or maximum (${\mathrm{C}}_{\text{max}}$) plasma concentrations as indicated by X. Adjustments for intracellular concentrations based on an in vitro mass-balance derived enrichment factor (EF) or a correction for unbound chemical (${\mathrm{f}}_{\mathrm{u}}$) available to interact with the biological target were applied as indicated by X.

^aThe PPK model is exposure route-agnostic.

^bThe HT3C and GP models explicitly include oral or injection dosing considerations.

Analysis of Model Performance

Overall performance of the eight model-adjustment combinations was assessed across all chemicals using the root mean squared error (RMSE), a standard statistical metric used to measure error between actual and predicted values. We used the mean residual values (MRV; Equation 5) to inform directional bias of error (over or under prediction).

$$MRV=\frac{1}{n}\sum _{i=1}^n\left(x_i-x_{true}\right)$$ (5)

For each PK model, we also evaluated whether the source of PK parameters ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ (experimental or predicted) affected predictive accuracy by assessing chemicals where both ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ were either determined experimentally or predicted using QSAR (${\mathrm{f}}_{\mathrm{u}}$) and QPPR (${\text{CL}}_{\text{int}}$) models. RMSE and MRV were calculated for each PK model using three groupings: all 29 chemicals (All), 12 chemicals with experimental values for ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ (EE), and 15 chemicals where QPPR and QSAR models were used to predict both ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$ (QQ), respectively. The RMSE and MRV values are presented in Table S2. Two chemicals (estrone and $17\mathrm{alpha}\text{-ethinylestradiol}$) had experimentally determined ${\mathrm{f}}_{\mathrm{u}}$ and QPPR-derived ${\text{CL}}_{\text{int}}$ (Table 1) and were not used in this portion of the analysis.

Based on the overall performance of the model-adjustment combinations, averaged across all chemicals, we evaluated the highest performing IVIVE approaches in a chemical-specific manner. The EADs were compared with the uterotrophic LELs for each chemical, and potential sources of under/over prediction were analyzed. The top performing approaches were then used to apply IVIVE to all 266 chemicals with significant activity in the ToxCast™ ER model (AUC-agonist score $>0.01$).

Results

Model Performance

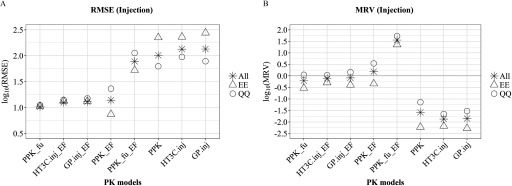
Plotting RMSE values for the injection models (including PPK, which is route-agnostic) revealed a clear separation of the eight model-adjustment combinations into two groups (low/high RMSE), “All” group, Figure 2A. All models using a single-adjustment ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$, PPK_EF, ${\text{HT}3\mathrm{C}}_{\text{inj}}\_\text{EF}$, ${\text{GP}}_{\text{inj}}\_\text{EF}$) had RMSE values between 1.00 and 1.15 log units, whereas all unadjusted models plus the PPK model with two adjustments ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}\_\text{EF}$) had RMSE values between 1.89 and 2.13 log units. Similar groupings were evident in the MRV analysis, which evaluates directional bias (Figure 2B). All three unadjusted models (PPK, ${\text{HT}3\mathrm{C}}_{\text{inj}}$, ${\text{GP}}_{\text{inj}}$) had MRV values between $-1.5$ and $-2.0\log \text{units}$, indicating a strong bias toward underprediction (producing injection EADs well below the observed LEL). Simultaneously adjusting both EF and ${\mathrm{f}}_{\mathrm{u}}$ in the PPK model resulted in a strong bias towards overpredicting uterotrophic LELs ($\text{MRV}=1.56\log \text{units}$), whereas all single-adjustment models were comparatively balanced with MRVs between $-0.20$ and 0.18 log units, “All” group, Figure 2B. As noted in the Methods section, the PPK model does not differentiate dosing routes, and the same (route-agnostic) EAD values are therefore used for comparison with route-specific EADs produced in the HT3C and GP models (injection and oral).

Figure 2.

Comparison of PK model-adjustment performance: injection dosing. The performance of 8 PK model-adjustment combinations (detailed in Methods and below) was compared using root mean squared error (RMSE) (A) and mean residual values (MRV) (B) between $\mathrm{lo}{\mathrm{g}}_{10}$ values of EAD and median LELs from uterotrophic injection studies, calculated for three groups of chemicals: all 29 chemicals (asterisk), 13 chemicals with experimental values for ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ (EE, triangle symbol), and 14 chemicals where QPPR and QSAR models were used to predict both ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$, respectively (QQ, circle symbol). PPK, one-compartment population-based pharmacokinetic model; ${\text{HT}3\mathrm{C}}_{\text{inj}}$, the httk “3compartment” model simulating injection exposure route; ${\text{GP}}_{\text{inj}}$, PBPK model built using GastroPlus™ software simulating injection exposure route. PPK_EF, ${\text{HT}3\mathrm{C}}_{\text{inj}}\_\text{EF}$, ${\text{GP}}_{\text{inj}}\_\text{EF}$ are corresponding PPK, ${\text{HT}3\mathrm{C}}_{\text{inj}}$ and ${\text{GP}}_{\text{inj}}$ models with EF adjustment applied for ${\text{ACC}}_{\text{ER}}$. $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ is PPK model with ${\mathrm{f}}_{\mathrm{u}}$ adjustment applied for in vivo ${\mathrm{C}}_{\text{ss}}$ in EAD calculation. $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}\_\text{EF}$ is PPK model with EF applied for ${\text{ACC}}_{\text{ER}}$ and ${\mathrm{f}}_{\mathrm{u}}$ adjustment applied for in vivo ${\mathrm{C}}_{\text{ss}}$ in EAD calculation. ${\text{ACC}}_{\text{ER}}$, pseudo median activity concentration at cutoff from estrogen receptor pathway model; ${\text{CL}}_{\text{int}}$, intrinsic clearance ($\mathrm{L}/\mathrm{h}$); EAD, equivalent administered dose; EF, enrichment factor; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein; LEL, lowest effect level; QPPR, quantitative property-property relationship; QSAR, quantitative structure-activity relationship; PK, pharmacokinetic.

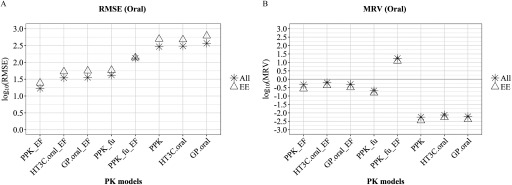
Results from the oral exposure models mirrored those from the injection models; RMSE values of the four single-adjustment models ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$, PPK_EF, ${\text{HT}3\mathrm{C}}_{\text{oral}}\_\text{EF}$, ${\text{GP}}_{\text{oral}}\_\text{EF}$) were uniformly lower (1.23 to 1.62 log units) than the unadjusted or double-adjusted oral models (2.13 to 2.57 log units, “All” group, Figure 3A). Similarly, all three unadjusted models (PPK, ${\text{HT}3\mathrm{C}}_{\text{oral}}$, ${\text{GP}}_{\text{oral}}$) had MRV values indicating a strong bias towards under prediction ($-2.12$ to $-2.25\log \text{units}$). Adjusting both EF and ${\mathrm{f}}_{\mathrm{u}}$ in the PPK model again resulted in a strong bias toward overpredicting uterotrophic LELs ($\text{MRV}=1.24\log \text{units}$), whereas all single-adjustment models had MRV values between $-0.21$ and $-0.68\log \text{units}$, “All” group, Figure 3B.

Figure 3.

Comparison of PK model-adjustment performance: oral dosing. The performance of 8 PK model-adjustment combinations (detailed in Methods and below) was compared using root mean squared error (RMSE) (A) and mean residual values (MRV) (B) between $\mathrm{l}\mathrm{o}{\mathrm{g}}_{10}$ values of EAD and median LELs from uterotrophic oral studies, calculated for three group of chemicals: all 8 chemicals (All, asterisk symbol), 6 chemicals with experimental values for ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ (EE, triangle symbol). PPK, one-compartment population-based pharmacokinetic model; ${\text{HT}3\mathrm{C}}_{\text{oral}}$, the httk “3compartment” model simulating oral route of exposure; ${\text{GP}}_{\text{oral}}$, PBPK model built using GastroPlus™ software simulating oral exposure route. PPK_EF, ${\text{HT}3\mathrm{C}}_{\text{oral}}\_\text{EF}$, ${\text{GP}}_{\text{oral}}\_\text{EF}$ are corresponding PPK, ${\text{HT}3\mathrm{C}}_{\text{oral}}$ and ${\text{GP}}_{\text{oral}}$ models with EF adjustment applied for ${\text{ACC}}_{\text{ER}}$. $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ is PPK model with ${\mathrm{f}}_{\mathrm{u}}$ adjustment applied for EAD calculation. $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}\_\text{EF}$ is PPK model with EF adjustment applied for ${\text{ACC}}_{\text{ER}}$ and ${\mathrm{f}}_{\mathrm{u}}$ adjustment applied for in vivo ${\mathrm{C}}_{\text{ss}}$ in EAD calculation. ${\text{ACC}}_{\text{ER}}$, pseudo median activity concentration at cutoff from estrogen receptor pathway model; ${\text{CL}}_{\text{int}}$, intrinsic clearance ($\mathrm{L}/\mathrm{h}$); ${\mathrm{C}}_{\text{ss}}$, steady state plasma concentration; EAD, equivalent administered dose; EF, enrichment factor; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein; LEL, lowest effect level; QPPR, quantitative property-property relationship; QSAR, quantitative structure-activity relationship; PK, pharmacokinetic.

We used RMSE to evaluate the impact on model performance when using chemicals with experimentally determined values for ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ (EE) in comparison with chemicals where in silico (i.e., QSAR or QPPR) approaches were used to estimate both values (QQ), Figures 2 and 3. The source of ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ values (experimental or in silico) had no impact on RMSE for three of the four top-performing injection models ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$, ${\text{HT}3\mathrm{C}}_{\text{inj}}\_\text{EF}$, ${\text{GP}}_{\text{inj}}\_\text{EF}$), whereas predictions made in the PPK_EF model using the in silico values had slightly higher errors in comparison with predictions made using experimental values: RMSE of 1.36 log units (QQ) vs. 0.87 log units (EE) (Figure 2). For chemicals with oral uterotrophic data, there is only one chemical (4-nonylphenol) where in silico (QSAR/QPPR) approaches were used to estimate both ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ values (QQ), in comparison with six chemicals with experimentally determined values for both parameters (EE). The prediction error using the in silico values (QQ) is lower than those predictions made using experimental values EE for seven of eight models (Excel Table S2). However, because it is unreasonable to calculate RMSE and MRV with sample size equal to one, values for QQ were not shown in Figure 3 for the oral data set. There was little difference across both RMSE and MRV values between “All” and “EE” sets (Figure 3).

Chemical-Specific EADs from Single-Adjustment Models

Our initial assessment of model performance, described above, was based on the mean of the EAD values from all 29 chemicals evaluated (i.e., RMSE and MRV). Based on these results, we chose to further evaluate chemical-specific EADs in the four best-performing models for each dosing route (oral and injection), which were the single-adjustment models in both cases: $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$, PPK_EF, HT3C_EF, and GP_EF. EADs for each of the 29 chemicals from each model were plotted against the median, highest, and lowest LELs from uterotrophic studies using either injection (Figure 4) or oral (Figure 5) dosing. As noted previously, the GP and HT3C models produce route-specific EADs that were used for comparison with oral or injection LELs from uterotrophic, as appropriate. However, the PPK model is route-agnostic, and we therefore used the same EAD values for comparison with both oral and injection LELs.

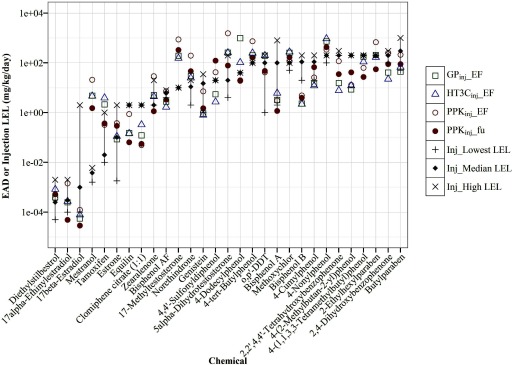
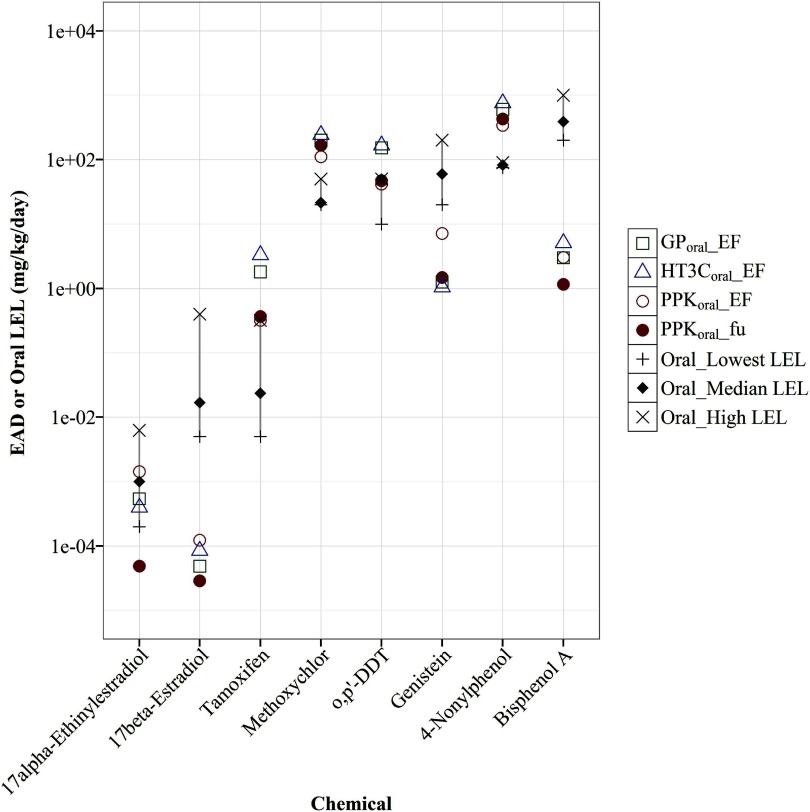
Figure 4.

Chemical-specific EAD predictions compared with injection LELs. EAD values (mg/kg/day) were predicted from ${\text{ACC}}_{\text{ER}}$ using ${\text{GP}}_{\text{inj}}$ (square), ${\text{HT}3\mathrm{C}}_{\text{inj}}$ (triangle) and PPK models (circle) with EF or ${\mathrm{f}}_{\mathrm{u}}$; adjustments were plotted against the median or mean (if only two studies), highest, and lowest LELs (mg/kg/d) of uterotrophic injection studies for 29 chemicals. The gray line highlights the range from lowest (“$+$”) to highest (“x”) LELs of all guideline-like uterotrophic injection studies. The chemicals are ordered from left to right based on their median or mean (if only two studies) LEL values, from low to high. Data for this figure are provided in Excel Table S1. ${\text{ACC}}_{\text{ER}}$, pseudo median activity concentration at cutoff from estrogen receptor pathway model; ${\text{CL}}_{\text{int}}$, intrinsic clearance ($\mathrm{L}/\mathrm{h}$); ${\mathrm{C}}_{\text{ss}}$, steady-state plasma concentration; EAD, equivalent administered dose; EF, enrichment factor; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein; LEL, lowest effect level; ${\text{GP}}_{\text{inj}}$, PBPK model built using GastroPlus™ software simulating injection exposure route; ${\text{HT}3\mathrm{C}}_{\text{inj}}$, the httk “3compartment” model simulating injection exposure route; PPK, one-compartment population-based pharmacokinetic model.

Figure 5.

Chemical-specific EAD predictions compared with oral LELs. EAD values (mg/kg/d) were predicted from ${\text{ACC}}_{\text{ER}}$ using ${\text{GP}}_{\text{oral}}$ (square), ${\text{HT}3\mathrm{C}}_{\text{oral}}$ (triangle) and PPK models (circle) with EF or ${\mathrm{f}}_{\mathrm{u}}$ adjustments were plotted against the median or mean (if only two studies), highest, and lowest LELs (mg/kg/d) from uterotrophic oral studies for 8 chemicals. The dashed line highlights the range from lowest ( “$+$”) to highest (“x”) LELs of all guideline-like uterotrophic oral studies. The chemicals are ordered from left to right based on their median or mean (if only two studies) LEL values, from low to high. Data for this figure are provided in Excel Table S1. ${\text{ACC}}_{\text{ER}}$, pseudo median activity concentration at cutoff from estrogen receptor pathway model; ${\text{CL}}_{\text{int}}$, intrinsic clearance ($\mathrm{L}/\mathrm{h}$); EAD, equivalent administered dose; EF, enrichment factor; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein; LEL, lowest effect level; ${\text{GP}}_{\text{oral}}$, PBPK model built using GastroPlus™ software simulating oral exposure; ${\text{HT}3\mathrm{C}}_{\text{oral}}$, the httk “3compartment” model simulating oral route of exposure; PPK, one-compartment population-based pharmacokinetic model.

All EADs from the four models were within 1 log of the lowest or highest LELs reported for 27 of the 29 chemicals tested in uterotrophic injection studies (Figure 4). For the remaining two chemicals, mestranol and 17-methyltesterone, all models produced EADs that were $>1\log$ higher than any reported injection LEL. Similar performance across all models was not entirely unexpected, as HT3C and GP both have injection-specific modules, and the PPK model assumes 100% delivery of chemical into blood as with injection dosing. However, there was no clear correlation between model structure or complexity and predictive performance.

All four oral models produced EADs that were within 1 log of the lowest or highest LELs reported for six of the eight chemicals tested in uterotrophic oral studies (Figure 5). For 17beta-estradiol and BPA, all models produced EADs that were $>1\log$ lower than any reported oral LEL. Unlike the case of injection dosing, similar performance between the models was not anticipated in light of the complex model structures built specifically to address oral dosing (i.e., gut absorption), which are absent from the PPK model.

Estimating EADs for the Extended ER Model Chemical Set

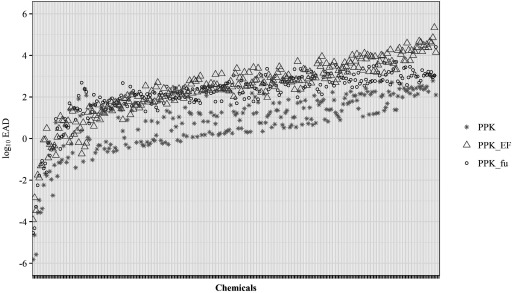
EADs from all PK models using single adjustments (EF or ${\mathrm{f}}_{\mathrm{u}}$) had significantly better performance than the unadjusted models when evaluated across all 29 chemicals from the validation set. Of these, the $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ model had the lowest RMSE (1.02 log units) when predicting LELs from uterotrophic injection studies, whereas the PPK_EF model had the lowest RMSE (1.23 log units) when predicting uterotrophic LELs from oral studies. Because neither single-adjustment PPK model had a clear advantage in performance over the other, we chose to use both models ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ and PPK_EF), in addition to the standard unadjusted PPK model, to calculate EADs for all 266 chemicals with activity in the ER model ($\text{AUC}>0.01$) (Figure 6, Excel Table S3).

Figure 6.

Estrogenic Dose Predictions for 266 Chemicals. EAD values (${\log }_{10}$ scale) were predicted from ${\text{ACC}}_{\text{ER}}$ for all 266 potential ER agonists from the ToxCast™ ER pathway model, using the PPK model (∗ symbol) and PPK model with EF (triangle) or ${\mathrm{f}}_{\mathrm{u}}$ (circle) adjustments. PPK, one-compartment population-based PK pharmacokinetic model; PPK_EF, PPK model with EF adjustment applied for ${\text{ACC}}_{\text{ER}}$ in EAD calculation. $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$, PPK model with ${\mathrm{f}}_{\mathrm{u}}$ adjustment applied for in vivo ${\mathrm{C}}_{\text{ss}}$ in EAD calculation. Data for this figure are provided in Excel Table S3. ${\text{ACC}}_{\text{ER}}$, pseudo median activity concentration at cutoff from estrogen receptor pathway model; ${\text{CL}}_{\text{int}}$, intrinsic clearance ($\mathrm{L}/\mathrm{h}$); ${\mathrm{C}}_{\text{ss}}$, steady-state plasma concentration; EAD, equivalent administered dose; EF, enrichment factor; ER, estrogen receptor; ${\mathrm{f}}_{\mathrm{u}}$, fraction of chemical unbound to plasma protein.

Discussion

We sought to evaluate and improve the predictive accuracy of IVIVE approaches for potential application to chemical prioritization, risk assessment, and regulatory decision-making. We chose estrogen receptor signaling as a case study because of its relevance to human and environmental health and availability of well-curated data obtained from validated in vitro (ToxCast™ ER pathway) and in vivo (uterotrophic) systems. In addition, the acute and specific nature of the uterotrophic response (ER agonist/uterine weight gain) provides an excellent corollary to the acute response measured in the in vitro assays, allowing a more direct comparison than would be afforded with a less specific mechanism of action (e.g., oxidative stress) or end point more distal from the molecular initiating event (e.g., tumorigenesis).

Three PK models (PPK, HT3C, GP) were used to estimate the daily EAD that would result in a plasma concentration corresponding to the in vitro ${\text{ACC}}_{\text{ER}}$, thereby approximating the LEL obtained from a uterotrophic bioassay conducted with the same chemical. We ran the models with user-provided values for in vitro activity (${\text{ACC}}_{\text{ER}}$), intrinsic clearance (${\text{CL}}_{\text{int}}$), and fraction of chemical unbound to protein (${\mathrm{f}}_{\mathrm{u}}$). We then applied adjustments to the model input parameters in an effort to improve the predictive performance. For all models, we applied a mass-balance derived EF, which adjusts the nominal concentration of test chemical (${\text{ACC}}_{\text{ER}}$) to reflect intracellular exposure. EAD calculations from the steady-state (${\mathrm{C}}_{\text{ss}}$) model were adjusted using fraction of unbound chemical in the plasma (${\mathrm{f}}_{\mathrm{u}}$) to approximate bioavailability. The accuracy of each model-adjustment combination was assessed by comparing model EADs for the 29 chemicals with corresponding uterotrophic LELs. Although it is certainly true that the in vivo data are less than a gold standard, these are the data currently used in regulatory screening and decision-making, and the uterotrophic dataset went through an extremely rigorous curation process (Kleinstreuer et al. 2016). Here, we used only uterotrophic studies that met all the criteria to be considered guideline-like, and only included chemicals that had multiple such studies in the evaluation set, to limit the impact of in vivo variability to the extent possible.

The three PK models used in this analysis had vastly different structures and complexity (Figure 1), and concomitant differences in predictive performance may therefore be expected among the models. However, our results show that the one-compartment steady-state PPK model had the best overall performance (lowest RMSE) in predicting uterotrophic LELs from both oral and injection dosing studies, and that model parameters for in vitro activity (${\text{ACC}}_{\text{ER}}$) and chemical bioavailability (${\mathrm{f}}_{\mathrm{u}}$) have a more significant impact on predictive performance than model complexity or structure (Figures 2 and 3).

Use of ${\mathit{\text{CL}}}_{\mathit{\text{int}}}$ and ${\mathit{f}}_{\mathit{u}}$ Values from in Silico Models

Chemical-specific values for ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$ are requisite parameters for all the PK models evaluated here, and for PK models in general. The lack of experimental values for these key parameters is often the limiting factor in developing IVIVE approaches for large chemical sets (e.g., HTS), as the assays used to determine ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$ are typically far costlier and more time-consuming than the in vitro assays used to assess chemical activity. Using in silico models to adequately estimate these values would therefore offer a path to greatly expand use and utility of IVIVE for risk assessment. We compared the accuracy of EADs generated from the same PK model, but for different chemicals having either experimentally determined or in silico predicted ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$ values (Table 1). In our study, a QSAR model developed in-house using published data (Ingle et al. 2016) was used to predict ${\mathrm{f}}_{\mathrm{u}}$ for 15 of 29 chemicals values and a published QPPR model (Kirman et al. 2015) was used to predict ${\text{CL}}_{\text{int}}$ for 17 of 29 chemicals. Octanol-water and air-water partition coefficients (${\mathrm{K}}_{\text{OW}}$ and ${\mathrm{K}}_{\text{AW}}$, respectively) are the two key parameters used in the QPPR models to predict ${\text{CL}}_{\text{int}}$. Values for ${\mathrm{K}}_{\text{OW}}$ and ${\mathrm{K}}_{\text{AW}}$ can, themselves, be predicted using in silico models. In our study, QSAR was used to estimate ${\mathrm{K}}_{\text{AW}}$ for 27 of 29 chemicals and for 16 of 29 ${\mathrm{K}}_{\text{OW}}$ values (the remainder having published experimental values). The source of these key parameters did not appear to affect the predictive performance of the top four (single-adjustment) models (Figures 2 and 3). Consequently, values for ${\text{CL}}_{\text{int}}$ and ${\mathrm{f}}_{\mathrm{u}}$, which are typically the most challenging experimental data to obtain, can be determined entirely through the use of in silico approaches without any apparent detrimental impact on PK model performance. This observation is addressed in additional detail in the Supplemental Material (Excel Table S2). Also, during the course of our in silico modeling efforts, we noted discrepancies in SMILES strings used to convey chemical structure information for the same chemicals from varying public resources. After investigating these inconsistencies, we decided to use the SMILES from the U.S. EPA Chemistry Dashboard (https://comptox.epa.gov/dashboard/) based on the high degree of manual and automated chemistry curation and the transparent, comprehensive nature of the resource (Williams et al. 2017).

Adjusting for in Vitro Nominal Concentration

IVIVE relies on measurements of chemical-specific activity from in vitro assays (e.g., ${\text{EC}}_{10}$, ${\text{AC}}_{50}$, ${\text{ACC}}_{\text{ER}}$) to estimate the daily exposure level yielding the corresponding plasma concentration in the exposed subject (human or animal). In our study, we used ${\text{ACC}}_{\text{ER}}$ as measurement of in vitro ER activity. ${\text{ACC}}_{\text{ER}}$ is one of the three critical chemical-specific values used in all three PK models, along with ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$. Of these, ${\text{ACC}}_{\text{ER}}$ values spanned the greatest numeric range in our study by $\sim 6$ orders of magnitude (${\text{ACC}}_{\text{ER}}$, $\sim 1\mathrm{E}–06$ to $10\mathrm{\mu }\mathrm{M}$; ${\mathrm{f}}_{\mathrm{u}}$ 0.005 to 1.000; ${\text{CL}}_{\text{int}}$, 0.16 to $4.78\mathrm{L}/\mathrm{h}$) and is the source of greatest potential variability in the PK models, as EAD varies proportionally with ${\text{ACC}}_{\text{ER}}$ (e.g., a twofold increase in ${\text{ACC}}_{\text{ER}}$ will result in a doubling of the EAD). This evidence suggests that of all variables influencing the PK models, in vitro potency values likely serve as the source of greatest potential uncertainty due to the wide range of possible numeric values and their proportional scaling with EADs. Model performance is therefore highly dependent on accurate measurements of chemical potency in vitro.

In vitro activity is typically reported with respect to the nominal concentration of chemical in the test medium, e.g., ${\text{ACC}}_{\text{ER}}$. However, chemical partitioning to various components of the assay systems (plastic, media proteins/lipids, head space, cells) can significantly affect the concentration of chemical acting on the (cellular) target of interest, thereby altering any measurement of chemical potency based on nominal concentration (Armitage et al. 2014; Fischer et al. 2017; Gülden et al. 2006). Partitioning is driven by the chemical’s physicochemical properties (e.g., ${\mathrm{K}}_{\text{OW}}$ and ${\mathrm{K}}_{\text{AW}}$) in combination with characteristics of the assay system (Armitage et al. 2014; Fischer et al. 2017; Kirman et al. 2015). Consequently, the nominal concentration in the medium does not always provide an adequate estimate of chemical potency when using in vitro activity to inform in vivo toxicity. Armitage et al. described a mass-balance model to calculate the mass distribution of a chemical in a user-defined in vitro test system at equilibrium (Armitage et al. 2014). This model relies on the assumption of instantaneous equilibrium and chemical partitioning in the in vitro test system after a single exposure and provides the cell/tissue enrichment factor (EF) metric that indicates the extent to which the nominal concentration reflects the exposure-relevant concentration in the cells at equilibrium (Armitage et al. 2014; Fischer et al. 2017). Applying the EF metric to adjust nominal ${\text{ACC}}_{\text{ER}}$ concentrations to reflect intracellular exposure resulted in a significant improvement in the predictive performance of all models, averaged across all chemicals in the validation set, which far exceeded any difference in performance attributable to model structure (Figures 2 and 3). Analysis of mean residual error (using MRV) demonstrated a strong bias toward underprediction in the unadjusted models (EADs well below observed uterotrophic LELs), which was negated in predictions from models using EF adjustment.

Adjusting for in Vivo Bioavailability

The one-compartment steady-state model (PPK) calculates chemical clearance via two routes: intrinsic (metabolic) clearance (${\text{CL}}_{\text{int}}$) and renal clearance by passive glomerular filtration. Both mechanisms are assumed to act only on unbound (freely available) chemical, (${\mathrm{f}}_{\mathrm{u}}$). However, the model does not incorporate the fraction of freely available chemical into calculations involving chemical potency, and the determination of chemical activity (i.e., EAD) is based on 100% bioavailability of chemical at a tissue level and molecular level. We therefore assessed the impact of applying a simple correction, using ${\mathrm{f}}_{\mathrm{u}}$ as a multiplicative factor to derive the unbound concentration at steady state. Adjusting EADs using ${\mathrm{f}}_{\mathrm{u}}$ improved the overall performance of the PPK model across all chemicals, resulting in RMSE values equivalent or better than those obtained using the EF (in vitro potency adjustment), and similarly reduced model bias (Figure 2A and Figure 3A). Theoretically, applying corrections to both in vitro (EF) and in vivo (${\mathrm{f}}_{\mathrm{u}}$) components of the model should result in the most accurate predictions. However, we found that applying both EF and ${\mathrm{f}}_{\mathrm{u}}$ adjustments simultaneously resulted in less-accurate predictions (higher RMSE) and a strong bias toward overprediction (EADs well above uterotrophic LELs). The cause of this overprediction is not entirely clear but is likely related to the error propagated with assumptions used in each approach (e.g., instantaneous equilibrium for EF, lack of on/off rate for ${\mathrm{f}}_{\mathrm{u}}$) when combined with the inherent error of the simple modeling approaches employed. We did not apply the free fraction correction to the other more complex models (HT3C, GP), as the linear relationships between dose and ${\mathrm{C}}_{\text{ss}}$ used for the PPK model may not be appropriate for models that do not yield steady-state predictions. Wetmore et al. (2015) also recommended adjusting for nonspecific binding in pharmacokinetic assays, including adjusting for fraction unbound in hepatocyte incubations (Wetmore et al. 2015) used to determine the intrinsic clearance rate in IVIVE models. However, as the chemicals included in this analysis were outside the domain of applicability ($\log \mathrm{P}>3$) (Kilford et al. 2008), the adjustment was not used in the present work.

Chemical-Specific Comparisons

Based on the above results, we limited our chemical-specific analyses to PK models with single adjustments applied (EF or ${\mathrm{f}}_{\mathrm{u}}$). For the majority of tested chemicals, all four models provided EAD values within $\sim 1\log$ of the reported range of LELs (minimum or maximum) from guideline uterotrophic studies (Figures 4 and 5). The RMSEs (vs. median LEL) for all single-adjustment models ranged from 1.02 ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$) to 1.14 (PPK_EF) for injection EADs and 1.23 (PPK_EF) to 1.62 ($\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$) for oral predictions (Figures 2A, 3A, and Excel Table S2). However, insufficient metabolic and clearance processes in the in vitro assays and failure to adequately account for these processes in the PK models resulted in EAD values that differed significantly from the uterotrophic LELs for a few chemicals. Proestrogens, such as mestranol, are known to require metabolic transformation to exert estrogenic effects (Schmider et al. 1997). Such requisite metabolism occurs in the rodent uterotrophic assay but not to an appreciable extent in the cell lines used for the ER model due to the poor metabolic capacity of the cell lines being used (relative to an in vivo rat liver), resulting in relatively high ${\text{ACC}}_{\text{ER}}$ values, and subsequent EAD calculations that overpredict the LELs observed in injection uterotrophic studies by 1–2 orders of magnitude (Figure 4). Likewise, 17-methyltesterone is readily aromatized in the liver to the potent estrogen, $17\mathrm{alpha}\text{-methylestradiol}$ (Hornung et al. 2004; Pawlowski et al. 2004), and therefore exhibits greatly reduced estrogenic activity in systems that are metabolically inert. It is worth noting that all single-adjustment model EADs for the known proestrogen, methoxychlor (Hu and Kupfer 2002), were within 1 log of the observed LEL values for both oral and injection studies, indicating that the in vitro assays were able to sufficiently characterize this chemical’s estrogenic properties.

Conversely, chemicals that are rapidly cleared or inactivated when administered orally, such as BPA or 17-beta-estradiol, are highly potent in the ER model but show significantly less activity in oral uterotrophic studies, resulting in EADs that are substantially ($>1\log$) below the observed oral LEL (Figure 5). Such underpredictions are consistent with the poor oral bioavailability of both chemicals (O’Connell 1995; Thayer et al. 2015), which would account for high potency activity only in the in vitro system that provides direct exposure to cells. Such underprediction could be addressed by inclusion or improved parameterization of processes, such as glucuronidation, that are important in gastrointestinal metabolism of many xenobiotics in rodent models (Kuester and Sipes 2007; Partosch et al. 2013). However, all models did produce EADs within the observed oral and injection uterotrophic LELs for genistein, which is metabolically cleared in a manner similar to that of BPA (Pritchett et al. 2008; Shelnutt et al. 2002). Surprisingly, route-agnostic EADs from the simple PPK model had an overall lower RMSE than the GP and HT3C models with oral dosing modules (i.e., simulating gut absorption) (Figure 3A). The route-specific predictions in this analysis should be viewed with caution given the small number of chemicals involved ($n=8$), but the results do call into question the advantage of (generalized) complex model structures and underscore the need for model validation using route-appropriate in vivo exposure and response data.

EADs for All ER Pathway-Active Chemicals

The PPK_EF and $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ models were used to calculate EADs for all 266 chemicals with activity in the ER model ($\text{AUC}>0.01$), using in silico approaches to estimate key model parameters (${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$) for the majority of chemicals (Excel Table S3). The two models produce EADs that were consistently $\sim 1.4\log$ higher than the unadjusted PPK model (Figure 6), and were correlated with an ${\mathrm{r}}^2=0.64$ (PPK_EF vs. $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$). There were insufficient in vivo data to adequately assess the difference in predictive performance between the two models, but the dynamic range of the $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ model may be limited by the analytical limits of the ${\mathrm{f}}_{\mathrm{u}}$ assay (typically truncated at 0.5%), as seen in the flattening of EADs values around $\sim 1000\mathrm{mg}/\mathrm{kg}/\text{day}$ in Figure 6. However, there are at least two advantages to using the $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ model. First, this model requires no additional information apart from the two values used to parameterize the model, ${\mathrm{f}}_{\mathrm{u}}$ and ${\text{CL}}_{\text{int}}$, which can both be estimated with QSAR/QPPR models. Calculation of EF requires the use of an additional (mass-balance) model, which itself requires the user to input values describing the specific in vitro assay system, and therefore adds a layer of complexity. The other advantage of the $\text{PPK}\_{\mathrm{f}}_{\mathrm{u}}$ model is the ability to apply it to data from cell-free assays (e.g., receptor–ligand binding). The use of both models to develop a consensus prediction or range is likely the best option, if available.

Conclusions

We applied three PK models with varying complexities to extrapolate in vitro to in vivo dosimetry for a group of 29 ER agonists, using data from validated in vitro (ToxCast™ ER model) and in vivo (uterotrophic) methods. We found little difference in model performance based on complexity or route-specific modifications. Simple adjustments, applied to account for in vitro intracellular exposure (EF) across all models or chemical bioavailability (${\mathrm{f}}_{\mathrm{u}}$) in the steady-state model, resulted in significant improvements in the predictive performance of all models. The simplest model (PPK), with application of either EF or ${\mathrm{f}}_{\mathrm{u}}$ adjustments, had the best overall performance for predicting both oral (EF) and injection (${\mathrm{f}}_{\mathrm{u}}$) LELs from guideline uterotrophic studies. Furthermore, this open-source model can be parameterized entirely with the use of open-source in silico tools to estimate ${\mathrm{f}}_{\mathrm{u}}$ and EF, thereby greatly expanding the accessibility and potential utility of IVIVE approaches for use in chemical risk assessment.