Few-Shot and Zero-Shot Multi-Label Learning for Structured Label Spaces

Abstract

Large multi-label datasets contain labels that occur thousands of times (frequent group), those that occur only a few times (few-shot group), and labels that never appear in the training dataset (zero-shot group). Multi-label few- and zero-shot label prediction is mostly unexplored on datasets with large label spaces, especially for text classification. In this paper, we perform a fine-grained evaluation to understand how state-of-the-art methods perform on infrequent labels. Furthermore, we develop few- and zero-shot methods for multi-label text classification when there is a known structure over the label space, and evaluate them on two publicly available medical text datasets: MIMIC II and MIMIC III. For few-shot labels we achieve improvements of 6.2% and 4.8% in R@10 for MIMIC II and MIMIC III, respectively, over prior efforts; the corresponding R@10 improvements for zero-shot labels are 17.3% and 19%.

1. Introduction

Unlike in binary or multi-class problems, for multi-label classification a model assigns a set of labels to each input instance (Tsoumakas et al., 2010). Large-scale multi-label text classification problems can be found in several domains. For example, Wikipedia articles are annotated with labels used to organize documents and facilitate search (Partalas et al., 2015). Biomedical articles indexed by the PubMed search engine are manually annotated with medical subject headings (Tsatsaronis et al., 2012). In healthcare facilities, medical records are assigned a set of standardized codes for billing purposes (NCHS, 1978). Automatically annotating tweets with hashtags, while the labels are not fixed, can also be represented as a large-scale multi-label classification problem (Weston et al., 2014).

There are two major difficulties when developing machine learning methods for large-scale multi-label text classification problems. First, the documents may be long, sometimes containing more than a thousand words (Mullenbach et al., 2018). Finding the relevant information in a large document for a specific label results in needle in a haystack situation. Second, data sparsity is a common problem; as the total number of labels grows, a few labels may occur frequently, but most labels will occur infrequently. Rubin et al. (2012) refer to datasets that have long-tail frequency distributions as “power-law datasets”. Methods that predict infrequent labels fall under the paradigm of few-shot classification which refers to supervised methods in which only a few examples, typically between 1 and 5, are available in the training dataset for each label. With predefined label spaces, some labels may never appear in the training dataset. Zero-shot problems extend the idea of few-shot classification by assuming no training data is available for the labels we wish to predict at test time. In this paper, we explore both of these issues, long documents and power-law datasets, with an emphasis on analyzing the few- and zero-shot aspects of large-scale multi-label problems.

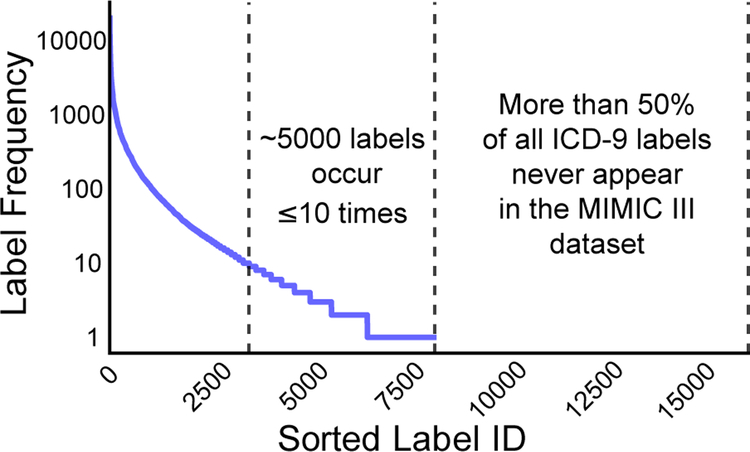
In Figure 1, we plot the label frequency distribution of diagnosis and procedure labels for the entire MIMIC III (Johnson et al., 2016) dataset. A few labels occur more than 10,000 times, around 5,000 labels occur between 1 and 10 times, and of the 17,000 diagnosis and procedure labels, more than 50% never occur. There are a few reasons a label may never occur in the training dataset. In healthcare, sevearl disorders are rare; therefore corresponding labels may not have been observed yet in a particular clinic. Sometimes new labels may be introduced as the field evolves leading to an emerging label problem. This is intuitive for applications such as hashtag prediction on Twitter. For example, last year it would not have made sense to annotate tweets with the hashtag #EMNLP2018. Yet, as this year’s conference approaches, labeling tweets with the #EMNLP2018 will help users find relevant information.

Figure 1:

This plot shows the label frequency distribution of ICD-9 codes in MIMIC III.

Infrequent labels may not contribute heavily to the overall accuracy of a multi-label model, but in some cases, correct prediction of such labels is crucial but not straightforward. For example, in assigning diagnosis labels to EMRs, it is important that trained human coders are both accurate and thorough. Errors may cause unfair financial burden on the patient. Coders may have an easier time assigning frequent labels to EMRs because they are encountered more often. Also, frequent labels are generally easier to predict using machine-learning based methods. However, infrequent or obscure labels will be easily confused or missed causing billing mistakes and/or causing the coders to spend more time annotating each record. Thus, we believe methods that handle infrequent and unseen labels in the multi-label setting are important.

Current evaluation methods for large-scale multi-label classification mostly ignore infrequent and unseen labels. Popular evaluation measures focus on metrics such as micro-F1, recall at k (R@k), precision at k (P@k), and macro-F1. As it is well-known that micro-F1 gives more weight to frequent labels, papers on this topic also report macro-F1, the average of label-wise F1 scores, which equally weights all labels. Unfortunately, macro-F1 scores are generally low and the corresponding performance differences between methods are small. Moreover, it is possible to improve macro-F1 by only improving a model’s performance on frequent labels, further confounding its interpretation. Hence we posit that macro-F1 is not enough to compare large-scale multi-label learning methods on infrequent labels and it does not directly evaluate zero-shot labels. Here, we take a step back and ask: can the model predict the correct few-shot (zero-shot) labels from the set of all few-shot (zero-shot) labels? To address this, we test our approach by adapting the generalized zero-shot classification evaluation methodology by Xian et al. (2017) to the multi-label setting.

In this paper, we propose and evaluate a neural architecture suitable for handling few- and zero-shot labels in the multi-label setting where the output label space satisfies two constraints: (1). the labels are connected forming a DAG and (2). each label has a brief natural language descriptor. These assumptions hold in several multi-label scenarios including assigning diagnoses/procedures to EMRs, indexing biomedical articles with medical subject headings, and patent classification. Taking advantage of this prior knowledge on labels is vital for zero-shot prediction. Specifically, using the EMR coding use-case, we make the following contributions:

1. We overcome issues arising from processing long documents by introducing a new neural architecture that expands on recent attention-based CNNs (ACNNs (Mullenbach et al., 2018)). Our model learns to predict few- and zero-shot labels by matching discharge summaries in EMRs to feature vectors for each label obtained by exploiting structured label spaces with graph CNNs (GCNNs (Kipf and Welling, 2017)).

2. We provide a fine-grained evaluation of state-of-the-art EMR coding methods for frequent, few-shot, and zero-shot labels. By evaluating power-law datasets using an extended generalized zero-shot methodology that also includes few-shot labels, we present a nuanced analysis of model performance on infrequent labels.

2. Related Work

Large-Scale Text Classification.

Linear methods have been successfully applied to large-scale problems (Tang et al., 2009; Papanikolaou et al., 2015; Rios and Kavuluru, 2015). For traditional micro- and macro-F1 measures, Tang et al. (2009) show that linear methods suffer using naive thresholding strategies because infrequent labels generally need a smaller threshold. Generative models have also been promising for datasets with many labels (Rubin et al., 2012). Intuitively, by using a prior distribution over the label space, infrequent labels can be modeled better. Finally, large-scale classification is also pursued as “extreme classification” (Yu et al., 2014; Bhatia et al., 2015) where the focus is on ranking measures that ignore infrequent labels. Neural networks (NNs) perform well for many small-scale classification tasks (Kim, 2014; Kalchbrenner et al., 2014). Recently, researchers have been exploring NN methods for large-scale problems. Yang et al. (2016) develop a hierarchical attentive NN for datasets with over a million documents, but their datasets contain few labels. Nam et al. (2014) show that feed-forward NNs can be successfully applied to large-scale problems through the use of a multi-label binary cross-entropy loss function. Vani et al. (2017) introduce a grounded recurrent neural network (RNN) that iteratively updates its predictions as it processes a document word-by-word. Baumel et al. (2018) experiment with both CNNs and RNNs for medical coding. Finally, Mullenbach et al. (2018) expand on prior ACNNs (Yang et al., 2016; Allamanis et al., 2016) to develop a label-wise attention framework where the most informative ngrams are extracted for each label in the dataset. Our attention mechanism extends their work to the zero-shot setting.

Few-Shot and Zero-Shot Learning.

While neural networks are generally considered to need large datasets, they have been shown to work well on few-shot classification tasks. To handle infrequent labels, most NN methods use a k-NN-like approach. Siamese NNs (Koch et al., 2015) learn a nonlinear distance metric using a pairwise loss function. Matching networks (Vinyals et al., 2016) introduce an instance-level attention method to find relevant neighbors. Prototypical Networks (Snell et al., 2017) average all instances in each class to form “prototype label vectors” and train using a traditional cross-entropy loss. In our prior work (Rios and Kavuluru, 2018), we combine matching networks with a sophisticated thresholding strategy. However, in Rios and Kavuluru (2018) we did not explore the few- and zero-shot settings.

Zero-shot learning has not been widely explored in the large-scale multi-label classification scenario. Like neural few-shot methods, neural zero-shot methods use a matching framework. Instead of matching input instances with other instances, they are matched to predefined label vectors. For example, the Attributes and Animals Dataset (Xian et al., 2017) contains images of animals and the label vectors consist of features describing the types of animals (e.g., stripes: yes). When feature vectors for labels are not available, the average of the pretrained word embeddings of the class names have been used. The attribute label embedding method (Akata et al., 2016) uses a pairwise ranking loss to match zero-shot label vectors to instances. Romera-Paredes and Torr (2015) introduced the “embarrassingly simple zero-shot learning” (ESZSL) method which is trained using a mean squared error loss. A few zero-shot methods do not translate well to multi-label problems. CONSE (Mikolov et al., 2013) averages the embeddings for the top predicted supervised label vectors to match to zero-shot label vectors. CONSE assumes that both supervised and zero-shot labels cannot be assigned to the same instance. In this paper, we expand on the generalized zero-shot evaluation methodology introduced by Xian et al. (2017) to large-scale multi-label classification. Finally, it is important to note that zero-shot classification has been previously studied in the multi-label setting (Mensink et al., 2014). However, they focus on image classification and use datasets with around 300 labels.

Graph Convolutional Neural Networks.

GCNNs generalize CNNs beyond 2d and 1d spaces. Defferrard et al. (2016) developed spectral methods to perform efficient graph convolutions. Kipf and Welling (2017) assume a graph structure is known over input instances and apply GCNNs for semi-supervised learning. GCNNs are applied to relational data (e.g., link prediction) by Schlichtkrull et al. (2018). GCNNs have also had success in other NLP tasks such as semantic role labeling (Marcheggiani and Titov, 2017), dependency parsing (Strubell and McCallum, 2017), and machine translation (Bastings et al., 2017).

There are three GCNN papers that share similarities with our work. (i) Peng et al. (2018) use a GCNN on a word co-occurrence graph for large-scale text classification where the GCNN operates on documents/words, while our GCNN operates on the labels. (ii) Chen et al. (2017) use GCNNs on structured label spaces. However, their experiments focus on smaller label spaces and do not handle/assess zero-shot and few-shot labels. Also, their experiments for text classification do not incorporate attention and simply use an average of word vectors to represent each document. (iii) Wang et al. (2018) propose a zero-shot GCNN image classification method for structured multi-class problems. We believe their method may transfer to the multi-label text classification setting but exact modifications to affect that are not clear (i.e., their semi-supervised approach may not be directly applicable). Likewise, porting to text is nontrivial for long documents.

3. Method

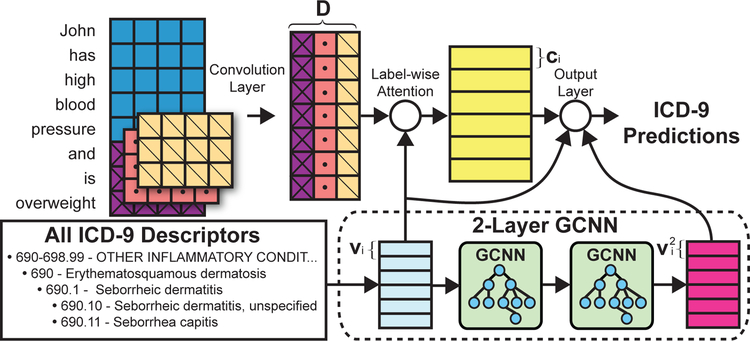
Figure 2 shows the overall schematic of our architecture. Intuitively, we incorporate four main components. First, we assume we have the full English descriptor/gloss for each label we want to predict. We form a vector representation for each label by averaging the word embeddings for each word in its descriptor. Second, the label vectors formed from the descriptor are used as attention vectors (label-wise attention) to find the most informative ngrams in the document for each label. For each label, this will produce a separate vector representation of the input document. Third, the label vectors are passed through a two layer GCNN to incorporate hierarchical information about the label space. Finally, the vectors returned from the GCNN are matched to the document vectors to generate predictions.

Figure 2:

This figure provides a visual overview of our method. Intuitively, our method has two main components. The first component is a CNN that operates operates on the EMRs. The other component is a 2-layer GCNN which creates the label-specific attention vectors and label-vectors used for ranking using ICD-9 descriptions as input.

Convolutional Neural Network.

Contrary to prior CNN methods for text (Kim, 2014), instead of using a max-over-time pooling layer, we learn to find relevant ngrams in a document for each label via label-wise attention (Mullenbach et al., 2018). The CNN will return a document feature matrix D ∊ ℝ ^(n−s+1)×u where each column of D is a feature map, u is the total number of convolution filters, n is the number of words in the document, and s is the width of convolution filters.

Label Vectors.

To be able to predict labels that were not in the training dataset, we avoid learning label specific parameters. We use the label descriptors to generate a feature vector for each label. First, to preprocess each descriptor, we lower-case all words and remove stop-words. Next, each label vector is formed by averaging the remaining words in the descriptor

$$v_i=\frac{1}{\left|N\right|}\sum _{j\in N}{w}_j,i=1,\dots ,L,$$ (1)

where v_i ∊ ℝ^d,L is the number of labels, and N is the index set of the words in the descriptor. Prior zero-shot work has focused on projecting input instances into the same semantic space as the label vectors (Sandouk and Chen, 2016). For zero-shot image classification, this is a non-trivial task. Because we work with textual data, we simply share the word embeddings between the convolutional layer and the label vector creation step to form v_i.

Label-Wise Attention.

Similar to the work by Mullenbach et al. (2018), we employ label-wise attention to avoid the needle in the haystack situation encountered with long documents. The issue with simply using a single attention vector or using max-pooling is that we assume a single vector can capture everything required to predict every label. For example, with a single attention, we would only look at one spot in the document and assume that spot contains the relevant information needed to predict all labels. In the multi-class setting, this assumption is plausible. However, for large multi-label problems, the relevant information for each label may be scattered throughout the document – the problem is worse when the documents are very long. Using label-wise attention, our model can focus on different sections. We also need to find relevant information for zero-shot classes. So we use the label vectors v_i rather than learning label specific attention parameters. First, we pass the document feature matrix D through a simple feed-forward neural network

$$D^2=\text{tanh}\left(D{W}_b+b_b\right)$$

where W_b ∊ ℝ^u×d and b_b ∊ ℝ^d. This mapping is important because the dimensionality of the ngram vectors (rows) in D depends on u, the number of scores we generate for each ngram. Given D², we generate the label-wise attention vector

$$a_i=\mathrm{softmax}\left(D^2{v}_i\right),i=1,\dots ,L,$$ (2)

where a_i ∊ ℝ^n−s+1 measures how informative each ngram is for the i-th label. Finally, we use D, and generate L label-specific document vector representations

$$c_i=a_i^{T}D,i=1,\dots ,L,$$

such that c_i ∊ ℝ^u. Intuitively, c_i is the weighted average of the rows in D forming a vector representation of the document for the i-th label.

GCNN Output Layer.

Traditionally, the output layer of a CNN would learn label specific parameters optimized via a cross-entropy loss. Instead, our method attempts to match documents to their corresponding label vectors. In essence, this becomes a retrieval problem. Before using each document representation c_i to score its corresponding label, we take advantage of the structured knowledge we have over our label space using a 2-layer GCNN. For both the MIMIC II and MIMIC III datasets, this information is hierarchical. A snippet of the hierarchy can be found in Figure 2.

Starting with the label vectors v_i, we combine the label vectors of the children and parents for the i-th label to form

$$v_i^1=f\left(W^1{v}_i+\sum _{j\in {\mathcal{N}}_p}\frac{W_p^1{v}_j}{\left|{\mathcal{N}}_p\right|}+\sum _{j\in {\mathcal{N}}_c}\frac{W_c^1{v}_j}{\left|{\mathcal{N}}_c\right|}+b_g^1\right)$$

where $W^1\in {ℝ}^{q\times d}$, $W_p^1\in {ℝ}^{q\times d}$, $W_c^1\in {ℝ}^{q\times d}$, $b_g^1\in {ℝ}^q$, f is the rectified linear unit (Nair and Hinton, 2010) function, and N_c (N_p) is the index set of the i-th label’s children (parents). We use different parameters to distinguish each edge type. In this paper, given we only deal with hierarchies, the edge types include edges from parents, from children, and self edges. This can be adapted to arbitrary DAGs, where parent edges represent all incoming edges and the child edges represent all outgoing edges for each node.

The second layer follows the same formulation as the first layer with

$$v_i^2=f\left(W^2{v}_i^1+\sum _{j\in {\mathcal{N}}_p}\frac{W_p^2{v}_j^1}{\left|{\mathcal{N}}_p\right|}+\sum _{j\in {\mathcal{N}}_c}\frac{W_c^2{v}_j^1}{\left|{\mathcal{N}}_c\right|}+b_g^2\right)$$

where W² ∊ ℝ^q×q, $W_p^2\in {ℝ}^{q\times q}$, $W_c^2\in {ℝ}^{q\times q}$, and $b_g^2\in {ℝ}^q$. Next, we concatenate both the averaged description vector (from equation (1)) with the GCNN label vector to form

$$v_i^3=v_i\Vert v_i^2,$$

where $v_i^3\in {ℝ}^{d+q}$. Now, to compare the final label vector $V_i^3$ with its document vector c_i, we transform the document vector into

$$e_i=ReLU\left(W_o{c}_i+b_o\right),i=1,\dots ,L,$$

where W₀ ∊ ℝ^(q+d)×u and b_o ∊ ℝ^q+d. This transformation is required to match the dimension to that of $V_i^3$. Finally, the prediction for each label i is generated via

$${\widehat{y}}_i=sigmoid\left(e_i^T{v}_i^3\right),i=1,\dots ,L.$$

During experiments, we found that using either the output layer GCNN or a separate GCNN for the attention vectors (equation (2)) did not result in an improvement and severely slowed convergence.

Training.

We train our model using a multi-label binary cross-entropy loss (Nam et al., 2014)

$$\mathcal{L}=\sum _{i=1}^L\left[-y_i\log \left({\widehat{y}}_i\right)-\left(1-y_i\right)\log \left(1-{\widehat{y}}_i\right)\right],$$

where y_i ∊ {0,1} is the ground truth for the i-th label and ${\widehat{y}}_i$ is our sigmoid score for the i-th label.

4. Experiments

In this paper, we use two medical datasets for evaluation purposes: MIMIC II (Jouhet et al., 2012) and MIMIC III (Johnson et al., 2016). Both datasets contain discharge summaries annotated with a set of ICD-9 diagnosis and procedure labels. Discharge summaries are textual documents consisting of, but not limited to, physician descriptions of procedures performed, diagnoses made, the patient’s medical history, and discharge instructions. Following a generalized zero-shot learning evaluation methodology (Xian et al., 2017), we split the ICD-9 labels into three groups based on frequencies in the training dataset: The frequent group S that contains all labels that occur > 5 times, the few-shot group F that contains labels that occur between 1 and 5 times, and the zero-shot group Z of labels that never occur in the training dataset, but occur in the test/dev sets. The groups are only used for evaluation. That is, during training, systems are optimized over all labels simultaneously. Instances that do not contain fewor zero-shot classes are removed from their respective groups during evaluation. This grouping is important to assess how each model performs across labels grouped by label frequency. Our evaluation methodology differs from that of Xian et al. (2017) in two ways. First, because each instance is labeled with multiple labels, the same instance can appear in all groups — S, F, and Z. Second, instead of top-1 accuracy or HIT@k evaluation measures, we focus on R@k to handle multiple labels. At a high level, we want to examine whether a model can distinguish the correct few-shot (zero-shot) labels from the set of all few-shot (zero-shot) labels. Therefore, the R@k measures in Tables 2 and 3, and Figure 3 are computed relative to each group.

Table 2:

MIMIC II results across frequent (S), few-shot (F), and zero-shot (Z) groups. We mark prior methods for MIMIC datasets that we implemented with a *.

	S		F		Z		Harmonic Average
	R@5	R@10	R@5	R@10	R@5	R@10	R@5	R@10
Random	0.000	0.000	0.000	0.000	0.011	0.032	0.000	0.000
Logistic (Vani et al., 2017) *	0.137	0.247	0.001	0.003	-	-	-	-
CNN (Baumeletal.,2018)*	0.138	0.250	0.050	0.082	-	-	-	-
ACNN (Mullenbach et al., 2018) *	0.138	0.255	0.046	0.081	-	-	-	-
Match-CNN (Rios and Kavuluru, 2018)	0.137	0.247	0.031	0.042	-	-	-	-
ESZSL + W2V	0.074	0.119	0.008	0.017	0.080	0.172	0.020	0.041
ESZSL + W2V 2	0.050	0.086	0.025	0.044	0.103	0.189	0.043	0.076
ESZSL + GRALS	0.135	0.238	0.081	0.123	0.085	0.136	0.095	0.152
ZACNN	0.135	0.245	0.103	0.149	0.147	0.221	0.128	0.205
ZAGCNN	0.135	0.247	0.130	0.185	0.269	0.362	0.160	0.246

Table 3:

MIMIC III results across frequent (S), few-shot (F), and zero-shot (Z) groups. We mark prior methods for MIMIC datasets that we implemented with a *.

	S		F		Z		Harmonic Average
	R@5	R@10	R@5	R@10	R@5	R@10	R@5	R@10
Random	0.000	0.000	0.000	0.000	0.038	0.052	0.000	0.000
Logistic (Vani et al., 2017) *	0.273	0.427	0.014	0.014	-	-	-	-
CNN (Baumeletal., 2018)*	0.269	0.413	0.058	0.085	-	-	-	-
ACNN (Mullenbach et al., 2018) *	0.288	0.458	0.130	0.168	-	-	-	-
Match-CNN (Rios and Kavuluru, 2018)	0.278	0.426	0.049	0.060	-	-	-	-
ESZSL + W2V	0.135	0.191	0.031	0.051	0.157	0.257	0.065	0.105
ESZSL + W2V 2	0.127	0.189	0.031	0.048	0.148	0.305	0.063	0.102
ESZSL + GRALS	0.256	0.393	0.033	0.060	0.076	0.138	0.064	0.114
ZACNN	0.278	0.435	0.152	0.195	0.364	0.442	0.232	0.310
ZAGCNN	0.283	0.445	0.166	0.216	0.428	0.495	0.252	0.337

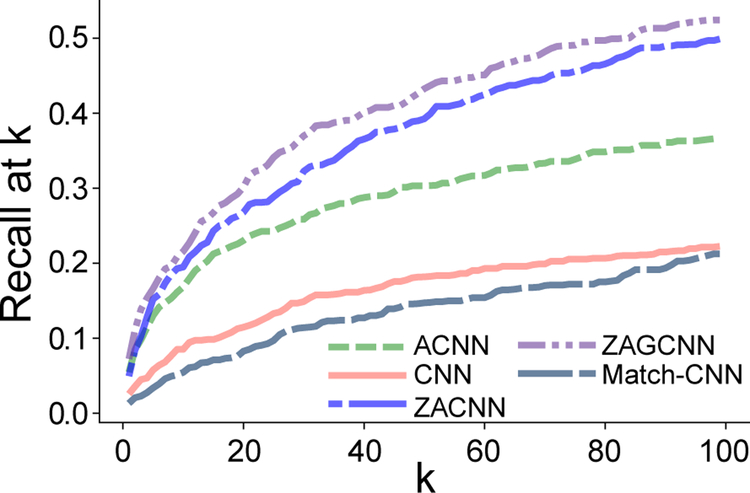
Figure 3:

This graph plots the MIMIC III R@k for few-shot (F) labels at different k values.

Evaluation Measures.

The overall statistics for these two datasets are reported in Table 1. For reproducibility purposes, we use the same training/test splits of the MIMIC II as Perotte et al. (2013). Following the procedures in Perotte et al. (2013) and Vani et al. (2017), for each diagnosis and procedure label assigned to each medical report, we add its parents using the ICD-9 hierarchy. Each report in MIMIC II is annotated with nearly 37 labels on average using hierarchical label expansion.

Table 1:

Dataset statistics for MIMIC II and MIMIC III.

Dataset	# Train	# Test	# Labels
			S	F	Z
MIMIC II	18822	1711	3228	3459	355
MIMIC III	37016	1356	4403	4349	178

MIMIC III does not contain a standardized training/test split. Therefore, we create our own split that ensures the same patient does not appear in both the training and test datasets. Unlike the MIMIC II dataset, we do not augment the labels using the ICD-9 hierarchy. The ICD-9 hierarchy has three main levels. For MIMIC III, level 0 labels make up about 5% of all occurrences, level 1 labels make up about 62%, and level 2 (leaf level) labels make up about 33%. Also, each MIMIC III instance contains16 ICD-9 labels on average.

ICD-9 Structure and Descriptors.

The International Classification of Diseases (ICD) contains alphanumeric diagnosis and procedure codes that are used by hospitals to standardize their billing practices. In the following experiments, we use the 9th edition of the ICD¹. Each ICD-9 identifier contains between 3 to 5 alphanumeric characters of the form abc.xy. The alphanumeric structure defines a simple hierarchy over all ICD-9 codes. For example, “systolic heart failure” (428.2) and “diastolic heart failure” (428.3) are both children of the “heart failure” code 428. Furthermore, sequential codes are grouped together. For instance, numeric codes in the range 390–459 contain “Diseases of the Circulatory System”. Furthermore, each code, including groups of codes (390–459), contain short descriptors, where the average descriptor length contains seven words². In this work, we use both the group descriptors and individual descriptors as input to the GCNN. At test time, we ignore the group codes.

Implementation Details.

For the CNN component of our model, we use 300 convolution filters with a filter size of 10. We use 300 dimensional word embeddings pretrained on PubMed biomedical article titles and abstracts. To avoid overfitting, we use dropout directly after the embedding layer with a rate of 0.2. For training we use the ADAM (Kingma and Ba, 2015) optimizer with a minibatch size of 8 and a learning rate of 0.001. q, the GCNN hidden layer size, is set to 300. The code for our method is available at https://github.com/bionlproc/multi-label-zero-shot.

Thresholding has a large influence on traditional multi-label evaluation measures such as micro-F1 and macro-F1 (Tang et al., 2009). Hence, we report both recall at k (R@k) and precision at k (P@k) which do not require a specific threshold. R@k is preferred for few- and zero-shot labels, because P@k quickly goes to zero as k increases and gets bigger than the number of group specific labels assigned to each instance. Furthermore, for medical coding, these models are typically used as a recommendation engine to help coders. Unless a label appears at the top of the ranking, the annotator will not see it. Thus, ranking metrics better measure the usefulness of our systems.

Baseline Methods.

For the frequent and few-shot labels we compare to state-of-the-art methods on the MIMIC II and MIMIC III datasets including ACNN (Mullenbach et al., 2018) and a CNN method introduced in Baumel et al. (2018). We also compare with the L1 regularized logistic regression model used in Vani et al. (2017). Finally, we compare against our prior EMR coding method, Match-CNN (Rios and Kavuluru, 2018).

For zero-shot learning, we compare our results with ESZSL (Romera-Paredes and Torr, 2015). To use ESZSL, we must specify feature vectors for each label. For zero-shot methods, the label vectors used are crucial regardless of the learning method used. Therefore, we evaluate ESZSL with three different sets of label vectors. We average 200 dimensional ICD-9 descriptor word embeddings generated by Pyysalo et al. (2013) which are pretrained on PubMed, Wikipedia, and PubMed Central (ESZSL + W2V). We lowercased descriptors and removed stop-words. We also compare with label vectors derived from our own 300 dimensional embeddings (ESZSL + W2V 2) pre-trained on PubMed indexed titles and abstracts. Finally, we generate label vectors using the ICD-9 hierarchy. Specifically, let Y ∊ ℝ^N×L be the document label matrix where N is the total number of documents. We factorize Y into two matrices U ∊ ℝ^N×300 and V ∊ ℝ^300×L using graph regularized alternating least squares (GRALS) (Rao et al., 2015). Finally, we also report a baseline using a random ordering on labels, which is important for zero-shot labels — because the total number of such labels is small, the chance that the correct label is in the top k is higher compared to few-shot and frequent labels.

We compare two variants of our method: zero-shot attentive GCNN (ZAGCNN), which is the full method described in Section 3 and a simpler variant without the GCNN layers, zero-shot attentive CNN (ZACNN)³.

Results.

Table 2 shows the results for MIMIC II. Because the label set for each medical record is augmented using the ICD-9 hierarchy, we expect methods that use the hierarchy to have an advantage. Table 2 results do not rely on thresholding because we evaluate using the relative ranking of groups with similar frequencies. ACNN performs best on frequent labels. For few-shot labels, ZAGCNN outperforms ACNN by over 10% in R@10 and by 8% in R@5; compared to these R@k gains for few-shot labels, our loss on frequent labels is minimal (< 1%). We find that the word embedding derived label vectors work best for ESZSL on zero-shot labels. However, this setup is outperformed by GRALS derived label vectors on the frequent and few-shot labels. On zero-shot labels, ZAGCNN outperforms the best ESZSL variant by over 16% for both R@5 and R@10. Also, we find that the GCNN layers help both few- and zero-shot labels. Finally, similar to the setup in Xian et al. (2017), we also compute the harmonic average across all R@5 and all R@10 scores. The metric is only computed for methods that can predict zero-shot classes. We find that ZAGCNN outperforms ZACNN by 4% for R@10.

We report the MIMIC III results in Table 3. Unlike for MIMIC II, the label sets were not expanded using the ICD-9 hierarchy. Yet, we find substantial improvements on both few- and zero-shot labels using a GCNN. ZAGCNN outperforms ACNN by almost 5% and ZACNN by 1% in R@10 on few-shot classes. However, ACNN still outperforms all other methods on frequent labels, but by only 0.3% when compared with ZAGCNN. For zero-shot labels, ZAGCNN outperforms ZACNN by over 5% and outperforms the best ESZSL method by nearly 20% in R@10. We find that ZACNN slightly underperforms ZAGCNN on frequent labels with more prominent differences showing up for infrequent labels.

In Table 4 we compare the P@10, R@10, and macro-F1 measures across all three groups (the union of S, F, and Z) on the MIMIC III dataset. We emphasize that the evaluation metrics are calculated over all labels and are not averages of the metrics computed independently for each group. We find that R@10 is nearly equivalent to the R@10 on the frequent group in Table 3. Furthermore, we find that ACNN outperforms ZAGCNN in P@10 by almost 4%. To compare all methods with respect to macro-F1, we simply threshold each label at 0.5. Both R@k and P@k give more weight to frequent labels, thus it is expected that ACNN outperforms ZAGCNN for frequent labels. However, we also find that ACNN outperforms our methods with respect to Macro-F1.

Table 4:

P@k, R@k, and macro-F1 results over all labels (the union of S, F, and Z).

	P@10	R@10	Macro-F1
CNN	0.562	0.407	0.028
ACNN	0.624	0.452	0.068
Match-CNN	0.561	0.415	0.033
ZACNN	0.577	0.429	0.037
ZAGCNN	0.587	0.439	0.038

Given macro-F1 equally weights all labels, does the higher macro score mean ACNN performs better across infrequent labels? In Figure 3, we plot the MIMIC III R@k for the neural methods with k ranging from 1 to 100. We find as k increases, the differences between ZAGCNN and ACNN become more evident. Given Figure 3 and the scores in Table 3, it is clear that ACNN does not perform better than ZAGCNN with respect to fewand zero-shot labels. The improvement in macro-F1 for ACNN is because it performs better on frequent labels. In general, infrequent labels will have scores much less than 0.5. If we rank all labels (S ⋃ F ⋃ Z), we find that few-shot labels only occur among the top 16 ranked labels (average number of labels for MIMIC III) for 6% of the test documents that contain them. This suggests that many frequent irrelevant labels have higher scores than the correct few-shot label.

Why do the rankings among few- and zero-shot labels matter if they are rarely ranked above irrelevant frequent labels? If we can predict which instances contain infrequent labels (novelty detection), then we can help human coders by providing them with multiple recommendation lists — a list of frequent labels and a list of infrequent/zero-shot labels. Also, while we would ideally want a single method that performs best for both frequent and infrequent labels, currently we find that there is a trade-off between them. Hence it may be reasonable to use different methods in combination depending on label frequency.

5. Conclusion and Future Work

In this paper, we performed a fine-grained evaluation of few- and zero-shot label learning in the large-scale multi-label setting. We also introduced a neural architecture that incorporates label descriptors and the hierarchical structure of the label spaces for few- and zero-shot prediction. For these infrequent labels, previous evaluation methodologies do not provide a clear picture about what works. By evaluating power-law datasets using a generalized zero-shot learning methodology, we provide a staring point toward a better understanding. Our proposed architecture also provides large improvements on infrequent labels over state-ofthe-art automatic medical coding methods.

We believe there are two important avenues for future work.

1. For medical coding, a wealth of unstructured domain expertise is available in biomedical research articles indexed by PubMed. These articles are annotated with medical subject headings (MeSH terms), which are organized in a hierarchy. Relationships between MeSH terms and ICD-9 codes are available in Unified Medical Language System (UMLS (Bodenreider, 2004)). If we can take advantage of all this structured and unstructured information via methods such as transfer learning or multi-task learning, then we may be able to predict infrequent labels better.

2. For our method to be useful for human coders, it is important to develop an accurate novelty detector. We plan to study methods for determining if an instance contains an infrequent label and if it does, how many infrequent labels it should be annotated with. In essence, this is an extension of the Meta-Labeler (Tang et al., 2009) methodology and open classification (Shu et al., 2017). If we can predict if an instance contains infrequent labels, then we can recommend few- and zero-shot labels only when necessary.