Production of acoustic radiation force using ultrasound: methods and applications

Abstract

Introduction:

Acoustic radiation force (ARF) is used in many biomedical applications. The transfer of momentum in acoustic waves can be used in a multitude of ways to perturb tissue and manipulate cells.

Areas Covered:

This review will briefly cover the acoustic theory related to ARF, particularly that related to application in tissues. The use of ARF in measurement of mechanical properties will be treated in detail with emphasis on the spatial and temporal modulation of the ARF. Additional topics covered will be the manipulation of particles with ARF, correction of phase aberration with ARF, modulation of cellular behavior with ARF, and bioeffects related to ARF use.

Expert Commentary:

The use of ARF can be tailored to specific applications for measurements of mechanical properties or correction of focusing for ultrasound beams. Additionally, noncontact manipulation of particles and cells with ARF enables a wide array of applications for tissue engineering and biosensing.

1. Introduction

Many biomedical applications have been developed over the past two decades that utilize acoustic radiation force. Before these methods were developed a considerable amount of theoretical and fundamental work was done which has been reviewed by Sarvazyan [1] Additional, application specific reviews of using acoustic radiation force have also been published in the literature [2, 3, 4, 5]. These reviews separately cover some of the topics addressed in this review. The general classes of applications include the measurement of mechanical properties, the manipulation of particles or cells, the modulation of cellular behavior, and the bioeffects related to the use of ARF. Ultrasound waves are transmitted into tissue or the medium of interest and the momentum of the waves is transferred to the medium to cause deformation or particle displacement. The interactions of the ultrasound waves can be tailored by different methods of focusing or utilizing specific boundary conditions for optimizing the use of acoustic radiation force to deliver forces in a noncontact manner. This review will focus on the how the application of acoustic radiation force both in time and space enables different biomedical applications. This review will also detail some of the commercial implementations that use ARF.

2. Theory

Acoustic radiation force (ARF) is the time-average force exerted by acoustic waves on an object [6, 7, 8, 9, 10]. Fundamentally, the ARF is caused by a change in the energy density of an incident acoustic wave. If a planar ultrasound wave is considered and interacts with an object that scatters and absorbs, the radiation force vector is [6]

$$\text{F}=d_{\text{r}}S\langle E_d\rangle ,$$ (1)

where d_r is the vector drag coefficient, S is the projected area of the wave on the object, and 〈E_d〉 is the time averaged energy density.

The drag coefficient represents the absorbing and scattering properties of the object [6]

$${\mathbf{d}}_{\mathbf{\text{r}}}=\widehat{p}\frac{1}{S}\left({\Pi }_a+{\Pi }_s-\int \gamma \cos {\alpha }_{s}dS\right)+\widehat{q}\frac{1}{S}\int \gamma \sin {\alpha }_{s}dS,$$ (2)

where $\widehat{p}$ and $\widehat{q}$ are the unit vectors in the direction of the beam and normal to the beam, respectively. The quantities Π_a and Π_s are the total absorbed and scattered powers, respectively. The parameter γ is the scattered intensity. The powers and intensity are expressed per unit incident intensity. The angle α_s is measured between the incident and scattered intensity and dS is the scalar area element. For a planar target, which is typically assumed, the normal component (second term in Eq. (2)) is set to zero [11] and we remove the unit vector $\widehat{p}$

$${\mathbf{d}}_{\mathbf{\text{r}}}=\frac{1}{S}\left({\Pi }_a+{\Pi }_s-\int \gamma \cos {\alpha }_{s}dS\right).$$ (3)

In the case when there is no absorption, Π_a = 0, the target is completely reflective (a_s = π) and the integral term results as -Π_s and the d_r = 2Π_s. This type of situation can occur in the case of transmitting through fluid and reflection occurring at a fluid-air interface or a fluid-solid interface where the acoustic impedance difference is large.

If we now consider the target as a Rayleigh scatterer (diameter smaller than the ultrasound wavelength), and the ultrasound is scattered in every direction, then the integral term in Eq. (3) will be zero. We can write the expression for the ARF by combining Eqs. (1) and (3) [12]

$$\text{F=}\left({\Pi }_a+{\Pi }_s\right)\langle E\rangle .$$ (4)

Now, if the soft tissue case is considered as a collection of randomly distributed Rayleigh scatterers where the magnitudes of the absorbed and scattered fields are compared, the absorbed power will be considerably higher than the scattered power and Eq. (4) reduces to [12]

$$\text{F}={\Pi }_a\langle E\rangle .$$ (5)

Using some simplifications of the absorbed power and the time-average of the energy density, we can write the ARF as [12]

$$\text{F}=\frac{2\alpha I}{c_l},$$ (6)

where the force is a body force or force per unit volume, a is the ultrasound attenuation, I is the intensity, and c_l is the longitudinal wave velocity. This expression is widely used as a simplified form of the ARF for many applications, particularly related to the measurement of mechanical properties.

3. Measurement of Mechanical Properties

One of the prominent uses of acoustic radiation force (ARF) in the biomedical field is for measurement of mechanical properties. The field of elasticity imaging or elastography has developed many different techniques for measuring mechanical properties of tissue. There are two common steps for each elastography measurement technique, applying a force to deform the tissue and measuring the tissue deformation [13]. One general assumption is that if a deformation is applied, a stiff material will deform less than a softer one.

One of the first applications of ARF for mechanical property measurement used this assumption to measure relative stiffness of rubber materials. A spherically focused ultrasound transducer was used to generate the ARF and a pulse-echo transducer was used to acquire data for measuring the resulting motion at the location of the deformation [14]. It was found that natural rubber deformed less than latex rubber.

One of the most important and widely used applications is the measurement of shear waves induced after ARF application, because the shear wave velocity, c_s, is proportional to the shear modulus, µ, of the material

$$\mu =\rho c_s^2.$$ (7)

where ρ is the mass density. In a homogeneous, elastic, isotropic, and incompressible (v = 0.5) tissue, then the Young’s modulus is approximately

$$E=2\left(1+v\right)\mu \approx 3\mu .$$ (8)

If a tone burst of ultrasound is transmitted into an absorbing medium, the momentum of the waves will be transferred to the tissue and the tissue will move [12]. When the toneburst ceases, the tissue will return to its equilibrium position. When this occurs, waves of axially polarized motion will propagate transverse to the direction of the ultrasound ARF application.

Several early developments were aimed at using ARF for the evaluation of mechanical properties using shear waves. Sarvazyan, et al., reported in their seminal publication on shear wave elasticity imaging (SWEI) the potentials for detecting the shear waves with magnetic resonance imaging (MRI), ultrasound pulse-echo measurements, or other acoustic means [15]. They demonstrated measurements of the shear waves produced by a focused ultrasound transducer with MRI techniques. They also developed theory related to the interaction of the force in a material and the resulting shear wave motion.

Dutt, et al., demonstrated measurements of shear waves produced by a focused ultrasound beam with pulse-echo measurements [16]. The pulse-echo transducer was translated to acquire different A-lines at different spatial locations while the ARF push was repeated for each measurement.

All of the previously mentioned applications were performed in an absorbing solid medium. When a focused ultrasound beam is transmitted into an absorbing or viscous fluid, acoustic streaming occurs which causes the fluid to flow [17, 18, 19]. Nightingale, et al., exploited this phenomenon to test whether breast cysts were filled with fluid or solid matter [20, 21]. Doppler ultrasound measurements were conducted after ARF application to evaluate if fluid flow was present. Several studies using ARF to initiate streaming were reported involving tests in phantoms and in patients [21, 22].

One of the next developments was reported by Fatemi and Greenleaf where two beams of ultrasound at different frequencies, f₁ and f₂, were co-focused, which caused the object at the focus to vibrate at the difference frequency ∆f = |f₁-f₂| [11, 23, 24]. The resulting acoustic signal produced by the vibration at the co-focus was measured by a nearby hydrophone, and this method was called vibro-acoustography.

As was mentioned above, the resulting motion from the application of ARF can be tracked using different modalities including ultrasound, MRI, and optical techniques [12, 15, 25, 26]. Separate studies by Bouchard, et al., and Czernuszewicz, et al., examined the accuracy of ultrasound-based methods for motion estimation after ARF application using optical detection as a comparison standard [25, 26]. These studies demonstrated good agreement with finite element modeling and underestimation with ultrasound-based techniques compared to optical detection.

These preliminary developments were very important for initiating a field that would continue to grow until the present day. For these methods and the ones that would follow (and will be described below), two aspects with respect to the ARF application should be noted, that is, the spatial and temporal modulation that is used.

3.1. Temporal Modulation

The goal of temporally modulating the ultrasound signals used to generate the ARF is to tailor the frequency of the applied stress. The temporal modulation of the ARF application has been studied extensively. One method that has been widely used is the impulsive application of ARF [12]. The impulse terminology applies to the short duration of the ARF application as it pertains to the tissue response. Typically the acoustic radiation force impulse (ARFI) is applied in less than 1 ms. In terms of ultrasound this can be a very long pulse. At 5 MHz, a 1 ms pulse is 5000 cycles, which can be assumed to be a continuous wave transmission. This is in contrast to a pulse that would be used for B-mode imaging that may only be 0.2–1.0 µs.

Soft tissue typically has a response time on the order of a few milliseconds, so from a linear systems point-of-view, the ARFI application can be considered nearly an impulse. In early work with ARFI, ultrasound-based measurements of the induced motion were performed both in the region-of-excitation (ROE) or lateral to the ROE [27]. In the case of the ROE measurement, the displacement amplitude, time-to-peak, and relaxation time were quantities that were under investigation to evaluate different materials or tissues [12, 28, 29]. The excitation beam can be moved about the array aperture to make measurements at different locations, which is called ARFI imaging. Images of the aforementioned parameters were formed, but in general the displacement amplitude at a given time or the peak displacement amplitude was typically used for the images. This modality is based on the assumption that stiffer regions would deform less than softer regions. ARFI imaging can produce images with good contrast between regions of different stiffness and has been commercialized as Virtual Touch Imaging by Siemens. Measurements lateral to the ROE can capture the resulting shear waves produced by ARF.

The kinetic acoustic vitreoretial examination (KAVE) method also takes advantage of ARFI excitations, but with much shorter pulses repeated at a relatively high rate [30, 31]. The pulses used are more typical of B-mode imaging pulses (1–2 µs), but many pulses were transmitted repeatedly every 1–2 ms for 1–2 seconds, and this sequence can be repeated several times a minute to obtain long-term data. This causes progressive displacement to occur in the ROE. The resulting displacement is fit to a rheological model for a viscoelastic material, that is, a material that has time-dependent behavior. A similar form of this method was developed into a method called sonothromboelastography or sonorheometry as it was used to measure the response of blood as it coagulated [32, 33, 34, 35]. The parameters that are fit by the viscoelastic model have been used to characterize clotting behavior.

Various groups have adapted the KAVE methodology to deform viscoelastic tissue and analyze the time course of the ARF-induced displacement and the tissue’s return to its equilibrium position. These methods include monitored steady-state excitation and recovery (MSSER), radiation force-induced creep (RFIC), radiation force-induced creep recovery (RFICR), and viscoelastic response (VisR) imaging [36, 37, 38, 39]. These methods are similar in their use of ARF to locally deform tissue, but the analysis of the resulting motion is very different for each of these methods. In addition, a calibration step, typically using shear wave velocity measurements, is needed to obtain absolute values for viscoelastic parameters [38, 39].

Another method called Harmonic Motion Imaging (HMI) has been developed that applies amplitude modulation to a continuous wave ultrasound transmission to cause vibration at a specific harmonic frequency [40, 41]. Exciting at a single harmonic frequency with sinusoidal modulation allows for high signal-to-noise ratio (SNR) detection of the resulting harmonic motion. The motion amplitude is used as a surrogate for how stiff a material is at the focal point of the transducer. This technology has been used to monitor the mechanical property changes after high intensity focused ultrasound (HIFU) ablation. Typically, tissue will become stiffer when the temperature in the tissue rises above 60–65 °C due to changes at the macromolecular level [42]. The HMI and HIFU methods have been combined for HMIFU, which alternates the excitation from a HIFU transducer between a longer, lower amplitude transmission for performing ablation to a shorter, higher amplitude transmission for interrogation of the ablated area [43, 44]. A small phased array transducer is co-focused with the HIFU transducer to perform motion detection for this HMIFU method.

Different types of modulation can be used with the ultrasound waves including a square wave for ARF generation. A repeated square wave can provide a repeated ARF pulse train, while a single square wave represents an ARF impulse. The concept of using repeated ARF pulses has been used in a method called shearwave dispersion ultrasound vibrometry (SDUV) [45]. This shear wave method is predicated on previous work that demonstrated that shear wave velocity varies with frequency, a concept called dispersion, in materials that are viscoelastic [46]. To obtain motion at prescribed harmonic frequencies with SDUV, the ARF pulses of length T_p are repeated at a rate of f_r = 1/T_r and a Fourier analysis of this resulting square wave excitation waveform has components at harmonics of f_r. The magnitude of the spectrum can be written as

$$F\left(f\right)=\left|a{f}_r{T}_p\sum _{n=-\infty }^{\infty }{e}^{-i\pi T_{p}n{f}_r}\text{sinc}\left(T_{p}n{f}_r\right)\delta \left(f-n{f}_r\right)\right|,$$ (9)

where a is an arbitrary amplitude, δ(⋅) is the Dirac function. The magnitude spectrum has a sinc-shaped envelope.

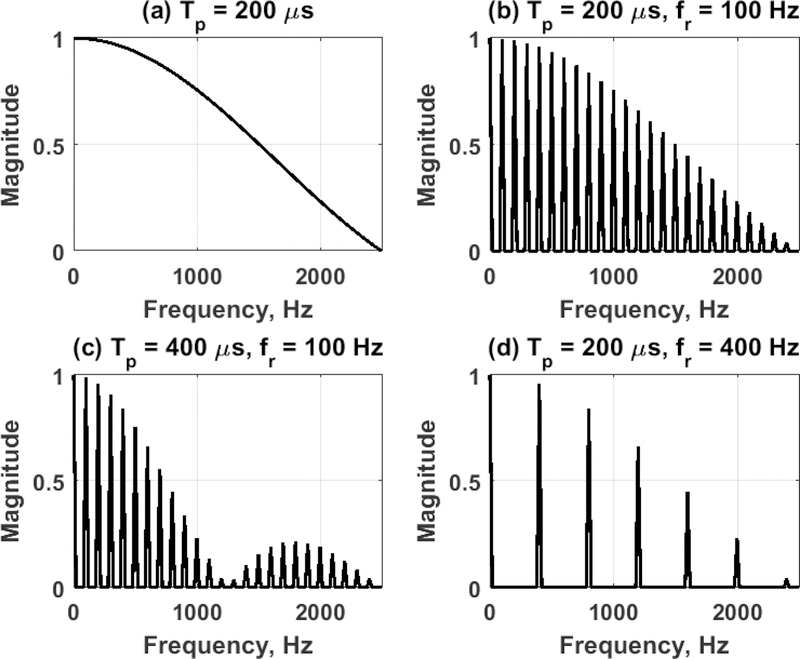
Figure 1 shows the magnitude spectrum for several different combinations of T_p and f_r computed with Eq. (9). Figure 1(a) shows the magnitude spectrum for a single push (single impulse) with T_p = 200 µs, which gives a decaying magnitude envelope. Figure 1(b) shows the magnitude spectrum when T_p = 200 µs with those pushes repeated at f_r = 100 Hz, which depicts components at multiples of 100 Hz. When the push length is increased to T_p = 400 µs, the component amplitudes change and there is a null at 1250 and 2500 Hz as shown in Fig. 1(c). Additionally, as shown in Fig. 1(d), if the f_r is increased to 400 Hz, the components are limited to those as multiples of 400 Hz.

Figure 1.

Normalized magnitude spectra from different SDUV pulse sequences. (a) Single push, T_p = 200 µs, (b) SDUV pushes, T_p = 200 µs, f_r = 100 Hz, (c) SDUV pushes, T_p = 400 µs, f_r = 100 Hz, (d) SDUV pushes, T_p = 200 µs, f_r = 400 Hz.

Therefore, with the SDUV excitation, multiple frequencies could be interrogated in a single acquisition with high SNR. Fourier analysis is performed on motion acquired at several locations lateral to the ARF application. A phase gradient is applied to the phase measurements (ϕ₁, ϕ₂) made at a particular frequency, f, from different locations r₁ and r₂ to estimate the shear wave velocity

$$c_s\left(f\right)=\frac{2\pi f\left(r_2-r_1\right)}{{\varphi }_2-{\varphi }_1}.$$ (10)

Additionally, a linear regression can also be utilized with several locations to make the phase velocity measurement more robust [45, 47].

A later modification of the SDUV methodology is called orthogonal frequency ultrasound vibrometry (OFUV) [48]. This method addresses the decaying amplitude of the ARF excitation of the SDUV method at higher frequencies. This is important, because shear wave attenuation increases with frequency, so components at higher frequencies may not have adequate amplitude. The OFUV method allows for the design of specific relative amplitudes at certain frequencies, and from the envelope, pulse width modulation can be applied to construct the excitation waveforms for achieving the desired excitation temporal profile.

In recent years, most shear wave elastography (SWE) methods have utilized a single impulsive ARF push of typically 100–800 µs for clinical applications. One reason is due to the requirements of the power source of the clinical or research ultrasound instrument being used and the need to sustain constant power for each push. Additionally, most clinical ultrasound scanners have implemented a time-domain group velocity measurement to quantify the shear wave velocity [49]. The measurement of the shear wave velocity in the time-domain does not require specific frequency-domain information and can be done by identifying features in the time-domain signal such as peak of particle displacement, peak of the particle velocity, or the peak of correlation functions to determine the time-of-flight between different locations [49, 50, 51, 52, 53, 54, 55, 56]. As a result, repeated pulses (SDUV, OFUV) are not necessary. Secondly, if shear wave velocity dispersion is to be explored, this can be evaluated using two-dimensional Fourier transform analysis on data from a single ARF push that was pioneered by Bernal, et al., and Couade, et al., originally for vascular applications [57, 58]. This method takes a two-dimensional Fourier transform of spatiotemporal (x,t) wave propagation data to transform to spatial frequency-temporal frequency (k,f) space. The wave velocities at specific frequencies can be extracted by locating peaks (k₀, f₀) in this Fourier distribution and computing

$$c_s\left(f\right)=\frac{2\pi f_0}{k_0}=f_0\times {\lambda }_s,$$ (11)

where λ_s is the wavelength [57]. Examples of the group and phase velocity estimation are depicted in a recent article related to simulating shear wave propagation in tissue-mimicking materials [59].

For the purposes of analysis of shear wave velocity dispersion from an ARF impulse, it should be noted that the frequency content is modulated by the size of the focal area of the pushing beam, the length of the ARF excitation push, and the stiffness of the medium [60]. For different media, frequency content needs to be addressed for the shear wave acquisition and in the post-processing. For example, shear waves in a normal liver have a lower frequency range compared to a cirrhotic liver. The impulse can be applied in general for many applications but may not be optimal for all applications.

Another method that has been utilized to quantify mechanical properties of tissues is using ARF to vibrate an inclusion (bubble or sphere) embedded in a medium. This work was motivated by a landmark paper by Oestreicher in 1951 [61]. Carstensen and Parker have published a review of the impact and the present use of this seminal work [62]. Chen, et al.,explored the use of the vibration of an embedded sphere to quantify viscoelastic parameters for gelatin phantoms [63]. Urban, et al., also used this concept to differentiate spheres of different materials [64]. Erpelding and colleagues developed methods for applying ARF to bubbles formed from laser-induced optical breakdown for estimation of mechanical properties in tissue mimicking materials and eye lenses [65, 66, 67]. Aglyamov, et al., investigated the impulsive excitation of embedded spheres and bubbles and found very good agreement between experimental results and their derived analytical result [68, 69]. The work by Aglyamov, et al., was derived using a Kelvin-Voigt material, and Urban, et al., extended this work for arbitrary rheological models [68, 70]. Other work has shown that different methods for modulating the ultrasound used to produce the ARF can be used to generate different sets of frequency components. This work by Urban, et al., utilized square, triangle, and sawtooth waveforms and modulation techniques such as double-sideband suppressed carrier, frequency shift keying, and frequency modulation [71]. Mitri, et al., extended similar models of vibration of embedded materials for detection of brachytherapy seeds by using modulated ultrasound to stimulate the seeds using VA to measure the acoustic response [72, 73, 74].

Frequency modulation of the ARF push has also been utilized for optical coherence elastography (OCE) to produce shear waves with large frequency bandwidth [75]. A matched filter approach is used to make measurements of shear wave velocity.

3.2. Spatial Modulation

The purpose of spatial modulation of the ARF is to distribute the ultrasound beams in the field-of-view in an advantageous ways to apply the stress in order to cause specific deformation in the tissue. In addition to the temporal modulation of the ARF excitation, the spatial distribution and focusing characteristics can also be varied for different applications. In general, ultrasound beams used for ARF pushes are focused using a fixed physical aperture (e.g. spherically focused surface) or by using electronic focusing with time delays applied to elements in an array transducer. Within the two-dimensional (x,z) imaging plane a single ARF beam will produce motion within the ROE and a left-traveling and right-traveling shear wave outside of the ROE [15]. In reality, a shear wave will propagate symmetrically or asymmetrically in a cylindrical fashion about the beam axis depending on the type of transducer and focusing that is used, but the motion is only measured in the B-mode imaging frame. Recent efforts have measured the motion spatially in three-dimensions [76, 77, 78, 79, 80].

Depending on the f-number of the ARF push beam, f/# = z_f/D, where z_f is the focal depth and D is the diameter or length of the aperture, the resulting motion can be very confined in the axial direction or can be very broad. As noted in Eq. (6), the ARF in an absorbing medium is proportional to the ultrasound intensity distribution. At one extreme end, an unfocused beam (f/∞) produces a very long axial beam, and a focused f/1 beam produces a beam similar to an hourglass shape (Fig. 2).

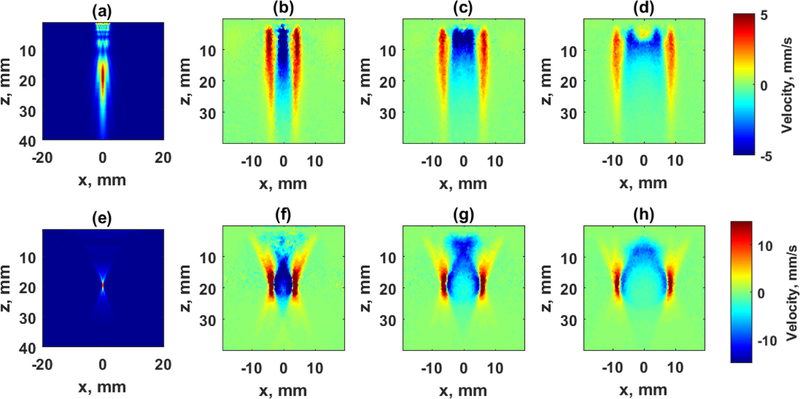
Figure 2.

Shear wave propagation in an elastic tissue mimicking phantom with different acoustic radiation force beams. The top row uses an unfocused beam, and the bottom row uses a focused beam. (a) Acoustic intensity for unfocused beam with 16 elements. (b)–(d) Snapshots of shear waves produced by an unfocused beam at 1.275, 2.550, and 3.825 ms, respectively. (e) Acoustic intensity for a focused beam with 64 elements focused at 20 mm. (f)–(d) Snapshots of shear waves produced by a focused beam at 1.275, 2.550, and 3.825 ms, respectively.

Figure 2 shows the intensity profile simulated for a linear array transducer (L7–4, Philips Healthcare, Andover, MA) for unfocused and focused beams as well as motion measured in an elastic phantom with c_s = 1.89 m/s (CIRS, Inc., Norfolk, VA) [81]. The top row of Fig. 2 shows the intensity profile of an unfocused beam using 16 elements and shear wave particle velocity at different time points measured with a research instrument (V1, Verasonics, Inc., Kirkland, WA). The bottom row of Fig. 2 shows the intensity profile of a focused beam with 64 elements and the resulting shear wave motion. The wave fronts for the unfocused front are relatively uniform with depth, while the focused beams produces shear waves with more curvature in the wave fronts.

The shape of the beam does affect the measurements made in the ROE for ARFI imaging. The size of f/# was analyzed extensively as it pertains to the robustness, reproducibility, and spatial coverage for the image reconstruction [82, 83, 84].

As it pertains to shear wave elastography (SWE), shear wave attenuation is high in soft tissues, so the shear waves do not typically travel very far (0.5–2.0 cm). To make an image that covers several centimeters laterally, multiple excitations are necessary, and the shear wave velocity results from each acquisition in the field-of-view (FOV) or region-of-interest (ROI) are combined to form the resulting image. Additionally, within the push beam, no shear wave is present, so measurement of the shear wave velocity in the area of the push beam can only be done from an excitation with a push beam located at another location which generates a shear wave through the region occupied by the push beam in question.

To address these limitations, Song, et al., proposed the comb-push ultrasound shear elastography (CUSE) method which uses several push beams distributed across the array aperture, and each of these beams could be unfocused or focused [85, 86]. The unfocused push beams are more optimal for measurements at shallow depths and the focused beams are more appropriate for deeper measurements. These multiple beams are transmitted simultaneously to create multiple shear waves. This addresses the aforementioned limitations in the following ways. First, distribution of the shear wave sources insures that a shear wave travels through all parts of the FOV before attenuating significantly. Adjacent push beams produce shear waves that cover other push beam areas so estimation of the shear wave velocity is possible at all locations. Simultaneously transmitting these push beams also allows for a single push event to occur to make a shear wave velocity image, assuming the use of plane wave imaging, as opposed to several acquisitions that are used by other techniques (even using plane wave imaging). When using unfocused beams, the method is known as unfocused CUSE (U-CUSE), and when using focused beams it is denoted as focused CUSE (F-CUSE). An extension of the CUSE methodology was to use multiple hybrid axicon beams or steered unfocused beams to generate even more ARF shear wave sources to enrich the shear wave content within the FOV [87, 88].

In addition to using unfocused, focused, or axicon beams, McAleavey, et al., proposed the use of spatially modulating the ultrasound transmitted [89, 90]. This generates a complicated ARF push waveform that has specific spatial wavelengths present depending on the modulation used.

3.3. Combined Temporal and Spatial Modulation

There are several methods that have combined temporal and spatial variations to generate shear waves in particular ways to provide reinforcement and increase the shear wave amplitude. Two of these methods, as described below, are shown in Fig. 3.

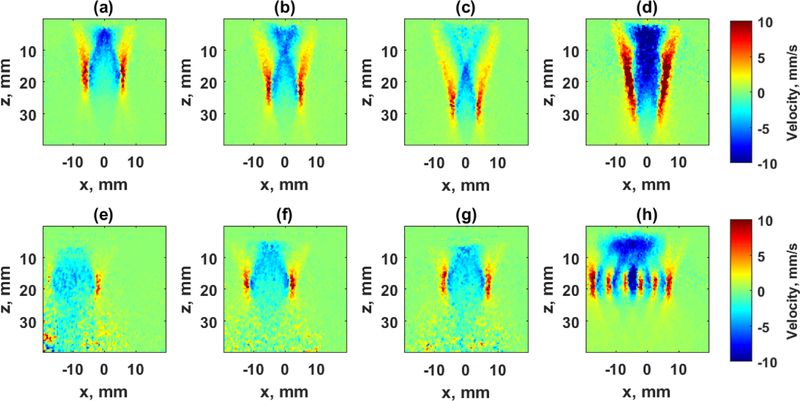
Figure 3.

Images of shear waves produced with different spatial and temporal modulation. The top row depicts the constituent pushes of a supersonic push and the bottom row shows the results of pushes using a marching CUSE excitation. (a)–(c) Shear waves produced from single pushes created with focused push beams with f/# = 1.55 focused at z = 20, 25, and 30 mm, respectively, at 1.275 ms after the push. (d) The shear wave produced by combining the pushes from (a)–(c) to create the supersonic push. (e)-(g) Shear waves produced from single pushes created with focused push beams with f/# = 1.00 focused at z = 20 mm, and x = −9.85, 0.00, +9.85 mm, respectively, at 1.275 ms after the push. (d) The shear wave produced by combining the pushes from (e)–(g) to create the marching CUSE excitation.

One of these methods is called supersonic shear imaging (SSI) [53]. The focused ARF push beam is moved axially to several locations faster than the medium’s shear wave velocity.This “supersonic” approach generates reinforced shear waves that mimic a Mach cone as produced when a jet crosses the sound barrier [91]. This reinforced shear wave can have a large axial extent to provide a large axial FOV for shear wave measurements. The supersonic push is depicted in the first row of Fig. 3 with the three component shear wave excitations with a f/1.55 push beam axially moved to three locations (z_f = 20, 25, 30 mm). The combination of all these components yields the result in Fig. 3(d), which is a push with large amplitude and a long axial wave front.

A variation of the CUSE methods is called marching CUSE (M-CUSE), which uses a focused ARF beam and moves it laterally at fixed time intervals [86]. This is most useful for deep excitations that may need many elements to be used for focusing whereas, other CUSE methods use smaller apertures to produce multiple beams across the aperture (typically 16–64 elements). The M-CUSE excitation is shown in the bottom row of Fig. 3. The f/1 push is translated to different lateral locations x = −9.85, 0.00, +9.85 mm. The resulting combination of the three excitations is shown in Fig. 3(d).

Another method that generates interfering waves called ARF crawling waves excites multiple ARF push beams, but instead of transmitting one temporal pulse, the temporal pulses are repeated at a particular rate to create multiple propagating waves [92]. In the CUSE methods, directional filtering is typically used to separate these waves and reconstructions are made from left-to-right (LR) and right-to-left (RL) traveling waves, and the resulting shear wave velocity images are combined at the end [85, 86]. In the ARF crawling waves, the local trajectories in the spatiotemporal domain are measured to reconstruct the shear wave velocity map.

Lastly, vibro-acoustography has used multiple focusing methodologies based on different transducer array types (sector, linear, 1.75D, reconfigurable) [23, 93, 94, 95, 96, 97, 98]. The aperture used for excitation can be moved along the transducer width for varying the spatial location of the ARF application. Additionally, multiple beams with different ultrasound frequencies and modulation have been utilized to generate multi-frequency ARF excitations in a single pushing event [99].

Multiplexing of different spatial distributions and temporal excitations can provide application-specific advantages that may optimize deformation or shear wave sources and enhance the frequency content of the excitation particularly in situations where shear wave attenuation is high and dissipates the waves before they travel appreciable distances. Table 1 summarizes the aforementioned methods with the temporal and spatial modulation characteristics as well as the primary measurement parameters.

Table 1.

Summary of ultrasound ARF-based elastography methods with temporal and spatial modulation characteristics.

Method	Temporal Modulation	Spatial Modulation	Measurement Location	Measurement Parameters
Acoustic Radiation Force Impulse Imaging (ARFI)	Impulse	Single Beam	ROE	• Peak displacement • Time-to-peak displacement • Relaxation time
Shear Wave Elasticity Imaging (SWEI)	Impulse	Single Beam	Lateral	Shear wave velocity
Vibro-acoustography (VA)	Harmonic	Co-focused Beams	ROE (Remote Hydrophone)	Acoustic emission
Harmonic Motion Imaging (HMI)	Harmonic	Single Beam	ROE	Displacement amplitude
Radiation Force Creep*	Repeated Impulse	Single Beam	ROE	Displacement creep response
Supersonic Shear Imaging	Impulse	Axially Moving Beams	Lateral	Shear wave velocity
Shearwave dispersion ultrasound vibrometry (SDUV)	Repeated Impulse	Single Beam	Lateral	Shear wave velocity dispersion
Orthogonal dispersion Ultrasound vibrometry (OFUV)	Repeated Impulse	Single Beam	Lateral	Shear wave velocity dispersion
Spatially Modulated Ultrasound Radiation Force	Impulse	Spatially Modulated Beam	Lateral	Shear wave velocity
Comb-push Ultrasound Shear Elastography (CUSE)	Impulse	Multiple Beams	Lateral	Shear wave velocity
Marching CUSE	Impulse	Laterally Moving Beams	Lateral	Shear wave velocity

^*Radiation force creep methods include KAVE, sonorheometry, MSSER, ViSR, RFIC, and RFICR.

3.4. Biomedical Applications of ARF-Based Elastography

All of the aforementioned methods have been used for in vitro, ex vivo, or in vivo testing to measure mechanical properties of soft tissues, and different methods may have particular advantages in these different tissues. Innumerable clinical papers have been published as ARFI imaging and different implementations of shear wave elastography has become available on multiple clinical ultrasound scanners. Based on this large body of work, general guidelines for these methods and more specific guidelines for certain organs have been developed [100, 101, 102, 103, 104, 105, 106]. However, these guidelines are continually evolving as the technology and body of knowledge changes.

Measurement of shear wave velocity in liver can provide information that is related to liver fibrosis as the liver gets stiffer as fibrosis increases up to the level of cirrhosis [102, 107]. Many different methods are suitable for this application with curved linear arrays. However, as like most soft tissues, the liver is viscoelastic and so special efforts need to be made to provide adequate frequency content to perform measurements of that viscoelasticity (e.g., shear wave velocity dispersion) [108, 109, 110].

Measurements in deep organs, such as portions of the liver or liver in obese patients, kidney, spleen, pancreas, heart may require more specialized focusing or particular transducers to achieve effective measurements. Also, using longer ARF push pulses may be necessary to induce sufficient motion for measurement.

Other organs that are thin may also require special focusing or considerations for shallow distances such as arteries, tendons, the urinary bladder, and the cornea [57, 58, 111, 112, 113]. Wave propagation is complicated in these structures and inverse approaches need to be customized for each of these cases.

Orientation of the ARF application is also necessary to consider in tissues that have directional dependence on their material properties. This condition is called anisotropy and is present in many soft tissues such as skeletal muscle, tendons, kidney, and myocardium [111, 114, 115, 116, 117, 118]. Results can be confounding or not as sensitive depending on the design of the ARF beam for either measurements in the ROE or of propagating shear waves in anisotropic tissues [119].

In applications that are targeted towards tumor characterization such as in the breast, thyroid, prostate, kidney, or liver, the lesion presents as an inhomogeneity in the surrounding normal tissue [101, 103, 104, 120]. This requires shear waves that can propagate some distance depending on the size of the lesion. Using multiple acquisitions or simultaneous use of multiple ARF push beams may be necessary to produce shear waves or other ARF interrogations over the region making up the lesion and the surrounding tissue to investigate the lesion with adequate contrast. In particular, directional filtering and having ARF pushes on both sides of the lesion can provide useful shear wave velocity reconstructions [85].

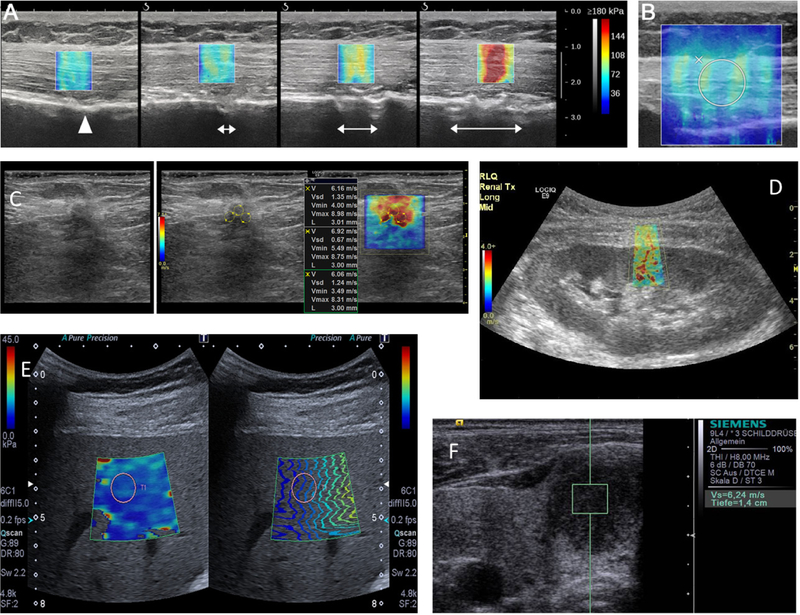
Example images of shear wave elastography measurements are shown in Fig. 4. Figures 4(a)–(b) show images of Young’s modulus in ex vivo deltoid muscle subjected to different levels of stretch acquired using a SuperSonic Imagine Aixplorer system [121]. The Young’s modulus increases as the stretch is applied. Figure 4(b) shows an example of a region-of-interest (ROI) typically used for measurements of mean, median, and standard deviation of the Young’s modulus or shear wave velocity. Figure 4(c) shows a B-mode ultrasound image, the same image with defined ROIs, and the shear wave velocity of a malignant invasive ductal breast carcinoma acquired using a General Electric Logiq E9. Figure 4(d) shows an example of the shear wave velocity map of a renal transplant using a General Electric Logiq E9. Figure 4(e) shows a shear wave velocity map and image of propagation time-of-flight in a liver acquired using a Toshiba Aplio 500 system. Figure 4(f) shows a shear wave velocity measurement in a hypoechoic thyroid nodule using a Siemens S2000 system.

Figure 4.

Example images with clinical SWE modes. a) Young’s modulus images of a deltoid muscle at different levels of stretch using a Supersonic Imagine Aixplorer [121], b) Region-of-interest used for analysis of SWE data containing the entire thickness of the muscle [121], c) Shear wave velocity map of a malignant invasive ductal carcinoma taken using a General Electric Logiq E9 [122]. d) Shear wave velocity map in a renal transplant taken using a General Electric Logiq E9. e) Young’s modulus images of a liver taken with a Toshiba Aplio 500 [123]. f) Shear wave velocity measurement of a thyroid nodule using a Siemens S2000 [124].

To facilitate clinical applications, many companies have implemented ARF-based methods to make measurements in various organs as demonstrated in Fig. 4. Table 2 summarizes a list of manufacturers, the devices that have ARF-based modes and their measurement capabilities. The manufacturers represent a wide array of companies from all over the world. Two companies that produce research devices, Verasonics [125] and S-Sharp, are also highlighted as having capabilities for producing ARF for developing new measurement techniques.

Table 2.

Summary of commercially implemented ultrasound ARF-based methods.

Manufacturer	Devices	Method	Manufacturer Name	Measurement Type
Supersonic Imagine (Aix en Provence, France)	Aixplorer, Aixplorer Ultimate Aixplorer Mach 30	SSI	Shear Wave Elastography	2D Image 3D Images
Siemens (Siemens Healthineers, Germany)	Acuson S2000 & 3000	ARFI imaging	Virtual Touch Imaging (VTI)	2D Image
		SWEI	Virtual Touch Quantification (VTQ)	Point
		SWEI	VTQ	2D Image
Philips (Philips Healthcare, Netherlands)	iU22, EPIQ 5, 7	SWEI	ElastPQ	Point
	EPIQ 5, 7	SWEI	ElastQ	2D Image
General Electric (General Electric Healthcare, United States)	Logiq E9, E10, S8	CUSE	Shear Wave Elastography	2D Image
Toshiba (Canon Medical Systems, Japan)	Aplio and Aplio i-Series	SWEI	Shear Wave Elastography	2D Image
Hitachi (Hitachi Ltd, Japan)	HI-VISION Ascendus, Arietta 70, 850	SWEI	Shear Wave Measurement	Point
Samsung (Samsung Medison, South Korea)	HS70A	SWEI	S-Shearwave	Point
Esaote (Esaote, Italy)	MyLabTwice, MyLab8, MyLab9	SWEI	QElaXto	Point
Mindray (Mindray, China)	Resona 7, DC-80	SWEI	Sonic Touch Elastography	2D Image
Verasonics (Verasonics Inc, United States)	V1, Vantage	--	Open Research Device	--
S-Sharp (S-Sharp Corporation, China)	Prodigy, Prospect T1	--	Open Research Device	--

Currently, ARF-based technologies are being used in many studies as evidenced by the large number of publications available for the applications detailed above. Additionally, these techniques have been and are being incorporated into clinical trials. A search using the term “shear wave” on ClinicalTrials.gov returned 145 completed or current studies in various organs. Additionally, a search using the term “acoustic radiation force” on ClinicalTrials.gov returned 42 completed or current studies. ARF-based techniques have been used widely in diagnosis of liver fibrosis and differentiating breast and thyroid lesions. Continued work for identifying clinical indications for ARF-based measurements will mature over time with more research and clinical use. One aspect that may be consistent within clinical practice is that elastographic measurements will typically be an additional complementary measurement in a standard anatomical clinical examination.

4. Manipulation of Particles for Biomedical Applications

As was detailed above, the ARF can be used to move solid tissues. However, ARF can also be used to manipulate small particles and cells in aqueous solutions to perform different objectives. This can be done with pulsed or continuous wave ultrasound application, and the choice of which will be detailed in the following paragraphs.

Particles can be propelled if they are in the path of an ultrasound beam. There has been considerable theoretical work on how the force changes for different shaped particles manipulated by different types of acoustic beams [126, 127, 128, 129, 130]. For biomedical applications, aggregation and separation of different cells has been explored. The field of acoustofluidics has arisen to incorporate surface acoustic waves to manipulate cells [3, 131, 132] and for separating cells from other particles [133, 134]. Acoustic tweezers have also been developed for manipulation of cells and particles [130, 135, 136, 137, 138, 139, 140]. Combination of microbubbles and ARF can also be used to probe the biomechanics of cells [141].

Acoustic radiation force has been shown to push microbubbles against vessel walls [142, 143, 144]. This can be very useful if the microbubbles are labeled with ligands designed to attach to epitopes for molecular imaging applications [145, 146, 147, 148, 149]. It has been shown that the image signal can be significantly enhanced by application of pulsed ultrasound [150, 151, 152].

In the previous case, the vessel wall served as a boundary to stop the microbubble. However, the vessel wall is not completely reflective. Ultrasound standing waves can be produced when a completely reflective interface is present and continuous ultrasound waves are used [153]. Nodes and antinodes will form at integral wavelengths of the ultrasound wave. Particles can be trapped in the nodes of the standing wave. The power of the ultrasound beam will determine how massive the particles can be that can be trapped [154].

An expression for the ARF in the standing wave, F_SW, is given as [155]

$$F_{SW}=ACF\left(\frac{-\pi P_0^{2}V{\beta }_o}{2\lambda }\right)\sin \left(\frac{4\pi z}{\lambda }\right),$$ (12)

where P₀ is the peak pressure amplitude, V is the spherical particle volume, λ is the ultrasound wavelength, and z is the perpendicular distance from nodal planes of the pressure. The ACF is defined as

$$ACF=\frac{5{\rho }_p-2{\rho }_o}{2{\rho }_p+{\rho }_o}-\frac{{\beta }_p}{{\beta }_o},$$ (13)

where the subscripts p and o refer to the particle and the suspending medium, respectively, and β is the compressibility.

Ultrasound standing waves can be used to pattern cells for tissue engineering applications to organize the cells and promote vascularization [155, 156, 157, 158, 159, 160, 161]. Yasuda, et al., reported the concentration of erythrocytes (red blood cells) using a standing wave and evaluated the amount of damage to the cells [162]. Manipulating the acoustic beams can provide a means for three-dimensional bioprinting [159, 163]. This involves manipulation, aggregation, and patterning of cells and other materials by acoustic means using standing waves. Ultrasound can also be used to stimulate cells to encourage proliferation and differentiation into tissues of interest for tissue engineering [164].

5. Phase Aberration Correction

When ultrasound beams are focused in tissue, a mean longitudinal velocity, typically 1540 m/s, is assumed to calculate electronic delays applied to the different elements. However, different tissues have different longitudinal velocities that will cause imperfect focusing. This is particularly exaggerated when large subcutaneous fat layers are encountered both due to increased ultrasound attenuation and lower longitudinal velocity (~1450 m/s) [165]. As a result, these tissue inhomogeneities in longitudinal velocity cause phase alterations between different ultrasound waves, or phase aberration. Many methods have been developed for correcting these time delays to alleviate the aberration that is present [166, 167, 168]. Many techniques assume that the phase aberration can be modeled as a phase screen close to the transducer even though the effects of defocusing are produced by propagation through several centimeters of tissue. These methods also do not typically compensate for amplitude attenuation that may be encountered.

One drawback for ultrasound-based methods is that they are based on coherent detection processes, that is, they are phase sensitive. Phase aberration is a problem that is not relegated only to ultrasound imaging, but is also present in astronomy and other imaging-based applications that require optically focusing. In these cases, the detection is incoherent, typically based on the intensity of the light.

An advantage for ultrasound-based methods would be to rely on an incoherent signal source such as the intensity or effects related to the intensity, i.e. the acoustic radiation force (Eq. 6). Urban, et al., recognized this aspect and designed and tested methods to perform phase aberration correction using measured motion produced by ARF on an embedded sphere as a metric to guide the correction through variation of the phase on each element of a 20 element annular array [169]. As the phase was changed progressively on each element, the motion of the sphere was increased as measured by a laser vibrometer and a pulse-echo transducer.

However, imaging array transducers have many elements, typically 128–256, and changing the phase of each element at a time may not affect the resulting motion in an appreciable manner, and doing an optimization for many elements in a sequential manner may be very time consuming depending on the number of transmissions needed for each element. To optimize this process, Herbert, et al., used Hadamard coding to obtain data so that fewer transmissions were needed to solve for the optimal time delays to apply to the elements in the array [170]. Using this type of scheme requires 4N transmissions where N is the number of elements in the array. In contrast, depending on the number of phase steps, N_Ф, the method proposed by Urban, et al., would take NN_Ф where N_Ф could be on the order of 3–10 but may not have the same sensitivity to finding a solution.

Another method that can be used for evaluating the focus of acoustic fields is magnetic resonance ARFI (MR-ARFI). High intensity focused ultrasound requires precise focusing for applications in the brain and in the abdomen. Typically, MR thermometry is used to measure the response of the HIFU therapy during the course of the ablation procedure. However, it is desirable to know the intensity distribution of the HIFU transmission. One way to do this is to transmit a shorter ARFI push pulse and measure the resulting displacement with MR phase techniques [171]. For applications in the brain, computed tomography (CT) scans can be used to estimate the skull thickness, and the appropriate phases for the ultrasound signals can be estimated [172, 173]. However, for real-time, in situ measurement of focusing of the skull, MR-ARFI has been used to evaluate the focal distribution and also use methods to focus the beam after it travels through the skull [172, 173, 174, 175]. Additionally, MR-ARFI has been used for applications in other soft tissue targets for evaluating the focus and refocusing [176, 177]. The MR-ARFI technique has also been utilized for mechanical property evaluation by measuring either induced displacements or shear wave velocities [178, 179].

6. Bioeffects Related to ARF Usage

In recent years, there has been considerable work in the areas of neuromodulation and activation of different channel-based cell signaling pathways using ultrasound. The mechanisms for activation of these pathways are still not totally understood, but there could be a role that ARF plays as many of the channels involved are mechanosensitive [164, 180, 181]. However, the ultrasound wavelength is typically much larger than the channels and cells themselves, so the role of ARF within these interactions needs further investigation [182].

There are safety issues related to the use of ARF in humans. The Food and Drug Administration (FDA) regulates the acoustic output of diagnostic ultrasound instruments in the United States, and the IEC 60601–2-37 provides international guidance for safety requirements for ultrasonic medical diagnostic and monitoring equipment [183]. The main bioeffects of ultrasound are thermal and mechanical. With intense, long duration pulses, there is a risk of heating the tissue either at the focal region or at the probe-skin interface, especially if the duty cycle of the ARF push pulses is high. The FDA places limits on the spatial-peak temporal average intensity (I_spta,0.3), which has to be under 720 mW/cm² for most diagnostic imaging applications that are not related to fetal or ophthalmologic imaging, where the limits are lower. The subscript 0.3 denotes that the pressure fields are derated by 0.3 dB/cm/MHz to conservatively account for attenuation experienced when propagating through soft tissues. Additionally, to prevent thermal damage for diagnostic uses, the Thermal Index must be lower than 6.0, which indicates that during the pulse sequence or scanning sequence, the temperature increase must be lower than 6.0 °C. Additionally, there are limits related to mechanical effects that are meant to prevent the occurrence of cavitation, or the creation of bubbles in the tissue. If the bubbles collapse at a high rate, they can produce high temperature and pressure, which can damage cells. The Mechanical Index (MI) is a predictor of the occurrence of cavitation, and the FDA sets the MI_0.3 limit at 1.9. The MI is calculated as

$$MI=\frac{P_{r,0.3}}{\sqrt{f}},$$ (14)

where P_r,0.3 is the derated peak rarefractional pressure in MPa and f is the frequency of the ultrasound wave in MHz. As can be observed from the equation, lower ultrasound frequencies (for the same pressure amplitude) will cause the MI limit to be encountered sooner. However, lower ultrasound frequencies to produce the ARF may be desirable to avoid excessive attenuation and phase aberration effects, so trade-offs may need to be made to optimize the resulting motion from ARF application. Typically, the MI limit is more restrictive in ARF applications unless the pulse or scanning sequence is very long and then the TI or I_spta limit may become more restrictive.

As these limits have been shown to be somewhat restrictive, especially for application of ARF in deeper tissues, there have been efforts to investigate the potential of using higher acoustic output and the general success of ARF-based measurements with these higher acoustic outputs [184, 185]. In general, using higher power for ARF excitations does produce motion at deeper focal depths that can be detected and increases the success rate of shear wave velocity measurements [185, 186]. However, this has been done on an exploratory basis and the FDA would have to alter regulatory limits for this to enter into widespread practice.

7. Conclusion

Acoustic radiation force has proved to be integral for new applications of biomedical ultrasound. Over the last three decades, there has been substantial development in the areas of elastography, phase aberration correction, manipulation of particles and cells, and biophysical modulation. ARF will continue to be used and its use will evolve and mature, and new areas for its use will emerge. Continued research and development will be targeted towards using this versatile tool to cause displacement in tissues in a noninvasive and noncontact fashion.

8. Expert Commentary

Acoustic radiation force is currently used in many biomedical applications. Currently, the main commercialized use of ARF is for measurement of mechanical properties in soft tissues. There has been considerable work done to optimize the application of ARF for the generation of internal displacements and shear waves. The depth of the target tissue dictates many parameters such as the array transducer, ultrasound frequency, dimensions of the push, and the time duration. It is generally desirable to have motion that has high bandwidth and, in the case of shear waves, propagates over a long distance.

In order to obtain tailored frequency content of the motion, temporal modulation has been employed. Responses that are broadband or have specific frequencies can be elicited using different strategies such as those described above for ARFI, SDUV, and OFUV. Likewise, to overcome issues related to shear wave attenuation, one can modify the spatial distribution or modulation of the applied ARF beams and use the constructive interference among several ARF sources to create stronger or a multiplicity of ARF sources. In essence, it may be advantageous to “flood” the FOV with ARF sources to generate motion at many spatial locations.

As was mentioned above, temporal and spatial modulation can be combined effectively to create motion with specific frequency content and spatially situated over a region within the tissue. The supersonic shear imaging, marching CUSE, and ARF crawling waves are examples of these combined techniques. Many other possible combinations could be created, by perhaps combining different spatial combinations from CUSE for example and combining with SDUV or OFUV.

Acoustic radiation force from pulsed or continuous wave transmissions has been used extensively in sorting or manipulation of small particles or cells. It has the advantage of being a relatively inexpensive way for moving particles or cells in a controlled, noncontact manner. Many biosensing and biological applications can utilize this type of technology. Considerable optimization needs to be done to be tuned for particles of different size or composition or particular types of cells. Likewise, ARF has been used for patterning of materials for bioprinting and tissue engineering applications. Bringing these applications to scale are issues that need to be addressed with further research and development.

Lastly, the bioeffects of ARF for causing desired changes in tissue such as neuromodulation or activation of cellular channels to affect a change in physiologic behavior need to be investigated in more detail. The purpose of this type of research is to better understand if ARF plays a role in these physiological changes. Additionally, using ARF can have deleterious effects on tissues due to the secondary effects of using high intensity of ultrasound such as thermal or mechanical mechanisms. Excessive repeated use of high intensity ultrasound to produce ARF could cause damage to tissues or ultrasound transducers. However, in general, clinical scanners and transducers are fairly robust and provide repeatable excitations for measurement and imaging applications.

One limitation of using ARF in tissue is the need for a substantial power source in the scanner. Adequate power supplies exist in the market, but incorporation into different ultrasound scanners is necessary to sustain ultrasound transmissions at high power. This limits the use of ARF in more modest ultrasound scanners including portable ultrasound units because of space and cost constraints, and to date has been relegated to more premium systems. Regulatory limits set for diagnostic ultrasound are adhered to and to the knowledge of the ultrasound community prevent tissue damage, but could be revisited to open up new areas or make ARF-based applications more efficacious in application areas where success rates may be diminished such as elastographic measurements at depth. However, for specialized applications such as particle and cell manipulation, the acoustic fields and ARF do not need to be as strong, because the targets are usually in an aqueous solution with very low attenuation.

One other limitation of using ARF in tissue, particularly for elastography-based applications, relies on clinical indications where the technology is efficacious. Currently, SWE has been used in liver, breast, and thyroid, and is being used in many other organs such as skeletal muscle, prostate, and kidney. With the large number of ultrasound manufacturers, there has been shown to be variation among different methods and scanners found in phantom studies [187, 188]. This level of variation has raised concerns of consistency of the measurements and comparability of studies using different scanners. Research, industry, and regulatory bodies have collaborated under the Radiological Society of North America’s Quantitative Imaging Biomarkers Alliance (RSNA QIBA) to work towards standardization of shear wave velocity measurements to address concerns related to reproducibility [189]. There is still work that needs to be done in this area to provide clinicians with confidence to use the measurements provided by different SWE modes, but efforts have been made towards developing a clinical profile for manufacturers to adhere for quality control purposes and clinical acceptance [189].

9. Five-Year View

The use of acoustic radiation force has become widely available, particularly in the elastography field where at least nine different companies have clinical systems available that can perform ARFI imaging or some form of shear wave measurement. Acoustic radiation force has the advantage of applying the force in a noninvasive and noncontact manner. This opens up numerous applications in different biomedical disciplines. More applications that utilize ARF for biosensing and tissue engineering will arise especially in the era of the need for in vivo sensing capabilities and personalized medicine. Alterations to FDA regulatory limits to increase levels of acoustic output would also provide more robust application of ARF in deep tissues, however, this may extend outside of the five year window of this perspective. Application of ARF is somewhat limited in some cases due to the need for a power supply that can produce adequate pulses for motion generation, so improvements in pulse sequences and ultrasound hardware may extend the use of ARF to more modest ultrasound systems to be used in lower resource environments.

Key Issues.

• Acoustic radiation force is used in many biomedical applications that require the deformation or displacement of soft tissues or cells.

• Spatial and temporal modulation of the ARF and the combination of the two can be used to make robust measurements in many diagnostic settings.

• ARF provides a means to focus acoustic beams by monitoring the displacement amplitude caused by the ARF excitation.

• ARF can be used extensively to move and manipulate cells, microbubbles, and other particles for applications in biosensing and tissue engineering.

• Due to the high intensity associated with ARF excitation used for producing measureable motion, bioeffects must be considered for developing ARF-based techniques.