Abstract
Genome-wide association studies (GWAS) typically search for marginal associations between a single nucleotide polymorphism (SNP) and a disease trait while gene-environment (GxE) interactions remain generally unexplored. More powerful methods beyond the simple case-control approach leverage either marginal effects or case-control ascertainment to increase power. However, these potential gains depend on assumptions whose aptness is often unclear a priori. Here, we review GxE methods and use simulations to highlight performance as a function of main and interaction effects and the association of the two factors in the source population. Substantial variation in performance between methods leads to uncertainty as to which approach is most appropriate for any given analysis. We present a framework that: (1) balances the robustness of a case-control approach with the power of the case-only approach; (2) incorporates main SNP effects; (3) allows for incorporation of prior information; and (4) allows the data to determine the most appropriate model. Our framework is based on Bayes model averaging, which provides a principled statistical method for incorporating model uncertainty. We average over inclusion of parameters corresponding to the main and GxE interaction effects and the G-E association in controls. The resulting method exploits the joint evidence for main and interaction effects while gaining power from a case-only equivalent analysis. Through simulations we demonstrate that our approach detects SNPs within a wide range of scenarios with increased power over current methods. We illustrate the approach on a gene-environment scan in the USC Children’s Health Study.
Keywords: Bayesian model, case-control studies, environmental factor, genome-wide scan, power
Introduction
Genome-Wide association studies (GWAS) have uncovered many trait-related SNPs to date, but many SNPs are likely yet undiscovered by GWAS due to insufficient power as a result of small effect sizes, low allele frequencies, or opposing effects in sample subgroups. Additionally, evidence suggests that marginal genetic effects alone may not explain all disease susceptibility (Manolio et al., 2009). It is therefore worthwhile considering GxE interactions when scanning for novel loci associations and for identifying genotypes with elevated susceptibility to complex diseases based on exposure to an environmental contributor. A conventional case-control logistic analysis is broadly acknowledged to suffer from low power to detect GxE interactions. The case-only design (Piegorsch, Weinberg, & Taylor, 1994) is an alternative which provides a substantial increase in power. However, the case-only design is subject to significant bias under non-independence of G and E in the source population, resulting in a highly increased Type I error and a large number of false discoveries. Numerous approaches have been developed to improve power while mitigating potential increases in Type I error. These include empirical Bayes (EB) (Mukherjee & Chatterjee, 2008), Bayes model averaging (BMA) (Li & Conti, 2009), numerous two-step methods (Gauderman, Zhang, Morrison, & Lewinger, 2013; Kooperberg & Leblanc, 2008; Murcray, Lewinger, & Gauderman, 2009), and two-degree of freedom joint tests of main and GxE interaction effects (Dai et al., 2012; Kraft, Yen, Stram, Morrison, & Gauderman, 2007; Tchetgen Tchetgen, 2011). In this paper, we extend the BMA approach proposed by Li and Conti (2009) and propose a novel Bayes model averaging approach to weight the case-only and case-control interaction effects within a two-degree of freedom test. We use simulations to show that this approach improves power in many scenarios while controlling the false discovery rate – even in the presence of non-independence of G and E in the source population. Our comparison study uses GxE approaches which are currently widely used, particularly powerful, similar to our novel approach, or a combination of the three. We used our proposed Bayes model averaging approach to analyze the role of air pollutants, Hispanicity and genotype on childhood asthma in the CHS dataset.
Methods
We first introduce the basic setup and notation, and briefly review standard G and GxE approaches. For simplicity, we consider a total sample size of N with equal numbers of cases and controls. Y is a binary indicator for disease status with baseline population disease risk Pr(Y = 1) = pY. Categorical exposure status is denoted as E, where E is binary for simplicity with population prevalence Pr(E = 1) = pE. Genotype is denoted as G, where for simplicity we use dominant coding (G = 1 for AA and Aa genotypes and G = 0 for aa genotypes), with Pr(G = 1) = qA as the probability of having the AA or Aa genotype.
Marginal Association Test (MA)
The most widely used method for finding an association between a genetic marker and a disease outcome in a GWAS is the marginal test of association (MA) carried out in samples of cases and controls. The MA method is typically comprised of a regression of a particular phenotype on a genetic variant (G) with a test of the association. Using a case-control sample with disease outcome Y, the MA test is typically characterized using the logistic equation:
| (1) |
with adjustment variables included when necessary. Here, βMAG denotes the log-odds ratio of G on the disease outcome, and a Wald, score, or likelihood ratio test is carried out to test the null hypothesis, βMAG = 0 of no genetic association. Within a GWAS, the MA model is repeated for each of the markers considered and tested using a specified P-value threshold α which is adjusted to maintain the family-wise error rate (FWER).
Case-Control Test of G × E Interaction (CC)
Using a sample of cases and controls, a test of GxE interaction with a binary disease outcome is often performed as a case-control (CC) model characterized by
| (2) |
Here, βccE and βccG represent the main effects of E and G respectively, while βccG×E is the log-odds ratio of the interaction of GxE. The null hypothesis of no interaction, H0: βccGxE = 0, is tested using either a Wald, score or likelihood ratio test. Though straightforward to implement and widely used, the CC test of interaction is also known to suffer from low power.
Case-Only Test of G × E Interaction (CO)
Using no information from controls, a case-only (CO) approach, where the association between the genetic variant and exposure is tested in affected individuals only, is often used as an alternative method to boost the power of detecting a GxE interaction over a CC approach. A CO logistic model is given by
| (3) |
Here, the term βcoG×E parameterizes the GxE interaction log odds ratio on disease status (Y) and in the presence of a rare disease and independence of G and E in the population, exp(βcoG×E) is a consistent estimator of the GxE interaction relative risk ratio (RR) (Piegorsch et al., 1994). The CO model yields biased estimates of effect and incorrect Type I error under violations of this independence assumption.
Weighted GxE Tests
To increase power while also mitigating bias under independence assumption violations, two methods have been introduced that combine CC and CO models as weighted averages. Li and Conti (2009) introduced a Bayes Model Averaging (BMA) approach which combines the GxE effect estimates from the two models via a weighted average determined by the posterior probabilities of each of the models. Using loglinear equivalent forms of Equation 2 (Bishop, Fienberg, & Holland, 1975) and Equation 3 (Umbach & Weinberg, 1997), βccG×E and βcoG×E are averaged using the posterior probabilities of their respective models given the data, D, hence incorporating model uncertainty within the resulting estimate. An overall interaction effect estimate is obtained by averaging the expectation of the interaction effect from each model and tested using a Wald statistic. A similar approach introduced by Mukherjee and Chatterjee (2008) is the Empirical Bayes approach, which also takes an average of GxE interaction effects from the CC and CO models. Rather than using posterior model probabilities as weights, the empirical Bayes approach uses the CC estimate, βccG×E, its variance, and the uncertainty about the independence assumption between G and E estimated by the G-E association in controls (Mukherjee & Chatterjee, 2008). Both methods consider the uncertainty of which model (CC vs. CO) is most appropriate while aiming to balance efficiency and bias when estimating the GxE interaction effect.
Two-step approaches
In a genome-wide setting, there are a variety of two-step GxE interaction methods based on an initial ‘screening’ followed by a ‘testing’ step. The screening step of a two-step procedure tests a given association and filters results based on a defined first-step P-value threshold, α1. Markers with P-values lower than α1 in the first step association test are then tested in the second step for a GxE interaction with appropriate control of the family-wise error rate, αFWER. To guarantee that Type I error is preserved at the nominal level, the test statistics used at each of the two steps must be independent. Several approaches exist for two-step methods that alter the first-step test of association (Gauderman et al., 2013; Kooperberg & Leblanc, 2008; Murcray et al., 2009). Gauderman et al. (2013) introduced the EDGE procedure, which combines the association between the disease and the genetic marker (Y-G) with the association between the environmental factor and the genetic marker (E-G) in the first step by summing the two independent test statistics, and testing the GxE interaction in step two using Equation 2. The test statistic for the Y-G association is calculated using Equation 1, while the statistic for the E-G association is calculated using a chi-square test of association between E and G in a combined case-control sample. Each test statistic has a χ2 distribution with one degree of freedom, and since the statistics are independent, their sum for the screening step has a χ2 distribution with two degrees of freedom. Step 1 P-values are ranked and the correction for multiple testing in step two of the process can occur in one of two ways. Using the subset testing approach, within the original group of W SNPs tested in step 1, a subset, w, of SNPs with P-value ≤ α1 are then included for the second step GxE test using a second threshold, αFWER/w, a Bonferroni correction for multiple testing. Alternatively, rather than a subset of SNPs, all W SNPs are tested in the second step according to a weighted significance threshold, whereby SNPs are tested against a threshold which increases in stringency with increasing screening step P-values (Ionita-Laza, McQueen, Laird, & Lange, 2007).
The EDGE approach is structurally very different from previous classes of models we have discussed and has been shown to be more powerful than many two-step methods in many of the scenarios that we use for comparing the GxE approaches (Gauderman et al., 2013). Thus, we include the EDGE approach as an important comparison to other GxE methods within our simulation study.
2 Degree of Freedom Tests
Unlike most single-degree-of-freedom test statistics of interaction, multiple-degree-of-freedom test statistics jointly test multiple parameters. The first of these tests was introduced by Kraft, et al. (2007) as a joint test of a main genetic effect and a GxE interaction effect using the CC model from Equation 2. This approach, denoted as DF2, tests the hypothesis of no main genetic effect and no GxE interaction effect (i.e., H0: βccG = βccG×E = 0) using a likelihood ratio test with two degrees of freedom. A similar test, denoted here as CO 2DF (Dai et al., 2012; Tchetgen Tchetgen, 2011), fits the MA model from Equation 1 and the CO model from Equation 3 and sums up the corresponding Wald test statistics from each of the models. The resulting test statistic has an (asymptotic) Chi-square distribution with two degrees of freedom. Because they are both constructed as omnibus tests, rejection of the null with the DF2 and CO 2DF indicates that at least one of the component parameters is equal to zero, revealing an association between a particular locus and a disease outcome but without pinpointing the driver of the association (i.e. marginal/main vs. interaction vs. both).
Novel Bayes Model Averaging Two Degree-of-Freedom Test (BMA 2DF)
We propose a Bayes model averaging (Hoeting, Madigan, Raftery, & Volinsky, 1999; A. E. Raftery, 1996; Adrian E. Raftery, Madigan, & Hoeting, 1997) two-degree-of-freedom test (BMA 2DF), that expands the BMA (Li & Conti, 2009) method. Our approach weights between the CC and CO models to test for both GxE interaction and G main effects using a multivariate Wald test with two-degrees of freedom. The approach is based on analogous loglinear models for CC and CO logistic models (Umbach & Weinberg, 1997) given respectively by:
| (4) |
| (5) |
Here, negy is the expected number of individuals per cell of the 2×2×2 contingency table of E, G, and Y, where e, g, and y denote the levels of E, G, and Y respectively. The estimators αcc0, αccG, αccE, and αccGE in Equation 4 parameterize the joint distribution of G and E in controls with αccGE denoting the association between G and E in controls. The parameters βcc0, βccG, βccE, and βccG×E in Equation 4 maintain the same interpretation they have in the logistic CC model in Equation 2, notably that βccG×E captures the CC interaction effect. Umbach & Weinberg (1997) showed that constraining αccGE = 0 (i.e. assuming independence of G-E in controls), produces a GxE interaction estimate, βcoG×E in Equation 5, that is approximately equivalent to the CO logistic estimate of βcoG×E in Equation 3 without reliance on controls and a smaller variance than βCCG×E.
We note that αco0, αcoG, and αcoE in Equation 5 parameterize the independent distribution of G and E in controls and that the CO model in Equation 5 still uses information from both cases and controls with estimates αcoG and αcoE based on marginal totals (Umbach & Weinberg, 1997). Similarly, main effects for E and G in Equation 5, βcoG and βcoE, are distinguished from βccG and βccE in Equation 4 because they are dependent on controls through marginal totals only and thus yield smaller variances. The smaller CO estimator variances results in expected improvement in power. The BMA 2DF approach takes a weighted average over the two disparate estimators, βccG and βcoG of a main G effect, as well as estimators, βccG×E and βcoG×E, for a GxE interaction from Equations 4 and 5, respectively. We then test the resulting averaged estimators, and simultaneously by using two degrees of freedom.
Letting and denote models represented in Equations 4 and 5 respectively, the BMA 2DF approach uses prior probabilities of the models, and , to be chosen by the investigator and to sum to one. Letting denote the BMA parameters of main and interaction effects and denote the BMA estimates of main and interaction effects, we define the posterior distribution of βBMAG and βBMAG×E given the observed data as:
| (6) |
For simplicity of notation, we let i ∈ {cc, co} and define the posterior model probability for each of the models given the observed data as . Here is the integrated likelihood of model over its parameters θi (Hoeting et al., 1999; Viallefont, Raftery, & Richardson, 2001), where is the prior distribution of parameters under model is estimated using a Laplace approximation as implemented in the R package GLIB (A. E. Raftery, 1996; A.E. Raftery & Richardson, 1996). and in Equation 6 denote the posterior probability distributions of βiG and βiG×E specific to model , and we estimate these model-specific effects using the expectations and from these distributions respectively. Model-specific multivariate vectors containing main and interaction effect estimates from each of the CC and CO models are denoted and respectively. The posterior mean and variance of the main and interaction effects are multivariate extensions to mean and variance presented by Hoeting et al. (1999) and are given by:
| (7) |
and
| (8) |
where
is the model-specific covariance matrix for . Letting Γ = Var(β|D), we can calculate the statistic to perform a multivariate Wald test (White, 1982). See the supplementary materials section I for more details.
Simulations
Evaluation of single-marker approaches.
We conducted single-marker simulations of a range of scenarios to compare empirical power. 1,000 replicate datasets were generated with 500 cases and 500 controls for a disease outcome (Y), a binary environmental exposure (E) with a marginal OR(E) = 1.2, and a binary genotype (G) assuming a dominant model. We used a population disease prevalence pY = 0.01, population exposure prevalence pE = 0.4, and genotype frequency of qA = 0.225. We simulated datasets across a range of log odds ratios [−1.0, +1.0] for main and interaction effects (i.e., βccG, βccG×E) as well as for G-E association, αccGE. Analyses and corresponding tests of association were performed for each scenario using α = 0.05 as the significance threshold. For scenarios simulated to have a non-zero GxE effect, empirical power was calculated testing GxE interaction as the proportion of replicates for which the given method detected a significant interaction at a given α-level. Power for the MA model was calculated as the proportion of simulated causal SNPs found to have a significant marginal effect on Y at threshold α.
Genome-wide.
Genome-wide simulations were done by generating W SNPs, d of which were designated as the disease-causing (DSL) SNPs and W – d of which were assumed to be independent of Y with neither main nor GxE interaction effect. The d ‘causal’ SNPs were simulated based on their specified associations with E and Y as in the single-marker simulation. Two sets of simulations were performed to assess power, sensitivity and specificity for discovery. The first set of simulations consisted of 1,000 replicates of N = 10,000 samples with equal numbers of cases and controls. We specified W = 1 million, d = 1, pE = 0.4, qA = 0.1, and pY = 0.05. The second set of genome-wide simulations consisted of 1,000 replicates of N = 3,750 samples with equal numbers of cases and controls, W = 10,000, d = 20, pE = 0.4, qA = 0.225 for all d SNPs, and pY = 0.01. We note that a smaller sample size was applied in the simulations used to create Receiver operating characteristic (ROC) curves in order to reduce sensitivity across all approaches and yield informative differentiation in results between methods. Such an approach was used because all methods in our comparison showed very high sensitivity, making it impossible to show differences between them. Unless otherwise specified, we simulated independent E and G, and ‘non-causal’ genetic variants with Pr(G = 1) sampled from a uniform distribution within the range [0.10, 0.40]. We set a null marginal environmental effect of OR(E) = 1.0 for both sets of simulations except for one instance in which we calculated power using induced main G effects. For induced main effects, we increased the effects of E and G with increasing interaction effect (See supplementary materials section II for more details). To measure empirical power in simulations with one designated ‘causal’ marker, we took the proportion of replicates in which the ‘causal’ marker was identified to be genome-wide significant (P-value ≤ 5 × 10−8). To create ROC plots, we repeatedly simulated sets of markers with d = 20 designated causal markers. The resulting P-values in each iteration were ordered from least to greatest, and the number of ‘causal’ markers ranked within the set of k smallest P-values, Pk were averaged across 1,000 repetitions. We then calculated sensitivity and specificity of discovery as follows:
And
Two-step approaches.
For two-step methods, we utilized the weighted hypothesis approach to test for interaction with bin size b = 5 and family-wise error rate of αFWER = 0.05, as it is generally more powerful than subset testing (Gauderman et al., 2013). For all one-step methods we used a αFWER = 0.05 with a correction for testing W SNPs, αFWER/W. Of the available two-step approaches, we include only the EDGE approach in our comparison study since Gauderman et al. showed that this approach has the best performance across a variety of scenarios. For performance comparisons among one-step approaches and the EDGE approach, empirical power was calculated as the proportion of replicates in which the designated ‘causal’ SNP was found to be significant, while Type I error was calculated as the proportion of replicates in which at least 1 of the W – d null SNPs was found to be significant.
Application to Asthma
We applied the novel BMA 2DF, MA, CC, CO and DF2 methods to the Children’s Health Study (CHS), an ongoing cohort study spanning 16 southern California communities investigating genetic and environmental factors leading to childhood respiratory outcomes. Using GWAS data on a nested case-control sample of 3,000 subjects, including 1,398 parent-identified Hispanic whites (HW) and 1,602 non-Hispanic whites (NHW) from the CHS, we analyzed GxE effects on childhood asthma. Childhood asthma status was based on questionnaire responses from parents affirming doctor-diagnosed asthma. We used a sample of 1,249 cases, of which 606 individuals were identified as Hispanic whites, and 1,751 controls, of which 792 individuals were identified as Hispanic whites. We analyzed two separate interactions: gene by self-reported Hispanicity (G x Hisp), and gene by ambient air pollution (G x PM2.5). We used microgram per cubic meter of PM2.5, particulate matter in the air smaller than 2.5 micrometers, as our measure of air pollution exposure. PM2.5 exposure was categorized into ‘low’ (≤ 15.12 μg/m3) and ‘high’ (> 15.12 μg/m3) exposure levels, classifying 58.6% of our sample as exposed to low levels and 41.4% to high levels of PM2.5. Measured genotype data consisted of 630,600 SNPs. These SNPs were phased using SHAPEIT and additional SNPs were imputed using IMPUTE2 separately for Hispanic and non-Hispanic whites against 1,000 Genomes Phase 1 integrated variant v3 phased reference. Imputed SNPs were filtered using the IMPUTE2 information metric removing SNPs with an information score < 0.7. SNPs with a combined minor allele frequency for both non-Hispanic whites and Hispanic whites less than 5% were removed from the analysis. After this QC, a total of 6,216,909 SNPs were available for analysis. In all analyses, we adjusted for sex, and Native American ancestry (<5%, 5–50%, and >50%). We further adjusted for self-reported Hispanicity in all analyses of G x PM2.5 interaction as well as for the analysis of marginal genetic effects on asthma status. Base on prior knowledge, prior weighting in the G x PM2.5 analysis was set to equally favor the CC and CO models (i.e. 1:1) while the prior weighting for the G x Hispanicity analysis was set at 100:1 odds that a CC model is more appropriate. These prior weights are supported empirically as the overdispersion parameter for the logistic CC and CO for the G x Hispanicity analyses are λ=1.0 and λ=1.8, respectively. Because we are using Laplace estimation to obtain marginal likelihoods, the computation time for the BMA 2DF model is relatively nominal. In a comparison of CPU run times, we found that the loglinear CC model in Equation 4 without specified prior distributions for parameters required 40% of the CPU run time of the CC logistic model in Equation 2. With specified priors, the CC loglinear model required 70% the run time necessary for a logistic CC model, and the BMA 2DF approach, estimating two nested loglinear models (See Equations 4 and 5), had the same run time requirements as the CC logistic approach outlined in Equation 2.
Results
Simulation
Single-marker.
Single marker simulations, depicted by heatmaps in Figure 1 show empirical power across a range of simulated main G and GxE interaction effects with each row indicating results for each approach and red indicating higher power. For the MA approach, power increases as the horizontal distance from 0 increases both to the left and the right, indicating an increase in power with larger main effects along the x-axis. Likewise for the CC, CO, and BMA approaches there is increasing power with distance in either direction along the y-axis away from a null GxE effect. Power for CC, CO, and BMA approaches increases mostly independent of changes in the main G effect. The 2-degree-of-freedom tests in Figure 1 show increasing power in both directions: increasing main effect size and GxE interaction effect size, since these approaches are testing both effects. As a result, the 2-degree-of-freedom approaches show a circular pattern around the null values of both parameters while the single-degree-of-freedom tests show a rectangular pattern surrounding null values of GxE interaction log odds. Visually, performance can be gauged by tightness of either the rectangle or the circle around the null parameter values. More frequently occuring warm colored areas, such as red and orange regions, indicate higher power for a larger proportion of the main and interaction effect pairwise combinations. For instance, the CO 2DF approach in Figure 1 has a much tighter circle surrounding the locus of null main and interaction effects, indicating higher power across more combinations of the two effects than other 2-degree-of-freedom approaches. However, Figure 1 shows the circle in the CO 2DF approach move across the three G-E association value columns, OR(G-E) = {0.8, 1.0, 1.2}, indicating a bias and an increase in Type I error with violations to the G-E independence assumption. Thus, Figure 1 shows CO 2DF to also be the most susceptible to violations to this assumption. Figure 1 also highlights the sensitivity of all models incorporating a CO design to G-E associations within the sample. While no method shows pronounced bias under the no G-E association (center) column in Figure 1, inflated Type I error rates for OR(G-E) = 0.8 and OR(G-E) = 1.2 are shown for CO, BMA, CO 2DF, and the BMA 2DF models. While these models have compromised robustness under independence violations, inflation of Type I error as the G-E association increases is largely mitigated for BMA and BMA 2DF by the models’ inherent averaging process. Figure 2 shows empirical power as a function of the G-E (αccGE) association for the CO 2DF model and the BMA 2DF approach in four scenarios. Figure 2 depicts two cases of empirical power for the CO 2DF model and the BMA 2DF test under no genetic effect with GxE interaction (A) and without GxE interaction (B). While the curves are close for very small values of αccGE, there is dramatic reduction in empirical power for the BMA 2DF test with increasing G-E association due to weighting the average more heavily toward a CC model via model posteriors. In the absence of genetic and interaction effects, empirical power effectively becomes the Type I error rate for a 2-DF test of both βG and βGxE. For scenarios in which a main effect exists (OR(G) = 1.2), the comparison in Figure 2.C and 2.D show a similar pattern with a shift upward to account for detection of a main genetic effect. More detailed Type I error across methods is displayed in Table I based on simulations of independent SNPs which do not interact with E in their effect on disease status. Table I shows Type I error across 1-step methods as measured by the proportion of SNPs identified to be statistically significant which do not have any main or interaction effects on disease status. The Type I error rate is inflated for the CO, BMA, and BMA 2DF in the presence of a G-E association, albeit less inflated for those BMA approaches weighted towards the CC model. Table I also shows Type I error (or empirical power) as measured by the proportion of SNPs identified to be statistically significant which do have a main effect on disease statust (OR(G) = 1.2) but which do not interact with E. Methods that include the CO model demonstrate an inflation with non-zero G-E association; however the BMA 2DF model has mitigated inflation compared with the CO and CO 2DF approaches which can be interpreted as power to detect the non-zero main G effect.
Figure 1.
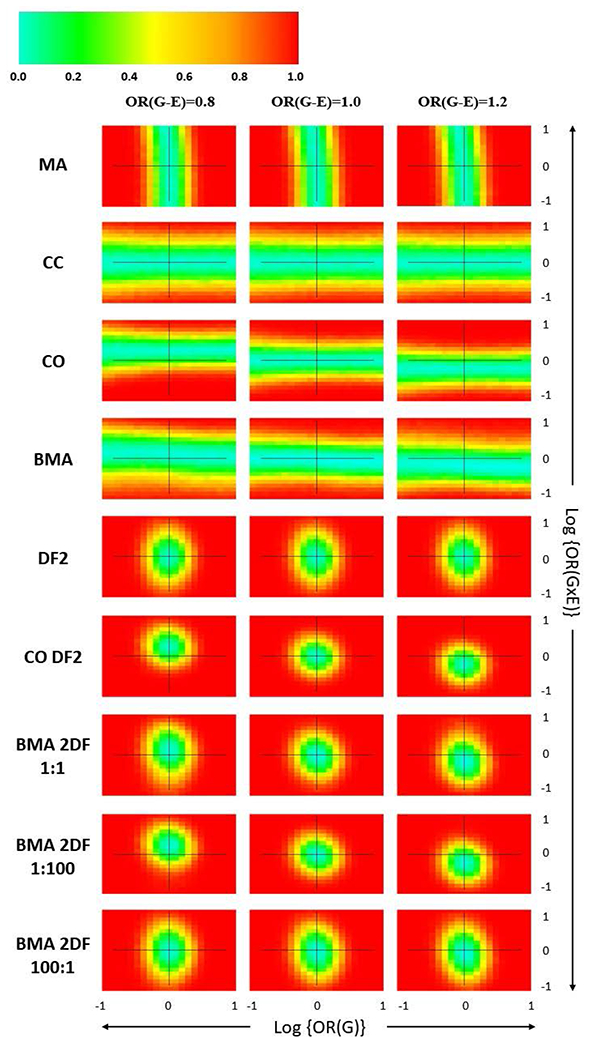
Heatmaps depicting power patterns for detection of GxE interaction across a marginal G and GxE interaction effect range r = [−1.0, +1.0] for one-step methods on 1,000 simulations of 500 cases and 500 controls. Within each heatmap plot in the grid, the x-axis shows the simulated marginal G effect with the null indicated by a vertical line. The y-axis is the simulated GxE effect with the null indicated by a horizontal line. The grid columns of Figure 1 represent the simulated G-E association in the population.
Figure 2.
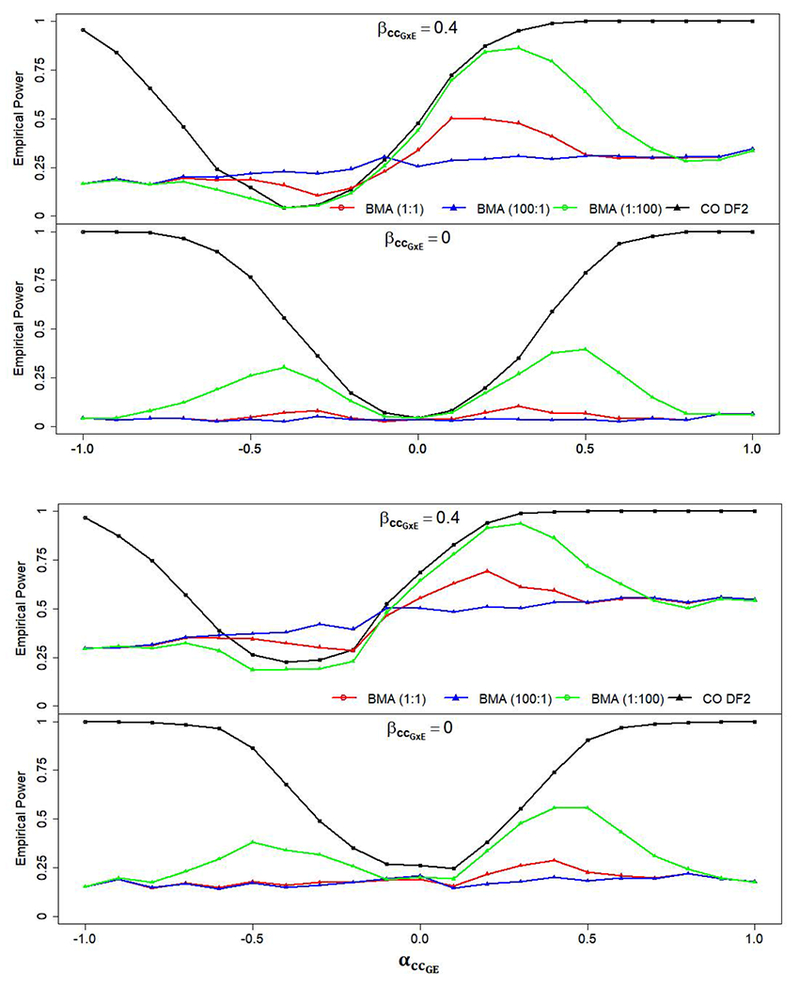
Empirical Power measured across a range r = [−1.0, +1.0] of G-E association with and without a GxE interaction and marginal effect for CO DF2 and BMA DF2 approaches. BMA(100:1) and BMA (1:100) represent an analysis of BMA DF2 with prior weighting based on a 100:1 and 1:100 odds of a CC model being more appropriate than a CO model respectively. A) OR(GxE)=1.0 & OR(G)=1.0, B) OR(GxE)=1.5 & OR(G)=1.0, C) OR(GxE)=1.0 & OR(G)=1.2, D) OR(GxE)=1.5 & OR(G)=1.2.
Table I.
Type I error rates across one – step methods in scenarios with and without G-E association
| OR(G) = 1.0 and OR(GxE) = 1.0 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | MA | CC | DF2 | CO | CO | BMA | BMA 2DF | BMA 2DF | BMA 2DF |
| 2DF | 1:1 | 1:100 | 100:1 | ||||||
| No G-E Association | 0.056 | 0.038 | 0.06 | 0.034 | 0.044 | 0.016 | 0.036 | 0.044 | 0.038 |
| G-E Association | |||||||||
| 0.8 | 0.05 | 0.058 | 0.048 | 0.228 | 0.172 | 0.054 | 0.044 | 0.13 | 0.038 |
| 1.2 | 0.052 | 0.05 | 0.052 | 0.258 | 0.198 | 0.096 | 0.072 | 0.17 | 0.04 |
| OR(G) = 1.2 and OR(GxE) = 1.0 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | MA | CC | DF2 | CO | CO | BMA | BMA 2DF | BMA 2DF | BMA 2DF |
| 2DF | 1:1 | 1:100 | 100:1 | ||||||
| No G-E Association | 0.320* | 0.048 | 0.264* | 0.062 | 0.260* | 0.028 | 0.190* | 0.200* | 0.208* |
| G-E Association | |||||||||
| 0.8 | 0.254* | 0.046 | 0.218* | 0.24 | 0.350† | 0.04 | 0.174† | 0.258† | 0.174† |
| 1.2 | 0.340* | 0.046 | 0.226* | 0.2 | 0.382† | 0.088 | 0.218† | 0.336† | 0.166† |
Error rate is calculated as the proportion of independent markers identified by a given method as having a significant interaction with E out of all independent markers simulated. Type I error rate for the marginal association model is calculated as the proportion of simulated SNPs identified by the marginal model as having a significant effect on outcome from all independent SNPs simulated. (Top) Error rates shown for null effects of both marginal G and GxE interaction; (Bottom) Error rates shown for marginal G effect OR(G)=1.2 and null GxE interaction effect;
Value is the power to detect a main G effect and does not represent inflated type I error accurately for GxE interaction
Value is a composite of 1) power to detect a main G effect and 2) type I error for testing GxE which is inflated by G-E association.
Genome-wide.
For our genome-wide simulation of 1 million SNPs with one designated causal SNP, we investigated empirical power under no violations of the G-E independence assumption. We investigated three scenarios (see Figure 3 (A-C)): A) a constant OR(G) = 1.0; B) a constant OR(G) = 1.2; and C) a main effect that increases due to induced effects from the increasing OR(GxE). These scenarios are indicated with red lines in the corresponding sub-graph to orient the figures presented within the heat maps in Figure 1. As expected, genome-wide simulations in Figure 3 show the BMA 2DF approach empirical power to consistently lie between that of the DF2 and CO 2DF models. When there is no main effect, Figure 3.A shows that a CC to CO weighting scheme of 1:100 towards a CO model coincides with the CO 2DF model, while using a 1:1 prior weighting scheme has power which lies between that of the CO 2DF and DF2 models and is nearly identical to the EDGE 2-step method. Figure 3.C shows empirical power when the main effect of G is induced by the interaction effect, rather than being held constant. In this scenario, approaches which incorporate a test of the SNP association are most sensitive and reflect the increase in the induced SNP effect with increasing power. In our second genome-wide simulation of 10,000 SNPs, we investigated the trade-off between increases in sensitivity and false discovery rates. ROC curves based on rankings in Figure 4 (A-C) show that the performance of the BMA 2DF approach again lies between the DF2 and CO DF2 models in the absence of SNPs, independent of the outcome, which are associated with E. Results in Figure 4 indicate that approaches which include a test of main effect gain sensitivity when there is a small genetic effect and lose sensitivity when there is no genetic effect. When SNPs which are associated with E but which are independent of the disease trait, are introduced into the same simulation, the CO model FDR (1-specificity) is notably higher (Figure 4.B). In this scenario, the BMA 2DF test offers improvement in sensitivity over the DF2 model while also showing an improvement in robustness over CO 2DF under violations of the independence assumption. Based on the sensitivity and specificity plots in Figure 4, it is evident that the set of top SNPs based on P-value rankings contains a large number of false-positives identified by the CO 2DF approach in the scenario where we have null SNPs associated with E. We exclude the two-step EDGE approach in Figure 4 in order to portray all SNPs tested rather than a subset resulting from a step 1 screen.
Figure 3.
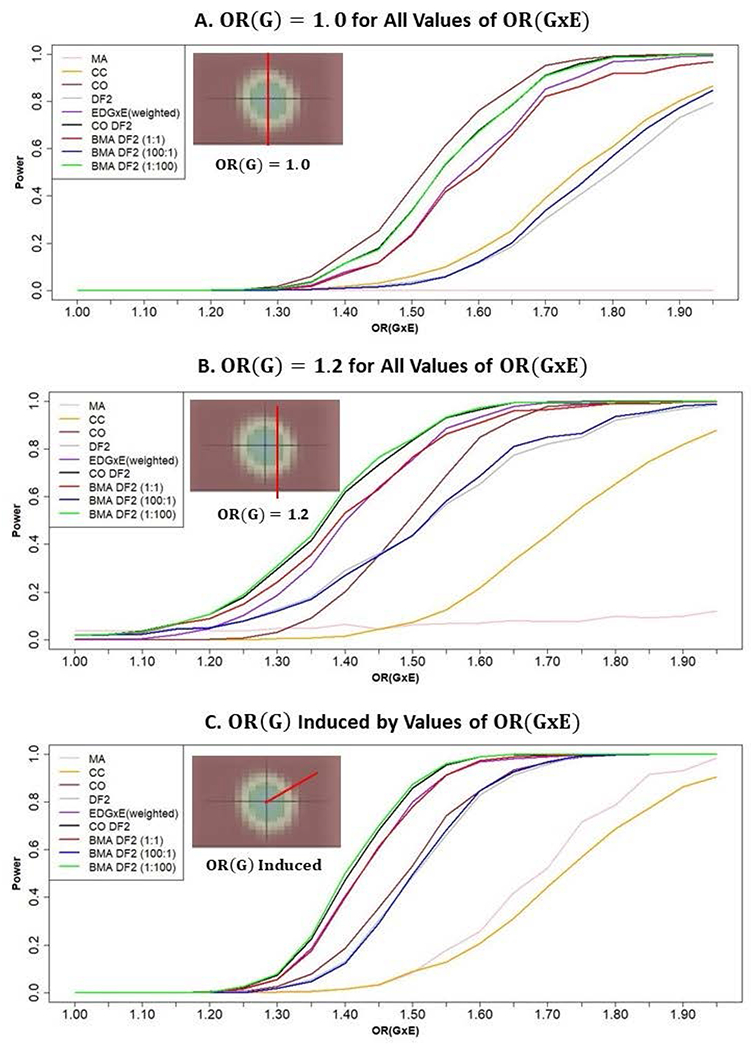
Empirical power vs. OR(GxE) with independence between G and E (plots A-C). Based on genome-wide simulations of 1 million SNPs with 1000 repetitions and one designated causal SNP in each repetition. A) OR(G) = 1.0 & OR(E) = 1.0; B) OR(G) = 1.2 & OR(E) = 1.2; C) Both OR(G) and OR(E) are induced by the interaction effect and are not held constant.
Figure 4.
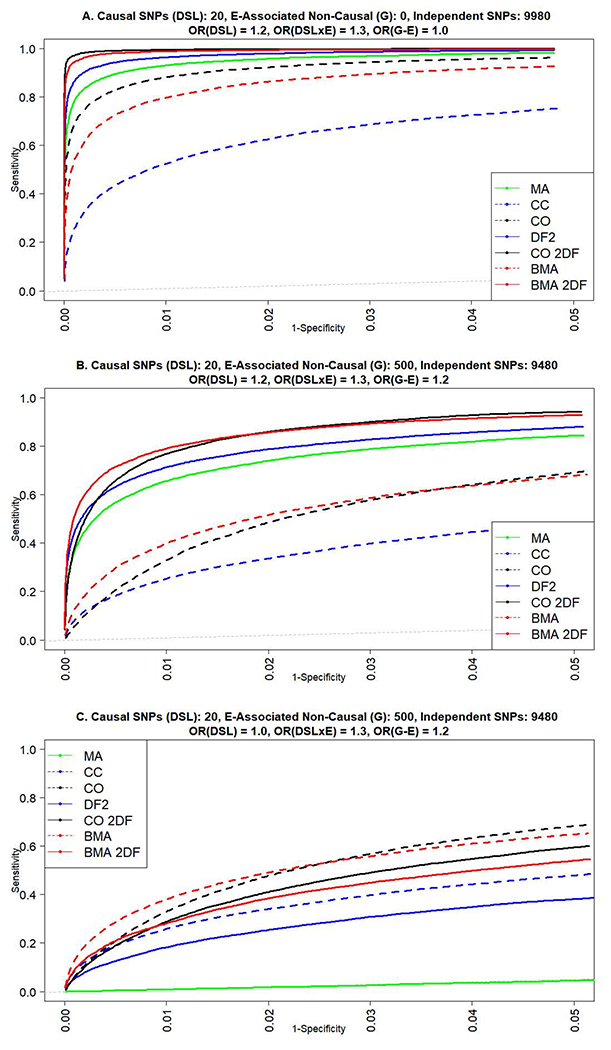
Receiver operating characteristic (ROC) curves for True and False positives in simulations of 1000 repetitions of 10,000 SNPs. A) 20 SNPs with non-zero GxE interaction (causal), no presence of non-causal SNPs associated with E, presence of marginal effect of causal SNPs. B) 20 SNPs with non-zero GxE interaction (causal), 500 non-causal SNPs associated with E, presence of marginal effect of causal SNPs. C) 20 SNPs with non-zero GxE interaction (causal), 500 non-causal SNPs associated with E, no marginal effect of causal SNPs.
Application to Asthma
In our analysis of G x PM2.5 interaction on asthma, the BMA 2DF approach identified a genome-wide significant region on chromosome 22, with the most significant SNP in the region having a P-value of 5.81 × 10−9 (Table II). Table II also shows the same region identified by the CC and DF2 models as having a significant interaction with PM2.5 on asthma. The MA model shows no main effect of the region on asthma while the CO model produces P-values which are low in the region, but do not reach genome-wide significance. Thus, the finding of rs62227671 by the BMA 2DF approach is largely driven by its adherence to the CC model with a posterior probability for the CC model of 0.993. A second region identified as marginally genome-wide significant by the BMA DF2 model on chromosome 20, rs6122625 (BMA 2DF P-value 5.97 × 10−8), was not identified by any of the other approaches as being genome-wide significant or marginally significant. While rs6122625 has no marginal effect on asthma (MA P-value 3.77 × 10−1), both CC and CO models yield relatively small P-values, implying that the finding is driven by the interaction alone, which is also true of the subsequent marginally significant BMA 2DF findings on chromosomes 2 and 8 for the G x PM2.5 analysis. The BMA 2DF test identifies rs6866110 on chromosome 5 as marginally significant (P-value 3.24 × 10−7) as well while the MA, CC and CO methods show relatively weaker signals. To investigate the weak signals from other approaches, we examine the marginal effect of rs6866110 by PM2.5 exposure group in Table IV. Table IV shows the marginal effects of rs6866110 in opposite directions according to the low/high exposure group.
Table II.
Top loci ranked by BMA 2DF P-value for G × PM2.5 interaction on asthma susceptibility
| Marginal (MA) | Case-Control (CC) | Case-Only (CO) | DF2 | BMA 2DF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chr | SNP | MAF | OR(G) | P-Value | OR(GxE) | P-Value | OR(GxE) | P-Value | P-Value | Posterior CC | Posterior CO | P-Value |
| 22 | rs62227671 | 0.25 | 0.92 | 2.68E-01 | 2.57 | 7.61E-10 | 1.83 | 4.06E-07 | 2.88E-08 | 0.993 | 0.007 | 5.81E-09 |
| 20 | rs6122625 | 0.11 | 0.92 | 3.77E-01 | 2.48 | 2.17E-06 | 1.91 | 3.05E-05 | 7.83E-06 | 0.024 | 0.976 | 5.97E-08 |
| 2 | rs57504074 | 0.13 | 0.97 | 7.61E-01 | 2.03 | 6.82E-05 | 1.81 | 2.40E-05 | 3.26E-04 | 0.031 | 0.969 | 2.84E-07 |
| 8 | rs11137048 | 0.08 | 1.16 | 1.82E-01 | 2.20 | 2.09E-04 | 1.92 | 7.71E-05 | 3.90E-04 | 0.026 | 0.974 | 2.99E-07 |
| 5 | rs6866110 | 0.08 | 1.5 | 3.54E-01 | 0.50 | 1.06E-03 | 0.59 | 1.50E-03 | 7.64E-06 | 0.028 | 0.972 | 3.24E-07 |
Table IV.
Stratified marginal analysis of rs6866110 and rs4672623 by exposure group
| Analysis | SNP | Exposure Group | Marginal OR(G) | Strata Specific |
|---|---|---|---|---|
| P-value | ||||
| G x PM2.5 | ||||
| rs6866110 | PM2.5 ≤ 15.12 | 1.89 | 1.62E-06 | |
| PM2.5 > 15.12 | 0.94 | 7.10E-01 | ||
| G x Hispanicity | ||||
| rs4672623 | Non-Hispanic White | 1.73 | 9.89E-08 | |
| Hispanic White | 0.71 | 0.00285 |
In the analysis of G x Hispanicity, the BMA 2DF approach identified a genome-wide significant SNP, rs4672623 (P-value 9.48 × 10−9) on chromosome 2 in Table III. Results for rs4672623 from the CC analysis show a marginally significant interaction, while the marginal test for association between rs4672623 and asthma shows a much weaker signal in the opposite direction from that of the GxE interaction. Due to effects of rs4672623 in opposite directions per Hispanicity group (OR[G|E = NHW] = 1.73 and OR[G|E = HW] = 0.71) as shown in Table IV, the marginal effect of G in the combined sample is weakened. However, testing both G and the interaction together in a 2-degree-of-freedom setting as both the BMA 2DF and DF2 methods do, yields a signal which reaches genome-wide significance. Additionally, the BMA 2DF test identified 3 marginally significant regions on chromosomes 8, 1, and 6. Each of these regions exhibit protective effects according to marginal tests of association between G and asthma, and interact with Hispanicity with effects in the same direction within a CC analysis. Table III shows rs10955770 on chromosome 8 has opposite CC and CO effects. Assuming this is a result of a G-E association in controls, the 1:100 prior weighting scheme makes the BMA 2DF P-value more plausible since it results in posteriors heavily in favor of a CC model.
Table III.
Top loci ranked by BMA P-value for G × Hispanicity interaction on asthma susceptibility
| Marginal (MA) | Case-Control (CC) | Case-Only (CO) | DF2 | BMA 2DF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chr | SNP | MAF | OR(G) | P-Value | OR(GxE) | P-Value | OR(GxE) | P-Value | P-Value | Posterior CC | Posterior CO | P-Value |
| 2 | rs4672623 | 0.34 | 1.23 | 6.98E-03 | 0.44 | 1.66E-07 | 0.69 | 6.31E-02 | 3.64E-08 | 1.000 | 0.000 | 9.48E-09 |
| 8 | rs10955770 | 0.15 | 0.75 | 1.30E-03 | 0.50 | 1.66E-04 | 1.45 | 1.37E-01 | 1.93E-06 | 1.000 | 0.000 | 7.98E-08 |
| 1 | rs70620 | 0.26 | 0.78 | 1.05E-03 | 0.57 | 2.78E-04 | 0.93 | 7.13E-01 | 3.16E-06 | 1.000 | 0.000 | 1.74E-07 |
| 6 | rs12664685 | 0.16 | 0.86 | 9.44E-02 | 0.46 | 1.02E-05 | 0.95 | 8.45E-01 | 1.20E-05 | 1.000 | 0.000 | 2.46E-07 |
Discussion
Within a genome-wide interaction scan, the BMA 2DF approach can provide a robust and powerful tool for identifying genetic loci with small effect sizes on disease outcomes, while also providing the flexibility of incorporating prior knowledge regarding the associations of G and E in the population. By producing a test which combines CC and CO methods and using two degrees of freedom to incorporate a test of main genetic effects along with interaction effects, the BMA 2DF method can provide increased power over many existing methods. BMA 2DF results are also more reliable than the most powerful CO and CO 2DF tests because we have shown that Type I error and bias are minimized by the BMA 2DF approach compared to these methods in Table I and Figure 2. Single-SNP and genome-wide simulation results presented have shown that the BMA 2DF approach is an appropriate method to use in situations where there may be G-E association present, particularly where there may be numerous genomic regions correlated with the environmental factor. Genome-wide simulations in Figure 3.B have shown the BMA 2DF method is also an appropriate approach in the situation where there are numerous SNPs which have null interaction and main effects on the outcome but are nevertheless associated with the environmental factor. In this specific situation, the BMA 2DF method parses out spurious associations by weighting more heavily to a CC analysis and gains robustness. In contrast, the CO 2DF method becomes subject to identifying spurious associations.
In our analysis of G × PM2.5 exposure using the Children’s Health Study, we identified a novel region on chromosome 22 which has a genome-wide significant interaction with PM2.5 (P-value = 5.8 × 10−9) on childhood asthma. The SNP with the greatest effect size in this locus, rs62227671, is in the PARVB gene region, a gene involved in cytoskeleton organization and cell adhesion, and with no previous record of association with either childhood asthma, or as an effect modifier of PM2.5 on childhood asthma. From Table II we can see that the association is largely driven by the interaction effect from a CC model where the interaction effect, OR(GxE) = 2.57 is highly significant (P-value = 7.6 × 1010). Since this SNP has no significant effect on childhood asthma marginally, the SNP would have likely been overlooked by a standard GWAS using an MA approach. Additional examination of the relationship of rs62227671 and PM2.5 to childhood asthma is necessary to determine the true effects and mechanisms of action of this genetic region on childhood asthma.
Due to the likely correlation expected between genetic markers and self-reported Hispanicity, we used a prior weighting scheme based on a CC to CO model odds of 100:1, favoring more weight toward a CC model. Using this weighting scheme, the BMA 2DF method identified rs4672623 on chromosome 2 as having a genome-wide significant interaction with self-identified Hispanicity (P-value = 9.48 × 10−9) as shown in Table III. This association is largely driven by the CC model, however it is not driven by the CC result alone. The MA and CO associations, though modest, appear also to be contributing to the BMA 2DF signal in this region. We note that like the BMA 2DF approach, the DF2 model also captures the association as genome-wide significant by its incorporation of the SNP effect in its 2-degree-of-freedom testing scheme. SNP rs4672623 is in the ErbB4 gene region on chromosome 2, which has been shown to regulate late fetal lung development (Liu et al., 2010; Zscheppang, Giese, Hoenzke, Wiegel, & Dammann, 2013), suggesting that the association is plausible. Further investigation is necessary to determine the true role of rs4672623 on childhood asthma in Hispanic white and non-Hispanic white children.
In practice, the BMA 2DF model is recommended for identifying genomic regions which interact with an environmental agent on a disease outcome in the context of a genome-wide study. By design, the approach is not meant to make inferences on genomic regions already known or suspected to be associated with an outcome as in candidate gene studies. Consideration should be given to the possible associations between the environmental factor E and genetic markers G when implementing the BMA 2DF approach. If association is suspected in the population studied, measures should be taken to account for likely bias which may result under violations of the G-E independence assumption. As in our G x Hispanicity analysis, directly assigning prior model weights to favor a CC model is an effective way to ensure that bias and spurious associations are kept to a minimum when a G-E association is suspected prior to analysis. We recommend setting prior model weights according to a 1:1 odds favoring both models equally in all scenarios where G-E correlation is not known or suspected. Consideration should also be given to setting prior effect hyperparameters as it is possible to influence the BMA 2DF approach’s inclination toward either the CC or CO approach by altering the precision around the prior mean of the αccGE model parameter. Given that the CC model (see Equation 4) is distinguished from the CO model (see Equation 5) by the assumption of a non-zero G-E association, decreasing the precision around the G-E association parameter αccGE allows for greater acceptance of G-E association in controls while still identifying αccG as zero and weighting toward a CO model. Some user-specified hyperparameters (Kass & Raftery, 1995; A. E. a. R. Raftery, S., 1996), can influence the posterior weight distribution between CC and CO models; however, we recommend using prior model weights exclusively to inform model posteriors. We have used values as recommended by A. E. Raftery, Madigan, D.M. and Hoeting, J. (1993) to obtain all results presented in this paper. See supplementary materials for details of hyperparameter values.
Due to the parameterization of the BMA 2DF model as a loglinear model, it is necessary to implement the approach using categorical variables in order to maintain equivalence of parameters between the logistic and loglinear models (Umbach & Weinberg, 1997). We have presented results and simulations using dichotomous environmental and confounding variables, but variables with three or more categories are also appropriate. We have used a dominant genetic model by analyzing genotypes as G = 0 or G = 1; however additive, dominant, recessive, or codominant analyses are also possible using the BMA 2DF approach, though additional levels of G will result in larger contingency tables (e.g., Trinary coding for G creates a 2×2×3 table whereas binary coding creates a 2×2×2 table) (Umbach & Weinberg, 1997). The parameterization of the BMA 2DF approach as a loglinear model poses additional considerations pertaining to confounding covariates. Such variables should be categorical and their inclusion must be carefully designed to retain equivalency of terms in loglinear equations to their counterparts in models using the logistic link (Agresti, 2002). While continuous variables can be used for adjustment in the BMA 2DF approach, the resulting estimates may no longer have the direct interpretation as when categorical variables are used. Equating models with logistic and loglinear links is beyond the scope of this paper, and we recommend that investigators maintain parsimonious models whenever possible. We have presented simulations with a case:control ratio of 1:1; however, we expect both power and Type I error of the BMA 2DF approach to increase as the number of cases increase and decrease with increasing controls (Li & Conti, 2009). Software to conduct our novel BMA 2DF approach is available as an R package with details provided within the supplementary materials section IV.
Supplementary Material
Acknowledgments
Research reported in this publication was supported by the National Institutes of Health under award numbers P01CA196569, R01CA201407, R01CA140561, ES024844, and R01ES016813, and by the National Institute of Environmental Health Sciences of the National Institutes of Health under Award Numbers P30ES007048 and T32ES013678. No conflict of interested is claimed.
References
- Agresti A (2002). Loglinear Models for Contingency Tables Categorical Data Analysis (2 ed., pp. 314–356). New Jersey: John Wiley & Sons. [Google Scholar]
- Bishop YMM, Fienberg SE, & Holland PW (1975). Discrete multivariate analysis : theory and practice. Cambridge, Mass. ; London: M.I.T. Press. [Google Scholar]
- Dai JY, Logsdon BA, Huang Y, Hsu L, Reiner AP, Prentice RL, & Kooperberg C (2012). Simultaneously testing for marginal genetic association and gene-environment interaction. Am J Epidemiol, 176(2), 164–173. doi: 10.1093/aje/kwr521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman WJ, Zhang P, Morrison JL, & Lewinger JP (2013). Finding novel genes by testing G x E interactions in a genome-wide association study. Genet Epidemiol , 37(6), 603–613. doi: 10.1002/gepi.21748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoeting JA, Madigan D, Raftery AE, & Volinsky CT (1999). Bayesian model averaging: A tutorial. Statistical Science, 14(4), 382–401. [Google Scholar]
- Ionita-Laza I, McQueen MB, Laird NM, & Lange C (2007). Genomewide weighted hypothesis testing in family-based association studies, with an application to a 100K scan. Am J Hum Genet, 81(3), 607–614. doi: 10.1086/519748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kass RE, & Raftery AE (1995). Bayes Factors. Journal of the American Statistical Association, 90(430), 773–795. doi: 10.1080/01621459.1995.10476572 [DOI] [Google Scholar]
- Kooperberg C, & Leblanc M (2008). Increasing the power of identifying gene x gene interactions in genome-wide association studies. Genet Epidemiol, 32(3), 255–263. doi: 10.1002/gepi.20300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft P, Yen YC, Stram DO, Morrison J, & Gauderman WJ (2007). Exploiting gene-environment interaction to detect genetic associations. Hum Hered, 63(2), 111–119. doi: 10.1159/000099183 [DOI] [PubMed] [Google Scholar]
- Li D, & Conti DV (2009). Detecting gene-environment interactions using a combined case-only and case-control approach. Am J Epidemiol, 169(4), 497–504. doi: 10.1093/aje/kwn339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Purevdorj E, Zscheppang K, von Mayersbach D, Behrens J, Brinkhaus MJ, … Dammann CE (2010). ErbB4 regulates the timely progression of late fetal lung development. Biochim Biophys Acta, 1803(7), 832–839. doi: 10.1016/j.bbamcr.2010.03.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, … Visscher PM (2009). Finding the missing heritability of complex diseases. Nature, 461(7265), 747–753. doi: 10.1038/nature08494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee B, & Chatterjee N (2008). Exploiting gene-environment independence for analysis of case-control studies: an empirical Bayes-type shrinkage estimator to trade-off between bias and efficiency. Biometrics, 64(3), 685–694. doi: 10.1111/j.1541-0420.2007.00953.x [DOI] [PubMed] [Google Scholar]
- Murcray CE, Lewinger JP, & Gauderman WJ (2009). Gene-environment interaction in genome-wide association studies. Am J Epidemiol, 169(2), 219–226. doi: 10.1093/aje/kwn353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piegorsch WW, Weinberg CR, & Taylor JA (1994). Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat Med, 13(2), 153–162. [DOI] [PubMed] [Google Scholar]
- Raftery AE (1996). Approximate Bayes factors and accounting for model uncertainty in generalized linear models Biometrika, 83(2), 251–266. [Google Scholar]
- Raftery AE, Madigan D, & Hoeting JA (1997). Bayesian Model Averaging for Linear Regression Models Journal of the American Statistical Association, 92(437), 179–191. [Google Scholar]
- Raftery AE, Madigan DM and Hoeting J (1993). Model selection and accounting for model uncertainty in linear regression models (U. o. W. Department of Statistics, Trans.) Technical Report. [Google Scholar]
- Raftery AE, & Richardson S (1996). Model selection for generalized linear models via GLIB, with application to epidemiology In Stangl D. A. B. a. D. K. (Ed.), Bayesian Biostatistics (pp. 321–354). New York: Marcel Dekker. [Google Scholar]
- Raftery A. E. a. R. S (1996). Model selection for generalized linear models via GLIB, with application to epidemiology In Stangl D. A. B. a. D. K. (Ed.), Bayesian Biostatistics (pp. 321–354). New York: Marcel Dekker. [Google Scholar]
- Tchetgen Tchetgen E (2011). Robust discovery of genetic associations incorporating gene-environment interaction and independence. Epidemiology, 22(2), 262–272. doi: 10.1097/EDE.0b013e318207ffc3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umbach DM, & Weinberg CR (1997). Designing and analysing case-control studies to exploit independence of genotype and exposure. Stat Med, 16(15), 1731–1743. [DOI] [PubMed] [Google Scholar]
- Viallefont V, Raftery AE, & Richardson S (2001). Variable selection and Bayesian model averaging in case-control studies. Stat Med, 20(21), 3215–3230. [DOI] [PubMed] [Google Scholar]
- White H (1982). Maximum-Likelihood Estimation of Mis-Specified Models. Econometrica, 50(1), 1–25. doi: Doi 10.2307/1912526 [DOI] [Google Scholar]
- Zscheppang K, Giese U, Hoenzke S, Wiegel D, & Dammann CEL (2013). ErbB4 is an upstream regulator of TTF-1 fetal mouse lung type II cell development in vitro. Biochim Biophys Acta, 1833(12), 2690–2702. doi: 10.1016/j.bbamcr.2013.06.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


