Estimating cross-population genetic correlations of causal effect sizes

Abstract

Recent studies have examined genetic correlations of single nucleotide polymorphism (SNP) effect sizes across pairs of populations to better understand the genetic architectures of complex traits. These studies have estimated ρ_g, the cross-population correlation of joint-fit effect sizes at genotyped SNPs. However, the value of ρ_g depends both on the cross-population correlation of true causal effect sizes (ρ_b) and on the similarity in linkage disequilibrium (LD) patterns in the two populations, which drive tagging effects. Here, we derive the value of the ratio ρ_g/ρ_b as a function of LD in each population. By applying existing methods to obtain estimates of ρ_g, we can use this ratio to estimate ρ_b. Our estimates of ρ_b were equal to 0.55 (s.e. 0.14) between Europeans and East Asians averaged across 9 traits in the Genetic Epidemiology Research on Adult Health and Aging (GERA) data set, 0.54 (s.e. 0.18) between Europeans and South Asians averaged across 13 traits in the UK Biobank data set, and 0.48 (s.e. 0.06) and 0.65 (s.e. 0.09) between Europeans and East Asians in summary statistic data sets for type 2 diabetes and rheumatoid arthritis, respectively. These results implicate substantially different causal genetic architectures across continental populations.

Introduction

There has been substantial recent interest in comparing the genetic architecture of complex traits across world populations (de Candia et al., 2013, Mancuso et al., 2016, Brown et al., 2016). The global phenotypic distributions of complex traits can vary based on a combination of genetic and environmental factors (Robinson et al., 2015, Burt et al., 1995), and uncovering these factors is key to both understanding complex traits and ensuring that medical genetics research is globally equitable(Popejoy and Fullerton, 2016). Multi-ethnic studies have analyzed the replication rates of associations from genome-wide association studies (GWAS)(Marigorta and Navarro, 2013), improved fine-mapping resolution(Zaitlen et al., 2010, Kichaev and Pasaniuc, 2015), increased meta-analysis power(Mahajan et al., 2014, Coram et al., 2015, Morris, 2011), and assessed the global relationships between allelic effect sizes via the genetic correlations(de Candia et al., 2013, Mancuso et al., 2016, Brown et al., 2016). However, differences in joint-fit effect sizes are influenced both by differences in causal variant effect sizes and by differences in linkage disequilibrium (LD) patterns between the populations. In this study, we derive an approach for estimating genetic correlations of causal variant effect sizes across populations, leveraging data from densely genotyped reference panels to apply a correction factor to conventional estimates of genetic correlations of joint-fit effect sizes.

The cross-population genetic correlation of joint-fit effect sizes (ρ_g) is a scalar quantity that summarizes the similarity of joint-fit allelic effects between two populations(de Candia et al., 2013, Mancuso et al., 2016, Brown et al., 2016). It is defined as the correlation between the vectors of joint-fit effect sizes at single nucleotide polymorphisms (SNPs) shared between two populations (see Materials and Methods). It is closely related to the genetic correlation of two phenotypes in a single population, which is a scalar quantity that summarizes the shared genetic architecture between the traits (Lee et al., 2013, Bulik-Sullivan et al., 2015a). Rather than focusing on a limited number of GWAS associations, the cross-population genetic correlation provides a genome-wide estimate of the similarity in genetic effects between the two populations.

Several recent studies have estimated cross-population genetic correlations (de Candia et al., 2013, Mancuso et al., 2016, Brown et al., 2016) by extending previous methods to estimate cross-trait genetic correlations from either raw genotype/phenotype data(Lee et al., 2012a, Lee et al., 2012b, Lee et al., 2013) or summary association statistic data(Bulik-Sullivan et al., 2015a). These studies estimated the correlation of joint-fit effect sizes at genotyped SNPs that are shared between the populations. However, ρ_g may depend on patterns of LD between SNPs, which differ across populations (Lee et al., 2013). For example, consider the case of an untyped causal SNP u with the same effect size in two populations, and two SNPs t₁ and t₂ that are genotyped in both populations. If t₁ perfectly tags u in population 1 (but not in population 2), and t₂ perfectly tags u in population 2 (but not in population 1), then the ρ_g at those genotyped SNPs will be 0 despite identical causal effects in the two populations.

In contrast, our goal here is to estimate the cross-population correlation of causal effect sizes (ρ_b; see Materials and Methods). To accomplish this, we derive the value of the ratio ρ_g/ρ_b as a function of LD patterns in each population, which can be obtained from a reference panel such as 1000 Genomes(Auton et al., 2015). We first estimate ρ_g as in previous studies, and then divide this estimate by the value of the ratio ρ_g/ρ_b to obtain an estimate of ρ_b. We validate our method using simulations, and apply the method to raw genotype/phenotype and summary association statistic data sets with 46K-116K European samples and 2K-23K East Asian or South Asian samples.

Materials and Methods

Genotype-phenotype model

For population k, let g_k,i denote the joint-fit effect size at SNP i in population k, so that g_k is the vector of joint-fit effect sizes at genotyped SNPs. Similarly, let b_k denote the vector of causal effect sizes at all SNPs (in practice, reference panel SNPs with minor allele frequency (MAF)>1%). We note that g_k and b_k are population-level parameters rather than estimates in a finite sample, but g_k can be viewed as the value of joint-fit effect size estimates in the limit of infinite sample size. We also note that values of g_k, but not b_k, depend on the LD patterns in the population and on the set of genotyped SNPs. We use “genotyped SNPs” as shorthand to denote the set of SNPs for which raw genotype/phenotype data or summary association statistic data is available; in some cases this may include both genotyped and imputed SNPs.

Let the heritability at genotyped SNPs of the trait in populations 1 and 2 be $h_1^2$ and $h_2^2$, respectively¹⁸. Likewise, let the heritability at causal SNPs in populations 1 and 2 be ${\sigma }_1^2$ and ${\sigma }_2^2$, respectively. We assume the additive infinitesimal model for a quantitative phenotype,

$$Y_k=X_{A,\mathrm{ }k}{b}_k+e_{b,k}$$

where Y_k is an N_k × 1 vector of phenotypes in N_k individuals from population k, X_A,k is an N_k × M matrix of mean-centered genotypes at all M SNPs, $b_k~N(0,{{\sigma }_k^{2}I}_M)\mathrm{ }$ is an M × 1 vector of causal effect sizes and $e_{b,k}~N(0,\left(1-{\sigma }_k^2\right)I_M)$ is an N_k × 1 vector of environmental noise.

For a fixed set of M_G genotyped SNPs, there also exists a vector of joint-fit effect sizes g_k such that

$$Y_k=X_{G,k}{g}_k+e_{g,k}$$

where X_G,k has dimension N_k × M_G and e_g,k is scaled such that the heritability explained by genotyped SNPs(Yang et al., 2010) is $h_k^2$. Here, A denotes all SNPs and G denotes genotyped SNPs, so that X_G,k represents a subset of the SNPs in X_A,k. In the first model, where all SNPs are observed, the vector e_b,k represents environmental noise. In the second model e_g,k represents a combination of environmental noise and the remaining un-modeled SNP effects. Thus, Var(e_g,k) ≥ Var(e_b,k) and $h_k^2\le {\sigma }_k^2$ We can relate g_k and b_k via

$$g_k=\underset{N\to \mathrm{\infty }}{\text{lim}}\widehat{g_k}=\underset{N\to \mathrm{\infty }}{\text{lim}}{\left({X_{G,k}^{T}X}_{G,k}\right)}^{-1}\left({X_{G,k}^{T}X}_k\right)b_k+\underset{N\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{\left({X_{G,k}^{T}X}_{G,k}\right)}^{-1}{X}_{G,k}^T{e}_{b,k}=S_{GG}^{-1}{S}_{GA}{b}_k\mathrm{ },$$

where the last step follows from the law of large numbers and the fact that E[e_b,k] = 0. Here, we introduce S as the M × M SNP cross-covariance matrix, which can be partitioned into genotyped and untyped SNPs (where G denotes genotyped SNPs, U denotes untyped SNPs and A denotes all SNPs):

$$S=\left(\begin{array}{c}{S}_{GA}\\ S_{UA}\end{array}\right)=\left(\begin{array}{cc}{S}_{GG}& S_{GU}\\ S_{UG}& S_{UU}\end{array}\right)\mathrm{ }.$$

The above model is based on genotypes X_{{G,A}, k} that have been mean-centered but not normalized. It may also be of interest to consider mean-centered, normalized genotypes W_k. We can then define normalized causal effect sizes β_k (instead of b_k) and normalized joint-fit effect sizes γ_k (instead of g_k), and relate γ_k and β_k using a normalized SNP cross-correlation matrix Σ_k. We employ this approach when estimating ρ_γ the cross-population correlation of normalized joint-fit effect sizes, and ρ_β, the cross-population correlation of normalized causal effect sizes. We note that previous work has reported similar estimates of ρ_γ and ρ_g, representing correlations of joint-fit effect sizes with or without normalization(Brown et al., 2016). We focus the derivations below on quantities without normalization (b, g, S, ρ_b, ρ_g), but all derivations are analogous when employing normalization (β, γ, Σ, ρ_β, ρ_γ).

Definition of ρ_g and ρ_b

We define the cross-population genetic correlation at genotyped SNPs as the correlation between g₁ and g₂,

$${\rho }_g=corr\left(g_1,g_2\right)=\frac{{\sum }_i{g}_{1,i}{g}_{2,i}}{\sqrt{h_1^2{h}_2^2}}.$$

Likewise, we define the cross-population genetic correlation at causal SNPs as the correlation between b₁ and b_2,

$${\rho }_b=corr\left(b_1,b_2\right)=\frac{{\sum }_i{b}_{1,i}{b}_{2,i}}{\sqrt{{\sigma }_1^2{\sigma }_2^2}}.$$

Based on these definitions, it follows that ρ_g (but not ρ_b) depends on the LD patterns in the two populations and on the set of genotyped SNPs.

The first step of our method for estimating ρ_b is to estimate ρ_g, the cross-population correlation of joint-fit effect sizes. When raw genotype/phenotype data is available, we use bivariate REML(Lee et al., 2013, Lee et al., 2012a, Lee et al., 2012b), as implemented in GCTA (see Web Resources). When only summary association statistic data is available, we use Popcorn(Brown et al., 2016) (see Web Resources), a maximum-likelihood based method that analyzes summary statistics and population-specific LD information from a reference panel.

Estimating ρ_g/ρ_b

The second step of our method for estimating ρ_b is to estimate the ratio ρ_g/ρ_b, which we derive as a function of LD in each population. We then divide our estimate of ρ_g by the value of ρ_g/ρ_b to obtain an estimate of ρ_b. In practice, this derivation requires that we estimate S, the cross-covariance LD matrix of all SNPs. We estimate S using an LD reference panel, because all SNP genotypes are unavailable in analyses of summary statistics and because SNP genotypes at untyped SNPs are unavailable in analyses of raw genotypes/phenotypes.

As noted above, the joint-fit effect sizes g (at genotyped SNPs) can be viewed as the value of joint-fit effect size estimates in the limit of infinite sample size:

$$g_k=\underset{N_k\to \mathrm{\infty }}{\text{lim}}{\widehat{g}}_k=\underset{N_k\to \mathrm{\infty }}{\text{lim}}{\left({X_{G,k}^{T}X}_{G,k}\right)}^{-1}{X}_{G,k}^T{Y}_k$$

$$=\underset{N_k\to \mathrm{\infty }}{\text{lim}}{\left({X_{G,k}^{T}X}_{G,k}\right)}^{-1}{X}_{G,k}^T\left[X_{A,k}{b}_k+e_{b,k}\right]$$

$$=\underset{N_k\to \mathrm{\infty }}{\text{lim}}{\left(X_{G,k}^T{X}_{G,k}\right)}^{-1}{X}_{G,k}^T{X}_{A,k}{b}_k$$

$$={\left[S_{GG}^{\left(k\right)}\right]}^{-1}{S}_{GA}^{\left(k\right)}{b}_k$$

where X_A,k is the N_k × M matrix of mean-centered genotypes for all SNPs in population k, $S_{GG}^{\left(k\right)}$ is the M_G × M_G cross-covariance sub-matrix between genotyped SNPs in population k and $S_{GA}^{\left(k\right)}$ is that M_G × M cross-covariance sub-matrix between genotyped SNPs and all SNPs in population k. It follows that $S_{GG}^{\left(k\right)}{g}_k=S_{GA}^{\left(k\right)}{b}_k$ and therefore that

$$Corr\left(S_{GG}^{\left(1\right)}{g}_1,\mathrm{ }{S}_{GG}^{\left(2\right)}{g}_2\right)=Corr\left(S_{GA}^{\left(1\right)}{b}_1,S_{GA}^{\left(2\right)}{b}_2\right).$$

where by Corr we refer to the scalar-valued correlation, rather than the matrix-valued cross-correlation. We now relate the right hand side of this equation to ρ_b. From the fact that E[b_k] = 0_M (the 0-vector) and properties of the trace, it follows that

$$Cov\left(S_{GA}^{\left(1\right)}{b}_1,S_{GA}^{\left(2\right)}{b}_2\right)=E\left[{\left(S_{GA}^{\left(1\right)}{b}_1-E\left[S_{GA}^{\left(1\right)}{b}_1\right]\right)}^T\left(S_{GA}^{\left(2\right)}{b}_2-E\left[S_{GA}^{\left(2\right)}{b}_2\right]\right)\right]$$

$$=E\left[{\left(S_{GA}^{\left(1\right)}{b}_1\right)}^T\left(S_{GA}^{\left(2\right)}{b}_2\right)\right]=E\left[b_1^T{S}_{GA}^{\left(1\right)T}{S}_{GA}^{\left(2\right)}{b}_2\right]$$

$$=E\left[tr\left(b_1^T{S}_{AG}^{\left(1\right)}{S}_{GA}^{\left(2\right)}{b}_2\right)\right]=tr\left(S_{GA}^{\left(1\right)}E\left[b_1^T{b}_2\right]S_{AG}^{\left(2\right)}\right)$$

$$={\rho }_b{\sigma }_{b_1}{\sigma }_{b_2}tr\left(S_{GA}^{\left(1\right)}{S}_{GT}^{\left(2\right)}\right),$$

so that

$$Corr\left(S_{GA}^{\left(1\right)}{b}_1,S_{GA}^{\left(2\right)}{b}_2\right)=\frac{Cov\left(S_{GA}^{\left(1\right)}{b}_1,S_{GA}^{\left(2\right)}{b}_2\right)}{\sqrt{Var\left(S_{GA}^{\left(1\right)}{b}_1\right)Var\left(S_{GA}^{\left(2\right)}{b}_2\right)}}$$

$$=\frac{{\rho }_b{\sigma }_{b_1}{\sigma }_{b_2}tr\left(S_{GA}^{\left(1\right)}{S}_{AG}^{\left(2\right)}\right)}{\sqrt{{\sigma }_{b_1}^{2}tr\left(S_{GA}^{\left(1\right)}{S}_{AG}^{\left(1\right)}\right){\sigma }_{b_2}^{2}tr\left(S_{GA}^{\left(2\right)}{S}_{AG}^{\left(2\right)}\right)}}$$

$$={\rho }_b\frac{tr\left(S_{GA}^{\left(1\right)}{S}_{AG}^{\left(2\right)}\right)}{\sqrt{tr\left(S_{GA}^{\left(1\right)}{S}_{AG}^{\left(1\right)}\right)tr\left(S_{GA}^{\left(2\right)}{S}_{AG}^{\left(2\right)}\right)}}.$$

We define a function τ to simplify our notation:

$$\tau \left(S_{GA}^{\left(1\right)},S_{GA}^{\left(2\right)}\right)=\frac{tr\left(S_{GA}^{\left(1\right)}{S}_{AG}^{\left(2\right)}\right)}{\sqrt{tr\left(S_{GA}^{\left(1\right)}{S}_{AG}^{\left(1\right)}\right)tr\left(S_{GA}^{\left(2\right)}{S}_{AG}^{\left(2\right)}\right)}},$$

so that

$$Corr\left(S_{GA}^{\left(1\right)}{b}_1,S_{GA}^{\left(2\right)}{b}_2\right)={\rho }_b\tau \left(S_{GA}^{\left(1\right)},S_{GA}^{\left(2\right)}\right).$$

It similarly follows that

$$Corr\left(S_{GG}^{\left(1\right)}{g}_1,S_{GG}^{\left(2\right)}{g}_2\right)={\rho }_g\tau \left(S_{GG}^{\left(1\right)},S_{GG}^{\left(2\right)}\right).$$

Combining the above equations, we have

$${\rho }_g\tau \left(S_{GG}^{\left(1\right)},\mathrm{ }{S}_{GG}^{\left(2\right)}\right)={\rho }_b\tau \left(S_{GA}^{\left(1\right)},\mathrm{ }{S}_{GA}^{\left(2\right)}\right)\mathrm{ },$$

so that

$$\frac{{\rho }_g}{{\rho }_b}=\frac{\tau \left(S_{GG}^{\left(1\right)},S_{GG}^{\left(2\right)}\right)}{\tau \left(S_{GA}^{\left(1\right)},\mathrm{ }{S}_{GA}^{\left(2\right)}\right)}\mathrm{ }.$$

We note that the trace of the product of the LD matrices in the numerator and dominator of the τ function corresponds to the sum of the entries of the Hadamard product of the two matrices:

$$tr\left({\left[S^{\left(1\right)}\right]}^T{S}^{\left(2\right)}\right)={\sum }_{i,j}{S}_{ij}^{\left(1\right)}{S}_{ij}^{\left(2\right)}\mathrm{ },$$

$$tr\left({\left[S^{\left(k\right)}\right]}^T{S}^{\left(k\right)}\right)={\sum }_{i,j}{\left[S_{ij}^{\left(k\right)}\right]}^2\mathrm{ }.$$

Thus, the denominator of the τ function contains the sums of LD scores, while the numerator contains the sum of a cross-population analog of LD scores(Brown et al., 2016). Since naïve estimates of squared correlations are upward biased, we adjust squared correlation estimates to remove this bias, as in previous work(Bulik-Sullivan et al., 2015b):

$${\widetilde{{\mathrm{\Sigma }}^2}}_{ij}^{\left(k\right)}={\left[{\widehat{\mathrm{\Sigma }}}_{ij}^{\left(k\right)}\right]}^2-\frac{1-{\left[{\widehat{\mathrm{\Sigma }}}_{ij}^{\left(k\right)}\right]}^2}{N_k-2},$$

where Σ denotes the SNP cross-correlation matrix. We propagate this adjustment to squared covariance estimates:

$${\widetilde{S^2}}_{ij}^{\left(k\right)}={\widehat{S}}_{ii}^{\left(k\right)}{\widehat{S}}_{jj}^{\left(k\right)}{\widetilde{{\mathrm{\Sigma }}^2}}_{ij}^{\left(k\right)\mathrm{ }}\mathrm{ },$$

$${\widehat{\tau }}_S\left({\widehat{S}}^{\left(1\right)},{\widehat{S}}^{\left(2\right)}\right)=\frac{{\sum }_{i,j}{\widehat{S}}_{ij}^{\left(1\right)}{\widehat{S}}_{ij}^{\left(2\right)}}{\sqrt{\left({\sum }_{i,j}{\widetilde{S^2}}_{ij}^{\left(1\right)}\right)\left({\sum }_{i,j}{\widetilde{S^2}}_{ij}^{\left(2\right)}\right)}}\mathrm{ }.$$

We only consider LD within 1Mb windows, setting ${\widehat{S}}_{ij}^{\left(k\right)}$ and ${\widehat{\mathrm{\Sigma }}}_{ij}^{\left(k\right)}$ to 0 if the distance between SNPs i and j is greater than 1Mb, similar to previous work(Bulik-Sullivan et al., 2015b, Kichaev and Pasaniuc, 2015).

Simulations with real genotypes and simulated phenotypes

To ensure realistic LD patterns, we performed simulations using real genotypes from the Genetic Epidemiology Research on Adult Health and Aging (GERA) data set and simulated phenotypes. The GERA data set contains 45,725 European ancestry (EUR) individuals, 3,357 East Asian ancestry (EAS) individuals, and 315,434 SNPs, after QC (see below). In each simulation, we sampled N₁ EUR and N₂ EAS samples, and restricted the simulation to all SNPs on chromosome 11 (we chose chromosome 11 because larger chromosomes tend to have higher LD, and smaller chromosomes tend to have lower LD). We selected a subset of M_G SNPs that were considered as “genotyped” SNPs for the purpose of the simulation, and selected a subset of M_C causal SNPs (from the set of all M SNPs) to simulate phenotypes. For each of the M_C causal SNPs, we sampled per-allele causal effect sizes in the two populations from a bivariate normal distribution with variance N(0, P_b), where P_b is a 2 × 2 matrix with diagonal entries equal to 1 and off-diagonal entries equal to ρ_b, the cross-population correlation of causal effect sizes. In each population, we multiplied the matrix of real genotypes by the vector of causal effect sizes to construct simulated genetic values. We scaled the genetic values to have mean 0 and variance h² and added environmental noise sampled from N(0, 1 – h²) to the genetic values to construct simulated phenotypes.

1000 Genomes data set

The 1000 Genomes data set(Auton et al., 2015) (see Web Resources) contains 503 individuals of European ancestry (EUR), 504 individuals of East Asian ancestry (EAS) and 489 individuals of South Asian ancestry (SAS). We performed QC in each population separately, retaining only bi-allelic SNPs in Hardy-Weinberg equilibrium (p>0.001) with MAF>0.1% and excluding SNPs with duplicate IDs, leaving 13,258,254 EUR SNPs, 12,285,372 EAS SNPs and 24,463,301 SAS SNPs. For each pair of populations analyzed (EUR-EAS and EUR-SAS), we restricted to SNPs with MAF>1% in each population (as in previous studies(Brown et al., 2016, de Candia et al., 2013, Mancuso et al., 2016)), resulting in 1,352,543 EUR-EAS SNPs and 2,115,911 EUR-SAS SNPs.

GERA data set

The Genetic Epidemiology Research on Adult Health and Aging (GERA) data set(Banda et al., 2015) (see Web Resources) includes 62,318 individuals of European ancestry (EUR) and 5,188 individuals of East Asian ancestry (EAS) genotyped on population-specific microarrays containing 657,184 and 694,877 SNPs, respectively. We performed QC in each population separately, retaining only bi-allelic SNPs with MAF>1% (as in previous studies(Brown et al., 2016, de Candia et al., 2013, Mancuso et al., 2016)) and missing genotype rate less than 2%. Only SNPs that passed QC in both populations were retained, resulting in 351,421 SNPs. This SNP set was further intersected with the 1000 Genomes EUR-EAS SNPs, resulting in 315,434 EUR-EAS SNPs. Related individuals and individuals with a greater than 2% missing data rate were also excluded from the study, resulting in 45,725 EUR and 3,357 EAS samples. We analyzed 9 traits that were previously analyzed in(Loh et al., 2015): allergic rhinitis, asthma, cardiovascular disease, type 2 diabetes, dyslipidemia, hypertension, macular degeneration, osteoarthritis and osteoporosis.

UK Biobank data set

The UK Biobank data set(Sudlow et al., 2015) (see Web Resources) includes 120,286 individuals of British ancestry QC-ed for GWAS analysis (EUR) and 1,784 individuals of South Asian ancestry (SAS) genotyped at 847,131 SNPs. We performed QC as with the GERA data set, resulting in 392,598 EUR-SAS SNPs, 116,478 EUR samples and 1,706 SAS samples. We analyzed 13 traits: bone-densitometry of heel, height, weight-height ratio, diastolic blood pressure, systolic blood pressure, college education, smoking status, eczema, asthma, hypertension, FEV1, FEV1-FCV ratio and age at menarche.

RA and T2D summary statistic data sets

We analyzed rheumatoid arthritis (RA) and type 2 diabetes (T2D) summary statistic data sets that were used to estimate ρ_g between Europeans and East Asians in a previous study(Brown et al., 2016). The RA data set included summary statistics from 58,284 European ancestry individuals(Okada et al., 2014) and summary statistics from 22,515 East Asian ancestry individuals(Okada et al., 2014), each computed at 2,539,629 genotyped or imputed SNPs. The T2D data set included summary statistics from 69,033 European ancestry individuals(Morris et al., 2012) and summary statistics from 18,817 East Asian ancestry individuals(Cho et al., 2011), each computed at 1,054,079 genotyped or imputed SNPs. For both RA and T2D, we used the estimates of ρ_g from the previous study(Brown et al., 2016), so that we only directly analyzed 1000 Genomes data (informed by the set of genotyped/imputed SNPs in the summary statistic data sets). As noted in the previous study(Brown et al., 2016), estimates of $h_g^2$ in these data sets were incorrectly scaled due to genomic control correction, which does not affect estimates of ρ_g, but were greater than 0 with very high statistical significance.

Results

Simulations with real genotypes and simulated phenotypes

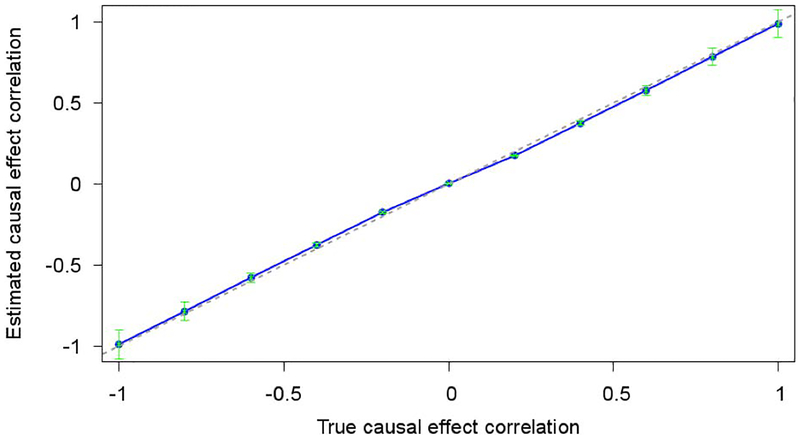
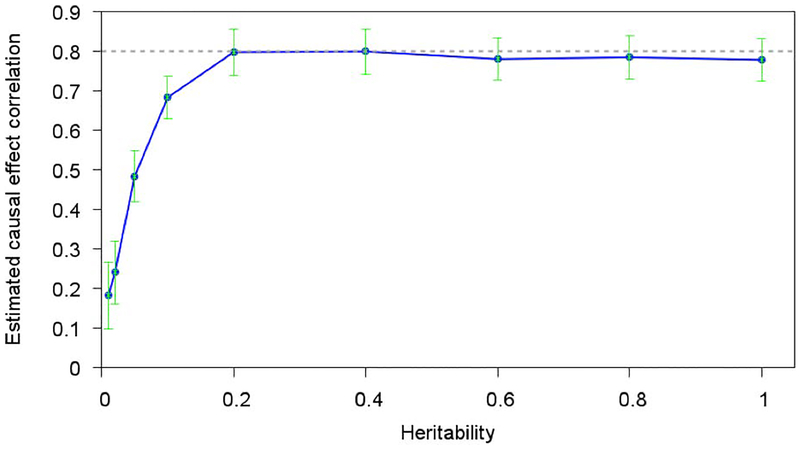
We first evaluated our method using simulations in which the true value of ρ_b is known. To ensure realistic LD patterns, we used real genotypes from chromosome 11 of the GERA data set and simulated causal effect sizes and phenotypes in EUR and EAS samples (see Materials and Methods). We included N_EUR=2K EUR samples, N_EAS=2K EAS samples, M_T=5,000 SNPs that were considered as “genotyped” SNPs (used to estimate ρ_g) and M_C=100 causal SNPs with nonzero causal effect sizes (selected from set of all M_T SNPs). We estimated ρ_g using bivariate REML, and transformed this into an estimate of ρ_b using our derivation of ρ_g/ρ_b (see Materials and Methods). We first fixed h²=0.8 and varied ρ_b. We determined that our method produced accurate estimates of ρ_b across all values of ρ_b (Figure 1). We then fixed h²=0.8 and ρ_b =0.8 and varied M_T, M_C, N_EUR=N_EAS, and N_EUR only, respectively. In each case, our method continued to produce accurate estimates of ρ_b (Figure S1). However, our results are subject to two caveats. First, we noted that regularizing LD estimates by restricting to 1Mb windows reduced slight biases (Figure S2). Second, we varied h² and determined that estimates of ρ_b were downward biased at very low values of h² (less than 0.2; Figure S3); this cannot be a limitation of our derivation of ρ_g/ρ_b, which does not depend on h² (or on any phenotypic values), and must instead be a limitation of estimation of ρ_g at very low values of h² (and $h_g^2$, although the true value of $h_g^2$ in these simulations is unknown). Thus, efforts to estimate either ρ_g or ρ_b should avoid traits with very low values of h².

Figure 1. Estimates of ρ_b are accurate in simulations at various values of ρ_b.

We report estimates of ρ_b for each value of true ρ_b. Dashed line is y=x.

Application to 9 traits from GERA data set

We applied our method for estimate ρ_b to 9 traits from the GERA data set, which includes data from 45,725 Europeans (EUR) and 3,357 East Asians (EAS) at 315,434 genotyped SNPs (see Materials and Methods). We first computed a value of 0.93 for the ratio ρ_g/ρ_b, for this set of genotyped SNPs relative to 1000 Genomes reference SNPs. We then used bivariate REML to estimate ρ_g for each trait (restricting the computation to 10K EUR and all EAS samples), and divided by 0.93 to obtain estimates of ρ_b. Estimates of ρ_g and ρ_b are reported in Table 1. The inverse-variance weighted average of ${\widehat{\rho }}_g$ was 0.51 with standard error 0.13, and the inverse-variance weighted average of ${\widehat{\rho }}_b$ was 0.55 with standard error 0.14. Estimates of cross-population correlations of normalized effect sizes (${\widehat{\rho }}_{\gamma }$ and ${\widehat{\rho }}_{\beta }$) were slightly lower, with inverse-variance weighted averages of 0.41 (SE=0.13) and 0.44 (SE=0.14) respectively.

Table 1. Estimates of cross-population genetic correlations for 9 GERA traits.

We report estimates of ρ_g, ρ_γ, ρ_b and ρ_β for each trait. (Adjusting estimates of ρ_g that are close to 1 by dividing by estimates of ρ_g/ρ_b can result in estimates of ρ_b that are greater than 1; although the true value of ρ_b cannot be greater than 1, it is possible for estimates of ρ_b to be greater than 1.) Numbers in parentheses denote standard errors. Standard errors of ${\widehat{\mathit{\rho }}}_{\mathit{g}}$ (resp. ${\widehat{\mathit{\rho }}}_{\mathit{\gamma }}$) are estimated by GCTA using bi-variate REML, while standard errors of ${\widehat{\rho }}_{\mathit{b}}$ (resp. ${\widehat{\mathit{\rho }}}_{\mathit{\beta }}$) are estimated by correcting the standard error estimated by GCTA by the estimated correction factor ρ_g/ρ_b (resp. ρ_γ/ρ_β).

Phenotype	${\widehat{\mathit{\rho }}}_{\mathit{g}}$	${\widehat{\mathit{\rho }}}_{\mathit{\gamma }}$	${\widehat{\mathit{\rho }}}_{\mathit{b}}$	${\widehat{\mathit{\rho }}}_{\mathit{\beta }}$
Allergic rhinitis	1.00 (1.06)	1.00 (1.00)	1.08 (1.14)	1.08 (1.08)
Asthma	−0.04 (0.40)	−0.34 (0.33)	−0.04 (0.43)	−0.37 (0.35)
Cardiovascular Disease	0.48 (0.35)	0.30 (0.32)	0.52 (0.38)	0.32 (0.34)
Type 2 Diabetes	0.35 (0.27)	0.29 (0.27)	0.38 (0.29)	0.31 (0.29)
Dyslipidemia	0.52 (0.21)	0.47 (0.21)	0.56 (0.23)	0.51 (0.23)
Hypertension	0.27 (0.19)	0.24 (0.19)	0.29 (0.20)	0.26 (0.20)
Macular Degeneration	1.00 (2.09)	1.00 (2.08)	1.08 (2.25)	1.08 (2.24)
Osteoarthritis	0.53 (0.35)	0.42 (0.32)	0.57 (0.38)	0.45 (0.34)
Osteoporosis	−0.07 (0.47)	−0.12 (0.53)	−0.08 (0.51)	−0.13 (0.57)

Application to 13 traits from UK Biobank data set

We next applied our method for estimating ρ_b to 13 traits from the UK Biobank data set, which includes data from 116,478 Europeans (EUR) and 1,706 South Asians (SAS) at 392,598 genotyped SNPs (see Materials and Methods). We first computed a value of 0.98 for the ratio ρ_g/ρ_b, for this set of genotyped SNPs relative to the 1000 Genomes reference SNPs. The larger value of ρ_g/ρ_b between Europeans and South Asians than between Europeans and East Asians (despite similar numbers of genotyped SNPs) is expected because Europeans and South Asians are more recently diverged than Europeans and East Asians(Sved et al., 2008). We then used bivariate REML to estimateρ_g for each trait (restricting the computation to 10K EUR and all SAS samples), and divided by 0.98 to obtain estimates of ρ_b. Estimates of ρ_g and ρ_b are reported in Table 2. The inverse-variance weighted average of ${\widehat{\rho }}_g$ was 0.53 with standard error 0.17, and the inverse-variance weighted average of ${\widehat{\rho }}_b$ was 0.54 with standard error 0.18. Estimates of cross-population correlations of normalized effect sizes (${\widehat{\rho }}_{\gamma }$ and ${\widehat{\rho }}_{\beta }$) were slightly lower, with inverse-variance weighted averages of 0.50 (SE=0.17) and 0.51 (SE=0.17) respectively.

Table 2. Estimates of cross-population genetic correlations for 13 UK Biobank traits.

We report estimates of ρ_g, ρ_γ, ρ_b and ρ_β for each trait. (Adjusting estimates of ρ_g that are close to 1 by dividing by estimates of ρ_g/ρ_b can result in estimates of ρ_b that are greater than 1; although the true value of ρ_b cannot be greater than 1, it is possible for estimates of ρ_b to be greater than 1.) Numbers in parentheses denote standard errors. Standard errors of ${\widehat{\mathit{\rho }}}_{\mathit{g}}$ (resp. ${\widehat{\mathit{\rho }}}_{\mathit{\gamma }}$) are estimated by GCTA using bi-variate REML, while standard errors of ${\widehat{\mathit{\rho }}}_{\mathit{b}}$ (resp. ${\widehat{\mathit{\rho }}}_{\mathit{\beta }}$) are estimated by correcting the standard error estimated by GCTA by the estimated correction factor ρ_g/ρ_b (resp. ρ_γ/ρ_β).

Phenotype	${\widehat{\mathit{\rho }}}_{\mathit{g}}$	${\widehat{\mathit{\rho }}}_{\mathit{\gamma }}$	${\widehat{\mathit{\rho }}}_{\mathit{b}}$	${\widehat{\mathit{\rho }}}_{\mathit{\beta }}$
Bone-densitometry of heel	0.60 (0.18)	0.49 (0.19)	0.62 (0.18)	0.50 (0.20)
Height	0.77 (0.26)	0.63 (0.24)	0.78 (0.26)	0.64 (0.24)
Weight-height ratio	1.00 (2.19)	1.00 (2.64)	1.02 (2.24)	1.02 (2.69)
Diastolic blood pressure	1.00 (0.56)	0.73 (0.35)	1.02 (0.57)	0.74 (0.36)
Systolic blood pressure	1.00 (0.91)	0.76 (0.59)	1.02 (0.93)	0.77 (0.60)
College education	0.36 (0.22)	0.38 (0.22)	0.37 (0.23)	0.39 (0.22)
Smoking status	0.37 (0.39)	0.22 (0.37)	0.38 (0.40)	0.22 (0.38)
Eczema	−0.19 (0.62)	0.14 (0.59)	−0.19 (0.63)	0.15 (0.60)
Asthma	0.92 (1.49)	0.65 (0.72)	0.94 (1.52)	0.66 (0.73)
Hypertension	0.32 (0.32)	0.38 (0.32)	0.32 (0.33)	0.38 (0.33)
FEV1	0.57 (0.27)	0.50 (0.29)	0.58 (0.28)	0.51 (0.30)
FEV1-FCV ratio	0.39 (0.29)	0.58 (0.41)	0.40 (0.30)	0.59 (0.42)
Age at menarche	0.70 (1.07)	0.59 (1.00)	0.71 (1.09)	0.60 (1.02)

Application to RA and T2D summary statistics

We next applied our method for estimating ρ_b to summary statistic data sets for RA (58,284 EUR and 22,151 EAS samples, 2,539,629 genotyped/imputed SNPs) and T2D (69,033 EUR and 18,817 EAS samples, 1,054,079 genotyped/imputed SNPs) that were used to estimate ρ_g in a previous study(Brown et al., 2016), which reported estimates of ρ_g of 0.463 (s.e. 0.058) for RA and 0.621 (s.e. 0.088) for T2D. We computed a value of 0.96 for the ratio ρ_g/ρ_b for the RA genotyped/imputed SNPs relative to the 1000 Genomes reference SNPs, and a value of 0.97 for the ratio ρ_g/ρ_b for the T2D genotyped/imputed SNPs relative to the 1000 Genomes reference SNPs. The larger values of ρ_g/ρ_b between Europeans and East Asians for these SNP sets, compared to 0.93 for the GERA genotyped SNP set, is expected due to the larger numbers of genotyped/imputed SNPs. We divided the previously reported estimates of ρ_g by the values of ρ_g/ρ_b to obtain estimates of ρ_b. The resulting estimates of ${\widehat{\rho }}_b$ were 0.48 (s.e. 0.06) for RA and 0.65 (s.e. 0.09) for T2D, which are still significantly less than 1.

Discussion

Recent work comparing the genetic architecture of complex traits across continental populations has established that GWAS results do not always transfer across populations(Brown et al., 2016, Mahajan et al., 2014), however, this finding may be explained by the fact that continental populations have different LD patterns. Our results demonstrate for the first time that causal genetic architectures differ between continental populations, and therefore that differences in GWAS results across populations cannot be explained by differences in LD patterns alone. We introduced a new method for estimating ρ_b, the cross-population correlation of causal effect sizes: we first estimate ρ_g (the cross-population correlation of joint-fit effect sizes) using existing methods(Brown et al., 2016, Lee et al., 2013, Lee et al., 2012a, Lee et al., 2012b), and then divide by the value of ρ_g/ρ_b that we obtain from 1000 Genomes reference data (as a function of the set of genotyped SNPs used to define ρ_g) using a new derivation. We applied our method to estimate ρ_b in GERA and UK Biobank data sets for which ρ_g and ρ_b had not previously been estimated, and to RA and T2D summary statistic data sets for which ρ_g (but not ρ_b) had previously been estimated. For each of the genotyped SNP sets and population pairs that we analyzed, ρ_g/ρ_b was only modestly smaller than 1, so that ρ_b was only modestly larger than ρ_g, and remained significantly smaller than 1. This could for example be explained by gene-gene or gene-environment interaction. Importantly, we have only analyzed data from European and Asian populations, which are known to have relatively similar LD patterns(Lonjou et al., 2003); our findings may not generalize to African-ancestry populations, which have more divergent LD patterns.

Our method is subject to several limitations. First, our method relies on LD information from a reference panel, and restricts to SNPs that are present in the reference panel. Methods that use LD information from a reference panel to analyze summary statistic data(Pasaniuc and Price, 2017) rely on the assumption that the LD in each study population is well approximated by the LD in the respective reference populations(Ni et al., 2018). In addition, due to complexities of admixture-LD, such methods may not work well in admixed populations(Bulik-Sullivan et al., 2015b, Brown et al., 2016), and thus our method is not currently applicable to populations such as African and Latin Americans that often provide the most practical route to assaying African and Native American genetic variation(Seldin et al., 2011). Second, limitations in existing methods for estimating ρ_g will carry over to our estimates of ρ_b; this is a particular concern for traits with very low heritability. Third, our method assumes that selection of the set of genotyped SNPs is independent of LD. This may not be strictly true in instances where the set of genotyped SNPs is selected based on their tagging efficiency, but restricting our analyses to SNPs that are genotyped in both populations minimizes the impact of SNPs with population-specific tagging efficiency. Finally, we restricted our analyses to SNPs with MAF>1% in both populations, as in previous studies(de Candia et al., 2013, Mancuso et al., 2016, Brown et al., 2016). Thus, many SNPs that have MAF<1% in either population are excluded (see Materials and Methods). It is possible that ρ_g/ρ_b would be smaller (i.e. ρ_b would be larger) when including the effects of rare (MAF<1%) causal variants. It will be possible to formally assess this when larger multi-ethnic reference panels become available, but we anticipate that the impact on our results will be small. This is because most common variation is shared across populations and because emerging research suggests that rare and low-frequency causal variants contribute only modestly to the heritability of complex traits(Yang et al., 2015, Zeng et al., 2018, Schoech et al., 2017) Despite these limitations, our method provides a promising way to assess cross-population correlations of causal effect sizes.

Supplementary Material

Supp figS1

Figure S1. Estimates of ρ_b are accurate in simulations at various parameter settings. We report estimates of ρ_b for various values of M_T, the number of “genotyped” SNPs; M_C, the number of causal SNPs; N_EUR=N_EAS; and N_EUR (with N_EAS fixed at 2K). The dashed line is the true value ρ_b =0.8.

Supp figS2

Figure S2. Regularizing LD estimates is necessary to minimize biases. We report the value of the correction factor ρ_g/ρ_b (resp. ρ_γ/ρ_β) as a function of the LD window used. We report estimates using only an LD window (dashed curve), as well as estimates using both an LD window and the regularization method of Wen & Stephens 2010 Ann Appl Stat (solid curve). The horizontal dashed line is the true correction factor, that is, the value of ${\widehat{\rho }}_{g,REML}/{\rho }_b$ (resp. ${\widehat{\rho }}_{\gamma ,REML}/{\rho }_{\beta }$). The results support the use of an LD window, and indicate than the regularization method of Wen & Stephens does not impact results when an LD window is used. Standardized and mean-centered approaches tend to give similar results in practice, but they assume a different trait model and therefore can give different results, especially if causal alleles have very different alleles frequencies between the two populations.

Supp figS3

Figure S3. Estimates of ρ_b are downward biased at very low values of h². We report estimates of ρ_b for various values of h². The dashed line is the true value ρ_b =0.8.

Figure 2. Estimates of ρ_b are downward biased at very low values of h².

We report estimates of ρ_b for various values of h². The dashed line is the true value ρ_b =0.8.