Abstract
The molecular dissociation constant, Kd, is a well-established parameter to quantitate the affinity of protein-protein or other molecular interactions. Recently, we reported the theoretical basis and experimental procedure for Kd determination using a quantitative FRET method. Here we report a new development of Kd determination by measuring the reduction in donor fluorescence due to acceptor quenching in FRET. A new method of Kd determination was developed from the quantitative measurement of donor fluorescence quenching. The estimated Kd values of SUMO1-Ubc9 interaction based on this method are in good agreement with those determined by other technologies, including FRET acceptor emission. Thus, the acceptor-quenched approach can be used as a complement to the previously developed acceptor excitation method. The new methodology has more general applications regardless whether the acceptor is an excitable fluorophore or a quencher. Thus, these developments provide a complete methodology for protein or other molecule interaction affinity determinations in solution.
Introduction
Protein interaction affinity as characterized by dissociation constant Kd is one of most important parameters for protein interactions in various physiological and pathological processes. Recently, a new effort to take advantage of FRET technology to determine protein interaction affinity has emerged1. Traditionally, a ratiometric method (acceptor emission/donor emission) has been widely used in quantifying the FRET signal. However, the ratiometric method for FRET analysis is not accurate measurement of absolute FRET signal. For example, bleed-through excitation occurs when an acceptor is excited by the donor’s excitation wavelength. Also, crosstalk in emission detection occurs when the emission of a donor contributes to the signal at the wavelength at which acceptor emission is measured. Because of these two types of signal contaminations, the ratiometric method (acceptor emission/donor emission) cannot accurately measure the absolute FRET signal, as it doubles the effect of bleed-through emission. Another effort to estimate the dissociation constant Kd by FRET assay was pioneered by Erickson et al., who measured quantitative “three-cube” FRET using fluorescent microscopy2,3. However, this methodology requires detailed knowledge of optical filter characteristics such as the average molar extinction co-efficiency of donor and acceptor over the bandwidth of FRET cube excitation filter. Although several improvements have been developed, microscopy images are blurred by the optical imaging process from out-focus image planes and adjacent points4,5. In addition, an independent estimation of FRET efficiency is needed to characterize protein binding. However, the FRET efficiency is affected by multiple factors, and accurate determination is often challenging. Recent studies of non-imaging-based FRET assay for Kd determinations have focused on the development of quantitative methodologies for steady-state and kinetic parameters of protein interactions or enzymatic reactions by photomultipliers (PMT)-based quantitative FRET assay6–8. In one study, CFP-SUMO1 and YFP-Ubc9 recombinant proteins were mixed, and the fluorescent spectra were compared with those from the same concentrations of separate CFP-SUMO1 or YFP-Ubc9 proteins to derive the FRET emission from YFP-Ubc96. The FRET emission intensity was then fitted with YFP-Ubc9 concentration to obtain the maximum FRET emission intensity, which is correlated with maximum bindings of two proteins. The bound YFP-Ubc9 concentration was calculated from the FRET emission with the assumption of a linear relationship. In the second study, the individual and quantified absolute fluorescence signals contributed by each component (i.e., donor, acceptor and FRET at the emission wavelength of acceptor) were determined using correlations of donor and acceptor fluorescence emissions. The absolute FRET signal was correlated with the amount of bound partners, which was then used to derive interaction affinity Kd7. A similar strategy was applied to Sentrin/SUMO-specific proteases 1 (SENP1) for its kcat/KM determinations8. The results from these quantitative FRET analyses are comparable to or more accurate than traditional biophysical or biochemical approaches, such as the surface plasmon resonance (SPR) or Western blot for estimating binding affinity constants. Furthermore, the FRET method provides free molecular interaction in solution and timely signal detection and therefore results in higher kinetic numbers6,7,9. In FRET, fluorescence quenching of a donor is proportional to the energy transferred to its acceptor, while fluorescence quenching is a more general approach than fluorescence emission as many FRET acceptors can be excitable fluorophores or quenching fluorophores. The fluorescence quenching approach was pioneered by Velick, et al. for characterizing antibody-hapten binding10. This approach was further developed by Liu and Schultz for characterizing binding between macromolecules11.
Here we report a more general method of quantitative FRET signal analysis-quantitative donor signal quenching for Kd determinations. New mathematical algorithms of nonlinear regression were developed, and experimental data were generated and analyzed. The estimated KdKd of SUMO1-Ubc9 interaction is in good agreement in general with those determined by the acceptor emission approach and the surface plasmon resonance (SPR). Our analysis is the first documentation of FRET quenching technique for protein dissociation constant determination. In addition, our method has broader applications regardless whether the acceptor is an emitting fluorophore or a quencher.
Methods
DNA constructs, protein expression and purification
Most of the plasmid constructs and protein expression procedures have been described7. Briefly, CyPet-SUMO1 and YPet-Ubc9 were cloned into the NheI/NotI sites of pET28(b) vector (Novagen). BL21(DE3) Escherichia coli cells were transformed with pET28 vectors encoding CyPet-SUMO1 or YPet-Ubc9. The expression of Poly-his tagged recombinant proteins was induced with 0.1 mM IPTG at 25 °C overnight. The recombinant proteins were then purified by Ni2+-NTA agarose beads (QIAGEN) and eluted by buffer containing 20 mM Tris-HCl, pH 7.5, 200 mM NaCl, and 150 mM imidazole. After the proteins were dialyzed in buffer containing 20 mM Tris-HCl, pH 7.5, 50 mM NaCl, and 1 mM DTT, they were concentrated and purified by gel filtration HPLC with Superdex75 10/300 GL column with a HPLC purification system (ÄKTATM purifier. GE Healthcare). Purity of proteins was confirmed by SDS-PAGE and Coomassie blue staining, and concentrations were determined by Coomassie Plus Protein Assay (Thermo-Fisher).
Fluorescence measurement of donor quenching
The FRET measurements were as previously described7. Briefly, recombinant CyPet-SUMO1 and YPet-Ubc9 proteins were diluted with Tris buffer (20 mM Tris-HCl, pH 7.5, 50 mM NaCl) in a total volume of 100 µL. For each set of measurements, the final concentrations of CyPet-SUMO1 were 0.5, 1.0 and 1.5 µM, respectively. The final concentrations of YPet-Ubc9 were increased from 0 to 4 µM. The fluorescence emission spectrum of each sample was determined using a fluorescence multi-well plate reader FlexstationII384 (Molecular Devices, Sunnyvale, CA). The fluorescence emission at 475 nm was measured at the excitation wavelength of 414 nm with a cutoff filter of 455 nm. For all the data points, the final fluorescent signals were obtained by subtracting the fluorescent signals with the background noise of blank well. The experiments were repeated three times and the average value of fluorescence were taken at each specific condition. The decrease of emission intensity at 475 nm (ΔEm475) is calculated by subtracting the emission intensity at a specific YPet-Ubc9 concentration by the emission intensity of CyPet-SUMO1 only:
Data processing and Kd determination
After ΔEm475 at each specific condition was calculated based on the method described above, a non-linear regression model was used to fit the datasets of ΔEm475 and the total concentration of YPet-Ubc9 ([YPetUbc9]total) by Prism 5 (GraphPad Software) to derive the value of Kd. In the non-linear regression model, the values of [YPetUbc9]total were put into X-series and the intensities of ΔEm475, which were determined in triplicate at each [YPetUbc9]total were put into Y-series.
Statistic Bootstrap Analysis
We denoted the Kd estimator based on the two methods by and , respectively. Based on the data from our experiments, and . We determined whether the difference of the two estimates is caused by the variation of the data and the true KdKd measured by the two methods are actually the same. This is equivalent to testing H0: Kd1 = Kd2 versus H1: Kd1 ≠ Kd2, where Kd1 and Kd2 are the true Kd measured by the two methods, respectively. To test this hypothesis, we examined the distribution of our test statistic under H0. To find out this distribution, we resort to the bootstrap method. More specifically, we simulated a new set of y’s from the two models using the estimated Kd and n as the true values plus some random noises which mimic the variation of the original data. Based on the new set of y’s, we obtained a new set of Kd estimates, denoted by and . We repeated this procedure 10,000 times, and the resulting Kd estimates are and The null distribution of then could be approximated by the empirical distribution of . Based on the approximated null distribution of , we obtained the p-value of the above hypothesis testing problem, which is p = 0.19148. Since the p-value is larger than 0.05, we do not have sufficient evidence to reject H0 and conclude that the true Kd measured by the two methods are actually identical.
Results
Measurement of Kd at the donor emission wavelength
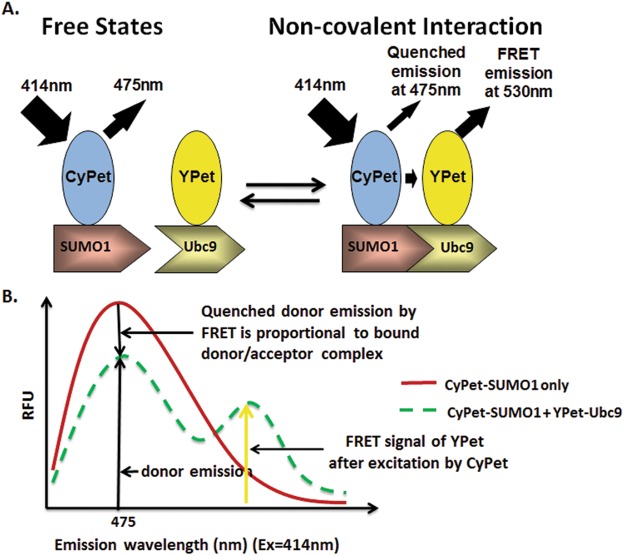
To determine the dissociation constant, Kd by FRET assay, we chose a high-efficiency FRET pair, CyPet and YPet, to fuse with SUMO1 and Ubc9, respectively (Fig. 1A). CyPet and YPet are fluorescent proteins engineered from CFP and YFP, respectively, with 20-fold greater ratiometric FRET signal than their parental FRET pair12.
Figure 1.
Schematic of the principle of donor quenching for protein interaction affinity determination by FRET assay. (A) Diagram of fluorescence emissions of FRET pair, CyPet and YPet, when tagged with interactive partners, SUMO1 and Ubc9, respectively. The fluorescence emission of donor CyPet-SUMO1 decreases when it binds acceptor Ypet-Ubc9. (B) Quantitative analysis of fluorescence signals. The decrease of CyPet emission is proportional the concentration of bound donor/acceptor complex.
In our previous development, the interaction affinity Kd was determined from the FRET acceptor emission signal at 530 nm after eliminations of direct emissions of CyPet-SUMO1 and YPet-Ubc97. As the fluorescent signal emitted by acceptor is proportional to the quenched fluorescent signal of donor in the FRET, we reasoned that the decrease in donor signal should also be proportional to the bound complex in the FRET assay, and therefore could be used for Kd determination. However, this is not true in a titration format when dilution also affects the donor emission signal. Therefore, donor concentration needs to be constant in a titration experiment.
Starting with the general law of mass action for protein-protein interaction,
The Kd can be calculated as follows:
| 1 |
The decrease of emission intensity of CyPet at 475 nm results from the quenching of CyPet-SUMO1 by acceptor YPet-Ubc9 as FRET occurs (Fig. 1B). Because the amount of quenched CyPet-SUMO1 fluorescence is proportional to the amount of bound protein complex, the relationship of emission decrease and concentration of bound protein can be represented by:
| 2 |
where n is a constant related to the FRET efficiency between CyPet-SUMO1 and YPet-Ubc9, [YPetUbc9]bound is the concentration of bound YPet-Ubc9, and ΔEm475 is the decrease of emission intensity at 475 nm with an excitation wavelength of 414 nm at each specific concentration of YPet-Ubc9,
| 3 |
where x is the concentration of YPet-Ubc9 in the FRET assay.
If we set the total concentration of CyPet-SUMO1 to a constant A, the concentration of total YPet-Ubc9 to the variable X, and ΔEm475 to the variable Y, we can convert the concentration of bound and free CyPet-SUMO1 or YPet-Ubc9 proteins in Equation 2 to:
| 4 |
and
| 5 |
and
| 6 |
Based on the definition of Kd and Equations 4 to 6, we can derive
| 7 |
After rearranging the above equations, the following equations are obtained:
| 8 |
| 9 |
| 10 |
Therefore, by fitting ΔEm475 (Y) and the total YPet-Ubc9 concentration (X) with Equation 10, we can derive the value of Kd and constant n.
Determination of the quenched donor emission ΔEm475
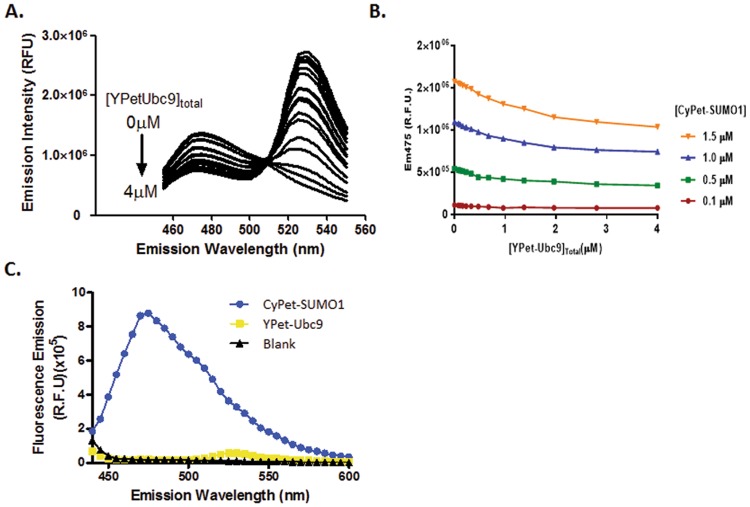
The Kd can be determined with a series of FRET assays, in which a single constant concentration of CyPet-tagged protein was used together with increasing concentrations of YPet-tagged interactive partner. However, to test the robustness of our approach, we set up the FRET experiments at different concentrations of CyPet-tagged protein. In our effort to determine Kd, we fixed the CyPet-SUMO1 concentration at 0.1, 0.5, 1.0, or 1.5 μM and increased the concentration of YPet-Ubc9 from 0 to 4 μM in a total volume of 100 μl13. The fluorescence emission spectra of the mixtures were then determined with a FlexstationII384 at an excitation wavelength of 414 ± 4 nm (Fig. 2A). As the concentration of YPet-Ubc9 was increased, the emission intensity at 475 ± 4 nm gradually decreased, indicating that CyPet-SUMO1 molecules were bound to YPet-Ubc9 and quenched by donor YPet-Ubc9 in the FRET assay. The range of acceptor signal increase was larger than that of donor signal decrease (Fig. 2A).
Figure 2.
Fluorescence emission from the mixture of CyPet-SUMO1 and YPet-Ubc9. (A) Spectrum changes of the mixture of CyPet-SUMO1 and YPet-Ubc9 proteins at increasing amount of acceptor when excited at 414 nm. The CyPet-SUMO1 concentration is fixed at 1.5 μM, and YPet-Ubc9 concentrations range from 0 to 4 μM. (B) Emission intensity of CyPet-SUMO1 at 475 nm (Ex = 414 nm) decreases at different concentrations of CyPet-SUMO1 with increasing YPet-Ubc9 concentrations. ● 0.5 μM of CyPet-SUMO1, ■ 1 μM of CyPet-SUMO1, and ▲ 1.5μM of CyPet-SUMO1. (C) The emissions of CyPet and YPet when excited at 441 nm.
The absolute quenched signal of CyPet-SUMO1 was obtained by Equation 3. At each CyPet concentration, the magnitude of quenching was obtained by subtracting the total fluorescence emission at 475 nm in the absence of YPet-Ubc9 from the remaining fluorescence emission at 475 nm in the presence of YPet-Ubc9 at different concentrations of YPet-Ubc9. The quenched signal of CyPet-SUMO1 shows a gradually decrease with increasing concentrations of YPet-Ubc9 (Fig. 2B). These data demonstrate that the degree of quenching of donor fluorescence increases with increased concentration of YPet-Ubc9 and it can be used to determine bound protein of protein interactions. In addition, because the YPet does not give emission at 475 nm when excited at 414 nm, this simplifies our analysis with only the emission of CyPet at 475 nm considered (Fig. 2C).
Determination of interaction affinity Kd by quenched donor emission
To determine the Kd and constant n simultaneously from the quenched FRET signals, we applied Equation 10 to ΔEm475 determined at each set of experiments with different [YPetUbc9]total, and fit the data using nonlinear regression. To apply the Equation 10, we determined ΔEm475 at each set of experiments with different [YPetUbc9]total, and then modeled the data into the equation by a least-square fitting. Four regression plots corresponding to the concentrations of CyPet-SUMO1 in our experiments (0.1, 0.5, 1.0, and 1.5 μM) were generated (Fig. 3). Nonlinear regression fitted the data reasonably well (R2 from 0.95 to 0.99).
Figure 3.
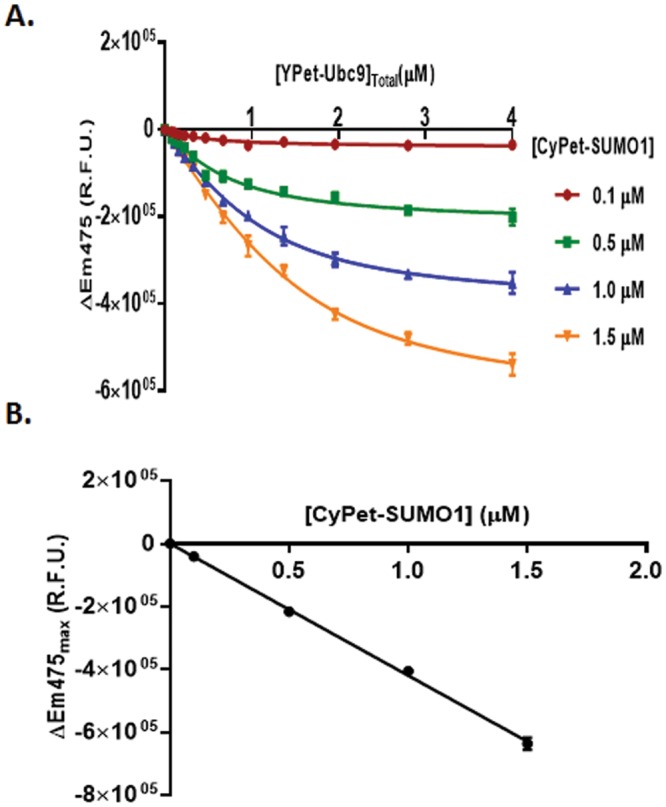
Curve fitting for Kd determination. (A) Decreased emission of Em475 was calculated by subtracting the emission intensity of CyPet-SUMO1 in the presence of YPet-Ubc9 from the emission in the absence of YPet-Ubc9. The value of decrease was then fitted with total YPet-Ubc9 concentration to derive the value of Kd according the formula Y = n/2 (A + X + Kd − √((A + X + Kd)^2−4AX)) (see text for details). (B) Linearity of maximum quenching signal of CyPet-SUMO1 by Ypet-Ubc9 at different concentrations was determined.
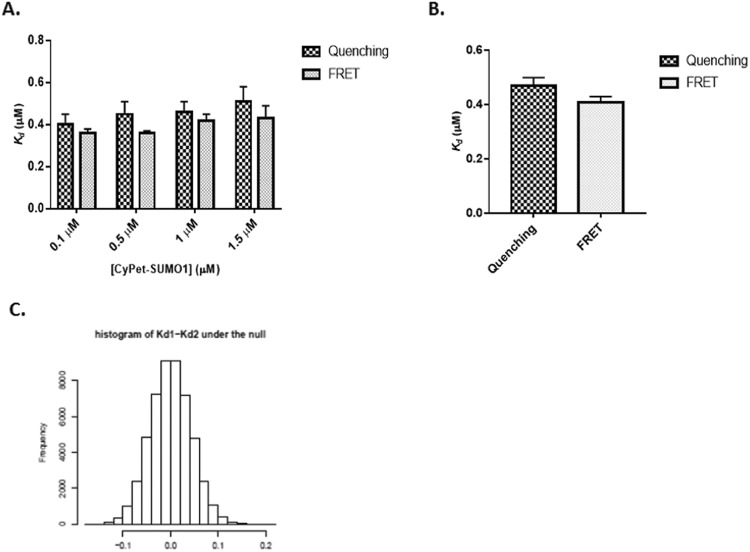
From the nonlinear regression of Equation 10, the Kd value can be determined from two parameter non-linear regression (n and Kd) because Y(CyPet quenched signal) and X(YPet-Ubc9 concentration) were known from experiments. The Kd values for these four independent experiments corresponding to different CyPet-SUMO1 concentrations were 0.40 ± 0.05, 0.45 ± 0.06, 0.46 ± 0.05, and 0.51 ± 0.07 μM, respectively (see Table 1). These Kd values are very similar to each other and also very close to previous results with acceptor excitation emission for Kd determination and are also very close to the results from other technologies(see Table 1)6,7 (see below).
Table 1.
Summary of fitting results for Kd determination.
| Donor Quenching | Acceptor Emission | Global Optimization | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [CyPet-SUMO1](μM) | 0.1 | 0.5 | 1 | 1.5 | 0.1 | 0.5 | 1 | 1.5 | Donor Quenching | Acceptor Emission |
| Kd (mM) | 0.40 ± 0.05 | 0.45 ± 0.06 | 0.46 ± 0.05 | 0.51 ± 0.07 | 0.36 ± 0.02 | 0.36 ± 0.01 | 0.41 ± 0.03 | 0.42 ± 0.06 | 0.47 ± 0.03 | 0.41 ± 0.02 |
By nonlinear regression, the constant n was also determined in each concentration of CyPet-SUMO1. The n numbers at each concentrations of CyPet-SUMO1 obtained from the non-linear regression were as −4.07 ± 0.15 × 105, −4.32 ± 0.15 × 105, −4.06 ± 0.10 × 105 and −4.24 ± 0.13 × 105, respectively. From its definition, n is a constant that converts the bound acceptor partner to the quenched signal of the donor (Equation 2). The slight fluctuation of n from these four sets of experiments likely suggest that the method is not equally sensitive at different dynamic ranges of readouts, in agreement with the results of different slopes at different concentrations.
Comparing affinity Kd determinations by donor quenching with FRET emission from acceptor
We previously developed a FRET-based method to determine Kd by acceptor excited emission7,13. That approach derives the FRET emission of acceptor from the whole spectrum by subtracting individual contributions of donor and acceptor. The Kd was then derived from the non-liner regression plot of the FRET emission plotted against the total concentration of acceptor.
To directly compare the sensitivity and accuracy of our newly developed donor quenching method and the FRET emission method, we also used FRET emission method to analyze the same data from the experiments at four different conditions in which [CyPet-SUMO1] is set to 0.1, 0.5, 1.0, or 1.5 μM, respectively and compared the values of Kd with those obtained using the donor quenching method. The Kd values obtained from the method of acceptor FRET emission were 0.36 ± 0.02, 0.36 ± 0.01, 0.41 ± 0.03, and 0.42 ± 0.06 μM at the same concentrations of CyPet, respectively (Fig. 4A). The data were similar across different concentration sets of experiment. To minimize the effect of variations, we performed global optimization for the Kd values from the two approaches, and the resulting Kd values from fluorescence quenching and emission are 0.47 ± 0.03 and 0.41 ± 0.02, respectively (Fig. 4B). These results suggest that the two methods give similar and consistent Kd measurements. We denote the Kd estimators using the two methods by and , respectively. Based on the data from our experiments, and . We next need to find out whether the difference of the two estimates is caused by the variation of the data and the true Kd measured by the two methods are actually the same. This is equivalent to testing versus , where Kd1 and Kd2 are the true Kd measured by the two methods, respectively. To test this hypothesis, we need to know the distribution of our test statistic under H0. To find out this distribution, we resort to the bootstrap method. More specifically, we simulate a new set of y’s from the two models using the estimated Kd and n as the true values plus some random noises which mimic the variation of the original data. Based on the new set of y’s, we obtain a new set of Kd estimates, denoted by and . We repeat this procedure 10000 times, and the resulting Kd estimates are and The null distribution of then can be approximated by the empirical distribution of . Figure 4 shows the approximated null distribution of if the two Kd are indeed equal using the bootstrap method. The observed from our experiment is 0.06 = 0.47 − 0.41. Based on the approximated null distribution of , we obtain the p-value of the above hypothesis testing problem, which is p = 0.19148. Since the p-value is larger than 0.05, we do not have sufficient evidence to reject H0 and conclude that the true Kd measured by the two methods are actually the same. Our Kd estimates are also very close to the Kd values from surface plasma resonance (BIACORE)(0.35 μM)7 and and isothermal titration calorimetry (0.25 μM)14, indicating a good agreement with others results.
Figure 4.
Comparison of Kd values obtained from two approaches by the quenched donor emission or acceptor emission. (A) Kd values determined by either FRET quenching or emission at different concentrations of CyPet-SUMO1 were compared. (B) Kd values after global optimization of either FRET quenching or emission datasets. (C) Bootstrap analysis of both Kd values revealed no significant difference.
Discussion
We have successfully developed a new mathematical algorithm, which allows us to derive Kd values from the FRET assay. This approach complements the previous approach utilizing acceptor fluorescence emission of FRET signal to determine the bound partner concentration and Kd, with an advantage of broader applications6,15. Like the previous approach, the new method offers an accurate and simplified Kd determination in a one-step procedure. Because YPet does not have an emission at 475 nm when excited at 414 nm, it does not contribute to the emission at 475 nm (Fig. 2C). The FRET signal can be derived from the total emission at 475 nm in the absence of acceptor by subtracting the emission at donor wavelength in the presence of acceptor. The quenched FRET signal is then converted to the concentration of bound partners, which is used to calculate affinity, Kd. The very similar Kd values generated from different concentrations and ratios of CyPet-SUMO1 and YPet-Ubc9 (from 0.1 to 1.5 μM of CyPet-SUMO1 and from a ratio of the binding partners of 4 to 40 fold) also demonstrate that the FRET-based Kd measurement approach is reliable and can provide consistent estimates of Kd.
The FRET-based Kd measurements, either from donor quenching-based or acceptor excitation-based methods, can provide several advantages over other current Kd measurement methods, such as radio-labeled ligand binding assay, such as SPR or ITC. First, fluorescent protein-tagged interaction partners provide FRET measurement in a solution phase, under conditions more physiological where the Kd is most likely to be close to the affinity of protein interaction in living cells, whereas other methods, such as SPR, require that the conjugations take place on a chip surface, which could interfere with the free interactions of proteins. Second, FRET-based method is very environmental friendly, and protein labeling method is universal. Other methods, such as radio-labeled method, need radioisotopes and special protection tools, and the labeling methodology is very tedious and varies depending on molecules. Third, FRET-based Kd measurement can potentially measure proteins interactions in the presence of other molecules, such as contaminated proteins, while other methods, such as ITC, require very pure proteins. Fourth, FRET-based Kd measurement only requires general fluorescence readers or fluorescence microscopes that are widely available. The Other approaches for Kd determination, such as SPR or ITC, require special instrumentation16,17. Finally, our approach provides a general platform for Kd measurements as long as the two interactive partners can be labeled by a FRET pair, such as protein-protein, protein–small molecule or small molecule–small molecule interactions. The mathematical algorithm and experimental procedure of Kd measurement by FRET technology can be generally applied to these cases.
These two approaches, namely donor quenching and acceptor emission, can be used in FRET-based methods for protein affinity determination. Compared to the method using increase in the acceptor emission, the method using quenched donor emission has more general applications because the acceptor can be excited fluorophores or quenchers. Different mathematical algorithms have been developed for these two approaches. The sensitivity and accuracy of FRET assays are dependent on the instrumentation and quantum yield of each partner of a FRET pair. Recently, extensive efforts have been made to develop new fluorescent proteins or small molecules for FRET assays18–20. Our methodologies of quantitative FRET assays for protein affinity and enzyme kinetics determination will provide powerful quantitative tools for future applications.
Acknowledgements
We thank Prof. Xuemei Chen for allowing us to use HPLC system. This work was supported by the National Institutes of Health Grant 5 R01 AI076504 to J. Liao, and National Natural Science Foundation of China (Grant No. 81503464), Scientific Research Foundation for the Returned Overseas Scholars in Hei Long Jiang Province of China (Grant No. LC2015032), Science Foundation of Heilongjiang University of Chinese medicine (Grant No. 2013bs01) and University Nursing Program for Young Scholars with Creative Talents in Heilongjiang Province, (Grant No. UNPYSCT-2016079) to J. Ling.
Author Contributions
J. Ling, Z.X., Y.S. conducted the experiments, Y.L., Y.C. contributed to manuscript writing and discussion, J. Li performed statistic data analysis. J.S.S. was involved in experimental idea and discussion. J. Liao designed the experiments, data analysis and manuscript writing.
Data Availability
The materials and protocols are available to public.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Liao JY, Song Y, Liu Y. A new trend to determine biochemical parameters by quantitative FRET assays. Acta Pharmacol Sin. 2015;36:1408–1415. doi: 10.1038/aps.2015.82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Erickson MG, Alseikhan BA, Peterson BZ, Yue DT. Preassociation of calmodulin with voltage-gated Ca(2+) channels revealed by FRET in single living cells. Neuron. 2001;31:973–985. doi: 10.1016/S0896-6273(01)00438-X. [DOI] [PubMed] [Google Scholar]
- 3.Erickson MG, Liang H, Mori MX, Yue DT. FRET two-hybrid mapping reveals function and location of L-type Ca2+ channel CaM preassociation. Neuron. 2003;39:97–107. doi: 10.1016/S0896-6273(03)00395-7. [DOI] [PubMed] [Google Scholar]
- 4.Chen H, Puhl HL, 3rd, Ikeda SR. Estimating protein-protein interaction affinity in living cells using quantitative Forster resonance energy transfer measurements. J Biomed Opt. 2007;12:054011. doi: 10.1117/1.2799171. [DOI] [PubMed] [Google Scholar]
- 5.Mehta K, Hoppe AD, Kainkaryam R, Woolf PJ, Linderman JJ. A computational approach to inferring cellular protein-binding affinities from quantitative fluorescence resonance energy transfer imaging. Proteomics. 2009;9:5371–5383. doi: 10.1002/pmic.200800494. [DOI] [PubMed] [Google Scholar]
- 6.Martin SF, Tatham MH, Hay RT, Samuel ID. Quantitative analysis of multi-protein interactions using FRET: application to the SUMO pathway. Protein Sci. 2008;17:777–784. doi: 10.1110/ps.073369608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Song Y, Madahar V, Liao J. Development of FRET Assay into Quantitative and High-throughput Screening Technology Platforms for Protein-Protein Interactions. Ann Biomed Eng. 2011;39:1224–1234. doi: 10.1007/s10439-010-0225-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu Y, Song Y, Madahar V, Liao J. Quantitative Forster resonance energy transfer analysis for kinetic determinations of SUMO-specific protease. Analytical biochemistry. 2012;422:14–21. doi: 10.1016/j.ab.2011.12.019. [DOI] [PubMed] [Google Scholar]
- 9.Reverter D, Lima CD. Structural basis for SENP2 protease interactions with SUMO precursors and conjugated substrates. Nat Struct Mol Biol. 2006;13:1060–1068. doi: 10.1038/nsmb1168. [DOI] [PubMed] [Google Scholar]
- 10.Velick SF, Parker CW, Eisen HN. Excitation energy transfer and the quantitative study of the antibody hapten reaction. Proc Natl Acad Sci USA. 1960;46:1470–1482. doi: 10.1073/pnas.46.11.1470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu BL, Schultz JS. Equilibrium binding in immunosensors. IEEE Trans Biomed Eng. 1986;33:133–138. doi: 10.1109/TBME.1986.325887. [DOI] [PubMed] [Google Scholar]
- 12.Nguyen AW, Daugherty PS. Evolutionary optimization of fluorescent proteins for intracellular FRET. Nature Biotechnology. 2005;23:355–360. doi: 10.1038/nbt1066. [DOI] [PubMed] [Google Scholar]
- 13.Song Y, Liao J. Systematic determinations of SUMOylation activation intermediates and dynamics by a sensitive and quantitative FRET assay. Mol Biosyst. 2012;8:1723–1729. doi: 10.1039/c2mb05465e. [DOI] [PubMed] [Google Scholar]
- 14.Tatham MH, et al. Role of an N-terminal site of Ubc9 in SUMO-1, -2, and -3 binding and conjugation. Biochemistry. 2003;42:9959–9969. doi: 10.1021/bi0345283. [DOI] [PubMed] [Google Scholar]
- 15.Song Y, Madahar V, Liao J. Development of FRET Assay into Quantitative and High-throughput Screening Technology Platforms for Protein–Protein Interactions. Annals of Biomedical Engineering. 2010;39:1224–1234. doi: 10.1007/s10439-010-0225-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Linman MJ, Abbas A, Cheng Q. Interface design and multiplexed analysis with surface plasmon resonance (SPR) spectroscopy and SPR imaging. Analyst. 2010;135:2759–2767. doi: 10.1039/c0an00466a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Perozzo R, Folkers G, Scapozza L. Thermodynamics of protein-ligand interactions: history, presence, and future aspects. J Recept Signal Transduct Res. 2004;24:1–52. doi: 10.1081/RRS-120037896. [DOI] [PubMed] [Google Scholar]
- 18.Sapsford KE, Berti L, Medintz IL. Materials for fluorescence resonance energy transfer analysis: beyond traditional donor-acceptor combinations. Angew Chem Int Ed Engl. 2006;45:4562–4589. doi: 10.1002/anie.200503873. [DOI] [PubMed] [Google Scholar]
- 19.Tsien RY. Constructing and exploiting the fluorescent protein paintbox (Nobel Lecture) Angew Chem Int Ed Engl. 2009;48:5612–5626. doi: 10.1002/anie.200901916. [DOI] [PubMed] [Google Scholar]
- 20.Goedhart J, et al. Bright cyan fluorescent protein variants identified by fluorescence lifetime screening. Nat Methods. 2010;7:137–139. doi: 10.1038/nmeth.1415. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The materials and protocols are available to public.