Abstract
Objectives
To formally identify and contrast the most commonly-employed quantifications of response time inconsistency (RTI) and elucidate their utility for understanding within-person (WP) and between-person (BP) variation in cognitive function with increasing age.
Method
Using two measurement burst studies of cognitive aging, we systematically identified and computed five RTI quantifications from select disciplines to examine: (a) correlations among RTI quantifications; (b) the distribution of BP and WP variation in RTI; and (c) the comparability of RTI quantifications for predicting attention switching.
Results
Comparable patterns were observed across studies. There was significant variation in RTI BP as well as WP across sessions and bursts. Correlations among RTI quantifications were generally strong and positive both WP and BP, except for the coefficient of variation. Independent prediction models indicated that slower mean response time (RT) and greater RTI were associated with slower attention switching both WP and BP. For selecting simultaneous prediction models, collinearity resulted in inflated standard errors and unstable model estimates.
Discussion
RTI reflects a novel dimension of performance that is a robust and theoretically informative predictor of BP and WP variation in cognitive function. Among the plenitude of RTI quantifications, not all are interchangeable, nor of comparable predictive utility.
Keywords: Central tendency, Cognitive aging, Inconsistency, Intraindividual variability, Response time, Measurement burst design
Intraindividual variability (IIV) is an approach for examining dynamic fluctuations in performance that confer meaning beyond estimates of central tendency (MacDonald & Stawski, 2015; Ram & Gerstorf, 2009; Stawski, Smith, & MacDonald, 2015). This approach holds promise for furthering our understanding of dynamic processes underlying adult development and aging (c.f., Benson, Ram, Almeida, Zautra, & Ong, 2017; Diehl, Hooker, & Sliwinski, 2015; Nesselroade & Salthouse, 2004). Trial-to-trial fluctuations on response time (RT) tasks, or response time inconsistency (RTI), is one particular instantiation of IIV that has been linked with deleterious age-related outcomes ranging from relatively transient lapses of attention (West, Murphy, Armilio, Craik, & Stuss, 2002) and neural deficiency in attentional control (Weissman, Roberts, Visscher, & Woldorff, 2006) to more durable and insidious correlates including normal and pathological cognitive decline, mild cognitive impairment, dementia, and compromised neural function (see Graveson, Bauermeister, McKeown, & Bunce, 2016; MacDonald & Stawski, 2015 for overviews). Thus, RTI represents a theoretically-valid indicator, emerging from the IIV tradition, with considerable promise for advancing our understanding of psychological function in general, and cognitive health in particular (MacDonald & Stawski, 2015; Stawski et al., 2015).
Although RTI has emerged as a potentially important behavioral indicator of cognitive status and function, several notable shortcomings obfuscate its meaning and practical utility. One critical shortcoming pertains to how best to operationalize RTI. Multiple quantifications are represented in the extant literature including: raw intraindividual standard deviation (ISD), coefficient of variation (CV), residualized ISD that attempts to control for select confounds (e.g., mean RT, time-based trends), variability for select portions of the RT distribution (e.g., based on percentiles for the fast vs slow tails), and mathematical models (e.g., ex-Gaussian distribution). The rationale, however, for the use of particular quantifications across studies is unclear, as is their comparability and predictive utility for theoretically-relevant outcomes. Without systematic examination of (a)symmetry in associations across multiple oft-used RTI quantifications, their comparability, interchangeability, meaning, and utility remains unclear.
A second critical issue pertains to the mismatch between theoretical and conceptual accounts of what RTI reflects, and the research designs employed to empirically study RTI. While RTI has been argued to reflect relatively labile phenomena such as lapses of attention (West et al., 2002) as well as more durable phenomena including mild cognitive impairment, dementia, and central nervous system (CNS) integrity, most research has focused on RTI as a between-person (BP) differences indicator. This, however, precludes an understanding of whether variation in RTI reflects an individual differences characteristic (e.g., having relatively poorer CNS integrity), a more labile characteristic attributable to proximal influences (e.g., daily variations in sleep or affect), or both (c.f., Hultsch, Strauss, Hunter, & MacDonald, 2008). Measurement burst designs (Nesselroade, 1991; Sliwinski, 2008; Stawski, MacDonald, & Sliwinski, 2016) facilitate the examination of such issues by allowing for the intensive assessment of RTI over shorter periods of time (e.g., days); repeating that intensive assessment protocol across longer intervals (e.g., semiannually, annually), for multiple persons. Thus, BP variability (i.e., individual differences) and short(er)-term variability within-persons (WP) over time can be distinguished. Applying measurement burst designs to the study of RTI will provide for a more nuanced understanding of RTI—one that more optimally matches a given study design to the phenomena under study (Neupert, Stawski, & Almeida, 2008).
Competing Quantifications of RTI
Clear theoretical or methodological rationale for selecting a specific RTI operationalization are lacking in many published studies of RTI and cognitive aging. To formally assess the extent of heterogeneity of RTI definitions employed within this field, we conducted a literature search with the goal of (a) identifying the most commonly employed RTI operationalizations, and (b) quantifying how frequently these definitions are employed. A search of the literature since 2000 in PubMed and PSYCInfo yielded 465 articles based upon key search terms (e.g., IIV, reaction time, response time, cognition, age). Of these, 186 empirical articles utilized one or more quantifications of RTI (222 total uses). The most prevalent RTI quantifications included the CV (30% of total uses), residualized ISD (29%), raw ISD (24%), and ex-Gaussian models (7%). For the remaining RTI quantifications, no single definition was used more than 3.6% of the time, with infrequently employed definitions including percentile approaches, log linear variance models, individual range and amplitude approaches, statistical (log-linear variance prediction) and mathematical (i.e., diffusion model, Weibull distribution) models, and raw between-group variability.
These frequencies underscore clear heterogeneity in RTI quantification, and unequivocally identify raw ISD, coefficient of variation, residualized ISD, and Ex-Gaussian models as the most frequently utilized quantifications in empirical work spanning the last 17 years. Although easy to compute, a raw ISD fails to control for mean RT, making it difficult to discern whether individual differences in variability (e.g., due to age) are an important phenomenon or merely an artifact of differences in mean RT. To address the concern of mean confounds, the CV is often derived to index RTI. However, the CV is a ratio of ISD to intraindividual mean, and use of such an interaction term makes it difficult to determine whether any observed effects reflect associations attributable to increased variability, mean slowing, or both (Hultsch et al., 2008). The residualized ISD controls for systematic between- (e.g., group differences in mean RT) and within-subject (e.g., polynomial time effects) confounds in the raw data (Hultsch et al., 2008). Finally, fitting explicit mathematical functions such as the ex-Gaussian distribution to raw RT data yields two parameter estimates: mean (mu) and SD (sigma) of the normally-distributed portion of the RT distribution, and a third parameter (tau) reflecting the M and SD of the positively skewed tail of the distribution. Although not solely a measure of RTI, larger estimates of tau are putatively driven by increased fluctuations in executive control processes (e.g., West et al., 2002). Notably, few studies report more than a single quantification of RTI (e.g., Deary & Der, 2005; Myerson, Robertson, & Hale, 2007), with seemingly no comparison of results across these competing definitions. As such, the comparability of RTI indices remains unknown.
The Present Study
We focus on several key research objectives using data from two measurement burst studies of cognitive aging. First, using the most commonly employed RTI quantifications (raw ISD, CV, residualized ISD, and ex-Gaussian) that vary in approach for addressing confounding influences, we compute corresponding RTI estimates for a similar RT measure from each study. We also include a fifth indicator of RTI, the mean squared successive difference (MSSD; von Neumann, Kent, Bellinson, & Hart, 1941), given its close computational association with the residualized ISD approach, and its use in neuroscience for minimizing the effect of within-subject trends by deriving RTI estimates from differences among successive adjacent trials. Second, given the advantages of measurement burst designs for studying RTI, we decompose the variability in RTI into BP and WP sources, and then systematically compare associations across the five RTI quantifications at each level of analysis. Specific questions addressed include: (a) What proportion of the variation for each RTI quantification is BP versus WP?, (b) Is a high degree of association observed across RTI quantifications both BP and WP?, and (c) Do the RTI quantifications share similar predictive associations for attention switching performance? Answers to these questions will inform the central issue of whether the disparate RTI quantifications are interchangeable. Finally, through parallel analyses across the two burst-design studies, an ancillary objective will address the generalizability of the individual RTI quantifications across measurement and sample.
Method
To address the research aims, the present study employs data from two measurement-burst studies—Project Mental Inconsistency in Normals and Demented (MIND) and the Cognition Health and Aging Project (CHAP).
Participants and Design
Project MIND
At baseline, 304 community-dwelling adults participated: 68.4% women, mean age = 74.02 years (SD = 5.95, range = 64–93), mean years of education = 15.15 (SD = 3.14). Exclusionary criteria included a diagnosis of dementia by a physician or Mini-Mental State Examination score <24, a history of significant head injury (defined as loss of consciousness for more than 5 min), other neurological or major medical illnesses (e.g., Parkinson’s disease, heart disease, cancer), severe sensory impairment (e.g., difficulty reading newspaper-size print, difficulty hearing a normal conversation), drug or alcohol abuse, current psychiatric diagnoses, psychotropic drug use, or lack of fluency in English.
Annually, participants completed a burst evaluation consisting of five individual testing sessions at year 1, with four sessions completed in years 2, 3, and 4. Each session was scheduled approximately 2 weeks apart, with participants completing a broad battery of RT tasks designed to assess short-term fluctuations in response speed. For each annual wave, the burst RT measures were identical and the order of presentation invariant. Up to four annual measurement occasions with burst data were available, and 76.9% (n = 242) of participants completed all four bursts.
CHAP
At baseline, 111 older adults participated: 72% female, mean age = 80.04 years (SD = 6.30, range = 66–95), mean years of education = 14.90 (SD = 2.40). All participants had confirmed intact mental status (i.e., fewer than 8 errors on the Blessed mental status exam; Blessed, Tomlinson, & Roth, 1968).
Participants completed six daily assessment occasions within a 14-day period, and this assessment protocol was repeated every 6 months for 2 years, yielding five bursts of data. Half of the sessions were scheduled in the morning (9 a.m. to 12 p.m.), and half in the afternoon (1–5 p.m.). Order of administration of RT measures was identical across sessions and bursts. Up to five bursts of data were available, with 78% (n = 90) completing all five bursts.
Measures
RT-based Measures of Cognition
Project MIND
Working memory was measured using a 1-back version of a 4-choice RT (60 trials) task. Participants indicated whether the current stimulus was the same or different than the previous stimulus. Attention switching was measured using a shape/color task-switching paradigm where figures varying in shape (square, circle) and color (red, green) were presented in a white frame. A cue indicating the currently relevant stimulus dimension (shape or color) was presented in random order above the stimulus, with 10 practice trials followed by 52 test trials. The average response time across correct trials was recorded. See Bielak, Hultsch, Strauss, MacDonald, & Hunter (2010) for additional task details.
CHAP
Working memory was measured using the 1-back version (60 trials) of the n-back task. Attention switching was measured using a serial counting task (Garavan, 1998), whereby participants maintained a running count of 2 objects simultaneously. Runs of 8, 10, 12, or 16 stimuli were administered, and performance was indexed as the average RT across runs where accurate counts were recorded. See Sliwinski, Smyth, Hofer, & Stawski (2006) for additional task details.
Quantification of RTI
Five estimates of RTI that have been used in existing empirical literature were computed for the 1-back working memory tasks. These included: (a) the raw ISD computed across RT trials for each session and burst, and providing no control for potential between- or within-subject confounds; (b) the residualized ISD computed across RT trials for each session and burst, residualizing select confounds from the raw data by employing linear mixed models to partial systematic between- (age group differences in response latency) and within-subject (trial, session, and burst trends) sources of variance, and their interactions (e.g., Hultsch et al., 2008); (c) CV computed as the ISD divided by the intraindividual mean to control for systematic between-subject (but not within-subject) confounds; (d) MSSD that controls for mean trends by estimating variability from differences among successive adjacent trials (von Neumann et al., 1941); and (e) tau, the exponential portion of the ex-Gaussian distribution, derived using Quantile Maximum Probability Estimation (QMPE) software (Heathcote, Brown, & Cousineau, 2004). For each operationalization, only RTs from accurate responses were included. Accuracy rates for the 1-back tasks were 92% for both studies.
Statistical Procedure
Given the nested data structure (i.e., sessions nested within bursts, nested within persons), all data were modeled using multilevel modeling (MLM) in SAS PROC MIXED v9.4 (SAS Institute, 2013). We used three-level MLMs to examine RTI, predicting attention-switching (AS) performance across sessions, bursts, and persons (Equation 1). Session- and burst-level effects of RTI were person-mean centered such that the session-level RTI variable reflects only variation across sessions (β3jk: RTIijk–RTI..k), and the burst-level RTI variable reflects only variation across bursts within a person (δ02k: RTI.jk–RTI..k). The person-level RTI variable was centered at the person’s mean across all sessions and bursts (γ002: RTI..k). Covariates for all models included linear (β1jk) and quadratic (β2jk) trends for performance across sessions, and linear trends across bursts (δ01k) to account for systematic trends in performance, as well as age at baseline (γ001). Random slopes for the linear session trend were included at both level 2 (U1jk) and level 3 (V10i), to allow for variation in these trends across bursts and persons, respectively. A random slope for the linear trend across bursts was also included at level 3 (V01i) to allow for variation across persons.
| (1) |
Analogous models, using the same centering approach, were estimated exchanging RTI for mean RT to evaluate associations between mean RT and attention switching across sessions, burst and persons, as well as models retaining both RTI and mean RT to evaluate their unique associations with attention switching. Decomposition of variation in RTI across session (eijk, level 1), bursts (U0jk, level 2), and persons (V00k, level 3) was done using an empty (i.e., no predictors) model based on Equation 1. All analyses were conducted using full information maximum likelihood estimation.
Results
First, we present variance decomposition of mean RT and RTI quantifications for the 1-back task. Second, we present correlations among mean RT and RTI quantifications across levels of analysis. Finally, we present results from multilevel models examining mean RT and RTI predicting attention-switching performance across sessions, bursts and persons.
Variance Decomposition of Mean RT and Inconsistency
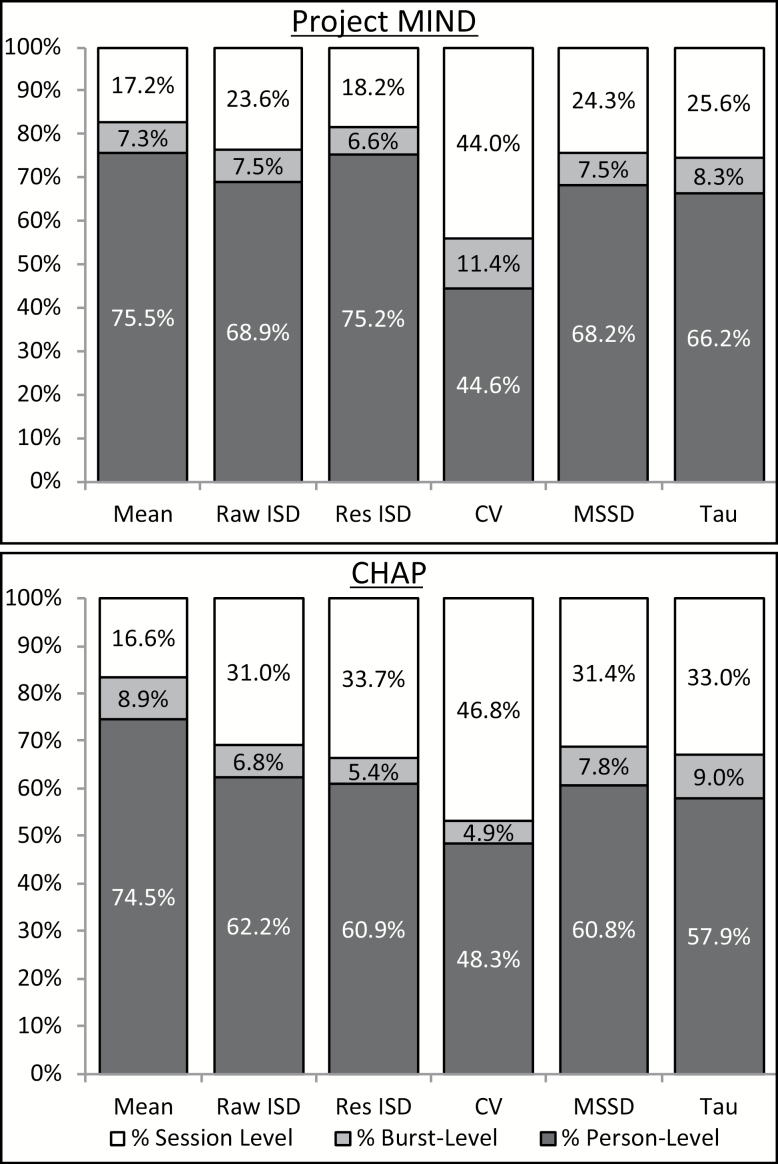
Empty multilevel models revealed significant variation in mean RT and RTI across sessions, bursts and persons, as well as across both studies (see Figure 1). With respect to mean RT, for both studies, the majority of variation was between persons (~75%), with the remainder reflecting variation WP across sessions (16.6–17.2%), and across bursts (7.3–8.9%). A similar pattern emerged for quantifications of RTI, with most variation observed between persons (44.6–75.2%), in contrast to WP across sessions (18.2–46.8%) or bursts (4.9–11.4%).
Figure 1.
Variance decomposition of 1-back mean RT and inconsistency in Project MIND (top panel) and CHAP (bottom panel). CV = Coefficient of variation; ISD = Intraindividual standard deviation; MSSD = Mean squared successive difference; Res ISD = Residualized intraindividual standard deviation; RT = Response time.
Correlations Among Mean RT and Inconsistency
Table 1 shows correlations among mean RT and RTI across sessions, bursts, and persons for each study. A few general patterns emerged. First, all correlations were positive and statistically significant, indicating that slower mean RT was associated with greater RTI. Second, correlations among RTI quantifications were positive, indicating rank-order stability. Third, correlations among mean RT and RTI, as well as across quantifications of RTI, tended to (a) be weakest WP across sessions, (b) increase in magnitude WP across longer intervals (semiannual or annual), and (c) be strongest BP. Finally, the CV exhibited weaker correlations with mean RT and other quantifications of RTI, regardless of study or level of association.
Table 1.
Correlations Among Mean RT and RTI Across Levels of Analysis
| MIND | CHAP | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Session | 1 | 2 | 3 | 4 | 5 | 6 | Session | 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | Mean | – | 1 | Mean | – | ||||||||||
| 2 | ISD | .78 | – | 2 | ISD | .83 | – | ||||||||
| 3 | rISD | .49 | .81 | – | 3 | rISD | .69 | .93 | – | ||||||
| 4 | CV | .09 | .59 | .64 | – | 4 | CV | .37 | .83 | .81 | – | ||||
| 5 | MSSD | .76 | .96 | .79 | .56 | – | 5 | MSSD | .76 | .96 | .89 | .78 | – | ||
| 6 | Tau | .72 | .86 | .72 | .49 | .85 | – | 6 | Tau | .56 | .63 | .56 | .48 | .60 | – |
| Burst | 1 | 2 | 3 | 4 | 5 | 6 | Burst | 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | Mean | – | 1 | Mean | – | ||||||||||
| 2 | ISD | .79 | – | 2 | ISD | .84 | – | ||||||||
| 3 | rISD | .49 | .80 | – | 3 | rISD | .74 | .92 | – | ||||||
| 4 | CV | .11 | .59 | .60 | – | 4 | CV | .36 | .77 | .76 | – | ||||
| 5 | MSSD | .75 | .98 | .80 | .60 | – | 5 | MSSD | .82 | .97 | .90 | .73 | – | ||
| 6 | Tau | .76 | .88 | .69 | .52 | .86 | – | 6 | Tau | .72 | .80 | .69 | .55 | .79 | – |
| Person | 1 | 2 | 3 | 4 | 5 | 6 | Person | 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | Mean | – | 1 | Mean | – | ||||||||||
| 2 | ISD | .94 | – | 2 | ISD | .90 | – | ||||||||
| 3 | rISD | .91 | .99 | – | 3 | rISD | .89 | .99 | – | ||||||
| 4 | CV | .32 | .59 | .60 | – | 4 | CV | .42 | .75 | .77 | – | ||||
| 5 | MSSD | .93 | .99 | .99 | .59 | – | 5 | MSSD | .89 | .99 | .99 | .76 | – | ||
| 6 | Tau | .91 | .98 | .97 | .61 | .97 | – | 6 | Tau | .89 | .96 | .96 | .69 | .94 | – |
Note: All correlations significant p < .05. CV = Coefficient of variation; ISD = Intraindividual standard deviation; MSSD = Mean squared successive difference; rISD = Residualized intraindividual standard deviation; RT = Response time; RTI = Response time inconsistency.
Associations Among Mean RT, RT Inconsistency, and Attention-Switching Performance
Independent prediction models
Initially, we examined the effects of mean RT and each RTI quantification in separate models. Mean RT was associated with attention-switching performance across sessions, bursts and persons in both MIND and CHAP (see Table 2). Participants’ attention switching was slower during sessions (MIND: Estimate = 0.05; CHAP: Estimate = 0.11) and bursts (MIND: Estimate = 0.06; CHAP: Estimate = 0.16) when their 1-back performance was slower than usual. Furthermore, across persons, individuals’ whose 1-back performance was slower also exhibited slower attention switching (MIND: Estimate = 0.20; CHAP: Estimate = 0.57).
Table 2.
Multilevel Model Estimates for Independent Effects of Session-, Burst-, and Person-Level Mean RT and Inconsistency on Attention Switching
| MIND | CHAP | ||||||
|---|---|---|---|---|---|---|---|
| Mean | Estimate | SE | p | Mean | Estimate | SE | p |
| WPS | 0.05 | 0.01 | <.01 | WPS | 0.11 | 0.02 | <.01 |
| WPB | 0.06 | 0.02 | <.01 | WPB | 0.16 | 0.06 | .01 |
| BP | 0.20 | 0.02 | <.01 | BP | 0.57 | 0.09 | <.01 |
| ISD | Estimate | SE | p | ISD | Estimate | SE | p |
|---|---|---|---|---|---|---|---|
| WPS | 0.07 | 0.01 | <.01 | WPS | 0.08 | 0.03 | <.01 |
| WPB | 0.08 | 0.02 | <.01 | WPB | 0.22 | 0.10 | .03 |
| BP | 0.35 | 0.03 | <.01 | BP | 1.05 | 0.18 | <.01 |
| rISD | Estimate | SE | p | rISD | Estimate | SE | p |
|---|---|---|---|---|---|---|---|
| WPS | 4.65 | 0.77 | <.01 | WPS | 2.79 | 1.02 | <.01 |
| WPB | 6.31 | 1.84 | <.01 | WPB | 9.79 | 3.99 | .01 |
| BP | 29.08 | 7.68 | <.01 | BP | 43.20 | 7.68 | <.01 |
| CV | Estimate | SE | p | CV | Estimate | SE | p |
|---|---|---|---|---|---|---|---|
| WPS | 17.62 | 13.74 | .20 | WPS | 33.50 | 35.95 | .35 |
| WPB | 33.15 | 37.21 | .37 | WPB | 147.97 | 158.49 | .35 |
| BP | 425.55 | 90.97 | <.01 | BP | 1,045.86 | 373.59 | <.01 |
| MSSD | Estimate | SE | p | MSSD | Estimate | SE | p |
|---|---|---|---|---|---|---|---|
| WPS | 0.04 | 0.01 | <.01 | WPS | 0.05 | 0.02 | <.01 |
| WPB | 0.05 | 0.02 | <.01 | WPB | 0.13 | 0.07 | .07 |
| BP | 0.24 | 0.02 | <.01 | BP | 0.72 | 0.13 | <.01 |
| Tau | Estimate | SE | p | Tau | Estimate | SE | p |
|---|---|---|---|---|---|---|---|
| WPS | 0.07 | 0.01 | <.01 | WPS | 0.04 | 0.02 | .01 |
| WPB | 0.06 | 0.02 | <.01 | WPB | 0.14 | 0.06 | .02 |
| BP | 0.37 | 0.02 | <.01 | BP | 0.71 | 0.12 | <.01 |
Note: BP = Between-persons; CV = Coefficient of variation; ISD = Intraindividual standard deviation; MSSD = Mean squared successive difference; rISD = Residualized intraindividual standard deviation; RT = Response time; WPB = Within-persons across bursts; WPS = Within-persons across session.
RTI was also associated with attention switching across sessions, bursts, and persons. In MIND, during sessions when a person’s 1-back RTI was greater than usual, their attention switching was slower than usual. This was true for RTI quantified by the raw ISD (Estimate = 0.07), residualized ISD (Estimate = 4.65), MSSD (Estimate = 0.04), and tau (Estimate = 0.07), but not CV. Similarly, across bursts when a person’s RTI was greater than usual, their attention performance was slower than usual. This was true for RTI defined by the raw ISD (Estimate = 0.08), residualized ISD (Estimate = 6.31), MSSD (Estimate = 0.05), and tau (Estimate = 0.06), but not CV. Lastly, across persons, individuals who exhibited greater RTI on average also exhibited slower attention switching performance, and this was true for all quantifications of RTI: raw ISD (Estimate = 0.35), residualized ISD (Estimate = 29.08), CV (Estimate = 425.55), MSSD (Estimate = 0.24), and tau (Estimate = 0.37).
Parallel analyses from CHAP revealed similar patterns. During sessions where a person’s 1-back RTI was greater than usual, their attention switching was slower. This was true for RTI quantified using the raw ISD (Estimate = 0.08), residualized ISD (Estimate = 2.79), MSSD (Estimate = 0.05), and tau (Estimate = 0.04), but not CV. Similarly, across bursts, when a person’s RTI was greater than usual, their attention switching was slower than usual. Again, this was true when RTI was quantified using the raw ISD (Estimate = 0.22), and residualized ISD (Estimate = 9.79), tau (Estimate = 0.14), and marginally for MSSD (Estimate = 0.13), but not CV. Lastly, across persons, individuals exhibiting greater RTI on average also exhibited slower attention switching performance, and this was true for all RTI quantifications: raw ISD (Estimate = 1.05), residualized ISD (Estimate = 43.20), CV (Estimate = 1,045.86), MSSD (Estimate = 0.72), and tau (Estimate = 0.71).
Simultaneous prediction models
Given concerns about mean and inconsistency reflecting similar sources of variance, we simultaneously modeled mean RT and RTI as predictors of attention switching to examine their unique effects, statistically adjusting for the other. For each RTI quantification, session-, burst-, and person-level effects of mean RT and inconsistency were examined.
For MIND, the simultaneous estimation patterns were largely similar to the univariate prediction models (see Supplementary Table 1). Across all models, mean RT was associated with attention-switching performance WP across session (Estimate = 0.03–0.05), WP across bursts (Estimate = 0.07–0.11) and across persons (Estimate = 0.11–0.19); attention switching was significantly slower on sessions and bursts for individuals who were slower than average. With respect to RTI, quantified as the raw ISD, attention switching was significantly slower on sessions (Estimate = 0.03) and for bursts (Estimate = 0.07) when RTI was greater than usual, and for individuals who exhibited greater RTI on average (Estimate = 0.17). Similar patterns emerged when RTI was quantified using the residualized ISD or MSSD, such that attention switching was slower during sessions (residualized ISD: Estimate = 1.86; MSSD: Estimate = 0.03) and bursts (residualized ISD: Estimate = 5.58; MSSD: Estimate = 0.05) when RTI was greater than usual, and for individuals who exhibited greater average RTI (residualized ISD: Estimate = 14.31; MSSD: Estimate = 0.11). RTI quantified as tau was not significantly associated with attention switching WP across bursts; however, attention switching was slower during sessions (Estimate = 0.04) when tau was greater than usual, and for individuals who exhibited greater average tau (Estimate = 0.19). In contrast, RTI quantified as CV was not significantly associated with attention switching WP across sessions or bursts; however, persons exhibiting greater RTI on average also exhibited slower attention switching performance (Estimate = 212.62).
For CHAP, a divergent pattern of results emerged (see Supplementary Table 2). Across all models, slower mean RT performance was associated with slower attention switching performance across sessions (Estimate = 0.13–0.19), bursts (Estimate = 0.29–0.41) and persons (Estimate = 0.52–0.60). With respect to RTI, session-, burst-, and person-level associations changed direction and were negative, except for person-level CV and tau. Additionally, few effects remained significant. Session-level associations between RTI and attention performance were significant for RTI quantified by the raw ISD (Estimate = −0.11), residualized ISD (Estimate = −3.16) and MSSD (Estimate = −0.06), indicating that attention switching performance was faster for sessions when individuals exhibited greater RTI than usual.
Quantifying collinearity
Collinearity is a concern with the simultaneous prediction models given stronger correlations between mean RT and RTI quantifications (see Table 2). Such collinearity can lead to inflated standard errors, unstable regression coefficients, and reduced power to detect reliable effects. Using methods described by Clark (2013), we computed multilevel variance inflation factors (MVIFs) for the effects of mean RT and RTI for each of the RTI quantifications (Table 3). For both studies, MVIFs for session- and burst-level mean RT and RTI effects were <3.5. However, the MVIFs for person-level mean RT and RTI effects were very large, ranging in value from 6.77 to 37.56 in MIND and 15.85 to 64.73 in CHAP. Taken together with the magnitude of correlations, there are noticeable issues and impacts of collinearity when considering the simultaneous effects of mean RT and RTI.
Table 3.
Multilevel Variance Inflation Factors
| MIND | ISD | rISD | CV | MSSD | Tau |
|---|---|---|---|---|---|
| Mean RT (Session) | 2.55 | 1.86 | 1.31 | 2.40 | 2.50 |
| Mean RT (Burst) | 3.01 | 2.60 | 1.55 | 2.72 | 3.03 |
| Mean RT (Person) | 37.56 | 29.03 | 6.77 | 33.05 | 30.60 |
| RTI (Session) | 2.27 | 1.43 | 1.02 | 2.11 | 2.08 |
| RTI (Burst) | 2.55 | 1.68 | 1.04 | 2.27 | 2.52 |
| RTI (Person) | 26.93 | 22.85 | 16.25 | 22.72 | 20.53 |
| CHAP | ISD | rISD | CV | MSSD | Tau |
|---|---|---|---|---|---|
| Mean RT (Session) | 2.75 | 2.23 | 1.29 | 2.45 | 1.54 |
| Mean RT (Burst) | 3.44 | 3.21 | 1.42 | 3.20 | 2.14 |
| Mean RT (Person) | 64.73 | 57.52 | 15.87 | 56.64 | 56.05 |
| RTI (Session) | 2.62 | 2.10 | 1.22 | 2.31 | 1.46 |
| RTI (Burst) | 3.12 | 2.62 | 1.16 | 2.85 | 1.94 |
| RTI (Person) | 34.22 | 31.44 | 28.57 | 27.48 | 24.60 |
Note: CV = Coefficient of variation; ISD = Intraindividual standard deviation; MSSD = Mean squared successive difference; rISD = Residualized intraindividual standard deviation; RTI = Response time inconsistency; WPB = Within-persons across bursts; WPS = Within-persons across session.
Discussion
The results of this comprehensive investigation yielded several major findings regarding RTI among older adults. First, based upon the advantages of the measurement burst design, we could delineate and quantify WP and BP variation in RTI. Second, correlations among five RTI quantifications, and RTI correlations with mean RT, were largely strong and positive, and increased in magnitude across levels of analysis from sessions to persons; the CV quantification shared the weakest association with the other four. Third, greater RTI was predictive of slower attention switching performance; patterns were largely consistent across RTI quantification, apart from the CV. Finally, results were largely consistent across two independent studies, underscoring the replicability of our findings.
Advantages of a Measurement Burst Design for Studying RTI
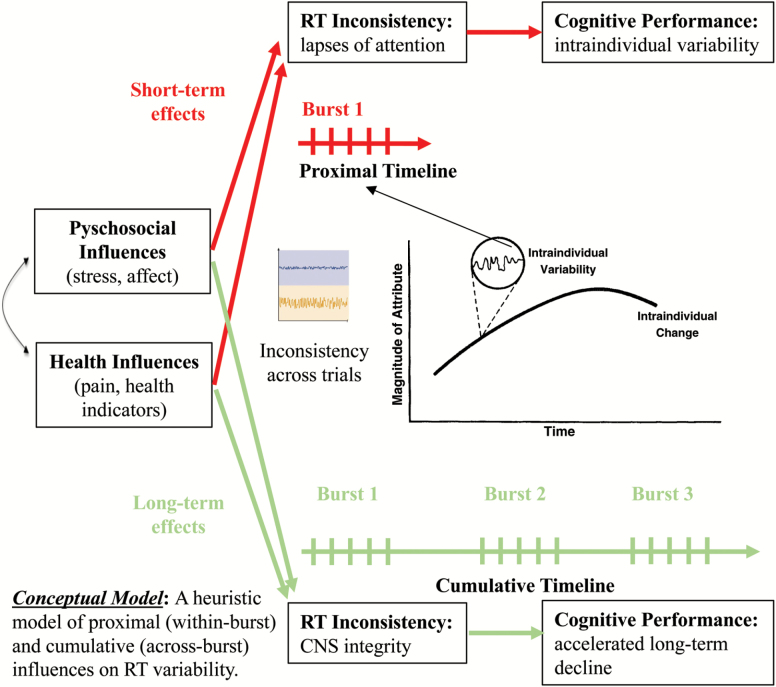
A unique feature of the current study is that two measurement burst designs were employed to investigate RT-based cognitive performance. In addition to distinguishing BP and WP sources of variation, the measurement burst design also facilitates the disambiguating of WP variation sources transpiring across different temporal intervals (see Figure 2). This latter advantage is critically important for the study of RTI, as theoretical accounts (for review, see Hultsch et al., 2008; MacDonald & Stawski, 2015) contend that increased RTI can reflect both short-term (e.g., transient lapses of attention due to proximal influences such as stress or affect) and long-term (e.g., year-over-year increases in RTI due to chronic health conditions) processes. As shown in Figure 2, distinct (or shared) influences may modulate both short- and long-term influences on RTI, and therein inform underlying mechanisms.
Figure 2.
A heuristic model of proximal (within-burst) and cumulative (across-burst) influences on intraindividual variability. Select modulating factors (e.g., psychosocial, health) may exert both short- and long-term influences on intraindividual variability in cognitive function. Determining how such factors influence variability from moment-to-moment, day-to-day, or year-to-year may further our understanding of potential underlying mechanisms, or how short-term processes map onto long-term cognitive change. Reproduced with permission. CNS = Central nervous system; RT = Response time.
The two measurement burst studies employed in the present investigation facilitate an optimal mapping of design-based sampling to the RTI phenomena under study (MacDonald & Stawski, 2015; Neupert et al., 2008; Ram & Gerstorf, 2009; see Figure 2). Project MIND involved 4–5 weekly assessments with this protocol repeated annually for 4 years, whereas CHAP incorporated six assessments over a 10-day period, with this protocol repeated every 6 months for 2.5 years—such complementary designs help to further our understanding of WP variation in RTI. Consistent with expectations, decomposition of variation in RTI revealed evidence of significant variability in RTI both WP (25%–55% of total variation), and BP (45%–75% of total variation), suggesting that variation in RTI does not strictly reflect individual differences.
Parsing BP and WP variation
Partitioning variance into BP and WP sources reflects one definitive advantage of employing a measurement burst design for the study of RTI, particularly given concerns regarding confounds at each level of analysis. In the present study, RTI exhibited less BP variation and more WP variation relative to mean RT. This pattern suggests that how fast someone performs on average is somewhat more reflective of who they are, with comparatively less WP variation in their performance. In contrast, RTI reflects a greater mixture of BP and WP variation. This difference in distribution of variation between mean RT and RTI further supports theoretical contentions that mean and variability in RT reflect qualitatively different theoretical variation (e.g., Jensen, 1992), and are potentially related to, and influenced by, both personal and contextual factors (Hultsch et al., 2008). We do, however, acknowledge that the larger proportion of WP across-session variation in RTI could reflect more measurement error (Schmiedek, Lövdén, & Lindenberger, 2009).
Parsing WP sources of variation
With regard to WP variation across shorter (sessions) and longer (bursts of assessment) intervals (c.f., Figure 2), the former may reflect variation more consistent with RTI reflecting transient phenomena reflected over a faster-moving time scale, such as lapses of attention or mental noise (Robinson & Tamir, 2005; Van Gemmert & Van Galen, 1997; West et al., 2002), whereas the latter may reflect more enduring processes reflected over a slower-moving time scale such as aging-related changes in brain and cognitive function. Although both sources of WP variation were significant, the proportion of observed variation was greater for the faster compared to the slower WP timescale. Taken together, the results of the two measurement burst studies suggest that RTI varies significantly BP and WP.
Are the RTI Quantifications Comparable?
Correlations among mean RT and RTI
In general, correlations between mean RT and RTI indicated that increased RTI was associated with slower mean RT, with largely strong and positive correlations among quantifications of RTI indicating rank-order stability both BP and WP. Two additional patterns emerged as well. First, BP correlations tended to be stronger than correlations WP across sessions or bursts. Second, the CV quantification of RTI exhibited markedly weaker associations with mean RT and the other quantifications of RTI. As suggested by Jensen (1992), these patterns of association among markers of central tendency and variability are consistent with distinct-but-related indices.
Mean RT and RTI as predictors of attention switching
In independent models, both mean RT and RTI were significantly predictive of attention-switching performance such that during sessions and for bursts when individuals were slower than usual or more inconsistent than usual, they also exhibited significantly slower (worse) attention-switching performance. Additionally, individuals who exhibited significantly slower and more inconsistent performance also exhibited slower attention-switching performance. RTI operationalized as the CV was a notable exception to this pattern. Taken together, these results suggest that both WP fluctuations and BP differences in RTI potentially undermine an individual’s ability to optimally switch their focus of attention. Given that attention switching is an integral part of working memory (Basak & Verhaeghen, 2011), the impact of RTI on cognitive performance is both theoretically and practically relevant for understanding complex cognitive function.
Collinearity concerns when simultaneously modeling mean and RTI
Results of simultaneous prediction models were informative in terms of both methodological practice and application. In Project MIND, all WP and BP effects of mean RT and RTI on attention switching remained positive and significant, consistent with patterns observed in the independent prediction models. In CHAP, the WP and BP mean RT effects remained positive and significant; however, nearly all RTI effects became negative in direction (i.e., higher RTI associated with faster attention switching), consistent with multicollinearity. To further inform the potential impact of multicollinearity on our prediction models, we computed MVIFs, which indicate the extent to which collinearity has resulted in high standard errors, unstable parameter estimates, and reduced statistical power (Clark, 2013). While conventions for evidence of high multicollinearity were not present (VIFs < 5) for WP effects, there was evidence of collinearity for BP effects (VIFs > 15). The square root of a VIF indicates how many times the SE for a given coefficient has been inflated (see Table 3), with obvious implications for the simultaneous modeling of RT and RTI. Given the somewhat higher correlations and MVIFs in CHAP, with its shorter interval between bursts and session, compared to MIND, our observed results are consistent with a potential threat due to collinearity when considering both mean RT and RTI simultaneous predictors. This underscores yet another advantage of employing a measurement burst design for the study of RTI; specifically, many published RTI studies rely solely upon BP estimates, and our partitioned findings clearly indicate that collinearity and variance inflation are of greatest concern for BP (vs WP) findings. Thus, variance partitioning in the burst design could be particularly advantageous as it facilitates (a) an opportunity to evaluate the relative impact of collinearity on BP estimates, as well as (b) the ability to shift the level of analysis WP, where the impact of variance inflation is less problematic. Exploration of alternative approaches for dealing with simultaneous modeling of mean and variability (e.g., Schmiedek et al., 2009), when these are also focal predictors of other outcomes, is an important endeavor for future research.
It is also important to note that estimates of mean have greater reliability than estimates of variability, which will likely threaten the predictive impact and pattern of variability more than mean when considered in a simultaneous model (Schmiedek et al., 2009). Conceptually, however, covarying for mean RT when examining the effect(s) of RTI (or vice versa) must be weighed. Despite their correlation, mean RT and RTI reflect different phenomena (Jensen, 1992). The mandate of simultaneous inclusion suggests that the validity of one only exists if it is uniquely predictive above and beyond the other. Placing the burden of proof on the maintained significance of RTI after adjusting for mean RT is tantamount to evaluating whether the effect of RTI is simply an artifact of being faster (or slower), or the effect of mean RT is an artifact of processing being more (or less) efficient (inconsistent). This, however, is not necessarily consistent with theory, and addresses a different set of questions. Mean and variability for any variable, including RT-based measures, will have shared method variance as they are derived from the same data. Theoretically-informed analyses and dissociative patterns reveal the validity of RTI. In the context of the current study, we would expect both mean RT and RTI to exhibit positive associations with attention switching—being slower and being more inconsistent should be associated with worse attention-switching performance. The fact that these associations operate in the same direction does not invalidate either index, as such patterns are consistent with theoretical predictions. Taken together, we believe the current results provide strong, theoretically-informed evidence for the systematic and reliable predictive validity of RTI, for both BP and WP variation in attention-switching performance.
Which Quantification of RTI?
Previous literature examining RTI has utilized numerous different quantifications, including raw ISD, residualized ISD, CV, the tau parameter of the ex-Gaussian distribution, and MSSD. To our knowledge, this study is the first systematic and comprehensive examination that compares and contrasts quantifications of RTI in a theoretically-informed fashion. Results of our analyses suggest that the effects of RTI on attention switching are robust to quantification, except for the CV. While the CV represents a quantitatively-simple approach to take mean into account when examining the effect of RTI, the index itself is a ratio—an interaction (ISD multiplied by the inverse of the mean). Interpreting this ratio is not straightforward as any observed association may reflect a relationship between ISD, the (inverse of the) mean, or their interaction. The transparency of CV and its association with other indices of RTI, as well as criterion outcomes, is further complicated by nonlinear associations between mean and variability in age heterogenous samples (Schmiedek et al., 2009). We observed marked consistency in rank-order stability and predictive utility of RTI across the other four quantifications, suggesting that each of these is a viable and valid quantification of RTI, at least with respect to our use of 1-back working memory tasks. Furthermore, these patterns were notably consistent across two independent studies, comparable in terms of constructs, but differing in terms of measures, number and temporal spacing of observations—a definitive strength clearly demonstrating the replicability of our findings. Taken together, the current results provide greater insight as to the critical question of which quantification of RTI to employ—perhaps surprisingly, the present patterns do not advocate for using any single quantification per se, but do imply avoiding the use of CV.
Limitations and Future Directions
Despite results being largely consistent with predictions, there were limitations. First, we restricted our focus to examining the most frequently employed quantifications of RTI from select disciplines. Advances in methodology and measurement certainly allow for additional and possibly superior and theoretically-informed operational definitions of RTI based upon diffusion models (e.g., Schmiedek, Oberauer, Wilhelm, Süss, & Wittmann, 2007). Some of these approaches, however, require a greater number of trials and would require additional resources for empirical study. Second, we examined RTI in a 1-back working memory task as it was a common task across the independent studies. It is unclear whether the consistency of results would maintain for RTI using different tasks with varying processing demands (e.g., simple or choice RT, and higher-order n-back tasks). Future research considering these comparatively gross quantifications of RTI with more sophisticated mathematical models, as well as (a)symmetries in patterns across different tasks and task dimensions will be important for understanding how best to measure and quantify RTI, maximizing its utility as a brief and inexpensive indicator of cognitive health. Finally, we focused on RTI as a predictor, not as an outcome. Hultsch et al. (2008) discussed the need for formal examination of labile influences that could underlie increased RTI, including pain, stress, and negative affect. Little empirical research has directly examined the influence of such labile influences of RTI; most research in this area has focused on mean RT outcomes (see however Sliwinski et al. 2006). Similarly, with respect to BP variation in RTI and its association with attention switching, identifying person-level factors (e.g., chronic conditions, systematic changes in brain structure or function) that contribute to increased RTI would help understand who is at risk for compromised CNS integrity, cognitive and brain health, as well as potential moderators or supports to mitigate these individual differences (see Figure 2). Thus, future research aimed at understanding the diverse factors contributing to BP and WP variation in RTI, as well as employing the advantages of measurement burst designs for examining phenomena varying from moment-to-moment over long periods of time and across persons, is warranted.
Conclusions
The present study aimed to provide the first systematic examination, comparing and contrasting quantifications, and evaluating evidence for BP and WP variation in RTI. Despite the variety of RTI quantifications, we have demonstrated that many but not all indices are of transparent quantitative and qualitative utility. In addition, using two independent measurement-burst studies of RT-based cognitive aging, we further demonstrated the utility of RTI for predicting poorer attention-switching performance among older adults, WP over shorter and longer temporal intervals, as well as between persons. Compared to mean RT-dominated research, RTI reflects a novel dimension of performance that represents a robust and theoretically-informative predictor of cognitive function. These findings furnish a cornerstone for future research examining the antecedents and consequences of RTI as a behavioral indicator of cognitive and brain health.
Supplementary Material
Supplementary data is available at The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences online.
Funding
This work was supported by the National Institute on Aging at the National Institutes of Health (R21 AG045575, R01 AG12448), the Natural Sciences and Engineering Research Council of Canada (418676-2012, 06468-2017), and the Michael Smith Foundation for Health Research (CI-SCH-01925(07-1)).
Conflict of Interest
None reported.
Supplementary Material
Acknowledgments
The authors thank Martin Sliwinski for providing data from CHAP.
R. S. Stawski and S. W. S. MacDonald contributed equally to this work.
References
- Basak C., & Verhaeghen P (2011). Aging and switching the focus of attention in working memory: Age differences in item availability but not item accessibility. Journal of Gerontology: Psychological Sciences, 66b, 519–526. doi:10.1093/geronb/gbr028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson L., Ram N., Almeida D. M., Zautra A. J., & Ong A. D (2017). Fusing biodiversity metrics into investigations of daily life: Illustrations and recommendations with emodiversity. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 73, 75–86. doi:10.1093/geronb/gbx025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bielak A. A. Hultsch D. F. Strauss E. MacDonald S. W. & Hunter M. A (2010). Intraindividual variability is related to cognitive change in older adults: Evidence for within-person coupling. Psychology and Aging, 25, 575–586. doi:10.1037/a0019503 [DOI] [PubMed] [Google Scholar]
- Blessed G. Tomlinson B. E. & Roth M (1968). The association between quantitative measures of dementia and of senile change in the cerebral grey matter of elderly subjects. The British Journal of Psychiatry: The Journal of Mental Science, 114, 797–811. doi:10.1192/bjp.114.512.797 [DOI] [PubMed] [Google Scholar]
- Clark P. C. (2013). ‘The Effects of Multicollinearity in Multilevel Models’. A dissertation submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy. Wright State University; <http://corescholar.libraries.wright.edu/cgi/viewcontent.cgi?article = 1879&context = etd_all>. [Google Scholar]
- Deary I. J. & Der G (2005). Reaction time explains IQ’s association with death. Psychological Science, 16, 64–69. doi:10.1111/j.0956-7976.2005.00781.x [DOI] [PubMed] [Google Scholar]
- Diehl M., Hooker K., & Sliwinski M. S (Eds.). (2015). Handbook of intraindividual variability across the life span. New York, NY: Routledge/Taylor & Francis. [Google Scholar]
- Garavan H. (1998). Serial attention within working memory. Memory & Cognition, 26, 263–276. [DOI] [PubMed] [Google Scholar]
- Graveson J. Bauermeister S. McKeown D. & Bunce D (2016). Intraindividual reaction time variability, falls, and gait in old age: A systematic review. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 71, 857–864. doi:10.1093/geronb/gbv027 [DOI] [PubMed] [Google Scholar]
- Heathcote A., Brown S. D., & Cousineau D (2004). QMPE: Estimating Lognormal, Wald and Weibull RT distributions with a parameter dependent lower bound. Behavior Research Methods, Instruments & Computers, 36, 277–290. doi:10.3758/BF03195574 [DOI] [PubMed] [Google Scholar]
- Hultsch D. F., Strauss E., Hunter M. A., & MacDonald S. W. S (2008). Intraindividual variability, cognition, and aging. In F. I. M. Craik & T. A. Salthouse (Eds.), The handbook of aging and cognition (3rd ed., pp. 491–556). New York: Psychology Press. [Google Scholar]
- Jensen A. R. (1992). The importance of intraindividual variation in reaction time. Personality and Individual Differences, 13, 869–881. doi:10.1016/0191-8869(92)90004–9 [Google Scholar]
- MacDonald S. W. S., & Stawski R. S (2015). Intraindividual variability -- an indicator of vulnerability or resilience in adult development and aging? In M. Diehl K. Hooker, & M. J. Sliwinski (Eds.), Handbook of intraindividual variability across the lifespan. New York, NY: Routledge/Taylor & Francis Group. doi:10.4324/9780203113066.ch13 [Google Scholar]
- Myerson J. Robertson S. & Hale S (2007). Aging and intraindividual variability in performance: Analyses of response time distributions. Journal of the Experimental Analysis of Behavior, 88, 319–337. doi:10.1901/jeab.2007.88-319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesselroade J. R. (1991). The warp and the woof of the developmental fabric. In R. Downs L. Liben, & D. S. Palermo (Eds.), Visions of aesthetics, the environment, & development: The legacy of Joachim F. Wohlwill (pp. 213–240). Hillsdale, NJ: Lawrence Erlbaum Associates. [Google Scholar]
- Nesselroade J. R., & Salthouse T. A (2004). Methodological and theoretical implications of intraindividual variability in perceptual-motor performance. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 59, P49–P55. doi:10.1093/geronb/59.2.P49 [DOI] [PubMed] [Google Scholar]
- Neupert S. D., Stawski R. S., & Almeida D. M (2008). Considerations for sampling time in aging research. In S. M. Hofer, & D. F. Alwin (Eds.), The handbook of cognitive aging: Interdisciplinary perspectives (pp. 492–505). Thousand Oaks: Sage Publications. [Google Scholar]
- Ram N. & Gerstorf D (2009). Time-structured and net intraindividual variability: Tools for examining the development of dynamic characteristics and processes. Psychology and Aging, 24, 778–791. doi:10.1037/a0017915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M. D. & Tamir M (2005). Neuroticism as mental noise: A relation between neuroticism and reaction time standard deviations. Journal of Personality and Social Psychology, 89, 107–114. doi:10.1037/0022-3514.89.1.107 [DOI] [PubMed] [Google Scholar]
- SAS Institute (2013). SAS (Version 9.4). Cary, NC: SAS Institute, Inc. [Google Scholar]
- Schmiedek F., Lövdén M., & Lindenberger U (2009). On the relation of mean reaction time and intraindividual reaction time variability. Psychology and Aging, 24, 841–857. doi:10.1037/a0017799 [DOI] [PubMed] [Google Scholar]
- Schmiedek F. Oberauer K. Wilhelm O. Süss H. M. & Wittmann W. W (2007). Individual differences in components of reaction time distributions and their relations to working memory and intelligence. Journal of Experimental Psychology. General, 136, 414–429. doi:10.1037/0096-3445.136.3.414 [DOI] [PubMed] [Google Scholar]
- Sliwinski M. J. (2008). Measurement-burst designs for social health research. Social and Personality Psychology Compass, 2, 245–261. doi:10.1111/j.1751-9004.2007.00043.x [Google Scholar]
- Sliwinski M. J. Smyth J. M. Hofer S. M. & Stawski R. S (2006). Intraindividual coupling of daily stress and cognition. Psychology and Aging, 21, 545–557. doi:10.1037/0882-7974.21.3.545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stawski R. S., MacDonald S. W. S., Sliwinski M. J (2016). Measurement burst design. The Encyclopedia of Adulthood and Aging, 2, 854–859. doi:10.1002/9781118521373.wbeaa313 [Google Scholar]
- Stawski R. S., Smith J., & MacDonald S. W. S (2015). Intraindividual variability and covariation across domains in adulthood and aging: Contributions for understanding behavior, health, and development. In M. Diehl K. Hooker, & M. J. Sliwinski (Eds.), Handbook of intraindividual variability across the lifespan (pp. 258–279). New York, NY: Routledge/Taylor & Francis Group. doi:10.4324/9780203113066.ch14 [Google Scholar]
- Van Gemmert A. W. & Van Galen G. P (1997). Stress, neuromotor noise, and human performance: A theoretical perspective. Journal of Experimental Psychology. Human Perception and Performance, 23, 1299–1313. [DOI] [PubMed] [Google Scholar]
- von Neumann J., Kent R. H., Bellinson H. R., & Hart B. I (1941). The mean square successive difference. The Annals of Mathematical Statistics, 12, 153–162. [Google Scholar]
- West R., Murphy K. J., Armilio M. L., Craik F. I. M., & Stuss D. T (2002). Lapses of intention and performance variability reveal age-related increases in fluctuations of executive control. Brain and Cognition, 49, 402–419. doi:10.1006/brcg.2001.1507 [DOI] [PubMed] [Google Scholar]
- Weissman D. H. Roberts K. C. Visscher K. M. & Woldorff M. G (2006). The neural bases of momentary lapses in attention. Nature Neuroscience, 9, 971–978. doi:10.1038/nn1727 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.