Abstract
For the two-sample problem the Wilcoxon-Mann-Whitney (WMW) test is used frequently: it is simple to explain (a permutation test on the difference in mean ranks), it handles continuous or ordinal responses, it can be implemented for large or small samples, it is robust to outliers, it requires few assumptions, and it is efficient in many cases. Unfortunately, the WMW test is rarely presented with an effect estimate and confidence interval. A natural effect parameter associated with this test is the Mann-Whitney parameter, ϕ = Pr[X < Y] + 0.5Pr[X = Y]. Ideally, we desire confidence intervals on ϕ that are compatible with the WMW test, meaning the test rejects at level α if and only if the 100(1 – α)% confidence interval on the Mann-Whitney parameter excludes 1/2. Existing confidence interval procedures on ϕ are not compatible with the usual asymptotic implementation of the WMW test that uses a continuity correction, nor are they compatible with exact WMW tests. We develop compatible confidence interval procedures for the asymptotic WMW tests, and confidence interval procedures for some exact WMW tests that appear to be compatible. We discuss assumptions and interpretation of the resulting tests and confidence intervals. We provide the wmwTest function of the asht R package to calculate all of the developed confidence intervals.
Keywords: Area under the curve, Mann-Whitney U test, Probabilistic index, Receiver operating characteristic curve, Wilcoxon rank sum test
1. Introduction
The Wilcoxon-Mann-Whitney (WMW) test ([1, 2]) is the widely used test derived as a permutation test on the difference in mean ranks between the two samples in the two-sample problem. The popularity of the WMW test is due to many reasons. It may be implemented exactly or asymptotically, on either continuous or ordinal responses. The WMW test is invariant to monotonic transformations and hence is robust to outliers. It is palindromically invariant, so the responses can be reversed and the inferences will match with the appropriate directional change [3]. The WMW test is often asymptotically more efficient that the t-test [4]. Finally, since the WMW test is nonparametric, it may be implemented with few assumptions.
Let X and Y represent arbitrary orderable (i.e., continuous or ordinal) responses from group 1 and group 2 respectively, where X ~ F and Y ~ G. The null hypothesis of the WMW test may be stated as H0: F = G and the alternative hypotheses is H1: F ≠ G (see [4] for other valid null and alternative hypotheses associated with the WMW decision rule). There are no parametric assumptions required on F and G, which is advantageous in terms of the breadth of applicability of the test; however, the lack of parametric assumptions hinders an easy and clear measurement of the effect associated with the test. Because of this, despite its wide popularity, the WMW test is rarely reported with effect estimates and confidence intervals. Ideally, we want an effect parameter associated with the WMW test to retain many of the analogous properties of the test: invariant to monotonic transformations, palindromically invariant, with few assumptions needed on F and G. Finally, we want the associated confidence interval to be compatible with the test, meaning that the value of the effect parameter under the null hypothesis when F = G is excluded from the 100(1 – α)% confidence interval if and only if the WMW test rejects at level α.
We briefly mention two parameters that do not meet these properties, but have been used with WMW tests. First, the difference in medians has the advantage of requiring no additional assumptions on F and G, but we show by example in Section 9 that this parameter is not compatible with the WMW test. When the data are continuous and a location shift model is appropriate, then the Hodges-Lehmann confidence interval on the location shift may be applied [5, 6]. Briefly, the Hodges-Lehmann confidence interval is calculated by subtracting different values of a shift parameter from all responses in one of the groups and for each potential shift parameter checking if the WMW test rejects on that adjusted data at level a. The 100(1 – α)% Hodges-Lehmann confidence interval consists of the values of the shift for which we fail to reach a statistically significant difference. The problem is that with discrete ordinal responses, the Hodges-Lehmann method may not give a good approximate confidence interval, and may fail spectacularly. In Section 9 we show a case with discrete data where if we try to apply the Hodges-Lehmann method by applying scores to the categories (and ignoring the necessary continuity assumption), then the location shift confidence interval is [0, 0] despite the WMW test showing a highly significant difference between the distributions. Further, the Hodges-Lehmann method confidence intervals are not invariant to monotonic transformations.
An alternative estimand that is invariant to monotonic transformations is the parameter from the proportional odds model. A proportional odds model says that
| (1) |
for all x and θ > 0. In other words, the odds that a response is larger than x is θ times larger for group 2 than for group 1, regardless of the value of x. There are two issues with associating the θ parameter and its usual confidence interval with the WMW test. First, the usual confidence intervals for θ are not compatible with the WMW test. We show this lack of compatibility for a simple example. Consider the two sample test with responses 2.1, 4.7, 6.8, 7.9, and 8.6 for treatment A and responses 7.5, 8.9, 9.2, and 9.3 for treatment B (see Kalbfleisch and Prentice [7], p. 222). The exact Wilcoxon-Mann-Whitney (WMW) test gives a two-sided p-value of 0.063 indicating not significant at the 0.05 level. Ideally, we would use an exact confidence interval on θ (or some other parameter) that is compatible with the exact WMW test, but none have been developed. One readily available proportional odds confidence interval estimate (the polr function in the MASS [version 7.3.47] R package[8]) is based on asymptotic normal approximation from the generalized linear model with N − 1 nuisance parameters, and for these data gives an estimate of θ = 25.2 with 95% confidence interval of (1.54,1170.1). One problem is that there are no degrees of freedom left when this model is applied to continuous responses and its properties are not known in this case. Further, even if the confidence interval could be applied, it implies that the odds ratio is significantly different from 1 at the 5% level, while the exact test implies no significant difference. Another case where the exact confidence intervals are needed is when the observed data are the most extreme, so that the maximum likelihood estimate of the proportional odds parameter is on the boundary of the parameter space and the usual asymptotic results do not hold.
The second issue with associating θ and its confidence intervals with the WMW test is that the interpretation of θ is not easy to explain to non-statistical audiences. Agresti and Kateri [9] address this interpretation issue and suggest that a parameter that is much easier to explain is . We call ϕ the Mann-Whitney parameter after [2], and it is also called the probabilistic index [10]. The ϕ parameter is equivalent to the area under the receiver operating characteristic (ROC) curve, where the two groups are diseased and non-diseased individuals and the response is an ordinal or continuous diagnostic variable [11]. Finally, the Mann-Whitney parameter is also known as the c-index or concordance index in regression models for binary outcomes used for predicting mortality (see for instance, Harrell et al. [12]). Besides its easy interpretation, ϕ is a natural parameter to use with the WMW test for several reasons. Like the WMW test, ϕ has interpretation for both continuous and discrete data. Further, ϕ may be defined without making any assumptions about the relationship between the distributions F and G Finally and importantly, ϕ defines the consistency of the WMW test. For alternative distributions where ϕ ≠ 1/2, the WMW test is consistent, meaning that the power of the test goes to 1 with infinite sample sizes.
Several recent papers have studied confidence intervals for ϕ [13, 14, 15, 16], but these papers do not study the issue of compatibility with the WMW test. For continuous data, Newcombe [14] performs simulations on several different confidence interval methods and suggests that the confidence interval that gives the best coverage is his method 5, which is a score-type modification of a method in [11]. In this paper, we propose a generalization of Newcombe’s confidence interval that is compatible with the usual asymptotic version of the WMW test. We also develop a confidence interval that appears to be compatible with one of the exact implementations of the WMW test.
Our confidence intervals require the proportional odds assumption, and the intervals may be applied to both continuous and discrete ordinal responses. One pleasing property of the proportional odds model is that the same parameter can be used for continuous responses and the ordinal responses that result from grouping the continuous responses into categories. This property does not always hold for the Mann-Whitney parameter. For example, grouped responses from latent continuous data will generally give a different Mann-Whitney parameter than the one from the latent continuous responses themselves. Agresti and Kateri [9] address this issue and propose using a cumulative probit model or some similar model to estimate the latent continuous Mann-Whitney parameter estimated from grouped data. In this paper, we propose a different way to estimate the latent continuous Mann-Whitney parameter directly from the nonparametric estimate of ϕ from the grouped data.
The WMW test is valid for H0: F = G without additional assumptions on F and G, and ϕ is defined with minimal assumptions also; however, our confidence intervals require the proportional odds assumption. After introducing the WMW test in Section 2, we discuss why some additional assumptions are required to get confidence intervals on ϕ that are compatible with the WMW test in Section 3. We formally define validity, palindromic invariance, and compatibility in Section 4. The bulk of the paper gives details on how to get valid, palindromic invariant, and compatible confidence intervals for different implementations of the WMW test. Compatible confidence intervals with the asymptotic WMW test for continuous or ordinal responses are developed in Sections 5 and 6. Confidence intervals that appear compatible with the exact WMW test (by complete enumeration or by Monte Carlo) are developed in Section 7. Simulations in Section 8 show that our developed confidence intervals have reasonable coverage under the proportion odds assumption. Practitioners not interested in the statistical details may wish to skip to Section 9 that gives some applications with interpretation. We provide the wmwTest R function in the asht R package to perform all versions of the WMW test with their associated compatible confidence intervals developed in this paper.
2. Wilcoxon-Mann-Whitney Test
Let X1, …,Xm and Y1, …,Yn represent the independent random variables from the first and second group respectively, and let X and Y denote an arbitrary response from each group. Let X ~ F and Y ~ G, and we assume the observations are orderable (e.g., continuous responses or scalar scores representing ordered categorical responses). Denote the Mann-Whitney functional as
| (2) |
We estimate ϕ using the empirical distributions, and as
| (3) |
where Sy is the sum of the n midranks from the second group, where the midranks are calculated by ranking all N = m + n responses together, breaking ties arbitrarily, and averaging the tied values. A WMW test is a permutation test using . We discuss several implementations of the WMW test: two asymptotic implementations (with and without a continuity correction), and four exact implementations (using either complete enumeration or Monte Carlo simulation, and each of those using either the absolute-value p-value or the central p-value). For large samples without ties, all implementations give similar results.
A complete enumeration exact WMW test can be performed by recalculating after permuting the treatment labels all different ways, using that permutation distribution to determine if the observed was extreme, and using the extent to extremeness to get the p-value. For example, we may define the exact absolute value p-value as
where I (A) = 1 when A is true and 0 otherwise, and are the estimates of ϕ under all J permutations, so that . The exact central p-value is pec = min(1, 2 * pel, 2 * peg), where and . Although it is computationally intensive to calculate the exact complete enumeration implementations of the WMW test, there are many fairly tractable algorithms (see e.g., [17, 18]).
The WMW test is testing the null hypothesis H0: F = G against the alternative Hi: F ≠ G. Under that null, ϕ =1/2 but under the alternative ϕ could be any value from 0 to 1, even including ϕ = 1/2 as long as F ≠ G (see Section 3). Under the assumption that m/N → λ with 0 < λ < 1, the asymptotic power of the WMW test goes to 1 for any alternative with ϕ ≠ 1/2; in other words, the WMW test is consistent under alternatives with ϕ ≠ 1/2 [19].
Despite the availability of exact p-values, asymptotic approximations are still used. The asymptotic approximation can be fairly accurate even for samples sizes as low at m = n = 8 (see e.g., [19] p. 17). The expected value of under the permutation distribution is 1/2. The permutational variance of is
where d1,…, dk are the number of tied responses from both groups in each of the k unique responses. Let
| (4) |
be the “tie adjustment factor”. If the responses are continuous, there are no ties and t =1. Under the null hypothesis that H0: F = G then ϕ = 1/2, and using a permutational central limit theorem [20] or some other methods (see e.g., Appendix 4 in [19])
is approximately distributed standard normal for large samples in both groups, as long as
Often a continuity correction is used so that the resulting p-values will be closer to the exact ones [21]. In that case, we treat Z as standard normal under the null hypothesis, where
| (5) |
and . Then the two-sided p-value for the asymptotic implementation of the WMW test is pa = 2 * {1 – Φ(|Z|)}, where Φ is the cumulative distribution of a standard normal.
3. Why We Need Extra Assumptions for Confidence Intervals
Because of the consistency of the WMW test with respect to ϕ, it is a natural parameter to use as an effect for the WMW test. Ideally, we would like a testing procedure that could test any in a series of hypothesis tests, H0: ϕ = ϕ0 versus H1: ϕ ≠ ϕ0, for many different values of ϕ0. Let p([x, y], ϕ0) be the p-value function associated with H0: ϕ = ϕ0 for one such testing procedure, where x and y are the vector of responses in both groups. Then we could invert the p-value function to create a 100(1 – α)% confidence region defined as all ϕ0 where p([x, y], ϕ0) > α. Unfortunately, the confidence region is not always an interval. Additionally, and more importantly, we need a valid p-value function p([x, y], ϕ0) that equals the WMW test p-value when ϕ0 = 1/2.
In order for this approach to work, we need some additional assumptions on the relationship between F and G. The problem is that without those additional assumptions, then the WMW test is not a valid test for H0: ϕ =1/2. Pratt [22] shows that, for example, if F and G are two normal distributions both with means 0 (and hence ϕ = 1/2) but different variances, then the asymptotic type I error rate can be greater than α. We simulate this with 104 replicates, m = 5000, n = 1000, Var(X) = 1, Var(Y) = 16, using Equation 5 with two-sided significance level of 5%, giving a simulated type I error rate of 15.9%. Thus, since the goal of this paper is to get a confidence interval compatible with the WMW test, our confidence interval derivation will require some extra assumptions on F and G to exclude examples like the heteroscedastic normal one in order to get coverage that is at least nominal.
If our goal is only to get a confidence interval on ϕ, we can use a different test procedure than the WMW test. If instead of permuting , we permute a studentized version of it (see Pauly, et al. [23] for details and related references), this gives an asymptotically valid test of H0: ϕ = ϕ0, and that procedure can be used to create an asymptotically valid confidence interval for ϕ as long as . However, because the permutation test on the studentized is more computationally intensive and gives different P values than the WMW test, it will not be discussed further.
4. Formal Statement of Properties
Let Ω(ϕ0) = {(F, G): hMW(F, G) = ϕ0}. A valid p-value for testing H0 : ϕ = ϕ0 has
| (6) |
where X and Y are random vectors. If a p-value procedure is valid for all possible ϕ0, then it may be inverted to create a valid confidence set,
| (7) |
and it is valid because Pr[ϕ0 ∈ Cs ([x, y], 1 – α)] ≥ 1 – α for all (F, G) ∈ Ω(ϕ0) (see e.g., [24] p. 421–422). The matching confidence interval just fills in any holes in the set if there are any, giving
| (8) |
By construction, if Cs is valid then the matching confidence interval must be valid, i.e.,
| (9) |
We say a p-value or confidence interval is asymptotically valid if expressions 6 and 9 are true asymptotically.
We say inferences are palindromically invariant if they remain unchanged when we change the order of the responses by multiplying them by −1 and switch the groups, in other words, if p([x, y], ϕ0) = p([−y, −x], ϕ0) and C([x, y], 1 – α) = C([−y, −x], 1 – α). Finally, we say the WMW test and a confidence interval are compatible when if and only if , since the null hypothesis of the WMW test is H0: F = G which implies for all F, G in the null hypothesis set.
5. Confidence Intervals Compatible with the Asymptotic Implementation
5.1. Acceptable Models
First, we generalize pa, as p([x, y], ϕ0) = 2 * {1 – Φ(|Z(ϕ0)|)} where
| (10) |
, and we require that V(1/2) = Vperm A sufficient condition for this p-value procedure to give asymptotically valid inferences is for Z(ϕ0) → N(0,1) whenever ϕ = ϕ0. When the p-value function is asymptotically valid for all ϕ0, we can create a matching asymptotically valid confidence interval as described in Section 4.
When X and Y are continuous, using U-statistics, the variance of is (see e.g., [25], p. 39)
| (11) |
So any assumption on the structure of F and G such that (ϕ = 1/2) ⇒ (F = G), will give
which equals Vperm for continuous data.
One simple assumption is the location-shift assumption: G(x) = F(x − Δ), where F is unspecified. This is the assumption needed for the Hodges-Lehmann method. An issue with this assumption is that the inferences will not be invariant to all monotonic transformations (e.g., if the original data follow a location-shift model then the log transformed data will not).
An alternative solution is to assume that there is some unknown strictly increasing transformation of the responses, say b(·), such that F(x) = F*(b(x)) and G(x) = F*(b(x) – β), where F* is a known distribution. This type of assumption is reasonable for rank tests, because it retains the robustness to outliers. Three special cases of this type of assumption are the proportional odds model, where F* is the standard logistic distribution; the proportional hazards model, where F* is the extreme minimum value distribution; and the probit model, where F* is the standard normal distribution. Under all these semi- parametric models, Ω(1/2) is the set of all F,G such that F = G, and therefore these models address the problem of Section 3. The proportional odds model is the best fit for our purposes as we discuss next.
5.2. Proportional Odds for Continuous Responses
The proportional odds model is a natural one for relating to the WMW test for two main reasons. First, the WMW test is the locally most powerful rank test for a shift in the logistic distribution (see e.g., [26], pp. 145–146). Second, both the proportional odds model and the WMW test are palindromically invariant.
The proportional odds model is given in Equation 1. Under this model we can show that if the transformation, b(·), is b(x) = F*−1(F(x)) where F* is the standard logistic, then the proportional odds model is the set of pairs of distributions F and G that by a strictly increasing transformation can be expressed as a location shift model on the standard logistic distribution (see Supplement Section S1). Since the WMW test is a rank test, the results will be the same for any strictly increasing transformation, so under a proportional odds model without loss of generality, we can treat the responses as if they belong to a location shift on the logistic distribution to calculate ϕ and (Supplement Section S2). For continuous data, the proportional odds model has ϕ = 0,1/2, and 1 when θ = 0,1, and ∞, respectively, otherwise
| (12) |
Let VPO (ϕ) be under the proportional odds model. Although there is no closed form of VPO (ϕ), it can be solved numerically (Supplement Section S2).
5.3. An Approximation for VPO
We can approximate VPO (ϕ) using a combination of the proportional hazards and the Lehmann alternative [27] (i.e., the reverse-time proportional hazards) models. In terms of relating F and G, the proportional hazards model is 1 − G(x) = {1 − F(x)}λ for all x with λ > 0, and the Lehmann alternative model is G(x) = F(x)ξ for all x with ξ > 0. The proportional hazards model gives a nice closed form expression for V(ϕ), but that model is not palindromically invariant. To get this invariance, we combine it with the Lehmann alternative model. For continuous data, our resulting confidence interval (without the continuity correction) is equivalent to “Method 5” of Newcombe [14], since any proportional hazards model can be written as a scale change of an exponential distribution (Supplement Section S4).
The Lehmann alternative model has and ξ = ϕ/(1 – ϕ) ([27], p. 32, Supplement Section S7.2). Inserting this into the expression for ([27], p. 32), we get
| (13) |
Just as the proportional odds model can be written as a strictly increasing transformation to a location-shift on the logistic distribution, the proportional hazards model can be written as a strictly increasing transformation to a location-shift on the extreme minimum value distribution (Supplement Section S3), or a scale-change in a exponential distribution (Supplement Section S4). Using the extreme minimum value distribution, λ = (1 – ϕ)/ϕ and under the proportional hazards model is defined as VPH (ϕ), where VPH (ϕ) is equal to VLA(ϕ) with the m and n switched (Supplement Section S7.1). Averaging those two variances gives
| (14) |
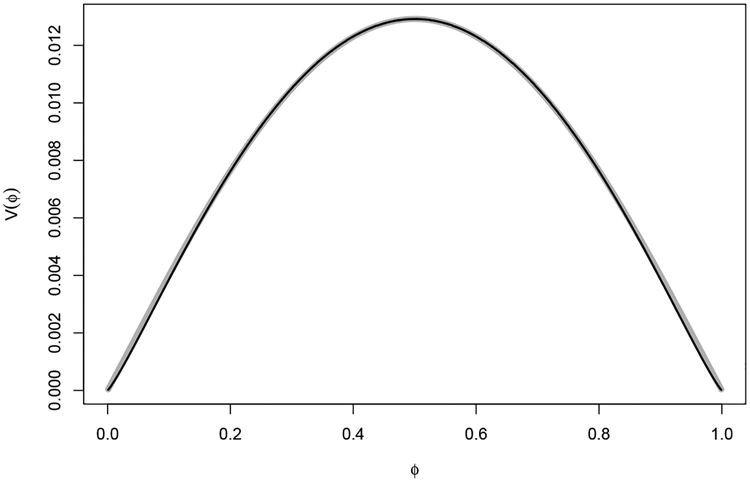
Unlike , VLA.PH(ϕ) is invariant to switching m and n, so because ϕ is invariant to switching groups and reversing the ordering of the responses, inferences based on Z(ϕ0) using V(ϕ0) = VLA.PH(ϕ) are palindromically invariant (see Supplement Section S5). The expression VLA.PH(ϕ) is an excellent approximation to the more complicated variance function for the proportional odds model (Figure 1).
Figure 1:
Comparison of VLA.PH(ϕ) from Equation 14 (thick gray line), with VPO(ϕ) from the proportional odds model (thin black line) (see Supplement Section S2), when m = 10 and n = 20. The lines are equal at ϕ = 1/2 and nearly indistinguishable otherwise.
6. Handling Tied or Ordinal Responses
6.1. Compatible Asymptotic Confidence Interval
The derivation of VPO (ϕ) and VLA.PH (ϕ) assumes continuous data. To account for ties and additionally give compatible inferences with the asymptotic WMW test we propose the following. For V(ϕ0) in Z(ϕ0) (Equation 10), we propose to use either V(ϕ0) = tVPO(ϕ0) or V(ϕ0) = tVLA.PH(ϕ0), where t is the tie adjustment factor of Equation 4. Then using that V(ϕ0) in Z(ϕ0) to get p([x, y], ϕ0) = 2 * {1 – Φ(|Z(ϕ0)|)}, our proposed 100(1 – α)% asymptotic confidence interval is given by equation 8.
Theorem 1 Our proposed asymptotic confidence interval with the continuity correction is compatible with the asymptotic WMW test with continuity correction. Similarly, the analogous confidence interval without the continuity correction is compatible with the asymptotic WMW test without a continuity correction.
The proof of Theorem 1 is given in Supplement Section S6.
6.2. Inferences on the Latent Continuous Mann-Whitney Parameter
Suppose the responses are ordinal or the responses have ties. We can still think of the data as coming from a continuous proportional odds model where the continuous responses are grouped into (perhaps very many) categories. The proportional odds parameter, θ, from the grouped responses may be translated into a Mann-Whitney parameter via Equation 12, except this Mann-Whitney parameter refers to the latent continuous responses. Let ϕ* denote the Mann-Whitney parameter of the latent continuous responses. This is different from ϕ = hMW(F, G), where F and G are the distributions of the grouped responses. The grouping pulls the latent Mann-Whitney parameter closer to 1/2.
We estimate ϕ* from grouped data by relating to the proportional odds model, then using Equation 12. Our method is non-parametric, depending only on , the proportion of samples in each group, and , the empirical distribution of the combined data. Let be the cumulative distribution that solves
where is the distribution for the second group under the proportional odds model with parameter . This can be solved for each unique response in the combined data using a quadratic equation. If θ was known, we could estimate ϕ with . But θ is not known. To relate our estimate to from the WMW test, we estimate θ with the value, , that solves . Then we estimate ϕ* by plugging in for θ in Equation 12. We also transform any other value on the original Mann-Whitney parameter space (e.g., lower and upper confidence limits for ϕ) to the latent Mann-Whitney parameter space in a similar manner. Nevertheless, for some values of and extreme values of ϕ, no solution exits. For example, consider the case with three ordinal categories with values 1, 2, and 3, with m = n and . When θ = 10−6 then and and ϕ ≈ 0.050. Smaller values of θ will just push and closer to 0 and not change by much. So there are no values of θ that will solve for ϕ < 0.05 for that . Analogously, there are no values of θ that will solve for ϕ > 0.95. Agresti and Kateri [9] discuss a different approximation to ϕ* using a cumulative probit model, which is closely related to the proportional odds model (called the cumulative logit model in [9]). That approximation allows for inclusion of other explanatory variables. We use our estimator of ϕ* because it is directly tied to from the WMW test.
7. Confidence Intervals Compatible with the Exact WMW Test
7.1. Complete Enumeration Implementation
Here is an overview of how we get confidence intervals that designed to be compatible with the exact WMW test. First, we generalize the distribution of the , the permutation estimates of ϕ, so that the distribution depends on a specific value of ϕ0 under some model. Second, we use this distribution to get pe(ϕ0), the p-value associated with the test H0: ϕ = ϕ0 versus H1: 0 ≠ ϕ0. Then the 100(1 − α)% confidence region is the set of all values of ϕ0 where pe(ϕ0) > α. If the region is valid and has a hole in it, we fill it to create an interval that will also be valid (see Section 4). This method is called the tail area modelling approach by Newcombe [13], except Newcombe uses a different model than we use. As in Section 5.3, we use a model that is a combination of the proportional hazards and the Lehmann alternative models.
For this section we introduce new notation. Take the original data, X1,…, Xm and Y1, …, Yn, and represent it as two N × 1 vectors: U = [U1, …,UN] is the vector of order statistics from the combined data, and W = [W1,…, WN] is the vector of group membership, where Wi = 1 if Ui represents a response from the second group (Y1, …,Yn) and Wi = 0 if Ui represents a response from the first group (X1, …, Xm). For example, the data from Kalbfleisch and Prentice [7] we mentioned in the introduction could be represented as either, x = [7.9, 6.8, 2.1, 4.7, 8.6] and y = [9.2, 8.9, 9.3, 7.5], or as u =[2.1, 4.7, 6.8, 7.5, 7.9, 8.6, 8.9, 9.2, 9.3] and w = [0, 0, 0,1,0, 0,1,1,1]. Since we only use the ranking information in u, we only need to work with w and the vector of midranks of u, say r. For continuous data r = [1, 2,…, N], but it will be different with ties.
Let w1, …, wJ be the unique permutations of the w vector. Let Tj = t(wj; ϕ0) and T0 = t(w; ϕ0), where t(·) is the test statistic that we use for the permutation test, and t(·) may depend on r. For this paper, we define t as a function of which by Equation 3 is a simple function of r and w. We define t such that larger values of T0 are more likely to reject. For example, for testing H0: ϕ ≤ ϕ0 versus H1: ϕ > ϕ0 we use , where is the estimated Mann-Whitney parameter associated with wj, while for testing H0: ϕ ≥ ϕ0 versus H1: ϕ < ϕ0 we use . For testing H0: θ = ϕ0 we can use . Suppose we had some model that defines the discrete distribution of W, an N × 1 vector with n 1’s and m 0’s. Denote the probability mass function as Pr [W = wj |ϕ0] = πj(ϕ0), where . Then an exact p-value of any of these hypotheses is
| (15) |
This generalizes the exact WMW test p-values whenever the model has πj (1/2) = 1/J for all j ∈ {1, …, J}.
We show in the Supplementary Section S7 that under the proportional hazards model,
| (16) |
where wj = [wj1, … wjN] and and . Under the Lehmann alternative model (reverse time proportional hazards) then
| (17) |
where and . Let
| (18) |
in Equation 15, and let the 100(1 – α)% confidence region for ϕ be
| (19) |
We show in Supplementary Section S5 that pe(ϕ0) using equation 18 for πj(ϕ0) is palindromically invariant. Unfortunately, the confidence region may not be an interval if the test statistic is the absolute value of the difference, (which gives equivalent p-values as using . Before addressing that issue, we discuss the two main choices for the two-sided p-value.
For the two-sided test, H0: ϕ = ϕ0 versus H1: ϕ ≠ ϕ0, the traditional way to define the WMW test is to use . We call this the absolute value method. However, often for two-sample tests we do not just want to know that ϕ ≠ ϕ0, but we want to know the direction of the effect. For example, we want to know not just that the treatment is significantly different from the control, but that the treatment is significantly better in terms of the ϕ parameter. This is known as a three-decision rule [19, 28]. After a test of H0: ϕ = ϕ0 we make one of three decisions: (1) fail to reject ϕ = ϕ0, (2) reject ϕ = ϕ0 and conclude ϕ > ϕ0, or (3) reject ϕ = ϕ0 and conclude ϕ < ϕ0. For three-decision rules, we use two one-sided p-values, and define the two-sided p-value as twice the minimum of those one-sided p-values (or 1 if twice the minimum is greater than 1). We call this two-sided p-value a central p-value.
In general, there is usually little difference between the central p-values and the absolute value p-values. When there are no ties and F = G, then the permutation distribution is symmetric (see [19], Chapter 1, section 5), and both p-values are equivalent. Further, asymptotically the permutation distribution is normally distributed and hence symmetric, so there is no difference between the methods in that case either. However, for small sample sizes in the presence of ties there is a difference. Further, there is an important difference in interpretation of the two-sided p-values when applying the three-decision rule. Let pe.abs and pe.centrai be the two-sided p-values under the two methods. For testing for any difference between the two distributions (i.e., H0: F = G versus H1: F ≠ G), then we reject at the 5% level when pe.abs ≤ 0.05 for the absolute value method and when pe.central ≤ 0.05 for the central method. But for showing that ϕ > ϕ0 in the three decision rule, we reject ϕ ≤ ϕ0 at the 2.5% level when and pe.abs ≤ 0.025 for the absolute value method, and we reject ϕ ≤ ϕ0 at the 2.5% level when and pe.central/2 ≤ 0.025 (i.e., pe.central ≤ 0.05) for the central method. So the absolute value method would appear to be more powerful for showing any difference, while the central method appears more powerful for showing one-sided differences in the three-decision rule. We simulate a simple situation to show this point. Simulate 104 data sets from a proportional odds model with (standard logistic but with a location parameter of −1) and , then group the data by rounding the exponentiated responses to the nearest integer (e.g., ). The proportion of the time that the two-sided p-value from the grouped data is less than or equal to 0.05 is 32.0% for the absolute value method and 29.5% for the central method. So the absolute value method appears more powerful to show that the two distributions are different. But to show that ϕ > 1/2 at level 0.025 we use the two-sided p-value for the absolute method, but one half of the two-sided p-value when for the central method. The proportion of rejections showing ϕ > 1/2 significant at the 2.5% level is 20.4% for the absolute value method and 29.5% for the central method. So the absolute value method appears more powerful to show ϕ ≠ 1/2 (e.g., there is a difference between treatment and control), while the central method appears more powerful to show ϕ > 1/2 (e.g., treatment is better than control).
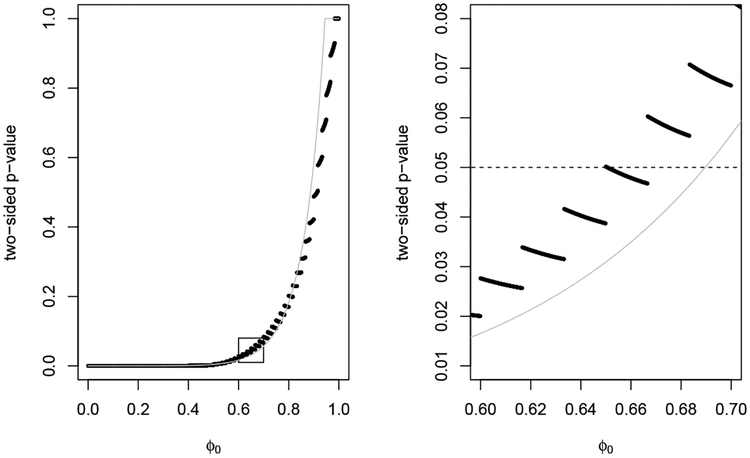
When inverting the pe.abs p-value, the confidence region may not be an interval. The issue is that the p-value function may have many local maxima in ϕ. In Figure 2 we show the 95% confidence regions by inverting the two different two-sided p-values. The confidence region associated with pe.abs is the union of two disjoint intervals, (0.6500, 0.6505)∪(0.6667,1). We create a confidence interval from the region by filling in the hole to get (0.65,1). When this problem occurs, it is impossible to create a confidence interval compatible with all tests of H0: ϕ = ϕ0. For example, for testing H0: ϕ = 0.66 then pe.abs = 0.0479, rejecting ϕ = 0.66 at the 5% level; however, the matching 95% confidence interval would include ϕ = 0.66 (because the hole is filled in). A similar issue occurs with the two different versions of the two-sided p-value from Fisher’s exact test [29, 30].
Figure 2:
Two-sided p-values for x = [1, 2, 3, 4, 5] and y = [6, 7, 8, 9, 10, 11]. Black dots are the absolute value method and the gray line is the central method. The 95% confidence region for the absolute value method is (0.6500, 0.6505) ∪ (0.6667, 1), while the one for the central method is (0.6897, 1).
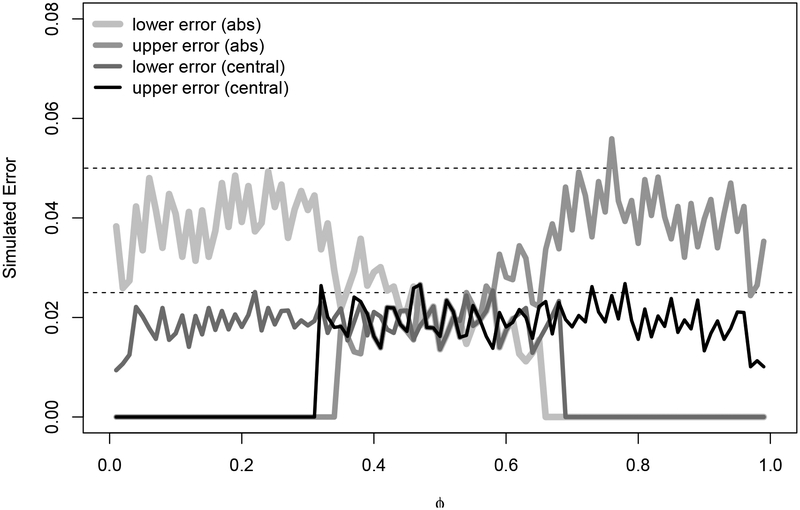
The three-decision rule issue remains when interpreting confidence intervals. Let the 95% central confidence interval based on the WMW test be (ϕl.c, ϕu.c). Then assuming the proportional odds model holds (and ignoring the error due to the fact that πj(ϕ0) is not exactly calculated under the proportional odds model but is an approximation based on combining the LA and PH models), if ϕ0 < ϕl.c we can conclude with 97.5% confidence that ϕ0 < ϕ. Alternatively, if we based our 95% confidence interval on the absolute value p-value, giving say (ϕL.a, ϕU.a), then if ϕ0 < ϕL.a we can only conclude with 95% confidence that ϕ0 < ϕ. In Figure 3 of Section 8, we show that the simulated error for the 100(1 – α)% confidence interval appears bounded by α for the absolute value method, but appears bounded by α/2 for the central method.
Figure 3:
Simulated error for 95% “exact” confidence interval procedures (Section 7.1) when m = 5 and n = 6. Dotted lines are at 0.05 and 0.025. The lower and upper simulated errors for the central method appear bounded at 2.5%, while those errors appear bounded at 5% for the absolute value method.
Although ties are handled straightforwardly, if we want to make statements about the latent Mann-Whitney parameter, we can adjust the estimates and confidence intervals for ϕ using the methods of Section 6.2.
7.2. Compatibility of Exact Methods
Since the matching confidence interval associated with pe.abs is not compatible with testing H0: ϕ0 = 0.66 as shown in the previous section, we do not try to show that it is compatible with the associated WMW test (i.e., compatible with testing H0: ϕ0 = 0.5). However, we strongly suspect that pe.centrai is compatible with the associated exact central WMW test.
We suspect this compatibility because of the following. First, pe.central(1/2) is equivalent to the exact central WMW test p-value. We can see this by noting that does not depend on wj. For example, when ϕ0 = 1/2 then
Thus, all permutations have equal probability, as in the calculation of the usual exact p-value for the WMW test. Second, pe.central(ϕ0) is continuous in ϕ0 as can be seen by inspection of the definition of πi(ϕ0). Third, all examples we calculated of pe.central(ϕ0) have only one local maximum and it is at 1. See Supplementary Section S8 (Figure S2) for examples. Finally, we suspect compatibility because of the following theorem.
Theorem 2 If a two-sided p-value function p([x, y], ϕ0) is continuous in ϕ0 with only one local maximum, then the matching confidence interval is compatible with the test of H0: ϕ0= ϕ0 using p([x, y], ϕ0).
The proof is on Supplementary Section S8.
7.3. Monte Carlo Implementation
The complete enumeration algorithm becomes intractable fairly quickly, since for example with m = n = 25 we get J ≈ 1.26 × 1014. An alternative to that algorithm and to the asymptotic method is a Monte Carlo implementation of the exact method. For this we estimate pe(ϕ0) by taking a random sample of B permutations of w, say w1, …, wB, and we use
| (20) |
where πobs(ϕ0) is the probability associated with w, the observed w-vector.
8. Simulations
All simulations are performed using our wmwTest R function that is demonstrated in Section 9. We first consider the exact method. We consider the continuous case so we need not deal with issues of latent continuous Mann-Whitney parameters versus grouped Mann-Whitney parameters. For sample sizes of m = 5 and n = 6, for all possible outcomes, we calculate the 95% central confidence intervals and the 95% absolute value method confidence intervals. Then we simulate 10, 000 data sets for each of ϕ = 0.01, 0.02, …, 0.99 under the continuous proportional odds model. For each ϕ we calculate the proportion of the 10, 000 data sets where its associated 95% confidence interval, say (L, U), has ϕ < L, which we call the lower simulated error, and the proportion with U < ϕ, which we call the upper simulated error. We plot the lower and upper simulated error for the 95% central intervals and 95% absolute value intervals in Figure 3. If one wants to make directional inferences (e.g., showing that new treatment is significantly better than control using three-decision rules), then the central confidence intervals show one-sided significances at the 2.5% level, while the absolute value method show one-sided significance at the 5% level only.
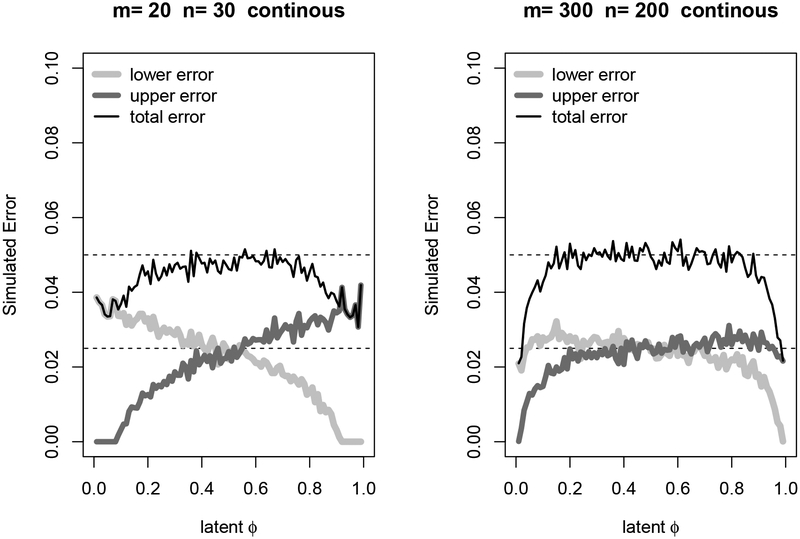
For the asymptotic method we perform several simulations, each using 104 replications. For each simulation we start with latent continuous proportional hazards model using a shift in the logistic distribution translating the location shift, log(θ), to the latent Mann-Whitney parameter, ϕ*, using Equation 12. In Figure 4 we plot the simulated errors in the continuous case where ϕ and ϕ* are the same, where the lower error is the proportion of times the lower limit is greater than the true ϕ, the upper error is analogous, and the total error is the sum of the lower and upper errors. We simulate for values of ϕ from 0.01, …, 0.99 with both smaller sample sizes (m = 20 and n = 30) and larger sample sizes (m = 300 and n = 200). The errors are not equal for small sample sizes for values of ϕ away from 1/2, but as the sample size gets larger the normal approximation becomes better and the errors are closer to equal.
Figure 4:
Simulated error for 95% asymptotic confidence interval procedures for the continuous proportional odds model. Dotted lines are at 0.05 and 0.025.
For the grouping, we perform the simulation similar to the one in Section 7.1. Let and , where θ = eβ is the proportional odds. Let and be the grouped data, except grouped values k − 1 or larger are all combined into the largest category, so that there are k categories of response, where we simulate two cases: k = 3 and k = 6. Let F and G be the distributions for the grouped responses, so the Mann-Whitney parameter is ϕ = hMW(F, G) and the latent Mann-Whitney parameter is ϕ* = hMW(F*, G*). We simulate for values of ϕ* ∈ {0.01, …, 0.99}, and also translate those values to ϕ for calculation of some errors.
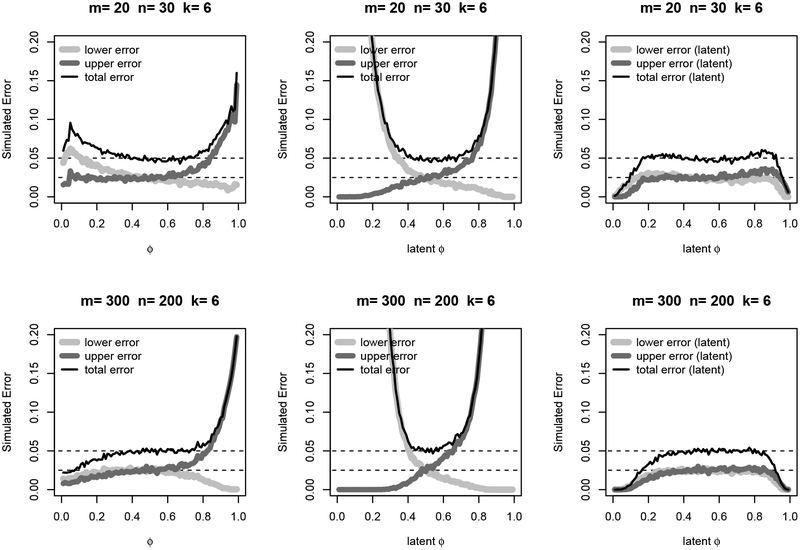
The results for the simulation with k = 6 are plotted in Figure 5. The first column shows the error of the asymptotic confidence interval for ϕ with respect to the true value ϕ. There the total error is close to the nominal 5% from about ϕ = 0.25 to ϕ = 0.75, but outside that range the error rates can be poor. The middle columns show the “error” of the asymptotic confidence interval for ϕ in covering ϕ*. This shows that the transformation to the latent scale is necessary. The third column shows the error rates with respect to ϕ* of the asymptotic confidence interval for ϕ transformed to the latent scale. For values at the edges, the confidence intervals are conservative because when a limit is too small or large to be transformed (see Section 6.2), then the software returns a limit of 0 or 1 respectively. Results for k = 3 are similar and given in the supplement.
Figure 5:
Simulated error for 95% asymptotic confidence interval procedures for the grouped proportional odds model with k = 6 categories. Dotted lines are at 0.05 and 0.025. The first column uses asymptotic confidence intervals for ϕ and calculates error with respect to ϕ. The second column uses asymptotic confidence intervals for ϕ but calculates error with respect to ϕ*. The third column uses asymptotic confidence intervals for ϕ transformed to the ϕ* (i.e. latent Mann-Whitney) scale, then calculates error with respect to ϕ*.
9. Examples and Software
In Table 1, we give data from [31] (see also Table 1 of [3]) on a study of children’s tonsil size comparing healthy children that are carriers of Streptococcus pyogenes or not. The data are heavily tied, but nevertheless we can perform an asymptotic WMW test corrected for ties giving a two-sided p-value of 0.009 (exact version gives the same result). Thus, we can reject the null H0: F = G at level α = 0.01. We see a highly significant difference between the two groups. Further, it looks like the carriers of the Streptococcus pyogenes tend to have larger tonsils than non-carriers.
Table 1:
Data from [31]. Tonsil size of carriers and non-carriers of Streptococcus pyogenes. Scores represent: 1=present but not enlarged, 2=enlarged, 3=greatly enlarged.
| Scores | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| Non-carriers | 497 | 560 | 269 |
| Carriers | 19 | 29 | 24 |
Now consider supplementing the test with an effect estimate and confidence interval. If we measure the effect size as a difference in medians, then the median score for non-carriers is 2 (i.e., enlarged) and the median score for carriers is 2 and the difference is 0. So we reject at the α = 0. 01 level, but the effect estimate is the same as the effect under the null hypothesis that F = G.
Now consider the Hodges-Lehmann estimator of location shift. The idea here is to shift the new treatment responses until the difference in mean ranks is about 0. This gives the Hodges-Lehmann estimator of location shift, say . This estimate (to four significant digits) is 0.0000. We can then get a 95% Hodges-Lehmann-type confidence interval by adding positive or negative shift to until we just barely reject at the α = 0.05 twosided level in either direction. This 95% confidence interval (to four significant digits) is (0.0000, 0.0000). This estimator and confidence interval can be found in standard software, for example using the wilcox.test function in R (version 3.3.3) or using Proc npar1way in SAS (version 9.4, which we used). This estimate and confidence interval say that there is no location shift, and we know that fairly precisely, while at the same time we reject the null hypothesis of F = G at the α = 0.01 level. The problem of course is that the continuity assumption needed for the validity of the Hodges-Lehmann estimator and confidence interval does not hold.
Using our wmwTest function in the asht R package [32], we can perform the asymptotic WMW test with a confidence interval for ϕ for these data.
> library(“wmwTest”)
> noncarriers<-rep(1:3, times=c(497, 560, 269))
> carriers<-rep(1:3, times=c(19,29,24))
> wmwTest(noncarriers, carriers)
Wilcoxon-Mann-Whitney test with continuity correction (confidence interval requires proportional odds assumption, but test does not)
data: noncarriers and carriers
Mann-Whitney estimate = 0.58499, tie factor = 0.86572, p-value = 0.008952
alternative hypothesis: two distributions are not equal 95 percent confidence interval:
0.5213330 0.6453915
sample estimates:
Mann-Whitney estimate
0.5849935
The interpretation is that we can reject the null hypothesis that the distribution of tonsil size is unrelated to whether a child is a carrier or not, H0: F = G. The p-value is valid without any proportional odds assumption. We estimate that the probability that the tonsil size of a randomly selected individual in the study that is a carrier will be larger than the tonsil size of a non-carrier (plus a correction for ties) is 0.585(95%CI: 0.521,0.645), where the confidence interval requires the proportional odds assumption. Using wmwTest(noncarriers, carriers, latentContinuous = TRUE) we get the same p-value, but now we transform the estimate and confidence limits to the latent Mann-Whitney parameter as 0.597(95%CI: 0.525, 0.665). The latent parameter represents the probability that the tonsil size of a randomly selected individual in the study that is a carrier will be larger than the tonsil size of a non-carrier under a continuous proportional odds model.
Returning to the data from [7] from the introduction, x = [2.1,4.7, 6.8, 7.9, 8.6] and y = [7.5, 8.9, 9.2, 9.3], we can use wmwTest(x, y) and the function automatically performs the exact WMW test with the associated confidence interval by the central method of Section 7.1 giving p = 0.063 with (95%CI: 0.477, 0.995). By the absolute value method (option tsmethod=“abs”) we get the same p-value p = 0.063 with (95%CI: 0.500,0.991).
The central method and absolute value method p-values may differ when there are ties. Consider the rounded data x = [2, 5, 7, 8, 9] and y = [8, 9, 9,9], then we get p = 0.143 and (95%CI: 0.390, 0.997) for the central method, while we get p = 0.1032 and (95%CI: 0.438, 0.995) for the absolute value method. For the three-decision rule the central method says that we can test H0: ϕ ≤ 0.5 with one-sided p-value of p = 0.071, while the absolute value method tests that hypothesis with p = 0.1032. Finally, we can transform the estimate and results to inferences on ϕ* (the latent Mann-Whitney parameter); using the central method we get (95%CI: 0.378,1.000).
10. Discussion
We have proposed confidence intervals for the Mann-Whitney parameter that are designed to be compatible with the WMW test, both the asymptotic and the exact versions. We have shown compatibility in the asymptotic case, and suspect compatibility in the exact case when using the central p-values. The confidence intervals require the proportional odds assumption. This assumption is much less restrictive than that of the Hodges-Lehmann interval which requires location shift and continuous responses. The proportional odds assumption is equivalent to saying that there exists some unknown strictly increasing transformation of the latent continuous responses such that the transformed responses represent a location shift on the logistic distribution. Further work is needed to determine how robust the coverage of the confidence intervals are if the data generating process is substantially different from the proportional odds one. The simulated error from the confidence intervals generally shows close to nominal error for values of ϕ close to one half, the area where coverage is most important.
The R function wmwTest in the asht R package [32] performs the methods of this paper.
Supplementary Material
Acknowledgements
The authors thank the reviewers for helpful comments that have improved the paper.
The authors gratefully acknowledge please remember to list all relevant funding sources in the unblended version
Footnotes
SUPPLEMENTARY MATERIAL
Supplement.pdf: A pdf file that gives mathematical details and simulation results related to this paper.
References
- 1.Wilcoxon F Individual comparisons by ranking methods. Biometrics bulletin 1945; 1(6):80–83. [Google Scholar]
- 2.Mann HB, Whitney DR. On a test of whether one of two random variables is stochastically larger than the other. The Annals of Mathematical Statistics 1947; 18(1):50–60. [Google Scholar]
- 3.McCullagh P Regression models for ordinal data (with discussion). Journal of the royal statistical society. Series B (Methodological) 1980;109–142. [Google Scholar]
- 4.Fay MP, Proschan MA. Wilcoxon-mann-whitney or t-test? on assumptions for hypothesis tests and multiple interpretations of decision rules. Statistics Surveys 2010; 4:1–39. URL http://www.i-journals.org/ss/viewarticle.php?id=51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hodges JL, Lehmann EL. Estimates of location based on rank tests. The Annals of Mathematical Statistics 1963;598–611. [Google Scholar]
- 6.Bauer DF. Constructing confidence sets using rank statistics. Journal of the American Statistical Association 1972; 67(339):687–690. [Google Scholar]
- 7.Kalbfleisch JD, Prentice RL. The statistical analysis of failure time data, second edition John Wiley & Sons, 2002. [Google Scholar]
- 8.Venables WN, Ripley BD. Modern Applied Statistics with S. Fourth edn., Springer: New York, 2002. URL http://www.stats.ox.ac.uk/pub/MASS4, iSBN 0-387-954570. [Google Scholar]
- 9.Agresti A, Kateri M. Ordinal probability effect measures for group comparisons in multinomial cumulative link models. Biometrics 2017; 73(1):214–219. [DOI] [PubMed] [Google Scholar]
- 10.Thas O, Neve JD, Clement L, Ottoy JP. Probabilistic index models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2012; 74(4):623–671. [Google Scholar]
- 11.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (roc) curve. Radiology 1982; 143(1):29–36. [DOI] [PubMed] [Google Scholar]
- 12.Harrell F, Lee KL, Mark DB. Tutorial in biostatistics multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Statistics in medicine 1996; 15:361–387. [DOI] [PubMed] [Google Scholar]
- 13.Newcombe RG. Confidence intervals for an effect size measure based on the mann-whitney statistic. part 1: general issues and tail-area-based methods. Statistics in medicine 2006; 25(4):543–557. [DOI] [PubMed] [Google Scholar]
- 14.Newcombe RG. Confidence intervals for an effect size measure based on the mann-whitney statistic. part 2: asymptotic methods and evaluation. Statistics in medicine 2006; 25(4):559–573. [DOI] [PubMed] [Google Scholar]
- 15.Ryu E, Agresti A. Modeling and inference for an ordinal effect size measure. Statistics in Medicine 2008; 27(10):1703–1717. [DOI] [PubMed] [Google Scholar]
- 16.Feng D, Cortese G, Baumgartner R. A comparison of confidence/credible interval methods for the area under the roc curve for continuous diagnostic tests with small sample size. Statistical methods in medical research (online early) 2015;D0I: 10.1177/0962280215602040. [DOI] [PubMed] [Google Scholar]
- 17.Mehta CR, Patel NR, Tsiatis AA. Exact significance testing to establish treatment equivalence with ordered categorical data. Biometrics 1984;819–825. [PubMed] [Google Scholar]
- 18.Hirji K Exact Analysis of Discrete Data. Chapman and Hall/CRC: New York, 2006. [Google Scholar]
- 19.Lehmann E Nonparametrics: Statistical Methods Based on Ranks. Holden-Day, Inc.: Oakland, Ca, 1975. [Google Scholar]
- 20.Sen P Permutational central limit theorems. Encyclopedia of Statistics (editors: Kotz S and Johnson NL) 1985; 6:683–687. [Google Scholar]
- 21.Lehman SY. Exact and approximate distributions for the Wilcoxon statistic with ties. Journal of the American Statistical Association 1961; 56(294):293–298. [Google Scholar]
- 22.Pratt JW. Robustness of some procedures for the two-sample location problem. Journal of the American Statistical Association 1964; 59(307):665–680. [Google Scholar]
- 23.Pauly M, Asendorf T, Konietschke F. Permutation-based inference for the AUC: A unified approach for continuous and discontinuous data. Biometrical Journal 2016; 58(6):1319–1337. [DOI] [PubMed] [Google Scholar]
- 24.Casella G, Berger RL. Statistical inference, second edition Duxbury Pacific Grove, CA, 2002. [Google Scholar]
- 25.Lee A U-Statistics: Theory and Practice. Marcel Dekker, Inc.: New York, 1990. [Google Scholar]
- 26.Hettmansperger TP. Statistical Inference Based on Ranks. Krieger Publishing Company: Malabar, Florida, 1984. [Google Scholar]
- 27.Lehmann EL. The power of rank tests. The Annals of Mathematical Statistics 1953;23–43. [Google Scholar]
- 28.Freedman LS. An analysis of the controversy over classical one-sided tests. Clinical Trials 2008; 5(6):635–640. [DOI] [PubMed] [Google Scholar]
- 29.Fay MP. Confidence intervals that match fisher’s exact or blaker’s exact tests. Biostatistics 2010; 11 (2):373–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fay MP. Two-sided exact tests and matching confidence intervals for discrete data. R journal 2010; 2(1):53–58. [Google Scholar]
- 31.Holmes MC, Williams R. The distribution of carriers of streptococcus pyogenes among 2,413 healthy children. Journal of Hygiene 1954; 52(02):165–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fay MP. asht: Applied Statistical Hypothesis Tests 2017. R package version 0.9.3 available on https://cran.r-project.org/package=asht.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.