Reducing Pulse Oximetry False Alarms Without Missing Life-Threatening Events

Abstract

Alarm fatigue has been increasingly recognized as one of the most significant problems in the hospital environment. One of the major causes is the excessive number of false physiologic monitor alarms. An underlying problem is the inefficient traditional threshold alarm system for physiologic parameters such as low blood oxygen saturation (SpO₂). In this paper, we propose a robust classification procedure based on the AdaBoost algorithm with reject option that can identify and silence false SpO₂ alarms, while ensuring zero misclassified clinically significant alarms. Alarms and vital signs related to SpO₂ such as heart rate and pulse rate, within monitoring interval are extracted into different numerical features for the classifier. We propose a variant of AdaBoost with reject option by allowing a third decision (i.e., reject) expressing doubt. Weighted outputs of each weak classifier are input to a softmax function optimizing to satisfy a desired false negative rate upper bound while minimizing false positive rate and indecision rate. We evaluate the proposed classifier using a dataset collected from 100 hospitalized children at Children’s Hospital of Philadelphia and show that the classifier can silence 23.12% of false SpO₂ alarms without missing any clinically significant alarms.

1. Introduction

The rapid pace of innovation in the medical device market has resulted in significant improvements in the devices used to monitor patients’ physiologic parameters in hospitals today. These devices provide rich information to doctors and nurses by monitoring vital signs and alerting clinicians of potential problems. However, studies have shown that more than 80% of hospital cardio respiratory monitor alarms are false or clinically insignificant (do not require bedside intervention) [1, 2, 3]. The excessive false alarms lead to alarm fatigue [4], such that life-threatening events are less likely to be addressed on time or can even be ignored, with potentially deadly consequences [5].

One of the most common continuously monitored vital signs is pulse oximetry, which is also the most common source of physiologic monitor alarms in the modern hospital [1]. Pulse oximetry is a non-invasive method for monitoring patient’s blood-oxygen saturation; it does so by providing peripheral oxygen saturation (SpO₂) readings. Since the oxygen saturation is a good indication of a person’s oxygen levels, clinicians set threshold alarms for low SpO₂ [6]. However, there are many factors influencing the effectiveness of the low SpO₂ alarm threshold such as patient size, skin condition, sensor technology, patient movement, and the employed signal processing algorithm. As a result, many low SpO₂ alarms do not require clinician intervention and contribute to the ”alarm hazards”, stated as the number one health technology hazard for 2015 by the ECRI Institute [7]. Therefore, our goal in this paper is to propose a new approach to reducing false low blood oxygen saturation alarms without silencing clinically significant alarms that represent life-threatening conditions.

Reducing false positive pulse oximetry alarms has been an active area of research for the past several decades. Low SpO₂ alarms can be significantly reduced by decreasing the low alarm threshold [8], adding a short delay [9], or combining both methods under continuous patient safety surveillance [10, 11]. However, by design these methods will also delay alerts for actionable alarms and potentially hide clinically significant fluctuations. On the other hand, pulse oximetry measurements can also be filtered statistically from noise and outliers, which then be used to compare with alarm thresholds instead of raw values [12, 13, 14]. As signal extraction algorithms, these approaches are limited with time series and cannot consider patient’s static information (e.g., patient age), which can help to reduce patient variabilities. While these technologies have been shown to significantly reduce the number of false low SpO₂ alarms, they also miss true low SpO₂ events – which raises significant clinical safety concerns.

In this paper, we propose to reduce the number of false SpO₂ alarms by developing an AdaBoost machine learning classifier with reject option that is tuned specifically to not silence valid alarms while suppressing as many of the false alarms as possible. We choose vital signs that are related to SpO₂ alarms (such as heart rate, SpO₂) to extract classifying features. Vital sign data, in the form of time series, are extracted into different numerical measurements within intervals before the alarm triggering time. These features are combined with patient information and related alarms that trigger during the monitoring window. In line with clinical guidelines that suggest that it may take up to 15 seconds to evaluate the validity of an alarm [11], our algorithm considers measurements for up to 15 seconds after an alarm.

AdaBoost is generally used in conjunction with other learning algorithms to improve the performance by iteratively adapting weak classifiers to misclassified samples during the previous iteration. To minimize the risk of silencing significant alarms, we introduce a reject option to not making any decision in case of doubt (i.e., a low confidence alarm). An alarm is considered high confidence if all the weak classifiers agree upon the validity outcome. On the other hand, due to the uncertainty involved, all low confidence alarms are immediately classified as clinically significant in order not to silent potentially life-threatening events. The proposed algorithm is optimized to achieve minimum false positive and indecision rate while maintaining false negative rate satisfying the upper bound condition.

We evaluate the proposed algorithm on a dataset of 100 hospitalized children at the Children’s Hospital of Philadelphia. The dataset includes patients’ information (e.g., age, weight), vital signs, and physiological monitoring alarms. For evaluation purposes, alarms were classified by clinicians (via video inspection) as (1) invalid, (2) valid but not clinically significant, and (3) clinically significant. To satisfy the conservative requirements of our algorithm, at the training stage we treat (2) and (3) as both valid. The results indicate that the classifier is able to silence a high number of false positive alarms without misclassifying any clinically significant alarms. Furthermore, we compare the performance of the proposed algorithm with the vanilla AdaBoost algorithm and show that AdaBoost with reject option can maintain the desired false negative rate while being able to silence false alarms.

In summary, the contributions of this paper are three-fold: (1) an AdaBoost classification method with reject option for reducing the number of false SpO₂ alarms without silencing any clinically significant alarms; (2) an evaluation of the proposed classifier on de-identified data obtained from the Children’s Hospital of Philadelphia; (3) a comparison of the proposed algorithm versus other state-of-the-art algorithms.

The remainder of this paper is organized as follows. In the next section, we briefly describe our dataset and formulate the problem. We discuss how the feature extraction and data preprocessing procedures in Section 3. Section 4 then introduces the proposed classifier in detail. We evaluate the performance of the proposed classifier in Section 5 and provide concluding remarks in Section 6.

2. Preliminaries and Problem Statement

This section describes the dataset used for evaluation in this paper. The large of number of false SpO₂ alarms is highlighted, followed by the statement of the problem addressed in this work.

The study was approved by the Institutional Review Board of the Children’s Hospital of Philadelphia (IRB #14-010846). As part of a larger study, the research team video recorded 551 hours of patient care on a medical unit at the Children’s Hospital of Philadelphia between July 2014 and November 2015 from 100 children whose families and nurses provided written informed consent. Beside patient background information (e.g., age group), continuously recorded blood oxygen saturation, heart rate, and respiratory rate were extracted from the physiologic monitoring network at a maximum sampling rate of 0.2 Hz. Each session lasted up to 6 hours and included up to 6 synchronized cameras per patient capturing multiple views of the patient and room as well as views of the monitoring device displays. In addition, all physiologic monitoring alarms were also extracted from the physiologic monitoring network with corresponding timestamps. These alarms were later reviewed, in conjunction with the video recordings, and annotated into four categories with the oversight of a physician expert: technical alarms, valid clinically significant alarms, valid non-clinically significant alarms and invalid alarms [15].¹

Technical alarms are caused by medical instruments such as electrocardiogram (ECG) lead displacement, while all others such as low oxygen saturation are clinical alarms. By reviewing the video, the team could further assess if the alarm correctly identified the physiologic status of the patient (i.e., valid) or was a false reading due to artifact (i.e., invalid). A valid alarm which led to a clinical intervention or consultation was further categorized as clinically significant alarm, while the rest were non-clinically-significant. Each alarm was annotated accordingly in the dataset; as noted in Section 1, for training purposes we consider both technical and invalid alarms as invalid, whereas valid clinically significant alarms and valid non-clinically-significant alarms are both considered valid.

As has been previously published [16], the study team trained a research assistant to review video and determine the validity of clinical alarms. During the training period, the research assistant reviewed every clinical alarm from the first 42 patients (with a total of 4675 alarms) with direct oversight from a physician expert in physiologic monitoring. The research assistant and expert then separately reviewed every clinical alarm that required interpretation from 10 additional patients (generating an additional 883 alarms). The research assistant and expert agreed on the validity determination for 99.3% of the 883 alarms. The research assistant then made the remaining validity determinations independently unless they were uncertain, in which case they consulted one or more experts.

Our study only considers a subset from the original dataset and includes:

• patient’s age group (less than one month old, from one to less than two months old, from two to less than six month old, older than six months),

• numerical measurements of pulse oximetry and heart rate (measured by pulse oximeter and 3-lead electrocardiography) at a maximum sampling rate of 0.2 Hz,

• annotated clinical alarms with corresponding alarm type and timestamp.

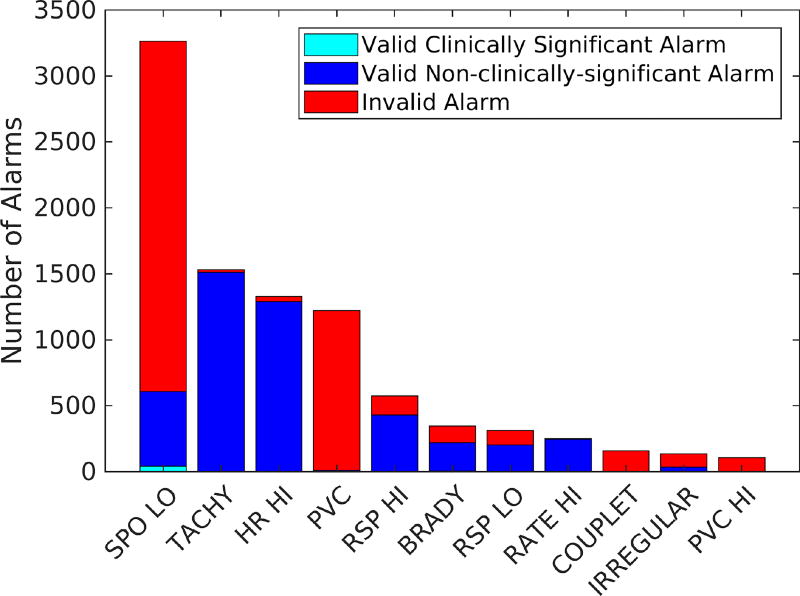
In summary, the extracted dataset contains 551 hours of recorded data with a total of 9547 clinical alarms in 26 different types. Vital signs were measured at 0.2 Hz rate and all the measurable data were recorded into one sample with patient ID and timestamp. Out of 9547 alarms, about 51% were invalid. Figure 1 shows the highest occurring alarm types² as the rest only accounted for fewer than 100 alarms each. As can be seen from Figure 1, low SpO₂ generated the highest number of alarms (34% of total alarms), for which 81% were invalid. It is clear that reducing invalid low SpO₂ alarms is an appropriate and potentially efficient target to address alarm fatigue.

Figure 1.

Number of alarms in different clinical categories for the top occurring physiologic monitoring alarms in the dataset.

Problem

The problem considered in this paper is to provide a robust classifier that can identify and silence false low SpO₂ alarms while ensuring zero misclassified clinically significant alarms.

3. Feature Extraction and Data Preprocessing

In this section, we first describe how we select and extract features from the given dataset. Then, the data preprocessing procedure is presented, namely removing samples without qualified information and performing dimensionality reduction.

3.1. Feature Extraction

There are three groups of variables in the dataset, namely: patient background information, vital sign measurements, and alarm data. Both patient information and alarm data (e.g., alarm type) are categorical data, which can be used directly as features in our machine learning algorithms. On the other hand, vital sign measurements are time series and need to be converted into usable forms. In medical datasets, the most recent patterns are the most significant ones; therefore, our approach is converting each vital sign measurement from the time an alarm occurred back to two minutes before that. In addition, it has been shown in previous works that the subsequent measurements in 15 seconds play an important role to suppress false positive alarms [9, 11], and thus, are also added to our feature set. Since we recorded vital signs every five seconds, this results in additional 27 features for each vital sign that we consider.³

The pulse oximetry sensor is capable of estimating both blood oxygen and pulse rate, provides a portable way to monitor heart rate in comparison with ECG monitoring [17]. Therefore, beside SpO₂ measurements, we also extract heart rate (denoted as HR) from electrocardiography and pulse rate (denoted as PuR) obtained by pulse oximeter. Since both methods are used to monitor the same vital sign, they are highly correlated and any difference between measurements is an indication of bad estimations (e.g., sensor misplacement) or, much less likely, poor perfusion to the extremity where the sensor is located. Hence, our feature set also includes the minimum, maximum, and median of the differences between heart rate and pulse rate within two minutes before the alarm timestamp. Intuitively, a false positive low SpO₂ alarm caused by sensor misplacement should also incur a higher than usual difference between these measurements.

Although blood oxygen saturation and heart rate are the most frequently monitored in hospital, respiratory rate has been shown to be an early and sensitive indicator of deterioration [18]. That is, an early respiratory rate alarm is more likely to validate a subsequent low SpO₂ alarm. To capture the correlation, we add a binary feature to indicate if a respiratory rate alarm was triggered within two minutes before each low SpO₂ alarm, and an additional similar binary feature for heart rate alarm.

Finally, Table 1 summarizes all the features that we use for our classifiers. Extracted data are parsed to generate corresponding feature data as listed above.

Table 1.

Extracted features for machine learning algorithms

Variable Group	Extracted Features
Patient Information	Age group
Vital Signs	27 SpO2 measurements
	27 HR measurements
	27 PuR measurements
	(HR - PuR) min
	(HR - PuR) max
	(HR - PuR) median
Alarms	Preceding respiratory rate alarm
	Preceding heart rate alarm

3.2. Data Preprocessing

Since the vital sign dataset was captured during routine clinical care, not all vital signs were collected for every patient. For instance, SpO₂ measurements were recorded for all 100 children, whereas only 79 children had heart rate obtained from electrocardiography available. Missing vital signs will eventually create multiple unknown values in our feature data and decrease the classifier’s performance. Therefore, we only keep alarm samples with at least 60% of the features available, which results in 2318 alarms left from the original 3265.

With 86 features for 2318 samples, our dataset forms a large multivariate matrix with many variables being extracted from the same signals; hence, it is often desirable to reduce the dimensionality, which results in lower memory consumption and faster classification without affecting the classification performance. Principle Component Analysis (PCA) is usually a good choice in this case. By transforming the data (i.e., linear projection) onto a lower dimensional space, PCA can reduce the dimensionality while preserving as much data variation as possible [19]. Mathematically, PCA tries to find a new set of uncorrelated variables (principle components), that are linear combinations but smaller in size than the original ones, to express the data in reduced form. We choose 95% explained fraction for our model since the feature set is highly correlated and are able to reduce the dataset dimension to 17 variables. PCA is only performed on training data to ensure test information is not leaked into training principle components.

4. Methods

This section first overviews the approach and AdaBoost algorithm, then describes the proposed AdaBoost with reject option in details.

4.1. Approach Overview

A robust alarm classifier should be able to suppress many false low blood oxygen saturation alarms and should not silence any clinically significant alarms. In order to achieve a low false negative rate, we need to capture as many patterns in the training data as possible while prioritizing clinically significant alarms. AdaBoost algorithm fits well in this context as the algorithm puts higher weights on previous misclassified points, which can be tuned specifically toward false negative points.

A general AdaBoost training algorithm minimizes the training error. In our application, we prioritize achieving a low false negative rate than the accuracy. Instead of the AdaBoost weighted sum output layer, we propose a different output layer that employs a softmax function to generate the probability distribution of the outcomes. Intuitively, classifying a low confidence alarm (i.e., both classes have either low probability or high probability) is high risk; hence, we want to be cautious and always classify the alarm as valid (i.e., not silence the alarm). On the other hand, high confidence alarms can be classified as the class with the higher probability.

4.2. AdaBoost Algorithm

In general, the AdaBoost algorithm is a boosting method which combines multiple weak and inaccurate classifiers to achieve a highly accurate prediction classifier as shown in Algorithm 1. On each training iteration t, the algorithm adds a weak learner with the aim of minimizing the training error ε_t such that the weights of incorrectly classified examples from previous iterations are increased (i.e., these examples will play more important roles in the training of the next iteration). Each weak classifier is assigned a weight corresponding to the training error of the iteration. The final classifier computes the sign of a weighted combination of weak classifiers (i.e., weighted majority vote).

Freund and Schapire proved that the training error of AdaBoost after T iterations is bounded by $\epsilon \le 2^T{\prod }_{t=1}^T\sqrt{{\epsilon }_t(1-{\epsilon }_t)}$, hence drops exponentially fast in the number of iterations T if each weak classifier is slightly better than random [20]. However, Freund and Schapire also proved that if the weak classifier are chosen from a class of VC-dimension d ≥ 2, then the final classifier after T iterations belong to a class of VC-dimension at most 2(d + 1)(T + 1) log₂(e(T + 1)), and the generalization error bound is of the form

$$\mathit{\text{err}}(H)=\widehat{\mathit{\text{err}}}(H)+\stackrel{\sim }{O}(\sqrt{\frac{\mathit{\text{dT}}}{m}})$$

Algorithm 1.

AdaBoost Algorithm

Given: -(x1, y1), …, (xm, ym) where xi ∈ χ, y ∈ {−1, +1} -Number of learning rounds T
1:	procedure Train(data)
2:	Initialize example i weight at iteration 1: D1(i) = 1/m for i = 1, …, m
3:	for t=1,…,T do
4:	Train weak classifier using distribution Dt
5:	Find weak learner at iteration t: $h_t=\text{arg }\underset{h_j\in H}{\text{min}}{\epsilon }_j={\sum }_{i=1}^m{D}_t(i)[y_i\ne h_j(x_i)$
6:	Choose weak learner weight ${\alpha }_t=\frac{1}{2}\text{ln}(\frac{1-{\epsilon }_t}{{\epsilon }_t})$
7:	Update $D_{t+1}(i)=\frac{D_t(i)\text{exp}(-{\alpha }_t{y}_i{h}_t(x_i))}{Z_t}$ where Zt is normalization factor
8:	Return final classifier: $H(x)=\mathit{\text{sign}}({\sum }_{t=}^T{\alpha }_t{h}_t(x))$

This bound implies that the generalization error decreases at first, yet finally increases as T increases, which is exactly the kind of overfitting behavior. This characteristic is important in our context since we want to capture all the clinically significant alarm patterns and AdaBoost tends to not overfit [21]. Hence, choosing the right T is a major consideration in the proposed algorithm as will be discussed in the next subsection.

4.3. AdaBoost with Reject Option Algorithm

On a high level, the proposed algorithm is a variant of AdaBoost with reject option by allowing a third decision (i.e., reject) expressing doubt. The predicted probability of each outcome j ∈ {−1, 1} (given the sample vector x and the weighting vector w) are input to a softmax function to generate a probability distribution over the two different possible outcomes:

$${\eta }_j=P(y=j\in \{-1,1\}|x)=\frac{e^{{\mathbf{w}}_j\top \mathbf{x}}}{{\sum }_k{e}^{{\mathbf{w}}_k^{\top }\mathbf{x}}}$$

Given a reject threshold β, the output function of the weak classifier in round t is then

$$h_t(x)=\{\begin{array}{c}-1\text{ if }{\eta }_{-1}\ge \beta \hfill \\ +1\text{ if }{\eta }_{+1}\ge \beta \hfill \\ \text{reject otherwise}\hfill \end{array}$$

Rather than using the usual prediction error, we ask that the weak classifiers satisfy a desired false negative rate (FNR) upper bound while minimizing the false positive rate (FPR) and the indecision rate (INDR). Note that the indecision rate may have a smaller effect than the false positive rate so that an indecision weight λ is used to express the relative ”importance” between these two rates. For example, an indecision weight of 0.5 means one false positive point is equal to two indecision points during optimizing. Hence, the weak learner’s goal is to find a hypothesis h_t and the corresponding confidence probability threshold β_t which minimizes:

$$\mathit{\text{FP}}+\lambda \ast \mathit{\text{IND}}$$

$$\text{subject to}\mathit{\text{FNR}}=\frac{\mathit{\text{FN}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}\le \epsilon$$ (1)

Algorithm 2.

AdaBoost with Reject Option Algorithm

Given: -(x1, y1), …, (xm, ym) where xi ∈ χ, y ∈ {−1, +1} -ε : false negative rate upper bound -λ : indecision weight -τ : stopping condition threshold -T : maximum allowed number of rounds
1:	procedure Train(data)
2:	Initialize example i weight at iteration 1: D1(i) = 1/m for i = 1, …, m
3:	for t=1,…,T do
4:	Train weak classifier using distribution Dt
5:	Find weak learner at iteration t: ht, ${\beta }_t=\text{arg }\underset{h_j\in H,{\beta }_t}{\text{min}}⧣\text{FP}+\lambda \ast ⧣\text{IND}$ $$\text{subject to}\mathit{\text{FNR}}=\frac{\mathit{\text{FN}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}\le \epsilon$$
6:	Choose weak learner weight ${\alpha }_t=\frac{1}{2}\text{ln}(\frac{1-{\epsilon }_t}{{\epsilon }_t})$
7:	Update $D_{t+1}(i)=\frac{D_t(i)\text{exp}(-{\alpha }_t{y}_i{h}_t(x_i))}{Z_t}$ where Zt is normalization factor
8:	If δFPR| ≤ 0 and δINDR ≥ τ then break
9:	Return final classifier: H(x)

Here, we denote the number of false positive points, the number of true positive points, and the number of false negative points as FP, TP, and FN respectively. Finally, the boosting algorithm repeatedly iterates in a series of rounds until maximum T rounds or until it reaches a stopping condition. We define two stopping conditions as below:

• Soft Condition: δ_FPR ≤ 0 and δ_INDR ≥ τ

• Hard Condition: δ_FPR ≤ −τ and δ_INDR ≥ τ

Both stopping conditions are used to prevent over-fitting with different levels of sensitivity. The soft condition detects a sharp increase in the indecision rate when the false negative rate is still decreasing. It happens when the algorithm is starting to learn harder cases and potentially over-fits the training data. We call this a “soft” condition as it allows the algorithm to continue improving the performance overall with a slight increase in the false negative rate. On the other hand, the hard condition detects sharp changes in both false negative rate and indecision rate, which indicates an apparent over-fit problem and the algorithm should not be allowed to continue. In summary, a strictly low false negative rate model can be achieved with the soft stopping condition while the hard stopping condition is suited for a better overall performance model.

Pseudocode for the proposed algorithm with the soft stopping condition is presented in Algorithm 2. Here we are given m labeled training examples with the labels y_i ∈ {−1, +1} for invalid/valid alarms. The algorithm has four hyper parameters: the desired false negative rate upper bound ε (ε should be set to 0 in the case of no false negatives), the indecision weight λ, the maximum number of rounds T, and the stopping threshold τ. On each round t = 1, …, T, a given weak learning algorithm is applied to find a weak hypothesis h_t and confidence probability threshold β_t that satisfies (1). The aim of the weaker learner is to guarantee that the false negative rate is below the pre-defined upper bound while minimizing false positive and indecision rate. The training algorithm results in a boosted classifier satisfying false negative rate with highest silencing alarm rate.

5. Results

In order to evaluate the performance of our approach, we perform 5-fold patient cross-validation on the obtained data such that the dataset is randomly partitioned into five equal sized partitions of patients: samples from four patient subgroups are used as training data, and the samples from the remaining subgroup are assigned as the validation set. The process is repeated five times such that each subgroup is used for validation exactly once. The results of our evaluation are presented in this section. First, we analyze the proposed algorithm’s performance. Then, we provide a discussion of motion artifact effects on the performance. Finally, we compare the performance of the final classifier with vanilla AdaBoost algorithm and other well-known algorithms.

5.1. Performance Analysis

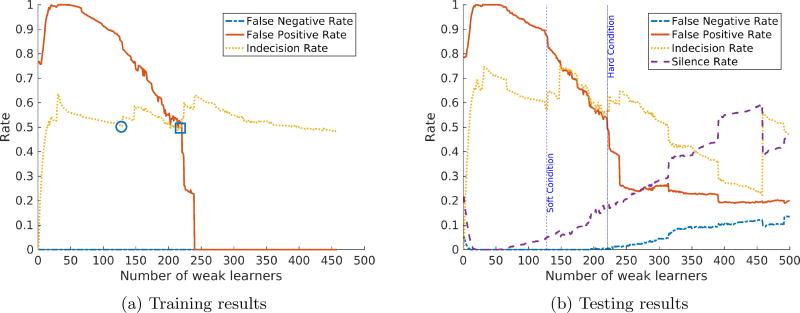
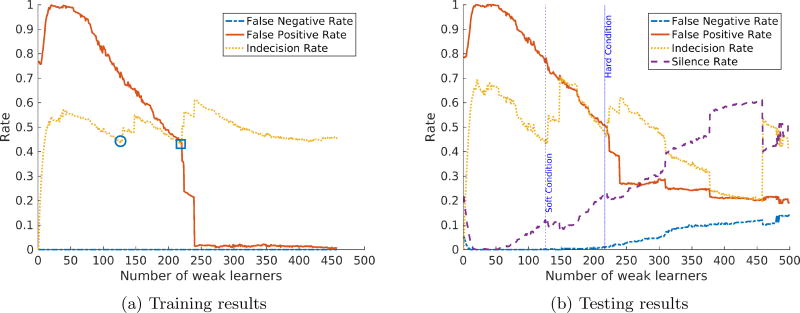
The false negative rate upper bound ε is crucial to the algorithm since it determines how much effort the weak classifiers need to expend in order to learn all the valid alarms. To ensure zero misclassified clinically significant alarms, we choose ε = 0.01. In addition, a good choice of indecision weight λ will balance the overall performance of the system. To illustrate, we analyze the classifier’s performance with λ = 0.01 and λ = 0.25 as shown in Figure 2a and Figure 3a respectively. In addition, we do not enforce the stopping condition to show the optimal number of weak learners selected by the algorithm and the effects of letting the algorithm choose a higher number of weak learners.

Figure 2.

AdaBoost with reject option performance with ε = 0.01 and λ = 0.01.

Figure 3.

AdaBoost with reject option performance with ε = 0.01 and λ = 0.25.

As can be seen from the training results of both figures, with a small number of weak learners, the final classifier has the false positive rate close to 1 to satisfy the false negative rate upper bound. This can be explained as for all decisions this classifier makes, the alarm is classified as valid due to inability to capture enough patterns. As the number of weak learners increases, the training false positive rate also decreases.

The algorithm stops the training phase when it reaches the soft stopping condition (denoted by a circle) or the hard stopping condition (denoted by a square) in Figure 2a and Figure 3a. The corresponding number of weak learners (approximately 130 and 220) are marked with vertical lines in the testing results respectively. Soft stopping condition results in models that meet false negative rate requirements and are able to silence 6% of the false alarms with λ = 0.01 and 9.38% of the false alarms with λ = 0.25.

On the other hand, if the algorithm is allowed to run until hitting the hard stopping condition, the final models have better performance (18% and 22% of false alarms are silenced for λ = 0.01 and λ = 0.25 respectively) with a slightly increase in false negative rate. The false negative rate starts to increase significantly as the number of weak learners is greater than the hard stopping condition cutoff, which confirms the overfitting hypothesis. The results show that AdaBoost with reject option can reduce a significant portion of false alarms at no (or very low) cost in false negatives. In addition, the cases of misclassified valid alarms are actually non-clinically-significant but require a great cost in performance to correctly classify as discussed in the next subsection.

5.2. Motion Artifact Effects

The proposed method offers a new approach to decrease false low SpO₂ alarms, and consequently reduce alarm fatigue. As an alternative to traditional delay method, we allow alarms to trigger but keep collecting new data to silent alarm as soon as we can identify false alarm.

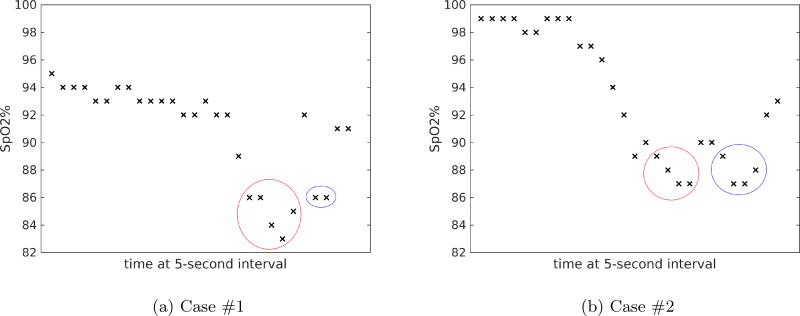
The results also reveal corner cases such that our classifiers can identify but with a great cost in performance, or cannot correctly classify at all. Further investigation on the two misclassified cases shows that they were preceded by invalid alarms within less than one minute. After our physician expert re-reviewed the video recordings of these alarms, we found out that these cases were largely affected by motion artifact. The patient’s vital sign measurements for both cases are shown in Figure 4 with invalid alarms denoted with red circles and valid alarms denoted with blue circles. For details, in the first case, the baby was being held and patted on the back by the caregiver, which led to preceding invalid alarms. After the baby was put back stably, measurements continue to drop. When the alarm was fluctuating between appearing valid and invalid, our standard was to be cautious and annotate as valid. In the second case, there were also significant motion artifacts that led to the invalid alarm. Since our dataset does not include the context information, these alarms appear to have similar features and cause the confusion. Importantly, in the original analysis [16] these cases were not clinically significant, i.e., the alarm did not lead to a clinical intervention or consultation.

Figure 4.

Patient’s SpO₂ measurements during monitoring interval for misclassified cases. Red circle denotes measurements during preceding invalid alarm. Blue circle denotes measurements during valid alarm.

Motion artifacts can be detected and reduced from photopleythysmograms (PPG - raw measurement obtained by pulse oximeter) as described in [22]. However, PPG waveform is not included in our dataset, which can be a next step for our future research. In addition, we can also use new sensor technology to detect motion [23] for the next study.

5.3. Comparison with Other Classifiers

In this subsection, we compare the proposed algorithm with other state-of-the-art classifiers. It is important to note that while the number of silenced alarms is the overall performance of the smart alarm, it is more critical to ensure that no clinically significant alarm is suppressed. In other words, we want to achieve close to one sensitivity (true positive rate) while maximizing specificity (true negative rate).

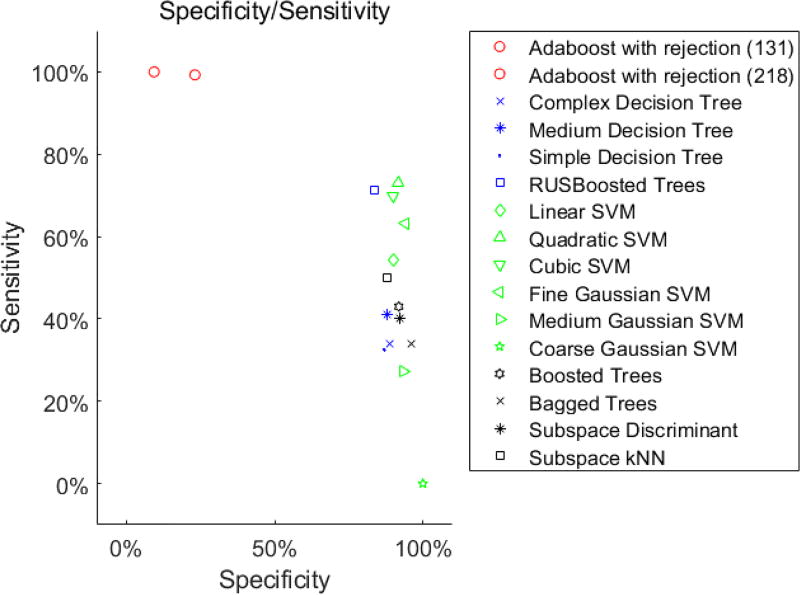
Table 2 shows the performance of the proposed classifier at two operating points (e.g., soft condition and hard condition) in comparison with the vanilla AdaBoost algorithm with the same settings. We can achieve 23.12% specificity, i.e., the proposed classifier is able to silent 23.12% of false SpO₂ alarms, while maintaining clinically significant alarm sensitivity at 99.27%. The vanilla AdaBoost algorithm even though achieves a higher number of silenced alarms, it also makes more mistakes to silence clinically significant alarms. In addition, we also compare with other well-known classifiers as listed in Figure 5. Similar to the vanilla AdaBoost, it can be seen that other classifiers can achieve a high specificity; however, requires a significant sacrifice in sensitivity. Thus, the proposed algorithm provides much better low false negative rate guarantees, while being able to achieve a reasonable false alarm detection rate.

Table 2.

Performance comparison between the proposed algorithm and the vanilla AdaBoost

	AdaBoost with Reject Option		Vanilla AdaBoost
	131 weak learners	218 weak learners	131 weak learners	218 weak learners
Number of Samples	2318
Valid / Invalid Alarms	549 / 1769
Sensitivity	100.00%	99.27%	95.26%	93.44%
Specificity	9.38%	23.12%	38.78%	43.81%
Silenced Alarms	166	413	712	813
Total False Negative	0	4	26	36

Figure 5.

Number of alarms in different clinical categories for the top occurring physiologic monitoring alarms in the dataset.

6. Conclusions

In this paper, we presented a robust false SpO₂ alarms classifier based on the AdaBoost algorithm with reject option by allowing a third decision expressing doubt. Weighted outputs of each weak classifier are input to a softmax function that is optimized to satisfy a desired false negative rate upper bound while minimizing the false positive rate and indecision rate. Finally, we evaluated the proposed classifier on a dataset collected from the Children’s Hospital of Philadelphia and showed that the classifier is able to suppress 23.12% of false SpO₂ alarms without missing any clinically significant alarms. The results show significant improvements over the vanilla AdaBoost algorithm and suggest that an avenue for future work is to detect motion artifacts.