Abstract
Ziff and Stell (Kinetics of polymer gelation, J. Chem. Phys., 73 (1980), 3492–3499.) pioneered the study of kinetic models of polymer growth and gelation which involve differential equations that describe the temporal evolution of oligomer concentrations and in which gelation is manifest as a finite-time singularity. Here we present a systematic framework for studying post-gelation behavior of these and related models that allows inclusion of the effects of diffusion and other transport mechanisms as well as those of sources and sinks, and which enables determination of, among other things, the final structure of the gel under a variety of conditions.
Keywords: coagulation, gel mass, gel front, generating function, kinetic gelation, polymer diffusion
AMS Subject Classifications: 80A30 (chemical kinetics), 82C26 (dynamic and nonequilibrium phase transitions), 82D60 (polymers)
1 Introduction
In a seminal paper on polymer gelation, Ziff and Stell [19] introduced and analyzed a set of kinetic models of polymer growth and gelation. The polymers were assumed to be made up of identical monomers each with a prescribed number f of reactive sites. Polymer chains comprised of k monomer units, denoted by Ck and referred to as ‘k-mers’, could form by the combination of two smaller chains whose combined number of monomer units equaled k. Ordinary differential equations were prescribed for the dynamics of the concentration ck of k-mers. As is explained below, they defined the onset of gelation to occur when the second moment of the {ck} distribution became infinite, and this event was interpreted as the formation of an oligomer of infinite size. Using a generating-function approach they computed the gel time at which this occurred. They also considered three models for continued reactions after the time a gel forms, which differed in the types of reactions in which the gel was allowed to participate. In another paper [18], Ziff and co-workers considered further two of these models, and in particular, presented asymptotic analyses and scaling laws for various quantities near the gel time and in the long-time limit. Still, their discussion of the post-gelation behavior of the different models was limited in that they did not present a unified framework for studying the model variants.
In the current paper, we present a systematic framework for studying post-gelation behavior of the Ziff-Stell models that allows us to also include the effects of diffusion and other transport mechanisms as well as those of sources and sinks. By comparison with stochastic simulations of the same processes, we identify one of the post-gelation variants as being most physically relevant. The framework we present is extendable to other, more complex, polymerization and gelation systems. In a separate paper [5], we apply it to study the post-gelation behavior in a model of fibrin polymerization, branching, and gelation during blood clotting [4].
Ziff and Stell were among the first to analyze formation of a gel in mean-field kinetic models of polymerization (see also [11]). There is now an extensive literature on kinetic models of polymerization, reviewed in [6, 12, 17]. Probabilistic approaches to gelation are reviewed in [1] and relations between gelation and percolation are reviewed in [15]. For other discussions of post-gelation behavior, see [3, 16], and other discussions of the effect of diffusion on gel formation can be found in [2, 9, 10, 13, 14]. We used an extension of the Ziff-Stell models to study fibrin formation under flow [8].
2 The Ziff-Stell Models
The reactions that Ziff and Stell considered are
| (1) |
provided i ≠ j, and
| (2) |
Here, ki,j = kgrirj, where kg is the reaction rate between a pair of reaction sites, and rj = (f − 2)j + 2 is the number of reactive sites on a j-mer. The second reaction differs from mass action kinetics in that the rate of reaction is , rather than ki,i. Making the assumption that no loops or cycles are allowed in the oligomers, Ziff and Stell proposed the dynamic equations for their model of polymerization
| (3) |
where R is the total concentration of reactive sites. The first term on the right-hand-side describes the production of k-mers from two smaller oligomers and the second term describes the consumption of k-mers to form larger oligomers. To close this system, we give an equation for the evolution of R:
| (4) |
To motivate this equation, note that another quantity of interest is the concentration of reactive sites on (finite-sized) oligomers
| (5) |
If R(t) = Rs(t), it follows from Eq. (3) that R satisfies Eq. (4). In anticipation of there being reactive sites that are not on finite-sized oligomers, in which case R(t) ≠ Rs(t), we define Rg(t) = R(t) − Rs(t), the concentration of reactive sites in a gel.
Several moments of the oligomer distribution of interest are , and . M0 is the total concentration of molecules and M1 is the total mass (measured in monomer units) of polymer per unit volume. An interpretation of M2 is obtained by noting that
| (6) |
where pk ≡ (kck)/(M1) is the probability that a randomly chosen monomer is in one of the k-mers. Thus, M2/M1 is the average oligomer size (aka cluster size) with respect to the probability distribution pk. Let Y (t) = (f − 2)M2(t)+ 2M1(t). Then, as shown in the Appendix, as long as R(t) = Rs(t), the following equations hold:
| (7) |
and it follows that, provided f > 2, Y (t)→∞ and, consequently, M2(t)→∞ as t → tgel where
| (8) |
is called the ‘gel-time’. Sometimes the blow-up of M2(t) is interpreted as indicating the appearance of an infinite-size cluster. Below, we characterize tgel in a different way and give other interpretations of it. Eqs. (7) break down at time tgel and cannot be used to determine dynamics after this time. For the rest of the paper, we assume that concentrations are scaled by a characteristic concentration C and that time is scaled by , so that henceforth ck and t are nondimensional concentrations and time, respectively. Then, Eqs. (3) – (8) hold with kg set to 1.
Ziff and Stell introduced an alternative way to study the infinite set of ordinary differential equations (3) using a generating function g(t, z) defined by
| (9) |
Using Eq. (3), it is straightforward to show that g(t, z) satisfies the non-linear partial differential equation
| (10) |
Now make the change of variables
| (11) |
From Eqs. (4) and (10) it follows that W(z, t) satisfies the inviscid Burger’s equation
| (12) |
Eq. (12) and Eq. (4) form a closed system from which we can determine W(t, z) and R(t) and therefore g(t, z). The moments of the oligomer distribution and other quantities of interest can be calculated directly from g(t, z) and its z-derivatives evaluated at z = 1. The concentrations ck(t) can be obtained from g and its z-derivatives evaluated at z = 0. The one use we make of this second fact is to evaluate the monomer concentration c1. From Eq. (9), we find that
and for the case f = 3, we have r1 = 3 and gzzz|z=0 = 6c1. It follows that the concentration of monomer is
| (13) |
The concentration of reactive sites in finite-sized oligomers is
| (14) |
We define Rg(t) by
| (15) |
to be the concentration of reactive sites not contained in finite-size oligomers, that is, the concentration of reactive sites contained in the gel. We see that
| (16) |
so that, in terms of W and R, Rg(t) = W(t, 1), and Rs(t) = R(t) − W(t, 1). As described below, an alternative characterization of tgel is the time at which a jump-discontinuity in W(t, z) develops at z = 1, and this is also the earliest time at which Rg is nonzero.
We introduce the quantity θs(t) defined by
| (17) |
which is the total mass density (number of monomeric units per unit volume) contained in finite-sized oligomers. We denote by θ(t) the total mass density and by θg(t) = θ(t) − θs(t) the total mass density contained in the gel. For brevity, we refer to these quantities as the sol mass, the total mass, and the gel mass, respectively. Note that
| (18) |
which follows from gz(t, 1) = (f−2)θs(t)+2g(t, 1) and W(t, z) = zR(t) − gz(t, z). For a situation in which there is no source or sink of oligomers, the total mass θ(t) = θ(0), and θg(t) = θ(0) − θs(t). If there are sources or sinks of monomers (or other oligomers), an appropriate equation for the dynamics of θ(t) must be introduced (see below).
Now we focus on the particular situation in which only monomer exists at time t = 0, so c1(0) = m0 and ck(0) = 0 for k > 1. It follows from their definitions that R(0) = Rs(0) = m0r1 = m0f and W0(z) = W(0, z) = m0f(z − zf−1). Using the method of characteristics, the solution W(t, z) to Eq. (12) is given implicitly by the formula
| (19) |
from which we calculate that
| (20) |
Since for z0 such that , Wz(t, z) blows up at a finite time
| (21) |
which is the same blow-up time as specified by Eq. (8).
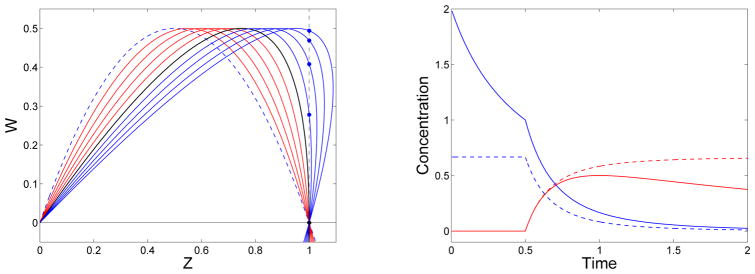
While the solution of the moment equations (7) cannot be continued past the time t = tg, that of the system comprised of Eqs. (4) and (12) can be. The left panel of Fig. 1 shows the solution W(t, z) of Eq. (12) obtained by the method of characteristics with and f = 3. For these parameter values, . We are interested in this solution for 0 ≤ z ≤ 1. The solution at z = 1 is multivalued for t > tg, but the branch of the curve W(t, z) starting at z = 0 and intersecting the line z = 1 above the z-axis is smooth. For the remainder of the paper we use W(t, 1) to refer to limz→1− W(t, z), the limiting value of W from the left along this branch. The right panel of Fig. 1 shows the reactive site concentrations and mass densities for the sol and gel as functions of t for the same parameters. We see sudden transitions in Rs and θs at t = tg, that almost all of the monomers are in the gel (not in finite-sized oligomers) by t = 2, and that the gel reactive site concentration first increases and then decreases tending eventually to 0.
Figure 1.
Left: Solution curves W(z, t) at selected times: At t = 0 (blue dashed), for t < tg (red), for t = tg (black), and for t > tg (blue). W(t, 1) for t > tg (blue star). Right: Reactive sites in sol Rs (blue) and in gel Rg (red). Mass in sol θs (blue-dashed) and in gel θg (red-dashed). f = 3, .
3 A Unified Framework
As we have seen, Eqs. (4) and (12) allow study of pre- and post-gelation behavior. Ziff and Stell presented two other variants of the kinetic gelation model. In this section we describe these models and, for each, present a pair of equations analogous to Eqs. (4) and (12) that allow study of their pre- and post-gelation behavior. To our knowledge, using these pairs of equations in this way has not been described in the literature.
The three kinetic gelation models that Ziff and Stell presented differ in what happens after gel time. For the model presented above, all reactive sites take part in reactions. For reasons given in their paper, Ziff and Stell refer to this as the Flory model. For the two variants, reactive sites in the gel (concentration Rg) either do not react at all or react with reactive sites in the sol but not with other reactive sites in the gel. The first of these they refer to as the Stockmayer model, and we regard it as uninteresting on physical grounds, because we see no reason that all gel reactive sites should be ignored. In contrast, for reasons we make clear below, we consider the model in which gel reacts only with the sol (referred to by Ziff and Stell only as the ‘third’ model) as the most interesting and physically relevant. We refer to the post-gel model in which gel reacts with both gel and sol as the GrGS model (this is the Flory model in Ziff and Stell’s terminology) and that in which gel reacts only with sol as the GrS model.
To derive a pair of equations, similar to Eqs. (12) and (4) above for the GrS model variant, note that the rate of disappearance of reactive sites in Eq. (4) can be written
with the individual terms in this sum corresponding, respectively, to reactions between sol oligomers, between a sol oligomer and the gel, or between different parts of the gel. For the GrS model, we drop the term in the evolution equation for R(t), while the g equation remains the same. Thus Eq. (4) is replaced by
| (22) |
For the GrS model, we make the same change of variables W = zR − gz as above, and find that W(z, t) satisfies the equation
| (23) |
Recalling that Rg(t) = W(t, 1), we see that the pair of equations, Eqs. (22) and (23) form a closed system for the GrS model. The system has the feature that its equations are nonlocal; the value of W at z = 1 enters into both of the differential equations in each system. Although we do not study it further, the Stockmayer model can be written as Rt = −(R − W(1, t))2 and Wt +WWz = zW(1, t)(2R − W(1, t)) and, like the GrS model, it is nonlocal.
For convenience, we combine the equations for the GrGS and GrS models into one set of equations
| (24) |
| (25) |
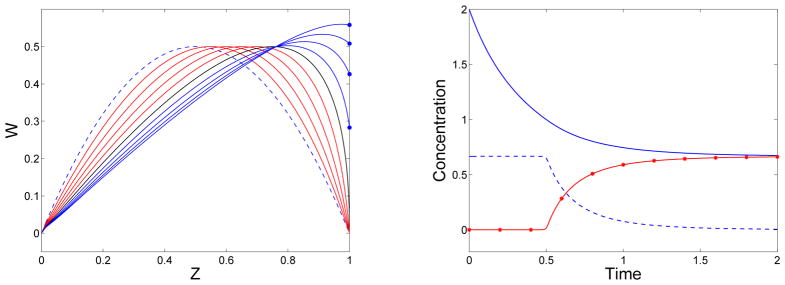
Here, χ = 0 for the GrGS model in which gel reactive sites interact with both gel and sol reactive sites, and χ = 1 for the GrS model in which gel reactive sites interact only with those in the sol. Fig. 2 shows numerical solutions with χ = 1 for W(t, z), the reactive site concentrations in the sol and gel, and the mass of polymeric material in the sol and gel. These solutions were computed using the second-order upwind method described in the Appendix. Several features of the solution are different from those when χ = 0. Firstly, W can achieve values higher than its maximum initial value. Secondly, the gel reactive site concentration does not vanish as t→∞.
Figure 2.
Left: Solution curves W(t, z) at selected times for model in which gel reacts only with sol (χ = 1): At t = 0 (blue dashed), for t < tg (red), for t = tg (black), and for t > tg (blue). W(t, 1) for t > tg (blue star). Right: For χ = 1, reactive sites in sol Rs (blue) and in gel Rg (red). Mass in sol θs (blue-dashed) and in gel θg (red-stars). f = 3, .
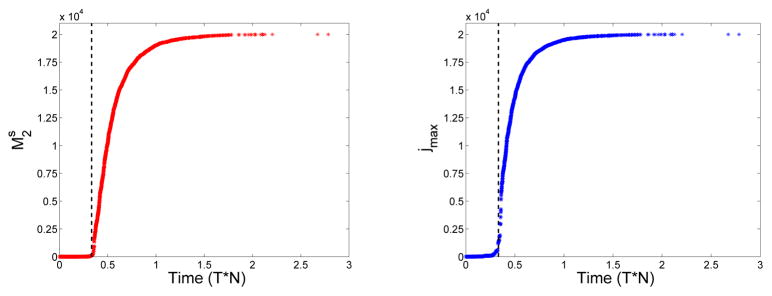
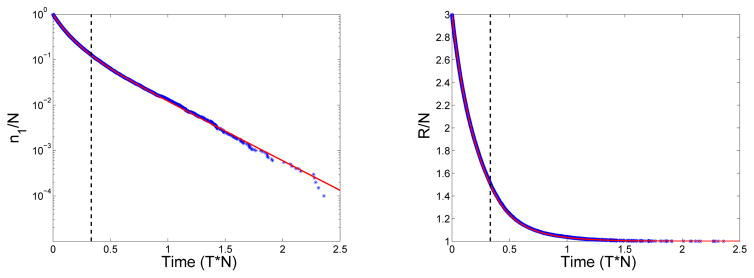
Of the three post-gelation time models considered by Ziff and Stell, the one we view as most reasonable is the GrS model, in which reactive sites in the gel react only with reactive sites in the sol. Only this model produces results that agree with those from stochastic simulations that start with a large, but finite, number of monomers. In the stochastic simulation of the Ziff-Stell model, the probability that a j-mer reacts with a k-mer (k ≠ j) during an infinitesimal time interval dt is rjnjrknkdt, where rj is defined above, and nj is the number of j-mer molecules. Similarly, the probability that a j-mer reacts with another j-mer is . We implemented the simulation using the Gillespie algorithm [7]. In the stochastic simulations, the second moment of the oligomer distribution cannot ‘blow-up’ because there are only a finite number of monomers in total; but, as shown in Fig. 3, the second moment does undergo a sharp transition at a time that agrees well with the gel time predicted by the deterministic continuum equations (3)–(4). At the same time, the size of the largest existing oligomer begins to grow very rapidly. Both before and after that time, the monomer concentration and reactive-site concentration from the stochastic simulations agree well with those from the GrS model, as shown in Fig. 4. In the GrS model, the gel, like all finite-size oligomers, cannot react with itself, i.e., no cycles are allowed to form. This model behaves very similarly to the discrete stochastic model with the gel reactive sites in the GrS model corresponding to those on the large oligomers in the stochastic model. In the stochastic model and the GrS model the reactive site concentration asymptotes to a nonzero level. In contrast, the reactive site concentration in the GrGS model decays with time as sites on the gel are lost because of gel-gel reactions, see Fig. 1.
Figure 3.
Left: (Asterisks) Second moment of oligomer size distribution vs. time from a stochastic simulation with N monomers, , where nj is the number of j-mers. N = 20000 and f = 3. Right: (Asterisks) Largest oligomer size vs. time from the same stochastic simulation. (Dashed Lines) Time of gel formation from the deterministic model for initial monomer concentration c1(0) = 1 with f = 3.
Figure 4.
Left: (Blue asterisks) Monomer fraction n1/N vs. time from a stochastic simulation with N monomers and (Red curve) monomer concentration c1 calculated using Eq. (13) from the deterministic GrS model. (Dashed Line) Time of gel formation from deterministic model. Right: (Blue asterisks) Concentration of reactive sites, (Σj rjnj)/N vs. time from the stochastic simulation and (Red curve) reactive site concentration R(t) from the deterministic GrS model. N = 20000, f = 3, n1(0) = N, and c1(0) = 1.
4 Diffusion and Sources
The models discussed above are based on the assumption that the oligomer concentrations are spatially uniform and that an initial supply of monomer is the only material from which the oligomers are built. In many situations, these assumptions are too restrictive. For example, monomers may be produced in part of a domain and they and the oligomers built from them may move by diffusion (e.g., see [8]). It is straightforward to add these extensions to the original systems of differential equations for the oligomer and reactive site concentrations. Suppose k-mers diffuse with diffusion coefficient Dk and that monomers are supplied at a rate (per unit volume) S1(x, t), where x denotes a spatial position. Then, the appropriate generalization of the Ziff-Stell equations is
| (26) |
where δk,1 is the Kronecker delta function and Δ is the Laplacian operator with respect to the spatial variable x. Because physical time has been scaled by , where kg is the polymerization second-order rate constant, to give the non-dimensional time variable t used here, Dk has dimensions of squared length and S1 is dimensionless. The physical diffusion coefficient and monomer supply rate are Dkkg and S1kgC, respectively.
We assume that gel does not diffuse. The analysis for the spatially-homogeneous system extends to this system if Dk = D for all k. We define the generating function by
| (27) |
and it follows easily that g satisfies the equation
| (28) |
where we have used that r1 = f. We assume that the reactive site concentration R(x, t) obeys the equation
| (29) |
Here, the diffusion term is DΔRs, rather than DΔR, because we have assumed that only finite-sized oligomers, and not gel, diffuse. We make a similar change of variables as in the spatially-homogeneous case by introducing a function W(x, t, z) defined by the relation
| (30) |
Then, since the concentration of reactive sites in finite-sized oligomers is Rs(x, t) = gz(x, t, 1), we have that the concentration of reactive sites in the gel Rg(x, t) = R(x, t) − Rs(x, t) is given by
| (31) |
as before. Making the change of variables in Eqs. (28)–(29), we obtain the system
| (32) |
It may be a more reasonable assumption about oligomer diffusion that the diffusion coefficient Dk should decrease with k. In general, the assumption that all of the Dk are different makes the generating function approach intractable. It is plausible that the diffusion coefficient decreases most rapidly as k increases for small values of k, since this corresponds to large relative changes in the oligomer size, and decreases much more slowly with k for large k. This can be approximated by assuming distinct diffusion coefficients for a small number of small oligomers, e.g., monomers and dimers, and a uniform smaller diffusion coefficient for all larger oligomers. With this approximation, the generating function approach is still useful. Suppose monomers have diffusion coefficient D1, dimers have diffusion coefficient D2, and larger oligomers have diffusion coefficient D. Then, for k ≥ 3, Eq. (26) describes the dynamics of ck(x, t), while for k = 1 and k = 2, we have the equations
| (33) |
and
| (34) |
Using these equations and Eq. (26), we find that the generating function g(x, t, z) satisifies that equation
| (35) |
and that the reactive site concentration equation is
| (36) |
Making the usual change of variables, W(x, t, z) = zR(x, t) − g(x, t, z), we find that W satisfies the equation
| (37) |
The system of equations (33), (34), (36), and (37) forms a closed system for the unknowns c1, c2, W, and R. Clearly, this approach generalizes to allow distinct diffusion coefficients for any finite set of oligomers.
To compute the total mass of the finite-sized oligomers θs, we use Eq. (18) as before. The evolution of the total mass θ(x, t) function must account for the diffusion of finite-sized oligomers
| (38) |
As usual, θg(x, t) = θ(x, t) − θs(x, t) gives the mass of the gel.
For the remainder of this paper, we consider the case of one spatial dimension and replace the operator DΔ above by . For polymerization reactions and diffusion on a finite interval a ≤ x ≤ b, boundary conditions are required at x = a and x = b. We are most interested in situations in which either all of the monomer is made available in the interior of the domain, or monomer enters the domain across the boundary at x = a. The boundary conditions on the oligomer concentrations are thus
| (39) |
Suppose monomers have diffusion coefficient D1 and all other oligomers have diffusion coefficient D. Then, from the definitions of g(x, t, z) and Rs(x, t), and the relation W(x, t, z) = zR(x, t) − gz(x, t, z), it follows that
| (40) |
| (41) |
and
| (42) |
At x = b, and . If D1 > 0 and D = 0, no boundary conditions are needed for Rs and W at x = a or x = b.
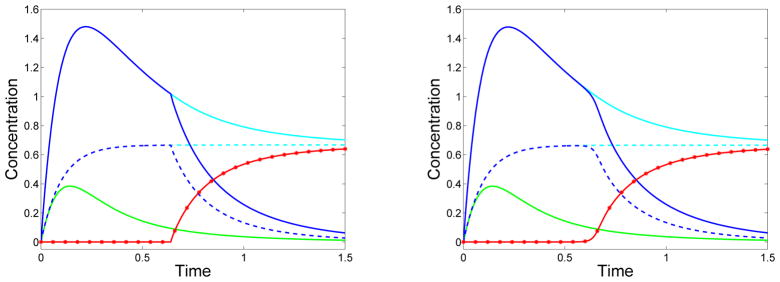
Fig. 5 shows solutions for a spatially-uniform source S1(t) = Smλ exp(−λt) with Sm = 1 and λ = 10 for the GrS model (χ = 1) generated in two distinct ways. One method of solving the system is to use the Method of Characteristics, in which the equations are recast into characteristic form
Figure 5.
Left: Solutions generated using the Method of Characteristics. Right: Solutions generated using the one-sided Beam-Warming finite-difference formula. Monomer is supplied at a rate S1(t) = Smλ exp(− λt). Monomer concentration c1(t) (solid green), total mass θ(t) (dashed cyan), sol mass θs(t) (dashed blue), gel mass θg(t) (red asterisks), total reactive site concentration R(t) (solid cyan), sol reactive site concentration Rs(t) (solid blue), gel reactive site concentration Rg(t) (solid red). f = 3, , λ = 10.
| (43) |
for j = 1, …,Nz, and
| (44) |
and then these equations are solved in time for a set of discrete initial values zj(0) of z. In each timestep, a spline is fit to the values of W(zj(t), t) at locations zj(t) ≤ 1 and evaluated at z = 1 to give Rg(t) = W(1, t). The second method uses the one-sided Beam-Warming discretization described in Appendix B. The two methods produce results (Fig. 5) that are almost indistinguishable. The only apparent difference is a slight smoothing of the transition from no gel to gel with the Beam-Warming scheme compared to that with the Method of Characteristics.
For problems with spatial, that is x-dependent, variations in the oligomer concentrations and transport by diffusion, we use a finite difference discretization of the equations in both z and x. The Method of Characteristics has the problem that characteristics starting at a particular value of z but for different x values generally move at different speeds in the z direction, making it difficult to approximate the x-diffusion operator. For the finite-difference discretization we combine the Beam-Warming discretization in z described in Appendix B with a standard second-order central difference approximation to the operator. Flux boundary conditions, e.g., Eq. (42), are discretized using a ghost cell at each x-boundary and a central difference approximation to at the grid points on the boundary. In the x-direction we use a uniform mesh spacing hx, while in the z-direction, we use a variable mesh spacing hz with smaller values of hz near z = 1.
4.1 Initial monomer supply
Results from a simulation of Eqs. (33), (36), and (37) with boundary conditions Eqs. (40)-(42), with Dk = D = 0.01 for all k, are shown in Fig. 6. The equations are solved on the x-interval [a, b] = [−L,L] for L = 0.5 with no-flux boundary conditions on all quantities at x = ±L, and with an initial distribution of monomers
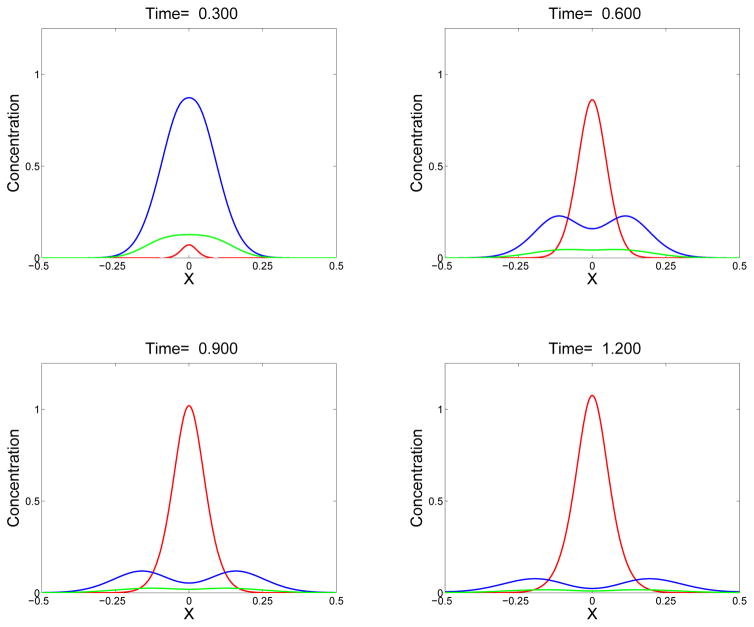
Figure 6.
Sequence of snapshots showing sol mass θs (blue), gel mass θg (red), and monomer concentration c1 (green) at the indicated times. Gel first appears shortly before t = 0.3. Simulations start with c1(x, 0) given by Eq. (45) with ε = 0.1 and Si = 1. D = D1 = 0.01.
| (45) |
with ε = 0.1 and Si = 1. In Fig. 6a, we see the start of gel formation centered at x = 0, and that the monomer and oligomer mass have spread from their initial support in [−0.1, 0.1] and dropped from their peak value of 1 at x = 0 at t = 0. While, c1(x, 0) = θs(x, 0), the monomer concentration at t > 0 is lower than the oligomer mass because many of the original monomers have been incorporated into larger oligomers. At this time, the net diffusive motion of oligomers is everywhere away from the domain center. By time t = 0.6, see Fig. 6b, the gel mass θg has increased substantially in the center of the domain and remains zero outside of a finite interval [−xg(t), xg(t)]. The oligomer (or sol) mass θs is now lower in the center than further toward the domain boundaries because of the incorporation of more mass into the gel. Thus, in portions of the domain, diffusion carries oligomers back toward the center of the domain from which the monomers comprising them originally came. As time progresses, the gel width grows, but more slowly than the oligomers diffuse outward, and the maximum gel mass density grows. At all times, the gel mass is confined to a proper subinterval of the domain. The total mass of sol and gel is constant throughout the simulation.
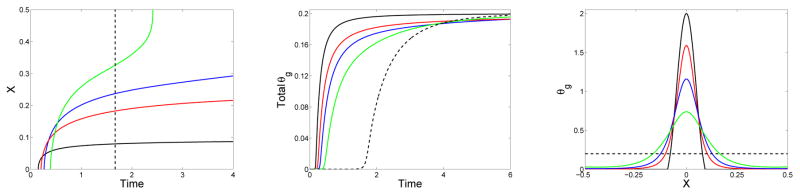
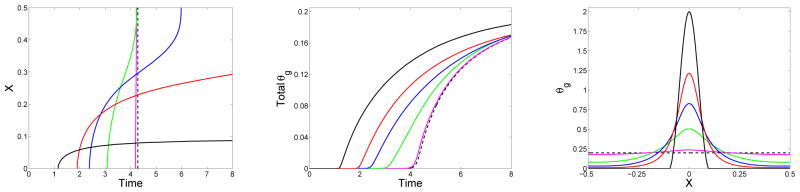
The progression of the gel front with time is shown in the left panel of Fig. 7. Here, the (approximate) edge of the gel at each time t is defined to be the point x where Rg(x, t) = 0.01. The figure shows the gel front for four simulations, all starting with the initial monomer distribution defined in Eq. (45). The simulations differ only in the value of the diffusion coefficient D =0, 0.005, 0.01, or 0.02. For all of these values of D, the gel first forms at x = 0 because the initial monomer concentration is highest at that location. Gelation occurs at x = 0 earlier for smaller values of D. For the simulation with D = 0, the spread of the gel is determined solely by how long it takes for the characteristics along each line x =constant to intersect at z = 1. Since it takes longer for this to happen for x with lower, but positive, values of c1(x, 0), the gel front progressively moves outward toward the edge of the initial monomer distribution at x = 0.1. For positive values of D, the gel grows to fill the entire domain. This occurs for D = 0.02 by t = 4, and occurs for D = 0.01 and D = 0.005 at later times (not shown). With D > 0, the onset of gelation at x = 0 is delayed compared to that with D = 0, more so for larger values of D, because the spread of oligomers in the x-direction reduces the rate at which very large oligomers and then gel form at x = 0. In contrast, the rate of gelation at locations remote from the initial support of the monomer concentration is greater with larger values of D. For each D, the propagation speed of the gel front decreases with t, until the gel front approaches the boundary where the no-flux boundary condition for the oligomer concentrations leads to faster accumulation of large oligomers and an increase in the front speed. The black line in the figure shows the gel time for the situation in which the same total amount of monomer is distributed uniformly in the domain at t = 0.
Figure 7.
Effect of diffusivity for monomer supplied at t = 0: (Left) Location of gel front xg(t) vs. time, (middle) time course of total gelation , and (right) final gel mass distribution (at t = 10) vs. x for simulations with initial monomer supply. Solid curves are for simulations which start with c1(x, 0) given by Eq. (45) with ε = 0.1 and Si = 1. D = D1 = 0 (black), D = D1 = 0.005 (red), D = D1 = 0.01 (blue), D = D1 = 0.02 (green). The dashed black lines are for a simulation with uniform initial monomer concentration c1(x, 0) = 0.2.
The middle panel shows how the total gel mass varies with t. This quantity begins rising earlier and early on grows more rapidly the smaller the diffusion coefficient. For each value of D the curve levels off, with the growth rate becoming larger for the smaller diffusivity cases at later times. The total gel mass goes to 0.1 in all of these simulations as t→∞. For all finite values of D, the diffusion time is slow compared to the instantaneous injection of monomer at t = 0, and the dynamics are determined by the value of D.
The right panel of Fig. 7 shows the final configuration of the gel for the same simulations. For any D > 0, the gel eventually occupies the entire domain, but the final distribution of gel mass is broader with larger values of the diffusion coefficient. The extreme case is that in which the monomers are initially uniformly distributed (corresponding to D →∞) in which case the final gel is, of course, also uniform in x.
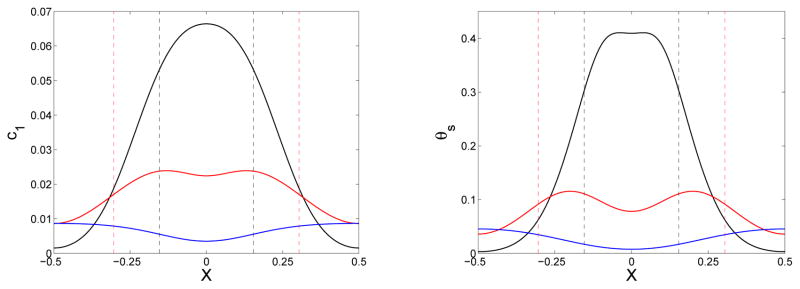
Fig. 8 shows the monomer distribution and sol mass distribution at several times for a simulation with D = D1 = 0.02. It reinforces the observation made above that the direction of oligomer movement changes during the course of gel development. At t = 0.5, the diffusive flux of monomer is everywhere outward from the domain center toward larger values of |x|. At t = 1.0, the direction of monomer flux has reversed near x = 0, but is unchanged for larger values of |x|. By t = 2.5, the diffusive flux of monomer is everywhere toward the center. Thus, the incorporation of oligomers into the gel in the center of the domain leads to ‘back diffusion’ of oligomers toward the center and further growth of the gel there.
Figure 8.
Plots of c1(x, t) (left) and θs(x, t) (right) at t = 0.5 (black), 1.0 (red), and 2.5 (blue).Note the reversal of the slope of the c1 and θs curves at later times. Dashed lines indicate location of gel front at t = 0.5 (black) and t = 1.0 (red). The gel front has reached x = 0.5 by t = 2.5. The simulations start with c1(x, 0) given by Eq. (45) with ε = 0.1 and Si = 1. D = D1 = 0.02.
4.2 Monomer source
If a fixed amount of monomer is introduced gradually through a source rather than all being present at t = 0, the spatial distribution of the source along with the relative rates at which the monomer is introduced and at which oligomers diffuse influence the propagation of the gel front, the rate of gel production, and the final distribution of the gel. We consider a source term of the form
| (46) |
for ε = 0.1 in the spatial domain −L ≤ x ≤ L with L = 0.5. For a situation in which Dk = D for all k, the (nondimensional) diffusion time scale is , and the (nondimensional) source time scale is . Figs. (9) and (10) show results from simulations in which λ was held fixed and D varied, or D was held fixed and λ varied.
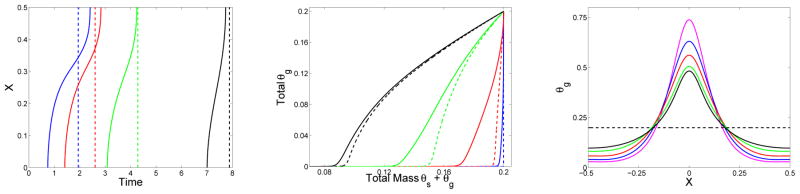
Figure 9.
Effect of diffusivity for monomer supplied over time: (Left) Location of gel front xg(t) vs. time, (middle) time course of total gelation , and (right) final gel mass distribution (at t = 24) vs. x (right) for simulations which start with ck(x, 0) = 0 and have a source of the form in Eq. (46) with Sm = 2, λ = 1. D = D1 = 0.00 (black), D = D1 = 0.005 (red), D = D1 = 0.01 (blue), D = D1 = 0.02 (green), and D = D1 = 0.08 (magenta). Also shown are the results for a spatially uniform source with the same rate constant λ and with the same total amount of monomer (dashed black).
Figure 10.
Effect of rate of monomer supply: (Left) Location of gel front xg(t) vs. time, (middle) total gel mass vs. total mass , and (right), final gel mass distribution (at t = 10) vs. x for simulations with D = D1 = 0.02 and source term Eq. (46) with Sm = 2 and various values of λ (solid curves), or spatially-uniform source term (dashed lines). (blue), (red), (green), (black). Final gel mass distribution vs. x (right) for an initial monomer supply Eq. (45) with Si = 2 (magenta) or for a spatially-uniform source with the same total amount of monomer (dashed black).
Fig. 9 shows results for simulations with source term Eq. (46) with λ = 1 and Sm = 2 for several values of the diffusion coefficients D = D1 ranging from 0 to 0.02. The left panel shows that the smaller the diffusion coefficient, the earlier gel forms near x = 0 and the later it forms for x near the domain boundary. The right panel shows that the final gel mass distribution is more peaked (right panel) for smaller values of D. The middle panel shows the growth in time of the total gel mass, i.e., the integral of θg(x, t) with respect to x. We see that the maximal gel mass growth rate (i.e., the maximum slope of each curve) varies non-monotonically as D increases, first decreasing and then rising (middle panel). The maximal growth rate occurs for the largest diffusion coefficient (D = 0.08). For this diffusion coefficient (magenta curves), the gel forms at close to the same time for all x, similar to what happens with a spatially-uniform source, and the widespread gelation results in the faster total mass growth rate. In this case, the final gel mass profile is close to uniform as well (dashed black curves).
Only for the D = 0.08 case is the diffusion time (≈ 1.5) scale approximately the same as that for the source, and in this case, the behavior is almost the same as if the monomer were supplied uniformly in space. For smaller values of D, diffusion is slower than the source, the gel front speeds vary in time, and the final mass distribution is significantly higher near x = 0 then for large values of |x|. Comparing results in the current figure with those in Fig. 7, we see that for each diffusion coefficient the gel forms much earlier at x = 0 when all of the monomer is supplied at the start of the simulation. As a consequence, there is less oligomer to diffuse to higher values of |x|, and so the gel front propagates to large |x| much more slowly in that case for each value of D, for example compare the green curves for D = D1 = 0.02 in the left panels of the two figures. For the same reason, the final gel mass is greater near x = 0 when all monomer is supplied initially.
Fig. 10 shows results for simulations with λ ranging between and , and for both the case of a source term as in Eq. (46) with D = D1 = 0.02, Sm = 2 and that of a spatially uniform source with Sm = 2. All of these simulations introduce the same total amount of monomer. Two types of comparison are of interest. For one, we fix the spatial variation of the source term and look at behaviors for different values of λ. For the other, we fix a value of λ and look at the differences between the case of a spatially-varying source and a spatially uniform one. The solid curves in the left panel show that gelation occurs earlier for each x for higher supply rates (larger λ). We see also that the gel front speed is non-monotone for each supply rate with more variation in the speed when the supply rate is sufficiently high that the source time scale is significantly shorter than the diffusive time scale. From the dashed lines in the left panel, we see that gelation at x = 0 occurs later for the spatially-uniform source than for the spatially-varying source concentrated near x = 0. The relative time of gelation for the two types of sources may switch for large values of x (blue and red curves), or not (green and black curves), depending on the relative rates of monomer supply and diffusion. The right panel of the figure shows that the faster the supply of monomer near x = 0, the more peaked is the final gel mass distribution. Again, for a fixed diffusion coefficient, the faster supply leads to greater buildup of oligomers and to earlier gelation, which ‘freezes’ mass near x = 0. With slower supply, gelation happens later giving the oligomers time to diffuse to larger |x| producing a more spread out gel. The case of infinite supply rate (i.e. an initial source) is shown in the figure for comparison.
In the middle panel of Fig. 10 we show curves of gel mass and total mass parameterized by t for each of the simulations. One behavior of interest revealed by these plots is that for slower source rates, the gel forms ‘sooner’ in terms of how much polymer mass has been injected, ranging from gelation when over 95% of the total mass has been injected for the fastest source rate to about 45% for the slowest one. The panel also shows that for each source rate, less mass was injected when gelation occurred for sources concentrated near x = 0 than in the spatially-uniform case. Comparing the concentrated source with the spatially-uniform one, we see two distinct behaviors. For the fastest and slowest source rates, there is little difference in the progression of gel mass with the cumulative injected mass for the two spatial source distributions. In contrast, for the intermediate source rates, substantially more mass must be injected in the spatially-uniform case to initiate gelation than in the concentrated case.
4.3 Other results
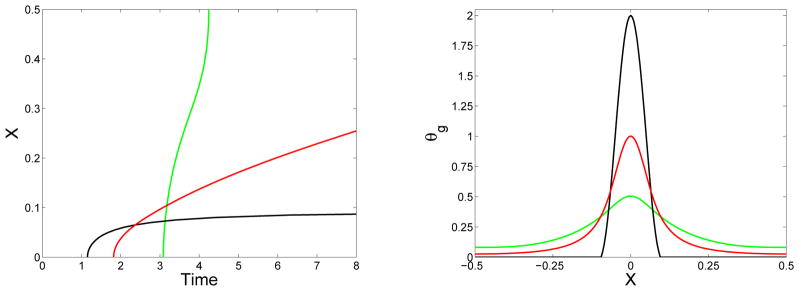
In Fig. 11 we show some results from simulations in which the source term was the same but the monomer and oligomer diffusion coefficients might differ. The simulations were run with D = D1 = 0.02, D = D1 = 0, and D = 0 and D1 = 0.02. The different pairs of diffusion coefficients produced substantially different patterns of gel front propagation and different final gel mass distributions. The sets of results for the cases D = D1 = 0.02 and D1 = 0.02 and D = 0 presumably bracket the results one would obtain with D1 = 0.02 and Dk a decreasing function of k for k ≥ 2.
Figure 11.
Effect of distinct monomer diffusivity: (Left) Location of gel front xg(t) vs. time and (right) final gel mass distribution (at t = 24) vs. x for simulations with source term Eq. (46) with Sm = 2 and , ε = 0.1, and D = D1 = 0.02 (green), D = D1 = 0 (black), and D = 0 and D1 = 0.02 (red).
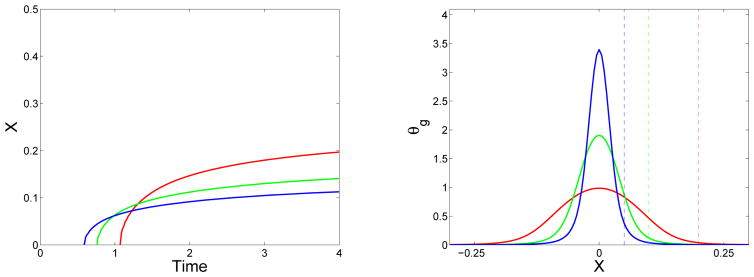
For all of the spatial simulations shown so far, the spatial support of the initial monomer supply or the source term was the same. In Fig. 12, three simulations are shown for which the diffusion coefficients D = D1 and the source rates λ were the same. The time course of total (integrated over space) mass injection is the same for the three simulations, but the width of the source terms is different. With a narrower source and therefore greater source rate (locally near x = 0), gelation occurs earlier and the final gel mass distribution is narrower and higher. The relative magnitude of the peak in the final gel mass distribution is not quite as large as the relative magnitude in the peak of the source distribution because the higher and narrower source leads to more rapid diffusion of oligomer away from the center of the source.
Figure 12.
Effect of monomer source width: (Left) Location of gel front xg(t) vs. time and (right) final gel mass distribution (at t = 24) vs. x for simulations with D = D1 = 0.001, source term Eq. (46) with Sm = 2 and λ = 1, and with support widths ε = 0.05 (blue), ε = 0.1 (green), and ε = 0.2 (red). In right panel, dashed lines show widths of source terms.
5 Discussion
In this paper, we have revisited the polymerization models studied by Ziff and Stell [19], and have introduced a systematic framework for studying these and related models both prior to gelation and after gelation. In their basic form, the models are kinetic descriptions of polymerization in which the time-evolution of the concentrations of oligomers with k subunits, ck(t), as well as the concentration of available reactive sites, R(t), are governed by ordinary differential equations Eqs. (3) and (4) or (25). Following Ziff and Stell, we introduce a generating function g(t, z) defined by Eq. (9) and then make a change of variables W(t, z) = zR(z) − gz(t, z). The dynamics of the polymer system are then completely determined by an advection-reaction partial differential equation (12) or (24) for W and the ordinary differential equation for R (along with initial conditions). The advection of W toward larger values of z ≤ 1 corresponds to the progression of polymerization toward larger oligomers.
Gelation occurs when the characteristic curves for W first intersect, and this happens at a finite time tgel with the singularity forming at z = 1. This event coincides with the blow-up of the second moment of the oligomer distribution, which is often interpreted as indicating the appearance of an infinite-size oligomer, and with the beginning of disappearance of mass and reactive sites from the finite-size oligomers. A singularity in W exists for all t ≥ tgel, but the branch of the graph of W(t, z) that connects z = 0 with z = 1 is smooth for z < 1. It can be computed with a numerical scheme, e.g., the Method of Characteristics or a Beam-Warming finite-difference method, that uses information only from the interval 0 ≤ z < 1 and accounts for the direction of advection appropriately. The limiting value of W as z → 1− is the concentration of available reactive sites in the gel Rg(t) and is known immediately provided W(t, z) for 0 ≤ z < 1 is known. The total mass of the finite-sized oligomers can also be computed by quadrature if the function W(t, z) is known for these z, and the mass of the gel can then be inferred provided the total mass of the system is computed. Different assumptions about with which species the gel reactive sites react lead to somewhat different equations, but in all cases, the dynamics before and after gelation are determined by the differential equations for W(t, z) and R(t) and the relationship Rg(t) = W(t, 1−). In general, the equations for W and R are coupled and nonlocal because of the presence of Rg(t) in them.
Ziff and Stell considered three reaction scenarios after gelation: (1) Reactive sites in the gel react with reactive sites on finite-sized oligomers and in the gel; (2) Reactive sites in the gel do not react at all; and (3) Reactive sites in the gel react only with reactive sites on finite-sized oligomers. We compared the predictions of the deterministic Ziff-Stell models with those from a direct stochastic simulation of the reaction system (1)–(2) using the Gillespie method. While the finite-size stochastic simulation could not produce a gel, there was a sharp transition in the value of the second moment of the oligomer distribution and in the size of the largest oligomer present in the system at the gelation time predicted by the deterministic models. After this transition, the monomer concentration and the reactive site concentration in the stochastic simulation matched those from the third of the Ziff-Stell scenarios. In effect, the large oligomers in the stochastic simulations behaved like the gel in that scenario. Because of this agreement, most of the simulations of the Ziff-Stell model that we carried out were done under the third scenario’s assumption using the model we referred to above as the GrS model.
Our framework for studying gelation extends readily to the spatially-nonuniform case in which oligomers move in space (in this paper we restrict our consideration to diffusive movement) and in which there may be source terms. The basis for the approach is then the partial differential equations (32) for W(x, t, z) and R(x, t) in the case that all oligomers have the same diffusion coefficient. Gelation occurs at spatial location x at the time tgel(x) when the z-characteristics along the line x constant first intersect at z = 1. The timing of gelation at x is, of course, influenced by diffusion because it affects the spatial distribution of oligomers, but note that there is no diffusion of W in x along z = 1 so there is no propagation of the singularity by diffusion along that line. So the effect of diffusion is limited to z < 1, but by altering the values of W(x, t, z), it alters the speed with which W(x, t, z) advects in z and therefore the speed with which oligomerization and gelation occur at each x. As in the spatially-uniform case, there is a smooth branch of the solution W(x, t, z) emanating from z = 0 and connecting to z = 1. A variant of the model in which the monomer diffusion coefficient differs from that of larger oligomers involves an additional partial differential equation for the monomer concentration and appropriate changes in the equations for W and R as given in Eqs. (36) and (37). We performed simulations of the spatial models in one dimension, using an algorithm that combines our Beam-Warming method in z with standard finite-difference approximations of differential operators in x.
The simulations either began with an initial distribution of monomers or introduced the same total quantity of monomers through a source term with an exponentially-decaying supply rate. The introduction of monomers was either spatially uniform or according to a bell-shaped distribution with a finite support centered at the domain center x = 0. The exponential supply rate λ was varied in some of the simulations and the oligomer diffusion coefficient was varied in other simulations. We tracked the location of the gel front as a function of time and the time course of the total mass of gel, and we computed the final spatial distribution of the gel mass under these different circumstances. The system’s behavior was influenced by the relative size of the non-dimensional diffusion and source time scales, but the ratio of these time scales does not fully characterize the system, as examination of the non-dimensional equations makes clear.
With positive diffusion coefficients and a non-uniform source concentrated near x = 0, the speed of the gel front was non-monotonic; fast for x near 0, slower for intermediate values of |x|, and then fast again as the no-flux boundary conditions caused the accumulation of oligomers near the boundary and led to faster gelation there. For a given supply rate, gelation happened earlier near x = 0 for smaller values of the diffusion coefficient and so the gel front moved from x = 0 earlier for small values of D. For larger values of D, once gelation started, the gel front propagated away from x = 0 more quickly and crossed the the gel front curves for smaller D. The final gel mass distributions had higher peaks near x = 0 and dropped off more quickly with |x| for smaller values of D. An interesting observation was the role of ‘back-diffusion’, particularly evident for larger values of D. Monomers introduced near the domain center initially diffused toward the boundary, but some of them later diffused back toward the center (either as monomers or part of larger oligomers) as gelation there consumed oligomers and reversed the direction of the concentration gradients.
The most important contribution of this paper is the development of a systematic framework for studying polymerization up to and beyond the time that a gel forms enabling us to determine, among other things, the final structure of the gel. While we demonstrated it for the relatively simple polymerization models studied by Ziff and Stell, the framework extends to more complicated models. In particular, we have applied it to our model of fibrin polymerization with branching in which both bi-molecular oligomer reactions (as in the Ziff-Stell models) and tri-molecular branch forming reactions occur and from which we compute the evolution of the gel mass distribution and the evolution of the distribution of branch points within the gel. This work will be described in a separate paper.
6 Appendix
A: Moment Equations
Note that replacing t by kgt eliminates the factor of kg in Eqs. (3–4). We calculate the rate of change of the first moment M1(t) = Σk kck.
| (47) |
So, as long as R(t) = Rs(t), M1(t) is constant. For the second moment,
| (48) |
Again, as long as R(t) = Rs(t),
| (49) |
Letting Y (t) = (f − 2)M2(t) + 2M1(t), it follows that as long as R(t) = Rs(t),
| (50) |
Hence, returning to the original time variable
| (51) |
and we see that Y (t)→∞ as t → tg ≡ 1/((f − 2)kgY (0)).
B: Beam-Warming Scheme
Consider the equation
| (52) |
We know that Wz develops a singularity at z = 1 at t = tg, but is smooth for 0 ≤ z < 1 for all t, and the branch starting from z = 0 is smooth for 0 ≤ z ≤ 1 for t < tg and t > tg. We therefore choose to discretize the above equation using a one-sided Beam-Warming type scheme, which we now derive.
| (53) |
| (54) |
Hence,
| (55) |
We approximate f(W)z at zj with a one-sided second order finite-difference quotient and we approximate (((f′ (W))2Wz)z) at zj with the usual approximation to a variable-coefficient diffusion term, but evaluated at zj−1. This gives an O(h) error for this quantity, but it is multiplied by k2, and so the overall scheme is still second-order. In the spatial discretization, we also allow for the spatial step size to vary hj = zj − zj−1, with z0 = 0. Let αj = hj/(hj−1(hj + hj−1)), βj = −(hj +hj−1)/(hj−1hj), and γj = −αj −βj, and make the approximation,
| (56) |
Note that if hj = h for all j, then αj = 1/(2h), βj = −4/(2h), and γj = 3/(2h).
The approximation to the diffusion term is
| (57) |
Here, , and in actual calculations, we use the approximation
| (58) |
The Beam-Warming scheme was validated by comparison with an analytic solution of Eqs. (24)–(25) in the case χ = 0 and by comparison with numerical solutions generated by the Method of Characteristics in the case χ = 1.
Footnotes
Version of March 18, 2015. This work was supported, in part, by NSF grant DMS-1160432 and NIH grant R01GM090203-04.
References
- 1.Aldous DJ. Deterministic and stochastic models for coalescence (aggregation, coagulation): Review of the mean-field theory for probabalists. Bernouilli. 1999;5:3–48. [Google Scholar]
- 2.Babovsky D. Gelation of stochastic diffusion-coagulation systems. Physica D. 2006;222:54–62. [Google Scholar]
- 3.Bak TA, Heilman OJ. Post-gelation solutions to Smoluchowski’s coagulation equation. J Phys A: Math Gen. 1994;27:4203–9. [Google Scholar]
- 4.Fogelson AL, Keener JP. Toward an understanding of fibrin branching structure. Phys Rev E. 2010;81:051922. doi: 10.1103/PhysRevE.81.051922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fogelson AL, Keener JP. Development of fibrin gel branch structure before and after gelation. in preparation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Galina H, Lechowicz JB. Mean-field kinetic modeling of polymerization: The Smoluchowski Coagulation Equation. Advances in Polymer Science. 1998;137:137–172. [Google Scholar]
- 7.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 8.Guy RD, Fogelson AL, Keener JP. Fibrin gel formation in a shear flow. Math Med Biol. 2007;24:111–130. doi: 10.1093/imammb/dql022. [DOI] [PubMed] [Google Scholar]
- 9.Herrero MA, Velazquez JJL, Wrzosek D. Sol-gel transition in a coagulation-diffusion model. Physica D. 2000;141:221–47. [Google Scholar]
- 10.Herrero MA, Rodrigo M. A note on Smoluchowski’s equations with diffusion. Applied Mathematics Letters. 2005;18:969–75. [Google Scholar]
- 11.Leyvraz F, Tschudi HR. Singularities in the kinetics of coagulation processes. J Phys A:Math Gen. 1981;14:3389–3405. [Google Scholar]
- 12.Lushnikov AA. Gelation in coagulating systems. Physica D. 2006;222:37–53. [Google Scholar]
- 13.Meakin M, Vicsek R, Family F. Dynamic cluster-size distributions in cluster-cluster aggregation: Effects of cluster diffusivity. Physical Review B. 1985;31:564–9. doi: 10.1103/physrevb.31.564. [DOI] [PubMed] [Google Scholar]
- 14.Sefcik J, Grass R, Sandkuhler P, Morbidelli M. Kinetics of aggregation and gelation in colloidal dispersions. Trans IChemE, Part A. 2005;83:926–32. [Google Scholar]
- 15.Stauffer D, Coniglio A, Adam M. Gelation and critical phenomena. Advances in Polymer Science. 1982;44:105–158. [Google Scholar]
- 16.van Roessel HJ, Shirvani M. A formula for the post-gelation mass of a coagulation equation with a separable bilinear kernel. Physica D. 2006;222:29–36. [Google Scholar]
- 17.Wattis JAD. An introduction to mathematical models of coagulation-fragmentation processes: A discrete deterministic mean-field approach. Physica D. 2006;222:1–20. [Google Scholar]
- 18.Ziff RM, Ernst MH, Hendriks EM. Kinetics of gelation and universality. J Phys A: Math Gen. 1983;16:2293–2320. [Google Scholar]
- 19.Ziff RM, Stell G. Kinetics of polymer gelation. J Chem Phys. 1980;73:3492–3499. [Google Scholar]