ECG Signal Classification for the Detection of Cardiac Arrhythmias Using a Convolutional Recurrent Neural Network

Abstract

Objective:

The electrocardiogram (ECG) provides an effective, non-invasive approach for clinical diagnosis in patients with cardiac diseases, such as atrial fibrillation (AF). AF is the most common cardiac rhythm disturbance and affects ~2% of the general population in industrialized countries. Automatic AF detection in clinics remains a challenging task due to the high inter-patient variability of ECGs, and unsatisfactory existing approaches for AF diagnosis (e.g., atrial or ventricular activity based analyses).

Approach:

We have developed RhythmNet, a 21-layer 1D convolutional recurrent neural network, trained using 8,528 single lead ECG recordings from the 2017 PhysioNet/Computing in Cardiology (CinC) Challenge, to classify ECGs of different rhythms including AF automatically. Our RhythmNet architecture contained 16 convolutions to extract features directly from raw ECG waveforms, followed by three recurrent layers to process ECGs of varying lengths and to detect arrhythmia events in long recordings. Large 15 × 1 convolutional filters were used to effectively learn the detailed variations of the signal within small time-frames such as the P-waves and QRS complexes. We employed residual connections throughout RhythmNet, along with batch-normalization and rectified linear activation units to improve convergence during training.

Main results:

We evaluated our algorithm on 3,658 testing data and obtained an F₁ accuracy of 82% for classifying sinus rhythm, AF, and other arrhythmias. RhythmNet was also ranked 5^th in the 2017 CinC challenge.

Significance:

Potentially, our approach could aid AF diagnosis in clinics and be used for patient self-monitoring to improve the early detection and effective treatment of AF.

1. Introduction

1.1. Background

Cardiovascular disease is one of the leading causes of death worldwide. An important class of cardiovascular disease is cardiac arrhythmia and is an abnormal heart rhythm that is too fast, too slow or erratic. Atrial fibrillation (AF) is the most common form of cardiac arrhythmia, it affects millions of people around the world and is also associated with substantial morbidity and mortality (Narayan et al., 2017; Zhao et al., 2017). Currently, 1 in 5 strokes in people aged over 60 years is caused by AF, and the prevalence of AF is ~2% of the general population (Lip et al., 2016). Electrocardiograms (ECG), discovered by Muirhead in 1872 to record heartbeats in a patient using wires attached to the patient’s wrists, is a widely used, non-invasive approach for clinical diagnosis in patients with cardiac arrhythmia, including AF. It has been suggested that early AF diagnosis from ECG recordings may enhance the effectiveness of clinical treatment and prevent serious complications (Artis et al., 1991). However, such diagnoses require specially trained health professionals to manually read and identify irregular ECGs, which is often a time consuming and a rather subjective process in some instances (Osowski et al., 2004). As a result, there is high interest in developing an automatic approach for AF detection from ECGs.

During AF, the electrical impulses that originate from the intrinsic cardiac pacemaker no longer pace the heart effectively, and are instead overrun by additional electrical sources (Haissaguerre et al., 1998). As a result, the P-waves in the surface ECG recordings devolve into a series of fibrillatory(f)waves with small magnitudes (Huang et al., 2011), and a fast and irregular heart rhythm is reflected in the short and variable R-peak-to-R-peak (RR) intervals (Tateno & Glass, 2001). Currently, two main approaches exist for AF detection from ECGs: atrial activity-based analyses detect AF by identifying the absence of P-waves and the presence of f-waves (Alcaraz et al., 2006; Du et al., 2014; García et al., 2016; Ladavich & Ghoraani, 2015; Pürerfellner et al., 2014; Ródenas et al., 2015), whereas ventricular activity-based analyses look for irregularity in the RR intervals of QRS complexes (Alcaraz et al., 2010; Carrara et al., 2015; DeMazumder et al., 2013; Huang et al., 2011; Lake & Moorman, 2010; Linker, 2016; Park et al., 2009; Sarkar et al., 2008; Tateno & Glass, 2001). However, atrial activitybased analyses are often error-prone when performed on noise contaminated ECGs. This is due to the small signal-to-noise ratio caused by the low amplitude f-waves (COLLOCA, 2013). On the other hand, ventricular activity-based analyses alleviate this problem due to the well-defined, large amplitude QRS complexes in the ECGs (Zhao et al., 2015b). However, ventricular activity based analyses require relatively long ECG recordings (>30s) of AF episodes for reliable detection (Petrėnas et al., 2015). Recent studies have combined both atrial and ventricular activity-based analyses for more accurate AF detection (Babaeizadeh et al., 2009; Colloca et al., 2013; Oster & Clifford, 2015), and have obtained promising results on diverse datasets.

Non-linear classifiers such as support vector machines (SVM) (Cortes & Vapnik, 1995) have been used to enhance the performance (Colloca et al., 2013; Couceiro et al., 2017; Li et al., 2014a; Li et al., 2014b). These methods involve the extraction of features from ECGs, such as those described in (Lake & Moorman, 2010; Linker, 2009; Sarkar et al., 2008) to learn which features are specific to AF and non-AF. This generally requires domain expertise in the field of ECG analysis, as a rigorous feature generation and selection procedure is required to find the optimal feature combination for learning, which can be extremely time-consuming.

Neural networks have been applied in many different fields, including medicine and bioengineering, to overcome the issues above by automating the feature extraction step (Krizhevsky et al., 2012; LeCun & Bengio, 1995; LeCun et al., 2015; LeCun et al., 2010). This allows the algorithms to not only learn “end-to-end” to make predictions directly from raw data but to also increase the effectiveness of the learning process when large datasets are available, as well as to enable an ease of adaptability to a wider range of tasks. Convolutional neural networks (CNNs) (LeCun & Bengio, 1995) have been widely applied in recent years for imaging tasks (He et al., 2016a; Krizhevsky et al., 2012; Szegedy et al., 2015). By applying a series of independent nested filters through multiple layers, CNNs have also been successful in setting state-of-the-art performance in tasks such as acoustic scene classification (Valenti et al., 2016). But a major disadvantage of CNNs is that they cannot be used on inputs with varying lengths. On the other hand, recurrent neural networks (RNNs) can model data of arbitrary lengths and have been widely used for modeling sequential data such as in speech recognition (Graves et al., 2013). However, an RNN usually requires the input to be encoded into a set of features, as they do not learn effectively from raw data, and are often more difficult to train (Pascanu et al., 2013).

1.2. Literature review on neural networks

This section describes the general concepts of the proposed method. It is organised as follows. Section 1.2.1 outlines the basic operations of CNNs, and how they can be applied to signals. Section 1.2.2 describes the use of residual connections to enhance CNNs. Section 1.2.3 outlines the basic operations of RNNs for sequence learning tasks.

1.2.1. 1D convolutional neural networks

The CNN is a type of ANN that excels in processing 2D data such as images. However, by considering signals as a 1D image, studies have shown promising results using convolutions for signal processing (Han & Lee, 2016; Hershey et al., 2017; Piczak, 2015).

The 1D convolution operation is performed by sliding a small 1D filter across the input one unit at a time and calculating the dot product between the two (Srivastava et al., 2014). This is computed as

$$l_i^{n+1}=f({\sum }_{a=1}^K{\kappa }_a{l}_{i+a}^n),\forall i\in l^n$$ (1)

for a K×1 filter, κ, at each index, i, over the entire input of layer lⁿ. The entries of the filter are the weight parameters to be trained, which vary spatially when used at each position along the input vector. In general, the entries of a filter would become more numerically significant at indices where important features that are characteristic of a certain class occur (LeCun & Bengio, 1995). To increase the degrees of freedom for optimization, the entire convolution operation can be repeated multiple times per layer to create multiple feature maps (LeCun & Bengio, 1995).

The 1D pooling operation is a common operation in 1D CNNs to down-sample patch size (Hu et al., 2014). By compressing certain layers, the total number of weight parameters in the network is decreased which in turn increases the efficiency of training. A commonly used pooling operation is max-pooling (Kim, 2014), where an input patch is down-sampled by keeping only the maximum value within each sub-region with a size of K:

$$l_i^{n+1}=max(l_{i+k}^n),\forall k\in [0,K-1].$$ (2)

The number of weight parameters in CNNs can easily reach hundreds of millions due to the complexity of the convolution operation. Therefore, overfitting is a major concern during training (Srivastava et al., 2014). Dropout is a technique that decreases overfitting by randomly setting weights parameters to zero (Srivastava et al., 2014). This forces the network to find unbiased features in the dataset that are representative of the data in general, instead of specific characteristics that appear only in the training data. A dropout rate, ϕ is added to (7) such that the layer l^N becomes

$$l_i^n=l_i^n{\varphi }_i^n,\forall i\in l^n$$ (3)

where ϕ equals zero with a pre-determined probability.

1.2.2. Residual blocks in CNNs

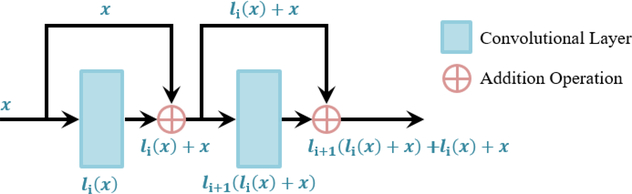
Since the optimization of neural networks is a gradient-based method, it can be enhanced via the use of residual connections. Residual connections provide an alternative pathway for the gradients to be propagated during backpropagation (Figure 1) (He et al., 2016a). The motivation of residual blocks stemmed from an optimization problem which occurred in traditional CNNs which do not contain skip connections. In traditional CNNs, it was observed that by utilizing a larger number of layers, which was previously thought to increase the effectiveness by increasing the degrees of freedom, resulted in a decrease in performance during training compared to CNNs with fewer layers. The vanishing gradient problem is a possible explanation to this phenomenon, where, in larger CNNs, the gradients of the layers that are deeper in the network progressively approach zero after many iterations due to the repeated derivative calculations in backpropagation, resulting in non-optimization (Bengio et al., 1993). By preserving the original gradient and combining it with the gradient after the convolution, skip connections can increase the efficiency of the propagation of gradients during weight parameter updates in SGD.

Figure 1.

A schematic to illustrate the basic operations for residual blocks. In residual blocks, the skip connections provide an alternative pathway for information to be propagated without introducing additional parameters. The original input data is merged with its respective transformed version via the use of an element-wise sum.

Within a residual block, a typical network includes a batch normalization (BN) layer, followed by a ReLU layer, and then a convolutional layer (He et al., 2016a). BN is a layer that constantly normalizes each mini-batch throughout the entire network, reducing the internal covariant shift caused by progressive transforms (Ioffe & Szegedy, 2015). BN uses the mean of the mini-batch, in a layer, x_mean, and their standard deviation, x_std, such that

$$BN\left(l_i\right)=\gamma \left(\frac{x_i-x_{mean}}{x_{std}}\right)+\beta$$ (4)

where x_i represents entries in the current mini-batch and γ and β are trained parameters. By applying ReLU before a convolution layer, as opposed to applying it after in the traditional fashion, the input values are further normalized to accelerate SGD.

1.2.3. Recurrent neural networks

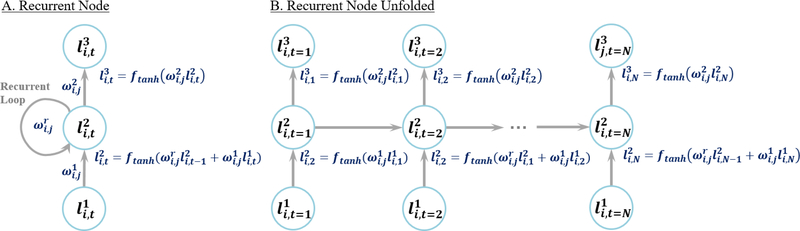
In RNNs, outputs of each neuron within the intermediate layers are cycled into its original input (Figure 2A). RNNs are widely used in the fields of speech recognition (Graves et al., 2013), language translation (Amodei et al., 2016) and video processing (Baccouche et al., 2011) as the cycling of information within each node allows sequential data to be processed efficiently. Hence, RNNs differ from CNNs as they can process data of variable input size. When many recurrent neurons exist in a recurrent layer, the sequential data is processed in parallel through different weights, allowing RNNs to generate multiple representations and create effective feature space separation.

Figure 2.

A recurrent layer with a single node. A) A compressed representation of the recurrent node. B) An unfolded version illustrating the cycling of weights inside a recurrent node at different time steps. Note that the weights within each layer are shared but applied to different time steps. The first node $l_{i,t=1}^2$ simply inputs the information from the previous layer as there is no previous time step.

In each RNN layer, lⁿ, for every node, information at different time steps, t, of an input is stored. The value of the layer in the next time step depends on the current time step of the layer, and the current time step of the previous layer such that

$$l_{i,t+1}^n=f_{tanh}({\omega }_{i,j}^r{l}_{i,t}^n+{\omega }_{i,j}^{n-1}{l}_{i,t}^{n-1})$$ (5)

where ωⁿ⁻¹ is the weight of the previous layer and ω^r is the weight of the recurrent node. The value of the next layer in the current time step depends on the current layer by

$$l_{i,t}^{n+1}=f_{tanh}({\omega }_{i,j}^n{l}_{i,t}^n)$$ (6)

The above operations are repeated to propagate the nodal values through several successive recurrent nodes (Figure 2B).

In this paper, we propose a neural network which combines the strengths of both CNNs and RNNs (Donahue et al., 2015; Pinheiro & Collobert, 2014) for the automatic detection of AF and other arrhythmias from ECGs. Our method is developed on the dataset provided by the organizers of 2017 PhysioNet/Computing in Cardiology Challenge (Clifford et al., 2017), the largest study of this kind. We also evaluate our algorithm against the other participants of the competition. The fully data-driven nature of our approach is an exciting development, and could potentially aid AF detection in clinics and patient self-monitoring from ECG recordings for early detection and effective treatment of AF.

2. Methods

2.1. Materials and pre-processing

The 2017 PhysioNet/CinC Challenge contained 12,186 single lead ECG recordings recorded by the patients from a self-diagnosis device, the AliveCor Kardia (California, United States) (Clifford et al., 2017). The ECG data contained four classes: normal rhythm (N), AF rhythm (AF), other rhythm (O) and noisy recordings (~). A typical waveform for each class is shown in Figure 3A. The ECG data used in this study was split into a training set with the manually annotated ground truths, and a test set. The training dataset consisted of 8,528 ECG recordings ranging from 9 to 60 seconds in length, with a sampling rate of 300 Hz. The testing set consisted of 3,658 recordings and was used to evaluate the performance of our algorithm in the 2017 CinC challenge. Figure 3B outlines the class distributions of the datasets.

Figure 3.

The data used in this study. A) Typical examples of single-lead ECG recordings for each of the four classes: normal rhythm (N), atrial fibrillation (AF), other rhythm (O) and noisy (~), in the provided dataset in the 2017 CinC Challenge. B) An illustration of the distribution of the four classes within the training set and within the test set hidden to the public.

Since the test set was inaccessible to the public, we performed 5-fold cross-validation on the training set, as a means to analyze the performance of RhythmNet and perform diagnostics. The training set generated from cross-validation was used to train our network, while the test set generated from cross-validation was used to preliminarily assess the performance of our network.

2.2. Proposed neural network architecture

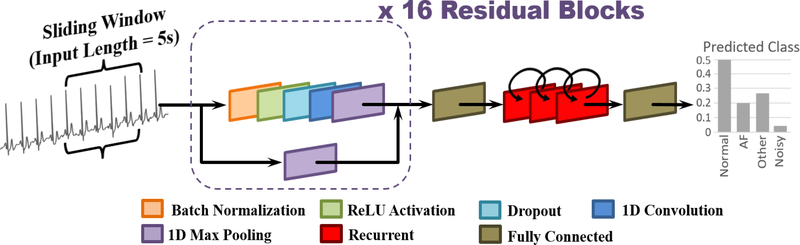
ECG classification is a challenging task due to the variable signal quality and lengths, ambiguity of labels as a result of multiple rhythm types in the same recording, variable human physiology, and the difficulty in distinguishing the features for cardiac arrhythmia such as AF. We propose a novel 21-layer residual convolutional recurrent neural network, with the alias RhythmNet (Figure 4), to effectively learn the features defining different single-lead ECG recordings. The network processes 5-second non-overlapping signal segments successively along the entire length of each ECG with convolutional layers and uses the recurrent layers to aggregate the individual outputs into a single prediction. 5 seconds was selected as the input length from hyper-parameter tuning, as input lengths which deviated from this value resulted in a decreased performance during cross-validation.

Figure 4.

The architecture of the proposed residual recurrent convolutional neural network (RhythmNet). The ECG signal is inputted in windows of 5 seconds and then passed through 16 repeated residual blocks containing convolutions of different depth. The output of the residual blocks is then flattened into a 1D vector, and fed through three recurrent layers to process the successive windows sequentially, 5 seconds at a time. The output of the recurrent layer is then mapped onto a fully connected layer with four nodes denoting the probabilities of the four classes to predict for.

Overall, RhythmNet consists of 16 convolutional layers within 16 residual blocks, three recurrent layers, and two fully connected layers. Each residual block consists of the BN, ReLU, convolution arrangement and an additional dropout layer, with a dropout rate of 0.8 as found from hyper-parameter tuning. Max pooling is added to decrease the number of parameters at the end of each residual block. Max pooling is also applied on the corresponding skip connection to maintain consistency of spatial size. All convolutional layers contain 15×1 filters to process the raw ECG waveform. After the 16 residual blocks, a fully connected layer with 1024 nodes is added to flatten the matrices from the convolutional layers, and to match the input requirements of the recurrent layer. Three recurrent layers, each with 512 nodes, are then used to learn an enhanced representation of the ECG signal for more accurate classifications by using convolutions as a preliminary feature extractor. Finally, the output of the recurrent layers is flattened through a fully connected layer to produce the probability of each ECG class via softmax activations.

The proposed neural network contains several hyper-parameters which were carefully selected after extensive experimentation. Each hyper-parameter was tuned by keeping all other parameters of the network constant and evaluating the effects of incrementally adjusting the value with 5-fold cross-validation on the training set. For each hyper-parameter, the value which resulted in the best cross-validation F1 score was selected for the final model. Initially, the RhythmNet was tested with 8, 16 or 32 residual blocks, followed by the use of 2, 3 or 4 recurrent layers. It was observed that 32 residual blocks and four recurrent independently resulted in substantial over-fitting as the training accuracy was much higher than the testing accuracy during cross-validation. On the other hand, eight residual blocks and two recurrent layers resulted in lower accuracies as the network did not contain sufficient parameters to learn the complex features in the ECG signals. The internal arrangement of each residual block and the progression of the number of feature maps in each convolutional layer was adapted from the architecture proposed by He in 2016 (He et al., 2016b) to 1D CNNs. The filter size in each convolutional layer was tuned by testing the entire network with 3×1, 5×1, 10×1 and 15×1 sized filters. Filters sized larger than this value was not tested due to the high computational costs which slowed down training and prediction run-time. Experiments testing the filter sizes showed that for 1D input, larger filters were more effective due to the increased receptive field being able to more effectively account for the variations of the signal over time. Adjusting the number of nodes of the recurrent layer did not result in any significant change as the majority of the processing was done by the residual blocks. Nevertheless, 512 proved to deliver a decent balance between learning capacity and avoiding over-fitting. Dropout was the last parameter to be tuned and various combinations were tested. Experiments showed that having a consistent dropout rate throughout all layers of RhythmNet improved the accuracy and stability of optimization during training while varying the dropout rate between layers decreased the accuracy. Dropout rates of 0.4, 0.5, 0.6, 0.7, 0.8 and 0.9 were tuned and 0.8 resulted in the best cross-validation accuracy. Larger dropout rates decreased the accuracy of the network as too many nodes were removed causing a decreased learning capacity and smaller dropout rates decreased the accuracy as the network was more prone to over-fit to the training set.

2.3. Training

The adaptive moment estimation (ADAM) optimizer, a type of SGD algorithm, was used to optimize the weight parameters (Kingma & Ba, 2014). The ADAM used consisted of an adaptive learning rate and momentum variable which increased the rate of convergence. An initial learning rate of 0.01 and exponential decay rates of 0.9 and 0.999 for the 1^st and 2^nd moment estimates were used. The training data was fed into RhythmNet in batches during training, and the accuracy was evaluated using cross-validation on the training set after each complete iteration of all the training data. This was repeated until the cross-validation accuracy stopped increasing, and the best performing model before this was chosen. The network was developed in Tensorflow, an open-source deep learning library for Python, and was trained on an NVIDIA Titan X-Pascal GPU with 3840 CUDA cores and 12GB RAM. The training phase took approximately two hours and predictions for each signal took ~0.01 seconds.

2.4. Evaluation

The F₁ score used for evaluation was the average of the individual F₁ scores for the normal rhythm, AF rhythm, and other rhythm. The classification accuracy of noisy signals was not considered, however, it implicitly impacted the F₁ scores of other classes when noisy signals were predicted incorrectly. The overall accuracy measure was defined as

$$F_1=\frac{1}{3}\left(\frac{2\times N_{truepositive}}{\sum N_{groundtruth}+\sum N_{predicted}}+\frac{2\times A_{truepositive}}{\sum A_{groundtruth}+\sum A_{predicted}}+\frac{2\times O_{truepositive}}{\sum O_{groundtru\text{th}}+\sum O_{predicted}}\right)$$ (7)

where for each class, the total number of correct predictions were multiplied by 2 and divided by the sum of the total number of signals within each class and the total number predicted for that class.

3. Results

RhythmNet achieved an overall F₁ accuracy of 0.864 from the 5-fold cross-validation experiments, with 0.919 for normal rhythms, 0.858 for AF rhythms and 0.816 for other rhythms. Figure 5 outlines the proportions of predictions for each class. RhythmNet had difficulties distinguishing normal rhythms from other rhythms, as 8.8% of the normal rhythm subgroup were mistakenly predicted as other rhythm, and 10% of the other rhythm subgroup was mistakenly predicted as normal rhythm. Many AF rhythms were also classified as other rhythms (9%). However, there was relatively small error between normal rhythm and AF as only a small proportion of either class were mistakenly classed as the one or another, implying that RhythmNet was effective in distinguishing AF and normal rhythms.

Figure 5:

Diagnostics of RhythmNet during cross-validation on the training set. A) A bar plot to visualize the proportions of the predictions vs ground truths. B) The corresponding confusion matrix with the proportions in %. The noisy class is in grey as it was not considered in the score.

The results from the 2017 CinC Challenge showed that our approach obtained an overall F₁ accuracy of 0.82 on the hidden test set, with 0.90 for normal rhythms, 0.82 for AF rhythms and 0.73 for other rhythms (Xiong et al., 2017). RhythmNet was only 0.01 from the top entry and achieved 5^th place out of the total 75 research groups that participated in the competition (Clifford et al., 2017). The lower score on the hidden test set compared to cross-validation showed that our algorithm over-fit during training. The fact that the model with the best performing accuracy during cross-validation was used as the entry in the challenge could cause the network to have the optimal predictions during cross-validation, but not on the hidden test set, hence, resulting in over-fitting.

4. Discussion and conclusions

Classification of arrhythmias such as AF from ECGs is a challenging task due to the high variability of the signals between different patients. The ECG dataset used in this study is especially difficult due to the severe class imbalance for the four different classes of signals, making it difficult for traditional learning algorithms such as SVMs or ANNs. The varying length of signals (9s to 60s) is also a challenge due to the occurrence of arrhythmia events which could only last a few seconds. These events could often be other rhythms or noisy segments which could confuse the classification of the entire signal. Mixtures of AF and other arrhythmic patterns, and normal -rhythm in the same recording complicate the decision further.

Recent studies have built upon traditional atrial and ventricular-based analyses by using them as features for non-linear classifiers such as SVMs to classify AF and other signals from ECGs. Many studies have been proposed which utilize feature extraction and selection tools to generate features for SVM classifiers (Lake & Moorman, 2010; Linker, 2009; Sarkar et al., 2008; Colloca et al., 2013), including the study from Li which used a genetic algorithm for feature selection (Li et al., 2014a; Li et al., 2014b), and have been successful on large databases.

Deep learning has become increasingly popular in recent years as it eliminates the need for feature extraction (LeCun et al., 2015). Our approach obtained 5^th place in the 2017 CinC challenge and had an F₁ score of 0.82, 0.01 less than the 4 top performing teams (Datta et al., 2017; Hong et al., 2017; Teijeiro et al., 2017; Zabihi et al., 2017). Although our study shows that deep learning without feature extraction is effective for ECG classification, the 4 top teams all used feature-oriented methods. Datta et al. and Zabihi et al used traditional non-linear classifiers (Datta et al., 2017; Zabihi et al., 2017), while Hong et al. and Teijeiro et al. (Hong et al., 2017; Teijeiro et al., 2017) used neural networks to classify sets of carefully generated and refined features. In contrast, our proposed RhythmNet does not require explicit feature extraction as the raw waveforms are processed by the network directly, which enables an automated workflow. However, the inherent limitations of our approach were reflected in the results. The lower performance of RhythmNet was primarily due to over-fitting on the cross-validation set and shows the difficulty of training large neural networks such as the one proposed in this study when limited data is available. This could be improved by increasing dropout or training the network for a shorter amount of time during cross-validation. It is difficult to precisely determine the optimal point between under and overfitting, as testing data such as that in the 2017 CinC challenge is often not accessible during training. Hence, the true performance accuracy of the network for any unseen dataset cannot be accurately measured. The most promising method to address this issue seems to be to introduce more test data to increase the robustness of validation.

The accuracy of RhythmNet could be further enhanced by incorporating more arrhythmia databases during training and testing, as our method is fully data-driven and will only improve with more data to learn from. This is especially the case for improving AF detection, as our study only used ~1000 ECGs containing AF rhythms, which is a small number by today’s standards. Data augmenting could be an alternate method to simulate more data, as well as generative neural networks which could be investigated in future studies (Van Den Oord et al., 2016).

ECG is a clinical approach that is widely used for detecting and classifying cardiac arrhythmias. In contrast to the traditionally-used ECG, which is a form of non-invasive measurement, invasive mapping approaches such as contact catheter mapping have become increasingly popular over the years. As a result, many methods have been proposed for processing atrial electrograms collected via invasive mapping approaches (Haïssaguerre et al., 2008; Pathik et al., 2017), including recurrence quantification analysis (Navoret et al., 2013; Yang, 2011) entropy measurements (Cervigón et al., 2010) and fast Fourier transforms (Zhao et al., 2015b). These invasive mapping and subsequent signal processing methods have enabled the construction of more accurate and local arrhythmia patterns, such as complex fractionated atrial electrograms (CFAE) (Nademanee et al., 2004; Navoret et al., 2013) and AF re-entrant driver regions (Hansen et al., 2015; Zhao et al., 2015a; Zhao et al., 2017) which have been used to guide ablation procedures to improve ablation success rates. The improved accuracy provided by direct contact mapping is extremely useful and desirable; however, its invasiveness does impose limitations and risks which largely restrict its use. Electrocardiographic imaging (ECGI) (Lim et al., 2017), on the other hand, is an approach that has the potential to combine the strengths of both invasive and non-invasive mapping approaches. As a result, it will be useful to extend our developed CNN approach to allow the processing of data collected from promising novel mapping approaches like ECGI.

In this study, we have developed and evaluated RhythmNet, a residual convolutional recurrent neural network for the classification of AF and other rhythms from single lead ECGs. RhythmNet is the highest performing fully data-driven model to have the capacity to analyze ECG signals of varying lengths. Our approach allows us to automatically detect AF from ECGs, which will potentially lead to enhance early detection and treatment of AF worldwide.