Stimulus complexity shapes response correlations in primary visual cortex

Significance

Whether the population activity in neuronal networks can be understood as the sum of individual activities or neurons jointly determine the state of populations is a fundamental question of neuroscience. Spike count correlations reflect coordination between pairs of neurons and therefore can be regarded as a signature of joint computations. So far, a majority of experimental and theoretical analyses considered these correlations noise and ignored stimulus-dependent aspects. Based on theoretical considerations, we argue that spike count correlations are stimulus dependent and variations in their structure can be predicted by stimulus content. Recording the activity of neurons from primary visual cortex in task-engaged monkeys, we confirm these predictions. These results provide insight into the computations performed by populations of cortical neurons.

Abstract

Spike count correlations (SCCs) are ubiquitous in sensory cortices, are characterized by rich structure, and arise from structured internal dynamics. However, most theories of visual perception treat contributions of neurons to the representation of stimuli independently and focus on mean responses. Here, we argue that, in a functional model of visual perception, featuring probabilistic inference over a hierarchy of features, inferences about high-level features modulate inferences about low-level features ultimately introducing structured internal dynamics and patterns in SCCs. Specifically, high-level inferences for complex stimuli establish the local context in which neurons in the primary visual cortex (V1) interpret stimuli. Since the local context differentially affects multiple neurons, this conjecture predicts specific modulations in the fine structure of SCCs as stimulus identity and, more importantly, stimulus complexity varies. We designed experiments with natural and synthetic stimuli to measure the fine structure of SCCs in V1 of awake behaving macaques and assessed their dependence on stimulus identity and stimulus statistics. We show that the fine structure of SCCs is specific to the identity of natural stimuli and changes in SCCs are independent of changes in response mean. Critically, we demonstrate that stimulus specificity of SCCs in V1 can be directly manipulated by altering the amount of high-order structure in synthetic stimuli. Finally, we show that simple phenomenological models of V1 activity cannot account for the observed SCC patterns and conclude that the stimulus dependence of SCCs is a natural consequence of structured internal dynamics in a hierarchical probabilistic model of natural images.

Spike count correlations (SCCs), covariation of neuronal responses across multiple presentations of the same stimulus, are ubiquitous in sensory cortices and span different modalities (1–3) and processing stages (4–7). In the visual system, SCCs, also termed noise correlations, have traditionally been considered to be independent of the stimulus and hence have been thought to impede stimulus encoding (8). Studies on stimulus-independent aspects of SCCs in the primary visual cortex (V1) sought to capture correlation patterns that were solely accounted for by differences in receptive field structure (9, 10). Initial investigations of dependence of SCCs on low-level stimulus features, such as orientation and contrast, focused on the population mean of SCCs (11–13), but stimulus-dependent changes in the mean are modest in awake animals (9, 14). Only recently has orientation and contrast dependence of the fine structure of SCCs been demonstrated in anesthetized cats and awake mice (15). Recent studies using calcium imaging of V1 in awake mice revealed a dependence of the fine structure of correlations on stimulus statistics (14, 16). These observations raise the possibility that not only single-neuron responses (mean activities) but joint response statistics (notably, correlations) too are tied to the properties of complex natural stimuli.

SCCs are emerging from the internal dynamics of cortical neuron populations. Internal dynamics is determined both by lateral connections and feedback from higher cortical areas, both of which have been demonstrated to shape the activity in V1 (15, 17–19). Lateral (20–23) and feedback interactions (24, 25) have been linked to regularities characteristic to natural stimuli, suggesting a possible role of internal dynamics in the interpretation of complex stimuli. Internal dynamics captured during spontaneous activity distorts the population activity directly evoked by the stimulus (26) and has been proposed to contribute toward the interpretation of naturalistic stimuli during perceptual inference (27). It is still unclear, however, whether stimulus-dependent SCCs can be explained by the internal dynamics implied by perceptual inference.

Natural visual stimuli are complex and provide insufficient information for unambiguous interpretation. Evidence suggests that the visual system represents an internal model of the environment, which serves the integration of information about the current stimulus with previously acquired knowledge of natural scene statistics (28, 29). Recently, it has been demonstrated that neural response variability can be linked to inference in the internal model (30) and that contextual influences in the internal model predict the stimulus dependence of surround suppression (31). Crucially, when interpreting complex stimuli, the context plays an essential role: the likelihood of the presence or absence of a particular visual feature is dependent on the presence or absence of a large number of contextual features. Indeed, when assessing the orientation of an edge in a small image patch, which V1 simple cells are selective to, the context of being on a pebbly beach or in a wheat field provides information about curvatures and spatial frequencies. Furthermore, given that the visual cortex processes visual information in a series of hierarchical processing stages, contextual information from the higher levels of the processing hierarchy can inform and constrain the activity at lower levels of processing through feedback (25, 32, 33). Thus, we argue that in the primary visual cortex high-level visual context introduces modulations of the internal dynamics, and ultimately results in stimulus-specific SCC structure.

Feedback modulation of higher-order statistics of responses, including variance (34) and correlations (35) in V1, were shown to contribute to multiplicative effects in activity fluctuations. Indeed, patterns in V1 SCCs in response to periodic grating stimuli were shown to be aligned with a simple phenomenological model of V1 responses that only considers stimulus dependence of neuronal responses in terms of tuning curves and assumes that joint modulations are stimulus independent (15). This model, however, does not aim to account for stimulus-dependent modulations of internal dynamics. Similarly, a functional account of V1 that links (co)variability of neuronal responses to perceptual uncertainty but lacks a representation of higher-order stimulus features fails to predict stimulus specificity in the correlation structure (30). Modulations of the fine structure of correlations have been predicted by functional models of attention (36, 37), which related changes in correlation structure to inference of task variables. Here, we go beyond these accounts and argue that hierarchical perceptual inference has a direct predictable effect on the structure of SCCs in V1, which is independent from task or attentional influences. We hypothesize that, for stimuli with high-order structure, inferences on the presence of high-level visual features modulate inferences on the presence of low-level features through top-down modulation of V1 responses, leading to stimulus specificity in SCC patterns. Conversely, we hypothesize that, without high-level structure, stimulus specificity of correlation patterns dwindles.

To test these hypotheses, we designed an experiment in which we can characterize the full correlation matrix, the so-called partial correlations. First, we established that correlation patterns in response to natural images are stimulus specific. We developed the contrastive rate matching (CRM) method to identify modulations in the correlation structure that are independent of changes in the mean of the responses. Second, we carried out a decoding analysis to test whether stimulus-specific correlations carry information about stimulus identity. Third, we designed synthetic image families with low-level or high-level structure. Importantly, in a hierarchical model of visual perception, high-level synthetic images, but not low-level synthetic images, are expected to elicit stimulus-specific top-down influences and consequently to introduce stimulus-specific correlations. Our V1 recordings confirm these predictions and demonstrate that the stimulus specificity of SCCs is dependent on stimulus structure: synthetic stimuli characterized solely by low-level structure elicit correlation patterns with reduced stimulus specificity, while synthetic stimuli characterized by high-level structure restore stimulus specificity of correlations. Finally, using surrogate datasets from phenomenological models of population responses, we demonstrate that accounts that do not consider stimulus-specific contextual modulation cannot account for the patterns observed in our recordings.

Results

To phrase predictions on the effect of top-down interactions on V1 internal dynamics and specifically on SCCs, we introduce a hierarchical model of visual processing in the ventral stream. The model naturally extends earlier probabilistic models of V1 activity (30, 38, 39) by assuming an additional layer of processing. The additional layer is analogous to higher processing layers in the ventral stream, and for simplicity, we identify it with the secondary visual cortex (V2). V2 neurons are assumed to be selective to texture-like patterns (40, 41) that emerge from combinations of elementary features (i.e., Gabor functions). Probabilistic models of perceptual inference, similar to the one proposed here, have been motivated by the fundamentally noisy and ambiguous nature of environmental stimuli and have gained extensive experimental support from behavioral studies (42, 43). Importantly, probabilistic models reveal that efficient computation requires the maintenance of uncertainty about the inferred environmental features; therefore, we consider neural representations that can represent such uncertainties (30, 32, 44).

Assuming a hierarchical internal model for the representation of natural images in the visual cortex (Fig. 1A), probabilistic inference in the model corresponds to stimulus perception (45). In this context, activities of neurons correspond to activation of variables, and selectivities of neurons correspond to filter properties of variables. In this model, the activity level of a neuron is assumed to represent the inferred intensity of its preferred visual feature. At different levels of the hierarchy, neurons are sensitive to features of different complexity. In a simple approximation, the receptive fields of V1 neurons can be characterized by Gabor filters, while the receptive fields of V2 neurons can be characterized by texture-like filters (40). Upon the presentation of a particular image, x, the posterior distribution for the activations of V1 neurons, y, conveys detailed information about the uncertainty of the features represented by V1 receptive fields, including the specification of not only mean activations but variances and covariances as well (see also SI Appendix):

$$\mathrm{P}\left(\mathrm{y}|\mathrm{x}\right)={\displaystyle \int \mathrm{P}\left(\mathrm{y}|\mathrm{x},\mathrm{z}\right)\hspace{0.17em}\mathrm{P}\left(\mathrm{z}|\mathrm{x}\right)\mathrm{dz}}.$$

The first term of the integral is the probability distribution of the joint activations of V1 neurons given a particular image and a particular set of activations, z, at a hierarchical level beyond V1 (Fig. 1B). The second term establishes weights for averaging over possible high-level activations. This equation highlights three important points: (i) activations at the lower level of the hierarchy, V1, depend on high-level activations, that is, specific predictions can be obtained from top-down interactions; (ii) activations at V1 can be correlated; that is, if a high-level feature represented in V2 assigns high probability to particular combinations of features, then variability in z will induce correlations in y (Fig. 1B); (iii) since the probability of different combinations of high-level activations, P(z | x), changes with the stimulus, correlations in V1 will be stimulus dependent. As a consequence, hierarchical statistical inference predicts stimulus-dependent correlations for structured stimuli, for example, for natural images, thus reflecting top-down influences (Fig. 1C). However, in the absence of high-level structure, stimuli will not be informative with respect to high-level inferences and therefore will result in unspecific top-down influences, and hence hierarchical statistical inference predicts unspecific correlations (Fig. 1D). These predictions are functional in nature and remain agnostic about the anatomical connections that contribute to the implementation of probabilistic computations in the hierarchical internal model. Nonlinear interaction patterns of receptive fields (22, 23, 46) that implement hierarchical computations are expected to involve not only bottom-up and top-down projections but lateral connections as well.

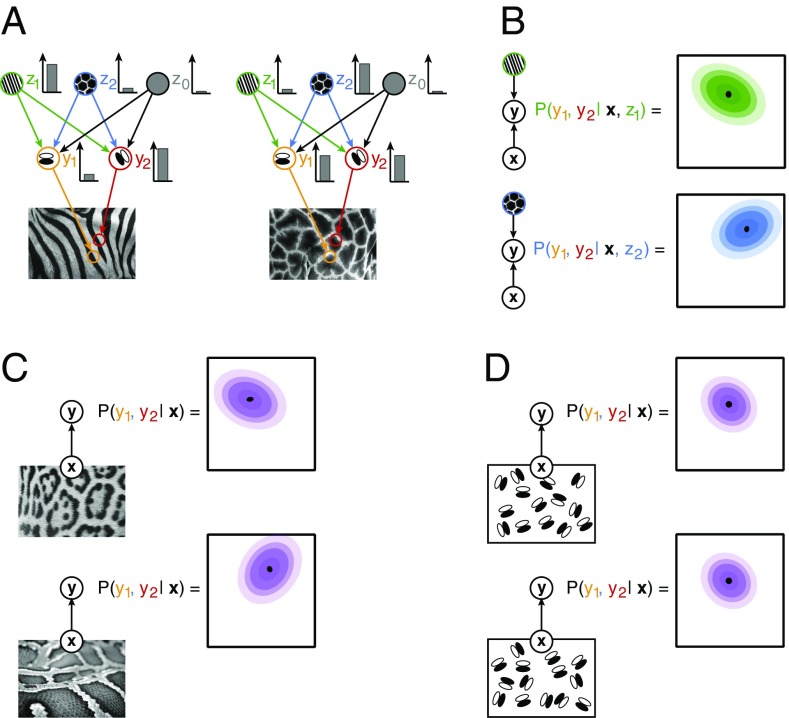
Fig. 1.

Illustration of inference in a hierarchical statistical model. (A) An image, x, is assumed to be generated by combining features of different complexity: high-level features, z_i (green and blue circles), determine the large-scale structure of low-level features, for example, textures determine the joint statistics of edges (z₀ is a bias term that represents an interpretation where no higher-order structure is present). Low-level features, y_i, capture simple regularities in images, for example, darker and lighter image areas underlying edges (orange and red circles). In the visual system, upon presentation of a stimulus, the contribution of different features to the observed image is inferred: different images (Left and Right) elicit different intensity responses from the neurons (Inset bar plots). (B) The statistical internal model establishes a joint probability distribution for the coactivation of low-level features upon observing a stimulus: beyond the most probable joint activations (black dots), a wide range of coactivations is compatible with the high-level percept, albeit with different probabilities (colors matching those on A). Given the activation of a particular high-level feature (z₁ or z₂ for the Left and Right, respectively), the joint distribution over activations of low-level features (contours) displays a covariance specific to the high-level feature. (C) The posterior distribution for low-level features is characterized both by the mean and covariance of the distribution (Top). Posterior distribution for a distinct structured image (Bottom) is characterized by a different mean and correlation structure. (D) A stimulus with no higher level structure is invoking an interpretation that low-level features are independent; therefore, the correlation structure of images with only low-level structure will be identical. Arrows define conditional dependencies throughout the figure.

Stimulus Dependence of SCCs.

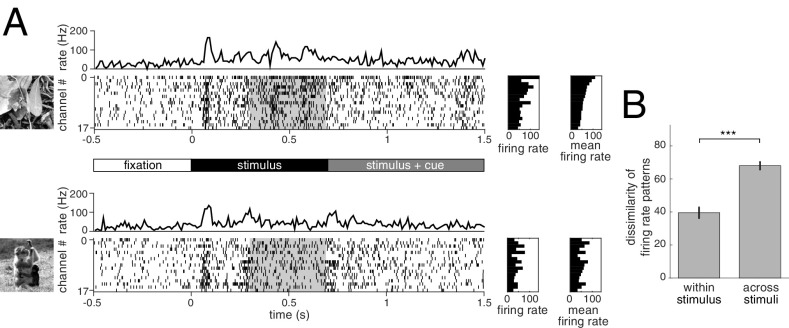
Parallel multielectrode recordings (32 channels) were obtained from area V1 of two awake behaving monkeys (Macaca mulatta). The receptive fields of the recorded units were located ∼2–4° (monkey A) and 3–7° (monkey I) from the fixation spot (SI Appendix, Fig. S1). Monkeys were trained to perform an attention task in which, after initiating fixation (Fig. 2A), they were presented with a pair of natural images located left and right from the fixation spot, one of which overlapped with the receptive fields of the recorded units. After 700 ms, a change in fixation spot color cued the monkeys to report an incoming change in either the left or right image. The task was used to ensure the engagement of the animal, and our analysis was constrained to neural responses evoked by stimulus presentation before appearance of the cue signal (Materials and Methods). Initial transient responses after stimulus onset were omitted from the analysis to reduce stimulus locked correlations, leaving a window of 400 ms to assess response statistics (Fig. 2A). Reliable estimation of the full SCC matrix between recorded channels required a large number of repetitions; therefore, the number of different images was limited to six or eight images per session, providing a range of 65–180 repetitions per image. The mean population response, as characterized by the average firing rate across units, was selective for stimulus identity (Fig. 2A) and exhibited a high level of dissimilarity of firing rate patterns in response to different natural images compared with a lower dissimilarity of responses to identical stimulus presentations (Fig. 2B).

Fig. 2.

Structure of the experiment and mean neural responses. (A) Time course of neural activity upon the presentation of two natural images (Top and Bottom). After presenting a fixation point for 500 ms (timeline in Middle), a pair of stimuli are presented off-foveally at equal distances from the fixation point. One of the images (shown on the Left for the example trial) covers the receptive fields of recorded V1 neurons. After another 700 ms, the color of the fixation point changes, cuing the monkey to which of the images it needs to focus its attention. In the following 800 ms, one of the images is rotated, and the monkey is asked to respond if the cued stimulus changes and to withhold responses to changes of the noncued stimulus. MUA is recorded on multiple channels and spiking activity is obtained (raster plots). After an initial transient following stimulus onset (peaks in the channel-averaged activity; top trace), a sustained but weaker activity follows. Analysis of spiking activity was constrained to this segment of 400 ms (gray shading). Mean firing rate of recorded channels in the presented trial (Left raster plot) and average across trials (Right side raster plot) display specificity to stimulus. Ordering of the channels was established based on the trial-average responses to the first image (Top Right raster). (B) Dissimilarity of patterns in average firing rates calculated either across subsets of trials using the same stimulus (within stimulus) or to different stimuli (across stimuli). *P < 0.05, **P < 0.01, ***P < 0.001; n.s., P ≥ 0.05 in this and all subsequent figures.

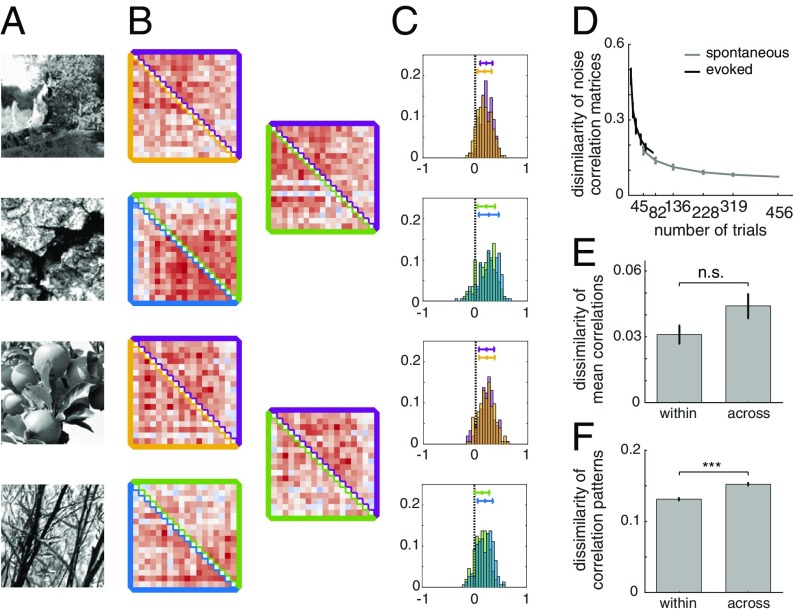
First, our goal was to establish the stimulus specificity of the fine correlation patterns in population responses to natural image patches. For each stimulus, we calculated a SCC matrix, by extracting correlations between the activities of any two neurons across repeated presentations of the same stimulus (Fig. 3A). We analyzed the stimulus specificity of the structure of SCC matrices by comparing the difference between the correlation matrices extracted in two different conditions: (i) from two independent subsets of data in response to the same stimulus (within-stimulus); (ii) from the responses of neurons to different stimuli (across-stimuli; Fig. 3B and SI Appendix, Fig. S2 B and C). This treatment goes beyond traditional approaches that only characterize the population mean of the distribution of correlations (Fig. 3C). In supplementary analysis, we characterized the stimulus dependence of correlations using additional techniques, sensitive to different properties of the response distribution. The linear predictability of SCCs across different conditions (SI Appendix, Fig. S2B) revealed stimulus-dependent structural changes in SCC matrices. Furthermore, we ranked SCCs according to one condition and measured rank correlation in SCCs in another condition, which yields a measure that is agnostic to changes in SCC magnitude. Measuring rank correlation across stimuli based on a rank established for a particular stimulus provided further support for the claim that stimulus content affected the structure of SCCs and their magnitude (SI Appendix, Fig. S2C).

Fig. 3.

Stimulus dependence of SCC. (A) Natural images used in the experiments. (B) Fine structure of SCCs calculated for two subsets of trials (upper and lower triangles of the SCC matrix) in response to the same image (Left column, within stimulus), or to different images (Right column, across stimuli, with colors matching those used for subsets of trials in the Left column). (C) Histograms of SCCs for two equal-sized subset of trials (two different colors on the same plot). (D) Dependence of within-stimulus dissimilarity of SCC matrices on the number of trials used for the estimation. (E) Dissimilarity of mean SCCs within stimulus and across stimuli. (F) Dissimilarity of SCC matrices within stimulus and across stimuli.

Measurement of SCCs from a finite number of trials is noisy, and therefore estimates of the SCC matrix are variable (Fig. 3A). As a consequence, the within-stimulus difference of SCC matrices can be used to establish a baseline for the estimates of across-stimuli differences of SCCs. The baseline shrinks with increasing the number of trials (set size). To establish the number of trials needed for a reliable estimate of SCCs, we assessed dissimilarity as a function of set size (Fig. 3D). There is a steep drop in dissimilarity at low trial counts due to high variance of correlation estimates. We balanced the trade-off between the number of repetitions and the size of the stimulus set in an experimental session by aiming for ∼80 repetitions per stimulus. We used the dependence of within-stimulus dissimilarity of SCCs on the number of repetitions to establish an approximate baseline for correlation dissimilarity. As within-stimulus difference could only be calculated from a lower number of repetitions than across-stimuli comparisons, this relationship was used to extrapolate the estimate for within-stimulus dissimilarity for higher number of trials.

We checked whether stimulus specificity of SCCs can be established based on the mean of the correlation distribution. Comparison of changes in the mean was not conclusive since the dissimilarity of the mean correlation across stimuli was not significantly higher than that within stimulus (t test, P = 0.064, t = −1.89, df = 58; Fig. 3E). Comparison of SCC matrices instead of the mean of SCC distributions is sensitive to changes in the patterns of correlations and therefore provides more detailed information on the stimulus dependence of population responses (Fig. 3F). Dissimilarity of SCC matrices was significantly higher across stimuli than within stimulus (t test, P = 7.4e-20, t = −9.14, df = 8,766). We also determined that the significance of the difference in dissimilarities is not merely the result of a larger sample size due to the large number of elements of correlation matrices. To this end, we constructed a measure that matches the sample size of the population mean of correlations. We calculated a single dissimilarity value for a particular pair of stimuli and compared this measure across conditions (t test, P = 1.76e-5, t = −4.68, df = 58; SI Appendix, Fig. S2F). Furthermore, both linear predictability of SCCs across conditions and rank correlations consistently showed similar changes across stimuli (t tests, Pearson correlation: P = 1.05e-05, t = 4.83, df = 58; Kendall rank correlation: P = 8.25e-06, t = 4.89, df = 58; SI Appendix, Fig. S2 D and E). Comparison of correlation matrices implicitly establishes a comparison between two multivariate normal distributions. A widely used measure to assess the dissimilarity of probability distributions is the Kullback–Leibler (KL) divergence, which can be calculated analytically for normal distributions and can be used to assess the dissimilarity of the correlation structures. We found a similar pattern in the difference in dissimilarities with KL divergence as with other measures (t test, P = 1.65e-3, t = −3.3, df = 58; SI Appendix, Fig. S2G). Taken together, these analyses indicate that, when natural scenes are presented, the resulting fine patterns in SCCs are specific to stimulus identity.

Contrastive Rate Matching.

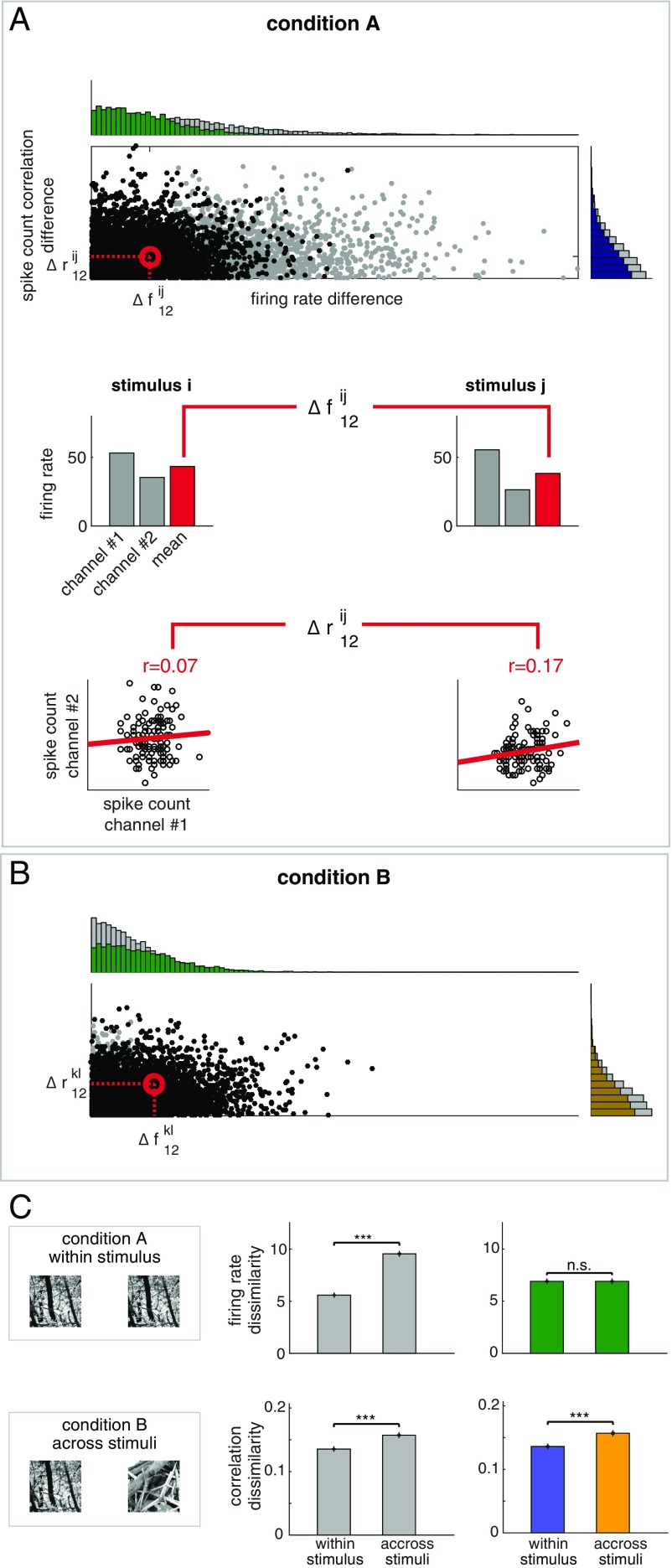
Firing rate has a major effect on the estimate of SCCs from spiking activity (47, 48). As a consequence, firing rate changes could constitute a potential confound for establishing stimulus specificity of SCCs. To address this potential confound, we devised the CRM method (SI Appendix and Fig. 4). Briefly, for a given condition, we calculated the 2D distribution of across-trial changes in firing rates and correlations (Fig. 4A). To eliminate the dependence of the estimate of correlation change on firing rate changes, the marginal distribution of firing rate changes is matched across the two conditions to be contrasted (Fig. 4B) by subsampling the data points. On these subsampled data, the magnitude of firing rate changes will be equal in the two conditions and the residual condition dependence of correlations can be assessed.

Fig. 4.

Contrastive rate matching (CRM) for controlling for the effects of firing rate changes on SCC distributions. (A) Distribution of the magnitude of changes in firing rates and correlations upon presenting stimulus “i” or “j.” One point on the scatter plot represents the response of a pair of channels to a pair of stimuli in a given condition (gray dots); horizontal and vertical histograms show marginal distributions for firing rate differences and correlation differences, respectively. Data from all sessions are aggregated. Difference in firing rates is calculated as the absolute difference between the geometric mean of the firing rates of the neuron pair (gray bars on Middle). SCC difference for a particular pair of neurons was calculated as the difference between the Pearson correlations in the two analyzed conditions (Bottom, dots represent individual trials). (B) Under a different condition where stimuli “k” and “l” are presented, joint distribution of firing rate differences and correlation differences for two novel stimuli (gray dots). To eliminate the effect of firing rate changes, the marginal distributions of firing rate differences in condition A and condition B are matched by subsampling the trials (green histograms). Firing rate difference-matched correlation differences are obtained by calculating correlation difference distributions (gold and purple histograms) from the subsampled joint distributions (black dots on the scatter on both A and B). (C) Using within-stimulus comparison as condition A and across-stimuli comparison as condition B (Left), dissimilarity of firing rates (Top row) and correlations (Bottom row) when the distributions of firing rate differences are intact (Middle) or matched (Right). Initial differences in firing rate dissimilarity (Top row, gray bars) are eliminated by CRM (Top row, green bars) but not in the dissimilarity of correlations (Bottom row, gray bars), which remain significant after CRM (Bottom row, colored bars, colors matching those of histograms at A and B).

To demonstrate the power of CRM, we used synthetic data in which the two conditions can be fully controlled (SI Appendix, Fig. S3). A network of 40 neurons was simulated in which membrane potential correlations and firing rates were set for each condition and the simulation matched the experimental conditions in terms of the amount of data used. In each experiment, the first condition assessed had identical firing rate and SCCs profiles in every trial (SI Appendix, Fig. S3A). We investigated three different scenarios for the second condition. First, dissimilarity of SCC matrices was assessed across trials with identical SCC patterns but different mean activations (SI Appendix, Fig. S3B). Under these conditions, we expect that, due to firing rate differences, SCCs will vary across trials. Indeed, dissimilarity of correlation matrices is higher in the condition where firing rate differences are present even though the membrane potential correlations are identical (SI Appendix, Fig. S3E). However, CRM eliminates this difference. Second, dissimilarity of SCC matrices was assessed across trials with identical mean activations but different SCC patterns (SI Appendix, Fig. S3C). As expected, dissimilarity of correlations remained significant in both the nonmatched and in the matched cases (SI Appendix, Fig. S3F). The last analysis tested the scenario where both firing rates and correlations show differences across trials (SI Appendix, Fig. S3D). Residual differences in correlation dissimilarity after CRM demonstrated that differences in membrane potential correlations can be identified in SCCs (SI Appendix, Fig. S3G).

We assessed within-stimulus and across-stimuli dissimilarity of SCC matrices using CRM on data recorded from V1 (Fig. 4C). As expected, CRM eliminates the condition dependence of firing rate dissimilarity (t test, P = 0.99, t = −0.02, df = 6,362). In addition, the analysis confirmed that differences in correlation dissimilarity are significant even after CRM (t test, P = 1.3e-13, t = −7.43, df = 6,362); therefore, stimulus specificity of the fine structure of SCC is not a result of changes in firing rates.

SCCs are dependent on tuning similarity (9, 10). We tested how this dependence may affect CRM on synthetic data. We used the same 40-neuron network as before but introduced dependence between the stimulus-driven changes in firing rates and correlations. First, only firing rates differed across conditions (SI Appendix, Fig. S4A). Second, across-condition firing rates were set such that for each pair of neurons firing rates were correlated with their membrane potential correlations. Increased SCC dissimilarity resulting from across-condition changes in firing rates could be removed with CRM at all levels of dependence between SCCs and tuning similarity. As expected, higher SCC dissimilarity was preserved when the two conditions differed both in firing rates and membrane potential correlations (SI Appendix, Fig. S4B).

Stimulus Structure Dependence of SCCs.

We argued that higher-order stimulus structure elicits differential responses at the network level both in V1 and at higher levels of processing. In our data, we identified stimulus-specific correlation structure in V1 activity congruent with the idea that high-level inferences impose differential top-down modulations at V1. This prediction, however, is not exclusive to hierarchical inference since it can be accounted for by alternative models. Therefore, we formulated a more specific prediction: if stimulus specificity is a consequence of stimulus-specific feedback from higher levels of processing, then removing higher-order structure from images should reduce stimulus specificity of correlations.

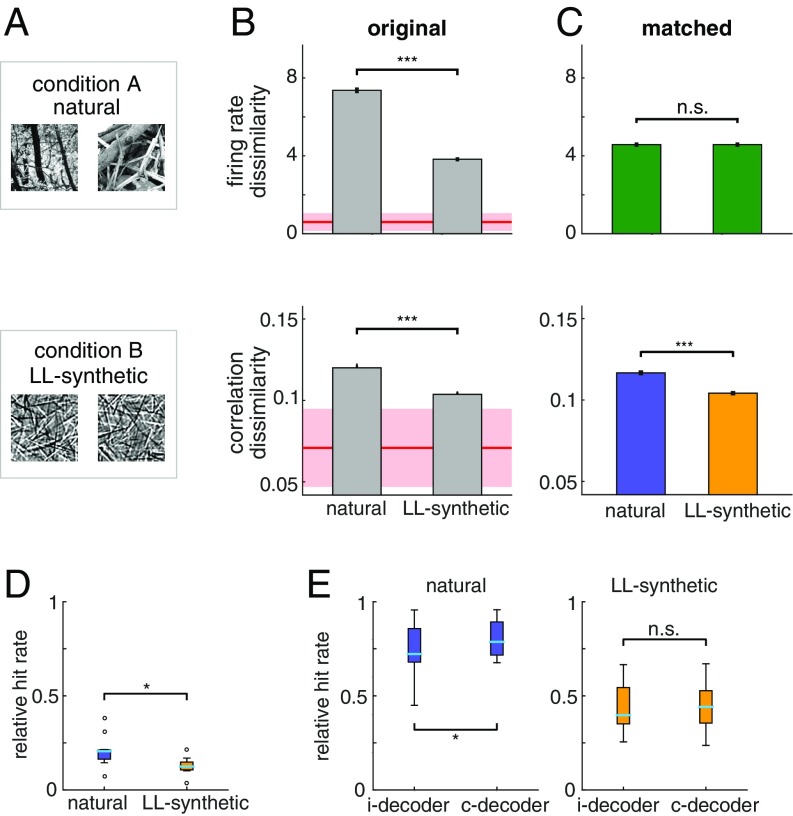
We tested this hypothesis explicitly by recording additional electrophysiological data in two monkeys, performing the same task. In these experiments, two sets of images were used: natural images and synthetic images. Synthetic images were constructed by overlaying Gabor functions with varying locations and orientations independently. These images retained the low-level structure preferred by V1 simple cells but contained no further dependencies [low-level (LL)–synthetic stimuli; Materials and Methods and SI Appendix, Fig. S5]. We calculated the average dissimilarity of firing rates and SCC matrices across natural images and compared them to the average dissimilarity of firing rates and correlations across LL-synthetic stimuli (Fig. 5A). We found that both firing rate dissimilarity and correlation dissimilarity were significantly higher for natural images than for LL-synthetic stimuli (Fig. 5B; t test, P = 7.4e-286, t = 37.29, df = 10,474, and P = 1.46e-21, t = 9.56, df = 10,474 for firing rate and correlation, respectively). Similar difference between the response distributions elicited by natural and LL-synthetic was found when we calculated the KL divergence of the correlations structures (paired t test, P = 1.44e-2, t = 3.11, df = 8; SI Appendix, Fig. S6A).

Fig. 5.

Comparison of stimulus specificity of correlation patterns induced by different stimulus structures. (A) Natural image patches and synthetic image patches generated from a V1 model of images (LL-synthetic) used in the experiments. (B) Stimulus specificity of firing rate responses (Top) and SCC patterns (Bottom) in the original (unmatched) data for natural and LL-synthetic images. While correlations show higher specificity for natural images, specificity of firing rate responses is also higher in the reference condition. Shaded areas show the extrapolated estimate of within-stimulus dissimilarity for both firing rates and correlations (SI Appendix). Note that the baseline for correlation dissimilarity is set to the mean of the extrapolated within-stimulus baseline minus 1SD. (C) CRM eliminates stimulus specificity of firing rate responses, but the residual dissimilarity of SCCs is still significantly higher for natural images than for LL-synthetic stimuli. Baseline for correlation dissimilarity as in B. (D and E) Decoding stimulus information from neuron population responses. (D) Performance of a decoder that learns about the correlation structure of the data using a z-scored version of the data. Z-scoring removes mean and variance information from the data leaving the correlations intact. The performance is calculated relative to the chance level (0 means chance performance, 1 means perfect performance). The decoder performs better than chance for the natural and LL-synthetic datasets but shows higher performance for natural stimuli. (E) Relative performance of the c-decoder and i-decoder on the original data for natural (Left) and LL-synthetic (Right) stimuli. The c-decoder performs better than the i-decoder for natural stimuli but not for synthetic stimuli.

The limited number of available repetitions establishes a lower bound on the dissimilarity measures (Fig. 3D). To directly obtain a lower bound for this experiment, the within-stimulus dissimilarities would have to be computed across data split into two halves. Such a manipulation, however, would result in higher variance in our primary measure of interest, the across-stimuli dissimilarity. Therefore, we obtained the lower bound indirectly, by extrapolating within-stimulus dissimilarity from dissimilarities calculated for lower numbers of repetitions (by subsampling the available data; SI Appendix).

Differences in firing rate dissimilarity can result in differences SCC dissimilarity. We applied CRM to eliminate such differences in firing rate dissimilarity (Fig. 5C; t test, P = 0.99, t = 0.015, df = 7,468). After this correction, residual SCC dissimilarity was still much higher for natural than for LL-synthetic stimuli and highly significant (t test, P = 4.17e-10, t = 6.26, df = 7,468). In addition, the difference was not sensitive to the time window chosen here: both the original and the matched data showed higher stimulus specificity to natural than to LL-synthetic stimuli for various temporally shifted windows (SI Appendix, Fig. S7).

Eye movements can introduce correlated changes in neuronal responses and can in principle lead to stimulus specificity of SCCs. While the difference in SCCs induced by natural and LL-synthetic images is a more specific prediction of hierarchical inference, similar patterns might arise from eye movements, under specific assumptions about neuronal sensitivities. A full receptive field characterization was not feasible in our paradigm (Materials and Methods); therefore, we investigated indirectly how eye movements affect our findings. We found that the frequency of saccades initiated after stimulus onset was similar for natural images and controls (t test, P = 0.84; SI Appendix, Fig. S8A), suggesting that the different stimulus types attracted eye movements in a similar manner. More interestingly, we identified a temporal window after the attentional cue onset, where saccade probability was dramatically reduced (SI Appendix, Fig. S8B). This temporal window coincided with that where the frequency of microsaccades decreases (49), which provided us with an ideal control opportunity. We repeated the SCC dissimilarity analysis with natural and LL-synthetic stimuli in two different time windows after cue onset. First, in the 300-ms time window in which both large and small eye movements are inhibited (SI Appendix, Fig. S8C; t test, P = 0.043, t = 2.022, df = 7,604), and second, in a slightly larger 400-ms window that matched our previous analysis (SI Appendix, Fig. S8D; t test, P = 0.002, t = 3.082, df = 7,494). The comparisons showed similar differences between natural and LL-synthetic images as found before, suggesting that eye movements are not the main drivers behind the observed effects.

Our analyses revealed that SCCs have stimulus-specific structure; however, it remains to be demonstrated whether stimulus-specific correlations convey information about stimulus identity. We tested whether such information can be recovered through simple decoding approaches. We constructed decoders that were sensitive to different aspects of the response statistics (SI Appendix). The stimulus-dependent correlation decoder (c-decoder) learned the stimulus-dependent mean responses and featured separate covariance structure for every stimulus. The independent decoder (i-decoder) learned about the mean responses but was agnostic to the correlation structure. We assessed the performance of the decoders on the spike count responses to natural images from all of the recorded sessions. We tested whether the stimulus specificity in the covariance structure alone is sufficient to obtain information about stimulus identity by z-scoring the data and applying the c-decoder. Higher-than-chance decoding performance demonstrated that the decoder could consistently discriminate stimulus information from the correlation structure alone (t test, P = 0.032, t = 2.34, df = 16; Fig. 5D). However, the decoding performance depended on the type of stimulus applied: decoding of z-scored responses was more efficient for natural than for synthetic stimuli (paired t test, P = 0.033, t = −2.57, df = 8; Fig. 5D). Finally, to test whether the correlation structure carries information beyond the mean and variance of the responses, we tested the decoders on the original data (not z-scored). The analysis revealed that the performance of the i-decoder was consistently lower than that of c-decoder for natural stimuli but not for synthetic stimuli (paired t test, P = 0.37, t = −0.94, df = 8; Fig. 5E), suggesting that correlations are more relevant for natural images.

Controls for Finite Data Effects and Global Fluctuations.

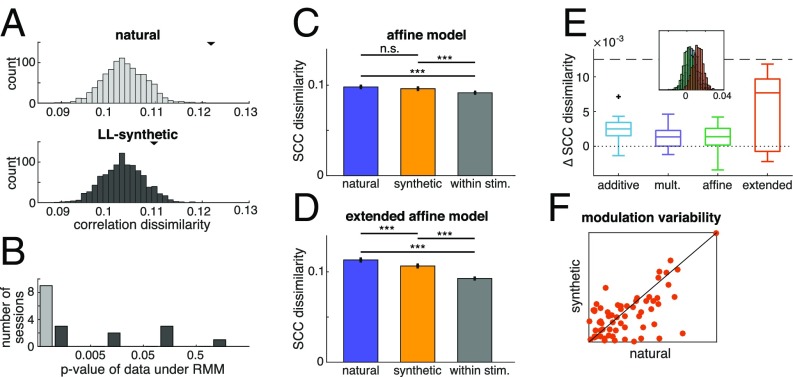
Since our measurements are based on a finite population, firing rate has an effect on the variability of measured correlations: higher firing rates can limit the number of possible binary words formed from spikes, which can affect dissimilarity measurements. We constructed surrogate data using a phenomenological model of population activity, the raster marginal model (RMM) (SI Appendix), to control for this effect. The RMM provided a distribution of correlation matrices for every single image. Correlation dissimilarities were calculated from 1,000 correlation matrices obtained from each distribution (Fig. 6A). The histogram of correlation dissimilarities determines how likely it is that the dissimilarity measured on the data can be traced back to changes in basic firing statistics. Histograms obtained for the two conditions did not show significant differences in their mean (t test, P = 0.12, t = 1.54, df = 1,998), but the histogram for natural images revealed that the dissimilarity obtained from the data were in the tail of the distributions of possible dissimilarities (P < 0.001; while for synthetic images, P = 0.076; Fig. 6A). Analysis of all recorded sessions reveals that, in all cases, the activity evoked by natural images is highly unlikely under the RMM model (Fig. 6B). However, responses to the LL-synthetic stimulus set were significantly different from an RMM account only in five out of nine sessions at the P < 0.05 level. Taken together, comparison of the results obtained with natural and LL-synthetic data, excludes the possibility that observed dissimilarities were merely resulting from changes accounted for by the RMM model.

Fig. 6.

(A) Raster marginal models (RMMs) fitted to the spike trains recorded in response to natural images and to LL-synthetic images in an example session (Top and Middle, respectively). Distributions of dissimilarities are calculated between correlation matrices sampled from RMMs obtained from the population activities recorded for individual stimuli. Black triangles mark the mean dissimilarity calculated from the electrophysiological data. (B) Likelihoods of recorded dissimilarity under the RMM model in all of the sessions in the natural and LL-synthetic conditions (colors match those of the Top and Middle). Dissimilarity indices of 500 pairs of correlation matrices sampled from the RMM model were used to assess the likelihood of the recorded data. Stimulus dependence of correlation matrices under natural image stimulation could not be explained by an RMM model in any of the recorded sessions. Dissimilarity determined for LL-synthetic stimuli was significantly different from the RMM model in five out of nine sessions. (C–F) Analysis of the joint-fluctuation models (JFMs). (C) SCC dissimilarity of synthetic data generated from the affine model fitted to an example recording session. SCC shows stimulus specificity both for synthetic and natural stimuli, but stimulus specificity of SCCs is not significantly different for synthetic and natural stimuli. (D) Same as C but for the extended affine model. Stimulus-specific additive component introduces sensitivity to the covariance structure characteristic of the responses of natural images, which supports a difference in SCC dissimilarity between natural and synthetic stimuli. (E) Multiple simulations with the same parameters yield a distribution of differences between SCC dissimilarities (Inset, colors of example models match those in the main panel). Sensitivity of the JFMs to differences in natural and synthetic stimuli was measured by the mean of the differences calculated for every given session was calculated for the four JFMs. (F) Comparison of stimulus specificity of parameters in the extended affine model for natural and LL-synthetic stimuli. Variability of the weight of the stimulus-specific additive component was measured. Individual points represent separate channels. All recording sessions are included.

We wanted to test whether simple collective modulations of the stimulus-induced drive can account for the patterns in correlation dissimilarities observed in our experiments. The phenomenological joint-fluctuation model (JFM), which incorporates collective additive and/or multiplicative noise components, has been shown to account for stimulus-specific SCCs in responses to superimposed grating stimuli (15). Three variants of the JFM include the following: (i) in the multiplicative model, featuring a common gain modulation, ${\text{g}}_{\text{t}}$, of the stimulus-specific drives of individual neurons (n), ${\text{d}}_{\text{n},\text{s}\left(\text{i}\right)}$, firing rates are covarying on a trial-by-trial basis, ${\text{f}}_{\text{n},\text{t}}={\text{g}}_{\text{t}}{\text{d}}_{\text{n},\text{s}\left(\text{i}\right)}$; (ii) in the additive model, the trial-by-trial collective fluctuation, ${\text{a}}_{\text{t}}$, is added to the stimulus-specific drive: ${\text{f}}_{\text{n},\text{t}}={\hspace{0.17em}\text{d}}_{\text{n},\text{s}\left(\text{i}\right)}+{\text{a}}_{\text{t}}{\hspace{0.17em}\text{h}}_{\text{n}}$; (iii) the affine model features both sources of joint fluctuations, ${\text{g}}_{\text{t}}$ and ${\text{a}}_{\text{t}}$: ${\text{f}}_{\text{n},\text{t}}={\text{g}}_{\text{t}}{\text{d}}_{\text{n},\text{s}\left(\text{i}\right)}+{\text{a}}_{\text{t}}{\text{h}}_{\text{n}}$. Stimulus dependence in JFM is established through the stimulus-specific drive, ${\text{d}}_{\text{n},\text{s}\left(\text{i}\right)}$, which is different from our proposed functional model where joint modulations can also have explicit dependence on stimulus. To obtain a phenomenological model with the same level of flexibility as our proposed model, we extended the JFM such that the additive component became dependent of the stimulus by fitting separate modulatory weights, ${\text{h}}_{\text{n},\text{i}}$, for each image i (extended affine model).

We synthetized population spike counts from the phenomenological models by fitting the values of trial-invariant variables, ${\text{d}}_{\text{n},\text{s}\left(\text{i}\right)}$ and h, and the distributions of trial-dependent variables, g and a, to spiking responses to natural or synthetic images (Materials and Methods). We calculated the dissimilarity of SCCs for natural and synthetic image pairs and provided a baseline by calculating within-stimulus dissimilarities. Dissimilarities of a set of synthetic trials with the parameters fit to one particular recording session from the affine model have the same magnitude as those in physiological data (Fig. 6C) and SCCs are specific to stimuli (across-stimulus dissimilarities vs. within-stimulus dissimilarity, t tests, for natural and synthetic images, P = 2.4e-4, t = −3.67, df = 14,004; P = 2.06e-7, t = −5.2, df = 14,004, respectively), confirming earlier results (15). However, difference between dissimilarities measured for natural and synthetic stimuli was not evident in the affine model (t test, P = 0.17, t = 1.37, df = 10,474) but was significant in the extended affine model (t test, P = 1.3e-4, t = 3.82, df = 10,474; Fig. 6D).

Simulations of multiple sets of trials introduce variability in SCC differences (Fig. 6E, Inset). We use the mean of SCC differences to compare how different phenomenological models can capture the stimulus specificity of SCC measured in recorded data (Fig. 6E). Differences between the dissimilarities in natural and synthetic stimuli were close to zero in all three variants of JFM, only the extended affine model could produce differences comparable to those measured from neuron populations. We assessed how fitted model parameters behave for different stimuli (Fig. 6F) to obtain an insight on why the extended affine model can replicate the physiological data.

We calculated the variability in the collective modulation across images for the two stimulus sets by calculating the variability in the fitted values of ${\text{h}}_{\text{n},\text{s}\left(\text{i}\right)}$ across stimuli. Comparing variability for natural and LL-synthetic images revealed higher variability in natural images and explained the higher stimulus specificity of SCCs in the extended affine model. In summary, differences in correlation dissimilarities for stimuli with different complexities could not be explained by phenomenological models that assumed stimulus-independent joint comodulation of neurons but could be reproduced by models that assumed stimulus-specific joint modulation, thus having a similar expressive capacity as the proposed hierarchical inference model.

Higher-Order Structure over Elementary Features Induces Stimulus-Specific Correlation Patterns.

Our experiment contrasting natural images and LL-synthetic images indicated that higher-order stimulus content contributes to the stimulus specificity of SCCs. LL-synthetic images were constructed to mimic filter properties of V1 simple cells. However, using Gabor functions to construct images with low-level structure also affected the spectral content of the stimuli. To rule out the possibility that changes in spectral content and not high-order structure underlie the observed differences in SCCs, we performed two control experiments.

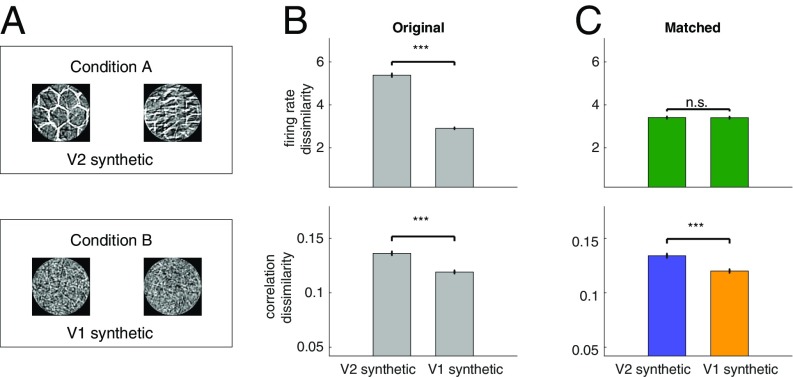
First, keeping the spectral content similar to the LL-synthetic stimuli, we constructed stimuli with high-level structure. In particular, we generated an additional set of synthetic stimuli that combined Gabor functions into texture-like patterns, thus introducing the kind of higher-level structure, which is expected to elicit differential responses in V2 (40). In additional recordings, we interleaved synthetic images characterized by low-level structure (LL-synthetic stimuli) with texture-like synthetic images characterized by high-level structure (HL-synthetic stimuli; Fig. 7A). Both firing rates and SCCs showed higher specificity for HL-synthetic stimuli than for LL-synthetic stimuli (Fig. 7B; t test, P = 2.6e-180, t = 29.3, df = 8,998, and P = 5.56e-16, t = 8.11, df = 8,998 for firing rates and correlations, respectively). Comparison of responses to HL-synthetic and LL-synthetic stimuli using KL divergence of SCCs distributions also showed a higher dissimilarity for HL-synthetic stimuli (paired t test, P = 1.9e-2, t = 4.63, df = 3; SI Appendix, Fig. S6B). CRM was applied to eliminate differences caused by firing rate dissimilarity (t test, P = 0.94, t = 0.076, df = 6,794; Fig. 7C). This manipulation did not alter the conclusion on stimulus specificity of SCCs: the difference between the correlation dissimilarity remained significant (t test, P = 8.55e-09, t = 5.76, df = 6,794).

Fig. 7.

Comparison of stimulus specificity of correlation patterns evoked by stimuli with different levels of statistical structure. (A) Condition A, a set of synthetic image patches in which filter co-occurrences define a texture structure (HL-synthetic stimuli); condition B, a set of synthetic image patches generated from a V1 model of images (LL-synthetic stimuli). (B) Stimulus specificity of firing rate responses (Top) and SCC patterns (Bottom) in the original (unmatched) data. While correlations show higher specificity for HL-synthetic images, specificity of firing rate responses is also higher in the first condition. The baseline for correlation dissimilarity is set to the baseline used in Fig. 5. (C) Firing and correlation dissimilarities after applying the CRM procedure. CRM eliminates stimulus specificity of firing rate responses, but the residual dissimilarity of SCCs is still significantly higher for HL-synthetic stimuli than that for LL-synthetic stimuli.

Second, we recorded data in which the natural images were contrasted to phase scrambled controls—altered images with identical spectral content (50–52) (Materials and Methods). We found a significant decrease in SCC dissimilarity to controls (t test, P = 2.12e-02, t = 2.31, df = 644; SI Appendix, Fig. S9) compared with the original images.

Taken together, these results demonstrate that SCCs are stimulus specific, and more importantly that the stimulus specificity hinges upon the presence of higher-order stimulus structure: removing high-level structure reduces stimulus specificity, while reintroducing high-level structure in controlled synthetic images restores the stimulus specificity of SCCs.

Discussion

We recorded population responses from area V1 of awake, task-engaged monkeys, and investigated how the correlation structure of V1 activity depends on stimulus content. Our analysis established that, upon presentation of natural scenes, the fine structure of correlations was stimulus specific. Crucially, by designing synthetic images with controlled statistical structure, we demonstrated that the stimulus specificity of SCCs was dependent on stimulus complexity: stimuli characterized by low-level structure elicited reduced stimulus specificity in SCCs, while images characterized by both low- and high-level structure elicited increased stimulus specificity. We developed a CRM technique and proved that the fine structure of SCCs could not be trivially explained by fluctuations in firing rates. Moreover, a decoding analysis confirmed that knowledge of the correlation structure was beneficial for decoding information on stimulus identity. We argued that the stimulus dependence of SCCs is a natural consequence of top-down modulations in the ventral stream: inferences about high-level structure of images provide context for the interpretation of low-level structure through the internal dynamics of the cortex. Finally, we showed that, while the qualitative changes in stimulus specificity of SCCs could be explained by a probabilistic hierarchical model of perceptual inference, they could not be accounted for by a range of other phenomenological models, based on either finite data effects or simple collective modulations of responses.

Parallel recordings from multiple neurons permit the investigation of higher-order statistics of neuronal responses. Hence, the assessment of SCCs, commonly addressed as “noise correlations,” has become a central topic in neuroscience (11, 13, 14, 52). Although measurement of SCCs only concern second-order statistics, accurate measurement (9, 13) and interpretation of variations in SCCs (53) proved to be challenging. Factors that affect SCC estimation include task design, wakefulness, eye movements, firing rate, cortical distance, tuning similarity, spike isolation, and spike width (13, 47, 48). We used a paradigm that permits a large number of repetitions, which limits sample variance in SCC measurements. Although anesthesia can permit a larger number of repetitions and/or a larger stimulus set, network-wide changes in the internal dynamics can introduce artificial correlation structures (19, 54). Using awake and task-engaged monkeys eliminates this confound (35). Eye movements have been shown to contribute to correlations in the visual cortex (55). We introduced an analysis that sought to reproduce our results under conditions in which saccades and microsaccades are minimized. This analysis confirmed a higher SCC specificity for stimuli with high-level structure immediately after the onset of the attentional cue when the occurrence of eye movements dwindles. We developed the CRM to control for firing rate changes across conditions and demonstrated its power on synthetic data before applying it to physiological data. This analysis confirmed that our conclusions on stimulus dependence of correlations were not a consequence of changing firing rates.

Earlier studies in mice used two-photon calcium imaging to characterize the changes in correlation structure that arise as a result of changes in stimulus statistics (14, 16), which extended earlier observations on the effects of stimulus statistics on higher-order single-cell statistics (52, 56). However, in these studies, pairwise correlations were assessed in response to movies and sequences of moving and static gratings, making it impossible to test the predictions of hierarchical inference on responses to individual stimuli.

Our approach can be regarded as an extension of earlier work investigating the patterns of mean responses in the hierarchy of the visual cortex (40). It has been shown that variance in mean responses in V2 can be well predicted by variations in factors that determine the statistics necessary for the generation of natural textures, while variations in mean responses in V1 can be predicted by variations in statistics at the level of independent Gabor-like edge filters. Similarly, contextual modulation of V1 activity by top-down influences from V2 neurons was demonstrated when high-level inferences were made in artificial images (24, 25). Furthermore, V1 was shown to receive delayed top-down influence relative to V2 (24). The long time window we used in our analysis to limit measurement noise was not effective to investigate such temporal dynamics in the interactions. Nevertheless, these observations complement our results and are fully compatible with probabilistic inference in a hierarchical internal model of natural images, in which mean responses correspond to the most probable interpretation of the stimulus.

Probabilistic computations require the representation of probability distributions. Representation of probability distributions was proposed to be achieved by stochastic sampling (32, 44), which interprets response variability as a direct consequence of perceptual uncertainty. The stochastic sampling framework generalizes naturally to hierarchical computations (32). Recently, it was shown that stimulus dependence of both membrane potential and spike count variability in V1 can be predicted by a model of natural images (30). This model, however, lacked the hierarchical structure presented here and was therefore unable to account for stimulus-dependent changes in correlation patterns. However, it provided a simple but important demonstration of contextual modulation of V1 responses: the assessment of stimulus contrast for a complete image patch affected the interpretation of local image elements (57). Such contextual modulation was shown to result in divisive normalization (39). Divisive normalization and more specifically surround suppression (58) are algorithmic motifs that can realize the computational principles put forward in our study. Such algorithmic motifs provide the nervous system with tools to calculate the quantities required by the functional model proposed here, and thus can highlight how processes within V1 can contribute to hierarchical inference. Our results fit naturally in the sampling framework by assuming that neural activity patterns represent multivariate samples from the probability distributions both at the level of V1 and higher-level areas, for example, V2 (Fig. 1).

Alternative Interpretations.

Patterns in higher-order statistics of neuronal responses beyond the mean activity, namely single-cell variability and SCCs, have been observed in association with task-related modulatory effects, such as those driven by attention (18, 19, 59) and in association with stimulus-related modulatory effects, such as those occurring during the perception of natural scenes (14, 52, 56). Computations underlying both of these processes invoke high-level inferences: inference of task variables in the case of attention and inference of high-level stimulus features, for example, object identity, in the case of perception. In both cases, inference of high-level variables breaks the feedforward processing hierarchy in the visual cortex and introduces top-down effects (33). Such modulatory effects of top-down computations related to attention have been demonstrated in population responses throughout the visual processing hierarchy, both regarding single-cell statistics [mean (60) and variance (34)] and pairwise statistics [SCCs (18, 19, 36, 37, 59)]. An interesting link between task execution and SCCs can be established by analyzing information limiting correlations (61). Information limiting correlation is a form of correlation that is aligned with the covariation of neural responses caused by perturbing the variable being assessed in the task. Such correlations depend on the task, that is, if the task is discrimination of a set of stimuli, information limiting correlations will depend on the stimuli. It is the subject of further investigations how the changes in correlations found in our study are related to information limiting correlations.

A recent phenomenological model of correlations suggested that multiplicative components might reflect top-down influences (15). Here, the so-called affine model could account for patterns in correlations emerging in anesthetized animals through collective gain modulation. However, our analyses demonstrated that, in awake task-engaged animals, stimulus structure dependence cannot be accounted for by this simple phenomenological model. A simple collective modulation of responses cannot explain our main experimental results, which show that joint activation patterns in V1 neuron populations depend on the presence of higher-level image features.

Deep networks, which are characteristically hierarchical architectures for image processing, have become vastly successful in recent years, closing the gap between human and machine performance in complex visual tasks (62, 63). Interestingly, the sensitivities of hierarchically organized neurons in the deep learning model show structural similarities to those in the biological system (64, 65). However, the predominantly feedforward architecture of deep networks remains at odds with the top-down, recurrent connections observed in the biological system. Recently, when performance of feedforward architectures was tested against that of humans and monkeys in an object perception task, systematic differences were found (66), possibly indicating the requirement of feedback. Our proposed probabilistic model differs from deep learning architectures by representing the uncertainty in inferences, which is intimately linked to the feedback influences incurred by the model. While the predictions of deep networks on mean responses provide valuable insights into hierarchical processing, the patterns in SCCs investigated here arise as a consequence of feedback and are not predicted by feedforward architectures. Recent advances may provide the tools to investigate hierarchical inference in deep generative models of vision (67, 68), allowing for further insights into the joint statistics of neuronal responses in the visual cortex.

Testable Predictions of the Model.

Analyzing mean responses of V1 and V2 neurons to texture images (41) revealed that the V1 and V2 neurons display different levels of invariance against manipulations at different levels of statistics: while mean responses of both V1 and V2 neurons showed a high level of variance to texture type (termed texture family), mean responses of V2 neurons, but not those of V1 neurons, were largely invariant across different image realizations from the same texture family. According to our account, it is the high-level inference that determines the correlation structure, and since different samples from the same texture family elicit similar responses in V2, we expect the correlation structure to be more similar across samples from the same texture family than across families. The same behavioral paradigm could accommodate an experiment with two or three texture families, each family containing three samples. Hierarchical probabilistic inference predicts that, while V1 responses will show high specificity to both sample identity and texture family, correlations show invariance across samples but not across families.

Materials and Methods

Electrophysiological Recordings.

This study was conducted on two adult rhesus macaques (Macaca mulatta; monkey A, male, 8 y; and monkey I, female, 12 y). All experimental procedures were approved by the local authorities (Regierungspräsidium, Hessen, Darmstadt, Germany) and were in accordance with the animal welfare guidelines of the European Union’s Directive 2010/63/EU. We recorded multiunit activity (MUA) from V1 using a chronically implanted microdrive containing 32 independently movable glass-coated tungsten electrodes with impedance between 0.7 and 1.5 MΩ and 1.5-mm interelectrode distance (SC32; Gray Matter Research; 69). The recording chamber was positioned based on stereotactic coordinates derived from MRI and CT scans following (70). Signals were amplified (TDT, PZ2 preamplifier) digitized at a rate of 25 kHz and bandpass filtered between 300 and 4,000 Hz for MUA recordings. For MUA analysis, a threshold was set at 4SD above noise level to extract spiking activity.

Behavioral Paradigm.

Animals were seated in a custom-made primate chair at a distance of 64 cm in front of a 477 × 298-mm monitor (Samsung SyncMaster 2233RZ; 120-Hz refresh rate). Eye tracking was performed using an infrared-camera eye-control system (ET-49; Thomas Recording). At the beginning of each recording week, the receptive field locations and orientation preferences of the recorded units were mapped with a moving light bar drifting in a randomized sequence in eight different directions (SI Appendix, Fig. S1) (71). The two monkeys performed an attention-modulated change detection task. To initiate a trial, the monkey had to maintain fixation on a white spot (0.1° visual angle) presented in the center of a black screen and press a lever. After 500 ms, two visual stimuli appeared in an aperture of 2.8–5.1° at a distance of 2.3–3.2° from the fixation point. One of the stimuli covered the receptive fields of the recorded units, the other was placed at the mirror symmetric site in the other hemifield. After an additional 700 ms, the color of the fixation spot changed, cuing the monkey to direct its covert attention to one of the two stimuli. When the cued image was rotated (20°), the monkey had to release a lever within a fixed time window (600 ms for monkey A; 900 ms for monkey I) to receive a reward. A break in fixation (fixation window, 1.5° diameter) or an early lever release resulted in the abortion of the trial, which was announced by a tone signal. The number of completed trials varied between 524 and 1,110 per recording session. No more than one session was recorded on a given day. To obtain a balance between the reliable estimation of SCCs (Fig. 3D) and the number of comparisons between stimulus pairs, we used six or eight different stimuli per session, resulting in 65–180 repetitions (124 on average) per stimulus, 64 stimuli in total for sessions showing natural and synthetic images and 24 for sessions showing only synthetic images. The order of stimulus presentations was randomized. The number of good channels varied between 15 and 23 per session. Trials in which the signals were contaminated by clear electrical artifacts were discarded from the analysis. The maximum number of trials discarded from a recording session was 3 (0.8 on average).

Visual Stimulus Design.

Stimuli were static, black and white natural images, phase scrambled versions of natural images, or synthetic images generated from an image model. Stimuli were presented in a square or circular aperture. Static stimuli were chosen to avoid potential confounds caused by firing rate-dependent or stimulus-dependent variances and correlations. Phase-scrambled images were generated by obtaining the Fourier-transformed versions of the original images and randomizing the phase spectrum under the constraint of symmetric complex conjugates. We generated synthetic control stimuli that matched the low-level statistical properties of the natural images, but lacked any high-level statistical structure. As neurons in V1 are sensitive to oriented edges, we designed a set of 3,000 Gabor functions adapted to the receptive field characteristics of the recorded neurons. The Gabor functions differed in their positions and orientations covering the image patch uniformly. Spatial scale of Gabor filters was matched to that of visual cortical neurons at the eccentricity our recordings were performed at. For each Gabor function, an activation variable was set that determined the level of contribution of the particular Gabor function to the image. The activation-scaled Gabor functions were linearly combined to obtain a synthetic image patch. For each synthetic control stimulus, we sampled the activations of 500–3,000 Gabor functions from the empirical distribution of Gabor filter responses to a particular natural image. The pixel distributions of synthetic control stimuli were then matched to the corresponding natural ones in terms of mean (luminance) and variance (contrast) (SI Appendix, Fig. S5). For a second set of experiments, we reintroduced higher-level statistical structure to synthetic images by calculating the responses of the filter set on photos of natural texture patterns, then setting up a correlation matrix for filter activations in such a way that two filters were more strongly correlated if their responses to the texture photo were more similar. Samples from this correlated filter activation distribution were used to linearly combine activation-scaled Gabor functions. This procedure resulted in texture-like synthetic patterns corresponding to the statistical structures typically represented in V2. In each recording session, half of the stimuli were synthetic images with statistical structure corresponding to the representation in V1 (LL-synthetic stimuli), and the other half consisted of natural and synthetic images with structures corresponding to representations in V2 (HL-synthetic stimuli), in the first and second set of experiments, respectively. An additional set of LL-synthetic stimuli was generated for HL-synthetic stimuli such that the spectral distribution of LL-synthetic images matched that of HL-synthetic images.

To generate images where the frequency spectrum is not affected but higher-order structure is removed, we generated phase scrambled versions of natural image patches. We computed a 2D fast Fourier transform (FFT), resulting in a complex magnitude/phase map of each image. The phase values were scrambled by assigning a random value to each element taken from a uniform distribution across the range (−π, π). An inverse FFT was then applied to the resulting magnitude/phase maps to produce scrambled control versions of the original images.