Transitions between foot postures are associated with elevated rates of body size evolution in mammals

Significance

Terrestrial mammals have evolved diverse foot postures, contributing to their ecological success. Yet, how postures evolved and how they affected body size evolution remain largely unknown. Here we statistically reconstruct the paths and trajectories in foot posture evolution and explicitly test the effects of posture on body size evolution, using phylogenetic Bayesian approaches. We found that upright foot postures evolved in a directional manner, from flat-footed ancestors, to tiptoed, and then to hooved descendants. Furthermore, transitions to different foot postures are associated with increases in rates of body size evolution, rapidly leading to larger descendants, demonstrating how transitions between foot postures have had profound influences on mammalian body size evolution.

Abstract

Terrestrial mammals have evolved various foot postures: flat-footed (plantigrady), tiptoed (digitigrady), and hooved (unguligrady) postures. Although the importance of foot posture on ecology and body size of mammalian species has been widely recognized, its evolutionary trajectory and influence on body size evolution across mammalian phylogeny remain untested. Taking a Bayesian phylogenetic approach combined with a comprehensive dataset of foot postures in 880 extant mammalian species, we investigated the evolutionary history of foot postures and rates of body size evolution, within the same posture and at transitions between postures. Our results show that the common ancestor of mammals was plantigrade, and transitions predominantly occurred only between plantigrady and digitigrady and between digitigrady and unguligrady. At the transitions between plantigrady and digitigrady and between digitigrady and unguligrady, rates of body size evolution are significantly elevated leading to the larger body masses of digitigrade species (∼1 kg) and unguligrade species (∼78 kg) compared with their respective ancestral postures [plantigrady (∼0.75 kg) and digitigrady]. Our results demonstrate the importance of foot postures on mammalian body size evolution and have implications for mammalian body size increase through time. In addition, we highlight a way forward for future studies that seek to integrate morphofunctional and macroevolutionary approaches.

Mammals have come to occupy a wide range of ecological niches; they span six orders of magnitude in body size (1) and inhabit most terrestrial environments. Adapting to diverse environments, mammals have evolved various foot postures that can be largely summarized into plantigrady (P; walking on the whole foot, e.g., mice, rats, squirrels, and humans), digitigrady (D; walking on toes, e.g., cats and dogs), and unguligrady (U; walking on hooved tiptoes, e.g., deer and horses) (2). These foot postures are tightly associated with the ecology of mammals: cursorial and graviportal mammals are digitigrade or unguligrade, whereas fossorial, arboreal, ambulatory, and saltatorial (2, 3) mammals are plantigrade (although ref. 2 considers salutatory as a distinct ecomorph). Ecological adaptations associated with each posture are most prominent in the morphology and biomechanics of the autopod (ulna + radius/tibia + fibula) and zeugopod (wrist + finger/ankle + toe), offering different advantages in various aspects of species biology (4–8).

Despite the evolutionary importance of autopod and zeugopod adaptations that are associated with foot postures, precisely how the different postures evolved across the mammalian tree of life remains poorly understood. Biomechanical predictions along with the fossil record provide us with some snapshots of how a few extinct species moved, which hint at how foot postures evolved (9–14). However, current hypotheses of locomotor evolution are yet to be tested statistically in an evolutionary context using empirical foot posture data covering a broad taxonomic sample.

Phylogenetic comparative methods are powerful tools with which one can statistically infer past events through Earth history while characterizing large-scale macroevolutionary processes (15). Accounting for and using shared ancestry as described by phylogeny is crucial in understanding evolution because apparent similarities/differences could simply owe to interrelationships (16, 17).

If we assume transitions between each pair of foot postures are equally probable, the expectation (the null hypothesis, H₀) would be that transitions among foot postures would have occurred in any direction between any pair (Fig. 1A). Hints from the fragmentary fossil record indicate that the null hypothesis may not be true, especially with regard to how unguligrady arose (9, 10, 12, 13) (Fig. 1B). To gain a more complete understanding of the evolution of foot postures we use a Bayesian phylogenetic approach (16, 18) to infer patterns of transitions among foot postures across the mammal tree of life using a comprehensive dataset collected for extant species. Our approach does not explicitly make any a priori assumptions or constraints on patterns of transitions among foot postures.

Fig. 1.

Null hypothesis and prior expectations of evolutionary transitions among foot postures. (A) Null hypothesis where transitions among all foot postures in any direction are equally probable. (B) Prior expectations of transitions between foot postures based on the phylogenetic distribution of data and the fossil record. Fossil evidence suggests that unguligrady evolved from digitigrady in artiodactyls and perissodactyls. Foot postures are represented by colored silhouettes: black, plantigrady; blue, digitigrady; and pink, unguligrady. Horse, opossum, and cat silhouettes courtesy of PhyloPic/Mercedes Yrayzoz, Sarah Werning, and Steven Traver.

Foot postures have been suggested to influence the evolution of body sizes (19). With this in mind, understanding how foot postures evolve may provide us with a better understanding of how body size evolved in mammals. Lovegrove and Haines (19) demonstrated that the distribution of mammalian body sizes may be explained by multiple distributions—with each subdistribution tied to a different foot posture (P, D, and U)—sufficiently better than by a single distribution, classically regarded as being right-skewed (SI Appendix, Fig. S1) (20–23). This notion fits with a previous empirical observation that the mammalian species body size distribution actually deviates from the classic single right-skewed distribution mainly owing to an underabundance of species around 1 kg and overabundance of species around 300 kg (24). Because different locomotor modes are associated with differences in body sizes (phylogenetic median body mass: plantigrady, 0.75 kg; digitigrady, 1.35 kg; and unguligrady, 78.1 kg) (Fig. 2), it follows that transitions from one posture to another may be accompanied by rapid changes in body size; these could be in line with Simpson’s (25) well-known notion of quantum evolution. Thus, we would expect accelerated rates of body size evolution along branches associated with transitions from one foot posture to another, particularly transitions into unguligrady given the extraordinarily larger average body sizes of unguligrade taxa compared with taxa of other foot postures (Fig. 2).

Fig. 2.

Phylogenetically corrected mean body sizes for each foot posture. Posterior distributions of estimated body mass accounting for shared ancestry for each foot posture, plantigrady (black), digitigrady (blue), and unguligrady (pink), using a variable-rates (VR) phylogenetic regression model (31) in BayesTraits. Differences between foot postures are calculated as the proportion of the posterior in which differences in estimated coefficients cross zero using a threshold value of 0.05 (p_MCMC < 0.05). Digitigrady and unguligrady are significantly different from plantigrady (p_MCMC < 0.05). Horse, opossum, and cat silhouettes courtesy of PhyloPic/Mercedes Yrayzoz, Sarah Werning, and Steven Traver.

Results and Discussion

We inferred transition rates among the different foot postures on a newly collected dataset from 880 species of extant mammals (Methods and SI Appendix) and a comprehensive species-level time-calibrated phylogeny (26), using a reversible-jump continuous time Markov model (16). We find strong support for the notion that the ancestral mammal was plantigrady P (probability of state P, P_P = 1). The dominant pattern that we reveal is that transition rates (q_ij, where i and j are two states) between P and D (q_PD and q_DP) and between D and U (q_DU and q_UD) are nonzero, with transition rates q_PU and q_UP being zero in the majority of the posterior sample (Fig. 3A), consistent with the fossil record (Fig. 1B) (2). This exact combination of nonzero transition rates (Fig. 3A) occurs as the predominant model in the posterior sample (57%) with the next most frequent model of transitions (37% of the posterior) having q_UP as a nonzero rate instead of q_UD (Fig. 3B).

Fig. 3.

Continuous time Markov multistate model. (A) The most frequent transition model in the posterior of models (57% of the posterior). Arrows represent nonzero median transition rates. The reconstructed ancestral mammalian foot posture is plantigrady (probability of state P, P_P = 1). (B) Second most frequent transition model (37% of the posterior of models). Arrows represent nonzero transition rate estimates. Histograms of transition rates across the posterior sample are shown for each nonzero transition. Foot postures are represented by colored silhouettes: black, plantigrady; blue, digitigrady; and pink, unguligrady. Horse, opossum, and cat silhouettes courtesy of PhyloPic/Mercedes Yrayzoz, Sarah Werning, and Steven Traver.

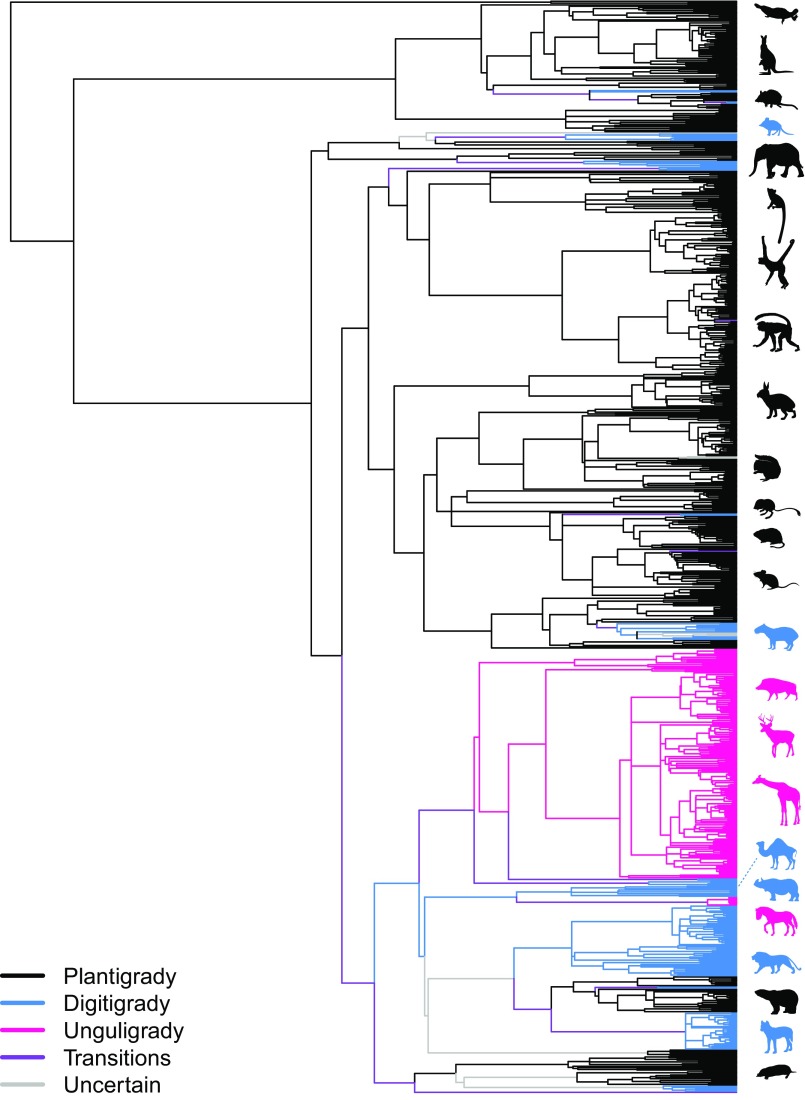
On average, there is a significant difference in body masses among the different foot posture groups: digitigrade taxa are larger than plantigrade taxa, whereas unguligrade taxa are larger than digitigrade taxa (Fig. 2). Thus, we hypothesize that transitions between foot postures would be associated with elevated rates in body size evolution compared with that within postures [${\sigma }_T^2$ > ${\sigma }_b^2$, where ${\sigma }_T^2$ is the rate of evolution associated with transitional branches, whereas ${\sigma }_b^2$ is the background (within-posture) rate of evolution]. To test whether rates of body size evolution differed between sets of branches along which transitions in foot posture occurred (Fig. 4, purple branches) with those that remained in the same posture [Fig. 4, black (P), blue (D), and pink (U) branches], we estimated separate rates of body size evolution for each partition of branches across the phylogenetic tree, where branches were partitioned according to differences in reconstructed nodal posture states (SI Appendix, Fig. S2). That is, for each branch of the phylogenetic tree, we compared the states of the ancestral and descendant nodes using ancestral state reconstructions (ASR) resulting from the top multistate model described in the text (Fig. 3A). We took the single ASR with the highest probability [at P_ASR > 0.67 (2/3), which is double the probability that a state can be reconstructed by chance alone (1/3); Fig. 4]. If the two states were identical (e.g., ancestor = D and descendant = D), then we would assign that branch to that specific posture (e.g., D) partition, but if they differed (e.g., ancestor = D and descendant = U), we would assign that branch to a transitional partition (SI Appendix, Fig. S2). Branches for which posture states could not be determined—i.e., a single ASR for either ancestral or descendant nodes cannot be assigned at P_ASR > 0.67—were partitioned as “uncertain.” Separate rates ${\sigma }_x^2$ of body size evolution were estimated for each partition. Additionally, individual branches or monophyletic groups were allowed to vary in rate ${\sigma }_v^2$ (27) on top of the partitioned rates, minimizing the effects of rare and exceptional rate shifts on partitionwise rate (${\sigma }_x^2$) estimates.

Fig. 4.

Branch partitions according to nodal states. Branches were partitioned according to differences in reconstructed nodal posture states or tip states. That is, for each branch of the phylogenetic tree, we compared the states of the ancestral and descendant nodes, using ancestral state reconstructions (ASR) resulting from the top multistate model described in the text (Fig. 3A). We took the single ASR with the highest probability (at P_ASR > 0.67), and if the two states were identical (e.g., ancestor = D and descendant = D), then we would assign that branch to the within-posture partition, but if they differed (e.g., ancestor = D and descendant = U), we would assign that branch to a transitional partition. Branches for which posture states could not be determined—i.e., a single ASR for either ancestral or descendant nodes cannot be assigned at P_ASR > 0.67—were partitioned as “uncertain.” Partitions are colored as shown in the legend. Kangaroo rat silhouette courtesy of Pixabay/Fran Barreto. Lemur silhouette courtesy of Wikimedia Commons/NMaia. Other animal silhouettes courtesy of PhyloPic/Steven Traver, Tracy A. Heath, Mathew Callaghan, Robbi Bishop-Taylor, Yan Wong, Catherine Yasuda, Natasha Vitek, Daniel Jaron, Pearson Scott Foresman, Birgit Lang, Mercedes Yrayzoz, Sarah Werning, and H. F. O. March.

We find that the rate of evolution of body size across transitions between foot postures (${\sigma }_T^2$) is significantly higher than that within postures (${\sigma }_b^2$; Fig. 5 and SI Appendix, Fig. S4); that is, the proportion of the posterior in which differences between rates straddle 0 is less than 0.05 (p_MCMC < 0.05) (Table 1). Elevated rates indicate that the statistically significant differences in body masses between P and D and between D and U (Fig. 2) were not attained gradually owing to the passage of time but through instances of elevated rates of evolution; transitional branches are associated with a sevenfold increase compared with rates associated with within-posture branches (Table 1).

Fig. 5.

Rates of body size evolution for each branch partition. Separate rates of body size evolution were estimated for each of the branch partitions, based on the state of foot posture along those branches, as in Fig. 4. The transitional partition (purple) is associated with significantly higher rates compared with the within-posture partition (dark gray).

Table 1.

Pairwise comparisons of branch partition-wise rate estimates

Partition	Within-posture	Transitions	Uncertain
Within-posture	0.007	6.924	2.927
Transitions	0.000*	0.049	0.423
Uncertain	0.022*	0.109	0.021

Diagonal elements of the table in bold are median values of the posterior estimates of evolutionary rates (${\sigma }_x^2$) for each branch partition, elements in the upper triangle of the table are the median partition rate scalars, and elements in the lower triangle of the table are pairwise p_MCMC values.

^*Significant at p_MCMC < 0.05.

That transitions between foot postures are associated with rate increases in body size evolution implies that morphological adaptations associated with changes in foot posture facilitate rapid changes in body size. For instance, upright foot postures are beneficial, if not necessary, for terrestrial animals having larger sizes and/or high-speed locomotion because they can compensate for increasing stresses on musculoskeletal systems that are associated with higher body masses or strenuous activities (4, 5, 7, 8). Upright foot postures have also been suggested as being an energy-saving mechanism, with lower metabolic costs to locomotion compared with nonupright foot postures (7). Morphological adaptations associated with upright foot postures thus were most likely advantageous with regard to efficient locomotion and reduction in metabolic costs, potentially enabling a burst of evolution to larger body sizes associated with acquisitions of more upright foot postures (i.e., P → D, D → U). In addition, secondary digitigrady in graviportal taxa like rhinos (i.e., U → D) would allow body size increases by reducing planter pressure with thick foot pads.

On the other hand, strong selection for rapid changes in body size may necessitate transitions in foot postures. That is, it has been previously hypothesized that plantigrade mammals were restricted to small body sizes throughout the Cenozoic owing to predation pressures from large cursorial digitigrade predators, whereas digitigrade and unguligrade mammals were free to increase in size presumably owing to reduced predation pressures (28). Thus, it is possible that for a small plantigrade taxon to rapidly increase in size to evade predation pressures, transitions in foot postures may be necessary for biomechanical and energetic reasons discussed above.

Because correlation does not imply causation, it is impossible to ascertain whether transitions between foot postures drove size changes or the other way around. Future studies incorporating fossil taxa may shed light on this issue. However, what is discernible is the discontinuity of body size evolution across foot postures—i.e., bursts of rapid evolution between significantly different group means (Figs. 2 and 5). That there is an interval in mean body sizes between two foot postures which is associated with rapid bursts of evolution to get from one to the other is reminiscent of the classic hypothesis of quantum evolution across adaptive zones (25).

The discontinuity in size between plantigrade and nonplantigrade (digitigrade and unguligrade) tetrapods seems to have existed, before that observed in mammals, for more than 200 million years since the emergence of the first digitigrade tetrapod, Dinosauromorpha (29), and is globally observed among extant nonvolant birds (29). Thus, it is possible that differences in foot postures have affected body size evolution universally throughout the evolutionary history of tetrapods; future collection of relevant autopod and zeugopod morphological data in a wide range of terrestrial tetrapods (living and extinct) and macroevolutionary statistical analyses (such as those conducted here) may shed light on this issue.

Methods

Data Collection.

Foot postures of mammals were grouped into three categories: plantigrady (P), digitigrady (D), and unguligrady (U). Categorization was based on analyses of videos of walking animals obtained from online resources (e.g., www.arkive.org/; see SI Appendix). Videos were searched for all terrestrial mammalian species (i.e., excluding Chiroptera and aquatic species), for which corresponding body mass data are available in the PanTHERIA database (1). When suitable videos were unavailable for a species, that species was excluded from subsequent analyses. When videos were unavailable for species within Artiodactyla, Perissodactyla, Canidae, Felidae, and Hyaenidae, foot posture was determined from photographs, and when photographs were unavailable, they were omitted. The criterion for foot posture categorization is as follows. The stance of the animal at which they paused during locomotion—i.e., when all four zeugopods are in contact with the ground for a few seconds—was used for judging its foot posture. A species was categorized as P if their tarso-metatarsal joint contacted the ground. If the tarso-metatarsal joints were clearly off the ground, they were categorized as D, and if the metatarso-phalangeal joints were off the ground, they were categorized as U. Graviportal species with elephantine feet, with thick foot pads underneath the metatarso-phalangeal joints that contacted the ground, were categorized as D (rhinos, tapirs, hippos, and camels), whereas elephants were categorized as P, based on the distribution of their planter pressure (SI Appendix).

We used the Time Tree of Life (26) and pruned out the tips for which we do not have posture data, resulting in 880 species (SI Appendix, Table S1). We also tested the effects of tree topology on our results using a tree with an alternate topology (SI Appendix).

Phylogenetic Comparative Methods.

To estimate transition rates among the different foot postures, we used the reversible-jump continuous time Markov model (16) in BayesTraits (18), simultaneously reconstructing ancestral states for each node in the tree. We ran three independent Markov Chain Monte Carlo (MCMC) chains for 10⁸ iterations sampling every 10⁵ iterations after burning in for 10⁷ iterations. We used an exponential (0, 1) hyperprior. We did not set any restrictions on transitions a priori for the initial model. We computed marginal log likelihoods using stepping stone sampling (30) over 1,000 stones at 250,000 iterations per stone.

To test whether rates of body size evolution differed among branches along which transitions in foot posture occurred, we estimated separate rates of body size evolution for each partition of branches across the phylogenetic tree, where branches were partitioned according to differences in reconstructed nodal posture states (SI Appendix, Fig. S2). That is, for each branch of the phylogenetic tree, we compared the states of the ancestral and descendant nodes using ASR resulting from the top multistate model described in the text (Fig. 3A). We took the single ASR with the highest probability [at P_ASR > 0.67 (2/3), which is double the probability that a state can be reconstructed by chance alone (1/3); Fig. 4], and if the two states were identical (e.g., ancestor = D and descendant = D), then we would assign that branch to that specific foot posture (e.g., D) partition, but if they differed (e.g., ancestor = D and descendant = U), we would assign that branch to a transitional partition. Branches for which posture states could not be determined—i.e., a single ASR for either ancestral or descendant nodes cannot be assigned at P_ASR > 0.67—were partitioned as “uncertain” (SI Appendix, Fig. S2). Separate rates ${\sigma }_x^2$ of body size evolution were estimated for each partition [three in total: within-posture (N = 1,616), transitional (N = 20), and uncertain (N = 18)] using the local transform option for the VR model in BayesTraits. We accounted for the large discrepancy in body size between graviportal and nongraviportal taxa within postures (e.g., elephants in plantigrady and rhinos in digitigrady) by allowing for an offset in means (intercept) under the VR phylogenetic regression framework (31). Additionally, individual branches were allowed to vary in rate ${\sigma }_v^2$ (27, 31) on top of the partitioned rates, minimizing the effects of rare and exceptional rate shifts on partitionwise background rate ${\sigma }_x^2$. We ran the MCMC chain for 10⁸ iterations after a burn-in period of 5 × 10⁷ iterations, sampling every 10⁴th iteration. We tested whether ${\sigma }_x^2$ differed among the branch partitions as the proportion of the posterior sample in which the difference in ${\sigma }_x^2$ between partitions crossed 0 using a critical level of 0.05 (p_MCMC < 0.05).

Data and BayesTraits infiles containing relevant command lines are provided as Datasets S1–S22 (see SI Appendix for description).