Limits of multifunctionality in tunable networks

Significance

Functionally optimized networks are ubiquitous in nature, e.g., in allosteric proteins that change conformation upon binding to a ligand or vascular networks that distribute oxygen and nutrients in animals or plants. Many of these networks are multifunctional, with proteins that can catalyze more than one substrate or vascular networks that can deliver enhanced flow to more than one localized region of the network. This work investigates the question of how many simultaneous functions a given network can be designed to fulfill, uncovering a phase transition that is related to other constraint–satisfaction transitions such as the jamming transition.

Abstract

Nature is rife with networks that are functionally optimized to propagate inputs to perform specific tasks. Whether via genetic evolution or dynamic adaptation, many networks create functionality by locally tuning interactions between nodes. Here we explore this behavior in two contexts: strain propagation in mechanical networks and pressure redistribution in flow networks. By adding and removing links, we are able to optimize both types of networks to perform specific functions. We define a single function as a tuned response of a single “target” link when another, predetermined part of the network is activated. Using network structures generated via such optimization, we investigate how many simultaneous functions such networks can be programed to fulfill. We find that both flow and mechanical networks display qualitatively similar phase transitions in the number of targets that can be tuned, along with the same robust finite-size scaling behavior. We discuss how these properties can be understood in the context of constraint–satisfaction problems.

Many naturally occurring and synthetic networks are endowed with specific and efficient functionality. For example, allosteric proteins globally adjust their conformation upon ligand binding to control the activity of a distant active site (1, 2). Venation networks in the leaves of plants are highly optimized for water and nutrient transport (3). In some cases, networks can change their function depending on the needs of the system; vascular networks in animals (4–6), fungi (7), and slime molds (8) can reroute the transport of fluids, enhancing or depleting nutrient levels to support local growth or activity. Modern power grids must precisely distribute electrical energy generated from a limited number of sources to a large number of consumers with widely varying consumption needs at different times (9). All of these networks are optimized to some degree, by evolution via natural selection, dynamic reconfiguration, or human planning.

A key aspect of such functionality is the complexity of a specific task. We define a “function” as an optimized response of a localized component of a network when another predefined, localized component of the system is activated. A “task” is then defined as the collective response of a set of individual functions due to a single input. The number of functions representing a specific task is the task complexity.

In this work we address the limits of complexity for a single task: How many functions composing a single task can be programed into a network? We consider two examples: (i) mechanical networks—in which nodes are connected by central-force harmonic springs—locally flexing in response to an applied strain and (ii) flow (or resistor) networks—in which nodes are connected by linear resistors—locally producing a pressure drop due to an applied pressure at the source. These systems are related; flow networks are mathematically equivalent to mechanical networks embedded in one spatial dimension—but with a nontrivial node topology (10).

Macroscopic properties of mechanical networks, such as their bulk and shear moduli, can be tuned by modifying only a tiny fraction of the springs between nodes (11–13) [in contrast to random removal (14)]. This idea was extended to show that such networks can be tuned to develop allosteric behavior via selective spring removal (15–17). Allostery in these systems is a single-function task in which a randomly selected spring (the target) responds in a specified way to a strain imposed on a separate pair of nodes (the source). Here we study complex tasks in which multiple targets are controlled by a single source. We study the scaling of the maximal complexity of a task with network size by asking how many individual targets can be successfully tuned simultaneously and show that in both flow and mechanical networks, the limit of task complexity is set by a phase transition.

Network Tuning Protocol

Our method for tuning networks follows the general scheme described in our previous work (15) with slight modifications. We start with 2D configurations of soft spheres with periodic boundary conditions created using standard jamming algorithms. We construct networks by placing nodes at the center of each sphere and links (edges) between nodes corresponding to overlapping particles. This ensemble of networks is used for both spring networks, in which edges are unstretched central-force springs, and flow networks, in which edges are resistive conduits. By using the same set of nodes and edges for both systems, we can directly compare results. We chose this ensemble because it is disordered and provides initial networks with properties reminiscent of the corresponding biological systems. Elastic networks with close-range interactions have often been used to model proteins (18), while many natural flow networks have high numbers of closed loops (19) and are highly interconnected (20). However, our networks do not exhibit modular topologies which can appear in some systems (9). While we briefly touch on modularity, an in-depth study of modular networks is outside the scope of this work.

For each network, a pair of source nodes is chosen randomly, along with a set of $N_T$ target edges. Our goal is to tune the extension (or pressure drop) $e_{\alpha }$ of each target edge, indexed by $\alpha$, in response to an extension (pressure drop) $e_S$ applied to the source nodes by adding and removing edges from the network. We explore two different types of sources: pairs of nodes connected by a randomly chosen edge and pairs of nodes that are each chosen randomly anywhere in the network (see SI Appendix for global compression and shear sources in mechanical networks).

To control the response of the targets, we define the response ratio ${\eta }_{\alpha }\equiv e_{\alpha }/e_S$ for each target. Each ${\eta }_{\alpha }$ is in general a collective property of the network; the response of each target is a function of the total network structure. Before tuning the network, we measure the initial extension (pressure drop) $e_{\alpha }^{\left(0\right)}$ to obtain the initial response ratio of each target ${\eta }_{\alpha }^{\left(0\right)}=e_{\alpha }^{\left(0\right)}/e_S$. We then tune the response ratio of each target so that its relative change compared with the initial state is greater than or equal to a specified positive constant $\mathrm{\Delta }$; that is, we tune each response ratio to satisfy the constraint

$$\frac{{\eta }_{\alpha }-{\eta }_{\alpha }^{\left(0\right)}}{{\eta }_{\alpha }^{\left(0\right)}}\ge \mathrm{\Delta },\hspace{1em}\alpha =1,\dots ,N_T.$$ [1]

Thus, for mechanical networks we require contracting edges to contract more and expanding edges to expand more. For flow networks, we require the magnitude of the pressure drop to increase without changing the direction of the flow through each target link.

Our optimization scheme involves minimizing a loss function which penalizes deviations from the constraints in Eq. 1 (Materials and Methods). Each optimization step consists of either removing a single link or reinserting a previously removed link to modify the network topology in discrete steps. More specifically, at each step we measure the resulting change in the loss function for each single-link removal or reinsertion and remove or reinsert the link to most decrease the loss function.

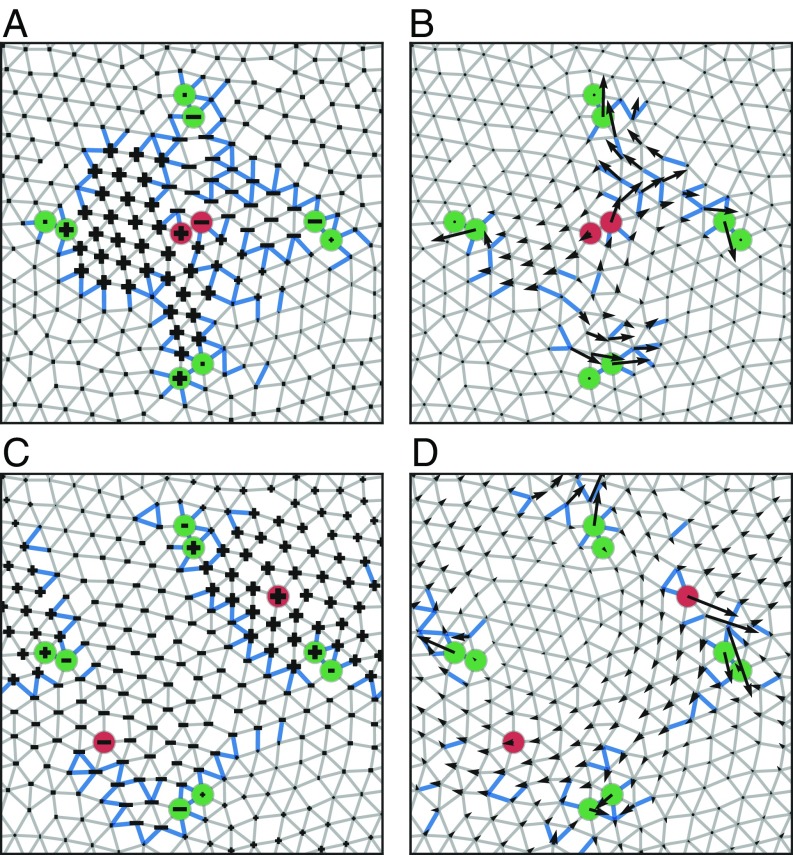
Fig. 1 depicts examples of both flow and mechanical networks which have been tuned using our prescribed method for the two different types of applied sources. Fig. 1 A and B shows flow and mechanical networks, respectively, tuned to respond to a source applied to a pair of nodes connected by an edge. Fig. 1 C and D shows the same networks, but with a pair of source nodes that are not connected by an edge.

Fig. 1.

Networks tuned to display multifunctional responses. Each network starts with the same initial topology and the same choice of four target edges (corresponding nodes shown in green). A and C are flow networks while B and D are mechanical networks. For each network a source extension (pressure drop) is applied to a pair of source nodes (shown in red). In A and B the pair of source nodes is connected by an edge, while in C and D the source nodes are not connected by an edge. For flow networks, response ratios are tuned to ${\eta }_{\alpha }\ge 0.5$, while for the mechanical networks they are ${\eta }_{\alpha }\ge 1.0$. The edges removed by tuning are shown as thick blue lines. For flow networks, the magnitude of the pressure on each node is indicated by the node size and the sign of the node pressure is represented by the shape. For mechanical networks, the node displacements are shown as black arrows.

Results

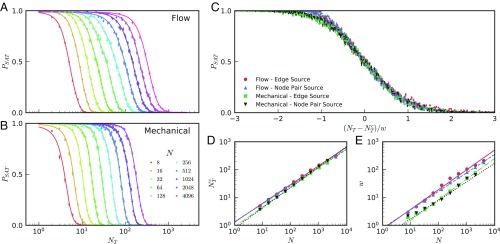
For both flow and mechanical networks, we explore the effects of various aspects of the tuning problem, with particular focus on task complexity. Fig. 2 A and B displays typical results for the fraction of networks that can be tuned successfully, $P_{SAT}$, for flow and mechanical networks, respectively. Data are shown for a randomly chosen edge source and $N_T$ randomly chosen target edges with a desired relative change in target response of $\mathrm{\Delta }=0.1$. System sizes range from $N=8$ to 4,096 nodes. Each value of $P_{SAT}$ is calculated by tuning at least 512 independent randomly generated networks. At low $N_T$, $P_{SAT}\approx 1$ while at large $N_T$, $P_{SAT}$ drops to zero.

Fig. 2.

(A and B) The fraction of satisfied configurations $P_{SAT}$ for (A) flow networks and (B) mechanical networks as a function of number of targets $N_T$ for systems of $N$ nodes. Results are shown for a pressure or extension applied to a single source edge with a desired response ratio of $\mathrm{\Delta }=0.1$. Curves are smoothing splines and estimated error bars are shown for binomially distributed data (SI Appendix). (C) Scaling collapse for all $N$ for four cases: flow networks with an edge source (red circles) and with a node pair source (blue triangles) and mechanical networks with an edge source (green squares) and with a node pair source (black triangles). In each case, we plot $P_{SAT}$ vs. $\left(N_T-N_T^c\right)/w$, where $P_{SAT}=\frac{1}{2}$ at $N_T^c$ and $w$ is the interval in $N_T$ over which $0.25<P_{SAT}<0.75$. (D and E) The transition points $N_T^C$ (D) and width of the transition $w$ (E) are reasonably described by power laws in $N$ with fits for $N_T^c$ giving exponents 0.67 and 0.65 for flow networks and 0.71 and 0.74 for mechanical networks with an edge and node pair source, respectively. In the same order, the power-law fits for $w$ have exponents of 0.71, 0.66, 0.74, and 0.66.

In Fig. 2C, we plot the transition curves for all system sizes for the four cases studied on the same axes. Using the smoothing spline interpolations shown in Fig. 2 A and B (SI Appendix), we estimate the number of targets $N_T^c$ at which $P_{SAT}=0.5$. Next, we estimate the width of the transition, $w$, taken as the interval in $N_T$ over which $0.25<P_{SAT}<0.75$. We attempt to collapse each curve by plotting $P_{SAT}$ vs. $\left(N_T-N_T^c\right)/w$. We find a similar functional form for all cases, with only a slight difference between flow and mechanical networks near $\left(N_T-N_T^c\right)/w\approx -1$.

Fig. 2 D and E shows that flow networks and mechanical networks have similar power-law behaviors for $N_T^c$ and $w$. Both the transition location and width scale approximately as $N^{\nu }$ with $\nu \approx 0.7$. Because the scaling exponent for $N_T^c$ is less than 1, the critical fraction of functions that can be tuned simultaneously approaches zero as $N$ goes to infinity, even though the number of simultaneously tuned functions diverges with system size. Thus, small networks are relatively more tunable than large ones. In addition, the sublinear scaling of the transition width shows that $P_{SAT}$ drops more rapidly with $N_T/N$ as $N$ increases, implying that the crossover becomes sharp as $N\to \infty$. At the same time, Fig. 3 shows that the average number of links that need to be removed for a successful tuning operation grows approximately linearly with the number of targets. Thus, those networks that can be tuned successfully typically require only removal of a constant fraction of edges. Together, our results suggest $P_{SAT}\left(N_T/N\right)\sim F\left[\left(N_T/N-{\rho }^{\infty }\right)N^{1-\nu }\right]$ with ${\rho }^{\infty }$ consistent with zero. For $\nu <1$, this implies a random first-order transition in the thermodynamic limit, with a discontinuity in $P_{SAT}$ and power-law finite-size scaling. Such hybrid transitions are typical of constraint–satisfaction problems.

Fig. 3.

(A and B) Power-law behavior of the average number of removed edges as a function of number of targets $N_T$ for (A) flow networks and (B) mechanical networks for various system sizes $N$. Included networks correspond to those that have been tuned successfully in Fig. 2 A and B with an edge source and desired change in target response of $\mathrm{\Delta }=0.1$. Error bars indicate the error on the mean. Power laws with an exponent of 1.0 are depicted as black dashed lines for comparison.

Discussion

We framed the problem of the maximum number of target edges that can be tuned successfully in a mechanical or flow network as a type of discrete constraint–satisfaction problem, in which we asked how many inequality constraints can be satisfied simultaneously. This places the tuning of multifunctionality in the context of a variety of other problems including jamming (21), spin glasses (22), the $k$-SAT problem (23), $k$-core percolation (24), and the perceptron (25). Much progress has been made by linking such transitions to the statistical physics of critical phenomena. The hallmark of these systems is the emergence of a SAT–UNSAT transition between regions in parameter space where the constraints can always (or with high probability) be satisfied and regions where the system is frustrated, such that not all constraints can be satisfied simultaneously (25). In mean-field and in some cases in finite dimensions, the SAT–UNSAT transition is a random first-order transition, with a discontinuous jump in the order parameter (the fraction of satisfied configurations $P_{SAT}$) as in a first-order phase transition, but with power-law scaling as in a second-order transition.

We have demonstrated a SAT–UNSAT transition in the complexity of a single task that can be tuned into disordered mechanical and flow networks. In both cases, the maximum task complexity diverges with a power law that is sublinear in $N$, the number of nodes in the network. The width of the SAT–UNSAT transition (relative to $N$) vanishes as $N$ diverges, showing that the transition is a true phase transition.

Although we find $P_{SAT}\left(N_T/N\right)\sim F\left[\left(N_T/N-{\rho }^{\infty }\right)N^{1-\nu }\right]$ for the four cases displayed in Fig. 2, both $F\left(x\right)$ and $\nu$ can vary, depending on a variety of factors. These factors include (i) the local or global nature of the source, (ii) the magnitude of desired change in target response $\mathrm{\Delta }$, (iii) disorder in the link topology, (iv) initial coordination of the network, and (v) the choice of whether to tune the link tensions (currents) or extensions (pressure drops) (SI Appendix). The values of $\nu$ lie in the range of 0.6–0.8, with the exception of one case of 1.0 for a very large relative change in target response of $\mathrm{\Delta }=\mathrm{1,000}$ (SI Appendix, Table S1). We find that the behavior is not well described by a power law for tuning negative relative changes in target response ($\mathrm{\Delta }<0$) and for tuning small changes in current or tension. The former case is still under investigation, while the latter exception has a simple explanation (SI Appendix).

Overall, the divergence of the maximum number of tunable targets with system size and the corresponding vanishing of the transition width (indicating the existence of a phase transition) are very robust observations for positive and sufficiently large relative changes in target responses. We note also that both mechanical networks and flow networks exhibit very similar quantitative behavior despite the fact that flow networks are purely topological, requiring no explicit spatial embedding.

The SAT–UNSAT transition of the task complexity problem introduced here represents a distinct class of discrete constraint–satisfaction transitions due to a complication that arises in the form of the constraints. When tuning a mechanical network, the removal of links can introduce soft modes, making it impossible to uniquely evaluate the network response and subsequently tune a given target. Similarly, in a flow network the tuning process can lead to regions being disconnected from the source, making it impossible to tune any target in that region. To avoid such cases, at each step of the tuning process we are forced to exclude specific link removals (Materials and Methods). In both mechanical and flow networks, we find that it becomes more and more likely to introduce a soft mode/disconnected region as the task complexity increases. This makes the problem more difficult to tackle both numerically and analytically compared with previously studied constraint–satisfaction transitions and may lead to differences in the nature of the transition.

For mechanical functions, a perfectly engineered mechanism (e.g., a pair of chopsticks, which creates a large displacement at the tips in response to strain applied where they are held) may perform exactly one function superlatively well, but we have shown that more complex network structures are able to adapt to a number of functions that diverge with the system size. The same argument holds for flow networks: An optimally engineered distribution network is a topological tree, perfectly suited for a specified task but at the same time “rigid,” in the sense that it cannot easily adapt to other tasks. The networks that we have studied are more complex than a pair of chopsticks or a topological tree, and this allows them to be tuned successfully to perform arbitrarily complex tasks.

Our finding that a disordered network topology allows for tunability may have relevance to real biological networks. For example, the development of certain vascular structures within animals is characterized by the initial appearance of a tightly meshed disordered network of veins (the vascular plexus) that is subsequently pruned and tuned to its function (26). The initial disordered network may be a prerequisite of the great variability and versatility seen in natural networks. The tuned mechanical networks serve as simple models for multifunctional allostery in proteins (with a single regulatory site that can control more than one active site, e.g., refs. 27 and 28) or multifunctional metamaterials. Our flow network results give insight into how to control, for example, blood and oxygen distribution in vascular systems or power in an electrical network. Indeed, we find very similar behavior in a flow network with nonplanar topology derived from the United Kingdom (UK) railroad network, which exhibits a high degree of modularity. $P_{SAT}$ exhibits a qualitatively similar transition in the number of targets that can be tuned compared to the transitions in the networks studied here (SI Appendix).

Our results raise a number of issues for future investigation. The divergence in the task complexity and vanishing of the transition width with system size are reasonably well approximated by power laws but may deviate for larger system sizes (SI Appendix). The measured exponents appear to depend on many specific properties of the problems studied. This may be due to corrections to scaling or to a more fundamental deviation from power-law scaling. Also, it is not clear what conditions on the network topology are necessary to observe the transition we see. For example, networks with high degrees of modularity may not be able to support tasks spanning multiple neighborhoods. However, our results for the UK railroad network suggest that even in this case, we observe identical qualitative behavior, but with an overall decreased $P_{SAT}$ corresponding to the possibility of choosing sources and targets in different neighborhoods (SI Appendix, SI Text). More generally, it has not been investigated how the results depend on network structure/topology and dimensionality nor how they depend on the tuning algorithm. For instance, the values of $N_T^c/N$ and $\nu$ might be higher for simulated annealing, which explores a wider region of solution space than the minimization algorithm studied here.

One further aspect of our results deserves mention: A simple function that controls only a single pair of target nodes can be achieved in an extremely large number of ways. We have shown that a task can be complex with $N_T$ randomly chosen target nodes controlled by a single source. However, if one is interested in controlling only a single target, one can create different paths for its control by choosing any of the $N$ other nodes in the system also to be a target. Likewise, one could specify a third node to be controlled as well, etc. That means that there are at least $\sim \left(N-1\right)!/\left(N-N_T^c\right)!\left(N_T^c-1\right)!$ ways of creating that simple function. Because we find $N_T^c\sim N^{\nu }$, for $\nu <1$ this lower bound is smaller than the prediction of $e^{\mathcal{O}\left(N\right)}$ solutions in the large-$N$ limit (16).

Here we studied the limits of the complexity of a single task. It would be interesting to understand how many different tasks can be designed successfully and whether that is controlled by a similar SAT–UNSAT transition. Finally, we note that for the mechanical and flow networks studied here, the behavior is governed by a discrete Laplacian operator (29)—mechanical networks obey force balance on each node and flow networks obey Kirchhoff’s laws. However, many networks, such as gene regulatory networks, metabolic networks, social networks, etc., are nonconservative. Moreover, the problems we have studied are linear in their couplings but ecological networks or neural networks, for example, are typically nonlinear. It is known that even nonconservative and/or nonlinear networks, such as the Hopfield model and jammed packings, can support SAT–UNSAT transitions as well (30, 31). It would interesting to study systematically how conservation constraints and linearity affect the nature of the transition.

Materials and Methods

Linear Response.

Our networks are described by a set of $N$ nodes and $N_E$ edges. The response of a flow network to external stimuli is represented by a pressure $p_i$ on each node $i$. Analogously, the response of a $d$-dimensional mechanical network is the $d$-dimensional displacement vector ${\overrightarrow{u}}_i$ of each node. Each edge linking nodes $i$ and $j$ is characterized by either a conductance or stiffness, denoted $k_{ij}$ in both cases. For mechanical networks, $k_{ij}={\lambda }_{ij}/{\ell }_{ij}$, where ${\lambda }_{ij}$ is the stretch modulus per unit length and ${\ell }_{ij}$ is the rest length. Initially, we set all stretch moduli ${\lambda }_{ij}$ identically to one. Similarly, for flow networks we set all conductivities $k_{ij}$ to one. Removing an edge $ij$ corresponds to setting $k_{ij}$ to zero, whereas reinserting an edge corresponds to setting $k_{ij}$ back to its original value.

To calculate the response of each type of network, we minimize the corresponding functional. In the case of flow networks, we minimize the power loss through the network,

$$P=\sum _{⟨ij⟩}{k}_{ij}{\left(p_j-p_i\right)}^2,$$ [2]

where $⟨ij⟩$ indicates a sum over all edges. For mechanical networks, we minimize the elastic energy

$$E=\frac{1}{2}\sum _{⟨ij⟩}{k}_{ij}{\left[{\widehat{b}}_{ij}\cdot \left({\overrightarrow{u}}_j-{\overrightarrow{u}}_i\right)\right]}^2,$$ [3]

where ${\widehat{b}}_{ij}$ is a unit vector pointing from node $i$ to node $j$ in the undeformed configuration. The power loss for a flow network can be mapped to the energy of a mechanical network for $d=1$ by mapping the pressure on each node to a 1D displacement (10). In this case, the unit vectors ${\widehat{b}}_{ij}$ are scalars with values of either $\pm 1$, which drop out when squared; the embedding of the network in space does not matter as is expected for flow networks.

Minimizing Eq. 2 for a flow network in the presence of externally applied boundary currents $q_i$ on each node $i$, we obtain a system of linear equations characterized by a graph Laplacian $L$,

$$L\left|p\right.⟩=\left|q\right.⟩,$$ [4]

where $|p⟩$ is an $N$-dimensional vector of node pressures and $|q⟩$ is an $N$-dimensional vector of external currents on nodes. We define the vector $|i⟩$ so that the pressure and current on the $i$th node are $p_i=⟨i\left|p\right.⟩$ and $q_i=⟨i\left|q\right.⟩$, respectively. Similarly for mechanical networks, minimizing Eq. 3 in the presence of externally applied forces, we obtain

$$H\left|u\right.⟩=\left|f\right.⟩,$$ [5]

where $|u⟩$ is a $dN$-dimensional vector of node displacements and $|f⟩$ is a $dN$-dimensional vector of external forces on nodes. Again we define the $N\times d$ matrix $\left|i_d\right.⟩$ to pick out the displacement and force on the $i$th node, ${\overrightarrow{u}}_i=⟨i_d\left|u\right.⟩$ and ${\overrightarrow{f}}_i=⟨i_d\left|f\right.⟩$. The matrix $H$ is the matrix of second derivatives known as the dynamical or Hessian matrix and can be interpreted as graph Laplacian where each element is a $d\times d$ matrix. We define the $d$ Laplacian, denoted $L_d$, as a generalized version of the standard Laplacian matrix. The case $d=1$ corresponds to the Laplacian of a flow network (or a 1D mechanical network) such that $L_1=L$, while for $d>1$, $L_d$ is a Hessian for a $d$-dimensional mechanical network; i.e., $L_{d>1}=H$. The $ij$th $d\times d$ block of the $d$ Laplacian is

$$\left.⟨i_d\right|L_d\left|\hspace{0.17em}{j}_d\right.⟩=\left\{\begin{array}{cc}\sum _{l\ne i}{k}_{il}{\widehat{b}}_{il}{\widehat{b}}_{il}^T\hfill & \hspace{1em}\text{if}\hspace{1em}i=j\hfill \\ -k_{ij}{\widehat{b}}_{ij}{\widehat{b}}_{ij}^T\hfill & \hspace{1em}\text{if}\hspace{1em}i\ne j\hfill \end{array}\right.,$$ [6]

where $k_{ij}$ is nonzero only if edge $ij$ exists.

Consequently, the response of either type of network is calculated by solving the corresponding set of linear equations rewritten as

$$L_d\left|u\right.⟩=\left|f\right.⟩,$$ [7]

where $|u⟩$ and $|f⟩$ are the appropriate $dN$-dimensional response and source vectors, respectively. To apply a pressure drop or edge extension source, we use a bordered Laplacian formulation.

Bordered Laplacian Formulation.

Calculating the linear response requires solving Eq. 7. However, there are two complications. The first is that the Laplacian operator is in general not invertible due to the presence of global degrees of freedom. For a periodic network, in $d$ dimensions, there are $d$ global translational degrees of freedom. Second, we apply edge extension (pressure drop) sources, rather than tension (current) sources. These sources can be applied as constraints on the system. Using a bordered Laplacian formulation, we add a constraint for each global translation and for the source.

First, we define the extension (or pressure drop) of the source as

$$e_S={\widehat{b}}_S\cdot \left({\overrightarrow{u}}_{S_2}-{\overrightarrow{u}}_{S_1}\right)=⟨S|u⟩$$ [8]

with source nodes $S_1$ and $S_2$. The unit vector ${\widehat{b}}_S$ points from node $S_1$ to $S_2$ and is a scalar in the case of a flow network. The vector $|S⟩$ is defined to extract the extension of the source from the full vector of node displacements. We specify the desired extension as $e{*}_S$. Additionally, we define the vectors $\left|G_i\right.⟩$ for $i=1,\dots ,d$ corresponding to translations of the entire system uniformly along the $i$th axis. We define the Lagrangian

$$\mathcal{L}=E-\sum _{i=1}^d{\lambda }_i⟨G_i|u⟩-{\lambda }_S\left(e_S-e{*}_S\right),$$ [9]

where the parameters ${\lambda }_i$ and ${\lambda }_S$ are Lagrange multipliers. We include the Lagrange multipliers as additional unknown parameters that must be determined in our calculations. We find solutions by extremizing the Lagrangian with respect to both the displacements and the Lagrange multiplier. We rewrite the Lagrangian in matrix form:

$$\mathcal{L}=\frac{1}{2}\left.⟨u\right|L_d\left|u\right.⟩-\left.⟨{\lambda }_G\right|G^T\left|u\right.⟩-{\lambda }_S\left(⟨S|u⟩-e{*}_S\right).$$ [10]

The vector $\left|{\lambda }_G\right.⟩$ is size $d$ with elements $⟨i|{\lambda }_G⟩={\lambda }_i$ and $G$ is a size $dN\times d$ matrix with columns $G\left|i\right.⟩=\left|G_i\right.⟩$. In this context we can further condense notation, writing the Lagrangian as

$$\mathcal{L}=\frac{1}{2}\left.⟨\overline{u}\right|{\overline{L}}_d\left|\overline{u}\right.⟩,$$ [11]

where we define the bordered Laplacian ${\overline{L}}_d$ as a block matrix of second derivatives of the Lagrangian:

$${\overline{L}}_d=\left(\begin{array}{ccc}\hfill L_d\hfill & \hfill -G\hfill & \hfill \left|S\right.⟩\hfill \\ \hfill -G^T\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⟨S\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$ [12]

We also define the bordered displacement and force vectors $\left|\overline{u}\right.⟩$ and $\left|\overline{f}\right.⟩$, respectively, each of size $dN+d+1$ as

$$\left|\overline{u}\right.⟩=\left(\begin{array}{c}\hfill \left|u\right.⟩\hfill \\ \hfill \left|{\lambda }_G\right.⟩\hfill \\ \hfill {\lambda }_S\hfill \end{array}\right),\hspace{1em}\left|\overline{f}\right.⟩=\left(\begin{array}{c}\hfill \left|f\right.⟩\hfill \\ \hfill 0\hfill \\ \hfill -e{*}_S.\hfill \end{array}\right).$$ [13]

As a result, the system of equations we must solve is now ${\overline{L}}_d\left|\overline{u}\right.⟩=\left|\overline{f}\right.⟩$. The bordered Laplacian is invertible due to the presence of the constraints and solving this equation is straightforward.

Tuning Loss Function.

Framed according to Eq. 1, the problem of tuning a complex task can be viewed as a constraint–satisfaction problem. The goal is to find a set of stiffnesses (conductivities) that simultaneously satisfy each constraint in Eq. 1. To study this problem numerically, we recast it as an optimization problem in the style of ref. 25, in which we define an objective function that penalizes deviation of the system’s behavior from the desired multifunctionality. Thus, we introduce the loss function

$$\mathcal{F}\left[\left\{k_{ij}\right\}\right]=\frac{1}{2}\sum _{\alpha =1}^{N_T}{r}_{\alpha }^2\mathrm{\Theta }\left(-r_{\alpha }\right),$$ [14]

which is a function of the set of all of the spring constants (conductivities) $\left\{k_{ij}\right\}$ and is composed of a sum over the set of $N_T$ target edges to be tuned. For each target edge $\alpha$ we define the residual

$$r_{\alpha }=\frac{{\eta }_{\alpha }-{\eta }_{\alpha }^{\left(0\right)}}{{\eta }_{\alpha }^{\left(0\right)}}-\mathrm{\Delta },$$ [15]

which measures how close each target is to being tuned successfully. The Heaviside function $\mathrm{\Theta }\left(-r_{\alpha }\right)$ is included so that if $r_{\alpha }>0$, i.e., the response ratio has increased at least by the desired proportion $\mathrm{\Delta }$, then the residual does not contribute to the loss function.

Optimization Method.

Our method for tuning a network involves minimizing the loss function in Eq. 14. In the spirit of refs. 11 and 15, our optimization consists of removing or reinserting previously removed edges from the network one at a time, modifying the network topology in discrete steps. More specifically, we use a greedy algorithm in which we remove or reinsert the edge which minimizes the loss function at each step. This requires a calculation of the new response for each possible move.

Suppose we have a network whose stiffnesses at the current step are $\left\{k_{ij}\right\}$ for all valid $ij$ where some $k_{ij}$ might already be zero, having been removed at previous steps. Our goal is to measure the change in response when the stiffness of edge $ij$ is changed by an amount $\mathrm{\Delta }{k}_{ij}$. We note that the Laplacian can be decomposed as

$$L_d=QK{Q}^T,$$ [16]

where the equilibrium (or incidence) matrix $Q$ of size $dN\times N_E$ defines the mapping of nodes to edges (29, 32) and $K$ is a size $N_E\times N_E$ diagonal matrix of edge stiffnesses such that $\left.⟨ij\right|K\left|lm\right.⟩=k_{ij}{\delta }_{ij,lm}$. We can define a bordered incidence matrix $\overline{Q}$ by appending $d+1$ rows of zeros to $Q$, giving us a corresponding decomposition of the bordered Laplacian ${\overline{L}}_d=\overline{Q}K{\overline{Q}}^T$. The change in response is

$$\left|\mathrm{\Delta }\overline{u}\right.⟩=\left[{\left({\overline{L}}_d+\mathrm{\Delta }{\overline{L}}_d\right)}^{-1}-{\overline{L}}_d^{-1}\right]\left|\overline{f}\right.⟩$$ [17]

with the corresponding change in the bordered Laplacian $\mathrm{\Delta }{\overline{L}}_d=\mathrm{\Delta }{k}_{ij}\left|q_{ij}\right.⟩\left.⟨q_{ij}\right|$ with the vector $\left|q_{ij}\right.⟩=\overline{Q}\left|ij\right.⟩$. We now need to calculate the inverse of the updated bordered Laplacian. This can be done using the Sherman–Morrison formula (33)

$${\left({\overline{L}}_d+\mathrm{\Delta }{\overline{L}}_d\right)}^{-1}={\overline{L}}_d^{-1}-\frac{{\overline{L}}_d^{-1}\mathrm{\Delta }{k}_{ij}\left|q_{ij}\right.⟩\left.⟨q_{ij}\right|{\overline{L}}_d^{-1}}{1-\mathrm{\Delta }{k}_{ij}\left.⟨q_{ij}\right|{\overline{L}}_d^{-1}\left|q_{ij}\right.⟩}.$$ [18]

The change in response is then

$$\left|\mathrm{\Delta }\overline{u}\right.⟩=-\frac{{\overline{L}}_d^{-1}\mathrm{\Delta }{k}_{ij}\left|q_{ij}\right.⟩\left.⟨q_{ij}\right|{\overline{L}}_d^{-1}\left|\overline{f}\right.⟩}{1-\mathrm{\Delta }{k}_{ij}\left.⟨q_{ij}\right|{\overline{L}}_d^{-1}\left|q_{ij}\right.⟩}.$$ [19]

The new response is then used to calculate an updated loss function.

To reduce numerical error and maintain the numerical invertibility of the bordered Laplacian, we define the quantity

$$S_{ij}^2\equiv 1-\mathrm{\Delta }{k}_{ij}\left.⟨q_{ij}\right|{\overline{L}}_d^{-1}\left|q_{ij}\right.⟩.$$ [20]

If $S_{ij}^2$ is less than $10^{-4}$, we do not remove an edge. This quantity can be shown to be the contribution of an edge to the states of self-stress in mechanical systems (12, 34). By ensuring that every removed edge has some contribution to the states of self-stress, then by Maxwell–Calladine counting, we are guaranteed that no zero modes are introduced (35).

We repeatedly add or remove edges until either the loss function is explicitly zero (i.e., all constraints are satisfied) or the relative change in the objective function is less than $10^{-8}$.