Thickness scaling of ferroelectricity in BiFeO₃ by tomographic atomic force microscopy

Significance

Intrinsic and extrinsic properties of ferroelectric materials are known to have strong dependencies on electrical and mechanical boundary conditions, resulting in finite size effects at length scales below several hundred nanometers. In ferroelectric thin films, equilibrium domain size is proportional to the square root of film thickness, which precludes the use of present tomographic microscopies to accurately resolve complex domain morphologies in submicrometer films. We report a subtractive experimental technique with volumetric resolution below 315 nm³, that allows for three-dimensional, tomographic imaging of materials properties using only an atomic force microscope. Multiferroic BiFeO₃ was chosen as a model system for illustrating the capabilities of tomographic atomic force microscopy due to its technological relevance in low-power, electrically switchable magnetic logic.

Abstract

Nanometer-scale 3D imaging of materials properties is critical for understanding equilibrium states in electronic materials, as well as for optimization of device performance and reliability, even though such capabilities remain a substantial experimental challenge. Tomographic atomic force microscopy (TAFM) is presented as a subtractive scanning probe technique for high-resolution, 3D ferroelectric property measurements. Volumetric property resolution below 315 nm³, as well as unit-cell-scale vertical material removal, are demonstrated. Specifically, TAFM is applied to investigate the size dependence of ferroelectricity in the room-temperature multiferroic BiFeO₃ across two decades of thickness to below 1 nm. TAFM enables volumetric imaging of ferroelectric domains in BiFeO₃ with a significant improvement in spatial resolution compared with existing domain tomography techniques. We additionally employ TAFM for direct, thickness-dependent measurements of the local spontaneous polarization and ferroelectric coercive field in BiFeO₃. The thickness-resolved ferroelectric properties strongly correlate with cross-sectional transmission electron microscopy (TEM), Landau–Ginzburg–Devonshire phenomenological theory, and the semiempirical Kay–Dunn scaling law for ferroelectric coercive fields. These results provide an unambiguous determination of a stable and switchable polar state in BiFeO₃ to thicknesses below 5 nm. The accuracy and utility of these findings on finite size effects in ferroelectric and multiferroic materials more broadly exemplifies the potential for novel insight into nanoscale 3D property measurements via other variations of TAFM.

The room-temperature multiferroic BiFeO₃ has become a material of fundamental importance, owing to the single-phase intrinsic coupling of electric, magnetic, and strain order parameters (1, 2), as well as the tunability and scalability of electronic properties (3–5) and the magnetic exchange bias in BiFeO₃ thin films (6, 7). Integration of BiFeO₃ into functional devices necessitates a thorough understanding of finite size effects on critical materials properties such as ferroic order parameter coupling, spontaneous polarization and magnetization, and hysteretic coercivity. In BiFeO₃, film thickness has been shown to have a substantial impact on ferroelectric domain size and morphology (8–11); however, quantification of the thickness dependence of the switchable polarization is most critical for leveraging functionality from BiFeO₃. The thickness dependence of the spontaneous polarization in BiFeO₃ has been investigated using macroscopic measurements (12), surface-sensitive electron microscopies (13), and piezoresponse force microscopy (PFM) (14), although PFM has been the only technique employed thus far to explore the thickness dependence of the ferroelectric coercive field in BiFeO₃ below 40 nm (14–16). The results of these studies point toward a robust and stable switchable ferroelectric state in BiFeO₃ at thicknesses below 10 nm; however, such studies are limited by the uncertainties inherent in performing experiments on discretely fabricated samples, namely fluctuations in structure and composition resulting from the imperfect nature of thin-film synthesis.

Since its invention, PFM has been adopted as a scanning probe technique for high-resolution imaging and manipulation of ferroelectric domains at nanometer length scales. However, like most scanning probe methods, PFM is largely limited to 2D surface studies where imaging artifacts that arise from structural or chemical modifications to the film during scanning are necessarily minimized. Several optical approaches have been successful for tomographic imaging of ferroelectric domains in bulk LaTiO₃ and LiNbO₃ single crystals (17–19), although necessarily limited by optical resolution on the order of 500 nm in any dimension. In this article, we present a scanning probe method, tomographic atomic force microscopy (TAFM), for the nanoscale thickness-resolved measurement of ferroelectric domain geometry, spontaneous polarization, and the ferroelectric coercive field in an epitaxial 120-nm BiFeO₃ (001)_pc/SrRuO₃ (001)_pc/DyScO₃ (110)_o thin-film heterostructure within a single imaging field of view. The subscripts “pc” and “o” denote pseudocubic and orthorhombic crystal axes, respectively. The ability to tomographically investigate the ferroelectric properties of BiFeO₃ within a single field of view (<20 μm) both minimizes the stoichiometric variability of the probed area and allows for high-accuracy z-position measurements of film thickness using the AFM. TAFM involves subtractive processing using the AFM probe with simultaneous acquisition of AFM images at progressively decreasing film thickness within a constant imaging area. This provides high-resolution (<50 nm) images and property measurements of subsurface structures throughout the thickness of a film. Employing TAFM, we report 3D PFM results, which provide quantitative 3D maps of the ferroelectric domain geometry in BiFeO₃ that strongly correlate with comparable cross-sectional transmission electron microscopy (TEM) analysis. The thickness dependence of the local piezoresponse acquired using TAFM has been analyzed in the context of Landau–Ginzburg–Devonshire phenomenological theory, which reveals the thickness dependence of the spontaneous polarization and critical switching thickness in BiFeO₃. Additionally, TAFM provides an experimental platform for thickness-dependent and defined-geometry experiments with site selectivity (20, 21). This capability is leveraged to perform polarization switching experiments on a programmed thickness gradient in BiFeO₃ following TAFM, and report localized, direct measurements of the electric field required for nucleation of ferroelectric domains as a function of film thickness. The thickness scaling of polarization switching in BiFeO₃ is found to obey the semiempirical Kay–Dunn scaling law to below 5 nm, which implies that ferroelectric switching in BiFeO₃ remains dominated by the electrostatics of the spontaneous polarization at nanometer length scales.

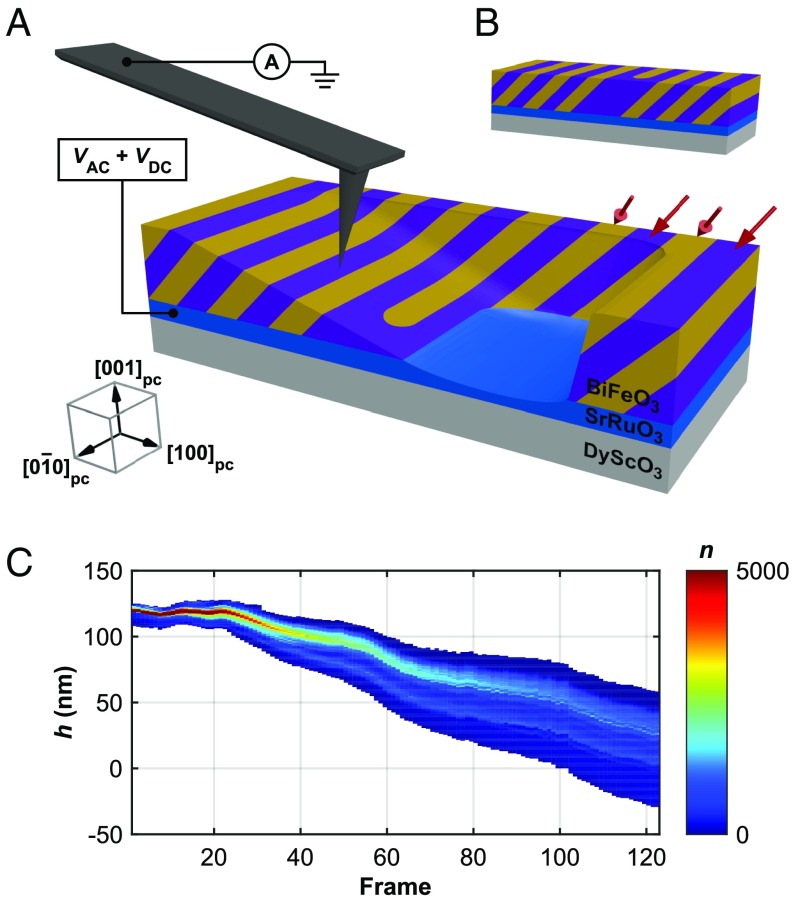
TAFM is the process in which a scanned probe, with downforces as high as micronewtons, performs mechanical removal (machining) of a specimen surface while simultaneously or sequentially recording one or more imaging modes, e.g., topography and PFM. The subtractive processing results in a series of conventional x-y plan-view images at continually increasing depths (decreasing film thickness, h), providing a 3D dataset of the desired imaging channel within the voided sample volume. Referenced to high-accuracy x, y, and z position data from the AFM, properties can thereby be volumetrically mapped throughout a portion or the entirety of a thin film. The concept is based on AFM micromachining methods previously reported for nanomechanical tooling (22–24) and fabrication of electron devices (25–27). The few reports of other TAFM variants have only characterized electrical conduction (28–30), and such methods are generally not applicable for high-modulus, electrically insulating materials such as ferroelectric oxides. Fig. 1A illustrates the application of TAFM for 3D PFM of ferroelectric domains throughout a multiferroic BiFeO₃ thin-film heterostructure. Fig. 1A depicts a single frame within a tomographic sequence, where the variable-thickness surface of BiFeO₃ has been created as a result of subtractive tomographic processing. The stripes shown in the BiFeO₃ film are ferroelectric/ferroelastic domains formed during film growth, with the direction of the spontaneous polarization indicated by red arrows. The subtractive nature of TAFM is apparent in SI Appendix, Fig. S1, which shows simultaneously acquired in-plane piezoresponse (u₁^ω) and surface topography, i.e., BiFeO₃ film thickness (h) throughout an ∼200-frame tomographic sequence. The resulting topographic depression posttomography is shown in SI Appendix, Fig. S2. The mechanical dynamics of TAFM can be inferred from the 2D histogram in Fig. 1C, which shows a smoothly decreasing BiFeO₃ film thickness (h) starting at frame ∼25 and continuing for the remainder of the measured sequence. Here, the material removal rate remains relatively constant throughout the experiment (linear dependence between BiFeO₃ film thickness, h, and imaging frame); however, a substantial increase in topographic roughness and nonplanarity is observed (σ = 0.2 nm at h = 120 nm and σ = 6.0 nm at h = 10 nm) as the tomographic sequence progresses. These observations are visually confirmed in SI Appendix, Fig. S1C.

Fig. 1.

TAFM of a BiFeO₃/SrRuO₃/DyScO₃ thin-film heterostructure. (A) PFM with probe current detection on a BiFeO₃ surface that has been prepared using TAFM, showing variable topography of BiFeO₃ and SrRuO₃ resulting from TAFM. Stripe-type contrast in BiFeO₃ represents ferroelectric domains with spontaneous polarization along [$\overline{1}1\overline{1}$]_pc and [$\overline{1}\overline{1}\overline{1}$]_pc, as indicated by red arrows. (B) Unprocessed, as-grown BiFeO₃/SrRuO₃/DyScO₃ heterostructure. (C) Two-dimensional histogram of z position as a function of imaging frame during TAFM of an h = 120 nm BiFeO₃ thin film.

The applied probe downforce was selected to simultaneously enable the controlled removal of surface layers of BiFeO₃ while preventing mechanically induced ferroelectric or ferroelastic switching of ferroelectric domains (31), and to image within the strong indentation regime for optimization of PFM contrast via minimization of nonlocal electrostatic interactions (32). Critical to the fidelity of TAFM measurements is the minimization of subsurface film damage during subtractive processing; any such damage would preclude accurate visualization and quantitative analysis of tomographic data. The relative frame-to-frame magnitude of the piezoresponse provides a continuous in situ indication of local crystal quality (14), which remained nearly constant during all TAFM scans on the BiFeO₃ film (SI Appendix, Figs. S1A and S3A); any subsurface defect formation or amorphization would result in suppressed piezoresponse relative to the as-grown film. In this work, an 11.4-µN mean probe downforce produced a mean vertical removal rate of 0.97 nm per frame (SI Appendix, Fig. S3B) and an overall tomographic sequence of ∼200 imaging frames on the h = 120-nm BiFeO₃ thin-film heterostructure. The in-plane piezoresponse increases slightly during the tomographic sequence commensurate with an increase in the mean probe downforce (32) (SI Appendix, Fig. S3A), both resulting from the broadening of the frame-to-frame surface roughness shown in Fig. 1C.

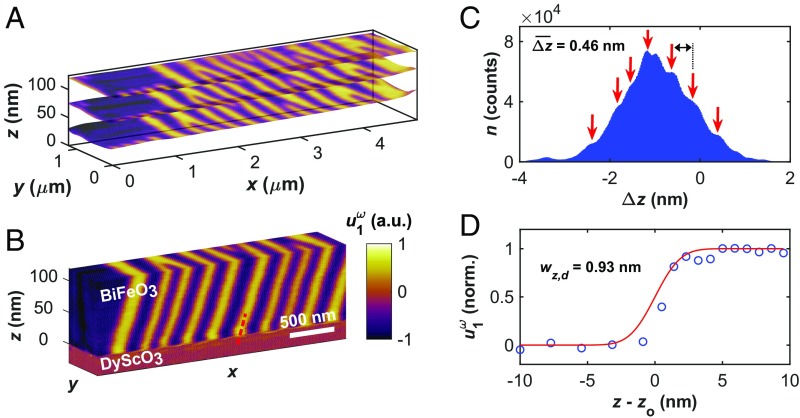
Fig. 2A superimposes three of the ∼200 sequential PFM images at mean z heights (film thickness, h) of 120 nm (frame 1), 77.8 nm (frame 65), and 33.8 nm (frame 120). For each of these frames, the in-plane piezoresponse (u₁^ω) is overlaid as color contrast on the simultaneously acquired surface topography. As with the schematics in Fig. 1A, the stripe-type domain pattern in the PFM contrast indicates 71° ferroelectric/ferroelastic domains with polarization orientations [$\overline{1}1\overline{1}$]_pc and [$\overline{1}\overline{1}\overline{1}$]_pc. To produce an accurate tomogram from AFM data with temporally evolving z positions, a postprocessing reconstruction algorithm is employed to map the through-thickness PFM response of BiFeO₃ onto a 3D rectilinear grid with x, y, and z axes parallel to the [100]_pc, [010]_pc, and [001]_pc crystal axes, respectively. The continuously decreasing, nonplanar z-position data obtained during TAFM cannot be accurately viewed in 3D due to the differential material removal rates throughout the imaging field of view (SI Appendix, Fig. S1C). Using simultaneously acquired z-position data, each (x, y, z) data point is used to translate the PFM response data onto a regular Cartesian grid using weighted trilinear interpolation within a standard 3D Delaunay triangulation routine. This procedure enables viewing and analysis of 3D data along correctly proportioned, pseudocubic crystal axes. To improve the accuracy of the z component of the tomogram, probe current is simultaneously measured to locally detect the zero-thickness position of the BiFeO₃ film, i.e., breakthrough to the conductive SrRuO₃ back electrode. The high conductivity of SrRuO₃ relative to BiFeO₃ provides a robust method for establishing the z position of the BiFeO₃/SrRuO₃ interface (SI Appendix, Fig. S4C), a critical parameter in the creation of spatially accurate tomograms constructed from AFM data. For reference, all z-position/film thickness (h) data presented in this work have been corrected for z drift and validated by setting the BiFeO₃/SrRuO₃ interface equal to h = z = 0.

Fig. 2.

Tomographic reconstruction of ferroelectricity from a BiFeO₃ thin-film heterostructure. Simultaneously acquired (A) PFM piezoresponse at h = 120 nm, h = 77.8 nm, and h = 33.8 nm from the ∼200-frame tomographic sequence superimposed onto the local surface topography (z position) for each imaging pixel. (B) Three-dimensional tomographic reconstruction of the thickness-resolved piezoresponse from a subregion of A (z dimension magnified ∼15× for viewing). (C) Histogram of the frame-to-frame change in the z position of the BiFeO₃ film surface (Δz), calculated on a per-pixel basis. Red arrows indicate apparent unit-cell steps in the fine structure of the histogram. (D) z resolution of tomographic PFM data calculated using the piezoresponse across the BiFeO₃/SrRuO₃ interface. The red line is an error function fit of the piezoresponse data (blue circles) centered around the interface, z_o.

Fig. 2B shows an isometric projection of a volumetric tomogram produced from a subsection of the reconstructed piezoresponse of BiFeO₃ shown in Fig. 2A. The z dimension in Fig. 2B is expanded by a factor of ∼15 for improved viewing of the x-z cross-sectional domain geometry. Both the 71° ferroelastic domain walls as well as “bifurcations” (i.e., defects) in the stripe pattern proceed throughout the entirety of the thickness of the film along the [101]_pc direction (SI Appendix, Fig. S4B). A continuous x shift in the domain configuration of ∼−200 nm throughout the thickness of the BiFeO₃ film indicates that the domain walls are tilted relative to the [001]_pc direction, an observation confirmed by TEM of equivalent specimens (4). At depths 120 nm below the as-grown surface (i.e., the BiFeO₃ film thickness, z = 0), an abrupt change in the PFM contrast from stripe-type domains to a uniform noise-limited signal indicates the complete removal of BiFeO₃ and the presence of either nonpiezoelectric SrRuO₃ or DyScO₃. The BiFeO₃/SrRuO₃ interface appears sharp and well-defined throughout the field of view in the tomograms of both piezoresponse and probe current. This is consistent with minimal subsurface structural damage during TAFM and is expected for the atomically precise interfaces commonly observed in epitaxial heterostructures synthesized using pulsed-laser deposition.

The vertical removal rate of 0.97 nm per frame during tomography of BiFeO₃ has been calculated using the mean z position of a given frame relative to the preceding frame; however, the large number of imaging pixels in the sequence (n > 10⁷) permits a more precise analysis of material removal rate. A histogram of the frame-to-frame change in the z position of the film surface (Δz) for each x-y imaging pixel for all frames on BiFeO₃ is shown in Fig. 2C. A pronounced peak is observed at the mean removal rate, Δz = −0.97 nm; however, the fine structure of the distribution contains shoulder peaks with a mean spacing of 0.46 nm (red arrows), which is within ∼15% of the room-temperature c-axis lattice parameter of BiFeO₃ (4.0 Å). This finding strongly suggests that material removal occurs in discrete multiples of unit cells, providing evidence of near-atomic-scale subtractive fabrication capabilities of TAFM. The resolution of the 3D PFM data on BiFeO₃ has been calculated using the piezoresponse across both an in-plane domain wall and the BiFeO₃/SrRuO₃ interface. The actual width of a ferroelectric domain wall, as well as a heteroepitaxial interface, is on the order of 1–2 unit cells, and the apparent width of these atomically-sharp interfaces provides a quantitative measure of the PFM spatial resolution, comparable to edge resolution in optical microscopy (33). Fitting the interfacial piezoresponse with an error function results in an x-y spatial resolution of 18.7 nm (SI Appendix, Fig. S5) and a z spatial resolution of 0.93 nm, shown in Fig. 2D. The BiFeO₃/SrRuO₃ interface used to quantify the z resolution is indicated with the dashed red line in Fig. 2B, and z_o is the location of the interface. These resolution figures result in a PFM spatial resolution and voxel size of less than 315 nm³ and 20 nm³_, respectively, among the highest reported 3D resolution for materials properties to date.

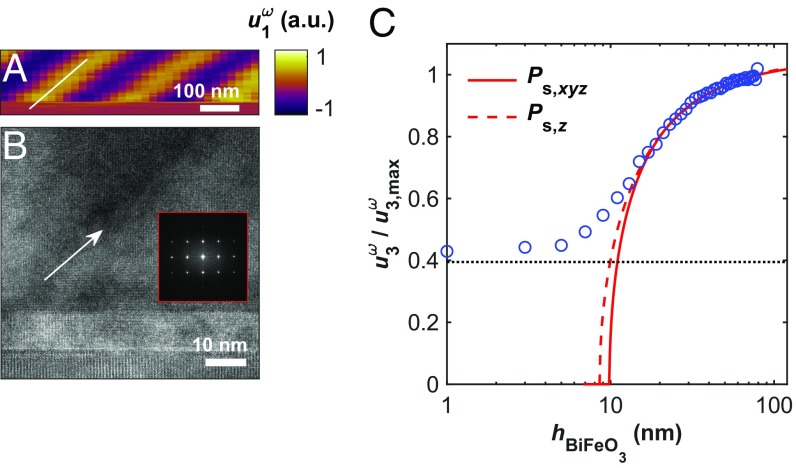
To verify the spatial fidelity of the tomographic PFM data, TEM was performed on the BiFeO₃ film following TAFM. Fig. 3A shows a representative x-z cross-section of the tomogram from Fig. 2B with correctly proportioned axes. The white reference line in Fig. 3A is tilted at 40° from the [100]_pc (x) crystal axis, and is shown to illustrate the vertical tilt of the 71° ferroelastic domain walls resolved by tomographic PFM. Fig. 3B shows a TEM cross-section taken along the [010]_pc zone axis (y direction, Fig. 2B), an identical perspective as Fig. 3A, where the white arrow indicates both the location of a 71° domain wall and a 40° domain wall inclination angle. Fig. 3B has been acquired from a region of BiFeO₃ where TAFM first partially removed the BiFeO₃ film above the imaging field of view. The as-grown tilting of 71° ferroelastic domain walls as well as the crystallinity of the BiFeO₃ (fast Fourier transform; Fig. 3B, Inset) are readily observed in Fig. 3B, establishing the complementarity of TAFM and TEM imaging techniques. Combined with the faithful reproduction of the domain wall geometry and the near-constant piezoresponse magnitude throughout the BiFeO₃ film (Fig. 3A), these observations provide evidence of the effectiveness of TAFM measurements for accurate, high-resolution 3D imaging of ferroelectric domains.

Fig. 3.

Validation of TAFM using high-resolution TEM and phenomenological theory. (A) x-z cross-section of tomographic PFM data depicting the true geometry of a 71° ferroelastic domain wall. (B) Cross-sectional TEM of BiFeO₃ showing an equivalent 71° domain wall with identical geometry, obtained below a TAFM processed surface. (Inset) The 2D fast Fourier transform from BiFeO₃ adjacent to the domain wall. (C) Semilogarithmic plot of normalized piezoelectric displacement as a function of thickness for BiFeO_3, with nonlinear regressions for 3D and one-dimensional LGD phenomenological models. Horizontal dashed line in C indicates the PFM signal noise floor.

Using TAFM, the thickness dependence of the spontaneous polarization in BiFeO₃ has been investigated within a single imaging field of view and validated with Landau–Ginzburg–Devonshire (LGD) phenomenological theory. The normal [001] component of the piezoelectric strain tensor in a piezoelectric crystal, x₃₃, is proportional to its spontaneous polarization, which in turn is a function of crystal thickness according to a 3D formulation of the LGD theory (13) (SI Appendix). Under the assumption of constant dielectric permittivity and electrostriction within the BiFeO₃ thickness range considered, the piezoelectric strain provides a measurement of the thickness-dependent spontaneous polarization in a ferroelectric such as BiFeO₃. Reformulating x₃₃ in terms of the out-of-plane cantilever displacement measured during PFM at frequency ω ($u_3^{\omega }$), the thickness dependence of the normalized piezoelectric displacement can be expressed as

$$\begin{array}{c}\frac{u_3^{\omega }}{u_{3,\text{max}}^{\omega }}=2Q_{33}{\mathit{ϵ}}_0{\mathit{ϵ}}_{33}{V}^{\omega }\cdot A\sqrt{B+\sqrt{1-\frac{h_{\text{cr}}}{h}}}\end{array},$$ [1]

where ε₀ is vacuum permittivity, Q₃₃ and ε₃₃ are z-oriented components of the electrostriction and dielectric permittivity tensors, respectively, V^ω is the oscillating PFM excitation voltage, A and B are temperature-dependent constants that incorporate multiple coefficients from the Landau free-energy expansion with respect to spontaneous polarization (13), and h_cr is the critical thickness for ferroelectricity, i.e., the thickness below which a switchable, spontaneous polarization is theoretically no longer stable. Fig. 3C (open circles) shows the normalized, [001]_pc-oriented piezoresponse ($u_3^{\omega }$) for BiFeO₃ plotted as a function of film thickness, h, acquired following TAFM (source data shown in SI Appendix, Fig. S6). A nonlinear least-squares regression of $u_3^{\omega }$ versus h using the model in Eq. 1 (Fig. 3C, solid line) results in a critical thickness, h_cr, of 6.8 nm, which is comparable to that calculated for BiFeO₃ by Rault et al. (13) (5.6 nm) using a combination of low energy and photoemission electron microscopy measurements. A fit of the data according to the one-dimensional LGD model derived by Maksymovych et al. (14) has been overlaid in Fig. 3C (dashed line) for reference. Deviation of the experimental piezoresponse from LGD theory can be partially attributed to a lower limit of measurable piezoresponse established by signal noise (dashed black line in Fig. 3C, $u_3^{\omega }/u_{3,\text{max}}^{\omega }$ = 0.39). The gradual approach to this limit is consistent with monotonically decreasing dielectric permittivity below an assumed constant (bulk) value at BiFeO₃ thicknesses below 15 nm.

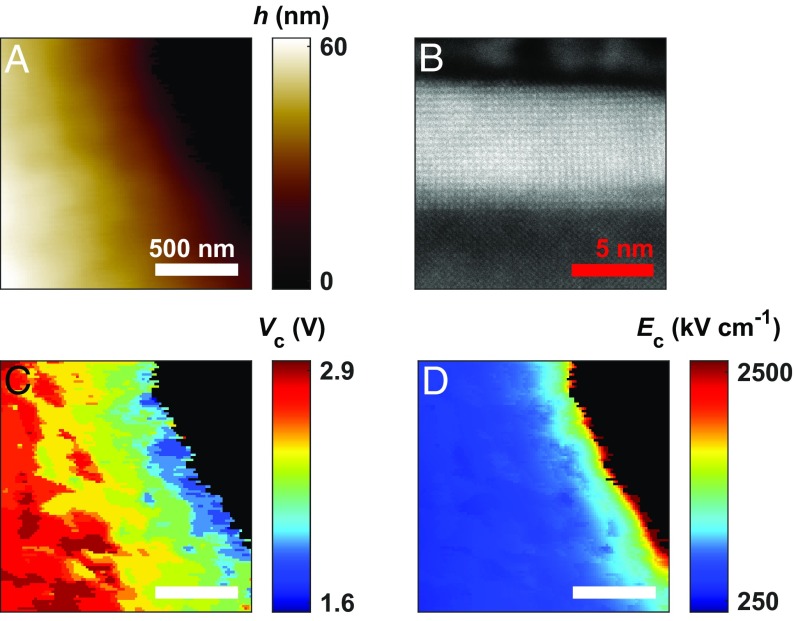
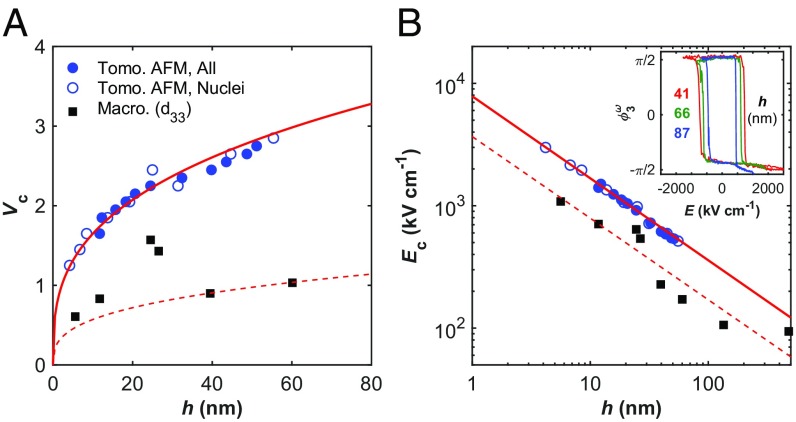
In addition to tomographic measurements of ferroelectric properties, TAFM provides an experimental platform for investigating the local dynamics of thickness-dependent spontaneous polarization reversal (switching). Dual-frequency, time-dependent PFM with a superimposed dc bias voltage was used to both induce and spatially map the evolution of ferroelectric polarization switching (34) within a region of BiFeO₃ where a predefined thickness gradient has been intentionally fabricated through TAFM (Fig. 1A). Fig. 4A displays a topographic map of a smoothly varying BiFeO₃ thickness gradient, 60 nm > h > 0 nm (i.e., SrRuO₃). Atomic-resolution high-angle annular darkfield scanning transmission electron microscopy (HAADF-STEM) for an equivalent region of BiFeO₃ is displayed in Fig. 4B and confirms the unperturbed crystal structure following TAFM at h = 7 nm. There is no visible dislocation formation, amorphization, or BiFeO₃/SrRuO₃ layer intermixing (SI Appendix, Fig. S7), and the pseudocubic lattice structure is clearly visible to within a single unit cell of the BiFeO₃ surface. Starting with a dc voltage of +0.6 V dc, the bias voltage was held constant until the spatial distribution of P⁺ and P⁻ domains (out-of-plane PFM phase, ${\varphi }_3^{\omega }$) within the field of view was invariant with respect to time (SI Appendix, Fig. S8). Following this criterion, the dc voltage was increased by 200 mV to induce further P⁻ → P⁺ polarization switching at thicker regions of BiFeO₃. This procedure was repeated until the out-of-plane ferroelectric polarization state had completely switched from P⁻ to P⁺ within the imaging field of view (+2.8 V dc). From this sequence, a nanoscale map of the local coercive voltage, V_c, can be constructed, shown in Fig. 4C. Coupling the spatially resolved V_c with the local BiFeO₃ thickness (h, Fig. 4A) enables the ferroelectric coercive field, E_c, to be mapped with nanometer-scale resolution, shown in Fig. 4D. This approach allows direct visualization of the thickness dependence E_c within a single imaging field of view. Clearly visible from these results is the direct proportionality of V_c and h (Fig. 4C) and the strong inverse proportionality of E_c and h for BiFeO₃ (Fig. 4D).

Fig. 4.

Spatially resolved polarization switching of variable-thickness BiFeO₃ following TAFM. (A) BiFeO₃ film thickness (h) and (B) cross-sectional HAADF-STEM of BiFeO₃ following TAFM showing unperturbed crystal structure. (C) Coercive voltage, V_c and (D) coercive field, E_c cospatial with A, determined at the onset of ferroelectric switching from P⁻ to P⁺ polarization.

The nucleation-based polarization reversal model of ferroelectrics proposed by Landauer (35) and Kay and Dunn (36) defines the thickness dependence of the electric field required to nucleate a semiprolate spheroidal domain of opposite polarization in a uniformly polarized crystal. The nucleation field obeys the semiempirical equation

$$\begin{array}{c}{E}_{\text{n}}=k{\left(\frac{b^{2}c}{a^3}\right)}^{1/3}{h}^{-2/3}\end{array},$$ [2]

where E_n is the coercive field at domain nucleation, k is a fixed constant, a, b, and c are constants that describe the geometry of the domain nucleus, and h is the crystal thickness. Several studies have reported Kay–Dunn coercive field scaling (i.e., E_c $\propto$ h^−2/3) in thin-film ferroelectrics (37, 38), while others have observed more general inverse power-law correlations between coercive field and film thickness (14, 39); all scaling experiments to date have been performed across multiple samples having discrete film thicknesses. Deviation from Kay–Dunn scaling in ultrathin films (h < 20 nm) has been attributed to perturbations in the depolarizing field acting antiparallel to the applied electric field (40), as well as a transition to cylindrically shaped domain nuclei at film thicknesses below 15 nm (41). Here, the spatially resolved h, V_c, and E_c data shown in Fig. 4 provide the basis for a comprehensive statistical analysis of the thickness dependence of ferroelectric coercivity in BiFeO₃. Fig. 5A shows a plot of V_c versus h for BiFeO₃ calculated using TAFM; closed blue circles represent the median thickness for all pixels that have switched from P⁻ to P⁺ at the corresponding applied voltage, V_c. The spatially resolved ferroelectric switching permits the identification of V_n (i.e., V_c) and h for individual P⁺ domain nuclei (open blue circles), in accordance with the theories of Landauer, and Kay and Dunn (SI Appendix, Fig. S8F). Reformulating Eq. 2 in terms of V_n and assuming E_n = V_n/h produces the relation $V_n\propto h^{1/3}$, a nonlinear power-law (Ax^b) regression of nuclei-V_c versus h in Fig. 5A yields the exponent b = 0.331 ± 0.045 for TAFM data (solid red line), in strong agreement with Kay–Dunn scaling. Macroscopic measurements of V_c obtained from d₃₃ measurements on discrete BiFeO₃ thin-film capacitors are also shown (black squares), along with the corresponding Ax^1/3 fit (dashed red line) for comparative visualization. The V_c offset between macroscopic and PFM data could result from several possible mechanisms. As with all PFM studies in ambient conditions as performed here, voltage losses at the tip–sample interface may occur due to parasitic capacitances (42). Differences in work function for patterned electrodes compared with the AFM probe may cause a voltage offset as well. But, the similarities acquired via PFM for discrete specimens (black squares, Fig. 5), over tens of thousands of data points in a single field of view (blue circles, Fig. 5), or from distinct PFM hysteresis loops on the same thickness gradient specimen (SI Appendix, Fig. S9), all indicate uniform if not completely negligible parasitic effects.

Fig. 5.

Thickness dependence of the coercive voltage (V_c) and coercive field (E_c) in BiFeO₃. (A) V_c vs. h, with TAFM data from all switched areas (closed blue circles), domain nuclei (open blue circles), and d₃₃-based measurements on macroscopic capacitor structures (black squares). Solid red line is a nonlinear power-law regression of V_c vs. h. (B) Logarithmic plot of E_c vs. h, using the same labeling convention as A. (Inset) Spectroscopic piezoresponse hysteresis loops (PFM phase) obtained at three discrete thicknesses following TAFM.

Fig. 5B shows a plot of E_c versus h in BiFeO₃ on logarithmic axes (same labeling as Fig. 5A); the strong linearity and precision of TAFM data relative to macroscopic measurements is apparent. A nonlinear power-law regression of nuclei-E_c versus h yields the exponent b = −0.670 ± 0.038, again in strong agreement with Kay–Dunn scaling. The minimum switched thickness measured using TAFM is 4.2 nm, in good agreement with the critical thickness predicted by the LGD fit of $u_3^{\omega }$ versus h (6.8 nm, Fig. 3C). Equivalent scaling behavior, albeit with lower precision, is observed in spectroscopic piezoresponse hysteresis loops acquired at several discrete thicknesses within the same region of BiFeO₃ (Fig. 5B, Inset and SI Appendix, Fig. S9). The scatter from discrete samples or hysteresis loop measurements does not represent intrinsic limitations, but rather extrinsic mechanisms that are often unavoidable for distinctly grown specimens or even positions on a single specimen. For tomographic PFM-based results, on the other hand, such extrinsic effects may be minimized. A statistical treatment of the thickness dependence of ferroelectric properties of BiFeO₃ obtained through TAFM is presented in SI Appendix, Fig. S10.

TAFM, augmented by direct identification of domain nuclei as a function of applied voltage and film thickness during ferroelectric switching, has enabled the observation that BiFeO₃ demonstrates Kay–Dunn scaling of E_c to below 5-nm thickness. This result is not immediately intuitive, since the stepwise polarization rotation known to occur in BiFeO₃ (2) is substantially different from the Ising-type polarization reversal in uniaxial ferroelectric materials (e.g., BaTiO₃) upon which the Landauer–Kay-Dunn theory is formulated. The Landauer–Kay-Dunn theory describes the electrostatics and geometry of ferroelectric domain nucleation; equivalent scaling in BiFeO₃ implies that its Bloch-like multistep polarization rotation is governed by the same electrostatic formulation of domain nucleation for Ising-type ferroelectrics. More specifically, the observed scaling of E_c suggests that the ferroelectric domain nuclei in BiFeO₃ retain semiprolate spheroidal geometry and that the effects of the depolarizing field remain constant throughout the two decades of film thicknesses measured, ∼1 nm < h < 120 nm. These analyses of nanoscale ferroelectric behavior in BiFO₃ represent an AFM-based approach for fundamentally understanding the size dependence of functional materials properties. TAFM allows for scaling phenomena to be explored on a single sample within a single imaging field of view, providing a high level of statistical confidence by representing each imaging pixel as a discrete capacitor element. By combining the subnanometer thickness resolution of AFM with the direct identification of domain nuclei, this work presents direct visualization reported of Kay–Dunn scaling in a ferroelectric. Unambiguous determination of absolute film thickness and local properties enabled by TAFM complements mean-thickness methods by providing access to thickness-dependent phenomena with precision, with broad potential for application across a range of material systems and AFM measurement variations.

In conclusion, we report a volumetric scanning probe microscopy investigation of ferroelectricity across two decades of thickness in a single field of view for the multiferroic BiFeO₃. Using a tomographic variant of AFM in conjunction with PFM, the full 3D geometry of nanoscale ferroelectric domains has been resolved. By combining nanoscale mapping capabilities with site selectivity and subnanometer thickness resolution, TAFM establishes an experimental platform for direct, high-accuracy correlations between film thickness and material properties. In this article, TAFM has provided access to the thickness dependence of two critical ferroelectric properties, spontaneous polarization and ferroelectric coercive field, enabling clear confirmation of both LGD phenomenological theory and Landauer–Kay-Dunn coercive field scaling in BiFeO₃ with a critical thickness for ferroelectricity on the order of 5 nm. These results more broadly illustrate the potential of TAFM for future investigations into the thickness dependence of materials properties, as TAFM extends the constellation of scanning-probe-based local property mapping techniques into all three spatial dimensions with better than 315 nm³ spatial resolution.

Materials and Methods

BiFeO₃ (001)_pc/SrRuO₃ (001)_pc heterostructures were grown epitaxially on DyScO₃ (110)_o substrates using pulsed-laser deposition, with nominal thicknesses of 120 and 10 nm, respectively. Pulsed-laser deposition was performed at 690 °C in a 100-mTorr oxygen environment using a KrF laser at 8 Hz. AFM measurements were performed in ambient conditions with an Oxford Instruments Asylum Research Cypher S AFM, along with a Zurich Instruments HF2LI lock-in amplifier and NanoSensors (NanoWorld)-type CDT-NCHR conductive diamond-coated probes having nominal stiffness k = 24 N m⁻¹ and resonance frequency f₀ = 325 kHz.