Experimental and computational analyses reveal dynamics of tumor vessel cooption and optimal treatment strategies

Significance

Vessel cooption is a strategy that many tumors employ to progress without creating new blood vessels but by exploiting preexisting vessels of the host tissue. In addition to promoting tumor growth, cooption is also associated with tumor resistance to antiangiogenic therapy. Despite the importance of this mode of tumor progression, the molecular and cellular mechanisms are not fully understood. Here, we combine intravital microscopy imaging and mathematical modeling to explore the dynamics of individual cancer cell cooption and collective response of the coopted cancer cells during antiangiogenic treatment. We also provide guidelines for effective therapeutic strategies that combine inhibition of both angiogenesis and cooption.

Abstract

Cooption of the host vasculature is a strategy that some cancers use to sustain tumor progression without—or before—angiogenesis or in response to antiangiogenic therapy. Facilitated by certain growth factors, cooption can mediate tumor infiltration and confer resistance to antiangiogenic drugs. Unfortunately, this mode of tumor progression is difficult to target because the underlying mechanisms are not fully understood. Here, we analyzed the dynamics of vessel cooption during tumor progression and in response to antiangiogenic treatment in gliomas and brain metastases. We followed tumor evolution during escape from antiangiogenic treatment as cancer cells coopted, and apparently mechanically compressed, host vessels. To gain deeper understanding, we developed a mathematical model, which incorporated compression of coopted vessels, resulting in hypoxia and formation of new vessels by angiogenesis. Even if antiangiogenic therapy can block such secondary angiogenesis, the tumor can sustain itself by coopting existing vessels. Hence, tumor progression can only be stopped by combination therapies that judiciously block both angiogenesis and cooption. Furthermore, the model suggests that sequential blockade is likely to be more beneficial than simultaneous blockade.

Originally developed to starve tumors, antiangiogenesis monotherapies have provided only modest or no survival benefits to cancer patients (1). The inability of antiangiogenic agents to consistently stop growth of primary or metastatic lesions is likely due to other compensatory mechanisms that the tumor can exploit to gain access to blood vessels. For example, some solid tumors grow without creating new blood vessels, instead exploiting the preexisting, host vasculature in a process termed vessel cooption. Nonangiogenic coopting tumors have been reported in the brain, lung, liver, and skin in both preclinical (mouse) models and patients (2–5). These coopting tumors grow by migrating along the existing vasculature rather than proliferating in place and recruiting new blood vessels. The cancer cells around coopted vessels, in turn, can grow and eventually compress these vessels, making them dysfunctional, causing hypoxia, and leading to hypoxia-induced angiogenesis (6–8). Cooption can involve individual cell migration or collective migration of cancer cells (9). Single cancer cells may adopt a coopting phenotype in the process of metastasis, either preceding intravasation at the primary site or following extravasation at the secondary site (5).

Because of its ability to circumvent the need for angiogenesis, vessel cooption confers resistance to antiangiogenic treatments, including anti-vascular endothelial growth factor (VEGF) therapies, which use monoclonal antibodies against VEGF or its receptor, or multitargeted receptor tyrosine kinase inhibitors (RTKIs). These therapies have failed to show overall survival benefit in unselected patients with glioblastoma (GBM) (1). Interestingly, in some orthotopic murine models of GBM, these agents increased survival, primarily by reducing edema rather than directly inhibiting tumor growth (10). Furthermore, studies have suggested that gliomas may increase their invasive phenotype in response to antiangiogenic therapy (11). Some studies have shown that antiangiogenic treatment can maintain and reinforce vessel cooption, allowing tumors to evade antiangiogenic therapy (12–14). This is especially relevant in primary and metastatic brain tumors where it is now accepted that invasion can be achieved not only by cell migration along the white matter tracks but also by coopting brain blood vessels (15). These results show that vessel cooption is a mechanism that tumors use to evade antiangiogenic treatment in animal models and patients (16).

The resistance to antiangiogenic therapy underscores the need to understand the mechanisms that drive cooption and raises two questions: (i) How do cancer cells interact with the host vasculature during cooption? (ii) Can we target cooption to improve therapy? Despite intense research in vessel cooption, a complete mechanistic understanding, as well as therapeutic targets, remains elusive (5, 9). To begin to understand this process, we followed the progression of two orthotopic models of invasive glioma (CNS-1 and GL261) using intravital multiphoton laser scanning microscopy (MPLSM) (10, 17). To simulate antiangiogenesis therapy of GBM, we treated one group of animals with a pan-VEGF RTKI, cediranib. We were able to visualize tumor growth and cell migration into the normal brain and to identify the regions of invasion with respect to structural and molecular markers of the brain parenchyma. In addition, we tested a model of brain metastasis from breast cancer using MDA-231BR cells (brain metastatic variant of a triple negative human breast cancer cell line) (18), which showed that metastatic cells also coopt the brain vasculature and that cooption can cause blood vessel compression.

To further probe the mechanisms and implications of vessel cooption, we developed a multiscale mathematical model that relates tissue level events to cellular and subcellular events to elucidate the mechanisms and dynamics of vessel cooption and response to antiangiogenic treatment. The model integrates multiple biological scales, spanning the microscopic cellular/subcellular scale of cancer and stromal cells and macroscopic tumor behavior (Fig. 1). Unlike previous efforts to model vessel cooption (SI Appendix, Table S1), our model accounts for the direct effects of cooption on the vascular density and the 3D growth of the tumor, the interactions between the tumor and the host tissue, the function of the tumor blood vessels, and the compression of coopted vessels that compromises their function. Model predictions were compared and validated against a large number of independent experimental studies summarized in Table 1—including our own experiments presented here—which were selected because they provide parameters measured both at the cellular and tissue level of a tumor. Model results agreed qualitatively with all sets of experiments, providing a mechanistic understanding of the kinetics and interactions among cancer cells and host vasculature, as well as the response of gliomas during antiangiogenic treatment. Finally, the model was employed to provide insights on the optimal use of antiangiogenic and anticooption therapeutic strategies.

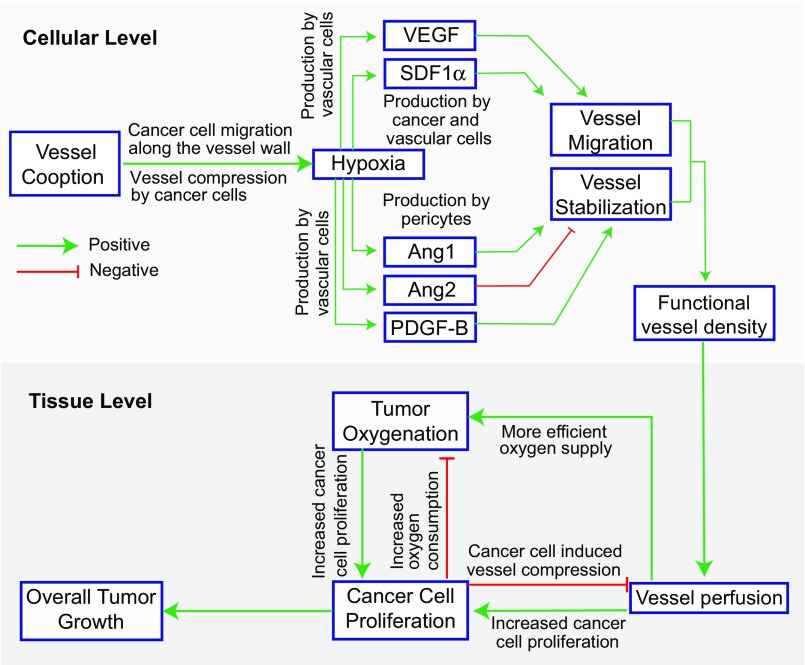
Fig. 1.

Schematic of components comprising the mathematical model and their interactions. The model considers events at both cellular and tissue levels. At the cellular level, cancer cells move toward the more oxygenated regions, coopting existing normal blood vessels. Cancer cell proliferation next to blood vessels can cause vessel compression, resulting in hypoxia, which drives a secondary angiogenic response as VEGF and SDF1α levels increase. This initiates angiogenesis through the proliferation and migration of vessels. Angiogenesis is enhanced by high levels of Ang2, which destabilizes vessels, and inhibited by Ang1 and PDGF-B, which recruit pericytes and stabilize vessels. From the vascular endothelial cell population, a tissue level functional vessel density is calculated that, in turn, determines the macroscopic oxygen transport, cancer cell proliferation, and overall tumor growth.

Table 1.

Experimental studies employed to validate model predictions

Tumor model	Parameters measured for model validation	Main findings	Source
Glioblastoma	Time required by cancer cells to coopt vessels	Kinetics of movement of cancer cells along blood vessels during cooption	(1)
Glioblastoma	Vessel diameter changes with respect to coopted cancer cell population	Decrease in diameter correlates with number of coopting cancer cells	(19)
Glioblastoma	Intratumor distribution of VEGF, Ang2, and vascular density	VEGF, Ang2, and vascular density are concentrated at tumor periphery	(6)
Colon carcinoma	Oxygen levels during tumor growth	Hypoxia is observed from the early stages of incipient angiogenesis	(20)
Glioblastoma	Tumor response to Wnt inhibition	Wnt inhibition reduced cooption (i.e., number of cancer cells in contact with vessels)	(9)
Glioblastoma	Tumor response to antiangiogenic treatment	Antiangiogenic treatment resulted in increased cooption at the tumor periphery	Current study

Also presented are parameters measured and main findings that were compared with model results.

Results

Kinetics of Host Vessel Cooption in an Invasive GBM Model in Mice.

We first examined the kinetics of vessel cooption in CNS-1 tumor—an invasive GBM model. CNS-1 tumor cells were implanted in the cerebrum of SCID mice bearing transparent cranial windows, and tumor development was monitored intravitally using MPLSM every 2 or 3 d. Fig. 2A shows representative images of vessel cooption over time. The invasive tumor cell line CNS-1 (Fig. 2A, red) invaded along the large meningeal vessels (Fig. 2A, green) of the brain. Readily observable vessel cooption occurred within the first 11 d after cell implantation in the meningeal layer; however, established tumors in the brain parenchyma grew more as a mass, with little vessel cooption at the tumor/brain interface.

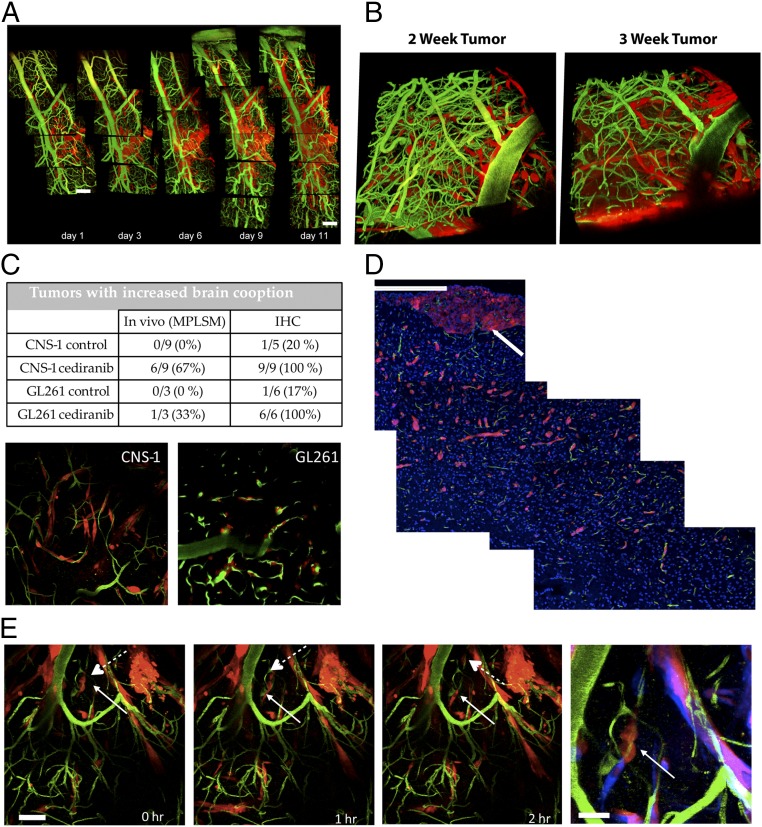
Fig. 2.

In vivo measurements of vessel cooption. (A) Using intravital microscopy, newly implanted CNS-1 tumor cells (red) were detected growing along the meningeal vessels of the brain vasculature (green). (Scale bar: 50 µm.) (B) In cases where the cells were implanted deeper in the brain parenchyma, after 2 to 3 wk (day 16 and 21, respectively), the tumor was fully established in the brain, as evidenced by the 3D projections. It should be noted that, at this stage of growth, a central tumor mass had formed below the displayed 3D volume. (C) Antiangiogenic treatment increases vessel cooption. Quantification performed in vivo or using immunostaining of harvested tissue showed increased vessel cooption by tumor cells, with less central mass growth and more preferential tumor growth along brain vessels. (D) The extent of tumor spread from the primary mass (white arrow) by cooption is shown in immunofluorescence sections of GL261 tumors following cediranib treatment (red, GL261 tumor cells; green, CD31⁺ vessels; blue, nuclei). (Scale bar: 200 µm.) (E) Typical trajectory of coopting tumor cells. Following a single cell division (solid and dash arrows), the daughter cells subsequently migrated in opposite directions along the vessel. (Scale bar: 50 μm.). The Right-hand panel shows an overlay of the displacements over the 2-h period for the region shown by the solid arrow, with the initial position appearing in red and the final positions in blue. (Scale bar: 20 μm.) (Magnification: B and C, 200×.)

Antiangiogenic Treatment Increases Vessel Cooption by GBM Cells.

Next, we studied the effect of antiangiogenic treatment on vessel cooption. Mice with invasive CNS-1 or GL261 gliomas were treated with 6 mg/kg cediranib, a vascular endothelial growth factor receptors (VEGFRs) tyrosine kinase inhibitor (TKI). During antiangiogenic treatment, infiltrative tumor cells appeared along brain vessels outside the main tumor mass (tumor mass below rendered 3D volume) (Fig. 2B). Quantification of cooption using both in vivo microscopy and immunohistochemistry (IHC) showed an increase in cooption in both tumor cell lines after long-term cediranib treatment (>2 wk) (Fig. 2C). Furthermore, mainly CNS-1 and, to a lesser extent, GL261 tumors invaded deeper into the perivascular space of the brain parenchyma following cediranib treatment. By imaging tissues more than 200 µm below the surface using multiphoton microscopy, we verified that most tumor cells (Fig. 2C, red) outside the main mass were invading along brain microvessels (Fig. 2C, green). Using IHC, we analyzed coopted vessels that extended over 1 mm from the primary lesion. Sections were stained with an anti-CD31 antibody (Fig. 2D, green) and DAPI (Fig. 2D, blue) to distinguish blood vessels and tumor cells (Fig. 2D, red). The IHC analysis showed that the invasion occurred preferentially along perivascular pathways (Fig. 2D), consistent with the intravital observations (Fig. 2C). To observe the dynamics of cooption directly, we performed time-lapse imaging of tumor cells in the brain during cediranib treatment (Fig. 2E). Consistent with the static data, proliferating tumor cells migrated along coopted brain vessels.

Tumor Cells Can Compress Coopted Vessels.

We next examined a model of breast cancer metastasis to the brain. MDA-231BR breast cancer cells were injected into the left ventricles of nude mice with cranial windows. Extravasation of the circulating cancer cells occurred within 7 d, and vessel cooption became apparent 4 wk after injection, with extensive cooption evident at 7 wk (Fig. 3 A–C). In this model, we found that vessel cooption can cause the compression of the affected vessels (Fig. 3 D–F) as vessels coopted by cancer cells often adopt elliptical shapes (Fig. 3 D and E) or have unusually small lumens compared with those not surrounded by cells (Fig. 3F). Both modes of vessel deformation can be caused by mechanical forces that cancer cells exert on the vessels (21–23). Therefore, apart from maintaining tumor progression under antiangiogenic treatment, vessel cooption can also cause compression of coopted vessels.

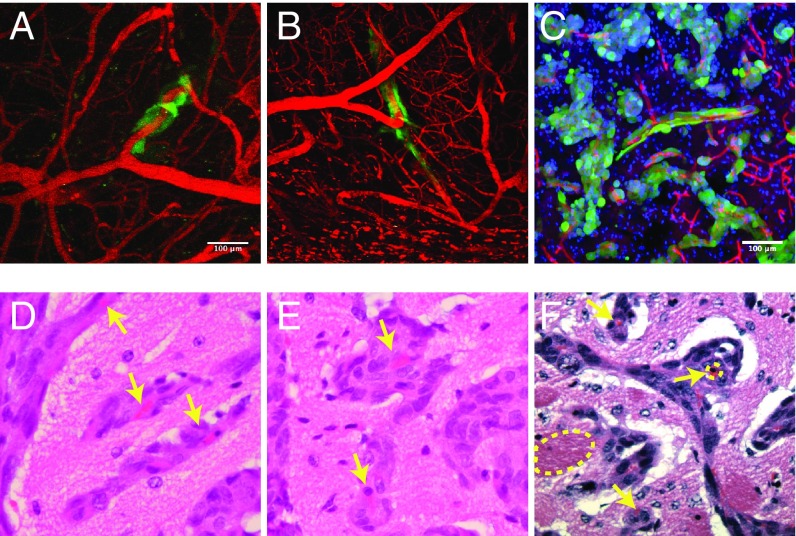
Fig. 3.

Proliferation of cancer cells that coopt blood vessels can compress tumor blood vessels. (A and B) Cooption of tumor blood vessels (red) by metastatic MDA-231BR cells (green) imaged by intravital microscopy. The two fields of view show typical cooption events. (C) The close association of cancer cells with blood vessels is further confirmed by immunofluorescence imaging. (D–F) H&E images of brain tumor sections show the compression of blood vessels due to the accumulation of perivascular cells (arrows), caused by cancer cell migration and proliferation along the vessel (blood vessel dimensions: compressed 4 to 6 µm and uncompressed 22 to 45 µm). The bright red objects are red blood cells trapped within the collapsed blood vessels and the dashed oval shows the vessel periphery. (Scale bars: A and C, 100 μm; scale identical in B.) (Magnification: D–F, 400×.)

Predictions and Insights from the Mathematical Model.

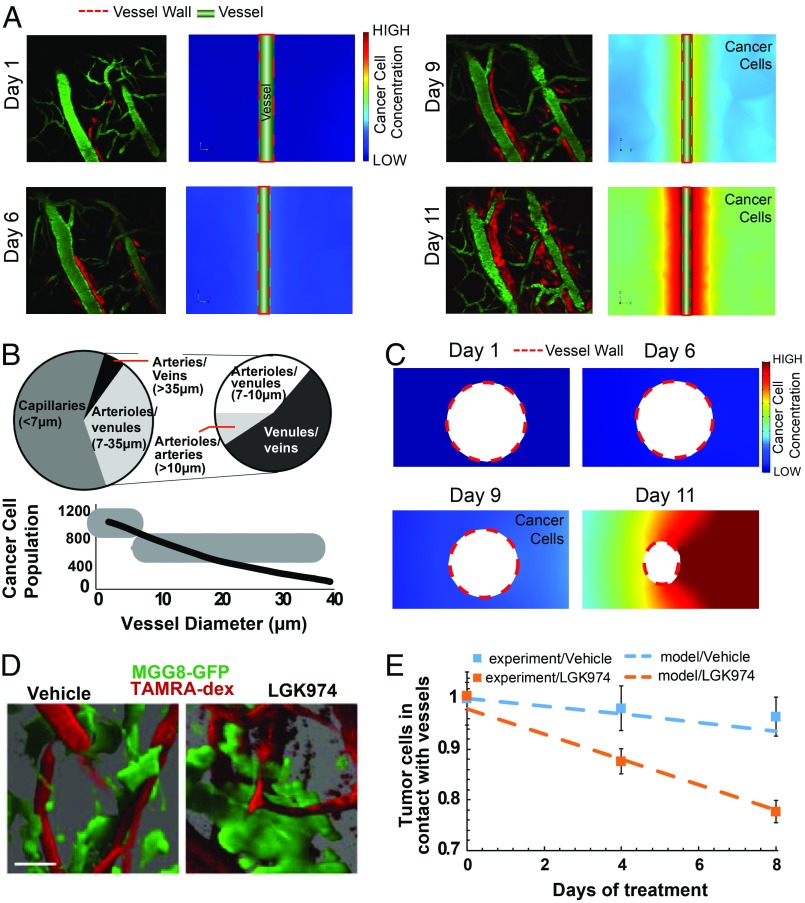
To better understand the mechanisms of vessel cooption and the effect of antiangiogenic and anticooption treatment, we developed a continuous mathematical model (Fig. 1). In the model, cancer cells migrate toward better oxygenated tissue using well-studied chemotaxis mechanisms. They can contact and move along the vessel wall and mechanically deform blood vessels. The growth and migration of the cancer cells can compress normal structures, such as blood vessels, reducing blood flow and producing hypoxia, which in turn triggers the production of angiopoietin 1 (Ang1) by pericytes, angiopoietin 2 (Ang2) and platelet-derived growth factor-B (PDGF-B) by tumor endothelial cells, as well as production of VEGF by cancer cells and stroma cell-derived factor 1 alpha (SDF1α) by both cancer and endothelial cells (24–26). Ang1 and PDGF-B stabilize blood vessels by increasing pericyte coverage whereas Ang2 destabilizes them, increasing their sprouting potential. In the model, VEGF and SDF1α gradients coordinate the processes of angiogenesis and vasculogenesis by directing the migration of endothelial cells and their progenitors (27). Macroscopic tumor growth is limited by the availability of endothelial cells, calculated based on VEGF- and SDF1α-driven growth and migration. The processes involved at cellular and tissue levels and their interactions are summarized in Fig. 1. We determined key parameters and validated the model using both our experiments and data extracted from the literature (Table 1). To demonstrate the ability of the model to predict cancer cell cooption around a single vessel and the resulting changes in vessel diameter due to cancer cell-induced compression, we extracted information on cellular events and vessel morphology from three independent studies of vessel cooption (1, 9, 19). The computational domain includes a vessel which bisects a rectangular domain representing the tissue. The cancer cells are located on one side of the domain (SI Appendix, Fig. S1A). The model accurately reproduces cell migration dynamics and the association between cells and the vessel wall observed in our experiments with orthotopic glioblastomas in mice (1) (DsRed-expressing CNS-1 cells) (Fig. 4A). Watkins et al. (19) correlated vessel diameters in gliomas in mice with the number of cancer cells associated with the vessel wall. Our model predictions agree with their experimental data (Fig. 4 B and C). To further explore mechanisms of cooption, we modeled the experiments of Griveau et al. (9), who utilized a patient-derived proneural GBM model by orthotopically implanting GFP-tagged MGG8 cells in cranial window-bearing nude mice. To detect colocalization of cancer cells and vessels, they injected tetramethylrhodamine (TAMRA) dextran i.v. (Fig. 4D), and treated the mice with the porcupine inhibitor LGK974, which blocks Wnt secretion. They found that LGK974 treatment significantly reduced the percentage of MGG8 cells in contact with blood vessels, suggesting that the treatment reduces cooption (Fig. 4E). To simulate this experiment with our model, we blocked cooption by eliminating cancer cell chemotaxis and found that model predictions agreed well with the experimental results (Fig. 4E). These results show that the model predictions are consistent with the evolution of cancer cell cooption around blood vessels.

Fig. 4.

Comparison between experimental data and the mathematical model of dynamics of vessel cooption. (A) Model simulations were compared with experimental data (1) for the temporal evolution of vessel cooption around a single vessel. Red represents glioblastoma cells (DsRed-expressing CNS-1 cells), and green represents perfused blood vessels (FITC-dextran injected intravenously). In our model, we adjusted the migration/diffusion coefficient of cancer cells to match the experimental observations of cooption (Color scale: low, 0; high, 18, dimensionless units). Reprinted from ref. 1. Copyright (2014), with permission from Elsevier. (Magnification: 200×.) (B) The decrease in vessel diameter as a function of the number of cancer cells attached to the vessel wall agrees well with published experimental data for D54 glioma cells found in ref. 19. Reprinted from ref. 9. Copyright (2018), with permission from Elsevier. (C) Model simulations for the evolution of cancer cell cooption around a blood vessel and the decrease in coopted vessel diameter were in agreement with experimental data in Fig. 2D (Color scale: low, 0; high = 18, dimensionless units). (D) Blood vessel cooption imaged using GFP tagged MGG8 cells and perfused blood vessels labeled with TAMRA-dextran. Images were created by high-resolution 3D reconstructions of intravital microscopy images of tumors from vehicle- and LGK974-treated MGG8-bearing mice (9). (Scale bar: 25 µm.) Reprinted by permission from ref. 19, Springer Nature: Nature Communications, copyright (2014). (E) Comparison of experimental data (squares, mean ± SEM) and model simulations (dash lines) for the number of MGG8 cancer cells in contact with the vessel wall. The y axis represents the ratio of the number of cancer cells during treatment divided by the number of cancer cells at day 0 for the experimental values and with the corresponding concentration of cancer cells in the model.

Validation of Model Predictions for Oxygenation, Ang2, VEGF, and Vascular Density.

Next, we expanded the model to include coupled cellular and tissue level processes. The 3D model domain includes a spherical tumor growing within a cubic volume of host tissue. Assuming symmetry, we solved the complete model equations in one-eighth of the domain (SI Appendix, Fig. S1B) and compared model predictions with two separate studies (6, 20). In the first study, Cao et al. (20), investigated the incipient tumor angiogenesis that is independent of hypoxia, using genetically engineered HCT116 human colon carcinoma cells, and found that initial tumor vessel recruitment precedes the hypoxic response, presumably due to cooption; a secondary, more intensive angiogenesis appeared after the onset of hypoxia. Specifically, they found that hypoxia appeared on day 3 following cancer cell implantation in the interior region of the tumor. The experimentally measured spatiotemporal evolution of hypoxia is consistent with the model predictions: a significant decrease in oxygen concentration at the center of the tumor starting on day 3 of tumor growth (SI Appendix, Fig. S2).

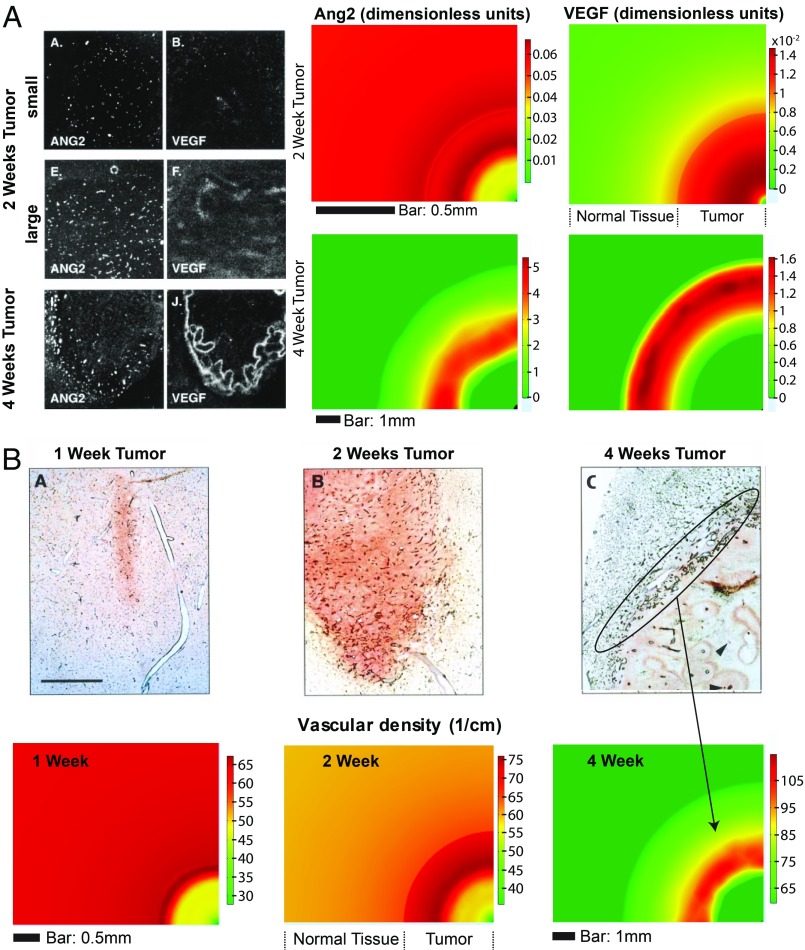
Hypoxia, in turn, up-regulates Ang2 and VEGF levels, driving VEGF-dependent tumor angiogenesis (6). Vessel cooption and its effects on the spatiotemporal evolution of Ang2 and VEGF, as well as on the resulting vascular network, were thoroughly studied by Holash et al. (6) using a rat glioma model. They found that the coopted host vasculature does not immediately undergo angiogenesis but first regresses, causing hypoxia, which is then rescued by robust angiogenesis regulated by Ang2 and VEGF. Specifically, it was shown that these two angiogenic molecules are up-regulated during the fourth week of glioblastoma growth and are concentrated at the tumor periphery where significant angiogenesis is observed. Our model accurately predicts the spatial distribution and temporal evolution of Ang2, VEGF, and angiogenesis (Fig. 5). Additionally, the model can be used to predict dynamics of cancer cells and Ang1 and SDF1α, that were not measured in Holash et al. (6) For example, the model predicts an increase in cancer cell density and Ang1 at the periphery of the tumor while the distribution of SDF1α is higher at the tumor center and decreases toward the periphery (SI Appendix, Fig. S3).

Fig. 5.

Model validation for VEGF, Ang2, and vascular density based on data taken from Holash et al. (6) using a rat glioma model. (A, Left) In situ hybridization analysis of Ang2 and VEGF mRNA in 2-wk-old rat gliomas and a 4-wk-old rat glioma. (Right) Model simulations of Ang2 and VEGF during tumor growth showing the concentrations of the two proteins at the tumor periphery at 4 wk of tumor growth. (B, Top) Sections from rat C6 gliomas showing vessel growth. At 2 wk, tumors continue to have extensive internal vasculature although the vessel density is less than that in the surrounding brain tissue. At 4 wk, the vessels inside the tumor regress, but robust angiogenesis is apparent at the tumor periphery. (Scale bar: 1 mm.) (Bottom) Model simulations agree with the experimental observations. The oval in C shows the region of robust angiogenesis at the tumor margin. From ref. 6. Reprinted with permission from AAAS.

Vessel Cooption Can Cause Resistance to Antiangiogenic Treatment.

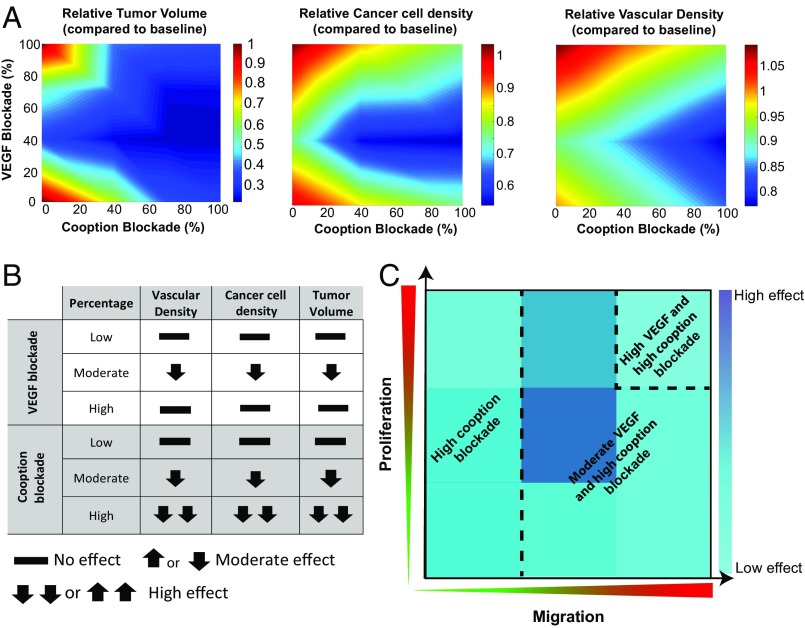
It has been reported that VEGF blockade and the subsequent inhibition of angiogenesis in glioblastomas can be compensated by persistent cooption, a process that may explain tumor resistance to antiangiogenic treatment (12–14). To investigate this mechanism using our model, we mathematically blocked VEGF signaling (and the resulting enhancement of endothelial cell migration), by making endothelial cells insensitive to VEGF gradients, and quantified the changes in vascular density, cancer cell population, and tumor growth. We simulated a murine tumor that grows within a period of 30 d based on the experimental studies that we used to validate the model. In these studies, the treatment period lasted from day 7 to day 25. The model predicts that low or high VEGF blockade does not have any effect on cancer cell density and final tumor volume, compared with the baseline simulations that do not include any treatment. Instead, moderate blocking of VEGF can be beneficial (Fig. 6A). The model also suggests that VEGF blockade does not lead to blood vessel pruning, but instead, the tumor remains well vascularized independently of the degree of VEGF blockade. This is consistent with the hypothesis that vessel cooption can act as a mechanism of resistance to antiangiogenic treatment in glioblastomas. In addition, the prediction of the model that tumors can continue to grow despite anti-VEGF treatment agrees with our experimental data using three different glioblastoma models in mice (10). Importantly, the model predicts that anti-VEGF treatment can be effective when an intermediate VEGF blockade is achieved with an optimum of 40% (Fig. 6A). In this case, a different response is observed, where both blood vessel density and the cancer cell population are uniformly distributed within the tumor, whereas, at lower or higher doses, they are concentrated toward the tumor periphery (SI Appendix, Fig. S4). This result is due to the fact that a low anti-VEGF dose does not cause any effect on the tumor vasculature, and, thus, the results are similar to the no-treatment condition. On the contrary, a high anti-VEGF dose causes excessive pruning of vessels, which creates hypoxia and increased concentration of angiogenic factors at the tumor periphery. This, in turn, results in a higher vascular density and cancer cell density at the periphery.

Fig. 6.

Phase diagrams of tumor volume, cancer cell concentration, and vascular density for (A) combined anti-VEGF and anticooption treatment. (B) Table summarizing the main effects of individual VEGF and cooption blockade from the results in A. (C) Schematic summarizing the optimal treatment condition as a function of cancer cell proliferation and migration rates based on the model results of SI Appendix, Fig. S5.

Interestingly, anti-VEGF treatment is more potent if vessel cooption is blocked at the same time. Drugs that interfere with cooption were modeled by decreasing the parameter that controls cancer cell chemotaxis toward oxygenated regions. Our model suggests that moderate or strong blockade of cooption can effectively reduce tumor volume, cancer cell concentration, and vascular density without the need for anti-VEGF treatment (Fig. 6A). However, the optimal treatment response is observed when 40% VEGF blockade is combined with strong inhibition of cooption. A summary of the results of the model simulations for the individual blockade of VEGF and cooption are presented in the table of Fig. 6B. Moderate VEGF blockade is beneficial compared with lower or higher doses, and cooption blockade improves efficacy in a linear fashion.

It should be noticed, however, that the efficacy of the combined treatment depends on the rates of cancer cell proliferation and migration. In Fig. 6A, results for the baseline values of cancer cell proliferation and migration are shown. Therefore, we repeated simulations of VEGF and cooption blockade by changing the proliferation and migration rate of cancer cells by an order of magnitude from the baseline values. The results are shown in SI Appendix, Fig. S5, and the optimal treatment conditions are summarized in Fig. 6C. The results depend significantly on these two parameters of cancer cells. At low cancer cell migration rates, VEGF blockade is not effective, and only cooption blockade can achieve a reduction in tumor volume. At intermediate migration rates or at high migration rates and low or intermediate proliferation rates, moderate VEGF blockade should be combined with cooption blockade whereas, at high proliferation and migration rates, both VEGF and cooption blockade should be more potent.

We next investigated if sequential blockade of VEGF and cooption can improve treatment compared with the simultaneous blockade studied thus far. Again, the treatments were applied from day 7 to day 25 of the 30-d simulation, and the durations of VEGF and cooption blockade were the same (7 d). A 40% VEGF blockade and a 100% cooption blockade were modeled based on the optimal conditions found in Fig. 6. Model predictions of final tumor volume and vascular and cancer cell density are presented in SI Appendix, Fig. S6. For these simulations, the baseline values of cancer cell proliferation and migration are used, and the results of tumor volume are compared with the optimal condition of simultaneous 40% VEGF and 100% cooption blockade. Four treatment scenarios were studied: (i) 40% VEGF blockade (days 7 to 14), (ii) 100% cooption blockade (days 7 to 14), (iii) cooption blockade (days 7 to 14) followed by a 3-d break (days 15 to 17) and 40% VEGF blockade (days 18 to 25), and (iv) 40% VEGF blockade (days 7 to 14) followed by a 3-d break (days 15 to 17) and cooption blockade (days 18 to 25). Interestingly, the model predicts that sequential inhibition of cooption followed by VEGF can reduce the final relative tumor volume by 40% compared with the simultaneous blockade.

Finally, given the importance of macrophages in glioma progression, we extended the model to account for the densities of the M1- and M2-like macrophages and repeated the simulations. The densities of the M1 and M2 populations depend on tumor oxygenation (28–30): i.e., a decrease in hypoxia skews macrophage polarization away from the M2- toward the tumoricidal M1- phenotype. Model predictions suggest that blocking VEGF and cooption improves tumor oxygenation, which in turn increases the M1-phenotype of macrophages, thus contributing to improved therapeutic outcome (SI Appendix, Figs. S7 and S8).

Taking all model results into consideration, we conclude that vessel cooption should be targeted either alone or in combination with VEGF targeting to achieve regression of tumors that are resistant to anti-VEGF therapy. However, this combinatorial treatment may not always lead to improved efficacy as the result will depend on cancer cell proliferation and motility. Furthermore, sequential targeting of cooption first followed by VEGF blockade appears to be advantageous over simultaneous treatment.

Discussion

Although approved for salvage treatment of recurrent GBM in the United States, bevacizumab does not improve overall survival, similar to various anti-VEGFR TKIs (e.g., cediranib) (4). It is therefore critical to understand the mechanisms of this failure. Here, using intravital microscopy, we found that long-term treatment of established GBMs with cediranib leads to an increase in tumor invasion along existing brain vessels. We also found that coopting cancer cells often compress vessels, which can trigger hypoxia-induced angiogenesis. Furthermore, to provide deeper insights into the mechanism of vessel cooption, we developed a mathematical framework for tumor growth and response to antiangiogenic treatment, taking into account the biological and physical events driving the process, from the early stage of vascular modifications through cooption of the host vasculature and the secondary, VEGF-dependent angiogenic process. The model was designed to integrate events from the cellular/subcellular level with overall tumor growth.

Model formulation was guided by multiple sets of experimental data, and its predictions agree qualitatively—and in many cases quantitatively—with data on the spatiotemporal evolution of vessel cooption and compression, VEGF and Ang2 levels, vascular density distribution, and tumor oxygenation. Interestingly, according to the model, inhibition of VEGF-dependent angiogenesis will not completely eliminate tumor vasculature (Fig. 6), and, hence, tumor growth can continue through this therapy. We found that anti-VEGF inhibition needs to be applied judiciously and that dual blocking of cooption and VEGF can decrease tumor vasculature and growth, but only under certain conditions of cancer cell proliferation and migration. Note, however, that GBMs are heterogeneous tumors and might contain some cancer cells that coopt vessels and others that induce angiogenesis. For example, both Olig2⁺ and Olig2⁻ cancer cells may be present in the same tumor. That means that Olig2⁺ will coopt vessels while Olg2⁻ will induce angiogenesis in the same tumor (9). Therefore, cooption blockade will counter the effect of the Olig2⁺ cancer cells, and VEGF blockade will target the Olig2⁻ cells. In this case, the treatment outcome of dual inhibition would also depend on the population ratio of the two cancer cell types.

Our model has certain limitations, including the fact that it includes only a subset of molecules (Ang1, Ang2, PDGF-B, VEGF, and SDF1α) that participate in the vascular response of tumors. Other molecules, such as hypoxia-inducible factor 1 (HIF1), bradykinin, inositol-requiring enzyme 1 (IRE1), Wnt7, and thrombospondin 1 (TSP-1)—also involved in tumor angiogenesis and vessel cooption—are not explicitly considered in the model (5, 7, 9). Also, some mechanisms have been simplified, including the assumption that VEGF is only produced by cancer cells; in reality, it can also come from host cells (31) or the production of SDF1α only by cancer and endothelial cells and not from neurons, subpial regions, and the white matter tracks (32). Additionally, the model does not account for other cell populations involved in tumor progression, including stem cell-like cancer cells and adaptive immune cells, which can significantly affect the efficacy of antiangiogenic therapy (33, 34), nor does it account for pseudopalisading necrosis. Nevertheless, the model is relatively comprehensive and reproduces complex, rich behaviors. It includes a large number of parameters associated with the motility of cancer and endothelial cells, their proliferation, angiogenic protein transport, physiological and mechanical tumor properties, and other functions (SI Appendix, Table S1). Baseline values of the model parameters were determined independently using data from the literature. Accordingly, model predictions are in good qualitative agreement with a large set of independent experimental data and could serve as a foundation for further experimental studies to examine the link between vessel cooption, VEGF-induced angiogenesis, tumor growth, and antiangiogenic treatments. Finally, model simulations were specified to address the specific questions in the current study about how cancer cells interact with the host vasculature and if we can target cooption to improve therapy. By comparing model predictions with a large set of experimental data and by performing simulations for different treatment protocols, we validated the basic assumptions of the model related to cancer cell–host vasculature interactions (for example, the importance of compression of coopted vessels by cancer cells, the cancer cell motility during antiangiogenic treatment, and the role of certain angiogenic factors). We also provided insights into the effects and the importance of blocking cooption. This detailed model of tumor progression can be employed to provide further insights in processes that involve angiogenesis and metastasis and be further developed to include other components of the tumor microenvironment, such as immune cells for the study of immunotherapy and related treatments.

Methods

Intravital Imaging of Glioblastomas.

CNS-1 (rat glioma) and GL261 (mouse glioma) were obtained from William F. Hickey, Dartmouth Medical School, Hanover, NH, and the National Cancer Institute Repository, Bethesda, MD, respectively, and were cultured as described in previous studies (35, 36). Both cell lines were transfected with DsRed fluorescent protein, sorted for 100% expression, and were maintained in culture as neurospheres. Then, 10,000 tumor cells were injected into the cerebrum (coordinates were 2 mm posterior and 1.5 mm lateral from bregma in the right cerebral hemisphere, and injection depth was 1.5 mm) of 8- to 12-wk-old male nonobese diabetic/SCID (CNS-1 cells per xenograft) or 8- to 12-wk-old male C57BL/6 (GL261/syngeneic) mice previously fitted with cranial windows. The tumor cells were imaged within the first week after implantation using a custom-built multiphoton microscope. Mice were injected i.v. with FITC Dextran (80 kDa) and imaged with an excitation wavelength of 840 nm to simultaneously excite FITC and DsRed. Mice were imaged every 1 to 2 d, and locations were tracked via vessel landmarks. For the antiangiogenic treatment studies, when tumors became detectable via intravital microscopy (typically 2 to 3 wk), we treated animals with 6 mg/kg cediranib (daily oral gavage), with control groups treated with the corresponding drug vehicle. Tumor cell dynamics relative to brain microvessels were measured with multiphoton microscopy. Following treatment and imaging, tissues were harvested, and brain sections were analyzed using tumor cell DsRed signal combined with CD31 staining.

Brain Metastasis Model from Breast Cancer Cells.

MDA-231BR cells were obtained from Patricia S. Steeg, National Cancer Institute, Bethesda, MD. For the brain metastasis model, a suspension of (0.25 million per 0.1 mL of PBS) MDA-231BR cells transfected with green fluorescence protein (GFP) was injected (intracardiac) into 4- to 5-wk-old female nude mice previously implanted with a cranial window. Mice were imaged every 3 d, and locations were identified and revisited using stable vessel landmarks. Transfection of cancer cells with GFP, immunofluorescence staining for cell nuclei (DAPI), and for functional blood vessels (biotinylated lectin), as well as hematoxylin and eosin (H&E) staining, were performed according to previous studies (37, 38).

All animal procedures were carried out following the Public Health Service Policy on Humane Care of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee of Massachusetts General Hospital. All cell lines tested negative for mycoplasma using the Mycoalert Plus Mycoplasma Detection Kit (Lonza) and were authenticated before use by IDEXX laboratories.

Description of the Mathematical Model.

A detailed description of the mathematical model can be found in SI Appendix and SI Appendix, Fig. S1.

Several molecules have been shown to affect the host and tumor vasculature, including Ang1 and Ang2, PDGF-B, VEGF, and SDF1α. The common feature of all these proteins is that they are overproduced under hypoxic conditions. Ang1 is produced by pericytes while Ang2 is mainly produced by endothelial cells, and the two act in an autocrine fashion: Ang1 and PDGF-β have been shown to stabilize endothelial cells, producing mature vessels, while Ang2 has the opposite effect, destabilizing endothelial cells favoring angiogenesis (6, 39–41). VEGF and SDF1α are mainly produced by tumor cells, and they coordinate endothelial cell migration and angiogenesis (7, 32, 40, 42–44). It has been further suggested that vessel cooption first increases autocrine expression of Ang2, which initiates endothelial cell migration, and, in the second stage, the formation of VEGF gradients guides the angiogenic processes (6, 45).

According to the literature, most pertinent mathematical models focus on VEGF-induced angiogenesis, with only a few accounting for vessel cooption. Furthermore, these models do not explicitly consider the effect of cooption on tumor growth (46–51) (SI Appendix, Table S1). Our mathematical framework for tumor growth accounts both for vessel cooption and VEGF-induced angiogenesis, coupling events at both cellular and tissue scales (Fig. 1).

Cellular level.

Cancer cells move toward regions with high oxygen levels (blood vessels), contributing to vessel cooption and compression. Vessel compression reduces oxygen delivery, creating hypoxia and triggering production of PDGF-B, VEGF, SDF1α, Ang1, and Ang2. Ang1 and PDGF-B stabilize endothelial cells whereas Ang2 destabilizes them. VEGF and SDF1α gradients drive endothelial cell migration and angiogenesis.

Cancer cell proliferation depends on oxygen concentration through a Michaelis–Menten kinetics equation while cancer cell movement is described by a diffusion process biased by oxygen and SDF1α gradients (52).

Two populations of endothelial cells are considered: endothelial cells that are maintained in a quiescent state and form stable blood vessels and endothelial cells that participate in angiogenic migration/sprouting. Production rates of both types of endothelial cells depend on VEGF and SDF1α (chemotactic term) concentrations as well as on their own concentrations. Endothelial cell migration is assumed to depend on VEGF and SDF1α gradients (52).

Two populations of pericytes are considered: pericytes that are tightly associated with endothelial cells and assumed to be immotile and pericytes that are dissociated from endothelial cells and can be motile. Production rates of both phenotypes depend on PDGF-B concentrations, as well as on their own concentrations (25).

VEGF concentration is determined by diffusion, production by cancer cells under hypoxic conditions, and binding to endothelial cell receptors (52).

SDF1α is also known as C-X-C motif chemokine 12 (CXCL12). We suggest in the model that VEGF released by hypoxic cancer cells up-regulates SDF1α from cancer cells and that SDF1α is also produced by endothelial cells in a VEGF-dependent manner (43).

Ang1 is assumed to be produced by pericytes and Ang2 by endothelial cells, respectively. Their production is enhanced by hypoxia based on VEGF levels (53).

PDGF-B is produced by endothelial cells and binds to pericytes (25).

Tissue level.

The tumor is assumed to be composed of a solid phase containing all cell types and extracellular matrix embedded in an interstitial fluid phase. Tumor growth is modeled based on principles of continuum mechanics and specifically employs the multiplicative decomposition of the deformation gradient tensor (33, 54–56). As the tumor grows, it mechanically displaces the surrounding host tissue, giving rise to the development of mechanical forces. A compressible neo-Hookean constitutive equation is used to describe the mechanical behavior of both the tumor and the host tissue (57). The solution of a force balance (i.e., linear momentum equation) between the tumor and the host determines the equilibrium position of the tumor.

Macroscopic tumor growth depends on the proliferation rate of cancer cells, which is a function of oxygen concentration (58). A standard convection–diffusion–reaction equation is used to calculate oxygen transport to the tumor, with the reaction term describing the oxygen supply from the vessels to the tumor tissue, Thus, tumor oxygenation is a function of functional vascular density. Functional vascular density is compromised if vessels are compressed by cancer cells. A relationship between cancer cells attached to blood vessels and the decrease in vessel diameter was derived previously based on experiments (21, 22), and it was validated here for a different set of experimental data (Fig. 3B).

Coupling of two length scales.

The cellular level equations provide a detailed description of the formation and remodeling of the tumor vasculature to calculate the functional vascular density, used at the tissue level, based on the endothelial cell population and the degree of vessel compression. The functional vascular density determines the oxygenation of the tumors and subsequently the proliferation rate of cancer cells and the overall tumor growth. A summary of model parameters, their values, and corresponding references are shown in SI Appendix, Table S2.

For the formulation of the model and the solution of the equations, the commercial finite elements software COMSOL Multiphysics v.5.2a was used.

Code availability.

The COMSOL code is available in SI Appendix.

Data Availability.

The authors declare that all other data supporting the findings of this study are available within the paper and SI Appendix.