Realizing the potential of dielectric elastomer artificial muscles

Significance

To build new robots that can safely interact with people, while completing complex tasks, we need artificial muscles. Ideally, these devices would be completely soft, as strong as natural muscles, and powered by electricity for easy integration with the rest of the robot. We found a materials solution that relies on an established technology, a dielectric elastomer soft capacitor, which deforms when an electric field is applied. By using a unique combination of nanoscale conductive particles and soft elastomers, we can apply high electric fields and reach contraction forces on par with natural muscles. Potential uses include novel surgical tools, prosthetics and artificial limbs, haptic devices, and more capable soft robots for exploration.

Abstract

Soft robotics represents a new set of technologies aimed at operating in natural environments and near the human body. To interact with their environment, soft robots require artificial muscles to actuate movement. These artificial muscles need to be as strong, fast, and robust as their natural counterparts. Dielectric elastomer actuators (DEAs) are promising soft transducers, but typically exhibit low output forces and low energy densities when used without rigid supports. Here, we report a soft composite DEA made of strain-stiffening elastomers and carbon nanotube electrodes, which demonstrates a peak energy density of 19.8 J/kg. The result is close to the upper limit for natural muscle (0.4–40 J/kg), making these DEAs the highest-performance electrically driven soft artificial muscles demonstrated to date. To obtain high forces and displacements, we used low-density, ultrathin carbon nanotube electrodes which can sustain applied electric fields upward of 100 V/$\mathrm{\mu }$m without suffering from dielectric breakdown. Potential applications include prosthetics, surgical robots, and wearable devices, as well as soft robots capable of locomotion and manipulation in natural or human-centric environments.

Soft robotics is a nascent subfield of robotics, with a broad range of applications (1–3), from wearable and rehabilitative devices (4) to novel surgical tools (5), as well as biomimetic robots for search, rescue, and exploration (6, 7). A fundamental challenge in developing these robots is the creation of effective actuators to deform a soft body to achieve locomotion, manipulation, or other tasks (8, 9). The gold standard for actuation in a soft body is natural muscle (10), which exhibits high energy density (0.4–40 J/kg), a broad range of frequencies (1–200 Hz), and large strains (5–30%). Since their initial development, dielectric elastomer actuators (DEAs) (11–13) have been hailed as artificial muscles, but material limitations typically constrain the user to choose between a truly soft actuator which exhibits low energy density (14) and an energy-dense actuator with multiple rigid components (15). Fundamentally, DEAs operate as compliant capacitors, in which the dielectric elastomer deforms in response to an applied electric field. In this work, we describe how, with careful material selection and processing, a DEA can be made to operate as a strong artificial muscle without requiring any rigid components.

In this work, we realize a longstanding vision for DEAs as fully soft, electrically driven, energy-dense artificial muscles (Fig. 1 A and B). Single-film dielectric elastomers are usually thin, to minimize the actuation voltage, which leads to small force outputs ($<$10 mN) and limited applications. To reach both the desired forces ($>$10 N) and displacements ($>$1 cm), we need to stack multiple layers. Here, we build upon our earlier work which combined UV-curable strain-stiffening elastomers (16) with ultrathin carbon nanotube (CNT)-based percolative electrodes (17) to make multilayered, robust, completely soft actuators. The use of strain-stiffening elastomers in a multilayered configuration bypasses the need to prestretch the elastomer (18), which otherwise negates the advantages of a soft actuator by surrounding it with a rigid frame. Without stiff constraints, DEAs can be made into linear contracting and expanding actuators (19) to mimic the function of natural muscle fibers (20) and muscular hydrostats (21), respectively. These linear actuators also serve as simple, yet reliable, tools to measure mechanical deformation and therefore quantify energy density, as well as other physical and electrical properties. The range of strains across different animal muscle types is fairly constant (5–10%), but power and energy densities depend on the type of locomotion (22). For example, the energy density ranges from 0.4 J/kg for a swimming bass at 4 Hz, to 6 J/kg at 25 Hz for the flight muscles in a locust, to 40 J/kg for a running rat at 7.5 Hz (23–25). With the goal of dielectric elastomer artificial muscles that achieve similar energy densities and bandwidths as natural muscles, we aimed for the following combination of actuator capabilities: (i) demonstrate linear contraction or expansion in fully soft DEAs, (ii) match the strain capability and energy density of natural muscle, and (iii) maximize the speed of deformation to reach the viscoelastic limits of the elastomer material.

Fig. 1.

Fabrication steps and breakdown performance. (A and B) Demonstration of muscle-like actuation. A contracting DEA is used to actuate a polymer replica of the bones of a human arm, with mechanics similar to a human bicep muscle. Metal wires serve as rigid links to connect the DEA to the bone. (C) A contracting actuator showing multiple stacks of active elements (dark gray) alternating with passive elements (light gray) for enhanced adhesion. (D) Zoomed-in image of the top six stacks in the contracting actuator. Each stack consists of 25 individual dielectric elastomer layers, each approximately 30 μm in thickness; the electrodes are made with ink B at areal density 15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. (E) Fabrication sequence for disk actuators used in breakdown testing. (F) Breakdown field of the disk actuator as a function of concentration of ink A used is indicated by the left y axis. Estimated areal coverage of CNTs as a function of concentration of ink used, based on SEM imaging, is indicated by the right y axis. The results indicate that lower areal densities of CNT reduce the chance of dielectric breakdown. The shaded region left of the 9-$\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$ mark indicates that no deformation was observed at any applied field. Dashed line corresponds to the breakdown field when using conventional carbon grease as an electrode determined in-house. Each datapoint corresponds to the average breakdown field of five different samples. The error bar corresponds to the SD of the dataset. (G) Breakdown field as a function of elastomer Young’s modulus, at two different areal densities of ink A. The results indicate that the areal density of CNTs dictates the onset of dielectric breakdown, and not the elastomer stiffness. Each datapoint corresponds to the average breakdown field of five different samples. The error bar corresponds to the SD of the dataset.

To achieve these goals, we optimized the electrode composition and multilayer processing to sustain high applied electric fields, without the onset of destructive dielectric breakdown. To understand this motivation in quantitative terms, for small deformations, on par with the strains observed in natural muscles ($<$20%), the strain in a linear DEA can be approximated as $s=ϵE^2/Y$, where $ϵ$ is the permittivity of the elastomer, $Y$ is the Young’s modulus of the elastomer, and $E$ is the applied electric field. The elastomers used in this work exhibit linear behavior in the range of strains of interest, as demonstrated earlier (17). To first order, the elastic energy density of the deformed elastomer can be approximated as $U_e=s^{2}Y/2$, leading to $U_e={ϵ}^2{E}^4/2Y$, meaning that energy density is highly sensitive to the applied electric field. In addition, we desire thin electrodes, to maximize the volume occupied by the elastomer in the final device.

CNTs meet the requirement for high conductivity at low thickness (26, 27) and could be easily integrated into a multilayer actuator. Other electrode materials considered were too thick [e.g., hydrogels (28) and ionogels (29, 30)], insufficiently conductive [e.g., crumpled graphene (31)], or difficult to integrate in a multilayered actuator [e.g., crumpled metal (32)]. The main drawback of CNTs is the early onset of dielectric breakdown (33) compared with more conventional electrodes, such as carbon grease. Earlier work (34) showed that dielectric breakdown occurs at low strains ($<20\%$), before the onset of strain stiffening in the elastomer. We hypothesized that the reason for early dielectric breakdown is due to nonhomogenous distribution of CNTs causing high electric field concentrations. Based on this hypothesis, we studied the relationship between the areal density of CNTs and the onset of dielectric breakdown.

Lower areal densities of CNTs in the electrodes may increase the sheet resistance, which in turn increases the actuator RC time constant (time constant of the circuit comprising a resistor and a capacitor). The response speed of DEAs is limited either by how quickly the compliant capacitor is charged or by how rapidly the elastomer can deform in response to the generated Maxwell stress between the electrodes. We aimed to find electrodes with sufficiently low sheet resistance that the deformation was limited by the elastomer viscoelasticity. As a result, the key actuator performance metrics (i.e., energy density and bandwidth) could be systematically varied by tuning different material properties (i.e., breakdown field and elastomer viscoelasticity, respectively).

Results

To test the hypothesis that breakdown field depends on nanotube areal density, we fabricated multilayered disk actuators with different CNT amounts and measured the dielectric breakdown field in each. A schematic of a disk actuator and the multilayering procedure is shown in Fig. 1F. The disk actuators were made by repeated spin-coating and UV-curing of acrylic elastomer precursors, alternating with stamping of electrodes from a supporting carrier film. The electrodes were made by filtering water-based CNT inks, diluted with isopropanol, through polytetrafluoroethylene (PTFE) filters, used as carrier films. We kept constant the area of the filter (9.62 ${\mathrm{c}\mathrm{m}}^2$) and ink concentration (determined by optical density, with transmittance equal to 17% at 550 nm). To systematically modify the CNT areal density, we varied the amount of ink used (50–600 $\mathrm{\mu }$L), leading to areal densities ranging from 5.19 to 62.37 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. We used two different inks: Ink A contained functionalized CNTs dispersed in water (average diameter = 5 nm), while ink B contained surfactant-coated CNTs dispersed in water (average diameter = 10 nm). The surfactants used for the stable dispersion of purified CNT in ink B at high concentrations in water can be removed at low temperatures by a heating process (2 h at $\mathrm{120}°$C), postdeposition. The multilayering fabrication process allowed for the electrodes to be heated while on the PTFE carrier films, thus eliminating the need to expose the elastomer to high temperatures. The actuators made with the two inks at varied amounts were tested at increasing electrical fields, as detailed in SI Appendix, until dielectric breakdown occurred.

CNT Electrode Optimization.

The results showed that, for both inks, there is a desirable, low CNT areal density region (7.79–15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$), in which the breakdown occurs at high electric fields. Reducing the areal density of CNTs increased the dielectric breakdown field to levels higher than more conventional carbon grease electrodes (Fig. 1F). Similar effects were observed for both types of ink used (SI Appendix, Fig. S1A). The onset of dielectric breakdown was found to be approximately inversely dependent with the areal coverage (Fig. 1F). Scanning electron microscopy (SEM) of the CNTs as dispersed on PTFE filters (SI Appendix, Fig. S1 B–J) showed that as the areal coverage of the electrode increases from 30% at an areal density of 5.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$ to ∼70–90% above 20.79 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. However, the electrodes are not homogenous: Patches of dense CNTs form at ∼10.39 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$, while some regions remain almost free of CNTs. To our surprise, increasing the elastomer modulus by a factor of 10$\times$ (through additional cross-linker in the elastomer precursor) did not impact the likelihood of breakdown as much as increasing the areal density of CNTs by a factor of 3$\times$ (Fig. 1G). SEM imaging of the electrodes on the transfer PTFE films show that the nonhomogeneity may be due to aggregation at the filter pores (SI Appendix, Fig. S2 A and C). The microstructure is retained after the electrode is transferred onto the elastomer (SI Appendix, Fig. S2 B and D). Overall, the results indicate that the process gives control over the areal density of the CNTs, which in turn allows the actuators to be powered to higher electric fields than previously demonstrated.

Although a low areal density of CNT electrodes reduces the likelihood of early breakdown, this can lead to poor electromechanical performance due to a low surface coverage of the elastomers. To quantify the effect of CNT areal density on mechanical performance, we built roll actuators (35) and measured their linear displacement in the axial direction (Fig. 2A). The expanding actuator consisted of 15 layers of elastomer (6 $\times$ 1 cm) and electrodes with either low (15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$) or high (46.77 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$) areal densities of ink B. The actuators were tested by applying increasing voltage steps, while measuring the actuator displacement and current drawn. In the initial test to 2 kV, the higher areal density electrodes drew higher currents than the low areal density electrodes (SI Appendix, Fig. S3 A–C), while showing smaller displacements. In the subsequent test, the same behavior was observed only when the applied voltage was the highest ever applied to the device (2–2.5 kV region; SI Appendix, Fig. S3 D–F). The behavior was repeated when the actuators were charged to 3 kV for the first time (Fig. 2 B, D, and F). By comparison, the current draws were similar at the 20th cycle (Fig. 2 C, E, and G), while the displacement was significantly smaller for the high-areal-density CNT electrodes. The leveling off in the current drawn suggested that a self-clearing mechanism was occurring during the initial charge of the actuators (36). Based on our observations and interpretation, the spikes in current caused localized heating and, therefore, partial damage to the electrode network. We expect that the same mechanism is responsible for the complete dielectric breakdown described in Fig. 1. Given that higher current spikes are correlated with higher-areal-density electrodes, it is likely that the CNT electrode morphology plays a significant role (SI Appendix, Fig. S1). The cause of the current spikes is still unclear: One hypothesis is that the ends of the CNTs enhance the local electric field. Alternatively, the denser CNT patches may cause excessive heating relative to the more uniform network nearby or poor bonding between adjacent layers. Given our interest in maximizing actuator performance, we focused on the more robust electrodes made with low areal densities of ink for the remaining demonstrations.

Fig. 2.

Performance of roll actuators. (A) Fabrication sequence for roll actuators used in CNT electrode optimization and ink selection. (B) Applied voltage in 0.3-kV steps every 1 s for two roll actuators using ink B, after thermal treatment, at areal densities of 15.59 and 46.67 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$, during the first test of the device. (C) Corresponding applied voltage during the 20th test of each device. The noise in the voltage applied to the actuator made with the higher ink concentration is due to high current peaks that reached the 2-mA safety limit of the power supply. (D) Current response to applied voltage from B, during the first test. (E) Current response to applied voltage from C, during the 20th test. (F) Actuator axial extension corresponding to B. The actuator heights are 1.1 cm for each device. (G) Actuator axial extension corresponding to C. The largest displacement is measured in electrodes made with low areal density of CNT ink, indicating that these materials are most suitable for building high-performance artificial muscles. (H) Actuator axial extension as a function of applied field for devices made with four different ink types. The dependence is parabolic: The displacement is proportional to the square of the applied electric field. (H, Inset) Graph shows the measured actuator capacitance for each ink type. The dashed line corresponds to the calculated capacitance of the device based on geometry and material parameters. The results indicate that ink B after thermal treatment creates the most effective CNT electrode and should be used in building artificial muscles.

The measured current and applied voltage (Fig. 2) were used to estimate the electrical energy input into the system: $U_{e_{total}}=Q\times V/2=200$ mJ for the low areal density actuator, where $Q$ is the charge stored in the capacitor, as a product of the current applied and time, and $V$ is the voltage at which the capacitor is charged. The measured displacement ($d$) and blocked force ($F_b$) of the actuator (SI Appendix, Fig. S4) were used to estimate the mechanical work output ($U_{mech}=d\times F_b/2=3.0$ mJ for the low areal density actuator), giving an energy efficiency ($u_{mech}/u_{e_{total}}$) of 1.5%. In addition, we also determined the electromechanical conversion efficiency of the actuator, by comparing the mechanical energy output to the stored electrical energy in the capacitor ($U_{e_{stored}}$). The electrical energy in the capacitor was calculated based on the measured capacitance ($C=10$ nF) and voltage across the capacitor ($V=3$ kV), using $U_{e_{stored}}=C\times V^2/2=45$ mJ. The electromechanical efficiency ($U_{mech}/U_{e_{stored}}$) of the expanding roll actuator was 6.7%.

To complete the electrode optimization, we considered the impact of thermal treatment on the two ink types for a constant CNT areal density. In addition to measuring the displacement of linear expanding axial actuators, we also quantified the electrode-sheet resistance and the actuator capacitance at low voltage (see description in SI Appendix, Fig. S5). We expected that electrodes which are not able to physically cover the entire elastomer surface effectively would have correspondingly high sheet resistance, lower than calculated capacitance values, and lower actuator displacement. Our expectation was confirmed: The actuators which exhibited the highest displacement also had the highest measured capacitance (Fig. 2F). The best-performing material was ink B after thermal treatment (vacuum for 2 h at $\mathrm{120}°$C), suggesting that the removal of surfactant molecules yields the most effective CNT network. SEM imaging of ink B electrodes showed no significant change in the microstructure before and after thermal treatment (SI Appendix, Fig. S6). Sheet-resistance measurements of the inks on PTFE supports were in agreement with this trend (SI Appendix, Table S1). Given the higher breakdown fields ($>$ 100 V/$\mathrm{\mu }$m) and large actuator displacements, we selected ink B, after thermal treatment, as the optimal electrode for our artificial muscles.

Artificial Muscle Demonstrations.

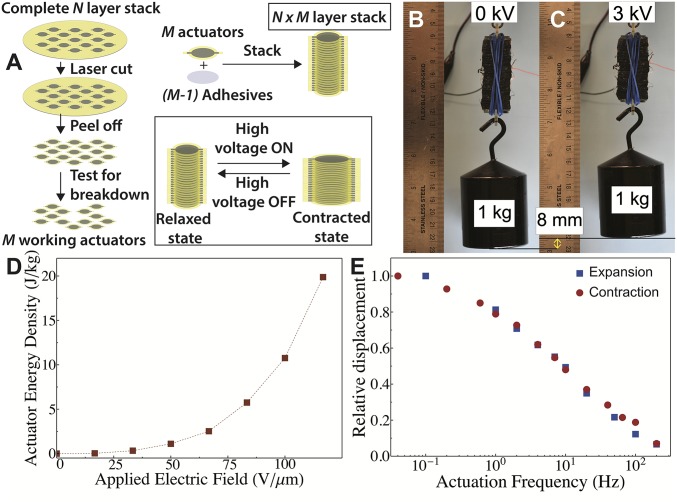
By multilayering our UV-curable elastomers and the optimized ink B electrodes, we built a linear contracting DEA to realize our goal of a fully soft, electrically driven artificial muscle. We adapted an established process (19, 37) by stacking 45 disks each of 26 layers to create a 1,170-layer cylinder (Fig. 3A and SI Appendix, Fig. S7A). To characterize the usable energy density, we measured the weight ($w$), pull force in a mechanical tester with no displacement ($F_b$), and free displacement ($d$) against gravity of the actuator as a function of the applied electric field (Fig. 3 B–D, SI Appendix, Fig. S7 B–E, and Movie S1). The pull force was measured by attaching one end of the actuator to a load cell and holding the other end fixed. The load cell had practically zero displacement, the actuator was powered, and the maximum force reading was recorded as the pull force. At high electric fields, the energy density ($=F_b\times d/2w$) reached 19.8 J/kg, while the displacement corresponded to 24% strain, covering a large segment of the performance envelope of natural muscles (38). For mammalian muscles, the typical energy density is 8 J/kg, while the typical strain is 20%. Compared with earlier demonstrations of stacked DEAs, our devices have higher-energy-density, thinner electrodes (Table 1). Furthermore, our fabrication process allows independent tuning of the properties and processing of the elastomer together with the electrode.

Fig. 3.

Performance of linear contracting actuators. (A) Fabrication sequence for linear contracting actuators used to measure energy density. (B) Contracting actuator attached to a 1-kg weight without electrical power applied. The actuator is 6.3 cm long, made of individual 30-$\mathrm{\mu }$m layers, weighs 20 g, and is made with ink B electrodes, after thermal treatment, at 15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. (C) Same actuator powered to 3.5 kV lifting a 1 = kg weight by 8 mm. (D) Energy density of the same actuator from B. The fitted line corresponds to a fourth power dependence of the energy density on the applied electric field, as predicted by our model. At the highest applied field, the actuator exhibits a peak energy density of 19.8 J/kg, on par with natural muscle. (E) Comparison of relative displacements of contracting cylinder and expanding roll actuators as a function of actuation frequency at 3 kV. The contracting actuator was a cylinder: 2 cm long, with a 1.2-cm diameter, made with ink B electrodes, after thermal treatment, at 15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. The expanding actuator was a cylinder: 2 cm long, with a 1-cm diameter, made with ink B electrodes, after thermal treatment, at 15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$.

Table 1.

Performance of DEAs in comparison with natural muscles

Electrode material	Natural muscle (22)	CNTs (this work)		Carbon powder (37)	Dispersed carbon (19)	Hydrogel (15)	Corrugated metal (39)
Action upon stimulation	Contraction	Contraction	Expansion	Contraction	Contraction	Contraction	Expansion
Prestrain, x $\times$y	N/A	1 $\times$ 1	1 $\times$ 1	1$\times$ 1	1 $\times$ 1	3 $\times$ 3.5	1 $\times$ 1
Electrode thickness, $\mathrm{\mu }$m	N/A	$<$0.1	$<$0.1	0.5–5	3–30	100–200	0.1–0.2
Applied field, V/$\mathrm{\mu }$m	N/A	100–150	100–150	62	12	33	35
Applied voltage, kV	N/A	3.75	3.75	4	6	24	2.8
Actuation strain, %	10–30	24	22	30	16	69	2.5
Bandwidth, Hz	2–180	1–10	1–10	N/A	N/A	20	10–100
Max power output, W/kg	9–280	30–80	30–80	N/A	N/A	60–600 *	5–50
Energy density, J/kg	0.2–40	19.8	13.75	13	10	7–70 *	0.5

Max, maximum; N/A, not available.

^*Lower bound includes estimated weight of fixtures required to maintain prestretch.

The same building blocks can be used to demonstrate high energy density in linear expanding actuators. A similar performance evaluation of the expanding actuators (low-areal-density ink actuators from Fig. 2E, using blocked force instead of pull force) demonstrated a peak energy density of 13.75 J/kg, while the displacement corresponded to 22% strain (SI Appendix, Fig. S4). The blocked force was measured by constraining the actuator between a mechanical ground and a load cell that was fixed in place. When an actuator was powered, its displacement was fully constrained: The maximum force reading was recorded as the blocked force. The lower energy density exhibited by the roll actuators compared with the contracting cylindrical actuators may be due to the mechanical energy lost to expanding the actuators radially. Relative to earlier examples (39), these linear actuators achieved a factor of almost 30$\times$ higher energy density, primarily due to the higher attainable applied electric field without dielectric breakdown. Despite the different geometry, both the expanding and contracting actuators exhibited similar bandwidth, by comparing displacement relative to the actuator length (Fig. 3E). The results indicate that the device performance is not dictated by the final actuator geometry, but by the properties of the materials used as the building blocks.

Discussion

To understand the electronic and viscoelastic limits of the device, we characterized the actuator bandwidth (i.e., response time) and electric properties. To this end, we compared two areal densities of ink B after heat treatment (15.59 and 46.77 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$) on the actuator’s linear expansion at a range of frequencies between 0.1 and 200 Hz. The test consisted of applying a sinusoidal voltage of 3 kV at a given frequency for 1–100 s and measuring the free displacement. We observed no significant difference in displacement between the two actuators, despite the 3$\times$ increase in CNT concentration and corresponding 4$\times$ decrease in sheet resistance. For comparison, the capacitances of the two actuators were similar: 9.6 and 9.9 nF, for the low and high concentrations, respectively. The resistances were 0.6 and 2.2 M$\mathrm{\Omega }$, respectively. Both the bandwidth data and the RC time constants (5–20 ms) indicate that the response was limited by material viscoelasticity (Fig. 4A). These actuators did not reach full displacement at frequencies >10 Hz, resulting in a power density on the lower end of the power density in mammalian muscles (100–400 W/kg). Increasing the power density further will require an increase in bandwidth and materials with lower viscoelastic losses.

Fig. 4.

Limits of performance. (A) Roll actuator extension as a function of actuation frequency at 3 kV for two different CNT ink compositions. Both expanding actuators were cylindrical: 1.2 cm long, with a 1-cm diameter, made with ink B electrodes, after thermal treatment, at 15.59 and 46.77 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. The similar performance of different-areal-density CNT inks indicates that the actuator response is limited by the viscoelasticity of the elastomer and not the RC constant of the circuit. (B) Roll actuator expansion as a function of number of cycles during continuous testing under a sine wave signal with 10-Hz frequency and 3-kV peak. The expanding actuator was a cylinder: 1.2 cm long, with a 1-cm diameter, made with ink B electrodes, after thermal treatment, at 15.59 $\mathrm{\mu }$L/${\mathrm{c}\mathrm{m}}^2$. The device is robust and can withstand 100,000 cycles without measurable degradation in mechanical performance. Each datapoint corresponds to the average displacement of the same device tested five times. The error bar corresponds to the SD of the dataset. (C–F) Complex actuators made from simple building blocks: a muscular hydrostat replica made from linear expanding actuators powered to 3 kV. (C) Relaxed state. (D) Column 1 actuated. (E) Column 2 actuated. (F) Column 3 actuated.

For completeness, a 0- to 3-kV, 10-Hz frequency signal was applied continuously to explore device robustness. We observed no measurable degradation in performance for actuators made with the low-areal-density electrodes of ink B (Fig. 4B) over the course of 100,000 cycles of continuous testing. The displacement of the actuators dropped to nearly half the initial value after 300,000 cycles. This fatigue may have been due to damage to the CNT network, which could be reduced by blending with different nanoscale conductors, such as silver nanowires (40). To match the robustness of natural muscles ($10^9$ cycles), we will need a better understanding of the device degradation. In addition, we used the established simple building blocks (expanding and bending actuators) to create more complex systems with additional capabilities. One example of these complex systems is as a muscular hydrostat replica made from linear expanding actuators, capable of both bending (tilt angles of $\mathrm{30}°$ in three independent directions) and expansion (10% strain) (Fig. 4 C–F and Movie S2). We envisioned that optimized versions of these types of enhanced actuators could find use in the manipulation of delicate objects or other complex manipulation tasks.

The DEAs presented in this work exhibit the highest peak energy density to date, while still being soft and stretchable, without incorporating any liquid components. By carefully selecting and processing ultrathin nanoscale conductors (SI Appendix, Fig. S8), we were able to apply high electric fields without risking premature dielectric breakdown. At high fields, the actuators show strain capability and energy density on par with natural muscles. We found that the actuator speed was limited by the elastomer viscoelasticity, not the electrode-sheet resistance. This work represents a major step toward the realization of fully stretchable, electrically driven, strong, and fast artificial muscles to be implemented in a variety of soft machines that can interact with, enhance, or restore the function of the human body.

Materials and Methods

In brief, we fabricated the artificial muscles using an established multilayering technique (17). The artificial muscles were made from UV-curable acrylic elastomers and ultrathin CNT mats. We quantified the actuator displacement, force output, and bandwidth for both contracting and expanding actuators using laser displacement sensors and load cells. Additional details are provided in SI Appendix.