Dynamics of frequency-swept nuclear spin optical pumping in powdered diamond at low magnetic fields

Significance

We articulate theory and experimental observations to understand the dynamic polarization of ¹³C spins in nitrogen vacancy (NV)-hosting diamond particles. The explored powder geometry is ideally suited to hyperpolarize fluids, as its inherently large surface-to-volume ratio is much greater than that possible in systems based on single crystals. Given the low-field magnets and low-intensity microwave and light sources we use, our technique promises to serve as a platform for low-cost, portable spin polarizers operating under ambient conditions. Alternatively, the diamond particles themselves could be exploited as background-free contrast agents for magnetic resonance imaging, a modality that builds on the biocompatibility of diamond and thus is complementary to the use of NV-hosting diamond particles as in vivo, fluorescent labels and drug delivery agents.

Abstract

A broad effort is underway to improve the sensitivity of NMR through the use of dynamic nuclear polarization. Nitrogen vacancy (NV) centers in diamond offer an appealing platform because these paramagnetic defects can be optically polarized efficiently at room temperature. However, work thus far has been mainly limited to single crystals, because most polarization transfer protocols are sensitive to misalignment between the NV and magnetic field axes. Here we study the spin dynamics of NV−¹³C pairs in the simultaneous presence of optical excitation and microwave frequency sweeps at low magnetic fields. We show that a subtle interplay between illumination intensity, frequency sweep rate, and hyperfine coupling strength leads to efficient, sweep-direction-dependent ¹³C spin polarization over a broad range of orientations of the magnetic field. In particular, our results strongly suggest that finely tuned, moderately coupled nuclear spins are key to the hyperpolarization process, which makes this mechanism distinct from other known dynamic polarization channels. These findings pave the route to applications where powders are intrinsically advantageous, including the hyperpolarization of target fluids in contact with the diamond surface or the use of hyperpolarized particles as contrast agents for in vivo imaging.

NMR has proven to be a powerful tool in areas ranging from molecular analysis to biomedical imaging. Unfortunately, the attainable nuclear spin polarization is often a small fraction of the possible maximum, thus imposing strict constraints on the minimum sample size and acquisition time. Dynamic nuclear polarization (DNP), i.e., the transfer of magnetization from electron to nuclear spins (1), is a route of growing popularity that substantially mitigates this problem. Enhanced polarization can be attained, e.g., with the aid of dissolved molecular radicals, although the most efficient implementations often rely on freeze−thaw protocols and high-frequency microwave (MW) excitation, which are expensive and technically demanding (2).

Adding to the library of DNP platforms, optically active spin defects in semiconductors are attracting widespread attention as alternative hyperpolarization agents. Among them, the negatively charged nitrogen vacancy (NV) center in diamond is arguably one of the most promising candidates, since it can be spin-polarized optically to a high degree with only modest illumination intensities and under ambient conditions (3). A variety of protocols have already been implemented to transfer NV spin polarization to surrounding nuclear spins, including level anticrossing-mediated transfer in the NV⁻ ground (4) and excited states (5), cross-relaxation with P1 centers (6–8), spin swap and population trapping (9), amplitude-matched MW excitation (10, 11), and transfer via MW sweeps (12, 13). Despite this progress, however, efficient hyperpolarization of randomly oriented samples at arbitrary magnetic fields has remained elusive, hence precluding applications where the use of diamond powders is desirable or necessary. Examples worth highlighting include the use of particles as contrast agents for in vivo magnetic resonance imaging [of interest given the biocompatibility of diamond (14)] or as a source of nuclear spin polarization in fluids (attractive given the enhanced surface-to-volume ratio inherent to powders).

Recent work demonstrated efficient ¹³C DNP in diamond powders simultaneously exposed to optical illumination and MW frequency sweeps (15), but gaining a detailed understanding of the microscopic mechanisms at play has proven subtle due to a complex interplay between the multiple degrees of freedom. Here we examine the dynamics of an NV−¹³C spin pair undergoing simultaneous optical illumination and MW excitation. We focus on the limit of low magnetic fields (∼10 mT to 30 mT) and consider the system evolution in the presence of MW sweeps of variable sweep rate. Through a transformation to the rotating frame, we show that the dynamics can be described in terms of a series of multibranched Landau−Zener (LZ) crossings; the branch-dependent degree of adiabaticity during these crossings combined with mild optical pumping of the NV spin leads to a net buildup of ¹³C polarization, which is robust against NV misalignment and efficient for hyperfine couplings as low as 0.2 MHz to 0.3 MHz. In particular, we show that moderately coupled carbons are dominant in driving the polarization dynamics of the bulk, a feature very much in contrast with prior spin transfer studies in diamond (mediated by first- or second-shell carbons). For the present experimental conditions, the observed level of ¹³C polarization is in the range 0.1 to 0.3%, corresponding to a 100- to 300-fold enhancement over the thermal polarization at 7 T. These results can be immediately extended to paramagnetic defects other than the NV [such as the neutrally charged silicon vacancy center (16, 17)] or to other wide-bandgap semiconductors (such as silicon carbide) hosting point defects that can be optically spin polarized (18).

Results and Discussion

Let us first consider an NV center spin interacting with a single ¹³C nucleus in the presence of an external magnetic field,

$$H=\mathrm{\Delta }\left({\left({\text{S}}^{\mathrm{z}}\right)}^2-\text{S}\left(\text{S}+1\right)/3\right)-{\gamma }_{\text{e}}\mathbf{B}\cdot \mathbf{S}-{\gamma }_{\text{C}}\mathbf{B}\cdot \mathbf{I}+\mathbf{S}\cdot \mathbf{A}\cdot \mathbf{I}\text{.}$$ [1]

Here, ${\gamma }_{\text{e}}$ and ${\gamma }_{\text{C}}$ stand for the electron and ¹³C gyromagnetic ratios, $\mathbf{B}$ is the external magnetic field, and $\mathbf{A}$ is the hyperfine coupling tensor between the NV electronic spin $\mathbf{S}$ and the ¹³C spin $\mathbf{I}$. Unless explicitly stated, we consider $\left|\mathbf{B}\right|=10\text{mT}$ and $100\text{kHz}\mathrm{\lesssim }\mathbf{A}\mathrm{\lesssim }10\text{MHz}$, meaning that the characteristic energy scales can be ordered as

$$\mathrm{\Delta }\approx 3\times {10}^3\text{MHz}>{\gamma }_{\text{e}}B\approx 3\times {10}^2\text{MHz}>\mathbf{A}>{\gamma }_{\text{C}}B\approx 1\times {10}^{-1}\text{MHz}.$$ [2]

In this regime, the crystal field $\mathrm{\Delta }$ is dominant and defines the main quantization direction, here chosen to coincide with the crystal frame z axis; accordingly, we write the magnetic field as $\mathbf{B}=B\left(\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta \right)$, where $\theta$ and $\varphi$ respectively denote the polar and azimuthal angles, changing randomly from one particle to another in the diamond powder. Further, the magnitude of the hyperfine coupling is greater than the nuclear Zeeman interaction, which makes the present regime different from that governing the integrated solid effect at high fields (19).

Extending the analysis above to identify the terms governing the nuclear spin dynamics is considerably more involved because, at the low magnetic fields considered herein, the hyperfine interaction can be dominant. An effective secular approximation valid for any choice of angles $\left(\theta ,\varphi \right)$ can be derived using Average Hamiltonian Theory (20, 21). Without loss of generality, we assume the carbon atom lies within the zx plane, and obtain (SI Appendix, section I)

$$H_{\text{sec}}=\mathrm{\Delta }\left({\left({\text{S}}^{\mathrm{z}}\right)}^2-\text{S}\left(\text{S}+1\right)/3\right)-{\gamma }_{\text{e}}B\cos \theta {\text{S}}^{\mathrm{z}}-{\gamma }_{\text{C}}\mathbf{B}\cdot \mathbf{I}+A_{\text{zz}}{\text{S}}^{\mathrm{z}}{\text{I}}^{\mathrm{z}}+A_{\text{zx}}{\text{S}}^{\mathrm{z}}{\text{I}}^{\mathrm{x}}-\frac{{\gamma }_{\text{e}}B\sin \theta }{\mathrm{\Delta }}\mathbb{M}\otimes \left[\cos \varphi \left(A_{\text{xx}}{\text{I}}^{\mathrm{x}}+A_{\text{zx}}{\text{I}}^{\mathrm{z}}\right)+\sin \varphi A_{\text{yy}}{\text{I}}^{\mathrm{y}}\right],$$ [3]

where $\mathbb{M}$ is a constant matrix defined in the Hilbert space $\left\{|m_{\text{S}}=+1\rangle ,|m_{\text{S}}=0\rangle ,|m_{\text{S}}=-1\rangle \right\}$ of the NV,

$$\mathbb{M}=\left[\begin{array}{ccc}1& 0& 0\\ 0& -2& 0\\ 0& 0& 1\end{array}\right].$$

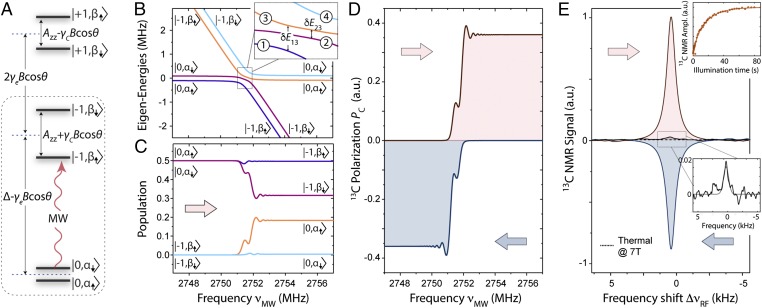
Fig. 1A shows a schematic representation of the NV–¹³C energy diagram: For the nuclear spin states, we use the notation $|{\alpha }_{\uparrow ,\downarrow }\rangle$ and $|{\beta }_{\uparrow ,\downarrow }\rangle$ to underscore the difference with the Zeeman basis states $|\uparrow ,\downarrow \rangle$ (even if they retain part of their character; see SI Appendix, section II). While the impact of the hyperfine field on the nuclear spin states in the $m_{\text{S}}=\pm 1$ subspaces is well documented (22), misalignment between the NV axis and the external magnetic field—unavoidable in a powdered sample—makes it necessary to take into account an additional contribution—last term in Eq. 3—active even when $m_{\text{S}}=0$ (23, 24). To illustrate its importance, we consider, for example, a hyperfine interaction $\mathbf{A}\approx 1\text{MHz}$, leading to matrix elements of order $\delta \approx {\gamma }_{\text{e}}\text{B}\mathbf{A}/\mathrm{\Delta }\approx 1\times {10}^{-1}\text{MHz}$. In the $m_{\text{S}}=0$ subspace, this contribution—which does not commute with $-{\gamma }_{\text{C}}B$—is comparable to the Zeeman splitting of the ¹³C states (Eq. 2) and hence cannot be disregarded. Note that this same term is less important in the $m_{\text{S}}=\pm 1$ subspaces (where the fourth and fifth terms in Eq. 3 become nonzero), since the factor scaling down the hyperfine coupling, ${\gamma }_{\text{e}}B/\mathrm{\Delta }$, amounts to only ∼0.1 for a 10-mT magnetic field.

Fig. 1.

Dynamic polarization of a ¹³C nuclear spin coupled to an NV center. (A) Schematics of the ground state energy diagram of an NV–¹³C pair. In each ket, the first (second) index refers to the electron (nuclear) spin quantum number, and we assume $A_{zz}$ is positive; all energy separations are approximate. (B) Four lowest eigenenergies of $H_{eff}$ as a function of the MW frequency ${\nu }_{\text{MW}}$ in the region near the $m_s=0\leftrightarrow m_s=-1$ transition. The labels denote the corresponding crystal frame eigenstates. The Inset is a zoomed plot of the main energy diagram within the region enclosed by the rectangle. (C) Population of the instantaneous eigenstates for the eigenenergies shown in B as the system undergoes an MW sweep at a velocity $\dot{\nu }$ = 40 MHz/ms. (D) Calculated ¹³C polarization during the sweep for (Upper) low-to-high and (Lower) high-to-low sweeps. (E) The ¹³C NMR spectrum at 7 T from single-crystal diamond upon 10 s of 532-nm, 1-W laser illumination and MW excitation at 38 mT followed by sample shuttling. The red (blue) trace corresponds to a low-to-high (high-to-low) MW frequency sweep after 20 repetitions of the polarization protocol; in both cases, the sweep rate is $\dot{\nu }=60$ MHz/ms and the frequency range is ∼0.37 GHz, from 3.507 GHz to 3.878 GHz (corresponding to a repetition rate of 164 Hz). The black trace is a reference spectrum from thermal polarization at 7 T for a total of 120 repeats separated by a 600-s wait interval; the attained enhancement relative to the 7-T signal is ∼300, corresponding to a bulk ¹³C polarization of ∼0.3%. In these NMR spectra, $\mathrm{\Delta }{\nu }_{\text{RF}}\equiv {\nu }_{\text{C}}^{\left(0\right)}-{\nu }_{\text{RF}}$ is the radio frequency (RF) shift relative to the high-field ¹³C resonant frequency ${\nu }_{\text{C}}^{\left(0\right)}=70$ MHz. Upper Inset shows the NMR peak amplitude as a function of the illumination time; Lower Inset is a blowout of the thermal ¹³C NMR spectrum. In B–D, we consider $A_{\text{zz}}=A_{\text{xx}}=A_{\text{yy}}=500\text{kHz}$, $A_{\text{zx}}=0.3A_{\text{zz}}$, $\text{Ω}=250\text{kHz}$, $B=10$ mT, and $\theta =65°,\varphi =0°$; in C and D, we assume that the electron spin has been fully initialized into $m_{\text{S}}=0$.

Building on Eq. 3, we can now extend our description to include the effect of MW driving: The MW field is modeled by a term $\propto {\text{S}}^{\mathrm{x}}\text{cos}(\omega \text{t})$, and, upon a unitary transformation into the frame rotating at the MW angular frequency $\text{ω}$ (SI Appendix, section I), we write the final effective Hamiltonian as

$$H_{\text{eff}}=\mathrm{\Delta }\left({\left({\text{S}}^{\mathrm{z}}\right)}^2-\text{S}\left(\text{S}+1\right)/3\right)-{\gamma }_{\text{e}}B\cos \theta {\text{S}}^{\mathrm{z}}+{\Omega \text{S}}^{\text{x}}-\omega {\left({\text{S}}^{\mathrm{z}}\right)}^2-{\gamma }_{\text{C}}\mathbf{B}\cdot \mathbf{I}+A_{\text{zz}}{\text{S}}^{\mathrm{z}}{\text{I}}^{\mathrm{z}}+A_{\text{zx}}{\text{S}}^{\mathrm{z}}{\text{I}}^{\mathrm{x}}-\frac{{\gamma }_{\text{e}}B\sin \theta }{\mathrm{\Delta }}\mathbb{M}\otimes \left[\cos \varphi \left(A_{\text{xx}}{\text{I}}^{\mathrm{x}}+A_{\text{zx}}{\text{I}}^{\mathrm{z}}\right)+\sin \varphi A_{\text{yy}}{\text{I}}^{\mathrm{y}}\right],$$ [4]

where we have introduced the Rabi frequency $\text{Ω}$. To illustrate the mechanism of spin polarization in the presence of an MW sweep, we first determine the eigenenergies of $H_{\text{eff}}$ as a function of the MW frequency ${\nu }_{\text{MW}}=\text{ω}/\left(2\text{π}\right)$ (Fig. 1B), and subsequently calculate the system evolution assuming initialization into $m_{\text{S}}=0$ (Fig. 1C) for the case of a positive hyperfine coupling (see below). As we tune the MW frequency in and out of resonance—in the present example, from lower to higher frequencies across the $m_{\text{S}}=0\leftrightarrow m_{\text{S}}=-1$ subset of transitions—the dynamics that follows can be interpreted in terms of an LZ population exchange near the avoided crossings. The corresponding energy gaps can be derived via second-order perturbation theory for the interlevel transitions in Eq. 4; using numeric labels 1 through 4 to identify branches in order of increasing energy (Fig. 1B, Inset), we find (SI Appendix, section II)

$$\delta E_{13}\approx \text{Ω},$$ [5]

and

$$\delta E_{23}\approx \left|\frac{{\omega }_{0I}}{2}+\frac{\left(A_{\text{zx}}^2-2{\text{Ω}}^2\right)}{8\left({\omega }_{0I}+A_{\text{zz}}\right)}-\frac{1}{2}\sqrt{{\left({\omega }_{0I}-\frac{A_{\text{zx}}^2}{4\left({\omega }_{0I}+A_{\text{zz}}\right)}\right)}^2+{\text{Ω}}^2}\right|.$$ [6]

Net nuclear spin polarization emerges from the nuclear spin-selective adiabaticity of the MW sweep. Assuming, for concreteness, a low-to-high-frequency sweep, the gap $\delta E_{13}$ yields an LZ jump probability between branches 1 and 3,

$$p\left(1|3\right)\approx \text{exp}(-2\pi {\text{Ω}}^2/\dot{\nu }),$$ [7]

where $\dot{\nu }$ is the frequency sweep rate. Therefore, assuming ${\text{Ω}}^2>\dot{\nu }$, the spin population initially in branch 1 remains unchanged throughout the LZ crossing. The situation is different, however, for the spin population in branch 2, whose jump probability to branch 3 is approximately given by

$$p\left(2|3\right)\approx \exp \left\{-2\pi {\left(\frac{\text{Ω}\left(G+A_{\text{zx}}\right)}{4\left({\omega }_{0I}+A_{\text{zz}}+F\right)}\right)}^2/\dot{\nu }\right\},$$ [8]

where $F$ and $G$ are functions of the relative orientation of the magnetic field $\left(\theta ,\varphi \right)$, and we are assuming ${\text{Ω}}^2>\dot{\nu }$; see SI Appendix, section II. The LZ dynamics in this case is partially nonadiabatic, meaning that the spin population initially in branch 2 bifurcates to create a net nuclear spin population difference (Fig. 1C). More generally, the condition for the generation of nuclear spin polarization during a sweep can be formally stated as $p\left(2|3\right)>p\left(1|3\right)$. We later show the carbon polarization in our simplified NV–¹³C model system (∼35% in the calculation of Fig. 1D) is consistent with the observed levels of bulk ¹³C polarization in our samples (typically in the 0.1 to 0.3% range). Interestingly, we note that, for a frequency sweep starting above, not below, the set of avoided crossings, it is the population in branch 3, not in branch 2, that bifurcates. Therefore, an adapted analysis shows that the sign of the end ¹³C polarization—calculated as a fractional population difference (see SI Appendix, section II)—depends on the direction of the frequency sweep, i.e., a low-to-high sweep yields positive nuclear magnetization, whereas the opposite is true for a high-to-low sweep (Fig. 1D).

A comparison with experiment is presented in Fig. 1E, where we probe the bulk ¹³C polarization induced at 38 mT under 532-nm illumination; inductive ¹³C detection upon MW and optical excitation is carried out at high field with the help of a 7-T NMR system adapted with a sample shuttling device (25). In this particular case, we use a single diamond crystal oriented so that all four NV orientations form the same angle with the applied magnetic field, and limit the MW sweep to a range around the $m_{\text{S}}=0\leftrightarrow m_{\text{S}}=-1$ subset of transitions. Consistent with theory (Fig. 1D), we find that reversing the sign of the frequency sweep yields a ¹³C NMR signal of opposite phase, indicative of polarization inversion. Note that the phase in the ¹³C NMR spectrum attained upon a low-to-high MW sweep coincides with that observed in the thermal signal at 7 T (acquired without optical excitation and/or sample shuttling), hence lifting the ambiguity in the absolute sign of the measured nuclear spin polarization.

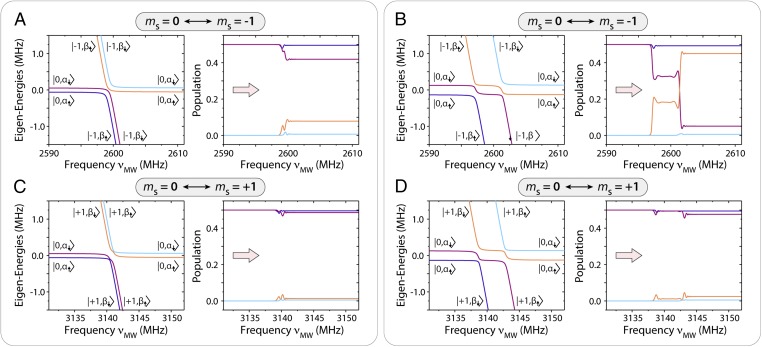
The structure of the LZ crossings is, in fact, more complex than the one presented in Fig. 1B (corresponding to a comparatively weak hyperfine coupling). Fig. 2 shows the typical energy diagrams for $A\approx 500$ kHz (Fig. 2 A and C) and $4$ MHz (Fig. 2 B and D), both near the $m_{\text{S}}=0\leftrightarrow m_{\text{S}}=-1$ (Fig. 2 A and B) and $m_{\text{S}}=0\leftrightarrow m_{\text{S}}=+1$ (Fig. 2 C and D) set of transitions. Comparing Fig. 2 A and B ($m_{\text{S}}=-1$ manifold), we find that, despite the growing frequency separation between the LZ crossings, the asymmetry in the gap size (and thus in the population transfer between branches) is not lifted, i.e., net nuclear spin polarization of the same (sweep-direction−dependent) sign is generated in all cases (even if the efficiency changes with hyperfine coupling strength and relative magnetic field alignment; see below).

Fig. 2.

Manifold-dependent nuclear spin polarization dynamics. (A) (Left) Eigenenergies of H_eff as a function of the MW frequency ν_MW near the m_S = 0 ↔ m_S = −1 subset of transitions; (Right) evolution of populations upon a single low-to-high-frequency sweep in the presence of a weak hyperfine coupling. (B) Same as in A but for a stronger hyperfine coupling where all transitions can be individually resolved. (C and D) Same as in A and B but for the $m_S=0\leftrightarrow m_S=+1$ subset of transitions. In A−D, the color code for Right follows the notation introduced in Left. In A and C, $A_{zz}=A_{xx}=A_{yy}=500$ kHz; in B and D, $A_{zz}=A_{xx}=A_{yy}=4$ MHz. In all cases, $A_{zx}=0.3A_{zz}$, $\Omega =250$ kHz, and $\theta =30°,\varphi =60°$.

By contrast, a quick inspection of Fig. 2 C and D shows that the energy level structure near the crossings—and corresponding polarization yield—is markedly different in the $m_{\text{S}}=+1$ manifold. Here, reversal in the order of the “allowed” and “forbidden” transitions traversed during a sweep (respectively connecting branches with the same “up” or “down” nuclear spin character) makes the generation of ¹³C polarization inefficient. The impact of the order reversal can be better visualized in Fig. 2D, where the greater hyperfine coupling leads to four resolved LZ crossings. Assuming initialization into $m_{\text{S}}=0$ and a low-to-high-frequency sweep, the large gap in the first avoided crossing—proportional to $\text{Ω}$—makes this passage predominantly adiabatic. Correspondingly, the subsequent population exchange during the second (narrower) crossing becomes ineffective in creating net nuclear polarization, as the probability of finding the NV–¹³C system in either branch still amounts to ∼50% (Fig. 2D, Right); a similar reasoning applied to the ensuing pair of crossings in the present example confirms that no net polarization can emerge from a sweep of the $m_{\text{S}}=0\leftrightarrow m_{\text{S}}=+1$ subset. Note, however, that because, in the present low-field regime, $\mathbf{A}>{\gamma }_{\text{C}}B$, the order in the transitions during a sweep depends on the sign of $A_{\text{zz}}$, which can be positive or negative with nearly equal probability. Therefore, there is no intrinsic difference in the polarization efficiency associated to the $m_{\text{S}}=-1$ or $+1$ manifolds, as the dynamics reverses upon an overall sign change of the hyperfine coupling constants. In other words, low-to-high (high-to-low) MW sweeps across either subset in a bulk crystal should yield net positive (negative) ¹³C spin polarization. We return to this point later in this section.

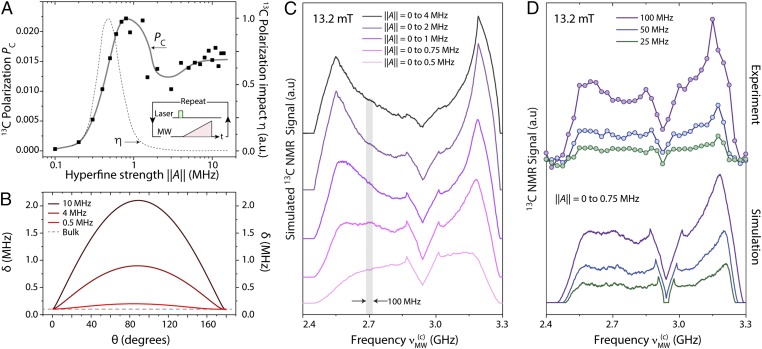
To gain a fuller understanding of the dynamics underlying the generation of bulk ¹³C magnetization, we investigate the polarization efficiency as a function of the hyperfine coupling. In Fig. 3A we spin initialize the NV electronic spin to about 5% and determine the steady-state polarization $P_{\text{C}}$ of the coupled ¹³C spin as we repeat the MW frequency sweep multiple times; this strategy more closely reproduces our experimental conditions (see Materials and Methods and SI Appendix). We attain comparable nuclear spin polarization for hyperfine couplings $\text{A}\mathrm{\gtrsim }500$ kHz and up to 10 MHz. As expected, the efficiency of the polarization transfer process decays for weaker couplings, although care must be exercised when correlating the end polarization of a particular ¹³C nucleus and its impact on the observed bulk NMR signal. Specifically, as the hyperfine interaction weakens, the number $N$ of carbon spins featuring a lower level of coupling increases (nearly quadratically). Further, weaker couplings considerably facilitate nuclear spin flip-flops between neighbors and hence are instrumental in enabling the generation of bulk nuclear polarization. This is shown in Fig. 3B where we plot the ¹³C spin energy splitting $\delta$ within the $m_{\text{S}}=0$ manifold assuming a 10-mT field: Except for NVs perfectly aligned with $B$, hyperfine contributions (stemming from the last term in Eq. 3) can quickly dominate over the Zeeman term, thus leading to a hyperfine-dependent frequency mismatch between carbons. This effect is only moderate when $\text{A}\mathrm{\lesssim }1$ MHz, suggesting that carbons featuring weak to moderate couplings have a comparatively larger influence on the observed ¹³C NMR signal.

Fig. 3.

”Strong” vs. “moderate” hyperfine couplings. (A) Calculated steady-state ¹³C spin polarization after repeated low-to-high-frequency sweeps across the $m_{\text{S}}=0\leftrightarrow m_{\text{S}}=+1$ subset for a variable hyperfine coupling $A_{zz}$; the initial NV spin polarization is 5%, the sweep rate is 40 MHz/ms, the Rabi field is 250 kHz, and we assume $A_{zz}=A_{xx}=A_{yy}$ and $A_{zx}=0.3A_{zz}$; the dots indicate a representative polarization for a given relative orientation of the magnetic field $B$, and the solid line is a guide to the eye. The dashed line indicates the estimated relative contribution $\eta$ to the observed ¹³C NMR signal amplitude (right vertical axis). (B) Calculated energy splitting $\delta$ between the NV–¹³C eigenenergies within the subspace $m_{\text{S}}=0$ as a function of $\theta$ for $\varphi =0$. (C) Modeled ¹³C spin NMR signal for a powdered diamond sample and a 100-MHz-wide MW frequency sweep centered at a variable frequency ${\text{ν}}_{\text{MW}}^{\left(c\right)}$. In all calculations, we assume the external magnetic field is $B=13.2$ mT and consider hyperfine interactions over the range 0 to A_max. (D) Same as in C but for a variable sweep range, as calculated numerically or observed experimentally (lower and upper trace sets, respectively). For the calculated plots, we use $A_{\text{max}}=750$ kHz, and all averages emerge over $1.5\times {10}^4$ configurations; throughout the experiments, the number of MW sweeps per data point is 10³, and the number of repeats is 30, with all other conditions remaining as in Fig. 1. In C and D, we displace all traces horizontally for clarity.

We can qualitatively gauge the influence of a given NV–¹³C pair with hyperfine coupling strength $A$ in generating the observed NMR signal through the “impact factor” $\eta \left(A\right)\propto \underset{0}{\overset{\pi }{{\displaystyle \int }}}d\theta {\sin }^2\theta \underset{0}{\overset{2\pi }{{\displaystyle \int }}}d\varphi N{P}_{\text{C}}g\left(\delta \right)$, where $N\propto 1/A^2$, and $g\left(\delta \left(\theta ,\varphi ,A\right)\right)$ is a function that quantifies the ability of a ¹³C spin to spin diffuse with its neighbors. Although the latter is presently unknown, we get a crude estimate by assuming $g\left(\delta \right)\propto \exp \left(-{\left(\delta -{\gamma }_{\text{C}}B/2\pi \right)}^2/2A_{\max }^2\right)$, where $A_{max}$ represents a critical hyperfine coupling, of order ∼1 MHz (see below). The result—shown as a dashed line in Fig. 3A—suggests that a very selective set of moderately coupled carbons—featuring $A$ between 0.5 MHz and 0.8 MHz—is effective in producing the observed bulk NMR signal, very much in contrast with prior studies (6, 11) where strongly coupled carbons (∼10 MHz and up) were seen to be dominant.

We confirm the ideas above through the observations in Fig. 3 C and D: Here, we consider NV–¹³C pairs extracted from a statistical distribution of hyperfine couplings, and calculate, for each pair, the ¹³C spin polarization after a 100-MHz local sweep of variable central frequency ${\nu }_{\text{MW}}^{\left(\text{c}\right)}$; throughout these calculations, we assume the relative orientations of the magnetic field and NV axis are random (SI Appendix, section III). Fig. 3C shows the results for distributions of hyperfine couplings with a variable upper threshold $A_{\max }$, ranging from 4 MHz down to 0.5 MHz (respectively ordered from top to bottom in the figure). Notably, the calculated responses display a marked asymmetry between the sides of the spectrum associated to transitions involving the $m_{\text{S}}=-1$ or $m_{\text{S}}=+1$ NV spin states (lower- and higher-frequency regions, respectively). Further, the overall spectral shape is sensitive to the range of hyperfine couplings taken into account, progressively evolving from a structured shape peaked at the edges of the spectrum toward a flatter, more uniform distribution for weaker $A_{\max }$.

Fig. 3D displays two sets of spectra, both experimental and calculated (upper and lower sets, respectively), which we now can use for direct comparison: In the upper set, each circle represents the amplitude of the measured 7-T ¹³C NMR signal upon multiple low-to-high-frequency sweeps over an MW band of predefined, variable width centered at a variable frequency ${\nu }_{\text{MW}}^{\left(\text{c}\right)}$. From an inspection of Fig. 3C, we find best agreement with experiment for carbon distributions where $A_{max}\approx 750$ kHz, hence indicating that strongly coupled carbons do not significantly contribute to the observed bulk NMR signal. Note that, despite the lineshape changes, the calculated spectra remain consistent with our observations even as we reduce the sweep bandwidth from 100 MHz to 50 MHz to 25 MHz (purple, light blue, and green traces, respectively). Further, because contributions to the calculated spectra stemming from carbons with hyperfine coupling lower than ∼200 KHz are negligible (SI Appendix, section III), the observed bulk nuclear spin polarization must be interpreted as mediated by a select shell of moderately coupled nuclei around the NV (i.e., 200 kHz $<A<$ 750 kHz), consistent with the calculated impact factor $\eta$ in Fig. 3A.

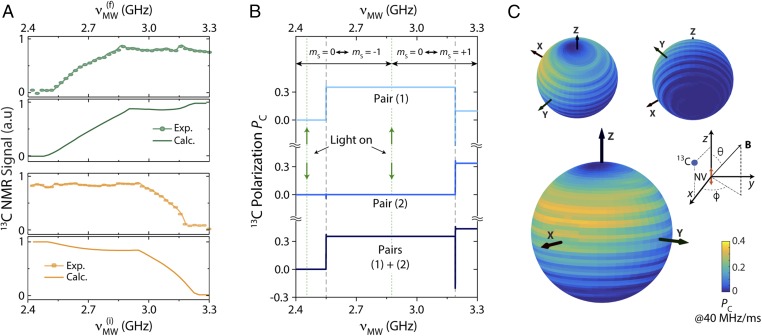
Although the broad spectra in Fig. 3 suggest nearly uniform contributions from NVs in all orientations, the process leading to bulk nuclear spin polarization is considerably more complex. The green circles in Fig. 4A show the result from an experiment where each data point reflects the ¹³C NMR signal amplitude upon multiple low-to-high MW frequency sweeps of increasing bandwidth, i.e., the start frequency ${\nu }_{\text{MW}}^{\left(\text{i}\right)}=2.4$ GHz remains unchanged while the end frequency ${\nu }_{\text{MW}}^{\left(\text{f}\right)}$ gradually increases. We find that the NMR signal first grows almost linearly, to subsequently plateau at a maximum once ${\nu }_{\text{MW}}^{\left(\text{f}\right)}\mathrm{\gtrsim }2.95$ GHz, i.e., once ${\nu }_{\text{MW}}^{\left(\text{f}\right)}$ reaches the set of transitions involving the $m_S=+1$ NV state; compared with the thermal signal amplitude, this maximum signal corresponds to a ¹³C spin polarization of order 0.2%. We find a similar (although complementary) result if we set the final MW frequency to ${\nu }_{\text{MW}}^{\left(\text{f}\right)}=3.3$ GHz and gradually change the start point in the sweep ${\nu }_{\text{MW}}^{\left(\text{i}\right)}$ toward lower frequencies (orange circles). These observations—qualitatively reproduced by our model (see solid traces in Fig. 4A)—can be interpreted in terms of a partial polarization cancellation during the sweep. Fig. 4B illustrates this process through a representative example in which we study the effect of a low-to-high-frequency sweep on two individual NV–¹³C pairs featuring hyperfine interactions of the same strength ($A=500$ kHz) but of opposite signs. In agreement with the results in Fig. 2, the carbon with a positive (negative) coupling polarizes positively upon crossing the set of transitions involving the $m_{\text{S}}=-1$ ($m_{\text{S}}=+1$) NV spin state. Interestingly, however, the positively coupled carbon loses its polarization when the MW reaches the subset of crossings involving $m_{\text{S}}=+1$, with the result that the net nuclear spin magnetization remains roughly unchanged during the second half of the sweep. In other words, no net increase in the ¹³C NMR signal is to be expected when extending the sweep range to include the full set of transitions, as observed experimentally.

Fig. 4.

Optimal spin polarization transfer: frequency and angular dependence. (A) (Upper) Measured (full circles) and calculated (solid line) ¹³C NMR signal upon multiple frequency sweeps; each sweep goes from a fixed MW start frequency ${\nu }_{\text{MW}}^{\left(\text{i}\right)}=2.4$ GHz to a variable end frequency ${\nu }_{\text{MW}}^{\left(\text{f}\right)}$. (Lower) Same as in Upper but for a variable start frequency ${\nu }_{\text{MW}}^{\left(\text{i}\right)}$ to a fixed final frequency ${\nu }_{\text{MW}}^{\left(\text{f}\right)}=3.3$ GHz. In both cases, the sweep is from low to high frequencies and thus yields a positive ¹³C polarization. All other experimental and modeling conditions are as in Fig. 3D. (B) Calculated ¹³C spin polarization for two example NV–¹³C pairs featuring similar hyperfine couplings ($A=500$ kHz) upon a low-to-high-frequency sweep; the NV–¹³C coupling is assumed positive (negative) for pair 1 (pair 2). Vertical dashed lines indicate the location of the crossings within the $m_{\text{S}}=\pm 1$ manifolds (we are assuming $\theta =30$°). For simplicity, we assume the NV is optically pumped into $m_{\text{S}}=0$ both at the beginning and midpoint of the sweep (dotted vertical line). (C) Calculated ¹³C spin polarization as a function of the orientation of the magnetic field relative to the NV axis, aligned parallel to the z axis. For these calculations, we use a hyperfine coupling tensor of the form $A_{\text{zz}}=A_{\text{xx}}=A_{\text{yy}}=0.5$ MHz and $A_{\text{zx}}=0.3A_{\text{zz}}$.

We gain additional insight on the NMR signal formation by calculating the steady-state nuclear spin polarization in an individual NV–¹³C pair ($A=500$ kHz) for different relative orientations of the magnetic field and NV axes. Despite the broad spectral response observed in Fig. 3 C and D—naively indicative of angle-insensitive nuclear spin polarization—we find a complex dependence, both in terms of the polar and azimuthal angles (Fig. 4C). Remarkably, our calculations indicate that nuclear spin polarization is more efficiently produced in the case of misaligned NVs (i.e., $\theta \ne 0$), which sheds light on why this approach works so effectively in a powdered sample. On the other hand, the polarization transfer process does not show cylindrical symmetry, a reflection of the azimuthal angle dependence in the last term of Eq. 3. Note that, although the calculated nuclear polarization is sizable only in the upper hemisphere of the plot, an equivalent response—this time with optimum in the lower hemisphere—can be attained by changing the sign of the hyperfine coupling, from positive (used in the present example) to negative. A crude estimate that takes into account the concentration of NVs and the ¹³C spin-lattice relaxation time, shows that the calculated average carbon polarization per sweep in our two-spin model (of order 5%; Fig. 4C) is consistent with the observed bulk ¹³C polarization (of order 0.1%; see SI Appendix, section IV).

Finally, we investigate the impact of the MW frequency sweep rate, set to ${\dot{\nu }}_{\text{MW}}=40$ MHz/ms in all of the results presented thus far. We start by calculating the ¹³C spin response in a moderately coupled NV–¹³C pair ($A=500$ kHz) for different orientations of the magnetic field. From a quick inspection of Fig. 5A, we conclude that the polarization transfer is most efficient at intermediate sweep rates—of order 40 MHz/ms to 50 MHz/ms—where nonadiabaticity at the LZ crossings is optimal. Consistent with the observations in Fig. 4C, the absolute ¹³C polarization attained at ${\dot{\nu }}_{\text{MW}}=40$ MHz/ms diminishes for NVs aligned with $\mathbf{B}$. On the other hand, the optimal sweep velocity can vary substantially depending on the exact field direction (Fig. 5B), although the absolute change is rather moderate within the set of angles ($\theta ,\varphi$) where the polarization transfer is most efficient. In particular, we find that the angular region where the ¹³C polarization is maximum remains similar to that in Fig. 4C, even if we choose, for each $B$ field direction, the optimal sweep rate (Fig. 5C).

Fig. 5.

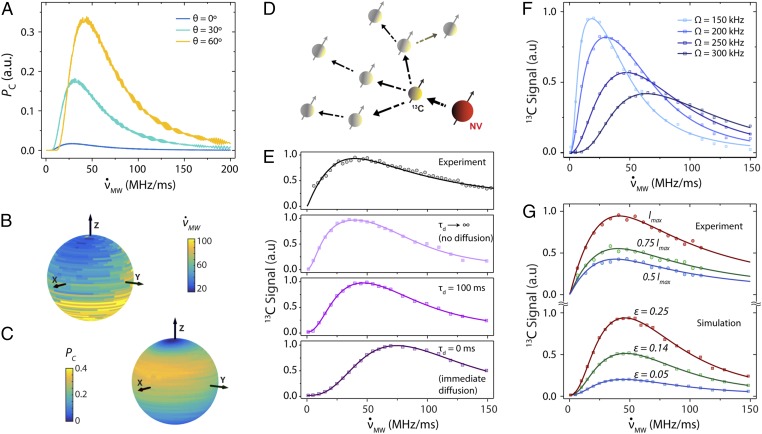
Impact of frequency sweep rate and illumination intensity on the ¹³C spin polarization. (A) Calculated ¹³C spin polarization upon a single sweep as a function of the MW frequency sweep rate for the case of a moderately coupled NV–¹³C pair ($A=500$ kHz) and different relative orientations of the external magnetic field. For simplicity, we assume the NV has been fully polarized into $m_{\text{S}}=0$ before the sweep and ignore the effect of illumination thereafter; all other conditions are as in Fig. 1. (B) Optimal frequency sweep velocity as a function of the magnetic field direction for the ¹³C spin considered in A. (C) Spin polarization for the same ¹³C spin as a function of the magnetic field direction assuming, in each case, the sweep rate is the optimum possible. (D) Nanoscale spin geometry. The polarization from a carbon coupled to an NV spin (yellow and red solid circles, respectively) diffuses via homo-spin couplings with its neighbors (semitransparent solid circles). (E) The upper trace is the measured ¹³C NMR signal amplitude (dark circles) as a function of the sweep rate; the total spin pumping time for each measurement is set to 10 s (see text). The lower traces are the calculated ¹³C signals assuming variable spin diffusion time ${\tau }_{\text{d}}$. (F) Calculated ¹³C magnetization for different Rabi field amplitudes as a function of the MW frequency sweep rate. (G) Measured and calculated ¹³C NMR signals (upper and lower sets, respectively) at different illumination intensities as a function of the MW sweep rate. In the experimental traces, the maximum laser intensity is $I_{\text{max}}=1$ W. For the calculated traces, we use a fixed Rabi field amplitude $\text{Ω}=250$ kHz and variable NV spin initialization into $m_{\text{S}}=0$ quantified via the parameter $\epsilon \in \left[\mathrm{0,2}\right]$; see SI Appendix, section IV. All calculations in E−G assume continuous laser excitation, a magnetic field $B=13.2$ mT, and a 100-ms spin diffusion time (unless explicitly noted otherwise). Each point emerges from average over all field orientations and hyperfine couplings assuming $A<1$ MHz; solid traces are guides to the eye.

Since the time required to complete multiple sweeps inherently depends on the chosen sweep rate, a comparison with experimental observations as a function of ${\dot{\nu }}_{\text{MW}}$ must necessarily take into account nuclear spin diffusion from the target carbon into the bath (Fig. 5D). While a full quantum mechanical description is difficult, we resort to a phenomenological approach where spin diffusion takes the form of a pseudo spin-lattice relaxation process affecting the polarization of the carbon directly coupled to the NV (26); our code, however, keeps track of the total magnetization injected into the nuclear spin system so as to make the end result proportional to the observed ¹³C NMR signal (SI Appendix, section IV).

Experimental plots of the dynamically pumped ¹³C NMR signal amplitude as a function of the MW sweep rate are presented in the upper trace of Fig. 5E; to maximize the polarization buildup, the total pumping time at each point is kept constant at $T_{1\text{C}}=$10 s (coincident with the ¹³C spin-lattice relaxation time at $B\approx 13.2$ mT), meaning that $n$, the number of sweeps, gradually changes depending on the specific value of ${\dot{\nu }}_{\text{MW}}$ according to the relation $n=T_{1\text{C}}{\dot{\nu }}_{\text{MW}}/\mathrm{\Delta }\nu$, where $\mathrm{\Delta }\nu =370$ MHz is the frequency bandwidth. The lower traces in Fig. 5E show the results of numerical simulations where we incorporate the above conditions; throughout these calculations, each data point emerges from a complex average, namely, we sample the hyperfine coupling from a statistical distribution (similar to that used in Fig. 3D, i.e., $0\le A\le 750$ kHz), and vary the magnetic field direction over all possible orientations relative to the NV axis. To save time (these calculations are demanding and thus require considerable computing power; see SI Appendix, section IV) we limit the total illumination time to 1 s.

In qualitative agreement with our experiments, we find a sharp initial growth followed by a slower decay at faster sweep rates, with an optimum around 40 MHz/ms to 50 MHz/ms. Taking spin diffusion into account (lower traces in Fig. 5E) shifts the optimum sweep rate to greater values, because the larger number of sweeps per unit time effectively enhances the total nuclear magnetization produced. It would be premature, however, to elaborate on the spin diffusion dynamics at play, as the overall shape of the response is sensitive to the Rabi field amplitude (Fig. 5F). Indeed, this latter dependence may be responsible for the main differences between theory and experiment, as the fixed direction of the MW field in the laboratory frame amounts to a random orientation relative to the NV axis, hence leading to a variable effective MW amplitude.

Interestingly, greater laser powers lead to greater ¹³C NMR signals without distorting the overall shape of the response (upper data set in Fig. 5G). This observation—correctly reproduced by our model (see lower data set in Fig. 5G)—is a consequence of the relatively mild illumination we employ herein (1-W laser focused over a 4-mm-diameter spot). Under these conditions, the probability of optically exciting an NV precisely during a subset of LZ crossings is relatively low—particularly if, as shown above, $A\mathrm{\lesssim }750$ kHz (Fig. 2)—meaning that the polarization transfer takes place coherently and NV repolarization preferentially occurs between successive crossings. More intense laser powers, therefore, lead to better NV spin initialization and, consequently, to enhanced ¹³C polarization, as observed experimentally. We caution, however, that this picture breaks down for strongly coupled carbons—where LZ crossings split into a resolved series (Fig. 2 B and D)—because optical reinitialization of the NV between crossings within the same $m_{\text{S}}=-1$ or $m_{\text{S}}=+1$ manifold typically causes depolarization (SI Appendix, section V).

Conclusions

Continuous optical illumination accompanied by repeated MW frequency sweeps leads to efficient spin polarization transfer from NVs to neighboring carbons in powdered diamond at 10 mT to 30 mT. Our observations can be reproduced via an average Hamiltonian describing the effective rotating-frame interaction between the NV and a neighboring ¹³C spin. In this picture, spin transfer takes place via an LZ-like process where nuclear polarization emerges as a consequence of the asymmetry in the adiabaticity parameter characterizing avoided crossings between branches with the same or opposite nuclear spin character; the polarization sign depends on the direction of the sweep, whereas its level relates to the hyperfine coupling, the misalignment, and the particular set of crossings involved. From comparison with ¹³C-NMR−detected NV spin spectra, we conclude that the polarization transfer to bulk nuclei is mediated by carbons with hyperfine couplings within a narrow range, $200\text{kHz}\mathrm{\lesssim }A\mathrm{\lesssim }750$ kHz. Although comparable levels of nuclear polarization can be attained virtually at all NV spin frequencies, the polarization transfer is sensitive to the relative direction of the magnetic field, with the optimum occurring for carbons associated to misaligned NVs. Further, competing nuclear spin polarization and depolarization processes limit the range of the frequency sweep necessary to attain maximum ¹³C NMR signals to approximately half the NV spin resonance spectrum. The NMR signal response as a function of the frequency sweep rate shows an optimum around 40 MHz/ms to 50 MHz/ms, consistent with the (calculated) values required to optimize the spin transfer during the LZ crossings.

Our findings open interesting opportunities for further optimization as well as for fundamental and applied work. For example, the angular dependence of the transfer on the $B$ field axis—particularly the azimuthal dependence (Fig. 4C)—suggests that additional NMR signal gain could be attained by making the field direction undergo a suitable time evolution. Also to consider is the sweep rate, which, rather than constant, could be gradually incremented with growing frequencies so as to match the optimum observed at different orientations (Fig. 5B). Along the same lines, another possibility is to use several MW sources to generate multiple sweeps running simultaneously but shifted in frequency; NMR signal amplification is expected when the time separation between successive sweeps—all sharing the same frequency sweep rate—are brought to a minimum defined by the NV repolarization time (27).

Additional work will be needed to investigate the impact of other experimental parameters such as the illumination conditions, and the influence of paramagnetic defects other than the NV. For example, at the relatively mild laser intensities used herein—of order 100 mW/mm²—the NV polarization rate amounts to ∼100 Hz, implying that the steady-state NV spin polarization, reaching at best 10%, is far below the optimum. On the other hand, light-induced decoherence during the LZ crossings must ultimately hinder the spin transfer process, which suggests there must be an optimum illumination intensity. Whether or not this regime can be reached without complications from NV photoionization (or the ionization of other impurities) is a question that can only be addressed through subsequent studies over a larger range of laser powers and using illumination wavelengths other than 532 nm.

Another pending question is the response as a function of the magnetic field amplitude, here constrained to less than 20 mT. Extending the present studies to greater fields—particularly those above 100 mT—is an attractive route to prolong the ¹³C spin-lattice relaxation time—here limited by cross-relaxation with paramagnetic nitrogen impurities (25)—and hence potentially augment the end polarization. Initial observations at ∼100 mT showed no enhancement, although a more systematic study—ideally encompassing greater fields—is in order. Several complications, both experimental and theoretical, must be overcome to accomplish this task. Among them is the limited frequency bandwidth typical in most MW sources and amplification systems, normally circumvented at high fields (e.g., $B\approx 300$ mT) through the use of tuned, narrow-band MW cavities and variable magnetic fields; it is not clear, however, that this strategy shares the same flexibility as the approach pursued herein. On the theoretical side, additional work will be necessary to extend the present formalism—valid in the limit where the impact of the magnetic field can be treated perturbatively—to the regime where the Zeeman interaction becomes dominant over the NV crystal field. Although some key ingredients remain unchanged (12), this regime is expected to differ from the present one in important ways, including the type of carbons mediating the polarization transfer to the bulk and, most notably, the impact of misalignment on the NV spin initialization. These studies must also encompass the case where the NV spin simultaneously interacts with more than one carbon nucleus, inherent to ¹³C-enriched samples and thus important in applications where diamond particles serve as an imaging contrast agent or as the source of hyperpolarization for target fluids.

Materials and Methods

Most experiments presented in this paper are carried out using E6 diamond particles with an average size of ∼200 µm and NV concentration of 1 ppm; more recent work, however, has attained virtually identical results with particle sizes down to 1 µm, either in the form of a dry powder or in solution. The mass of the entire sample of particles is 7.50 ± 0.25 mg. Using the known density of diamond (3.51 mg/mm³), the total sample volume is calculated to be 2.14 ± 0.07 mm³. Dividing by the individual particle volume, the number of diamond particles is found to be 287 ± 27 diamonds. For the experiments in Fig. 1E, we employ a $3\times 3\times 0.3$ mm³ type 1b single-crystal diamond oriented so that all four NV directions form a 54.7° angle with the applied magnetic field.

To induce and detect DNP, we use a custom-built sample shuttling device. In a typical experiment, simultaneous MW excitation and 1-W, 4-mm-diameter optical illumination at 532 nm take place at a variable low magnetic field (5 mT to 36 mT), upon which the sample quickly moves to the sweet spot of a 7-T NMR magnet for inspection; the NMR signal amplitude is extracted from the height of the ¹³C spectrum obtained upon Fourier transform of the free-induction decay resulting from resonant single-pulse radio frequency excitation at 7 T. We refer the reader to ref. 25 for further details.

Our numerical calculations are conducted using a Matlab code developed in-house (SI Appendix, section IV). We consider individual NV–¹³C pairs whose dynamics follows the effective rotating-frame Hamiltonian presented in Eq. 4; we model the impact of light through sudden projections into the $m_{\text{S}}=0$ subspace. We sample over all relative orientations of the magnetic field, and, when necessary, over all hyperfine couplings using suitable statistical distributions. To reduce the computing time, we resort to the facilities of the City University of New York (CUNY) High Performance Computing Center. We refer the reader to SI Appendix, section IV for additional details.