Thermodynamically reversible paths of the first fusion intermediate reveal an important role for membrane anchors of fusion proteins

Significance

The isolated transmembrane domains (TMDs) of fusion proteins such as SNARE molecules drastically lower the free energy of both the stalk barrier and metastable stalk, which is not trivially explained by molecular shape arguments. The here-demonstrated methodology may have far-reaching applications in the fields of medicine and pharmacology because it enables screening and rational design of novel fusion inhibitors and accelerators.

Abstract

Biological membrane fusion proceeds via an essential topological transition of the two membranes involved. Known players such as certain lipid species and fusion proteins are generally believed to alter the free energy and thus the rate of the fusion reaction. Quantifying these effects by theory poses a major challenge since the essential reaction intermediates are collective, diffusive and of a molecular length scale. We conducted molecular dynamics simulations in conjunction with a state-of-the-art string method to resolve the minimum free-energy path of the first fusion intermediate state, the so-called stalk. We demonstrate that the isolated transmembrane domains (TMDs) of fusion proteins such as SNARE molecules drastically lower the free energy of both the stalk barrier and metastable stalk, which is not trivially explained by molecular shape arguments. We relate this effect to the local thinning of the membrane (negative hydrophobic mismatch) imposed by the TMDs which favors the nearby presence of the highly bent stalk structure or prestalk dimple. The distance between the membranes is the most crucial determinant of the free energy of the stalk, whereas the free-energy barrier changes only slightly. Surprisingly, fusion enhancing lipids, i.e., lipids with a negative spontaneous curvature, such as PE lipids have little effect on the free energy of the stalk barrier, likely because of its single molecular nature. In contrast, the lipid shape plays a crucial role in overcoming the hydration repulsion between two membranes and thus rather lowers the total work required to form a stalk.

Membrane fusion, one of the most fundamental processes in life, occurs when two separate lipid membranes merge into a single continuous bilayer (1). In the last 40 y, much understanding has been gained about the intermediate stages of this process due to extensive theoretical and experimental research (2). Notwithstanding this progress, there remain many open and exist newly emerging questions regarding the nature of the rate-limiting steps of the fusion reaction and how fusion proteins lower the free-energy barriers along the transition path (3–5). Furthermore, since membrane fusion is an essential step in the infection process of enveloped viruses, gaining further understanding of membrane fusion is ultimately driven by the need to control it. The ability to theoretically quantify how molecules alter the free-energy landscape of membrane remodeling may have far-reaching applications in the fields of medicine and pharmacology because it enables (high-throughput) screening and rational design of novel fusion effectors. Moreover, as we will illustrate within this work, such an ability can gain important new insights into the essential structural characteristic of existing fusion proteins such as, for example, SNARE proteins. However, theoretically quantifying these free energies poses a major challenge because the essential reaction intermediates in biological membrane fusion are complex and of a molecular length scale.

Most if not all of the physical driving forces that govern the reaction path of nonchemical biological reactions are inherently encoded within the complexity of classical molecular force fields, i.e., a set of parameters that describe the Newtonian forces between atoms or coarse-grained groups of atoms in silico. Therefore, in silico modeling in principle enables an explicit description of the full molecular complexity of biological membrane fusion. To quantify transformations one often uses reaction paths and the free-energy barriers along them. However, using molecular force fields for the quantification of free energies is severely limited by the computational mining or sampling of all of the accessible states of a physical system (phase-space). For example, umbrella sampling methods (6, 7) reconstruct the free energy from the effective equilibrium force, which is required to drive the reaction along an a priori known reaction coordinate, e.g., the distance between two molecular groups (8, 9). In case of collective processes, which involve many different molecules, such as membrane fusion or fission, it is often rather unclear how the reaction path should look like or how to control it. A related question is whether an a priori chosen reaction path represents a thermodynamically reversible reaction path. Moreover, experimental studies (10), field-theoretical studies (11, 12), and molecular simulations (9, 13–19) have illustrated the existence of multiple competitive paths in membrane fusion, which proceed through structurally and topologically different intermediates.

In contrast, traditional equation-based free-energy descriptions, such as Helfrich elastic continuum modeling, must coarse-grain the effects of lipids and proteins into a few parameters, which mathematically describe the molecular shape (spontaneous curvature) and the elastic moduli of the membrane (20–22). While these models provide physical insights into the universal aspects of the free-energy landscape, they lack molecular details that may become important, particularly for protein-mediated fusion.

Here, we will demonstrate the unique capability of an enhanced sampling method – the string method – to self-resolve a thermodynamically reversible path of minimum free energy of the fusion reaction by using the information encoded within molecular force fields. To this end, we will focus on the transition between two apposed membranes (the reactant) and the first metastable fusion intermediate state, the so-called stalk (the product state). For calculation of the free energy, we introduce a high-dimensional collective order parameter, $m\left(\mathbf{r}\right)$—hydrophobic membrane density on a grid (23)—that should completely characterize the membrane conformation. The collective lipid density is an appropriate choice because it has a slow relaxation time as compared with the single-lipid conformations.

We consider two mechanically coupled but distinct levels of description: (i) an instantaneous atomic level described by a molecular force field in conjunction with a molecular dynamics (MD) engine and (ii) the local hydrophobic density of the membrane system, $m\left(\mathbf{r}\right)$, which is obtained by averaging the position of atoms over discretized space. The free-energy functional, $F\left[m\right]$, describes the free-energy landscape of the membrane transformation but its functional form is not explicitly known.

Our method is in the flavor of other earlier ’unbiased’ methods such as transition path sampling (24, 25) and so-called chain-of-states based methods (26). The main idea is to describe the most likely reaction path—the minimum free-energy path (MFEP)—by a sequence of membrane configurations: the string $m_s\left(\mathbf{r}\right)$ that connects the reactant state, $s=0$, and product state, $s=1$. To this aim, we first construct an initial sequence of sample configurations based on simple, linear interpolation between the known densities of the reaction and product state. Each of these sample configurations is studied by a separate, independent MD simulation and the local chemical potential (i.e., the derivative of the free energy with respect to density) is obtained. Knowledge of this chemical potential is exploited to update all sample configurations that comprise the path within an additional but separate pseudodynamical step. This update locally minimizes the free energy, subject to a constraint that the distance between neighboring sample configurations along the path remains uniform (27, 28), ensuring that the sampled path locally converges to a MFEP, i.e., the most likely path. The string method, as any other free-energy calculation method, is a local optimization method (local minimum), which finds a thermodynamically reversible free-energy path. Therefore, different choices of the initial path may result in different pathways. However, based on the observation of stalk formation in MD simulation studies, alternative pathways seem unlikely, i.e., stalk formation always proceeds via formation of an essential, initial lipidic connection between the apposed membranes (8, 29, 30). In our example, we initiated the string using snapshots (structures) along the stalk transformation path derived in our previous work (8). Further details about the simulation model and free-energy calculation can be found under Materials and Methods and in SI Appendix.

To illustrate the capabilities of the string method, we will first revisit the theoretically well-studied process of protein-free stalk formation between two apposed flat membranes and study the role of intermembrane separation distances ($d_w$). We calculate the free-energy profiles for stalk formation while keeping track of the additional (equilibrium) work associated with adopting such separation distance via membrane dehydration. Finally, we will address whether the transmembrane domains (TMDs) of fusion proteins can alter the free-energy landscape of stalk formation in two already apposed membranes or whether they are inert at such a stage, i.e., they rather only serve as membrane anchors to bring the membranes in close proximity (1, 31). Specifically, we will focus on the TMDs of neuronal SNAREs – one of the most studied fusion proteins (4). It is an open question what the active role of SNARE TMDs is in regulating pre-fusion stages and fusion pore dynamics (5). By resolving the MFEP of the stalk formation we will illustrate that the inherent interactions between the membrane and TMDs can significantly influence biological fusion.

Results and Discussion

Free Energy of the Stalk Is Mostly Determined by Intermembrane Distance.

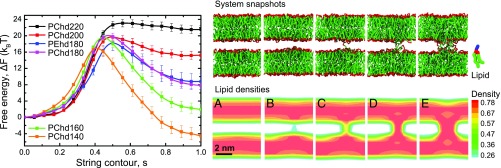
The classical model for theoretically studying fusion intermediates is a system comprised of two flat bilayers (Fig. 1, Right, snapshot A). This setup mimics the adhesion zone of two vesicles with large radii (much larger than the bilayer thickness). We chose the simulation box of about the same size as the unit cell of the rhombohedral structure formed between multilamellar stacks at low hydration (32), and vary the intermembrane separation distance from $d_w=1.2$ nm to about 1 nm (or 5 nm between the centers of mass of membranes). In this narrow distance interval, we obtained five MFEPs for phosphatidyl choline (POPC) bilayers and one for phosphatidyl ethanolamine (POPE) membranes. To feed the free-energy resolver, we used a near-atomic coarse-grained model, the Martini model (33, 34), because of its fast-convergence properties, together with the Gromacs MD engine (35). However, we emphasize that the application of this approach is general. Fig. 1, Left shows the free energy along the MFEPs obtained for different distances, $d_w$. An example of the corresponding lipid configurations and hydrophobic densities for $d_w=1.01$ nm along the transition path are also shown in Fig. 1, Right. This calculation uses the string method to obtain the MFEP of molecular-detailed membranes. Our results illustrate that the stalk stability rapidly increases with decreasing intermembrane distance, $d_w$, whereas the free-energy barrier decreases only marginally. The observed values are in good agreement with the metrics resolved by X-ray studies, which revealed that the stalk structure becomes energetically more favorable than the apposed bilayers ($\mathrm{\Delta }G<0$) at $0.9\pm 0.05$ nm (32) independent of lipid type, as well as our previous simulations (8), where the stalk barrier was estimated around 20$k_{B}T$ using umbrella sampling method. The stalk metastability disappears for larger distances, $d_w>1.24$ nm (“stretched stalk/worm-like micelle”), since the free-energy profile does not have a local minimum. It is interesting to note that, even when the membranes are at small intermembrane separation distances, the free-energy barrier to form the stalk structure is in the range $16-24k_{B}T$.

Fig. 1.

(Left) MFEPs for five POPC systems with different hydration levels: $d_w=1.0$ nm (PChd140: orange), $d_w=1.01$ nm (PChd160: green), $d_w=1.09$ nm (PChd180: blue), $d_w=1.13$ nm (PChd200: red), and $d_w=1.20$ nm (PChd220: black curve); and one POPE system with $d_w=1.06$ nm (PEhd180: magenta). Bars represent standard deviations. (Right) Snapshots depict configurations along the transformation path for the POPC system with $d_w=1.01$ nm (160 solvent beads between membranes). Color coding is as follows: hydrophobic beads, green; hydrophilic beads, blue (shown only for selected lipid); glycerol backbone, red. The slices (at $x=3$ nm) of the system hydrophobic densities (nm⁻³) are shown below the corresponding snapshots. The lamellar structure is at $s=0$ (A), $s=0.28$ (B), the barrier corresponds to $s=0.42$ (C), $s=0.56$ (D), and the stalk structure is at $s=1$ (E).

The advantage of using a collective order parameter, i.e., the lipid density field, in conjunction with the string method, is that we do not need an a priori knowledge of a suitable reaction coordinate; instead, the optimal reaction coordinate is automatically obtained from the collective order parameter after the path converged: It is a single-lipid protrusion before the barrier and a radial stalk thickening after the barrier. We note that the initial (equilibrium) simulations of product and reactant state are performed in the $NPT$ ensemble to ensure tension-less systems of the metastable end states. However, the path does not necessarily conserve this tension-less condition since the free-energy calculation steps are performed in the canonical $NVT$ ensemble. Therefore, to access the influence of a potentially introduced tension, we have extensively repeated these calculations for systems under controlled, initial tension and found no significant effect on the free-energy profiles (SI Appendix, Fig. S2).

Additionally, to independently verify the string method in its ability to resolve the free-energy landscape of protein-mediated membrane fusion, we calculated the relative free-energy differences between the two metastable end points of the MFEP, i.e., the apposed membrane system and the stalk, using the thermodynamic integration method (7), and found a good quantitative agreement between these different methods (SI Appendix, Table S1).

Finally, to localize the transition state and to verify that it indeed corresponds to the free-energy barrier, we performed a committor probability analysis (SI Appendix, Fig. S3). For six configurations around the free-energy barrier, for the system with $d_w=1.01$ nm, we generated around 200–500 trajectories and calculated the probability that the starting structure transforms to the bilayer state. We note that the transition state is in fact an ensemble of structures. About $66\%$ of the configurations at the transition state correspond to the splayed-lipid-bond configuration where a single lipid inserts its tails in the apposing bilayers (Fig. 1, Right, snapshot C), and the other configurations are represented by solvent-exposed tails from few different lipids (SI Appendix, Fig. S3).

POPE Lipids Do Not Affect the Inherent Stalk Barrier.

A compelling amount of experimental evidence suggests that POPE lipids enhance hemifusion (2). This effect is commonly understood from matching the effective shape of POPE lipids (negative spontaneous curvature) with the stalk’s overall structure. However, the stalk is evidently not the barrier state in our simulations but a metastable structure, whereas the stalk barrier itself is characterized by the structure of one or very few molecules, whose tails are exposed to the hydrophobic environment. The (near) single-molecular structure at the barrier state is not trivially related to the effective shape of a molecule in a bilayer.

To discern the effects of effective molecular shape, we additionally studied the fusion between two pure POPE membranes at $d_w=1.06$ nm (Fig. 1). Indeed, despite of POPE’s negative spontaneous curvature, the free-energy barrier is similar for both POPC and POPE lipid membranes, whereas the stability of the stalk is slightly increased. Although these results may seem paradoxical with respect to the hitherto hypothesized effect of POPE on membrane fusion, we emphasize that the effect of POPE on the total stalk barrier—the one that is experimentally observed—is chiefly determined by the work required to first bring the membranes in close proximity, i.e., to adopt a certain intermembrane distance, $d_w$ (SI Appendix, Fig. S4). This work has so far been omitted within our calculations. Thus, the here-reported barrier is an intrinsic stalk barrier.

Before membranes can fuse they must be positioned at close distance (2). We have already illustrated that distance matters—it has a pronounced effect on the free energy of the stalk. The closer the better. Therefore, fusion proteins, such as SNARE complexes, must overcome large repulsive (hydration) forces at short distances due to the structuring of water molecules near membrane interfaces (36). The presence of adhesion sites, charged lipids and ions additionally alter the free energy of interacting membranes. Also varying the hydrophobicity of interacting neutral membranes results in less repulsion for more hydrophobic interfaces (37). The spontaneous curvature of a lipid essentially provides an effective, coarse-grained description of the head group’s ability to shield the hydrophobic tails from solvent. Therefore, a smaller head group, i.e., a negative spontaneous curvature, will result in more exposure of the tails to the solvent, and thus generally in a reduced membrane-membrane repulsion. This trend is evident from the effective (equilibrium) work required to dehydrate stacked membrane systems in experiments (32). In correspondence, the coarse-grained model, which quantitatively model spontaneous curvature (33), reveals a similar trend within the overall free-energy cost of membrane dehydration (38).

Membrane elasticity (spontaneous curvature) and membrane repulsion are thus generally correlated because they share similar underlying physical driving forces (e.g., hydrophobic effects, area compressibility). Therefore, POPE lipids lower the total stalk barrier by affecting the cost required to bring membranes in close proximity, or alternatively, increasing the probability that membranes come in close proximity. Notably the effective shape of a molecule or spontaneous curvature is an outcome of the combined chemical features of both the hydrophilic head-group and hydrophobic tail—similar spontaneous curvatures can thus have rather different chemical origins. For example, the presence of lipids with shorter tails—this imposes a more positive spontaneous curvature—can alternatively increase the intrinsic stalk barrier because shorter-tailed lipids are less able to form splayed intermediates, i.e., the here-observed stalk barrier (39).

SNARE TMDs Substantially Lower the Free Energy of both the Metastable Stalk and Its Barrier.

The structure and function of SNARE TMDs has been extensively investigated over the past decades by means of experiments and simulations (4, 5, 40–49). Replacements of TMDs by various lipid anchors, different mutants, and partially truncated transmembrane peptides have suggested that TMDs are not only anchors for cytoplasmic SNARE domains, but play an active role in both, the formation of the initial stalk (or hemifusion state) as well as the further progression to full fusion.

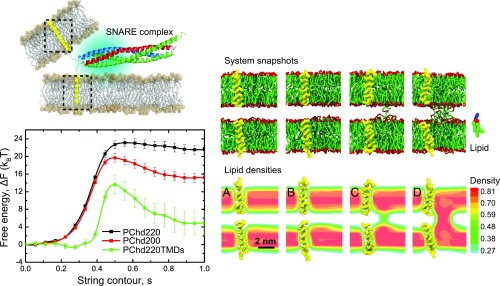
Since TMDs span a membrane area, which is on the order of the area per lipid, we do not expect that insertion of TMDs—given the small number of SNARE complexes that is typically required for fusion [one to eight complexes (50, 51)]—have a large influence on the here-calculated hydration repulsion free energy. Although high concentrations of viral TMDs can lower the hydration repulsion (52). A more intriguing question is whether TMDs are able to affect the intrinsic stalk barrier—thus quite in contrast to the effect observed for POPE lipids. To this aim, we inserted the TMDs in the membrane to mimic the biologically relevant situation when these anchoring peptides are linked to the rest of the SNARE complex (Fig. 2). This simulation models a scenario where the membranes are already brought within close proximity by the SNARE complex, i.e., $d_w=1.2$ nm, being our largest intermembrane distance.

Fig. 2.

(Top Left) Schematic representation of the SNARE complex with TMDs, selected by dashed lines. Reprinted from ref. 4. (Bottom Left) MFEPs for two systems without TMDs [PChd220, $d_w=1.2$ nm (black); and PChd200, $d_w=1.13$ nm (red)] and with TMDs [PChd220TMDs, $d_w=1.16$ nm (green)]. The hydration level is 220 solvent beads between membranes for the black and green curves and 200 for the red curve. Bars represent standard deviations. (Right) Snapshots depict lipid and peptide (yellow) configurations, and hydrophobic densities are shown below the corresponding snapshots: $s=0$ (A), $s=0.23$ (B), $s=0.5$ (C), and $s=1$ (D).

Fig. 2 presents the converged MFEPs. Indeed, the system with TMDs shows a substantial decrease of the stalk free energy as well as a reduction of the free-energy barrier compared with the pure lipid systems at $d_w=1.2$ and 1.13 nm. The increased stability of the stalk structure is additionally reflected by the tendency of the stalk to increase its otherwise costly perimeter in the presence of the TMDs (SI Appendix, Fig. S9A). Detailed analysis of the position and orientation of the TMDs during the reaction can be found in SI Appendix. It is interesting to note that the position and orientation of the TMDs closely correlate with the region of membrane thinning around the base of both the metastable stalk and stalk-barrier structure (Fig. 2 and SI Appendix). By partitioning in the region of large packing frustration, TMDs lower the excess free energy of the highly bent stalk structure. Such a reduction of the stalk’s free energy will result in a mutual attraction between the stalk and TMDs. Indeed, such an attraction is confirmed by unbiased equilibrium simulations (SI Appendix, Fig. S9B). Thus, we hypothesize that TMDs enhance fusion because of their favorable structural compatibility with the stalk structure and the stalk-barrier structure.

One of the most important findings of our current work is that the intrinsic stalk barrier and metastability are largely determined by distance between the opposed membranes—distance matters a lot. In contrast to the general consensus of membrane fusion, the effective shape of a molecule is not a main determinant of the intrinsic stalk barrier but, rather, plays an important role in the effective, total stalk barrier by affecting the free energy required to bring the membranes into close proximity. Such a lack of influence on the intrinsic stalk barrier is most likely explained by the observed single-molecular nature of the stalk barrier. Furthermore, we have illustrated that transmembrane proteins, although they are not trivially characterized by a molecular shape, can substantially affect the free energy of both the stalk and its barrier. TMDs alternatively reduce the elastic energy by thinning and softening the membrane (53–55). We hypothesize that the observed mutual attraction between stalk and the TMDs, which is analogous to the line tension driven attraction between stalks and (leakage) pores (9, 12, 14, 15, 56), plays an important role in the self-organization of fusion proteins at the biological fusion site and may be essential to overcome the additional fusion barriers after a stalk has formed. We therefore predict that the TMDs of fusion proteins generally prefer a (slight) negative hydrophobic mismatch, i.e., too short, with respect to their native membranes (57). In support of such a notion, a negative mismatch has been experimentally shown to promote the formation of inverted membrane phases (58). Finally, our results also highlight the importance of membrane anchors from a different perspective, i.e., they are essential tools for lowering fusion barriers by bringing the membranes in close proximity (3).

We foresee that the here-demonstrated methodology may find important applications in the fields of medicine and pharmacology because it enables screening and rational design of novel fusion inhibitors or accelerators. The power of the string method lies within its unique unbiased, equation-free description of the path of minimum free energy, which enables the integration of molecular complexity by parameterized classic force fields. Since the string method can quantify and thus score the direct effect of chemical alternations or biological mutations on a modeled molecule of interest (i.e., via the free energy), it can be suitably combined with state-of-the-art artificial intelligence methods to identify an optimal effector of the studied reaction. One can additionally exploit the reduced chemical degrees of freedom of coarse-grained models to reduce chemical space (59) and sample the effect of general physical properties, such as hydrophobicity or flexibility, within different regions of the molecule. The gained knowledge can be subsequently exploited to pinpoint interesting regions within full chemical space.

Materials and Methods

Simulation Setup.

All simulations were performed using the Gromacs 4.5 package (35) with the Martini coarse-grained force field for lipids and proteins (33, 34) in the canonical $NPT$ or $NVT$ ensemble at the temperature 300 K and with the typical length of simulations 1–2 $\mathrm{\mu }$s. The typical system contained two POPC or two POPE membranes, each consisting of 128 lipids, and 2,080 solvent beads. To control the intermembrane distance, $d_w$, we varied the number of solvent molecules between membranes, keeping the total number of solvent beads constant. The intermembrane distance was defined as in ref. 23, i.e., the distance between the equal densities of the glycerol backbone and phosphate group of the apposed leaflets. All systems were preequilibrated in the $NPT$ ensemble and further free energy calculations were performed in the $NVT$ ensemble. The implementation of the discretized densities and force calculations in Gromacs 4.5 were straightforward in the constant volume ensemble. However, we do not expect that our results will deviate much in the $NPT$ ensemble even for small system sizes.

To investigate finite size effects, we also performed simulations of large systems, obtained by periodically multiplication of the corresponding reference systems in $x$ and $y$ dimensions. The typical size of the reference systems was $6\times 6\times 15\hspace{0.17em}{\mathrm{n}\mathrm{m}}^3$, and that of the large system was $12\times 12\times 15\hspace{0.17em}{\mathrm{n}\mathrm{m}}^3$.

To study effects of SNARE TMDs, we placed the isolated TMD of synaptobrevin (bottom membrane) and syntaxin (top membrane) opposite to each other in the reference system with $d_w=1.2$ nm. Syntaxin peptide has 23 amino acids, IleMetIleIleIleCysCysValIleLeuGlyIleIleIleAleSerThrIleGlyGlyIlePheGly, and synaptobrevin has 22 amino acids, MetMetIleIleLeuGlyValIleCysAlaIleIleLeuIleIleIleIleValTyrPheSerThr (60). To study finite size effects, we inserted transmembrane peptides in the large membrane system. The size of the reference (small) system with TMDs was $6\times 7\times 15\hspace{0.17em}{\mathrm{n}\mathrm{m}}^3$, and the large system with TMDs was $12\times 14\times 15\hspace{0.17em}{\mathrm{n}\mathrm{m}}^3$.

The fusion transmembrane peptides (TMDs) were inserted in each membrane such that they were on top of each other along the $z$ axis, and the position of the center of mass of each peptide was restrained to prevent translational motion in the $xy$ plane at the beginning of the free-energy calculations; after equilibration, these restrains were removed. This setup mimics the connection of the transmembrane peptides via the linker peptides to the rest of the SNARE proteins.

MFEP Calculation Using the String Method.

The strategy consists in finding a string of morphologies (a path), characterized by a spatially varying density field (order parameter), $m_s\left(r\right)$, where $r$ denotes the spatial coordinate and $0\le s\le 1$ is the contour parameter along the transformation path. The transformation path was discretized by $n=19$ replicas. The reaction coordinate for $s=0$ corresponded to the system of two apposed membranes, $s=1$: the stalk structure. The MFEP is characterized by the condition that the variation of the free energy perpendicular to the path vanishes (28).

$${\left({\mu }_s\right)}_{\perp }\equiv {\left(\frac{\delta F\left[m_s\right]}{\delta m_s\left(\mathbf{r}\right)}\right)}_{\perp }=\frac{\delta F\left[m_s\right]}{\delta m_s\left(\mathbf{r}\right)}-\frac{\mathrm{d}{m}_s\left(\mathbf{r}\right)}{\mathrm{d}s}\frac{\int {\mathrm{d}}^3\mathbf{r}\hspace{0.17em}\frac{\delta F\left[m_s\right]}{\delta m_s\left(\mathbf{r}\right)}\frac{\mathrm{d}{m}_s\left(\mathbf{r}\right)}{\mathrm{d}s}}{\int {\mathrm{d}}^3\mathbf{r}\hspace{0.17em}{\left(\frac{\mathrm{d}{m}_s\left(\mathbf{r}\right)}{\mathrm{d}s}\right)}^2}\stackrel{!}{=}0.$$ [1]