Significance
Knots and entanglements occur in proteins, DNA, and synthetic polymers and are being used to form the basis of interwoven nanomaterials. Understanding how the tautness of molecular entanglements affects properties is crucial for the future design of knotted, woven, and entangled molecules and materials. However, while there are many theoretical studies on such systems there are very few experimental studies. Here we investigate the influence of knot tightness in a range of physical and chemical properties for three knots tied in 20-, 23-, and 26-nm closed-loop strands. We find that the tightness of the molecular knots significantly affects reactivity, conformation, and the expression of chirality.
Keywords: molecular knots, supramolecular chemistry, chemical topology
Abstract
Three 819 knots in closed-loop strands of different lengths (∼20, 23, and 26 nm) were used to experimentally assess the consequences of knot tightness at the molecular level. Through the use of 1H NMR, diffusion-ordered spectroscopy (DOSY), circular dichroism (CD), collision-induced dissociation mass spectrometry (CID-MS) and molecular dynamics (MD) simulations on the different-sized knots, we find that the structure, dynamics, and reactivity of the molecular chains are dramatically affected by the tightness of the knotting. The tautness of entanglement causes differences in conformation, enhances the expression of topological chirality, weakens covalent bonds, inhibits decomplexation events, and changes absorption properties. Understanding the effects of tightening nanoscale knots may usefully inform the design of knotted and entangled molecular materials.
Knots are found in some proteins (1), linear and circular DNA (2), and polymers of sufficient length and flexibility (3). The strand entanglements affect molecular size (4), stability (5), and various mechanical properties (6–8), although much of the understanding as to how and why remains unclear. To date the influence of various structural traits, such as the number of knot crossings (9), writhe (10), backbone crossing ratio (BCR) (11), and the global radius of curvature (12), on properties has mainly been studied by simulations (13–16) rather than experiment (17, 18). Knot tightness (19–21) is a particularly easy-to-appreciate characteristic, familiar from our everyday experience in the macroscopic world, that may also have significant effects at the molecular level (4, 22–27). Long polymers are predicted to have knotted regions that are both frequent and tight (25). The tightness of knotting is implicated in variations in the thermostability of entangled proteins (26) and is thought to have consequences for tensile strength (27). However, it is difficult to assess intrinsic effects of knotting by comparing structures with rather different chemical compositions. Monodispersed synthetic molecular knots are ideal models through which to evaluate the influence of knot tightening on physical and chemical properties (17, 18). Here we report experimentally determined property differences in a set of three knotted molecules that differ only in the length of flexible regions (alkyl chains) that separate more rigid sections (composed of aromatic rings) of the strand. Using a braiding strategy previously used to assemble (28) an extremely tightly knotted 192-atom loop 819 knot (1) (29), the alkene-terminated chains used to close the knotted structure were extended without otherwise altering the outcome of the knot synthesis (Fig. 1). This resulted in a set of three 819 molecular knots that differ only in the length of the alkyl chains in the loop (1 is 192 atoms long, 2 is 216 atoms long, and 3 is 240 atoms long, a 25% variation in strand length involving only the flexible regions). We probed the properties of the different-sized knots by 1H NMR spectrometry, mass spectrometry, UV spectroscopy, and circular dichroism, and used computational studies to help explain the role the increasing tightness of knotting plays in altering physical and chemical behavior.
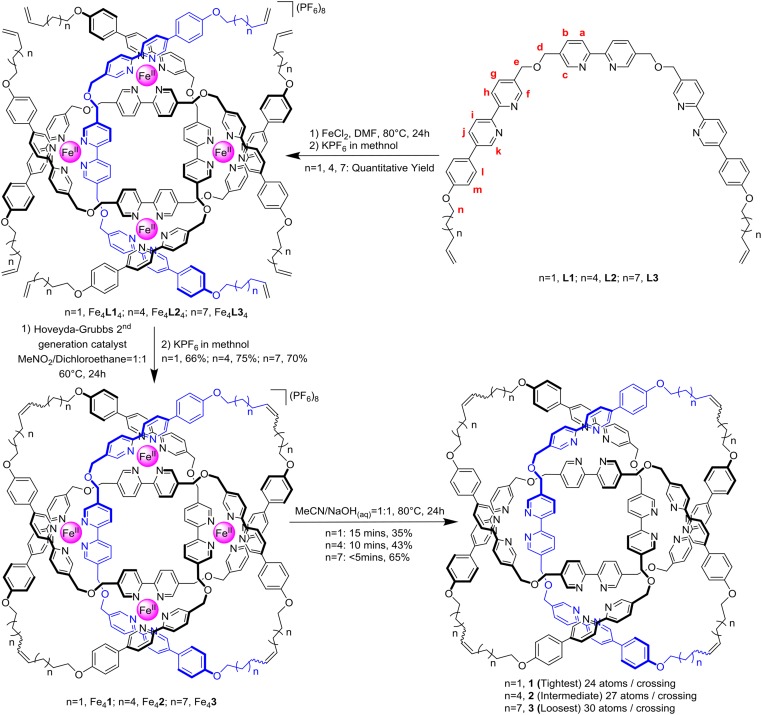
Fig. 1.
Synthesis of [Fe4Knot](PF6)8 (Knot = 1–3) and their subsequent demetallation to 819 knots 1–3.
Ligand strands L1–L3 bearing Tris(2,2′-bipyridine) motifs with different lengths of alkene-terminated alkyl chains were prepared by analogy to that previously used to prepare 1 (29). Treatment of the ligands with equimolar amounts of FeCl2, followed by ring-closing metathesis (30), gave the corresponding 819 knot complexes [Fe4Knot](PF6)8 (Knot = 1–3; Fig. 1) which were isolated and characterized by electrospray ionization mass spectrometry and 1H NMR spectroscopy (SI Appendix, Figs. S1–S8). The 1H NMR spectra of the three knotted complexes are essentially superimposable (SI Appendix, Figs. S14 and S15), other than the alkyl region due to the differences in chain length, indicating that metal coordination of the knotted ligands holds the three complexes in similar conformations. Subjecting the metallated knots to a 1:1 MeCN/NaOHaq (1 M) solution at 80 °C, followed by size-exclusion chromatography, afforded the corresponding demetallated knots 1–3 with different degrees of tightness (Fig. 1 and SI Appendix, Figs. S9–S12). The BCRs (11) of 1–3 are 24, 27, and 30, respectively. The diffusion coefficients (D) values of the three knots were measured by diffusion-ordered spectroscopy experiments; the relative effective hydrated radius of the knots increases by 8% from 1 to 2 and 16% from 2 to 3 in line with the 12.5% and 25% increase in the length of the flexible regions, respectively (SI Appendix, Figs. S19–S21). The optimized reaction times used in the demetallation process were 15 min for [Fe41](PF6)8 (resulting in a 35% yield of 1), 10 min for [Fe42](PF6)8 (43% yield of 2), and less than 5 min for [Fe43](PF6)8 (65% yield of 3). The differences in reactivity (yield and reaction time) can be rationalized by loosening of the knot giving the strand significantly greater flexibility, particularly after displacement of the first iron cation. This makes it easier for hydroxyl ions to access the remaining iron centers (31), decreasing the amount of the poorly soluble iron bipyridine hydroxide by-products (32) that reduce the yield of metal-free knot. The yields of the demetallated 819 knots did not increase with longer reaction times.
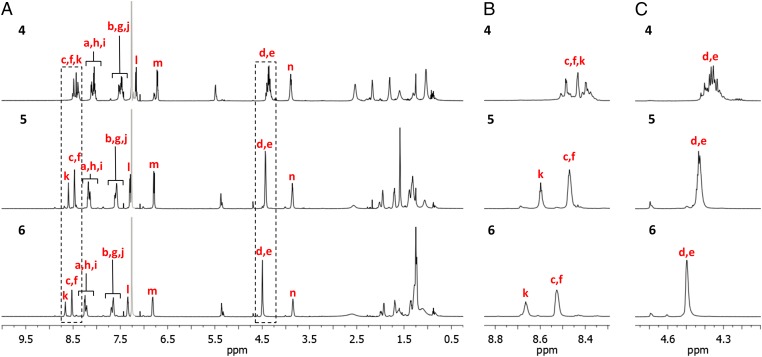
In contrast to the similar chemical environments observed for the protons of the metallated knots, the 1H NMR spectra of 1–3 differ markedly from each other in several regions (Fig. 2). Methylene (CH2) groups Hd and He in the tightest knot, 1, appear as multiplets because the constricted chiral environment accentuates their diastereotopicity. With the loosening of the knot from 1 to 2, the signals of Hd and He broaden, becoming a single broad signal (at 600 MHz in CDCl3) in 3 in line with the protons occupying less-constricted, less well-defined, environments (Fig. 2C). Variable-temperature 1H NMR spectra of 1–3 show little change over a large temperature range (238–318 K), indicating that the variances in the 1H NMR spectra of the three knots are primarily due to the differences in tightness affecting conformation and not general dynamic phenomena (SI Appendix, Figs. S16–S18).
Fig. 2.
Partial 1H NMR spectra (600 MHz, CDCl3, 298 K) of 819 knots 1, 2, and 3; (A) region 0.25–10.0 ppm. (B) Expanded regions 8.3–8.8 ppm. (C) Expanded regions 4.1–4.7 ppm. Residual solvent peaks are shown in gray. The lettering corresponds to the proton labeling in Fig. 1.
The resonances of the aromatic protons in the looser knots, 2 and 3, shift to low field, their chemical shifts moving closer to those of the corresponding building blocks (L2 and L3). The shielding of Hd, He, Hf, and Hk, in particular, are intermediate between that of the corresponding protons in 1 and 3. Concomitantly, the resonances of most of the alkyl protons (e.g., Hn) move upfield. Both effects are consistent with a loss of π–π interactions in the tightly knotted structures and the rise of CH–π interactions between the alkyl protons and aromatic motifs in the looser knots (Fig. 2B and SI Appendix, Fig. S22 and Table S1). It suggests that the conformation of the tightest knot, 1, is stabilized by π–π stacking with the aromatic groups involved in the entangled region of the structure with the alkyl chains to the outside. In 2 and 3, the longer alkyl chains slip into the knotted region while the aromatic groups move to the periphery, thus generating fewer π–π interactions but more CH–π interactions. These observations provide experimental evidence in support of the migration of entanglements from rigid to flexible regions, behavior that has been predicted in simulations of knotted polymers (33, 34).
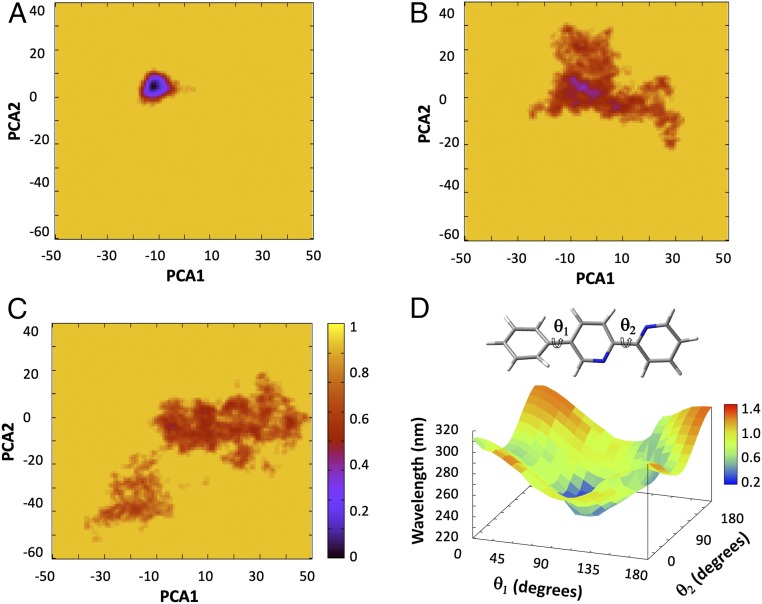
To help explain the experimental data, molecular-dynamics calculations were performed on 1–3. The starting geometries were based on the X-ray structure of the metallated knot [Fe41](PF6)7Cl (29), removing the iron cations and counteranions, and increasing the chain length for 2 and 3. A summary of the dynamics in terms of principal component analysis (PCA) maps is shown in Fig. 3 A–C. (For illustrative examples of populated conformations during the simulations, see SI Appendix, Figs. S32–S34.) The tightest knot 1 shows markedly different dynamics with respect to knots 2 and 3 and is locked into essentially a single conformation stabilized by strong π–π interactions that involve every aromatic ring (Fig. 3A and SI Appendix, Fig. S32). The knot of intermediate tightness, 2, populates a larger variety of conformations in which π–π interactions are limited (Fig. 3B and SI Appendix, Fig. S33), while the loosest knot, 3, has no particularly preferred conformation (Fig. 3C and SI Appendix, Fig. S34). The Tris(2,2′-bipyridine) units, the most rigid part of the structure, largely move out of the entangled region—and the alkyl chains, the more flexible region, move into it—in most of the thermally equilibrated conformations of the loosest knot, 3. This is consistent with the experimentally observed 1H NMR shifts and illustrates how local flexibility of the strand affects both conformation and the position of the entanglement. The results of both experiment and simulation indicate that the dynamic properties of the 819 knots are profoundly influenced by the tightness of the entanglements.
Fig. 3.
Normalized free energy surfaces, according to PCA of (A) knot 1. (B) Knot 2 and (C) knot 3. The x and y axis are displacement vectors spread over the entire system, i.e., how much each atom “moves.” They are calculated with respect to an average structure (physically meaningless) and can be thought of directions of flexibility. (D) TD-DFT (M06-2X/6–31G*) calculated four-dimensional plot of θ1 and θ2 together with the associated wavelength of excitation and the oscillator strength (in color scale of the phenyl-bipyridine fragment).
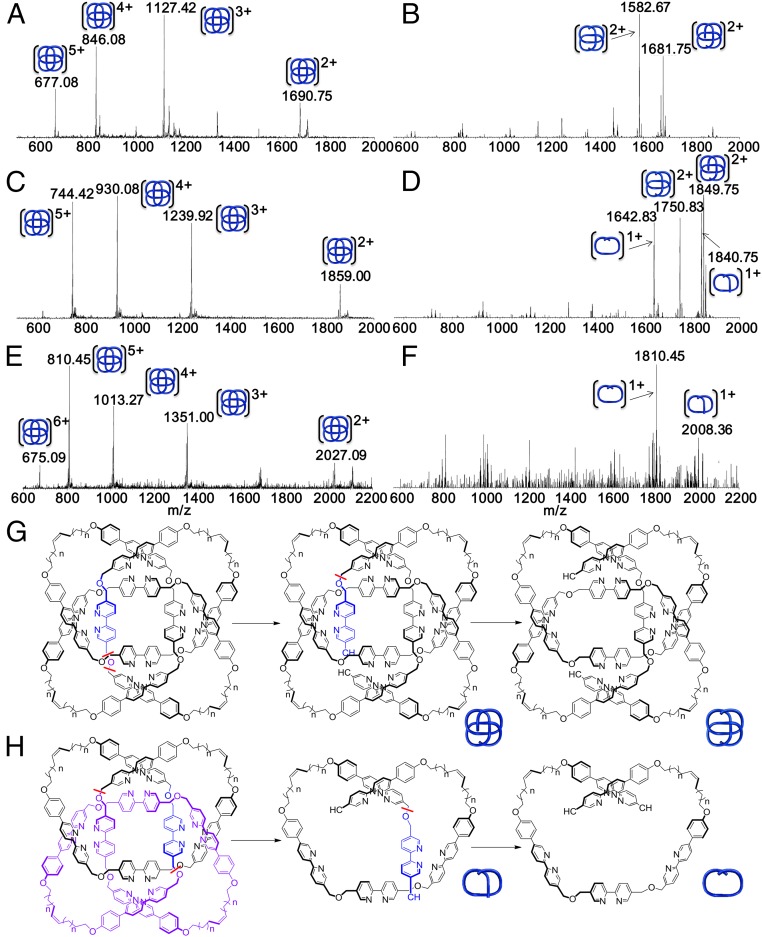
To evaluate the effect of knot tightness on covalent bond strengths, tandem mass spectrometry (MS-MS) experiments were conducted on the [M + 2H]2+ peak (Fig. 4 A, C, and E) of knots 1–3 activated by collision-induced dissociation (CID). This resulted in multiply charged ions with a loss of mass consistent with covalent bond scission and subsequent unraveling of the knotted strand (Fig. 4 B, D, and F). Upon increasing the normalized collision energy in 1-eV steps until bond cleavage occurred, the looser knots (2 and 3) required significantly higher energies (35 and 55 eV, respectively) to fragment than 1 (28 eV). For each knot scission always occurs at the carbon–oxygen bond between the central bipyridine and phenyl–bipyridine units, but the knots showed two distinct types of fragmentation pattern (type I, Fig. 4G and type II, Fig. 4H). For the tightest knot 1, fragmentation (loss of a water molecule; m/z = 1,681.75) is followed by loss of an adjacent central bipyridine unit (m/z = 1,582.67; Fig. 4B, type I). In contrast, the loosest knot 3 requires a minimum of 55 eV to fragment and directly forms two breakdown products that each contain half of the knot (m/z = 2,008.36 and 1,810.45; Fig. 4F, type II). Both types of fragmentation pattern are observed with knot 2 at 35 eV (Fig. 4D, m/z = 1,849.75 and 1,750.83 for type I and m/z = 1,840.75 and 1,642.83 for type II). Clearly knot tightness significantly affects covalent bond strength; the tighter the knot, the more easily some bonds can be broken. The experimental results are consistent with the simulations that suggest that tight knotting forces the adoption of conformations with strained bond lengths and angles.
Fig. 4.
Fragmentation of 819 knots 1–3 under CID-MS experiments. (A) CID-MS of knot 1. (B) MS-MS of [M+2H]2+ (m/z = 1,690.75) from knot 1, only type I fragmentation is observed. (C) CID-MS of knot 2. (D) MS-MS of [M+2H]2+ (m/z = 1859.00) from knot 2, both types of fragmentations are observed. (E) CID-MS of knot 3. (F) MS-MS of [M + 2H]2+ (m/z = 2,027.09) of knot 3, only type II fragmentation is observed. No fragment ions corresponding to macrocycles, which could arise from molecular links (e.g., a [2]catenane or Solomon link) upon fragmentation of one ring (17), was observed over a range of collision energies, further demonstrating that only knots are present. (G and H) Two different fragmentation pathways (type I, G; type II, H) for the 819 knots corresponding to the MS-MS results shown in B, D, and E; bond cleavage is indicated with a red wavy line, the residues lost in the first step are colored purple, and those lost in the second step are colored blue.
Wiberg bond indices analysis, as implemented in the Gaussian09 suite of programs (35) was conducted with the Minnesota 2006 hybrid meta exchange-correlation functional (M06-2X) (36) and Pople's basis set with polarization functions, 6-31G(d), on the global minimum energy structures of doubly charged 1 and 3 to calculate the bond order of the carbon–oxygen bond between the central bipyridine and phenyl–bipyridine units (Ce–O–Cd, Fig. 1). The calculations on the tightest knot, 1, show that one of these carbon–oxygen bonds is significantly weaker than others and is more likely to break in the CID-MS experiments (SI Appendix, Fig. S38). After cleavage, the resulting terminal oxygen atom can reorganize its electronic structure to allow loss of a water molecule (Fig. 4G). In the loosest knot, 3, the carbon–oxygen bonds all have similar bond orders that are higher than the weak C–O bond in 1. This can result in near-simultaneous cleavage of two C–O bonds at higher energy (SI Appendix, Fig. S38), to produce the two halves of 3 observed experimentally (Fig. 4H).
The effect of knot tightness on the spectral properties of 1–3 was also investigated. The UV-vis spectra of knots 1 and 2 are similar, with a slight decrease in absorption at λmax = 306 nm for 2. However, the absorption of the loosest knot, 3, decreases significantly and is associated with a 10-nm red shift (SI Appendix, Fig. S25). Simulated spectra, generated from time-dependent density functional theoretical (37) calculations at the M06-2X/6–31G(d) level of theory, show that the electronic spectra of the knots are highly sensitive to the two torsional angles, θ1 and θ2, within the phenyl–bipyridine moieties (Fig. 3D and SI Appendix, Figs. S35–S37). The observed red shift of knot 3 is due to the variation of θ1 and θ2 as the increased flexibility of the loose knot allows the chromophores to populate more conjugated, flatter, conformations.
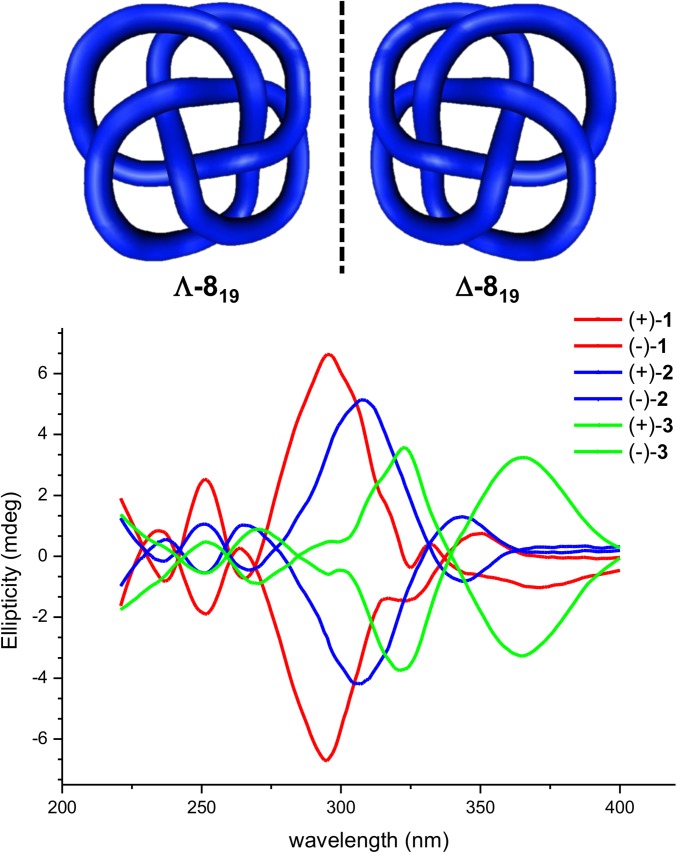
An 819 knot is intrinsically chiral by virtue of its topology. The enantiomers of 1–3 were isolated by chiral high-performance liquid chromatography (HPLC) and analyzed by CD spectroscopy (Fig. 5 and SI Appendix, Figs. S23 and S24). Each pair of knot enantiomers gives CD spectra of equal but opposite shape and sign (38, 39). As the knots become looser from 1 to 3, the change in the environment around the chromophores results in a red shift of the CD signal in the spectra of the respective molecules. The simulations and 1H NMR experiments suggest that the bipyridine and phenolic ethers are locked in a chiral conformation in the tightest knot, 1, which features strong π–π interactions. However, the looser knots have a variety of conformations that average out to give a weaker CD response. The red shift is a consequence of the more conjugated, flat, conformations of the chromophores in the looser knots. The dynamics and conformation of the knotted structures are clearly significantly affected by tightness, with the expression of chirality tunable by tightening or loosening the entanglement.
Fig. 5.
CD spectra of each enantiomer of molecular 819 knots 1, 2, and 3.
Analysis of the molecular-dynamics simulations suggests that the property trends observed for 819 knots 1–3 are not a specific consequence of the particular aromatic-ring–based backbones of their structures. Atomic fluctuations measure the flexibility of (large) molecular systems. They are connected to the temperature B factor (40) that can be measured experimentally and is usually reported together with a protein structure in the Protein Data Bank. In the molecular-dynamics simulations, the size of the atomic fluctuations of the aromatic rings, the aliphatic chains, and the entire knot were found to be a function of tightness (Table 1): the tighter the knot, the smaller the fluctuations. The trends are broadly similar for each of the three structural elements monitored (aromatics, aliphatics, and the whole molecule).
Table 1.
Atomic fluctuations, Δ (Å2), aromatic fragment interactions, Efrag (kcal/mol), and strain energy of the alkyl chain, Estrain (kcal/mol), of the three knots (1–3)
| Knot | Δaromatic rings | Δentire knot | Δalkyl chain | Efrag | Estrain |
| 1 | 2.26 | 2.31 | 2.66 | −48.3 | 53.8 |
| 2 | 4.95 | 5.39 | 6.86 | −40.1 | 160.0 |
| 3 | 7.43 | 8.42 | 10.77 | −23.6 | 260.1 |
The structures of snapshots of the molecular dynamics that successfully simulated the experimental data were used to investigate the interactions between the aromatic fragments and the strain energies of the alkyl chains in the three knots (Table 1). The calculations were performed at the M06-2X/6-31G(d) level of theory. For the interactions between aromatic rings, the correction for basis-set superposition error was determined using the counterpoise method (41). In order of decreasing knot tightness (1 to 2 to 3), the average interaction energy between aromatic fragments reduces from −48.3 to −40.1 to −23.6 kcal/mol (Table 1). The variation reflects the greater strand dynamics as the knots become looser. In the same series the average strain energies of the alkyl chains increase from 53.8, 160.0, and 260.1 kcal/mol, as more methylene groups are added to each chain, forced by the knot topology to adopt strained dihedral angles and CH–CH steric clashes. Aromatic stacking interactions do not generate favored conformations in the more flexible knots, but rather form to alleviate strain when the tightness of knotting forces the molecule to become more compact. The stacking of aromatic rings is a consequence of knot tightness rather than the driving force behind its conformation/structure. The aromatic rings in the Tris(2,2′-bipyridine) ligand strands are necessary for the knot synthesis and, in some cases (1H NMR, CD spectra), provide useful probes for the experimental detection of behavior. If π-stacking was the dominating interaction that determined their conformation, the knots would not be the highly dynamic systems that experiments and simulations show them to be. It therefore seems likely that the trends observed for 1–3 are not directly related to their particular molecular make-up but will more generally reflect aspects of behavior regarding knot tightness at the nanoscale.
Conclusions
A series of molecular 819 knots that differ only in the length of alkyl chains that connect rigid aromatic regions enable the investigation of the influence of knot tightness on a range of physical and chemical properties, allowing experimental observations to be rationalized through computational simulations. The tightness of molecular 819 knots affects reactivity (the rate of demetallation of knotted ligands and collision energies required for bond breaking), conformation (rigid regions preferring to be outside the region of entanglement in looser structures), and the expression of topological chirality (manifest in CD and 1H NMR spectra). These results provide some experimental evidence of the effects of tightening knots at the molecular level, which should prove useful in understanding the role of knotting in entangled polymers and in the design of future knotted and interwoven nanomaterials (42–45).
Materials and Methods
Synthesis.
Molecular knots 2 and 3 were prepared by modifying the braiding strategy previously used (29) to assemble knot 1 (Fig. 1). Subjecting each metallated knot ([Fe41](PF6)7Cl, [Fe42](PF6)7Cl, or [Fe43](PF6)7Cl) to a 1:1 MeCN/NaOHaq (1 M) solution at 80 °C, followed by size-exclusion chromatography, afforded the corresponding demetallated knots 1–3, which were characterized by NMR and mass spectrometry. The enantiomers of 1–3 were isolated by chiral HPLC and analyzed by CD spectroscopy.
Molecular-Dynamics Simulations.
Molecular-dynamics simulations were carried out with the AMBER 12.0 suite of programs. The knots were parametrized using the general AMBER force field and the standard restrained electrostatic potential procedure carried out to assign charges to atoms by Antechamber. The crystallographic structure of metallated knot [Fe41]8+ was used as the starting structure for 1 and as a template for 2 and 3.
Supplementary Material
Acknowledgments
We thank the China 1000 Talents Plan, East China Normal University, the Engineering and Physical Sciences Research Council (EP/P027067/1) and the European Research Council, Advanced Grant 339019 for funding, and the University of Manchester for a President’s Doctoral Scholar Award (to L.Z.). D.A.L. is a China 1000 Talents “Topnotch Talent” Professor and Royal Society Research Professor.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1815570116/-/DCSupplemental.
References
- 1.Sułkowska JI, Rawdon EJ, Millett KC, Onuchic JN, Stasiak A. Conservation of complex knotting and slipknotting patterns in proteins. Proc Natl Acad Sci USA. 2012;109:E1715–E1723. doi: 10.1073/pnas.1205918109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wasserman SA, Cozzarelli NR. Biochemical topology: Applications to DNA recombination and replication. Science. 1986;232:951–960. doi: 10.1126/science.3010458. [DOI] [PubMed] [Google Scholar]
- 3.Tubiana L, Rosa A, Fragiacomo F, Micheletti C. Spontaneous knotting and unknotting of flexible linear polymers: Equilibrium and kinetic aspects. Macromolecules. 2013;46:3669–3678. [Google Scholar]
- 4.Dzubiella J. Sequence-specific size, structure, and stability of tight protein knots. Biophys J. 2009;96:831–839. doi: 10.1016/j.bpj.2008.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sułkowska JI, Sułkowski P, Szymczak P, Cieplak M. Stabilizing effect of knots on proteins. Proc Natl Acad Sci USA. 2008;105:19714–19719. doi: 10.1073/pnas.0805468105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Saitta AM, Soper PD, Wasserman E, Klein ML. Influence of a knot on the strength of a polymer strand. Nature. 1999;399:46–48. doi: 10.1038/19935. [DOI] [PubMed] [Google Scholar]
- 7.Caraglio M, Micheletti C, Orlandini E. Stretching response of knotted and unknotted polymer chains. Phys Rev Lett. 2015;115:188301. doi: 10.1103/PhysRevLett.115.188301. [DOI] [PubMed] [Google Scholar]
- 8.Ziegler F, et al. Knotting and unknotting of a protein in single molecule experiments. Proc Natl Acad Sci USA. 2016;113:7533–7538. doi: 10.1073/pnas.1600614113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alexander JW, Briggs GB. On types of knotted curves. Ann Math. 1926;28:562–586. [Google Scholar]
- 10.Bates A. DNA Topology. Oxford Univ Press; Oxford: 2005. pp. 36–37. [Google Scholar]
- 11.Fenlon EE. Open problems in chemical topology. Eur J Org Chem. 2008;2008:5023–5035. [Google Scholar]
- 12.Gonzalez O, Maddocks JH. Global curvature, thickness, and the ideal shapes of knots. Proc Natl Acad Sci USA. 1999;96:4769–4773. doi: 10.1073/pnas.96.9.4769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Orlandini E, Polles G, Marenduzzo D, Micheletti C. Self-assembly of knots and links. J Stat Mech. 2017;26:034003. [Google Scholar]
- 14.Orlandini E, Whittington SG. Statistical topology of closed curves: Some applications in polymer physics. Rev Mod Phys. 2007;79:611–642. [Google Scholar]
- 15.Dai L, van der Maarel JRC, Doyle PS. Effects of nanoslit confinement on the knotting probability of circular DNA. ACS Macro Lett. 2012;1:732–736. doi: 10.1021/mz3001622. [DOI] [PubMed] [Google Scholar]
- 16.Baiesi M, Orlandini E, Whittington SG. Interplay between writhe and knotting for swollen and compact polymers. J Chem Phys. 2009;131:154902. doi: 10.1063/1.3244643. [DOI] [PubMed] [Google Scholar]
- 17.Fielden SDP, Leigh DA, Woltering SL. Molecular knots. Angew Chem Int Ed Engl. 2017;56:11166–11194. doi: 10.1002/anie.201702531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lim NCH, Jackson SE. Molecular knots in biology and chemistry. J Phys Condens Matter. 2015;27:354101. doi: 10.1088/0953-8984/27/35/354101. [DOI] [PubMed] [Google Scholar]
- 19.Dommersnes PG, Kantor Y, Kardar M. Knots in charged polymers. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;66:031802. doi: 10.1103/PhysRevE.66.031802. [DOI] [PubMed] [Google Scholar]
- 20.Metzler R, Hanke A, Dommersnes PG, Kantor Y, Kardar M. Equilibrium shapes of flat knots. Phys Rev Lett. 2002;88:188101. doi: 10.1103/PhysRevLett.88.188101. [DOI] [PubMed] [Google Scholar]
- 21.Zheng X, Vologodskii A. Tightness of knots in a polymer chain. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;81:041806. doi: 10.1103/PhysRevE.81.041806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Arteca GA. Externally steered relaxation of tight polyethylene tangles with different initial knot topologies. Theor Chem Acc. 2007;118:549–556. [Google Scholar]
- 23.Mansfield ML. Tight knots in polymers. Macromolecules. 1998;31:4030–4032. [Google Scholar]
- 24.Cantarella J, Kusner RB, Sullivan JM. Tight knot values deviate from linear relations. Nature. 1998;392:237–238. [Google Scholar]
- 25.Katritch V, Olson WK, Vologodskii A, Dubochet J, Stasiak A. Tightness of random knotting. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 2000;61:5545–5549. doi: 10.1103/physreve.61.5545. [DOI] [PubMed] [Google Scholar]
- 26.King NP, Yeates EO, Yeates TO. Identification of rare slipknots in proteins and their implications for stability and folding. J Mol Biol. 2007;373:153–166. doi: 10.1016/j.jmb.2007.07.042. [DOI] [PubMed] [Google Scholar]
- 27.Arai Y, et al. Tying a molecular knot with optical tweezers. Nature. 1999;399:446–448. doi: 10.1038/20894. [DOI] [PubMed] [Google Scholar]
- 28.Orlandini E, Polles G, Marenduzzo D, Micheletti C. Self-assembly of knots and links. J Stat Mech Theory Exp. 2017;2017:034003. [Google Scholar]
- 29.Danon JJ, et al. Braiding a molecular knot with eight crossings. Science. 2017;355:159–162. doi: 10.1126/science.aal1619. [DOI] [PubMed] [Google Scholar]
- 30.Garber SB, Kingsbury JS, Gray BL, Hoveyda AH. Efficient and recyclable monomeric and dendritic Ru-based metathesis catalysts. J Am Chem Soc. 2000;122:8168–8179. [Google Scholar]
- 31.Zhang L, et al. Stereoselective synthesis of a composite knot with nine crossings. Nat Chem. 2018;10:1083–1088. doi: 10.1038/s41557-018-0124-6. [DOI] [PubMed] [Google Scholar]
- 32.Meyer M, Albrecht-Gary A-M, Dietrich-Buchecker CO, Sauvage J-P. Dicopper(I) trefoil knots: Topological and structural effects on the demetalation rates and mechanism. J Am Chem Soc. 1997;119:4599–4607. [Google Scholar]
- 33.Orlandini E, Baiesi M, Zonta F. How local flexibility affects knot positioning in ring polymers. Macromolecules. 2016;49:4656–4662. [Google Scholar]
- 34.Poier P, Likos CN, Matthews R. Influence of rigidity and knot complexity on the knotting of confined polymers. Macromolecules. 2014;47:3394–3400. doi: 10.1021/ma5006414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Frisch MJ, et al. Gaussian 09. Gaussian, Inc.; Wallingford, CT: 2009. [Google Scholar]
- 36.Zhao Y, Truhlar DG. Density functionals with broad applicability in chemistry. Acc Chem Res. 2008;41:157–167. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
- 37.Adamo C, Jacquemin D. The calculations of excited-state properties with time-dependent density functional theory. Chem Soc Rev. 2013;42:845–856. doi: 10.1039/c2cs35394f. [DOI] [PubMed] [Google Scholar]
- 38.Rapenne G, Dietrich-Buchecker C, Sauvage J-P. Resolution of a molecular trefoil knot. J Am Chem Soc. 1996;118:10932–10933. [Google Scholar]
- 39.Vögtle F, et al. Novel amide-based molecular knots: Complete enantiomeric separation, chiroptical properties, and absolute configuration. Angew Chem Int Ed. 2001;40:2468–2471. doi: 10.1002/1521-3773(20010702)40:13<2468::AID-ANIE2468>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 40.Frauenfelder H, Petsko GA, Tsernoglou D. Temperature-dependent X-ray diffraction as a probe of protein structural dynamics. Nature. 1979;280:558–563. doi: 10.1038/280558a0. [DOI] [PubMed] [Google Scholar]
- 41.Boys SF, Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol Phys. 1970;19:553–566. [Google Scholar]
- 42.Liu Y, et al. Weaving of organic threads into a crystalline covalent organic framework. Science. 2016;351:365–369. doi: 10.1126/science.aad4011. [DOI] [PubMed] [Google Scholar]
- 43.Marcos V, et al. Allosteric initiation and regulation of catalysis with a molecular knot. Science. 2016;352:1555–1559. doi: 10.1126/science.aaf3673. [DOI] [PubMed] [Google Scholar]
- 44.Lewandowska U, et al. A triaxial supramolecular weave. Nat Chem. 2017;9:1068–1072. doi: 10.1038/nchem.2823. [DOI] [PubMed] [Google Scholar]
- 45.Wang Z, et al. Molecular weaving via surface-templated epitaxy of crystalline coordination networks. Nat Commun. 2017;8:14442. doi: 10.1038/ncomms14442. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.