Volumetric quantitative optical coherence elastography with an iterative inversion method

Abstract

It is widely accepted that accurate mechanical properties of three-dimensional soft tissues and cellular samples are not available on the microscale. Current methods based on optical coherence elastography can measure displacements at the necessary resolution, and over the volumes required for this task. However, in converting this data to maps of elastic properties, they often impose assumptions regarding homogeneity in stress or elastic properties that are violated in most realistic scenarios. Here, we introduce novel, rigorous, and computationally efficient inverse problem techniques that do not make these assumptions, to realize quantitative volumetric elasticity imaging on the microscale. Specifically, we iteratively solve the three-dimensional elasticity inverse problem using displacement maps obtained from compression optical coherence elastography. This is made computationally feasible with adaptive mesh refinement and domain decomposition methods. By employing a transparent, compliant surface layer with known shear modulus as a reference for the measurement, absolute shear modulus values are produced within a millimeter-scale sample volume. We demonstrate the method on phantoms, on a breast cancer sample ex vivo, and on human skin in vivo. Quantitative elastography on this length scale will find wide application in cell biology, tissue engineering and medicine.

1. Introduction

Measuring the mechanical properties of a biological sample, from the sub-cellular [1] to the whole-organ scale [2], has proven useful in a variety of ways. In the field of cell mechanics, where the emphasis is on the cellular and sub-cellular levels, such data assist in revealing new knowledge on how cells migrate and differentiate, and on how diseases emerge [3]. At these scales, mechanical properties and forces are measured with a variety of methods, including atomic force microscopy, micropipette aspiration, optical tweezers and traction force microscopy [4]. In the field of medicine, where the emphasis is on the scale of whole organs, elastography has become a mainstream component of ultrasonography instruments [5] and is utilized in a range of clinical applications that include improved detection, diagnosis and staging of disease [6]. Elastography is also rapidly becoming a part of magnetic resonance imaging instruments [7]. However, there is a relative dearth of methods that can image the mechanics of aggregates of cells or regions of tissue, in the range from tens of micrometers to tens of millimeters. Such requirements, which are necessary to migrate research in cell mechanics to a 3D in vivo or in situ context and reconcile it with whole tissue pathophysiology, exceed the range of most cellular-scale methods, and generally exceed the resolution capacity of non-optical methods.

Optical elastography methods have recently made great strides in mapping the microscale mechanical properties of tissue [8]. Amongst these methods, optical coherence elastography (OCE), in particular, has experienced great advances [9] and is intrinsically suited to mapping mechanical properties over this intermediate range. Quantitative elastography methods, i.e., those seeking to retrieve an absolute mechanical property, typically operate by imparting a load onto the sample, and relating the resulting displacement to an elastic modulus by solving an inverse problem [10]. The inversion from displacement to elastic modulus should be consistent with physical principles that govern the deformation of a three-dimensional elastic continuum with spatially varying mechanical properties, but most current approaches in OCE do not comply with this requirement [9,11]. Instead, current approaches assume some form of local homogeneity for the material distribution, and/or uniformity in the stress state. In this manuscript, we describe a method that does not make these assumptions, but leads to a challenging inverse problem in OCE. Previously, we have demonstrated such a method in two dimensions, using the assumption of plain strain [12]. However, the direct extension of such a method to three dimensions is not tractable, due to the large number of optimization parameters. We demonstrate here, for the first time, its iterative solution in three dimensions. This solution is made computationally feasible by using adjoint-based algorithms [13], developing adaptive meshing techniques that focus computational efforts in regions with most significant spatial variations, and domain decomposition techniques to analyze different sub-regions in parallel and independently of each other. We note that Khalil et al. [14,15] proposed a method within which local homogeneity is not assumed; instead the problem is simplified by using prior information about the spatial distribution of mechanical properties. For most problems, especially in in vivo and in situ settings, this prior information is not available.

In this paper, we demonstrate our method in the context of compression OCE [16–18], in which the whole field of view being imaged undergoes quasi-static compression, and phase-sensitive optical coherence tomography (OCT) is used to determine the resulting displacement field along the optical axis. We insert a transparent, compliant layer with known shear modulus between the sample and the compressor [18], and use this knowledge, along with the measured axial displacement in the layer and the sample, to recover the quantitative shear modulus map. The combined experimental and computational method to recover shear modulus distribution is applied to tissue-mimicking phantoms, and to ex vivo and in vivo human tissue samples. The tissue-mimicking phantom study highlights the ability of this method to recover accurate, absolute quantitative estimates and spatial variations of shear modulus. The ex vivo human tissue study, performed on a breast specimen containing invasive ductal carcinoma, demonstrates its capability to visualize cancerous tissue and its robustness in heterogeneous materials. Finally, the in vivo study, which is performed on human skin, points to the applicability of this method in resolving small, localized features. Overall, we demonstrate an important advance towards the accurate determination of the elasticity of soft tissue with micrometer-scale resolution over millimeter-scale regions.

2. Methods

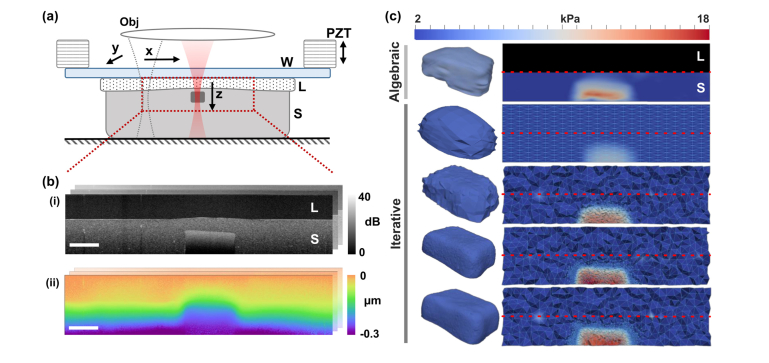
In this section, we first describe the overall approach to generating quantitative volumetric images of mechanical properties and, thereafter, we describe each component of this approach in detail. In our approach, the whole sample volume to be imaged and the transparent, compliant layer are subjected to microscale, quasi-static compression [18]. Figure 1(a) shows the imaging setup of the system. The sample (in this case, a silicone phantom with a stiff inclusion embedded in a soft surrounding material, described in detail in Section 2.5) and the layer are pre-compressed between a rigid back-plate and a glass window. A piezoelectric ring actuator provides the loading synchronized with the OCT acquisition, as illustrated in Fig. 1(b). OCT is used to image the sample structure, with 5-20 µm resolution (see Section 2.1) over 10 mm lateral fields of view and 1-2 mm penetration depth in turbid tissue, as well as the axial (relative to the imaging beam) displacement between compression steps with nanometer-scale sensitivity (see Section 2.1). The displacement field and the known shear modulus in the layer are inputs to the inversion method, resulting in an estimate of the local shear modulus throughout the imaged sample volume. Figure 1(c) shows such a reconstruction of the inclusion phantom, demonstrating four steps of adaptive mesh refinement. We begin by solving the inverse problem on a uniform coarse mesh, which is selectively refined in regions of high shear modulus gradient in the subsequent step. This process is repeated until the smallest mesh elements anywhere in the reconstruction domain, as indicated by the triangular faces in Fig. 1(c), are as small as the voxel size over which the displacement data is obtained. In the top panel of Fig. 1(c), we also show a reconstruction from a previously published inversion method, which relies on the assumption of uniaxial and uniform stress (method outlined in ref [18]. and Section 2.3), and is referred to here as the algebraic method. The improvement in accuracy afforded by the iterative method can be seen by comparing the modulus image and the thresholded volume for the iterative method (bottom panel in Fig. 1(c)) with their counterparts for the algebraic method (top panel in Fig. 1(c)), and using the OCT image (Fig. 1(b)) as a reference.

Fig. 1.

(a) Imaging set up of compression OCE, illustrating a sample (S) with a stiff inclusion and a transparent, compliant layer (L) compressed between a rigid back-plate and a window (W). OCE is illustrated by a tomographic scanning of a beam, focused by an objective lens (Obj). The scanning is synchronized with microscale loading and unloading by a piezoelectric actuator (PZT). The field of view is outlined by a red dashed line. (b) Cross-sectional images of sample structure (i), and axial (z) displacement (ii), measured by OCE. Scale bar is 500 µm. (c) Reconstructed maps of shear modulus using the iterative inversion method, compared to the algebraic method in the top panel, illustrating steps of adaptive mesh refinement (top to bottom). The compliant layer is masked out in blank in the algebraic reconstruction. Cross-sectional slices are shown on the right, where for the iterative method, the nodes and the edges of the finite element mesh are marked in light blue. The interface between the compliant layer and the sample is marked by a red dotted line. Thresholded (by shear modulus) reconstructions that pick out the stiff inclusion are on the left, showing an increasing resolution in each refinement step.

2.1 OCE hardware (OCT system and mechanical loading)

OCE data was acquired with two systems, one for the phantom and ex vivo samples and one for the in vivo data, discussed here in turn. For the phantom and ex vivo samples, OCE was performed using a fiber-based Fourier-domain OCT system operating at a center wavelength of 835 nm and a 3-dB bandwidth of 50 nm. The axial and lateral resolution were measured to be 7.8 μm (in air) and 11 μm, respectively. For the skin data, OCE was performed using a fiber-based Fourier-domain OCT system operating at a center wavelength of 1300 nm and a 3-dB bandwidth of 170 nm. The axial and lateral resolution were measured to be 5.5 μm (in air) and 20 μm, respectively. The displacement sensitivity for both systems was measured to be <2.2 nm.

Prior to OCE acquisition, a compliant layer was placed on top of the sample. The imaging probe, consisting of a glass window attached to a piezoelectric actuator (PZT), was used to preload the layer and the sample, such that complete contact was achieved between the window, layer and sample surface within the OCT field of view. Further, the preload was used to ensure that the majority of the sample was under compressive strain. This preload was in the range 5–10% in the phantoms and 10–20% in the tissues.

After the initial preload, the PZT was used to provide sequential step-wise loading and unloading on the scale of a few micrometers. OCE acquisition was synchronized with the loading, and cross-sectional data (B-scans) were captured in each location in the field of view, sequentially, in the loaded and unloaded positions, assembling volumetric data. For the breast tumor, four acquisitions in multiple lateral locations were stitched together to obtain a larger field of view.

2.2 Displacement estimation

We denote an OCT A-scan as $I(z)=a(z)\exp (\iota \varphi (z))$, where $I(z)$ is the complex-valued intensity associated with the pixel at depth z. Displacement data is obtained by acquiring two A-scans, one denoted $I^0(z)=a^0(z)\exp (\iota {\varphi }^0(z))$, with the sample experiencing a preload and another denoted $I^{\downarrow }(z)=a^{\downarrow }(z)\exp (\iota {\varphi }^{\downarrow }(z))$, with the sample experiencing additional microscale mechanical loading. The axial displacement component in response to mechanical loading is then found according to $u(z)=\lambda ({\varphi }^{\downarrow }(z)-{\varphi }^0(z))/(4\pi n)$, where λ is the mean wavelength of the OCT system and n is the refractive index of the sample (assumed to be 1.4).

2.3 Algebraic method

The algebraic method for solving the inverse elasticity problem in compression OCE operates under the assumption of uniform and uniaxial compression. It was proposed and described in detail by Kennedy et al. [18], and we describe it briefly here. Under the assumption of uniaxial compression, shear modulus is given as: $\mu =\sigma /3\epsilon$, where σ is the axial stress, and ε is the axial strain. ε is evaluated from the gradient of displacement using a weighted least mean square estimator [19]; σ is estimated from the strain of the compliant layer, and its well-characterized shear modulus at the particular preload. The stress is assumed to propagate uniformly in depth. The shear modulus becomes: $\mu (x,y,z)={\mu }_c(x,y){\epsilon }_c(x,y)/\epsilon (x,y,z)$, where ${\mu }_c(x,y)$ is the tangent shear modulus and ${\epsilon }_c(x,y)$ is the strain of the compliant layer. Here, (x, y, z) denote the lateral and axial coordinates.

2.4 Inverse problem solution

We partition the domain of interest, Ω, into the volume occupied by the compliant layer, ${\Omega }_c$, and the volume occupied by the sample, ${\Omega }_s$, and let $u(x,y,z)$ denote the axial component of measured displacement. We model the compliant layer and the sample as incompressible elastic materials, with the stress tensor given by $\sigma =-pI+2\mu \epsilon$, where p is the pressure, I is the identity tensor, μ is the shear modulus, and ε is the strain tensor. Within the compliant layer, we measure the average axial strain through the thickness, ${\epsilon }_c(x,y)$, that is applied to ensure proper contact. This, in conjunction with the knowledge of the elastic behavior of the calibration material [18], allows us to calculate the tangent shear modulus, ${\mu }_c(x,y)$, within the compliant layer, at the particular preload.

The inverse problem we wish to solve is: given u and ${\mu }_c$, determine the spatial distribution of the shear modulus, $\mu (x,y,z)$, in the tissue. This problem is supplemented by the constraint that the equations of equilibrium must be satisfied, that is $\nabla \cdot \sigma =0$. We solve this problem as a minimization problem, where we seek to find the distribution μ that minimizes the functional [20]:

$$\pi ={\int }_{\Omega }T{(u-\tilde{u})}^{2}d\Omega +\alpha {\int }_{\Omega }\sqrt{{\left|\nabla \mu \right|}^2+c^2}d\Omega \cdot$$ (1)

In the equation above, the first term represents the data mismatch and the second term represents regularization. In the data mismatch term, $\tilde{u}$ is the axial component of the predicted displacement field, which is constrained to satisfy the equations of equilibrium for a linear, incompressible elastic solid, and T is a spatially varying weighting function that accounts for spatial dependence of noise in the measured displacement. The regularization term, which is of the total variation (TV) type, addresses the ill-posed nature of the inverse problem and penalizes large variations in the recovered shear modulus. It does so without regard to the steepness of the slope of these variations and is, therefore, ideally suited for recovering the shear modulus when working with sharp features; like the presence of a stiff tumor within soft glandular tissue. In this term, α is the regularization parameter, and c is another parameter that ensures that this term has continuous derivatives (with respect to μ) when $\nabla \mu =0$.

We note that the shear modulus, μ, influences the data mismatch term indirectly via the predicted displacement, $\tilde{u}$, since the spatial distribution of μ determines $\tilde{u}$ through the solution of the equations of equilibrium. Any change in μ leads to a change in $\tilde{u}$, which changes the data mismatch term. The goal is to find the distribution of μ that minimizes the sum of the mismatch and the regularization terms. This is accomplished by representing both μ and $\tilde{u}$ using the standard finite element basis functions, and then using a gradient-based quasi-Newton algorithm to solve the minimization problem Eq. (1). The gradient vector, whose components represent the change in π due to change in the value of μ at a finite element vertex, is determined by solving the forward problem (equations of equilibrium) and an adjoint problem. At every iteration of the quasi-Newton algorithm, given the current estimate for the shear modulus distribution, the following tasks are performed: (1) A forward elasticity problem with the boundary conditions derived from the measured displacement is solved to generate the predicted displacement field; (2) An adjoint elasticity problem, which is driven by the difference between the measured and predicted displacement fields, is solved to determine the adjoint displacement field; and (3) Using the forward and adjoint displacement fields, the gradient vector is determined and supplied to the quasi-Newton method, which then returns with an improved estimate for the shear modulus field. These steps are repeated until convergence, which is obtained when the gradient vector is smaller than a specified tolerance, or when the change of the displacement mismatch over the last five iterations is smaller than a specified tolerance. We note that while this method is relatively new to OCE, it has been used quite extensively in ultrasound based elastography [13,20,27].

The algorithm described above is efficient; however, its cost can become prohibitive when solving problems in 3D on a fine grid. For example, if we were to apply this algorithm to the problem of a tissue- mimicking phantom with a single inclusion (as in Fig. 1), we would solve for 31 million optimization variables, which is very challenging. To address this challenge, we have incorporated two novel approaches. First, when solving the inverse problem, we make use of adaptive spatial resolution. In particular, we first solve the inverse problem on a coarse grid. Thereafter, we define a mesh size field that is inversely proportional to the absolute value of the gradient of the recovered shear modulus. This is used to generate a new finite element mesh that has finer resolution wherever the shear modulus varies sharply. We repeat this step several times and arrive at a final mesh whose resolution is optimal for the problem at hand. We terminate the process of mesh modification when we arrive at a mesh where the group of smallest elements has a mesh size that is comparable to the pixel size for the displacement field. The final mesh is fine where the gradients in μ are large, and coarse in other places. This procedure is shown in Fig. 1(c), where four successive steps of mesh refinement and the corresponding shear modulus distributions are shown for the tissue phantom considered in Section 3.1. As we move from one step to another, the mesh clusters near the interface between inclusion and the background where the finer spatial resolution is most needed. This process is also illustrated in Visualization 1 ^{(1.7MB, mp4)} , where the evolution of the shear modulus distribution and the underlying mesh is captured for the breast tissue example described in Section 3.2.

The approach described above works well for problems with a large field of view and relatively few significant features. In cases where there are many features within the field of view, this approach will lead to a fine resolution everywhere and, therefore, a very large computational problem. In order to tackle these types of problems, we combine this approach with a domain decomposition method. In this approach, the overall problem is simultaneously solved on N distinct meshes. In each mesh, an adaptive strategy is applied to a smaller subdomain of the total volume, and a fixed, coarse mesh is used in the rest of the domain. The fact that the adaptive strategy is applied to a single subdomain in each problem allows us to focus on the features contained within that subdomain, and the fact that the region outside this subdomain is represented through a coarse discretization, allows us to account for the effect of the remainder of the region without expending large computational resources. Another advantage of this method is that it is “trivially parallelizable”; that is, each of the N problems described above can be solved independently of each other on separate processors or computers, with no communication. In this manuscript, this domain decomposition approach was applied to the in-vivo imaging of the skin presented in Section 3.3 and is described in Fig. 5 for N = 3 subdomains.

The algorithms described above were implemented within our in-house finite element code written in Fortran 90. All problems were solved on multi-processor machine with eight 2.3 GHz CPU cores and a total memory of 16 GB. For a typical 3D problem with around 50,000 grid points and 400 iterations of the inverse algorithm, our code takes around 20 hours of wall clock time with the majority of this time spent solving the linear systems at each iteration.

2.5 Construction and characterization of phantom

Tissue-mimicking phantoms and the compliant layers were fabricated from two-compound room-temperature vulcanizing silicone. Two compounds were used: Elastosil P7676 and Elastosil RT601 (Wacker Chemie AG, Munich, Germany). The optical properties were controlled through the addition of titanium dioxide particles of known size distribution. The refractive index of the silicones is 1.4 and 2.5 for the titanium dioxide [21]. The mechanical properties were controlled by changing the mixing ratio of the two components of the silicone (Parts A and B), and further varied by diluting the silicone parts with polydimethylsiloxane (PDMS) oil (AK50, Wacker Chemie AG, Munich, Germany). PDMS oil was also used to lubricate the samples to minimize friction in the experiments. Each composition is presented as Compound A:B:Oil (e.g., P7676 2:1:0.3). The phantom mixture was mixed and sonicated to ensure uniform distribution of constituents and scatterers, and was oven-cured at 80°C.

The compliant layers were fabricated from P7676 1:1:0 with no added scattering. The layers were fabricated to a 500-μm thickness. The bulk of the four-inclusion phantom, described in Section 3.1, was fabricated from P7676 1:1:0, and the inclusions were fabricated from (in order of descending modulus): RT601 5:1:0, RT601 10:1:10, RT601 10:1:30 and P7676 2:1:0.3. 1 g/L of titanium dioxide was added to the bulk and 2.5 g/L was added to the inclusions to provide optical contrast. Each inclusion material was fabricated independently and then manually cut into an approximately rectangular shape, and incorporated into the bulk during its curing process. Each inclusion was designed to be 6 × , 3 × , 1.5 × and 0.5 × the bulk stiffness, with actual values shown in Fig. 2(a). Mechanical properties of each material were independently characterized using uniaxial compression testing (Instron, Norwood, MA, USA).

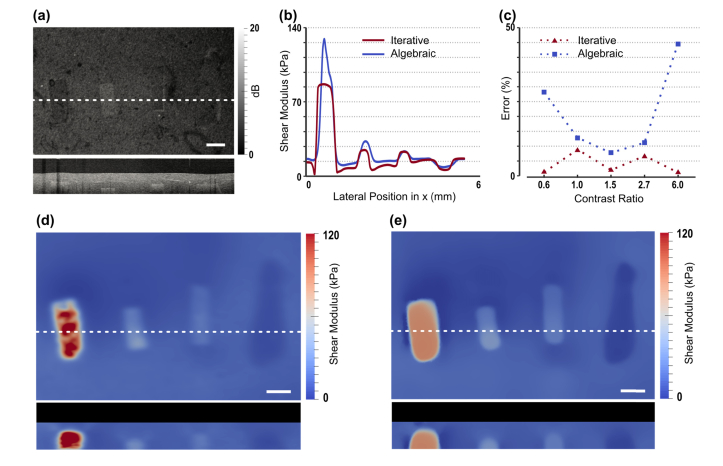
Fig. 2.

Tissue-mimicking phantoms with multiple inclusions of varying shear modulus. (a) OCT structural image, showing en face (upper) and cross-sectional views. (b) Plots of reconstructed shear modulus along the white-dashed line in (a) using the iterative and algebraic methods. (c) The error in the estimated shear modulus compared with experimentally measured values with respect to the contrast ratio in modulus between the inclusion and the surrounding material. (d) and (e) are corresponding maps of shear modulus (en face and cross-sectional views) reconstructed using the algebraic and iterative methods, respectively. Scale bars are 500 µm.

2.6 Preparation of breast tumor sample

Informed consent was obtained from patients and the study approved by the Human Research Ethics Committee of Royal Perth Hospital, Perth, Western Australia. The breast tumor sample was freshly excised and dissected for scanning, with approximate dimensions (x × y × z) of 2 × 2 × 1 cm³ [18]. The sample was kept hydrated in saline until imaging, which occurred within 3 hours of excision. After imaging, samples were fixed in 10% neutral buffered formalin, embedded in paraffin, sectioned and stained with haematoxylin and eosin (H&E) following the standard histopathology protocols used at Royal Perth Hospital. Interpretation of histology was performed by an experienced pathologist.

2.7 Preparation of skin sample

Skin imaging was approved by The University of Western Australia Human Research Ethics Committee. Imaging was performed on a 26-year-old Caucasian male. Prior to imaging, the fingertip was cleaned and lubricated with PDMS oil. The compliant layer was also lubricated and placed on top of the fingertip. The finger was placed on a cushion to minimize discomfort and movement. The imaging probe was then brought into contact with the fingertip, preloading it until there were no observable movement artifacts and bulk motion in the displacement images. It was also preloaded to ensure that there was complete contact, and that all layers were undergoing strain due to compression.

3. Results

3.1 Tissue-mimicking phantom

Figure 2 shows images of a phantom containing four inclusions spanning a range of shear moduli, including one that is less than that of the bulk matrix material. The raw OCT and shear modulus reconstructions are presented in both en face and B-scan images. The dashed line in the en face images indicates the position of the corresponding B-scan image. The primary purpose of this figure is to assess the performance of the reconstruction method on a sample whose mechanical properties have been measured through a standard compression test performed on a custom-built rig. We also compare the performance of the algebraic (Fig. 2(d)) and the iterative (Fig. 2(e)) methods. OCT images of the phantom (Fig. 2(a)) are presented in correspondence with the shear modulus images. Plots of the reconstructed shear modulus using the algebraic and iterative methods, along the white-dashed line on the en-face plane shown in Fig. 2(a), are shown in Fig. 2(b). Also, the percentage error in the average shear modulus for each inclusion and the surrounding material as a function of the modulus contrast (with respect to the background) is shown in Fig. 2(c) for the two methods. The mean and the standard deviation of the modulus within the inclusions and the background are reported in Table 1. These statistics were calculated by averaging the shear modulus over all mesh nodes within each region. The boundaries between the inclusion and the background were determined from the OCT volumes. The compression test was performed on separate samples that were created from the same mixture as the inclusions.

Table 1. Mean and standard deviation (SD) of the shear modulus values within the inclusions and the background as determined by the algebraic and iterative methods, and independent mechanical testing.

μ (kPa)	Experimental		Algebraic		Iterative
	Mean	SD	Mean	SD	Mean	SD
Inclusion 1	66	3	110	50	80	10
Inclusion 2	30	4	28	7	29	6
Inclusion 3	17	3	18	3	19	3
Inclusion 4	7	2	9	1	6	2
Background	11	2	13	4	12	3

Figure 2(c) demonstrates the accuracy of the iterative method in recovering the average shear modulus for all inclusions. The error is less than 10% for all inclusions, and the accuracy is retained for inclusions with large contrast ratios; whereas, the error in the algebraic method grows with increasing contrast. Since the algebraic method is based on the assumption of homogeneity, which is clearly violated in inclusions with large contrast, this degradation in accuracy is expected. The relationship of contrast ratio to accuracy has been identified as a fundamental limitation in elastography [22], which is overcome, in part, by the iterative method.

Beyond the accuracy of mean modulus values, the iterative method is accurate in mapping the spatial distribution of elasticity. A distinction between the algebraic (Fig. 2(d)) and iterative (Fig. 2(e)) methods is the homogeneity of the modulus retrieved for each inclusion. In particular, the modulus distributions arising from the iterative solution are significantly more homogeneous than the algebraic case, which is expected as the inclusions are fabricated from the same uniform material. This is clearly seen by plotting the modulus along the white-dashed line for the two methods (Fig. 2(b)). In Fig. 2, we also observe an artifact produced by the iterative method, in that it leads to “undershoots” in the predicted modulus in the background close to the interface with the stiffest (left-most) inclusion. Whilst it is difficult to specify the cause of this artifact without detailed simulations, it is likely that it results from the restricted lateral expansion of the soft material at the interface with the stiff inclusion. This issue could be addressed by supplying the iterative algorithm more information about the local deformation near the interface by measuring all three components of the displacement field in that region.

3.2 Ex vivo malignant breast tumor

Several studies have demonstrated that OCE can visualize tumor in excised human breast tissue [18,23–26]. Eventually, OCE may provide intraoperative feedback to surgeons to assist in the detection of tumor, which may reduce the number of re-excision surgeries required to remove residual tumor missed during the initial surgery. In Fig. 3, we demonstrate our technique’s ability to visualize tumor elasticity in human breast tissue acquired from a specimen containing invasive ductal carcinoma excised during a mastectomy procedure performed on a 60-year-old patient. Some of this data has previously been published based on the algebraic method [18]. The evolution of the shear modulus and the underlying mesh at various stages of the iterative inversion is shown in Visualization 1 ^{(1.7MB, mp4)} . The haematoxylin and eosin (H&E) histology image in Fig. 3 shows a large region of invasive tumor cells (T, stained purple) with local regions of benign ducts (D) in desmoplastic stroma. A region of stromal tissue (S), comprising a mixture of collagen, normal ductal structures, and microcystic structures, extends into the adipose tissue (A). The en face views in Figs. 3(c) and 3(d) show shear modulus images at a depth of 150 μm beyond the tissue-layer interface. The most striking difference between the images is the number of pixels with negative shear modulus value (marked by yellow) in the algebraic case, due largely to the problem of positive/tensile strain reported previously for OCE imaging of breast tissue [23]. In mechanically heterogeneous tissue, the algebraic method can result in strain in the direction opposite to the applied load, particularly at boundaries between tissue features. As the corresponding boundary stress is not considered by the algebraic method, this can lead to negative shear modulus values that are not physically meaningful. Furthermore, it is likely that these regions of non-physical shear modulus imply a reduced accuracy in the regions where the extracted modulus is physically plausible. In this case, depicted in Fig. 3(c), the pixels corresponding to regions of negative modulus are masked in yellow in the elastogram [18]. This problem is not present in the iterative method, where the shear modulus parameter is constrained to remain positive throughout the domain leading to a more accurate representation of the elasticity (Figs. 3(d)).

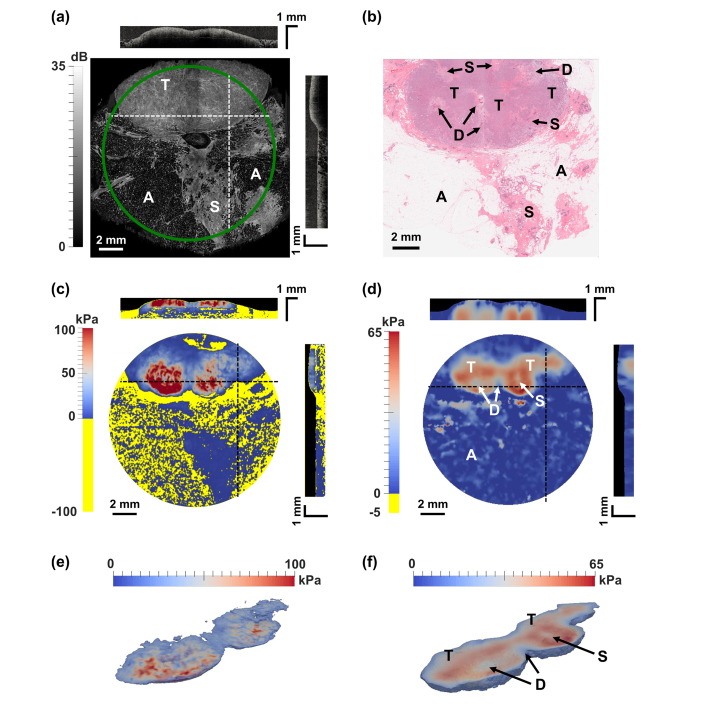
Fig. 3.

Ex vivo OCE images from a human breast specimen containing invasive ductal carcinoma. (a), (c), and (d) en face views of OCT, shear modulus from the algebraic method, and shear modulus from the iterative method, respectively, with cross-sectional views taken at the dashed lines. The compliant layers in the modulus images are masked in black. Negative modulus values produced by the algebraic method are indicated in yellow. (b) Corresponding H&E histology. (e) and (f) 3D segmentation of tumor mass from the shear modulus reconstruction of the algebraic and iterative inversion methods, respectively. A = adipose tissue, S = stroma, T = tumor, D = benign duct in desmoplastic stroma.

Although the elasticity is more faithfully estimated in adipose tissue using the iterative approach, the strongly fluctuating and low OCT signal typical of adipose tissue inevitably leads to an inaccurate result, as displacement accuracy and, therefore, elasticity accuracy are directly related to the OCT intensity. This could be the reason why adipose tissue and stroma show similar modulus values in the lower half of Fig. 3(d). In addition, in the region of tumor (T), a more uniform shear modulus is recovered using the iterative method, with the shear modulus in the range 60-65 kPa. By comparison, the corresponding region recovered using the algebraic method shows shear modulus values in the range 20-100 kPa. As the histology image demonstrates, there is relative uniformity in the structure of the tumor region, which is replicated in the shear modulus provided by the iterative method. It is worth noting that the uniform composition of the tumor here is distinct from many tumors previously scanned using compression OCE, where more commonly the intermingling of tumor with desmoplastic stroma creates heterogeneous strain as a hallmark of disease [26,27]. Also, in the histology image (Fig. 3(b)), local regions of benign ducts in desmoplastic stroma are visible within the larger region of tumor. These regions are more clearly visible in shear modulus distributions obtained using the iterative solution by their lower modulus. The central duct descends past the tumor mass to the stromal region, whilst the others are circumscribed by the tumor. This is reflected in the iterative solution, suggesting that this approach can more faithfully reproduce features within mechanically heterogeneous tissue.

3.3 In vivo human skin

Figure 4 shows in vivo OCE images of a human fingertip. The OCT images show the ridges of the fingerprint in the epidermis and the layered structure of the skin (Fig. 4(a)), from top to bottom: the stratum corneum (SC), a protective layer of dead anucleated keratinocytes (corneocytes); the living section of the epidermis (E); and the dermis (D), typically comprising dense, irregular connective tissue. Sweat ducts (SD) can be readily seen as spiraling structures in the stratum corneum, descending past the epithelium and into the dermis; however, there is insufficient contrast to resolve the sweat ducts in the epidermis and dermis due to the higher scattering of surrounding tissues.

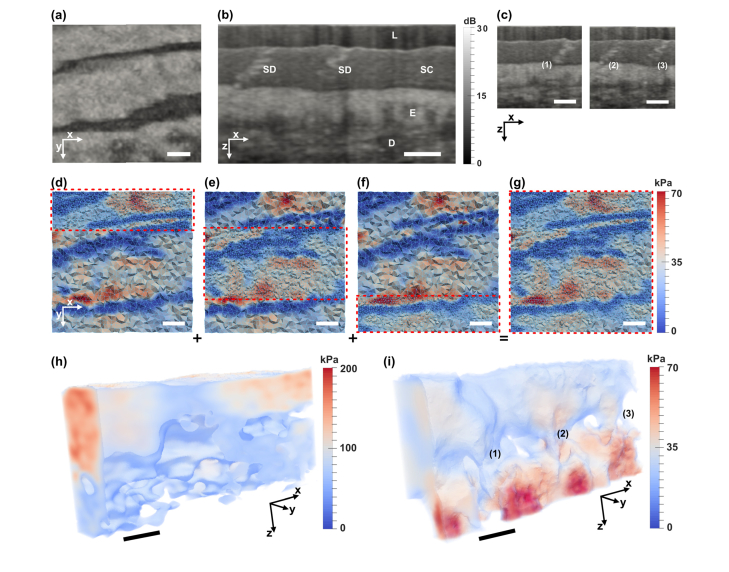
Fig. 4.

In vivo OCE images of a human fingertip. (a) En face view of OCT showing epidermal folds in a fingerprint. (b) OCT cross-sectional structural image. (c) OCT cross-sections associated with sweat duct structures (1), (2) and (3) in (i). OCT images are smoothed by a Gaussian filter (σ = 4 µm). (d)-(g) illustrate the method of domain decomposition, and correspond to the OCT in (a). (d)-(f) show inversion and meshing in three sub-domains that combine to form (g). (h) and (i) 3D shear modulus reconstructions using the algebraic and iterative methods, respectively. The volumes are visualized by overlaying a thresholded volume with a sub-surface projection of shear modulus values. Scale bars are 500 µm. L = compliant layer, SC = stratum corneum, E = epidermis, D = dermis, SD = sweat duct.

The algebraic (Fig. 4(h)) and iterative (Fig. 4(i)) reconstructions show the shear modulus distribution, in 3D, between the skin layers (excluding the compliant layer (L)). It is evident that the iterative method identifies the layers and features of the skin more clearly, and further preserves the fidelity of the shear modulus reconstruction at depth. Particularly, in Fig. 4(i), the layers are identified by the variation in their mean modulus and also the modulus distribution. The continuation of the sweat ducts into the epidermal layer (corresponding to Fig. 4(c)) are readily identified in the elastograms generated by the iterative method; whereas, these features are not observed in the OCT or algebraic method images.

The mean shear modulus values for the three layers, calculated using the iterative method, are: 34 kPa (SC), 27 kPa (E), and 53 kPa (D), which are within the expected ranges [28,29]. These average values are calculated by segmenting the shear modulus image into three layers using the OCT data (where the layers are seen clearly) and then calculating the volumetric mean within each layer. Direct comparison of shear modulus values between different methods is challenging. Skin tissue is typically non-linear elastic, such that with increasing pre-strain, the effective shear modulus increases [28]. Further, bulk characterization techniques, such as indentation, assess the cumulative properties (in depth) of the skin tissue (or an aggregate of a few layers), thereby, representing average values.

Skin tissue is highly heterogeneous; thus, a high mesh density is desired in the iterative method. Performing inversion over the entire tissue volume with a high mesh density is computationally demanding. As shown in Figs. 4(d)-4(g), this is made feasible through domain decomposition, where multiple independent inversions were performed, still over the entire domain, however, with separate complementary partitions being refined with a dense mesh (Figs. 4(d)-4(f)). The results from each refined partition in each inversion were fused to obtain a full, high-resolution reconstruction of shear modulus (Fig. 4(g)).

Accurate mapping of mechanical properties in vivo in skin may find clinical application in dermatology in characterizing conditions such as cancer [30], pathological scarring [31] and scleroderma [32]. Further, it may find application in the cosmetics industry, where the mechanical properties of skin are important in aging, treatment and regeneration [33]. The first steps toward this with OCE have been recently demonstrated, showing the capacity to distinguish burn scars, moles and image other locations of the skin, however, all based on the algebraic method [34]. The iterative reconstruction method presented here will likely further improve the clinical diagnostic capacity of OCE.

4. Discussion

Optical coherence elastography has demonstrated great promise in mapping the mechanical properties of tissues on the hundreds of micrometer to millimeter scale, showing clinical potential, for example, in ophthalmology and oncology [8]. It has also started to emerge in cell mechanics, where the impetus is on understanding how cells interact with their mechanical microenvironment through physical forces [11]. The iterative inversion method presented in this paper will benefit all these applications of OCE leading to high-resolution and higher-accuracy shear modulus maps.

The iterative method to modulus reconstruction presented here makes no assumptions regarding homogeneity of stress or elastic properties. As a result, it produces modulus distributions that are more accurate when compared with the algebraic method, especially for samples that are inherently heterogeneous. As shown in the Results section, in the case of a phantom with multiple inclusions, it leads to more accurate average modulus values, especially when the contrast between the inclusion and the background is large. Also, consistent with how the sample was manufactured, it leads to a more uniform distribution within each inclusion. In the case of the ex vivo imaging of a malignant breast cancer specimen, the iterative method avoids the appearance of regions of negative modulus, and produces modulus images that are qualitatively more consistent with histology. Finally, in the case of in vivo imaging of skin, the iterative method better resolves the three layers of the skin (stratum corneum, epidermis and dermis), and the spiral structure of individual sweat ducts.

The improved accuracy of the iterative method comes at the cost of solving a complex inverse problem which is computationally intensive. These computational costs are mitigated by the use of an adjoint solver, an adaptive grid resolution algorithm, and a domain decomposition algorithm. The computational gains from this relatively simple approach are substantial. For example, in the multiple inclusion problem, using this approach, the number of unknown parameters in the inverse problem reduces from ~28.9 million to ~42 thousand, a reduction by a factor of 680 that makes the solution of this problem feasible in about 6 hours on an off-the-shelf desktop computer. Similar savings are observed for other problems reported in this paper.

It is interesting to consider the spatial resolution of the modulus images and the least count error for the modulus estimate produced by the iterative method. However, these quantities are not easily estimated because the modulus is determined from the displacement field by solving a complex nonlinear inverse problem on an adaptive unstructured grid, and the displacement estimate is itself obtained from phase differences between collocated pixels in successive OCT B-scans. One approach to estimating the spatial resolution would be to determine the point-spread function (PSF) for each of these steps and then convolve them in order to determine a cumulative PSF for the entire problem. However, for the complex, nonlinear inverse problem we are solving, it is not possible to determine the PSF. Thus, in order to gain some understanding of the spatial resolution and the least count error of the method, we must rely on some other approach. In particular, we make use of the validation results obtained for the multiple inclusion problem described in Fig. 1.

We assume that the interface between the inclusion and the background is infinitesimally thin, and that this discontinuity is smeared out in the modulus image. By measuring the rise-distance, which is defined as the distance taken for the modulus value to rise from 10% to 90% of its value, we can obtain an estimate of the spatial resolution of the method. This distance was calculated for the inclusion in Fig. 1, and is equal to 62 μm. In order to estimate the least count error, we assume that the modulus distribution within the inclusion is homogeneous. This is a reasonable assumption since the modulus of the inclusions was controlled by the mixing ratio of the PDMS. Further, the addition of scatterers did not show a change in overall mechanical properties when assessed by uniaxial compression tests. Thus, any variation reported in the modulus value can be ascribed to an error in the reconstruction. The root mean square (RMS) of this error is, therefore, an estimate of the least count error. The RMS error value for the inclusion is ~4 kPa.

It is interesting to consider the effect of overall noise, as well as it spatial variation, on the results of the iterative method, especially since we expect the noise in the displacement measurement to vary spatially in inverse proportion to the OCT signal intensity. Any increase in the overall level of noise leads to an increase in the regularization parameter through the L-curve procedure, which in turn leads to smoother reconstructions with lower contrast due to the effect of the TV regularization.

The spatial variation in noise is accommodated through the spatially varying weighting function T in Eq. (1). This function determines the relative importance of data mismatch and regularization terms at any point in the domain. In regions with large noise this function is set to a small value thereby effectively increasing the importance of regularization. When viewed from a Bayesian inference perspective, with a Gaussian model for noise, this function is the inverse of the covariance of noise in the measured data. To understand what effect this might have on a reconstruction, let’s consider two regions: one where the noise estimate is small (T is large) and another where it is large (T is small). In the region with small noise (large T) the regularization term will have a lesser effect and the modulus reconstruction will have significant spatial variations. In the region where noise is large (small T), the regularization term will be more important and the solution will be smoother. In the context of the examples considered in this manuscript, where we have varied T in inverse proportion to OCT intensity, this implies that regions with lower OCT intensity will have relatively smoother reconstruction when compared with regions with higher OCT intensity.

While the method described in this paper does not require the assumption of homogeneity that is invoked in the algebraic method, it retains some other assumptions, namely linear elasticity, and isotropy. For the phantom and breast samples considered in this paper, isotropy is likely a reasonable assumption. However, it is also likely that given the amount of pre-compression, these samples are not in the linear-elastic regime. Thus, the modulus we recover can be interpreted as a tangent modulus about the pre-compression strain, which can be characterized by the absolute deformation state of the compliant layer. A natural extension of the iterative method discussed here would be to include non-linear elastic behavior, anisotropy, and perhaps even poroelastic behavior in the inverse problem. We note that the iterative method provides a framework to include all of these effects [20,35–37]. However, to successfully do so will require collecting additional independent displacement data that may be obtained by altering the spatial and/or temporal characteristics of the excitation, and enriching the forward solver within the iterative method with the appropriate mechanical models.

5. Conclusion

We have demonstrated, for the first time, a tractable method for the measurement of shear modulus in three dimensions on length scales highly relevant to biological and disease processes on the scale between cells and whole tissues. This approach is free from simplifying assumptions that have been invoked in other methods and are routinely violated in heterogeneous samples. Undoubtedly, there is still much to learn in the application of these methods to a wide variety of biological constructs and tissue types. However, the results demonstrated here suggest that our approach will find many applications in the future, in research and with prospects for translation to applications from tissue regeneration to clinical medical imaging.

Funding

Australian Research Council; the Cancer Council, Western Australia; and the Department of Health, Western Australia. PM is supported by a Royal Society University Research Fellowship.

Disclosures

DDS and BFK hold shares in a startup company, OncoRes Medical, developing optical coherence elastography for surgical applications (I). BFK receives research funding from this company (F). The other authors declare no conflicts of interest related to this article.