Aperture phase modulation with adaptive optics: a novel approach for speckle reduction and structure extraction in optical coherence tomography

Abstract

Speckle is an inevitable consequence of the use of coherent light in imaging and acts as noise that corrupts image formation in most applications. Optical coherence tomographic imaging, as a technique employing coherence time gating, suffers from speckle. We present here a novel method of suppressing speckle noise intrinsically compatible with adaptive optics (AO) for confocal coherent imaging: modulation of the phase in the system pupil aperture with a segmented deformable mirror (DM) to introduce minor perturbations in the point spread function. This approach creates uncorrelated speckle patterns in a series of images, enabling averaging to suppress speckle noise while maintaining structural detail. A method is presented that efficiently determines the optimal range of modulation of DM segments relative to their AO-optimized position so that speckle noise is reduced while image resolution and signal strength are preserved. The method is active and independent of sample properties. Its effectiveness and efficiency are quantified and demonstrated by both ex vivo non-biological and in vivo biological applications.

1. Introduction

Speckle is a long-standing problem in all imaging technologies that use coherent light sources [1–4]. Speckle originates in interference between light scattered by a randomly distributed scatterers in the system point-spread function (PSF) volume, and is observed as voxel-to-voxel intensity fluctuations in the image [5,6]. Although speckle can provide potentially useful information about the dynamics of sample microstructure, in most applications it acts as a major source of noise that degrades image quality. Optical coherence tomography (OCT) is a volumetric imaging technology developed in 1991 [7], which was soon adopted in biomedical applications [8–13]. However, as a method dependent on the coherent properties of light, OCT images suffer from speckle noise [14–16].

Many approaches have been taken to suppress speckle, including generation by various means of multiple images with uncorrelated speckle patterns followed by averaging [17–20]. A weakness of these methods is that the number of uncorrelated speckle patterns that can be created is typically small, limiting the degree of speckle suppression by averaging. Speckle reduction methods using digital post-processing have also been proposed [21–25]. However, digital post-processing usually reduces speckle by spatial averaging or filtering, which necessarily reduces image resolution. Recently, it was shown that simple averaging of suitably numerous, well aligned images can reduce speckle for in vivo imaging, and it was hypothesized that the subcellular motility of scatterers was responsible for varying the speckle pattern between frames [26–28]. Because this latter method relies on time-dependent variation in the sample microstructure, it is inherently passive and dependent on the underlying dynamics of the mobile scatterers. As a way of potentially overcoming the limitations of passive averaging, speckle modulating OCT (SM-OCT) was recently developed [29]. By introduction of a ground-glass diffuser in the external optical path, the method generates random, time-varying changes in the sample beam. The authors hypothesize that SM-OCT introduces axial phase variation in the imaging plane, but the variation is not completely under experimenter control, and the phase variation cannot be readily repeated. In contrast, as characterized in classical optical theory and applied in adaptive optics (AO) imaging [30], the wavefront phase across the system aperture can be precisely controlled by manipulation of a wavefront corrector conjugate with the pupil aperture, and this insight suggests the possibility of using AO technology to create a method for speckle suppression that would be readily controllable and broadly applicable to OCT.

The core of all AO-enhanced imaging is the active control of the wavefront phase across the system aperture. This control is implemented by means of a deformable mirror (DM) or spatial light modulators (SLMs), and typically optimizes the wavefront over the pupil to allow the system to operate at or near diffraction-limited performance [31–34]. Here, we take advantage of this exquisite control to create a novel method for speckle noise reduction - aperture phase modulation AO-OCT (APM-AO-OCT). This method employs sub-micrometer piston modulations of the DM segments to introduce random phase variation for all segments in both spatial and temporal dimensions. In describing APM-AO-OCT, we first present the hypothesized underlying mechanism, namely that the modulations of DM segments about their AO-optimized positions slightly alter the PSF, randomizing over samples the contributions from different scatterers to create uncorrelated speckle patterns, so that averaging can efficiently reduce the speckle. We then address the inherent conflict between speckle noise reduction and preservation of signal resolution and strength by determining an optimum mirror segment displacement range. We further identify a relatively small subset of the total set of mirror configurations with displacements in this range that maximally reduce speckle while preserving resolution and signal strength. Finally, we demonstrate the success of APM-AO-OCT with in vivo mouse retina imaging applications.

2. Methods

2.1 AO-OCT system configuration

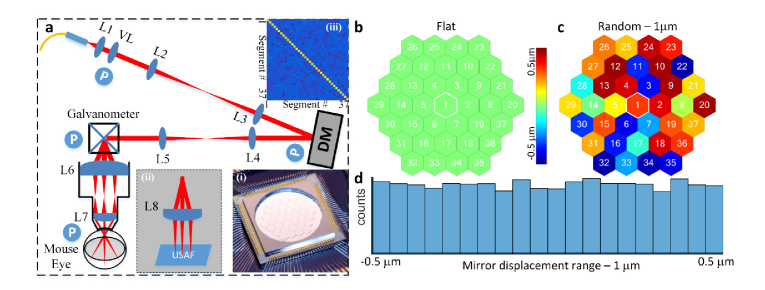
In adaptive optics (AO) systems used in vision science [30], a deformable mirror (DM) is placed in an optical plane conjugate with the pupil aperture to correct aberrations of the cornea and lens, as shown in Fig. 1(a), which provides a schematic of the sample arm of our AO-OCT system built for in vivo mouse retinal imaging. The DM (PTT111, IRIS AO, Inc., photo in Fig. 1(a), bottom right inset) has 37 segments with 111 actuators (3 actuators per segment to independently control the displacement/piston, tip and tilt). The DM segments have nanometer level displacement resolution (z-offset of the mirror surface) with a working range of [-2, 2] μm. When the DM operates in ‘flat’ mode, the displacements of all segments are zero (Fig. 1(b)). The piston of each segment can be independently controlled to operate in a ‘random’ mode (Fig. 1(c)).

Fig. 1.

System setup and the geometry of the segmented deformable mirror. (a), OCT sample arm (Inset: (i) - Photo of the DM; (ii) - setup for USAF 1951 resolution test target; (iii) - covariance analysis of the random segments’ pistons). (b), Mirror configuration – Flat. (c), Mirror Configuration - mirror segments with random displacements. (d), Histogram of the mirror displacements for 100 mirror configurations in which the displacement range was 1μm (0 ± 0.5 μm); Abbreviations: L#: Lens, VL: variable focus length liquid lens, DM: Deformable mirror, USAF: 1951 USAF (U.S. Airforce) resolution test target, P (circled in blue) optical planes conjugate with the pupil.

The lenses used in the sample arm are VIS-NIR coated achromatic lenses (400-1000 nm, Edmunds Optics). A reference arm was built with dispersion compensation prisms. A SLD (T-870-HP, Superlum, 180 nm full width at half maximum bandwidth centered at 870 nm) served as the light source for NIR OCT with a power at mouse pupil of 900 μW. A customized spectrometer with 2048 pixels was used to acquire the OCT spectra.

2.2 Data acquiring, post-processing and quantification

OCT spectra were acquired at a 100 kHz A-scan rate using customized Labview software. Each B-scan comprised 550 A-scans, resulting in a B-scan rate of 30 Hz that included data acquisition, display and storage. Post-processing was implemented by customized Matlab™ code with standard functions including DC subtraction, dispersion compensation, wavelength-to-k-space interpolation, Hann windowing, and FFT [35,36]. The results, intensity-based B-scans (not complex OCT signals), were further processed by averaging or other analysis as indicated. The raw spectrum of each A-scan acquired with OCT and APM-OCT was processed in exactly the same way to create images in the spatial domain for comparison.

A metric, normalized speckle contrast (NSC), was used to quantify and compare the speckle noise suppression effect between images. NSC is defined as the standard deviation (s.d.) of the image intensity in a given region divided by its average image intensity. For simplicity, speckle contrast, instead of its full name, is used in the main text.

The registration of B-scans collected in vivo was done either with ImageJ TurboReg / StackReg plugin [37,38] for B-scan averaging, or with phase variance OCT software developed for intensity averaging and/or blood vessel map extraction [39,40] for volume data averaging.

2.3 Wavefront sensorless (WFSL) adaptive optics aberration correction

The imaging beam at the mouse pupil has a diameter of 0.93 mm, a size for which ocular aberration is non-negligible [41,42]. The mouse eye’s aberrations were first corrected using wavefront sensorless (WFSL) aberration correction software [36,43,44] with image intensity-based optimization metric. The software automatically calculates the brightness in a user-defined region of interest (ROI) layer, while varying the shapes of the DM controlled by superposition of Zernike polynomials (ANSI standard [45]) over a search range. After the search process found the optimal mirror configuration for correcting the aberrations of the individual eye, the mirror configuration was loaded into the Labview-based data acquisition software.

2.4 Aperture phase modulation

In an optimized AO system, the DM defines a wavefront across the system aperture to correct aberrations so as to approach diffraction-limited performance for the system NA, resulting in the most compact PSF possible for that NA [30]. The aperture phase distribution was modulated about its optimum AO configuration by random displacements of the mirror segments using a uniform distribution centered on zero, with displacement ranges varied from 0 (no displacement) to 1.0 μm (0 ± 0.5 μm). Histogram analysis of the mirror segments established the uniform distribution of the displacements (Fig. 1(d)). Covariance analysis of the mirror position matrix from 100 trials showed that the displacements of the different DM segments are uncorrelated (Fig. 1(a) top right inset).

2.5 3D PSF of the AO-OCT system

In a scanning imaging system, the 3D distribution of power at the focal point in the sample defines the system’s PSF. For diffraction-limited systems employing non-coherent light sources and having a circular aperture, the 3D PSF has an analytic form [46] that can be approximated by a 3D ellipsoid. In OCT, which relies on partially coherent light for interferometry, beam propagation into the sample is governed by the NA of the system in the same manner as for non-coherent light, but the axial direction is further sectioned in the detector by the coherence length, which is inversely proportional to source bandwidth [35]. In the AO-OCT system used here the PSF has a calculated axial (coherence) length of ~2.5 μm in tissue, assuming a refractive index of 1.35. In Fourier domain OCT the sampling unit is the A-scan, which provides an axial profile of the backscattered light along the beam propagation axis. While the coherence length of the PSF is invariant with A-scan depth, the lateral (x-, y-) width of the PSF varies according to the NA, being wider away from the center focus. This lateral variation can be particularly notable in AO-OCT, where a higher NA is achieved, an effect that diminishes both the lateral resolution and the power density (imaging brightness) at axial distances away from the focal plane.

2.6 Timing and scanning protocol

The configuration of the DM was changed immediately before each B-scan. For AO-OCT, the DM was flattened for resolution target imaging or optimized for aberration-corrected mouse retinal imaging; For APM-AO-OCT, the DM adds random mirror segment displacements on top of the optimal mirror shape for AO-OCT:

• i)For the B-scan based comparison between AO-OCT and APM-AO-OCT, the x-scanner repeatedly scanned the same line on the sample. N samples (N = 100 for ex vivo imaging, N = 1 for in vivo imaging) AO-OCT and APM-AO-OCT were acquired one right after the other one.
• ii)For the enface comparison, N samples (N = 20, 50 or 100 for ex vivo imaging, N = 50 for in vivo imaging) OCT and APM-OCT B-scans were acquired in same location one after the other, then the y-scanner move to the next location to repeat the previous process until it covered the ROI.

Note that there was only a N/30 s time (30 is the B-scan rate in Hz) difference between data sets taken with AO-OCT and with APM-AO-OCT, to ensure strictly comparable conditions.

2.7 Animal handling

All mice husbandry and handling were in accordance with protocols approved by the University of California Animal Care and Use Committee, which strictly adheres to all NIH guidelines and satisfies the Association for Research in Vision and Ophthalmology guidelines for animal use. Adult pigmented C57BL/6J and albino BALB/c mice were obtained from Jackson Laboratories and maintained on a 12:12, ∼100-lux light cycle. During our measurements, mice were anesthetized with the inhalational anesthetic isoflurane (2% in O₂), and their pupils dilated with medical grade tropicamide and phenylephrine. A contact lens and gel (GelTeal Tears, Alcon, U.S.) was used to maintain the cornea transparency for in vivo retinal imaging [47,48].

3. Results

3.1 Effect of aperture phase modulation and hypothesized mechanism of speckle noise reduction

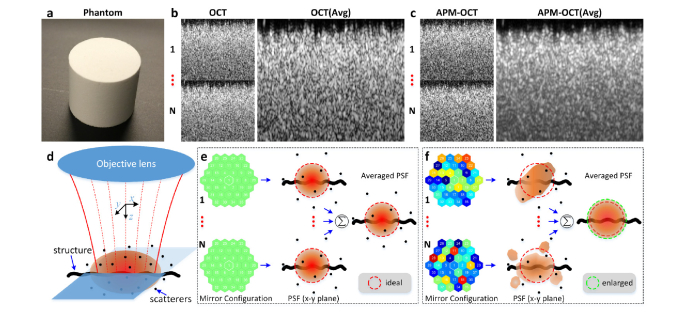
As described in the Introduction, speckle noise in OCT images arises from the interference between light backscattered from different scatterers within the PSF, and is observed as voxel-to-voxel intensity fluctuations in the image [5,49]. In a single OCT B-scan of a Lambertian target (Fig. 2(a)), the speckle pattern predominates to the extent that no structure can be discerned below the surface (Fig. 2(b)). Averaging 100 B-scans with an unchanged DM configuration does little to suppress the speckle, since the scan-to-scan speckle pattern doesn’t change, as dictated by physics, given that the scatterers in the object are immobile for non-biological target (Fig. 2(b)).

Fig. 2.

Effect of aperture phase modulation and hypothesized mechanism of speckle noise reduction. (a), the reflectance standard phantom (Fluorilon 99W, Avian Technologies LLC). (b), individual (1…N) and 100-frames-averaged OCT B-scans. (c), individual (1…N) and 100-frames-averaged APM-OCT B-scans (DM displacement range: 0.3 μm). (d), representation of the in-focus 3D OCT PSF (reddish ellipse). (e), when the DM was configured as flat mode, a static PSF always selects the same set of scatterers; (f), when the DM was configured in ‘random’ mode, a dynamically varied PSF selects different sets of scatterers. Avg: 100 frames averaged.

The OCT imaging system has a deformable mirror (DM) whose actuators have a rapid response time, and so afford the possibility of manipulating the wavefront phase at the system aperture in real time. If prior to the collection of each B-scan the DM mirror facets are randomly displaced a sub-micrometer distance, the speckle pattern changes between B-scans, so that averaging can suppress the speckle noise (Fig. 2(c)).

For non-living tissue, when the DM of the AO-imaging system is optimized, the PSF realizes its most compact form in the sample (Fig. 2(e), PSF, x-y plane) and does not change, so that the set of scatterers sampled by the PSF is always the same. This results in an un-changing speckle pattern for successive B-scans, explaining why the average B-scan appears very similar to any individual scan. Conversely, random displacements of the DM segments from their optimum positions alter the wavefront phase across the system aperture, resulting in a PSF distorted from the optimum to varying degrees (Fig. 2(f), PSF, x-y plane). This altered PSF will probe a different set of scatterers, so that speckle pattern becomes less correlated between B-scans, but still sufficiently compact to reveal spatial structure in the sample (Fig. 2(f), thick wavy line, larger than the PSF in either of 3 dimensions). Averaging over a population of B-scans taken with a different DM patterns can thus reduce speckle while preserving signal from the structures (Fig. 2(f)).

APM-OCT clearly holds promise in reducing speckle noise but faces several challenges. One of these is the inherent conflict between the goal of reducing speckle noise and that of maintaining maximal image resolution. A second challenge is that the potential number of DM configurations is vast: for a mirror with 37 segments and a uniform, only 11-step distribution over the displacement range, the total number of possible configurations is very large (11³⁷), and it is unclear which subset of these configurations will be optimal. A third problem is that any method that perturbs the PSF from its most compact shape will reduce signal strength. Practical implementation of APM-OCT as a method of speckle noise reduction must provide an efficient way of selecting a manageable subset of the mirror configurations that also resolves the conflict between speckle noise reduction, and preservation of resolution and signal strength.

3.2 Finding the DM displacement range that both reduces speckle and preserves resolution

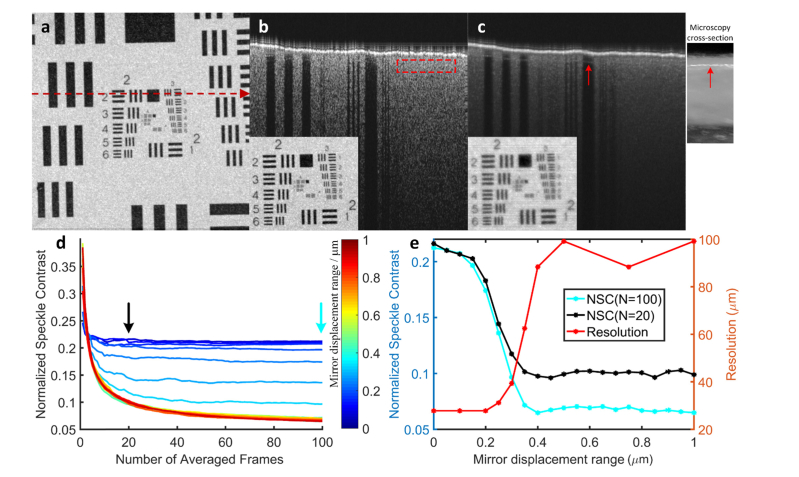
To address the conflict between reducing speckle noise and preserving resolution we performed OCT imaging on a printed 1951 USAF resolution test target (Newport, Irvine, CA, U.S.). The B-scan of the target averaged from an ensemble of 100 scans taken with no DM modulation exhibits speckle noise (Fig. 3(b)), while the average of 100 scans taken with each DM facet displaced randomly over a 0.3 μm range (0 ± 0.15 μm) shows strongly reduced speckle (Fig. 3(c)). The dependence of speckle noise reduction on the number of averaged B-scan and mirror displacement range was quantified by calculating the normalized speckle contrast (Fig. 3(d)). Here the displacement ranges were varied from 0 (no displacement) to 1.0 μm with a uniform distribution centered on zero. Speckle contrast rapidly declined with increased displacement range and/or number of B-scans averaged (Fig. 3(d)), approaching an asymptotic value. Image resolution loss and speckle contrast reduction from these experiments were then compared as a function of the DM displacement range (Fig. 3(e)): the curves for the two measures cross at a displacement range of ~0.3 μm, implying that an arrangement of mirror displacements derived from a distribution with this range is the best choice for simultaneously preserving resolution and reducing speckle noise for this sample.

Fig. 3.

Finding an optimal displacement range for minimizing speckle while preserving target resolution. (a), OCT enface projection of a 1951 USAF resolution test target. The red dashed line indicates the location of OCT B-scans for panels (b) and (c)). (b), OCT B-scan obtained by averaging 100-frames when the DM was set to ‘flat’ mode (red dashed rectangle: region used for speckle contrast quantification; inset: enface projection). (c), APM-OCT B-scan obtained by averaging 100-frames when the facets of the DM were randomly modulated with a uniform distribution having a displacement range of 0.3 μm (0 ± 0.15 μm) (inset: enface projection). Note that the second layer of the target became visible (red arrows, right inset shows side view cross section obtained with a fiber microscope). (d), Speckle contrast as a function of the number of B-scans averaged for different random mirror displacement ranges; the color bar specifies the displacement range. (e), Speckle contrast as function of mirror displacement range replotted from (d) N = 20 and N = 100 (the black and cyan arrows in (d) identify the curves from the points were extracted). Note that NSC declines rapidly towards its asymptote over the same displacement range for N = 20 and N = 100. The target resolution (red curve) was obtained from N = 20 for efficiency, since each of the points on the curve required acquisition and processing of an ensemble of N OCT volumes.

3.3 Defining an optimum subset of deformable mirror configurations for preserving the resolution and signal intensity

While the above results show that an optimum mirror displacement range of ~0.3 μm can be found (Fig. 3), there is still considerable loss of resolution and signal intensity (compare Figs. 3(b) and 3(c)). Moreover, the huge number of potential DM configurations makes it very inefficient to search for a global optimum DM configuration set to mitigate the resolution and signal loss. In analyzing the results, however, we found that the APM-OCT image average intensity varied substantially between B-scans (over 3-fold on linear scale). Based on general principles, it could be expected that the brighter an individual image, the less distorted was the underlying PSF, suggesting that the subset of mirror displacement patterns yielding the brightest images might correspond to a set of minimally distorted PSFs.

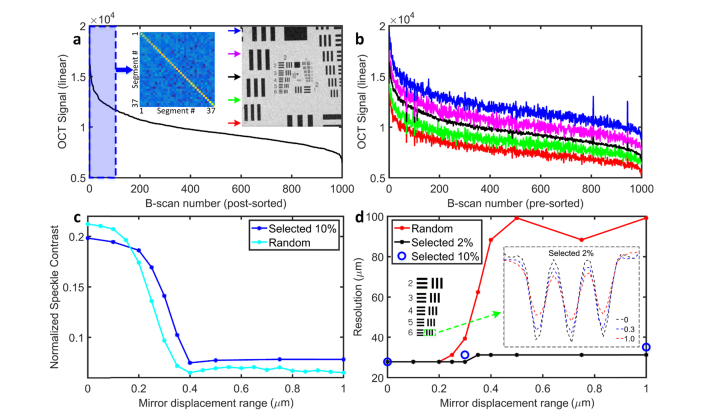
To examine this hypothesis, we generated an ensemble of 1000 B-scans for a mirror displacement range of 0.3 μm and sorted them by their average signal intensities (Fig. 4(a)). Then, we applied the same mirror configurations at 5 different locations (ROIs identified by colored arrows in inset of panel (a)). While the average intensity varied somewhat for B-scans taken at these different positions (Fig. 4(b)), the overall OCT signal plots were very similar, consistent with the idea that the shape of the plot was dictated by the PSFs corresponding to each mirror configuration, rather than by properties of the sample. The subset of the first 100 mirror configurations (Fig. 4(a) blue region marked) corresponding to the brightest 10% of the images for various displacement ranges was selected for further examination. We next compared the performance of the “top 10%” configurations for each displacement range with that of an equal number (100) of purely random configurations, and found that the selected top 10% sets performed almost as well as the purely random sets with the same displacement range (Fig. 4(c)). Remarkably, however, the selected subset of configurations provided resolution up to ~3-fold greater than the randomly generated configurations (Fig. 4(d)). In conclusion, although the “top 10%” subset of mirror configurations with displacement range of around 0.3 μm is slightly less efficient than a purely random set of the same size and displacement range in reducing speckle, it satisfies the triple constraints of greatly reducing speckle noise while simultaneously maximally preserving resolution and signal strength. More generally, the approach provides a rapidly implemented method for programming a deformable mirror to achieve these goals.

Fig. 4.

A subset of the mirror configurations reduces speckle while preserving resolution and signal strength. (a), Average intensity of 1000 APM-OCT B-scans plotted in descending order (the mirror displacement range was 0.3 μm). Left inset: covariance analysis of the top 100 mirror configurations). Right inset: enface test target image identifies the B-scan locations for (b). (b), APM-OCT signals from 1000 B-scans with the mirror configuration set used in (a), but taken at different locations on the target; the signal distributions from different locations have a form similar to that in (a), and have been offset arbitrarily for clarity. (c), Comparison of speckle contrast for APM-OCT images averaged from 100 frames, and obtained either with the selected “top 10%” or with purely random DM configurations for different displacement ranges; (d), Resolution plotted as a function of displacement range for different sets of configurations: purely random (red symbols and line); the top 10% (blue circles); top 2% (black symbols and line). The resolution achieved with the selected DM configurations is always better than that obtained with random configurations for displacement range greater than 0.25 μm and is asymptotically ~3-fold better. Left inset: location on target grid for results plotted in right inset. Right inset: vertically averaged cross-section OCT signal changes for different displacement ranges using the selected 2% configurations, showing there is a continuous contrast loss. Because there was very little difference in the resolution achieved with the top 2% (black symbols and curve) and top 10% (blue circles) DM configuration sets at three critical displacement ranges, and the latter required acquisition and processing of 100 OCT volumes for each point, we limited analysis of the top 10% to these three critical displacement ranges.

3.4 In vivo application of APM-AO-OCT reduces speckle efficiently and reveals novel structure

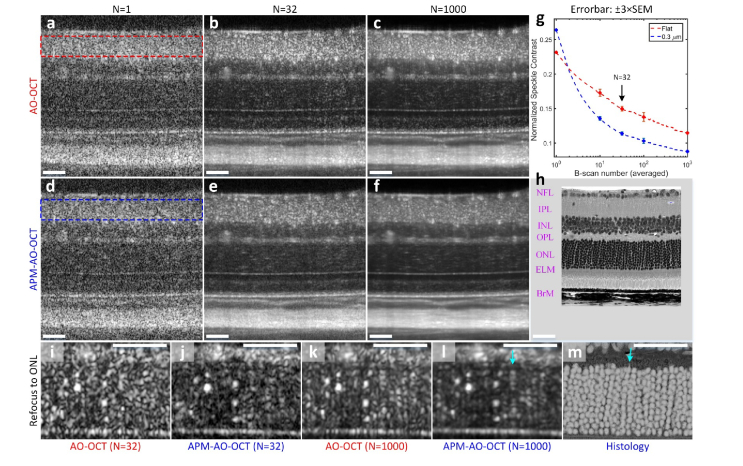
To examine the in vivo applicability of APM-AO-OCT we imaged the retinas of Balb/c mice using an interlaced B-scan acquisition protocol in which successive scans were acquired with or without APM. Single B-scans exhibited substantial speckle that obscured even highly scattering and extended structures, with little noticeable difference between scans taken with and without APM (Figs. 5(a) and 5(d)). The averages of 32 B-scans with and without APM had noticeably reduced levels of speckle (Figs. 5(b) and 5(e)); notably, extended structures such as the ELM and Bruch’s membrane appeared clearer in the image generated with APM. We quantified the speckle contrast in the region of the B-scans corresponding to the inner plexiform layer (IPL; dashed rectangles in Figs. 5(a) and 5(d)), as this region was bright, but showed no apparent structure. This quantification revealed that the average of 32 scans taken with APM-AO-OCT had a reliably reduced level of speckle contrast relative to average of 32 scans taken with AO-OCT alone (Figs. 5(b) and 5(e); Fig. 5(g), arrow). The reduction in speckle contrast was evident for all sample sizes between 10 and 1000 (Fig. 5(g)). The AO-OCT results are consistent with previous observations showing that averaging per se leads to reduction in speckle contrast in in vivo imaging [26,27]. This reduction was hypothesized to arise from the movements of subcellular organelles whose scattering gives rise to speckle. This hypothesis is supported by our observation that averaging of AO-OCT images of non-living targets (e.g., Figs. 2 and 3) does not per se much reduce speckle. Nevertheless, APM-AO-OCT more efficiently reduces speckle. Thus, the average of 32 scans with AMP-AO-OCT (Fig. 5(e)) appears comparable to that of 1000 scans taken with AO-OCT alone (Fig. 5(c)).

Fig. 5.

Comparison of the efficiency of the averaging of APM-AO-OCT vs AO-OCT results in reducing speckle and revealing novel cellular structure in vivo. (a-c), AO-OCT B-scans with N representing the number of images averaged. (d-f), APM-AO-OCT B-scans with sample averaging corresponding to that used in panels (a-c). The data in these panels were acquired with interlaced protocol. The focus of the AO-system was set to the IPL. The retinal layers are indicated in (h), which is provided at the same scale as the OCT B-scans. (g), Normalized speckle contrast of the IPL, for AO-OCT (red rectangle in a; red symbols and line in g) and for APM-AO-OCT (blue rectangle in d; blue symbols and line in g), plotted as function of the number of B-scan averaged. (h), Retinal plastic section of a C57Bl/6 mouse imaged with a 40X objective in a Nikon A1 microscope. (i-l), Averaged B-scans with the focus of the AO system shifted to the ONL; the shifted focus both increases the overall brightness of the images and narrows the width of the ONL scattering spots relative to those in panels (a-f). (m), Histology of the ONL from (h) presented with inverted contrast and magnified so as to have the same scale as panels (i-l); scale bar 50 μm. Cyan arrow in (l) points to a periodic series of spots which is very similar to stacks of rod cell bodies in m. Abbreviations: NFL - nerve fiber layer, IPL - inner plexiform layer, INL - inner nuclear layer, OPL - outer plexiform layer, ONL - outer nuclear layer, ELM - external limiting membrane, BrM - Bruch’s membrane. For APM-OCT, the top 10% mirror configurations were used (DM displacement range: 0.3 μm).

In addition to its greater efficiency than pure averaging in reducing speckle noise, APM-AO-OCT also serves to increase the confidence with which the experimenter can draw conclusions about structures. To illustrate this point, we compare OCT images taken with the two methods after shifting the focus of the AO-system to the ONL (Figs. 5(i)-5(l)). The ONL comprises the cell bodies of the photoreceptors, which are developmentally arranged in vertical stacks of 10-11 (Fig. 5(h), histology). The average of 32 AO-OCT scans (Fig. 5(i)) shows spots of increased scattering that might be hypothesized to arise from the photoreceptor nuclei. However, the speckle noise is such that the hypothesis is dubitable. The average of 32 APM-AO-OCT B-scans strengthens the hypothesis (Fig. 5(j)). The comparison of averages of 1000 B-scans (Figs. 5(k) and 5(l)) leads to even greater conviction that the bright spots arise from rod nuclei: thus, for example, in Fig. 5(l) one can observe a number of rows of such spots which have the same vertical spacing and, in some cases, the expected total number as rod nuclei seen in ONL histology (Fig. 5(m); contrast-inverted from Fig. 5(h)). While the hypothesis that photoreceptor nuclei can be visualized with APM-AO-OCT (and to a lesser extent, AO-OCT) needs to be tested further, the evidence from the vertical and lateral spacing as well as size is substantial and demonstrates the potential for APM-AO-OCT for producing novel discovery. Thus, for example, it is possible that the variation in the brightness of the ONL spots reflects diurnally or otherwise changing structural and/or functional properties of the cell bodies and nuclei.

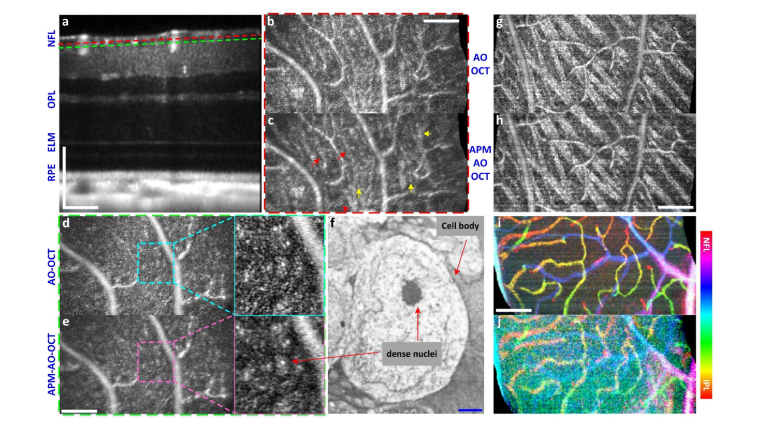
To explore the full potential of APM-AO-OCT to reduce speckle and uncover structure in vivo, we applied the method to volumetric data acquisition, arranging the focus of the AO-system to be at the uppermost retinal layers (Fig. 6(a)), and comparing AO-OCT with APM-AO-OCT as before. Enface presentation of single layer of the averaged volume showed an enhanced reduction of speckle by APM-AO-OCT (Fig. 6(c) vs. Figure 6(b)) and several linear structures (arrows) not discernible in the corresponding AO-OCT image. The averaged single layer about 10 μm deeper in the retina (Figs. 6(d) and 6(e)) revealed several regions with intensity greater than the surround which include bright spots. Based on a comparison with published histology (Fig. 6(f), Low-power electron microscopy [50]), we hypothesize that these regions represent displaced amacrine cells. Another comparison at the level of the NFL is provided in Figs. 6(g) and 6(h). Here APM-AO-OCT provides a greater reduction of speckle noise and improved confidence in the discrimination of blood vessels from ganglion cells axon fiber bundles. A potential downside of APM-AO-OCT is that its utility for OCT angiography [40,51] is reduced (Figs. 6(i) and 6(j)). However, this problem can be dealt by using the interlaced scanning protocol, as the AO-OCT-alone scans retain the angiographic information (Fig. 6(i)). Furthermore, the comparison of the averages from the interlaced protocol may lead to insight into the scattering structures seen with the AO-OCT images (compare Figs. 5(k) and 5(l)).

Fig. 6.

Visualization of cellular scale structures in retinal layers with in vivo volumetric APM-AO-OCT. (a), B-scan from a 560 × 280 × 320 μm³ retinal volume imaged 50 times with interlaced AO-OCT and APM-AO-OCT, aligned and averaged; the AO system was optimized for focus on the outer retina. The dashed lines indicate planes at which enface images were extracted for panels (b-e), respectively; (b, c), Enface presentation of a 0.85 μm digital section at the depth locus indicated by red dashed line in (a) for AO-OCT (b) and APM-AO-OCT (c) respectively. Red arrows point to thin line structures that can be excluded as being blood vessels, and likely represent the outermost ganglion cell axons; (d, e), Enface presentation of a 0.85 μm digital section at the depth locus indicated by green dashed line in (a), 10 μm deeper into the retina than (b, c). Magnified presentations reveal relatively brighter (gray) contiguous regions with especially bright dots inclosed; these regions are hypothesized to reveal displaced amacrine cells, which are known to reside in this layer; (f), Electron microscopic image of an amacrine cell image (from [50], with permission). (g, h), Enface presentations of 0.85 μm digital sections for AO-OCT and APM-AO-OCT with focus on the NFL. Speckle noise reduction by APM-AO-OCT enables more confident discrimination between blood vessels and axon fiber bundles; interlaced protocol; (i, j) OCT angiography (phase-variance analysis) with AO-OCT (i) and APM-AO-OCT (j). The aperture phase modulation substantially reduces the phase-variance OCT signal contrast in the APM-AO-OCT data, while the interlaced AO-OCT data preserves the signal contrast. Scale bar 100 μm (white) for all panel except (f), where it represents 1 μm (blue). Abbreviations: NFL - nerve fiber layer, OPL - outer plexiform layer, ELM - external limiting membrane, RPE - retinal pigment epithelium. For APM-OCT, the top 10% mirror configurations were used.

4. Summary and discussion

Adaptive optics has revolutionized image science by enabling image systems to perform at their diffraction limits, and thereby reveal a wealth of novel structure [31]. AO systems operate by actively controlling the wavefront at the system pupil aperture and have been implemented in imaging systems for in vivo ophthalmic imaging, including Scanning Laser Ophthalmoscopy (SLO) and OCT systems [52–56]. OCT imaging systems employ partially coherent light sources to extract depth scattering profiles of tissue, and as with all systems that use such sources, are subject to speckle noise, which substantially reduces their signal-to-noise ratio. Here we have presented a novel approach to speckle noise reduction in OCT. This approach exploits small scan-to-scan modulations of the phase across the aperture of an AO-OCT system produced by sub-micrometer displacements of the segments of a deformable mirror (DM) (Fig. 1). We established that an optimum mirror displacement range can be found which simultaneously greatly reduces speckle noise and maintains image resolution (Fig. 3), and that an algorithmically selected subset of the mirror configurations can further improve resolution and preserve signal intensity (Fig. 4). Finally, we demonstrated APM-AO-OCT can be used in vivo to efficiently reduce speckle noise and discover novel structure (Figs. 5 and 6).

4.1 Mechanism of APM-AO-OCT: selected perturbations of the system PSF

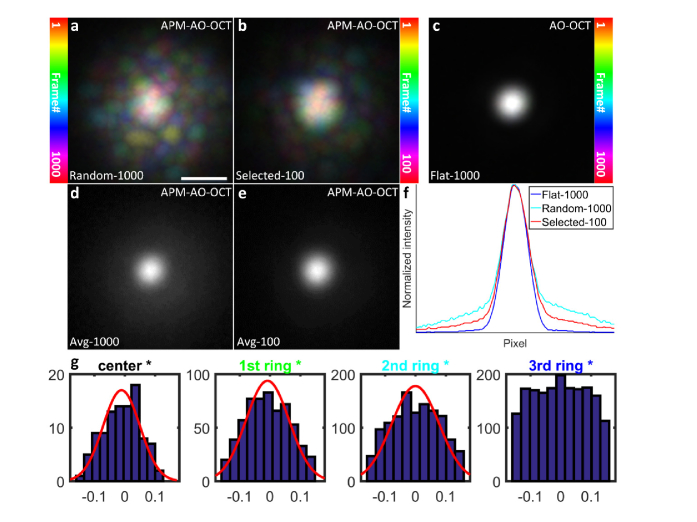
In an OCT system, the PSF is defined axially by the source coherence length and determined laterally by the NA of the system (Methods). Because the sampling unit in Fourier domain OCT is the A-scan, the lateral extent of the PSF varies with depth, achieving its diffraction-limited minimum at the focal depth. Aperture phase modulation (APM) necessarily perturbs the OCT PSF shape, but primarily affects its x-, y- distribution. The effects of APM on the PSF can be visualized by focusing the OCT beam onto a CMOS camera (Fig. 7). Each of a series of 1000 APM-AO-OCT PSFs exhibit a central power density with random extensions of lower power (Fig. 7(a)), while a similar sample of 1000 AO-OCT PSFs are identical (Fig. 7(c)). The PSFs of the selected “top 10%” of the APM-AO-OCT sample are more compact (Fig. 7(b)), as further emphasized by comparison of the averages (Figs. 7(d) and 7(c)), and comparison of line scans through the averaged PSF centers (Fig. 7(f)). This analysis provides support for the hypothesis (Fig. 2) that the averaging of scans taken with APM-AO-OCT efficiently reduces speckle contrast because the randomly distorted PSFs encompass different sets and numbers of scatterers, while the maintained centroid of the PSFs captures information from larger scale structural elements in the sample.

Fig. 7.

Comparison of the lateral extent of AO-OCT and APM-AO-OCT PSFs at the focus. All PSF images were obtained by focusing the beam onto a CMOS camera. (a), Color-coded projection of 1000 APM-AO-OCT PSFs produced with a DM displacement range of 0.3 μm. Colors were assigned according to the position in the series as indicated in the colorbar at left. (b), Color-coded projection of the “top 10%” PSFs from the sample of 1000 presented in (a). (c), Color-coded projection of 1000 AO-OCT PSFs (no DM modulation); the 1000 PSFs were indistinguishable from one another. (d), Average of the 1000 APM-AO-PSFs presented in (a). (e), Average of the “top 10%” APM-AO-OCT presented in (b). (f), Line profiles of the averaged PSFs; see legend. Note that, these images represent the “1-way” or incoming PSF of the system, whereas in application the effective PSF results from two passes through the system aperture. (g), Histogram analysis of deformation range for different groups of segments for “top 10%” optimum subset of DM configurations, show that the range of deformations depends on the distance from the DM center: the innermost DM segments and those in the first ring can be described by Gaussian distributions, while the outermost ring displacements have a nearly uniform distribution.

We believe that further insight into the class of mirror displacement configurations that minimize speckle contrast while maintaining resolution and image brightness will be obtained both by additional characterization of the DM configurations that yield optimum performance, and by theoretical analysis of the corresponding perturbed wavefronts. Thus, for example, histogram analysis of the DM segment displacements of the “top 10%” configurations as a function of distance from the DM pupil center revealed that the outermost actuators varied nearly uniformly over the full range of deformation, while the inner actuator displacements followed a Gaussian distribution with a restricted range (Fig. 7(g)). This observation suggests the hypothesis that configurations characterized by Zernike aberrations of the class Z_j ^{± j} (j≥2) may be especially useful for optimizing APM-AO-OCT. Interestingly, recent research [57] using astigmatism as an aberration-diverse source to vary speckle is consistent with this hypothesis, as astigmatism is characterized by non-zero Z₂ ^{± 2} terms. These ideas and results suggest how APM-AO-OCT might be extended to non-segmented DMs, which are widely used in AO imaging. Thus, the use of non-segmented DMs to generate class Z_j ^{± j} aberrations for producing uncorrelated speckle patterns while maintaining imaging resolution is a promising direction. Moreover, this suggests that theoretical analysis in which such higher order Zernike components are perturbed from their AO optima may lead to a deeper understanding of how the contributions of different scatterers within the PSF volume may be systematically manipulated.

4.2 Analysis of speckle statistics and estimation of the generated uncorrelated speckle patterns

In work presented above, we used the normalized speckle contrast (NSC) metric to quantify speckle reduction in multi-frame averaging. The averaging of independent speckle patterns is widely understood to be the primary mechanism by which speckle is reduced. If in a depth-restricted portion of a B-scan the intensity of all pixels is independent and identically distributed, and M uncorrelated speckle patterns are averaged, the contrast of the speckle of the average will obey the following general relation [5]:

$$\frac{NS{C}_M}{NS{C}_1}={(\frac{{\sigma }_I}{\overline{I}})}_M/{(\frac{{\sigma }_I}{\overline{I}})}_1=\frac{1}{\sqrt{M}}$$ (1)

where I is the random variable of intensities, $\overline{I}$ is the mean value of the intensity, and ${\sigma }_I$ is the standard deviation of the intensity variation. In the more general case where the mean intensity at different locations may vary in a sample, the speckle distribution has been described as a case of the full K distribution [58,59]. This distribution has a parameter (m) that can be used to estimate the number of independent speckle patterns [58]:

$$p_K(I_{sp}|\alpha ,\mu ,m)=\frac{2}{\Gamma (\alpha )\Gamma (m)}{I}_{sp}^{\frac{\alpha +m-2}{2}}{(\frac{\alpha m}{\mu })}^{\frac{\alpha +m}{2}}\times K_{\alpha -m}(2\sqrt{I_{sp}m\alpha /\mu })$$ (2)

where $I_{sp}$ represents the possible values of intensities in the fully-developed speckle pattern. Here α and µ are the shape parameter and expected value respectively of the local mean intensity variation, (assumed to follow a Gamma distribution), K_α(x) is the modified Bessel function of the second kind with order α, and m is the number of uncorrelated speckle patterns [58].

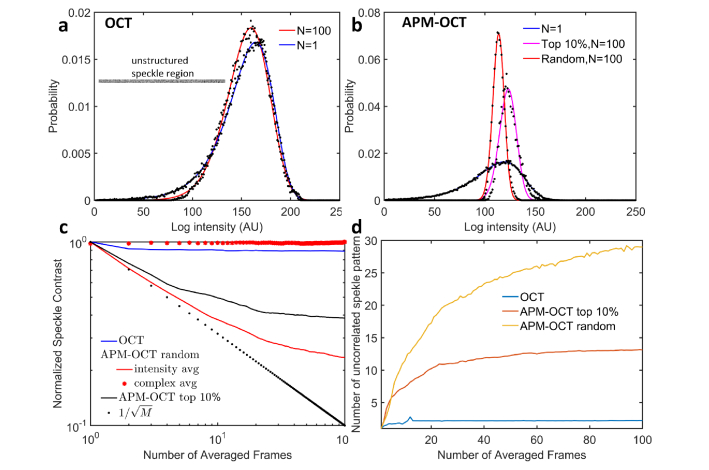
To estimate of the effective number of independent speckle patterns produced in different conditions, we first fitted speckle histograms of an unstructured region of the target imaged with normal OCT and APM-OCT B-scans, with and without averaging (Fig. 8(a), inset). As expected, the speckle intensity distributions for normal OCT changed little with averaging even 100 scans (Fig. 8(a)). In contrast, the speckle intensity distributions obtained with APM-OCT became much narrower with averaging (Fig. 8(b)). Two analyses were performed to estimate the number of independent speckle patterns. First, normalized NSC values were calculated and plotted as a function of the size of the scan sample averaged for different conditions (Fig. 8 (c)). APM-OCT is seen to yield a steeper decline in NSC with sample size than conventional OCT, but deviates from the theoretical limit given by E.q. (1). Under some conditions complex averaging has been shown to improve the signal-to-noise ratio in OCT [60]. However, such averaging produces negligible change in NSC with increased sample size for the unstructured field analyzed here (Fig. 8(c), red dots) [57]. As a second approach to determining the number of independent speckle patterns, speckle histograms were fitted with the full K distribution (Eq. (2)), and the number estimated with the appropriate parameter (m), and plotted in Fig. 8(d). This analysis also reveals that APM-OCT produces effectively uncorrelated speckle patterns, but the number is substantially lower than total number of patterns generated.

Fig. 8.

Analysis of speckle statistics of an unstructured target. (a) Experimental (black dots) and best fitting theoretical distributions (lines) of speckle intensity from a 500 × 15 pixel portion of the Air Force target obtained from a single B-scan and from the average of 100 B-scans (inset shows a single scan). The fitted curves were generated with Eq. (2) with m = 1 (blue curve, α = 23, μ = 2.4 × 10³) and m = 2.2 (red curve, α = 2.2, μ = 2.3 × 10³). (b) Experimental data and fitted curves for results collected with APM-OCT: N = 1 (black dots, blue curve; Eq. (2), m = 1, α = 30, μ = 287); average of N = 100 with random DM configurations (black dots, red curve; Eq. (2), m = 29, α = 29, μ = 212); average N = 100 using top 10% DM configurations (black dots, magenta curve; Eq. (2), m = 13, α = 13, μ = 339). The conversion of the histograms to a logarithmic axis and least-squares fitting were performed with the code provided in [58]. (c) Dependence of speckle contrast on the number of B-scans averaged for different cases (see legend). (d) The estimated number m of uncorrelated speckle patterns as a function of the number of B-scan frames averaged.

4.3 Comparison with similar methods of speckle reduction

Many different approaches to reducing speckle noise in imaging systems employing coherent light have been proposed [2,16] (cf. Introduction). Methods such as that of Liba et al. [29] provide relatively little control: first, because the distorted PSF is not readily determined, which decrease the capability for optimization; second, because the class of permitted distortions is limited and cannot be easily and precisely varied as would be needed in application with different wavelength and/or samples. APM-AO-OCT overcomes these limitations, and “gives the experimenter precise control of the PSF on a rapid trial-by-trial basis, providing a quantifiable and repeatable way to explore and optimize the method. Furthermore, APM-AO-OCT is intrinsically compatible with adaptive optics, offering a natural way to reduce speckle while preserving AO-enhanced lateral resolution.

Recently, it was also reported that averaging of multiple, precisely aligned volumes obtained in vivo OCT imaging can reduce speckle noise and reveal novel cellular scale structure [26,27]. It was hypothesized that such averaging is effective because of the random movement of sub-PSF size scattering elements in cells. This approach is passive, however, and limited by the time scale and extent of the underlying scatterer motions, which imposes a characteristic time window for the decorrelation of the speckle pattern between images. The in vivo results presented here confirm the effectiveness of pure averaging, but also show that the active approach of APM-AO-OCT can be considerably more efficient (Figs. 5 and 6).

4.4 Future directions

The broad adoption of adaptive optics continues to revolutionize imaging science and has spurred the development of wavefront correctors with increasing numbers of segments and speed, at even lower cost. In principle, APM-AO-OCT could also be implemented with spatial light modulators (SLM) [61], or other deformable mirrors (e.g. AlpAO, BMC Inc., etc.) [62–64]. Exploration of alternative PSF shaping methods [65] and more efficient ways of generating appropriate wavefront deformations should speed the routine implementation of APM-AO-OCT. Moreover, OCT systems capable of megahertz A-scan rates have been developed [66,67]. The marriage of modern AO and ultrahigh speed OCT scan technologies should enable routine implementation of APM-AO-OCT in clinical and research settings, enhancing cellular resolution clinical diagnosis as well as basic science discovery. For example, implementation of APM-AO-OCT should lead to broader application of OCT to brain structural imaging [68,69] where the presence of speckle in images remains a major obstacle. It may also help to suppress the speckle introduced by OCT contrast agents, such as gold nanoparticles [70–72]. Finally, thanks to the improvement in the visualization of subcellular structure, APM-AO-OCT should enable a more precise localization and quantification of retinal optophysiological signals, which provide non-invasive, label-free measurement of photoreceptor function [73–77].

Funding

UC Davis Research Investments in the Sciences and Engineering (RISE) program; National Science Foundation (NSF) (I/UCRC CBSS Grant); National Eye Institute (NEI) (EY026556, EY02660, EY012576 (Core Grant), T32 EY015387).

Disclosures

R.J.Z, E.N.P and P. Z are listed as inventors on a patent application related to the work presented in this manuscript.