Physiologically-based modeling of monoclonal antibody pharmacokinetics in drug discovery and development

Abstract

Over the past few decades, monoclonal antibodies (mAbs) have become one of the most important and fastest growing classes of therapeutic molecules, with applications in a wide variety of disease areas. As such, understanding of the determinants of mAb pharmacokinetic (PK) processes (absorption, distribution, metabolism, and elimination) is crucial in developing safe and efficacious therapeutics. In the present review, we discuss the use of physiologically-based pharmacokinetic (PBPK) models as an approach to characterize the in vivo behavior of mAbs, in the context of the key PK processes that should be considered in these models. Additionally, we discuss current and potential future applications of PBPK in the drug discovery and development timeline for mAbs, spanning from identification of potential target molecules to prediction of potential drug-drug interactions. Finally, we conclude with a discussion of currently available PBPK models for mAbs that could be implemented in the drug development process.

INTRODUCTION

Monoclonal antibody (mAb)-based therapeutics rank among the best-selling and fastest growing classes of therapeutics available on the market, with indications in many significant disease areas, including cancer, autoimmune diseases, infectious diseases, and cardiovascular disease [1,2]. These molecules are highly attractive drug candidates due to their high affinity and specificity for a target of interest. However, their high affinity for target molecules can be a double-edged sword, as interaction with target can often lead to non-linear pharmacokinetics (PK), which generally is not well-predicted using interspecies scaling approaches such as allometry. Accurate projection of human pharmacokinetics and pharmacodynamics (PK/PD) using in vitro and preclinical in vivo data would be useful in facilitating translation to clinical studies with a high probability of success. One approach that could be used in a translational setting would be scaling of mechanism-based PK/PD models from preclinical species to man; however, to date, reported model-based scaling efforts have had mixed results in the prediction of the clinical PK of mAbs.

The use of mechanism-based mathematical models to guide drug development, termed model-based drug development (MBDD), has been identified as an approach to improve decision-making throughout the drug discovery/development timeline, from lead compound selection through clinical trial design [3]. Recently, Hu and Hansen have highlighted the role that MBDD has taken in the development of antibody therapeutics, describing the utility of various types of models throughout the development timeline [4]. In their review, the authors discuss model-based approaches for target identification, lead optimization, human PK prediction, and optimization of dosing regimens; however, they suggest that different types of models may be optimal at different stages of development [4]. In an ideal scenario, a model developed at the target identification stage of drug discovery could be scaled and extended to provide utility throughout the entire development process, incorporating knowledge as it is gained.

Physiologically-based pharmacokinetic (PBPK) models are a platform that has become prevalent in recent years to predict the in vivo behavior of small molecule drugs, partially due to commercially available software for PBPK such as Simcyp and GastroPlus. The use of PBPK models represents an attractive approach for prediction of plasma and tissue pharmacokinetics (PK), as they are able to integrate knowledge across various levels, from the “macroscopic” (anatomical) space all the way down to the molecular level (protein-protein interactions). A recent review that summarized applications of PBPK in the pharmaceutical industry highlighted prediction of cytochrome P450 (CYP)-mediated clearance, CYP-based drug-drug interactions (DDIs), and prediction of food effects on absorption as areas where PBPK is routinely used in drug development [5]. In that same review, it was stated that there is only low-to-moderate confidence in the prediction of large molecule (e.g. therapeutic protein) PK using PBPK modeling, due to uncertainties in parameters related to target-mediated disposition (TMD) and the neonatal Fc receptor (FcRn)-mediated recycling pathway [5]. However, despite potential uncertainty in key parameters, there have been several predictive PBPK models of antibody disposition published that are able to well-describe the time course of drug exposure. While the limitations highlighted in the aforementioned review do present a hurdle in the development of predictive PBPK models for antibodies, published models have used ‘best guess’ approximations and assumptions based on available information in the literature to facilitate model-building efforts.

PBPK has been utilized for mAbs for over 30 years, and a brief summary of select publications in this field can be found in Table 1. The first PBPK model developed for antibodies was described in 1986 by Covell and colleagues, and it included 6 tissues (lung, gut, liver, spleen, kidney, carcass) divided into 3 layers (capillary plasma, interstitial space, cell-associated space) [6]. While this model relied on fitting of several parameters, it was able to well-characterize plasma and tissue concentration vs. time profiles for IgG, (Fab)₂, and Fab following administration to mice [6]. Several years later, Baxter et al. put forth a series of papers that were the first to describe mAb-target binding and elimination [7] and interspecies scaling to predict disposition of a targeted mAb in man [8]. In more recent years, antibody PBPK models 4 have become more complex and mechanistic in nature, expanding to include the FcRn-mediated recycling pathway, first described by Ferl only in skin and muscle [9], and later included in all tissues by Garg and Balthasar [10]. Davda and colleagues have described a PBPK model that includes FcRn in all tissues, which was able to well-characterize the target-mediated disposition of mAb CC49, and two fragments ([sc(Fv)₂]₂ and sc(Fv)₂) both in monkeys and in man [11]. More recently, the Garg model has been modified to account for the time course of endosomal transit and acidification, to more appropriately describe the IgG-FcRn interaction [12]. Shah and Betts have utilized a similar model structure as Garg and Balthasar to propose a ‘platform’ PBPK model to describe antibody disposition across several species (mouse, rat, monkey, and man) [13]. The platform PBPK model has since been applied to infer antibody biodistribution coefficients, which could be used to project tissue concentrations from plasma data for mAbs [14] and for antibody fragments [15]. These models have since been expanded to describe target-mediated, non-linear PK of mAbs in mice [16,17], in monkeys [18], and in man [19,20].

Table 1:

Timeline of select publications in mAb PBPK

Year	Authors	Key Advances	Reference
1986	DG Covell et al.	First PBPK model for IgG	[6]
1994	LT Baxter et al.	Impact of target binding in PBPK	[7]
1996	LT Baxter et al.	Interspecies scaling of PBPK to man	[8]
2005	GZ Ferl et al.	Incorporation of FcRn in some tissues	[9]
2007	A Garg and JP Balthasar	Incorporation of FcRn in all tissues	[10]
2008	JP Davda et al.	Consideration of TMDD for mAb fragments	[72]
2012	L Abuqayyas and JP Balthasar	A priori prediction of non-linear PK in mice	[16]
2012	Y Chen and JP Balthasar	Inclusion of endosomal transit/acidification	[12]
2012	DK Shah and AM Betts	Platform PBPK model across several species	[13]
2013	Y Cao et al.	First minimal PBPK model for mAbs	[24]
2015	PM Glassman et al.	A priori prediction of non-linear PK in monkeys	[18]
2016	PM Glassman and JP Balthasar	A priori prediction of non-linear PK in humans	[19]

In addition to the use of full PBPK models to describe the disposition of mAbs, several groups have proposed the use of ‘minimal’ or ‘lumped’ PBPK mode ls for antibody therapeutics. Rather than including a large number of tissues in the model, these approaches reduce the structure to only include key sites of distribution (e.g. tumor) or lump tissues with similar properties (e.g. perfusion, permeability, etc.) to simplify the overall model structure. Notably, these simplified model structures have been employed in commercially available PBPK software, such as Simcyp, which includes both a reduced structure that only includes crucial tissue sites of distribution [21,22] and full PBPK models for protein therapeutics [23]. Additionally, a series of papers has been published that lumps tissues with similar permeabilities to describe the plasma PK of mAbs [24–27]. While these simplified models do not retain the capacity of more complex models (e.g. full PBPK) to predict the behavior of several species of mAb (free mAb, mAb-target complexes) in plasma and in tissues, they do present a ‘middle ground’ between simple compartmental models and full PBPK. By including physiological parameters into these models, groups are able to include a level of anatomical relevance without requiring the complexity of full PBPK models.

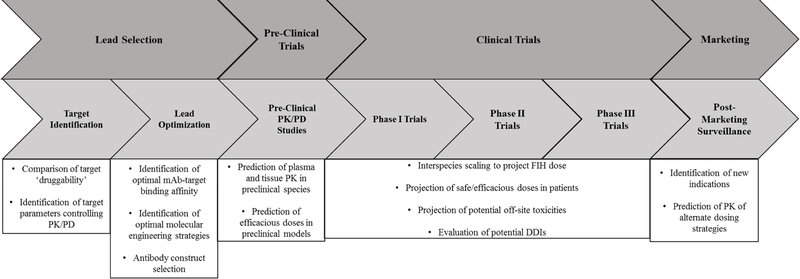
In this review, the general determinants of mAb PK will be discussed in the context of crucial parameters for PBPK model development (for a more focused discussion of mAb PK/PD, interested readers are directed to [28]). A schematic showing the key points in the drug development timeline where PBPK could be useful for antibody therapeutics is shown in Figure 1. Following these discussions, a broad overview of the current state of antibody PBPK modeling will be given, with a particular emphasis placed on the use of PBPK in the drug discovery and development process.

Figure 1.

Applications of PBPK in mAb discovery and development.

DETERMINANTS OF ANTIBODY PHARMACOKINETICS

Understanding of the processes controlling drug distribution is crucial in the development of mechanistic PBPK models. However, many parameters required for building of PBPK models, particularly for therapeutic proteins, are associated with significant uncertainty, potentially hindering development and application of these models. In this section, critical parameters related to mAb PK will be discussed in the context of the development and application of PBPK models. A general schematic of a PBPK model for IgG disposition is shown in Figure 2.

Figure 2. General structure of a PBPK model of IgG disposition.

The model includes key sites of antibody distribution, such as plasma, lung, spleen, gastrointestinal (GI) tract, liver, kidney, heart, skin, muscle, and others, as required. Tissues are connected in an anatomical fashion by plasma (Q_tissue) and lymph (L_tissue) flows. The inset shows a typical organ sub-model. Organs are divided into spaces representing the vasculature, endosomal space of the vascular endothelium, interstitial, and cellular spaces. IgG in the vascular space can enter tissue either via convection, controlled by L_tissue and the vascular reflection coefficient (σ_V), directly into the interstitial space or via fluid-phase endocytosis (CL_uptake) into the endosomal space. IgG in the endosomal space is able to interact with the neonatal Fc receptor (FcRn) either via equilibrium or kinetic binding (shown here as equilibrium for simplicity). Unbound IgG in the endosomal space is degraded and FcRn-bound IgG is recycled either to the vascular or interstitial space. Within the interstitial space, IgG can enter the endosomal space via fluid-phase endocytosis or leave the tissue via the lymphatics at a rate controlled by L_tissue and the lymphatic reflection coefficient (σ_L). If target is present, mAb within the interstitial space is able to bind to target present on the surface of cells. Target turnover is described using a zero-order synthesis rate constant (k_syn) and a first-order elimination rate constant (k_deg), and mAb-target complex elimination is described using a first-order rate constant (k_int).

Absorption

Following subcutaneous (SC) administration, antibodies are generally well-absorbed, with absolute bioavailabilities typically ranging from 50 – 100% [28]. Due to the high molecular weight and hydrophilicity of IgG molecules, it is generally accepted that the predominant route of absorption of antibody therapeutics following SC administration is via the lymphatics [29,30]. Additionally, it has been reported that SC absorption of IgG is FcRn dependent, with bioavailability of 7E3 dropping from 82.5% in wild-type mice to 28.3% in FcRn^−/− mice [28]. Later studies by Shah and Balthasar demonstrated the saturable nature of mAb absorption in mice, with an observed reduction in absolute bioavailability of 8C2 from 82% at a 10 mg/kg dose to 15% at a 3.77 g/kg dose [31]. For the development of a mechanistic SC absorption component in a PBPK model, crucial parameters would be the rate of fluid flow from injection site through the lymphatics to the circulation and the expression of FcRn in cells present in the lymphatics and lymph nodes. Values related to these parameters have not been reported with high confidence in the literature, thereby limiting development of a mechanistic, physiologically-based absorption model for mAbs.

While there has been some interest in development of mechanism-based SC absorption models for IgG [32], these models have been linked to compartmental models for systemic exposure, and there has been no evaluation of a mechanistic SC absorption model within a full PBPK model for IgG. In published PBPK models, SC absorption is simply described through administration of mAb to the interstitial space of the skin. From this site, mAb is able to leave the tissue via the lymphatics and travel through the lymph node. One example of the use of a PBPK model to describe SC bioavailability of mAbs utilized an empiric function relating the fraction of mAb returning to plasma from the lymph node to FcRn binding affinity [12]. Simulations with this model were able to predict SC bioavailability of a series of 4 Fc variant mAbs administered to mice within 40% of observed values (unpublished data). While this approach has shown predictive utility in mice, it is unclear whether this simple function will be able to predict bioavailability in higher species (e.g. monkeys and man), due to potential differences in catabolism within the subcutaneous space and FcRn capacity. Use of a model structure that mechanistically describes the capacity-limited nature of FcRn-mediated protection would likely have a greater predictive ability across species, and would instill greater confidence in a priori predictions of SC bioavailability of antibody therapeutics.

Distribution

Unlike small molecule drugs that enter tissues primarily via diffusion or transporter-mediated uptake, the primary route of tissue uptake of antibodies is via convective transport, with modeling analyses suggesting that greater than 98% of mAb enters tissue via a convective pathway [7]. For antibody to distribute into tissues, it must leave the vasculature and pass through paracellular pores to reach the interstitial space. This pathway of uptake would be dependent on the size of pores relative to the size of the antibody molecule and on the rate of fluid movement into the tissue. Mathematically, the movement of antibody from the vasculature into the interstitial space is typically described as a function of lymph flow (L_organ) and the vascular reflection coefficient (σ_V), which represents the fraction of mAb in plasma that is unable to pass through paracellular pores. The value for σ_V is often fixed to a constant value of 0.95 in healthy tissues [12,10] as a simplifying assumption, but in reality, the true reflection coefficient would differ between tissues as a function of the relative vascular ‘leakiness’. For example, a tissu e such as the spleen, which has an ‘open’ circulation and maximum pore sizes approaching 5 µm would be expected to present relatively little resistance to antibody uptake, while a tissue like the brain, which has very tight junctions, has pore sizes that are typically estimated as <1 nm, which would provide heavy resistance to antibody passage [33]. Nonetheless, in the absence of validated tissue-specific reflection coefficients, the simplifying assumption of a single vascular reflection coefficient has allowed for accurate predictions of both plasma and tissue concentration vs. time profiles of untargeted mAb administered to mice [10].

In addition to consideration of the overall resistance to antibody convection due to pore size, it is appreciated that all paracellular pores do not have the same dimensions, even within a tissue, which could provide further complications in identification of reflection coefficients. Many PBPK models of antibody disposition have considered tissue distribution using the ‘two pore formalism’, a concept proposed by Rippe and Haraldsson to describe transport across the endothelial layer via convection through large pores and fluid circulation through small pores [34]. This conceptualization of tissue uptake was applied in early PBPK models to account for fluid recirculation and IgG tissue uptake at a rate greater than possible to explain via bulk fluid flow [7]. However, in several other models a ‘one pore formalism’ has been applied where there is only one size pore present in the endothelium, and direct movement of mAb from the vasculature to interstitium is described only via convection. Justification for this approach includes the model-generated hypothesis that the vast majority of antibody that enters tissue is via convection (e.g. that very little antibody enters tissue through small pores) [7]. In many models employing the ‘one pore formalism’, IgG is described as entering tissue via FcRn-mediated transcytosis across the vascular endothelium, in addition to convective uptake (see discussion of FcRn-mediated protection of IgG in Elimination).

Further complicating prediction of antibody distribution from the vasculature into tissues are inter-antibody differences in distribution and clearance that are mediated by factors that have not yet been well described using simple quantitative relationships. It has been reported by several groups that changes in antibody charge (defined by molecular or variable domain isoelectric point) can lead to changes in tissue distribution and clearance of mAbs, potentially through altered electrostatic interactions with the glycocalyx decorating the surface of endothelial cells [35,36]. However, despite these observations, there is still some controversy as to whether the effect of charge on PK is generalizable, as it has been observed in some cases that changes in isoelectric point did not lead to changes in disposition [37]. More recently, it has been noted that the critical molecular factor in charge-mediated antibody PK may not be overall variable domain charge, but rather the presence of large patches of charge within the variable domain [38]. Despite the increased amount of available data describing the role of charge on antibody PK, there is still no quantitative relationship describing the impact of physicochemical properties (e.g. charge) of mAbs on pharmacokinetics. In several recent PBPK models, inter-antibody differences in PK have been described using empiric factors that modulate the rate of fluid-phase pinocytosis and the vascular reflection coefficient [12]. As quantitative relationships are developed that describe the role of charge (and other physicochemical properties) on mAb PK, they could readily be incorporated into PBPK models, allowing for removal of empiric scaling factors.

Distribution of antibody within tissues is typically described using several well-mixed compartments representing the tissue vascular space, endosomal space of the vascular endothelium, interstitial space, and cell-associated space. However, from a physiological perspective, it is appreciated that these spaces, particularly the interstitial space, are not entirely well-mixed. Within the interstitial space, components of the extracellular matrix (ECM) can reduce the available volume in which antibody can distribute and lead to a heterogenous distribution of drug molecules [39]. As many antibody targets are expressed on epithelial cells, and thereby are accessible to mAb within the interstitial space, this tissue heterogeneity can lead to reduced amounts of accessible target compared to what would be calculated from total target load in the tissue. Therefore, the use of well-mixed compartments may lead to estimations of receptor occupancy and target-mediated elimination from tissue that may not accurately represent the ‘true’ occupancy. Nonetheless, current models are able to make reasonable predictions of the pharmacokinetics of mAbs using this physiologically-flawed assumption of a well-mixed interstitial space; however, predictions, particularly of tissue concentrations and receptor binding, may be improved with knowledge of the ‘available’ volume and receptor quantity.

In addition to the challenges described above for accurate description of antibody distribution, tumors present further challenges to antibody uptake due to their altered physiology. Antibodies extravasating into tumor are faced with additional barriers to distribution, relative to a healthy tissue, such as abnormal vasculature, high interstitial pressure, and poor lymphatic drainage [40]. In order to describe the altered vascular permeability, several PBPK models of IgG disposition have utilized a lower value for the vascular reflection coefficient, to represent the leaky vasculature [31,30]. Following extravasation, the high affinity interaction between antibody and target can lead to a perivascular distribution pattern, due to the presence of the ‘binding site barrier’ [41–45]. Briefly, the ‘binding site barrier’ occurs due to high affinity binding between antibody and target immediately following antibody extravasation, thereby preventing distribution deeper into the tissue. To describe the observation that not all expressed target is accessible to antibody molecules, PBPK models have used an accessibility term to describe the fraction of target in tumor available for mAb binding [17,16]; however, this may change with higher doses or altered affinity, as the importance of the ‘binding site barrier’ is altered. In addition, the ‘well-mixed’ d escription of the interstitial space would not capture this perivascular distribution, but rather would describe distribution as homogeneous throughout the tumor. Two model structures have been proposed that could be useful in description of heterogeneous antibody distribution within solid tumors. First, a spherical tumor model has been proposed to describe the heterogenous distribution of drug within tumor, separating the tumor into several layers with changes in permeability between layers [46]. An advantage of this model would be that it would be able to mechanistically describe the ‘binding site barrier’ by includi ng target within each layer of the tumor, describing the rapid binding of mAb to target immediately following extravasation and poor penetration deeper into the tumor. A second structure that has been proposed to describe heterogeneous tumor distribution is a Krogh cylinder, which is able to describe the 11 distribution of antibody within tissue as a function of distance traveled from the vasculature [47]. Recently, this model structure has been linked to a PBPK model for antibody-drug conjugates (ADC) and used to simulate the effect of increasing doses of ‘naked’ antibody on ADC tumor penetration [48]. It is feasible that these model structures could be used to replace the current ‘well-mixed’ structure used to describe tumors in PBPK models, and improve predictions of heterogeneous intratumoral antibody distribution.

Elimination

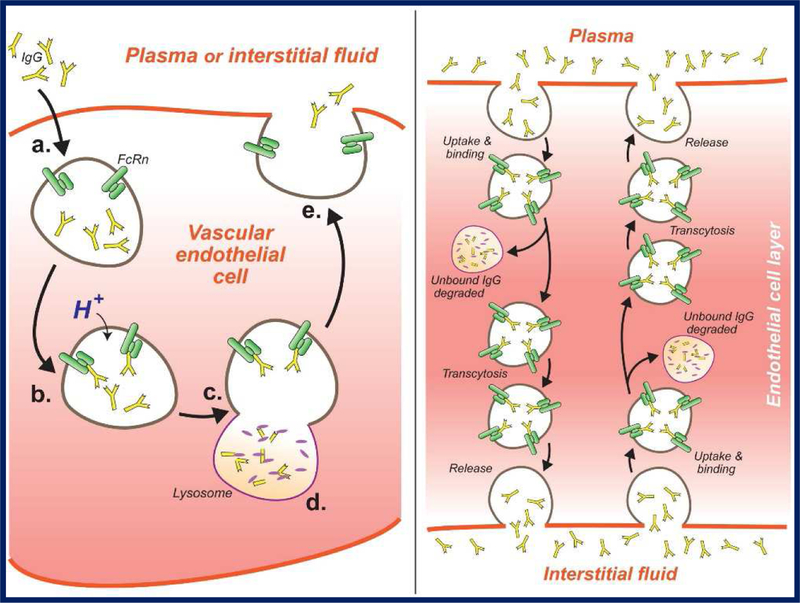
Similar to distribution, the pathways of antibody elimination differ from small molecule drugs in that they are not typically eliminated by renal filtration or by Phase I/II metabolism mediated by enzymes such as cytochrome P450s (CYP450s). Instead, antibodies are mainly eliminated via catabolism following endocytosis and transport to the lysosome. However, the efficiency of the endo-lysosomal route of elimination is blunted for antibodies following non-specific uptake due to interactions with FcRn. The presence of a protection receptor for IgG, first proposed by F.W. Brambell in the 1960s [49] and confirmed by several groups in the mid-1990s [50–52], confers IgG with its long circulating half-life (~21 days in man). Following uptake and endosomal acidification, any mAb that is bound to FcRn is protected from degradation and recycled, while unbound mAb is directed to the lysosome for degradation. This protective pathway is highly efficient, as demonstrated by the ~10-fold increase in mAb clearance observed for FcRn^−/− mice, compared to wild-type mice [10]. A summary of the intracellular trafficking and processing of IgG can be found in Figure 3.

Figure 3. FcRn-mediated protection and transport of IgG.

Left panel: Proposed mechanism for IgG protection by FcRn. (a) IgG molecules enter cells (e.g., vascular endothelial cells) via fluid-phase endocytosis; (b) H+ enters the endosome, reducing pH, and IgG binds with FcRn; (c) the endosome fuses with the lysosome, but FcRn-bound IgG is not released to the lysosome; (d) unbound IgG is released to the lysosome and catabolized by proteases; (e) the endosome fuses with the plasma membrane, the FcRn-IgG complex is exposed to physiologic pH, and IgG is released into plasma (or interstitial fluid). Right panel: Proposed mechanism for IgG transcytosis by FcRn. Following endocytosis and FcRn binding, antibody may transcytosed; antibody endocytosed at the apical membrane may be released at the basolateral membrane, and antibody endocytosed at the basolateral membrane may be released at the apical membrane. Thus, FcRn may contribute to the rate and tissue selectivity of antibody distribution (right panel based on Israel et al. [50]).

In PBPK models, FcRn-mediated protection of IgG is typically described in as occurring within the endosomes of the vascular endothelium, and is described either via equilibrium [10] or kinetic [12] binding parameters. In order to appropriately describe FcRn within the framework of PBPK models, data describing FcRn expression and the rate of uptake into endothelial cells are required. However, in addition to FcRn protection in endothelial cells, it has been reported that a significant portion of FcRn-mediated protection occurs in hematopoietic cells [53–55], which has not been described in published PBPK models to date. In recent models, uptake has been described in a rate consistent with fluid-phase pinocytosis of cultured endothelial cells [12], likely giving physiologically-relevant endosomal antibody concentrations. However, FcRn expression data has been more challenging to come by, with models relying on various estimates of protein quantity, including model-generated estimates [10,31], mRNA expression data [12], quantitative protein expression data (Western Blot or mass spectroscopy), or a mixture of multiple methods. While it is feasible to measure total tissue amounts of FcRn protein in tissue via methods such as Western Blot (Li and Balthasar, manuscript in preparation) or mass spectroscopy [56,57], the physiologically-relevant concentrations of FcRn is currently unknown. The relevant pool of FcRn that protects IgG from degradation is that which is present in recycling endosomes, and no direct measurement of this pool has been made to date. This has led to reliance on estimates of tissue-level FcRn expression values to describe FcRn-mediated protection of IgG, and while this has allowed for good characterization of antibody disposition, these assumptions may not be useful for prediction of antibody PK following administration of an FcRn inhibitor to reduce pathogenic IgG concentrations [58]. Improved understanding of the concentration of antibody within recycling endosomes should allow for improved confidence in model-based predictions following changes in FcRn expression (either pharmacologic or disease-induced).

Despite these limitations, PBPK models have been utilized to predict the sites of elimination for mAbs in the absence of target interaction. The model developed by Garg and Balthasar for 7E3 pharmacokinetics in mice predicted that skin, muscle, liver, and gastrointestinal tract were the major sites of IgG catabolism. More recently, it has been proposed that by comparing tissue uptake of mAbs conjugated to so-called “non-residualizing” (e.g. ¹²⁵I) and “residualizing” (e.g. ¹¹¹In) radiolabels could be used to infer the degree of IgG catabolism within tissues, as “re sidualizing” radiolabels would be expected to remai n within sites of catabolism following breakdown, while “non-residualizing” radiolabels would be rapidly effluxed and eliminated from the body [59]. In a recent publication, Eigenmann and colleagues have proposed a PBPK model to describe the degree of mAb clearance from tissues, utilizing data from ¹²⁵I- and ¹¹¹In-labeled antibodies with wild-type, enhanced, and reduced affinities for FcRn [60]. Their modeling suggests that liver, skin, and muscle have the greatest tissue-specific intrinsic clearances for IgG, and that the whole-body pattern of catabolism can be shifted by modulating FcRn affinity [60].

Due to the high affinity interaction between antibody and target, mAbs are often susceptible to target-mediated disposition. This process is dependent on several parameters, including antibody dose, target expression, target turnover, and target accessibility. As discussed above, the well-mixed assumption used to describe the interstitial space of organs may lead to projections of receptor occupancy (and thus target-mediated elimination) that are not in agreement with ‘true’ values. In addition to this assumption, parameters describing target expression and turnover are neither easily nor routinely measured using quantitative methods, particularly in higher species such as monkeys and man. In xenograft mouse models, target expression is typically only in the tumor, due to poor cross-reactivity of mAbs developed against human proteins to corresponding murine proteins. In this case, from knowledge of receptor number on tumor cell lines and tumor growth kinetics, the total receptor pool in tumor is easily calculated, and can be used to generate accurate predictions of antibody pharmacokinetics [16]. However, in monkeys and in man, there is often expression of target not only in diseased tissue (e.g. solid tumors), but also in ‘normal’ tissue. Therefore, c onsideration of receptor expression in all tissues is critical for the prediction of antibody PK. However, direct, quantitative measurements of tissue concentrations, particularly in healthy tissue, are neither readily available nor easily accessed in monkeys and man, limiting the available information for use in model development. Recently, PBPK models have been proposed that can generate reasonable, a priori predictions of non-linear, target-mediated pharmacokinetics of mAbs both in monkeys [18] and in man [19]. In the development of these models, an algorithm was proposed to convert semi-quantitative immunohistochemical (IHC) scores into target concentrations, using relationships developed from cells in culture. While this approach has its limitations, it has been shown to be reasonable for generating predictions of non-linear PK of several mAbs directed against multiple targets in two species. With respect to target turnover, direct measurement of membrane-bound target turnover in vivo is challenging; however, a common approach is to use in vitro data describing target turnover from internalization or pulse-chase studies to obtain estimates of the target turnover rate [16,18]. In addition to simple considerations of basal target turnover, it is often observed that binding between mAb (or ligand) and target stimulates target internalization, which can in turn affect target suppression and the degree of target-mediated clearance. This could lead to a reduced impact of target-mediated elimination upon multiple dosing, as previously observed for anti-CD3 mAbs [61]. Therefore, careful consideration of the relative rates of target turnover in the presence and absence of binding is critical for prediction of target-mediated elimination, particularly following multiple doses.

An additional complication that is present for certain targets is the shedding of antigen by tumor cells, which can lead to high local concentrations of target in the tumor interstitium as well as in the systemic circulation. This additional pool of target can affect the PK and biodistribution of therapeutic mAbs and can be driven by the degree of antigen shedding, the turnover of shed antigen from the circulation, and the elimination of mAb-antigen complexes from the blood. Recently, Malik et al have proposed a population PBPK model for trastuzumab (anti-HER2) that included inter-individual variability in key parameters, mainly related to HER2 expression, shedding and turnover. This model was able to well-characterize the mean and variation in plasma PK of trastuzumab in patients [62]. Li and colleagues have utilized a minimal PBPK format with antigen shedding to describe the same antibody-target system, and have investigated the interplay between various factors (e.g. degree of target shedding, shed target turnover, binding to shed antigen), on the plasma PK of trastuzumab [63]. These approaches may be useful not only for prediction of the non-linear, target-mediated PK of mAbs that bind to shed antigens, but also for mAbs against soluble targets (e.g. IgE or PCSK9).

Many mAbs are directed against targets not present within tissues, but rather on the surface of blood cells such as lymphocytes, including CD4 and CD20. Development of PBPK models for mAbs directed against these targets represents a unique opportunity, as the target cells are readily accessible via a blood draw, and the degree of target expression can be directly measured in patient populations. However, these cells are not exclusively present in the circulation, but rather are constantly cycling throughout the body, and may reside within lymphoid organs (e.g. lymph nodes, spleen, and bone marrow) [64]. This cellular trafficking behavior has been previously described in compartmental PK models for antibody therapeutics using rate constants for transfer [65,66]. Recently, we have developed a PBPK model for lymphocyte-targeted mAbs that describes cellular trafficking between the blood and lymphoid organs using the spleen as a representative lymphoid organ [20]. Not only was this model able to well-characterize the plasma PK of anti-lymphocyte mAbs, but also the time course of receptor occupancy and expression following antibody administration.

APPLICATIONS OF FULL PBPK MODELS FOR MONOCLONAL ANTIBODIES

With growing understanding of the determinants of IgG disposition, the complexity and predictive capabilities of PBPK models for mAbs have greatly improved since the description of the first antibody PBPK model three decades ago. In this section, several applications of mAb PBPK models will be discussed, with particular emphasis on the use of modeling in the drug discovery and development timeline.

Identification of ‘Druggable’ Targets

At the onset of any drug discovery program, identification of a target of interest is a critical step. Part of the target selection process is identification of the ‘druggability’ of a target of interest, through analysis of expression patterns in healthy and in diseased tissue, the target’s role in disease development and progression, and how target properties might play a role in efficacious dose (i.e. would the theoretical efficacious dose be feasible to administer to patients). One approach that could be used to identify possible targets for drug discovery programs would be to use PBPK models to generate predictions of doses required to achieve a targeted receptor occupancy. Using assumptions highlighted in previous sections and measurements of key target parameters (e.g. expression and turnover), simulations could be performed for a target of interest to determine dose levels that would be required to achieve a targeted exposure or receptor occupancy. While, to date, there has been no published example of the use of a mAb PBPK model to identify target ‘druggability’, it is not unreasonable to project that this approach could be used with success by an early discovery group. A potential exercise to validate this approach would be to retrospectively project receptor occupancy and efficacious doses for mAbs directed against successful and failed antibody targets, either using in-house or published data. In addition to demonstrating the utility of this approach to discovery teams, this could also lend mechanistic insights into the reasons why development programs for certain targets were unsuccessful, potentially leading to hypotheses as to what properties a potential drug against this target might require.

Design of Lead Molecules

Following identification of a ‘druggable’ target, selection of a lead compound from a library of possible molecules would be the next significant step in a discovery timeline during which PBPK could play a significant role. At this stage, groups must make decisions regarding the desired target binding properties (equilibrium affinity and binding rate constants), FcRn binding properties, effector functions, and what antibody construct would be optimal for the proposed indication (e.g. IgG, Fab, scFv, etc.). In many cases, molecules with the highest target binding affinity are selected and cloned into an IgG backbone with the desired effector functions; however, this approach is empirical in nature and may not necessarily provide the ‘best’ molecule to treat the disease of interest. For simple affinity or Fc engineering, sensitivity analyses with a PBPK model may provide insight as to how changes in a parameter of interest could lead to changes in PK/PD properties for a mAb directed against a target of interest. One example of the use of PBPK to predict ‘optimal’ molecular engi neering strategies was described by Chen and Balthasar. In this work, the authors used a catenary PBPK model of IgG disposition (where binding between mAb and FcRn is described using a series of transit compartments representing different pH values) to predict how changes in binding rate constants for the interaction between IgG and FcRn would change antibody half-life in mice. Simulations suggested that increases in the association rate constant (k_on) at pH 6.0, but not decreases in the dissociation rate constant (k_off) at pH 6.0 would be expected to lead to improvements in antibody half-life [12]. In addition, it was hypothesized that increases in k_on at intermediate pH values of 6.5 – 7.0 in combination with increases in k_on at pH 6.0 would be expected to lead to large, synergistic improvements in PK [12]. The mechanistic rationale for these hypotheses is the observation that the reported dissociation half-life (~6–60 minutes) between IgG and FcRn at pH 6.0 is often much longer than the half-life of endosomal recycling (~7.5 minutes), thereby further decreases in the dissociation rate would not lead to enhancements in the fraction of IgG that is bound by FcRn, and thus protected from lysosomal degradation, within the endosome [12].

In addition to simple affinity and Fc engineering, there have several recent publications describing a more exquisite antibody engineering strategy, development of ‘catch and release’, or pH-sensitive, mAbs [67,68]. Briefly, ‘catch and release’ mAbs have hi gh affinity binding to target at extracellular pH (7.4), but rapidly dissociate from target at pH values associated with the early endosome (pH 5.5 – 6.0), typically through protonation of histidine residues in the complementarity-determining region (CDR) of the antibody or in the target epitope recognized by the mAb. These engineered molecules have been shown to lead to selective elimination of target molecules following endocytosis and abrogation of target-mediated elimination (and enhancement of exposure) in preclinical models [67,68]. Recently, we have published a PBPK model that is able to describe a significant portion of the difference in clearance observed between a wild-type and a ‘catch and release’ anti-PCSK9 mAb [69]. Using this model, simulations were performed that suggested that rapidly turned over targets with high baseline expression relative to the targeted therapeutic dose would be those for which development of ‘catch and release’ antibodies would have the most benefit over conventional mAbs [69].

Beyond manipulation of individual amino acids responsible for binding to target or to FcRn, there has been interest in the development of antibody-based molecules that retain key features of the parent molecule (e.g. high target affinity) while altering other properties (e.g. size, toxic payload, etc.) to obtain the desired PK/PD properties. As the processes controlling distribution of these antibody constructs are similar to those which control IgG disposition, PBPK models based on those developed for full mAbs have been utilized to characterize the PK of other constructs. In fact, the first two publications describing PBPK models for IgG also utilized PBPK to characterize the disposition of untargeted and targeted F(ab’) ₂ and Fab’ fragments in mice [6,7]. In a later publication, Ferl and colleagues utilized PBPK to describe the plasma and tissue pharmacokinetics of scFv-Fc fusion proteins; however, this model did not incorporate FcRn-mediated protection of these molecules [70]. Davda and colleagues have reported the use of a PBPK model developed for targeted IgG to describe the disposition of di- and tetravalent scFv constructs of the parent IgG [11]. More recently, Sepp et al used a full PBPK model to characterize the PK of a domain antibody and mice, including FcRn recycling and renal filtration of the construct [71]. In addition to various sized constructs, PBPK has been used to describe the disposition of antibody constructs, both for antibody-directed enzyme prodrug therapy (ADEPT) [72] and for antibody-drug conjugates [48,73]. The use of these models to describe the disposition of various antibody constructs suggests that PBPK may be useful in characterizing how various strategies may alter antibody PK, and could be used to inform groups seeking to determine the ‘optimal’ construct for a given application.

Prediction of Mouse Pharmacokinetics and Distribution

After lead selection and characterization of in vitro properties of the test antibody (e.g. binding affinity, cytotoxicity, etc.), lead mAb pharmacokinetics and efficacy are typically first assessed in mouse models. PBPK models, informed by prior information regarding target properties in the model system of interest and in vitro properties of the lead molecule, can be used to simulate plasma and tissue concentration vs. time profiles and anticipated receptor occupancy at a range of doses. Most PBPK models of IgG disposition published to date have focused on characterization of mAb PK in mice [16,7,12,11,9,10,17]. One recent example of the use of PBPK to predict the PK and distribution of mAbs in mice is the model described by Garg and Balthasar, which was the first antibody PBPK model to incorporate FcRn-mediated recycling of IgG in all tissues. In this work, using physiological parameters, simulations (with no fitting of parameters) were able to generate good predictions of the plasma and tissue pharmacokinetics of 7E3, a mAb with no target in mice) both in Swiss-Webster mice (wild-type) and in FcRn^−/− mice, demonstrating the utility of this model structure for prediction of the non-specific distribution and elimination of mAbs [10]. The Garg model was later extended by Urva et al to include a tumor compartment [17], and this model was utilized by Abuqayyas and Balthasar to predict the plasma and tissue pharmacokinetics of an untargeted antibody (8C2, anti-topotecan) and an anti-carcinoembryonic antigen (CEA) antibody (T84.66) in mice bearing tumor xenografts with high (LS174T) and low (HT29) CEA expression [16]. Values of key parameters (receptor number, receptor turnover, tumor vascular reflection coefficient, binding affinity, etc.) were obtained from the literature and Monte Carlo simulations were used to make predictions of plasma and tissue PK. Simulated profiles were in good agreement with observed data across a range of doses in both plasma and in tissues [16]. These publications demonstrate the utility of PBPK models in the a priori prediction of both plasma and tissue pharmacokinetics of mAbs administered to mice (both healthy and tumor-bearing).

Interspecies Scaling of Pharmacokinetics

As a molecule moves through early development and progresses from rodent studies to non-human primates and finally moves into clinical studies, accurate projection of PK can be very useful, particularly in the design of clinical trials and selection of the first in human (FIH) dose. Due to the conserved nature of processes controlling non-specific elimination of mAbs (e.g. linear processes), scaling of mAb PK in the absence of target-mediated elimination is relatively straightforward, and often can be described using the same model structure as for preclinical species (e.g. rodents) [13]. However, as discussed above (see Elimination), target expression in both healthy and tumor tissue can contribute to target-mediated elimination in monkeys and in man, and these values are not easily measured in higher species. Protein expression data is very rarely reported quantitatively for humans, particularly in healthy tissue; however, other semi-quantitative measurements of protein expression are available in the literature (e.g. IHC scores and proteomic datasets). Through the use of an algorithm relating IHC scores to interstitial receptor concentrations, we have recently scaled a PBPK model to monkeys [18] and to man [19] and have shown its ability to make reasonable predictions of the plasma PK of several antibodies exhibiting non-linear PK, using a strategy similar to that described for mice (see Prediction of Mouse Pharmacokinetics and Distribution) [16]. While the limitations of this approach are acknowledged, the use of IHC scores to make ‘best guesses’ as to tissue target concentrati ons presents one possibility for mechanistic description of target-mediated processes (binding and elimination) in PBPK models.

These recent publications describing the use of PBPK models for a priori prediction of the plasma PK of mAbs in monkeys and in man suggest that this platform has potential to be a useful tool in translational research. While published work has only focused on prediction of the plasma PK of mAbs directed against epithelial antigens, extensions of this model to predict the PK of mAbs directed against other classes of targets (e.g. soluble targets and lymphocyte antigens) are a logical progression from the currently published work. Additionally, it would be relatively simple to adjust model outputs to make predictions of the time course of receptor occupancy or tissue mAb concentrations. In a translational setting, PBPK could be used to identify potential FIH or efficacious doses, through the use of simulations to predict targeted plasma concentration vs. time profiles or efficacious receptor occupancies. Also, through consideration of target occupancy in healthy tissues, it could be feasible to make predictions of potential sites of toxicity and toxic doses. Using a validated model, these approaches could lead to an informed clinical trial design with a high probability of success.

Prediction of Potential Drug-Drug Interactions

While drug-drug interactions are frequently considered for small molecule therapeutics, particularly with respect to drug-metabolizing enzymes and transport proteins, the potential for DDIs involving mAbs is just now starting to gain appreciation. With an understanding of the underlying mechanisms driving DDIs, PBPK can be useful in the prediction of the potential significance of DDIs involving antibody-based therapeutics. In their PBPK model of anti-CEA mAb disposition, Abuqayyas and Balthasar used prior information describing the influence of anti-VEGF treatment on tumor vascular volume, plasma flow rate, lymph flow rate, and vascular permeability to make predictions of the influence of anti-angiogenic therapy on mAb disposition. Simulations with this model were able to well-predict (with no fitting of parameters) the observed decrease in anti-CEA mAb tumor exposure observed following anti-angiogenic therapy [16]. While this example demonstrates the potential for prediction of DDIs with ‘naked’ antibody therapy, other antibody-based cons tructs may also lead to DDIs. In some cases, the small molecule component of antibody-drug conjugates could be susceptible to transporter or enzyme-mediated DDIs (either as victim or as perpetrator). A recent publication used a semi-physiologic model to describe potential CYP3A-mediated DDIs observed following treatment with monomethyl auristatin E 22 (MMAE)-containing ADCs. The authors were able to well-characterize the time course of free MMAE following brentuximab vedotin treatment, and simulated changes in MMAE disposition following treatment with a CYP3A inhibitor (ketoconazole) and inducer (rifampicin) [74]. By combining PBPK models of antibody disposition and small molecule drug disposition, not only will prediction of ADC PK be facilitated, but it also may be possible to predict the impact of co-administered drugs on the pharmacokinetics of released payload.

CURRENTLY AVAILABLE PBPK MODELS

As previously discussed, a recent review of the use of PBPK modeling in the pharmaceutical industry indicated that there is low to moderate confidence in the prediction of large molecule PK using PBPK due to lack of characterization of drug disposition mechanisms and target-mediated processes [5]. However, the use of PBPK-based models for prediction of antibody PK has grown due to the release of commercially available platforms. In this section, currently employed approaches for the development and application of PBPK in antibody discovery/development will be discussed.

Commercially Available Models

One hurdle to the routine implementation of PBPK models in drug discovery and development is the technical skills necessary to develop and validate these models. However, in recent years Simcyp, GastroPlus, and PK-Sim have incorporated modules for antibody PBPK into their commercially available software packages. The Simcyp platform uses a lumped approach, where organs are combined into a “Tissue Space” that is subdivided into vascular, en dothelial, and interstitial spaces. This model has been used to make reasonable predictions of the PK/PD of an anti-CD11a mAb, efalizumab [21], anti-TNFα mAb adalimumab [22], and anti-ALK1 mAb PF-03446962 [22]. In addition, this model has been extended to include the antigen shedding from tumor cells, and used to predict how changes in circulating HER2 could alter the plasma PK of trastuzumab [63]. More recently, the model has been extended to a full PBPK model for therapeutic proteins, and has demonstrated an ability to well-predict SC absorption of a range of therapeutic proteins [23]. Recently, a generic PBPK model for therapeutic proteins was described in PK-Sim, which was able to generate reasonable predictions of blood and tissue PK of mAbs and antibody fragments [75]. These pre-developed platforms such as Simcyp, GastroPlus, and PK-Sim represent useful tools for prediction of antibody PK/PD for groups lacking the resources or expertise to develop full models in house.

Minimal PBPK Models

In addition to the lumped models that have been made commercially available by Simcyp, several groups have developed minimal PBPK (mPBPK) models for therapeutic antibodies. Cao and Jusko have published a series of papers describing the use of PBPK for both small molecules and antibodies, which lumps tissues with similar permeability to drug (i.e., with “tight” and “leaky” vasculature) while describing tissue distribution as a function of lymph flow and a vascular reflection coefficient [24]. They have demonstrated that these models have utility in characterization of the plasma PK of untargeted mAbs administered to mice [24], interspecies scaling of mAb PK [76], description of non-linear, target-mediated mAb PK [25], and characterization of the clinical PK of mAbs against a wide variety of targets [26]. More recently, these models have been extended to account for the time course of endosomal transit, in order to characterize the behavior of Fc engineered and of ‘catch and release’ mAbs [77,78]. In addit ion to these general examples demonstrating the utility of this model structure, Chen and colleagues have extended the mPBPK model to include a diseased tissue (synovial fluid) and have used this structure to characterize the time course of plasma and joint concentrations of CNTO 345 (anti-interleukin 6 (IL-6)) and IL-6 in a collagen-induced arthritis mouse model [79], as well as for the PK/PD of an anti-IL-23 mAb in a psoriasis model [27]. Another extension of the mPBPK model was proposed by Chadha and Morris, who linked a mechanistic kidney model to a mPBPK model to describe the influence of diabetic nephropathy on IgG PK in a rat model [80]. While these models do not have the capacity to predict drug concentrations in all tissues simultaneously, they do represent a potential platform for groups whose interest lies in characterization of mAb PK in plasma and a tissue of interest.

CONCLUSIONS AND FUTURE PROSPECTUS

In the above sections, the integration of crucial determinants of antibody disposition into PBPK models has been discussed, with particular focus paid to those parameters that are associated with significant uncertainty. In addition, current and potential uses of PBPK throughout the drug discovery and development timeline were discussed, with several potential applications of this type of modeling being highlighted. It is anticipated that as confidence improves in critical parameters controlling antibody disposition that confidence will also grow in the applications of PBPK models throughout antibody drug discovery and development. Potential extensions of the PBPK approaches discussed here would be to generate PBPK models to predict the behavior of ‘next generation’ antibody therapeutics such as bispecific T cell engagers (BiTEs). As PBPK models of IgG disposition integrate up to date knowledge of determinants of mAb PK, the predictive abilities of these models is likely to grow. With improved predictive capacities, the use of PBPK may become routine in development of new biologics, at steps including, but not limited to, those summarized in Figure 1.