Allosteric DNAzyme-based DNA logic circuit: operations and dynamic analysis

Abstract

Recently, due to the dual roles of DNA and enzyme, DNAzyme has been widely used in the field of DNA circuit, which has a wide range of applications in bio-engineered system, information processing and biocomputing. In fact, the activity of DNAzymes was regulated by subunits assembly, pH control and metal ions triggers. However, those regulations required to change the sequences of whole DNAzyme, as separating parts and inserting extra DNA sequence. Inspired by the allosteric regulation of proteins in nature, a new allosteric strategy is proposed to regulate the activity of DNAzyme without DNA sequences changes. In this strategy, DNA strand displacement was used to regulate the DNAzyme structure, through which the activity of DNAzyme was well controlled. The strategy was applied to E6-type DNAzymes, and the operations of DNA logic circuit (YES, OR, AND, cascading and feedback) were established and simulated with the dynamic analyses. The allosteric regulation has potential to construct more complicated molecular systems, which can be applied to bio-sensing and detection.

INTRODUCTION

Recently, DNA nanotechnology becomes an attractive area that synthetic biomolecular systems are established to achieve programmable genetic information storage and transmission, such as nano-devices (1), computing operations (2), DNA-based circuits (3,4), and DNA storage (5,6). Among them, DNA logic circuit has been a rapidly developed research hot spot related to molecular sensing, information processing, computing and nano-robotics. Meanwhile, to realize the complicated DNA computing systems, lots of bio-engineered methods have been employed, such as proteins catalysis (7–9), DNAzymes cleavage (10–26), DNA/RNA strand displacement (27–34), DNA photoregulation (35), and FRET method (36).

In particular, DNAzymes (37,38) have been widely used in the field of molecular computing systems, such as primitive logic gate (39), DNA circuit (11,12), and half adder/subtractor (14,15). In a typical DNAzyme-based reaction, DNAzymes are used as computing operators by catalysing the scission of ribophosphodiester linkage. Subsequently, the separations of the cleaved substrates result in the generation of another DNAzymes or DNA strands, serving as signals to trigger downstream reactions. Therefore, it is a critical step to control the activity of DNAzyme in the reaction. In biosystems, the enzymatic activity is usually regulated by an allosteric effect, in which catalytic functions are determined by the structural changes of enzymes. Recently, the activities of DNAzymes are controlled in several ways, such as subunits assembly (11–15), pH control (40,41) and metal ions triggers (42). In these researches, the conserved domain of DNAzyme plays an important role (13) to control the activity of DNAzyme.

However, the activity of DNAzyme not only depends on the conserved domain, but also is controlled by the secondary structure. Similar to the action of other biological enzymes in nature, such as protein enzymes and ribozymes (43–45), the catalytic activity of DNAzymes can be activated or inhibited through a conformational alternation in secondary structure. Moreover, as catalytically active DNA molecules, DNAzymes play a double role in applications: to encode information used as storage media, and to catalyze specific chemical reactions serving as computing operators. So, in practice use, to keep information in an integral state and minimize extra distractions, the allosteric regulation of DNAzymes should not damage the completeness of DNA sequences and avoid introducing external contributions. In short, besides the previous DNAzyme regulation, a simple and programmable method is still required to regulate DNAzyme activity in a controllable and modular manner.

On the other hand, DNA strand displacement, a well-developed DNA regulation method, has been widely applied to the areas of nano-engineering (46), gene regulation (47), molecular detection (48) and biomolecular computing (49). It is suitable to regulate the configurations of DNA assembled structures. In addition, strand displacement is particular to facilitate the regulation of multi-level cascading DNA system (50). Therefore, it is advantageous to use strand displacement to control DNAzyme activity in an allosteric and hierarchical way.

In this study, inspired by the allosteric regulation of protein enzymes, an allosteric strategy is presented and applied to E6-type DNAzymes (10). Here, the key method is a specific strand displacement-mediated allosteric regulation that induces a conformational alteration of DNAzyme from an open to a closed structure, promoting the activity of DNAzyme from an inactive to an active state. Based on the allosteric strategy, three basic DNA logic gates, such as YES gate, OR gate and AND gate were established. Meanwhile, two-level DNA logic circuits, cascading and feedback circuit, were also established by the connection of basic logic gates. In addition, as an effective analysis method, the reaction-based numerical simulation provides feasibilities to have an insight into the reaction process and many unobservable experimental details can be revealed in quantity (51–55). To obtain a general insight into the circuit's behavior, we firstly modeled the experiments in all cases. And then, the simulations and dynamic analyses were carried out to evaluate the performance of DNA logic circuits. Using the simulation, the phenomena of response delay, activity adjustment and signal synchronization in the cascading DNA circuit, as well as the damped oscillation in the feedback circuit, were observed, demonstrating the feasibilities of regulating DNA logic circuits.

The concept of strand displacement-mediated allosteric regulation of E6-type DNAzyme is consistent with other DNAzymes with stem-loop structure, indicating that such an allosteric design can be applied to regulate more complicated activities of DNAzymes. And the DNA logic circuits presented here have the potential to be extended to achieve establishing various molecular computing systems, nano-devices, bio-sensing and disease diagnostics.

MATERIALS AND METHODS

Materials

All DNA strands were purchased from Sangon Biotech Co., Ltd. (Shanghai, China). Unmodified strands were purified by polyacrylamide gel electrophoresis (PAGE), and modified DNA strands with RNA base and fluorophore were purified by high-performance liquid chromatography (HPLC). The sequences of all strands are listed in Table S1 and simulated using Nupack as shown in Supplementary Figures S25 and S26. DNA strands were dissolved in water as stock solution and quantified using a Nanodrop 2000 spectrophotometer (Thermo Fisher Scientific Inc. USA), and absorption intensities were recorded at λ = 260 nm. Other chemicals were of analytical grade and were used without further purification.

Preparation of DNA logic gate

All DNA logic gates were formed by annealing twice: firstly, the mixture of the inhibitor DNA strands and E6-type DNAzymes in 1× TAE/Mg²⁺ buffer (40 mM Tris, 20 mM acetic acid, 1 mM EDTA2Na and 12.5 mM Mg(OAc)₂, pH 8.0) was heated at 95°C for 4 min, 65°C for 30 min, 50°C for 30 min, 37°C for 30 min, 22°C for 30 min, and preserved at 20°C; and then the substrates were added into the annealed mixture and incubated at constant temperature 20°C for 4 h. Note that no PAGE purifications were applied in all experiments.

Displacement reaction of triggering logic gates

Logic gates were triggered through displacement reaction in 1× TAE/Mg²⁺ buffer (40 mM Tris, 20 mM acetic acid, 1 mM EDTA2Na, and 12.5 mM Mg(OAc)2, pH 8.0). The input DNA strands were added to a solution containing DNA logic gates and reacted for >2 h at 20°C. Next, the displaced products were stored at 20°C for native PAGE or fluorescence detection.

Native PAGE

Samples were mixed with 6× loading buffer (Takara or TransBionovo) or 36% glycerine solution and run on 12% native polyacrylamide gel in 1× TAE/Mg²⁺ buffer (40 mM Tris, 20 mM acetic acid, 1 mM EDTA2Na, and 12.5 mM Mg(OAc)₂, pH 8.0) at 100 V for no >2 h at 4°C.

Fluorescent signal detection

The fluorescent results were obtained using real-time PCR (Agilent, G8830A) equipped with a 96-well fluorescence plate reader. The reactions were performed in 1× TAE/Mg²⁺ buffer (40 mM Tris, 20 mM acetic acid, 1 mM EDTA2Na, and 12.5 mM Mg(OAc)₂, pH 8.0) and in a typical 24-ul reaction volume at 25°C.

Simulation

The simulation and dynamic analyses of the reaction kinetics were carried out based on nonlinear grey-box model (56) using MATLAB 2017b. Firstly, all reaction formulas were modeled using explicit state-space forms (57) in a uniform schema. Secondly, the experimental data were used to estimate the unknown parameters in the mathematical model. Finally, based on mathematical model, the reaction process was simulated using updated parameters. More details can be found in Supplementary note S3.

RESULTS AND DISCUSSIONS

YES gate

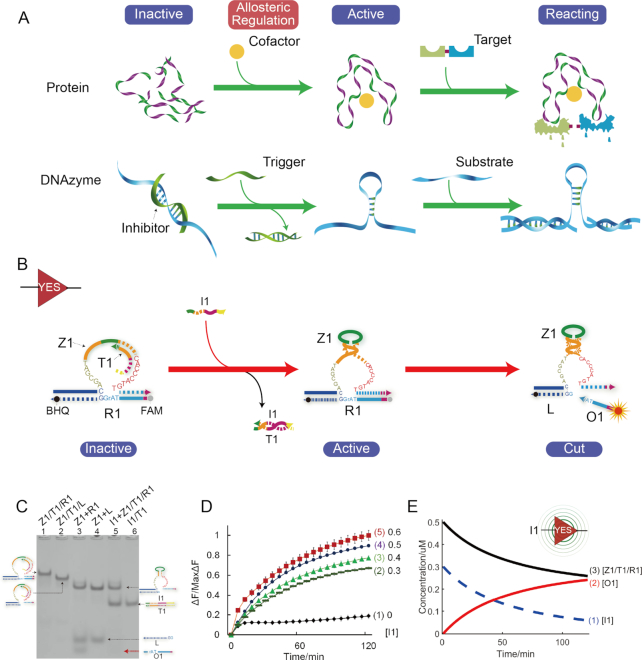
As shown in Figure 1A, similar to the conformational change of proteins in nature, for the DNAzyme with stem-loop structure, the DNAzyme function can be regulated by the inhibitor or trigger strand from an inactive to an active state coupled with the conformational alternation of stem-loop structure from an open to a closed structure. In this regulation process, the completeness of DNAzyme sequence is kept and no external contributions are needed. To demonstrate the feasibility of allosteric regulation of DNAzyme, a basic YES gate was directly constructed as follows.

Figure 1.

(A) Schematic comparison of allosteric regulation of protein and DNAzyme. (B) Illustration of YES gate. The fluorophore FAM and the quencher BHQ are functionalized at either end of substrate strand R1. And DNAzyme Z1 can cleave substrate R1 to make outputs and trigger fluorescent signals. (C) Native PAGE analysis of YES-gate products. The strands and complex involved were labeled above the lane number. The DNA complex was represented by its elements linked by slashes. Lane 1, gate complex Z1/T1/R1 consisting of strand Z1, T1 and R1; lane 2, DNAzyme complex Z1/T1/L; lane 3, products of DNAzyme digestion ([Z1]:[R1] = 1:3); lane 4, products of DNAzyme Z1 mixed with strand L, ([Z1]:[L] = 1:3); lane 5, products of YES logic operation triggered by input I1; lane 6, duplex I1/T1. (D) Time-dependent normalized fluorescence changes (ΔF/MaxΔF) at different levels of input concentrations. The sample interval was 3 min. Curves (1) to (5) demonstrate the gate responses at different concentrations of I1 as 0, 0.3, 0.4, 0.5 and 0.6μM, respectively. All data represent the average of three replicates. Error bars represent one standard deviation from triplicate analyses. (E) Time-dependent changes of concentrations of reactants during YES logic operation. Curves (1)–(3) denote time-dependent changes of concentrations of input strand I1, output strand O1 and YES gate complex Z1/T1/R1, respectively.

The YES gate (Figure 1B) is composed of three strands, DNAzyme Z1, inhibitor T1 and RNA-modified substrate R1. The YES gate can be triggered by the addition of input I1 that can displace inhibitor T1 from the allosteric regulation domain of DNAzyme Z1 (the hairpin region). After that, DNAzyme Z1 is activated and cut substrate R1 into two pieces at the cleavage site ‘TrAGG’. Then, the cleaved short segment O1 is released serving as one output and the long segment L still hybridizes with DNAzyme Z1 forming DNAzyme complex Z1/L as the other output. To monitor the YES gate in real time, fluorescence modifications were also used by modifying fluorophore and quencher at both 5′ and 3′ ends of strand R1, respectively.

Here, the YES gate was verified by PAGE gel firstly. As shown in Figure 1C, the YES-gate complex Z1/T1/R1 can be observed clearly in lane 1 as a single gel band. When triggered by input I1, DNAzyme Z1 was activated and substrate R1 was cleaved subsequently. After the digestion, segment O1 and DNAzyme complex Z1/L were released from the gate complex as shown in lane 5. Note that in the presence of excess substrate R1, segment L can be displaced from DNAzyme complex Z1/L by free substrate R1 (lane 3). To avoid this, the molar ratio of DNAzyme, inhibitor and substrate in development of all gate complexes was 1:1.2:1. Moreover, when the substrate was replaced by DNA, DNAzyme displacement still happened (Supplementary Figures S2 and S3) and some remote displacement induced by magnesium ion could be achieved (58). According to the design (Figure 1B), possible reactions of DNAzyme digestion in this study were confirmed in Supplementary Figure S1. And, the optimization of gate complex was analysed in Supplementary note S1.3. In addition, a YES gate with sticky end was constructed (Supplementary Figure S7) in which the length of substrate is increased to ensure the released segment long enough to displace the inhibitor of next gate.

A fluorescence assay was also conducted to monitor the YES gate in real time. Moreover, to better demonstrate the input-output response, a control experiment by varying the concentrations of input strand I1 was implemented (Figure 1D). In the presence of input strand I1, the significant fluorescence signal was produced (curves 2–5). In contrast, no remarkable increase of fluorescence signal could be observed in curve 1 without the addition of input strand I1. The results demonstrate the successful performance of YES gate.

To reveal the detailed behaviors in the reaction process, the simulative results are shown in Figure 1E. It can be observed clearly that the input strand I1 (curve 1) was transformed to the output segment O1 (curve 2) in proportion to the consumption of gate complex Z1/T1/R1 (curve 3). As the reaction progressed, the gate complex Z1/T1/R1 would be exhausted and input strand I1 would be transformed to output segment O1 completely.

OR and AND gate

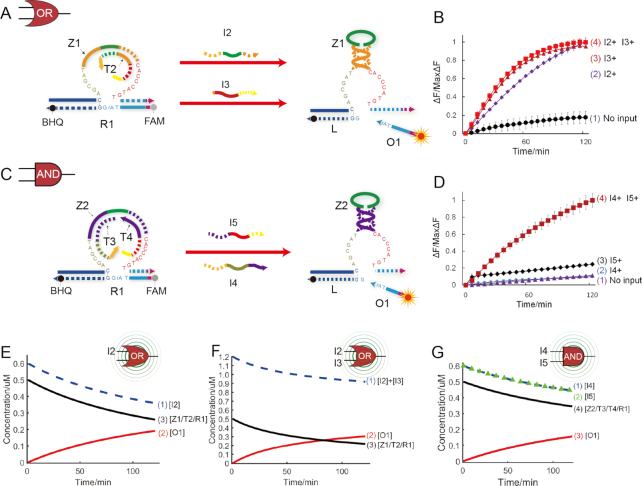
To further test the allosteric regulation mechanism, another two basic logic gates, an OR gate and an AND gate, were also established (Figure 2).

Figure 2.

(A) Illustration of OR gate. The fluorophore FAM and the quencher BHQ are functionalized at either end of substrate strand R1. (B) Time-dependent normalized fluorescence changes (ΔF/MaxΔF) during 2-h reaction process. The sample interval was 3 min. Curves (1) to (4) demonstrate the gate responses to different inputs. Here, symbol + denotes the addition of strand and symbol—denotes the absence of strand. All data represent the average of three replicates. Error bars represent one standard deviation from triplicate analyses. (C) Illustration of AND gate. The fluorophore FAM and the quencher BHQ are functionalized at either end of substrate strand R1. (D) Time-dependent normalized fluorescence changes (ΔF/MaxΔF) during 2-h reaction process. The sample interval was 3 min. Curves (1) to (4) demonstrate the gate responses to different inputs. Here, symbol + denotes addition of the strand and symbol − denotes absence of the strand. All data represent the average of three replicates. Error bars represent one standard deviation from triplicate analyses. (E) Time-dependent changes of concentrations of reactants during OR logic operation triggered by only one input I2. Curves (1)–(3) denote time-dependent changes of concentrations of input strand I2, output O1 and OR gate complex Z1/T2/R1, respectively. (F) Time-dependent changes of concentration of reactants during OR logic operation triggered by both inputs I2 and I3. Curves (1)–(3) denote time-dependent changes of concentrations of input strands I2 and I3, output strand O1 and OR gate complex Z1/T2/R1, respectively. (G) Time-dependent changes of concentrations of reactants during AND logic operation triggered by both inputs I4 and I5. Curves (1)–(4) denote time-dependent changes of concentrations of input strands I4, I5, output strand O1 and AND gate complex Z2/T3/T4/R1, respectively.

The OR gate was designed to be able to response to either trigger I2 or I3. Accordingly, two toehold regions were designed at 5′ and 3′ends of inhibitor T2, which can react with trigger I2 or I3, respectively. As illustrated in Figure 2A, upon activating with either trigger I2 or I3, the substrate R1 can be cleaved into two pieces and the fluorescence signal increase will be produced. To analyse the OR gate in quantity, a fluorescence assay was also employed. It is easy to observe that when adding either or both of triggers I2 and I3, significant fluorescence intensity increases were obtained (Figure 2B), consisting with the gel results in Supplementary Figure S8. More experimental details of OR gate can be found in Supplementary note S2.2. In addition, to demonstrate the flexibility of the allosteric regulation mechanism, Supplementary Figures S11 and S12 present another two versions of OR gate in which the inhibitor strand and trigger strand had hairpin structure.

Next, the AND gate is composed of 4 stands, DNAzyme Z2, inhibitors T3 and T4, and substrate R1 (Figure 2C). Different from the YES and OR gates, the regulation domain of DNAzyme was designed to be inhibited by two strands T3 and T4 at the same time. When adding triggers I4 or I5, only the partial of the regulation domain can be released and the activity of DNAzyme Z2 was still hindered. If and only if both of the triggers I4 and I5 are introduced at the same time, the inhibitors T3 and T4 can be released and the whole regulation domain can be released to achieve DNAzyme Z2 activation. In the fluorescence assay, the significant signal increase can be observed when using both of the triggers I4 and I5 (curve 4 in Figure 2D). In the case of inputting only one of the triggers, there was no significant fluorescence intensity increase can be obtained (curves 1, 2 and 3 in Figure 2D), consisting with the gel results in Supplementary Figure S13. Interestingly, different leakages between curves 2 and 3 can be observed, which may be attributed to the asymmetric conserved domains of DNAzyme Z2. To evaluate the stability of DNAzyme's allosteric regulation, a control experiment with variation in allosteric regulation domain was done (Supplementary Figure S14), indicating that the mutation in the allosteric regulation domain of DNAzyme had little impact on the allosteric regulation of DNAzyme.

Simulative results of the two gats were drawn in Figure 2E–G. When only trigger I2 was added (Figure 2E), the OR gate made response similar to the YES gate. But when both triggers I2 and I3 were added (Figure 2F), the OR gate could make response much more quickly (curves 1 and 2 intersected). This is due to the fact that the OR gate can be triggered by either trigger I2 or I3 (curve 1). In the presence of both triggers I4 and I5 (curve 1 and 2 in Figure 2G), the AND gate was triggered and made output (curve 3 in Figure 2G). Different from YES and OR gate, the rate of AND gate consumption (curve 4 in Figure 2G) was much slower. This is due to the fact that the trigger of AND gate is dependent on the combined effect of both triggers I4 and I5. In addition, although similar reaction formulas (equations <11> and <14> in Supplementary note S3), it can be observed from simulative results that the two gates (OR and AND) showed different input-output behaviors confirming the different reaction or response mechanisms between the two gates.

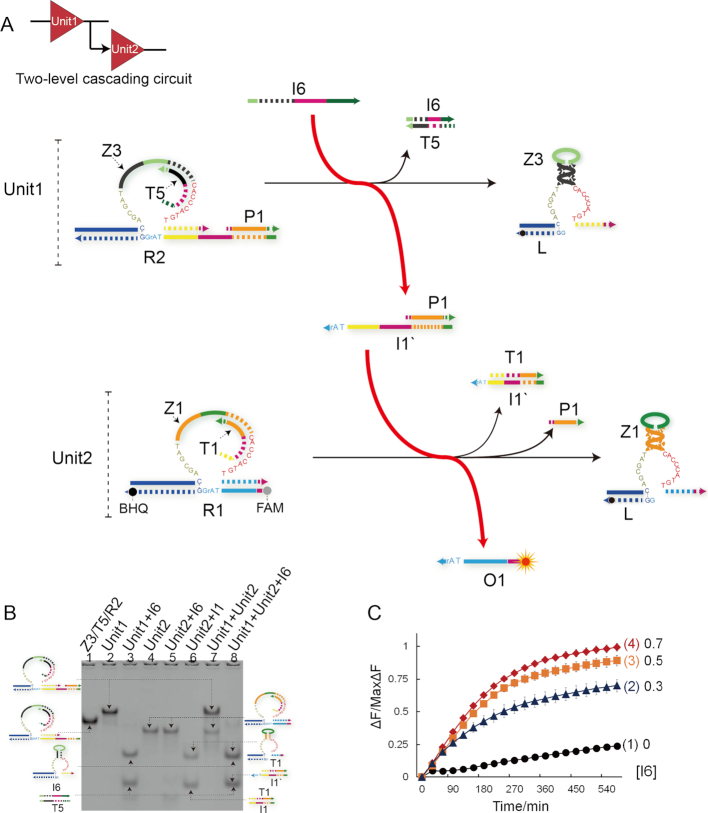
Two-level cascading logic circuit

To test the possibility of cascading logic operations, two-level logic circuit was established (Figure 3) in a modular manner. In the cascading logic circuit, the product of the upstream logic gate serves as the input targeting at the downstream gate. As shown in Figure 3A, the two-level logic circuit is composed of two YES gates in a hierarchical way: gate Unit1 → gate Unit2. The trigger I1′, targeting at downstream inhibitor T1, is designed to be initially protected by hybridizing with DNAzyme Z3. After triggered by strand I6, the DNAzyme Z3 can be activated to digest substrate R2 and release the downstream trigger P1/ I1′. Then, the DNAzyme Z1 can be activated to cleave substrate R1, thus resulting in the separation between fluorophore and quencher to produce a significant signal increase. Here, the duplex P1/I1′ plays a role of message linker to connect Unit1 with Unit2. Notably, strand P1 here is used as an assistant protector to avoid the direct crosstalk between the upstream substrate R2 and downstream gate.

Figure 3.

(A) Illustration of two-level cascading circuit. The fluorophore FAM and the quencher BHQ are functionalized at either end of substrate strand R1. (B) Native PAGE analysis of two-level cascading circuit products. Lane 1, DNA complex Z3/T5/R2; lane 2, Unit1 complex Z3/T5/R1/P1; lane 3, products of Unit1 triggered by input I6; lane 4, Unit2 complex Z1/T1/R1; lane 5, products of Unit2 in presence of input I6; lane 6, products of Unit2 triggered by input I1; lane 7, mixture of Unit1 complex and Unit2 complex; lane 8, products of two-level cascading circuit consisting of Unit1 and Unit2 triggered by input I6. (C) Time-dependent normalized fluorescence changes (ΔF/MaxΔF) at different levels of input concentrations. The sample interval was 6 min. Curves (1) to (4) demonstrate the cascading circuit responses at different concentrations of I6 as 0, 0.3, 0.5, 0.7 μM, respectively. All data represent the average of three replicates. Error bars represent one standard deviation from triplicate analyses.

The experimental results were firstly verified by PAGE gel. From Figure 3B, Unit1 and Unit2 can be clearly observed in lanes 2 and 4. And when mixing Unit1 and Unit2 together without any trigger strand, no gel band shift can be observed indicating no cross reaction occurred (lane 7). From lanes 3 and 6, the two units could make right response to the triggers I6 and I1′, respectively. But strand I6 cannot trigger Unit2 (lane 5). When strand I6 was introduced to the mixture of Unit1 and Unit2, both digested products of units and the waste I1′/T1 were produced and the gel bands of Unit1 and Unit2 disappeared (lane 8). From these facts, it can be concluded that the gel band shifts in lane 8 must be due to the trigger of stand I6, thus demonstrating well performance of the cascading circuit. The whole PAGE gel results can be found in Supplementary Figure S15.

In the fluorescence assay, to demonstrate the regulation effect of strand I6, a concentration gradient analysis was implemented as shown in Figure 3C. From Figure 3C, significant increases of fluorescence intensity change can be obtained after 10-h reaction (curves 2–4). The results show that the cascading circuit can dependently respond to the addition of input I6 at varying concentrations.

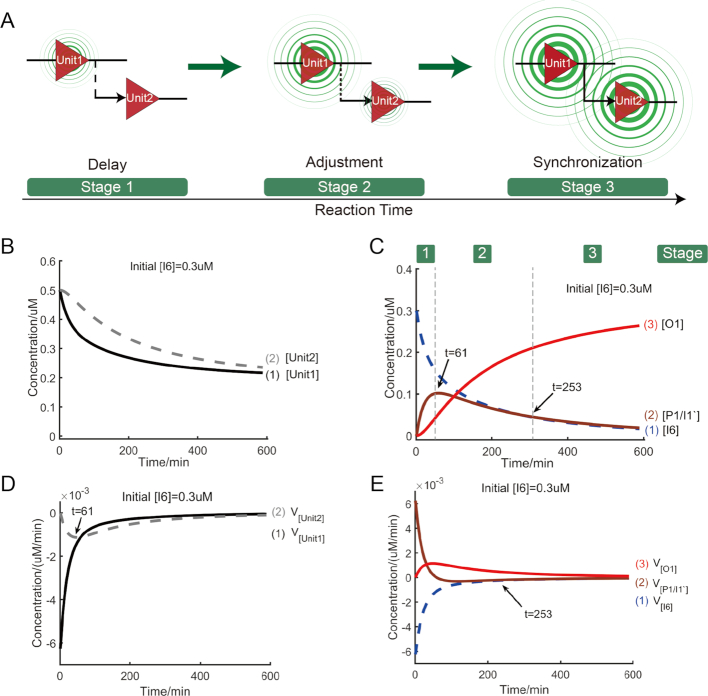
Because of sequential executions and time delay of reactions, we speculate that the cascading process can be roughly divided into three stages (Figure 4A): stage 1-delay in which Unit1 is triggered by input I6 firstly and some delays exist in the trigger of Unit2, stage-2 adjustment in which the activity of Unit2 is adjusted by the output of Unit1 P1/I1′ (also serving as the linker strand between the two gates) and stage 3-synchronization in which the activities of the two gates cooperate at a constant pace forming signal outputs in synchronization. To support our hypothesis, the theoretical model of the two-level cascading circuit (more details in Supplementary note S3.4) is constructed and the simulative results and analyses are presented in Figure 4B–E.

Figure 4.

Simulative analysis for two-level cascading circuit. The symbol V with subscript denotes the reaction rate of reactant. (A) Illustration of stage evolution of circuit. (B) Time-dependent changes of concentrations of reactants: Unit1 and Unit2. (C) Time-dependent changes of concentrations of reactants: input strand I6, linker strand P1/I1′ and output strand O1. Reaction stage was labeled on the top of the figure. (D) Time-dependent changes of reaction rates of reactants: Unit1 and Unit2. (E) Time-dependent changes of reaction rates of reactants: input strand I6, linker strand P1/I1′ and output strand O1.

From Figure 4B, within approximate 61 min, Unit1 was triggered firstly (curve 1 in Figure 4B) and the output of Unit1 P1/I1′, also as the linker of two gates, increased sharply (curve 2 in Figure 4C). While during this period, there was a delay in the response of Unit2 (curve 2 in Figure 4D) and the output of Unit2 O1 increased slowly (curve 3 in Figure 4C). The growth difference between the two outputs, P1/I1′ and O1, illustrates the time delay between the two gates in response to their respective inputs. And most of P1/I1′, as free linker strands between the two gates, did not participate the reaction of triggering Unit2 in initial stage. After the approximate 61th minute, for the consumption of Unit2, the concentration of P1/i1′ decreased gently in the cascading process (curve 2 in Figure 4C) and the circuit entered the stage adjustment. In this stage, the rate of consumption of Unit2 followed up the rate of consumption of Unit1 (curves 1 and 2 in Figure 4D). As the cascading reaction proceeding, in the second half of the reaction process (approximately after 253 min), it can be observed that the reaction rates of P1/I1′ and I6 were almost the same (curves 1 and 2 in Figure 4E), which reflected the fact that the cascading reaction entered a stage of synchronized development. In this stage, the cascading reaction pathway, I6→Unit1→P1/I1′→Unit2→O1 (red line in Figure 3A), was steadily developed and two gates cooperate in synchronization. These simulative results verified our stage-division hypothesis on cascading circuit, demonstrating the feasibility of regulating cascading circuit at different points in time.

Feedback logic circuit

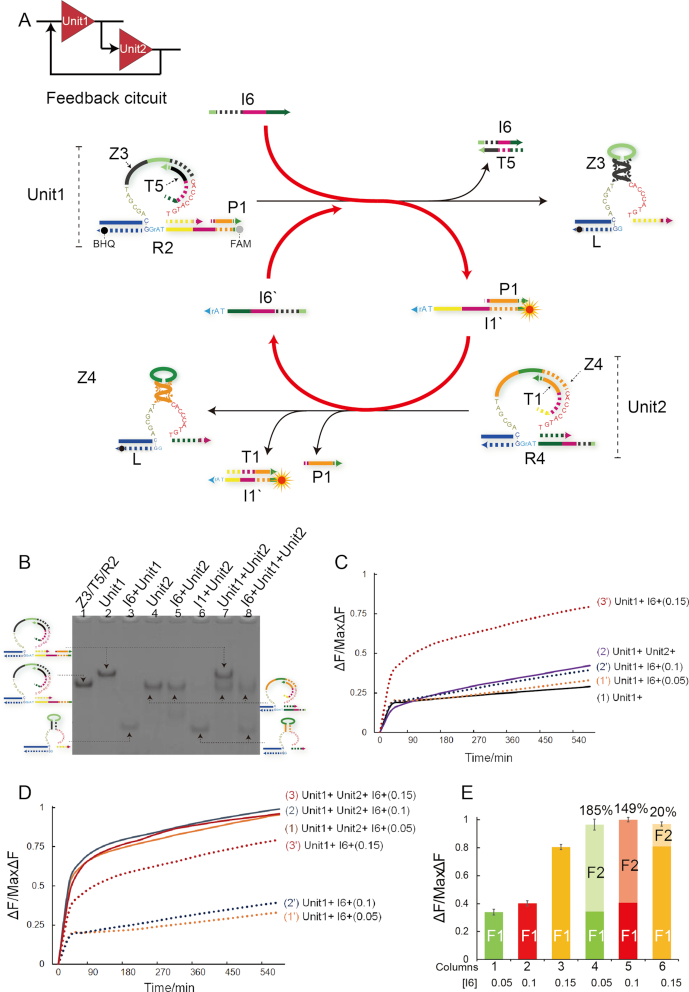
In this study, a feedback circuit (Figure 5) was also established. As shown in Figure 5A, the feedback circuit consists of two components: Unit1 and Unit2, where a cascading reaction sequence is designed as trigger I6→Unit1→Unit2→trigger I6′→Unit1 (red line in Figure 5A). In the presence of input strand I6, the Unit1 can be activated and the released duplex P1/I1′ can act on the next gate Unit2. Notably, the activated Unit2 will release the pre-protected strand I6′, which can target at Unit1 to promote the whole reaction. Therefore, the Unit2 here not only serves as a logic gate, but also a signal amplifier or energy storage element. Importantly, different from the cascading circuit above, the fluorescence reporter was designed in Unit1 as FAM and BHQ modified on two ends of strand R2, and the fluorescence intensity can increase after the cleavage of R2.

Figure 5.

(A) Illustration of feedback circuit. The fluorophore FAM and the quencher BHQ are functionalized at either end of substrate strand R2. (B) Native PAGE analysis of feedback-circuit products. Lane 1, DNA complex Z3/T5/R2; lane 2, Unit1 complex Z3/T5/R2/P1; lane 3, products of Unit1 triggered by input I6; lane 4, Unit2 complex Z4/T1/R4; lane 5, products of Unit2 in presence of input I6; lane 6, products of Unit2 triggered by input I1; lane 7, mixture of Unit1 complex and Unit2 complex; lane 8, products of feedback circuit consisting of Unit1 and Unit2 triggered by input I6. (C) Time-dependent normalized fluorescence changes (ΔF/MaxΔF) during 10-h reaction process. The sample interval was 6 min. As baselines, curve (1) demonstrates the leakage level of Unit1 and curve (2) demonstrates the leakage level of feedback circuit in absence of trigger I6. Curve (1′)-(3′) demonstrate the Unit1 responses at different concentrations of I6 as 0.05, 0.1 and 0.15 μM, respectively. All data represent the average of three replicates. Error bars represent one standard deviation from triplicate analyses. (D) Time-dependent normalized fluorescence changes (ΔF/MaxΔF) during 10-h reaction process. The sample interval was 6 min. Curves (1)–(3) demonstrate the feedback-circuit responses at different concentrations of I6 as 0.05, 0.01, 0.15 μM, respectively. Curves (1′)–(3) demonstrate the Unit1 responses at different concentrations of I6 as 0.05, 0.1 and 0.15 μM, respectively. All data represent the average of three replicates. Error bars were not plotted to avoid curves overwriting each other. (E) Fluorescence signal analysis in form of bars. The columns 1–3 correspond to the normalized fluorescence changes (ΔF/MaxΔF) of the Unit1 triggered by input I6 at 0.05, 0.1, 0.15 μM, respectively, after 10 h. The columns 4–6 correspond to the normalized fluorescence changes (ΔF/MaxΔF) of feedback circuit triggered by I6 at 0.05, 0.1, 0.15 μM, respectively, after 10 h. And the relative fluorescence increase percentage (F2/F1%) was labeled at the top of bars in columns 4–6.

Figure 5B presents the PAGE gel results of the feedback circuit. Unit1 and Unit2 can be triggered by strands I6 and I1 (lanes 3 and 6), respectively. But Unit2 cannot be triggered by strand I6 (lane 5). In addition, when Unit1 and Unit2 were mixed together without any trigger (lane 7), two separate gel bands can be observed clearly, thus indicating the stability of the gate structures and no crosstalk occurred. Interestingly, upon addition of trigger i6 (0.05 μM, very small concentration, where [Unit1] = 0.5 μM and [Unit2] = 0.3 μM), the initial gel band of Unit1 disappeared and the gel band corresponding to Unit2 faded (lane 8), demonstrating the activation of the feedback circuit. Similar to the analysis in cascading circuit, it can be concluded that the gel band shift in lane 8 must be due to the feedback of Unit2. More PAGE gel results can be found in Supplementary Figure S16.

However, more exquisite fluorescence assay was needed to confirm the feedback effect caused by Unit2. In Figure 5C, curves 1 and 2 were used as baselines to measure the leakage levels of Unit1 and the mixture of Unit1 and Unit2. In the absence of Unit2 (curves 1′–3′), the Unit1, as a YES gate, made different responses to trigger I6 at varying input concentrations. It can be observed that, in the case of low initial input concentrations of strand I6 (curves 1′ and 2′), the Unit1 cannot be triggered effectively. This is because the free inhibitor T5 (∼0.1 μM, where [Unit1] = 0.5 μM) hybridized with the input I6 and hindered the trigger of Unit1. Moreover, even some of Unit1 were triggered and released linker P1/I1′, the free inhibitor T1 (approximate 0.05μM, where [Unit2] = 0.25 μM) could break the feedback pathway (red line in Figure 5A) by hybridizing with the linker in advance (see Supplementary note S3.5 for simulative analysis). So, no significant fluorescence increase was observed in curves 1′ and 2′ except curve 3′ in Figure 5C. But once mixed with Unit2 (curves 1–3 in Figure 5D), the input I6, regardless of the initial input concentrations, would trigger the feedback circuit and significant fluorescence increases were obtained. From these facts, it can be concluded that Unit2 did feedback the Unit1.

Basic statistical analysis on the feedback effect was done in Figure 5E. In the feedback circuit, the fluorescence intensity increase is derived from the cleavage of substrate R2, which are triggered by initial input I6 and subsequent trigger I6′. Thus, the fluorescent signal increase ΔF can be divided into two categories: (i) F1, triggered by initial input I6; (ii) F2, generated from the feedback of Unit2. We speculate that feedback-induced F2 will take up larger proportion of signal increase than F1 in the case of a very small concentration of initial input I6. To verify this hypothesis, the differences between non-feedback reaction and feedback reaction were illustrated as shown in Figure 5E. In non-feedback reactions (columns 1, 2 and 3), only the Unit1 was triggered by input I6 with varying concentrations as 0.05, 0.1 and 0.15 μM, respectively. Accordingly, the obtained fluorescence intensity can be deemed as F1. On the other hand, in feedback reactions (columns 4, 5 and 6), both Unit1 and Unit2 were introduced to perform feedback circuit. All the three reactions have the significant fluorescence intensity increase as 185%, 149% and 20%, respectively. The experimental results well confirmed our speculation of the feedback effect. Besides, it is worth noting that although all three feedback reactions have almost the same fluorescence intensities changes, the results are due to the excess of inhibitor T5 which consumed some of initial input I6 in reactions 5 and 6.

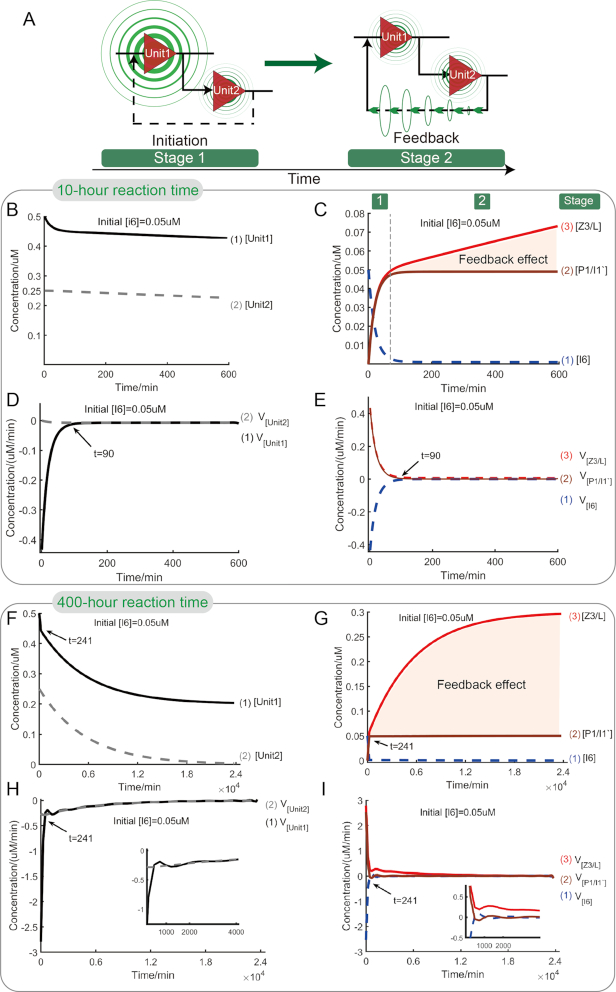
Inspired by the reaction pathway (red line in Figure 5A), we roughly divide the feedback process into two stages (Figure 6A), stage 1-initiation in which the feedback circuit is triggered by the initial input, stage 2-feedback in which the two gates promote each other for the feedback connection. To better clarify the detailed process of feedback reaction, we modeled the feedback reaction (Supplementary note S3.5) and the simulative results were analysed as shown in Figure 6B–I. For the one-one correspondence between DNAzyme complex Z3/L and strand I1′ modified by fluorophore, we selected DNAzyme Z3/L as the output to simplify the theoretical model.

Figure 6.

Simulative analysis for feedback circuit. (A) Illustration of stage evolution of circuit. (B) Time-dependent changes of concentrations of reactants, Unit1 and Unit2, during 10-h reaction process. (C) Time-dependent changes of concentrations of reactants, input strand I6, linker strand P1/I1′ and output complex Z3/L, during 10-h reaction process. Reaction stage was labeled on the top of the figure. The shaded area demonstrates the feedback effect of Unit2 to Unti1 in 10-h reaction process. (D) Time-dependent changes of reaction rates of reactants, logic units Unit1 and Unit2, during 10-h reaction process. (E) Time-dependent changes of reaction rates of reactants, input strand I6, linker strand P1/I1′ and output strand Z3/L, during 10-h reaction process. (F)–(I) present asymptotic analysis for the feedback circuit. (F) Time-dependent changes of concentrations of reactants, Unit1 and Unit2, during 400-h reaction process. (G) Time-dependent changes of concentrations of reactants, input strand I6, linker strand P1/I1′ and output complex Z3/L, during 400-h reaction process. The shaded area demonstrates the feedback effect of Unit2 to Unti1 in 400-h reaction process. (H) Time-dependent changes of reaction rates of reactants, Unit1 and Unit2, during 400-h reaction process. (I) Time-dependent changes of reaction rates of reactants, input strand I6, linker strand P1/I1′ and output strand Z3/L, during 400-h reaction process.

From Figure 6B and D, when triggered by initial input I6, Unit1 was consumed rapidly (curves 1 in Figure 6B and D) and Unit2 responded gently (curves 2 in Figure 6B and D) within initial ∼90 min. Different from the response of Unit2 in cascading circuit (curve 2 in Figure 4D), the reaction rate of Unit2 in feedback circuit shows approximate linear change during the whole 10-h reaction time, demonstrating different connection mechanism of the two gates. And due to mutual promotion, the two gates in feedback shows tighter coupling than that in cascading circuit. Correspondingly, as the output of Unit1 and the linker between the two gates, P1/I1′ was generated rapidly (curve 2 in Figure 6C). Importantly, the almost identical changes of circuit output Z3/L and linker P1/I1′ (curves 2 and 3 in Figure 6C and E) means that the responses of Unit2 and Unit1 were synchronized, demonstrating different dynamic properties from that in cascading circuit. And this result shows that in the presence of initial input I6, even very small concentration, it is the whole feedback circuit that is initiated, which is different from the sequential triggers of gates in cascading circuit. After almost 90th minute, as the linker of two gates, [P1/I1′] (curve 2 in Figure 6C) gradually approached to the initial value of [I6]. And almost at the same time, the reaction rates of input I6, linker P1/I1′, and circuit output Z3/L started to converge (Figure 6E). The fact shows that from now on, the feedback reaction sequence, I6→Unit1→P1/I1′→ Unit2→I6′→Unit1, was steadily developed until the feedback element Unit2 was completely exhausted. Moreover, as illustrated in Figure 6C, when the linker P1/I1′ almost kept constant concentration, the concentration of output Z3/L still increased significantly. So according to the mechanism of feedback circuit, the difference between [Z3/L] and [P1/I1′] must result from the feedback of Unit2 (marked region between curves 2 and 3 in Figure 6C). Based on the above simulative results, the feedback process can be regarded as a process consisting of two stages. In stage 1, the feedback circuit was initiated and the initial input I6 was transformed into circuit output with little or no loss in quantity. Meanwhile, the feedback or amplification effect was insignificant. In addition, stage 1 can also be viewed as a process of energy storage. In this stage, the drive energies needed by feedback mechanism were gradually accumulated in the form of linker strand P1/I1′ until its concentration reached the concentration of initial input I6. In stage 2, the feedback effect showed up and the initial input signal was amplified until the feedback element Unit2 was exhausted completely.

Next, to predict the final feedback effect, the asymptotic analysis for feedback circuit is presented. From Figure 6F–I, the two-stage division of the feedback process is conspicuous (the boundary time coordinates, dependent on the observation scale, were marked on the curves). Moreover, for time delay of reaction process, the damped oscillation of reaction rate can be observed in the feedback reaction sequence, I6→Unit1→P1/I1′→ Unit2→I6′→Unit1, in stage 2 (Figure 6H and I). Comparing circuit's behaviors in the two cases (Figure 6C and G), the feedback element Unit2 can be used as a linear signal amplifier in the short term (curve 3 in Figure 6C) and used as a nonlinear signal amplifier in the long term (curve 3 in Figure 6G). The above simulative results reveal more details of the feedback-circuit behavior and support our stage-division statement on feedback circuit, providing the feasibility of regulating feedback circuit at different stages.

CONCLUSIONS

In this study, a strategy of strand displacement-mediated allosteric regulation of DNAzyme is proposed and applied to E6-type DNAzymes. Based on the regulation strategy, series of basic DNA logic gates including YES gate, OR gate and AND gate were constructed, and two kinds of two-level logic circuits including cascading and feedback circuits were established in a controllable and modular manner. The experimental results indicate that the DNA logic circuits were well implemented and performed reliably. Through simulation, more details of circuit's behavior are revealed and the insight into the reaction process provides the feasibility to regulate DNA logic circuit. The concept of allosteric regulation of E6-type DNAzymes is consistent with other DNAzymes with stem-loop structure, suggesting that such a strategy is a general strategy to be applied in construction of DNA logic circuits. And the strand displacement-mediated allosteric regulation provides a simple method to control the activity of DNAzyme. We envision that, the DNA logic circuits here have potentials to construct more complicated molecular computing systems. It may open up more possible concepts and strategies in dynamic molecular control, which can lead to the development of novel nano-machine, bio-sensing and disease diagnostics.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Natural Science Foundation of China [61425002, 61572093, 61751203, 61772100, 61702070, 61672121, 61872002 and 61802040]; Program for Changjiang Scholars and Innovative Research Team in University [IRT_15R07]; Scientific Research Staring Foundation of Shenyang Aerospace University [18YB38]; Program for Liaoning Innovative Research Team in University [LT2015002]; Basic Research Program of the Key Lab in Liaoning Province Educational Department [LZ2015004]; Joint Fund of the Equipment Pre Research Ministry of Education [6141A02033607]; Beijing Natural Science Foundation [4182027]; Natural Science Foundation of Liaoning Province [20180551241]. Funding for open access charge: National Natural Science Foundation of China [61425002, 61572093, 61751203, 61772100, 61702070, 61672121, 61872002 and 61802040]; Program for Changjiang Scholars and Innovative Research Team in University [IRT_15R07]; Scientific Research Starting Foundation of Shenyang Aerospace University [18YB38]; Program for Liaoning Innovative Research Team in University [LT2015002]; Basic Research Program of the Key Lab in Liaoning Province Educational Department [LZ2015004]; Joint Fund of the Equipment Pre Research Ministry of Education [6141A02033607]; Beijing Natural Science Foundation [4182027]; Natural Science Foundation of Liaoning Province [20180551241].

Conflict of interest statement. None declared.