Abstract
Vascular smooth muscle cells (VSMCs) can regulate arterial mechanics via contractile activity in response to changing mechanical and chemical signals. Contractility is traditionally evaluated via uniaxial isometric testing of isolated rings despite the in vivo environment being very different. Most blood vessels maintain a locally preferred value of in vivo axial stretch while subjected to changes in distending pressure, but both of these phenomena are obscured in uniaxial isometric testing. Few studies have rigorously analyzed the role of in vivo loading conditions in smooth muscle function. Thus, we evaluated effects of uniaxial versus biaxial deformations on smooth muscle contractility by stimulating two regions of the mouse aorta with different vasoconstrictors using one of three testing protocols: (i) uniaxial isometric testing, (ii) biaxial isometric testing, and (iii) axially isometric plus isobaric testing. Comparison of methods (i) and (ii) revealed increased sensitivity and contractile capacity to potassium chloride and phenylephrine (PE) with biaxial isometric testing, and comparison of methods (ii) and (iii) revealed a further increase in contractile capacity with isometric plus isobaric testing. Importantly, regional differences in estimated in vivo axial stretch suggest locally distinct optimal biaxial configurations for achieving maximal smooth muscle contraction, which can only be revealed with biaxial testing. Such differences highlight the importance of considering in vivo loading and geometric configurations when evaluating smooth muscle function. Given the physiologic relevance of axial extension and luminal pressurization, we submit that, when possible, axially isometric plus isobaric testing should be employed to evaluate vascular smooth muscle contractile function.
Keywords: wall stress, mechanotransduction, vasocontraction, smooth muscle function
Introduction
Arterial vasoactivity is an important consideration when investigating mechanisms that prevent or drive cardiovascular disease. Maintenance of smooth muscle tone contributes to vascular homeostasis in many ways: it modulates systemic blood pressure, it regulates local blood perfusion to tissues, and it can prevent pressure overloading of the microcirculation and associated organ damage. Endothelial cells and vascular smooth muscle cells (VSMCs) work together to regulate the local mechanical environment in part by modulating vasoactivity [1]. Impaired regulation of vascular tone can manifest due to dysfunction of either cell type: endothelial dysfunction (e.g., decreased production of endothelial nitric oxide synthase) impairs vascular relaxation and contributes to the development of hypertension [2], and loss of smooth muscle function can predispose to thoracic aortic aneurysm and dissection [3–5]. Thus, rigorous evaluation of arterial contractility is essential for understanding vascular health and disease.
Length-dependent vascular smooth muscle contractility was shown in the 1960s to exhibit maximal active tension at an optimal value of circumferential stretch [6], a finding that has become fundamental to understanding arterial mechanics and physiology. Experimental protocols seeking to characterize contractile dysfunction of blood vessels often employ uniaxial isometric conditions, which do not mimic in vivo conditions [7]. The arterial wall and hence VSMCs are exposed in vivo to axial extension and circumferential distension, with these cells in turn modulating circumferential geometry in response to changing chemical cues and mechanical demands. To understand better the physiological behavior of vascular smooth muscle in vivo, it is prudent to evaluate function under conditions that resemble the in vivo loading and geometric configuration of the tissue. Here, we compare three well-known experimental methods: uniaxial isometric testing, biaxial isometric testing, and axially isometric plus isobaric (biaxial isometric–isobaric) testing, in two aortic regions subject to different in vivo conditions to investigate the influence of mechanical loading on overall contractile behavior. Such a comparison suggests that the maximum contractile response of vascular smooth muscle is achieved under an optimal biaxial stretch condition that depends on aortic region.
Materials and Methods
Vessel Isolation.
All animal procedures were approved by the Yale Institutional Animal Care and Use Committee. Male wild-type C57BL/6J mice were obtained from Jackson Laboratories and euthanized at 18.9 ± 1.0 weeks of age by intraperitoneal injection of Beuthanasia-D (150 mg/kg). Immediately following euthanasia, the heart was perfused with Hank's buffered saline solution (HBSS, Gibco) via a left ventricular puncture, and the aorta was excised and separated into the descending thoracic aorta (DTA), which spans from the left subclavian artery to the diaphragm, and the infrarenal abdominal aorta (IAA), which spans from the left renal artery to the iliac bifurcation. DTA segments were shortened to include only the first 4–5 pairs of intercostal arteries. Each segment was carefully cleaned of loose perivascular tissue and branches were ligated using individual threads from 9-0 nylon suture. For uniaxial isometric testing, two ring segments were cut from the distal region of each isolated vessel and the remaining vessel segment was used for one of two biaxial testing protocols. In total, 14 mice were used for this study.
Uniaxial Isometric Testing.
Ring segments (n = 7 DTA, n = 7 IAA) were mounted on opposing posts in a multichannel muscle myograph [8] and submerged in a 10 ml open organ bath at 37 °C in Krebs–Ringer solution (123 mM NaCl, 4.7 mM KCl, 1.2 mM MgCl2, 20 mM NaHCO3, 1.2 mM KH2PO4, 5.6 mM glucose, and 2.5 mM CaCl2) oxygenated with 95% O2 and 5% CO2 to maintain a pH of 7.4. The unloaded ring circumference was estimated by increasing the distance between the mounting posts until the force increased above its zero baseline. The segments were stretched circumferentially (defined as the ratio of loaded post-to-postdistance to unloaded post-to-postdistance) to 1.1 and allowed to equilibrate for 15 min, and thereafter contracted for 5 min by adding 100 mM KCl followed by washout for 10 min with Krebs–Ringer solution to reorient the smooth muscle cells toward an in vivo configuration, hereafter referred to as “active preconditioning.” This procedure was repeated at a circumferential stretch of 1.2. The optimal circumferential stretch was determined by measuring active force generation in response to 100 mM KCl at multiple values of circumferential stretch and inferring the stretch at which active force was maximal. Thereafter, dose–response curves were generated for KCl and phenylephrine (PE) by separate serial addition of each to obtain the desired vasoconstrictor concentration in the organ bath. Active dose–response curves for KCl were generated from 0 to 100 mM in increments of 20 mM; dose–response curves for PE were generated from 10−11 M to 10−4 M with each increment increasing one order of magnitude. Segments were stimulated for 5 min at each concentration with each of the vasoconstrictors.
Biaxial Isometric Testing.
Vessel segments (n = 5 DTA, n = 5 IAA) were mounted on a custom computer-controlled biaxial testing apparatus [9] and submerged in Krebs–Ringer solution, warmed to 37 °C, and bubbled with 5% CO2 as described for uniaxial testing. Unloaded axial length was determined as the length at which the segment ceases to buckle when unloaded axially at a transmural pressure of 10 mmHg, thus allowing determination of axial stretch, , where is the loaded length, and is the unloaded length. Vessels then underwent two isobaric active preconditioning contraction cycles at transmural pressures of 40 mmHg and 60 mmHg and axial stretches of either 1.10 and 1.20 (DTA) or 1.15 and 1.30 (IAA), respectively. The different axial stretches were based on previous observations of regional differences in estimated in vivo values [10]. Active preconditioning was performed by stimulating the specimens for 15 min with 100 mM KCl followed by a 10 min washout with fresh Krebs solution. The estimated in vivo axial stretch was then determined by identifying the value of at which axial force remains nearly constant over the range of pressurization from 80 to 100 mmHg. Vessels were subsequently pressurized to 90 mmHg and extended to the estimated in vivo value of axial stretch. Preliminary experiments suggested minimal differences in contractile function between 70 and 90 mmHg when vessels were within 5% of the estimated in vivo stretch (data not shown); thus, 90 mmHg was chosen based on its closeness to mean arterial pressure. Basal diameter (i.e., diameter prior to addition of vasoconstrictors) was recorded, then biaxial isometric dose–response curves were generated for KCl and PE by raising the luminal pressure to maintain outer diameter constant despite different degrees of smooth muscle contraction. For example, if the diameter of a DTA segment at 90 mmHg is 1300 μm, then addition of 5 mM KCl may require a pressure increase of 3 mmHg to maintain the diameter at 1300 μm. Dose–response curves for KCl were generated from 0 to 60 mM every 5 mM up to 20 mM and every 20 mM thereafter. The small initial step change was chosen based on preliminary observations of increased K+ sensitivity in biaxial isometric testing. Dose–response curves for PE were generated from 10−11 M to either 10−5 M (DTA) or 10−4 M (IAA) with each increment increasing by one order of magnitude. Segments were stimulated for a minimum of 5 min or until equilibration at each concentration with each vasoconstrictor.
Following active testing, the bath was changed to room temperature HBSS, which reduces SMC tone [11], and passive mechanical preconditioning was performed by pressurizing the vessels from 10 to 140 mmHg for four cycles at the estimated in vivo stretch after which the true unloaded configuration was recorded. Such passive preconditioning has previously been shown to minimize viscoelastic behavior without inducing damage such that a quasi-static state can be assumed during cyclic loading [12]. Note that active preconditioning, which involves high-potassium stimulation at fixed geometric conditions to facilitate reorientation of VSMCs toward their in vivo configuration, is distinct from passive preconditioning, which involves cyclic loading without a smooth muscle contribution.
Biaxial Isometric–Isobaric Testing.
Vessel segments (n = 7 DTA, n = 5 IAA) were mounted and preconditioned in the same manner as described for biaxial isometric testing. The in vivo axial stretch was estimated, and vessels were pressurized to 90 mmHg and extended to the estimated in vivo value of axial stretch. Dose–response curves for KCl and PE were generated separately by adding each in series and allowing the diameter to reach a steady-state minimum value at a constant pressure of 90 mmHg. Dose–response curves for KCl were generated from 0 to 100 mM every 20 mM; dose–response curves for PE were generated from 10−10 M to either 10−5 M (DTA) or 10−4 M (IAA) with each increment increasing by one order of magnitude. Segments were stimulated for a minimum of 5 min or until equilibration (often up to 15 min) at each concentration with each of the vasoconstrictors. Vessels were rendered passive by switching the solution to room temperature HBSS, and passive preconditioning was performed by cyclically loading the vessels from 10 to 140 mmHg at the estimated in vivo axial stretch for four cycles. The true unloaded configuration was then determined as described for biaxial isometric testing.
Mechanical Analysis.
Unloaded wall thickness and axial ring segment length were determined for the ring samples using a custom matlab program to analyze digital pictures of the specimens. The axial vessel length and unloaded outer diameter of the biaxial specimens were measured with the biaxial testing apparatus, as usual [10].
For uniaxial testing, loaded geometry was determined by first calculating the loaded inner circumference
| (1) |
where is the diameter of the mounting posts, and is the measured length between the posts. An effective inner diameter was calculated from this relation and, consequently, an effective circumferential stretch was
| (2) |
where is the effective inner diameter, is the unloaded outer diameter as determined from biaxial testing, is the loaded thickness, and is the unloaded thickness. Assuming incompressibility (), and equal deformations in radial and axial directions in the uniaxial ring test (), the circumferential stretch can be calculated as . With the radial stretch ratio defined as , the loaded thickness was then expressed as , and the effective circumferential stretch was solved numerically using the matlab subroutine fsolve. Values of uniaxial circumferential force prior to beginning the dose–response tests were considered to be passive, and active force was calculated as the difference between total and passive force. Note that passive preconditioning was not performed under uniaxial testing conditions to maintain general consistency with similar studies in the literature. The total circumferential Cauchy stress was calculated in the ring tests at each condition as
| (3) |
where is the measured circumferential force, and is the unloaded ring length. Note that active circumferential stress is calculated similar to active force, that is, active stress ( equals the difference between total and passive stress.
For biaxial testing, circumferential stretch was calculated as the ratio of loaded midwall diameter to unloaded midwall diameter, . The mean total value of circumferential Cauchy stress was calculated using Laplace's Law
| (4) |
where is the transmural pressure, is the loaded inner radius, and is the loaded wall thickness, which can be calculated assuming incompressibility. This mean value represents the actual value reasonably well because of residual stresses in the arterial wall [13]. The active stress for biaxial isometric testing was calculated as with 90 mmHg the initial value of . For biaxial isometric–isobaric testing, the basal stress was calculated using the loaded geometry prior to stimulation with any vasoconstrictor, with total stress calculated using Eq. (4) for each equilibrium configuration and active stress calculated as the absolute value of the difference between total and passive stress (noting that isobaric testing results in decreasing stress whereas isometric testing results in increasing stress); the effective circumferential force production was derived with a simple force balance approach using known loaded geometries and calculated circumferential stresses at passive and active states.
The axial stress can be calculated from
| (5) |
where is the axial force and accounts for the pressure acting on the cannula due to pressurization. Passive and active axial stresses were calculated similarly. Axial force is measured directly and does not need to be calculated.
The concentration corresponding to 50% of the maximum force generation, or [EC50], a metric used to evaluate the sensitivity of cells to a particular vasoconstrictor [14], was calculated by nonlinear regression analysis, namely
| (6) |
where = {uni, biax}, is prescribed as the minimum active stress, and is the maximum observed active stress generation for the given protocol , noting that the absolute maximum may be slightly higher than the observed maximum, is the concentration of the vasoconstrictor in mol/L, and is the Hill constant governing the slope of the sigmoidal curve. Nonlinear regression was performed with the matlab subroutine lsqnonlin to estimate [EC50] and .
Statistics.
To test for normality, data were mean centered and variance scaled, and a one-sample Kolmogorov–Smirnov test was performed. The Kolmogorov–Smirnov test suggested that all data were normally distributed; thus, a two-way analysis of variance with a Tukey's posthoc comparison was performed to test differences between protocol and aortic region. The statistical analysis was performed only on metrics that were appropriate for comparison across the three groups; namely, normalized mechanical metrics, including stretch and stress as well as measures of contractile sensitivity and strength. All data are presented as mean ± standard error of the mean (SEM).
Results
Data from uniaxial isometric, biaxial isometric, and biaxial isometric–isobaric testing of segments of DTA and IAA are shown in Fig. 1 in terms of changes in circumferential force, transmural pressure, and outer diameter in response to increasing concentrations of KCl (Figs. 1(a)–1(c)) or PE (Figs. 1(d)–1(f)). To facilitate equal comparison across groups, normalized values of Cauchy wall stress are shown in Fig. 2. Table 1 lists all observed and computed metrics, and Table 2 lists all relevant p-values for statistical comparison across testing protocols and regions.
Fig. 1.
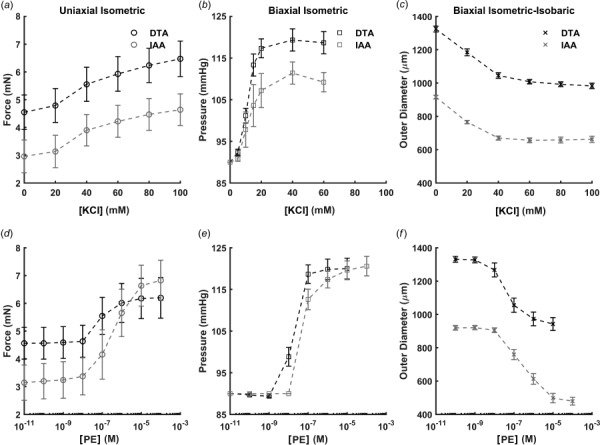
Dose–response data collected for DTA (black) and IAA (gray) using three different classes of mechanical testing protocols (left-to-right) to assess responses to KCl ((a)–(c)) and PE ((d)–(f)). Direct quantitative comparison between methods is difficult since each experimental framework naturally yields different quantities: circumferential force (uniaxial isometric testing; (a), (d)), transmural pressure (biaxial isometric testing; (b), (e)), and outer diameter (biaxial isometric–isobaric testing; (c), (f)). Data are presented as mean ± SEM.
Fig. 2.
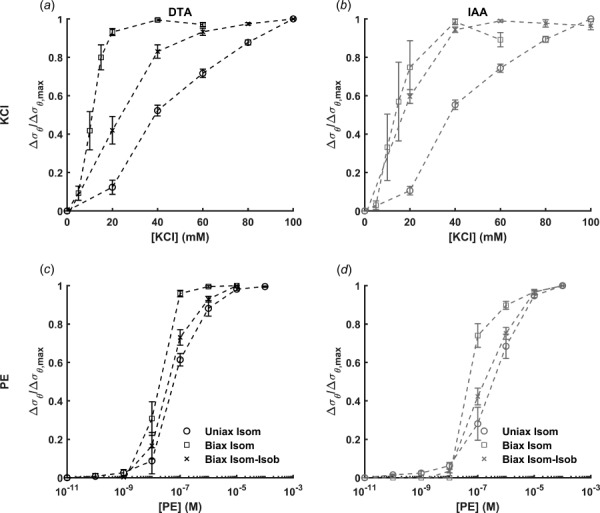
Active circumferential stress responses to KCl ((a), (b)) or PE ((c), (d)) in the DTA ((a), (c)) and IAA ((b), (d)) normalized to the maximum change in circumferential stress for uniaxial isometric (uniax isom), biaxial isometric (biax isom), and biaxial isometric–isobaric (biax isom-isob) testing. Note that calculation of Cauchy stress facilitates direct comparison across methods. These results suggest a markedly different sensitivity of potassium channels due to axial loading (uniaxial versus biaxial testing) and ability to change configuration (isometric or fixed diameter versus isobaric or fixed pressure testing) while α-adrenergic receptors were less sensitive to the type of mechanical loading. Data are presented as mean ± SEM.
Table 1.
Summary of all observed and calculated metrics for the DTA and IAA in response to KCl or PE using three experimental testing protocols. Data are presented as mean ± SEM.
| DTA | IAA | ||||||
|---|---|---|---|---|---|---|---|
| Uniaxial | Biaxial isometric | Biaxial isobaric | Uniaxial | Biaxial isometric | Biaxial isobaric | ||
| n = 7 | n = 6 | n = 7 | n = 7 | n = 5 | n = 5 | ||
| Unloaded passive configuration | |||||||
| Outer diameter (μm) | 946 ± 11 | 890 ± 32 | 929 ± 17 | 681 ± 8 | 645 ± 17 | 681 ± 15 | |
| Thickness (μm) | 120 ± 3.5 | 115 ± 2.8 | 125 ± 4.1 | 99 ± 3.9 | 100 ± 2.4 | 101 ± 3.9 | |
| Axial length (mm) | 0.87 ± 0.06 | 5.07 ± 0.14 | 5.28 ± 0.10 | 0.84 ± 0.05 | 5.58 ± 0.36 | 4.61 ± 0.12 | |
| Fixed loaded configuration for active testing | |||||||
| Axial stretch | 0.86 ± 0.01 | 1.46 ± 0.03 | 1.45 ± 0.02 | 0.91 ± 0.01 | 1.69 ± 0.02 | 1.64 ± 0.03 | |
| Potassium chloride | Loads and configurations | ||||||
| Relaxed pressure (mmHg) | — | 90 ± 0.0 | 90 ± 0.0 | — | 90 ± 0.0 | 90 ± 0.0 | |
| Pressure at maximal contraction (mmHg) | — | 120 ± 2.7 | 90 ± 0.0 | — | 112 ± 2.8 | 90 ± 0.0 | |
| Relaxed outer diameter (μm) | 1218 ± 33 | 1301 ± 46 | 1316 ± 17 | 803 ± 22 | 897 ± 18 | 909 ± 11 | |
| Outer diameter at maximal contraction (μm) | 1218 ± 33 | 1301 ± 46 | 983 ± 17 | 803 ± 22 | 897 ± 18 | 658 ± 17 | |
| Maximum change in outer diameter (%) | — | — | −25 ± 1.1 | — | — | −28 ± 2.3 | |
| Relaxed wall thickness (μm) | 104 ± 2.8 | 49 ± 2.0 | 55 ± 21 | 89 ± 4.0 | 38 ± 1.4 | 41 ± 2.0 | |
| Wall thickness at maximal contraction (μm) | 104 ± 2.8 | 49 ± 2.0 | 75 ± 3.0 | 89 ± 4.0 | 38 ± 1.4 | 60 ± 4.7 | |
| Stress calculations | |||||||
| Circumferential calculations | |||||||
| Relaxed circumferential stretch | 1.35 ± 0.03 | 1.62 ± 0.03 | 1.57 ± 0.03 | 1.22 ± 0.03 | 1.58 ± 0.03 | 1.50 ± 0.03 | |
| Circumferential stretch at maximal contraction | 1.35 ± 0.03 | 1.62 ± 0.03 | 1.13 ± 0.03 | 1.22 ± 0.03 | 1.58 ± 0.03 | 1.04 ± 0.06 | |
| Maximum change in circumferential stretch (%) | — | — | −28 ± 1.3 | — | — | −31 ± 2.8 | |
| Relaxed circumferential stress (kPa) | 30 ± 3.8 | 149 ± 9.2 | 133 ± 5.9 | 23 ± 5.4 | 132 ± 5.5 | 122 ± 5.7 | |
| Circumferential stress at maximal contraction (kPa) | 42 ± 4.1 | 197 ± 10.8 | 66 ± 3.5 | 35 ± 5.2 | 163 ± 3.1 | 54 ± 5.7 | |
| Maximum change in circumferential stress (kPa) | 13 ± 1.1 | 48 ± 4.0 | −68 ± 4.0 | 12 ± 0.5 | 31 ± 3.3 | −68 ± 4.4 | |
| Active circumferential force (mN) | 1.9 ± 0.1 | 3.9 ± 0.4 | 18 ± 1.0 | 1.7 ± 0.1 | 2.9 ± 0.4 | 14 ± 1.1 | |
| Axial calculations | |||||||
| Relaxed axial force (mN) | — | 12.0 ± 1.0 | 13 ± 0.5 | — | 5.9 ± 0.8 | 10 ± 0.5 | |
| Axial force at maximal contraction (mN) | — | 8.2 ± 1.1 | 15 ± 0.6 | — | 4.3 ± 1.0 | 10 ± 0.5 | |
| Maximum change in axial force (%) | — | 33.1 ± 4.5 | 7.6 ± 2.2 | — | 31.4 ± 8.8 | 0 ± 1.8 | |
| Relaxed axial stress (kPa) | — | 134 ± 7.3 | 127 ± 6.3 | — | 122 ± 10.8 | 147 ± 9.3 | |
| Axial stress at maximal contraction (kPa) | — | 138 ± 8.7 | 99 ± 5.6 | — | 121 ± 12.1 | 114 ± 9.1 | |
| Maximum change in axial stress (kPa) | — | 3.3 ± 1.6 | −27 ± 09 | — | −0.7 ± 1.8 | −32.3 ± 1.2 | |
| Dose–response parameters | |||||||
| Hill constant | −6.62 ± 0.31 | −11.29 ± 1.99 | 6.75 ± 0.32 | −7.16 ± 0.35 | −17.47 ± 3.36 | 7.90 ± 0.61 | |
| [EC50] (mM) | 39.62 ± 2.00 | 10.73 ± 1.03 | 23.58 ± 2.46 | 38.81 ± 1.17 | 14.03 ± 2.80 | 18.80 ± 0.86 | |
| Phenylephrine | Loads and configurations | ||||||
| Relaxed pressure (mmHg) | — | 90 ± 0.0 | 90 ± 0.0 | — | 90 ± 0.0 | 90 ± 0.0 | |
| Pressure at maximal contraction (mmHg) | — | 120 ± 2.5 | 90 ± 0.0 | — | 121 ± 2.4 | 90 ± 0.0 | |
| Relaxed outer diameter (μm) | 1218 ± 33 | 1314 ± 46 | 1329 ± 18 | 803 ± 22 | 917 ± 21 | 917 ± 14 | |
| Outer diameter at maximal contraction (μm) | 1218 ± 33 | 1314 ± 46 | 942 ± 39 | 803 ± 22 | 917 ± 21 | 479 ± 23 | |
| Maximum change in outer diameter (%) | — | — | −29 ± 2.3 | — | — | −48 ± 1.9 | |
| Relaxed wall thickness (μm) | 104 ± 2.8 | 48 ± 1.9 | 78 ± 3.2 | 89 ± 4.0 | 37 ± 1.3 | 84 ± 7.9 | |
| Wall thickness at maximal contraction (μm) | 104 ± 2.8 | 48 ± 1.9 | 119 ± 11.1 | 89 ± 4.0 | 37 ± 1.3 | 181 ± 18.7 | |
| Stress calculations | |||||||
| Circumferential calculations | |||||||
| Relaxed circumferential stretch | 1.35 ± 0.03 | 1.64 ± 0.02 | 1.59 ± 0.03 | 1.22 ± 0.03 | 1.62 ± 0.03 | 1.51 ± 0.03 | |
| Circumferential stretch at maximal contraction | 1.35 ± 0.03 | 1.64 ± 0.02 | 1.07 ± 0.03 | 1.22 ± 0.03 | 1.62 ± 0.03 | 0.68 ± 0.04 | |
| Maximum change in circumferential stretch (%) | — | — | −32 ± 2.6 | — | — | −55 ± 2.6 | |
| Relaxed circumferential stress (kPa) | 30 ± 3.5 | 152 ± 9.1 | 136 ± 4.6 | 24 ± 5.8 | 139 ± 6.3 | 124 ± 5.7 | |
| Circumferential stress at maximal contraction (kPa) | 40 ± 4.5 | 202 ± 9.9 | 59 ± 5.1 | 52 ± 7.2 | 185 ± 4.8 | 19 ± 3.7 | |
| Maximum change in circumferential stress (kPa) | 11 ± 1.4 | 50 ± 3.1 | −77 ± 5.7 | 28 ± 1.8 | 47 ± 2.0 | −105 ± 4.6 | |
| Active circumferential Force (mN) | 1.6 ± 0 2 | 4.0 ± 0.3 | 22 ± 2.0 | 3.7 ± 0.2 | 4.1 ± 0.3 | 26 ± 0.9 | |
| Axial calculations | |||||||
| Relaxed axial force (mN) | — | 10.5 ± 0.8 | 13 ± 0.4 | — | 5.5 ± 0.9 | 9 ± 0.6 | |
| Axial force at maximal contraction (mN) | — | 7.0 ± 0.7 | 15 ± 0.5 | — | 3.2 ± 1.1 | 10 ± 0.6 | |
| Maximum change in axial force (%) | — | 33.6 ± 1.2 | 18 ± 2.5 | — | 52.1 ± 15.0 | 17 ± 2.0 | |
| Relaxed axial stress (kPa) | — | 128 ± 7.7 | 124 ± 5.3 | — | 121 ± 12.9 | 140 ± 9.9 | |
| Axial stress at maximal contraction (kPa) | — | 134 ± 6.9 | 100 ± 5.0 | — | 120 ± 13.6 | 112 ± 10.0 | |
| Maximum change in axial stress (kPa) | — | 5.7 ± 1.7 | −24 ± 1.5 | — | −0.2 ± 1.0 | −27 ± 4.7 | |
| Dose response parameters | |||||||
| Hill constant | −3.16 ± 0.56 | −9.90 ± 2.45 | 2.73 ± 0.35 | −2.24 ± 0.12 | −6.28 ± 1.14 | 1.76 ± 0.07 | |
| [EC50] (nM) | 83.06 ± 17.75 | 14.59 ± 2.26 | 53.73 ± 11.08 | 509.92 ± 147.97 | 72.97 ± 8.42 | 303.56 ± 77.52 | |
Table 2.
Calculated p-values from two-way analysis of variance accounting for differences between testing protocol and aortic region
| Relaxed configuration | Potassium chloride | Phenylephrine | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λθ | λz | σθ | σz | [EC50] | [EC50] | |||||||
| Method comparisons | ||||||||||||
| DTA uniax isom | Versus | DTA biax isom | 0.0000 | 0.0000 | 0.0000 | — | 0.0000 | — | 0.0000 | 0.0000 | — | 0.0031 |
| DTA uniax isom | Versus | DTA biax isom-isob | 0.0001 | 0.0000 | 0.0000 | — | 0.0000 | — | 0.0030 | 0.0000 | — | 0.8796 |
| DTA biax isom | Versus | DTA biax isom-isob | 0.8808 | 1.0000 | 0.4597 | 0.9028 | 0.0009 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0438 |
| IAA uniax isom | Versus | IAA biax isom | 0.0000 | 0.0000 | 0.0000 | — | 0.0025 | — | 0.0000 | 0.0105 | — | 0.0095 |
| IAA uniax isom | Versus | IAA biax isom-isob | 0.0000 | 0.0000 | 0.0000 | — | 0.0000 | — | 0.0002 | 0.0000 | — | 0.9977 |
| IAA biax isom | Versus | IAA biax isom-isob | 0.5414 | 0.6279 | 0.8963 | 0.2179 | 0.0000 | 0.0000 | 0.1835 | 0.0000 | 0.0000 | 0.0506 |
| Regional comparisons | ||||||||||||
| DTA uniax isom | Versus | IAA uniax isom | 0.0442 | 0.5302 | 0.9572 | — | 1.0000 | — | 1.0000 | 0.0121 | — | 0.0030 |
| DTA biax isom | Versus | IAA biax isom | 0.9618 | 0.0000 | 0.4405 | 0.7120 | 0.0108 | 0.2158 | 0.7229 | 0.9862 | 0.3480 | 0.0063 |
| DTA biax isom-isob | Versus | IAA biax isom-isob | 0.5756 | 0.0000 | 0.7700 | 0.3425 | 1.0000 | 0.0803 | 0.7370 | 0.0001 | 0.6992 | 0.0018 |
Numbers in bold denote statistical significance defined as p < 0.05. Metrics for the relaxed configuration were taken from data prior to KCl stimulation, noting that comparisons for data prior to PE stimulation yielded similar results.
Axial Extension Alters Sensitivity to Vasoconstrictors.
In DTA segments, the optimal uniaxial stretch for maximal active force development was a modest 1.35 ± 0.03. In contrast, the estimated in vivo midwall circumferential stretches during biaxial isometric testing were 1.62 ± 0.03 during KCl stimulation and 1.64 ± 0.02 during PE stimulation. The slight difference in optimal stretch between vasoconstrictors could be due to minimal loss in tone over the course of testing. Though statistical comparison between vasoconstrictors was not the focus of this study, a two-tailed paired t-test was performed between vasoconstrictors for the relaxed circumferential stretch of the DTA during biaxial protocols, and the differences were not statistically significant (p = 0.30 and 0.10 for isometric and isobaric protocols, respectively), suggesting that loss of tone was negligible. Calculating the active circumferential stress and normalizing it to the maximum value revealed a qualitatively increased sensitivity to KCl and PE when comparing biaxial isometric and uniaxial isometric testing (Figs. 2(a) and 2(c)). Regression analysis revealed decreased [EC50] values (i.e., increased sensitivity) for KCl (39.62 ± 2.00 mM versus 10.73 ± 1.03 mM) when comparing uniaxial versus biaxial isometric testing (Fig. 3(a)), suggesting a critical role of axial stretch in VSMC response to KCl. Similar but less dramatic differences were observed for responses to PE.
Fig. 3.
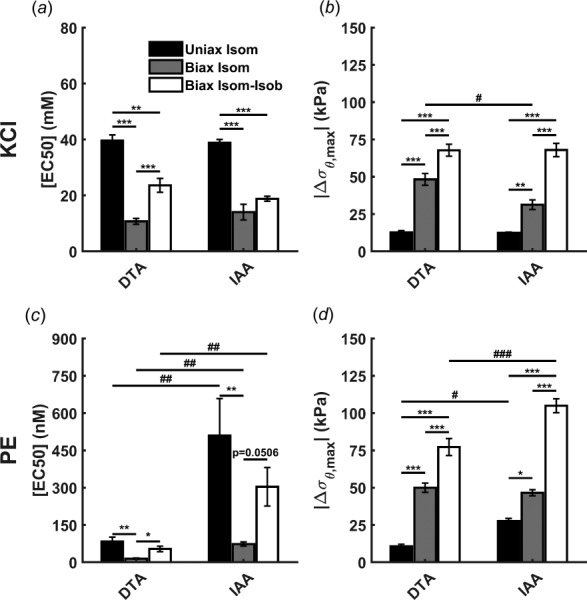
Variation in [EC50] ((a), (c)) and maximum change in circumferential stress ((b), (d)) in response to KCl ((a), (b)) and PE ((c), (d)) as evaluated by uniaxial isometric (uniax isom), biaxial isometric (biax isom), and biaxial isometric–isobaric (biax isom-isob) testing of murine DTA and IAA. Maximum change in circumferential stress is largest in biaxial isometric–isobaric testing and best reflects the true in vivo capability of VSMCs to regulate the mechanical environment. Data are presented as mean ± SEM. (*) p < 0.05, (**) p < 0.01, (***) p < 0.001 denote differences between testing protocols. (#) p < 0.05, (##) p < 0.01, (###) p < 0.001 denote differences between aortic regions.
For the IAA, the optimal circumferential stretch under uniaxial isometric testing conditions was 1.22 ± 0.03. Similar to the DTA, the circumferential stretch value increased for biaxial isometric testing to 1.58 ± 0.04 during KCl stimulation and 1.62 ± 0.03 during PE stimulation. Similar to the DTA, a two-tailed paired t-test between vasoconstrictors for the relaxed circumferential stretch of the IAA during biaxial protocols suggested that loss of tone, though small, was statistically significant (p = 0.01 and 0.06 for isometric and isometric–isobaric protocols, respectively). Active circumferential stress values revealed increased sensitivity to both KCl and PE when comparing biaxial isometric to uniaxial isometric testing. [EC50] values were significantly decreased (38.81 ± 1.17 mM versus 14.03 ± 2.80 mM) when comparing uniaxial versus biaxial isometric protocols (Figs. 3(a) and 3(c)). Again, similar observations were noted for the response to PE.
Axial Extension Increases Contractile Capacity and Suggests a Regionally Distinct Optimal Biaxial Configuration for Achieving Maximal Smooth Muscle Response.
In addition to contractile sensitivity, changes in contractile strength were evaluated in terms of the maximum change in circumferential stress. For the DTA, the maximum change in circumferential stress in response to KCl under isometric conditions increased with axial extension (12.7 ± 1.1 kPa at = 0.86 ± 0.01 versus 48.3 ± 4.0 kPa at = 1.46 ± 0.03, Figs. 3(b) and 3(d)). Similar observations held for PE, supporting the hypothesis that axial stretch augments VSMC contractility. For the IAA, contractile capacity similarly increased with axial extension, from 12.4 ± 0.5 kPa at = 0.91 ± 0.01 in uniaxial isometric testing to 31.3 ± 3.3 kPa at = 1.69 ± 0.02 in biaxial isometric testing. PE-induced contractility also increased with axial stretch in the IAA.
Maximum contractility is typically evaluated at an optimal circumferential stretch in uniaxial tests. Our results suggest that the optimal configuration for achieving true maximum contractility requires biaxial stretch and that the optimal condition differs between aortic regions. “Optimal” is defined by the basal or relaxed condition prior to addition of vasoconstricting agents. In both aortic regions, maximum contractility was higher under biaxial conditions despite the basal circumferential stretch being significantly higher than the optimal circumferential stretch in uniaxial conditions (e.g., for DTA prior to KCl stimulation, = 1.35 ± 0.03 versus 1.62 ± 0.03 in uniaxial isometric versus biaxial isometric testing, respectively). Notably, the axial stretch in biaxial testing conditions was significantly higher in the IAA compared to the DTA (Fig. 4). Despite the regional difference in axial stretch, the basal axial stress did not differ between regions, suggesting an optimal state of stress to achieve maximal contractility that depends on locally distinct configurations.
Fig. 4.
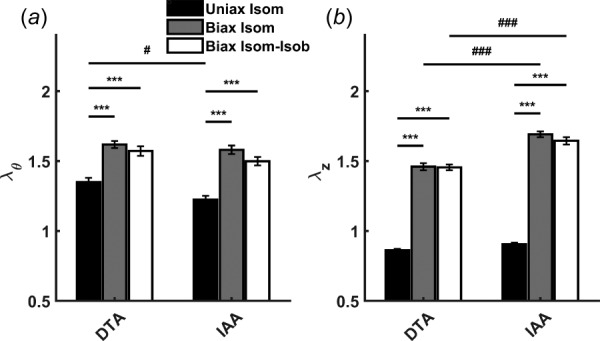
Optimal biaxial configuration of aortic segments prior to KCl stimulation. Circumferential (a) and axial stretches (b) were higher in biaxial testing protocols (biax isom, biax isom-isob) compared to uniaxial testing (uniax isom). Axial stretches in biaxial testing were larger in IAA segments compared to DTA segments, suggesting regionally distinct optimal biaxial configurations for achieving maximal smooth muscle contractility. Data are presented as mean ± SEM. (*) p < 0.05, (**) p < 0.01, (***) p < 0.001 denote differences between testing protocols. (#) p < 0.05, (##) p < 0.01, (###) p < 0.001 denote differences between aortic regions.
Physiologic Changes in Configuration Further Alter Contractile Sensitivity and Strength.
Unlike biaxial isometric testing, biaxial isometric–isobaric testing allows the vessel diameter to decrease under a constant pressure of 90 mmHg in response to stimulation of VSMCs. Sensitivity to KCl and PE decreases in both segments when comparing isometric–isobaric to isometric conditions, though the decrease is not statistically significant in the IAA (Fig. 3(a)). Interestingly, [EC50] values were still lower for biaxial isometric–isobaric testing than for uniaxial isometric testing for KCl, while they were not significantly different in response to PE. Given the differences between these methods (i.e., fixed circumferential and unconstrained axial configuration in uniaxial testing versus unconstrained circumferential and fixed axial configuration in biaxial isometric–isobaric testing), comparisons should be drawn with caution. Similarly, the maximum change in circumferential stress was highest in biaxial isometric–isobaric testing for both vasoconstrictors in both aortic regions (Figs. 3(b) and 3(d)). It should be noted that this change is a reduction in stress in biaxial isometric–isobaric testing but an increase in uniaxial and biaxial isometric testing (Table 1). Increases in contractile strength from uniaxial isometric to biaxial isometric–isobaric conditions were similar between regions for both KCl and PE and captured well the regional difference in response to PE. Comparison of biaxial protocols also facilitates evaluation of changes in axial stress. Maximum change in axial stress in the DTA in response to KCl was larger with biaxial isometric–isobaric testing compared to biaxial isometric testing (3.3 ± 1.6 kPa versus −27 ± 0.9 kPa, respectively). Similar observations held for the response to PE as well as for all responses in the IAA.
Discussion
Axial loading is critical to arterial growth and remodeling, serving both as a driver and indicator in development, adaptation, and disease [15–17]. In regulating the local mechanical environment, it is important that smooth muscle cells respond appropriately to contractile stimuli, which is frequently assessed through uniaxial ring tests wherein axial stretch is neglected. Although the effect of axial loading on VSMC tone has been studied in arteries [18–21], it has not been evaluated in the context of different vasoconstrictors or different experimental testing conditions. Here, we demonstrate that maximum smooth muscle contractility depends on both circumferential and axial stretch and that such an optimal configuration reveals differences in vasoconstrictor sensitivity when evaluated under physiologically relevant pressurization. The DTA and IAA underwent one of three activation protocols: (i) uniaxial isometric testing, (ii) biaxial isometric testing, and (iii) axially isometric plus isobaric testing. These different protocols address two considerations: first, the influence of axial deformation on the contractile behavior of VSMCs and, second, the physiologic relevance of fixed geometry versus fixed loading conditions, noting that neither need be constant in vivo.
We first investigated the role of axial deformation in the sensitivity and strength of the VSMC contractile response to KCl and PE. Comparisons of isometric protocols in uniaxial versus biaxial testing revealed statistically significant increases in sensitivity to both KCl and PE when segments are stretched circumferentially and axially to their estimated in vivo values. Length dependence of sensitivity is well documented in VSMCs [14], but uniaxial testing has previously evaluated such dependencies primarily in the circumferential direction, with few exceptions addressing axial extension [7,22]. Importantly, a study comparing uniaxial and biaxial isometric testing between carotid and iliac arteries found no differences between protocols [7], but determination of in vivo axial stretches was not reported, and the experimental procedure differed significantly from that which is detailed here. Thus, the differences as a function of testing protocol observed herein do not necessarily conflict with previous results.
Similarly, maximum change in circumferential stress was increased in biaxial isometric testing compared to uniaxial isometric testing in response to both KCl and PE despite the circumferential stretch being markedly higher in the biaxial configuration. A recent study used a finite elasticity framework [23] to investigate the effects of axial stretch on KCl-induced VSMC contractility using both uniaxial isometric and biaxial isometric–isobaric experimental data of mouse DTA [8,24]. It was demonstrated that when using a VSMC model with only a circumferential-dependent description of the myosin and actin filament overlap [25], the model was able to predict the magnitude of active tone observed in uniaxial isometric contraction but not in biaxial isometric–isobaric contractions. However, when including radial and axial stretch dependencies in the model based on experimental observations of filament lattice spacing-dependent myosin filament polymerization [26], the model was able to accurately simulate both uniaxial isometric and biaxial isometric–isobaric contractions. Our experimental data confirm these model simulations and suggest that microstructural organization of myosin and actin filaments could play an important role in biaxial stretch-sensitive VSMC contractility.
In addition to quantifying roles of axial stretch in vasoactivity, comparing biaxial isometric and isobaric testing allows one to quantify roles of geometric changes in regulating vasoactivity. First, alterations in the mechanical environment were of similar orders of magnitude but in different directions; circumferential stress increases during isometric testing and decreases during isobaric testing due to VSMC contraction. Allowing vessels to change diameter under a constant load increases contractile capacity as measured by the change in circumferential stress, but decreases sensitivity to both KCl and PE regardless of aortic region, noting that the difference in response to KCl in the IAA was not statistically significant. One previous study addressed this issue in canine carotid arteries and reported that maximum contractile force occurs at 100 mmHg [22], but axial stretch was not reported and vasoconstrictor sensitivity was not investigated. Although results from each testing protocol may be equally “true” in that cells respond differently under isometric versus isobaric conditions, isobaric testing may mimic better in vivo VSMC mechanosensitivity and mechanoregulation. Indeed, a key function of VSMCs is to maintain a target value of wall shear stress on the endothelium, which is achieved by modulating the diameter of the vessel [1]. The maximum change in wall shear stress, , may be estimated from the observed change in inner diameter from isobaric testing (given a constant flow rate). The target value of has been observed in multiple species and vascular locations, with the set-point depending on local physiologic flow rates [27]. Isometric testing does not reveal contraction-mediated changes in wall stress that would be “sensed” by mural cells in vivo, which is thought to be important in aortic diseases related to cellular mechanotransduction [28]. Thus, we assert that axially isometric plus isobaric testing is necessarily superior given both the extra data available for analysis and its greater relevance to in vivo interpretation.
We also sought to delineate possible regional variations in axial dependence of contractility. Regionally dependent responses to vasoconstrictors have been reported under uniaxial [29–31] and biaxial [20] testing conditions. In general, imposing axial stretch showed expected regional differences without revealing new or unexpected observations. For example, it is expected that the IAA has lower sensitivity but stronger overall contractility than the DTA in response to PE, which is captured well in both uniaxial isometric and biaxial isobaric testing (Fig. 3, Table 2). While this may seem unremarkable, it is important that these observations remain consistent across protocols despite the regional difference in axial stretch that is imposed in biaxial but not uniaxial protocols. Similar changes in contractile sensitivity and strength between regions despite differences in axial stretch suggest that optimal VSMC function depends on proper maintenance of locally preferred mechanical environments. Importantly, relaxed values of axial stress were not different between regions under biaxial testing despite differences in configuration, further supporting a critical role of axial stretch in the maintenance of a locally preferred mechanical environment and mechanically mediated VSMC function.
Of note, as VSMCs in the DTA and IAA derive from the same embryonic origin [32], it seems likely that regional responses depend more on mechanical environment than inherent cellular differences, though constitutive differences in the perivascular environment (e.g., abdominal versus thoracic cavity) could play a role. Further studies should examine carefully the mechanisms of regional differences when evaluating contractile behavior in the ascending thoracic aorta, of which VSMCs derive from the neural crest and second heart field [32]. Additionally, it is unknown how structural differences between thoracic and abdominal aorta may contribute to regional variations in contractility. Small but statistically significant differences in collagen orientation between regions have been reported in apolipoprotein E-null mice [33], which could influence the ability of smooth muscle cells to deform the matrix during contraction (assuming the observation holds for wild type mice). Similarly, thoracic segments of apolipoprotein E-null mice have thicker medial layers and thus more elastin but proportionally lower smooth muscle content than abdominal segments [34], which may explain the slightly higher changes in stress achieved in the IAA. Furthermore, key vasoactive receptors are in many cases differentially expressed between vascular regions, which clearly drive disparate regional contractile responses to specific vasoconstrictors [35].
Mechanosensitivity may be affected by changes in local tissue mechanical properties or by changes in the cell “sensing” apparatus, either in transmembrane proteins such as integrins or by differences in intracellular signaling. Observed differences between testing protocols suggest axial mechanosensitivity of VSMCs, but such differences may occur either because cells are sensing changes in the local mechanical environment due to axial stretching or because physical stretch of the cells directly alters vasoactive channels and receptors. Mechanosensitivity of ion channels and G-protein coupled receptors has been reported in vascular smooth muscle cells [36,37], suggesting that the physical alterations of the vessel segments may have a direct impact on cellular mechanosensing, perhaps via conformational changes of key ion channels and vasoactive receptors. Alternatively, it is possible that physical stretch does not alter the conformation of ion channels and vasoactive receptors, but rather intracellular calcium handling may depend directly on cellular sensing of the mechanical environment, which changes with axial stretch. Such a distinction is difficult to delineate experimentally, but should nonetheless be a topic of further investigation.
Various limitations herein warrant a brief discussion. First, sensitivity to PE was highly variable in the IAA. While this created difficulty in achieving statistical power when comparing methods, this variability appears to be an inherent property of the IAA rather than a limitation of the method because the responses to KCl produced relatively little variability. Second, the study was limited to male mice only. The role of sex hormones in regulation of vascular tone has been demonstrated extensively [38]. Although sex differences in vascular tone have been observed in multiple species, observed differences in maximal contractility have not been studied in detail. Sex differences in response to PE have been reported in rat thoracic aorta using uniaxial tests [39]. Various studies demonstrate sex differences in contractility under pathogenic conditions in mice, but baseline sex differences are negligible [40]. Given these observations, sex differences should be considered in future studies using the axially isometric plus isobaric protocol.
Conclusion
Understanding the contractile capability of vascular smooth muscle is critical to evaluating both the in vivo mechanical environment within the vascular wall and its overall mechanical function. We submit that the best test for evaluating smooth muscle contractility requires biaxial deformations, and the methods offer considerable new information regarding the ability of vascular smooth muscle to regulate the mechanical environment by closely mimicking in vivo loading and changes in configuration. Given axially dependent differences in vasoconstrictor sensitivity, which are not observed under uniaxial testing, biaxial tests are particularly useful. These observations have important implications when attempting to model active wall mechanics [23,41]. Data reporting quantitative descriptions of vascular sensitivity and strength under nonphysiologic conditions should be interpreted with caution when informing mechanistic models of smooth muscle-mediated biomechanical behavior of arteries. Future studies should incorporate biaxial contractility frameworks to identify changes in smooth muscle function that may not otherwise be observed and, in so doing, provide greater clarity in calculating in vivo mechanical conditions, which are critical in directing cell signaling.
Contributor Information
Alexander W. Caulk, Department of Biomedical Engineering, , Yale University, , New Haven, CT 06520
Jay D. Humphrey, Fellow ASME, Department of Biomedical Engineering, , Yale University, , New Haven, CT 06520; Vascular Biology and Therapeutics Program, Yale University, , New Haven, CT 06520
Sae-Il Murtada, Department of Biomedical Engineering, , Yale University, , 55 Prospect Street, , New Haven, CT 06520 , e-mail: sae-il.murtada@yale.edu.
Funding Data
National Heart, Lung, and Blood Institute (5R01HL105297).
References
- [1]. Furchgott, R. F. , and Zawadzki, J. V. , 1980, “ The Obligatory Role of Endothelial Cells in the Relaxation of Arterial Smooth Muscle by Acetylcholine,” Nature, 288(5789), pp. 373–376. 10.1038/288373a0 [DOI] [PubMed] [Google Scholar]
- [2]. Dharmashankar, K. , and Widlansky, M. E. , 2010, “ Vascular Endothelial Function and Hypertension: Insights and Directions,” Curr. Hypertens. Rep., 12(6), pp. 448–455. 10.1007/s11906-010-0150-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Ferruzzi, J. , Murtada, S.-I. , Li, G. , Jiao, Y. , Uman, S. , Ting, M. Y. L. , Tellides, G. , and Humphrey, J. D. , 2016, “ Pharmacologically Improved Contractility Protects Against Aortic Dissection in Mice With Disrupted Transforming Growth Factor-β Signaling Despite Compromised Extracellular Matrix Properties,” Arterioscler., Thromb., Vasc. Biol., 36(5), pp. 919–927. 10.1161/ATVBAHA.116.307436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Guo, D.-C. , Pannu, H. , Tran-Fadulu, V. , Papke, C. L. , Yu, R. K. , Avidan, N. , Bourgeois, S. , Estrera, A. L. , Safi, H. J. , Sparks, E. , Amor, D. , Ades, L. , McConnell, V. , Willoughby, C. E. , Abuelo, D. , Willing, M. , Lewis, R. A. , Kim, D. H. , Scherer, S. , Tung, P. P. , Ahn, C. , Buja, L. M. , Raman, C. S. , Shete, S. S. , and Milewicz, D. M. , 2007, “ Mutations in Smooth Muscle α-Actin (ACTA2) Lead to Thoracic Aortic Aneurysms and Dissections,” Nat. Genet., 39(12), pp. 1488–1493. 10.1038/ng.2007.6 [DOI] [PubMed] [Google Scholar]
- [5]. Milewicz, D. M. , Guo, D.-C. , Tran-Fadulu, V. , Lafont, A. L. , Papke, C. L. , Inamoto, S. , Kwartler, C. S. , and Pannu, H. , 2008, “ Genetic Basis of Thoracic Aortic Aneurysms and Dissections: Focus on Smooth Muscle Cell Contractile Dysfunction,” Annu. Rev. Genomics Hum. Genet., 9(1), pp. 283–302. 10.1146/annurev.genom.8.080706.092303 [DOI] [PubMed] [Google Scholar]
- [6]. Speden, R. N. , 1960, “ The Effect of Initial Strip Length on the Noradrenaline-Induced Contraction of Arterial Strips,” J. Physiol., 154(1), pp. 15–25. 10.1113/jphysiol.1960.sp006561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Cox, R. H. , 1983, “ Comparison of Arterial Wall Mechanics Using Ring and Cylindrical Segments,” Am. J. Physiol., 244(2), pp. H298–H303. 10.1152/ajpheart.1983.244.2.H298 [DOI] [PubMed] [Google Scholar]
- [8]. Murtada, S.-I. , Ferruzzi, J. , Yanagisawa, H. , and Humphrey, J. D. , 2016, “ Reduced Biaxial Contractility in the Descending Thoracic Aorta of Fibulin-5 Deficient Mice,” ASME J. Biomech. Eng., 138(5), p. 051008. 10.1115/1.4032938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Gleason, R. L. , Gray, S. P. , Wilson, E. , and Humphrey, J. D. , 2005, “ A Multiaxial Computer-Controlled Organ Culture and Biomechanical Device for Mouse Carotid Arteries,” ASME J. Biomech. Eng., 126(6), pp. 787–795. 10.1115/1.1824130 [DOI] [PubMed] [Google Scholar]
- [10]. Ferruzzi, J. , Bersi, M. R. , Uman, S. , Yanagisawa, H. , and Humphrey, J. D. , 2015, “ Decreased Elastic Energy Storage, Not Increased Material Stiffness, Characterizes Central Artery Dysfunction in Fibulin-5 Deficiency Independent of Sex,” ASME J. Biomech. Eng., 137(3), p. 031007. 10.1115/1.4029431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Ferruzzi, J. , Collins, M. J. , Yeh, A. T. , and Humphrey, J. D. , 2011, “ Mechanical Assessment of Elastin Integrity in Fibrillin-1-Deficient Carotid Arteries: Implications for Marfan Syndrome,” Cardiovasc. Res., 92(2), pp. 287–295. 10.1093/cvr/cvr195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Ferruzzi, J. , Bersi, M. R. , and Humphrey, J. D. , 2013, “ Biomechanical Phenotyping of Central Arteries in Health and Disease: Advantages of and Methods for Murine Models,” Ann. Biomed. Eng., 41(7), pp. 1311–1330. 10.1007/s10439-013-0799-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Humphrey, J. D. , 2002, Cardiovascular Solid Mechanics: Cells, Tissues, and Organs, Springer, New York. [Google Scholar]
- [14]. Price, J. M. , Davis, D. L. , and Knauss, E. B. , 1981, “ Length-Dependent Sensitivity in Vascular Smooth Muscle,” Am. J. Physiol., 241(4), pp. H557–H563. 10.1152/ajpheart.1981.241.4.H557 [DOI] [PubMed] [Google Scholar]
- [15]. Brozovich, F. V. , Nicholson, C. J. , Degen, C. V. , Gao, Y. Z. , Aggarwal, M. , and Morgan, K. G. , 2016, “ Mechanisms of Vascular Smooth Muscle Contraction and the Basis for Pharmacologic Treatment of Smooth Muscle Disorders,” Pharmacol. Rev., 68(2), pp. 476–532. 10.1124/pr.115.010652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16]. Gleason, R. L. , and Humphrey, J. D. , 2005, “ Effects of a Sustained Extension on Arterial Growth and Remodeling: A Theoretical Study,” J. Biomech., 38(6), pp. 1255–1261. 10.1016/j.jbiomech.2004.06.017 [DOI] [PubMed] [Google Scholar]
- [17]. Jackson, Z. S. , Gotlieb, A. I. , and Langille, B. L. , 2002, “ Wall Tissue Remodeling Regulates Longitudinal Tension in Arteries,” Circ. Res., 90(8), pp. 918–925. 10.1161/01.RES.0000016481.87703.CC [DOI] [PubMed] [Google Scholar]
- [18]. Zulliger, M. A. , Kwak, N. T. M. R. , Tsapikouni, T. , and Stergiopulos, N. , 2002, “ Effects of Longitudinal Stretch on VSM Tone and Distensibility of Muscular Conduit Arteries,” Am. J. Physiol.: Heart Circ. Physiol., 283(6), pp. H2599–H2605. 10.1152/ajpheart.00298.2002 [DOI] [PubMed] [Google Scholar]
- [19]. Rachev, A. , and Hayashi, K. , 1999, “ Theoretical Study of the Effects of Vascular Smooth Muscle Contraction on Strain and Stress Distributions in Arteries,” Ann. Biomed. Eng., 27(4), pp. 459–468. 10.1114/1.191 [DOI] [PubMed] [Google Scholar]
- [20]. Wagner, H. P. , and Humphrey, J. D. , 2011, “ Differential Passive and Active Biaxial Mechanical Behaviors of Muscular and Elastic Arteries: Basilar Versus Common Carotid,” ASME J. Biomech. Eng., 133(5), p. 051009. 10.1115/1.4003873 [DOI] [PubMed] [Google Scholar]
- [21]. Agianniotis, A. , Rachev, A. , and Stergiopulos, N. , 2012, “ Active Axial Stress in Mouse Aorta,” J. Biomech., 45(11), pp. 1924–1927. 10.1016/j.jbiomech.2012.05.025 [DOI] [PubMed] [Google Scholar]
- [22]. Dobrin, P. B. , 1973, “ Isometric and Isobaric Contraction of Carotid Arterial Smooth Muscle,” Am. J. Physiol., 225(3), pp. 659–663. 10.1152/ajplegacy.1973.225.3.659 [DOI] [PubMed] [Google Scholar]
- [23]. Murtada, S.-I. , Humphrey, J. D. , and Holzapfel, G. A. , 2017, “ Multiscale and Multiaxial Mechanics of Vascular Smooth Muscle,” Biophys. J., 113(3), pp. 714–727. 10.1016/j.bpj.2017.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Murtada, S.-I. , Lewin, S. , Arner, A. , and Humphrey, J. D. , 2015, “ Adaptation of Active Tone in the Mouse Descending Thoracic Aorta Under Acute Changes in Loading,” Biomech. Model. Mechanobiol., 15(3), pp. 579–592. 10.1007/s10237-015-0711-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Murtada, S. C. , Arner, A. , and Holzapfel, G. A. , 2012, “ Experiments and Mechanochemical Modeling of Smooth Muscle Contraction: Significance of Filament Overlap,” J. Theor. Biol., 297, pp. 176–186. 10.1016/j.jtbi.2011.11.012 [DOI] [PubMed] [Google Scholar]
- [26]. Liu, J. C.-Y. , Rottler, J. , Wang, L. , Zhang, J. , Pascoe, C. D. , Lan, B. , Norris, B. A. , Herrera, A. M. , Paré, P. D. , and Seow, C. Y. , 2013, “ Myosin Filaments in Smooth Muscle Cells Do Not Have a Constant Length,” J. Physiol., 591(23), pp. 5867–5878. 10.1113/jphysiol.2013.264168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Baeyens, N. , Nicoli, S. , Coon, B. G. , Ross, T. D. , den Dries, K. V. , Han, J. , Lauridsen, H. M. , Mejean, C. O. , Eichmann, A. , Thomas, J.-L. , Humphrey, J. D. , and Schwartz, M. A. , 2015, “ Vascular Remodeling Is Governed by a VEGFR3-Dependent Fluid Shear Stress Set Point,” eLife, 4, p. e04645. 10.7554/eLife.04645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Humphrey, J. D. , Schwartz, M. A. , Tellides, G. , and Milewicz, D. M. , 2015, “ Role of Mechanotransduction in Vascular Biology Focus on Thoracic Aortic Aneurysms and Dissections,” Circ. Res., 116(8), pp. 1448–1461. 10.1161/CIRCRESAHA.114.304936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. Asbún-Bojalil, J. , Castillo, E. F. , Escalante, B. A. , and Castillo, C. , 2002, “ Does Segmental Difference in Α1-Adrenoceptor Subtype Explain Contractile Difference in Rat Abdominal and Thoracic Aortae?,” Vascul. Pharmacol., 38(3), pp. 169–175. 10.1016/S1537-1891(02)00164-7 [DOI] [PubMed] [Google Scholar]
- [30]. Kleinbongard, P. , Schleiger, A. , and Heusch, G. , 2013, “ Characterization of Vasomotor Responses in Different Vascular Territories of C57BL/6J Mice,” Exp. Biol. Med., 238(10), pp. 1180–1191. 10.1177/1535370213502621 [DOI] [PubMed] [Google Scholar]
- [31]. Leloup, A. J. A. , Hove, V. E. C. , Heykers, A. , Schrijvers, D. M. , Meyer, D. Y. G. R. , and Fransen, P. , 2015, “ Elastic and Muscular Arteries Differ in Structure, Basal NO Production and Voltage-Gated Ca2+-Channels,” Front. Physiol., 6, p. 375 10.3389/fphys.2015.00375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Majesky, M. W. , 2007, “ Developmental Basis of Vascular Smooth Muscle Diversity,” Arterioscler., Thromb., Vasc. Biol., 27(6), pp. 1248–1258. 10.1161/ATVBAHA.107.141069 [DOI] [PubMed] [Google Scholar]
- [33]. Watson, S. R. , Liu, P. , Peña, E. A. , Sutton, M. A. , Eberth, J. F. , and Lessner, S. M. , 2016, “ Comparison of Aortic Collagen Fiber Angle Distribution in Mouse Models of Atherosclerosis Using Second-Harmonic Generation (SHG) Microscopy,” Microsc. Microanal., 22(01), pp. 55–62. 10.1017/S1431927615015585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Bersi, M. R. , Khosravi, R. , Wujciak, A. J. , Harrison, D. G. , and Humphrey, J. D. , 2017, “ Differential Cell-Matrix Mechanoadaptations and Inflammation Drive Regional Propensities to Aortic Fibrosis, Aneurysm or Dissection in Hypertension,” J. R. Soc. Interface, 14(136), p. 20170327. 10.1098/rsif.2017.0327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35]. Poduri, A. , Iii, A. P. O. , Howatt, D. A. , Moorleghen, J. J. , Balakrishnan, A. , Cassis, L. A. , and Daugherty, A. , 2012, “ Regional Variation in Aortic AT1b Receptor MRNA Abundance is Associated With Contractility but Unrelated to Atherosclerosis and Aortic Aneurysms,” PLoS One, 7(10), p. e48462. 10.1371/journal.pone.0048462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Park, K. S. , Kim, Y. , Lee, Y.-H. , Earm, Y. E. , and Ho, W.-K. , 2003, “ Mechanosensitive Cation Channels in Arterial Smooth Muscle Cells Are Activated by Diacylglycerol and Inhibited by Phospholipase C Inhibitor,” Circ. Res., 93(6), pp. 557–564. 10.1161/01.RES.0000093204.25499.83 [DOI] [PubMed] [Google Scholar]
- [37]. Schnitzler, M. M. y , Storch, U. , Meibers, S. , Nurwakagari, P. , Breit, A. , Essin, K. , Gollasch, M. , and Gudermann, T. , 2008, “ Gq‐Coupled Receptors as Mechanosensors Mediating Myogenic Vasoconstriction,” EMBO J., 27(23), pp. 3092–3103. 10.1038/emboj.2008.233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Orshal, J. M. , and Khalil, R. A. , 2004, “ Gender, Sex Hormones, and Vascular Tone,” Am. J. Physiol.: Regul., Integr. Comp. Physiol., 286(2), pp. R233–R249. 10.1152/ajpregu.00338.2003 [DOI] [PubMed] [Google Scholar]
- [39]. Stallone, J. N. , Crofton, J. T. , and Share, L. , 1991, “ Sexual Dimorphism in Vasopressin-Induced Contraction of Rat Aorta,” Am. J. Physiol.: Heart Circ. Physiol., 260(2 Pt 2), pp. H453–H458. 10.1152/ajpheart.1991.260.2.H453 [DOI] [PubMed] [Google Scholar]
- [40]. Gros, R. , Van Wert, R. , You, X. , Thorin, E. , and Husain, M. , 2002, “ Effects of Age, Gender, and Blood Pressure on Myogenic Responses of Mesenteric Arteries From C57BL/6 Mice,” Am. J. Physiol.: Heart Circ. Physiol., 282(1), pp. H380–H388. 10.1152/ajpheart.2002.282.1.H380 [DOI] [PubMed] [Google Scholar]
- [41]. Zahalak, G. I. , 1996, “ Non-Axial Muscle Stress and Stiffness,” J. Theor. Biol., 182(1), pp. 59–84. 10.1006/jtbi.1996.0143 [DOI] [PubMed] [Google Scholar]


