Abstract
The efficacy of reduced order modeling for transstenotic pressure drop in the coronary arteries is presented. Coronary artery disease is a leading cause of death worldwide and the computation of pressure drop in the coronary arteries has become a standard for evaluating the functional significance of a coronary stenosis. Comprehensive models typically employ three-dimensional (3D) computational fluid dynamics (CFD) to simulate coronary blood flow in order to compute transstenotic pressure drop at the arterial stenosis. In this study, we evaluate the capability of different hydrodynamic models to compute transstenotic pressure drop. Models range from algebraic formulae to one-dimensional (1D), two-dimensional (2D), and 3D time-dependent CFD simulations. Although several algebraic pressure-drop formulae have been proposed in the literature, these models were found to exhibit wide variation in predictions. Nonetheless, we demonstrate an algebraic formula that provides consistent predictions with 3D CFD results for various changes in stenosis severity, morphology, location, and flow rate. The accounting of viscous dissipation and flow separation were found to be significant contributions to accurate reduce order modeling of transstenotic coronary hemodynamics.
Keywords: coronary artery stenosis, fractional flow reserve, hemodynamics, image-based modeling, noninvasive pressure drop
1. Introduction
Coronary artery disease is a leading cause of death worldwide [1]. Atherosclerotic lesions in the coronary arteries and their rupture can obstruct blood flow and result in angina and myocardial ischemia, necessitating medical intervention with angioplasty, stenting, or bypass surgery. Coronary computed tomography angiography (CCTA) enables noninvasive imaging of the coronary lumens for identification of stenotic lesions. However, the previous studies have reported unreliable relationship between angiographic measures of stenosis and ischemia, with, for example, reports of fewer than half of CCTA-identified obstructive lesions causing ischemia [2,3].
Ischemia is directly related to how much a coronary lesion reduces hydrodynamic pressure. Congruently, fractional flow reserve (FFR), which is the ratio of the mean blood pressure distal to a coronary stenosis to the mean aortic root pressure (FFR = Pdist/Pao) upstream during maximal hyperemia, is considered as a gold standard to determine the functional significance of a coronary stenosis [4]. Due to the invasive nature of FFR measurement, a noninvasive method to estimate FFR could improve the safety, accessibility, and cost-effectiveness of coronary artery disease management. Recently, the technique of FFRCT [5] has emerged as the standard to noninvasively calculate FFR and has demonstrated high diagnostic performance compared to invasively measured FFR for identification of patients with coronary lesions causing ischemia [6,7].
Transstenotic pressure drop, and related measures such as FFRCT, can be computed using image-based computational fluid dynamics (CFD) modeling to simulate coronary blood flow and pressure. This can be achieved by constructing a three-dimensional (3D) computer model of the coronary arteries (cf. Fig. 1) from CCTA, modeling blood as a fluid, and using CFD to solve the Navier–Stokes equations (NSEs) subject to appropriate boundary conditions. These simulations require significant computational effort, which may only be necessary if the flow itself is highly 3D, or localized flow behavior is sought. In some scenarios, blood flow may be considered approximately one-dimensional (1D), and the NSEs can be appropriately simplified [8–10]. This leads to an equation that is easier to numerically solve but incurs some level of model-form error stemming from the simplifying assumptions. Notably, the cross-sectional velocity profile must be assumed in order to estimate convective acceleration and friction terms in the 1D equations, which may be particularly limiting for scenarios of estimating pressure drop, especially where flow separation is expected. Recently, Ghigo et al. [11] proposed a two-dimensional (2D) “multiring” method that avoids the need to assume a cross-sectional velocity profile and provides the ability to capture flow separation. The 1D and 2D multiring models provide computationally efficient alternatives for solving global features of blood flow in deformable vessels compared to 3D time-dependent modeling.
Fig. 1.
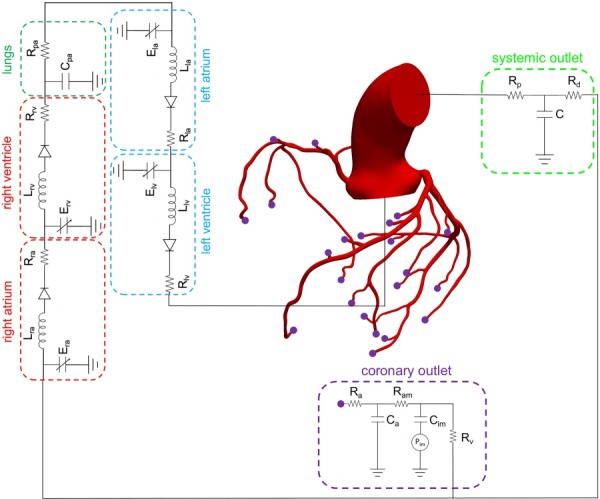
Schematic of image-based 3D model of an aorta and coronary arteries coupled to closed-loop lump parameter (0D) models of the heart, pulmonary arteries, and systemic and coronary circulations
The models described earlier are governed by partial differential equations (PDEs), which are capable of spatially resolving the pressure (and velocity) field. Alternatively, algebraic formulas have been proposed to simplify the calculation of net pressure drop across a stenosis based on blood flow rate and geometrical properties. Also from the practical standpoint, while FFR is often measured in reference to aortic root pressure, transstenotic pressure drop models could be of value to FFR estimation because the value of FFR can be approximately related to the amount of pressure drop across a stenosis (FFR ∼ 1 − ΔP/Pao), assuming that the pressure drop in the coronary segments proximal to the stenosis is negligible. An early transstenotic pressure drop model was developed by Young and Tsa [12,13], including empirical parameters determined from a series of steady and unsteady in vitro experiments. Seeley and Young [14] modified this model to better consider geometric factors affecting pressure drop and verified their model by in vitro experiments. Garcia et al. [15] proposed and validated a simple theoretical model from an energy loss concept to describe the instantaneous pressure drop across the aortic valve. Itu et al. [16] proposed a pressure-drop model for aortic coarctation by assuming specific formulations of the viscous and the inertial terms. The models referenced above include empirical parameters, which may limit the generalizability of the model in flow regimes not dynamically similar to those the models were derived for. Huo et al. [17] presented an analytical model derived from the general Bernoulli equation by considering various energy losses along the length of a lesion, which does not contain empirical parameters, and applied this model to coronary artery stenosis. Other reduced order and regression-based models have been developed to predict transstenotic pressure drop based on geometry and predicted velocity profile in mildly stenosed arteries [18,19].
In this study, a comprehensive range of computational hydrodynamic models is considered, which includes algebraic formulations, the 1D blood flow equations, a 2D multiring method, and 3D image-based CFD coronary flow modeling. The objective is to evaluate if reduced order models can reasonably predict transstenotic pressure drop and FFR in comparison with 3D CFD simulations. A reasonably diverse range of coronary stenoses is considered including symmetric, asymmetric, curved, and patient-specific stenosis geometries, as well as differing stenosis location and transstenotic flow rate.
2. Methods
Here, we discuss the modeling of coronary blood flow and transstenotic pressure drop using image-based CFD, 2D multiring, 1D, and algebraic (0D) models. Image-based CFD modeling results were considered as the gold standard to which results from the reduced order (2D, 1D, and 0D) models were compared. The image-based CFD models included the aorta and all major coronary arteries—this, among other reasons described below, enabled the volumetric flow rate through the stenotic artery to be computed from basic physiological data. However, to provide more direct comparison of transstenotic pressure drop prediction, the reduced order models only modeled the stenotic artery, with the time-varying volumetric flow rate prescribed from the 3D CFD results to maintain consistency.
Note that fluid properties (blood density and blood viscosity ) were common among all models.
2.1. Image-Based Three-Dimensional Coronary Flow Modeling.
Image-based CFD modeling of blood flow and pressure in human coronary arteries was performed using the open source software package SimVascular [20], following the methods described in Refs. [21] and [22]. This entailed constructing a 3D model of the aorta and coronary arteries from CCTA data, employing and tuning lumped parameter network (LPN) models to specify boundary conditions representative of cardiac physiology, finite element simulation of the 3D time-dependent Navier–Stokes equations, and postprocessing to compute relevant indices, including FFR.
A representative image-based model including the aortic root and coronary arteries coupled with a closed-loop LPN that models the heart, pulmonary arteries, and systemic and coronary circulation is shown in Fig. 1. The image-based CFD models included the aorta and major coronary branches for several reasons. First, this enabled coupling to cardiac and coronary microcirculation models, which strongly determine coronary hemodynamics. Second, this enabled transstenotic flow rate to be computed from basic physiological data, and more natural modeling of hyperemia. Third, inclusion of the aorta, major coronary branches, and lumped parameter models of the heart and coronary microcirculation is similar to the method described in Ref. [5] to compute FFR, which has gained clinical adoption and has been extensively compared to invasive measurements [6,7,23–25].
A three-element “RCR” Windkessel model was used to model the systemic circulation. Distal to each coronary outlet in the model, separate coronary-specific LPNs were coupled that consider the influence of intramyocardial pressure on coronary flow [21]. (Note, only one coronary LPN is shown in Fig. 1 to reduce clutter although this model contains 24 coronary-specific LPNs.) A time-dependent intramyocardial pressure was prescribed to represent the influence of myocardial contraction in coronary flow. A detailed description of the differential equations governing the heart model and coronary LPNs is given in Sankaran et al. [22]. The LPN parameters were tuned to match target pressure and flow splits to the aorta and systemic and coronary outlets. In this tuning process, relationships between vessel size and flow rate according to a modified Murray's law were used to estimate resistances and capacitances at the outlets [22,26]. Blood flow was modeled by the Navier–Stokes equations
| (1) |
These equations were used to solve for fluid velocity and pressure using the SimVascular CFD flow solver. Note that vessel walls were assumed rigid as fluid-structure interaction modeling in SimVascular demonstrated insignificant (<2%) changes to transstenotic pressure drop and computed FFR values.
2.1.1. Modeling Hyperemia.
Since the coronary microvascular resistance varies based on cardiac demand, it is desirable to saturate vasodilation to properly evaluate the functional significance of a coronary stenosis. FFR is typically measured invasively under a hyperemic condition caused by the administration of adenosine. Wilson et al. [27] showed that the 140 µg/kg/min infusion of adenosine causing maximal hyperemia reduced total coronary resistance to 0.22–0.24 of the resting values. Furthermore, they reported 5±5 (mmHg) reduction in mean blood pressure but insignificant changes to heart rate. Therefore, to model hyperemia in our 3D time-dependent simulations, we reduced coronary resistance to 0.22 of the resting values, while keeping other parameters fixed. Note, although the coronary bed distal to a stenosis may have compromised vasodilatory response, consistent with [5], the hyperemic microcirculatory resistance distal to a stenosis was assumed to be the same as that in the case of coronary arteries without disease (0.22 of resting value).
2.2. Two-Dimensional Multiring Method.
The 2D multiring method [11] decomposes the vessel cross section into concentric rings and integrates the NSEs assuming that axial velocity is constant over each ring (annulus). This enables a radial distribution of the axial velocity to be computed, instead of assumed. Furthermore, the velocity profile at each cross section can be different along the axial coordinate and, in particular, phenomena such as flow separation can be considered.
After integrating the axisymmetric NSEs simplified using the long wave assumption for each ring, the equations for the balance of mass and momentum in ring are as follows:
| (2) |
| (3) |
where
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Eqs. (2) and (3) are similar to the 1D NSEs (described below); however, these equations hold for each ring, and source terms are added to the right-hand side representing the radial mass and momentum exchanges between adjacent rings at each cross section. To complete the system of equations, the arterial wall is assumed thin, cylindrical, isotropic, homogeneous, incompressible, and linearly elastic, and each cross section deforms independently, yielding the following pressure-area relationship [9]:
| (9) |
where is Young's modulus of the vessel wall, is the vessel wall thickness, is the external pressure acting on the vessel wall (assumed zero), and and are the diastolic pressure and area, respectively.
We developed an in-house flow solver for multiring modeling using a finite volume axial discretization with the kinetic scheme [28] and the hydrostatic reconstruction [29]. Verification of the 2D multiring solver is described in the Appendix. For each stenotic artery considered in the 3D CFD modeling, the 2D multiring method was also used to model pressure drop in that artery. The time-varying volumetric flow rate from the 3D CFD simulation was specified at the artery inlet using a parabolic profile since the Womersley number was close to unity in all cases, and a time-varying pressure from the 3D CFD simulation was specified at the outlet. The arterial geometry (radius as a function of axial location) was derived from the corresponding 3D arterial model. Because the 3D simulations assumed rigid walls, we synthetically increased the value of Young's modulus (i.e., ) in the pressure law of Eq. (9) to maintain consistency.
2.3. One-Dimensional Navier–Stokes Model.
Derivations of the 1D equations for flow and pressure in a deformable tube can be found in numerous publications, e.g., Refs. [8], [30], and [31]. Alternatively, the 1D equations can be interpreted as a particular case of the 2D multiring equations with only one ring and a particular velocity profile being assumed. Regardless, the resulting equations can be expressed as
| (10) |
| (11) |
where is the axial coordinate, is the time, is the cross-sectional area of the vessel, is the volumetric flow rate, is the blood pressure averaged at each cross section, and determines the frictional force due to viscosity of the blood and depends on the chosen velocity profile. The axisymmetric velocity profile is assumed to fit the form [10]
| (12) |
from which it can be shown that [31], where is the averaged velocity and R is the vessel radius. To complete the system of equations for , , and , the pressure law of Eq. (9) is employed.
The above conservative system of equations was solved using a finite volume numerical scheme. The kinetic flux function approach [28] coupled with a well-balanced hydrostatic reconstruction technique [29] was used to calculate the required numerical flux and source terms in the finite volume scheme. Verification of the 1D solver is described in the Appendix. For each stenotic artery considered using 3D CFD modeling, the 1D equations were also used to model pressure drop in that artery. The same boundary conditions as described in Sec. 2.2 were applied for the 1D modeling, and a parabolic velocity profile () is assumed.
2.4. Algebraic Models.
We considered four algebraic (“0D”) models of pressure drop. Although, these models were derived for different applications—including general vascular stenosis, aortic stenosis, aortic coarctation, and coronary artery stenosis—as we will show in the results, these differences were not necessarily indicative of model accuracy. Thus, it was important to consider a range of transstenotic pressure drop models despite their origin. Moreover, all models are similar in that they treat a stenosis as a simple area reduction of a 1D internal flow, and all models can be considered to be effectively generalizations of Bernoulli's equation, or energy balance equation. For each stenotic artery considered using 3D CFD modeling, each algebraic 0D model was also used to model pressure drop across the stenosis based on the flow rate determined from the 3D CFD. Several of the 0D models contain empirical parameters; however, we did not tune these parameters to match the 3D simulations.
Model 1 [15]
| (13) |
where is the (unsteady) flow rate, is the stenosis minimum cross-sectional area, is the nominal cross-sectional area of the native vessel that is the average between the cross-sectional area of the artery proximal and distal to the stenotic region, and and are empirically derived [15].
Model 2 [14]
| (14) |
where the first term captures the viscous losses by considering the empirical parameter related to and , which are minimum and nominal cross-sectional areas of the vascular segment, respectively. The second term represents the empirically corrected energy dissipation due to flow separation with “turbulence” coefficient . The third term represents the inertial effect of blood flow in a stenotic region with an inertial coefficient . Additional parameters are as follows: and are radius of the stenosis and native vessels, respectively. Although the cross sections are not always circular, and are calculated to be the radius of a circle with areas and , respectively. is the length of the stenosis that is calculated such that the cross-sectional area in that region is between and 1.1 , and denotes the absolute value of flow rate.
Model 3 [16]
| (15) |
Model 3 is similar to model 2 but the viscous loss is modified by considering an integral form of viscous resistance based on Poiseuille's law. The empirical parameters are modified specially to relate the viscous dissipation not only to the geometrical properties of the stenosis but also to the Womersley number, , which quantifies the relative importance between pulsatile inertial effects and viscous effects. The frequency is related to the patient heart rate (HR) via . Moreover, the fourth term is a continuous component to model the phase difference between flow rate and pressure drop, where is the mean flow rate over one cardiac cycle.
Model 4 [17]
| (16) |
where is the vessel length, indicates the stenosis length, and are the inlet and outlet cross-sectional areas of vascular lesion, respectively. The first term of Eq. (16) represents the convective pressure drop and the second term represents the diffusive pressure drop by considering the entrance region of stenosis through a dimensionless radius of inviscid core () in which the velocity is uniform [32]. The remainder of the equation takes into account the pressure drop due to expansion of the cross-sectional area by assuming a parabolic flow. Detailed information about how to calculate the value of inviscid core for stenotic regions is available in Huo et al. [17].
3. Results
3.1. Image-Based Computational Fluid Dynamics Modeling.
Modeling of blood flow and pressure in image-based 3D models was performed using the methods described in Sec. 2.1. Baseline resting hemodynamics for all models were simulated by tuning the LPNs to match target values in Table 1. Coronary resistances were then updated to model hyperemia. Representative results are shown in Fig. 2 for the model shown in Fig. 1. For these results, unstructured tetrahedral meshes of 4,629,813 elements, including boundary layer meshing, and a time-step size of 1 ms were used, which are representative of mesh and time-step resolution used in the other image-based CFD models presented. The solutions were run until the pressure fields at the inlet and outlets did not change more than 1.0% compared to the solutions at the same time point in the previous cardiac cycle (typically at least six cardiac cycles were needed to reach convergence). Figure 2 displays the computed aortic pressure, the pressure-volume loops of the left and right ventricles, and the flow waveforms in representative left and right coronaries. These results demonstrate realistic coronary flow waveform dynamics consistent with Ref. [24], namely, the left coronary flow peaks during diastole and dips in early systole, and right coronary flow demonstrates commensurate peaks in systole and diastole [33]. The parameter values of the closed-loop heart model, aortic outlet, and coronary outlets for these results are given in Tables 2–4, respectively. In addition to recovering realistic flow and pressure waveforms, the results showed consistent agreement with target data as shown in Table 1. The results of simulated of hyperemia, compared against those from the rest condition, agreed with clinical observations [27]. Namely, simulated hyperemia resulted in approximately 5 mmHg reduction in blood pressure and insignificant changes in cardiac output, while the flow split ratio between coronary and systemic outlets increased from 4.8% to 16.7% (see Table 5).
Table 1.
Comparison of “clinical targets” with computed values from the 3D patient-specific coronary flow and pressure simulation for the healthy case shown in Fig. 2(a)
| Clinical targets | Computed values | |
|---|---|---|
| Aortic flow rate (cc/s) | 83.33 | 82.89 |
| Maximum aortic pressure (mmHg) | 120 | 119.2 |
| Minimum aortic pressure (mmHg) | 80 | 81.1 |
| Mean aortic pressure (mmHg) | 100 | 99.92 |
| Mean pulmonary artery pressure (mmHg) | 18 | 17.6 |
| Ejection fraction | 50–60% | 55% |
| Flow split ratio between coronary and systemic outlets | 4–6% | 4.8% |
| Flow split ratio between left and right coronaries | 70–80% | 79% |
Fig. 2.
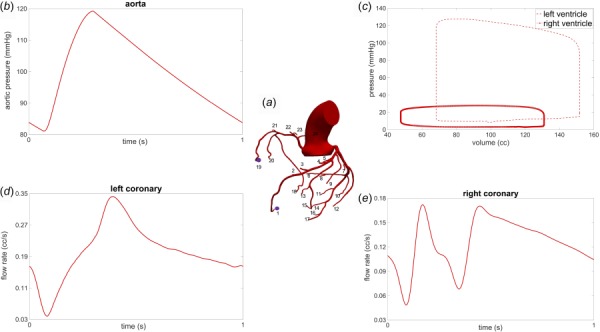
Simulation results for image-based 3D CFD coronary modeling: (a) image-based geometry with 24 coronary outlets, (b) computed aortic pressure waveform, (c) computed pressure-volume loops of the left and right ventricles, (d) typical computed left coronary artery flow waveform with minimum flow in systole and maximum flow in diastole, and (e) typical computed right coronary artery flow waveform with commensurate peaks in systole and diastole
Table 2.
Parameters of the heart model (in c.g.s. units) shown in Fig. 1 for the healthy patient-specific geometry of Fig. 2(a)
| Parameter | Value |
|---|---|
| Lra | 0.50 |
| Rra | 10 |
| Lrv | 0.25 |
| Rrv | 20 |
| Rpa | 120 |
| Cpa | 0.003 |
| Lla | 0.10 |
| Rla | 5 |
| Llv | 0.65 |
| Rlv | 10 |
Table 4.
Parameters of the coronary outlets (in c.g.s. units) for the healthy patient-specific geometry of Fig. 2(a)
| Outlet number | Ra 103 | Ram 103 | Rv 103 | Ca 10−6 | Cim 10−6 |
|---|---|---|---|---|---|
| 1 | 208.77 | 339.25 | 44.74 | 0.011 | 1.780 |
| 2 | 159.56 | 259.28 | 34.19 | 0.014 | 2.189 |
| 3 | 142.10 | 230.91 | 30.45 | 0.015 | 2.393 |
| 4 | 147.27 | 239.31 | 31.56 | 0.014 | 2.328 |
| 5 | 262.65 | 426.81 | 56.28 | 0.009 | 1.492 |
| 6 | 206.83 | 336.09 | 44.32 | 0.011 | 1.793 |
| 7 | 309.52 | 502.98 | 66.33 | 0.008 | 1.315 |
| 8 | 428.21 | 695.85 | 91.76 | 0.006 | 1.024 |
| 9 | 258.56 | 420.16 | 55.41 | 0.009 | 1.510 |
| 10 | 229.76 | 373.36 | 49.23 | 0.010 | 1.654 |
| 11 | 284.16 | 461.77 | 60.89 | 0.009 | 1.404 |
| 12 | 292.69 | 475.63 | 62.72 | 0.008 | 1.373 |
| 13 | 361.95 | 588.18 | 77.56 | 0.007 | 1.166 |
| 14 | 164.24 | 266.89 | 35.19 | 0.013 | 2.141 |
| 15 | 272.67 | 443.10 | 58.43 | 0.009 | 1.449 |
| 16 | 249.07 | 404.74 | 53.37 | 0.010 | 1.554 |
| 17 | 222.16 | 361.01 | 47.61 | 0.010 | 1.697 |
| 18 | 293.61 | 477.10 | 146.82 | 0.33 | 11.12 |
| 19 | 148.78 | 241.65 | 74.32 | 0.56 | 18.78 |
| 20 | 486.92 | 791.33 | 243.52 | 0.22 | 7.54 |
| 21 | 218.54 | 355.01 | 109.12 | 0.41 | 13.97 |
| 22 | 363.24 | 590.22 | 181.67 | 0.28 | 9.45 |
| 23 | 719.31 | 1168.85 | 359.60 | 0.17 | 5.58 |
| 24 | 449.6 | 730.6 | 224.83 | 0.24 | 8.02 |
Table 5.
Comparison between major hemodynamic indices at rest and hyperemia for the case shown in Fig. 2(a)
| Rest condition | Hyperemic condition | |
|---|---|---|
| Cardiac output (cc/s) | 82.89 | 82.97 |
| Mean blood pressure (mmHg) | 99.92 | 95.23 |
| Flow split ratio between coronary and systemic outlets | 4.8% | 16.7% |
| Flow split ratio between left and right coronaries | 79% | 81% |
Table 3.
Parameters of the systemic outlet (in c.g.s. units) for the healthy patient-specific geometry of Fig. 2(a)
| Parameter | Value |
|---|---|
| Rp | 142.47 |
| Rd | 1440.51 |
| C | 0.0015 |
3.2. Comparison of Model Results for Synthetic Symmetric Stenoses.
In this section, we calculate the amount of pressure drop across various synthetic stenoses in order to quantify the reliability of transstenotic pressure drop prediction from each model for varying the degree of stenosis in a systematic manner; patient-specific stenoses will be considered below. We created 50%, 75%, and 90% area reduction stenosis in one branch of the left anterior descending coronary artery of an image-based model that did not otherwise contain any major stenoses (see Figs. 3(a), 3(d), and 3(g)), and simulated the blood flow and pressure under hyperemia using the image-based 3D CFD methods described earlier. Computed flow rate and measured geometrical properties of the respective stenosis (see Table 6) were used to parameterize the algebraic, 1D and 2D multiring models. Note, the synthetic increase in Young's modulus for the 1D and 2D multiring models (used to maintain consistency with the 3D model) results in an increased pressure drop across the stenotic region, and leads to more favorable comparison as the 1D and 2D models systemically underpredicted pressure drop as shown below. The 1D solutions were obtained using 300 cells, and the multiring vessels were discretized with 30 rings and 800 cells.
Fig. 3.
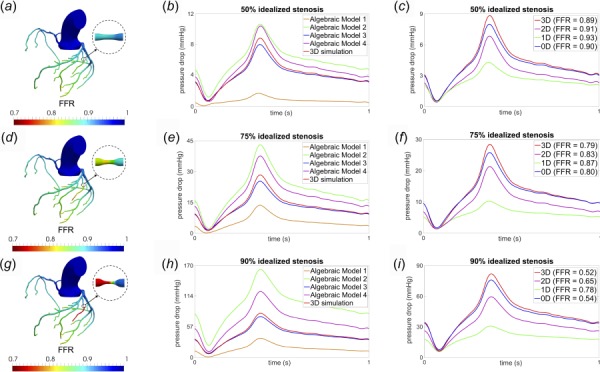
Comparison of results for models with 50%, 75%, and 90% idealized stenosis: (a), (d), (g) computed FFR distribution throughout the coronary trees from 3D CFD, (b), (e), (h) comparison of pressure drop across the respective coronary stenosis for four different algebraic models and the full 3D CFD simulation, and (c), (f), (i) comparison of pressure drop across the respective coronary stenosis obtained from algebraic model 3 (0D), 1D, multiring (2D), and the full 3D CFD simulation
Table 6.
Physical and geometrical properties (in c.g.s. units) of all respective stenosis models
| A0 | As | Lv | Ls | Womersley number () | Mean flow rate | |
|---|---|---|---|---|---|---|
| 50% Idealized stenosis | 0.013 | 0.0063 | 0.52 | 0.18 | 0.82 | 0.44 |
| 75% Idealized stenosis | 0.013 | 0.0028 | 0.51 | 0.17 | 0.82 | 0.40 |
| 90% Idealized stenosis | 0.013 | 0.0011 | 0.52 | 0.19 | 0.82 | 0.34 |
| 73% Nonsymmetric stenosis | 0.050 | 0.0125 | 1.47 | 0.71 | 1.20 | 1.93 |
| 90% Nonsymmetric stenosis | 0.013 | 0.0012 | 0.48 | 0.10 | 0.83 | 0.35 |
| 70% Patient-specific stenosis | 0.041 | 0.0108 | 3.27 | 1.04 | 0.91 | 1.06 |
| 88% Patient-specific stenosis | 0.061 | 0.0073 | 2.10 | 1.34 | 1.10 | 1.61 |
| 84% Patient-specific stenosis | 0.017 | 0.0027 | 0.56 | 0.21 | 0.86 | 0.48 |
Figures 3(a), 3(d), and 3(g) display the spatially resolved distribution of computed FFR throughout the coronary tree and demonstrate potential for ischemia for 75% and 90% area stenosis, but no potential ischemia for the 50% stenosis. Figures 3(b), 3(e), and 3(h) compare the results of the four algebraic models described in Sec. 2.4. The pressure drop results of Model 3 for all degrees of stenosis are consistent with those from the 3D simulations. Figures 3(c), 3(f), and 3(i) provide comparison between the amount of pressure drop calculated by model 3 (abbreviated henceforth in the figures as 0D), 1D, multiring (abbreviated as “2D”), and 3D simulations. The multiring method is able to better predict pressure drop than the 1D model for all degrees of stenosis considered, however, the estimated pressure drop from both the 1D and multiring methods deviate significantly from the 3D CFD results, particularly when the stenosis becomes clinically significant. The algebraic model 3 maintains consistent predictions for varying degrees of stenosis. A comparison of the computed FFR values calculated distal to the coronary stenoses for different models is presented in the inset legends of Figs. 3(c), 3(f), and 3(i), and similarly demonstrate the reliability of model 3 for different degrees of stenosis and the unreliability of the 1D and multiring methods as the stenosis becomes clinically significant. It was found that algebraic models 1, 2, and 4 produced consistently inaccurate results compared to 3D simulations, and thus, were not included in the subsequent comparisons presented below for asymmetric and patient-specific stenoses; algebraic model 3 was hence used as the de facto 0D model.
3.3. Comparison of Model Results for Synthetic Nonsymmetric Stenoses.
The idealized stenosis considered in Fig. 3 was locally symmetric. However, most patient-specific coronary stenoses have irregular and nonsymmetric geometries. To study robustness to asymmetry, we created nonsymmetric stenoses in different arteries with different degrees of area reduction. A nonsymmetric 73% stenosis with curvature was created in a different coronary artery, which had a mean flow that was five times greater compared to the symmetric 75% stenosis case presented earlier. Thus, this model considers large perturbations to stenosis shape, location, and flow rate. The model 3 prediction of pressure drop for this scenario remained consistent to the 3D CFD simulation results as shown in Figs. 4(a) and 4(b). As another test, a 90% highly asymmetric stenosis was considered, in the same arterial segment of the idealized 90% symmetric stenosis. Figures 4(c) and 4(d) demonstrate that model 3 maintained consistent prediction of transstenotic pressure drop even for this high degree of asymmetry and high severity of area reduction.
Fig. 4.
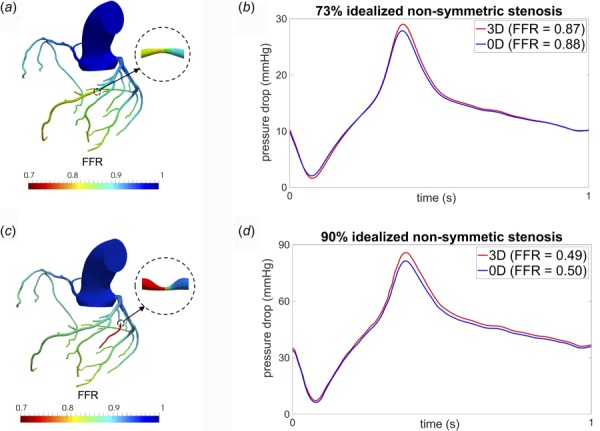
Comparison of results for models with asymmetric stenoses: (a) computed FFR distribution from 3D CFD for a 73% asymmetric stenosis, (b) pressure drop across stenosis for model 3 (0D) and full 3D CFD simulation for the 73% asymmetric stenosis, (c) computed FFR distribution from 3D CFD for a 90% asymmetric stenosis, and (d) pressure drop across stenosis between model 3 (0D) and full 3D CFD simulation for the 90% asymmetric stenosis
3.4. Comparisons for Patient-Specific Stenosis.
CCTA images of three patients with different degrees of stenosis were used to evaluate if the algebraic model 3 maintained reasonably consistent predictions for patient-specific stenosis geometries. Figures 5(a), 5(c), and 5(e) display the computed FFR distribution throughout the coronary trees of three patients with approximately 70%, 88%, and 84% area reduction stenosis, respectively, which spans FFR values from clinically acceptable (not likely to cause ischemia) to significant (likely to cause ischemia). These stenoses were located in different left and right coronary arteries with different flow rates of 1.06, 1.61, and 0.48 (cc/s), respectively. Moreover, it should be noted that the first patient (70% case) had two consecutive stenoses, which is not uncommon of lesion complexity encountered clinically. In the patient with consecutive stenosis, the amount of pressure drop due to the first stenosis was first calculated, then resulting values were used to calculate the pressure drop over the second stenosis, and finally, the results were combined. It was observed that the transstenotic pressure drop predicted by model 3 maintained reliable agreement with 3D simulation results in all cases. While the peak pressure drop showed moderate deviation, the computed FFR values varied by less than 4% between the 0D and 3D simulations.
Fig. 5.
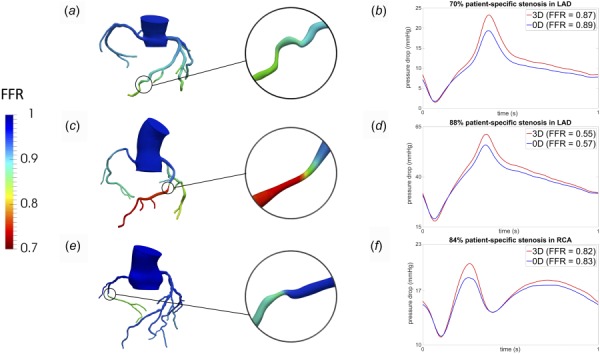
Comparison of models for patient-specific coronary stenoses: (a) computed FFR distribution for a patient with two consecutive stenosis in the left anterior descending (LAD) coronary artery with maximum value of 70%, (b) pressure drop across the consecutive stenoses from the algebraic model 3 (0D) and full 3D simulation, (c) computed FFR distribution for a patient-specific 88% stenosis in the left anterior descending (LAD) coronary artery, (d) pressure drop across the patient-specific 88% stenosis for algebraic model 3 (0D) and full 3D simulation, (e) computed FFR distribution for a patient-specific 84% stenosis in the right coronary artery (RCA), and (f) pressure drop across the patient-specific 84% stenosis for algebraic model 3 (0D) and full 3D simulation
4. Discussion
We compared the ability of various algebraic and PDE models to predict transstenotic pressure drop and noninvasive FFR estimation in the coronary arteries for a range of stenosis severity, morphology, location, and flow rate. The reduced order PDE models (1D and 2D multiring methods) consistently underestimated pressure drop and overestimated FFR. The algebraic pressure-drop models varied widely; however, one model (model 3) provided consistent prediction with 3D time-dependent CFD simulations. These results support the notion that an algebraic pressure-drop model may provide useful diagnostic value compared to more complex and computationally expensive methods.
Although the transstenotic pressure drop models considered here were developed for differing vascular applications, it was important to consider a range of models because model origin was generally not predictive of accuracy. For example, transstenotic pressure drop models developed for general vascular stenosis or coronary artery stenosis (e.g., Models 2 and 4) were found to perform poorly when compared to 3D simulations, whereas model 3 showed strong agreement over a range of scenarios. This may be considered surprising since model 3 was developed in the context of aortic coarctation where Reynolds number Re ∼ 2000, Womersley number ∼ 15, and area reduction 1 − As/A0 ∼ 40–60%. These key nondimensional parameters are on the order of Re ∼ 100, ∼ 1, and 1 − As/A0 ∼ 50–90% for coronary applications herein. Thus, the application here was not dynamically or kinematically similar to that considered in Ref. [16]. Despite the relative agreement of model 3 with the 3D results, the model does appear to systematically underpredict pressure drop slightly, which indicates that more favorable agreement may be achieved by appropriate tuning of model parameters for coronary applications.
To provide more general insight into reduced order modeling, we note that in most algebraic models the pressure drop is predicted based on energy losses due to viscosity, sudden expansion, convective and unsteadiness effects of the flow. Model 1 largely underestimates the value of pressure drop even for mild (50%) stenosis. The reason for this could be that viscous dissipation is neglected. Model 2 takes into account viscous dissipation, but the empirical parameters used in this model appear to result in significant overestimation of pressure drop as compared to model 3, which is of mostly similar functional form. Namely, the modifications introduced in model 3 appear to improve the accuracy, and robustness to changes in the shape, location, and degree of stenosis. Model 4 has the advantage of no empirical parameters, however, the results from this model appear sensitive to how the length of the stenosis is chosen. Knowing how to choose the length of the stenosis is generally difficult in practical applications.
The results of model 3 indicate that dissipation due to viscosity and flow separation downstream of the stenosis has the highest contributions to the total pressure drop. Pressure drop due to viscous dissipation is sensitive to the flow profile, which must be assumed in the 1D model, and it is difficult to anticipate a suitable flow profile a priori, if one even exists. Pressure drop due to flow separation is neglected in the 1D model since the velocity profile is assumed fixed at all cross sections. For this reason, one might not expect the 1D model to perform well; however, it is useful to quantify the amount of error incurred by 1D modeling since 1D modeling is employed for coronary flow simulations [34]. Flow separation and viscous effects are more accurately captured in the multiring method since the time- and space-varying velocity profiles are computed rather than assumed, which results in better prediction of pressure drop, as shown in Figs. 3(c), 3(f), and 3(i). However, the multiring method is relatively computationally expensive, and despite its improved accuracy, its results differed noticeably from the 3D simulations as the stenosis becomes clinically significant. A main assumption in the multiring method is axisymmetric velocity. However, even for a locally symmetric stenosis, the overall curvature of the artery in 3D leads to nonsymmetric and intricate stenotic flow patterns. This distortion of the velocity profile due to vessel curvature causes extra viscous dissipation as compared to a straight vessel with similar length and radius. Consequently, the axisymmetric assumption of the multiring model, and 1D model, could be a significant source of error in predicting pressure drop in realistically arterial geometries. Considering additional terms in 1D and multiring models to capture energy dissipation due to vessel curvature is likely to improve the accuracy of these models for predicting pressure drop [35].
We note that although FFR is based on mean differences in pressure, the comparisons of transstenotic pressure drop that we presented are temporally resolved. Thus, transient differences between the models can be evaluated. It is observed that model 3 maintained relative agreement with the 3D computations throughout the cardiac cycle. The comparison over time can also be loosely interpreted as comparison overflow rate since flow rate through the artery changes dramatically over the cardiac cycle. This is noteworthy for at least two reasons. First, uncertainty in cardiac output (upstream) or microvascular resistance, vascular reactivity or collateralization (downstream) would manifest in difference in flow rate through a stenotic artery. Second, the location (artery) of the stenosis mainly affects flow rate through the stenosis. Therefore, demonstrating that a model maintains consistent agreement over a range of flow rate is important.
All reduced order models used flow rates obtained from the 3D CFD simulation. This is reasonable from a comparison standpoint to reduce extraneous differences that might bias the comparisons. However, from a practical standpoint, one would want to avoid 3D CFD in order to estimate the flow rate in the stenotic artery for reduced order modeling to be worthwhile. However, this can be handled by either obtaining noninvasive estimation of flowrate in the effected coronary artery [36] or using a reduced order model of the coronary arterial tree in order to obtain flow rate through the stenotic artery. Another limitation is that we mostly considered isolated stenosis, however, atherosclerotic arteries can have highly diffuse lesions and/or lesions in proximity to bifurcations. Algebraic models are generally not designed to account for such geometric complexity, and such cases should likely be excluded from consideration in practical applications. Indeed, for translational efforts, a far greater number and variety of patient-specific stenosis should be considered. However, the results herein indicate that reduced order modeling may be sufficiently accurate to be of clinical value for a relatively broad range of cases.
5. Conclusion
Fast and accurate noninvasive identification of coronary transstenotic pressure loss can have important clinical significance for management of coronary artery disease. Here, we compared pressure-drop estimations from models diversely ranging from algebraic relations to 3D time-dependent CFD simulations in coronary stenoses that ranged in severity, shape, and location. We observed the capability of a simple algebraic model to maintain reasonable agreement with fully 3D patient-specific CFD simulations, providing evidence that an algebraic pressure-drop model may provide high diagnostic value for evaluating the functional significance of a coronary stenosis.
Funding Data
This work was supported by the NIH (Grant No. R01HL103419, Funder ID. 10.13039/100000002).
Author HIL is supported by research grants from Siemens Healthineers related to FFR research (Funder ID. 10.13039/501100004830).
Appendix
Verification of One-Dimensional Solver.
To verify our 1D solver, we considered the benchmark study in Boileau et al. [37]. The vessel had uniform geometry and wall properties, with nominal radius of 0.3 cm and length of 12.6 cm. A pulsatile periodic flow waveform with a period of = 1.1(s) (see Fig. 6(a)) was imposed as an inlet boundary condition and a three-element Windkessel model was employed at the outlet boundary. All the mechanical and geometrical parameters for this model are given in Table 7. Figure 6 displays the numerical predictions of inlet pressure (Fig. 6(b)), flow rate at the midpoint (Fig. 6(c)), and pressure gradient between inlet and outlet of the model (Fig. 6(d)). These waveforms are in excellent agreement with the corresponding waveforms calculated in Boileau et al. [37].
Fig. 6.
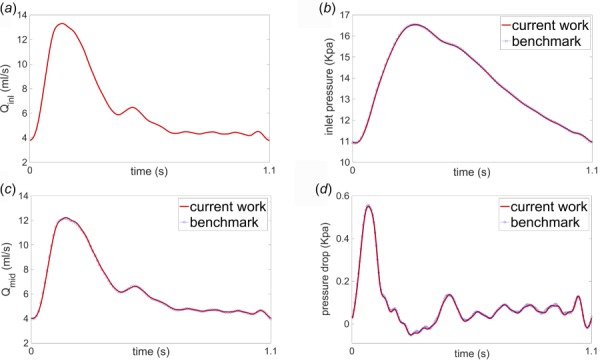
Results of 1D simulations of flow and pressure in an idealized common carotid artery from our in-house solver and benchmark [37]: (a) imposed inlet flow rate, (b) computed inlet pressure, (c) computed flow rate at the vessel midpoint, and (d) computed pressure difference between the inlet and outlet
Table 7.
Model parameters of the common carotid artery taken from Boileau et al. [37]
| Property | Value |
|---|---|
| Length, | 126 mm |
| Radius at diastolic pressure, | 3 mm |
| Area at diastolic pressure, | 0.28274 cm2 |
| Initial cross-sectional area, | 0.22038 cm2 |
| Initial flow velocity, | 0 |
| Initial pressure, | 0 |
| Wall thickness, | 0.3 mm |
| Blood density, | 1060 Kg m−3 |
| Blood viscosity, | 4 m Pa s |
| Velocity profile order, | 2 |
| Young's modulus, | 700.0 kPa |
| Diastolic pressure, | 10.933 kPa |
| Windkessel resistance, | 2.4875 × 108 Pa s m−3 |
| Windkessel compliance, | 1.7529 × 10−10 m3.Pa−1 |
| Windkessel resistance, | 1.8697 × 109 Pa s m−3 |
Verification of Multiring Solver.
The analytical linear Womersley solution for flow in a deformable tube was used to verify our numerical implementation of the multiring method. Details of the analytical derivation of the Womersley solution can be found in the previous works [11]. Since the multiring method can produce the velocity profile at each cross section over differing axial locations, it is expected that the longitudinal and radial variation of the axial velocity component from the Womersley solution can be reproduced by the multiring method. All model parameters used in the comparison are listed in Table 8.
Table 8.
Geometrical and mechanical parameters for the artery, inlet and outlet boundary conditions taken from Ghigo et al. [11]
| Property | Value |
|---|---|
| Length, | 200 cm |
| Initial radius, | 1 cm |
| Wall rigidity, | 104 dyn cm−3 |
| Initial flow rate, | 0 |
| Initial pressure, | 0 |
| Blood density, | 1 g cm−3 |
| Blood viscosity, | dyn s cm−2 |
| Inlet pressure amplitude, | |
| Womersley number, | 5, 20 |
For the multiring model, a periodic pressure with = 0.5 was imposed at the inlet of the tube and a nonreflecting boundary condition was imposed at the outlet. The multiring vessel was discretized with 120 rings and 1600 cells. Figure 7 shows the velocity profile at = 25 (cm) at different time points for both the multiring and Womersley solutions, with Womersley numbers of 5 and 20. For both Womersley numbers, the multiring method demonstrates very close agreement with the Womersley solution for both flow and pressure.
Fig. 7.
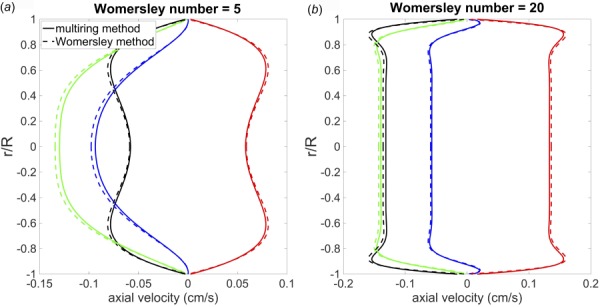
Comparison of velocity profiles from the analytical linear Womersley solution (dashed line) and multiring method (solid lines) at x = 25 cm and different time points
Contributor Information
Mehran Mirramezani, Department of Mechanical Engineering, , University of California, , Berkeley, CA 94720;; Department of Mathematics, , University of California, , Berkeley, CA 94720
Scott L. Diamond, Department of Chemical and , Biomolecular Engineering, , Institute for Medicine and Engineering, , University of Pennsylvania, , Philadelphia, PA 19104
Harold I. Litt, Department of Radiology, , Perelman School of Medicine , of the University of Pennsylvania, , Philadelphia, PA 19104
Shawn C. Shadden, Department of Mechanical Engineering, , University of California, , Berkeley, CA 94720 , e-mail: shadden@berkeley.edu.
References
- [1]. Heidenreich, P. , Trogdon, J. , Khavjou, O. , Butler, J. , Dracup, K. , Ezekowitz, M. D. , Finkelstein, E. A. , Hong, Y. , Johnston, S. C. , Khera, A. , Lloyd-Jones, D. M. , Nelson, S. A. , Nichol, G. , Orenstein, D. , Wilson, P. W. F. , and Woo, Y. J. , 2011, “ Forecasting the Future of Cardiovascular Disease in the United States a Policy Statement From the American Heart Association,” Circulation, 123(8), pp. 933–944. 10.1161/CIR.0b013e31820a55f5 [DOI] [PubMed] [Google Scholar]
- [2]. Meijboom, W. B. , Mieghem, C. A. V. , Pelt, N. V. , Weustink, A. , Pugliese, F. , Mollet, N. R. , Boersma, E. , Regar, E. , van Geuns, R. J. , de Jaegere, P. J. , Serruys, P. W. , Krestin, G. P. , and de Feyter, P. J. , 2008, “ Comprehensive Assessment of Coronary Artery Stenoses: Computed Tomography Coronary Angiography Versus Conventional Coronary Angiography and Correlation With Fractional Flow Reserve in Patients With Stable Angina,” J. Am. Coll. Cardiol, 52(8), pp. 636–643. 10.1016/j.jacc.2008.05.024 [DOI] [PubMed] [Google Scholar]
- [3]. Schuijf, J. D. , and Bax, J. J. , 2008, “ CT Angiography: An Alternative to Nuclear Perfusion Imaging?,” Heart, 94(3), pp. 255–257. 10.1136/hrt.2006.105833 [DOI] [PubMed] [Google Scholar]
- [4]. Pijls, N. H. , Son, J. A. , Kirkeeide, J. A. , De Bruyne, R. L. , and Gould, B. , 1993, “ Experimental Basis of Determining Maximum Coronary, Myocardial, and Collateral Blood Flow by Pressure Measurements for Assessing Functional Stenosis Severity Before and After Percutaneous Transluminal Coronary Angioplasty,” Circulation, 87(4), pp. 1354–1367. 10.1161/01.CIR.87.4.1354 [DOI] [PubMed] [Google Scholar]
- [5]. Taylor, C. A. , Fonte, T. A. , and Min, J. K. , 2013, “ Computational Fluid Dynamics Applied to Cardiac Computed Tomography for Noninvasive Quantification of Fractional Flow Reserve,” J. Am. Coll. Cardiol., 61(22), pp. 2233–2241. 10.1016/j.jacc.2012.11.083 [DOI] [PubMed] [Google Scholar]
- [6]. Min, J. K. , Leipsic, J. , Pencina, M. J. , Berman, D. S. , Min, B. K. , Leipsic, J. , Pelcina, M. J. , Berman, D. S. , Koo, B.-K. , van Mieghem, C. , Erglis, A. , Lin, F. Y. , Dunning, A. M. , Apruzzese, P. , Budoff, M. J. , Cole, J. H. , Jaffer, F. A. , Leon, M. B. , Malpeso, J. , Mancini, G. B. J. , Park, S.-J. , Schwartz, R. S. , Shaw, L. J. , and Mauri, L. , 2012, “ Diagnostic Accuracy of Fractional Flow Reserve From Anatomic CT Angiography,” JAMA, 308(12), pp. 1237–1245. 10.1001/2012.jama.11274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Nakazato, R. , Park, H. B. , Berman, D. S. , Gransar, H. , Koo, B. K. , Erglis, A. , Lin, F. Y. , Dunning, A. M. , Budoff, M. J. , Malpeso, J. , Leipsic, J. , and Min, J. K. , 2013, “ Noninvasive Fractional Flow Reserve Derived From Computed Tomography Angiography for Coronary Lesions of Intermediate Stenosis Severity: Results From the DeFACTO Study,” Circ. Cardiovasc. Imag., 6(6), pp. 881–889. 10.1161/CIRCIMAGING.113.000297 [DOI] [PubMed] [Google Scholar]
- [8]. Barnard, A. C. L. , Hunt, W. A. , Timlake, W. P. , and Varley, E. A. , 1966, “ Theory of Fluid Flow in Compliant Tubes,” Biophys. J., 6(6), pp. 717–724. 10.1016/S0006-3495(66)86690-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Formaggia, L. , Lamponi, D. , Tuveri, M. , and Veneziani, A. , 2006, “ Numerical Modeling of 1D Arterial Networks Coupled With a Lumped Parameters Description of the Heart,” Comput. Methods Biomech., 9(5), pp. 273–288. 10.1080/10255840600857767 [DOI] [PubMed] [Google Scholar]
- [10]. Hughes, T. J. , and Lubliner, J. , 1973, “ On the One-Dimensional Theory of Blood Flow in the Larger Vessels,” Math. Biosci., 18(1–2), pp. 161–170. 10.1016/0025-5564(73)90027-8 [DOI] [Google Scholar]
- [11]. Ghigo, A. R. , Fullana, J. M. , and Lagrée, P. Y. , 2017, “ A 2D Nonlinear Multi-ring Model for Blood Flow in Large Elastic Arteries,” J. Comput. Phys., 350, pp. 136–165. 10.1016/j.jcp.2017.08.039 [DOI] [Google Scholar]
- [12]. Young, D. F. , and Tsa, F. Y. , 1973, “ Flow Characteristic in Models of Arterial Stenosis—I, Steady Flow,” J. Biomech., 6(4), pp. 395–410. 10.1016/0021-9290(73)90099-7 [DOI] [PubMed] [Google Scholar]
- [13]. Young, D. F. , and Tsa, F. Y. , 1973, “ Flow Characteristic in Models of Arterial Stenosis—II, Unsteady Flow,” J. Biomech., 6(5), pp. 547–559. 10.1016/0021-9290(73)90012-2 [DOI] [PubMed] [Google Scholar]
- [14]. Seeley, B. D. , and Young, D. F. , 1976, “ Effect of Geometry on Pressure Losses Across Models of Arterial Stenosis,” J. Biomech., 9(7), pp. 439–448. 10.1016/0021-9290(76)90086-5 [DOI] [PubMed] [Google Scholar]
- [15]. Garcia, D. , Pibarot, P. , and Duranda, L. G. , 2005, “ Analytical Modeling of the Instantaneous Pressure Gradient Across the Aortic Valve,” J. Biomech., 38(6), pp. 1303–1311. 10.1016/j.jbiomech.2004.06.018 [DOI] [PubMed] [Google Scholar]
- [16]. Itu, L. , Sharma, P. , Ralovich, K. , Mihalef, V. , Ionasec, R. , Everett, A. , Ringel, R. , Kamen, A. , and Comaniciu, D. , 2013, “ Non-Invasive Hemodynamic Assessment of Aortic Coarctation: Validation With In Vivo Measurements,” Ann. Biomed. Eng., 41(4), pp. 669–681. 10.1007/s10439-012-0715-0 [DOI] [PubMed] [Google Scholar]
- [17]. Huo, Y. L. , Svendsen, M. J. , Choy, S. , Zhang, Z. D. , and Kassab, G. S. , 2012, “ A Validated Predictive Model of Coronary Fractional Flow Reserve,” J. R. Soc., Interface., 9(71), pp. 1325–1338. 10.1098/rsif.2011.0605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Schrauwen, J. T. C. , Wentzel, J. J. , Steen, A. F. W. V. , and Gijsen, F. J. H. , 2014, “ Geometry-Based Pressure Drop Prediction in Mildly Diseased Human Coronary Arteries,” J. Biomech., 47, pp. 1810–1815. 10.1016/j.jbiomech.2014.03.028 [DOI] [PubMed] [Google Scholar]
- [19]. Schrauwen, J. T. C. , Koeze, D. J. , Wentzel, J. J. , Vosse, F. N. V. , Steen, A. F. W. V. , and Gijsen, F. J. H. , 2015, “ Fast and Accurate Pressure-Drop Prediction in Straightened Atherosclerotic Coronary Arteries,” Ann. Biomed. Eng., 43(1), pp. 59–67. 10.1007/s10439-014-1090-9 [DOI] [PubMed] [Google Scholar]
- [20]. Updegrove, A. , Wilson, N. M. , Merkow, J. , Lan, H. , Marsden, A. L. , and Shadden, S. C. , 2016, “ Simvascular—An Open Source Pipeline for Cardiovascular Simulation,” Ann. Biomed. Eng., 45(3), pp. 525–541. 10.1007/s10439-016-1762-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Kim, H. J. , Vignon-Clementel, I. E. , Coogan, J. S. , Figueroa, C. A. , Jansen, K. E. , and Taylor, C. A. , 2010, “ Patient-Specific Modeling of Blood Flow and Pressure in Human Coronary Arteries,” Ann. Biomed. Eng., 38(10), pp. 3195–3209. 10.1007/s10439-010-0083-6 [DOI] [PubMed] [Google Scholar]
- [22]. Sankaran, S. , Moghadam, M. E. , Kahn, A. M. , Tseng, E. E. , Guccione, J. M. , and Marsden, A. L. , 2012, “ Patient-Specific Multiscale Modeling of Blood Flow for Coronary Artery Bypass Graft Surgery,” Ann. Biomed. Eng., 40(10), pp. 2228–2242. 10.1007/s10439-012-0579-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Nørgaard, B. L. , Gaur, S. , Leipsic, J. , Ito, H. , Miyoshi, T. , Park, S. J. , Zvaigzne, L. , Tzemos, N. , Jensen, J. M. , Hansson, N. , Ko, B. , Bezerra, H. , Christiansen, E. H. , Kaltoft, A. , Lassen, J. F. , Bøtker, H. E. , and Achenbach, S. , 2015, “ Influence of Coronary Calcification on the Diagnostic Performance of CT Angiography Derived FFR in Coronary Artery Disease: A Substudy of the NXT Trial,” JACC: Cardiovasc. Imag., 8, pp. 1045–1055. 10.1016/j.jcmg.2015.06.003 [DOI] [PubMed] [Google Scholar]
- [24]. Miyoshi, T. , Osawa, K. , Ito, H. , Kanazawa, S. , Kimura, T. , Shiomi, H. , Kuribayashi, S. , Jinzaki, M. , Kawamura, A. , Bezerra, H. , Achenbach, S. , and Nørgaard, B. L. , 2015, “ Non-Invasive Computed Fractional Flow Reserve From Computed Tomography (CT) for Diagnosing Coronary Artery Disease,” Circ. J., 79(2), pp. 406–412. 10.1253/circj.CJ-14-1051 [DOI] [PubMed] [Google Scholar]
- [25]. Lu, M. T. , Ferencik, M. , Roberts, R. S. , Lee, K. L. , Ivanov, A. , Adami, E. , Mark, D. B. , Jaffer, F. A. , Leipsic, J. A. , Douglas, P. S. , and Hoffmann, U. , 2017, “ Noninvasive FFR Derived From Coronary CT Angiography: Management and Outcomes in the PROMISE Trial,” JACC: Cardiovasc. Imag., 10, pp. 1350–1358. 10.1016/j.jcmg.2016.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Changizi, M. A. , and Cherniak, C. , 2000, “ Modeling the Large-Scale Geometry of Human Coronary Arteries,” Can. J. Physiol. Pharm., 78(8), pp. 603–611. 10.1139/y00-024 [DOI] [PubMed] [Google Scholar]
- [27]. Wilson, R. F. , Wyche, K. , Christensen, B. V. , Zimmer, S. , and Laxson, D. D. , 1990, “ Effects of Adenosine on Human Coronary Arterial Circulation,” Circulation., 82(5), pp. 1595–1606. 10.1161/01.CIR.82.5.1595 [DOI] [PubMed] [Google Scholar]
- [28]. Perthame, B. , 2002, Kinetic Formulation of Conservation Laws, Oxford Press, New York. [Google Scholar]
- [29]. Audusse, E. , and Bristeau, M. O. , 2005, “ A Well-Balanced Positivity Preserving Second-Order Scheme for Shallow Water Flows on Unstructured Meshes,” J. Comput. Phys., 206(1), pp. 311–333. 10.1016/j.jcp.2004.12.016 [DOI] [Google Scholar]
- [30]. Formaggia, L. , Lamponi, D. , and Quarteroni, A. , 2003, “ One-Dimensional Models for Blood Flow in Arteries,” J. Eng. Math., 47(3/4), pp. 251–276. 10.1023/B:ENGI.0000007980.01347.29 [DOI] [Google Scholar]
- [31]. Sherwin, S. J. , Franke, V. , Peiro, J. , and Parker, K. H. , 2003, “ One-Dimensional Modelling of a Vascular Network in Space-Time Variables,” J. Eng. Math., 47(3/4), pp. 217–250. 10.1023/B:ENGI.0000007979.32871.e2 [DOI] [Google Scholar]
- [32]. Fargie, D. , and Martin, B. W. , 1971, “ Developing Laminar Flow in a Pipe of Circular Cross-Section,” Proc. R. Soc. Lond. A., 321(1547), pp. 461–476. 10.1098/rspa.1971.0043 [DOI] [Google Scholar]
- [33]. Opie, L. H. , 2003, Heart Physiology: From Cell to Circulation, Lippincott Williams and Wilkins, Philadelphia, PA. [Google Scholar]
- [34]. Boileau, E. , Pant, S. , Roobottom, C. , Sazonov, I. , Deng, J. , Xie, X. , and Nithiarasu, P. , 2017, “ Estimating the Accuracy of a Reduced-Order Model for the Calculation of Fractional Flow Reserve (FFR),” Int. J. Numer. Meth. Biomed. Eng., 34(1), p. e2908. 10.1002/cnm.2908 [DOI] [PubMed] [Google Scholar]
- [35]. Dean, W. R. , 1927, “ Note on the Motion of Fluid in a Curved Pipe,” Phil. Mag., Ser., 4(20), pp. 208–223. 10.1080/14786440708564324 [DOI] [Google Scholar]
- [36]. Molloi, S. , Zhou, Y. , and Kassab, G. S. , 2004, “ Regional Volumetric Coronary Blood Flow Measurement by Digital Angiography: In Vivo Validation,” Acad. Radiol., 11(7), pp. 757–766. 10.1016/j.acra.2004.04.002 [DOI] [PubMed] [Google Scholar]
- [37]. Boileau, E. , Nithiarasu, P. , Blanco, P. J. , Müller, L. O. , Fossan, F. E. , Hellevik, L. R. , Donders, W. P. , Huberts, W. , Willemet, M. , and Alastruey, J. , 2015, “ A Benchmark Study of Numerical Schemes for One-Dimensional Arterial Blood Flow Modelling,” Int. J. Numer. Meth. Biomed. Eng., 31(10), p. e02732. 10.1002/cnm.2732 [DOI] [PubMed] [Google Scholar]


