ABSTRACT
MicroRNAs (miRNAs) play an important role in prevention, diagnosis and treatment of human complex diseases. Predicting potential miRNA-disease associations could provide important prior information for medical researchers. Therefore, reliable computational models are expected to be an effective supplement for inferring associations between miRNAs and diseases. In this study, we developed a novel calculative model named Negative Samples Extraction based MiRNA-Disease Association prediction (NSEMDA). NSEMDA filtered reliable negative samples by two positive-unlabeled learning models, namely, the Spy and Rocchio techniques and calculated similarity weights for ambiguous samples. The positive samples, reliable negative samples and ambiguous samples with similarity weights were used to construct a Support Vector Machine-Similarity Weight model to predict miRNA-disease associations. NSEMDA improved the credibility of negative samples and reduced the impact of noise samples by introducing ambiguous samples with similarity weights to train prediction model. As a result, NSEMDA achieved the AUC of 0.8899 in global leave-one-out cross validation (LOOCV) and AUC of 0.8353 under local LOOCV. In 100 times 5-fold cross validation, NSEMDA obtained an average AUC of 0.8878 and standard deviation of 0.0014. These AUCs are higher than many classical models. Besides, we also carried out three kinds of case studies to evaluate the performance of NSEMDA. Among the top 50 potential related miRNAs of esophageal neoplasms, lung neoplasms and carcinoma hepatocellular predicted by NSEMDA, 46, 50 and 45 miRNAs were verified to be associated with the investigated disease by experimental evidences, respectively. Therefore, NSEMDA would be a reliable calculative model for inferring miRNA-disease associations.
KEYWORDS: Microrna, disease, association prediction, reliable negative sample, positive-unlabeled learning
Introduction
MicroRNAs (miRNAs) are a class of short non-coding RNAs of about 22 nucleotides in length [1]. It normally suppresses gene expression by binding to the 3ʹ untranslated regions (UTRs) of the target mRNAs through base pairing that will inhibit translation and reduce mRNA stability [2]. Meanwhile, some miRNAs also promote the expression of the target mRNAs according to scientific studies. The first two known miRNAs lin-4 and let-7 were discovered more than twenty years ago [3,4], and they both act as positive regulators. According to previous studies, miRNAs play an important role in many cellular and biological processes such as cell growth [5], cell aging [6], cell proliferation [7], signal transduction [8], tumor invasion [9], and so on. Understanding the molecular mechanism of miRNA may provide new ideas for overcoming complex diseases. Zheng et al. [10] found that the levels of miR-106b were upregulated in both tissue and plasma samples from breast cancer patients and patients with high miR-106b expression levels tended to have shorter disease-free survival times and overall survival times. Besides, Heegaard et al. [11] accurately measured expression levels of miRNAs in serum of 220 patients with early stage non-small cell lung cancer and 220 matched controls. As a result, the expression of miR-27a, miR-106a, miR-221, miR-146b, miR-155, miR-17-5p and let-7 were lower compared with controls, meanwhile the expression of miR-29c was increased. In addition, Wang et al. [12] surveyed the function and expression level of miR-22 in patients with esophageal squamous cell carcinoma. They found that there was a clear positive correlation between the expression of miR-22 and the survival rate of patients receiving radiotherapy. There is no doubt that collecting and making full use of information of associations between miRNAs and diseases could help researchers to discover pathogenesis of human complex diseases at the molecular level. Furthermore, uncovering the miRNA-disease associations would improve the diagnostic and therapeutic level of human complex diseases. However, seeking such associations between miRNAs and diseases through experiments is extremely inefficient and pay a lot in manpower, materials and finance. Therefore, efficient computational methods are expected to predict more reliable associations between miRNAs and diseases for further experiments.
In the past few years, plenty of computational models have been developed to infer potential associations between miRNAs and diseases [13]. Under the hypothesis that functionally related miRNAs are more likely to be linked with phenotypically similar diseases, Jiang et al. [14] constructed a phenome-microRNAome network by merging functionally related miRNA network, disease phenotype similarity network, and known human disease-miRNA association network. They developed a scoring system based on hypergeometric distribution to predict potential miRNAs associated with the investigated disease. The functionally related miRNA network in their study was constructed just according to the hypothesis that two miRNAs are functionally related if the number of target genes shared by them was statistically significant. However, two miRNAs may be functionally related if their target genes are in the same cellular pathways or functional modules. Moreover, based on the hypothesis that if a miRNA’s targets are related with disease genes, the miRNA is more likely to be associated with this disease, Shi et al. [15] proposed a method to identify miRNA-disease association by mapping miRNA targets and disease genes on a protein-protein interaction (PPI) network and using the random walk with restart (RWR) algorithm in the PPI network. Pasquier et al. [16] developed a model named MiRAI which concatenated five different matrices, namely, the miRNA-disease association matrix, the miRNA-neighbor association matrix, the miRNA-target association matrix, the miRNA-word association matrix and the miRNA-family association matrix. Then they cut down the dimension of the larger matrix by Singular Value Decomposition and calculated the cosine distance between the miRNA vector and the disease vector as the association score for this miRNA-disease pair. Nevertheless, high false-positive and false-negative miRNA-target interactions or incomplete network information of disease-gene associations would damage the predicted performance of these models mentioned above.
Researchers also made use of miRNA functional similarity network which do not rely on miRNA-target interactions to represent miRNAs information in some computational methods. Xuan et al. [17] developed a reliable computational model named Human Disease-related MiRNA Prediction (HDMP) to predict potentially related miRNAs for disease through surveying k most similar neighbors of candidate miRNAs respectively. The functional similarity of each two miRNAs used in HDMP was calculated by utilizing the semantic similarity and phenotype similarity of their related diseases. Compared to previous studies, HDMP distributed higher weight to neighbors of candidate miRNA if they belong to the same miRNA family or cluster, which improved prediction accuracy. However, HDMP could not infer potentially related miRNAs for novel diseases without any known associated miRNAs. In addition, HDMP only used k neighbors’ information of candidate miRNA rather than global miRNA functional similarity network that would limit the prediction performance. Chen et al. [18] developed Random Walk with Restart for MiRNA–Disease Association (RWRMDA) to infer potential disease-related miRNAs by implementing random walk algorithm on miRNA functional similarity network. RWRMDA made full use of known miRNA-disease associations and miRNA functional similarity network, which is the first global similarity-based prediction method. Nevertheless, it still could not work for novel diseases without any known associated miRNAs. Xuan et al. [19] proposed another computational model of MIRNAs associated with Diseases Prediction (MIDP) to predict disease-associated miRNAs based on random walk, which utilized the characteristics of the nodes and prior information of miRNA-disease associations. MIDP separated the transition matrix into two transition matrices about the labeled nodes and the unlabeled nodes which were distinguished according to prior information of nodes and gave higher weight to the former. MIDP succeeded in working for novel diseases without known associated miRNAs by extending the walking on a miRNA-disease bilayer network. Chen et al. [20] developed another model named Within and Between Score for MiRNA-Disease Association prediction (WBSMDA). They calculated within-score by surveying the similarity between known miRNAs (diseases) which are related with the disease (miRNA) of target miRNA-disease pair and the miRNA (disease) of target miRNA-disease pair. Besides, between-score was computed by surveying the similarity between miRNAs (diseases) which are unrelated with the disease (miRNA) of target sample and the miRNA (disease) of target sample. By this way, WBSMDA can work for novel disease without associated miRNAs and novel miRNA without associated diseases respectively. Recently, Chen et al. [21] presented a model of Heterogeneous graph inference for miRNA-disease association prediction (HGIMDA). They complemented the similarity information of miRNAs and diseases through computing Gaussian profile kernel similarities of miRNAs and diseases respectively. These similarity information and miRNA-disease associations information were integrated into a heterogeneous graph. The association scores of potential associated miRNA-disease pairs can be obtained by considering all paths with the length equal to three. Recently, Li et al. [22] proposed a calculated model of Matrix Completion for MiRNA Disease Association (MCMDA) in which the matrix completion procedure was accomplished by utilizing the singular value thresholding (SVT) algorithm. MCMDA predicted the miRNA-disease associations only depended on the known miRNA–disease associations. Yu et al. [23] developed a model of Maximizing Network Information Flow (MaxFlow) to infer miRNA-disease associations. Initially, a query disease and candidate miRNAs were introduced in a network. The maximum information flow between two nodes was calculated using the push-relabel algorithm. Then they computed the amount of flow leaving a candidate miRNA by summing all maximum information flow between the miRNA and other nodes in the network. Finally, the amount of flow leaving the candidate miRNA was utilized to evaluate the extent of association between the miRNA and the query disease. More recently, Chen et al. [24] proposed a model of Triple Layer Heterogeneous Network based inference for MiRNA-Disease Association prediction (TLHNMDA). The triple layer heterogeneous network was constructed by integrating miRNA-disease associations, interactions between miRNAs and long non-coding RNAs (lncRNAs) and similarity networks of miRNAs, diseases and lncRNAs. Then they built two iterative updating algorithms that propagate information across the constructed heterogeneous network for the identification of potential miRNA-disease associations and miRNA-lncRNA interactions, respectively. In each step, once a new miRNA-lncRNA interaction was obtained, it would be used as new information for the identification of miRNA-disease associations. Similarly, once a new miRNA-disease association was obtained, a new miRNA-lncRNA interaction would be obtained. The two algorithms would be stable after some steps and final probability scores of potential miRNA-disease associations would be obtained. Chen et al. [25] also developed a computational model of Inductive Matrix Completion for MiRNA-Disease Association prediction (IMCMDA). They applied miRNA similarity matrix and disease similarity matrix as the feature matrix of miRNA and disease respectively. Based on the information of known miRNA-disease associations and these feature matrices, the inductive matrix completion algorithm was used to complete the missing entries of known miRNA-disease association matrix by constructing an optimization problem. Then they searched the optimal solution with an alternating gradient descent algorithm. Finally, the completed matrix was used to measure the correlations between miRNAs and diseases.
In addition, there were some calculated models constructed based on machine learning methods. Chen et al. [26] proposed a model of Regularized Least Squares for MiRNA-Disease Association (RLSMDA). RLSMDA created two optimal classification functions by solving two similar optimization problems in miRNA space and disease space respectively. The two optimal classifiers were combined to predict miRNA-disease associations based on a simple weighted average operation. RLSMDA can infer potential miRNAs for all diseases simultaneously and predict associated miRNAs for diseases without any known associated miRNAs. The problem of this model is how to directly obtain a single classifier from miRNA space and disease space. Chen et al. [27] presented another calculated model of Restricted Boltzmann machine for multiple types of miRNA-disease association prediction (RBMMMDA) based on the restricted Boltzmann machine (RBM) which is a two-layer undirected graphical model composed of layers of visible and hidden units. It is worth noting that RBMMMDA could not only predict potential miRNA-disease associations but also give types of the corresponding association. However, it is hard to select parameters in RBMMMDA. More recently, Chen et al. [28] developed a Ranking-based KNN for miRNA-Disease Association prediction (RKNNMDA) method in which k-Nearest Neighbor (KNN) algorithm and Support Vector Machine (SVM) ranking model were used to find k-nearest-neighbors for miRNA and disease. They calculated the weight score 1 (WS1) between a miRNA and a disease by integrating the feature scores of the disease. Similarly, the weight score 2 (WS2) was calculated by integrating the feature scores of the miRNA. Finally, they added WS1 and WS2 together and ranked the potential miRNA-disease associations.
The methods mentioned above had their own highlights, meanwhile some limitations also existed. In this study, we developed a novel computational model of Negative Samples Extraction based MiRNA-Disease Association prediction (NSEMDA) (motivated by the study of Peng et al. [29]). As we know, negative samples of miRNA-disease pairs are hard to come by and some machine learning-based methods randomly selected samples from unlabeled miRNA-diseases pairs as negative samples. The false negative rate of these negative samples obtained by randomly selection would be high. In our model, negative samples were extracted from unlabeled samples by using two positive-unlabeled learning (PU learning) technologies. In addition, the noise in training samples was unavoidable. Thus, we calculated similarity weights for ambiguous samples which represent probabilities that the ambiguous samples belong to the negative and positive categories to demonstrate different noise levels of the ambiguous samples. Finally, training samples including positive samples, negative samples and ambiguous samples with similarity weights were used to train prediction model based on SVM-Similarity Weight (SVM-SW). We carried out leave-one-out cross validation (LOOCV) and five-fold cross validation to evaluate performance of NSEMDA. As a result, the model obtained AUC of 0.8899 in global LOOCV and 0.8353 in local LOOCV. The AUC based on 5-fold cross validation of NSEMDA was 0.8878 ± 0.0014. Besides, three kinds of case studies were used in several common human diseases that are Esophageal Neoplasms, Lung Neoplasms and Hepatocellular Carcinoma. NSEMDA predicted potentially associated miRNAs for them, and there were 46, 50 and 45 of top 50 predicted miRNAs which were verified by biological evidences, respectively. The results of cross-validation and case studies reveal the reliability of our method.
Results
Performance evaluation
In this study, both global and local LOOCV were applied based on the known associated miRNA-disease pairs to evaluate the performance of NSEMDA. The known 5430 miRNA-disease associations were obtained from HMDD v2.0 involving 383 diseases and 495 miRNAs. In global LOOCV, each of 5430 miRNA-disease associations was left out as a test sample in turns. Then the test sample and all unknown miRNA-disease pairs between 383 diseases and 495 miRNAs were scored by the prediction model. We could obtain the rank of the test sample after ranking these scores in descending order. Finally, we got 5430 rankings in total. We drew a Receiver Operating Characteristics curve (ROC) with the true positive rate (TPR, sensitivity) versus the false positive rate (FPR, 1-specificity) at different thresholds. Sensitivity means the percentage of test samples ranked above the threshold and specificity represents the percentage of candidates ranked below the threshold. Area under the ROC (AUC) curve was widely used to assess the performance of a calculation model and the higher the AUC value, the better the model performance. As shown in Figure 1, NSEMDA obtained higher global LOOCV AUC of 0.8899 compared with 0.8781, 0.8426, 0.8366, 0.8030, 0.8795, 0.8749 and 0.8624 of previous models corresponding to HGIMDA, RLSMDA, HDMP, WBSMDA, TLHNMDA, MCMDA and MaxFlow, respectively. In local LOOCV, it was different from global LOOCV that test sample and unknown miRNA-disease pairs which contain the same disease in the test sample were scored by our prediction model. Similarly, we could obtain the rank of the test sample after ranking these scores in descending order. Then we drew a ROC curve in the same way and the local LOOCV AUC of NSEMDA was 0.8353 which was still higher than AUCs of 0.8077, 0.6953, 0.7702, 0.8031, 0.7756, 0.7718, 0.6299, 0.7774 and 0.8196 obtained from HGIMDA, RLSMDA, HDMP, WBSMDA, TLHNMDA, MCMDA, MiRAI, MaxFlow and MIDP, respectively. Note that MIDP and MiRAI only appeared in local LOOCV comparison. On the one hand, MIDP was based on random walk which is a local method and could not predict for all diseases simultaneously. Thus, we can’t obtain AUC of MIDP under global LOOCV. On the other hand, each miRNA-disease pair’s association score computed by MiRAI was extremely correlated with how many known miRNAs associated with the disease. In other words, for a disease with more associated miRNAs, prediction scores between the disease and its candidate miRNAs would be higher. Therefore, it is unfair to compare prediction scores of candidate samples for different diseases. MiRAI had a lower AUC using our training dataset because the kernel of the model was collaborative filtering that suffers from the data sparsity problem. Our training dataset was sparse; it contained 383 diseases, of which the majority were related with only a few miRNAs. It is obvious that AUCs of NSEMDA were higher than the above previous methods both in local and global LOOCV which showed its excellent performance.
Figure 1.
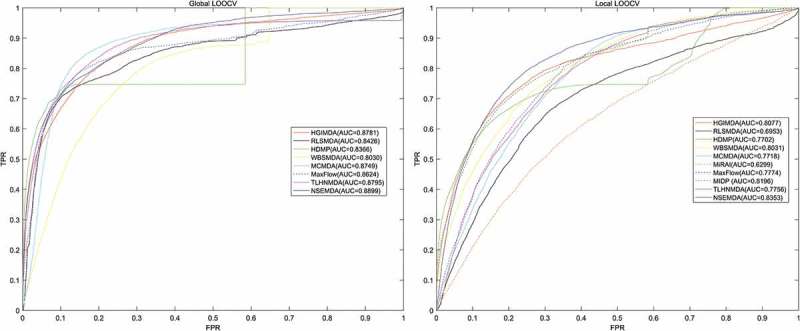
AUCs (left) of NSEMDA as well as HGIMDA, RLSMDA, HDMP, WBSMDA, MCMDA, MaxFlow, TLHNMDA under global LOOCV. AUCs (right) of NSEMDA as well as HGIMDA, RLSMDA, HDMP, WBSMDA, TLHNMDA, MCMDA, MiRAI, MaxFlow, MIDP under local LOOCV. As we can see NSEMDA achieved AUCs of 0.8899 and 0.8353 under global LOOCV and local LOOCV which were higher than that of previous models.
In the 5-fold cross validation, we randomly divided known miRNA-disease associations into five subsets with an equal size. Each subset would be regarded as the test set in turns and the rest four were utilized as the training samples. The miRNA-disease pairs in the test set and all miRNA-disease pairs without known association evidences would be scored by NSEMDA. Each sample in the test set would be ranked with all unknown samples through their scores in descending order. We repeated this procedure for 100 times to achieve a sound estimate of the average prediction accuracy of NSEMDA. As a result, NSEMDA achieved average AUC and standard deviation of 0.8878 and 0.0014 respectively. Compared with AUCs of 0.8569 ± 0.0020, 0.8342 ± 0.0010, 0.8185 ± 0.0009, 0.8795 ± 0.0010, 0.8767 ± 0.0011 and 0.8579 ± 0.001 respectively from previous models of RLSMDA, HDMP, WBSMDA, TLHNMDA, MCMDA and MaxFlow, NSEMDA still demonstrated its outstanding ability to predict miRNA-disease associations.
Case studies
Based on the model of NSEMDA, potentially related miRNAs of three common human cancers, Esophageal Neoplasms, Lung Neoplasms and Hepatocellular carcinoma, were inferred in three different case studies. We surveyed how many of top 10, top 20 and top 50 inferred miRNAs were verified to be associated with cancers mentioned above. In the first type case study on Esophageal Neoplasms, the training data was from HMDD v2.0. We validated potentially relevant miRNAs inferred by our model according to the miR2Disease and dbDEMC databases. In addition, we provided associated scores of all predicted miRNA-disease associations that would offer the reference for biological researchers (See Supplementary Table 1). To evaluate the performance of NSEMDA in predicting potential miRNAs for diseases without any known associated miRNAs, we implemented the second type of case study on Lung Neoplasms. The training data still came from HMDD v2.0, but all known associations containing Lung Neoplasms were regarded as unlabeled pairs. In the third kind of case study, the training data was from HMDD v1.0 database including 1395 known miRNA-disease associations between 137 diseases and 271 miRNAs. NSEMDA model was used to predict related miRNAs for Hepatocellular carcinoma, meanwhile HMDD v2.0, miR2Disease and dbDEMC databases were utilized to verify predicted results. By this way, we could see the performance of our model in different datasets. Concrete verification results of three cancers were presented as follows.
Esophageal Neoplasms is one of eight most common cancers whose mortality was in top six among human cancers all over the word [30]. China has one of the highest incidence of Esophageal Neoplasms [31]. The survival rate of five-year maintained at 15% to 25% even though multimodal therapeutic means were utilized to treat Esophageal Neoplasms [32,33]. Esophageal Neoplasms survival rate would be improved to 90% if we could diagnose the cancer more earlier [34]. It is obvious that discovering symptoms of Esophageal Neoplasms in early stage is crucial for successful treatment. More and more studies indicated that a mass of miRNAs linked with Esophageal Neoplasms. For example, the overexpression of miRNA-99a and miRNA-100 suppressed cell proliferation by inducing the apoptosis of Esophageal Neoplasms cell lines through the transient transfection with the corresponding precursor molecules [35]. And researchers have discovered that there were obvious links between decreased expression of miRNA-99a/100 and survival rates of Esophageal Neoplasms patients in clinical observation [35]. The expression of let-7 in Esophageal Neoplasms could be utilized to infer reaction to chemotherapy based on cisplatin. The chemo sensitivity to cisplatin could be adjusted by let-7 via affecting IL-6/STAT3 pathway in Esophageal Neoplasms [36]. NSEMDA was used to infer potential associated miRNAs for Esophageal Neoplasms based on the first type case study. Finally, 9 out of the top 10 and 46 out of the top 50 miRNAs were verified by miR2Disease and dbDEMC databases (See Table 1).
Table 1.
Top 50 Esophageal Neoplasms-associated miRNAs predicted by NSEMDA based on database of HMDD v2.0. The first column records top 1–25 predicted miRNAs, while the third column records the top 26–50 predicted miRNAs. 9, 18 and 46 out of top 10, 20 and 50 miRNAs were verified by evidence of dbDEMC and miR2Disease databases.
| miRNA | Evidence | miRNA | Evidence |
|---|---|---|---|
| hsa-mir-122 | unconfirmed | hsa-let-7i | dbDEMC |
| hsa-mir-30a | dbDEMC | hsa-mir-19b | dbDEMC |
| hsa-mir-195 | dbDEMC | hsa-mir-15b | dbDEMC |
| hsa-mir-182 | dbDEMC | hsa-mir-181a | dbDEMC |
| hsa-mir-1 | dbDEMC | hsa-mir-107 | dbDEMC and miR2Disease |
| hsa-mir-24 | dbDEMC | hsa-mir-23a | dbDEMC |
| hsa-mir-7 | dbDEMC | hsa-mir-17 | dbDEMC |
| hsa-mir-222 | dbDEMC | hsa-mir-103a | unconfirmed |
| hsa-let-7g | dbDEMC | hsa-mir-125a | dbDEMC |
| hsa-mir-221 | dbDEMC | hsa-mir-18a | dbDEMC |
| hsa-mir-29a | dbDEMC | hsa-mir-125b | dbDEMC |
| hsa-let-7f | unconfirmed | hsa-mir-206 | dbDEMC |
| hsa-mir-133b | dbDEMC | hsa-mir-142 | dbDEMC |
| hsa-mir-200b | dbDEMC | hsa-mir-93 | dbDEMC |
| hsa-let-7e | dbDEMC | hsa-mir-224 | dbDEMC |
| hsa-mir-9 | dbDEMC | hsa-mir-23b | dbDEMC |
| hsa-mir-16 | dbDEMC | hsa-mir-193b | dbDEMC |
| hsa-let-7d | dbDEMC | hsa-mir-429 | dbDEMC |
| hsa-mir-106a | dbDEMC | hsa-mir-199b | dbDEMC |
| hsa-mir-146b | dbDEMC | hsa-mir-124 | dbDEMC |
| hsa-mir-106b | dbDEMC | hsa-mir-132 | dbDEMC |
| hsa-mir-181b | dbDEMC | hsa-mir-335 | dbDEMC |
| hsa-mir-29b | dbDEMC | hsa-mir-30c | dbDEMC |
| hsa-mir-10b | dbDEMC | hsa-mir-96 | dbDEMC |
| hsa-mir-218 | unconfirmed | hsa-mir-20b | dbDEMC |
Lung Neoplasms is the second leading disease contributing to years of life lost because of premature mortality [37]. Among histologic types of lung cancer, adenocarcinoma is the most common subtype in Asians but not in Europeans [38]. Typical risk factors for lung neoplasms include smoking and exposure to arsenic, chromium, radon, or air pollution [39]. The 5-year overall survival rate of Lung Neoplasms patient was about 70% in clinical stage I but only 30% in stage III of non small-cell lung neoplasms which account for 80% of Lung Neoplasms [40]. Unfortunately, Lung Neoplasms is almost always discovered in late stages by traditional methods [41]. There is a lot of evidence that the abnormal expression of miRNA may be used as evidence for Lung Neoplasms diagnosis. According to study [42], crk (v-crk sarcoma virus CT10 oncogene homolog) is one of adaptor proteins which can change cell proliferation, migration and adhesion. Expression of crk in Lung Neoplasms tend to be higher than normal people. Meanwhile, researchers found that crk could be decreased when over-expression of miRNA-126 occurred in Lung Neoplasms cell lines. Besides, the expression of miRNA-137 was reduced in Lung Neoplasms cells. We carried out the second type of case study on Lung Neoplasms using NSEMDA to find more Lung Neoplasms-related miRNAs. As a result, all of top 50 potential miRNAs predicted by NSEMDA were confirmed according to HMDD v2.0, miR2Disease and dbDEMC (See Table 2).
Table 2.
Top 50 Lung Neoplasms-related miRNAs inferred by NSEMDA after hiding all known associations about Lung Neoplasms based on HMDD v2.0 database. Top 1–25 predicted miRNAs are recorded in the first column while top 26–50 predicted miRNAs are recorded in the third column. As shown in Table 2, all top 50 predicted miRNAs were verified by databases.
| miRNA | Evidence | miRNA | Evidence |
|---|---|---|---|
| hsa-mir-155 | dbDEMC;miR2Disease; HMDD |
hsa-mir-222 | dbDEMC;HMDD |
| hsa-mir-92a | HMDD | hsa-let-7b | miR2Disease;HMDD |
| hsa-mir-15a | dbDEMC | hsa-let-7c | dbDEMC;miR2Disease;HMDD |
| hsa-mir-16 | dbDEMC;miR2Disease | hsa-mir-146b | miR2Disease;HMDD |
| hsa-mir-17 | miR2Disease;HMDD | hsa-mir-142 | HMDD |
| hsa-mir-34a | dbDEMC;HMDD | hsa-mir-106b | dbDEMC |
| hsa-mir-20a | dbDEMC;miR2Disease; HMDD |
hsa-mir-9 | miR2Disease;HMDD |
| hsa-mir-19b | dbDEMC;HMDD | hsa-mir-200b | dbDEMC;miR2Disease;HMDD |
| hsa-mir-21 | dbDEMC;miR2Disease; HMDD |
hsa-mir-210 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-29a | dbDEMC;miR2Disease; HMDD |
hsa-mir-200c | dbDEMC;miR2Disease;HMDD |
| hsa-mir-29b | dbDEMC;miR2Disease; HMDD |
hsa-mir-150 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-146a | dbDEMC;miR2Disease; HMDD |
hsa-mir-15b | dbDEMC |
| hsa-mir-18a | dbDEMC;miR2Disease; HMDD |
hsa-mir-133a | dbDEMC;HMDD |
| hsa-mir-145 | dbDEMC;miR2Disease; HMDD |
hsa-let-7d | dbDEMC;miR2Disease;HMDD |
| hsa-mir-125b | miR2Disease;HMDD | hsa-let-7e | miR2Disease;HMDD |
| hsa-mir-221 | dbDEMC;HMDD | hsa-mir-24 | miR2Disease;HMDD |
| hsa-mir-19a | dbDEMC;miR2Disease; HMDD |
hsa-mir-182 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-126 | dbDEMC;miR2Disease; HMDD |
hsa-mir-181b | dbDEMC;HMDD |
| hsa-let-7a | dbDEMC;miR2Disease; HMDD |
hsa-mir-34c | dbDEMC;HMDD |
| hsa-mir-29c | dbDEMC;miR2Disease; HMDD |
hsa-mir-31 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-223 | HMDD | hsa-mir-195 | dbDEMC;miR2Disease |
| hsa-mir-143 | dbDEMC;miR2Disease; HMDD |
hsa-mir-200a | dbDEMC;miR2Disease;HMDD |
| hsa-mir-1 | dbDEMC;miR2Disease; HMDD |
hsa-let-7f | miR2Disease;HMDD |
| hsa-mir-181a | dbDEMC;HMDD | hsa-mir-203 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-199a | dbDEMC;miR2Disease; HMDD |
hsa-let-7i | dbDEMC;HMDD |
Hepatocellular carcinomas recognized as the third most common cause for cancer-related mortality because of a lack of effective treatment options [43]. Currently, surgery is still an effective strategy for increasing the survival rate of Hepatocellular carcinoma, but low resection rate together with high recurrence and metastasis rates mainly affect the clinical treatment outcomes [44]. Therefore, it is urgent to find better prevention, diagnosis and treatment methods for Hepatocellular carcinoma [45]. There were also many miRNAs reported to be associated with Hepatocellular carcinoma. For example, down-regulation of Bcl-w by miRNA-122 results in a decrease in the Bnmcl-w/Bax ratio, ultimately leading to apoptosis in Hepatocellular carcinoma-derived cell lines. The third type case study was implemented on Hepatocellular carcinoma. As a result, 10 out of the top 10 and 45 out of the top 50 predicted miRNAs were verified by HMDD v2.0, miR2Disease and dbDEMC databases (See Table 3).
Table 3.
Top 50 Hepatocellular Carcinoma-related miRNAs predicted by NSEMDA based on known associations in HMDD v1.0 database. Top 1–25 predicted miRNAs are recorded in the first column while top 26–50 predicted miRNAs are recorded in the third column. As we can see 10, 20 and 45 out of the top 10, top 20 and top 50 were verified by databases.
| miRNA | Evidence | miRNA | Evidence |
|---|---|---|---|
| hsa-mir-16 | dbDEMC;miR2Disease; HMDD |
hsa-let-7b | miR2Disease;HMDD |
| hsa-mir-15a | dbDEMC;miR2Disease; HMDD |
hsa-mir-206 | unconfirmed |
| hsa-mir-155 | dbDEMC;miR2Disease; HMDD |
hsa-let-7c | dbDEMC;miR2Disease;HMDD |
| hsa-mir-181b | dbDEMC;miR2Disease; HMDD |
hsa-mir-34b | unconfirmed |
| hsa-mir-181a | dbDEMC;miR2Disease; HMDD |
hsa-mir-106b | dbDEMC;miR2Disease;HMDD |
| hsa-mir-451 | dbDEMC | hsa-mir-124 | miR2Disease;HMDD |
| hsa-mir-373 | HMDD | hsa-mir-214 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-372 | HMDD | hsa-mir-199b | miR2Disease;HMDD |
| hsa-mir-29b | dbDEMC;HMDD | hsa-mir-34c | HMDD |
| hsa-mir-143 | dbDEMC;miR2Disease | hsa-mir-191 | dbDEMC;HMDD |
| hsa-mir-29a | dbDEMC;HMDD | hsa-mir-205 | miR2Disease;HMDD |
| hsa-let-7a | dbDEMC;miR2Disease; HMDD |
hsa-mir-25 | dbDEMC;miR2Disease;HMDD |
| hsa-mir-126 | dbDEMC;miR2Disease; HMDD |
hsa-mir-31 | miR2Disease;HMDD |
| hsa-mir-29c | dbDEMC;HMDD | hsa-mir-142 | miR2Disease;HMDD |
| hsa-let-7g | miR2Disease;HMDD | hsa-mir-339 | unconfirmed |
| hsa-mir-146b | HMDD | hsa-mir-302b | HMDD |
| hsa-mir-9 | miR2Disease | hsa-mir-196b | unconfirmed |
| hsa-mir-141 | miR2Disease;HMDD | hsa-mir-181d | dbDEMC;HMDD |
| hsa-mir-15b | dbDEMC;HMDD | hsa-mir-182 | miR2Disease;HMDD |
| hsa-mir-24 | miR2Disease;HMDD | hsa-mir-96 | miR2Disease;HMDD |
| hsa-mir-150 | dbDEMC;miR2Disease; HMDD |
hsa-mir-23b | miR2Disease |
| hsa-mir-133a | miR2Disease | hsa-mir-200c | HMDD |
| hsa-let-7f | miR2Disease;HMDD | hsa-mir-107 | dbDEMC;miR2Disease;HMDD |
| hsa-let-7i | dbDEMC;HMDD | hsa-mir-429 | unconfirmed |
| hsa-let-7d | miR2Disease;HMDD | hsa-mir-93 | dbDEMC;miR2Disease;HMDD |
Discussion
MiRNAs play an important role in processing of disease prevention, diagnosis and treatment. More effective computational models to predict potential miRNA-disease associations have been developed to provide relevant information for subsequent experiments, which will greatly improve efficiency in discovering novel associations between miRNA and disease. In this study, we proposed a model of NSEMDA to infer potential miRNA-disease association. We regarded 5430 known miRNA-disease associations in HMDD v2.0 as positive samples and remaining pairs between 383 diseases and 495 miRNAs as unlabeled samples. The negative samples are difficult or impossible to get, so we extracted reliable negative samples for training model through PU learning. Furthermore, the remaining unlabeled samples after extraction were considered as ambiguous samples which were given probabilities belonging to positive and negative classes by integrating global and local similarity weights. Finally, a SVM-SW method was used to train prediction model. We carried out local and global LOOCV to evaluate the performance of NSEMDA and our model obtained higher AUCs than nine classical models of HGIMDA, RLSMDA, HDMP, WBSMDA, TLHNMDA, MCMDA, MiRAI, MaxFlow and MIDP. The results of 5-fold cross validations also demonstrated reliable predictive ability of NSEMDA. Three different kinds of case studies were implemented on common human cancers and the overwhelming majority of top 50 potential miRNAs inferred by NSEMDA were verified by several databases.
The reliable performance of NSEMDA was due to three main factors. First, NSEMDA integrated various biological information including miRNA functional similarity, disease semantic similarity, Gaussian interaction profile kernel similarity of disease and miRNA to construct feature vector. And a feature selection method was implemented to reduce the dimension of feature vector and choose robust features. Second, NSEMDA could extract negative samples from unlabeled samples based on two kinds of PU learning models of Spy and Rocchio techniques. Application of more than one PU learning models will enhance credibility of negative samples extraction. Third, noise would appear in training samples in the process of inferring potential miRNA-disease associations. We calculated similarity weights for ambiguous samples to represent different levels of noise. Thus, SVM-SW model possessed better tolerant capacity when faced with different noise level of training samples.
However, there are also some limitations affecting performance of predicting miRNA-disease associations. First, the unlabeled sample set for training consists of samples that were randomly selected from unknown miRNA-disease pairs, which may affect the accuracy of our model. Besides, the parameters in SVM-SW model were hard to selected. Finally, there were only 5430 known associations between 383 diseases and 495 miRNAs in HMDD v2.0 database and the number of unknown miRNA-disease pairs is more than 30 times that of known associations. We believe that the predictive accuracy can be improved as more and more novel miRNA-disease associations are discovered in the future.
Materials and methods
Human miRNA-disease associations
There were 5430 miRNA-disease pairs involving 383 diseases and 495 miRNAs proved to be related through experiments. These known associations can be downloaded from HMDD v2.0 database [46]. We regarded the rest of miRNA-disease pairs as unlabeled pairs. Variable nd and nm denotes the number of diseases and miRNAs investigated in this study. To express association information clearly, an adjacency matrix A with a size of nd rows and nm columns was constructed in which the element A(i,j) is equal to 1 if miRNA m(j) and disease d(i) were verified to be related, otherwise 0.
Mirna functional similarity
MiRNAs functional similarity score can be computed under the hypothesis that similar miRNAs are more likely to link with phenotypically similar diseases according to previous study [47]. They developed a method, MISIM (miRNA similarity), to calculate the functional similarity of miRNAs. MISIM mainly contains four steps calculating the functional similarity between miRNA m(i) and m(j). First, the diseases associated with the two miRNAs were put into associated-disease set D(i) and D(j) respectively. Then the diseases’ semantic values were calculated based on their DAGs. Third, the semantic similarity for each pair of diseases between D(i) and D(j) can be computed based on their semantic value. Finally, the functional similarity between miRNA m(i) and m(j) was calculated based on the semantic similarity mentioned in the third step. In our study, miRNA functional similarity score can be downloaded via the link http://www.cuilab.cn/files/images/cuilab/misim.zip. Similarly, we represented this information through a miRNA functional similarity matrix FS in which the element FS(m(i),m(j)) is the functional similarity score of miRNA m(i) and miRNA m(j).
Disease semantic similarity model 1
To calculate semantic similarities between different diseases, we downloaded MeSH descriptors for diseases from the National Library of Medicine (http://www.nlm.nih.gov/). Then we can obtain Directed Acyclic Graphs (DAGs) of diseases according to MeSH descriptors. All nodes in the DAG are connected by a direct edge from parent node to child node. DAGD = (D,TD,ED) was utilized to denote the disease D, where TD represents the node set containing node D and its ancestor nodes and ED is the set of all direct edges [47]. The diseases semantic similarity model 1 was constructed according to previous study [17]. Specifically, the semantic value DV1(D) of disease D can be calculated by summing up the contributions from disease D itself and other diseases:
| (1) |
where D1D(t) was defined as the contribution of disease t to DV1(D), and it can be calculated as follows:
| (2) |
where is the semantic contribution factor. was set as 0.5 according to previous literature [17]. The contribution of disease D to the semantic value of itself is 1. The contributions of other diseases to the semantic value of disease D are weaken by and the farther the distance between disease t and disease D, the smaller the contribution of disease t.
The semantic similarity value between disease d(i) and d(j) can be calculated based on the conjecture that two diseases will have larger semantic similarity if they share larger part of their DAGs as follows:
| (3) |
where SS1 is the disease semantic similarity matrix and the element SS1(d(i),d(j)) denotes the semantic similarity between d(i) and d(j) calculated based on disease semantic similarity model 1.
Disease semantic similarity model 2
In disease semantic similarity model 1, the contributions of other diseases to the semantic value of disease D will be distinguished by the distance between disease D and other disease. Therefore, different diseases in the same layer of DAGD have the same contribution to the semantic value of disease D. That may be not very reasonable, because different diseases in the same layer of DAGD may appear in other DAGs and the number of DAGs they appear may be different. Obviously, the disease appearing in less DAGs is more specific and the contribution of the more specific disease to the semantic value of disease D should be lager than other diseases in the same layer. Thus, the disease semantic similarity model 2 was established according to previous study [17]. Here, the contribution of disease t to the semantic value of disease D can be calculated as follows:
| (4) |
We defined the semantic similarity value between disease d(i) and d(j) similar to model 1 as follows:
| (5) |
where DV2(d(i)) and DV2(d(j) are semantic values of d(i) and d(j) which can be calculated similar to formula [1]. SS2 is a disease semantic similarity matrix with nd rows and nd columns and the element SS2(d(i),d(j)) represents the semantic similarity of d(i) and d(j) calculated based on disease semantic similarity model 2.
Gaussian interaction profile kernel similarity for diseases
Gaussian interaction profile kernel similarity for diseases can be calculated through investigating the information of known miRNA-disease associations under the assumption that functional similar miRNAs are more likely to be associated with similar diseases according to the previous method [48]. Binary vector IP(d(u)) was utilized to represent the interaction profiles of disease d(u) by observing whether d(u) is associated with each one of nm miRNAs or not. The binary vector IP(d(u)) and the u-th row vector of adjacency matrix A are equivalent. Then Gaussian interaction profile kernel similarity between d(u) and d(v) was defined as follows:
| (6) |
where parameter was implemented to control the kernel bandwidth which can be calculated via normalizing original parameter as follows:
| (7) |
where is equal to 1 based on previous study [49].
Gaussian interaction profile kernel similarity for miRNAs
Based on previous method of calculating Gaussian interaction profile kernel [48], the Gaussian profile kernel similarity between miRNAs was calculated as follows:
| (8) |
| (9) |
where binary vector IP(m(u)) or IP(m(v)) represented the interaction profiles of miRNA m(u) or m(v) by observing whether m(u) or m(v) is related with each one of nd diseases which is equivalent to the u-th or v-th column vector of adjacency matrix A. And is equal to 1 according to previous literature [49].
Integrated similarity for diseases
In order to make full use of disease semantic similarity 1, disease semantic similarity 2 and disease Gaussian interaction profile kernel similarity, an integrated disease similarity matrix SD was constructed by integrating the above similarities based on the method in previous study [20]. The element SD(d(u),d(v)) represented integrated similarity between disease d(u) and d(v) which was defined as follows:
| (10) |
where d(u) and d(v) has semantic similarity if both d(u) and d(v) have their own DAG.
Integrated similarity for miRNAs
We integrated miRNA functional similarity and miRNA Gaussian interaction profile kernel similarity according to the method of previous study [20]. Thus, the integrated similarity between miRNA m(i) and m(j) was calculated as follows:
| (11) |
NSEMDA
In this study, we proposed NSEMDA to infer potential miRNA-disease associations. The model can be divided into six steps (See Figure 2):
Establish positive sample set P and unlabeled sample set U for training
Represent each miRNA-disease sample as a vector.
Select the feature subsets of miRNA-disease samples.
Extract reliable negative miRNA-disease samples, obtain ambiguous samples and add positive samples.
Calculate the similarity weights of the ambiguous samples.
Train the prediction model and predict potential miRNA-disease associations.
Figure 2.
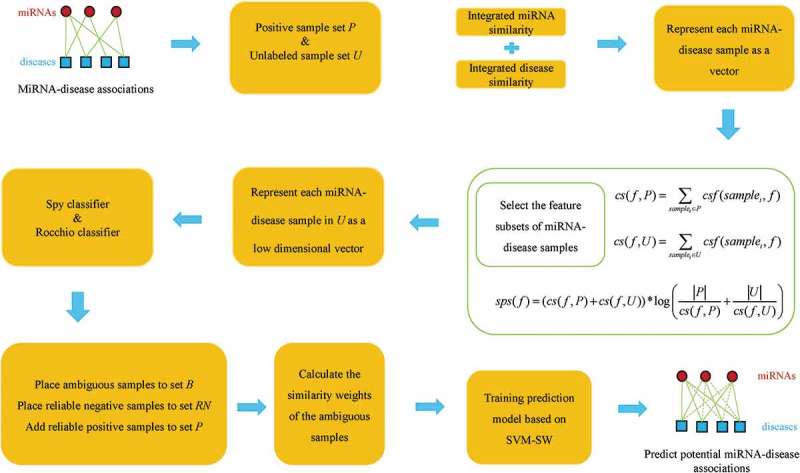
Flowchart of NSEMDA model to predict potential associations between miRNAs and diseases.
Firstly, the positive sample set P consisted of 5430 known miRNA-diseases associations. To ensure the adequacy of unlabeled samples for training and the computational efficiency of our model, the size of unlabeled sample set is twice that of the positive sample set. Thus, the unlabeled sample set U contained 10,860 unlabeled miRNA-disease pairs which are randomly selected from all unlabeled miRNA-disease pairs.
Secondly, each miRNA-disease pair can be represented by a vector based on integrated similarity of miRNA and disease. For one miRNA m(i), there were nm integrated similarity values, and then we utilized a nm-dimensional vector to represent m(i) as follows:
| (12) |
where SM(m(i)) is the i-th row vector of matrix SM.
Similar, for one disease d(j), there were nd integrated similarity values, and then we used a nd-dimensional vector to express d(j) as follows:
| (13) |
where SD(d(j)) is the j-th row vector of matrix SD.
Therefore, each miRNA-disease sample can be expressed by a (nd+nm)-dimensional vector as follows:
| (14) |
F(m(i),d(j)) = (f1, f2, …, fnm, … fnm+nd), where (f1, f2, …, fnm) represents the nm integrated similarity between the miRNA i and other miRNAs including itself, and (fnm+1, fnm+2, … fnm+nd) represents the nd integrated similarity between the disease j and other diseases including itself.
Thirdly, to efficiently distinguish related miRNA-disease pairs from unrelated miRNA-disease pairs, we choose robust features among 878 features. For each feature f, we calculated its cumulative score in P and U (cs(f,P) and cs(f,U)) as follows:
| (15) |
| (16) |
where samplei is the i-th miRNA-disease pair. csf(samplei, f) represents feature value of the feature f of samplei.
We calculated the specificity score of f in P and U as follows:
| (17) |
For a feature f, if cs(f,P) is large but cs(f,U) is small or cs(f,U) is large but cs(f,P) is small, the value of sps(f) will be higher because and are both relatively large. Otherwise, when both cs(f,P) and cs(f,U) are large or small respectively, the value of sps(f) will be lower. Considering the effectiveness and richness of features, 100 robust features were selected in our study. Roughly based on the original ratio between features of miRNA and features of disease, we selected 60 features from (f1, f2, …, fnm) whose specificity score are top 60 of specificity scores of all nm features and 40 features from (fnm+1, fnm+2, … fnm+nd) whose specificity score are top 40 of specificity scores of all nd features.
Fourthly, as well known, both positive and negative samples are indispensable in supervised learning-based models. However, negative samples are hard to obtain or even unavailable. In addition, known miRNA-disease associations between nd diseases and nm miRNAs occupy a small proportion of all miRNA-disease pairs. To achieve a good predictive performance, we extracted reliable negative samples from unlabeled sample set U based on two PU learning models, i.e. the Spy and Rocchio techniques [50,51]. Moreover, some reliable positive samples were added to the positive sample set P. Specifically, the training sample sets for two PU learning models were P and U mentioned in the first step. Once the two classifiers, namely, Spy classifier and Rocchio classifier were established, we could classify samples in U. For each sample in U, if both two classifiers put it into positive class, we regarded the sample as reliable positive sample and added it into P; If both two classifiers put it into negative class, we regarded the sample as reliable negative sample. If one classifier put it into positive class while another classifier put it into negative class, we regarded it as ambiguous sample. All the reliable negative samples were placed in reliable negative sample set RN and all ambiguous samples were placed in ambiguous sample set B.
Fifthly, we could train prediction model utilizing SVM in positive sample set P and negative sample set RN mentioned above. However, some noise samples may reduce the performance of our model. Therefore, we added ambiguous samples in B to training set and constructed a SVM-SW prediction model. Note that, each sample in B was given two SWs which denote the probabilities belonging to positive sample and negative sample respectively. To calculate SWs for ambiguous samples, we divided samples in RN into n groups (RN1, RN2,…RNn) using the k-means clustering algorithm. Then we computed the representative positive and negative miRNA-disease association prototypes as follows:
| (18) |
| (19) |
where Fi denoted the feature vector of i-th sample. And the parameter n was set as , in which |B| and |RN| represent the number of samples in B and RN respectively according to previous study [29]. Besides, 30, 16 and 4 were assigned to parameter of t, α and β according to previous study [52].
SWs of ambiguous samples can be obtained by integrating global similarity weights and local similarity weights. Before computing global similarity weights and local similarity weights, we defined similarities between an ambiguous sample and representative prototypes (pi and ni) as follows:
| (20) |
| (21) |
where x denotes the feature vector of ambiguous sample x.
Then we carried out pseudocode I (See Supplementary File) to calculate local similarity weights (LswPi(x), LswNi(x)) of ambiguous sample. Obviously, samples in the same group (for example Bi) have the same local similarity weights. Therefore, to reveal the difference of ambiguous samples in the same group, we computed global similarity weights for each sample in B as follows:
| (22) |
| (23) |
where GswP(x) and GswN(x) denote the probabilities that sample x belongs to positive class and negative class respectively from a global perspective. Finally, we can obtain similarity weights of ambiguous by integrating local and global similarity weights as follows:
| (24) |
| (25) |
where the parameter is equal to 0.6 which is utilized to balance the importance between the global similarity and the local similarity.
Finally, the training sample sets consist of the positive sample set P, the negative sample set RN and the ambiguous sample set B. These training samples may include parts of noisy data. Therefore, we constructed a SVM-SW model to predict miRNA-disease associations which can reduce the influence of noisy data. The input data of the model was shown as follows:
| (26) |
where denotes the feature vector of the positive sample Pi, the is equal to 1 and the is equal to 1. Besides, denotes the feature vector of the ambiguous sample Bj, the is equal to 1 and the is equal to the similarity weight SWp(Bj), meanwhile, the is equal to 0 and the is equal to the similarity weight SWn(Bj). Furthermore, represents the feature vector of the negative sample RNl, the is equal to 0 and the is equal to 1. As a result, we can get final prediction model after training the input data based on SVM-SW. The objective function and constraint conditions of SVM-SW can be described as follows:
| (27) |
where ζiP and ζiP*, ζjB, ζjB*, ζkB, ζkB*, ζiRN and ζiRN* are error terms. C is the penalty parameter of error terms. The weights of SWp(xj) and SWn(xk) will rescale effect of the penalty parameter C. Higher weights force the classifier to put more emphasis on these points. More specifically, the ambiguous example xj with higher SWp(xj) tend to belong to the positive class. Similarly, xk with smaller SWn(xk) is less significant toward the negative class. In this study, we employed the package of sklearn.svm.SVR based on the above description to construct the prediction model of SVM-SW. The final prediction model can be used to predict potential miRNA-disease associations by marking candidate miRNA-disease pairs. And the score denotes the possibility that the miRNA-disease pair is associated miRNA-disease pair.
Funding Statement
This work was supported by the National Natural Science Foundation of China [61772531].
Acknowledgments
XC was supported by National Natural Science Foundation of China under Grant No. 61772531.
Disclosure statement
No potential conflict of interest was reported by the authors.
Supplementary Material
Supplemental data for this article can be accessed here.
References
- [1].Ambros V. microRNAs: tiny regulators with great potential. Cell. 2001;107(7):823–826. Epub 2002/ 01/10 PubMed PMID: 11779458. [DOI] [PubMed] [Google Scholar]
- [2].Behm-Ansmant I, Rehwinkel J, Doerks T, et al. mRNA degradation by miRNAs and GW182 requires both CCR4: nOTdeadenylase and DCP1: DCP2decapping complexes. Genes Dev. 2006;20(14):1885–1898. Epub 2006/07/04PubMed PMID: 16815998; PubMed Central PMCID: PMCPMC1522082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Lee RC, Feinbaum RL, Ambros V. The C. elegans heterochronic gene lin-4 encodes small RNAs with antisense complementarity to lin-14. Cell. 1993;75(5):843–854. Epub 1993/12/03 PubMed PMID: 8252621. [DOI] [PubMed] [Google Scholar]
- [4].Reinhart BJ, Slack FJ, Basson M, et al. The 21-nucleotide let-7 RNA regulates developmental timing in Caenorhabditis elegans. Nature. 2000;403(6772):901–906. Epub 2000/ 03/08 PubMed PMID: 10706289. [DOI] [PubMed] [Google Scholar]
- [5].Ambros V. MicroRNA pathways in flies and worms: growth, death, fat, stress, and timing. Cell. 2003;113(6):673–676. Epub 2003/ 06/18 PubMed PMID: 12809598. [DOI] [PubMed] [Google Scholar]
- [6].Alshalalfa M, Alhajj R. Using context-specific effect of miRNAs to identify functional associations between miRNAs and gene signatures. BMC Bioinformatics. 2013;Suppl 12:S1 Epub 2013/12/07 PubMed PMID: 24267745; PubMed Central PMCID: PMCPMC3848857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zhang K, Guo L. MiR-767 promoted cell proliferation in human melanoma by suppressing CYLD expression. Gene. 2017. Epub 2017/ 10/22 PubMed PMID: 29054757 DOI: 10.1016/j.gene.2017.10.055. [DOI] [PubMed] [Google Scholar]
- [8].Cui Q, Yu Z, Purisima EO, et al. Principles of microRNA regulation of a human cellular signaling network. Mol Syst Biol. 2006;2:46 Epub 2006/09/14 PubMed PMID: 16969338; PubMed Central PMCID: PMCPMC1681519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Ma L, Teruya-Feldstein J, Weinberg RA. Tumour invasion and metastasis initiated by microRNA-10b in breast cancer. Nature. 2007;449(7163):682–688. Epub 2007/ 09/28PubMed PMID: 17898713. [DOI] [PubMed] [Google Scholar]
- [10].Zheng R, Pan L, Gao J, et al. Prognostic value of miR-106b expression in breast cancer patients. J Surg Res. 2015;195(1):158–165. Epub 2015/01/27 PubMed PMID: 25619461. [DOI] [PubMed] [Google Scholar]
- [11].Heegaard NH, Schetter AJ, Welsh JA, et al. Circulating micro-RNA expression profiles in early stage nonsmall cell lung cancer. Int J Cancer. 2012;130(6):1378–1386. Epub 2011/ 05/06PubMed PMID: 21544802; PubMed Central PMCID: PMCPMC3259258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Wang XC, Zhang ZB, Wang YY, et al. Increased miRNA-22 expression sensitizes esophageal squamous cell carcinoma to irradiation. J Radiat Res. 2013;54(3):401–408. Epub 2012/ 11/29 PubMed PMID: 23188185; PubMed Central PMCID: PMCPMC3650739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Chen X, Xie D, Zhao Q, et al. MicroRNAs and complex diseases: from experimental results to computational models. Brief Bioinform. 2017. Epub 2017/ 10/19 PubMed PMID: 29045685 DOI: 10.1093/bib/bbx130 [DOI] [PubMed] [Google Scholar]
- [14].Jiang Q, Hao Y, Wang G, et al. Prioritization of disease microRNAs through a human phenome-microRNAome network. BMC Syst Biol. 2010;4(Suppl 1):S2 Epub 2010/06/11 PubMed PMID: 20522252; PubMed Central PMCID: PMCPMC2880408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Shi H, Xu J, Zhang G, et al. Walking the interactome to identify human miRNA-disease associations through the functional link between miRNA targets and disease genes. BMC Syst Biol. 2013;7:101 Epub 2013/10/10 PubMed PMID: 24103777; PubMed Central PMCID: PMCPMC4124764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Pasquier C, Gardes J. Prediction of miRNA-disease associations with a vector space model. Sci Rep. 2016;6:27036 Epub 2016/06/02 PubMed PMID: 27246786; PubMed Central PMCID: PMCPMC4887905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Xuan P, Han K, Guo M, et al. Prediction of microRNAs associated with human diseases based on weighted k most similar neighbors. PloS One. 2013;8(8):e70204 Epub 2013/08/21 PubMed PMID: 23950912; PubMed Central PMCID: PMCPMC3738541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Chen X, Liu MX, Yan GY. RWRMDA: predicting novel human microRNA-disease associations. Mol Biosyst. 2012;8(10):2792–2798. Epub 2012/ 08/10PubMed PMID: 22875290. [DOI] [PubMed] [Google Scholar]
- [19].Xuan P, Han K, Guo Y, et al. Prediction of potential disease-associated microRNAs based on random walk. Bioinformatics. 2015;31(11):1805–1815. Epub 2015/01/27 PubMed PMID: 25618864. [DOI] [PubMed] [Google Scholar]
- [20].Chen X, Yan CC, Zhang X, et al. WBSMDA: within and between score for MiRNA-disease association prediction. Sci Rep. 2016;6:21106 Epub 2016/ 02/18 PubMed PMID: 26880032; PubMed Central PMCID: PMCPMC4754743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Chen X, Yan CC, Zhang X, et al. HGIMDA: heterogeneous graph inference for miRNA-disease association prediction. Oncotarget. 2016;7(40):65257–65269. Epub 2016/ 08/18PubMed PMID: 27533456; PubMed Central PMCID: PMCPMC5323153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Li JQ, Rong ZH, Chen X, et al. MCMDA: matrix completion for MiRNA-disease association prediction. Oncotarget. 2017;8(13):21187–21199. Epub 2017/ 02/09PubMed PMID: 28177900; PubMed Central PMCID: PMCPMC5400576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Yu H, Chen X, Lu L. Large-scale prediction of microRNA-disease associations by combinatorial prioritization algorithm. Sci Rep. 2017;7:43792 Epub 2017/03/21 PubMed PMID: 28317855; PubMed Central PMCID: PMCPMC5357838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Chen X, Qu J, Yin J. TLHNMDA: triple layer heterogeneous network based inference for MiRNA-disease association prediction. Front Genet. 2018;9:234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Chen X, Wang L, Qu J, et al. Predicting miRNA-disease association based on inductive matrix completion. Bioinformatics. 2018. Epub 2018/ 06/26 PubMed PMID: 29939227 DOI: 10.1093/bioinformatics/bty503. [DOI] [PubMed] [Google Scholar]
- [26].Chen X, Yan GY. Semi-supervised learning for potential human microRNA-disease associations inference. Sci Rep. 2014;4:5501 Epub 2014/07/01 PubMed PMID: 24975600; PubMed Central PMCID: PMCPMC4074792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen X, Yan CC, Zhang X, et al. RBMMMDA: predicting multiple types of disease-microRNA associations. Sci Rep. 2015;5:13877 Epub 2015/ 09/09 PubMed PMID: 26347258; PubMed Central PMCID: PMCPMC4561957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Chen X, Wu QF, Yan GY. RKNNMDA: ranking-based KNN for MiRNA-Disease Association prediction. RNA Biol. 2017;14(7):952–962. Epub 2017/ 04/20PubMed PMID: 28421868; PubMed Central PMCID: PMCPMC5546566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Peng L, Zhu W, Liao B, et al. Screening drug-target interactions with positive-unlabeled learning. Sci Rep. 2017;7(1):8087 Epub 2017/08/16 PubMed PMID: 28808275; PubMed Central PMCID: PMCPMC5556112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Giri S, Pathak R, Aryal MR, et al. Incidence trend of esophageal squamous cell carcinoma: an analysis of Surveillance Epidemiology, and End Results (SEER) database. Cancer Causes Control. 2015;26(1):159–161. Epub 2014/ 11/08PubMed PMID: 25376829. [DOI] [PubMed] [Google Scholar]
- [31].Yu C, Guo Y, Bian Z, et al. Association of low-activity ALDH2 and alcohol consumption with risk of esophageal cancer in Chinese adults: A population-based cohort study. Int J Cancer. 2018. Epub 2018/ 05/01 PubMed PMID: 29707772 DOI: 10.1002/ijc.31566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Torre LA, Bray F, Siegel RL, et al. Global cancer statistics, 2012. CA Cancer J Clin. 2015;65(2):87–108. Epub 2015/ 02/06PubMed PMID: 25651787. [DOI] [PubMed] [Google Scholar]
- [33].Sjoquist KM, Burmeister BH, Smithers BM, et al. Survival after neoadjuvant chemotherapy or chemoradiotherapy for resectable oesophageal carcinoma: an updated meta-analysis. Lancet Oncol. 2011;12(7):681–692. Epub 2011/ 06/21 PubMed PMID: 21684205. [DOI] [PubMed] [Google Scholar]
- [34].Daly JM, Fry WA, Little AG, et al. Esophageal cancer: results of an American college of surgeons patient care evaluation study. J Am Coll Surg. 2000;190(5):562–572. discussion 72–3 Epub 2000/ 05/09.PubMed PMID: 10801023. [DOI] [PubMed] [Google Scholar]
- [35].Sun J, Chen Z, Tan X, et al. MicroRNA-99a/100 promotes apoptosis by targeting mTOR in human esophageal squamous cell carcinoma. Med Oncol. 2013;30(1):411 Epub 2013/ 01/08 PubMed PMID: 23292834. [DOI] [PubMed] [Google Scholar]
- [36].Sugimura K, Miyata H, Tanaka K, et al. Let-7 expression is a significant determinant of response to chemotherapy through the regulation of IL-6/STAT3 pathway in esophageal squamous cell carcinoma. Clin Cancer Res off J Am Assoc Cancer Res. 2012;18(18):5144–5153. Epub 2012/ 08/01 PubMed PMID: 22847808. [DOI] [PubMed] [Google Scholar]
- [37].Murray CJ, Atkinson C, Bhalla K, et al. The state of US health, 1990-2010: burden of diseases, injuries, and risk factors. Jama. 2013;310(6):591–608. Epub 2013/ 07/12 PubMed PMID: 23842577; PubMed Central PMCID: PMCPMC5436627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Yang SC, Lai WW, Su WC, et al. Estimating the lifelong health impact and financial burdens of different types of lung cancer. BMC Cancer. 2013;13:579 Epub 2013/12/07 PubMed PMID: 24308346; PubMed Central PMCID: PMCPMC4234193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Ahsan H, Thomas DC. Lung cancer etiology: independent and joint effects of genetics, tobacco, and arsenic. Jama. 2004;292(24):3026–3029. Epub 2004/ 12/23PubMed PMID: 15613673. [DOI] [PubMed] [Google Scholar]
- [40].Dominioni L, Imperatori A, Rovera F, et al. Stage I nonsmall cell lung carcinoma: analysis of survival and implications for screening. Cancer. 2000;89(11 Suppl):2334–2344. Epub 2001/01/09 PubMed PMID: 11147608. [DOI] [PubMed] [Google Scholar]
- [41].Wang Y, Zhang X, Liu L, et al. Clinical implication of microrna for lung cancer. Cancer Biother Radiopharm. 2013;28(4):261–267. Epub 2013/03/19 PubMed PMID: 23496233. [DOI] [PubMed] [Google Scholar]
- [42].Crawford M, Brawner E, Batte K, et al. MicroRNA-126 inhibits invasion in non-small cell lung carcinoma cell lines. Biochem Biophys Res Commun. 2008;373(4):607–612. Epub 2008/07/08 PubMed PMID: 18602365. [DOI] [PubMed] [Google Scholar]
- [43].Kim HY, Park JW. Clinical trials of combined molecular targeted therapy and locoregional therapy in hepatocellular carcinoma: past, present, and future. Liver Cancer. 2014;3(1):9–17. Epub 2014/ 05/08PubMed PMID: 24804173; PubMed Central PMCID: PMCPMC3995399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Matsuda T, Saika K. Trends in liver cancer mortality rates in Japan, USA, UK, France and Korea based on the WHO mortality database. Jpn J Clin Oncol. 2012;42(4):360–361. Epub 2012/03/30PubMed PMID: 22457364. [DOI] [PubMed] [Google Scholar]
- [45].Huang J, Yang G, Huang Y, et al. 1,25(OH)2D3 induced apoptosis of human hepatocellular carcinoma cells in vitro and inhibited their growth in a nude mouse xenograft model by regulating histone deacetylase 2. Biochimie. 2018;146:28–34. Epub 2017/ 11/22 PubMed PMID: 29158005. [DOI] [PubMed] [Google Scholar]
- [46].Li Y, Qiu C, Tu J, et al. HMDD v2.0: a database for experimentally supported human microRNA and disease associations. Nucleic Acids Res. 2014;42(Database issue):D1070–D1074. Epub 2013/ 11/07 PubMed PMID: 24194601; PubMed Central PMCID: PMCPmc3964961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wang D, Wang J, Lu M, et al. Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases. Bioinformatics. 2010;26(13):1644–1650. [DOI] [PubMed] [Google Scholar]
- [48].van Laarhoven T, Nabuurs SB, Marchiori E. Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics. 2011;27(21):3036–3043. Epub 2011/09/07PubMed PMID: 21893517. [DOI] [PubMed] [Google Scholar]
- [49].Chen X, Yan GY. Novel human lncRNA-disease association inference based on lncRNA expression profiles. Bioinformatics. 2013;29(20):2617–2624. Epub 2013/ 09/05PubMed PMID: 24002109. [DOI] [PubMed] [Google Scholar]
- [50].Liu B, Lee WS, Yu PS, et al, editors. Partially Supervised Classification of Text Documents. Nineteenth International Conference on Machine Learning; 2002 Jul 8–12; Sydney, NSW, Australia; 2002. [Google Scholar]
- [51].Li X, Liu B, editors. Learning to classify texts using positive and unlabeled data. International Joint Conference on Artificial Intelligence; 2003 Aug 9–15; Acapulco, Mexico; 2003. [Google Scholar]
- [52].Li XL, Yu PS, Liu B, et al, editors. Positive unlabeled learning for data stream classiflcation. Siam International Conference on Data Mining, SDM 2009; 2009 Apr 30–May 2; Sparks, Nevada; 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


