Detecting repeated cancer evolution in human tumours from multi-region sequencing data

Abstract

Cancer evolution is driven by the accumulation of (epi)genomic aberrations. Recurrent sequences of genomic changes, between and within patients, reflect repeated evolution that is valuable for anticipating cancer progression. Multi-region sequencing allows inference of some temporal orderings of genomic changes within a tumour. However, the inherent stochasticity of the evolutionary process makes different patients appear very distinct, preventing the robust identification of repeated evolution. Here we present a novel machine learning method based on Transfer Learning that overcomes the stochastic effects of cancer evolution and noise in the data, highlighting hidden evolutionary patterns in cancer cohorts. When applied to multi-region sequencing datasets from lung, breast, renal and colorectal cancer (768 samples from 178 patients), our method detected repeated evolutionary trajectories in subgroups of patients, which reproduced in single-sample cohorts (n=2,935). Our method provides novel ways to classify patients based on how their tumour evolved, with implications for anticipating cancer evolution.

Introduction

The biggest clinical challenge in oncology is the fact the tumours change over time, progressing from benign to malignant, becoming metastatic, and developing treatment resistance^1,2. This occurs through a process of clonal evolution involving cancer cells and their microenvironment³. Intra-tumour heterogeneity (ITH), or the genetic and phenotypic variation of cancer cells within the same tumour, is the natural consequence of this evolutionary process. ITH is also a key factor contributing to the lethal outcome of cancer, as it provides the substrate of phenotypic variation upon which adaptation can occur⁴. A fundamental question in oncology is therefore: can we predict a cancer’s next evolutionary “step”? Our ability to predict cancer evolution has tremendous implications for clinical care and therefore the question of predictability of evolutionary processes, first posed by evolutionary biologist Stephen Jay Gould for species evolution⁵, is also central in oncology.

Clonal evolution results from the interplay of random mutations, genetic drift, and non-random selection⁶, leading to complex patterns in the data and implying some limits of predictability of cancer evolution due to stochastic forces⁷. However, the prognostic value of histopathological staging and molecular markers indicate that, at least in part, tumour evolution is predictable. Moreover, several observations suggest that despite its stochastic nature, micro-environmental, epistatic, and lineage constraints may allow for the prediction of a limited set of subsequent evolutionary moves². Previous approaches based on single-sample cross-sectional data have shown that indeed there are recurrent sequences of genomic events in cancer cohorts^8–11.

More recent seminal studies based on multi-region sequencing of tumours however, have shown how the partial order of somatic aberrations in a patient’s tumour can be determined using phylogenetic analysis, revealing the spatio-temporal dynamics of single malignancies². However, truncal (clonal) alterations cannot be ordered in most cases and phylogenetic trees from different patients often appear very distinct^12–18. The underlying variability and complexity of the evolutionary process, as well as the high levels of noise and uncertainty in the data, is such that with current analysis techniques we are generally unable to robustly identify repeated evolutionary trajectories across patients. Characterising repeated evolution in cancer would have important implications both for our ability to stratify patients in the clinic, as well as for predicting cancer progression.

Here we exploit the fact that tumours in different patients represent multiple instances of the same evolutionary process. This is an opportunity that is missing in classical evolutionary biology where data come from a unique stream of evolution. To leverage this observation, we devised REVOLVER (Repeated EVOLution in cancER), a novel method that for the first time jointly analyses multi-region sequencing data from patient cohorts by using a Machine Learning approach called Transfer Learning (TL)¹⁹. REVOLVER infers n patient evolutionary models jointly, with the aim of increasing their structural correlation. Our method exploits multiple independent noisy observations (i.e. single patients), and “transfers” information between patients to de-noise data and highlight hidden evolutionary patterns (Figure 1). The n models still explain the data in each patient, while at the same time highlighting subgroups of tumours that evolved similarly.

Figure 1. Identifying repeated evolution in cancer multi-region sequencing data using Transfer Learning.

(A) Cancer evolution studies often employ multi-region sampling (red circles) and genomic profiling to characterise intra-tumour heterogeneity (ITH). The data may encode specific sequences of somatic driver aberrations that correspond to repeated evolutionary trajectories common to patient subgroups (e.g. group red vs group purple). However, due to the underlying stochasticity of cancer evolution and inherent noise in the data, genomic patterns usually appear very variable between patients, and the details of the evolutionary process remain hidden. Considering ITH data from n patients with the same tumour type, we want to find n models that describe the evolution of each tumour, while at the same time highlighting the presence of repeated evolutionary trajectories across patients. (B) The standard approach is to infer one evolutionary model per patient at a time (i.e. a phylogenetic tree), and then compare the n trees. Because the models are inferred independently and are therefore uncorrelated, the statistical signal of repeated evolutionary trajectories is weak and all tumours seem different. (C) This leads to few repeated evolutionary trajectories identified (e.g. only part of the purple trajectory is identified). (D) REVOLVER uses Transfer Learning to infer n models jointly, with the aim of increasing their structural correlation. We obtain n trees that explain the data in each patient while highlighting repeated evolutionary trajectories in the cohort. (E) This results in a stronger statistical signal of repeated cancer evolution and recurrent trajectories are identified.

Results

Approach and method description

Genomic profiling of multiple regions of the same tumour is the established approach to study the evolutionary history of human malignancies⁴. Multi-region sequencing allows assessing ITH in individual patients, with particular focus on recurrent driver alterations. To detect repeated evolutionary trajectories across patients (e.g. purple subgroup vs red subgroup in Figure 1A), the classical approach exploits methods that reconstruct the phylogenetic tree of each tumour (Figure 1B). However, standard tools determine one tree per patient at a time, leading to solutions that are uncorrelated (i.e., the model that we fit to a patient is independent from the models that we fit to the rest of the cohort). The stochasticity and complexity of the evolutionary process, the extensive inter-patient variability, as well as the inherent ambiguity and noise in the data, render the statistical signal of repeated trajectories very weak (Figure 1C).

The problem is exacerbated by the fact that multi-region bulk samples are mixtures of cancer cell populations. This requires subclonal decomposition for each sample²⁰, i.e. transforming the measured allelic abundance of a mutation into the proportion of cancer cells carrying the mutation, the so-called Cancer Cell Fraction (CCF). However, high levels of tumour sampling bias (several admixed subpopulations) confound CCF estimates, rendering difficult to infer the correct phylogenetic tree via the pigeonhole principle. This commonly adopted principle is used to layout an evolutionary tree from CCF estimates, stating that if the sum of the CCF of two subpopulations is more than 1, then one subpopulation must be nested in the other²¹ (Supplementary Notes). In many such cases, however, the pigeonhole principle does not allow disambiguating the true model (see Supplementary Figure 1, ambiguity between linear versus branched evolution). Moreover, CCF estimation requires correcting sequencing data for purity, ploidy, absolute copy number status, and mutation multiplicity (number of genomic copies carrying a mutation) for each single variant used for phylogenetic reconstruction. This process of correction inevitably propagates a significant amount of noise into the final CCF estimates and, consequently, in the associated phylogenetic trees.

REVOLVER implements a Maximum Likelihood (ML) method to jointly fit n models from n datasets D₁, …, D_n of alterations, for which either CCF or simpler binary annotations of presence/absence are available (Figure 1D). The method will process any alteration that can be annotated in these formats (e.g. mutation, copy number alteration, etc.). Each model is a tree that represents a partial ordering of the annotated alterations. To perform the fit, REVOLVER analyses a set of trees per patient (solutions) via a two-steps Transfer Learning strategy that outputs n correlated evolutionary trees T₁, …, T_n, (Supplementary Figure 2 and 3). Possible solutions can be pre-computed with external phylogenetic tools^22–27 and passed to REVOLVER, or can be directly computed within REVOLVER, for both CCF and binary data. The method requires a score per tree, which can be the model’s likelihood against data, e.g., p(D|T) for tree T, or any other suitable scalar that we seek to maximize. See Online Methods for full details on the methodology.

REVOLVER uses fits to measure the heterogeneity of the trajectories, and to calculate an evolutionary distance to compare patients and identify tumours shaped by similar trajectories (stratification, Figure 1E). The overall confidence in the predictions can be assessed with a jackknife approach²⁸ (see Supplementary Notes).

Finally, the genomic features of the evolutionary trajectories identified using a multi-region dataset (training set) can be used to classify single-sample cohorts (test set). This allows exploiting multi-region datasets to extract information from larger, single-sample cohorts. We note that the annotations of the genomic features (e.g. drivers) are left to the user to make REVOLVER applicable to different cohorts.

Synthetic test and biological validation of the method

We performed in silico validation of REVOLVER against synthetic data (1,620 cohorts, >86,000 patients and 200,000 samples; Supplementary Notes). Our analysis verified the internal consistency of the methodology, and demonstrated its superiority to standard methods based on uncorrelated phylogenetic inference. In every test, we generated n random phylogenetic trees and simulated consistent CCF values from multi-region bulk profiling. In every such cohort, the true models were associated to repeated evolutionary trajectories, which we sought to retrieve with REVOLVER and standard uncorrelated phylogenetic inference. To render this task realistic and account for allele sampling bias that can prevent the identification of the true phylogenetic tree via the pigeonhole principle²¹, we simulated a fraction p of the n cases so that multiple solutions are equally likely (ambiguous CCFs, Supplementary Figure 1). To model uncertainty in CCF estimates due to technical noise, we also added Gaussian noise to simulated data (Figure 2A). Standard phylogenetic approaches use CCF data from a single patient to score and rank a set of possible phylogenetic trees, eventually returning the one that explains best the data (top-rank). However, due to the uncertainty described above, the true solution does not always rank top (Figure 2B). This confounds the identification of the true model, and the detection of repeated evolutionary trajectories. REVOLVER allows de-noising the data by transferring information across phylogenetic trees, thus resolving this ambiguity. Results demonstrate that in the presence of sampling bias (e.g. linear and branched evolution are undistinguishable with the pigeonhole principle), with and without technical noise, REVOLVER is better than standard approaches in identifying the true evolutionary model, even when a large proportion of tumours have ambiguous solutions (Figure 2C; Supplementary Figure 4).

Figure 2. Synthetic test of the method and biological validation.

(A) To test our method, we generated n random phylogenetic trees and used them to sample synthetic CCF data for n patients. Due to tumour sampling bias (multiple subpopulations admixed in a bulk sample with unknown phylogenetic relationship), CCF data from a proportion of cases (red) may be ambiguous. For example, using the pigeonhole principle alone it may not be possible to discern linear from branched evolution (Supplementary Figure 1). Moreover, technical noise in the estimation of CCF values further exacerbates the problem. (B) When we analyse data with standard phylogenetic methods, we rank the best tree for a given patient. Due to sampling bias and technical noise, the true tree may remain hidden amongst lower ranking solutions in ambiguous samples (red). (C) REVOLVER transfers information across patients to de-noise the dataset and identify the true tree, even for patients with ambiguous data. We simulated 20 cohorts of n = 50 patients with 1-3 bulk regions each (extended tests in Supplementary Figure 4) and modelled sampling bias in a percentage p = 10, 30, 50% of patients, as well as Gaussian technical noise (σ = 0.05). Compared to standard uncorrelated phylogenetic inference in terms of trajectories retrieved (rate of true positives). Boxplots show mean and inter quartile range (IQR), upper whisker is 3^rd quartile +1.5 * IQR and lower whisker is 1^st quartile − 1.5 * IQR. (D) We performed biological validation of REVOLVER using data describing the adenoma-to-carcinoma evolutionary transition. We analysed a multi-region sequencing dataset comprising of n = 19 colorectal cancer patients (9 adenomas, and 10 carcinomas)³². REVOLVER detected repeated evolutionary trajectories (e.g. APC→KRAS, GL:germline, each column is a patient) involving key colorectal drivers such as APC, KRAS, TP53 and PIK3CA, which we can use to stratify patients (complete data in Supplementary Figure 5). In the bottom heatmap are putative driver alterations shaded by proportion of samples with the alteration. REVOLVER trees (bottom) show that by transferring information across patients, repeated evolution in early-stage tumours (adenomas) become informative of evolutionary trajectories in late-stage tumours (carcinomas), in which many alterations appear clonal and cannot otherwise be ordered. This analysis confirms the identification of the expected evolutionary trajectories of APC→KRAS→PIK3CA and APC→TP53 that drive malignant transformation.

We then sought to validate REVOLVER against established biological knowledge of evolutionary trajectories describing pre-malignant to malignant transition. Arguably, the best studied evolutionary transition in solid tumours is the adenoma-to-carcinoma sequence in colorectal cancer²⁹. In this scenario, carcinogenesis is a step-wise process of accumulation of genomic aberrations transforming a benign colon adenoma into carcinoma. Although not all colorectal cancers necessary develop from an adenoma, a significant proportion do, as demonstrated by the successes of bowel cancer screening and polypectomy procedures worldwide^30,31. We leveraged on a recent multi-region sequencing colorectal cancer dataset involving mutations in 9 adenomas and 10 carcinomas³² (95 total samples, median 5 per patient; Supplementary Table 1, Supplementary Figure 5). The stage of disease (adenoma or carcinoma) was hidden to REVOLVER. The dataset recapitulated the evolutionary transition from adenoma to carcinoma, which involves known colorectal cancer driver genes such as APC, KRAS, TP53 and PIK3CA. Figure 2D shows the heatmap of alterations in these driver genes (rows) for every patient (columns). Shade of blue represents the proportion of samples bearing the alteration (driver alterations are annotated as present/absent in a sample; truncal alterations are highlighted with orange squares). Our method identified multiple evolutionary transitions between pairs of events that characterise key evolutionary trajectories (Figure 2D). For instance, REVOLVER leveraged on information transferred from adenomas to detect trajectories that were hidden in carcinomas (truncal mutations, red arrows). For instance, the complete trajectory APC→KRAS→PIK3CA was never explicitly observed in a single patient but became detectable when patients were jointly analysed with TL. These known evolutionary trajectories demonstrate the ability of REVOLVER to systematically identify and compare repeated evolution from multi-region datasets, even in cases where noise and partial observations obscure the true trajectory in most patients.

Recurrent evolutionary trajectories in non-small cell lung cancer

We applied REVOLVER to the TRACERx dataset, the largest multi-region profiling effort to date, currently comprising n = 100 non-small cell lung cancers¹⁸ (Supplementary Table 2, Supplementary Notes). In this cohort, each tumour underwent whole-exome sequencing (500x depth) of multiple spatially separated regions, and a set of putative driver mutations and focal copy number alterations were annotated (302 total samples, median 3 per patient; 65421 total alterations, 450 drivers). We analysed the CCF values for all available patients (n = 99) and used the putative driver mutations and copy number alterations annotated in the original study. We considered recurrent drivers those appearing in at least 2 patients. We note that in our study we focus on a gene level analysis (i.e. we do not consider where the mutation occurs within a gene) to maximise the number of recurrent alterations. Although hotspot-level analysis could be performed, larger cohorts are required to achieve a suitable level of recurrence and transfer information across patients.

REVOLVER outputs n = 99 correlated models, and several measures of confidence and heterogeneity of the cohort. REVOLVER identified several repeated evolutionary transitions that characterised 10 clusters C1-C10 (Figure 3A; Supplementary Figures 6, 7). A jackknife approach²⁸ (Supplementary Notes) confirmed cluster robustness, with 80% median cluster stability and strongest signal for C2, C3, C4, C6 and C8 (Supplementary Figure 8). Clusters C4 and C6 have slightly weaker separation across resamples, and lower support is observed for small clusters like C10, or for C1 which has no clear signature. Importantly however, the individual evolutionary trajectories (e.g. CDKNA→TP53) were highly robust (Supplementary Notes). Cluster C5 describes the trajectory CDKNA→TP53→TERT (overall support >90%), suggesting progressive cell-cycle deregulation, anti-senescence, genomic instability and cell-death bypassing (Figure 3B). Two other clusters, C4 and C6, are associated with early EGFR alterations, with C4 also acquiring late TP53 loss. It is important to note that clustering the occurrences of driver alterations alone does not identify clear subgroups, even if one accounts for clonality status (Supplementary Figure 9). Furthermore, a comparative analysis against approaches based on single-sample cross-sectional cohorts¹¹, akin to refs^8–10,33,34, demonstrates the additional power in the predictions of REVOLVER, which combines multi-region data, phylogenetic theory and Transfer Learning (Supplementary Figure 10). By transferring information across patients, REVOLVER can also retrieve the temporal ordering of events within the same node of a tree (that could not be timed otherwise). This feature is called expansion, and it is illustrated for patient CRUK0016 (cluster C5) where we could identify the ordering in the trunk of the tree (Figure 3C). We also note that the phylogenetic tree fit for CRUK0016 ranked 5^th out 56 possible alternatives with a standard approach, and thus would not have been inferred without TL.

Figure 3. Repeated evolutionary trajectories in lung cancer.

(A) REVOLVER analysis of Cancer Cell Fraction (CCF) data from n = 99 non-small cell lung cancers from the TRACERx study¹⁸ (columns are patients). Top heatmap shows the most recurrent repeated evolutionary trajectories identified by our method (GL: germline, complete data in Supplementary Figure 6). Bottom heatmap shows most recurrent putative driver genes reported as average CCF values as provided in¹⁸. Alterations are ordered by frequency in the cohort, truncal alterations highlighted with orange squares. REVOLVER stratified this cohort in 10 evolutionary subgroups characterized by repeated evolution (Supplementary Figure 7). Subgroup stability was estimated via jackknife (N = 1,000 resamples, leave out p = 10%; Supplementary Figure 8) and annotated in the dendrogram (median per cluster). These groups can be used to derive a decision-tree classifier that stratifies n = 589 tumours in orthogonal single-sample cohorts (Supplementary Figure 11). (B) Repeated trajectories characterising cluster C5. In each edge of the graph we report the number of times a transition x →y is observed in the group, which contains 9 patients. For each alteration, we also annotate the number of times it is clonal or subclonal in the cohort, as well as the probability of detecting the edge across resamples (Supplementary Notes). (C) The phylogenetic model for patient CRUK0016 (cluster C5) has 13 clones (CCFs clusters), 5 with drivers annotated (in colour). The REVOLVER tree ranked 5th of 56 alternative ones. Via Transfer Learning, REVOLVER can also estimate the intra-clone orderings, for example the trajectory CDKNA→TP53→TERT can be expanded.

Finally, repeated evolutionary trajectories extracted from multi-region sequencing data with REVOLVER can be used to derive a decision tree that classifies large single-sample cohorts. In this case, stratification of n = 883 single-sample tumours^35–37 demonstrate that many of the REVOLVER subgroups show significant differences in disease-free survival (Supplementary Figure 11). Notably, previous large-scale single sample studies did not find clinically relevant subgroups using standard approaches³⁸.

Recurrent evolutionary trajectories in breast cancer

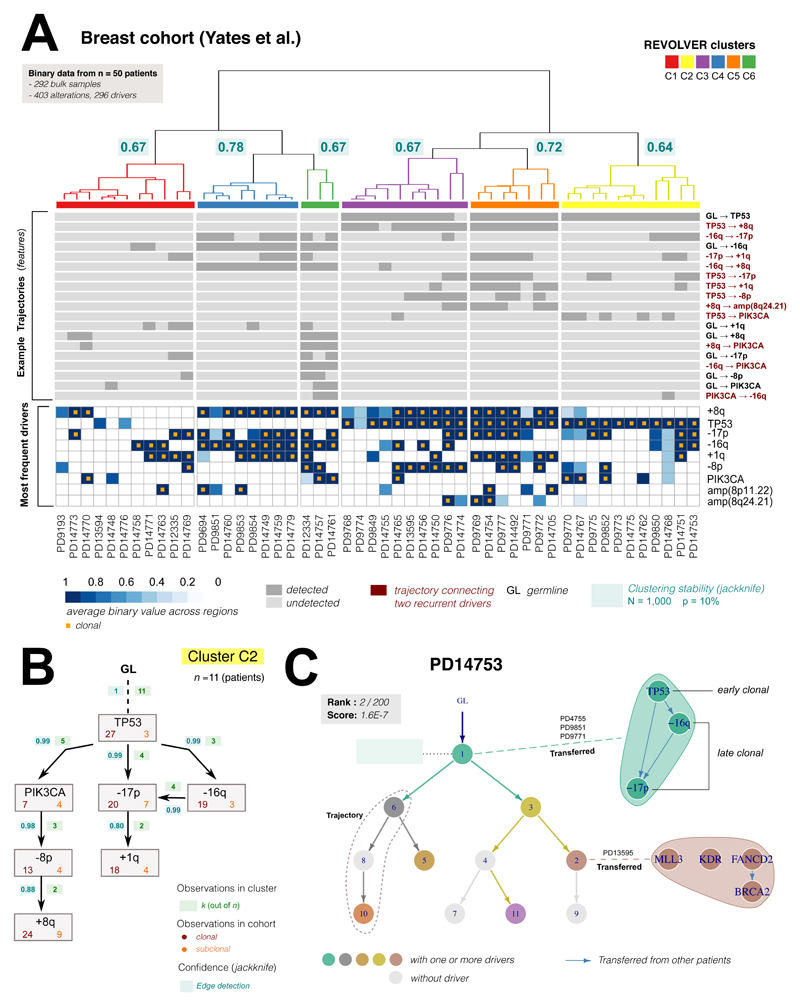
We applied REVOLVER to a cohort of n = 50 primary breast cancers where multi-region whole-genome and targeted deep sequencing was available¹⁵ (292 total samples, median 6 per patient; 403 total alterations, 296 drivers; Supplementary Table 3, Supplementary Notes). In each sample, a panel of mutations and CNAs (cytoband-level and whole-arm) in breast cancer putative driver genes were annotated¹⁵. For this study, we processed all annotated mutations and CNAs as presence/absence in a sample, and considered recurrent those in at least 2 patients. REVOLVER identified several repeated evolutionary transitions (Figure 4A) that characterised 6 evolutionary groups (Supplementary Figures 12, 13). Again, the results were robust, but with slightly lower scores than the one observed in the lung cohort possibly due to the lower resolution of binary data compared to CCF, which renders it more difficult to retrieve temporal orderings. However, the inferred trajectories were well supported by the data (Supplementary Figure 14). For example, subgroup C2 described the repeated evolutionary trajectory TP53→PIK3CA→-8p→+8q (Figure 4B), identified with >90% support (Supplementary Notes). Figure 4C shows the fit for patient PD14753, from subgroup C2. Again, standard clustering based on the patterns of occurrences of driver alterations does not identify similar groups (Supplementary Figure 15).

Figure 4. Repeated evolutionary trajectories in breast cancer.

(A) REVOLVER analysis of data from n = 50 breast cancers from Yates et al. 2015¹⁵ (columns are patient). Top heatmap shows the most common repeated evolutionary trajectories identified by our method (GL:germline, complete data in Supplementary Figure 12). Bottom heatmap shows most recurrent putative driver genes reported as average CCF values as provided in¹⁵ (data were presence/absence). Alterations are ordered by frequency in the cohort, truncal alterations annotated with orange squares. REVOLVER stratified this cohort in 6 evolutionary subgroups characterized by repeated evolution (Supplementary Figure 13). Subgroup stability was estimated via jackknife (N = 1,000 resamples, leave out p = 10%; Supplementary Figure 14), and annotated in the dendrogram (median per cluster). (B) Repeated trajectories in cluster C2. In each edge of the graph we report the number of times a transition x → y is observed in the group, which contains 11 patients. For each alteration, we also annotate the number of times it is clonal or subclonal in the cohort, as well as the probability of detecting the edge across resamples. This group highlights the evolutionary trajectory TP53→PIK3CA→-8p→+8q. (C) The clone tree for patient PD14753 (cluster C2) had 11 nodes, 7 of which containing drivers (in colour). With a standard approach, this tree would have scored 2/200 alternative trees. By transferring information from other patients in the cohort (dashed lines), REVOLVER can expand evolutionary transitions within the same node. In this case, we identified TP53 as tumour-initiating alteration (early clonal), followed by loss of 16q/17p (late clonal). Uncertainty on -16q and -17p ordering remains because of equally likely observations in the cohort. Transfer Learning also works at the subclonal level, identifying the trajectory FANCD2→BRCA2. The order of MLL3 and KDR remained uncertain.

We used repeated trajectories to create a decision tree (Figure 5A) and stratify n = 1,752 single-sample breast cancer cases from the METABRIC^39,40 (n = 1,318) and BRCA TCGA⁴¹ (n = 434) studies. We found that our evolutionary subgroups replicated in these cohorts (Figure 5B), and survival analysis highlighted significant differences between clusters (Figure 5C). Our evolutionary subgroups are enriched for specific breast cancer subtypes from the IntClust (based on both transcriptomic and copy number alterations) and PAM50 (transcriptomics alone) classifications (Figure 5D, 5E). Interestingly, REVOLVER group C3, which shows significantly poorer survival and is characterised by the evolutionary trajectory TP53→+8, was enriched for IntClust 10 and basal subtypes. This analysis demonstrates how evolutionary groups identified with REVOLVER can be combined with cancer subtypes to inform on how these tumours evolved.

Figure 5. Stratifying single-sample cross-sectional cohorts with repeated evolutionary trajectories.

(A) From the subgroups identified with REVOLVER using multi-region sequencing (in this example the breast cancer dataset), we can build a decision tree. (B) The decision tree was used to classify n = 1,752 single-samples tumours from large cross-sectional cohorts (METABRIC and TCGA BRCA2012), showing that REVOLVER subgroups reproduced in large orthogonal datasets. Most recurrent driver alterations, PAM50 and IntClust classifications are reported. (C) The evolutionary subgroups identified by REVOLVER were prognostic (two-tailed log-rank test, p < 0.05, 95% confidence interval shaded). Interestingly, poor survival group C3 was enriched for a specific subset of basal tumours characterised by trajectory TP53→+8q. See Supplementary Figure 11 for the same analysis in lung cancer. (D, E) Enrichment of REVOLVER clusters for IntClust classification and PAM50 classifications (one-tailed Fisher’s Exact test, p < 0.05 adjusted with Bonferroni correction, odds ratio and confidence interval in Supplementary Table 3).

Recurrent evolutionary trajectories in renal cancer

We used REVOLVER to analyse somatic mutations in a cohort of n = 10 clear cell renal cell carcinomas (79 samples, median 8 per patient; 843 alterations, 75 drivers)¹². We could identify repeated evolution involving mutations in PBRM1 and BAP1, well-known predictors of the evolution of this malignancy¹², further validating the approach. The identified trajectories reproduced in single-sample cohorts and have prognostic significance, in line with previous literature⁴² (Supplementary Table 4, Supplementary Notes).

Discussion

Detecting repeated evolution in cancer is critical for the implementation of evolutionary approaches to disease management. Stratifying patients based on their recurrent evolutionary patterns facilitates the prediction of the future steps of malignant progression, thus potentially allowing taking optimal and personalised clinical decisions.

Although the application of ‘artificial intelligence’ algorithms based on machine learning methods to biomedical datasets is becoming popular⁴³, the use of these methods as ‘black boxes’ to mine cancer genomic data is unlikely to be successful unless combined with clinical and biological knowledge of human malignancies to annotate input data and interpret results. Moreover, analysing the results in light of the cancer evolution paradigm is essential.

Here we presented a novel Transfer Learning approach that combines high-quality multi-region sequencing data of driver alterations and phylogenetic theory to detect the hidden signal of repeated evolution within multiple tumour types. We have demonstrated how apparently hidden evolutionary trajectories can be identified using this method. Approaches that do not exploit the observation of repeated evolution in multiple patients, and that attempt either a comparison of uncorrelated evolutionary models, or a clustering of alterations’ patterns, fail to identify signs of repeated evolution between patients. Our approach also helps to reconcile multi-region sequencing data with large single-sample cohorts by combining different data types and extracting more information on the evolutionary process from both strategies concurrently.

As our method is flexible in terms of input data, it can be used with both binary and CCF values and can be employed in conjunction with any phylogenetic method providing multiple scored phylogenetic tree solutions per patient. Importantly, our method is adaptable to a wide range of input data, and as higher resolution datasets will become available, our tool would be readily usable to detect evolutionary patterns in those. Moreover, the stratification power could be further increased with larger datasets, and it is readily applicable to single-cell sequencing data. The repeated evolutionary trajectories we identified were associated with subsets of patients with distinct prognosis, demonstrating the likely clinical value of stratifying patients based on how their tumours evolved.

Online Methods

The number of cancer evolution studies involving multi-region sequencing are rapidly growing (see, e.g., the case studies in^{12–15,17,18,44}), and intra-tumour heterogeneity profiling allows reconstructing the spatio-temporal evolutionary history of a patient tumour².

REVOLVER takes as input n multi-region sequencing datasets from n patients D₁, … , D_n. Each sample from a patient contains information on what genomic alterations are present in that specific sample. Our method is agnostic to the type of alteration annotated, which could be a nucleotide substitution (SNV), a copy number alteration (CNA) or any other (epi)genomic event. For each event, two data formats can be processed:

• Cancer Cell Fractions (CCF), or the proportion of cancer cells in the sample that bear the alteration.

• If CCF values are unavailable, a simpler binary format with presence/absence of the alteration in a sample.

The method also requires to specify for every patient when sets of alterations occur together in the same clone:

• For CCF data, clones are estimated via subclonal reconstruction (i.e., CCF-based clustering);

• For binary data, alterations are assumed to be in the same clone if found in the same set of samples.

For each genomic alteration, the input should also clarify if it is a putative driver, and/or truncal (i.e., present in 100% of cancer cells, or in the case of binary format, present in all samples; see Supplementary Notes for details on the input format).

In REVOLVER, we call alterations that are detected in multiple patients recurrent. We will use a parameter to determine a minimum recurrence threshold.

Evolutionary trajectories using a standard approach

For each patient, we can construct an evolutionary model (e.g. a phylogenetic tree) that explains the data via a standard approach such as those presented in refs^{12–15,17,18,44}. In what follows, we will seek to compare our method to the principles underpinning those approaches.

For a cohort of n patients, we would identify n evolutionary models T₁, … , T_n where:

• Each T_i is a tree describing the evolutionary history of a patient’s tumour. Its nodes are the groups of input alterations. In the case of CCF data this is a clone tree and each node is a clone, whereas in the case of binary data this is a mutation tree⁴⁵. The tree encodes the (partial) temporal ordering of the alterations in the tumour.

• An evolutionary trajectory is defined as a path x₁ → x₂ → ⋯ that connects alterations x_i, and describes their order of accumulation: x₁ is earlier than x₂, x₃, etc, while x₂ is earlier than x₃, x₄ etc. It can be computed from the ordering of the nodes in a tree.

Ideally, in order to interpret the data from a whole cohort of patients in light of tumour evolution, one would like to identify recurrent evolutionary trajectories describing repeated evolution across patients. Repeated evolution in cancer describes recurrent sequences of events that fundamentally underpin tumorigenesis and progression in a given subgroup of patients. Repeated evolutionary trajectories pinpoint evolutionary “steps” of a tumour, and could underlie advantageous phenotypic changes to the cancer clone.

Therefore, one needs a method that identifies trajectories that 1) are repeated across the cohort, and (hence) 2) involve recurrent alterations (drivers). Specifically, we need a method that correlates a trajectory involving recurrent drivers x and y, present within a sequence that may include passengers p_i:

$$\dots \to x\to p_1\to \dots \to p_w\to y\to \dots$$

See Supplementary Figure 2.

Using a standard approach based on phylogenetic theory, such as Maximum Parsimony⁴⁶ or Maximum Likelihood²⁷, one would infer each phylogenetic model T_i independently for each patient. A Bayesian approach would compute independently n posteriors p(T_i|D_i) for i=1,.., n, and use them to sample models with high likelihood.

With n independent models, we could evaluate post hoc structural similarities between patients. However, visual inspection of a set of phylogenetic trees is impractical with complex models or large n. Automatic approaches that use structural distances, or that measure similarities among the distributions induced by these probabilistic models, can help. Nevertheless, this approach to the detection of repeated evolutionary trajectories remains impractical because cancer multi-region cohorts exhibit a high degree of heterogeneity both between and within patients (see ref1,2 for a review), as well as inherent noise in the data.

Evolutionary trajectories using Transfer Learning

We propose a new approach to detect repeated evolutionary trajectories from noisy multi-region sequencing data of cancer patients. We assume that the recurrent trajectories can be modelled as a tree, which is hidden in the data. To capture heterogeneity across patients, we consider each input tumour as a noisy realisation from such tree (a realisation being the evolutionary trajectories for a patient, and its associated dataset).

In probabilistic terms, the individual patient trees are coupled through a shared prior, so that the (marginal) posterior distribution of patient trees no longer factorises across patients. Consider a joint posterior over T₁,…, T_n; we expect the solutions to differ in the following statistical sense

$$p\left(T_1,\dots ,T_n|D_1,\dots ,D_n\right)\ne {\displaystyle \prod _{i=1}^{n}p\left(T_i|D_i\right).}$$

In practice, a joint inference correlates explicitly n models of evolutionary processes: the solutions will be statistically dependent, and hence correlated across patients.

We argue that the detection of statistically significant regularities from correlated models is a better approach to exploit data of n (independent) evolutionary processes that describe the same tumour. Synthetic tests show that this method improves over standard uncorrelated methods, particularly in the presence of sampling bias and technical noise in CCF (Supplementary Notes).

The REVOLVER algorithm

In REVOLVER -- Repeated evolution in cancer -- we adopt an Expectation Maximisation (EM) strategy for Maximum Likelihood (ML) estimation of the n trees (Supplementary Notes). The structural correlation among each model is measured via a parameter w, which we maximise. From w, we estimate repeated evolution of the n input tumours, and induce a distance metric for cohort stratification.

First, REVOLVER processes input data and group (clone) assignments to pre-compute a set of scored trees for every patient. This is done differently depending on whether CCF or binary data is available and can be modified to accommodate custom tree learning methodologies (see below).

Then, a two-steps Transfer Learning (TL) strategy computes the joint ML estimates of T₁, …, T_n. Very broadly, TL is a Machine Learning paradigm to exploit knowledge gained while solving multiple related tasks. Here, the inference of the model for a patient (one task) becomes informative for the inference of other models (other tasks)¹⁹. The features shared among correlated tasks are recurrent drivers and their evolutionary trajectories (i.e., orderings). We remark that TL is sometimes used to indicate a broader class of problems; in the Machine Learning literature, our approach could be more specifically called multi-task learning.

Precisely, REVOLVER does the following steps (Supplementary Figures 2, 3):

• computes n correlated models T₁, …, T_n, from the ones available for each patient;

• computes the evolutionary trajectories within each group of alterations annotated in every patient and refines fit estimates accordingly. These trajectories cannot be detected unless we analyse data from multiple patients, and we “transfer” trajectories across inference tasks.

REVOLVER is a model-selection strategy. We first discuss how it computes correlated models, and then how its input models can be computed from CCF or binary data.

Correlating evolutionary trajectories across patients

A dataset D_i of a single patient is a matrix with alterations as columns, and samples sequenced from the i-th patient as rows. With input CCF, each entry of D_i is a real value in [0,1]; with binary data 1s report where the alteration is detected. We assume that D_i has no 0 columns and denote as {D_i|i = 1,.., n} the data from the whole cohort. $V={\cup }_{i=1}^n{V}_i$ is the whole set of alterations in the cohort; V_i the ones that occur in the i-th patient.

Evolutionary trajectories from groups (Supplementary Figure 2)

Consider a driver x, and denote with k_x the number of patients where it occurs; define

$$\Gamma =\{x\in V|k_x\ge \theta \}\cup \{\star \}$$

the set of recurrent alterations that occur in at least θ > 1 patients, plus a special symbol ⋆ that stands for “germline” ancestor. REVOLVER processes the whole dataset and induces correlation among drivers in Γ.

We write x → y ∈ T for an edge appearing in a tree T and introduce a special definition of the transitive closure of →, usually denoted as →* (Supplementary Figure 2,3). In general, the transitive closure of a path x → y → z is the set of edges →*= {x → y, y → z, x → z}; x → z follows by →’s closure. In this work, we have a special interest for evolutionary trajectories among recurrent drivers. Consider for the i-th patient the trajectory

$${{{\displaystyle p}}^{\prime }}_1\to \cdots \to {{{\displaystyle p}}^{\prime }}_z\to x\to p_1\to \cdots \to p_w\to y\to \cdots \text{where}{p}_i,{{{\displaystyle p}}^{\prime }}_i\notin \Gamma \text{and}x,y\in \Gamma$$

We write ${\pi }_y^i=x$ to denote the recurrent driver upstream of y in this patient; these trajectories are correlated in REVOLVER. We indicate them by the notation ${\pi }_y^i=x\to *y,$ or when it is clear by x →* y.

Because input alterations are grouped into clones, we need to account for groups when we create trajectories. If g₁ → g₂ are two groups in a model’s path, and x_j and y_j are the driver alterations in those groups, we account for all combinations of orderings in the two groups with the trajectories

$$g_1=\{x_1,\dots ,x_w\}\to g_2=\{y_1,\dots ,y_l\}=\{\begin{array}{c}{x}_1\to y_1\\ \cdots \\ x_w\to y_l\end{array}$$

This creates a combinatorial number of trajectories according to the number of drivers annotated in each group of a patient’s alterations. Clearly, the trajectory within a patient’s group is a linear ordering of its alterations that, however, cannot be estimated from a single patient. This is a confounding factor that renders the inference harder. However, by leveraging cross-sectional data from multiple patients diagnosed at different evolutionary times, one can recovery such trajectories and average out the confounders.

Multinomial counts of trajectories

To measure the structural correlation among the models, we count how often they contain a path that connects x and y in Γ; the minimum among k_x and k_y is an upper bound to this count.

Definition (Multinomial consensus) Given n trees T₁, …, T_n, we define the |Γ| × |Γ| discrete-valued consensus matrix w with entries

$${\mathit{\text{w}}}_{x,y}=|\{T_i|x\to *y\in T_i;x,y\in \Gamma \}|$$

where x →* y is a trajectory defined as explained above (Supplementary Figure 3).

Clearly, w_x,y/k_y is an empirical probability for the observation of x upstream y in the n models. By construction, we are detecting a statistical signal among x and y, recurrent driver alterations that intertwine with passengers. The role of ⋆ is to capture which x ∈ Γ is earliest in the trunk of a model (the associated trajectory is ⋆→* x); so w_⋆,x counts how many tumours are predicted to initiate via x. It must follow by tree construction that no alteration is upstream ⋆, and hence w_x,⋆ = 0.

Model-selection via Transfer Learning

REVOLVER requires a pre-computed set of trees per patient, and their scores (that must be sortable values); the algorithm uses those sets of models and w as estimator of their structural correlation and selects each patient’s most correlated tree. Procedures to create trees are implemented in the framework, according to the input data; see Supplementary Notes, for the algorithms’ pseudocode.

REVOLVER’s score of a model T_i is a rescaling of its pre-computed score by a factor that measures its structural deviation from the models of the other patients. The pre-computed score acts as a log-likelihood of the data under the model: p(T_i |D_i).

Definition (Model's score) Let Γ_i = V_i∩Γ be the recurrent drivers in patient i. A model T_i for this patient has score

$$f_{T_i}=\text{log}p(T_i|D_i)+\text{log}p{(T_i|\mathit{\text{w}})}^{\alpha }$$

for α ≥ 1. The latter term is a regularization term

$$p(T_i|\mathit{\text{w}})={\displaystyle \prod _{x\in {\Gamma }_i}\left(1-\frac{{\sum }_y{\mathit{\text{w}}}_{y,x}-{\mathit{\text{w}}}_{{\pi }_x^i,x}}{k_x}\right)}.$$

If the pre-computed scores factorize over models' edges, we can decompose the score as

$$\text{log}p(T_i|D_i)\propto \text{log}{\displaystyle \prod _{x\to y\in T_i}p(y|x;D_i)}$$

where p(y|x; D_i) are the edge terms obtained by fitting the tree’s parameters to D_i. This factorization is common but is not a requirement. Technically, f_Ti is a penalised log-likelihood; we refer to 1– p(T_i |w) as the penalty that re-scales T_i ’s likelihood at polynomial rate with degree α. This overall quantity is the “information transfer” (Supplementary Figure 2); α is a scaling factor that “shrinks” the penalty effect; in practice we always set it to 1 but it could be easily used to induce a stronger effect of the information transfer in shaping the gradient. In Supplementary Notes, we show power calculations for the minimum information transfer to induce an ordering's swap.

We observe the following properties of the above definition:

1. the information transfer considers only penalties by predictions that disagree with T_i. In fact, for any ${\pi }_x^i\to *x$ x in T_i, term ${\mathit{\text{w}}}_{{\pi }_x^i,x}$ is subtracted from the penalty;

2. we penalise independently each recurrent driver x ∈ Г_i, proportionally to the consensus of its evolutionary trajectories ∑_y w_y,x across the cohort;

3. ⋆ does not have incoming edges; only its outgoing edges contribute to p(T_i|w).

Definition (Model selection) To select n models T_* = [T₁, …, T_n], we solve a problem of discrete optimisation

$${\mathbf{\text{T}}}_{*}={\text{arg max}}_{\mathit{\text{T}}=[T_1,\dots ,T_n]}[f_{T_1},\dots ,f_{T_n}]$$

This problem is approached with an EM procedure. Because the trees are pre-computed for each model, a global solution for each initial EM condition is guaranteed. Given an initial estimate of the trees, T⁽⁰⁾ we compute w⁽⁰⁾ to select the T⁽¹⁾ that maximise REVOLVER’s score under w⁽⁰⁾. We then iterate by estimating w⁽¹⁾ from T⁽¹⁾, etc.; we stop when we reach a fix-point T⁽ⁱ⁺¹⁾ = T⁽ⁱ⁾ for some i, which is the ML estimate of T_*.

Precisely, the E and M steps are (Supplementary Figure 3):

• [E-step] from the current estimates of [T₁, … , T_n], compute w;

• [M-step] use w to compute the penalty; for every patient update the scores of its pre-computed models, and determine the highest scoring (ML estimate).

The ML estimates push to minimise the penalties in the sense that the optimisation gradient pushes p(T_i |W) to 1. In fact, with penalty 1 all the models predict the same trajectories for the variables in Γ, and we reach the objective of maximising the number of models, out of k_x, that predict the same driver upstream x. To start this EM, one can sample multiple random initial conditions, and select the solution with lowest penalty; this can be done in parallel. Equivalence classes of solutions with the same score and penalty might exist; this depends on the distribution of the input pre-computed scores. The method, however, is more powerful than its un-correlated counterpart in estimating the true model, as we measured via synthetic tests.

Computing trajectories within groups (expansion)

We know that, in every model T_i, we cannot compute trajectories for the alterations x₁,… , x_w that map to the same group g (e.g., those in the same clone). However, their trajectories might be detectable in those patients T_j ≠ T_i whose alterations overlap with g, if they are sampled at an earlier time. Because the hidden model is assumed to be the same tree for all patients, T_j’s trajectories are representative of the ones hidden in T_i.

In a TL approach, we transfer this information to T_i and split g accordingly; we can do that once the first EM strategy has converged. We call this procedure “expansion” of a group (Supplementary Figure 3). This heuristic first subsets the entries of x₁,… , x_w from w, and then selects, for each x_i, the most frequent parent driver. This is the multinomial ML estimate in w; if this does not exist because there is no evidence of any of the drivers in g to be upstream x_i, then x_i cannot be ordered and will be associated to the node upstream g. Ideally, if the input tumours were homogenous and we add observations from patients at different steps of progression, we could retrieve the unknown linear ordering (i.e., a topological sort) of x₁,… , x_w. In realistic cases, because of the uncertainty in the estimation of these trajectories and drivers’ annotation, we expect the expansion to be a graph that, of course, does not represent branched evolution.

Notice that the expansion does not change T_i ’s original likelihood (since its data was uninformative of g's trajectories), but it still changes the tree structure, and hence w and the penalty. We expect expansion to reduce the variance of w; if the cohort were truly homogenous, the penalty should decrease as well since we are selecting one particular ordering of x₁,…, x_w from a homogenous cohort.

Building input models from CCFs

Consider a patient with c groups – in what follows called clones for consistency with CCF-based studies – from r sequencing samples, its CCF data is stored in a c × r real-valued a matrix M. Each entry is a value in [0, 1], estimated from read counts, the input clone assignments of each alteration, copy number segments and tumour purity. REVOLVER’s implementation provides a method to compute phylogenetic trees to use as input for the tool. The tool allows one to input also a custom set of trees and scores. See also Supplementary Notes.

Generating trees

The method implemented exploits a modified version of ClonEvol, a tool for phylogenetic inference from CCF clusters⁴⁷. This tool first enumerates, independently for each sample, all trees compatible with M and rooted in z, the truncal clone. Then, it tries to build a “consensus” tree model that fits all the r regions at once. To build a tree, ClonEvol uses the standard pigeonhole principle²¹: for a node x to branch towards y₁, … , y_k, the parent's CCF must be greater than the sum of y_i’s CCF, that is

$$\mathbf{\text{ccf}}(\text{x})>{\sum }_{i=1}^k\mathbf{\text{ccf}}(y_i).$$

Clearly, certain combinations of CCF values are ambiguous, and support alternative trees. For instance, if x has CCF 1 and y and z 0.3 and 0.1, then both the linear path x → y → z, and the branched model (x towards y and z) are plausible under the pigeonhole principle. Because of noise in CCF estimation and tumour sampling bias, a consensus model might only be available if we allow for violations of such principle.

Ranking phylogenetic trees

We are not interested in a perfect consensus model, but rather we want to generate several alternative trees to input to REVOLVER. We modified ClonEvol to skip its last step and return the trees computed per region. With that, we could create a distribution of trees plausible under the input CCF, with a probability mass proportional to the extent to which a tree violates the pigeonhole principle under M, and the empirical evidence of each edge (obtained from ClonEvol estimates). This ensures that, even without perfect CCF, we can still compute a model for the data, and quantify its goodness of fit, without sub-setting input.

We proceeded as follows. Consider C, the set of clones annotated in M, and merge all trees into a weighted direct acyclic graph D whose nodes are C, and the weights are the average frequency of detection of the edges in each region, as estimated in ClonEvol. For each edge x → y, this is the empirical probability λ_x,y of clone x to be a direct parent of y in the phylogenetic trees, according to the trees estimated by ClonEvol. Thus, D is a generator of the distribution of phylogenetic trees for data M, assuming all edges to be independent.

The support of this distribution is the set of all minimum-spanning trees rooted in the truncal clone, which is known. This can be generated exhaustively only for small number of clone c = |C|, i.e., for a few thousand trees. If this is not the case, we can Monte Carlo sample a desired number of distinct trees for this patient; for each node y, its parents are sampled from the discrete marginal distribution λ_y = {λ_x,y}. This exploits a factorization of the distribution over the tree’s nodes and leads to sample trees that maximize the observed frequencies of edges, as we might desire.

Definition (Phylogenetic score) For a set of phylogenetic trees $𝒯$, each T ∈ $𝒯$ can be scored as

$$\begin{array}{cc}\eta (T)={\displaystyle \prod _{x\in T}ϵ(x){\displaystyle \prod _{x\to y\in T}{\lambda }_{x,y}}}& ϵ(x)=\frac{1}{r}\end{array}{\displaystyle \sum _{i=1}^r{\mathbf{1}}_{\mathbf{\text{ccf}}}(x,i)}$$

where 1_ccf is an indicator function that evaluates to 1 if x satisfies the pigeonhole principle in the i-th region,and 0 otherwise.

This score has the following desirable properties:

• η(T) and ϵ(x) span in [0,1], and allow for equivalent-scoring models;

• ϵ(x) is a goodness-of-fit measure: lower values indicate increasing violations of the principle, for x in T, under data M.

• terms λ_x,y is a probability that measures how often ClonEvol predicts x upstream of y; when this approaches 1 we have stronger evidence that x is upstream of y.

• η(T) = 1 only when 1) there is a unique possible assignment to the parents of every clone, and 2) there are no violations of the pigeonhole principle.

This score η(T) is a joint likelihood: the probability of each parent of a clone is weighted by a multinomial likelihood of error ϵ(x) estimated from the tumour data. This part of the algorithm can accommodate several customizations, and it is straightforward to use phylogenetic tools that provide alternative scoring function^22–27.

For our score or variations thereof, the following min/max interpretation holds. If we maximize η(T) alone we select the tree with most-frequent structure (max), and the smallest violations (min). When η(T) is combined within REVOLVER we expect a min/max-max shrinkage effect where, at the same time, we minimize errors in each phylogeny, and maximize both tree edges that are frequent and represent repeated evolution in the cohort.

Building input models from binary observations

Binary data is lower-resolution than CCFs but can still be used to create a mutation tree for a patient. To do that, REVOLVER implements a method that links Suppes' theory of probabilistic causation to cancer progression^11,48,49, see also Supplementary Notes.

Definition (Suppes' probabilistic causation in cancer) For any two variables x and y, edge x → y can exist in Suppes’ probabilistic model only if p(x) ≥ p(y) and p(y|x) ≥ p(y|¬x), where p(·) are empirical multinomial probabilities estimated via ML from binary data.

A Suppes' partially ordered set (poset) Π_i is the set of edges that satisfy probabilistic causation. We estimate for patient i its poset by data D_i, and use it as building blocks of our mutation trees. Temporal priority acts as both an infinite sites assumption, and a no back-mutations model (in phylogenetic jargon). In practice, we are assuming that alterations are persistent and, accordingly, we estimate temporal precedence via marginal frequencies. Probability rising, instead, is a measure of the degree of association between two variables, which implies statistical dependence as it is symmetric (like correlation), see Supplementary Notes.

A poset is also a weighted directed graph with constant normalized weights, if we assume all poset’s parents equally likely. So, it can be used to generate all minimum spanning trees rooted in the clonal group, which is the one whose alterations appear in all samples. Mutation trees can be sampled as done for phylogenetic trees, either exhaustively or by Monte Carlo, and can be scored via standard information theory. Each such model is a well-known Chow-Liu tree, a generator of the joint distribution p(c₁, … , c_w) if c₁, … , c_w are the w groups for this patient – i.e., the probability of observing the presence/absence of the corresponding alterations in a sample⁵⁰. A Chow-Liu tree contains second-order terms p(y|x) for the product approximation of the joint distribution that we factorise. It is well known that it has the minimum Kullback-Leibler divergence to the true distribution, being its closest approximation in an information-theoretic sense.

Definition (Binary tree score) For a set of Chow-Liu trees $𝒯$, each T ∈ $𝒯$ can be scored as

$$\tau (T)={\displaystyle \prod _{x\to y\in T}\mathbf{\text{mutinf}}(x,y)}$$

where mutinf(x, y) is the mutual information associated to random variables that take values x and y

$$\mathbf{\text{mutinf}}(X,Y)={\displaystyle \sum _{x,y}\frac{p(x,y)}{p(x)p(y)}}.$$

Thus, the highest-scoring Chow-Liu tree is the optimal solution to this model-selection task. REVOLVER’s input Chow-Liu trees can be ordered by decreasing mutual information; our method will fit lower-rank ones only if they have smaller penalty.

Synthetic tests

We carried out synthetic tests with CCF data to validate and assess the performance of REVOLVER under different configurations of cohort size, number of samples per patient and other covariates modelling confounding factors. Tests and results are detailed in Supplementary Notes and Supplementary Figure 4.

In a first batch of tests, we generated phylogenetic trees and CCF data under a combined model of tumour sampling bias. Statistically speaking, in some patients CCF will be hard to process (i.e., noisy): they will suggest linear and branched models of evolution with the same score. In other patients, CCF data will top-score the true evolutionary model. Results show that REVOLVER, by transferring information across patients, can retrieve the true model also for patients with noisy CCF data. Uncorrelated inference (the baseline method that we compare against), instead, suffers from sampling bias and uncertainty in tree estimation. This shows that joint ML estimation of the correlated trees can de-noise genomics data, improving on the uncorrelated counterpart.

In a second batch of tests, we investigated resistance to noise of our estimator. REVOLVER’s information transfer is estimated from data, thus if CCF data are dominated by noise, the algorithm will transfer “noise” and might fit repeated errors. We investigate this phenomenon with synthetic datasets affected by different intensities of Gaussian noise (technical noise) and show that REVOLVER is robust for reasonable ranges of those parameters.

Further material and case studies

REVOLVER is a framework with other features beyond its main inferential algorithm.

In Supplementary Notes we present:

1. Power calculations to correlate evolutionary trajectories;

2. A scalar index of divergent evolution that measures the heterogeneity of the trajectories inferred;

3. A REVOLVER-derived evolutionary distance (grounded in ecological theory for species’ diversity) to stratify the cohort into subgroups of tumours that harbour similar evolutionary trajectories.

4. A jackknife approach to estimate the stability of clusters and trajectories.

5. Further commentary on the approach;

6. Algorithmic settings for the analysis of real data.