Just-in-Time but Not Too Much: Determining Treatment Timing in Mobile Health

Abstract

There is a growing scientific interest in the use and development of just-in-time adaptive interventions in mobile health. These mobile interventions typically involve treatments, such as reminders, activity suggestions and motivational messages, delivered via notifications on a smartphone or a wearable to help users make healthy decisions in the moment. To be effective in influencing health, the combination of the right treatment and right delivery time is likely critical. A variety of prediction/detection algorithms have been developed with the goal of pinpointing the best delivery times. The best delivery times might be times of greatest risk and/or times at which the user might be most receptive to the treatment notifications. In addition, to avoid over burdening users, there is often a constraint on the number of treatments that should be provided per time interval (e.g., day or week). Yet there may be many more times at which the user is predicted or detected to be at risk and/or receptive. The goal then is to spread treatment uniformly across all of these times. In this paper, we introduce a method that spreads the treatment uniformly across the delivery times. This method can also be used to provide data for learning whether the treatments are effective at the delivery times. This work is motivated by our work on two mobile health studies, a smoking cessation study and a physical activity study.

1. INTRODUCTION

Recent advances in mobile technologies have generated increased scientific interest in the use and development of Just-in-Time Adaptive Interventions (JITAIs) in mobile health. Wearable devices and/or smartphones can be used to unobtrusively collect data from users in real time, such as busyness, location, weather, step count and heart rate [13,17, 18]. The JITAI involves treatments that are delivered via notifications on a smartphone or a wearable and which are designed to help users make healthy decisions to effectively manage their health and health behaviors. To be most effective in influencing health, the combination of both the right treatment and right delivery time is likely critical [13]. Many prediction/detection algorithms have been developed in order to provide potential delivery times. For example, physiological measurements collected from wearable sensors can be used to detect physiological stress [7]. Impending negative mood or detections of current negative mood [12] and detections of risky locations [6, 25] are additional examples of risk predictions/detections. Alternatively, the algorithms may detect times of potential receptivity or interruptibility [14].

Scientists are increasingly interested in designing mobile interventions in which treatments can be delivered to the user at these times. For example, in smoking cessation, we might aim to deliver a reminder to practice stress management skills when the user is detected to be stressed in order to limit potential relapse. Depending on the user and the day, there may be many such times. However, it is well understood that delivering too many treatments can cause undue user burden [9], possibly leading to app disengagement. Furthermore, repeatedly providing similar treatments may lead to habituation, where users begin to pay less attention to each subsequent treatment, decreasing its effectiveness [5, 13]. Thus, scientists often impose constraints on the number of times the mobile device should deliver treatments. Consider, for instance, the HeartSteps V1 physical activity study [3, 10, 11] in which activity suggestions are delivered to the user’s phone. In this study, considerations of burden and habituation led to the constraint that, on average, three activity suggestion messages would be delivered per day. In the planned next version of HeartSteps - referred to as HeartSteps V2 throughout - one of the treatment components is an anti-sedentary message. Here, the scientific team aims to provide an average of 1.5 anti-sedentary messages per day at sedentary times.

Here, times at which treatment may be provided are referred to as risk times. Ideally, it is best to deliver the treatments uniformly across the risk times so as to randomly sample the full variety of contexts in which risk times occur. Uniform sampling benefits the study design in two ways: first, uncertainty in when the treatments are delivered can reduce user habituation [5]; second, the uniform sampling of risk times enhances the ability of data analyses to learn if and in which contexts there is a causal effect of the treatment.

This paper develops a “Sequential Risk Time Sampling” (SeqRTS) algorithm that both satisfies the desired constraint on the total number of treatments in a day and spreads these treatments uniformly across all risk times. The SeqRTS algorithm combines forecasts of the remaining number of risk times within future blocks of time with a sequential algorithm that, at each risk time, provides a probability for triggering delivery of treatment.

This work is motivated by our collaboration on two mHealth studies - a smoking cessation trial currently in the field, Sense2Stop [2, 17], and in planning the next version of a physical activity trial, HeartSteps V2 [10]. In both cases, the approach developed here is currently being used or will be used to sample risk times to provide treatment. In both of the motivating studies, a primary goal is to learn if and in which contexts there is a causal effect of the treatment in altering health behaviors. In HeartSteps V2, for example, one goal is to determine if the anti-sedentary messages are effective at times the user is detected to be sedentary and how this effectiveness might be impacted by current context. In the smoking cessation study, Sense2Stop, one goal is to learn whether the reminders to practice stress management skills are effective at times the user is detected to be stressed.

2. RELATED WORK

A natural approach to developing a method to meet the constraints and deliver treatments uniformly across risk times is to build on methods from the ecological momentary assessment (EMA) [4, 15, 19–22] literature. Recall an EMA is a self-report collected via a mobile device as the user goes about his/her life [21, 22]. However, due to the high user burden imposed by frequent requests for self-reports, scientists often set a budget for the number of EMA requests within a day. Indeed, a higher average EMA response rate is observed in nonclinical studies when users are prompted for self-report fewer times per day [23]. In addition, usually scientists aim to uniformly spread out the EMA data collection across the day so that the self report answers more accurately reflect the user’s mood/behaviors in different contexts throughout the day.

A classical approach for timing the EMA is to split each day into some number of blocks, say K, and assign each block with certain number of treatments to achieve the constraint [4, 19, 20]. In a recovery support services study [20], for example, the day was split into K = 5 blocks. Within each block, a time was uniformly sampled and an EMA was delivered via the mobile device to the user at the sampled time. This method achieves the budget constraint exactly of five EMA messages every day. Of course, the number of messages can be randomized. For instance, if we want to achieve an average of 3 messages per day and we keep the 5 blocks from the prior example, then we can send a message with probability 3/5 = 0.6 in each block. If a block is selected for a message then the time at which the EMA message is sent is sampled uniformly within the block.

Rathbun et al. [15] consider alternative approaches to sending EMA. They sample times at which to send EMA according to a Poisson process with intensity ${\lambda }_t\left({\mathcal{H}}_t\right)={\lim }_{\delta \to 0}{\delta }^{-1}\mathbb{E}[N[t,t+\delta )|{\mathcal{H}}_t]$, where N[a, b) is the number of EMA sent within the time interval [a, b) and ${\mathcal{H}}_t$ denotes history of all the EMA times before time t. One option they consider for the intensity is ${\lambda }_t\left({\mathcal{H}}_t\right)=\exp (\alpha +\beta (t-\rho N[0,t)))$ for some $\mathit{\beta },\rho >0$. This intensity self-corrects when the system has sent more EMA than was desired. That is, if N[0, t), the number of EMA sent prior to time t, goes well-above the target t/ρ then the probability of sending an EMA is decreased.

However, these methods were not developed to deliver treatment. The method developed in this paper generalizes ideas from the above methods to the setting in which EMA messages are only to be sent at risk times and in addition, we do not know how many risk times will occur within any block of time. We will see that, when there is high variability in the number of risk times within the block, the SeqRTS algorithm outperforms simple extensions of the block sampling approach in achieving the desired average number of treatments and in spreading the treatments uniformly across risk times. We will also see that this performance depends on the forecast quality.

In the next section, we introduce notation for the longitudinal data collected from wearable devices. Next, in section 4, we introduce the SeqRTS algorithm. We discuss each tuning parameter, what it controls, and how to set their values. We then present a toy example to demonstrate how the tuning parameters and the forecasts impact the performance of the SeqRTS algorithm. We evaluate the performance of the SeqRTS algorithm in two mHealth studies - the Minnesota smoking study and HeartSteps V1. Studying performance on the Minnesota study informs expected performance in Sense2Stop. Similarly, performance on HeartSteps V1 informs expected performance in HeartSteps V2. We end with a discussion of limitations and suggestions regarding practical implementation in future studies.

3. DATA COLLECTED FROM WEARABLE DEVICES

Write the user’s longitudinal data recorded via mobile devices as the sequence $\left\{O_0,O_1,A_1,O_2,\dots ,O_t,A_t,O_{t+1},\dots \right\}$, where t indexes regularly-spaced times (e.g., every minute, five-minutes, thirty-minutes, hour, etc.); O₀ contains the baseline information; the observation O_t (t ≥ 1) is the vector of sensed and self-report observations collected between time t − 1 and t; and A_t is the treatment at time t. Choice of time-scale is usually determined by the frequency with which the risk detections can be made. In the smoking cessation study, the temporal frequency is set to every minute; in the physical activity study, the frequency is every five minutes. For simplicity, we consider binary treatment, i.e., A_t = 1 if treatment is delivered, A_t = 0 otherwise. Denote by H_t = $\{O_0,O_1,A_1,O_2,\dots ,A_{t-1},O_t\}$ the observation history up to time t as well as the treatment history at all times up to, but not including, time t.

The observations, O_t, include a variable that indicates risk, X_t. For example, in the physical activity study, described below, X_t = 1 if the user’s wristband tracker records less than 150 steps in the past 40 minutes (i.e., user is sedentary) and X_t = 0 otherwise. The activity suggestion messages are designed to be delivered when the user is sedentary, e.g., when X_t = 1. A risk time is a time t at which the user is detected to be at risk. In the physical activity study, “at risk” implies X_t = 1; however, in other studies, multiple levels of risk may exist. In the smoking cessation study, for example, X_t = 1 (i.e., time is not classified as stressed) and X_t = 2 (time is classified as stressed) are two levels of risk. Write X_t = 0 to denote the user is not at risk, and $X_t=x\in \{1,\dots ,\chi \}>0$ to denote the user is at risk level x at time t (i.e., a risk time at level x). The risk variable at time t, X_t, is contained in H_t.

At some risk times, however, feasibility and ethics considerations imply that the individual is unavailable for treatment. For example, if sensors indicate that the user might be driving a car [18], then the message should not be sent; that is, the user is unavailable for treatment. The observation, O_t, includes an availability indicator I_t to capture this information; that is, I_t = 1 if the individual is “available” for treatment and I_t = 0 otherwise. An available time is a time t at which the user is available for treatment, i.e., when I_t = 1. The availability indicator at time t, I_t, is contained in H_t. An available risk time is a time t at which the user is available for treatment and at risk. Finally, times t such that X_t = x > 0 and I_t = 1 are referred to as available risk times at level x.

4. THE SEQUENTIAL RISK TIME SAMPLING ALGORITHM

As mentioned above, the proposed sequential risk time sampling (SeqRTS) algorithm generalizes blocking as well as the use of a sequential algorithm from the EMA literature. For simplicity, assume that each day is split into K time blocks, i.e., $\mathcal{\tau }={\cup }_{k=1}^K{\mathcal{B}}_k$ and denote the size of each block $\left|{\mathcal{B}}_k\right|=T$. The following method can be easily generalized to allow for different numbers of blocks per day or differently sized blocks depending on the time of day. Suppose there are multiple levels of risk indexed by $x\in \{1,\dots ,X\}$. And suppose that each day, an average of $N_x^{*}$ available risk times at level x are to be sampled for treatment delivery (A_t = 1). Mathematically, the average constraint can be written as

$$\mathbb{E}\left[\sum _{t\in \mathcal{T}}{A}_t{\mathcal{1}}_{\left\{X_t=x,I_t=1\right\}}\right]=N_x^{*}$$ (1)

for each value of x. Note the expectation is over the distribution of available risk times at level x within a given day. Furthermore, a secondary goal is to deliver treatment uniformly over available risk times at every level x such that the above constraint is satisfied. Operationally, the goal is to design a probability to assign treatment or, equivalently, a probability that is used to sample available risk times at level x.

Intuitively, at each available risk time in a block, SeqRTS calculates the number of remaining available risk times to be sampled for treatment in the block and divides this by the expected number of available risk times remaining in the block. More precisely suppose time t is an available risk time in the k-th time block at level x for a user. Then, SeqRTS delivers treatment with probability

$${\pi }_t={\varphi }_{ϵ}\left(\frac{N_{x,k}-C_{t,\lambda }(x)}{1+g(x|H_t)}\right).$$ (2)

Where $\lambda \in [0,1]$ is a tuning parameter,

• (1)$N_{x,k}\ge 0$ (i.e., the block budget) is a tuning parameter. Roughly speaking, $N_{x,k}$ is the average number of treatments delivered in block k at level x. So $\sum {}_{k=1}^K{N}_{x,k}\approx N_x^{*}$.
• (2)
  $C_{t,\lambda }(x)$ denotes a soft version of number of treatments that have been triggered so far in current block at the risk level x; that is,

  $$C_{t,\lambda }(x)=\sum _{s\in {\mathcal{B}}_k,s\le t-1}{\mathcal{1}}_{\left\{I_s=1,X_s=x\right\}}({\lambda }^{t-s}{A}_s+\left(1-{\lambda }^{t-s}\right){\pi }_s).$$ (3)

  C_t,1(x)(i.e., setting $\lambda =1$) equals the exact number of treatments that have been triggered so far in the current block at risk level x. C_{t, 0} (x) (i.e., setting $\lambda$ = 0) equals the sum of probabilities of triggering treatment at previous available risk times at level x in the current block. The former uses the observed history. The latter uses the “expected” history. The choice of $\lambda \in [0,1]$ smoothly adjusts between these extremes. As will be seen below, the tuning parameter $\lambda$ controls the variability in sampling the risk times; see below for futher details.

• (3)$g\left(x|H_t\right)$ denotes a forecast of the number of available risk times at risk level x left in the current block, i.e., ${\sum }_{s\in {\mathcal{B}}_k,s\ge t+1}{\mathcal{1}}_{\left\{I_s=1,X_s=x\right\}}$, given the observed history up to time t, H_t. We build this forecast from training data. See section 6 for a discussion of the limitations of forecasting in our current setting.
• (4)Lastly ${\varphi }_{ϵ}(x)=x{\mathcal{1}}_{\left\{x\in \left[{ϵ}_L,{ϵ}_U\right]\right\}}+{ϵ}_U{\mathcal{1}}_{\left\{x>{ϵ}_U\right\}}+{ϵ}_L{\mathcal{1}}_{\left\{x<{ϵ}_L\right\}}$ denotes a truncation function with pre-specified upper and lower limits $ϵ=\left\{{ϵ}_L,{ϵ}_U\right\}$. The truncation function ensures the output value stays within $\left[{ϵ}_L,{ϵ}_U\right]$ (i.e., bounded away from 0 and 1) to allow for causal inference with the collected data. This truncation function is intended as a last resort as generally N_x,_k and $\lambda$, when well tuned, will ensure that the fraction in (2) is bounded away from 0 and 1.

To recap, the numerator in (2) takes the block budget N_x,k for level x and subtracts the amount that has been “used” by time t (i.e., C_{t, λ} (x)); this is, roughly speaking, the number of remaining times to be sampled for treatment in the block where the user will be available and at risk level x. This “remaining budget” is then divided evenly among the expected number of available risk times at level x remaining in the block (i.e., $1+g(x|H_t)$). Algorithm 1 provides pseudocode for the SeqRTS algorithm at a particular risk time t.

In general, we aim to sample times for treatment with probabilities bounded away from 0 and 1; this enhances our ability to learn the casual effect of the treatment and how this causal effect is impacted by the user’s context. However, if ${ϵ}_L=0,{ϵ}_U=1$ and $\lambda =1$, then it is possible, given the history, for a time at which the user is available and at risk level x to be sampled for treatment with zero probability. This is because the numerator becomes zero whenever the past number of treatments in the current block equals the target N_x, _k. Additionally, for certain histories, the probability of sending treatment can be one. Consider a toy example with a perfect forecast, the block is a day and every day has five available risk times. Suppose the goal is to achieve an average of one treatment per day. Then if $\lambda =1$, once a treatment within the block is provided, the probability of treatment at any future available risk time in the day is zero. Or if no treatment has been provided in the first four risk times, then the probability of sending treatment at the fifth risk time becomes 1. To avoid these settings we select $\lambda <1$ and, in addition, we employ the truncation function, ${\varphi }_{ϵ}$, with ${ϵ}_L>0$ and ${ϵ}_U<1$. Furthermore, if $\lambda =0$, the algorithm, because it does not take into account past treatments but only the probabilities of past treatments, may sample many more or much fewer risk times than desired. Consider the toy example once more, in which the block is an entire day. Then if $\lambda =0$, the average number of treatments per day is equal to 1 as desired, but on 19% of the days, the user will receive more than 3 treatments. For studies where treatment may cause high undue user burden, this might be considered to be excessive. In Sense2Stop, for instance, an excessive number of treatments at times classified as “Stressed” may only exacerbate stress. Tuning of $\lambda$ guards against the likelihood of over-treating at these times. See section 5.1 for a more complex example of this trade-off.

When the scientific team believes the variation in the number of treatments under $\lambda =0$ is too high, one could choose a non-zero λ to reduce the variation. Additionally, the use of discounted weights ${\lambda }^{t-s}$, instead of a fixed, time-invariant weight, is to help spread out the treatments, as the probability of sending treatments would decrease if a treatment was delivered in the recent past and such impact would be weaken as time goes on (discounted by the length of separation t − s). This is similar to the use of the self-correcting process in the point-process sampling method for EMA discussed in section 2.

A key difference between the SeqRTS algorithm and the block sampling method discussed in section 2 is the use of forecast, $g(x|H_t)$. Essentially, we replace the crude estimate of the average number risk times per block by time-varying forecasts of the remaining risk times at risk level x within the block. These forecasts allow us to use user-specific time varying covariates and baseline characteristics to account for the potentially high variability in the number of risk times and in how the risk times are spread out within a block and thus better achieve the average constraint and uniformly spread out the treatments across the risk times.

4.1. Selecting Tuning Parameters

SeqRTS requires selection of blocks, the construction of the forecasts ($g(x|H_t)$) and the tuning parameters $\lambda$ and $\mathit{N}=\left\{N_{x,k},x=1,\dots ,\chi ,k=1,\dots ,K\right\}$. We assume that the blocks and bounds e have been selected. Because there are a variety of high quality prediction/forecasting methods available, here we focus on tuning of $\lambda$ and N. See below for comments on the selection of the number of blocks as well as the prediction method. The TUNE algorthim is given in Algorithm 2.

Training data is used to tune $\lambda$ and N. This training data must include all of the features needed by the forecasting method as well as the risk X_t and availability I_t variables. Here, our training data is from similar studies to Sense2Stop and HeartSteps V2 for which the same sensing suites are deployed – the Minnesota smoking study and HeartSteps V1 respectively. Below the Minnesota smoking study does not include treatment whereas HeartSteps V1 does include treatment.

As previously discussed, the value of N_x,k controls the total number of treatments in the k-th block. When there is more than one time block in a day (i.e. K > 1), in order to choose an appropriate value of N_x,k we first construct a target average number of treatments for each block, denoted by $N_{x,k}^{*}$, by splitting the overall daily constraint $N_x^{*}$ into K time blocks such that $N_x^{*}={\sum }_{k=1}^K{N}_{x,k}^{*}$. Here we use $N_{x,k}^{*}=N_x^{*}/K$.

To tune the parameters $\left(\lambda ,\mathit{N}\right)$, we use (2) to determine the probability ${\pi }_t$ to generate an A_t at each available risk time. This is done for each block in each day in the training data, 1000 times. We then compute the average number of treatments in the k-th block at each level x (across all days and the 1000 runs of the algorithm) and

denote the averages by $F_{x,k}(\lambda ,\mathit{N})$. For each $\lambda$ in a grid, we search for the optimal tuning value of ${\mathit{N}}_{x,k}$, such that the computed average number of treatments is equal to the target constraint $N_{x,k}^{*}$; more precisely, we minimize the objective function $J(\mathit{N})={\sum }_{k=1}^K{\sum }_{x=1}^{\chi }{\left({\mathit{N}}_{x,k}^{*}-F_{x,k}(\lambda ,\mathit{N})\right)}^2$. The remaining problem is how to tune $\lambda$. Recall that we aim to select a value of $\lambda <1$ so as to ensure the sampling probabilities lie in (0,1). However small values of $\lambda$ can potentially result in too much variance in the number of treatments (e.g. sampled risk times) across days. Our approach, as part of the scientific team, is to decide what level of daily variation in treatments is tolerable and use this to tune $\lambda$. That is, we specify a probability, p, and a range [l, u] so that the probability of total treatments within a given range [l, u], i.e., $\text{Pr}\left(l\le {\sum }_{t\in \mathcal{T}}{A}_t{\mathcal{1}}_{\left\{I_t=1,X_t=x\right\}}\le u\right)\ge p$ for each level of risk $x\in \{1,\dots ,\chi \}$. For each value of $\lambda$, the training data to estimate this probability under the optimal, tuned N. Then the smallest $\lambda$ that achieves the above inequality is selected. For example, besides providing on average 2 notifications per day, we might want to ensure that the probability of sending 1 to 3 notifications is at least p = 0.95 (e.g., l = 1, u = 3). In section 5.1, we use a toy example to illustrate the selection of tuning parameters.

Recall that the forecast $\left(g\left(x|H_t\right)\right)$ predicts the number of remaining available risk times at risk level x in the current time block. As pointed out earlier, the quality of the forecast determine the ability of SeqRTS in spreading out the treatments uniformly across the risk times at risk level x. Note that the size of time block also affects the forecast quality since the forecast needs to look more into the future if the size of the block is big. However, the block lengths should not be too short as then there will be blocks with no risk times. We suggest using a block length that is short, yet ensures that with high probability there will be at least N_x/K risk times at risk level x.

As the main focus of this work is on discussing the timing of treatment problem and the use of (2) along with how best to select the tuning parameters, we assumed that a method for forecasting is given. In practice, one can use the study data to both choose the tuning parameters and build the forecasts; we do this below. There are a number of existing methods for prediction and forecasting for the time-series, e.g., exponential smoothing and ARIMA model; see [1] for a review. In the Sense2stop example, we use forecasts obtained by Poisson regression. In the HeartSteps V2 example, we construct the forecasts by using the fact that if X_t = 1 then X_{t + 1} is highly likely to be 1 as well (see section 5.3.1)

4.2. Cross Validation Using Study Data

The TUNE algorithm (2) selects tuning parameters using a training dataset. In both examples below, prior real mHealth studies exist that can be used for constructing training datasets and assessing performance via cross validation. Figure 1 visualizes the sequence of actions to perform cross validation and assess performance. In both examples, a fraction of the person-days from the study data is used as the training data, while the remainder is used as the test data (Step 1). The TUNE algorithm is applied to the training data to obtain tuning parameters (i.e., Step 2). A particular person-day is extracted from the test data (i.e., Step 3). Then the SeqRTS algorithm is applied to test data (i.e., Step 4) to generate multiple treatment sequences; in our examples, 1000 treatment sequences are generated. Step 5 is cross validation to build performance summaries. This procedure outputs performance summaries for a particular chosen forecasting model. Therefore, the procedure must be run again for each proposed forecasting model. Alternatively, Step 1 could split the data by person rather than person-days; however, in these studies the resulting performance summaries are very similar.

Fig. 1.

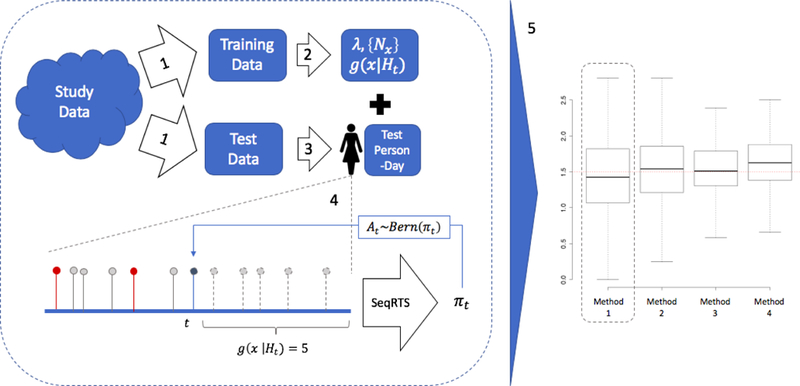
Flowchart for studying performance of the SeqRTS algorithm. In step 1, study data is split into training and test data. In step 2, TUNE is used to construct all tuning parameters and fit parameters for a chosen forecasting method. In Step 3, a person-day is extracted from the test data. In Step 4, SeqRTS is applied sequentially. The blue point indicates that time t is an available risk time at level x for the user; the prior red and gray points indicate past available risk times at level x. Prior points in red indicate treatment was provided. In this example, there are 6 prior available times at risk level x. Combining this information with the forecast of 5 future available times at risk level x, SeqRTS is applied using the given tuning parameters and forecasting method to construct the probability of treatment at time t. In step 5, summaries of the performance on test data are aggregated using cross-validation. Each new forecasting method requires the left-hand block to be re-run (i.e., current flowchart builds summaries for Method 1).

5. STUDIES

Here the SeqRTS algorithm is contrasted with a natural extension of the blocking method used in standard EMA setting. This extension considers the setting in which only risk times should be sampled for treatment and in which there is an average constraint on the number of treatments. This natural extension is a good comparator to our proposal because it is a simple extension that may achieve the desired soft constraint and uniformity across risk times.

To describe the extended version of block sampling method suppose there is only one level of risk (i.e., $X_t\in \{0,1\}$) and the goal is to send treatment only at risk times (i.e., when X_t = 1). As in the standard blocking design, first construct K blocks of time within each day. If the average number of treatments per day is N, then in each block the goal is to provide an average of n = N/K treatments. Suppose prior scientific knowledge and/or data from a prior study is used to estimate the number of expected risk times within each block, denoted by M_k for the k-th block. The number of blocks, K, would be chosen based on prior data and scientific rationale so that one can expect more risk times per block than the desired average number of treatments per block (i.e., M_k > n). Then at each risk time within each block, a treatment is sent with probability n/M_k. This “extended EMA blocking method” implicitly assumes that risk times are spread uniformly within blocks and that there is little between-user variability in the number of risk times per block.

Two metrics are used to compare SeqRTS with the above block sampling method. The first metric is graphical and the second metric uses a divergence function to assess divergence from uniform sampling of risk times for treatment. Recall that a training set is used to build the forecasts method as well as the select tuning parameters. These two metrics will be evaluated on a test data set. See Figure 1 for the cross validation procedure. Given the forecasts and selected tuning parameters, user-day trajectories within the test data are used to generate 1,000 treatment sequences (sequences of A_t’s) per user-day. Each A_t is generated with the probability given by (2).

In the first, graphical metric, the 1000 generated treatment sequences are used to compute the total number of treatments provided per day. The average over these treatment sequences is used to compute the average number of treatments per user-day. A box-plot across all user-day combinations of this average number of treatments summarizes performance. It is expected that the mean and median to agree with desired number of treatments per day, $N_x^{*}$. Methods with low variability around this mean are preferable. For the physical activity study, HeartSteps V1, for each user we compute the average of these user-day averages (i.e., average across days per user). A box-plot summarizes performance and highlights across-user variability in performance.

The second metric again uses the 1,000 treatment sequences and computes the fraction of time treated per risk time at risk x for each day d. As treatment can only be provided at risk times, we extract these times out to construct the vector ${\widehat{p}}_{u,d,x}$ (i.e., fraction of time treated for user u on day d at risk level x). Let N_u,_d,_x be the number of risk times for user u on day d at risk x. Recall one of the goals for this algorithm is uniformity across risk times. To assess whether this goal is achieved we use the Kullback-Leibler divergence measure - a measure of “how one probability distribution diverges from a second, expected probability distribution” [24]. To assess uniformity, the second, “expected probability distribution” is the targeted uniform probability distribution across the true risk times. That is, knowing N_u,_d,x and the budget N_x, treatment should be provided marginally at each available risk time at level x with probability $N_x\text{/}{N}_{u,d,x}$. Therefore, the Kullback-Leibler divergence measured is between the sampling probabilities achieved by SeqRTS, e.g. ${\widehat{p}}_{u,d,x}$ and the targeted uniform probabilities, $N_x/N_{u,d,x};$ that is,

$$\frac{1}{N_{u,d,x}}\sum _{i=1}^{N_{u,d,x}}\left(N_x^{*}/N_{u,d,x}\right)\log \left(\frac{{\widehat{p}}_{u,d,x,i}}{N_x^{*}/N_{u,d,x}}\right)$$

Where ${\widehat{p}}_{u,d,x,i}$ is sampling probability for the ith risk time for user u on day d at risk level x vector ${\widehat{p}}_{u,d,x}$. A box-plot of this quantity across user-days (all (u, d)’s) summarizes performance. Smaller Kullback-Leiber divergence indicates that the sampling is closer to uniform sampling and low overall variability indicates the sampling of risk times is closer to uniform for all user-days.

We start with a toy example to demonstrate how the tuning parameter impacts the SeqRTS algorithm and illustrate tuning parameter selection using the TUNE algorithm. Afterwards, the procedure in Figure 1 is applied to two real mHealth studies - the Minnesota smoking study and HeartSteps V1 study - used to design Sense2Stop and HeartSteps V2 respectively.

5.1. Toy Example

A toy example illustrates how the tuning parameters $\left(\mathit{N},\lambda \right)$ and the forecasts impact the performance of the SeqRTS algorithm and illustrate the selection of tuning parameters. For simplicity, consider the case where the user is always available for treatment (i.e., I_t = 1) and the risk variable is binary, $X_t\in \{0,1\}$. Temporal frequency is every fifteen minutes and we consider providing treatments in a 10-hour day (T = 40). In this toy example, there is a single level of risk (i.e., X_t = 1) and a single whole day block for simplicity (i.e. K = 1). The risk variables $\left\{X_1,\dots ,X_T\right\}$ are generated i.i.d. with probability 0.5. The goal is to provide on average 3 treatments per day (i.e., $N_0^{*}=0$ and $N_1^{*}=3$) at risk times. The training dataset is 100 randomly generated user-days.

A series of three simulations illustrate the performance of the SeqRTS algorithm. The first simulation (S1) illustrates how the tuning parameters impact the average number of daily treatments. Algorithm performance is evaluated with tuning parameters $N_{1,1}\in \{2.95,3,3.05,3.1\}:=G_N$ and $\lambda \in \{0,0.1,\dots ,0.9\}:=G_{\lambda }$ using the test set. In the second simulation (S2), the value of N_1,1 is tuned (using training set) so as to achieve the average constraint under each $\lambda$. In both S1 and S2, the forecasts are correct in expectation, e.g. $g\text{(}1\left|H_t\right)=0.5(T-t\text{)}$. The simulation results are provided in Figure 2. The left graph in this figure illustrates N_1,1 together with the choice of $\lambda$ control the total number of notifications. The appropriate value of N_1,1 to achieve the average constraint (i.e., 3 in this toy example) depends on the value of $\lambda$ For example, when $\lambda =0,N_1{{}_{,}}_1$ needs to be greater than 3, whereas in the case of $\lambda =0.8$, the appropriate choice of N_1,1 is less than 3. After properly choosing N_1,1 for each $\lambda$, the right graph in Figure 2 shows that incorporating $\lambda$ allows the algorithm to control the variability in number of treatments yet achieve the average constraint. The y-axis is the probability that the number of treatments sent lies in the range of 1 to 5.

Fig. 2.

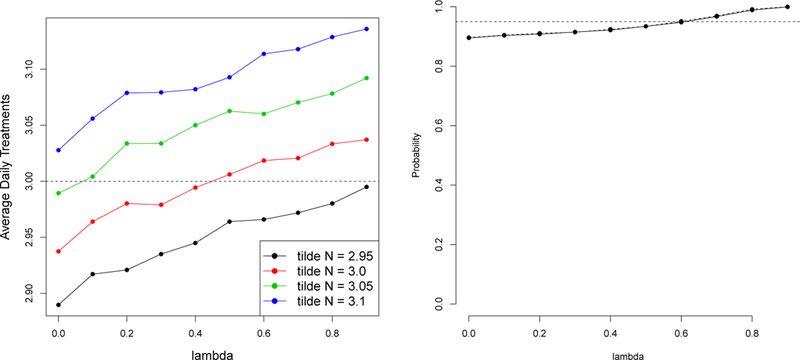
Simulation results of S1 and S2. Left: the average number of daily treatments under different values of $\lambda$ (x-axis) and N_1,1 (in color). Right: the probability that the number of treatments sent ranges between 1–5 treatments. Here N_1,1 is tuned for each $\lambda$.

The last simulation (S3) illustrates the impact of an inaccurate forecasting method on SeqRTS. A class of forecasts indexed by a constant τ are considered, i.e., $g(1|H_t)=(T-t)\tau$. For each forecast, the tuning parameter $\lambda$ is chosen using training set to be the smallest one over the grid set $\{0,0.05,\cdots ,0.95\}$, such that with at least 0.95 probability the number of treatments sent lies in the range of 1 to 5. Here, the parameter N_1,1 is tuned for each $\lambda$ as in S2. In all cases, N_1,1 can be tuned to achieve the average constraint of 3, and $\lambda$ tuned to achieve at least 0.95 probability that the number of treatments sent lies in the range of 1 to 5. However, as shown in Figure 3, the more inaccurate the forecast (i.e. $\tau$ far from 0.5), the less uniform the distribution of treatments assigned across hour blocks (note that the times when X_t = 1 are uniformly distributed across time in this toy example).

Fig. 3.

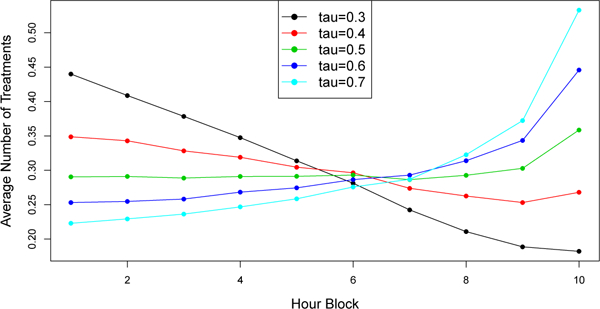
Simulation results of S3. Average number of treatments triggered in each hour block in testing data set. Solid lines = “forecast”; dashed line = “oracle”

5.2. Minnesota Smoking Study

To design Sense2Stop, data from a smoking cessation study [16, 17] (here on called the “Minnesota smoking study”) is used to construct forecasts, tune the parameters, and assess expected performance. The Minnesota dataset is a no treatment, smoking study. Sensor data collected from wearable devices (e.g., the electrocardiogram (ECG) and respiration data) are used to produce an online, time-varying stress likelihood for each minute [18]. Next, a Moving Average Convergence Divergence approach (MACD) is adopted to locate an episode based on the time-series of stress likelihood; the episode consists of the start (the trend in stress likelihood changes from decreasing (−) to increasing, (+), the peak (from + to −) and end time (from − to +). At the peak time, a classification of the episode is made; we set X_t = 2 if the classification is “Stress”, X_t = 1 if “Not Stress” and X_t = 0 is “Unknown”(when too much of the sensor data used for stress classification is missing or is of low quality due to sensor detachment or intermittent loosening); see [17] for details.

The dataset is restricted to user-days for which the duration of a day is at least 12 hours. Each user-day is truncated to 12 hours. This results in 54 user-days of 12 hours each. Three-fold cross validation is used to construct the training and test sets and assess performance. Specifically, user-days of the Minnesota dataset are randomly divided into three approximately equal subsets of user-day’s data. Two subsets are used as the training set and the remaining one subset as the test set. This is repeated 2 further times to allow each subset to play the role of a test set. This reflects the procedure outlined in Figure 1.

5.2.1. Sense2Stop: Smoking Cessation Study.

Performance assessment on the Minnesota smoking study informs expected performance in Sense2Stop [2, 17], an mHealth smoking cessation study currently underway; this study includes a 10-day post-smoking-quit phase in which users may receive a reminder to practice self-regulation exercises installed on the smart phone [8]. These exercises are designed to help users manage their stress as stress is a risk factor for relapse to smoking. Time frequency is every minute during a 12-hour day (T = 720). Sensor data collected from wearable devices matches the Minnesota smoking study (e.g., the same suite of sensors are worn), and the time-varying stress likelihood for each minute is computed in the same manner.

Availability I_t is set to 0 except for the peak time; furthermore, even at peak times, I_t = 0 if a treatment was provided within the prior hour or if self-report assessments (randomly assigned in each of 4-hour window) were requested from the user in the prior 10 minutes. Availability is similarly encoded in the study of the performance of the SeqRTS algorithm using the Minnesota study. Treatment at time t, A_t, is an indicator of whether a reminder is delivered at a time t (e.g., 1 = “deliver reminder” and 0 = “no reminder”). The goal is to provide, on average, 1 treatment at “Stress” and 1.5 treatments at “Not Stress” times per day, and no treatment if “Unknown;” that is, $N_2^{*}=1,N_1^{*}=1.5$ and $N_0^{*}=0$.

5.2.2. SeqRTS.

To design SeqRTS, the training set is used to build the forecasts for both the stress and non-stress episodes. There is a single block per day (i.e. K = 1) and thus, forecasts of the number of available stressed and non-stress episodes in the remaining of the day are required. Forecasts are built separately for stress and non-stress. Specifically, a Poisson regression is first fit using the training set with the outcome being the count of future “Stress” or “Not Stress” episodes and the input features: the remaining time of the day, the numbers of “Stress “, “Not Stress” and the “Unknown” episodes so far in the day and the indicator of lapse. To account for availability, these forecasts are further discounted by a constant (i.e. a guess of the fraction of future available stress/non-stress episodes). Bounds are set to ${ϵ}_L=0.01$ and ${ϵ}_U=0.99$. Next as described in subsection 4.1, the training data is used to select the tuning parameters $\lambda$ and N using Algorithm 2—that is, for each $\lambda$, the parameters N are chosen to achieve the average constraints (an average of 1,1.5 treatments per day at stressed, non-stress times respectively) and then the value of $\lambda$ is chosen such that the probability of receiving at least 1 to at most 5 treatments (across both stress and non-stress episodes) in a day is at least 0.95.

5.2.3. Extended Block Sampling.

Here, the block sampling approach used in EMA setting to handle the risk setting with average constraints is adapted and used as a comparison to SeqRTS. As is customary with EMA, the 12-hour day is split into three four-hour blocks. Three-fold cross validation is applied as above using the procedure outlined in Figure 1. Using the training set, the average numbers of “Stress” episodes within each block in the training set are calculated and then discounted by a constant (to account for availability) to form an estimate of the number of available stress episodes in each block. Denote these numbers by M₁, M₂, M₃. This results in the block sampling method where, in each block, available stress times are randomly selected for treatment with probability (1/3)/M_k in the k-th block at the “Stress” times (recall the goal is to send on average 1 treatment at “Stress” times). The same procedure is applied to “Not Stress” times.

5.2.4. Comparison of SeqRTS and Extended Block Sampling.

To compare SeqRTS with Extended Block Sampling, we use the test subset of the Minnesota data set. Since the Minnesota data set does not include all sources of un-availability, to more accurately represent availability as it occurs in Sense2Stop, we also generate the random self-report assessments (three times per day and randomly selected in each four-block block) and take into account availability constraints; here these are that the reminder messages can occur only after 10 or more minutes following a random self-report assessments and only after 60 or more minutes following a prior reminder message.

Using SeqRTS, we generate 1,000 treatment sequences for each real user-day in the test set. We also use Extended Block Sampling to generate 1,000 treatment sequences for each real user-day in the test set. For each user-day, we compute the average number of treatments at “Stress” and “Not stress” episodes and the percentage of sending 1 to 5 total treatments in a day over the 1,000 treatment sequences for both block sampling and the sequential sampling method. Recall we use 3-fold CV to train then test, thus the results are averaged over the 3 test sets. The results are shown in Figure 4 and Table 1. Recall that our goal is to achieve on average 1.5 reminders at “Not stress” and 1 reminder at “Stress” times and to ensure that with at least 0.95 probability of at least 1 and no more than 5 treatments are provided during the day. SeqRTS meets the desired desired average constraints; the average numbers of treatments at stress and not-stress over all user-days of 1.004 and 1.521. The block sampling method performs similarly in terms of the number of treatments at stress and not-stress times (0.912 and 1.426); however, SeqRTS is able to significantly reduce the variation of the average treatments across all 54 user-days in the test sets. For the “Stress” case, the standard deviations of the average treatments across user-days is 0.557 and 0.364 for extended block sampling and SeqRTS, respectively. For the “Not stress” case, the standard deviations are given by 0.612 and 0.298. The large variation of the average number of treatments for extended block sampling is due to the high variation of number of “Stress” and “Not Stress” times in each block, shown in Table 2. SeqRTS allows us to better achieve the average constraint across the user-days.

Fig. 4.

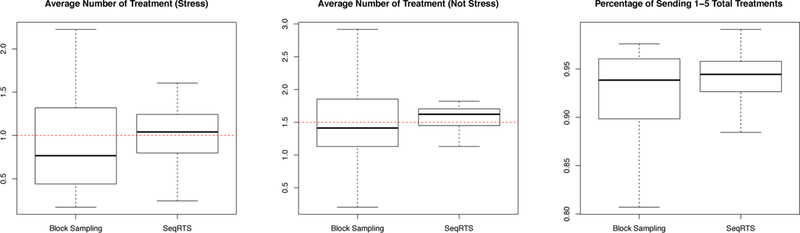
Three-fold cross validation results of Block Sampling and Sequential Risk Times Sampling (SeqRTS) algorithms. The average number of treatments at stress and not-stress episodes and the percentage of sending 1 to 5 total treatments achieved by each user-day in 1,000 runs.

Table 1.

Three-fold cross validation results of Extended Block Sampling (BS) and proposed Sequential Risk Times Sampling (SeqRTS): average number of treatments at “Stress” and “Not stress” times and the percentage of sending 1 to 5 total treatments achieved in each user-day across the 1,000 treatment sequences.

	Min	1st Qu.	Median	Mean	3rd Qu.	Max.
# Treatments at NS (BS)	0.203	1.132	1.411	1.426	1.854	2.917
# Treatments at NS (SeqRTS)	0.275	1.454	1.601	1.521	1.710	1.830
# Treatments at S (BS)	0.172	0.451	0.766	0.912	1.317	2.225
# Treatments at S (SeqRTS)	0.245	0.797	1.037	1.004	1.240	1.705
Prob. of 1–5 Treatments (BS)	0.401	0.902	0.939	0.910	0.961	0.976
Prob. of 1–5 Treatments (SeqRTS)	0.785	0.929	0.947	0.948	0.958	0.991

Table 2.

Summary statistics of the number of “Stress” and “Not Stress” times in each block. MAD: mean absolute deviation.

	Not Stress			Stress
	Block 1	Block 2	Block 3	Block 1	Block 2	Block 3
Mean	8.98	8.37	7.52	1.65	1.59	1.74
MAD	3.91	4.35	3.48	1.51	1.30	1.65

Additionally extended block sampling produces high variance in the total number of treatments in a day (across the stress and non-stress times). The overall percentage of sending at least 1 and no more than 5 treatments in the blocking method is 0.910. SeqRTS controls this probability via the use of λ: the overall percentage is 0.948 as desired. The variations across the user-days is also significantly smaller (see Figure 4).

As discussed in the beginning of this section, we assess whether a method achieves uniform sampling across risk times via the average KL divergence. The results are provided in Figure 5. We see that SeqRTS achieves smaller average KL over all user-days in the case of “Stress” times comparing with extended block sampling (i.e. more uniform distribution of treatment across “Stress” times), but larger in the “Not Stress” times. The latter is mainly due to the quality of the estimated forecast. This can be seen as follows. We run SeqRTS replacing the forecast of future stress and non-stress episodes by the weighted average of the estimated forecast from the model and the oracle (i.e. the true number of the future “Stress” and “Not Stress” episodes). As we can see in Figure 6, the average KL can be significantly reduced comparing with extended block sampling when we have high quality forecasts. The results of the average number of treatments and the variation in the total treatments are similar using these hypothetical forecasts and thus are omitted.

Fig. 5.

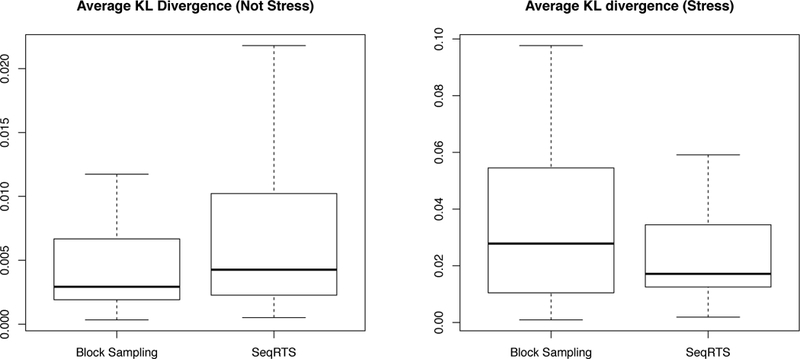
Three-fold cross validation results of Block Sampling and Sequential Risk Times Sampling (SeqRTS) algorithms. The average KL divergence at stress and not-stress episodes by each user-day in 1,000 runs.

Fig. 6.

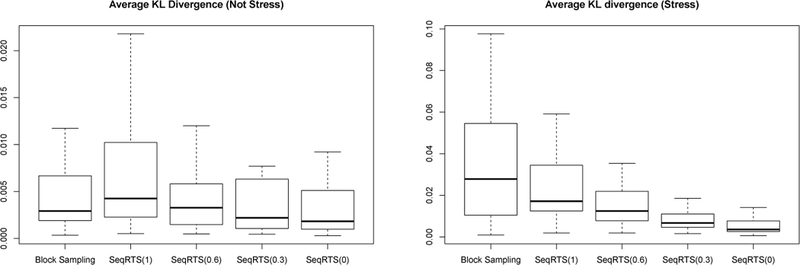
Three-fold cross validation results of Block Sampling (BS) and Sequential Risk Times Sampling algorithms (SeqRTS(w)) method using hypothetical forecasts : the average KL divergence at “Stress” and “Not Stress” episodes by each user-day in 1,000 runs. w is the proportion of the estimated forecasts in the constructing the hypothetical forecasts used in SeqRTS

5.3. HeartSteps V1: Physical Activity Study

We use data from HeartSteps V1 [10] to design HeartSteps V2. HeartSteps V1 is a mobile health study focused on promoting physical activity among sedentary individuals. We restrict to the user-days in HeartSteps V1 for which there is at least one five-minute window with step count. This avoids using days in which the user may not be wearing the wrist sensor. We restrict to 9AM to 9PM as this range had the most reliable step count data. This results in 1,543 12-hour user-days. In both SeqRTS and the Extended Blocked Sampling, we use 3 even blocks (i.e., K = 3) each of size 4 hours. Descriptive statistics for these blocks are provided in Table 3. The fact that the mean absolute deviation is smaller than the mean number of sedentary times indicates that there are a small number of days with blocks that include very high numbers of sedentary times as compared to most blocks. This occurs for all 3 blocks in the day. Additional descriptive statistics for these blocks are provided in Table 4. Here, the average number of sedentary times is computed per user-block. The mean and mean absolute deviation of these averages is reported. Table 4 indicates high between-person variation in the mean number of sedentary times across users.

Table 3.

Summary statistics of the number of “Sedentary” times in each block. MAD: mean absolute deviation.

	Block 1	Block 2	Block 3
Mean	35.91	33.24	34.14
MAD	20.76	19.27	19.27

Table 4.

Summary statistics for mean number of “Sedentary” times per user in each block.

	Block 1	Block 2	Block 3
Mean	35.69	33.01	33.91
MAD	7.17	7.22	8.47

We use five-fold cross validation to design both methods and contrast them. In particular, we randomly divide into five subsets of user-day’s data. A single test subset is extracted and the remaining four subsets of HeartSteps V1 are used as the training set. Below we repeat the training and testing 5 times so as to allow each subset to play the role of a test set. This is in line with the procedure outlined in Figure 1.

5.3.1. HeartSteps V2: Physical Activity Study.

In the upcoming HeartSteps V2, patients with blood pressure in the stage 1 hypertension range (120–130 systolic) will be provided a wrist tracker and a mobile phone application intended to help them maintain recommended levels of physical activity over the long term. For the anti-sedentary suggestions in HeartSteps V2, time frequency is every five minutes within a 12-hour day (T = 144). Only a subset of these times are risk times. The binary risk factor X_t is set to 1 if the user has less than 150 steps within the prior 40 minutes; otherwise the user is classified as “Not Sedentary” (X_t = 0). The risk times are the times with X_t = 1. The treatment, A_t is an indicator of whether an anti-sedentary message is sent at risk time t (e.g., 1 = “Send Message” and 0 = “Provide Nothing”). If, at a risk time, the user received an anti-sedentary message within the past hour, then availability I_t is set to 0, otherwise I_t = 1. In this study, the goal will be to provide on average 1.5 anti-sedentary messages per day when X_t = 1 and no anti-sedentary message when X_t = 0; that is, $N_1^{*}=1.5$ and $N_0^{*}=0$ in (1).

5.3.2. SeqRTS.

To design the SeqRTS algorithm, training data is extracted from HeartSteps V1 in order to tune parameters, and build the forecasts of the number of available sedentary times during the remaining time in a block. The forecast (g(1|H_t)) is constructed based on the concept of a “run”. When X_t = 1, it is likely that X_t+1 = 1 since the prior 40-minute step count is used to define X_t+1. Since X_t and X_t+1 have 35-minute overlap if X_t = 1 then X_t+1 is likely to be 1 as well. Specifically, using the training set we build a non-parametric forecast that is a function of run length and the current hour.

The tuning parameter ${\tilde{N}}_1$ is selected to achieve the desired average constraint (N₁ = 1.5) in the training step. The tuning parameter $\lambda$ is set to 0 because the scientific team decided the variation in the number of treatments was not too high. The rationale was that the anti-sedentary messages cause low user burden and, therefore, will not substantially aggravate the user. Figure 7 shows the expected number of times the user will receive 4 or more anti-sedentary messages is very low. These messages are low burden in comparison to the reminders in Sense2Stop; therefore, the scientific team decided the variability when $\lambda =0$ was not an issue. Bounds are set to ${ϵ}_L=0.005$ and ${ϵ}_U=0.995$.

Fig. 7.

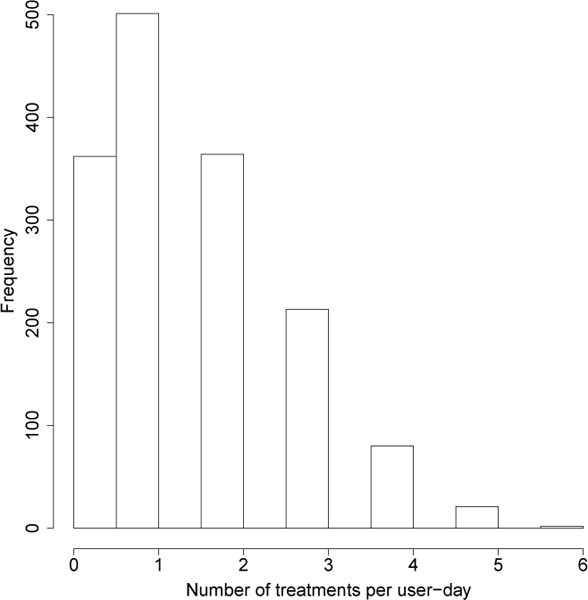
Histogram of user-day number of treatments from a single iteration through the training data, showing the chance of receiving more than 4 treatments per day is low.

5.3.3. Extended Block Sampling.

The blocking sampling algorithm as described in section 5.2.3 was implemented using the three four-hour blocks.

5.3.4. Comparison of SeqSeqRTSRTS and Extended Block Sampling.

To compare SeqRTS with Extended Block Sampling, we use the test subsets from HeartSteps V1. For each user-day in the test subset, we compute the average number of treatments at sedentary times in a day over the 1,000 treatment sequences for both extended block sampling and SeqRTS. Recall we use 5-fold CV to train then test, thus the results are averaged over the 5 test sets.

The results are shown in Figure 8 and Table 5. Recall the goal is to achieve on average 1.5 messages at sedentary times per day. Using the SeqRTS algorithm, the average numbers of treatments at sedentary times (averaged over all user-days) is 1.53, which achieves the desired average constraints. The block sampling method does achieve the desired number of treatments (on average 1.45), with slightly higher variation across user-days. However, when examining averages per user rather than user-day, the block sampling method has much higher variation across users. This is likely due to high between-person variability in the number of of sedentary times in each block as illustrated by Table 4.

Fig. 8.

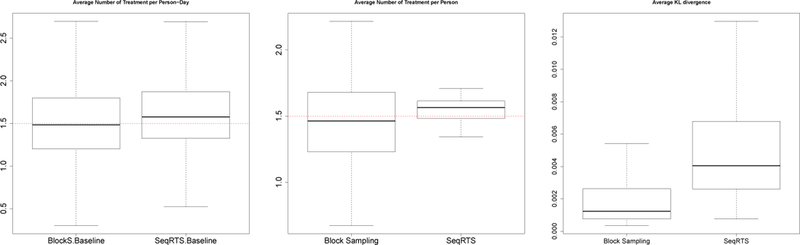
Five-fold cross validation results of Extended Block Sampling and SeqRTS. The average number of treatments (Left) and the average KL divergence (Right) at sedentary times averaged 1,000 treatment sequences. The average number of treatments per user (Middle), which takes the average across 1,000 treatment sequences and days

Table 5.

Five-fold cross validation results of Block Sampling and Sequential Risk Times Sampling (SeqRTS) algorithms: average number of treatments at sedentary times averaged across user-days/users and the 1,000 treatment sequences.

Average over	Method	Min	1st Qu.	Median	Mean	3rd Qu.	Max.
User-day	Block sampling	0.00	1.07	1.42	1.45	1.82	2.80
	SeqRTS	0.00	1.30	1.51	1.51	1.79	2.39
User	Block sampling	0.67	1.23	1.46	1.45	1.67	2.21
	SeqRTS	0.99	1.41	1.55	1.51	1.63	1.83

The average KL divergence for each user-day are provided in Figure 8. We see that SeqRTS produces slightly larger average KL over all user-days compared to the block sampling method. Again one can lower the deviation from uniformity by building better forecasts.

6. LIMITATIONS: IMPLEMENTATION AND TUNING

There are several important limitations regarding the proposed SeqRTS approach:

• (1)Non-simulated testing required to assess impact: Validation of the SeqRTS algorithm is preliminary and based on simulated-based testing procedures. The algorithm needs to be tested as an online algorithm within an mHealth study to demonstrate real-life utility. To this end, it is currently being employed in the Sense2Stop study and will be employed in the upcoming HeartSteps V2 study. This data will then be used to complete validation and perform non-simulated testing.
• (2)Initial user checks: To ameliorate any potential issues discussed below, a number of test users can be recruited prior to the start of the upcoming study. This is being performed prior to both Sense2Stop and HeartSteps V2. Test users can help identify software bugs and improve implementation; data from these test users can be used to further update the tuning parameters.
• (3)Prior studies with similar sensor suites: the SeqRTS algorithm requires the prior study to collect data on the risk and availability factors using similar, not necessarily identical, sensor suites. The Minnesota and Sense2Stop studies use the exact same sensor suite; however, HeartSteps V1 used the Jawbone activity tracker, while HeartSteps V2 will use the Fitbit activity tracker. It is only required that the measurement devices have similar measurement-error properties. In situations where this may be violated, additional work is necessary to translate between measurements made via different sensor suites. In settings where no prior study has been completed, a pilot study with a few participants may be run in order to collect preliminary data and inform simple forecasting methods.
• (4)TUNE performed under hypothesis of mild to no treatment effect of intervention components in prior study: The Minnesota study was a no treatment, smoking study, while the HeartSteps V1 study had multiple intervention components. Regardless of whether the prior study included treatments, the randomization design is under the hypothesis of mild to no treatment effects for the upcoming study. Also, some intervention components included in the prior study may be different from those considered in the upcoming study; ignoring potential treatment effects averages over the distribution of risk and availability induced by these intervention components. Therefore, the “no-treatment” model may be off-target. The worst case scenario is that, in the upcoming study, too few or too many treatments will provided on any given day. If there are strong concerns about this, then one can adjust the truncation function to ensure a minimal opportunity to provide treatment.
• (5)Population in prior study may vary: it may be that the prior study is on a different population than the current study. The Minnesota smoking study recruited smokers who reported smoking 10 or more cigarettes per day for the prior 2 years, a high motivation to quit, and willingness to participate in a 4-day observation trial (1 day pre-quit, 3 days post-quit). The Sense2Stop study is recruiting smokers who smoke 1+ cigarettes per day for past year who are willing to try to quit smoking for at least 48 hours during a 15-day quit trial. They must be willing to not use non-cigarette tobacco products or nicotine replacement therapy during the study period. HeartSteps V1 recruited sedentary adults with “regular” daytime jobs, while HeartSteps V2 recruited patients with blood pressure in the stage 1 hypertension range (120–130 systolic). While the populations may differ, if the underlying dynamics of risk and availability factors are similar, then assessing performance using the prior study will give a strong indication of expected performance in the upcoming study.
• (6)Forecasts and prior data: Forecasts were assumed given in order to derive the SeqRTS algorithm. In sections 5.2 and 5.3, forecasting methods were derived using the training data. For the Minnesota smoking study, the forecast was based on a generative model. For HeartSteps V1, a non-parametric method was constructed. In both settings, prior data was small, motivating us to use simple methods to avoid over-fitting. However, forecast complexity can increase substantially as data on additional participants is collected in subsequent studies. Over multiple studies, enough data may be collected to use more advanced forecasting methods (e.g., deep learning algorithms). Precision/recall can be used as informative performance measures to assess relative performance of various forecasting methods. This is one of the main benefits of the SeqRTS algorithm - the forecasting method is explicitly incorporated as a subcomponent that can be improved.
• (7)Uniformity assessment via Kullback-Leibler divergence: Kullback-Leibler divergence is an entropy-based metric which quantifies the similarity between two distributions. Here, we have used it to measure similarity to the marginal uniform distribution. However, KL-divergence suffers from lack of specificity. Therefore, other measures that are more standard like precision and recall may be used in assessment. Note that precision and recall are typically designed for the classification context. Our current setting is decision to treat or not. While both are binary processes, they are distinct scientific problems. Thus, precision and recall must be properly redefined to yield appropriate metrics when the goal is assessment of uniformity of treatment across available risk times.
• (8)User burden and choice of $\lambda$: In HeartSteps V1, the tuning parameter $\lambda$ is set to 0 because the scientific team decided the variation in the number of treatments was not too high. The rationale was that the anti-sedentary messages cause low user burden and, therefore, will not substantially aggravate the user. In mHealth intervention studies, setting $\lambda$ to 0 is justifiable when the intervention option is not likely to substantially aggravate the user. However, in intervention studies like Sense2Stop, the scientific team may believe the intervention will cause high user burden. In such settings, the scientific team may decide the variability when $\lambda =0$ is too high and investigate reducing variability in the number of interventions by setting $\lambda >0$.

7. CONCLUSION AND FUTURE WORK

In this paper, we have proposed a new approach to design the timing of just-in-time treatments when there is a soft constraint on the number of treatments per day. We have illustrated how one selects tuning parameters so as to achieve the constraint, yet maintain an acceptable level of variance in number of treatments delivered. If there is within- and between-user variation in the risk pattern and this variability is well explained by (time-varying) covariates, then the use of forecasts based on these time-varying covariates allows SeqRTS to sample risk times with a uniform distribution thus providing data that allows scientists to learn if and in which contexts the treatment is effective. Extended block sampling achieves uniform sampling of the risk times when there is minimal within- and between-user variation in the risk pattern.

The micro-randomized trial [10] is a previously introduced experimental design to assess if and in which contexts treatment is effective. Treatment randomization is allowed to depend on time, but cannot depend on the entire observable history. Therefore, the micro-randomized trial could not achieve the soft constraint across risk levels. The SeqRTS algorithm improves upon the micro-randomized trial, allowing us to ensure sufficient randomizations at each risk level. In particular, some risk levels occur more rarely and thus to ensure sufficient treatment exposure at these values, the SeqRTS algorithm stratifies randomization [2].

We foresee several opportunities for future work. First, viewing SeqRTS as a warm-start, one could update the tuning parameters and the forecasts as information accumulates on a user during the study. This personalization might occur by making the tuning parameters person-specific. Second, depending on the amount of training data, a variety of forecasting algorithms might be considered including deep learning algorithms, such as the Long Short Term Memory algorithm; these methods would facilitate the investigation of how to combine/fuse multiple data streams (stress, location, eating, etc.) in forecasts and thus enable prediction of more complex risk variables. Finally, there it would be interesting to develop a version of the SeqRST algorithm that includes assumptions about non-zero treatment effects.