Emotionally Aversive Cues Suppress Neural Systems Underlying Optimal Learning in Socially Anxious Individuals

Abstract

Learning and decision-making are modulated by socio-emotional processing and such modulation is implicated in clinically relevant personality traits of social anxiety. The present study elucidates the computational and neural mechanisms by which emotionally aversive cues disrupt learning in socially anxious human individuals. Healthy volunteers with low or high trait social anxiety performed a reversal learning task requiring learning actions in response to angry or happy face cues. Choice data were best captured by a computational model in which learning rate was adjusted according to the history of surprises. High trait socially anxious individuals used a less-dynamic strategy for adjusting their learning rate in trials started with angry face cues and unlike the low social anxiety group, their dorsal anterior cingulate cortex (dACC) activity did not covary with the learning rate. Our results demonstrate that trait social anxiety is accompanied by disruption of optimal learning and dACC activity in threatening situations.

SIGNIFICANCE STATEMENT Social anxiety is known to influence a broad range of cognitive functions. This study tests whether and how social anxiety affects human value-based learning as a function of uncertainty in the learning environment. The findings indicate that, in a threatening context evoked by an angry face, socially anxious individuals fail to benefit from a stable learning environment with highly predictable stimulus–response–outcome associations. Under those circumstances, socially anxious individuals failed to use their dorsal anterior cingulate cortex, a region known to adjust learning rate to environmental uncertainty. These findings open the way to modify neurobiological mechanisms of maladaptive learning in anxiety and depressive disorders.

Introduction

Economics, psychology, and neuroscience have often assumed that emotions compete with reason during decision-making (Cohen, 2005; Kahneman, 2011). Recent theories challenge this notion, suggesting that in fact emotions are deeply embedded within decision-making computations (Phelps et al., 2014; Lerner et al., 2015). For instance, recent work has shown that trait-anxiety and stress sensitivity influence learning rate, a quantity reflecting the rate at which decision values are updated by new information (Browning et al., 2015; de Berker et al., 2016). These observations are in line with older descriptive studies suggesting that emotions modulate cognitive flexibility (Dreisbach and Goschke, 2004; van Steenbergen et al., 2010). Although recent studies have revealed neural correlates of dynamic learning rate (Behrens et al., 2007, 2008; Li et al., 2011), particularly in the dorsal anterior cingulate cortex (dACC; Behrens et al., 2007, 2008), the computational and neural mechanisms by which emotional cues and emotion-related traits modulate learning rate are unknown.

Psychological models of conditioning, such as Rescorla–Wagner (Rescorla et al., 1972), suggest that animals learn by computing prediction errors. Such errors are positive when an outcome (reward or punishment) is better than expected and negative when the outcome is worse than expected. According to these models, animals learn by updating their expectation in proportion to the prediction error multiplied by a learning rate. In Rescorla–Wagner models, the learning rate is assumed to be a constant parameter between zero and one. Models of associative learning, such as Pearce–Hall (Pearce and Hall, 1980), however, suggest that animals learn stimulus–outcome associations by tracking associability, a quantity reflecting the extent to which each cue has previously been accompanied by surprise (unsigned prediction errors). This quantity guides animals' attention toward cues with large associability. According to these models, the associability signal gates the amount of future learning about the cue on the basis of whether it has been a reliable or poor predictor of reinforcement in the past. Bayesian or temporal difference models proposed for learning in uncertain environments essentially combine the key features of both accounts, in which error-driven learning depends on a dynamic learning rate closely resembling the notion of associability (Behrens et al., 2007, 2008; Li et al., 2011; Iglesias et al., 2013). These models indicate that when the environment is highly surprising, the learning rate should be higher allowing expectations to get updated quickly. This causal inference about changes in the environment might be particularly disrupted in anxiety and depressive disorders, which are associated with self-blame symptoms. As noted by Beck (1967), self-blame in a depressed patient “expresses a patient's notion of causality”. In other words, in an uncertain environment, these patients might attribute negative outcomes to their own actions instead of the stochasticity of the environment and change their decisions frequently. This view is consistent with theories suggesting that emotion-related traits modulate associability tracking in uncertain environments (Paulus and Yu, 2012; Mason et al., 2017). Relatedly, a recent study has reported that trait anxiety is negatively correlated with the ability to adjust learning rate in uncertain environment (Browning et al., 2015). However, the neural mechanisms by which learning rate is related to trait anxiety are still unknown. Furthermore, it is not clear whether emotionally aversive cues in the environment mediate such relation.

Here, we combine functional neuroimaging and computational modeling to investigate whether and how emotions modulate learning rate and whether those modulations depend on individual variation in the personality trait of social anxiety. A hybrid computational model was considered, in which error-driven learning depends on a learning rate containing both dynamic-, similar to Pearce–Hall, and constant-, similar to Rescorla–Wagner, components. Model-based analysis of task-related fMRI data was conducted to investigate the neural correlates of dynamic learning rate in the dACC, a region previously shown to encode dynamic learning rate in uncertain environments (Behrens et al., 2007, 2008). We hypothesized that the dynamic adjustment of learning rate and its neural correlates depend on emotional state and trait social anxiety.

Materials and Methods

Participants

Forty-five female volunteers gave written informed consent approved by the local ethical committee (“Comissie Mensgebonden Onderzoek”, Arnhem-Nijmegen) and participated in the study. Only women have been recruited to have a relatively homogeneous sample in terms of emotional reactivity (Koch et al., 2007; Domes et al., 2010). Exclusion criteria were claustrophobia; neurological, cardiovascular, or psychiatric disorders; regular use of medication or psychotropic drugs; heavy smoking; and metal parts in the body. Participants were selected from an online pool of students based on their scores on the Liebowitz social anxiety scale (Liebowitz, 1987). Thus, participants were recruited to have either low (not >13, n = 23) or high scores (not <25, n = 22) on this test. One participant did not finish the experiment because of headache (from the high-score group). Data from all other 44 participants were analyzed (all right-handed, mean age of 20.7). We used data from a previously published study (Ly et al., 2014) focused on the association between emotional biasing of go/no-go responding and individual differences in social avoidance. Unlike the current study, Ly et al. (2014) did not consider any form of learning and only focused on behavioral inhibition.

Probabilistic reversal learning task

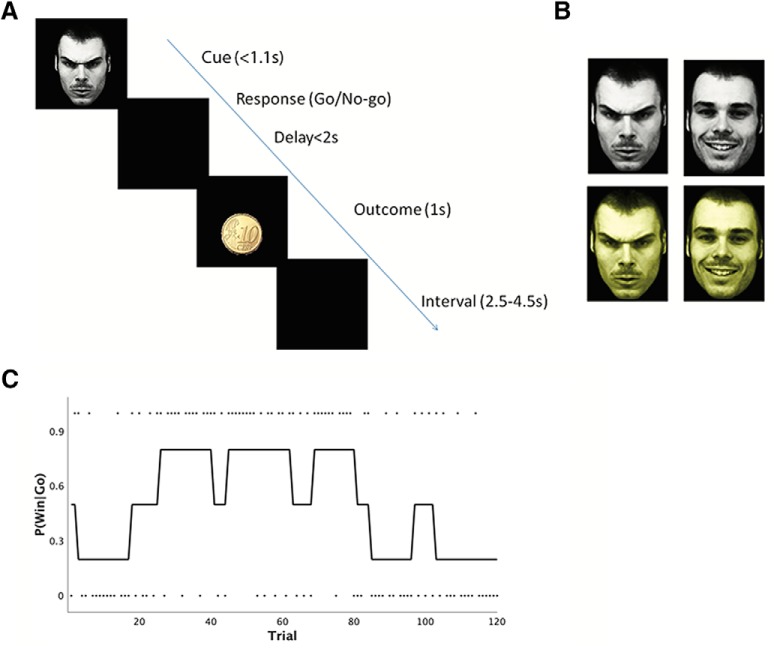
Each participant completed 480 trials of a probabilistic learning task in the scanner. Each trial started with a face cue (happy or angry) presented on a color frame indicating the type of outcome valence (reward or punishment) at the end of the trial. Thus, there were four trial types in a 2 × 2 factorial design with factors emotion (happy or angry) and valence (reward or punishment). There were 120 trials per trial type. Participants were instructed that the combination of emotional content of the face cue and color frame distinguished the four trial types and that they had to learn the optimal response for each of the four cue-types separately. The response–outcome contingency was probabilistic and independent for each trial type. The response–outcome contingency was reversed several times for each trial type, resulting in different degree of volatility in the course of experiment, while remaining counterbalanced across trial types. Specifically, each participant completed three sessions, with a 1 min break in between the sessions. Each session consisted of 160 trials, with 40 trials per trial type. For each trial type within a session, the probability of a positive outcome given a go response could take one of the following combinations in two consecutive blocks: (1) 0.5, 0.2, 0.5, 0.2; (2) 0.5, 0.2, 0.5, 0.8; and (3) 0.5, 0.8, 0.5, 0.8, where each session was associated with one of these combinations. The blocks with probability of 0.5 were short blocks with average length of five trials, and other blocks were long blocks with average length of 15 trials.

Emotional stimuli were adult Caucasian faces from 36 models (18 men) taken from several databases (Ekman and Friesen, 1976; Matsumoto and Ekman, 1988; Lundqvist et al., 1998; Martinez and Benavente, 1998). Model faces were trimmed to exclude influence from hair and non-facial contours (van Peer et al., 2007; Roelofs et al., 2009). Model identity was counterbalanced, such that the model occurred equally often for each trial type. The color frame (yellow or gray) indicating the possibility of reward or punishment was also counterbalanced across participants. On each trial, one of the face cues was presented centrally. Participants were then allowed to make a response 100 ms after cue onset, where they were required to make either a go or a no-go response within 1000 ms. If no response was made within 1000 ms, then a no-go response was recorded. After a response–outcome delay of maximally 2000 ms (depending on the response time), the outcome was presented for 1000 ms (+10 cents for reward, −10 cents for punishment, and 0 cents for omitted reward or avoided punishment). The intertrial interval was jittered (2500–4500 ms).

The relatively long time window for responding (1000 ms) ensured that no-go responses are not because of failure in making a go response. To illustrate this point, we tested each participant response time separately for go responses in every trial type. This test revealed that for all participants and all trial types, response times are significantly <1000 ms window (t test, all p values <10⁻¹⁰).

Computational models

In this section, we describe the computational learning models compared in this study. A common choice model was then used in combination with each of these learning models to predict the probability of choices, which will be presented later.

All learning models track expected value x_t on trial t of each stimulus and action pair. Thus, if s_t is the stimulus presented on trial t, c_t is the choice taken and o_t is the received outcome, all models compute a prediction error signal and update the corresponding expected value:

where δ_t is the prediction error on trial t and α_t is the learning rate representing the degree to which the prediction error influences the current expected value. The learning models are different in how they conceptualize the learning rate.

M1: Rescorla–Wagner model.

This model (Rescorla et al., 1972) is the simplest model among the tested models, containing only one free learning parameter as constant learning rate, κ, bounded in the unit range, [0 1]. Therefore, for this model, α_t is equal to κ on all trials.

M2: hybrid model.

This model and its variant (M4) are the main models of interest in this study. The hybrid model quantifies associability, A_t, and constructs the learning rate accordingly in two steps. First, it constructs K_t:

where w is the weight parameter constrained to lie in the unit range. Therefore, K_t is a weighted combination of a constant- and a dynamic-component according to w. If w = 0, the dynamic component, A_t, has no influence on K_t and therefore the learning rate is a constant. Conversely, if w = 1, K_t has no constant component and therefore it is fully dynamic. Note that, regardless of the value of w, the maximum possible value (i.e., the scale) of K_t is 1. The learning rate is then defined as follows:

where κ is another free parameter, which indicates the scale of learning rate. Thus, for any value of κ, the learning rate on every trial lies between 0 and κ.

In this model, the associability also gets updated. On every trial, two factors influence the associability update, similar to update rules in Bayesian dynamic models such as Kalman filter (Daw et al., 2006). First, similar to the gain in the Bayesian models (e.g., Kalman gain), associability gradually reduces because of random diffusion:

Second, after observing the outcome of the trial, the associability gets updated according to the surprise (i.e., squared prediction error):

Note that, on every trial, the learning rate, α_t, depends on A_t, which itself depends on squared prediction errors from the past trials, but not the current one. Therefore, δ_t is not double counted in the value update.

Together, this learning model contains three free learning parameters, κ, w and λ, which are all constrained to lie in the unit range. Moreover, because squared prediction errors in this task are between 0 and 1 (as outcomes are binary), associability will also always lie in the unit range. Consequently, learning rates will always be between 0 and 1 ensuring that expected values are well defined for any set of parameters.

M3: reinforcement learning model.

The reinforcement learning model of Li et al. (2011) model also combines error-driven learning with an associability signal. The important difference between this model and M2 is that, whereas in M2 the learning rate is a weighted combination of a dynamic and a constant component, M3 only contains a dynamic component. Also, the way that M3 quantifies surprise is slightly different compared with the M2 by updating associability according to the absolute value of previous prediction error (instead of squared value of prediction error).

where μ and κ are free parameters (bounded in the unit range) determining the step size for updating associability and the scale of learning rate, respectively.

M4: hybrid emotion-specific w model.

This model is identical to M2 except that it assumes two different weight parameters, w_a and w_h, for angry and happy trials, respectively. Therefore, this model has one more free parameter compared with M2.

M5: hybrid emotion-specific κ model.

This model is also identical to M2 except that it assumes two different overall scale, κ, parameters for angry and happy trials.

M6: hybrid valence-specific w model.

This model is also identical to M2 except that it assumes two different weight, w, parameters for reward and punishment trials.

Choice model.

Each of the learning models was combined with a choice model to generate probabilistic predictions of choice data. Expected values were used to calculate the probability of actions, a₁ (go response) and a₂ (no-go response), according to a sigmoid (softmax) function:

where β is the decision noise parameter encoding the extent to which learned contingencies affect choice (constrained to be positive) and b(s_t) is the bias toward a₁ because of the stimulus presented independent from learned values. The bias is defined based on three free parameters, representing bias because of the emotional content (happy or angry), b_e, bias because of the anticipated outcome valence (reward or punishment) cued by the stimulus, b_v, and bias because of the interaction of emotional content and outcome, b_i. No constraint was assumed for the three bias parameters. For example, a positive value of b_e represents tendencies toward a go response for happy stimuli and for avoiding a go response for angry stimuli (regardless of the expected values). Similarly, a positive value of b_v represents a tendency toward a go response for rewarding stimuli regardless of the expected value of the go response. Critically, we also considered the possibility of an interaction effect in bias encoded by b_i. Therefore, the bias, b(s_t), for the happy and rewarding stimulus is b_e + b_v + b_i, the bias for the angry and punishing stimulus is −b_e − b_v + b_i, the bias for the happy and punishing stimulus is b_e − b_v − b_i and the bias for the angry and rewarding stimulus is −b_e + b_v − b_i.

Model fitting

We fitted parameters in the infinite real-space and transformed them to obtain actual parameters fed to the models. Appropriate transform functions were used for this purpose: the sigmoid function to transform parameters bounded in the unit range (the learning parameters in all models) and the exponential function to transform the decision noise parameter in the choice model. No transformation was needed for the bias parameters of the choice model as they were not bounded.

Free parameters of each model were estimated in two stages. In the first stage, a set of parameters, θ_MAPⁿ, maximizing log-likelihood of data plus log-prior [maximum a posteriori (MAP)] was estimated for every participant separately (n is the index of participant) similar to our previous study (Piray et al., 2016). A wide Gaussian prior was assumed for all parameters (with 0 mean and a variance of 6.25). This initial variance is chosen to ensure that the parameters could vary in a wide range with no substantial effect of prior. Specifically, the log-effect of this prior is less than one chance-level choice (i.e., log0.5) for any value of w between 0.05 and 0.95. This is also the case for all other free parameters constrained in the unit range. A nonlinear derivative-based optimization algorithm (as implemented in the fminunc routine in MATLAB, MathWorks) was used for fitting. To overcome bias of the optimization algorithm to the initial point, the optimization was repeated multiple times and the best set of parameters was selected.

In the second stage, a hierarchical fitting procedure was used to fit the models to participants' choices. An expectation-maximization algorithm was used for optimizing group and individual parameters in an iterative fashion, with Laplace approximation for approximating the posterior distribution (Huys et al., 2011). This method estimates the mean and the variance of parameters across all participants (group parameters) in the first step. In a subsequent step, that mean and variance is used to define a normal prior distribution of parameters and to estimate parameters of each individual participant using Laplace approximation. This procedure is then continued iteratively to reach convergence. Group parameters was initialized according to the mean and variance of the individual parameters, θ_MAPⁿ, fitted in the first stage. This procedure regularizes individual fitted parameters according to group parameters, thereby decreases fitting noise and protects against outliers. The final estimated values for the group parameters, Θ, were used to generate the regressors used in the fMRI analyses, as they are less biased by fitting noise. For details of the hierarchical fitting procedure, see Huys et al. (2011).

All codes used for fitting are publically available online (https://github.com/payampiray/cbm_v0). The Gramm plotting tools (Morel, 2018) were used for visualization.

Model selection

We used a Bayesian model comparison approach to assess which model better captures participants' choices. This approach selects the most parsimonious model by quantifying model evidence, a metric which balances between model fits and complexity of the model (MacKay, 2003). Notably, this procedure penalizes complexity induced by both group and individual parameters using Laplace approximation and Bayesian information criterion, respectively. For each model fitted using the hierarchical fitting procedure, the log-model evidence is penalized for complexities at both individual and group levels, which can be quantified using Laplace approximation and Bayesian information criterion, respectively (Piray et al., 2014):

where Dⁿ is the set of choice data for the nth participant θⁿ, is the fitted individual parameters for nth participant, Θ and Σ is the mean and variance for the group distribution, respectively, d is number of free parameters of the model, N is the number of participants, and |H_n| is the determinant of the Hessian matrix of the log-posterior function at θⁿ. The log-likelihood function is the predicted probability of choice data given the model and parameters defined as log p(Dⁿ|θⁿ) = Σ_tlog p_t(c_t), where the sum is over all trials. Therefore, the first term on the right-hand side of the equation is how well the model predicts data. The sum of the next three terms together is the penalty because of individual parameters. The last term represents the penalty approximated for 2d (mean and variance together) group parameters as quantified using Bayesian information criterion.

fMRI data acquisition and preprocessing

Whole-brain imaging was performed on a 3T MR scanner (Magnetom Trio Tim, Siemens Medical Systems) equipped with a 32-channel head coil using a multiecho GRAPPA sequence [Poser et al., 2006; repetition time (TR): 2.32 ms, echo times (TEs): 9.0/19.3/30/40 ms, 38 axial oblique slices, ascending acquisition, distance factor: 17%, voxel size 3.3 × 3.3 × 2.5 mm, field-of-view (FoV): 211 mm; flip angle, 908]. At the end of the experimental session, high-resolution anatomical images were acquired using a magnetization prepared rapid gradient echo sequence (TR: 2300 ms, TE: 3.03 ms, 192 sagittal slices, voxel size 1.0 × 1.0 × 1.0 mm, FoV: 256 mm).

Given the multiecho GRAPPA MR sequence (Poser et al., 2006), the head motion parameters were estimated on the MR images with the shortest TE (9.0 ms), because these images are the least affected by blood oxygenation level-dependent (BOLD) signals. These motion-correction parameters, estimated using a least-squares approach with six rigid body transformation parameters (translations, rotations), were then applied to the four echo images collected for each excitation. After spatial realignment, the four echo images were combined into a single MR volume using an optimized echo weighting method (Poser et al., 2006). Noise effects in data were removed using FMRIB's ICA-based Xnoiseifier tool, which uses independent component analysis (ICA) and classification techniques to identify noise components in data (Salimi-Khorshidi et al., 2014). Other preprocessing steps were performed in SPM12. The T1-weighted image was spatially coregistered to the mean of the functional images. The fMRI time series were transformed and resampled at an isotropic voxel size of 2 mm into the standard Montreal Neurological Institute space using both linear and nonlinear transformation parameters as determined in a probabilistic generative model that combines image registration, tissue classification, and bias correction (i.e., unified segmentation and normalization) of the coregistered T1-weighted image (Ashburner and Friston, 2005). The normalized functional images were spatially smoothed using an isotropic 6 mm full-width at half-maximum Gaussian kernel.

Statistical analysis of imaging data

General linear model (GLM) was used to model effects at the single-subject level (first-level analysis). Four sets of four regressors, each containing one regressor per trial type, were considered: one set was time-locked to the visual presentation of cues; one set was time-locked to the visual presentation of outcomes; one set was parametrically modulated by prediction error and time-locked to the presentation of the trial outcome; one set was parametrically modulated by dynamic learning rate and time-locked to the presentation of the trial outcome. Group parameters obtained through the hierarchical fitting procedure, Θ, were used to generate these signals. Twelve motion regressors representing six motion parameters obtained from the brain-realignment procedure and their first derivative were also included.

Contrasts of interests were estimated at the subject-level. These contrast images were then used in a second-level GLM to make inference at the group level (t test). The region-of-interest analysis in the dorsal anterior cingulate was performed in anatomically defined mask of the rostral cingulate motor area, which has been shown to correlate with learning rate and has distinct connectional fingerprints. The rostral cingulate motor area mask was created based on a diffusion-parcellation atlas of human medial and ventral frontal cortex (thresholded at p < 0.25; Neubert et al., 2015).

Results

Forty-four participants performed a probabilistic learning task. Participants were selected from an online pool of students based on their scores on the Liebowitz social anxiety scale (Liebowitz, 1987). Thus, participants were recruited to have either low (not >13) or high scores (not <25) on this test. Participants were accordingly divided into two groups with low (n = 23, mean = 8.26, SE = 0.76) or high (n = 21, mean = 31.00, SE = 1.37) social anxiety.

In the experiment (Fig. 1), participants were presented with validated images of faces (happy or angry) and were asked to make either a go or a no-go response (i.e., press a button, or withhold a button press, respectively) for each of these facial cues to obtain monetary reward or avoid monetary punishment. There were four trial types: happy face–reward outcome trials, happy punishment, angry reward, and angry punishment trials. Participants were also informed about outcome valence at the start of each trial by presenting the face image in a background color (yellow or white) indicating whether, at the end of a trial, a win outcome consisted of obtaining a reward or avoiding a punishment. Crucially, the response–outcome contingencies for the cues were probabilistic and manipulated independently, and reversed after a number of trials, varying between 5 and 15 trials, so that the experiment consisted of a number of blocks with varying trial length (Fig. 1C). Within each block, the probability of a win was fixed. There were matched numbers of action–outcome contingency reversals across trial types, with 120 trials in each of the four trial types (see Materials and Methods for details).

Figure 1.

Probabilistic reversal learning task. A, Timeline of the task. Participants had to respond (either go or no-go) after a face cue was presented. A probabilistic outcome was presented following a delay. Importantly, the presented cues were used as conditioned stimuli and the optimal response is a function of the probability of a win given a go, which varied across trials, independent of the emotional content of the cue (C). B, There were four different trial types in the task. The cue of each trial could vary in emotional content (an angry or happy face) and in color (gray, yellow). The color indicates whether the outcome of a trial is a reward or punishment. C, An example of probability sequence of win given a go response for one of the four trial types. The dots show the actual feedback seen by the participant, which are drawn from this probability distribution. Probability of a win given the no-go response is the reverse of the probability of a win given the go response (e.g., when probability of a win given go is 0.8, probability of win given no-go is 0.2). Note that the probability sequence (and thus the optimal response) is reversed multiple times for each cue. The underlying probability sequence is manipulated independently for each cue.

Participants learned the task effectively: performance quantified as the number of correct decisions given the true underlying probability was significantly higher than chance across the group (t₍₄₃₎ = 14.68, p < 0.001). Importantly, participants responded to reversals. As Figure 2 shows, their performance was approximately at chance level immediately after reversals and improved slowly for all trial types and both type of responses. Note that, as Figure 2 shows, the effects of reversal learning on performance is not different between go and no-go responses as the slope of the two curves is not substantially different.

Figure 2.

Performance after reversals. Data has been shown separately for each trial type and response type (go vs no-go). Performance was about the chance level immediately after reversal and improved over the course of learning. For each participant, a learning curve is defined by averaging performance after multiple reversals occurred for the corresponding trial type and response type. Mean learning curve across all participants and corresponding standard error of the mean are plotted. Note that the x-axis displays trials after reversals (reversal occurred at trial 0). HR, Happy and reward trial type; HP, happy and punishment trial type; AR, angry and reward trial type; AP, angry and punishment trial type.

The emotional cues did not influence overall task performance (t₍₄₃₎ = −0.37, p = 0.71), nor participants' bias toward go responses (t₍₄₃₎ = −1.39, p = 0.17). However, longer latencies of go responses following the presentation of angry face cues relative to happy face cues indicated that participants did process the emotional content of those cues (t₍₄₃₎ = 3.72, p < 0.001). Latencies of go responses, however, did not vary as a function of social anxiety (t₍₄₃₎ = 0.68, p = 0.5).

Emotional cues modulate adaptive learning rate

We tested whether participants adjusted their learning rate dynamically according to the history of surprises. First, we considered a Rescorla–Wagner model in which expected value is updated by the product of prediction errors and a constant learning rate (Model M1). We then focused on assessing the additional explanatory power of a class of an augmented hybrid Pearce–Hall Rescorla–Wagner models in which the learning rate depends on another variable, K_t, that combines the learning rate of Rescorla–Wagner with that of Pearce–Hall model. The dynamic component of K_t was adjusted according to the history of surprises (or sample variance equal to squared prediction error), similar to the Pearce–Hall associability rule.

Therefore, we built a model (Model M2) in which K_t is a weighted combination of a constant- and a dynamic-component according to a weight parameter, w. The weight parameter, w, indicates the degree to which this dynamic associability component influences on K_t and thereby contributes to the learning rate. If w = 0, the dynamic component has no influence on K_t and therefore the learning rate is a constant. Conversely, if w = 1, K_t has no constant component and therefore the learning rate is fully dynamic.

On every trial, the product of K_t with another free parameter, κ, indicates the learning rate on that trial, in which κ indicates the overall scale of learning rate (also constrained to lie in the unit range). Thus, whereas w indicates the degree to which learning rate is changing over time, κ determines the maximum of learning rate. In other words, on every trial, learning rate lies between zero and κ. In sum, this augmented hybrid model contains both a model with a constant learning rate (if w = 0) for which the learning rate is always κ, and a model with a fully dynamic learning rate (if w = 1) as special cases.

We used a choice model to generate probability of choice data according to action values derived for each model. Note that the choice model controlled value-independent biases in making or avoiding a go response because of the emotional or reinforcing content of the cues (see Materials and Methods for formal definition). We then used a hierarchical Bayesian estimation algorithm (Huys et al., 2011, 2012; Piray et al., 2014) to obtain parameters of the model given the data. This is an algorithm with the advantage that fits to individual subjects are constrained according to the group-level distribution. For each model, this procedure also calculates its evidence (Piray et al., 2014), a measure of goodness of fit of the model penalized by the complexity of the model (MacKay, 2003), which can be used for Bayesian model comparison. This analysis revealed that the hybrid model explains data better than the simpler model with a constant learning rate (Table 1). As a control analysis, we compared M2 with two other models. First, we considered the reinforcement learning model implemented by Li et al. (2011) (Model M3), which was inferior to our original model. Unlike M2, this reinforcement learning model contains only a dynamic component in its learning rate. Note that whereas the weight parameter of M2 enables us to quantify individual differences in the degree to which participants followed the Pearce–Hall associability rule, M3 does not have such parameter. In other words, under M3, all individuals equally follow the Pearce–Hall associability rule.

Table 1.

Bayesian model comparison

	Model	No. free parameters	Relative log-model evidence
M1	Rescorla–Wagner	5	−15.02
M2	Hybrid	7	−7.13
M3	Li et al. (2011) model	6	−14.78
M4	Hybrid emotion-specific w	8	0
M5	Hybrid emotion-specific κ	8	−7.77
M6	Hybrid valence-specific w	8	−8.85

For each model, differential log-model evidence is shown. Higher values indicate more evidence in favor of the model. The hybrid model with emotion-specific w (M4) has the highest Bayesian model evidence among all models. Note that models are only different in the number of learning parameters. Additionally, all models contain four parameters for generating choice including three value-independent biases in making a go or no-go response and one inverse-temperature parameter. See Materials and Methods for formal definition of all models. See Table 2 for further statistics on fitted parameters of the winning model.

We then asked whether emotional cues modulate learning rate. Specifically, we considered a variant of the hybrid model M2 with emotion-specific weight parameters (Model M4). This dual weight model contains separate weight parameters for happy and angry trials. We used the same Bayesian model comparison procedure to compare this model with model M2. We found that this model outperformed M2 despite the penalty for one extra parameter. We also used classical likelihood ratio tests for comparing this model (M4) with the original hybrid model (M2), as M2 is nested within M4. The results confirmed the Bayesian model comparison results indicating that the hybrid model with emotion-specific w parameters (M4) is better given the data (χ₍₂₎² = 21.84, p < 0.0001).

We also considered control analyses to test modulation of M2 parameters across different factors. First, we fitted a model in which κ rather than w was assumed to be emotion-specific (M5). This model tested the idea that emotions reduce or increase scale of learning rate regardless of the dynamics of the environment. The evidence for this model, however, was lower than that for the original one (M2) ruling out that emotions affect the overall scale of learning rate rather than its sensitivity to environmental dynamics (Table 1). Second, we tested a control model in which the weight parameters varied as a function of the valence of the outcome (Model M6). In this model, w was different for reward and punishment trials. This model also did not outperform the original model, M2. Altogether, these results suggest that emotional state modulates the degree to which people adapt their learning rate dynamically as a function of the history of surprises Table 2.

Table 2.

Fitted parameters of the winning model (hybrid emotion-specific w model) individually using maximum a posteriori (MAP) and the hierarchical fitting procedure (HFP)

	MAP 25th percentile	MAP median	MAP 75th percentile	HFP group mean, Θ
wh	0.2	0.372	0.546	0.397
wa	0.21	0.426	0.649	0.403
κ	0.789	0.868	0.909	0.922
λ	0.404	0.539	0.673	0.458
β	1.321	1.822	2.619	1.646
bν	0.021	0.181	0.339	0.152
be	−0.12	0.029	0.181	0.032
bi	−0.052	0.056	0.14	0.045

Trait social anxiety predicts dynamic learning rate in states evoked by angry face cues

Trait social anxiety is a predictor of vulnerability to depression and anxiety disorders (Mineka and Oehlberg, 2008), pathologies hypothesized to be related to disrupted learning in uncertain environments (Paulus and Yu, 2012; Huys et al., 2015). Furthermore, a recent study has shown that variability in learning rate in a probabilistic learning task is associated with individual differences in trait anxiety (Browning et al., 2015). Here, we build on these prior findings by assessing whether individual differences in the effect of emotional cues on the dynamic learning rate, w, are related to individual variability in social anxiety. To this end, we tested how individual differences in parameters of the winning model, M4, are related to social anxiety. We analyzed estimated weights, w, using individually fitted parameters. Unlike parameters estimated by the hierarchical Bayesian procedure that are regularized according to all subjects' data, the individually fitted parameters are independently estimated and therefore can be used in regular statistical tests. Nonparametric Wilcoxon rank (two-tailed) tests were used, because of the non-Gaussian distribution of the weight parameters (as they were constrained to lie in the unit range).

The weight, w, differed significantly between the low and high social anxiety groups on angry trials (p = 0.001, z = 3.20; Fig. 3A), but not on happy trials (p = 0.56, z = −0.59; Fig. 3B) and the difference in weights (angry vs happy) was also significantly different between the two groups (p = 0.033, z = 2.14). Thus, participants with high versus low social anxiety exhibited reduced dynamic adjustment of learning rate on trials starting with an angry, but not a happy, face. No significant difference between the two groups was found for the other parameters of the model (all p > 0.05).

Figure 3.

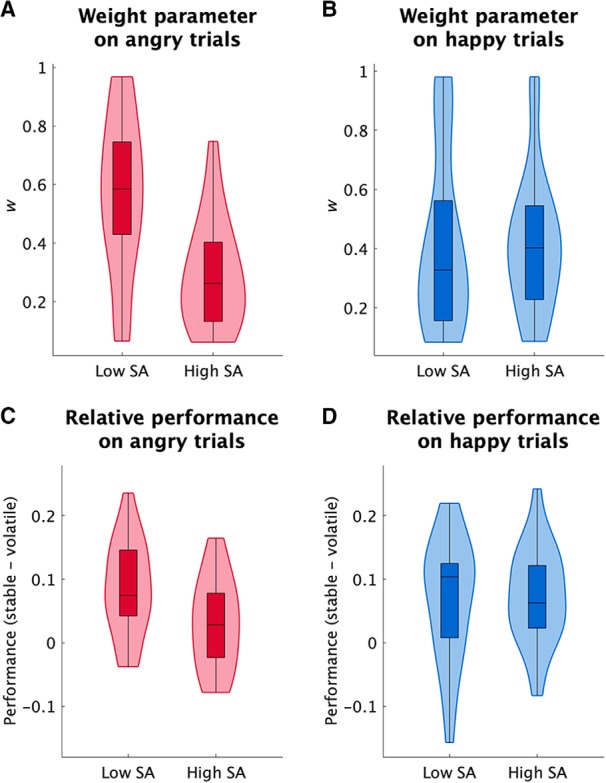
Effects of social anxiety on learning rate. A, B, Effects of social anxiety (SA) on the weight given to the dynamic component of the learning rate in angry (A) and happy (B) trials. High socially anxious individuals showed less dynamic adjustment of learning rate (indexed by parameter w) on angry trials. There was no effect of social anxiety on dynamic learning rate on happy trials. C, D, Effects of social anxiety on performance in stable and volatile epochs in angry (C) and happy (D) trials. In line with the weight parameter results, high socially anxious individuals showed less benefit of stability in their performance than the low social anxiety group on angry trials. There was no significant interaction on the happy trials. Standard boxplots are plotted, in which the box is drawn between the 25 and 75 percentiles with a line indicating the median. The distribution of data is also shown.

An obvious next question is how the low weight parameter in the high socially anxious group affected their choice. Because the weight parameter, w, indicates sensitivity of the learning rate to changes in the environment, its effects on learning is manifested in the relative performance in the stable versus volatile epochs. For example, a model with a low weight, w, would change its decisions on the basis of a few bad outcomes that could be because of noise. This model feature can cause poor performance especially in relatively stable conditions in which the action–outcome contingency does not change and optimal learning relies on a reduced learning rate.

To demonstrate this quantitatively and in a relatively theory-neutral fashion, we analyzed performance of participants on the angry trials in two different conditions. We dissociated stable and volatile epochs, depending on whether there has been at least a change in action–outcome contingencies in the last 10 preceding trials. Thus, a trial was defined as stable if no change occurred in the action–outcome contingency in the last 10 trials. Otherwise, it was defined as a volatile trial. Performance in the stable and volatile epochs was quantified in terms of the average optimal choice (i.e., the probability of choosing the action with the highest probability of winning). Because our task is stochastic (action–outcome probability is never >80% and there are frequent reversals) and the average length of stable blocks (with probability of 80%) was 15 trials, the window of 10 trials provide a reasonable criterion for defining stability. Note that the modeling results presented above are not sensitive to such criteria in defining stability versus volatility and rather define volatility based on the sequences of choices and surprises. Nevertheless, to ensure that the results presented here are robust against the 10-trial criterion, we considered other definition of stability in which the window length was >10 trials. The pattern of results found for those alternatives were consistent with the one presented here.

First, we analyzed optimal choice probability on angry trials as a function of condition (stable vs volatile) using nonparametric Wilcoxon tests (because of its non-Gaussian distribution, all tests are two-tailed). Across all participants, optimal choice probability was higher for stable than volatile trials (p < 0.0001, z = 4.04). This is expected because making an optimal choice after a change in action–outcome contingency (i.e., in volatile trials) is more difficult than the stable condition in which there is no change in contingency. The important question, however, is whether this analysis confirms the model-based results, which suggest that social anxiety affects optimal choice probability differentially for the stable and volatile conditions. As predicted, we found a significant interaction between social anxiety and epoch, with the high social anxiety group showing less difference between optimal choice probability in stable and volatile epochs than the low social anxiety group (p = 0.02, z = 2.33; Fig. 3C). Post hoc tests revealed that the low social anxiety group benefited from stability of the environment as their performance was significantly better in the stable than the volatile epoch (p < 0.0001, z = 3.83). This effect was not present in the high social anxiety group (p = 0.12, z = 1.55). Note that the difference in relative performance is not because of better performance of the high social anxiety group in volatile conditions. Specifically, no significant difference in optimal choice probability on the volatile epoch was found between the two groups (p = 0.88, z = −0.15) indicating that the high social anxiety group did not perform better in volatile conditions. Significant effects were found when we considered different window length for defining stability (windows with 11–14 trials, all p values <0.05).

We also performed the same analysis for the happy trials, which, as predicted by the model-based analyses, did not reveal any group by epoch interaction effect (p = 0.91, z = −0.11; Fig. 3D).

Trait social anxiety predicts dorsal anterior cingulate cortex activity related to learning rate in states evoked by angry face cues

The dACC has been proposed to contribute to learning from experience by computing learning rate (Behrens et al., 2007, 2008; Rushworth et al., 2011). In nonhuman primates, lesions to dACC results in an inability to use more than the most recent outcome to guide decisions (Kennerley et al., 2006). In humans, BOLD responses in the dACC have been shown to correlate with learning rate in a probabilistic learning task. Another study using the same task has reported that the dynamic learning rate depends on trait anxiety scores (Browning et al., 2015). The next question we ask here is whether learning rate-related signals in the dACC depend on emotion-related traits, such as social anxiety, and emotional states, as manipulated using emotional facial cues.

To answer this question, we performed model-based fMRI analysis (Cohen et al., 2017) to isolate BOLD signals that correlate with learning rate in different emotional contexts. Our linear regression model included not just dynamic learning rate, but also prediction error to control for prediction error-related effects. These model-derived time series were considered as parametric regressors at the time of outcome, separately for each of the four trial types, leading to eight regressors. Eight regressors-of-no-interest were added to account for trial-type-specific effects at the time of cue presentation (4 regressors) and of outcome presentation (4 regressors). To generate regressors for fMRI analysis on a common scale, we used the average parameters estimated by the hierarchical Bayesian procedure across all subjects as the common values for all parameters. This is a common approach in model-based neuroimaging, which enables us to draw inferences about individual differences in the neural correlates of model-derived regressors (Daw et al., 2006; Daw, 2011). In other words, any effect regarding individual differences in neural correlates should be attributed to neural signal rather than the parameters used to generate regressors correlating with those signals. Importantly, we used parameters of the hybrid Model M2 (rather than M4) to ensure that any difference in correlation between BOLD and learning rate in angry versus happy trials is not confounded with different weight parameters. An anatomically defined mask of the dACC (the rostral cingulate motor area in the connectivity-based parcellation atlas of medial frontal cortex (Neubert et al., 2015) was used for region-of-interest analysis.

In line with previous findings, we found that BOLD signal in the dACC, across all trials and participants, correlated with learning rate (bilaterally, peak at x = 8, y = 26, z = 42, voxel-level familywise small-volume corrected at p < 0.05; Fig. 4A). Post hoc test at the peak revealed that the effects are significantly stronger for the angry than happy trials (t₍₄₃₎ = 2.11, p = 0.041; Fig. 4B). Similar effects were found when considering activity of all voxels within the dACC mask showing a significant (at p < 0.001 uncorrected) learning rate activity (t₍₄₃₎ = 2.11, p = 0.041). Further tests also revealed that dACC correlation with learning rate was driven by the angry trials. Specifically, BOLD signal in the dACC exhibited a significant correlation with learning rate during angry trials (bilaterally, peak at x = −8, y = 24, z = 40, voxel-level familywise small-volume corrected at p < 0.05), but not during happy trials (no voxel survived uncorrected threshold of 0.001). Therefore, we focused on angry trials and asked whether high social anxiety individuals show weaker learning rate related activity than the low social anxiety group, as suggested by the modeling findings.

Figure 4.

Effects of social anxiety (SA) on learning rate-related activity in the dACC. A, Across all trials, dACC correlated with the learning rate (LR), although (B) the effects were stronger during angry trials and was mainly driven by the angry trials. C, On angry trials, learning rate-related activity in the dACC was present in the low SA group, which showed significantly greater activity than the high SA group. For a, t map (degrees of freedom = 43) is shown with all voxels within the anatomical mask of dACC with p < 0.005 (uncorrected for display). B, The effect size is defined as the β coefficient at the peak voxel of learning rate-related activity in the dACC. C, The effect size is defined as the β coefficient at the peak voxel of learning rate-related activity in the dACC on angry trials. B, C, The corresponding mean and SEM are plotted. The distribution of data is also shown. For further details of statistical analysis, see Table 3.

We found that individual differences in social anxiety covaried strongly with learning rate-related signals in the dACC on angry trials (Fig. 4C). Specifically, the learning rate signal in the dACC during angry trials (at the peak voxel x = −8, y = 24, z = 40) was stronger for the low than the high social anxiety group (t₍₄₂₎ = 3.05, p = 0.004). Similar effects were found when considering activity of all voxels within the dACC mask showing a significant (at p < 0.001 uncorrected) learning rate activity on angry trials (t₍₄₂₎ = 2.37, p = 0.023). Post hoc tests at the peak voxel revealed that the high social anxiety group did not show a significant correlation (t₍₂₀₎ = 0.93, p = 0.36). These results demonstrate that, compared with the low social anxiety group, the high social anxiety dynamically adapted their learning rate to a lesser degree on trials involving presentation of an angry face. Moreover, unlike the low social anxiety group, their dACC BOLD signal did not covary with the learning rate on these trials.

We looked at two control contrasts in the above neuroimaging analysis. First, we found strong prediction error related signal in the ventral striatum (bilaterally, peak at 14, 12, −8, voxel-level familywise small-volume corrected at p < 0.05), consistent with previous studies (McClure et al., 2003; O'Doherty et al., 2003; Daw et al., 2006). Second, we performed a region-of-interest analysis in the amygdala. We focused on the amygdala given its important role in emotional processing (Weiskrantz, 1956; Ledoux, 1996; Phelps and LeDoux, 2005), and previous reports on amygdala sensitivity to learning rate (Li et al., 2011). Despite the presence of clear emotion-related main effects of cue in the amygdala (bilaterally, peak at −14, −8, −16, voxel-level familywise small-volume corrected at p < 0.05), with stronger signal during the presentation of the angry faces, there were no significant effects of learning rate in the amygdala (p < 0.001 uncorrected; Table 3).

Table 3.

Statistics of the neuroimaging analysis of the main effects of learning rate in the dACC mask (small-volume voxel-level familywise error corrected)

	Cluster-level statistics		Voxel-level statistics
	PFWE	k	PFWE	t(43)	Peak, mm
Learning rate across all trials	0.034	38	0.032	+3.75	8	26	42
	0.038	32	0.035	+3.72	−10	18	44
Learning rate on angry trials	0.017	77	0.013	+4.14	−8	24	40
	0.033	38	0.017	+4.03	10	28	42

Discussion

In daily life, it is important to adaptively learn from the outcomes of our decisions, even in environments with threat cues. The adaptation should depend on the history of outcomes and the degree to which those previous outcomes were surprising. When the environment is full of surprises, recent experiences are more predictive of future events than remote experiences. In those circumstances, a higher learning rate is optimal. We found evidence that social anxiety is associated with reduced adaptation of learning rate, particularly in aversive states, such as those evoked here by exposure to images of angry faces.

Our findings are in line with theories looking at psychiatric disorders linked to social anxiety from the perspective of decision neuroscience (Hartley and Phelps, 2012; Paulus and Yu, 2012; Huys et al., 2015). These disorders are hypothesized to be accompanied by deficits in learning and decision-making, particularly in uncertain environments requiring dynamic learning (Paulus and Yu, 2012; Browning et al., 2015). Here, we focused on trait social anxiety in healthy participants, as trait social anxiety is a factor predicting vulnerability to anxiety and depression (Barlow, 2004; Mineka and Zinbarg, 2006; Mineka and Oehlberg, 2008). Our data indicate that the presence of maladaptive biases in learning, at both computational and neural levels, even in healthy individuals. These findings suggest a particular computational mechanism by which social anxiety might impact decisions in threatening situations. In those situations, the weight of dynamic learning rate is too low for anxious individuals, making them oversensitive to noisy outcomes of their decisions. Suboptimal decisions and oversensitivity to outcomes exacerbate each other, generating a dysfunctional loop.

Inspired by these modeling results, we found signatures of disrupted adaptation of learning rate in the behavioral data (Fig. 3C). In threatening situations evoked by angry face images, the high social anxiety group did not benefit from stability in the environment and showed similar levels of performance in both stable and volatile situations. In contrast, the low social anxiety group showed a much better performance in the stable situation compared with the volatile situation. These results are consistent with a recent report by Browning et al. (2015). They showed that anxiety is associated with inability to adjust learning in stable and volatile situations. Our data adds to those findings by showing that inability in optimal learning is also a function of emotional cues. Furthermore, our findings elucidate corresponding neural mechanisms in socially anxious individuals by showing that disruption in optimal learning is accompanied by disruption in dACC activity related to learning rate. The dACC has been argued to specifically contribute to reinforcement learning by computing learning rate in uncertain environments (Behrens et al., 2007, 2008; Rushworth et al., 2011). However, so far, it has remained unclear whether dACC computations of learning rate are modulated by emotional cues or by traits such as social anxiety. Showing those modulations is particularly important, because the dACC is a central node of the brain system processing negative affect (Shackman et al., 2011), suggesting that its computations might be sensitive to negative emotions. Here, we replicated previous findings, namely covariation between dACC activity and learning rate (Behrens et al., 2007, 2008). Furthermore, we added to those reports by demonstrating that learning rate-related computations are stronger when responding to emotional cues. More importantly, our results suggest that high socially anxious individuals show disrupted dACC activity in relation to learning rate.

Influences of emotional conditioned stimuli on optimal learning, as found in this study, might be because of effects of those stimuli on emotions, and subsequent effects of negative emotions on optimal learning and decision-making. Another possibility is that social threat cues disrupt optimal learning directly, even when they are not accompanied with negative emotions. Future studies should address this question, in particular by analyzing choice data and simultaneously recorded physiological signals related to experienced emotions, such as skin conductance response. Importantly, although current research on defensive behavior is mainly focused on elicited reactions, new theories emphasize active responses to threat cues (LeDoux and Daw, 2018). The neural processes underlying those active responses are not yet clear, although amygdala is hypothesized to influence active decisions by signaling threats to the striatum (LeDoux and Daw, 2018), which plays a key role in learning and decision-making. The role of the dACC in these neural processes are not yet known, although dACC has dense connectivity with both the amygdala and the striatum (Draganski et al., 2008; Shackman et al., 2011).

In this study, in addition to emotional content of conditioned stimuli, we manipulated valence of outcomes independently. However, no significant effect of outcome valence on optimal tuning of learning rate was found. Nevertheless, further studies are needed to investigate effects of outcome valence on optimal learning. First, optimal learning might be more sensitive to primary punishments such as shocks. In this study, however, we used monetary outcomes as instrumental reinforcers both as reward and punishment. Second, the outcome manipulation of the present study might not be sufficiently powerful to be detected in our sample size. Third, in our paradigm, the punishment is avoidable (outcome contingency is instrumental), although the facial expression is not. This difference might lead to potentiated effects for the negative facial expression versus the negative outcome.

In this study, unlike the recent study by Li et al. (2011), we did not find associability related activity in the amygdala, even when we focused only on angry trials. However, there are important differences between the paradigm used in this study and that of Li et al. (2011). First, Li et al. (2011) used shocks as negative outcomes, whereas we used financial losses as negative outcomes. Second, Li et al. (2011) fitted their model to skin conductance response data, whereas we fitted models to choice data. Finally, Li and colleagues examined amygdala activation in the context of a Pavlovian task that did not require making decisions, whereas the current study required decision-making. Consistent with our findings, a recent study in monkeys did not find significant effects of amygdala lesions on associability in a stochastic two-arm bandit task (Costa et al., 2016). It should be noted, however, that the role of amygdala regarding associability computations in threat situations might be to signal presence of threat to other regions (Fox et al., 2015), such as dACC.

The biases induced by threatening social cues, such as angry faces, reflect Pavlovian biases in learning. These Pavlovian biases are not always the most rational responses, but they are generally useful heuristics as they reflect predominant statistics of the environment around us, for example threatening angry cues are more likely to be followed by negative outcomes. Importantly, unlike Pavlovian response biases, such Pavlovian learning biases affect causal inference. Therefore, our findings suggest that threatening angry cues affect how high trait social anxiety individuals make causal inference. In the context of social threat cues, those individuals are unable to dissociate a bad outcome that happened by chance from an actual mistake caused by their own actions. This might be related to symptoms of “self-blame” in anxiety and depression disorders (Beck, 1967), although further studies are needed to investigate this somewhat speculative hypothesis. Previous works have linked Pavlovian biases to neuromodulatory systems (den Ouden et al., 2013; Swart et al., 2017), particularly dopaminergic (although see the recent study by Rutledge et al., 2017) and serotonergic systems. Whether and how these, or other neuromodulatory (Iglesias et al., 2013; Payzan-LeNestour et al., 2013), systems modulate such Pavlovian biases in learning rate in socially anxious individuals are open questions for future studies.

Psychological, temporal difference and Bayesian accounts of learning suggest that learning rate is a crucial element of learning, which should be adaptively adjusted according to the history of surprises to support optimal learning (Pearce and Hall, 1980; Yu and Dayan, 2005; Behrens et al., 2007; Li et al., 2011; Mathys et al., 2011; Iglesias et al., 2013). Here, we used an augmented hybrid Rescorla–Wagner model in which learning rate was a weighted combination of a dynamic and a constant component. The dynamic component was gradually updated according to the sample variance (squared error) on every trial. The hybrid model can be treated as a proxy model of fully Bayesian accounts, which has the benefit to be close to classical psychological models. An important open question for future studies is whether the inability to adjust learning rate in socially anxious individuals is caused by disruptions in computationally higher levels of reasoning that are responsible for detecting changes in the environment. Hierarchical Bayesian models are particularly useful to address this question (Behrens et al., 2007). Another important question remained to be addressed is whether these hierarchically computed learning rates vary as a function of the valence of prediction errors, which is shown to influence baseline learning rates in humans (Frank et al., 2004, 2007; Piray et al., 2014) as well as monkeys (Piray, 2011) and supported by neural models of prefrontal cortex–basal ganglia (Frank et al., 2004; O'Reilly and Frank, 2006) and mesostriatal circuits (Haber et al., 2000; Piray et al., 2017).

In this study, we characterized the computational and neural mechanisms by which emotional context modulated optimal learning in an uncertain environment and how those mechanisms are disrupted in high trait social anxious individuals. These findings open the way to test and modify the neurobiological underpinnings of maladaptive learning in pathologies related to social anxiety.