Electron Delocalization in Planar Metallacycles: Hückel or Möbius Aromatic?

Abstract

In this work the relationship between the formal number of π‐electrons, d‐orbital conjugation topology, π‐electron delocalization and aromaticity in d‐block metallacycles is investigated in the context of recent findings concerning the correlation of π‐HOMO topology and the magnetic aromaticity indices in these species. It is demonstrated that for π‐electron rich d‐metallacycles the direct link between aromaticity, the number of π‐electrons and the frontier π‐orbital topology does not strictly hold and for such systems it is very difficult to unambiguously associate their aromaticity with the “4n+2” (Hückel) and “4n” (Möbius) rules. It is also shown that the recently proposed electron density of delocalized bonds (EDDB) method can successfully be used not only to quantify and visualize aromaticity in such difficult cases, but also – in contrast to magnetic aromaticity descriptors – to provide a great deal of information on the real role of d‐orbitals in metallacycles without the ambiguity of bookkeeping of electrons in the π‐subsystem of the molecular ring. Interestingly, some of the metallacycles studied cannot be classified exclusively as Hückel or Möbius because they have a hybrid Hückel‐Möbius or even quasi‐aromatic nature.

1. Introduction

Over the last decades the transition‐metal metallacycles has been receiving a substantially increasing attention as important catalyst precursors and intermediates in organometallic chemistry.1,2 From the molecular‐structure perspective, a d‐metallacycle can be regarded as a derivative of the carbocyclic system with at least one carbon atom replaced by the d‐block metal atom. Although d‐metallacycles were many times confirmed experimentally to be more reactive than their aromatic hydrocarbon precursors,2 the cyclic delocalization of π‐electrons has been considered to play a crucial role in determining their physicochemical properties from the very beginning.3 Unfortunately, semiquantitative (aromaticity is a concept and not an observable in a strict quantum‐mechanical sense) analysis of aromatic stabilization in metallacycles faces serious difficulties.1f In particular, anisotropy of the metal center, non‐local character and influence of ligands on diatropic ring current are the main reasons why the aromaticity predictions based on magnetic criteria, such as the nucleus‐independent chemical shift (NICS),4 should be taken with caution.5 On the other hand, aromaticity descriptors that depends on the definition of a reference system, such as the harmonic‐oscillator model of aromaticity (HOMA)6 or the aromaticity fluctuation index (FLU),7 cannot straightforwardly be used due to lack of parameterization for bonds with metal atoms. Calculations of aromatic stabilization energies (ASE),8 in turn, usually requires design of different isomerization reaction scenarios, which may lead to a lot of arbitrariness and makes it limited in applications.1f One of the most promising aromaticity descriptors in the context of organometallic systems is the multicenter index (MCI).9 MCI quantifies the effect of cooperativity of all ring members in the cyclic delocalization of π‐electrons (a multicenter sharing of π‐electrons); it is a non‐reference quantity that can be calculated from both the molecular wave function as well as the n‐electron density.9 Unlike with other descriptors, the multicenter index enables one to study almost all types of aromaticity that can be found in the literature, including the all‐metal aromaticity,10 and it is one of the few descriptors that successfully passed a set of rigorous tests for aromaticity indices, designed by our group.11 Unfortunately, the calculations of MCI face several challenges such as high computational cost, numerical accuracy problems, ring‐size extensivity issue,5l and considerable sensitivity to the level of the theory (and even the choice of the exchange‐correlation functional at the DFT level).10,12

Despite the difficulties with quantification of aromaticity, also the nature of the aromatic stabilization in d‐block metalloaromatic systems itself remains under continuous debate,1f because it can involve contribution of different d‐orbitals of the transition metal to the π‐electron delocalization.3a As shown in Figure 1a, chemical bonding between transition metal and the adjacent atoms allows two different topologies of d‐orbital conjugation within the system of molecular π‐orbitals (MO): 1) the π‐type (Hückel) topology without phase inversion, involving the d_yz metal orbital, and 2) δ‐type (Möbius) topology, in which d_xz metal orbital acts as a “phase switch” allowing cyclic delocalization to fall into the opposite phase side over the cyclic unit.13 In contrast to typical twisted Möbius hydrocarbon aromatics, both the MO topologies co‐exist within the same π‐system and deciding which of them determines aromaticity in particular case is not straightforward. Interestingly, Mauksch and Tsogoeva have recently shown that there is a relationship between the magnetic aromaticity by NICS and the topology of the highest occupied molecular π‐orbital (π‐HOMO), which comes down to the following rule:14

Figure 1.

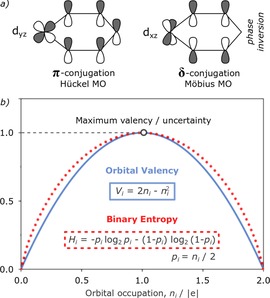
a) Schematic representation of two different topologies of π‐MOs involving d‐orbitals. b) The approximate relationship between orbital occupation number n_i, valency V_i, and the binary (Shannon) entropy H_i within the closed‐shell π‐electron system.

“The metallacycle is aromatic (antiaromatic) when the number of π‐MOs is even and the π‐HOMO is of Möbius (Hückel) topology‐and vice versa when the number of π‐MOs is odd”.

This frontier π‐orbital topology rule, however, depends upon bookkeeping of electrons in the π‐system (which itself can be very difficult even for planar rings due to the extensive π‐MO delocalization nature) and it does not explicitly take into account the effect of cyclic delocalization of electrons. It should be emphasized that, from the electronic point of view, aromaticity is always a result of specific interference between molecular orbitals and, according to the balance‐equivalence theorem by Klein and Balaban,15 the link between size of the π‐system and its aromaticity (antiaromaticity) holds strictly only for the annulene‐like systems. This is because annulene represents a perfect balance between the number of occupied bonding and unoccupied antibonding valence π‐MOs or, equivalently, the number of π‐electrons equals the number of 2p_z orbitals.

In this work the link between the number of electrons in the π‐system, d‐orbital conjugation topology, electron delocalization and aromaticity in d‐metallacycles will be studied in the context of the frontier π‐orbital topology rule.14 In particular, we will use the test set of metallamonocycles (in silico designed by Mauksch and Tsogoeva in their seminal proof‐of‐concept work)13 and several representative d‐metallabicyclic aromatics.

2. Methodology

To quantify cyclic delocalization of π‐electrons in metalloaromatic rings we used the electron density of delocalized bonds (EDDB).16 The EDDB method has originally been proposed to facilitate visualization and quantitative study of chemical resonance and multicenter bonding in molecular systems with different topology and size.16b It has recently been demonstrated, however, that also the quantitative predictions of aromaticity by EDDB are in excellent agreement with a wide range of descriptors based on structural, magnetic, and electronic‐structure criteria of aromaticity.17 There are several important features, that set the EDDB method apart from other aromaticity descriptors: 1) EDDB does not suffer from the ring‐size extensivity issue and can be used to study electron delocalization in any type of aromatic system regardless of its size and topology (in contrast to NICS); 2) EDDB does not depend upon parametrization to the reference model system (in contrast to HOMA and FLU); 3) EDDB provides aromaticity predictions very similar to MCI but it is much less computationally expensive and does not share the numerical‐accuracy problems;10a 4) EDDB enables one to quantify cyclic delocalization of electrons within the framework of the first‐order population analysis (the number of electrons delocalized through the system of conjugated bonds), so the results are much easier to interpret than those from other approaches.16b

The EDDB(r) function is defined in the basis of Weinhold's natural atomic orbitals (NAO)18 as

$${\displaystyle \mathrm{EDDB}\left(r\right)=\sum _{\mu ,\nu }{\chi }_{\mu }^{†}\left(r\right){\mathrm{D}}_{\mu \nu }^{\mathrm{DB}}{\chi }_{\nu }\left(r\right),}$$ (1)

where the corresponding DB‐density matrix reads:

$${\displaystyle {\mathbf{D}}^{\mathrm{DB}}=\frac{1}{2}\mathbf{D}\left[\sum _{\alpha ,\beta \ne \alpha }^{\Omega }{\mathbf{C}}_{\alpha \beta }{ϵ}_{\alpha \beta }{\lambda }_{\alpha \beta }{\mathbf{C}}_{\alpha \beta }^{†}\right]\mathbf{D}.}$$ (2)

In the above equation D represents the standard one‐electron density matrix, C _αβ collects linear‐combination coefficients of the orthogonalized two‐center bond orbitals (2cBO),16a,19 λ _αβ is a diagonal matrix collecting the corresponding 2cBO squared occupation numbers, ϵ _αβ is a diagonal matrix of the bond‐orbital delocalization factors (ϵ_αβ is close to 1 for delocalized bonds and approaches 0 for the localized ones), and Ω={(X_α, X_β)} denotes a set of all the atomic pairs in a molecular ring.16a,16b The definition of ϵ _αβ involves a series of projections of 2cBO onto their three‐center counterparts (3cBO), followed by the projection onto the occupied molecular orbitals (MO), which significantly extends the electron delocalization over all the ring members; such projection cascade is deeply rooted in the formalism of the so called orbital communication theory.20 The trace of the D ^DB matrix from Eq. (1) can be interpreted as the population of electrons delocalized through the system of conjugated bonds in the molecular ring Ω; in contrast, summation (over NAOs centered on the ring members only) of diagonal elements of D gives the corresponding overall (natural) population of electrons in the cycle. In this work, these electron populations will be denoted simply as EDDB and ED, respectively.

For planar aromatics the subset of occupied π‐MOs can be used to get the corresponding π‐ED and π‐EDDB components. Furthermore, since within the NAO representation both D and D ^DB have the same atomic‐block structure, it is possible to separate aromatic ring from the rest of the molecule (simply by zeroing the corresponding off‐diagonal elements of the density matrix) and partition both the electron density, π‐ED(r), and the electron density of delocalized bonds, π‐EDDB(r), into components representing metal atom and the rest of ring members:

$${\displaystyle \pi \text{-}\mathrm{ED}\left(r\right)=\pi \text{-}\mathrm{ED}{}_{\mathrm{Me}}\left(r\right)+\pi \text{-}\mathrm{ED}{}_{\mathrm{R}}\left(r\right),}$$ (3)

and

$${\displaystyle \pi \text{-}\mathrm{EDDB}\left(r\right)=\pi \text{-}\mathrm{EDDB}{}_{\mathrm{Me}}\left(r\right)+\pi \text{-}\mathrm{EDDB}{}_{\mathrm{R}}\left(r\right).}$$ (4)

Finally, diagonalization of the metal atomic‐blocks of such π‐density matrices gives rise to the effective p_z, d_xz, and d_yz atomic orbitals polarized within the molecular environment.21 It should be noticed that the orbital decomposition of π‐ED leads to the overall orbital populations (occupation numbers), n_i, while in the case of π‐EDDB we get the corresponding orbital contributions to the cyclic delocalization of π‐electrons in the aromatic ring, θ_i. One should realize that for an idealized aromatic ring the latter is very close to the orbital valency, V_i, which in the case of closed‐shell π‐systems at the one‐determinant theory level reads:

$${\displaystyle \theta {}_i\approx V{}_i=2n{}_i-n{}_i{}^2.}$$ (5)

The above relation follows directly from duodempotency of the π‐density matrix and strictly holds for unhybridized orbitals only. As illustrated in Figure 1b, orbital valency is closely related to the Shannon (binary) entropy from information theory, H_i,19 and it reaches maximum for the atomic orbitals occupied exactly by one electron (maximum uncertainty of electron=maximum valency). In other words, the contribution of each of these orbitals to the π‐delocalization in a closed‐shell aromatic ring is always lower than or at most equal to 1 electron. This fact is of crucial importance in the context of π‐conjugation topology in aromatic d‐metallacycles and it will we discussed in the next section.

3. Results and Discussion

Let us begin with the model of hypothetical ferracycloheptatriene, [Fe(CH)₆H₂],13 with the π‐system consisting of 5 doubly occupied MOs (Figure 2a); however, since HOMO‐3 is in 99 % localized on the metal atom, it does not contribute to the cyclic delocalization of π‐electrons and, consequently, the ferracycloheptatriene ring can be regarded as a 8π system. Indeed, the electron population analysis based on the LCAO π‐MO coefficients (Figure 2b) shows that 5.970|e| is assigned to the carbon fragment (ED_R) while 1.922|e| comes from the metal atom (ED_Me). The orbital‐decomposition of ED_Me reveals that it is predominated by the 3d_xz orbital (1.697|e|, i. e. ∼88 %) with only a small admixture of 3d_yz (0.225|e|, i. e. 12 %), which makes this particular metallacycle a perfect candidate for being a Möbius aromatic system. In fact, aromaticity in [Fe(CH)₆H₂] manifests itself through significant reduction of the carbon‐carbon bond length alternation, HOMA=0.930, and negative value of the axial component of the nucleus‐independent chemical shift at 1 Å above the ring plane, NICS(1)_zz=−15.0.13 Moreover, the highest occupied molecular π‐orbital is of Möbius type (see Figure 2a), which, in accordance with the recent findings on the relationship between NICS and π‐HOMO topology,14 seems to confirm the existence of Möbius aromaticity in [Fe(CH)₆H₂]. It should be noticed that, although including HOMO‐3 in the π‐electron population analysis increases the 3d_yz orbital occupation number for about four times (grey numbers in Figure 2b), it does not change the final conclusion about predominating role of the δ‐conjugation topology in this particular d‐metallacycle.

Figure 2.

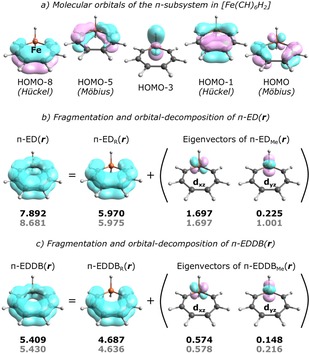
a) Contour plots of the occupied molecular π‐orbitals in [Fe(CH)₆H₂]. b,c) Results of the analysis of d‐orbital contributions to π‐ED(r) and π‐EDDB(r) with the electron populations corresponding to the 8π‐ (black) and 10π‐system (grey).

Figure 2c, in turn, presents the results of the corresponding partition and orbital‐decomposition of the π‐EDDB(r) function. The resulting EDDB populations indicate that about 69 % (i. e. 5.409|e|) of the total population of π‐electrons in the aromatic ring is delocalized and the contribution from 3d_xz to the cyclic delocalization is up to 0.574|e| (i. e. only 33 % of the corresponding orbital occupation number). Although these electron populations significantly differ from the ED‐based ones, they seem to be quite reasonable as long as EDDB is considered a quantitative criterion of aromaticity. In fact, metallacycles are commonly known to be less aromatic than their classical counterparts, and it has recently been shown using the EDDB method that in the case of benzene about 90 % of electrons are delocalized within the π‐system.17a In this context, the cyclic delocalization of electrons in [Fe(CH)₆H₂] is at least 20 % less effective than in C₆H₆. On the other hand, the orbital valency approximated by Eq. (5), V_3dxz=2×1.7–1.7²≈0.5, is very close to the corresponding eigenvalue of the π‐EDDB_Me density matrix, ϑ_3dxz=0.574, which clearly shows that the 3d_xz orbital contributes to electron delocalization to very limited extent (and hence it preserves to some degree the non‐bonding nature). Moreover, since the π‐electron delocalization in aromatics relies on the cooperativity of all ring members in the electron sharing, one should expect the sum of ϑ_3dxz and ϑ_3dyz to be more or less equal to the average EDDB population per carbon atom; indeed, the former is 0.722|e| while the latter is 0.781|e| (for comparison, in the case of benzene, the corresponding π‐EDDB population per each ring member is 0.889|e|). The reduced aromaticity in the ring is in line with noticeable alternation of the calculated NAO‐based Wiberg π‐bond orders,20 i. e. 0.296, 0.479, 0.386, and 0.458 (going from the Fe−C bond). Furthermore, the EDDB analysis involving separate subsets of the Möbius‐ and Hückel‐type π‐MOs reveals that their mutual interference leads to ∼23 % drop of the metal contribution to aromaticity, i. e. from 0.938|e| (π‐EDDB_Me,δ+π‐EDDB_Me,π) to 0.722|e| (π‐EDDB_{Me, δ+π}); in particular, it decreases ϑ_3dxz for about 31 % (i. e. from 0.833|e| to 0.574|e|) and increases ϑ_3dyz for nearly 41 % (i. e. from 0.105|e| to 0.148|e|). The opposite effect is observed for the carbon fragment where the interference of the π‐MO subsets of different types reinforces the cyclic delocalization of electrons for nearly 70 % (from 2.756|e| to 4.687|e|). All in all, the results presented in Figure 2c show that in [Fe(CH)₆H₂] 3d_xz prevails over 3d_yz as regards participation in cyclic delocalization of electrons, which allows one to draw the conclusion that [Fe(CH)₆H₂] is indeed a Möbius aromatics (with minor ‘assistance’ of the π‐conjugation topology). Moreover, although the aromatic ring in ferracycloheptatriene seems to represent a perfect balance between the number of electrons and atomic orbitals within the π‐system (8 : 8), it is much less aromatic than benzene because of the π/δ anti‐cooperativity and, consequently, limited participation of the metal 3d_xz and 3d_yz orbitals in the cyclic delocalization of electrons. In fact, both d‐orbitals together are in total less effectively conjugated with other AOs in the metallacyclic ring than a single 2p_z orbital in benzene.

It should be noticed that, in contrast to the ED‐based results depicted in Figure 2b, the EDDB analysis gives rise to practically the same picture of cyclic delocalization of π‐electrons regardless of the assumption about the size of the π‐MO subspace (i. e. with or without HOMO‐3) – the total EDDB populations differ by less than 0.5 %. But the EDDB method can easily be used also for d‐metallacycles with aromatic rings significantly distorted from planarity, for which a strict separation of σ‐ and π‐MOs may be not possible. To demonstrate the performance of the EDDB‐based orbital‐decomposition method in such cases, let us consider a test set of 15 d‐metallacycles in silico designed by Mauksch and Tsogoeva,13 but re‐optimized without symmetry and geometrical constrains forcing planarity. The results of the EDDB partition and orbital‐decomposition are collected in Table 1 and depicted in Figure 3; the corresponding values of HOMA (based only on the C–C bonds) and NICS(1)_zz (taken from Ref. [13]) has been added for comparison. As regards the orbital decomposition, only the first five highest occupied eigenvectors of the EDDB_Me matrix were analyzed reproducing in most cases (except 8) up to 99 % of the overall EDDB_Me population (see Figure 3b). It should be noted that in several cases (especially molecular rings significantly distorted from planarity) metal contributes to electron delocalization mainly through the σ‐delocalization involving d_x2‐y2 orbitals, while the π‐delocalization involves additionally d_z2 and p_z orbitals along with the d_yz ones.1h

Table 1.

Averaged NICS(1)_zz (in ppm), HOMA and the results of the EDDB‐based partition and orbital‐decomposition (in |e|) for d‐metallacycles 1–15.^a

	NICS(1)zz	HOMA	EDDB	EDDBR	EDDBMe
					σ	π	δ
1	−4.9	0.984	4.415	3.634	0.342	0.327	0.098
2	−23.0	0.955	5.562	4.710	0.115	0.326	0.406
3	−27.6	0.971	5.976	4.811	0.142	0.479	0.539
4	−4.9	0.925	5.541	4.355	0.138	0.433	0.611
5	−15.0	0.930	6.017	5.068	0.112	0.254	0.578
6	−25.6	0.970	5.465	4.722	0.210	0.232	0.297
7	−40.3	0.935	5.620	4.584	0.398	0.225	0.391
8	−9.4	0.973	5.297	4.524	0.221	0.276	0.196
9	−9.5	0.947	5.425	4.684	0.543	0.057	0.137
10	−27.4	0.980	6.781	5.544	0.248	0.272	0.714
11	−57.0	0.946	7.119	5.966	0.084	0.104	0.962
12	−19.7	0.958	7.076	5.996	0.266	0.144	0.665
13	−65.3	0.958	7.808	6.389	0.144	0.255	0.974
14	−8.2	0.957	7.782	6.242	0.151	0.415	0.932
15	−1.2	0.945	7.220	5.955	0.189	0.221	0.849

^a The NICS(1)_ZZ values taken from Ref. [13]

Figure 3.

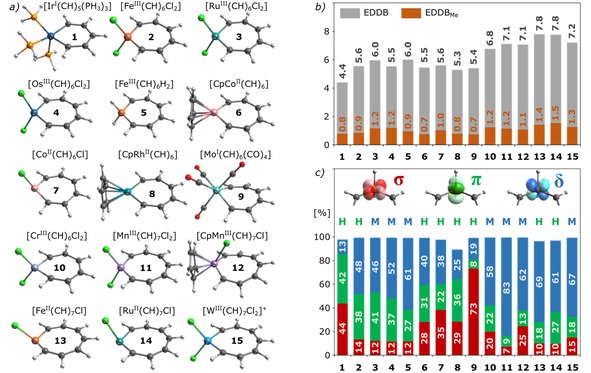
a) Ball‐and‐stick models of the optimized structures of d‐metallacycles 1–15. b,c) Graphical representation of the EDDB results presented in Table 1; labels H (Hückel) and M (Möbius) refer to the topology of π‐HOMO.

At first glance, it is clear from Table 1 that all the indices predict metallacycles 1–15 to be aromatic (negative NICS values, HOMA close to unity, and the EDDB populations in the range of 4.4–7.8|e|), although the dramatic deviations of NICS(1)_zz – even for metallacycles of the same type and size (e. g. 13 and 14) – are difficult to explain; thus, the results of aromaticity quantification based on NICS(1)_zz should be taken with caution.5 Admittedly, the direct comparison of HOMA and EDDB_R misses the point since the systems consist of different numbers of atoms and π‐electrons, however, the averaged EDDB_R populations calculated per carbon atom for 6‐, 7‐, and 8‐membered d‐metallacycles from Table 1 represent respectively about 82 %, 90 %, and 98 % of the corresponding EDDB_R per ring‐member population in benzene (0.889|e| per each C). Thus, the overall population of π‐electrons delocalized in metallacycles 1–15 increases with the number of ring members, although the C−C bond‐length equalization seems to not follow this trend; this, however, should not be surprising since the latter is regarded as the effect of σ‐system rather than π‐delocalization.23 Also, the ratio between different metal d‐orbital contributions to delocalization changes significantly as the ring size increases (although the average EDDB_Me over the entire test set is ∼1|e|). In particular – leaving aside electron delocalization within the σ‐system – the iridabenzene core in the archetypical metallabenzene 1 is predominantly Hückel aromatic with only a small dope of δ‐conjugation topology by the 5d_xz orbital (∼13 %); since the π‐HOMO is of Hückel‐type topology, aromaticity in 1 follows the frontier π‐orbital topology rule. Admittedly, this result pleads in favor of the 6π metallabenzene model system as reported by Thorn and Hoffmann,3a but to some extent it also reconciles the influence of the doubly‐occupied 5d_xz orbital, as suggested by Schleyer and supported later by Jia et al.24 It has to be noticed that Hückel aromaticity has also been confirmed for octahedral Fe, Mn, Os, and Rh‐benzenes with neutral electron‐pair donors such as PH₃ or CO.1f In contrast, within 7‐membered systems 2–10 δ‐conjugation topology is slightly more favorable, albeit the ratio between d_yz and d_xz orbital contributions to π‐delocalization is in many cases (especially in 2–4, and 6) much more a one‐to‐one like, which suggests a hybrid Hückel‐Möbius nature. Interestingly, the highest occupied molecular π‐orbitals in 3–5 and 10 are of Möbius type, while for the rest of the 7‐membered rings they have Hückel topology; this shows certain incompatibility between topological criterion of aromaticity based on the π‐HOMO shape and the cyclic delocalization of π‐electrons (see Figure 3c). It should be noticed, however, that in 2, 3, 5, and 9 two of the highest occupied molecular π‐orbitals are nearly degenerated (Δe≤0.01 a.u.) having the opposite topology types; moreover, some of the Hückel‐type π‐HOMOs, especially 6, 7, and 8, contain noticeable contribution from d_z2 orbitals,13 which, together with substantial delocalization of π‐MOs over the ligand atoms, hinders one from classifying them as ‘pure’ Hückel aromatics. Finally, 11–15 with metallacyclooctatetraene cores represent predominantly Möbius aromatics (EDDB_Me,δ reaches a maximum of ∼1|e| in 11 and 13) with up to 27 % support of the π‐topology (14). Admittedly, 13 and 14 have the π‐HOMOs of Hückel type, but again, they consist of d_z2 rather than d_yz orbitals and thus (following suggestions by Mauksch and Tsogoeva to rely on the π‐MOs containing only d_xz and d_yz orbitals)14 both these systems could be regarded Möbius aromatics according to their HOMO‐1 topology.

To sum up, the results presented in Table 1 and Figures 3b,c indicate that the exclusive classification of Hückel or Möbius aromaticity in d‐metallacycles misses the point as both d_yz and d_xz contribute to the cyclic delocalization of electrons (but to a variable extent). Interestingly, δ‐type conjugation involving the d_xz orbitals becomes more important as the ring size increases, which can be explained in terms of the overlapping between atomic orbitals of the metal center and two adjacent carbon atoms (see Figure 1a). E.g., going from 1‐chloroferrabenzene through its 7‐ (2) to 8‐membered (13) homologues the percentage of the 3d_xz orbital‐contribution to the cyclic π‐delocalization increases from 27 % through 48 % up to 69 % following the corresponding change of the C−Me−C bond angle from 96° through 109° up to 114°; accordingly, the opposite trend is observed for the 3d_yz orbital, i. e. its contribution to EDDB_Me systematically decreases from 57 % through 38 % to 18 %, respectively.

It has to be emphasized that the EDDB orbital‐decomposition scheme principally does not rely on bookkeeping of electrons within the π‐subsystem of the metallacyclic ring; in other words, no assumption on the formal number of π‐electrons (“4n+2” or “4n”) is needed to assess aromaticity and the orbital‐conjugation topology in d‐metallacycles. In this context, the proposed methodology can easily be used for metallacycles with extensively delocalized π‐MOs involving more than one cyclic unit. For instance, let us consider the metallabicyclic core of one of the osmapentalenes recently reported by Zhu et al.25 Figure 4 collects π‐MOs and the results of the EDDB analysis with the corresponding populations based on the LCAO‐MO coefficients for two isomeric structures of osmapentalene; the anisotropy of the current induced π‐density (π‐ACID)26 isosurfaces and the averaged π‐NICS(1)_ZZ values are added for comparison. Figure 4a indicates that both isomers have the π‐MOs delocalized over the entire molecule (including metal atom), but they differ in the size of the π‐system and topology of π‐HOMO. In fact, according to the Mauksch‐Tsogoeva rule,14 one could expect that both isomers are antiaromatic (6 π‐MOs, π‐HOMO of Hückel topology in isomer I and 5 π‐MOs, π‐HOMO of Möbius topology in isomer II), but this is inconsistent with their structural, thermochemical and magnetic properties.25 Indeed, large negative values of π‐NICS(1)_ZZ supported by the π‐ACID plots unquestionably shows that both isomers are aromatic. It should be noticed, however, that due to influence of the local currents associated with metal‐ligand bonds it is very difficult to assess the topology of d‐orbital conjugation based exclusively on the π‐ACID surfaces (in this context, also the π‐NICS(1)_ZZ values should be taken with caution). In contrast, even a nodding glance at the π‐EDDB(r) contours in Figure 4b leaves no doubt that significant delocalization of π‐electrons through the osmium atom involves mainly the 5d_xz orbital (especially in II) advocating for Möbius aromaticity. The corresponding EDDB‐based populations indicate that in each case about 6.0–6.5|e| are delocalized within the π‐system (thus, the average π‐EDDB population per ring member in isomers I and II reaches respectively about 91 % and 85 % of the corresponding π‐EDDB value for benzene), and the metal contribution is indeed predominated by 5d_xz (up to 85 % in isomer II). Interestingly, participation of 5d_yz in cyclic delocalization is much better marked in isomer I (0.3|e| vs ∼0.1|e|), suggesting that the π‐type topology involving the bridgehead Os atom is necessary to correctly represent electron delocalization over the smaller 5‐membered cycles. Moreover, just like in the case of [Fe(CH)₆H₂], the mutual interference of the subsets of Hückel‐ and Möbius‐type molecular orbitals significantly decrease the overall metal contribution to the cyclic delocalization (for up to ∼50 % in isomer II), thus confirming the anti‐cooperativity of π‐ and δ‐conjugation topologies. Admittedly, the 5d_z2 metal orbital builds π‐HOMO and two of the lowest lying π‐MOs in isomer I, but it does not participate in electron delocalization. In fact, since the Os−H bond is perpendicular to the ring plane it makes 5d_z2 an inherent part of the π‐system (with the occupation number equals to 1.152|e|). With that in mind, one could subtract the 5d_z2 orbital population from the total population of π‐electrons in the ring to obtain 9.995|e|, i. e. a formally 10π Hückel aromatic system. Furthermore, taking into account that the orbital population of 5d_yz (1.905|e|) is determined mainly by the HOMO‐1 (localized in 84 % on the metal atom) allows one to identify isomer I as the 8π Möbius aromatics (the highest occupied and delocalized π‐MO containing either 5d_xz or 5d_yz is HOMO‐2). Similarly, excluding from consideration HOMO‐5, which is in 81 % localized on the [H₂Os] fragment (although it is not so obvious from the first glance at the isosurface contour plot), makes isomer II the 8π Möbius aromatic system as well.

Figure 4.

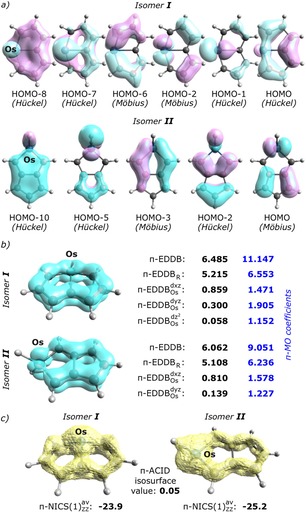
a) Contour plots of the occupied π‐MOs in two different isomers of osmapentalene. b) Results of the π‐EDDB analysis with the corresponding electron populations based on the LCAO MO coefficients (blue numbers). c) The π‐ACID isosurfaces with the corresponding averaged π‐NICS(1)_ZZ values.

The example of osmapentalenes clearly shows that without careful analysis of the LCAO‐MO coefficients and, even more important, without any initial assumption about the role of different d‐orbitals, the qualitative criterion based on the formal number of π‐electrons and the π‐MO topology may lead to conclusions that are inconsistent with quantitative criteria of aromaticity. But the situation becomes even more complicated in the case of planar d‐metallaheterobicyclic aromatics like the one presented in Figure 5. According to the original report by Rimola et al.,27 this formally 16π system is regarded Möbius aromatic mainly due to significant equalization of the C−C, C−N, and C−O bond lengths (HOMA=0.939), the normalized multicenter index9c being half as large as in benzene (I_NG=0.020), and characteristic shape of the lowest lying occupied π‐MO. One should realize, however, that HOMO‐15 is actually of Hückel type because here the copper atom does not allow cyclic delocalization to fall into opposite phase over a single cyclic unit. Interestingly, also the highest occupied molecular π‐orbital (here HOMO‐1) possess the Hückel‐type topology, which, following the frontier π‐orbital rule by Mauksch and Tsogoeva,14 indicates Hückel antiaromaticity. What is more, the π‐component of the anisotropy of the current induced density together with the marginal value of π‐NICS(1)_ZZ complicates the case even further suggesting non‐aromaticity of the system: at the (standard) isovalue of 0.05 π‐ACID shows predominating role of the local (atomic and diatomic) ring currents, especially over the metal center (see Figure 5c). However, the results of the EDDB orbital‐decomposition presented in Figure 5b seem to rationally reconcile this incompatibility between structural, topological, and magnetic characteristics unambiguously identifying the cupraheterobicycle as quasi‐aromatic.28 Indeed, since neither 3d_xz nor 3d_yz contribute to electron delocalization (acting as doubly‐occupied lone‐pair‐like orbitals) there is no cyclic delocalization in each heterocyclic unit and consequently no diatropic ring current can be observed; this is in full agreement with the previous findings by Krygowski et al.28a On the other hand, electrostatic interactions with the copper cation (the natural charge on Cu is +1.308) and noticeable σ‐delocalization involving 3d_x2‐y2 orbital and the lone‐pairs from heteroatoms (which seem to hold the structure in a plane) support delocalization of π‐electrons in both quasi‐rings. It is worth noting that, according to the π‐EDDB_R and LCAO π‐MO‐based electron populations, only a half of the total number of π‐electrons in the heterocyclic quasi‐rings (6.076|e|) is delocalized, which gives on average 0.608|e| per each quasi‐ring member; for comparison, the corresponding values for furan and pyrrole are 0.503|e| and 0.724|e|, respectively.12a Interestingly, both quasi‐rings contain in total ten atoms and therefore, in accordance with Figure 1b, the maximum of number of electrons that can be delocalized through the π‐system of conjugated 2p_z orbitals is 10. Thus, since the π‐system contains more electrons (12.023|e|) than can actually be delocalized, the balance‐equivalence rule15 is not satisfied and, consequently, the direct link between the number of “4n+2” (“4n”) π‐electrons and aromaticity (antiaromaticity) no longer holds. In fact, the overlapping of the metal 3d_xz and 3d_yz orbitals with 2p_z orbitals of the heteroatoms makes it very difficult to predict quasi‐aromatic character of cupraheterobicycle basing exclusively on the frontier π‐orbital topology rule.14 Admittedly, negligible d‐orbital valencies can be deduced straightforwardly from the LCAO π‐MO coefficients, but still, the effect of π‐conjugation of all the 2p_z orbitals is assessable only within the framework of the electronic criterion of aromaticity, i. e. by means of the EDDB method.

Figure 5.

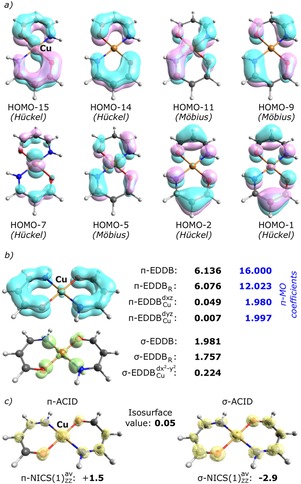
a) Contour plots of the occupied π‐MOs in cupraheterobicycle. b) Results of the σ‐ and π‐EDDB analyses with the corresponding electron populations based on the LCAO MO coefficients (blue numbers). c) The σ/π‐ACID plots with the corresponding averaged σ/π‐NICS(1)_ZZ value.

4. Conclusions

The results presented in this study clearly show that the reported by Mauksch and Tsogoeva correlation of aromaticity and the topology of the π‐HOMO (provided it contains neither p_z nor d_z2 metal orbitals)14 strictly holds only for the d‐metallacycles with the total population of electrons (based on the LCAO‐MO coefficients) approximately equal to the number of members in the ring. And so, 6‐membered 6π‐electron metallacycles are predominated by the π‐conjugation topology and hence they are mainly Hückel aromatics. In contrast, in the 8‐membered 8π‐electron systems δ‐type topology (involving the d_xz metal orbitals) prevails over the π‐type one, thus indicating Möbius aromaticity (usually with small dope of the d_yz orbital contributing to the cyclic delocalization of electrons). But, for the 7‐membered 8π‐electron d‐metallacycles as well as the studied d‐metallabicycles, there is more electrons in the π‐system than can actually be delocalized, and thus the direct link between aromaticity and the π‐HOMO topology no longer holds. For such systems it is very difficult to predict the effect of the π‐MO interference on the orbital valency and overlapping, and their aromaticity is hardly assessable by means of the magnetic, structural, and topological criteria; good examples here are 7‐membered metallacycles and the cupraheterobicycle molecule revealing a hybrid Hückel‐Möbius aromatic and quasi‐aromatic nature, respectively.

In this work we have demonstrated that the EDDB method can successfully be used not only to quantify and visualize aromaticity in such difficult cases, but also – in contrast to ACID plots or NICS values – to provide a great deal of information on the real role of the metal d‐orbitals in metallacycles. Moreover, the proposed methodology does not rely on bookkeeping of electrons within the π‐system of the metallacyclic ring (no dissection into σ‐ and π‐MOs is needed); in other words, no assumption on the formal number of π‐electrons (“4n+2”/“4n”) is required to assess aromaticity and the d‐conjugation topology in metallacycles.

Computational Details

All the DFT calculations with full geometry optimizations were performed using Gaussian 09;29 the standard B3LYP30 exchange‐correlation functional was used in all cases and the stationary points showed minima within the frequency calculations. All species studied, except the cupraheterobicycle one, have singlet closed‐shell ground states. Optimized geometries are available on request. For the 15 test‐set d‐metallacycles we employed two basis sets: Stuttgart‐Dresden (SDD)31 with effective core potentials (4d and 5d metals) and 6‐31G* (other atoms). For osmapentalenes we used SDD (Os) and 6‐31G** (C,H), while the restricted open‐shell calculation of the cupraheterobicycle in its doublet ground state was performed using 6‐31++G** (C,H,N,O) and the Watcher's primitive 14s9p5d set supplemented with s, p, d (diffuse), and f (polarization) functions (Cu).32 The axial (zz) components of the nucleus‐independent chemical shifts calculated at 1 Å above/below the ring centroids for the test‐set d‐metallacycles were taken from Ref. [13] while for other systems NICS(1)_ZZ was calculated using Gaussian 09 (the values were averaged over both cyclic units and the positions relative to the ring plane). ACID plots were generated using the ACID 2.0 program provided by the authors26a and Gaussian 09; the continuous set of gauge transformation (CSGT) was used to calculate the ring currents.33 HOMA was calculated using only the C−C, C−N and C−O bonds and the calculation‐consistent parameters from Ref. 6c (d‐metallamonocycles) and the standard parameters provided by Krygowski et al.6b,27 The EDDB‐based partition and orbital‐decomposition were performed within the representation of natural atomic orbitals (NAO)18 as implemented in the NBO 6.0 software34 and the script program written by one of the authors (DS).35 The corresponding EDDB(r) isosurfaces were generated by means of the standard tools from the Gaussian 09 package (Formchk and Cubegen).29 To depict ACID and EDDB(r) we used popular molecular editor and visualizer Avogadro 1.0.36

Conflict of interest

The authors declare no conflict of interest.

D. W. Szczepanik, M. Solà, ChemistryOpen 2019, 8, 219.