Visualization of Neuronal Structures in Wide-Field Microscopy Brain Images

Abstract

Wide-field microscopes are commonly used in neurobiology for experimental studies of brain samples. Available visualization tools are limited to electron, two-photon, and confocal microscopy datasets, and current volume rendering techniques do not yield effective results when used with wide-field data. We present a workflow for the visualization of neuronal structures in wide-field microscopy images of brain samples. We introduce a novel gradient-based distance transform that overcomes the out-of-focus blur caused by the inherent design of wide-field microscopes. This is followed by the extraction of the 3D structure of neurites using a multi-scale curvilinear filter and cell-bodies using a Hessian-based enhancement filter. The response from these filters is then applied as an opacity map to the raw data. Based on the visualization challenges faced by domain experts, our workflow provides multiple rendering modes to enable qualitative analysis of neuronal structures, which includes separation of cell-bodies from neurites and an intensity-based classification of the structures. Additionally, we evaluate our visualization results against both a standard image processing deconvolution technique and a confocal microscopy image of the same specimen. We show that our method is significantly faster and requires less computational resources, while producing high quality visualizations. We deploy our workflow in an immersive gigapixel facility as a paradigm for the processing and visualization of large, high-resolution, wide-field microscopy brain datasets.

1. INTRODUCTION

The understanding of neural connections that underline brain function is central to neurobiology research. Advances in microscopy technology have been instrumental in furthering this research through the study of biological specimens. High-resolution images of brain samples obtained using optical microscopes (average resolution of 200 nm/pixel) and electron microscopes (average resolution of 3 nm/pixel) have made it possible to retrieve micro- and nano-scale three-dimensional (3D) anatomy of the nervous system. The field of connectomics [47] and relevant studies in image processing have developed methods for the reconstruction, visualization, and analysis of complex neural connection maps. Insights gained from these reconstructed neuron morphologies, often represented as 3D structures and 2D graph layouts, can lead to a breakthrough understanding of human brain diseases.

A wide-field (WF) microscope [55] is a type of fluorescence microscope that is often preferred by neurobiologists since it can image a biological sample orders of hours faster than a confocal microscope. Imaging a 40×slice of a sample using a confocal microscope would take 15 hours, whereas a WF microscope would take approximately 1.5 hours for the same sample. Moreover, WF microscopy (WFM) scanners are thousands of dollars cheaper and cause minimal photobleaching to the specimens, in comparison to a confocal or electron microscope. However, due to its optical arrangement, a WF microscope collects light emitted by fluorescent-tagged biological targets in the focal plane, plus all the light from illuminated layers of the sample above and below the focal plane (Fig. 2). As a result, the acquired images suffer from a degraded contrast between foreground and background voxels due to out-of-focus light swamping the in-focus information, low signal-to-noise ratio, and poor axial resolution. Thus, analysis and visualization of WF data is a challenge for domain experts.

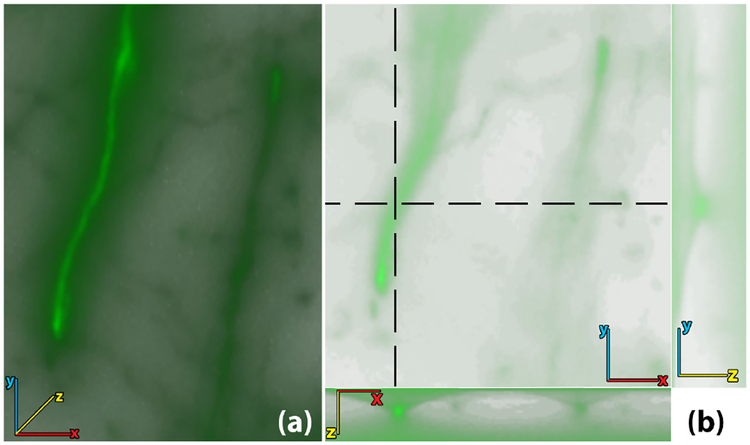
Fig. 2.

WFM images are volumes obtained by focusing at different depths of a thinly sliced specimen. (a) Volume rendering of an unprocessed WFM brain image. (b) Top-left: a 2D cross-sectional view of the volume in the x-y plane. (b) Top-right: 2D cross-section in the y-z plane cut along the vertical dotted line. (b) Bottom: a 2D cross-section in the x-z plane cut along the horizontal dotted line. The cross-sections show how out-of-focus light occludes the low intensity features, making it difficult to analyze structures in 3D.

Most available techniques for 3D visualization of neuronal data are designed specifically for electron [14] and confocal [52] microscopy. Transfer function designs for the volume rendering of microscopy images [6, 53] do not yield effective results when applied to WFM images. Furthermore, the accuracy of neuron tracing and morphology reconstruction algorithms depends on pre-processing image restoration steps [28]. 3D deconvolution techniques [40] attempt to reverse the out-of-focus blur and restore the 3D WFM images with improved contrast and resolution. However, they are complex and time-consuming to compute, often requiring rounds of iterative approximations to produce the corrected image [45], and depend on detailed parameter inputs. These limitations compel neurobiologists to use rudimentary methods, such as manually traversing 2D slices of the volumetric image or using maximal intensity projections for better visibility of features at the cost of losing 3D information.

In collaboration with neurobiologists, we have designed a pipeline for the meaningful visualization of WFM brain images. Rather than employing computationally demanding and time-consuming image processing techniques, we propose a pipeline of simple and efficient visualization-driven techniques as a more practical solution in the daily workflow of neurobiologists. To achieve this goal, we propose a new kind of a distance transform algorithm, called the gradient-based distance transform function. Applying a curvilinear line filter [41] and a Hessian-based enhancement filter to the computed distance field, we generate an opacity map for the extraction of neurites (axons and dendrites) and cell bodies, respectively, from raw WFM data. We enable the effective visualization and exploration of complex nano-scale neuronal structures in WFM images by generating three visualization datasets: the bounded, structural, and classification views. This eliminates the occlusion and clutter due to out-of-focus blur.

We demonstrate our visualization on two display paradigms. For a standard desktop computer display, we use FluoRender [53] as the volume rendering engine since it is specially designed for visualization of microscopy data and can handle rendering large volumes without the requirement for high-end hardware. Additionally, we present a novel visualization paradigm that could be instrumental for future research in neurobiology. We utilize Stony Brook University Reality Deck (RD) [30], the world’s largest immersive gigapixel facility, as a cluster for the processing and visualization of large, high-resolution, microscopy data. We provide neurobiologists with an interactive interface to naturally perform multiscale exploration of the visualization modes generated using our pipeline.

Our workflow allows researchers to visualize results without having to adjust image-correction parameters and transfer functions for the retrieval of useful information. In addition to being more efficient, we show that our method yields better visualization of neuronal structures compared to results from publicly available deconvolution software, as well as compare our results with confocal microscopy volumes of the same specimen. We summarize the contributions of our paper as follows:

• To the best of our knowledge, we are the first to present a framework for the meaningful visualization of neuronal structures in WFM images of brain samples.

• We introduce a novel algorithm to overcome out-of-focus blur in WFM, and extract and visualize neuronal structures efficiently.

• We develop our framework based on feedback and evaluation from neurobiologists and demonstrate its effectiveness on practical WFM brain data.

• We evaluate our method by comparing against confocal microscopy data and the output from a well-known deconvolution algorithm.

• We maximize the visual acuity of the domain scientists for the visualization of massive brain datasets by deploying our visualizations on the RD, the world’s first immersive gigapixel-resolution facility.

2. RELATED WORK

The growing use of high-resolution microscopy technology by neurobiologists and the introduction of recent major initiatives, such as the BRAIN initiative [29], the BigNeuron project [31], and the DIADEM challenge [7], have considerably gained the attention of researchers to develop techniques for qualitative and quantitative analysis of 3D neuron morphology.

Qualitative analysis

Volume rendering systems have been developed for visualizing, segmenting, and stitching microscopy data. Mosaliganti et al. [26] proposed a method for the 3D reconstruction of cellular structures in optical microscopy data sets and correcting axial undersampling artifacts. Wan et al. [53] developed an interactive rendering tool for confocal microscopy data that combines the rendering of multi-channel volume data and polygon mesh data. Jeong et al. [14] extended the domain of microscopy visualization tools by developing a system for the visualization, segmentation, and stitching analysis of large electron microscopy datasets. The techniques proposed in these works are designed specifically for confocal, two-photon, or electron microscopy data, where the acquired images contain only the light emitted by the points in the focal plane. However, due to out-of-focus light spreading through the WFM data and its poor axial resolution, the naïve application of these techniques on WFM data, does not produce effective visualizations.

Another group of techniques aims to segment or classify voxels based on neuronal structures. Janoos et al. [13] presented a surface representation method for the reconstruction of neuron dendrites and spines from optical microscopy data. As a pre-processing step, their method requires the deconvolution of the microscopy images. Nakao et al. [27] proposed a transfer function design for two-photon microscopy volumes based on feature spaces. The feature space they explored for the visualization of neural structures included local voxel average, standard deviation, and z-slice correlation. These features would be ineffective for WFM data, mainly because the intensity values due to the super-imposition of light emitted from the neurons can be greater than weak neurons and there is a low correlation for thin neuronal structures within z-slices. This makes transfer function adjustment an arduous task for neurobiologists. Close to neuron morphology, Läthén et al. [18] presented an automatic technique to tune 1D transfer functions based on local intensity shift in vessel visualization. However, overlapping intensity ranges of the out-of-focus light and neuronal structures make this technique inapplicable to WFM datasets.

Quantitative analysis.

Neuron tracing algorithms and the field of connectomics were introduced for the quantitative analysis of neuron morphology and functioning. Connectomics [47] aims to develop methods to reconstruct a complete map of the nervous system [2,4,57] and the connections between neuronal structures [15,23,46]. Neuron tracing algorithms are designed to automatically or interactively extract the skeletal morphology of neurons. Available tools, such as NeuronJ [24], Reconstruct [9], NeuroLucida 360 [22], and Vaa3D [32] provide methods for semi-automatic interactive tracing and editing of neurons. Automated tracing methods use either global approaches [8,20,49,54,56] or local cues [3,39,58] to trace neuronal skeletal structures. We refer the reader to a detailed chapter by Pfister et al. [34] on visualization in connectomics and a recent survey by Acciai et al. [1] for a full review and comparison of recent neuron tracing methods.

Image processing of WFM data.

The optical arrangement of a WF microscope lacks the capability to reject out-of-focus light emitted by fluorescent-tagged biological targets. The mathematical representation of this blurring is called a point spread function (PSF), which can be determined experimentally [43] or modeled theoretically [5,11,36]. However, it depends on a detailed set of microscopy parameters and is subject to changes in the experimental procedure. Deconvolution is an image processing technique designed to reverse the attenuation caused by the PSF and to restore, as far as possible, the image signals to their true values. Often, deconvolution techniques are iterative since they follow an expectation-maximization framework [21, 37]. Blind deconvolution techniques [19] are used to bypass the need for PSF modeling or for cases where the parameters for PSF estimation are unknown. DeconvolutionLab2 [38] is an open-source software that contains a number of standard deconvolution algorithms commonly used by neurobiologists. Even though deconvolution is an effective method for restoring microscopy images, the time and memory requirements to process large microscopy images make them less practical for regular use by domain experts.

Immersive Visualization.

Immersive visualization systems tap into the human peripheral vision and allow a more effective exploration of three- and higher dimensional datasets. Prabhat et al. [35] performed a user study on the exploration of confocal microscopy datasets on different visualization systems. Their findings reflected that, for qualitative analysis tasks, users perform better in immersive virtual reality environments. Laha et al. [17] examined how immersive systems affect the performance of common visualization tasks. Their studies showed that immersive visualization environments improve the users’ understanding of complex structures in volumes. Specifically in neurobiology, Usher et al. [51] designed a system for interactive tracing of neurons, using consumer-grade virtual reality technology.

3. DOMAIN GOALS

We design our pipeline for visualization and analysis of WFM brain images based on the guidance provided by our neurobiologist collaborators. We identify the following goals:

G1 - Improved quality of neuronal structure visualization.

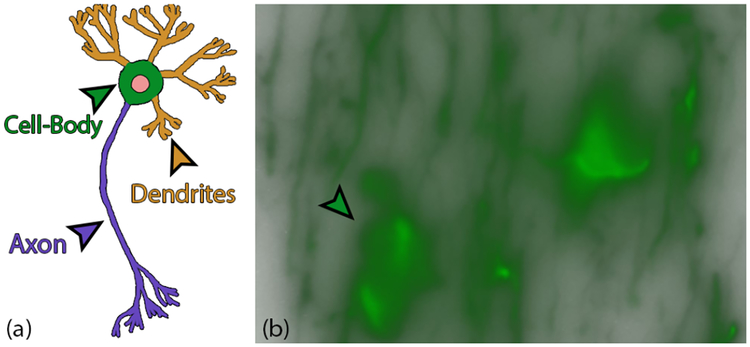
Thresholding is a common practice of domain scientists for the removal of the out-of-focus blur contamination in WFM brain images. This poses two problems: (a) in the process of removing noise, thresholding may also remove neurites and cell-bodies with lower intensities, and (b), since the biological targets do not emit light uniformly, thresholding may cause ‘holes’ or create discontinuity within the structure. Our collaborators want to be able to analyze the 3D structure of the neurites (Fig. 3) and cell-bodies (Fig. 3 (b)) without losing information due to thresholding.

Fig. 3.

(a) Diagram of the anatomy of a neuron. (b) Neurons seen under a WF microscope. The bright green spots in (b) are the cell bodies and the remaining thread-like structures are neurites (axons and dendrites).

G2 - Facilitate quantitative analysis.

Due to limitations on preparation of specimens and the optical arrangement of a WF microscope, some neurites have considerably low intensities. Within the scope of the domain, lower intensity structures cannot be concluded as ‘less significant’, and the relationship between intensity and functioning strength of neuronal structures is open to research. For quantitative analysis, our neurobiologist collaborators consider all structures to be equally important. In practice, the microscopy data is binarized, following thresholding. Our collaborators want to study the axons and dendrites rendered at a uniform intensity value but with some visualization cues that could represent the intensity strength observed in the microscopy output.

G3 - An efficient pipeline to handle large datasets.

The limitation of processing and visualization tools in handling large microscopy datasets can hinder the efficiency of neurobiologists’ workflow to analyze experimental results. Our collaborators want our pipeline to be efficient with the ability to be deployed on commonly available desktop workstations.

4. OUR VISUALIZATION WORKFLOW

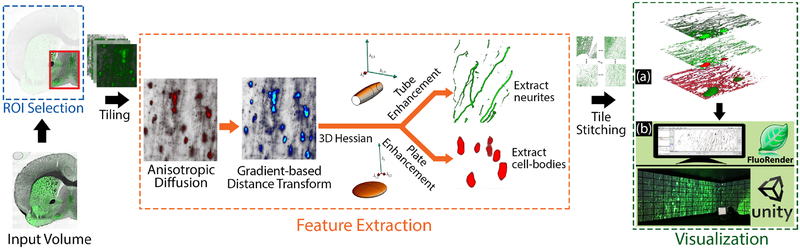
Based on the goals enumerated in Section 3, we present a workflow to overcome the out-of-focus blur in WFM brain images, making them more accessible to domain experts for visual and quantitative analysis. Fig. 4 summarizes our feature extraction and visualization pipeline. Following the region-of-interest (ROI) selection by the users, we divide the ROI into smaller tiles for parallelization of the feature extraction steps. In the following sections, we describe our feature extraction pipeline, where we introduce our novel gradient-based distance transform function followed by the use of structural filters to extract neurites and cell-bodies. We use a desktop setup and an immersive gigapixel facility as two display paradigms for the visualization and exploration of the extracted neuronal information.

Fig. 4.

Our workflow for the visualization of neuronal structures in WFM brain data. The user first selects a ROI from the input volume which is then tiled for effective memory management during the feature extraction stage. Following the gradient-based distance transform algorithm, we process the output tiles to extract neurites and cell-bodies. The final output of our algorithm allows three visualization modes shown in (a): bounded view (top), structural view (center), and classification view (bottom). We present two display paradigms for the visualization of these modes, as shown in(b): FluoRender is used as the volume rendering engine for visualization on a personal desktop computer, and we developed a Unity 3D tool for the interactive exploration of these modes on the RD, an immersive gigapixel facility.

4.1. Feature Extraction

Given the challenges of WFM data, fine structural details are swamped by out-of-focus light voxels and thus visualized with reduced contrast. We design a new gradient-based distance transform function based on the fast marching framework [44] to capture of neuronal features in WFM brain data. Current distance transform functions are introduced for the skeletonization of neurites in confocal and multi-photon microscopy datasets. When applied to WFM data, the computed distance transform blends neurites that run close to each other, and fails to isolate structures that have low contrast with the background (Fig. 5 (b)). The goal of our novel gradient-based distance transform function is to suppress background voxels and grow regions of increasing intensity from the boundary of the neuronal structures to their center. The thresholded response from this distance function is used as a bounding mask to isolate in-focus features in the volume.

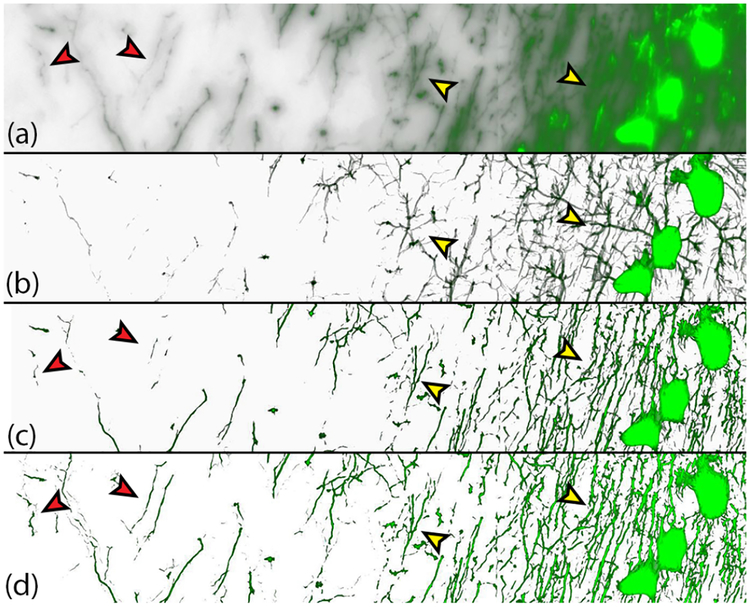
Fig. 5.

Improvements in feature extraction due to our novel gradient-based distance transform function. (a) Raw WFM brain volume. (b) The application of the distance transform function in Eqn. 2. This distance function causes false branching between the neurites, because of the spreading of out-of-focus light, and is unable to recover neurites with lower intensities. (c) Improvements in neurite extraction due to the anisotropic diffusion term we introduce in Eqn. 4. The yellow arrows compare the incorrect branching of features in (b). (d) Improvements due to the introduction of the z distance condition in Eqn. 4. The red arrows compare how some neurites, incomplete or missing in (b), are recovered in (d).

4.1.1. Fast Marching and Gray-Weighted Distance Transform

Fast marching (FM) is a region growing algorithm that models a volume as a voxel-graph and recursively marches the graph from a set of seed points to all the remaining voxels, in a distance increasing order. The voxels are divided into three groups: alive, trial, and far. In the initialization step of the framework, voxels with intensity values corresponding to the ‘background’ are initialized as seed points and are labeled alive, the neighbors of the seed points are labeled trial, and the remaining voxels are labeled far. In each iteration, a trial voxel x, with the minimum distance to the set of alive voxels, is extracted and changed from trial to alive. For an iteration n + 1, the distance d of each non-alive neighbor y of x is updated to the following:

$$d{(y)}_{n+1}=min\left\{d{(y)}_n,d{(x)}_n+e(x,y)\right\}$$ (1)

where d(y)_n is the current distance value of voxel y, and e(x,y) is a distance function that determines the distance value between voxels x and y. Conventionally, distance functions were only applicable to thresholded binary values. APP2 [56], a neuron tracing algorithm, defined a new distance function for grayscale intensities:

$$e(x,y)=\Vert x-y\Vert \cdot I(y)$$ (2)

where ||x − y || is the Euclidean distance between two neighboring voxels x and y, and I(y) is the intensity of voxel y in the raw data. The scalar multiplication between the distance and its intensity in Eqn. 2 results in the FM algorithm outputting increasing distance values towards the center of neuronal structures.

4.1.2. Gradient-based Distance Transform

In WFM images, the intensity of light emitted by biological targets decays with the square of the distance from the focal point in an airy pattern [16]. We introduce a novel gradient-based distance transform function that is modeled on the emission of light in the sample, penalizes voxels contributing to the out-of-focus blur, and effectively recovers neurites with weak intensities.

To automatically select an intensity value for initializing the set of background voxels as seed points, we determine a computed minimum intensity value that would work effectively with our proposed algorithm. The minimum intensity for each z-slice is calculated from the input volume and the distance transform value ϕ(x) for each voxel x in the slice, is initialized as,

$$\varphi (x)=\{\begin{array}{ll}0,alive\hfill & x\in background\hfill \\ \infty ,far\hfill & x\notin background\hfill \end{array}$$ (3)

Our choice of this minimum value is because in WFM data, z-slices away from the focal plane have decreasing intensities and reduced sharpness. Therefore, neurites away from the focal plane may have intensity values smaller than the intensity values of light-blur closer to the focal plane. Thus, to avoid weak intensity neurites being included as seed points, a minimum is calculated for each z-slice.

In the next step, the neighbors of all the background voxels are set as trial, their distance value (ϕ) initialized as the intensity (I) of the voxel in the raw data, and pushed into a priority queue. The trial voxel x with the minimum ϕ value is extracted from the queue and its label is changed to alive. For each non-alive neighboring voxel y of x, ϕ(y) is updated as follows:

$$\varphi {(y)}_{n+1}=\{\begin{array}{ll}min\left\{\varphi {(y)}_n,\varphi (x)\cdot \Vert x-y\Vert +\Delta G\cdot I(y)\right\}\hfill & \Vert x_z-y_z\Vert >0\hfill \\ min\left\{\varphi {(y)}_n,\varphi (x)\cdot \sqrt{\Vert x-y\Vert }+\Delta G\cdot I(y)\right\}\hfill & \Vert x_z-y_z\Vert =0\hfill \end{array}$$ (4)

where ΔG = ||G(x) − G(y)|| is the magnitude difference between the anisotropic diffusion values at x and y, and || x_z − y_z || is the z distance of the voxels. If y is a far voxel, the label is changed to trial and pushed into the priority queue. The trial voxels are iteratively extracted until the priority queue is empty.

The new distance-transform function we propose in Eqn. 4 aims to identify the ‘neuriteness’ of each voxel. Therefore, two new variations are introduced to the gray-weighted distance transform in Eqn. 2. First, the propagation of the distance transform value with respect to the z distance, attributing to the spreading of light from the targets in an airy pattern. Second, the addition of the term ΔG. We observed that regions of out-of-focus light have relatively uniform intensities, and the edge-enhancing property of anisotropic diffusion results in a gradient around the neuronal structures. Therefore, we include the difference in the anisotropic diffusion values between x and y as a weight in Eqn. 4. As a result, the out-of-focus blur regions have ϕ values close to 0. Fig. 5 shows how the new variations introduced in Eqn. 4 improve the extraction of neurites.

The properties that differentiate the neuronal structures from the out-of-focus light are similar to the three criteria motivating the anisotropic diffusion proposed by Perona and Malik [33]: (1) any feature at a coarse level of resolution is required to possess a scale-space at a finer level of resolution and no spurious detail should be generated passing from finer to coarser scales; (2) the region boundaries should be sharp and coincide with the semantically meaningful boundaries at that resolution; and (3) at all scales, intra-region smoothing should occur preferentially over inter-region smoothing. In our workflow, we calculate the anisotropic diffusion G, of the raw volume, as a preprocessing step:

$$G=div\left(D\left(|\Delta u{|}^2\right)\cdot \Delta u\right)$$

with the diffusiveness function,

$$D\left(|\Delta u{|}^2\right)=\frac{1}{1+{(\left|\Delta u\right|/\lambda )}^2}$$

Here, Δu is the convolution of the 3D volume with a gradient kernel, and λ plays the role of a contrast parameter. λ enforces smoothing in regions of out-of-focus light that inherently have low contrast, and enhancement at the boundaries of neuronal structures that inherently have high contrast. We set Δu to be a 3D convolution mask of 26 neighboring voxels that computes finite differences between the voxel intensity values. For λ, we studied the intensity histograms of the neurites and out-of-focus light voxels and determined its value, for our WFM datasets, to be 50 (for an intensity range of 0 − 255).

4.1.3. Extraction of Neurites

From the generated 3D data of intensity values, we use the vesselness feature of the neurites to extract their geometric structure. We apply the 3D multi-scale filter for curvilinear structures, proposed by Sato et al. [41], to extract tubular structures from ϕ. The response from this filter is used to bound the voxels in the raw microscopy volume and thus used as an opacity map. This thresholding results in the removal of the background out-of-focus blur in the visualizations described in Section 4.2.

4.1.4. Extraction of Cell-bodies

The eigenvalues (λ₁,λ₂,λ₃) of the Hessian of a 3D image can indicate the local shape of an underlying object. A cell-body can be identified as an irregular-disk structure in a brain sample (the bright green ‘spots’ in Fig. 10 (a)). Substituting the geometric ratios introduced in Frangi’s vesselness measure [10], an enhancement filter for a 2D plate-like structure can be defined as:

$$O(\lambda )=\{\begin{array}{ll}{e}^{-\frac{R_B^2}{{}_2{\beta }^2}}\cdot (1-e^{-\frac{s^2}{2^{{\gamma }^2}}})\hfill & {\lambda }_j<0\hfill \\ 0\hfill & \text{ otherwise }\hfill \end{array}$$

where s² is the Frobenius norm of the Hessian matrix and R_B is expressed as $R_B=\frac{\left|{\lambda }_2\right|}{\left|{\lambda }_3\right|}$. We apply a 2D plate enhancement filter on each z-slice of the image stack, instead of applying a 3D ‘blob’ filter on the volume, because the poor axial resolution of a WF microscope diminishes the ellipsoidal attribute of the cell-body. Simply applying a blob filter will only extract the centroid of the cell-body. To properly bound the cell-body, the response of the 2D filter from each z-slice is then diffused in the z direction using a Gaussian blur to form a 3D bounding structure. This bounding structure is then used to extract the cell-bodies from the raw data.

Fig. 10.

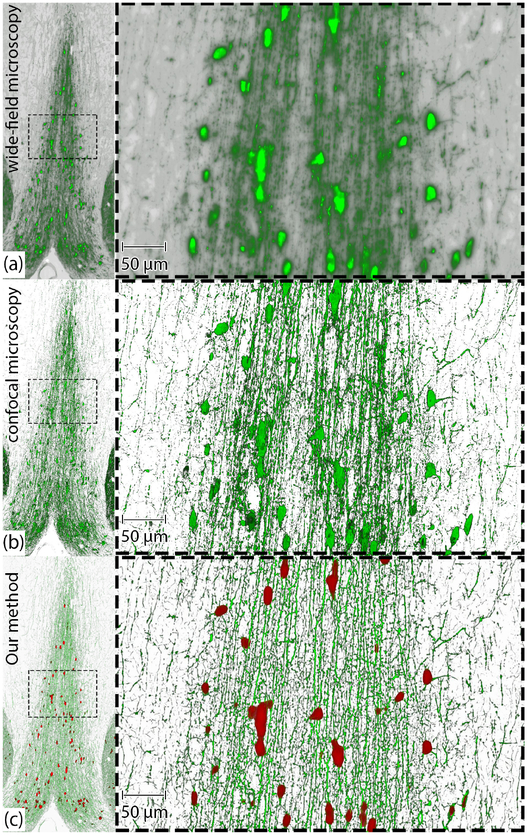
A comparison between volume rendering of (a) raw WFM image (A-20wf), (b) confocal microscopy image (A-20c) of the same specimen, and (c) visualization of A-20wf generated by our workflow. All three sub-figures show the medial septum region of the same mouse brain specimen.

4.2. Feature Visualization

To satisfy G1, improved visualization of the neuronal structures, and G2, binary visualization of neurites, the next step of our workflow generates three visualization modes: (a) bounded view, (b) structural view, and (c) classification view. We use FluoRender as our volume rendering engine for the qualitative visualization of our outputs on a desktop computer. Our choice is attributed to FluoRender’s ability to handle large microscopy data, multi-modal rendering of different volume groups, and its simple and interactive parameter settings.

Bounded view.

We use an opacity map to separate features from out-of-focus blur and background noise, as shown in Fig. 6. The opacity map is computed from our feature extraction pipeline and forms a conservative bound around the neuronal structures. This enables the domain experts to investigate their data without having to threshold and adjust parameters to remove the out-of-focus blur. In contrast, transfer functions and visualization parameters can now be effectively used to adjust the rendering of neuronal structures in the data.

Fig. 6.

Visualization using the bounded view. (a) Volume rendering of raw WFM data. (b) Bounded view visualization eliminating the out-of-focus light noise.

Structural view.

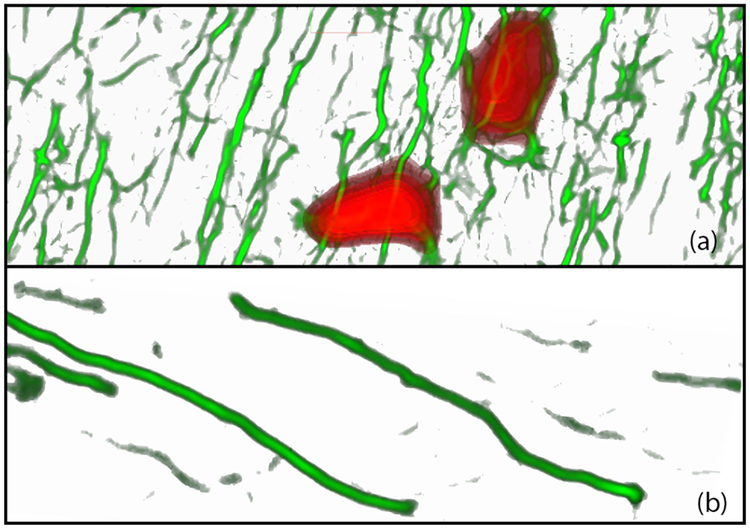
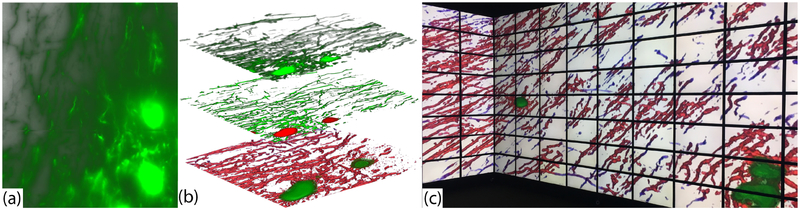
3D analysis of neurites is difficult in regions of dense neuronal network, since the structures in raw WFM are not continuous. To this end, we generate a volume from the responses of the curviliniear and cell-body extraction filters. For this visualization, we use two layers: the neurite layer and the extracted cell-bodies layer. Fig. 7 shows an example of the structural view - the red structures in (a) are the cell-bodies and the green vessel-like structures are the neurites.

Fig. 7.

Visualization of the structural view. (a) The rendering of the extracted geometry of both the neurites (in green) and the cell bodies (in red). (b) The structural view of the neurites seen in Fig. 6 (b).

Classification view.

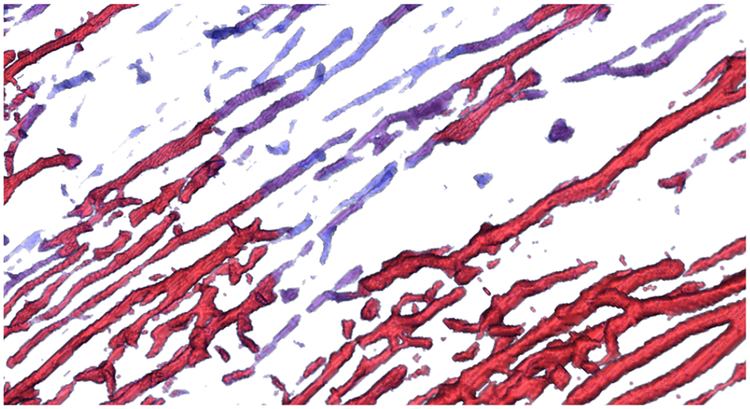
Neurites can have variable intensity in WFM images due to various reasons, such as the structure moving in and out of the sample and due to experimental limitations in the image acquisition process. However, weak intensity neurites are still relevant for domain analysis. Since the bounded and structural views are visualizations of the raw WFM data, our collaborators wanted an additional view that would allow them to analyze all the neuronal structures in the sample, at a uniform intensity, but with a cue that would represent the strength of the structures observed in the raw data. To this end, we make these structures distinguishable by classifying the extracted neurites based on average intensities from the raw images. Such a classification allows us to render the weak and strong structures with different colors rather than using variable opacity, which would make them less visible. Fig. 8 shows an example of the classification view.

Fig. 8.

Classification view of neurites based on feature intensity. Blue color indicates weak intensity neurites while red indicates stronger intensity neurites. This classification helps in locating neurites that may be fragmented or moving across different specimen slices.

Essentially, we classify the neurites into weak and strong based on their signal strength in the original images. We achieve this classification in the following manner. First, we threshold and binarize the extracted structure of neurites from our pipeline to remove noisy fragments and artifacts. Second, we compute the Gaussian-weighted average intensity for every voxel in the original raw image using a standard deviation of 10× the voxel width. Finally, voxels of the binary mask computed in the first step are classified based on the weighted averages computed in the second step. We use an adjustable diverging (blue-to-red) transfer function [25] with uniform opacity to visualize this classification as shown in Fig. 8.

4.3. GigaPixel Visualization

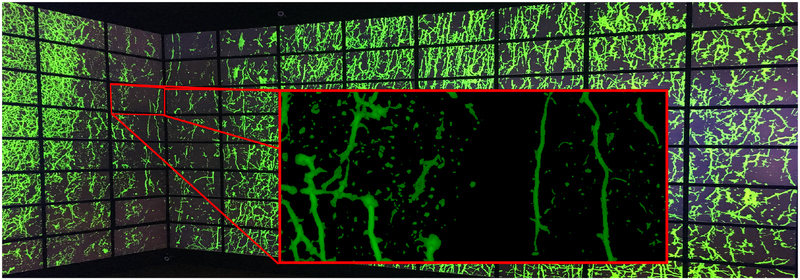
We extend the exploration of WFM brain data to a novel visualization paradigm that could be instrumental for future research in neurobiology. We utilize Stony Brook University RD [30], the world’s largest immersive gigapixel facility, as a cluster for the processing and visualization of massive, high-resolution, microscopy data. The facility offers more than 1.5 gigapixels of resolution with a 360° horizontal field-of-view. Given the complex nano-scale structure of the neuronal network of a brain, we provide our collaborating neurobiologists with the ability to interactively analyze their data and improve their visual acuity on the display platform (Fig. 9).

Fig. 9.

Exploration of the structural view of A-7 from our visualization pipeline on the RD. The inset tile shows the amount of detail that is visible by physically approaching the display walls.

We have developed an application for the rendering of the three data views on the Reality Deck. Users mark their ROI using a desktop computer placed inside the facility. The data is then processed using our workflow and rendered on the display walls. Interaction is driven by two components: (a) using a game controller to globally rotate and translate the data; and (b) by physically approaching the display surfaces and naturally performing multiscale exploration. Additionally, by deploying our visulizations on the RD, we enable neurobiologists with the ability to collaboratively explore their large experimental data. Furthermore, this visualization cluster serves as a computational resource for our processing pipeline, thus achieving G3, an efficient pipeline to handle large datasets.

5. IMPLEMENTATION

WF microscopes with a lateral resolution of 160 nanometers can image a brain slice with dimensions 4mm × 5mm × 0.00084mm that results in an image stack of approximately 10 gigabytes. Processing these large images on a regular basis poses an additional challenge to domain experts. We implement a workflow as shown in Fig. 4 to accommodate G3 of the domain goals. The input format used in our workflow is TIFF, which is commonly used in neurobiology research and is a standard image format used by microscopy manufacturer softwares. First, we use MATLAB to load the microscopy volume, as input from the user, and display a lower resolution 2D maximum-intensity projection for the user to efficiently select an ROI. Since diffusion-based algorithms involve local and identical computations over the entire image lattice, the ROI is then divided into smaller tiles for better memory management during the feature extraction stage.

For each tile, in parallel, the anisotropic diffusion volume is then generated. Next, the anisotropic diffusion volumes and raw tiles are set as input to our gradient-based distance function, implemented in C++. The priority queue was implemented as a Fibonacci heap to efficiently obtain the minimum trial voxel in each iteration. Finally, for extracting the 3D neuronal features from the output of the gradient-based distance function, we used ITK’s [42] Hessian computation functionality and the multi-scale vesselness filter. Based on the anatomical radii of the neurites and cell-bodies, provided by neurobiologists, we used a σ value of 1.0 to 2.0 for the Hessian matrix computation of the neurites, and a σ value of 5.0 for the cell-bodies. After generating the output data from the filter responses for the three visualization modes, the processed tiles are automatically stitched together to create the full ROI volumes as a final output for the user.

We use FluoRender’s [53] rendering engine for the visualization of our modes and introduced the tool to our collaborators for the qualitative analysis of their experimental studies for the desktop setup. The interactive tool for the visualization of the output views on the RD is implemented in Unity3D [50]. We use UniCAVE [48], a Unity3D-based setup for virtual reality display systems. The tool is developed using C# and uses sparse textures to render the large microscopy volumes.

6. RESULTS AND EVALUATION

In this section, we provide a qualitative evaluation of the output volume and visualizations generated using our workflow as compared to Richardson-Lucy (RL) deconvolution results and confocal microscopy images of the same specimen. We also provide a computational performance evaluation by comparing with the RL deconvolution algorithm. This is followed by feedback and discussion on the features from our collaborators.

6.1. Data Preparation

We tested our workflow on WFM datasets of mouse brain slices, imaged by our collaborating neurobiologists. The WF microscope used was an Olympus VS-120, and the imaging parameters were set to a numerical aperture of 0.95 at 40× magnification, with xy resolution of 162.59 nm/pixel and z spacing of 0.84 μm. The results shown in this section are artificial chromosomes-transgenic mice, expressing a tau-green fluorescent protein (GFP) fusion protein under control of the ChAT promoter (ChAT tau-GFP) [12]. Coronal brain sections of 30μm thickness were cut with a cryostat. Serial sections were collected onto slides. Table 1 provides details of the datasets used.

Table 1.

Datasets used in the evaluation of our workflow. A-20wf and A-20c are WF and confocal images of the same specimen, respectively. A-7tile is a smaller region extracted from A-7.

Dataset	Dimensions	Microscopy	Uncompressed size (GB)
A-20wf	3000 × 6500 × 20	WF	0.85
A-20c	3000 × 6500 × 20	Confocal	1.05
A-7	11000 × 12400 × 20	WF	3.10
A-7tile	2750 × 3100 × 20	WF	0.22

6.2. Evaluation

Qualitative comparison.

The primary benchmark, for the qualitative evaluation of our results, is to compare the volume generated by our workflow with raw data obtained using a confocal microscope. In terms of microscopy, the principle advantage of using a confocal microscope over a WF microscope is its optical arrangement: a confocal microscope operates on the principle of a pinhole, which eliminates out-of-focus light, thus improving the fidelity of a 3D image and increasing the contrast of fine structural details. To evaluate our result, a mouse brain-slice was first imaged using WFM, and since a WF microscope does not completely bleach the biological sample, the slice was re-imaged using a confocal microscope. It took 10 minutes to image the slice using a WF microscope and approximately 2 hours for the same slice to be imaged using a confocal microscope.

Fig. 10 shows the volume rendering of (a) the raw WF data, (b) the raw confocal data, and (c) the volume generated using our method for the A-20wf dataset. The left column in Fig. 10 is the zoomed out image of the ROI selected from the brain slice and the right column is 20× magnification into the dotted area of the region in the left column. The bright green irregular plate-like structures in Fig. 10 (a) and (b) are the cell-bodies in the brain, and the remaining vessel-like structures are the neurites. In comparison to confocal microscopy, the neuronal structures in WF data are blurred due to out-of-focus light, making it difficult to study the geometry of the dendrites in 3D. The rendering of our result in (c) shows that our workflow eliminates the out-of-focus blur noise from WFM data and successfully captures the neuronal structures in the slice. The red irregular structures in (c) are the cell-bodies and the green structures are the dendrites. On comparing our result with confocal data, the neurobiologists commented that the visualizations from our pipeline are qualitatively similar to confocal microscopy data.

An alternate method for the removal of out-of-focus blur from WFM data is using image restoration deconvolution algorithms. RL is a standard algorithm readily available in deconvolution tools, such as DeconvolutionLab2 or MATLAB’s deconvolution functions and is widely-used by domain experts. Despite research efforts in image processing, deconvolution is a challenge because the PSF is unknown. Even though blind deconvolution algorithms are proposed to eliminate the need of an accurate PSF, the efficacy of these algorithms depends on an initial estimate. Since our pipeline is designed based on the strength of visualization techniques, our method does not require any input microscopy parameters.

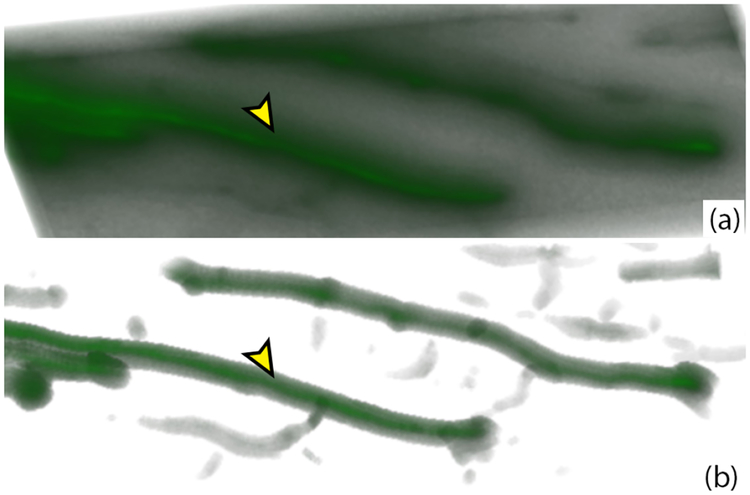
A qualitative comparison between the RL algorithm and the results generated using our method is shown in Fig. 11. The first row shows an area of densely packed neuronal structures (in the striatum region of a mouse brain), the second row shows an area with axons, dendrites, and cell-bodies (in the medial septum region of a mouse brain), and the third row shows a 40× magnification into an area annotated in the medial septum. The volume renderings in each row are of the raw WFM data, the output from RL deconvolution, and the output from our method, from left to right. The parameters for the PSF estimation were obtained from the microscope settings (numerical aperture, objective magnification, CCD resolution, and z-spacing) and the slice preparation information (refractive index of the immersion medium, sample dimensions, and cover glass thickness). The PSF was calculated using Richards and Wolf [36], a shift invariant, vectorial-based diffraction PSF estimation model. We ran the RL algorithm several times, changing the number of iterations for each attempt and found that the algorithm visually converges after 150 iterations based on visual comparison by the domain experts. Therefore, the images shown in the deconvolution column of Fig. 11 are the outputs from 150 iterations of the RL algorithm. It can be observed from the different projections of the zoomed-in dendrite, in the last row of Fig. 11, that even though deconvolution removes most of the surrounding out-of-focus blur, and improves the contrast between background and foreground structures, the area around the dendrite is still cluttered with noise. The result from our method allows the user to directly visualize the dendrite structures, without having to adjust for the out-of-focus light obstruction.

Fig. 11.

Qualitative comparison of volume renderings of raw WFM brain data, Richardson-Lucy (RL) deconvolution of the raw data, and the output result from our workflow for the A-7 dataset. The first row shows a region of the brain with dense neurites, the second row is a region with neurites and cell-bodies, and the last row is a μm-level zoom into the indicated region of the data.

Quantitative comparison.

Cell-body count and terminal field density are two commonly used measures for the quantification of experimental findings in neurobiology. The number of cell-bodies in a brain sample signifies the health of the brain and the network of axons neurites manifests the communication in the brain. In order to compute cell-body count and terminal density, the images are first maximum intensity projected along the z-axis. The images are converted to grayscale, and a threshold is set to determine what gray value is considered signal and what is considered background. Images are binarized after thresholding. For cell-body counts, a diameter criteria is set and counted using a cell counter plugin in ImageJ, which records a total count and tags each included cell-body to ensure no cell is counted twice. Terminal density is computed as a ratio of white (signal) pixels to black (background) pixels.

The results in Table 2 reflect that, compared to the quantitative measurements calculated using confocal imaging, much of the neuronal information in WFM is lost. This is primarily due to thresholding of the WFM data, in order to remove the out-of-focus blur pixels from the calculations. Even though the result from deconvolution improves the quantifications, some useful pixels are still thresholded in the process of removing residual noise. On the other hand, the quantitative measurements of the output generated from our workflow have similar values to that of confocal imaging and no thresholding was required to remove noise from our result. Thus, our method can aid neurobiologists to not only achieve qualitative renderings, but also quantitative results similar to that of confocal microscopy.

Table 2.

Comparison of quantitative measurements performed on the A-20wf WF, A-20wf with the RL-deconvolution, A-20wf with our method, and A-20c confocal data. The output of our method produces measurements that are closer to the confocal benchmark image (A-20c).

Calculation	Raw WFM	RL	Our Method	Confocal Microscopy
Cell-body Count	91	101	128	127
Terminal Field Density	16%	22%	35%	39%

Performance measure.

Our pipeline was tested on two systems, a desktop workstation and the RD. The desktop workstation system was a Windows PC with Intel Xeon E5–2623 CPU, 64 GB RAM, and an NVIDIA GeForce GTX 1080 GPU. The RD is a visualization cluster with 18 nodes. Each node is equipped with dual hexacore Intel Xeon E5645 CPUs, 64 GB RAM, and four AMD FirePro V9800 GPUs. Dataset A-20wf was evaluated on the desktop system and A-7 was evaluated on the RD. Since deconvolution is an alternative method for the restoration of WFM images, for improved qualitative and quantitative analysis of brain samples, we compare the performance of our pipeline with the RL algorithm. Deconvolution was carried out using DeconvolutionLab2 [38], an ImageJ plug-in. Table 3 reports the performance measurements for the two methods.

Table 3.

Performance comparison for datasets A-20wf and A-7 between RL deconvolution algorithm and our method. A-20wf was evaluated on a desktop workstation and A-7 was evaluated on the RD.

Dataset	Method	Peak Memory (GB)	Total Time (hours)	Process
A-20wf	Deconvolution	52.6	23.6	Serial
	Our Method	11.5	1.35	Serial
A-7	Deconvolution	62	18.2	Parallel
	Our Method	8.7	0.45	Parallel

The peak memory, in Table 3, is the maximum amount of RAM required at any stage of the process, and total time is the time elapsed from the start of the processing pipeline until the final output results are generated. Dataset A-7 was divided into 16 tiles and each node of the RD processed two tiles. For both deconvolution and our method, 8 nodes of the RD were used for processing. The performance numbers show that our workflow is orders of hours faster, and more memory efficient than deconvolution. A domain expert would need a powerful, high performance computer to run the deconvolution process on their experimental data and it would make it even more challenging to process microscopy data in a large volume. Our pipeline can be executed on a standard desktop machine and generates results in a reasonable amount of time.

6.3. Domain Expert Feedback

Bounded view.

Our collaborating neurobiologists found that, through this view, they could adjust the gamma and the luminance settings, provided in FluoRender, for their qualitative analysis, which otherwise would have been impossible due the obstructions caused by the amplified noise voxels (Fig. 12).

Fig. 12.

Comparison of visualization parameter adjustment between the raw and bounded view. Column (a) shows a rendering of the raw volume (top) and a bounded view (bottom), at gamma value 1. Column (b) shows their corresponding renderings when the gamma value is changed to 2. Changing visualization parameters makes it difficult to study the features in the raw volume, due to the obstruction caused by noise, whereas for the bounded view, the parameters are only applied to the features bounded by the mask extracted using our algorithm.

Structural view.

This output is particularly useful for our collaborators for their quantitative analysis. The cell-bodies layer gave them a direct cell-body count, without having to perform thresholding to remove all other structures, and the neurite layer can be projected directly in 2D for the terminal field density calculation. Additionally, they found it very useful to be able to shift between the structural and bounded visualization for a detailed analysis of their samples.

Classification view.

In the ROI studied by our collaborators, the neurites often enter from and exit to the surrounding brain slices. The reason why some structures (or part thereof) have weaker intensities in the imaged data, is because the majority of structural mass could be in neighboring slices. Analyzing the result of the classification view, they could identify the region of the neurite entering/exiting the focal plane.

GigaPixel Visualization.

The RD is actively being used by our collaborators in understanding the disposition of complex terminal field networks and the functional mapping of individual cholinergic neurons. Typically, when wanting to visualize a single region of the brain, scientists would have to zoom in to the ROI, and thus, lose the context of the entire brain slice. The panoramic projection of the data on the RD enable domain experts to notice details in the organization of structures from one brain region to another, which otherwise they would not have at such high resolution, side by side. This also allows for mapping of structures within the field of view as experts found they were able to follow structures across large distances, which would have been difficult or impossible on standard desktop screens.

7. CONCLUSION AND FUTURE WORK

We designed a visualization workflow, in collaboration with neurobiologists, for WFM volumes of brain specimens. We achieve this by building a visualization pipeline for a data modality where visualization tools, to the best of our knowledge, have been virtually non-existent. We overcome the inherent out-of-focus blur caused in the WFM images through a novel gradient-based distance transform computation followed by extraction of 3D neuronal structures using 3D curvlinear and 2D plate enhancement filters. Our exploration system provides three different visualization modes (bounded, structural, and classification view) that aim to meet the domain goals. A combination of these views and the ability to switch between them provide with the ability to explore local features through our visualization and compare with the raw images without losing context. Moreover, the ability of our workflow to separate cell-bodies from neurites provides a clutter-free and effective visualization. It also overcomes the unnecessary pre-processing procedures that are otherwise required of WF images for quantitative analyses, such as cell-body counting and estimating neurite density. We evaluated our workflow by providing a qualitative and quantitative comparison between our results, a standard deconvolution technique, and confocal microscopy imagery for the same specimen.

For future work, we plan to upgrade our framework to a complete exploration system by incorporating more sophisticated interaction techniques under immersive visualization platforms, such as gigapixel walls and head-mounted displays. Such immersive platforms can be leveraged for better exploration of large WFM images. Furthermore, we will investigate a GPU-based implementation of our feature extraction workflow to accelerate the computation of our distance function and the Hessian matrix calculation for the feature extraction filters. As a result, this would allow the users to interactively change the parameters of the neurite and cell-body extraction filters and observe their results reflected in the changing opacity maps.

Fig. 1.

Visualization of neuronal structures in wide-field microscopy volumes. (a) Volume rendering of an unprocessed wide-field microscopy volume of a brain slice. (b) Our workflow provides different visualization modes for analysis of the region-of-interest shown in (a): bounded view (top), structural view (center), and classification view (bottom). (c) Visualization deployed on the Reality Deck, an immersive gigapixel resolution platform at Stony Brook University, for effective exploration of large datasets.