Probabilistic Asymptotic Decider for Topological Ambiguity Resolution in Level-Set Extraction for Uncertain 2D Data

Abstract

We present a framework for the analysis of uncertainty in isocontour extraction. The marching squares (MS) algorithm for isocontour reconstruction generates a linear topology that is consistent with hyperbolic curves of a piecewise bilinear interpolation. The saddle points of the bilinear interpolant cause topological ambiguity in isocontour extraction. The midpoint decider and the asymptotic decider are well-known mathematical techniques for resolving topological ambiguities. The latter technique investigates the data values at the cell saddle points for ambiguity resolution. The uncertainty in data, however, leads to uncertainty in underlying bilinear interpolation functions for the MS algorithm, and hence, their saddle points. In our work, we study the behavior of the asymptotic decider when data at grid vertices is uncertain. First, we derive closed-form distributions characterizing variations in the saddle point values for uncertain bilinear interpolants. The derivation assumes uniform and nonparametric noise models, and it exploits the concept of ratio distribution for analytic formulations. Next, the probabilistic asymptotic decider is devised for ambiguity resolution in uncertain data using distributions of the saddle point values derived in the first step. Finally, the confidence in probabilistic topological decisions is visualized using a colormapping technique. We demonstrate the higher accuracy and stability of the probabilistic asymptotic decider in uncertain data with regard to existing decision frameworks, such as deciders in the mean field and the probabilistic midpoint decider, through the isocontour visualization of synthetic and real datasets.

1. Introduction

Uncertainty visualization has been recognized as one of the top research challenges in the domain of scientific visualization [16,17]. Algorithmic and hardware limitations can modulate data in unexpected ways as data is processed through various phases of the visualization pipeline. The noise introduced in data due to limitations on data processing can significantly impact the final visualization. Brodlie et al. studied the sources of errors in the visualization pipeline [5] and demonstrated that the quantification of uncertainty in visualization is important in avoiding misleading interpretations regarding underlying data. In other words, uncertainty quantification can potentially improve the reliability of decision support systems [9, 40], especially for sensitive applications. We study uncertainty quantification in the context of level-set visualization.

Level-set visualization is one of the fundamental data visualization paradigms for interpreting scalar and vector field data in a broad spectrum of applications, such as medical imaging and flow visualizations for aerodynamics and hydrodynamics. The marching squares (MS) algorithm is a 2D version of the marching cubes algorithm [23] for level-set visualizations. The MS algorithm assumes a piecewise bilinear interpolation model, and the equation for the bilinear interpolant corresponds to the equation for hyperbolae. The robust implementation of the MS algorithm aims to reconstruct an isocontour that is topologically and geometrically consistent with the piecewise bilinear interpolation model.

For the MS algorithm, saddle points are the points where curves of hyperbolae intersect asymptotically. Hence, saddle points are considered as critical points in scalar and vector fields since they represent points where the topology for isocontours can either merge or split. The topological ambiguity in the MS algorithm, therefore, arises near saddle points since they can represent either a split or a merge configuration. A careful analysis is needed near the saddle points to avoid topological inconsistencies with the piecewise bilinear interpolation. The midpoint and asymptotic decider are well-known mathematical techniques for resolving topological ambiguities. The latter has been shown to be more accurate than the former [21]. The existing methods for topological ambiguity resolution assume that the sampled data values at the grid vertices are certain. However, in uncertain data, the ambiguity or uncertainty in topological configurations escalates. In our contribution, we address the issue of topological ambiguity resolution in the MS algorithm when sampled data is uncertain.

The uncertainty in data leads to uncertainty in the underlying bilinear interpolation function for each cell of a grid and, hence, their saddle points. We, therefore, define three terms relevant to the bilinear interpolation model for uncertain data. First, we define an uncertain cell as the cell with uncertain data at the cell vertices. Second, we define saddle points for an uncertain cell as a union of the saddle points of all possible bilinear interpolation functions for an uncertain cell. Lastly, we define saddle values for an uncertain cell as the data values attained at the saddle points for the same uncertain cell. In our contribution, we analytically derive variations in the saddle values for an uncertain 2D cell without needing to actually compute its saddle points.

The proposed derivations assume uniform and nonparametric noise for modeling data uncertainty at grid vertices. The nonparametric density models have been advocated for a more realistic characterization of noise distributions when compared to parametric density models [32]. Nonparametric models add flexibility to capture multimodal distributions. We initially assume a uniform noise model for deriving variations in saddle values of an uncertain cell. The density characterization for uniform noise assumption works as a building block for characterizing saddle value densities assuming nonparametric noise. Our results in Figure 8 show that the nonparametric noise assumption successfully captures multimodel probabilistic variations in saddle values for an uncertain 2D cell.

Fig. 8:

Topological ambiguity resolution for a 2D uncertain cell using probabilistic decision frameworks. In the left two columns, the similar shapes of the distributions for the Monte Carlo simulations and the analytical approach confirm the correctness of the derivations in sections 5.1 and 5.2. The right column illustrates the inconsistency of the topological decisions for the probabilistic asymptotic and the probabilistic midpoint deciders.

Athawale et al. [2,3] recently investigated positional uncertainty in level-set visualizations for uncertain scalar fields. Our work is primarily motivated by two major aspects of their contributions, specifically an analytic framework for fast and accurate characterization of the densities at the spatial positions of interest and a probabilistic decision framework for topological ambiguity resolution in uncertain data. In their work, the advantages of analytical models for level-set extraction in uncertain data over Monte Carlo simulations were demonstrated for nonparametric density estimation. Analytical models provide performance gain and higher computational accuracy. In our work, we devise an analytic solution that exploits the framework for the probabilistic midpoint decider [3] (also discussed in section 3) to resolve topological ambiguities for isocontours in uncertain 2D data.

Contributions:

Our contribution in this paper is threefold. First, we derive the density, in closed form, that characterizes variations in saddle values for an uncertain 2D cell. The derivation assumes uniform and nonparametric densities for modeling data uncertainties at the cell vertices, and it uses the concept of ratio distribution [2] for analytic formulation. Second, we study the issue of topological ambiguity resolution in uncertain data by leveraging the framework for the probabilistic midpoint decider [3]. We devise the probabilistic asymptotic decider for resolving topological ambiguities in noisy data. The probabilistic asymptotic decider leverages the computation of saddle value densities derived in our first contribution to efficiently decide topology in the marching squares (MS) algorithm. The proposed probabilistic framework allows us to quantify and visualize uncertainty in topological decisions. We encode topological uncertainty into visualization by employing a colormapping technique. Lastly, we confirm the higher accuracy and resilience of the statistical model for the proba bilistic asymptotic decider with regard to existing decision frameworks through visualization. The existing frameworks include the asymptotic and midpoint deciders in the mean field and the probabilistic midpoint decider. The superiority of isocontour reconstruction for the probabilistic asymptotic decider is confirmed in the results shown in Figure 1.

Fig. 1:

The comparison of the topological decision frameworks for isocontour reconstruction in uncertain data. The marked squares (white/colored) in all images denote underlying grid cells that have topological ambiguity. In uncertain data, the proposed probabilistic asymptotic decider (image (d)) recovers the groundtruth isocontours better than the isocontours reconstructed using the decision frameworks for images (b) and (c). Moreover, the probabilistic decision frameworks allow us to encode the confidence in topological decisions into the visualization. For example, in images (c) and (d), red indicates relatively low, white denotes moderate, and blue denotes relatively high confidence in isocontour topology. The isocontour breaks more often near the red cells.

The rest of the paper is organized as follows: In section 2, we briefly discuss advances in the fields of topological analysis of level-set extraction and uncertainty visualization. In section 3, we summarize the asymptotic, midpoint, and probabilistic midpoint decider [3] frameworks for topological ambiguity resolution in the MS algorithm. Next, we mathematically present the research question of the characterization of uncertainty in saddle values for an uncertain 2D cell in section 4. The probabilistic asymptotic decider is derived in closed form in section 5 for the uniform and nonparametric noise models. Finally, we show the visualization results for the probabilistic asymptotic decider in section 6.

2. Related Work

The state-of-the-art techniques in the field of uncertainty visualization have been reviewed by Bonneau et al. [4]. We briefly discuss important contributions to uncertainty visualization relevant to the fields of level-set topology and statistical modeling. Two popular techniques for summarizing spatial variations in uncertain data are contour [38] and surface boxplots [8]. Both methods derive quartiles of positional variations in level sets using the concept of functional data depth [22]. Pöthkow and Hege [31, 33] devised probabilistic marching cubes for the visualization of spatial uncertainty in isosurfaces when data noise is modeled using Gaussian distributions. The analysis of probabilistic marching cubes was further expanded to take into account nonpara-metric models [32]. The contour tree data structure proposed by Carr et al. [6] is useful for gaining insight into topological events associated with isosurfaces. These events include appearance, disappearance, merging, or splitting of the geometric components of isosurfaces at critical points, such as local minimum/maximum or saddles, in a scalar field. Wu and Zhang [39] studied the effect of data uncertainty on contour trees and devised novel methods for integrating data uncertainty into contour trees. Agarwal et al. [1] developed probabilistic models for characterizing the variation in distance between the nodes of contour trees for uncertain data.

The visualization of distribution datasets is another important research challenge. In distribution datasets, each spatial data point is modeled as a distribution function. Kao et al. [19] and Luo et al. [25] devised statistical shape descriptors for visualization of uncertainty in distribution datasets with the least possible clutter. The ProbVis system developed by Potter et al. [34] enables users to explore the probability and cumulative density functions interactively. Hazarika et al. [13] characterized data uncertainty using copula-based mixed distribution models to study isosurface topology. The copula-based mixture models add the flexibility to characterize dependency between multiple random variables while allowing users to choose among a family of distributions for each random variable independently.

A considerable body of literature addresses the challenge of uncertainty quantification for visualizing vector field data and direct volume rendering. Otto et al. [28] studied uncertainty in streamline flows, as well as positional uncertainty in critical points for 2D and 3D flow fields assuming Gaussian noise models. Djurcilov et al. [7] mapped the opacity in transfer functions to data uncertainty and colormapped scatter plot space by segmenting out regions of low and high spatial variations. Sakhaee and Entezari [36] and Liu et al. [20] modeled data uncertainty with parametric, nonparametric, and Gaussian mixture models and integrated uncertainty into the ray-casting technique for direct volume rendering. Colormapping [35], point-displacement [10, 11], animation [24], and glyphs [14] are a few of the techniques to encode quantified uncertainty into visualization.

3. Topological Deciders for the MS Algorithm

In this section, we briefly describe the asymptotic, midpoint, and probabilistic midpoint decider frameworks for topological ambiguity resolution in the MS algorithm. Let (x,y) represent the cell domain, where x ∈ [0,1] and y ∈ [0,1]. Let d₀₀, d₀₁, d₁₀, and d₁₁ denote the data values at the cell corners. For the bilinear interpolation model, the data values within a cell can be represented with the following hyperbolic equation:

$$d_{xy}=a_{1}x+a_{2}y+a_{3}xy+a_4$$ (1)

Let s represent the data values at the intersection of asymptotes (saddle points) of the equation of hyperbolae presented in Equation (1), and let m represent data values at the midpoints of 2D cells. The values of s and m can be derived using the following two equations [21,27]:

$$s=\frac{d_{01}\cdot d_{10}+d_{00}\cdot d_{11}}{d_{00}-d_{01}-d_{10}+d_{11}}$$ (2)

$$m=\frac{d_{00}+d_{11}+d_{10}+d_{01}}{4}$$ (3)

The asymptotic decider and the midpoint decider resolve ambiguous isocontour topology by investigating values of the variables s and m, respectively (section 17.4.1, [21])

The probabilistic midpoint decider (section 3.3, [3]) resolves topological ambiguities when sampled data is uncertain and data uncertainty is characterized by noise distributions. The uncertainty in data values at the position (x,y) is represented by a random variable D_xy. Thus, the random variable corresponding to the midpoint of a 2D cell can be represented as M = D_0.5,0.5. For the independent noise assumption, the density of M is computable in closed form through the convolution of densities at the cell vertices. The density of the random variable M can be leveraged to probabilistically decide the isocontour topology.

4. Problem Description

The noise in data values at the cell vertices introduces uncertainty in the values attained by the saddle points of the bilinear interpolant for (unknown) groundtruth data. We represent a random variable S to denote the variations in the saddle values for an uncertain 2D cell. A range of the values for the random variable S can be derived using the following formula:

$$S=\frac{D_{01}\cdot D_{10}+D_{00}\cdot D_{11}}{D_{00}-D_{01}-D_{10}+D_{11}}$$ (4)

For the isovalue k, the topological ambiguity can be resolved by computing the most frequent sign attained by the saddle points for an uncertain cell. We presume that the saddle points for an uncertain cell are the proper positions for investigating data to decide topology because of the constant choice of the interpolation model (bilinear) for all realizations of uncertain data. Mathematically, we compute the probability that the saddle values for an uncertain 2D cell are less than k:

$$Pr(S<k)=Pr\left(\frac{D_{01}\cdot D_{10}+D_{00}\cdot D_{11}}{D_{00}-D_{01}-D_{10}+D_{11}}<k\right)$$ (5)

If Pr(S < k) > 0.5, the most probable sign for the saddle point of the groundtruth data is presumed to be negative and vice versa. We name this decision framework the probabilistic asymptotic decider. We rewrite Equation (5) in terms of two new random variables P and Q, where each random variable represents a combination of the sum and the product of the random variables D_xy at the cell corners:

$$\begin{array}{l}Pr(S<k)\hfill \\ =Pr\left(D_{01}\cdot D_{10}+D_{00}\cdot D_{11}<k\cdot \left(D_{00}-D_{01}-D_{10}+D_{11}\right)\right)\hfill \\ =Pr\left(D_{01}\cdot D_{10}+D_{00}\cdot D_{11}-k\cdot \left(D_{00}-D_{01}-D_{10}+D_{11}\right)<0\right)\hfill \\ =Pr\left(D_{01}\cdot D_{10}+k\cdot \left(D_{01}+D_{10}\right)+D_{00}\cdot D_{11}-k\cdot \left(D_{00}+D_{11}\right)<0\right)\hfill \\ =Pr\left(S^{\prime }=P+Q<0\right),\text{ where}\hfill \\ P:=D_{01}\cdot D_{10}+k\cdot \left(D_{01}+D_{10}\right)\hfill \\ Q:=D_{00}\cdot D_{11}-k\cdot \left(D_{00}+D_{11}\right)\hfill \end{array}$$ (6)

In a similar manner, the decision framework for the probabilistic midpoint decider can be modeled by turning each quantity in Equation (3) into a random variable:

$$\begin{gathered} Pr\left(M<k\right)=Pr\left(\frac{D_{01}+D_{10}+D_{00}+D_{11}}{4}<k\right) \\ =Pr\left(M^{\prime }=D_{01}+D_{10}+D_{00}+D_{11}-4k<0\right) \end{gathered}$$ (7)

5. Saddle Value Density for an Uncertain Cell

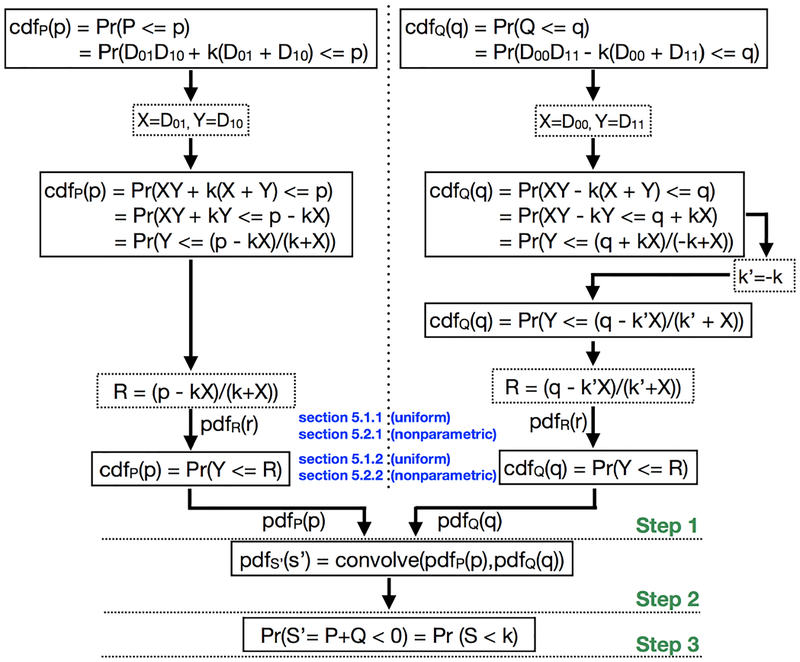
In this section, we present an analytic derivation for computing Pr(S < k) = Pr(S′ = P+Q < 0) (Equation (6)). The topological decision of the probabilistic asymptotic decider depends upon the value of Pr(S < k), as described in section 4. The steps for computing Pr(S < k) are depicted in Figure 2. The approach consists of three primary steps. First, we compute the probability densities pdf_P(p) and pdf_Q(q) for the independent random variables P and Q, respectively. The independent computation of pdf_P(p) and pdf_Q(q) is shown by the two columns of Figure 2 separated by a dotted vertical line. Second, the density of a random variable S′ is computed through convolution of the densities pdf_P(p) and pdf_Q(q) computed in step one since S′ = P + Q. Lastly, the density pdfs′ (s′) is integrated to evaluate Pr(S′ < 0), which is equivalent to computing Pr(S < k) (Equation (6)).

Fig. 2:

The steps for computing Pr(S < k). Step 1: Computation of the densities pdf_P(p) and pdf_Q(q). Both densities are computed independently, as indicated by the two columns separated by a dotted vertical line. The dotted blocks denote the temporary renaming of variables. Step 2: Computation of pdf_S′ (s^′). Step 3: Computation of Pr(S^′ = P + Q < 0).

We provide a closed-form derivation of step 1, i.e, the computation pdf_P(p) and pdf_Q(q) in sections 5.1 (uniform noise) and 5.2 (non-parametric noise). We show only the derivation for the computation of pdf_P(p) (the left column in Figure 2) because pdf_Q(q) (the right column in Figure 2) is derived using a similar approach. A short description of steps 2 and 3 is provided in section 5.3.

5.1. Formulation of pdf_P(p) Assuming Uniform Noise

Initially, we derive the cumulative density function of a random variable P, cdf_P(p). The process is depicted in the left column of Figure 2. The pdf_P(p) is obtained by taking the derivative of cdf_P(p) with respect to variable p. The cumulative density function of a random variable P can be represented as:

$$\begin{gathered} cd{f}_P\left(p\right)=Pr\left(P\le p\right) \\ =Pr\left(D_{01}\cdot D_{10}+k\cdot \left(D_{01}+D_{10}\right)\le p\right) \end{gathered}$$ (8)

For simplicity of discussion, we rename the variables D₀₁ and D₁₀ as X and Y, respectively. The temporary renaming of random variables is indicated by the dotted blocks in Figure 2. Equation (8) can be alternatively written as follows:

$$\begin{gathered} cd{f}_P\left(p\right)=Pr\left(P\le p\right) \\ =Pr\left(XY+k\left(X+Y\right)\le p\right) \\ =Pr\left(XY+kX+kY\le p\right) \\ =Pr\left(XY+kY\le p-kX\right) \\ =Pr\left(Y\le \frac{p-kX}{k+X}\right) \\ =Pr\left(Y\le R\right),\text{ where }R=\frac{p-kX}{k+X} \end{gathered}$$ (9)

Thus, the computation of Pr(Y ≤ R) is equivalent to computing cdf_P(p). We show the analytic formulation of Pr(Y ≤ R) when random variables X and Y are uniformly distributed. Let X ~ U(a,b) and Y ~ U(c,d). For both uniform distributions, we assume a < b and c < d. We break down the formulation of Pr(Y ≤ R) into two steps. First, the distribution of a ratio random variable $R=\frac{p-kX}{k+X},$ pdf_R(r), is derived analytically. The second step uses pdf_R(r) computed in the first step to evaluate Pr(Y ≤ R) in closed form. The computation of pdf_R(r) is indicated on arrows in Figure 2 since it is fed as input for the computation of Pr(Y ≤ R).

5.1.1. Step 1: Formulation of pdf_R(r)

We use the concept of ratio distribution [2] for the formulation of pdf_R(r). Let $R=\frac{R_1}{R_2},$ where R₁ p − kX and R₂ = k + X. We break down the computation of pdf_R(r) into three parts. First, we compute the joint density of R₁ and R₂. In the second part, the cumulative density cdf_R(r) is computed from the joint density computed in the part one. Last, pdf_R(r) is computed by taking the derivative of cdf_R(r) with respect to r.

We initially describe an approach for computing the joint density of random variables R₁ and R₂, as depicted in Figure 3. For axis R₁, p−kb < p−ka or p ka < p−kb depending upon the isovalue k. On the contrary, order of the quantities k + a and k + b on the axis R₂ does not depend upon the isovalue k, and in all cases k + a < k + b since a < b. For now, let p kb − p<ka on the axis R₁. The support of joint density of random variables R₁ and R₂ is a line since both random variables depend only on X. In Figure 3, the tilted solid line segment between points end₁ and end₂ denotes the support of the joint density of R₁ and R₂. Throughout this paper, end₁ and end₂ indicate the positions (k+a, p−ka) and (k+b, p kb), respectively. Also, note that the height of the joint density at all points between end₁ and end₂ is constant since X assumes a uniform distribution.

Fig. 3:

The ratio distribution of random variable $R=\frac{p-kX}{k+X}.$ The tilted solid line depicts the support of the joint distribution of random variables R₁ and R₂. The cumulative density function cdfR(r) is proportional to the length of the line segment bounded by the point I and the endpoint end2 on which R ≤ r.

Next, we derive cdf_R(r). The cumulative density can be computed by sweeping the dotted line $\frac{R_1}{R_2}=r$ depicted in Figure 3 from r = −∞ to r = ∞. For the specific value of r, cdf_R(r) is an integral of the joint density of variables R₁ and R₂, where $R=\frac{R_1}{R_2}\le r.$ For example, for the dotted line shown in Figure 3, the line segment $\left(I=\left(\frac{k^2+p}{k+r},\frac{r\left(k^2+p\right)}{k+r}\right),en{d}_2\right)$ represents a portion of the joint density of R₁ and R₂ where $\frac{R_1}{R_2}\le r.$ Thus, cdf_R(r) can be computed by finding the length of the line segment (I, end₂) and dividing it by the total length of a line segment (end₁, end₂).

Lastly, pdf_R(r) is obtained by taking the derivative of cdf_R(r) with respect to r. For uniformly distributed random variable X, the probability density of a random variable $R=\frac{p-kX}{k+X},$ in closed form, is given by:

$$pd{f}_R\left(r\right)=\frac{k^2+p}{{\left(k+r\right)}^2\left(b-a\right)}$$ (10)

Figure 4 shows a sample result for the closed-form computation of pdf_R(r). For the result presented, X ~ U(2,4), the isovalue k is 4, and p is chosen as 40. The same shapes of Monte Carlo simulations and the analytical formulation validate the derivation of pdf_R(r).

Fig. 4:

Monte Carlo (left) vs analytic computation (right) of pdf_R(r).

The approach presented for computation of pdf_R(r) is applicable when the support of the joint density of R₁ and R₂ lies in any of the four quadrants or spans multiple quadrants. For the quadrants other than the first quadrant, the distribution function pdf_R(r) stays the same; however, the domain of pdf_R(r) can be finite and continuous or infinite and discontinuous. Figure 5 illustrates the two cases. In Figure 5a, the support of the joint density of R₁ and R₂ spans the second and the third quadrants. In this case, the domain of pdf_R(r) is finite and continuous, where r ∈ [end₁,end₂]. Here, r∈ [end₁,end₂] indicates that the ratio r lies between the slopes for the2 points end₁ and end₂. In Figure 5b, the support of the joint density of R₁ and R₂ spans the first, second, and fourth quadrants. In this case, the domain of pdf_R(r) is infinite and discontinuous, where $r\in \left[-\infty ,en{d}_1\right]\cup \left[en{d}_2,\infty \right].$ We tabulate the domain of integration cdf_R(r) for all quadrant cases in the supplementary material.

Fig. 5:

The domain of pdf_R(r): (a) r [end₁,end₂]. (b) r [−∈,end₁] U [end₂, ∞]. The domain of integration in both cases can be interpreted by finding the slopes of the dotted line for which it intersects the tilted solid line, as the slope is varied from −∞ to ∞.

5.1.2. Step 2: Formulation of Pr(Y ≤ R)

In this section, we derive Pr(Y≤ R) in closed form using pdf_R(r) formulated in step 1. Pr(Y ≤ R) is equivalent to computing the cumulative distribution function of a random variable P = kX +kY +XY (Equation (9) and Figure 2 (left column)). We present the derivation of Pr(Y ≤ R) for two cases, specifically when the domain of pdf_R(r) is either finite or infinite, as illustrated in Figure 5.

To compute Pr(Y < R), we again find the joint density of random variables Y and R. Figure 6a illustrates the joint density of random variables Y and R when R is finite and continuous, and Figure 6b illustrates the joint density when R is infinite and discontinuous. The joint density is a product of distributions pdf_Y(y) and pdf_R(r) since random variables Y and R are independent. The support of the joint density is a rectangle. The rectangle is bounded by the range [c,d] along the Y axis, and the range $\left[\frac{p-kb}{k+b},\frac{p-ka}{k+a}\right]$ along the R axis. Note that c < d, but the order of $\frac{p-kb}{k+b}$ and $\frac{p-ka}{k+a}$ is interchangeable for the axis R depending upon the signs of p, k, a, and b.

Fig. 6:

The joint density of random variables Y and R assuming the uniform noise model. In both subfigures, the distribution is bounded on the Y axis in the range [c,d]. In subfigure (a), the distribution along the R axis is bounded between $\left[\frac{p-kb}{k+b},\frac{p-ka}{k+a}\right].$ In subfigure (b), the distribution along the R axis is in the range $\left[-\infty ,\frac{p-kb}{k+b}\right]\cup \left[\frac{p-ka}{k+a},\infty \right].$ In the blue regions, Y≤ R at any position R = r₁ (illustrated by the purple line), and brown highlights the domain of integration for computing Pr(Y ≤ R).

Having computed the joint density of random variables Y and R, we take a two-step approach for evaluating Pr(Y ≤ R). First, we find the positions where Y≤ R. Second, we integrate the joint density of Y and R at positions where Y≤ R. The blue region highlighted in Figure 6 represents the half space generated by line $\frac{Y}{R}=1$ and indicates positions where Y≤ R at any position R = r₁. For example, the position R = r₁ is indicated by a purple line in Figure 6, and every point on the purple line has Y≤ R₁. The domain of integration to compute Pr(Y≤R) is the intersection of the blue region and the support of the joint distribution of Y and R. The domain of integration is highlighted in brown.

The joint density of Y and R is integrated over the brown regions in Figure 6a to obtain the closed-form formulation of Pr(Y≤R). In Figure 6a, Pr(Y ≤ R) can be computed using a double integration over the brown area as follows:

$$Pr\left(Y\le R\right)={\int }_{r=\frac{p-kb}{k+b}}^{r=\frac{p-ka}{k+a}}{\int }_{y=c}^{y=r}pd{f}_Y\left(y\right)\cdot pd{f}_R\left(r\right)dydr$$ (11)

We substitute $pd{f}_Y\left(y\right)=\frac{1}{d-c}$ and pdf_R(r) derived in Equation (10) into Equation (11). The substitution simplifies the double integration into a single integration as:

$$Pr\left(Y\le R\right)={\int }_{r=\frac{p-kb}{k+b}}^{r=\frac{p-ka}{k+a}}\frac{r-c}{d-c}\cdot \frac{k^2+p}{{\left(k+r\right)}^2\left(b-a\right)}dr$$

In Figure 6b, Pr(Y < R) can be computed as a sum of three double integrations over the brown area:

$$Pr\left(Y\le R\right)={\int }_{r=c}^{r=\frac{p-kb}{k+b}}{\int }_{y=c}^{y=r}pd{f}_Y\left(y\right)\cdot pd{f}_R\left(r\right)dydr+{\int }_{r=\frac{p-ka}{k+a}}^{r=d}{\int }_{y=c}^{y=r}pd{f}_Y\left(y\right)\cdot pd{f}_R\left(r\right)dydr+{\int }_{r=d}^{r=\infty }{\int }_{y=c}^{y=d}pd{f}_Y\left(y\right)\cdot pd{f}_R\left(r\right)dydr$$ (12)

Although the limits of the last integral in Equation 12 contain ¥, it is computable in closed form. A single integral corresponding to the third double integral in Equation 12 after substitution of pdf_Y(y) and pdf_R(r) is:

$$Pr\left(Y\le R\right)={\int }_{r=d}^{r=\infty }\frac{k^2+p}{{\left(k+r\right)}^2\left(b-a\right)}dr$$ (13)

The integration in Equation (13) is an inverse function of r, specifically $\frac{k^2+p}{\left(k+r\right)\left(a-b\right)}.$ Thus, the integration value goes to zero in the limit when r = ∞. Thus, the computation of Pr(Y ≤ R) can be obtained in closed form even if the domain of R is infinite. We tabulate the cases for the domain of integration of cdf_P(p) in the supplementary material when the support of the joint density of Y and R is finite or infinite. Having computed cdf_P(p) = Pr(Y≤ R) (Equation (9)), we take the derivative of cdf_P(p) with respect to p to compute pdf_P(p).

5.2. Formulation of pdf_P(p) Assuming Nonparametric Noise

The kernel density estimation for a random variable X is mathematically represented as:

$$\begin{gathered} pd{f}_X\left(x\right)=\frac{1}{n}\sum _{i=1}^{i=n}{K}_h\left(x-x_i\right),\text{ where} \\ n=\text{Number of kernels} \\ h=\text{Bandwidth} \\ {K}_h\left(x-x_i\right)=\text{Kernel of width }h\text{ centered at }{x}_i \end{gathered}$$ (14)

Equation (14) represents a uniform noise model when n = 1 and the kernel is uniform. When n > 1, we repeat the steps described in subsection 5.1 for computing pdf_P(p).

5.2.1. Step 1: Formulation of pdf_R(r)

Let n₁ denote the number of kernels in nonparametric density pdf_X(x), and let cdf_Rki(r) denote the cumulative density function for the i’th kernel k_i in pdf_X(x). Then cdf_R(r) is a sum of the cumulative density functions computed over all base kernels of pdf_X(x). Mathematically,

$$cd{f}_R\left(r\right)=1/n_1\sum _{i=1}^{i=n_1}cd{f}_{R_{ki}}\left(r\right)$$ (15)

For example, consider Figure 7a for the computation of cdf_R(r). Suppose pdf_X(x) has a kernel count of n₁ = 2 and pdf_Y(y) has a kernel count of n₂ = 2. Let the base kernel for both nonparametric distributions be uniform. Let k₁ and k₂ denote base uniform kernels of pdf_X(x). In Figure 7a, the two solid lines indicate the domain of integration for kernels k₁ and k₂ in order to compute cdf_R(r). We process each line individually using the approach in section 5.1.1 to compute cdf_Rki and sum the cumulative density over all kernels, as presented in Equation (15). The derivative of Equation (15) with respect to r gives us pdf_R(r).

Fig. 7:

Computation of Pdf_P(p) for nonparametric models when the number of base kernels in pdf_X(x) and pdf_Y(y) is two. (a) The joint density of R₁ = p − kX and R₂ = k + X. The two solid lines represent the joint density for two kernels (k₁ and k₂) of nonparametric density pdf_X(x). (b) The joint density of random variables Y and R. Two kernels of pdf_Y(y) are in the range [c₁,d₁] and [c₂,d₂]. pdf_R(r) varies for kernels k₁ and k₂ of pdf_X(x) in ranges [r1_k1,r2_k1] and [r1_k2,r2_k2], respectively. The four rectangles depict the joint density for each pair of ranges of Y and R. The rectangles for ranges [c₁,d₁] and [c₂,d₂] are colored in red and green, respectively. In the blue regions, Y≤R at any position R = r. Brown and orange together highlight the domain of integration for computing Pr(Y≤ R). Orange denotes the regions where the rectangles of the joint density overlap.

5.2.2. Step 2: Formulation of Pr(Y≤ R)

We compute Pr(Y≤ R) by finding the joint distribution of random variables Y and R. As Y and R are independent, the joint density of Y and R is the product of pdf_Y(y) and pdf_R(r):

$$Pr\left(Y=y,R=r\right)=\frac{1}{n_1\cdot n_2}\sum _{i=1}^{i=n_2}K\left(y-y_i\right)\cdot \sum _{j=1}^{j=n_1}pd{f}_{R_{kj}}\left(r\right),\text{ where }$$ (16)

Equation (16) can be expanded as the sum of the product of densities for each pair of ranges of random variables Y and R. Thus, the computational complexity of (16) is quadratic to the number of kernels. For example, in Figure 7b, the joint density of Y and R is depicted for a range of R corresponding to Figure 7a. The joint density of Y and R shown in Figure 7b is a superimposition of four rectangles. The base kernels of pdf_Y(y) vary in the ranges [c₁,d₁] and [c₂,d₂]. The pdf_R(r) for kernels k₁ and k₂ varies in ranges [r1_k1,r2_k1] and [r1_k2,r2_k2], respectively. Blue denotes the region where Y≤ R for any R = r. Brown and orange regions together highlight the domain of integration for the computation of Pr(Y≤ R). Orange indicates areas of overlap be tween rectangles of the joint densities of Y and R, and hence, higher probability.

The results of the nonparametric density estimation have a relatively higher sensitivity to the choice of the bandwidth h than the choice of the kernel [3,18]. We use Silverman’s rule of thumb [37] for bandwidth estimation of a uniform kernel. The formula for the bandwidth of a uniform kernel using Silverman’s rule of thumb (appendix, [3]) is:

$$h=\left({4.5}^{1/5}\right){\left(\frac{3}{8}{\pi }^{-1/2}{\sigma }^{-5}\right)}^{-1/5}{n}^{-1/5}$$

5.3. Formulation of pdf_S′ (s′) and pdf_M′ (m′)

In subsections 5.1 and 5.2, we derived density pdf_P(p) in closed form for uniform and nonparametric noise models, respectively. We show the derivation when random variable P takes the form P = kX + kY + XY. We similarly compute the density of a random variable Q, which takes the form Q = −kX − kY + XY (the right column in Figure 2), in which we flip the sign of the isovalue k. Variables P and Q in Equation (6) are independent. Thus, the density of a random variable S′ introduced in Equation (6) can be computed through convolution of the densities of random variables P and Q (step 2 in Figure 2). The density function pdf_M′ (m) of a random variable M′ corresponding to the probabilistic midpoint decider (Equation (7)) can be obtained through the convolution of densities at the cell vertices (section 3) since we assume an independent noise model. The topological ambiguity can be probabilistically resolved by slicing pdf_S′ (s^′) and pdf_M′ (m^′) at 0 (step 3 in Figure 2).

6. Results and Discussion

We design three experiments to validate and demonstrate the effectiveness of the proposed methods. In the first experiment, we confirm the correctness of the derivation for density computation of saddle values for an uncertain 2D cell described in section 5 for uniform and non-parametric noise assumptions. The results shown in Figure 8 validate the correctness of the derivation. In the second experiment, we demonstrate the higher decision accuracy and stability of the probabilistic asymptotic decider in uncertain data for deciding the contour topology when compared to the other decision frameworks. We support our claim of the higher reliability of the probabilistic asymptotic decider in uncertain data by presenting the results for the synthetic datasets in Figures 1, 9, 10, and 11. In the last experiment, we visualize the results for the real datasets in Figure 12.

Fig. 9:

The sensitivity of the decision probabilities to kernel bandwidth for the data used in the result in 8b. The isovalue is k = 4. The variable b denotes the bandwidth estimated using Silverman’s rule of thumb.

Fig. 10:

A comparison of the decision frameworks for resolving topological ambiguities. The decision plots are a function of isovalue k. 1 and −1 indicate the positive and the negative decider signs, respectively. The left and the right columns depict the topology by considering the sign computed at the saddle point and the midpoint, respectively. The top row shows the sign decisions for the groundtruth data. The top left image is considered as the gold standard. The middle row shows the decider signs for the probabilistic deciders in uncertain data along with the confidence information. The confidence map is shown in pink. The bottom row depicts topological decisions for the mean of uncertain data. The probabilistic asymptotic decider (left image in the middle row) is the most consistent with the gold standard when compared to the other decision frameworks.

Fig. 11:

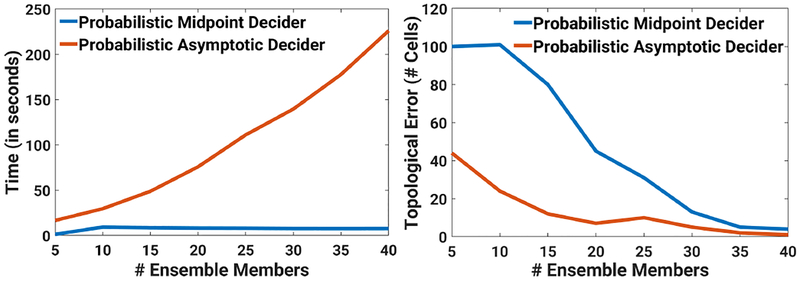
The comparison of performance (left image) and topological error (right image) for probabilistic deciders.

Fig. 12:

The visualization of the real datasets for the comparison of the probabilistic asymptotic decider and the probabilistic midpoint decider. The dotted boxes colored in magenta mark positions with topological differences. Red denotes relatively low and blue denotes relatively high confidence in the isocontour topology.

6.1. Probabilistic Asymptotic Decider for an Uncertain Cell

A topological ambiguity resolution for a 2D cell is illustrated for the uniform noise model in the top row of Figure 8. The uniform noise at the cell vertices is modeled by random variables D₀₀ ~ U(9,11), D₀₁ ~ U(−2,2), D₁₀ ~ U(1,3), and D₁₁ ~U(6,7). For the isovalue k = 4.5, the most probable signs of random ~ variables D₀₁ and D₁₀ are negative, whereas the most probable signs of random variables D₀₀ and D₁₁ are positive. Therefore, the cell denotes an ambiguous configuration. Figures 8a.I and 8a.II compare the results of the Monte Carlo simulations and the analytic formulation for the densities pdf_P(p) and pdf_Q(q), where P = D₀₁ D₁₀ +k (D₀₁ +D₁₀) and Q = D₀₀ Dk –k (D₀₀ + D₁₁) (Equation (6)). The analytic results are obtained using a derivation in section 5.1 for the uniform noise models. The same shapes for the densities of Monte Carlo sampling and the analytical formulation confirm the correctness of the proposed derivation.

Figure 8a.III illustrates the inconsistency in the decisions of the probabilistic asymptotic decider and the probabilistic midpoint decider. pdf_S′ (s^′) is computed by convolving the densities pdf_P(p) and pdf_Q(q) (step 2 in Figure 2). The density pdf(m^′) is computed by convolving the densities of random variables D₀₀, D₀₁, D₁₀, and D₁₁. For the iso-value k = 4.5, the most probable sign for the saddle point of the underlying bilinear interpolant is negative since Pr(S^′ < 0) = 0.5187 > 0.5. In the case of the probabilistic midpoint decider, the most probable sign is positive since Pr(M^′ < 0) = 0.3553 < 0.5. We also studied topological decisions for the asymptotic and midpoint deciders in the mean of uncertain data. However, the decisions for the asymptotic and the midpoint deciders in the mean field are the same when compared with the probabilistic asymptotic and the probabilistic midpoint deciders, respectively, for the uniform noise assumption. The advantage of the probabilistic asymptotic decider is evident when data noise is modeled with nonparametric densities.

In Figure 8, the bottom row shows the results for the non-parametric noise models. We describe the process for drawing noise samples to show the advantage of nonparametric distributions over uniform noise models. We draw noise samples close to a user’s choice of the groundtruth value in addition to a few outlier samples. For example, if a user selects the groundtruth value to be 1.5, then the sample array for this experiment looks like [1.4,1.2,1.3,2.9]. Sample 2.9 is an outlier in this example. For the results shown in Figure 8, we choose kernel densities at each cell vertex, such that the kernel means for D₀₀, D₀₁, D₁₀, and D₁₁ are positioned at [10,10.2,10.3,10.3,11], [−1,−1.1,−1.3,−0.8,−1.6], [1,1.3,1.2,1.3,2.8], and [6,6.1,6.2,6.3,6.9], respectively. The iso-value is k = 4.2. Our results show that the outliers can significantly affect the mean of uncertain data, and hence, can result in misleading interpretations. In contrast, the nonparametric densities show higher resilience to the outliers. The bandwidth estimation for nonparametric densities is performed using Silverman’s rule of thumb for the uniform kernel, as described in the last paragraph of section 5.2.

In Figures 8b.I and 8b.II, the shapes of the densities for the Monte Carlo simulations and the analytic formulation are the same for pdf_P(p) and pdf_Q(q), which proves the correctness of the derivation described in section 5.2. The nonparametric densities successfully capture the multimodel behavior of probabilistic variations in the saddle values for an uncertain cell. Figure 8b.III illustrates the inconsistency in topological decisions for the probabilistic asymptotic and the probabilistic midpoint deciders. The probability of a negative sign for the saddle point of the underlying bilinear interpolant is significantly different when compared with the midpoint. Specifically, the probability of the underlying saddle point being negative is 0.9175, and it is 0.3928 at the midpoint for the isovalue k = 4 2.

In Figure 9, we test the effect of the bandwidth estimation on the saddle value probabilities for the data used in obtaining the results in Figure 8b. A nonoptimal choice of bandwidth can result in under-smoothing or oversmooting of kernel density estimates. Since decision probabilities depend upon the evaluation of the integral Pr(S^′ < 0), the shape variations in distribution of S^′ caused by the bandwidth variations do not severely affect the integral computation. For example, for the variation of 0.1 in bandwidth b computed using Silverman’s rule of thumb, the estimation of the saddle probabilities varied by approximately 0.02, as depicted in Figure 9. Thus, the decisions of the probabilistic deciders are stable to the choice of the bandwidth for nonparamtric density estimation.

In Figure 10, we study the inconsistency in topological decisions for various decision frameworks as a function of isovalue k. We perform the study on noise samples consisting of outliers, similar to the ones used for obtaining the nonparametric density results in Figure 8b. The left and right columns in Figure 10 resolve topological ambiguities based on the signs derived at the cell saddle points and the midpoints, respectively. The top row shows the variation in the decider sign for the groundtruth data as a function of isovalue k. The groundtruth data was chosen to be d₀₀ = 10.1, , d₀₁ = −1, d₁₀ = 1.2, and d₁₁ = 6.1. 200 equispaced k values were sampled from the range [3.5,4.7]. The data values at the saddle point and midpoint are computed for each k using Equations (2) and (3), respectively. The vertex sign at the saddle point in the groundtruth data is considered as the gold standard.

The middle row shows the variation in the decider sign for uncertain data computed using the probabilistic asymptotic decider (section 5) and the probabilistic midpoint decider (section 3). The vertex signs reported by the probabilistic asymptotic decider match closely with the decisions for the gold standard, which illustrates the robustness of the probabilistic asymptotic decider to noise or the outlier samples. Moreover, the decisions of the probabilistic asymptotic decider can be computed fast because of the proposed analytical derivation. The vertex signs reported by the probabilistic midpoint decider are in disagreement with the gold standard in the isovalue range k = [3.9,4.25]. The pink plots represent confidence information regarding the decisions made by the probabilistic deciders. Due to the uncertainty in the data, the confidence value for the probabilistic asymptotic decider is the lowest near k = 3.85 where the saddle point sign is flipped in the gold standard. However, the confidence for the probabilistic midpoint decider is the lowest near k = 4.25. The shift in k is because of the outlier samples. The bottom row in Figure 10 plots decisions of the asymptotic decider and the midpoint decider for the mean of the uncertain data. The results again show the inconsistency in decisions with respect to the gold standard in the approximate isovalue range k = [3.9,4.2]. The inconsistencies in the results for the mean field are again due to a significant shift in the mean caused by the outlier samples. Also, the mean field technique does not provide any confidence information regarding the vertex signs.

6.2. Visualization of an Uncertain Scalar Field Using the Probabilistic Asymptotic Decider

We demonstrate the higher reconstruction accuracy of the probabilistic asymptotic decider compared to the other decision frameworks through an experiment on a synthetic dataset. We use the Blobs image shipped with MATLAB as the groundtruth data. For the isovalue k = 0.49, the image has 145 2D cells with ambiguous cell configurations. Figure 1a visualizes isocontours corresponding to two concentric circles in a portion of the groundtruth image. The white areas represent the cells with ambiguous topology for k = 0.49 in the MS algorithm, whereas gray denotes cells without any topological ambiguity. To compare the visualization performance of various decision frameworks, we inject the groundtruth image with noise to create an ensemble representing uncertain data. The noise samples are generated by following the same process as for the nonparametric density results in Figure 8b. We visualize the results of the comparison of various decision frameworks in Figure 1.

In the first step for extracting isocontours from uncertain data, the most probable vertex sign is determined at each cell vertex. We follow the vertex-based classification approach (section 3.1, [3]) for closed-form computation of the most probable signs for grid vertices. The most probable vertex signs for the scalar grid decide whether the cell topology is ambiguous or not. Note that the computation of the cell configuration (ambiguous or not ambiguous) stays the same for all decision frameworks in Figure 1 since all frameworks are tested on the same ensemble data. The difference in isocontour topology in Figure 1 for various decider frameworks is because of their statistical properties.

For each cell with an ambiguous configuration, we make the topological decisions using three statistical frameworks, specifically the asymptotic decider in the mean field (Figure 1b), the probabilistic midpoint decider (Figure 1c), and our probabilistic asymptotic decider (Figure 1d). In the results for the mean field, the isocontour breaks at many positions because of the incorrect topological decisions for ambiguous cells, where ambiguous cells are marked in white. Moreover, the mean field result does not give any cues regarding confidence in the topological decisions. The probabilistic midpoint decider [3] recovers isocontours for the concentric circles reasonably well when compared with the mean field result. Moreover, the probabilistic midpoint decider allows us to encode confidence in the topological decision into the visualization. In Figure 1c, the cells with relatively low confidence are colored in red, whereas the cells with relatively high confidence are colored in blue.

Although the reconstruction performance for the probabilistic midpoint decider is better than the mean field decider, the reconstructed isocontour contains a considerable number of holes. The isocontour holes are prominent, especially in the regions of low confidence (red cells). Figure 1d visualizes the result of the proposed probabilistic asymptotic decider. The isocontours for the concentric circles are recovered considerably well when compared with the other two decision frameworks. The isocontours for the probabilistic asymptotic decider are recovered at all groundtruth positions except for two places: one position on the southeast and one position on the west side of the concentric isocontours. Moreover, the closed-form formulation of the probabilistic asymptotic decider allows fast and accurate computation of the probabilities as opposed to expensive Monte-Carlo simulations.

Figure 11 visualizes a comparison of the time complexity and the accuracy of the probabilistic deciders for the uncertain Blobs dataset. The results are taken by increasing the number of ensemble members from five to 40 at intervals of five. The time complexity of the probabilistic asymptotic decider (Figure 11a) grows quadratically with the number of ensemble members/kernels, as we had anticipated from Equation (16). The time complexity of the probabilistic midpoint decider is, how ever, constant since its computation consists of a single convolution per cell, as described in section 3. Figure 11b plots the number of grid cells where the topology for each of the probabilistic deciders differs from the groundtruth topology. The topological inconsistency or the topological error of the proposed probabilistic asymptotic decider is lower than the probabilistic midpoint decider throughout. However, the inconsistency in decisions converges as we get more samples from the underlying distribution or for higher numbers of ensemble members.

In the last experiment, we compare the results of the probabilistic deciders for the real datasets in Figure 12. Figure 12a visualizes isocon-tour reconstruction in the temperature dataset. The temperature dataset is courtesy of the DEMETER project [29]. The isocontours are visualized in the temperature field for isovalue k = 10°. The dataset consists of nine ensemble simulations for 2-meter temperature data collected in years 2000–02. We perform nonparametric density estimation and visualize the results for the probabilistic asymptotic and the probabilistic midpoint deciders. The positions of inconsistent topological decisions for the two methods are indicated by the dotted boxes colored in magenta. The cells with relatively low confidence in topology are colored in red, whereas those with relatively high confidence in topology are colored in blue.

Figure 12b visualizes the results similar to the temperature dataset for flow simulations. We generate 15 simulations of the Kàrmàn vortex street with Gerris [30]. All simulations were run for a fixed amount of time with uncertain viscosity parameters (section 5.2, [12]). The analysis of the Kàrmàn vortex street plays a critical role in engineering applications, such as structural engineering [15]. The inconsistency in isocontour reconstruction of the probabilistic deciders for the velocity magnitude field of Kàrmàn vortex street is visualized in Figure 12b. In the majority of cells, the probabilistic asymptotic decider resolves the topology with the high confidence value, whereas the topological confidence of the probabilistic midpoint decider seems to vary considerably because of the outliers.

7. Conclusion and Future Work

The asymptotic and the midpoint decider are standard techniques for resolving topological ambiguities in the marching squares (MS) algorithm. The issue of topological ambiguity escalates for uncertain data. None of the existing work, to the best of our knowledge, has rigorously analyzed topological ambiguity resolution in uncertain data. In our contribution, we address the issue of ambiguity resolution in uncertain data by proposing a closed-form statistical framework. We analytically derive the density of the data values at the saddle points of uncertain bilinear interpolation functions for the MS algorithm assuming uniform and nonparametric noise models. The density formulation allows us to decide topology probabilistically and efficiently when compared to expensive Monte Carlo simulations. Our experiments show that the probabilistic asymptotic decider framework is the most stable and accurate when compared with other decision frameworks in uncertain data. The probabilistic models allow us to quantify the confidence in topological decisions and integrate it into the visualization.

The methods proposed in this paper are the building blocks for studying the research question of topological ambiguity resolution in the case of 3D isosurfaces. The probabilistic asymptotic decider can be directly applied to resolve the face ambiguities for the marching cubes algorithm. However, topological ambiguity resolution in 3D is a complex problem, especially when a cell has more than one ambiguous face. Accurate resolution of topological ambiguities for uncertain data in 3D requires the study of the probabilistic variations in data at the points in the interior of a 3D cell, e.g., body saddle points [26, 27]. As the next step of our work, we plan to study the question of density characterization at the saddle points of uncertain trilinear interpolation functions.

In the future, we also plan to take into account data correlation and kernels other than the uniform kernel for deriving the closed-form probabilistic asymptotic decider. The higher order kernels pose the challenge of computing complex integrals. It would be interesting to investigate the research question of probabilistic placement of saddle points in uncertain cells. Finally, we would like to investigate the impact of variations in data at the saddle points of uncertain fields in visualization applications, such as contour trees and flow field topologies.