Advances in Micropipette Aspiration: Applications in Cell Biomechanics, Models, and Extended Studies

Abstract

With five decades of sustained application, micropipette aspiration has enabled a wide range of biomechanical studies in the field of cell mechanics. Here, we provide an update on the use of the technique, with a focus on recent developments in the analysis of the experiments, innovative microaspiration-based approaches, and applications in a broad variety of cell types. We first recapitulate experimental variations of the technique. We then discuss analysis models focusing on important limitations of widely used biomechanical models, which underpin the urge to adopt the appropriate ones to avoid misleading conclusions. The possibilities of performing different studies on the same cell are also considered.

Main Text

The mechanical behavior of cells is central to the cell state and functions, including growth (1), degree of differentiation (2, 3), ability to migrate (4, 5), immune cell activation (6), and fate (7). Current research in cell mechanics spans a broad spectrum of cellular events that underlie mechanical responses, including mechanosensing mechanisms, cytoskeleton dynamics, adhesion, cell-cell communication, and interaction with the extracellular matrix (8, 9, 10, 11). Because of the heterogeneity and anisotropy of cellular constituents (solid-like, fluid, and viscous materials) and the multiple regulatory mechanisms involved in mechanosensing, determining the mechanical behavior of a living cell presents great modeling difficulties.

Multiple experimental tools exist to both probe cells and quantify the forces that cells exert (12, 13, 14). These growing methods are creating new avenues to capture the mechanical fingerprint of different cell types (15, 16, 17). From the 1970s, microaspiration experiments have remained widely used in the study of cell mechanics, comprising assays of suspended cells—mainly blood cells (1, 18, 19, 20, 21, 22)—and adherent cells—adhered cells or resuspended cells (5, 23, 24, 25, 26, 27) —, cell nucleus (28), cell blebs (29), giant unilamellar vesicles (30, 31, 32, 33), extracellular matrices (24), and tissues (34, 35).

The deformation behavior of cells, apart from depending on the length scale of observation, is affected by active change and internal structure determined by the state of the cell (36). Hence, the simplest continuum models, commonly used (37, 38), do not reflect heterogeneity, anisotropy, and dynamic changes. However, they are very useful to assess mechanical parameters, allowing the comparison of cells in different states or different cells. A helpful review by Hochmuth, published in 2000, covered practical and simple equations that are extensively used to estimate mechanical parameters (38). Nevertheless, lacunae underlying the physical assumptions in some of those equations or an inappropriate application could preclude accurate estimations. To overcome these limits, improved models of micropipette aspiration have recently enabled more robust analyses.

This article aims to serve as a consult guide for researchers seeking to conduct and interpret the versatile measurements of micropipette-aspiration experiments. We highlight novel microaspiration-based approaches and the models to quantify biomechanical properties.

Classical approach: Observing the cell shape during the aspiration process

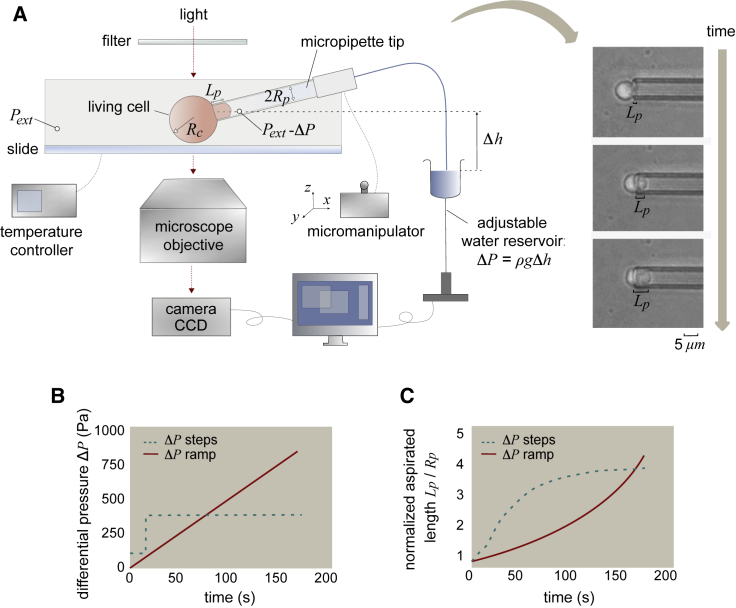
In micropipette-aspiration experiments, a suction pressure ΔP is applied by connecting the micropipette (microcapillary) to an adjustable water reservoir (Fig. 1 a) or a pump. Cell changes (Fig. 1 c) are determined microscopically by means of image analysis (39). The suction pressure is given by the height difference between the tip of the micropipette and the top of the reservoir h and the specific weight of water ρg: ΔP = ρgh. If there is a flow, the pressure drop along the microcapillary must be taken into account, and the following equation may be used (40):

$$\mathit{\Delta }P=\rho gh\left(1-U/U_f\right),$$ (1)

where U is the velocity of the aspirated material and U_f is the velocity that it would have if flowing freely. Typically, U_f is several orders of magnitude higher than U (U_f ≈ 4 μm/s for a capillary of internal radius R_p ≈ 5 μm and for a low value ρgh = 1 Pa (40)). Therefore, the correction factor (1 − U/U_f) may be taken equal to 1 in experiments of tens of seconds or longer. To prevent adhesion of the membrane to the glass in micropipette-aspiration experiments (41), which could lead to overestimates of the cell mechanical properties, different experimental protocols have been reported in the literature (28, 42).

Figure 1.

Scheme of the micropipette-aspiration experiments. (A) Experimental setup was used to simultaneously adjust the differential pressure ΔP, the temperature and the position of the micropipette, and the representative sequence of images of an experiment. (B) The graph shows two types of curves for the differential pressure ΔP applied over time: creep experiments at constant pressure (dashed line) and ramp experiments (solid line). (C) Plot of the aspirated length as a function of time for the two types of experiments. To see this figure in color, go online.

Biomechanical models

In this section, we summarize biomechanical models that allow researchers to quantify cellular mechanical properties using the cell-surface shape information from the aspiration experiments.

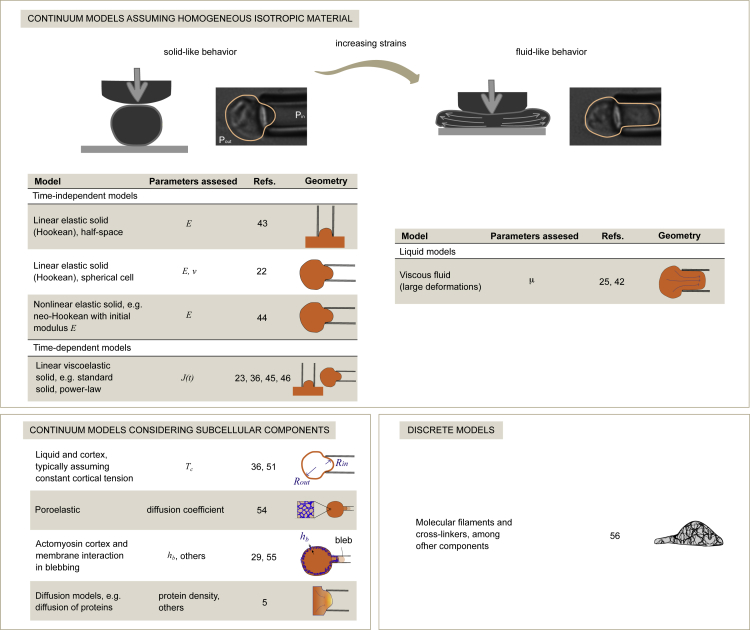
Continuum-medium models assuming homogeneity

The simplest models adopt continuum-modeling approaches (Fig. 2). The computed parameters are typically phenomenological without a direct link to subcellular components. The classic work by Theret et al. (43) provided one equation to compute the elastic modulus E of a sample, assumed to be a homogeneous incompressible linear-elastic half space:

$$\frac{\mathit{\Delta }P}{E}=\frac{2\pi }{3{\varphi }_p}\frac{L_p}{R_p},$$ (2)

where ΔP is the differential pressure, L_p is the aspirated length, and R_p is the pipette radius (Fig. 1). The term ϕ_p depends weakly on the thickness of the pipette wall, and the value ϕ_p ≈ 2.1 is typically used. In this linear model, the slope of the curve ΔP/E versus L_p/R_p is 2π/3ϕ_p ≈ 1.0.

Figure 2.

Models to analyze the mechanical properties of cells by micropipette aspiration. The figure summarizes continuum and discrete strategies for modeling the mechanical behavior of cells. To see this figure in color, go online.

For suspended nearly spherical cells, accurate mechanical models should take into account the finite size. Zhou et al. studied the aspiration of a homogeneous neo-Hookean (incompressible) spherical cell (44). From their computed curves, they fitted a nonlinear equation, from which we obtained a linearized version (37):

$$\frac{\mathit{\Delta }P}{E}=c_l\frac{L_p}{R_p}.$$ (3)

The function c_l takes into account the relative size of the cell through the ratio between the radius of cell R_c and pipette R_p and is given by

$$c_l={\beta }_1\left[1-{\left(R_p/R_c\right)}^{{\beta }_3}\right]/3,$$ (4)

where β₁ = 2.0142 and β₃ = 2.1187 are constants obtained by Zhou et al.

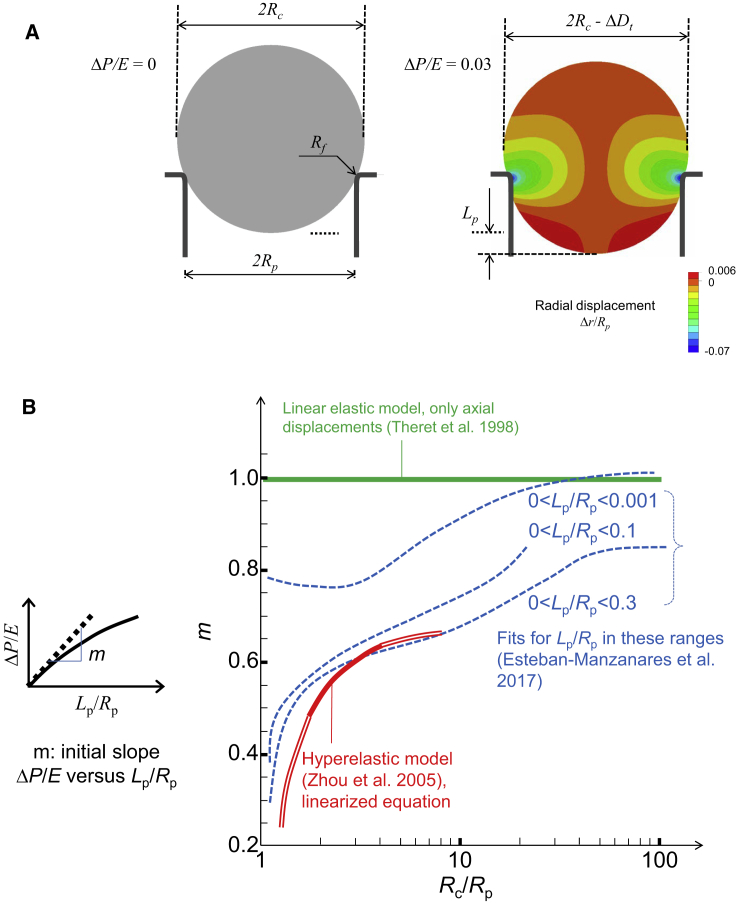
Additionally, we studied the aspiration of a homogeneous linear-elastic spherical cell (22), addressing the influence of the Poisson’s ratio ν. First, we found that the influence of the fillet radius R_f (see Fig. 3 a) is important, and its value should not be smaller than the size associated to the cell-surface roughness; we proposed to set a value of R_f = R_p/20. To obtain an equation to estimate E, we investigated the importance of the range of values of L_p used to fit the aspiration curve (Fig. 3 b) and proposed to use the range 0.0 < L_p/R_p < 0.3. In the case of incompressible material, the relationship between aspiration pressure and aspirated length is similar to the one obtained by Zhou et al. (for not very large cells). Hence, we concluded that Eq. 3 is suitable to compute the elastic modulus when cells are assumed to be homogeneous, spherical, incompressible, and elastic. If the resolution of experimental images allows for measurements of radial displacements (i.e., ΔD_t in Fig. 3 a), it is possible to assess both E and ν (22).

Figure 3.

Modeling the aspiration of a homogeneous, isotropic, and spherical cell. (A) Schemes showing geometrical parameters and radial displacements for a linear elastic sphere and a suction pressure ΔP/E = 0.03 (22). (B) Plot of the initial slope of the curves ΔP/E versus L_p/R_p as a function of R_c/R_p; slope was computed for Theret et al.’s model of a semi-infinite space (43), for Zhou et al.’s model of a hyperelastic sphere (44) (the linearized expression (30) is used, see (3), (4); the bold line represents the range originally studied by Zhou et al.), and for Esteban-Manzanares et al.’s model of a linear elastic sphere (22). In the latter case, the slope is represented for three ranges of fitting of the curve ΔP/E versus L_p/R_p. To see this figure in color, go online.

Theret et al.’s equation has been widely used, even for nearly spherical cells (disregarding that the finite size of the cells may produce differences in size, which are incorrectly interpreted as differences in rigidity). Nevertheless, this model did not take into account the nonlinearity of the contact between pipette and cell. As shown in Fig. 3 b, for a sufficiently large spherical cell, the slope of the curve ΔP/E versus L_p/R_p is close to 1.0 when the curve is fitted for very small values 0 < L_p/R_p < 0.001. However, in practice, such small displacements are impossible to measure in optical images. We determined that for a fitting in the range 0.0 < L_p/R_p < 0.3, the slope would be ∼0.8 for large cells. Hence, we propose to use the factor 0.8 to analyze adhered cells or large suspended cells (R_c/R_p ≥ 10). We underline that the factor 0.8, instead of 1.0, is obtained by enhancing the analysis without simplifications of the theory. The use of the factor 0.8 would reduce the differences between the elastic modulus estimated by aspiration and by other techniques usually yielding higher values (13).

The previous models may be extended to a linear incompressible viscoelastic material; the evolution of the aspirated length L_p(t) may be computed by replacing the constant 1/E by a creep function J(t). For instance, the modified version of Eq. 3 is (37):

$$\frac{L_p\left(t\right)}{R_p}=\frac{\mathit{\Delta }P}{c_l}J\left(t\right).$$ (5)

Regarding the creep function J(t), the standard linear solid model with three parameters and the power-law rheological model with two parameters are customarily used for aspiration experiments (45, 46). Eq. 5 may be directly used in experiments with constant pressure applied instantaneously at time t = 0. If the pressure varies, the appropriate equation is obtained using the Boltzmann superposition principle (37).

When a cell undergoes large deformations, it evolves from a solid-like to a fluid-like behavior (47, 48), and it is possible to quantify its apparent viscosity (21, 42). Based on the relation obtained by Needham and Hochmuth (42), we derived an equation to estimate the apparent viscosity μ (at time t₁) from one single picture (25):

$$\mu =\frac{3{\int }_0^{t_1}\mathit{\Delta }Pdt}{4m\frac{V_{\text{in}}}{V_{tot}}\left(1-\frac{R_p}{R_c}\right)}{\left(\frac{R_p}{R_c}\right)}^3,$$ (6)

where R_c is the initial radius of the cell (m = 6), V_in is the aspirated volume (at t₁), and V_tot is the total volume of the cell. The approximation was found to be valid for R₀/R_p < 2.5 and V_in/V_tot < 0.

The models discussed above assume that the aspirated cell is homogeneous and are useful for quantitative analysis allowing comparison of different cells. However, cells highly depart from an ideal homogenous isotropic medium. Dynamic changes, heterogeneity, and anisotropy are not taken into account by these models and may contribute to the variability of the evaluated deformability parameters (for instance, because of a mechanosensing-related evolution of a nonhomogeneous cytoskeletal cortex) (49).

Models taking into account subcellular-component parameters

A simple approach, suitable for some suspended cells and taking into account the actomyosin cortex contractility, is to consider the cell mechanically equivalent to a liquid drop, its shape being determined by the cortical tension T_c (38, 50) produced by the actomyosin cortex (51). The equilibrium shape corresponds to spherical surfaces inside and outside the microcapillary, respectively, with radii R_in and R_out, and the Laplace equation is used:

$$\mathit{\Delta }P=2T_c\left(\frac{1}{R_{in}}-\frac{1}{R_{out}}\right).$$ (7)

Eq. 7 is easily modified if the cortical tension is considered different inside and outside the pipette (52). When the length of suction surpasses the radius of the microcapillary, the cell is unable to stay in equilibrium, and it is freely aspirated, as observed in cells with low viscosity (38, 42). It is possible to calculate the equivalence between the measured cortical tension of the cell T_c and apparent modulus E given by (3), (5) (37):

$$T_c\approx \frac{R_0^2\left[{\left(1-{\left(R_p/R_0\right)}^2\right)}^{-1/2}-1\right]}{2R_p{c}_l}E.$$ (8)

The interior of the cell is a complex fluid with active microdomains that can be tuned by the cell to control its structure and function (53). Indeed, given the large amount of understudied species of molecules (54), biomechanical modeling cannot yet describe in full detail the response of cells and is therefore an active area of research. In poroelastic (and poroviscoelastic) models, the cell is described as an elastic (or viscoelastic) porous structure dispersed in a viscous fluid (48, 55). The time dependency of deformability is given by a poroelastic diffusion constant that scales as E_matξ²/μ_cyt, E_mat being the elastic modulus of the drained matrix, μ_cyt being the cytosol viscosity, and ξ being the characteristic pore radius (55). In this context, Brugués et al. worked on an analytical model and performed micropipette-aspiration experiments to study the dynamical interaction between the actomyosin cortex and the plasma membrane (29). Their simplified equation for the critical thickness of the actomyosin cortex h_b, for which the plasma membrane would detach, producing blebs, is

$$h_b=\frac{f_b{d}_b{R}_p}{2{\sigma }_{myo}},$$ (9)

where f_b is the bond force, d_d is the surface density of bonds between cortex and plasma membrane, and σ_myo is the cortex stress due to myosin contractility. Alert et al. obtained a model that would allow for estimations of the membrane-cortex ligand density and the contractile activity of the cortex (56) in experiments combining micropipette aspiration and interferometric spectroscopy.

Lykov et al. developed a discrete particle-based model of a spherical cell, describing the cell membrane, nucleus, and cytoskeleton during the aspiration process (57). Their analysis of experiments indicated that the main contributor to cell stiffness is its cytoskeleton, filaments, and cross-links being equally important.

Out of the membrane: Models to study the extracellular matrix or the cell wall

To study the stiffness of chondrocyte pericellular matrix, Alexopoulos et al. developed a theoretical model based on the elastic semispace, with the addition of a superficial layer that would represent the pericellular matrix (24). They obtained an equation similar to Eq. 2:

$$\frac{\mathit{\Delta }P}{E_{layer}}=\frac{1}{C\ast }\frac{L_p}{R_p}.$$ (10)

The constant C^∗ depends on the ratio of shear moduli of the surface layer and the internal semispace and on the thickness of the layer. Boudou et al. obtained correction factors for the model of Theret et al. for elastic layers attached to semi-infinite substrates (58).

Recently, micropipette aspiration has been used to study fungal cells, characterized by a cell wall resisting a great turgor pressure. We developed a procedure to study the influence of the differential pressure applied at the tip, ΔP, on the growth rate dL_p/dt (59), predicting and measuring a ΔP value that arrests the cell growth.

New approaches: The need for additional measurements

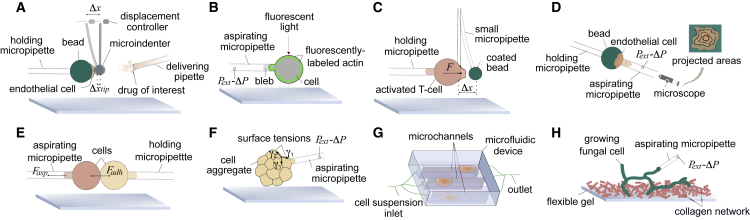
Micropipette aspiration has evolved to quantify both local and global mechanical properties of cells (see Fig. 4). To carry out local analyses, Guillou et al. (60) developed the profile microindentation technique. It requires holding a cell by a micropipette while using a profile microindenter (Fig. 4 a). An additional micropipette may be used to deliver molecules onto the cell. This procedure has enabled, for example, the study of endothelial cells when whiffed by a drug. In local analyses, micropipette aspiration and fluorescence or confocal microcopy can be combined to integrate molecular observations with mechanical assays (Fig. 4 b), which permits inferring mechanosensing activity (49, 61). For instance, micropipette aspiration combined with single-particle tracking has been employed in mechanosensitive studies of membrane-embedded ion channels and proteins (62).

Figure 4.

Schematic of micropipette-aspiration-based techniques. (A) Microindenter force tool to locally deform an attached cell. (B) Pipette aspiration was combined with confocal microscopy to relate protein expression (as measured by fluorescent microscopy intensity) and cell mechanical behavior. (C) Pipette-based force apparatus to measure cell pulling and pushing forces. (D) Cell-detachment technique was used to characterize adhesion forces. The resulting cell projected area as a function of time is related to the cell-substrate adhesion forces. (E) Dual-pipette aspiration was used to quantify intracellular forces. (F) Microaspiration device was used to map the surface tension of cell-aggregate interfaces. This mapping can be used to study morphogenesis and cell division. (G) Microfluidic high-throughput method was used to characterize single-cell mechanics. (H) Tip-pressure probe was used to assess the rate of growth of polarized cells. To see this figure in color, go online.

Micropipette force probe (Fig. 4 c) uses a micropipette holding a functionalized bead coated with molecules of interest. To quantify the pushing or pulling forces, the bead is brought in contact with a cell that is fixed by a micropipette. Micropipette force probe has been used to assess the pushing force by activated T cells (6, 63). A strategy to quantify cell-substrate adhesion force entails measuring the aspiration pressure required to modify the geometry and detach a cell from a surface (64) (Fig. 4 d). Similarly, cell-cell detachment forces may be assessed by a dual micropipette-aspiration system (65), in which two antiparallel micropipettes regulate the negative pressure applied to each of the cells (Fig. 4 e). Cell-cell forces are particularly important during morphogenesis: a growing cell aggregate may need to rearrange its cellular interfaces, thus requiring changing the surface tensions in the different parts. Aspiration can be directly applied to quantify the effective surface tensions of all interfaces of a group of cells (Fig. 4 f) (7, 66).

A variation of micropipette aspiration has recently overcome a key limitation of the technique: the relatively low throughput of the experiments (∼20 cells/h). Lee et al. developed a new microfluidic device based on microaspiration that has greatly increased the throughput of the technique (∼1000 cells/h) (67), complementing other microfluidics approaches to measure cell-deformability parameters with a high throughput (68) (Fig. 4 g).

A future development of the technique on which we are currently working will offer the possibility of performing different analyses on the same cell sequentially. Such sequential single-cell characterization could be implemented by collecting the aspirated cells and keeping them identified for different studies. In particular, this extension of the technique could enable measurements of cell deformability, followed by biochemical assays or detailed optical or electron imaging of cellular components.

Concluding remarks and new avenues

An important feature of micropipette aspiration is the possibility of performing single-cell experiments of increasing complexity. An array of variations recently developed of micropipette aspiration allows for the manipulation of cells to measure their mechanical properties as well as for the development of sophisticated analyses of a biochemical and microstructural nature. Such studies are only now beginning to be exploited, basically being limited to the combination of mechanical measurements with fluorescence-microscopy analyses. Microfluidics devices are making inroads to improve the throughput of aspiration-like experiments. However, the widespread use of these devices is still hindered by technical limitations to keep repeatability and smooth flow in the microchannels at low cost for nonexperts.

Future extensions of micropipette aspiration to perform sequential single-cell measurements that may help to explain the biomechanical cell behavior will include the collection of the cells after their aspiration for an ulterior characterization via optical or electron imaging or biochemical or genetics assays, for instance. The observation of internal components will provide a better understanding of the effect of heterogeneity and anisotropy on deformability. Furthermore, by altering the expression, and thus the concentration of specific proteins in cells, researchers can employ single-cell microaspiration experiments to directly test more complex mechanical models. We consider that such single-cell studies will be at the heart of future developments.

Editor: Brian Salzberg.