A novel perturbation based compression complexity measure for networks

Abstract

Measuring complexity of brain networks in the form of integrated information is a leading approach towards building a fundamental theory of consciousness. Integrated Information Theory (IIT) has gained attention in this regard due to its theoretically strong framework. Nevertheless, it faces some limitations such as current state dependence, computational intractability and inability to be applied to real brain data. On the other hand, Perturbational Complexity Index (PCI) is a clinical measure for distinguishing different levels of consciousness. Though PCI claims to capture the functional differentiation and integration in brain networks (similar to IIT), its link to integrated information is rather weak. Inspired by these two perspectives, we propose a new complexity measure for brain networks – ${\mathrm{\Phi }}^C$ using a novel perturbation based compression-complexity approach that serves as a bridge between the two, for the first time. ${\mathrm{\Phi }}^C$ is founded on the principles of lossless data compression based complexity measures which is computed by a perturbational approach. ${\mathrm{\Phi }}^C$ exhibits following salient innovations: (i) mathematically well bounded, (ii) negligible current state dependence unlike Φ, (iii) network complexity measured as compression-complexity rather than as an infotheoretic quantity, and (iv) lower computational complexity since number of atomic bipartitions scales linearly with the number of nodes of the network, thus avoiding combinatorial explosion. Our computations have revealed that ${\mathrm{\Phi }}^C$ has similar hierarchy to <Φ> for several multiple-node networks and it demonstrates a rich interplay between differentiation, integration and entropy of the nodes of a network.

${\mathrm{\Phi }}^C$ is a promising heuristic measure to characterize network complexity (and hence might be useful in contributing to building a measure of consciousness) with potential applications in estimating brain complexity on neurophysiological data.

1. Introduction

Φ, a measure of network complexity, has drawn a lot of attention recently because it claims its inspiration from the nature of consciousness. Consciousness is our inner “experience”, which is subjective, distinct and unique – such as the feeling of pain, perception of the color green, or in the most general sense, the felt experience – “what's it like to be?” [1] by an organism. Consciousness is hard enough to be defined in words but easiest to be accepted, as it is something rather than nothing, which each of us is experiencing right now. The problem of measuring consciousness is difficult because of the presence of different levels of conscious experience [2] and first person reports of consciousness might not be accurate. It might also be interesting to use the measures of consciousness and brain networks' complexity in deciphering if neural networks as the ones in [3] possess any consciousness. It has also been suggested that we need a mix of theoretical and practical approaches to be able to characterize consciousness mathematically in terms of quality as well as quantity [4], [5].

On the basis of various scientific theories, different measures of consciousness are suggested in the literature – both on behavioral and neurophysiological basis [2]. The idea that consciousness is the result of a balance between functional integration and differentiation in thalamocortical networks, or brain complexity, has gained popularity [6], [7], [8], [9], [10].

We intend to analyze, in particular, a measure of complexity called Integrated Information – Φ [5] which has gained much popularity because of Integrated Information Theory of Consciousness (IIT) [5]. Though theoretically well founded, IIT 3.0 suffers from several limitations such as current state dependency, computational intractability and inability to be used with neurophysiological data. There are two other measures viz. Neural Complexity [11] and causal density [12] as well, which also capture the co-existence of integration and differentiation serving as measures of consciousness [2]. Apart from the individual challenges that these measures have, the common fundamental problem to use them in clinical practice is that they are very difficult to calculate for a network with large number of nodes such as the human brain [2]. In the recent past, a clinically feasible measure of consciousness – Perturbational Complexity Index (PCI) was proposed as an empirical measure of consciousness. PCI has been successfully tested in subjects during wakefulness, dreaming, non-rapid eye movement sleep, anesthesia induced patients, and coma patients. Although the authors of [6] claim that PCI is theoretically based, they don't explicitly and formally establish a link to information integration.

1.1. Dependence of Φ on the current state

Φ, as defined in [5], is heavily dependent on the current state of a system. This fact is supported by referring to the framework of IIT 3.0 – (i) firstly, the notion of intrinsic information that Tononi propounds is defined as “difference that make a difference” to a system, which is based on how an element of a system constrains the past of other node of the same system depending on its mechanism and its current state [5], (ii) secondly, IIT is based on a basic premise that if integrated information has to do something with consciousness, then it must not change, howsoever, the system is divided into its parts. Therefore we require a crucial cut – Minimum Information Partition (MIP) which is the weakest link of the system [13]. MIP is dependent on the current state of the system because it requires the identification of that partition which makes the least difference to the cause-effect repertoires of the system [5].

Therefore, following from the above, we can infer that Φ is dependent on the current state of a system. However, this can be problematic as shown in Figure 1. Figure 1(A) shows a system ABC with 3 different mechanisms and Figure 1(B) shows different values of Φ for the different current states of ABC, which shows the current state dependence of Φ.

Figure 1.

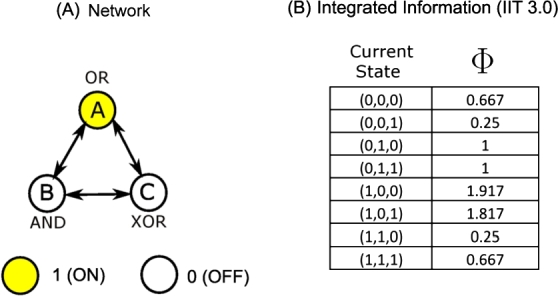
Dependence of Φ on current state. (A) A 3-node network ABC with 3 different mechanisms OR, AND, XOR respectively. (B) The table of values of Φ for all current states of the network ABC.

1.2. Theoretical gap in Perturbational Complexity Index (PCI)

PCI is defined as “the normalized Lempel–Ziv complexity of the spatiotemporal pattern of cortical activation triggered by a direct Transcranial Magnetic Stimulation (TMS) perturbation” [6]. PCI computes the algorithmic complexity of the brain's response to the perturbation and determines two important components of complexity: integration and differentiation, for the overall output of the corticothalamic system.

Perturbational Complexity Index (PCI) [6] is proposed as an objective measure for the determination of consciousness in the clinic and for distinguishing the level of consciousness in 3 scenarios: (i) healthy subjects in wakefulness, non-rapid eye movement (NREM) sleep and dreaming states, (ii) subjects sedated by anesthetic agents (midazolam, xenon, and propofol), and (iii) patients who emerged from coma (vegetative/minimally conscious state, and locked-in syndrome) [6].

PCI faces certain drawbacks which needs to be addressed: a) the authors of PCI have not explicitly shown the mapping between the values of their measure (for example, high in wakefulness and low in NREM sleep) and the amount of integration and differentiation present in the cortical responses, b) PCI measures complexity of (averaged) TMS evoked potentials from one particular target region (single type of external perturbation) [14], and c) it is not known whether TMS-induced perturbations in PCI are random in nature or not.

1.3. The new measure – ${\mathrm{\Phi }}^C$

On one hand we have theoretically well founded measures such as Integrated Information, Causal Density and Neural Complexity, which are currently impossible to be tested in the clinic on a real subject; on the other hand we have the very promising and successful candidate – PCI, which is applicable in the clinic, but lacks a clear connection to these theoretical measures. Our aim is to bridge this gap.

Inspired by the theoretical framework of IIT 3.0 and empirical measure PCI, we propose a perturbation based compression-complexity measure for brain networks – ${\mathrm{\Phi }}^C$. The idea of Compression-Complexity is motivated by observing the similarity between data compression performed by compression algorithms and ability of the human brain to make holistic sense of the different stimuli received by the brain. The link between data compression and Tononi's integrated information is highlighted by the fact that the information encoded by the bits of a compressed file are more tightly integrated than the original uncompressed file.1 Complexity measures based on lossless data compression algorithms such as Lempel–Ziv Complexity (LZ) [15] and Effort-To-Compress (ETC) [16] are known to outperform infotheoretic measures such as entropy for characterizing the complexity of short and noisy time series of chaotic dynamical systems [16], [17]. The newly proposed compression-complexity measure ${\mathrm{\Phi }}^C$ characterizes complexity of networks using LZ and ETC measures.

${\mathrm{\Phi }}^C$ is defined and computed as the maximally-aggregate differential normalized Lempel–Ziv (LZ) or normalized Effort-To-Compress (ETC) complexity for the time series data of each node of a network, generated by perturbing each possible atomic bipartition of an N-node network with a maximum entropy perturbation and a zero entropy perturbation. The detailed explanation is given in Methods section and in ‘Supplementary Text’. ${\mathrm{\Phi }}^C$ has the following advantages – theoretically well-bounded and independent of current state of the system, linear correlation with entropy of the nodes, and approximates integrated information with both aspects – ‘process’ and ‘capacity’. ${\mathrm{\Phi }}^C$ attempts to capture the co-existence of differentiation, integration, as well as entropy in networks and shows a similarity with Φ in its performance on 3, 4 and 5-node networks.

2. Results

The Results section is structured as follows: we start by analyzing IIT 3.0 and its limitations, in particular, its dependence on current state which makes Φ a non-robust measure. This limitation is one of the motivations for proposing a new measure. We also demonstrate the correlation between <Φ> (mean value of Φ) and the entropy of the nodes of the network. In the next section, we allude to the lack of a clear theoretical framework in PCI which makes it an empirical measure. To address these limitations, we first introduce the idea of compression-complexity and then propose a new measure – ${\mathrm{\Phi }}^C$. The steps for the computation of the new measure are provided and its properties are enlisted. We also contrast the hierarchy of <Φ> with $<{\mathrm{\Phi }}^C>$ for all 3, 4, 5-node networks formed by logic gates: OR, AND and XOR.

2.1. Model assumptions

We make the following model assumptions in our paper:

• •Although certain states may be forbidden in a given network, to ease analysis, we generically assume that any state is equally likely at time $t=0$. Hence, while computing all measures in the paper, we consider all possible current states to be equally likely.
• •Each network that we consider is fully connected (bi-directionally) and no node has self-loops unless otherwise specified.
• •We assume all networks to be composed of binary logic gates (OR, AND and XOR) and both the perturbation and output time series are also binary. However, our methods can be extended for networks which are non-boolean.
• •At certain places in this paper, we have used the term ‘element’ and ‘system’ to mean ‘node’ and ‘network’ respectively.

2.1.1. <Φ>: incorporating current states of a network

Taking a cue from the previous section, we performed computer simulations to compute the values of Φ for all 3-node networks consisting of OR, AND and XOR gates, and for every current state (details in Methods section). We then compute mean value of Φ across all current states of a network – <Φ>. Table 1 shows Φ for all current states, along with the <Φ> and standard deviation. We repeat this exercise for 4 and 5-node networks as well, and the results are presented in Table S1 (Supplementary Tables).

Table 1.

Integrated information (Φ) computed for all current states of different 3-node networks.

Network No.	Networks	$(0,0,0)$	$(0,0,1)$	$(0,1,0)$	$(0,1,1)$	$(1,0,0)$	$(1,0,1)$	$(1,1,0)$	$(1,1,1)$	<Φ> ± Stdev.
1	XOR–XOR–XOR	1.875	4.125	4.125	1.875	4.125	1.875	1.875	4.125	3 ± 1.203
2	XOR–XOR–OR	2.937	3.229	4.187	0.854	4.187	0.854	2.187	2.104	2.568 ± 1.312
3	XOR–XOR–AND	2.104	2.187	0.854	4.187	0.854	4.187	3.229	2.937	2.568 ± 1.312
4	OR–OR–XOR	2.500	0.250	4.167	0.917	4.167	0.917	0.357	0.357	1.704 ± 1.680
5	AND–AND–XOR	0.357	0.357	0.917	2.042	0.917	2.042	0.250	4.500	1.422 ± 1.434
6	OR–AND–XOR	0.667	0.250	1	1	1.917	1.817	0.250	0.667	0.946 ± 0.636
7	AND–AND–OR	0.383	0.334	0.264	0.243	0.264	0.243	0.500	0.264	0.312 ± 0.091
8	OR–OR–AND	0.264	0.500	0.243	0.264	0.243	0.264	0.334	0.383	0.312 ± 0.091
9	AND–AND–AND	0.194	0.243	0.243	0.264	0.243	0.264	0.264	0.500	0.277 ± 0.093
10	OR–OR–OR	0.500	0.264	0.264	0.243	0.264	0.243	0.243	0.194	0.277 ± 0.093

For each possible network formed by three different logic gates: OR, AND and XOR, the values of Φ and <Φ> (± standard deviation) for all 8 current states are calculated. The computation of Φ is done using Python library for Integrated Information [18], [5] which is based on the theoretical framework of IIT 3.0 [14].

<Φ> exhibits a unique property of integrated information: the hierarchy in its values for all possible 3, 4, 5-node networks formed by all possible combinations of 3 distinct mechanisms: AND, OR, and XOR. As we can observe in Table S1 (Supplementary Tables), <Φ> leads to a natural hierarchy of networks based on the entropy of its individual nodes and how they combine. The higher the number of high entropy nodes present in the network, the more it contributes to integrated information of the corresponding network (Figure 2). Thus, a 3-node network consisting of all XORs has higher value of <Φ> (=3.0) as compared to a network consisting of all ANDs ($<\mathrm{\Phi }>=0.277$) (please refer to Table S1(a)). It is easy to verify that XORs have the highest Shannon entropy (=1.0 bit/symbol) followed by AND and OR, both of which have an entropy of 0.8113 bits. It is pertinent to note that the natural hierarchy is exhibited by <Φ> alone and not when the values of Φ are compared across different networks for any single current state.

Figure 2.

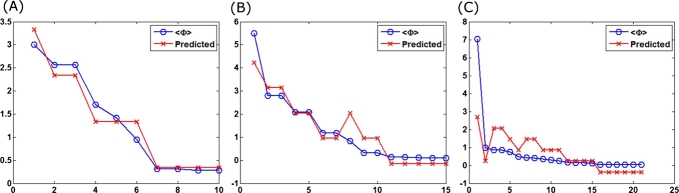
Linear regression of <Φ> as a function of entropy of nodes for all 3, 4 and 5-node networks. A linear fit is obtained between the dependent variable <Φ> and the explanatory variables ‘entropy’ of nodes and ‘number of nodes’. Y-axis represents the mean value of integrated information in all 3 graphs. (A) X-axis represents 10 different 3-node network configurations (refer Table S1(a) in ‘Supplementary Tables’). (B) X-axis represents 15 different 4-node network configurations (refer Table S1(b) in ‘Supplementary Tables’). (C) X-axis represents 21 different 5-node network configurations (refer Table S1(c) in ‘Supplementary Tables’). The blue plot represents the <Φ> values for each network configurations and the red plot represents the predicted values of <Φ> as a function of ‘entropy’ for each network configuration in all 3 graphs. The predicted <Φ> (in red) obtained from linear regression is a good fit when compared to the actual <Φ> (in blue) as indicated by the linear correlation coefficient values between them: 0.9746 (3-nodes), 0.9275 (4-nodes) and 0.6262 (5-nodes) respectively. For further details, please refer to ‘Supplementary Text’.

In order to understand the dependence of <Φ> with entropy of the nodes, we performed a linear regression (least squares) between the dependent variable <Φ> and the explanatory variables ‘entropy’ of the nodes and the ‘number of nodes’ (for further details, please refer to ‘Supplementary Text’). The predicted values obtained from the linear fit closely tracks the actual values of <Φ> as shown in Figure 2 and the linear correlation coefficient values between them are: 0.9746 (3-nodes), 0.9275 (4-nodes) and 0.6262 (5-nodes) respectively. This confirms our intuition that there is a linear correlation between the values of <Φ> and the entropy and of the nodes and their number.

In this section, we have shown that Φ is heavily dependent on current states of a network, which makes it non-robust measure of integrated information and <Φ> has linear correlation with the entropy of nodes. Φ also suffers from the limitations such as computational explosion for estimation in large networks and inability to handle neurophysiological data which is continuous in nature (for example, time series data) and thus not immediately applicable in the clinic. The new measure ${\mathrm{\Phi }}^C$ that we propose tries to address these limitations.

Nevertheless, in spite of the individual drawbacks that IIT 3.0 and PCI have, the former is strongly theoretically grounded and latter has succeeded empirically. Inspired by the both of these approaches, we propose new approach based on perturbational compression-complexity, which attempts to bridge the gap between IIT and PCI.

2.2. Comparing $<{\mathrm{\Phi }}^C>$ with <Φ>

In this section, we intend to evaluate how $<{\mathrm{\Phi }}^C>$ does in comparison with <Φ> for 3, 4, 5-node networks. It is shown through simulations that $<{\mathrm{\Phi }}^C>$ aligns very well with <Φ> in terms of hierarchy for 3-node networks and to a certain extent with 4 and 5-node networks as shown in Table S2 and Table S3 (please refer to ‘Supplementary Tables’) and Figure 3.

Figure 3.

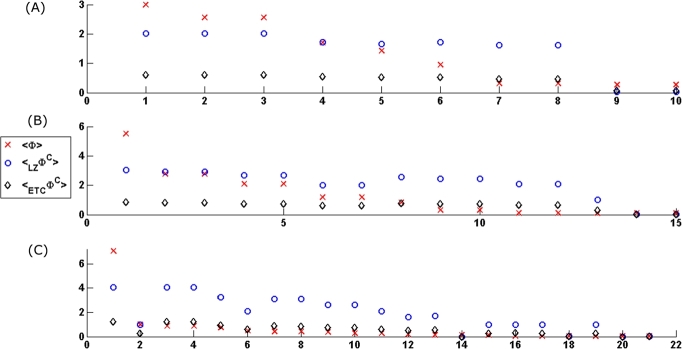
Plots of <Φ^C> and <Φ> (across all current-states) for all (A) 3-node, (B) 4-node, (C) 5-node networks. X-axis of each graph represents the different configurations of networks and Y-axis represents mean values of complexity of brain networks (here, integrated information) corresponding to the tables in ‘Supplementary Tables’. (A), (B) and (C) show the mean value of network complexity for ten configurations 3-node networks, 15 configurations of 4-node networks, 21 configurations of 5-node networks respectively. The trends in the values of <Φ> and <Φ^C> across different networks, depicted in this figure, are similar.

The trends in the values of <Φ> and $<{\mathrm{\Phi }}^C>$ across different networks are depicted in Figure 3 and they are similar. To quantify this, we compute the linear correlation coefficients between <Φ> and ${<}_{LZ}{\mathrm{\Phi }}^C>$: 0.6851 (3-nodes), 0.6154 (4-nodes) and 0.4877 (5-nodes). Similarly, linear correlation coefficient values between <Φ> and ${<}_{ETC}{\mathrm{\Phi }}^C>$ were: 0.7118 (3-nodes), 0.5561 (4-nodes) and 0.4977 (5-nodes). The linear correlation coefficients between ${<}_{LZ}{\mathrm{\Phi }}^C>$ and ${<}_{ETC}{\mathrm{\Phi }}^C>$ were very high (>0.99 in all cases). Also, as shown in Figure 4, we depict box-plots of the values of Φ and ${\mathrm{\Phi }}^C$ for all networks and for all current states.

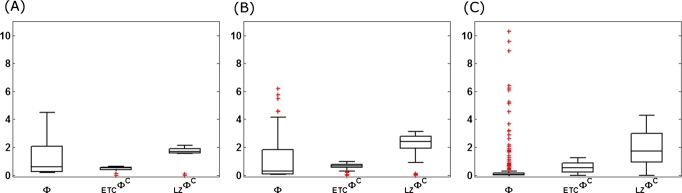
Figure 4.

Box-plots of the values Φ, ${}_{ETC}\mathrm{\Phi }^C$ and ${}_{LZ}\mathrm{\Phi }^C$ for all (A) 3, (B) 4, (C) 5-node networks and for all current states. The resolution of <Φ> across different networks is best among all the three measures.

For the sake of exhaustive analysis, we present mean and standard deviation of ${\mathrm{\Phi }}^C$ and Φ for all current-states of each network (Table S2 and Table S3 in ‘Supplementary Tables’). $<{\mathrm{\Phi }}^C>$ is observed to have similar hierarchy as <Φ> but with lesser standard deviation across current-states for all 3, 4, 5-node networks. As depicted in Table S1(a), Table S2(a) and Table S3(a) in ‘Supplementary Tables’, 3-node networks exhibit a similar hierarchy in values of ${<}_{ETC}{\mathrm{\Phi }}^C>$ and ${<}_{LZ}{\mathrm{\Phi }}^C>$ when compared to the values of <Φ>. This order is found to some extent in 4 and 5-node networks (refer to ‘Supplementary Tables’). However, there are some departures in the ordering of $<{\mathrm{\Phi }}^C>$ and <Φ>. For example, while comparing <Φ> and ${<}_{LZ}{\mathrm{\Phi }}^C>$ and taking the <Φ> values in Table S1(a) (‘Supplementary Tables’) as a reference for 3-node networks, there is a minor shuffling in the hierarchy (this is clear when you look at the column ‘Network No.’). For 4-node and 5-node, the departure from the hierarchy with respect to <Φ> is higher. As an example, AND–AND–AND–AND–AND and AND–AND–AND–AND–XOR stand at #20 and #2 respectively in the hierarchy for <Φ>, whereas for $<{\mathrm{\Phi }}^C>$ they are much closer in hierarchy. It is more intuitive that a single XOR replacement of an AND gate should not yield such a drastic change in complexity of brain networks.

Also, the standard deviation of ${\mathrm{\Phi }}^C$ for 3, 4 and 5-node networks is much lower than that of Φ: ($0.0\text{–}0.184$) for ${}_{ETC}\mathrm{\Phi }^C$, ($0.0\text{–}0.558$) for ${}_{LZ}\mathrm{\Phi }^C$ and ($0.0\text{–}2.062$) for Φ. In order to measure the dispersion of the three measures across all networks and all states, we compute the coefficient of variation (CoV).2 This is plotted in Figure 5, from which it is evident that both ${}_{LZ}\mathrm{\Phi }^C$ and ${}_{ETC}\mathrm{\Phi }^C$ have better (lower) values of CoV than Φ, barring a few exceptions (network $\mathrm{\#}9,10$ for 3-node networks, $\mathrm{\#}14,15$ for 4-node networks and $\mathrm{\#}14,18,20,21$ for 5-node networks). Therefore, in practice, we recommend choosing any single current state at random and then computing the value of ${\mathrm{\Phi }}^C$ for that current state. This is also one of the reasons why our measure is computationally efficient.

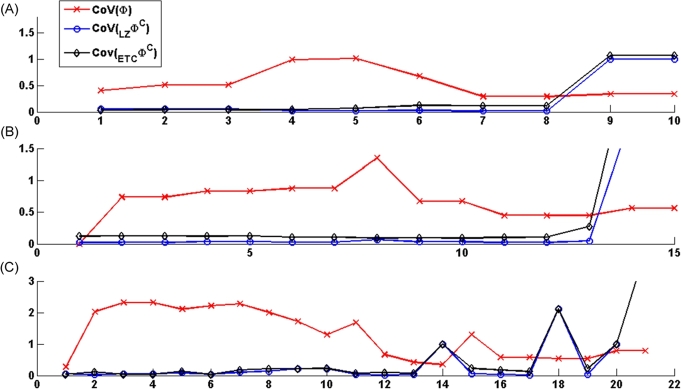
Figure 5.

Coefficient of variation (CoV) for measuring the complexity of brain networks. CoV of ${}_{LZ}\mathrm{\Phi }^C$, ${}_{ETC}\mathrm{\Phi }^C$ and Φ for (A) 3-node, (B) 4-node, and (C) 5-node networks. X-axis of each graph represents the different configurations of networks and Y-axis represents CoV values. (A), (B) and (C) show the mean value of integrated information for ten configurations of 3-node networks, 15 configurations of 4-node networks, 21 configurations of 5-node networks respectively (refer to ‘Supplementary Tables’ for the network configurations). Both ${}_{LZ}\mathrm{\Phi }^C$ and ${}_{ETC}\mathrm{\Phi }^C$ have better (lower) values of CoV than Φ in most networks barring a few exceptions.

2.3. Properties of ${\mathrm{\Phi }}^C$

• 1.Current-state independence: Unlike other measures of brain network complexity such as causal density [12], Neural complexity [11], Φ (IIT 1.0) [9], φ (IIT 2.0) [19], [20], [21], ${\mathrm{\Phi }}^{Max}$ (IIT 3.0) [4], [5], ${\mathrm{\Phi }}^{⁎}$ and ${\mathrm{\Phi }}_{MMP}^{⁎}$, which demonstrate the state-dependence of integrated information, the proposed measure ${\mathrm{\Phi }}^C$ has negligible dependence on the current state of the nodes of the network. There have been earlier attempts to propose a state-independent measure: (i) ${\mathrm{\Phi }}_E/{\mathrm{\Phi }}_{AR}$ proposed by [21] aims to measure the average information generated by the past states rather than information produced by the particular current state, (ii) ψ proposed by Griffith [22] also suggests stateless ψ as <ψ>, but this results in weakening of ψ, (iii) ${\mathrm{\Phi }}_{MMP}^{AR}$ suggested by Toker et al. [23] based on the foundations of ${\mathrm{\Phi }}_{AR}$ using Maximum Modularity Partition seems to be state-independent when utilized for neural data that cannot be transformed into a normal distribution. But, these measures too, have not been extensively tested with different networks to show a lower standard deviation when computed across all current states. However, as it can be seen from ‘Supplementary Tables’, the standard deviation of the values of ${\mathrm{\Phi }}^C$ across all current states for 3, 4, 5-node networks is very low. We expect this property to hold even for networks with larger number of nodes.
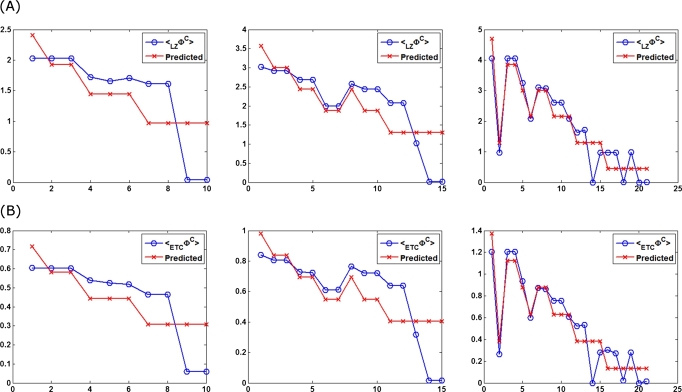
• 2.Linear correlation of ${\mathrm{\Phi }}^C$ with entropy of nodes: Similar to <Φ>, $<{\mathrm{\Phi }}^C>$ also exhibits a linear correlation with the entropy of the nodes. As shown in Figure 6, linear regression (least squares) is performed with the dependent variable $<{\mathrm{\Phi }}^C>$ and the explanatory variables ‘entropy’ of the nodes and the ‘number of nodes’ (for further details, please refer to ‘Supplementary Text’). The predicted values obtained from the linear fit closely tracks the actual values of $<{\mathrm{\Phi }}^C>$ as shown in Figure 6. This is indicated by the linear correlation coefficient values between ${<}_{LZ}{\mathrm{\Phi }}^C>$ and the predicted values: 0.6654 (3-nodes), 0.7524 (4-nodes), 0.9378 (5-nodes); and between ${<}_{ETC}{\mathrm{\Phi }}^C>$ and the predicted values: 0.6879 (3-nodes), 0.6957 (4-nodes), 0.9361 (5-nodes). As it can be seen, the prediction improves as the number of nodes increases.
• 3.Information theoretic vs. Compression-Complexity measure: Existing measures of brain network complexity are all heavily based on information theoretic measures such as entropy, mutual information, intrinsic information, etc. However, ${\mathrm{\Phi }}^C$ is built on complexity measures (ETC, LZ) which have roots in lossless compression algorithms. ETC is related to a lossless compression scheme known as NSRPS [16], [24] and LZ is based on a universal compression algorithm [25]. These complexity measures do not directly model the probability distribution of potential past and future states of a system, but learn from the patterns in the time series. This approach is known to be more robust even with small set of measurements and in the presence of noise [16].
• 4.Boundedness: ${\mathrm{\Phi }}^C$ is well defined mathematically and is bounded between 0 and $N-1$, where N is the number of nodes in the network. Since we use normalized values for both ETC and LZ complexity measures to define ${\phi }^C$ at every node, therefore ${\phi }^C$ is bounded between 0 and 1. Further, since ${\mathrm{\Phi }}^C$ is computed as the maximum of aggregated values of ${\phi }^C$, and for every atomic bipartition there are $N-1$ pairs of output time series, the maximum aggregated value of the differential complexity measure can be utmost $N-1$ (the maximum value is attained if complexity value obtained from MEP time series is 1 and 0 from ZEP time series for each bipartition). Therefore, $0\le {\mathrm{\Phi }}^C\le N-1$. Even though LZ complexity is also normalized, its value can exceed one at times [26], [27]. This is a problem due to finite data lengths. But, normalized ETC does not have this problem and it is always bounded between 0 and 1 [16]. Hence, we would recommend the use of normalized ETC complexity measure over normalized LZ complexity.
• 5.Process vs. capacity: ${\mathrm{\Phi }}^{Max}$ measures consciousness as brain network complexity which is represented by the capacity of the system [21], while PCI measures the same as a process by recording the activity of the brain generated by perturbing the cortex with TMS using high-density electroencephalography [6]. However, ${\mathrm{\Phi }}^C$ as a measure of integrated information encapsulates both the ideas of ‘capacity’ and ‘process’. The Differential Compression-Complexity Response Distribution (dCCRD) for each atomic bipartition is measuring integrated information as a process for time-series data from each node. The Aggregate Differential Compression-Complexity Measure captures the network's capacity to integrate information. Therefore, ${\mathrm{\Phi }}^C$ incorporates ideas from both IIT and PCI, for measuring network complexity.
• 6.Discrete and continuous systems: ${\mathrm{\Phi }}^C$ can be easily extended to continuous measurements such as neurophysiological data. We could sample the continuous measurements to yield discrete samples on which ${\mathrm{\Phi }}^C$ can be estimated or apply techniques which maximize the information transfer (or minimizes the loss) [28]. Thus, our measure applies equally to both discrete and continuous systems.
• 7.Lower computational complexity: Since ${\mathrm{\Phi }}^C$ employs atomic bipartitions it has lower computational complexity than the case where computation is performed over all possible partitions. This is because the number of atomic bipartitions increases linearly with the number of nodes in the network whereas the total number of bipartitions increases exponentially.

Figure 6.

Linear regression of (A) <_LZΦ^C> and (B) <_ETCΦ^C> as a function of entropy of nodes for all 3, 4 and 5-node networks. A linear fit is obtained between the dependent variable <_LZΦ^C> (or <_ETCΦ^C>) and the explanatory variables – ‘entropy’ of nodes and ‘number of nodes’. In each of the graphs above, X-axis of each graph represents the different configurations of networks and Y-axis represents the mean value of brain network complexity. The leftmost, middle and rightmost graph in both (A) and (B) shows the mean value of integrated information for ten configurations 3-node networks, 15 configurations of 4-node networks, 21 configurations of 5-node networks respectively (refer to ‘Supplementary Tables’ for the network configurations). For each network configuration, the blue plot represents <_LZΦ^C> or <_ETCΦ^C> values respectively in (A) and (B) and the red plot represents their predicted values as a function of ‘entropy’. For further details, please refer to ‘Supplementary Text’.

3. Methods

In this section, we detail all the methods pertaining to the new measure ${\mathrm{\Phi }}^C$.

3.1. ${\mathrm{\Phi }}^C$: moving towards a new approach

To address the aforementioned limitations of Φ (IIT 3.0) and PCI, we propose a new measure ${\mathrm{\Phi }}^C$ and formally introduce the required steps for its computation.

3.1.1. Data compression and integrated information

As Maguire notes, there is an integration of our current experience with memories that already exist within us, and this unique binding lends ‘subjectivity’ to our experience [29]. This relates to the notion of integrated information. For example, a video camera which is capable of recording several amounts of visual data, is not conscious in the same way as we human beings are [29]. This is because, one can selectively delete the memory of the video camera unit whereas it is nearly impossible to do so in the human brain. The different parts of the brain are tightly integrated such that they have significant causal interactions amongst them and the information of an external stimulus is ‘encoded’ (or integrated) to the existing information in the brain. Thus, the brain responds more like a singular unified integrated system.

The notion of data compression is a good example for integrated information [30]. Every character in an uncompressed text file is carrying nearly independent information about the text while in a compressed (lossless) file, no single bit is truly independent of the rest. As observed in [29], “the information encoded by the bits of a compressed file is more than the sum of its parts”, highlighting connections between data compression and Tononi's concept of integrated information.

Compressionism is a term coined by Maguire and Maguire [30], [31] to characterize the sophisticated data compression which the brain performs to bind information with experience that we associate with consciousness. Therefore, information integration in brain networks could be captured by data compression.

3.1.2. Compression-Complexity

There is a deep relationship between data compression and several complexity measures, especially those measures which are derived from lossless compression algorithms. Lempel–Ziv complexity (LZ) [15] measures the degree of compressibility of an input string, and is closely related to Lempel–Ziv compression algorithm (a universal compression algorithm [25] which forms the basis of WinZip, Gzip, etc.). Similarly, a recently proposed complexity measure known as Effort-To-Compress (ETC) [16] characterizes the effort to compress an input sequence by using a lossless compression algorithm. The specific compression algorithm used by ETC is Non-Sequential Recursive Pair Substitution Algorithm (NSRPS) [24]. ETC and LZ have been demonstrated to outperform Shannon entropy for characterizing the complexity of short and noisy time series from chaotic dynamical systems [16], [17]. It is difficult to evaluate entropy since it involves estimation of probability distribution which requires extensive sampling that usually cannot be performed [32]. However, LZ and ETC complexities are properties of individual sequences (or time series) and much easier to compute in a robust fashion. Hence, we make use of these for computing compression-complexity of time series. Brief descriptions of LZ and ETC are given below.

Lempel–Ziv complexity (LZ):

Given the input time series, $X={\{x_i\}}_{i=1}^{i=n}=x_1{x}_2\dots x_n$, it is parsed from left to right so as to identify the number of distinct patterns it contains. This parsing scheme has been proposed in [15].

We reproduce a slightly modified description of the algorithm for computing LZ complexity, adapted from [27]. Let the input sequence be denoted by $S=s_1{s}_2\cdots s_n$; and let $S(i,j)$ represent a substring of S that begins at position i and ends at position j; let $W(S)$ denote the set of all substrings $\{S(i,j),i=1,2,\cdots n;j\ge i\}$. For example, let $S=def$, then $W(S)=d,e,f,de,ef,def$. The parsing mechanism is a left-to-right scan of the symbolic sequence S. Start with $i=1$ and $j=1$. A substring $S(i,j)$ is compared with all strings in $W(S(i,j-1))$ (let $W(S(1,0))=\{\}$, the empty set). If $S(i,j)$ is present in $W(S(1,j-1))$, then increase j by 1 and repeat the process. If the substring is not present, then place a dot after $S(i,j)$ to indicate the end of a new component, set $i=j+1$, increase j by 1, and the process continues. This parsing procedure continues until $j=n$, where n is the length of the symbolic sequence. For example, the sequence ‘$aacgacga$’ is parsed as ‘$a.ac.g.acga$.’. By convention, a dot is placed after the last element of the symbolic sequence and the number of dots gives us the number of distinct words which is taken as the LZ complexity, denoted by $c(n)$. In this example, the number of distinct words (LZ complexity) is 4. To facilitate the comparison of LZ complexity values of sequences of different lengths, a normalized measure is used [26]:

$$C_{LZ}=(c(n)/n)lo{g}_{\alpha }n,$$ (1)

where α denotes the number of unique symbols in the input time series.

Effort-To-Compress complexity (ETC):

At the first iteration of ETC, that pair of symbols (in the input time series/sequence) which has maximum number of occurrences is replaced by a new symbol. For example, the input sequence ‘22020020’ is transformed into ‘23303’ in the first iteration since the pair ‘20’ has maximum number of occurrences (when compared with the pairs ‘00’, ‘02’ and ‘22’). In the second iteration, ‘23303’ is transformed to ‘4303’. The algorithm proceeds in this manner until the length of the transformed string shrinks to 1 or the transformed sequence reduces to a constant sequence. In either cases, the algorithm terminates. For our example, the algorithm transforms the input sequence $22020020\mapsto 23303\mapsto 4303\mapsto 503\mapsto 63\mapsto 7$, and thus takes 5 iterations to halt.

The ETC complexity measure, $ET{C}_{val}$, is given by the number of iterations required to transform the input sequence to a constant sequence by repeated application of the pair substitution algorithm just described. $ET{C}_{val}$ is always a non-negative integer, bounded between 0 and $L-1$, where L is the length of the input sequence. The normalized version of the measure is given by: $ET{C}_{norm.}=\frac{ET{C}_{val}}{L-1}$. Note that $0\le \frac{ET{C}_{val}}{L-1}\le 1$. For our example, $ET{C}_{norm.}=\frac{5}{8-1}=\frac{5}{7}=0.7143$.

Difference that makes a difference:

In the light of the advantages which LZ and ETC provide over information theoretic measures such as entropy, we are motivated to employ these in determining complexity in brain networks. Therefore, we introduce “Compression-Complexity” measures which characterize complexity of brain networks using lossless compression algorithm based complexity measures.

Our goal is to use these complexity measures (LZ and ETC) to propose a network complexity measure which can approximate the integrated information in a network. When a single node of a network is perturbed by a random input, this perturbation travels through the network to other nodes. By capturing the output at all the other nodes and computing the complexity of their outputs, we intend to study the degree of information integration in the network. As a baseline, we also compute the complexity of the response of all the other nodes for a zero-entropy perturbation of the input node. We then compute the difference between the two responses and aggregate them. A network which is more strongly integrated will exhibit strong causal interactions among its nodes. This means that in such a network, the perturbations travel throughout the network causing high entropy output in other nodes as well (since the input is a random perturbation, it is a high entropy input to the network). By aggregating the differential compression-complexity of the output of all the other nodes (leaving out the input node which is perturbed), we get a sense of integrated information. This is because, we are computing information as difference that makes a difference [33], here the difference is calculated between the response for a maximum-entropy perturbation and a zero-entropy perturbation. We then take a maximum of all such aggregated differential compression-complexity measures across all possible perturbations (if a network has N nodes, then we have N pairs of perturbations in total). The reason for taking the maximum is that it indicates that specific atomic bipartition which characterizes integrated information as maximum difference in the input perturbations (as measured by Shannon entropy or compression-complexity) that makes a maximum difference in the aggregated output response (measured by compression-complexity). Thus, we define the maximum differential compression-complexity (aggregated) response that is triggered by a maximum differential entropy perturbation as a measure of the capacity of the network to integrate information. In a way, this is what PCI is also measuring, but it makes use of a single perturbation (which is not a maximum entropy one either).

3.1.3. Defining and computing the new measure ${\mathrm{\Phi }}^C$

${\mathrm{\Phi }}^C$ for a network (with randomly chosen current state of the network) is computed by performing the following steps, as also depicted in Figure 7: (i) bipartitioning a network into its all atomic bipartitions, (ii) perturbing the atomic node for each bipartition with random input time series (maximum entropy), and followed by a zero entropy time series (constant sequence), (iii) recording the output time series from all the other nodes of the network and computing the LZ/ETC complexities of these individual time series for each bipartition, for both perturbations and computing their difference (denoted by 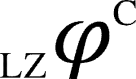or 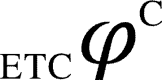), (iv) computing the aggregate of these differential complexity measures (LZ/ETC) for each bipartition of network, (v) reporting the maximum value across all such computed aggregate differential complexity measures ( 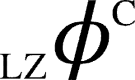or ) 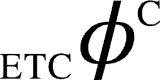obtained in step (iv) as the value of 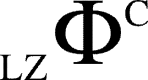(or ).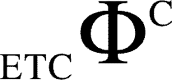

Figure 7.

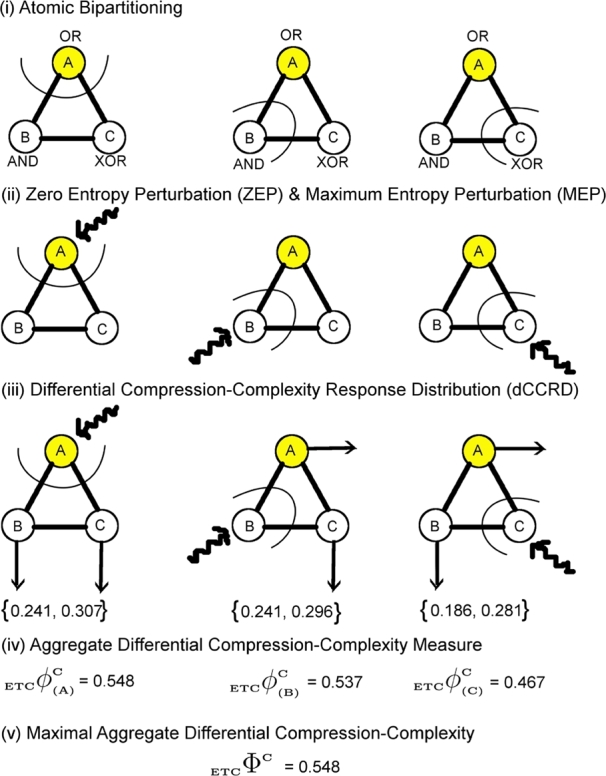
Algorithm for the computation of Φ^C is illustrated through diagrams. The network ABC (current state = (1,0,0)) constitutes three logic gates: OR, AND, XOR for which the value of Φ^C is computed. (i) The network is partitioned into 3 possible atomic bipartitions, (ii) each atomic bipartition is perturbed with a Maximum Entropy Perturbation (MEP) which is a random input binary time series (length = 200) as well as Zero Entropy Perturbation (ZEP) which is a constant sequence (length = 200), (iii) Differential Compression-Complexity is computed by taking the difference between complexities for MEP and ZEP for each output time series from the remaining two unperturbed nodes. This forms the Differential Compression-Complexity Response Distribution (dCCRD) for each bipartition. For example, 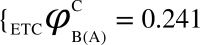, , 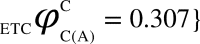represents the dCCRD of the time series obtained from the nodes B and C respectively, when the node A is perturbed. Similarly, the dCCRD for the other two bipartitions are: 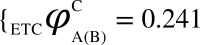, 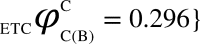and 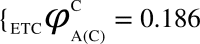, , 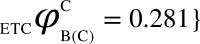(iv) the individual values of each dCCRD are summed up to obtain ‘Aggregate Differential Compression-Complexity Measure’ for each bipartitioned-perturbed network. Therefore, 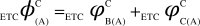and similarly 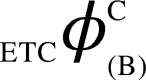and 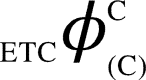can be computed. All corresponding values are: 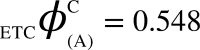, , 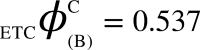, 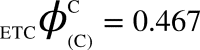(v) Maximal-Aggregate Differential Compression-Complexity, Φ^C, is nothing but the maximum of the Aggregate Differential Compression-Complexity measures: 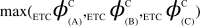. Thus, 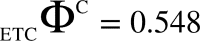. For more details, please refer to ‘Supplementary Text’.

Definition

${\mathrm{\Phi }}^C$ is defined as the maximally-aggregate differential normalized Lempel–Ziv (LZ) or normalized Effort-To-Compress (ETC) complexity for the time series data of each node of a network, generated by perturbing each possible atomic bipartition of an N-node network with a maximum entropy perturbation and a zero entropy perturbation. The mean of ${\mathrm{\Phi }}^C$ across all states of a network is denoted as $<{\mathrm{\Phi }}^C>$. ${}_{ETC}\mathrm{\Phi }^C$ and ${}_{LZ}\mathrm{\Phi }^C$ denote ${\mathrm{\Phi }}^C$ computed using ETC and LZ complexity measures respectively.

For the sake of clarity and completeness, we define the following terms:

Network: A system with N nodes $A_1,A_2,\dots ,A_N$ with all bi-directional connections and no self-loops.

Atomic bipartition: A division of a network with two parts with one part containing only one node ($A_i$) and the other part containing the rest $\{A_1,A_2,\dots ,A_j,\dots ,A_N\}$ where $j\ne i$.

Maximum Entropy Perturbation (MEP): It is defined as the uniform random input perturbation time series (with maximum entropy) injected to $A_i$ of the atomic bipartition.

Zero Entropy Perturbation (ZEP): It is defined as a constant input perturbation time series (with zero entropy) injected to $A_i$ of the atomic bipartition.

Differential Compression-Complexity Response Distribution (dCCRD): It is defined as the distribution of difference between complexities of the responses from each node of the network in each atomic bipartition of the network when one of the nodes is perturbed – first with a random maximum entropy perturbation and next with a zero entropy perturbation (see Methods for details).

3.1.4. An example of ${\mathrm{\Phi }}^C$

${\mathrm{\Phi }}^C$ serves as a measure of integrated information (similar to Φ). We provide two examples to demonstrate the correspondence of ${\mathrm{\Phi }}^C$ with Φ. For two 2-node networks as shown in Figure 8, the values of ${\mathrm{\Phi }}^C$ and Φ are similar – both are lower for OR–AND than OR–XOR network.

Figure 8.

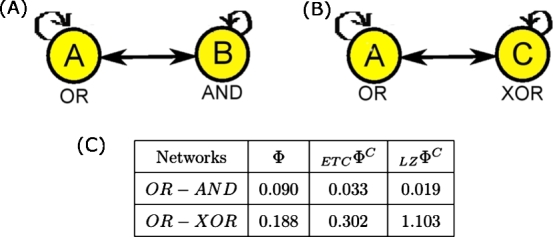
Resemblance of Φ^C with Φ for two 2-node networks. (A): OR–AND network, (B) OR–XOR network. (C) The table lists the corresponding values of Φ^C and Φ for the current state (1,1). It can be seen that similar to Φ, Φ^C is lower for OR–AND when compared to OR–XOR.

3.2. Calculation of ${\mathrm{\Phi }}^C$ (${}_{LZ}\mathrm{\Phi }^C$ and ${}_{ETC}\mathrm{\Phi }^C$)

To compute the proposed compression-complexity measure, ${\mathrm{\Phi }}^C$, the methods employed are described below.

3.2.1. Maximum Entropy Perturbation (MEP)

The input to the perturbed node is a maximum entropy time series $\{P_t\}$ which is obtained as follows:

$$\begin{array}{ccc}\hfill RAN{D}_t& \hfill =\hfill & rand(0,1),\hfill \\ \hfill P_t& \hfill =\hfill & 0,\text{if }0\le RAN{D}_t\le 0.5,\hfill \\ \hfill & \hfill =\hfill & 1,\text{if }0.5<RAN{D}_t\le 1,\hfill \end{array}$$ (2)

where $rand(0,1)$ generates a uniform random variable between 0 and 1; discrete time $t=1,2,\dots ,LEN$, where LEN is the length of the time series generated. We have chosen $LEN=200$ in our computations.

3.2.2. Zero Entropy Perturbation (ZEP)

The input to the perturbed node is a zero entropy time series $\{Q_t\}=\mathit{constant}$ of length $LEN=200$.

3.2.3. Differential Compression-Complexity Response Distribution (dCCRD)

The perturbation to the i-th node is done by independently injecting the MEP and ZEP time series $\{P_t\}$ and $\{Q_t\}$ to node i. The two independent sets of output time series $\{T_j^{MEP}\}$ and $\{T_j^{ZEP}\}$ from the remaining $N-1$ nodes (indexed by $j\ne i$) are collected. We compute the differential compression-complexity of the j-th time series for the i-th perturbed node as follows:

(3)

where $j=1,2,\dots ,N$ and $j\ne i$. Thus, dCCRD for the i-th perturbed node is obtained as the following set:

(4)

We thus obtain $\{dCCR{D}_{ETC}(i)\}$ for all perturbed nodes $i=1,2,\dots ,N$. The subroutine $\text{Compute}\mathrm{\_}\text{ETC}\mathrm{\_}\text{Complexity}(\cdot )$ employs the normalized Effort-To- Compress (ETC) complexity measure. ETC uses the lossless compression algorithm called Non-Sequential Recursive Pair Substitution (NSRPS) and it denotes the number of iterations needed for NSRPS to transform the input sequence to a constant sequence. ETC has been found to be more successful as a complexity measure in practical applications (in short and noisy real-world sequences) than infotheoretic measure such as entropy [16], [17].

3.2.4. Aggregate Differential Compression-Complexity Measure

Once we have the dCCRD for all the perturbed nodes, the aggregate differential compression-complexity measure is obtained as follows:

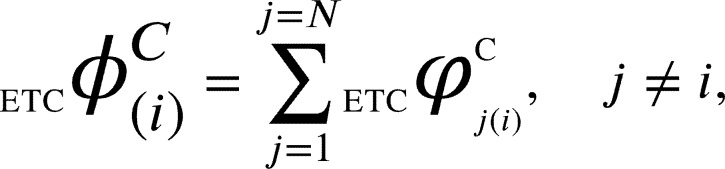(5)

where $i=1,2,3,\dots ,N$.

3.2.5. Maximal Aggregate Differential Compression-Complexity

We finally obtain:

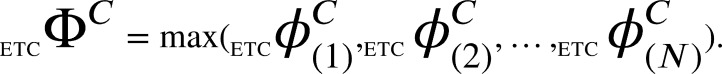(6)

For obtaining the other measure ${}_{LZ}\mathrm{\Phi }^C$, we replace $\text{Compute}\mathrm{\_}\text{ETC}\mathrm{\_}\text{Complexity}(\cdot )$ in Eq. (3) with $\text{Compute}\mathrm{\_}\text{LZ}\mathrm{\_}\text{Complexity}(\cdot )$. The subscript LZ instead of ETC is carried forward, but the steps remain effectively the same. $\text{Compute}\mathrm{\_}\text{LZ}\mathrm{\_}\text{Complexity}(\cdot )$ employs the normalized Lempel–Ziv complexity measure.

3.2.6. An example implementation of ${}_{ETC}\mathrm{\Phi }^C$ in MATLAB

As supplementary code to this paper, we provide MATLAB program ‘PhiC_ETC_Fig7.m’ which performs step-by-step computation of ${}_{ETC}\mathrm{\Phi }^C$ for the example network ABC with 3 nodes, as depicted in Figure 7. ‘ETC.m’ is the MATLAB subroutine for the computation of normalized “Effort-To-Compress” (ETC) measure (required to run ‘PhiC_ETC_Fig7.m’). ‘MEP_TimeSeries.txt’ and ‘ZEP_TimeSeries.txt’ are the text files containing the time-series for the network ABC when each of its bipartition is perturbed with a random binary sequence and a constant binary sequence (either all zeros or all ones) respectively.

3.3. Calculation of Φ

For the sake of completeness, we give details of computation of Φ in this work. We compute Φ for the following configuration – all possible 3-node networks with logic gates: XOR, OR, AND. The network is fully connected i.e. each node is connected to every other node in the network with a bi-directional connection and no node has any self-loop. In this case, there are a total of 10 distinct possible networks and for each 3-node networks there are 8 possible current states of the network.

Using the PyPhi 0.7.0 Python library [18], [5] for computing integrated information, we calculate the values of Φ for the current state of each network and then calculate the mean of all values (<Φ>). We repeat the same experiment for 4 and 5-node networks. For further details on computing Φ, refer to [5].

4. Discussion

In this paper, we proposed a new measure for quantifying complexity in brain networks (which could also contribute in developing a potential measure of consciousness) called ${\mathrm{\Phi }}^C$, which is defined as the largest aggregated differential compression-complexity measure (ETC/LZ) computed from time series data of each perturbed node of the atomic bipartition of an N-node network.

We have discussed the motivation behind such a compression-complexity approach to measure integrated information. The perturbational perspective to measure compression-complexity is inspired by PCI and is also computationally efficient (we need to consider only N bipartitioned perturbations). ${\mathrm{\Phi }}^C$ is a measure of the maximum difference in complexity of outputs resulting from a maximum difference in entropy of input perturbations across all nodes of a network. ${\mathrm{\Phi }}^C$ exhibits the following salient innovations: (i) negligible current state dependence (as indicated by a very low standard-deviation of ${\mathrm{\Phi }}^C$ across all current states of a network), (ii) network complexity measured as compression-complexity rather than as an infotheoretic quantity, and (iii) quick computation by a perturbational approach over atomic bipartitions (which scales linearly with number of nodes), thus avoiding combinatorial explosion. Our computer simulations showed that $<{\mathrm{\Phi }}^C>$ has similar hierarchy to <Φ> for 3, 4, 5-node networks, thus conforming with IIT. Moreover, the hierarchy of $<{\mathrm{\Phi }}^C>$ follows intuitively from our understanding that integrated information is higher in a network which has more number of high entropy nodes (for example, more number of XOR gates than AND, OR gates) for a fully connected network.

4.1. Advantages of ${\mathrm{\Phi }}^C$

Our novel approach provides several advantages over other measures of measuring brain network complexity: i) suggesting atomic bipartitioning instead of MIP which avoids combinatorial explosion, ii) introducing Maximum Entropy Perturbation (MEP) and Zero Entropy Perturbation (ZEP), and iii) proposing Differential Compression-Complexity Response Distribution (dCCRD) allowing us to measure ${\mathrm{\Phi }}^C$ for continuous time series data.

${\mathrm{\Phi }}^{Max}$ as a measure of Integrated Information to quantify consciousness needs the identification of MIP in a network [5]. But, finding MIP faces practical and theoretical roadblocks which are unresolved till now [14]. The practical issue is: locating MIP requires investigation of every possible partition of the network, which is realistically unfeasible as the total number of possible partitions increase exponentially with the size of the network leading to combinatorial explosion [14], [23], [34]. In fact, this approach is impractical for a network with more than dozen nodes [5]. In order to overcome these issues, other approaches have been suggested, such as Minimum Information Bipartition (MIB) and Maximum Modularity Partition (MMP). Though MIB is faster to compute than MIP [23] and has been used by various measures of integrated information [9], [7], [35], [14], [20], [36], [37], it also has two issues to be addressed. Firstly, the time to find MIB also grows exponentially with larger networks and secondly, it is not certain if MIB is a reasonable approach to disintegrate a neural network (since it is dubious that functional subnetworks divide the brain exactly in half) [23]. Hence, MIB is inapplicable to real brain networks as of now. We tackle this practical issue by using atomic bipartitions, whose number increases linearly with the size of the network. Atomic bipartitions have been recommended by other researchers too in lieu of MIP [23], [14].

Compression-Complexity approach conferred certain desirable properties to ${\mathrm{\Phi }}^C$. Firstly, this approach allowed us to measure the dynamic complexity of networks as a process for the output time-series data in the form of distribution of differential responses (dCCRD) to Maximum Entropy Perturbation (MEP) and Zero Entropy Perturbation (ZEP) and secondly, dCCRD provided us with the distribution of differential complexity values which could be useful in multitude of ways to be explored in the future. Furthermore, since ${\mathrm{\Phi }}^C$ employs complexity measures such as LZ and ETC instead of infotheoretic quantities (such as entropy, mutual information, etc.), it is more robust to noise, and efficient with even short and non-stationary measurement time series. Also, we have already noted that ${\mathrm{\Phi }}^C$ has negligible dependence on current-state of a network, unlike other measures.

Thus, ${\mathrm{\Phi }}^C$ is a potentially promising approach for fast and robust empirical computation of brain network complexity.

4.2. Interplay between differentiation, integration and entropy

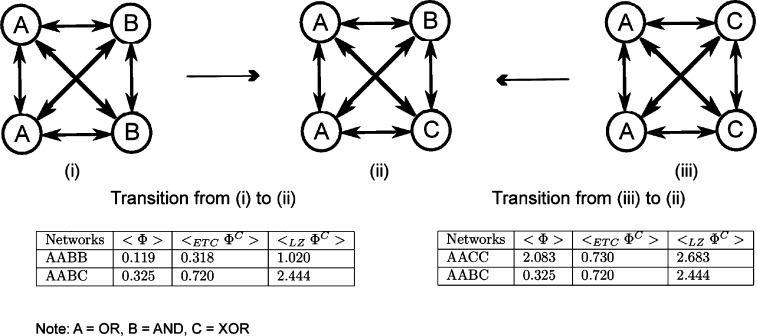
Researchers have already acknowledged that consciousness could be a result of the complexity of neuronal network in our brain which depicts ‘functional differentiation’ and ‘functional integration’ [6], [7], [8], [9], [10], [21], [38]. For example, referring to Figure 9, when we compare the two networks (i) and (iii) with the network (ii), we note that the latter is more heterogeneous (since it has three different types of gates as opposed to the former which has only two types of gates). Griffith [22] makes the point that in such a scenario, it is intuitive that the integrated information is larger for the more heterogeneous network. But, it is not as intuitive as it seems, since the entropy of the gates play an important role as well.

Figure 9.

Interplay between differentiation, integration and entropy. (i) AABB has <Φ > =0.119, <_ETCΦ^C > =0.318, <_LZΦ^C > =1.020, (ii) AABC has <Φ > =0.325, <_ETCΦ^C > =0.720, <_LZΦ^C > =2.444, (iii) AACC has <Φ > =2.083, <_LZΦ^C > =0.730, <_ETCΦ^C > =2.683. The complexity of the simulated network AABB is lower than that of AABC, which is lesser than the complexity of AACC. This may seem counter-intuitive, but it is not, since the entropy of C (XOR gate) is higher than the entropies of both B (AND gate) and A (OR) gate. Thus, heterogeneity alone is insufficient to increase the value of integrated information of the network; the entropy of the individual nodes and their number in the network also matter.

As shown in the Figure 9, the integrated information (<Φ>, ${<}_{LZ}{\mathrm{\Phi }}^C>$ and ${<}_{ETC}{\mathrm{\Phi }}^C>$) of the network $AABB$ is lower than that of $AABC$ which is in turn lesser than the integrated information of $AACC$ (with $A=OR$, $B=AND$, $C=XOR$). This may appear counter-intuitive at first, but it makes sense when we realize that the entropy of C is higher than both A and B. Thus, it is not universally true that heterogeneous networks have higher amounts of integrated information, as it very much depends on the entropy of the individual nodes as well as their number. In the case of the brain, cortical neurons are known to exhibit different firing patterns whose entropy varies widely. As an example, we simulate a cortical neuron from the Hindmarsh–Rose neuron model [39] which is a widely used model for bursting-spiking dynamics of the membrane voltage of a single neuron which we describe below.

Hindmarsh–Rose neuron model

The equations of the Hindmarsh–Rose neuron model [39] in dimensionless form are:

$$\begin{array}{ccc}\hfill \dot{S}& \hfill =\hfill & P+3S^2-S^3-Q+I,\hfill \\ \hfill \dot{P}& \hfill =\hfill & 1-5S^2-P,\hfill \\ \hfill \dot{Q}& \hfill =\hfill & -r[Q-4(S+\frac{8}{5})],\hfill \end{array}$$ (7)

where S(t) is the membrane voltage of a single neuron, P(t) measures the rate of sodium and potassium ions through the fast ion channel, and Q(t) measures the rate of other ions through slow channels. P(t) is called the spiking variable and Q(t) is called the bursting variable. The model has the following control parameters: I and r, where the former is the external current applied and the later is the internal state of the neuron. In our simulations we have chosen $r=0.0021$. The values of I chosen are $I=3.31$ for simulating regular spiking and $I=3.28$ for simulating irregular/chaotic spiking. We have used a window of length 2 and if the value of $S(t)$ exceeded a threshold of −0.1 in this window, we count it as a spike (‘1’). The resulting sequence of 0s (no-spike) and 1s (spike) is used for computing Shannon entropy, LZ and ETC complexities.

The same neuron exhibits regular spiking (Figure 10(A)) when the external current applied is $I=3.31$ and chaotic or irregular spiking (Figure 10(B)) when $I=3.28$. We computed the Shannon entropy, ETC, and LZ complexity values for the two cases. It can be seen that the same neuron shows a lower value of entropy and complexities ($H=0.8342$ bits, $ETC=0.1910$ and $LZ=0.6879$) when it is spiking in a regular manner as compared to its behavior in a chaotic manner ($H=0.9295$ bits, $ETC=0.2211$, $LZ=0.7262$). Thus, for the same neuronal network, under two different excitations, the neurons can behave with different entropies/complexities. This will have a significant impact on the values of integrated information and it is hard to predict how this interplay between functional integration, differentiation and entropy will pan out in reality.

Figure 10.

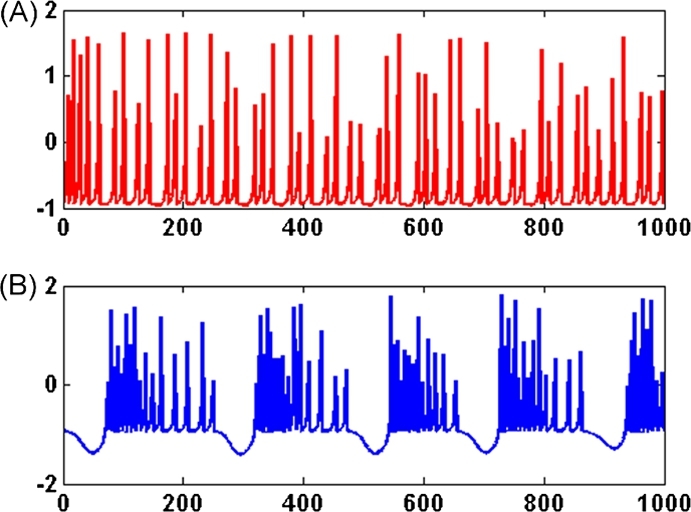
A single neuron exhibits low and high entropy firing patterns. Simulation of a single cortical neuron from the Hindmarsh–Rose neuron model [39] showing two different kinds of behavior. (A) Membrane voltage as a function of time for regular firing exhibited by the neuron when the external current applied is I = 3.31. Entropy and Complexities: H = 0.8342 bits and ETC = 0.1910, LZ = 0.6879. (B) Membrane voltage as a function of time for chaotic or irregular spiking exhibited by the neuron when I = 3.280. Entropy and Complexities: H = 0.9295 bits and ETC = 0.2211, LZ = 0.7262. Thus, for the same neuron, under two different excitations, the neuron manifests low as well as high entropy behavior (low and high ETC/LZ complexities correspondingly). Note: The model in [39] treats voltage and time as dimensionless quantities.

4.3. A remark on Aggregate Differential Compression-Complexity Distribution

One drawback of integrated information as well as $<{\mathrm{\Phi }}^C>$ (mean value), is the fact that they are scalar quantities and thus there is a possibility of ambiguity.

It is possible that two different networks could end up having the same value for the measure. For example, consider two 5-node networks (current state ‘11101’): Network I – XOR–XOR–XOR–AND–XOR and Network II – XOR–XOR–XOR–OR–XOR, both of which turn out to have the same mean ${}_{ETC}\mathrm{\Phi }^C=1.175$. However, the ‘Aggregate Differential Compression-Complexity Distribution’ (Aggregate dCCRD) turns out to be different for the two networks. Aggregate dCCRD for Network I is $[0.709,0.709,0.709,1.176,0.884]$ and that for Network II is $[0.719,0.719,0.719,1.176,1.161]$. Thus, aggregate dCCRD is able to resolve this ambiguity by providing a rich vector-valued distribution worth of complexity values for all the nodes of the network. Further uses of aggregate dCCRD need to be explored in future.

4.4. Testing ${\mathrm{\Phi }}^C$ on larger sized networks

Testing of our proposed measure on real-world brain networks is outside the purview of this work. However, we shall demonstrate how our measure performs on various simulated directed graphs with different topologies (by varying the number of edges and their connectivity).

We simulated directed graphs with $V=100$ nodes and different number of directed edges E. We consider three well known topologies namely – (a) Ring, (b) Random, (c) Perfect graph. In the case of Ring topology, the nodes are connected in a circular fashion with each node having only 2 neighbors (a node $v_k$ has a node $v_{k-1}$ that feeds into it and in turn the node $v_k$ feeds into $v_{k+1}$). In case of Perfect graph topology, every node feeds into every other node (except itself). For the Random network topology, we generated the adjacency matrix with every entry having a 1 as its value with probability of 0.5 (we eliminated self-loops). This would mean that between any two distinct nodes the probability of having a directed edge is 0.5. This resulted in a random network with $E=5012$ edges. We additionally changed this probability of edge formation to create several random networks with different number of directed edges ($E=986,2964,3953,6929,8019$). Thus we have generated a total of 8 directed networks (1 each for Ring and Perfect and 6 for Random).

The nodes are assumed to have chaotic dynamics (similar to Hindmarsh–Rose neuron in chaotic spiking mode). For this, we simulated different time series of length 200 samples from the well known discrete chaotic dynamical system – Logistic map3 [40] with a randomly chosen initial value from the interval $(0,1)$ (with bifurcation parameter set to 4.0). We quantized the resulting real-valued chaotic time series into a symbolic sequence of two symbols with 0.5 as the threshold. For a directed edge between vertices $v_i$ and $v_j$, we assumed an XOR operation of the input node dynamics at $v_i$ with the output node dynamics at $v_j$. When the vertex $v_i$ is perturbed, we replace its input time series with ZEP (or MEP) before taking the XOR operation. In this case, we took ZEP to be the all-zero sequence and MEP to be a perfectly random binary sequence, both with a length $L=200$.

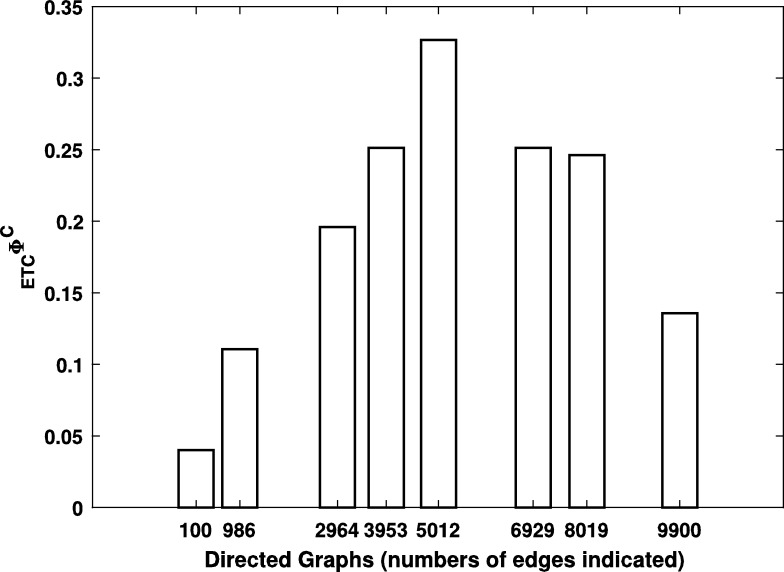
From Table 2 and Figure 11 we can infer that the proposed complexity measure ${}_{ETC}\mathrm{\Phi }^C$ is quite low for both ring topology and perfect graph topology. It is generally higher for a random network topology, and highest when the probability of having a directed edge between any two nodes is 0.5. This is intuitive since a random network exhibits heterogeneous nodes (nodes with different degrees) and should have higher complexity when compared to ring and perfect graph topologies which have homogeneous nodes (all nodes have the same number of edges). Small-world networks (a type of random network) are believed to exist in the brain. It is considered to be a vital aspect of efficient brain organization that confers significant advantages in information processing and is deemed essential for healthy brain function [41]. Deviation from small-world features are observed in patient groups with various brain-related disorders. We conjecture that such small-world networks (being random networks) would also exhibit a high amount of ${}_{ETC}\mathrm{\Phi }^C$ and worth further exploring.

Table 2.

Performance of Φ^C on directed networks (nodes modeled as chaotic neurons) with different topologies. Number of vertices or nodes V = 100 and number of directed edges E varies as indicated.

No.	Topology	Number of directed edges	${}_{ETC}\mathrm{\Phi }^C$
1	Ring	100	0.0402
2	Random	986	0.1106
3	Random	2964	0.1960
4	Random	3953	0.2513
5	Random	5012	0.3266
6	Random	6929	0.2513
7	Random	8019	0.2462
8	Perfect	9900	0.1357

Figure 11.

Performance of ${}_{ETC}\mathrm{\Phi }^C$ on networks with V = 100 nodes (chaotic neurons) with very different topologies: Ring topology (E = 100), Perfect graph topology (E = 9900) and Random graph topology (E = 986,2964,3953,5012,6929,8019.)

5. Conclusions

In Table 3, we provide an exhaustive chronological list of brain complexity measures with their short definitions, theoretical strengths, process/capacity, current state dependency, experimental readiness and remarks. Since ${\mathrm{\Phi }}^C$ provides certain benefits over other measures of complexity of brain networks, it has potential in transitioning it to the real-world – for measuring brain complexity in the clinic. We list below a few of these ways and provide tentative approaches towards harnessing the true potential of ${\mathrm{\Phi }}^C$. By no means is this an exhaustive list.

• •Test on very large sized networks. We have demonstrated our measure on networks with chaotic dynamics (100 nodes) but it is still nowhere close to the size of brain networks. We need to explore how the measure behaves with very large sized networks.
• •Examining the appropriate bipartitions of realistic applications. Even though number of required perturbations for atomic bipartitions scale linearly with the increase in the number of nodes, it is still a mammoth task to perturb all atomic bipartitions for a larger network like the human brain. A heuristic approach can be developed to ${\mathrm{\Phi }}^C$ to determine the right number of bipartitions for evaluating ${\mathrm{\Phi }}^C$ to differentiate different levels of consciousness.
• •Generate MEP and ZEP using TMS. It may be possible to shape the TMS perturbation to yield different entropy perturbations. Whether can we exactly replicate a ZEP and MEP is difficult to say (without doing the actual experiments). But, we believe that an innovation in shaping the perturbations empirically to simulate low and high entropies may be a worthwhile generalization of PCI that needs to be explored. This will also enable our measure to be applied in a clinical setting.

Table 3.

An exhaustive chronological list of brain complexity measures with their short definitions, theoretical strengths, process/capacity, current state dependency, experimental readiness and remarks.

Name	Definition	Tht. strength	Process/capacity	Ct. St. dependency	Exp. readiness	Remarks
Neural Complexity [11] (1994)	Sum of average mutual information for all bipartitions of the system.	Strong	Process	Yes	Low
Causal Density [12] (2003)	“A measure of causal interactivity that captures dynamical heterogeneity among network elements (differentiation) as well as their global dynamical integration [12].”	Strong	Process	Yes	Low	Calculated by applying “Granger causality”.
Φ (IIT 1.0) [9] (2004)	It is the amount of causally effective information that can be integrated across the informational weakest link of a subset of elements.	Medium	Capacity	Yes	Low	Provided the hypothesis for “Information Integrated Theory of Consciousness.” Applicable only to stationary systems.
φ (IIT 2.0) [19], [20], [42] (2008)	Measure of the information generated by a system when it transitions to one particular state out of a repertoire of possible states, to the extent that this information (generated by the whole system) is over and above the information generated independently by the parts.	Strong	Capacity	Yes	Low	Extension of IIT 1.0 to discrete dynamical systems.
ΦE and ΦAR[21] (2011)	Rather than measuring information generated by transitions from a hypothetical maximum entropy past state, ΦE instead utilizes the actual distribution of the past state. “ΦAR can be understood as a measure of the extent to which the present global state of the system predicts the past global state of the system, as compared to predictions based on the most informative decomposition of the system into its component parts [21].”	Strong	Process	No	Medium	ΦE is applicable to both discrete and continuous systems with either Markovian or non-Markovian dynamics. ΦAR is same as ΦE for Gaussian systems [21]. ΦE and ΦAR fail to satisfy upper and lower bounds of integrated information [14]. However, the authors propose variants of these measures which are well bounded.
PCI [6] (2013)	“The normalized Lempel–Ziv complexity of the spatiotemporal pattern of cortical activation triggered by a direct Transcranial Magnetic Stimulation (TMS) perturbation [6].”	Weak	Process	Unknown	High	While PCI proves to be a reasonable objective measure of consciousness in healthy individuals during wakefulness, sleep and anesthesia, as well as in patients who had emerged from coma, it lacks solid theoretical connections to integrated information theories.
ΦMax (IIT 3.0) [4], [5] (2012–14)	Measure of the Information that is specified by a system that is irreducible to that specified by its parts. “It is calculated as the distance between the conceptual structure specified by the intact system and that specified by its minimum information partition [43].”	Strong	Capacity	Yes	Low	IIT 3.0 introduces major changes over IIT 2.0 and IIT 1.0: (i) considers how mechanisms in a state constrain both the past and the future of a system; (ii) emphasis on “a difference that makes a difference”, and not simply “a difference”, (iii) concept has proper metric – Earth Mover's Distance (EMD) [5]. Limitations: Current-state Dependency, Computational intractability, Inability to handle continuous neurophysiological data.
ψ[22] (2014)	ψ is a principled infotheoretic measure of irreducibility to disjoint parts, derived using Partial Information Decomposition (PID), that resides purely within Shannon Information Theory.	Medium	Capacity	No	Low	ψ compares to φ (IIT 2.0) instead of ΦMax (IIT 3.0). Address the three major limitations of ϕ in [20]: State-dependency and entropy; issues with duplicate computation and mismatch of the intuition of “cooperation by diverse parts” [22]. Has desirable properties such as not needing a MIP normalization and being substantially faster to compute.
Φ⁎[14] (2016)	“It represents the difference between “actual” and “hypothetical” mutual information between the past and present states of the system.” It is computed using the idea of mismatched decoding developed from information theory [14].	Strong	Capacity	Yes	Medium	Emphasis on theoretical requirements: First, the amount of integrated information should not be negative. Second, the amount of integrated information should never exceed information generated by the whole system. Focuses on IIT 2.0, rather IIT 3.0.
${\mathrm{\Phi }}_{MMP}^{⁎}$ and ${\mathrm{\Phi }}_{MMP}^{AR}$[23] (2016)	Introduction of Maximum Modularity Partition (MMP), which is quicker than MIP to compute the integrated information for larger networks. In combination with Φ⁎ and ΦAR, MMP yields two new measures ${\mathrm{\Phi }}_{MMP}^{⁎}$ and ${\mathrm{\Phi }}_{MMP}^{AR}$.	Strong	Capacity (${\mathrm{\Phi }}_{MMP}^{⁎}$), Process (${\mathrm{\Phi }}_{MMP}^{AR}$)	Yes (${\mathrm{\Phi }}_{MMP}^{⁎}$), No (${\mathrm{\Phi }}_{MMP}^{AR}$)	Medium	The new measures are compared with Φ⁎, ΦAR and Causal Density and based on the idea that human brain has modular organization in its anatomy and functional architecture. Calculating Integrated Information across MMP reflects underlying functional architecture of neural networks.
ΦC (this paper)	The maximally-aggregate differential normalized Lempel–Ziv (LZ) or normalized Effort-To-Compress (ETC) complexity for the time series data of each node of a network, generated by maximum entropy and zero entropy perturbations of each possible atomic bipartition of an N-node network.	High	Both	Low	Medium	Bridges the gap between theoretical and empirical approaches for computing brain complexity. Based on the idea that brain behaves as an integrated system and acknowledging the similarity between compressionism and integrated information, ΦC is based on compression-complexity measures and not infotheoretic measures.

In summary, we proposed a perturbation based Compression-Complexity measure of network complexity which operates on time series measurement and can approximate Tononi's integrated information (which is known to be computationally intractable). The new measure ${\mathrm{\Phi }}^C$ incorporates various well-supported approaches to estimate network complexity such as: using atomic bipartitions which reduces computational effort, moving beyond MIP approach [23], MEP and ZEP and then recording activity from all the nodes of the network (to measure ‘difference that makes a difference’), employed ETC measure which outperforms LZ and Shannon Entropy. Furthermore, we have proposed, for the first time, the Differential Compression-Complexity Response Distribution (dCCRD), which can potentially play an important role going forward in understanding the distribution of compression-complexity values in a network.

Declarations

Author contribution statement

Mohit Virmani, Nithin Nagaraj: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by Consciousness Studies Programme, National Institute of Advanced Studies (NIAS), IISc Campus, Bengaluru, India. Mohit Virmani was supported by the NIAS Mani-Bhaumik Research Fellowship (provided by Consciousness Studies Programme, NIAS). Nithin Nagaraj was supported by Tata Trusts and SATYAM grant (DST/SATYAM/2017/45(G)).

Competing interest statement

The authors declare no conflict of interest.

Additional information

Supplementary content related to this article has been published online at https://doi.org/10.1016/j.heliyon.2019.e01181.

No additional information is available for this paper.

Supplementary material

The following Supplementary material is associated with this article:

Supplementary Text.pdf

In this supplementary text, we give a detailed computation with explanation of the example in Figure 7 of the main manuscript as well as details pertaining to linear regression of measures of integrated information as a function of entropy of nodes with an example.

Supplementary Tables.pdf

Supplementary tables.

PhiC_ETC_Fig7.m

Main MATLAB code that performs step-by-step computation of ${}_{ETC}\mathrm{\Phi }^C$ for the example network ABC with 3 nodes, as depicted in Figure 7.

ETC.m

MATLAB subroutine for the computation of normalized Effort-To-Compress (ETC) measure (required to run ‘PhiC_ETC_Fig7.m’).

MEP_TimeSeries.txt

Text file containing the time-series for the network ABC when each of its bipartition is perturbed with a random binary sequence (required to run ‘PhiC_ETC_Fig7.m’).

ZEP_TimeSeries.txt

Text file containing the time-series for the network ABC when each of its bipartition is perturbed with a constant (either all zeros or all ones) binary sequence (required to run ‘PhiC_ETC_Fig7.m’).