Phonon confinement and size effect in Raman spectra of ZnO nanoparticles

Abstract

We study Raman spectra of ZnO nanoparticles of 5–12 nm size in the whole range of the first-order phonon bands. We apply the 3D phonon confinement model (PCM) for the interpretation of the observed Raman spectra. It is found that PCM is well applicable to the acoustic modes as well as to the optical ones, despite the fact that PCM has been thought not to be suitable for acoustic phonons. We show that the asymptotic behavior of PCM for the small-size limit is more consistent with the observation than that of the elastic sphere model (ESM). Furthermore, PCM gives detailed information on the complex size-dependent shapes of the phonon bands.

1. Introduction

It is well known that phonon Raman spectra show pronounced size effect, which makes Raman spectroscopy a highly important characterization tool for nanoparticles [1, 2]. To make it practically useful, a consistent analytical interpretation of the spectra is required in terms of the “Raman size”, or the phonon propagation scale. For nanoparticles, two major approaches are used currently: Phonon Confinement Model (PCM) [1, 3, 4] and Elastic Sphere Model (ESM) [1, 5]. PCM treats the vibrations in nanoparticles as confined phonons of the crystalline solid, while ESM models them as vibrations of a uniform isotropic sphere. The main objective of these two models is to derive the size information from the Raman spectra. Of special interest are the low-wavenumber Raman (LWR) modes of nanoparticles, sometimes referred to as confined acoustic phonons [5, 6, 7, 8]. It has been shown that acoustic phonon modes are highly sensitive to the particle size [9, 10], which make them highly valuable for characterizing nanoscale materials. The interpretation of acoustic phonon modes, however, is more challenging than that of optical ones. Currently, ESM is more favorably used [1, 6, 10], or, alternatively, direct quantum-chemical calculations are applied to all vibrations of nanoparticles as big molecules [9]. The key value calculated by ESM is the band position for a given sphere diameter; neither the band shape nor the intensity can be estimated. Moreover, Lamb's theory, on which ESM is based, is strictly applicable only to isotropic homogeneous particles of spherical shape. The Lamb model for more realistic anisotropic systems requires additional assumptions on sound velocity [5], making the ESM treatment more arbitrary. Unlike ESM, PCM possesses the correct asymptotic behavior; for the small size limit it converges to the spectrum of amorphous material, while for the large size limit, it approaches the spectrum of the bulk crystal [4]. Moreover, its application is not limited to particles of certain particular shape [11].

Quantum dots of wurtzite-type materials are of high practical importance for a wide range of applications [12]. ZnO is a good model system of wurtzite structure and several studies [6, 13, 14, 15, 16, 17, 18, 19, 20] have attempted to establish the correlation between the Raman spectral pattern and crystallite size for ZnO nanoparticles. In particular, it was shown by resonance Raman spectroscopy that the E₁(LO) band at 585 cm⁻¹ shows low-wavenumber shift upon confinement [13, 14, 15, 20]. The interpretation of ZnO phonons with PCM has been attempted for the upper optical modes within the 1D approximation without discussing the assumed dispersion curves [18]. The localized acoustic bands were also studied [6]; pronounced size dependence of the Raman spectra in LWR was found. The data were interpreted within the ESM model; a good agreement between calculation and experiment was reported [6]. However, the applicability of ESM to ZnO is questionable, because ZnO nanoparticles are anisotropic [16] and, especially for the small size, far from being homogeneous [1]. ESM was criticized also for the failure to reproduce the experimental data for silicon nanoparticles, which is a system simpler than ZnO [5].

Since the pioneering work of Richter [3], the PCM approach is being constantly developed. The original 1D description of the phonon dispersion may introduce arbitrariness in the model; several improvements have been proposed to address this issue [21, 22, 23, 24]. Herein, we use the recently developed 3D version of the model with quantum-chemically calculated phonon dispersion [4].

In the present work, we study the applicability of the PCM approach for Raman spectra of ZnO nanoparticles. Though only optical phonons have been treated by PCM so far, we attempt to use PCM also for the description of the acoustic phonons.

2. Experimental

Four ZnO nanoparticle samples, with particle size of 4.8, 6.4, 8.6 and 12 nm, were obtained by the hydrothermal synthesis (sol-gel) described elsewhere [25]. The particle size was estimated by the previously found correlation between the size (from TEM and XRD data) and the emission spectra [26]. The peak positions of the emission spectra were 366, 371, 374 and 376 nm, respectively for the 4.6, 5.6, 9.0 and 12 nm samples. It was shown that for the sol-gel ZnO nanoparticles, the size distribution is very narrow, with the standard deviation within 10% of the size. The reason for the narrow size distribution is the Ostwald ripening kinetics, such that the growth rate decreases with the size of the ZnO QDs [26].

The Raman measurements were carried out with a laboratory built spectroscopic system described elsewhere [27]. Excitation wavelength was 532 nm with laser power of 12 mW at the sample point. 8 spectra were averaged for each sample with acquisition time of 30 s. The measured spectra were reduced with the Boltzmann factor and corrected for the ν³ frequency dependence [27].

3. Model

In the case of polar anisotropic systems like ZnO, the Raman intensity near gamma-point strongly depends on the scattering direction. This effect is not taken into account with the basic equation of conventional PCM [4]:

$$I\left(\omega \right)\cong \text{∫}\text{∫}\text{∫}\frac{{\Gamma }_0\left(\sigma \right)*{\left|C\left(q_{\mathit{0}},q\right)\right|}^{\mathit{2}}}{{\left(\omega -\omega \left(q\right)\right)}^2+{\left({\Gamma }_0\left(\sigma \right)/2\right)}^2}{d}^{3}q\text{,}$$ (1)

where ω is the wavenumber, σ is the confinement size, Γ₀ is the natural linewidth, C(q₀,q) is the Fourier coefficient for a given confinement shape and size at a given wave vector q of the Brillouin zone (BZ) with q₀ being the wave vector of the bulk crystal.

In the present work, this problem has been solved by considering the differential intensity A(q, φ, θ) for different scattering angle φ, θ and then integrating it over the polar coordinates. With the Sortphon algorithm making use of the phononic k.p theorem [28], this approach ensures the “confined” phonon being spread only within the same band without band index permutation. For each scattering direction, we take a uniform path (grid in q) and sort the phonon wavenumbers by band index according the vibrational modes.

The intensities at the BZ center A_i (q₀, φ, θ) are calculated for each scattering direction using the ab initio determined Raman tensor with the electric field vectors orthogonal to the scattering direction with subsequent numerical averaging over different polarizations. Note that experimental Raman spectra discussed in this study were obtained in the non-polarized geometry.

It was shown by TEM studies that the spherical particle shape is a good description for ZnO nanoparticles [13]. As was shown before, the Fourier coefficients C(q₀,q) for this case have a form of Bessel-like function [4] (eq. 2):

$$C\left(q_{\mathit{0}},q\right)\cong \frac{\sin \left(qR\right)-qR*\cos \left(qR\right)}{{\left(qR\right)}^3}\text{,}$$ (2)

where R is the radius of the sphere.

Next, intensities are integrated (numerically) over the scattering directions in polar coordinates:

$$I\left(\omega \right)\cong \sum _i\text{∫}\text{∫}\text{∫}\frac{A_i\left({\mathit{q}}_{\mathbf{0}},\phi ,\theta \right)*{\Gamma }_{0,i}*{\left|C\left({\mathit{q}}_{\mathbf{0}},\mathit{q}\right)\right|}^{\mathit{2}}*q^2}{{\left(\omega -{\omega }_i\left(\mathit{q}\right)\right)}^2+{\left({\Gamma }_{0,i}/2\right)}^2}dqd\phi d\theta \text{,}$$ (3)

where i is the band number and q is the norm of q. The integration in Eq. (3) is done within [0,2] range of the reduced wavevector. Since the calculated Raman intensities of the acoustic modes are zero, the corresponding A_i values were adjusted to the values matching the experimental data (no direction dependence was assumed). For the optical modes, the intensities were scaled to the observed spectra for each band.

It is interesting to compare the PCM spectral pattern with the theory of Raman intensity for amorphous solid. It was discussed previously that, in the asymptotic limit, PCM should approach the amorphous [29]. Indeed, if all k-points contribute equally to the spectrum (i.e. C(q₀,q) becomes constant), the integral (1) reduces to DOS g(ω) convoluted with the Lorentzian profile of the width Γ₀. Therefore, in this limit PCM converges to the Shuker-Gammon formulation of the Raman intensity for amorphous solid [30]:

$$I\left(\omega \right)\cong C\left(\omega \right)g\left(\omega \right)/\omega \text{,}$$ (4)

where C(ω) is the average light-vibration coupling coefficient [31] (Bose-Einstein population factor is omitted in Eq. (4) because we already discuss the reduced spectra). It has been shown that for low-wavenumber region C(ω) ∝ ω [32, 33]. The ab initio Raman intensities of acoustic phonon bands for the bulk crystal are zero. However, upon confinement this situation changes. According to the Shuker-Gammon formulation, the wavenumber-dependent intensity factor should be assumed. For the spectral region where the contribution of acoustic modes is significant (in the present calculation, below 200 cm⁻¹), the linear wavenumber-dependent intensity dependence was applied.

Phonon lifetime, and, as a consequence, the natural linewidth Γ, depends on the confinement size [34]. To take this fact into account, the following dependence was assumed: Γ_0,i = Γ_0,i(bulk)*(1 + 4/σ). For the optical phonons, the natural linewidths for the bulk Γ_0,i(bulk) were estimated from fitting of the experimental data; for the acoustic modes, the data for the bulk crystal are not available, and Γ_0,i(bulk) was estimated more roughly from PCM; from this, Γ_0,ac(bulk) = 8 cm⁻¹.

The DFT phonon dispersion (ω_i(q)) as well as the Raman tensor were provided by courtesy of Dr. Calzolari. The details of the computational procedures are described elsewhere [35]. Briefly, the Quantum Espresso package [36, 37] was used with the Perdew-Burke-Ernzerhof (PBE) functional; Hubbard-like potential with U = 12.0 eV and U = 6.5 eV was applied on the 3d orbitals of zinc and on the 2p orbitals of oxygen, respectively. The phonon dispersion was shown to give an excellent agreement with the available experimental data [35].

4. Results and discussion

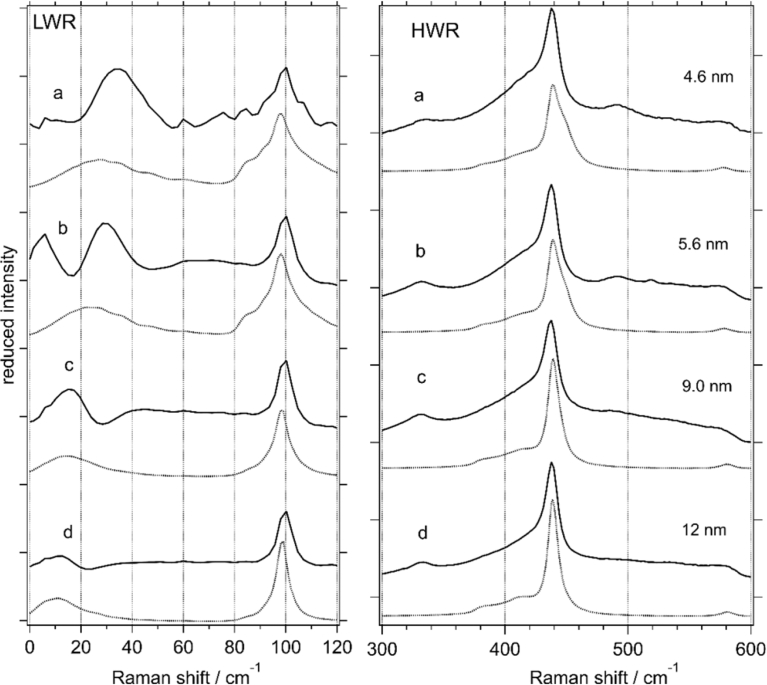
Raman spectra of ZnO nanoparticles of different sizes are shown in Fig. 1 for the high wavenumber region (HWR, 300–600 cm⁻¹) and for the low wavenumber region (LWR, 0–120 cm⁻¹). The corresponding PCM simulated spectra are also shown together. The HWR spectrum is dominated by the E₂ optical phonon band at 438 cm⁻¹ the position of which is practically independent on the size. This observation is in agreement with the previously reported data [18]. The possible reason for this is the specifics of the E₂^high band, which shows an unusually strong anharmonicity and, as a result, well-pronounced asymmetry even for the bulk ZnO crystal [38]. We need to admit that this band does not follow the typical behaviour of Raman bands observed in other materials at nanoscale.

Fig. 1.

Raman spectra (reduced, background subtracted) of ZnO nanoparticles (solid curves) and the corresponding simulated spectra (dotted lines) for the particle size 4.6 nm (a), 5.6 nm (b), 9.0 nm (c) and 12 nm (d). Left pane: low-wavenumber region (LWR), right pane: high-wavenumber region (HWR). The LWR spectra are scaled by a factor of 20.

The E₁(T) and A₁(T) optical phonon modes (407 and 380 cm⁻¹ for the bulk ZnO [39]) contribute to a broad shoulder of the E₂ band, while the weak broad band at around 570 cm⁻¹ is assigned to the E₁(L) and A₁(L) optical phonons (583 and 574 cm⁻¹ for the bulk). The peak at 330 cm⁻¹ belongs to the second-order spectrum of ZnO [40] and will not be discussed in this work. The low-wavenumber optical phonon E₂ mode is observed at around 100 cm⁻¹. Broad bands below 50 cm⁻¹ belong to the localized acoustic phonon modes [6] (the features below 10 cm⁻¹ belong to the artefacts of the Rayleigh line filtering).

The simulated spectra show a high-wavenumber shoulder of the E₂ band (as expected from the dispersion of this optical phonon band [35]), which is not clearly observed in the experiment. At this point we must note that for the bulk ZnO, the E₂ band also cannot be described by a symmetric Lorentzian band. Instead, it shows distinct asymmetry that is attributed to the anharmonic interaction with acoustic phonons [38]. For the bulk crystal, the spectral profile can be well fitted with an asymmetric pseudo-Voigt function [41], however, the use of such line shape in PCM needs a solid justification. The spectral profile of the optical phonons in ZnO nanoparticles therefore is more complex than the PCM predictions. The E₁(LO) band at 585 cm⁻¹ shows low-wavenumber shift upon confinement, which corroborates experimental results for resonant Raman scattering by Cheng [20] and Yoshikawa [14].

In contrast to the optical phonons, the acoustic phonon band in LWR shows significant size dependence, both in the band position and the shape. The peak maximum increases with decreasing size; 11.7 cm⁻¹ (12 nm), 12.6 cm⁻¹ (9.0 nm), 26.2 cm⁻¹ (5.6 nm) and 32.6 cm⁻¹ (4.6 nm). From the lattice dynamics of ZnO, it is known that the acoustic phonons are significantly more dispersive than the optical ones [35], therefore, the LWR is more sensitive to the confinement size, as is expected from Eq. (1), where the changes with the size are related to the “steepness” of the phonon dispersion (or, for acoustic phonons, the speed of sound). The PCM simulated spectra reproduce well this tendency.

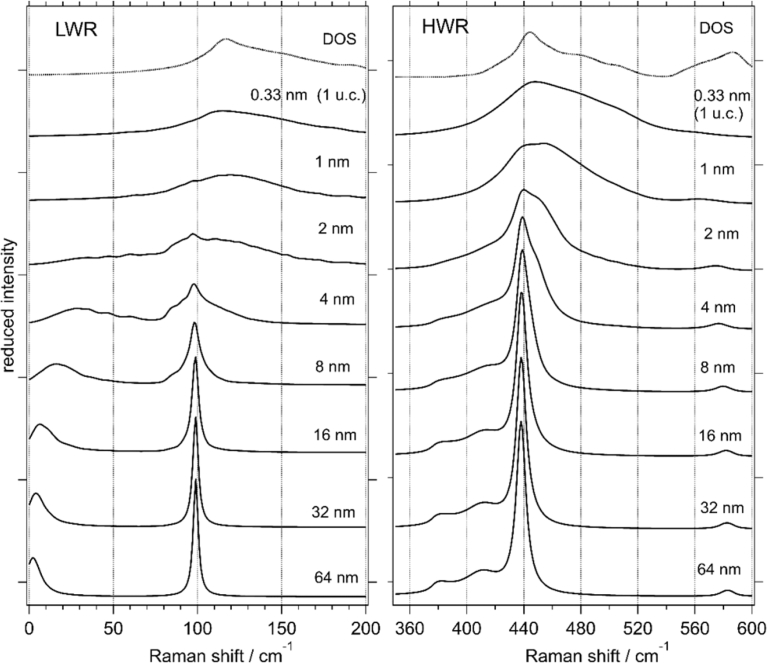
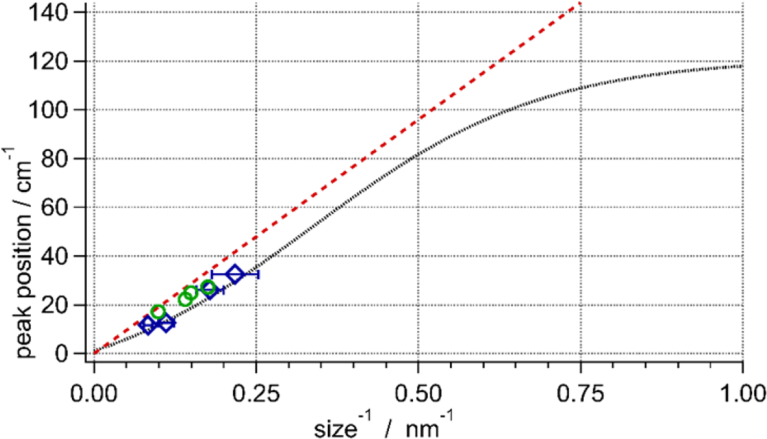
In order to confirm the correct asymptotic behavior of PCM, the simulated Raman spectra of ZnO nanoparticles are shown in Fig. 2 for the particle sizes from 64 nm to 0.325 nm (one unit cell). For the large size limit, the simulated spectrum approaches that of the bulk crystal, while for the small size limit it converges to that of the amorphous solid [4, 30]. For the large size limit, PCM intrinsically approaches to the bulk crystal. For the small size limit, PCM also shows a good agreement with the DOS (Fig. 2) and the available experimental data for amorphous ZnO [42, 43, 44]. In the few-nm size range, the PCM and ESM predictions of the peak position agree well with each other (Fig. 3). It was shown however that ESM is applicable only in the limited range of confinement size and shape [1]. Moreover, while ESM predicts only the band position, PCM allows to predict the band shape as well. While ESM describes Raman pattern as two dominant modes, PCM takes into account wide range of lattice vibrations.

Fig. 2.

PCM calculated Raman spectra for different confinement sizes (solid lines) and the Density of States (DOS) of amorphous ZnO (dotted line). Left pane: low-wavenumber region (LWR), right pane: high-wavenumber region (HWR). The LWR spectra are scaled by a factor of 20.

Fig. 3.

LWR peak position vs inverse size for ZnO nanoparticles. Dash red line: ESM predictions; dotted black line: PCM; blue squares: experimental data from this work; green circles: experimental data from the work [6].

From a thorough quantum-chemical analysis of the vibrational modes of nanoparticles, the acoustic band region in the Raman spectra is a superposition of multiple vibrations [9]. The band shape as calculated by PCM comes from superposition of Lorentzian profiles from different q-points, and this “envelope” is close to more strict quantum-chemical description. Therefore, in this aspect the PCM provides more physically sound description than ESM.

It should be noted that the linewidth predicted by PCM has two contributions: (1) natural linewidth (the phonon lifetime changes upon confinement) and (2) the envelope linewidth. The first contribution was addressed above; the second contribution comes from Eq. (3) and is a result of superposition (integration) of many Lorentzian profiles, each of which has the linewidth Γ_0,i(σ). Unlike the width of the Lorentzian line, the width of the envelope is not strictly defined. Fitting of the resulting spectral pattern with Lorentzian or Gaussian equation allows the approximate estimation of the bandwidth. The resulting linewidths and band positions are summarized in Table 1.

Table 1.

Peak positions and linewidths (full width at half maximum) for the confined acoustic phonon bands, in cm⁻¹.

Size	Experimental		PCM
	Position	FWHM	Position	FWHM
12 nm	11.7	11.4	9.9	21.8
9.0 nm	12.6	16.1	13.3	26.3
5.6 nm	26.2	22.3	23.1	31.1
4.6 nm	32.6	20.8	29.5	38.2

The experimental spectral data and basic quantum-chemical results required to reproduce these findings are available on request from VK.

5. Conclusions

We have studied the Raman spectra of ZnO nanoparticles of 4.6, 5.6, 9.0 and 12 nm sizes in both the optical and acoustic regions. While the optical phonon bands show minor changes with the particle size, the acoustic bands show significant changes. We have examined the applicability of the phonon confinement model (PCM) to the whole range of the first-order phonon bands including the acoustic. The PCM calculated spectra show a good agreement with the experimental data. In the case of ZnO nanoparticle, acoustic phonons have much steeper dispersion than the optical ones, showing much higher sensitivity to the particle size. Application of PCM to the acoustic phonons has successfully analyzed the size dependent Raman spectra of ZnO nanoparticles. Broad applicability of PCM has thus been demonstrated.

Declarations

Author contribution statement

Vitaly I. Korepanov: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Si-Yuan Chan: Performed the experiments; Analyzed and interpreted the data.

Hsu-Cheng Hsu: Analyzed and interpreted the data.

Hiro-o Hamaguchi: Conceived and designed the experiments; Wrote the paper.

Funding statement

This work was supported by the Ministry of Education of Taiwan (“Aim for the Top University Plan” of National Chiao Tung University) Vitaly Korepanov was supported by the Ministry of Science and Higher Education of the Russian Federation (075-00475-19 -00). Si-Yuan Chan and Hsu-Cheng Hsu were supported by the Ministry of Science and Technology of Taiwan (MOST 105-2112-M-006-004-MY3).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.