Skip to main content
PMC home page
iScience logoLink to iScience
. 2019 Feb 6;13:9–19. doi: 10.1016/j.isci.2019.02.002

Spatiotemporally Controlled Myosin Relocalization and Internal Pressure Generate Sibling Cell Size Asymmetry

Tri Thanh Pham 1, Arnaud Monnard 1,2,6, Jonne Helenius 3,6, Erik Lund 1,5, Nicole Lee 1,4, Daniel J Müller 3, Clemens Cabernard 1,7,∗
PMCID: PMC6383127  PMID: 30785031

Summary

Metazoan cells can generate unequal-sized sibling cells during cell division. This form of asymmetric cell division depends on spindle geometry and Myosin distribution, but the underlying mechanics are unclear. Here, we use atomic force microscopy and live cell imaging to elucidate the biophysical forces involved in the establishment of physical asymmetry in Drosophila neural stem cells. We show that initial apical cortical expansion is driven by hydrostatic pressure, peaking shortly after anaphase onset, and enabled by a relief of actomyosin contractile tension on the apical cell cortex. An increase in contractile tension at the cleavage furrow combined with the relocalization of basally located Myosin initiates basal and sustains apical extension. We propose that spatiotemporally controlled actomyosin contractile tension and hydrostatic pressure enable biased cortical expansion to generate sibling cell size asymmetry. However, dynamic cleavage furrow repositioning can compensate for the lack of biased expansion to establish physical asymmetry.

Subject Areas: Biomechanics, Biophysics, Cell Biology, Methodology in Biological Sciences

Graphical Abstract

graphic file with name fx1.jpg

Open in a new tab

Highlights

  • •

    Fly neural stem cells display stiffness asymmetry during mitosis

  • •

    Hydrostatic pressure increases in fly neural stem cells before anaphase

  • •

    Coordination of Myosin relocalization and pressure enables biased cortical expansion

  • •

    Changes in hydrostatic pressure affect physical asymmetry

Biomechanics; Biophysics; Cell Biology; Methodology in Biological Sciences

Introduction

Sibling cell size asymmetry, here also called physical asymmetry, refers to the formation of unequally sized cells during cell division. Metazoan cells tightly regulate the mechanisms controlling symmetric or asymmetric physical cell divisions, but the mechanics and physiological roles are still unclear (Roubinet and Cabernard, 2014).

The anaphase spindle has been proposed to be the primary determinant for the positioning of the cleavage furrow (D'Avino et al., 2015, Rappaport, 1986, Glotzer, 2017, Green et al., 2011). Regulating spindle positioning, orientation, and geometry thus offers a mechanism for the generation of equal- or unequal-sized sibling cells (White and Glotzer, 2012, Roubinet et al., 2017, Albertson and Doe, 2003, Cai et al., 2003). For instance, changing spindle position or metaphase plate location of symmetrically dividing cultured human cells can induce physically asymmetric cell divisions (Kiyomitsu and Cheeseman, 2013, Tan et al., 2015). Flies and ascidians control spindle symmetry and positioning through microtubule-depolymerizing kinesin family proteins such as Klp10A or Kif2A (Costache et al., 2017, Derivery et al., 2015, Chen et al., 2016).

Drosophila neuroblasts, the neural stem cells of the developing central nervous system are an ideal system to investigate sibling cell size asymmetry. These cells divide asymmetrically by size and fate, forming a large self-renewed neuroblast and a small differentiating ganglion mother cell (GMC). Neuroblasts are intrinsically polarized (Homem and Knoblich, 2012, Gallaud et al., 2017), and changes in cell polarity affect spindle geometry and sibling cell size asymmetry (Albertson and Doe, 2003, Cabernard and Doe, 2009, Cai et al., 2003). However, findings from Drosophila and C. elegans neuroblasts suggest that cell size asymmetry is also regulated by asymmetric localization of non-muscle Myosin II (Myosin hereafter) (Cabernard et al., 2010, Connell et al., 2011, Ou et al., 2010). Fly neuroblasts relocalize Myosin to the cleavage furrow at anaphase onset through a basally directed cortical Myosin flow followed by, with a 1-min delay, an apically directed cortical Myosin flow. The molecular mechanisms triggering apical-basal cortical Myosin flow onset are not entirely clear but involve apically localized Partner of Inscuteable (Pins; LGN/AGS3 in vertebrates), Protein Kinase N, and potentially other neuroblast-intrinsic polarity cues. On the basal neuroblast cortex, spindle-dependent cues induce an apically directed cortical Myosin flow to the cleavage furrow. The correct timing of these Myosin flows is instrumental in establishing biased Myosin localization and sibling cell size asymmetry in fly neuroblasts (Tsankova et al., 2017, Roth et al., 2015, Roubinet et al., 2017).

Spatiotemporally controlled Myosin relocalization provides a framework for the generation of unequal-sized sibling cells, but the forces driving biased cortical expansion are still unknown. Here, we use atomic force microscopy (AFM) to measure dynamic changes in cell stiffness and cell pressure (Krieg et al., 2018), combined with live cell imaging and genetic manipulations in asymmetrically dividing neuroblasts. We found that physical asymmetry is formed by two sequential events: (1) internal pressure initiates apical expansion, enabled by a Myosin-dependent softening of the apical neuroblast cortex and (2) actomyosin contractile tension at the basally shifted cleavage furrow subsequently initiates basal expansion while maintaining apical membrane expansion. Thus, spatiotemporally coordinated Myosin relocalization combined with hydrostatic pressure and cleavage furrow constriction enables biased membrane extension and the establishment of stereotypic sibling cell size asymmetry. Furthermore, we found that if biased cortical expansion is compromised, either by removing hydrostatic pressure or by altering spatiotemporally regulated Myosin relocalization, a dynamic adjustment of the cleavage furrow position compensates for the lack of biased expansion to rescue the establishment of physical asymmetry.

Results

A Cell-Intrinsic Stiffness Asymmetry Precedes the Formation of the Cleavage Furrow

Cell shape changes are largely controlled by changes in mechanical stress and tension at the cell surface (Clark et al., 2015). During physical asymmetric cell division, cortical proteins are subject to precise spatiotemporal control (Roubinet et al., 2017, Tsankova et al., 2017), but how this impacts cell surface tension to allow for dynamic cell shape changes is incompletely understood (Figure 1A). To this end, we set out to measure cell stiffness—a measure of the resistance of the cell surface to an applied external force—of asymmetrically dividing larval brain neuroblasts with AFM. As in vivo these neural stem cells are surrounded by cortex glia apically, and GMCs and differentiating neurons basally, we established primary neuroblast cultures so that the AFM tip could directly probe the neuroblast surface. Cultured larval brain neuroblasts showed normal polarization and cell cycle timing (Figures S1A–S1C and Berger et al., 2012).

Figure 1.

Figure 1

Open in a new tab

Cortical Stiffness Only Partially Correlates with Myosin Localization and Curvature

(A) Wild-type neuroblasts undergo biased membrane expansion (orange arrows) concomitant with spatiotemporally controlled Myosin relocalization (green arrows). Apical Myosin flows (green arrows) toward the cleavage furrow before the onset of an apically directed Myosin flow (green arrows).

(B) Schematic representation showing cortical stiffness measurement points along the cell cortex (colored circles) throughout mitosis. Measurements were binned into five cortical regions along the apical-basal neuroblast axis.

(C) Representative image sequence showing a wild-type neuroblast expressing Sqh:GFP (Myosin; green) and the centrosome marker Cnn:GFP (bright green dots) throughout mitosis. Positions where AFM measurements were performed are labeled with colored circles (see also Figure S1).

(D) Distribution of mean cortical stiffness and standard error of the mean (top row, n = 25) in all regions along the division axis throughout mitosis in reference to anaphase onset (0 s). The bottom row shows the corresponding heatmap for cortical stiffness.

(E–J) (E) Mean Myosin intensity (n = 19) at all sub-binned regions for wild-type neuroblasts; time axis is relative to anaphase onset. Mean stiffness (n = 25) and mean curvature (dimensional unit is μm−1, n = 19) are shown in (F) and (G), respectively. Deviation coefficients (see Methods) were plotted to correlate Myosin intensity with cortical stiffness (H), curvature with stiffness (I), and Myosin intensity with curvature (J).

Scale bar, 5 μm.

We used a rounded, 300-nm-radius AFM tip and measured neuroblast stiffness on ∼20 positions along the apical-basal division axis every 30 s. The averaged measurements (n = 25 neuroblasts) were binned in five regions (apical, sub-apical, middle, sub-basal, and basal) (Figure 1B). Cell cycle stages and the position of measurement were determined using Sqh:GFP (Royou et al., 2002) (labeling Myosin's regulatory light chain) and GFP-tagged centrosomin (cnn:GFP, labeling centrosomes; Zhang and Megraw, 2007) (Figures S1D–S1H and Methods).

Our AFM measurements revealed that cell stiffness was mostly uniform before anaphase onset ranging from 0.5 to 0.8 nN μm−1. At anaphase onset and 60 s thereafter (“0 s” marks anaphase onset in Figures 1C and 1D), we observed a noticeable increase in stiffness in the mid and sub-basal regions, reaching almost 1.0 nN μm−1. Interestingly, this increase in stiffness appeared in the region of the prospective cleavage furrow, most likely coinciding with the localization of the centralspindlin component Tumbleweed (MgcRacGAP in vertebrates) (Roubinet et al., 2017). However, stiffness dropped over most of the cell cortex 90 s after anaphase onset, eliminating this apparent stiffness asymmetry. In late anaphase, stiffness increased again, predominantly in the cleavage furrow region. Taken together, these measurements revealed a stereotypic increase in neuroblast stiffness until anaphase onset before it dropped significantly thereafter. Furthermore, stiffness was not uniform but distributed asymmetrically in early anaphase and was at its highest in a basally shifted region corresponding to the prospective cleavage furrow.

Neuroblast Stiffness Is a Combination of Actomyosin Contractile Tension and Other Biophysical Parameters

Previously, it was suggested that cortical relaxation at the poles was responsible for biased membrane expansion during physical asymmetric cell division (Connell et al., 2011). Cortical relaxation could be induced through Myosin relocalization, prompting us to correlate stiffness changes with Myosin relocalization dynamics. As the wide-field imaging data were not sufficiently reliable to extract Myosin intensity we imaged third instar neuroblasts expressing Sqh:GFP with spinning disk microscopy and correlated the resulting intensity and curvature profiles with AFM stiffness data by calculating the relative change between Myosin intensity and cell curvature, and between Myosin intensity and cell stiffness. As reported previously (Roubinet et al., 2017), apical Myosin intensity started to decrease at anaphase onset, although stiffness increased again apically (Figures 1E and 1F). In the mid and sub-basal regions, both Myosin intensity and stiffness increased. Similarly, high Myosin intensity was visible at the forming cleavage furrow later in anaphase, concomitant with detectable changes in cell surface curvature. The most noticeable curvature changes became apparent in the furrow region from 120 s after anaphase onset onward (Figures 1E–1G). The resulting deviation coefficients revealed that Myosin intensity and curvature strongly correlate early (−120 to 30 s) on the apical neuroblast cortex and later in the cleavage furrow region (120 to 240 s); the shift in Myosin intensity from the apical cell cortex toward the furrow region, previously described as a cortical flow (Roubinet et al., 2017), was accompanied by a shift in curvature changes. Until 120 s after anaphase onset, stiffness correlated best with Myosin intensity in the cleavage furrow region. However, it is noticeable that Myosin intensity poorly correlated in many cortical regions with either curvature or stiffness (Figures 1H–1J and 2G–2J).

Figure 2.

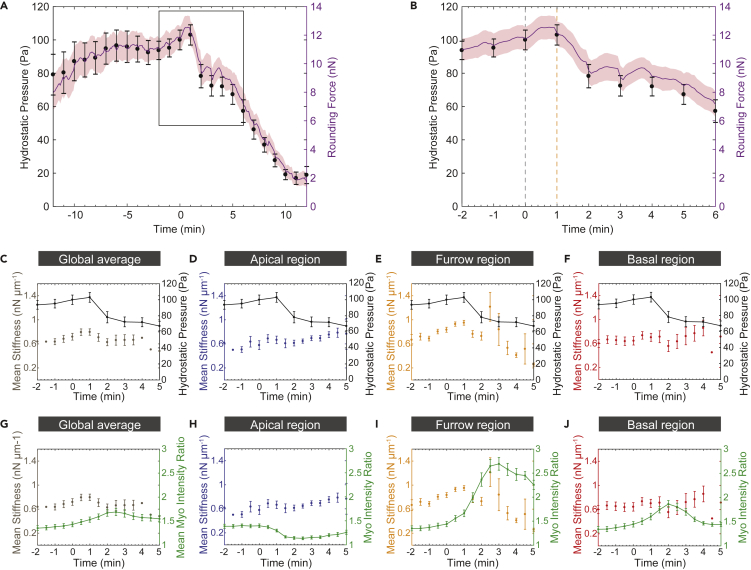
Figure 2

Open in a new tab

Hydrostatic Pressure Increases during Mitosis, Peaking Right after Anaphase Onset

(A–J) (A) Mean rounding force (magenta line) and mean hydrostatic pressure (black balls) measured by AFM using the parallel plate assay (see Figure S2 for more details; error bars represent standard error of the mean, n = 13) throughout mitosis for wild-type neuroblasts. The boxed measurements are shown enlarged in (B). The gray vertical line refers to anaphase onset (0 min). The orange vertical line highlights the onset of the hydrostatic pressure drop. Graphs showing the mean cortical stiffness and mean hydrostatic pressure throughout mitosis for (C) the entire neuroblast (global average) and the (D) apical, (E) furrow, and (F) basal regions. Graphs showing the mean cortical stiffness and mean Myosin intensity throughout mitosis for (G) the entire neuroblast (global average) and the (H) apical, (I) furrow, and (J) basal regions.

We conclude that asymmetrically dividing fly neuroblasts dynamically change stiffness locally, which only partially correlates with local Myosin accumulation and cell shape changes. We hypothesize that the local accumulation of Myosin filaments directly or indirectly affects cell surface properties in cortical regions with low Myosin filament concentration. For example, actomyosin constriction at the furrow can stretch the cortex in the apical region, which could result in a high stiffness value even in the absence of apical Myosin. Alternatively, the registered neuroblast stiffness could be a combination of Myosin activity and other biophysical parameters.

Neuroblasts Build up Hydrostatic Pressure until Anaphase Onset, Followed by a Pressure Drop in Early Anaphase

As cells increase their hydrostatic pressure during mitosis (Stewart et al., 2011), we wondered whether changes in neuroblast stiffness could be attributed to changes in hydrostatic pressure. We used a parallel plate assay to measure rounding force by pressing a wedge onto cultured neuroblasts expressing the membrane marker PH:GFP (see also Methods and Figure S2A). Rounding force gradually increased during mitosis before dropping sharply shortly after anaphase onset (Figure S2B). From these measurements, we used two methods to calculate the corresponding hydrostatic pressure. (1) We measured the surface area in contact with the AFM wedge for each time point and divided the registered rounding force by this value. (2) We used the Young-Laplace formula (Yoneda, 1964, Yoneda, 1980) (see also Methods) to obtain the contact area before anaphase. At these stages, Young-Laplace calculations are very precise because cells are predominantly spherical before elongation in anaphase. However, because our contact area measurements were much higher than the calculated Young-Laplace surface area, probably due to optical aberrations, we calculated a correction factor and applied it to the detected contact area to extract hydrostatic pressure at all time points (Figures S2C and S2D). These measurements showed that cultured neuroblasts increase their intracellular hydrostatic pressure up to 105 Pa (Figures 2A and 2B; mean p = 103; SD = +/− 6.08; n = 13) 1 min after anaphase onset. However, 2 min after anaphase onset, hydrostatic pressure has already dropped by 20% compared with its peak value. Once division is completed, neuroblasts have a significantly lower hydrostatic pressure (mean p = 10.92; SD = ±3.72; n = 13) compared to the pressure at' the onset of mitosis.

Stiffness averaged over the entire neuroblast cortex followed hydrostatic pressure and also concomitantly increased at the apical, basal, and furrow regions. However, apical and basal stiffness poorly correlated with hydrostatic pressure from approximately 2 min after anaphase onset. Similarly, stiffness increased sharply in the cleavage furrow region 2.5 min after anaphase onset, whereas hydrostatic pressure had already dropped (Figures 2C–2F).

Taken together, these data suggest that at the cellular level, changes in hydrostatic pressure match neuroblast stiffness. However, on a subcellular level, local stiffness differs spatiotemporally from global hydrostatic pressure.

The Coordination between Hydrostatic Pressure and Myosin Relocalization Enables Biased Cortex Expansion

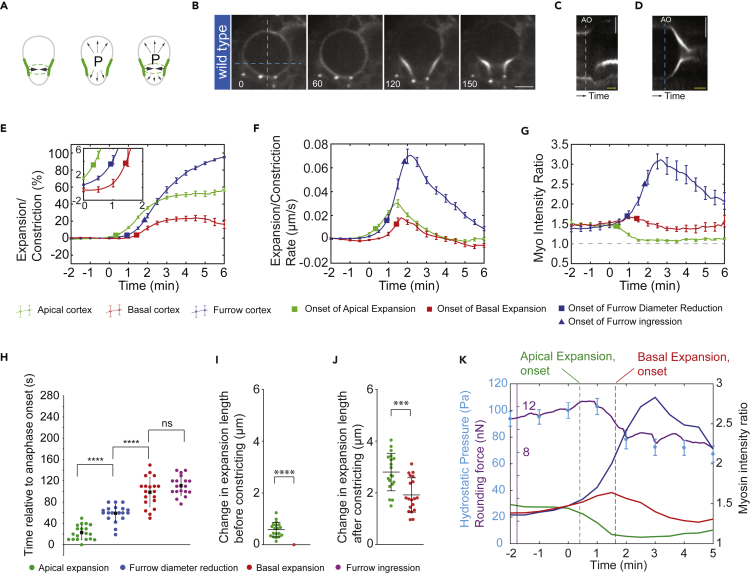
Next we asked how these dynamic changes in cell surface stiffness and hydrostatic pressure contribute to the establishment of sibling cell size asymmetry. Previously, we showed that Myosin relocalization dynamics strongly correlates with physical asymmetry (Roubinet et al., 2017, Tsankova et al., 2017, Connell et al., 2011), but the force underlying biased cortex expansion remained unexplained. Neuroblast cortex and membrane extension could be driven by (1) actomyosin contractile tension at the cleavage furrow (furrow constriction) displacing fluid and cytoplasmic material, (2) internal pressure, or (3) a combination of both (Figure 3A). We thus analyzed how dynamic changes in neuroblast pressure during mitosis correlate with Myosin relocalization, constriction, and biased cortical expansion. To this end, we imaged neuroblasts in intact brains, expressing Sqh:GFP and the spindle marker Cherry:Jupiter, and quantified the extent of apical and basal cortical expansions in relation to anaphase onset and cleavage furrow ingression, constriction, and expansion rates, and Myosin intensity at the apical, basal, and furrow cortex (Figures 3B–3G, S3A, and S3B). Here, we consider furrow diameter reduction as the earliest sign of furrow constriction because it can be uncoupled from cortical extension (see below). We found that wild-type neuroblasts always started to expand shortly after anaphase onset on the apical neuroblast cortex first, followed by furrow diameter reduction. Expansion of the basal cell cortex occurred after furrow diameter reduction, almost at the same time as furrowing (furrow ingression) was detectable (Figure 3H). Before constriction, neuroblasts expanded by ∼0.6 μm on the apical cortex, but no expansion was detected basally. Once constriction started, expansion was measureable on both the apical and basal neuroblast cortex (Figures 3I and 3J). These data suggest that (1) initial apical expansion is primarily driven by hydrostatic pressure and (2) sustained apical and all basal expansion is driven by furrow constriction. Furthermore, biased cortical expansion could correlate with Myosin relocalization dynamics. Indeed, apical expansion occurred shortly after anaphase onset, coinciding with a drop in apical Myosin intensity and high internal pressure. The onset of basal cortex expansion—∼90 s after anaphase onset—coincided with decreasing levels of basal Myosin, dropping hydrostatic pressure, and an increase in Myosin intensity at the cleavage furrow (Figure 3K).

Figure 3.

Figure 3

Open in a new tab

Internal Hydrostatic Pressure and Myosin Relocalization Dynamics Drive Asymmetric Cortical Expansion in Fly Neuroblasts

(A) Biased membrane expansion could be driven by furrow constriction, intracellular hydrostatic pressure, or a combination of both.

(B–G) (B) Representative image sequence showing a wild-type neuroblast expressing Sqh:GFP (white). Kymographs obtained along the apical-basal axis (orange dotted line) are shown in (C) or the furrow region (blue dotted line) in (D). Mean change in the expansion/constriction length (E), rate of change (F), and Myosin intensity (G) are plotted for the apical cortex (green), the basal cortex (red), and the furrow site (blue). Vertical bars refer to standard error of the mean (n = 19). The time axis is relative to anaphase onset (0 s). The inset in (E) shows a magnification of the 0- to 2-min time window.

(H–J) (H) Scatterplot showing the onset of apical expansion (green), onset of furrow diameter reduction (blue), onset of basal expansion (red), and onset of furrow initiation (when the curvature first changes from a straight line to an inward bending curve; purple). Changes in expansion length for both apical (green) and basal (red) cortex before and after furrow constriction (furrow diameter reduction) are shown in (I) and (J), respectively.

(K) Graph showing the mean rounding force (purple), mean hydrostatic pressure (cyan circles with error bars), mean Myosin intensity at the apical cortex (green), mean Myosin intensity at the basal cortex (red), and mean Myosin intensity at the furrow site cortex (blue). The green and red dashed lines represent the mean onsets of apical and basal expansions, respectively. Scale bar, 5 μm. Yellow timescale bar in kymographs, 2min.

Asterisks denote statistical significance, derived from unpaired t tests: ***p ≤ 0.001, ****p ≤ 0.0001; n.s., not significant.

We conclude that in wild-type neuroblasts, apical membrane expansion occurs when hydrostatic pressure is the highest. Basal cortical expansion coincides with an increase in Myosin at the cleavage furrow and a reduction of basally located Myosin. These data suggest that apical expansion is driven by high hydrostatic pressure and permitted by decreasing actomyosin contractile tension on the apical cortex. Basal membrane expansion, however, is primarily driven by an increase in cleavage furrow constriction and enabled by a lowering of actomyosin contractile tension on the basal cell cortex.

Spatiotemporal Control of Actomyosin Contraction Affects Expansion Dynamics and Sibling Cell Size Asymmetry

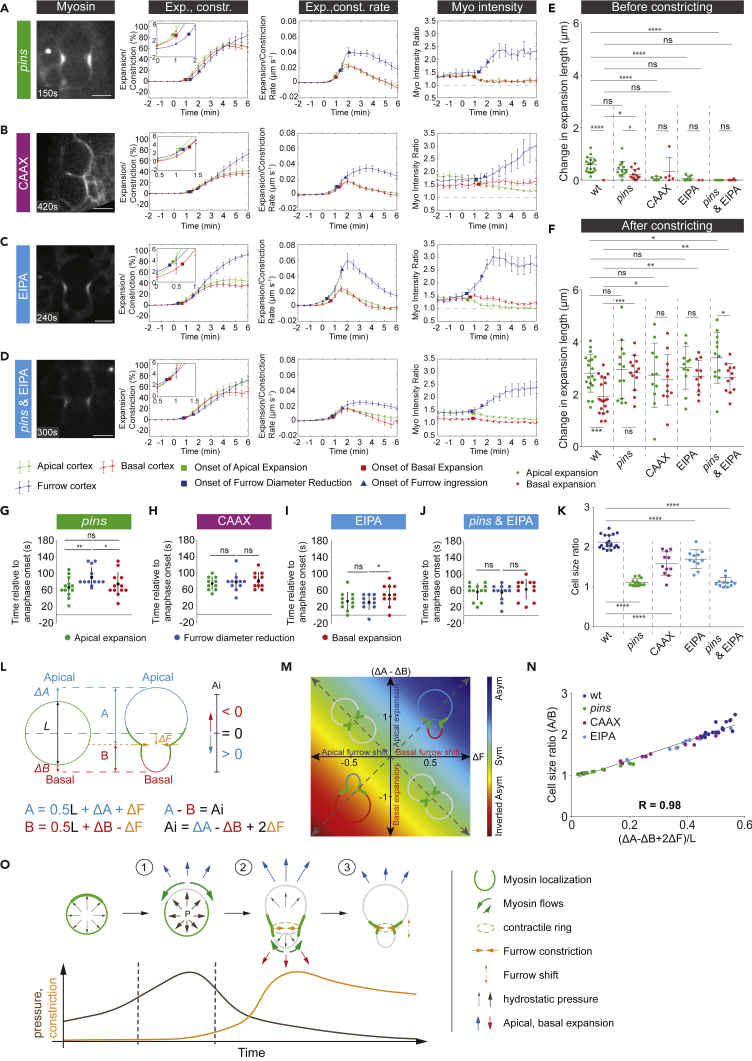
Next, we tested how global or local modulations in actomyosin contractile tension and changes in hydrostatic pressure affected biased cortical extension dynamics. We reasoned that relieving both the apical and basal cortices from actomyosin contractile cortical tension should permit hydrostatic pressure to drive symmetric expansion. To test this hypothesis, we analyzed pins mutant neuroblasts, which have been shown to clear Myosin from both the apical and basal cell cortex simultaneously (Cabernard et al., 2010, Tsankova et al., 2017, Roubinet et al., 2017). Indeed, in contrast to wild-type, apical and basal extension occurred to the same extent before furrow constriction in pins mutant neuroblasts (Figures 4A, 4G, 4E, 4F, S3C, and S3D). Similarly, delaying Myosin relocalization from both cell poles should prevent initial pressure-driven expansion and bias it toward constriction-driven expansion. To this end, we coexpressed Sqh:GFP together with the membrane-tethered nanobody ((pUAST-CAAX:vhhGFP4); vhhGFP4 has a high affinity for GFP; Saerens et al., 2005), thereby delaying Myosin relocalization on the apical and basal neuroblast cortex (referred to as CAAX hereafter). This manipulation abolished initial apical expansion, causing the apical and basal cell cortex to predominantly expand during furrow ingression (Figures 4B, 4H, 4E, 4F, S3E, and S3F).

Figure 4.

Figure 4

Open in a new tab

Physical Asymmetric Cell Division Is a Two-Step Process Driven by Internal Pressure and Spatiotemporally Controlled Myosin Relocalization

(A–J) Representative anaphase images, change in expansion/constriction length, expansion/constriction rate, and Myosin intensity shown for (A) pins (n = 13), (B) CAAX:vhhGFP4 expressing (n = 11), (C) EIPA-treated wild-type (n = 11), and (D) EIPA-treated pins mutant (n = 12) neuroblasts expressing Sqh:GFP (white). Measurements are shown for the apical cortex (green), the basal cortex (red), and the furrow site (blue). Time axis is relative to anaphase onset (0 s). Scatterplots showing the change in expansion length for the apical (green) and basal (red) cortex before (E) and after (F) constriction (furrow diameter reduction). Scatterplots showing the onset of apical expansion (green), furrow diameter reduction (blue), and basal expansion (red) for (G) pins, (H) CAAX:vhhGFP4-expressing, (I) EIPA-treated wild-type, and (J) EIPA-treated pins mutant neuroblasts.

(K) Scatterplots showing the cell size ratio for wild-type (n = 19), pins (n = 13), CAAX:vhhGFP4-expressing (n = 11), EIPA-treated wild-type (n = 11), and EIPA-treated pins mutant neuroblasts.

(L) Theoretical model describing the contribution of cortical expansion and furrow shift to daughter cell size difference (Ai, asymmetry index).

(M) Simulated heatmap defining different asymmetry regions based on the contribution of cortical expansion and the change in furrow positioning to the asymmetry index.

(N) Scatterplots showing the correlation between daughter cell size ratio and the normalized asymmetry index.

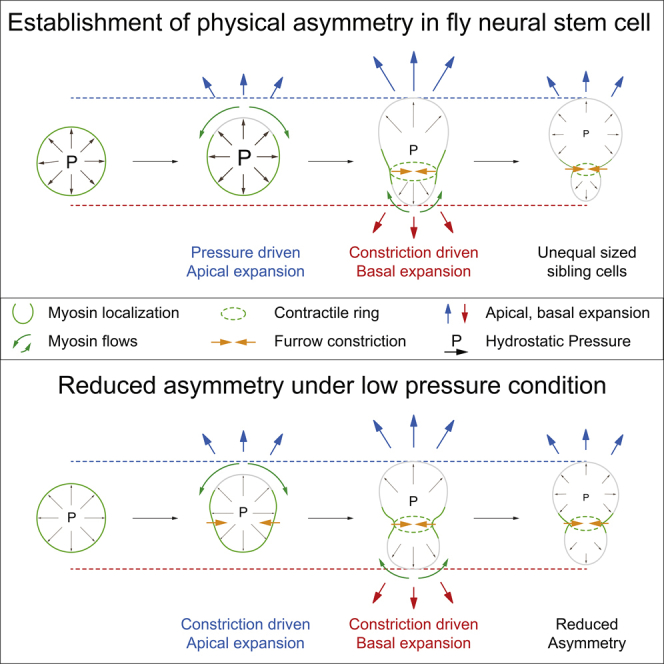
(O) Model. (1) Spatiotemporally regulated Myosin relocalization permits initial internal-pressure-driven apical expansion. (2, 3) Subsequently, owing to dissipation of internal pressure, sustained apical and subsequent basal expansion is driven by actomyosin-dependent furrow constriction. (3) Shifting or late positioning of the cleavage furrow can compensate for the lack of biased cortical expansion (see Figure S3 for more details).

See text for details. Scale bars, 5 μm. Asterisk denote statistical significance, derived from unpaired t tests: *p ≤ 0.05, **p ≤ 0.01, ***p ≤ 0.001, ****p ≤ 0.0001; n.s., not significant.

Myosin relocalization dynamics can also be biased by removing the mitotic spindle using colcemid, a condition delaying basal Myosin relocalization while still permitting normal apical clearing (Roubinet et al., 2017, Roth et al., 2015). Although the lack of the mitotic spindle prevented us from determining anaphase onset, we found that expansion only occurred apically before constriction, followed by a late constriction-driven basal expansion event. As Myosin was retained basally, the basal cortex initially retracted, and we measured the extent of expansion following this initial retraction only (Figures S3G, S3H, and S3Q–S3S).

If hydrostatic pressure drives initial apical expansion, then lowering hydrostatic pressure should delay apical expansion until constriction sets in. In cells, hydrostatic pressure can be generated by an osmolarity gradient; if the osmolarity is higher inside the cell than outside, inflowing water will create hydrostatic pressure. Osmolarity and thus hydrostatic pressure can be changed by inhibiting ion transporters at the plasma membrane. We used ethylisopropylamiloride (EIPA), an inhibitor of Na+/H+ antiporters to reduce hydrostatic pressure (Stewart et al., 2011) in neuroblasts, and measured the subsequent expansion dynamics. EIPA did not affect Myosin dynamics, but wild-type or pins mutant neuroblasts exposed to EIPA predominantly abolished pre-constriction-driven expansion. Apical and basal expansion predominantly occurred after constriction started (Figures 4C–4F, 4I, 4J, and S3I–S3L).

Cell rounding is also regulated by a balance between actomyosin contractile tension and hydrostatic pressure (Stewart et al., 2011). Thus we hypothesized that lowering actomyosin contractile tension by reducing the amount of activated cortical Myosin should diminish intracellular hydrostatic pressure, thereby altering expansion dynamics. Adding the Rho kinase inhibitor Y-27632 to wild-type neuroblasts significantly lowered cortical Myosin intensity; complete Rok inhibition showed no difference between cortical and cytoplasmic signals, whereas partial inhibition still contained lowered cortical Myosin levels (Figures S3M–S3P). Strong Rok inhibition prevented all apical and basal membrane extension and constriction (Figures S3M and S3N), but partial inhibition of Rok allowed apical and basal membranes to expand at the onset of furrow diameter reduction (Figures S3O and S3P). However, similar to EIPA-treated neuroblasts, most expansion occurred predominantly after furrow constriction set in (Figures S3Q–S3T). Thus lowering actomyosin contractile tension shifted the initial pressure-driven expansion toward constriction-driven expansion.

We conclude that Myosin localization and activity, as well as hydrostatic pressure, determine the cortical expansion dynamics. In the absence of hydrostatic pressure, or if actomyosin contractile tension is maintained, membrane expansion is primarily driven by cortical constriction. Furthermore, the spatiotemporal regulation of Myosin relocalization underlies biased cortical expansion dynamics.

Cleavage Furrow Shifting Can Compensate for the Lack of Biased Cortical Expansion

Finally, we tested how pressure-driven and constriction-driven expansions contribute to the establishment of physical asymmetry. In most cases, alterations in either cortical expansion dynamics by changing Myosin dynamics (pins mutants, CAAX neuroblasts), hydrostatic pressure (EIPA treatment), or both also affected sibling cell size asymmetry (Figures 4K and S3U). However, we noticed that some EIPA-treated and CAAX neuroblasts showed wild-type-like asymmetry ratios, although they expanded to the same extent on both the apical and basal cell cortex. We hypothesized that a shifting cleavage furrow could provide a mechanism to correct for the lack of expansion-driven physical asymmetry establishment. Indeed, EIPA-treated neuroblasts preferentially shifted the cleavage furrow toward the basal cortex, whereas wild-type neuroblasts can shift it in either direction (Figures S3V–S3X). We established a mathematical model that calculates an asymmetry index (Ai) as a measure of the degree of sibling cell size asymmetry (Figures 4L and 4M). This asymmetry index includes both polar cell expansion and cleavage furrow shift. For instance, in the absence of biased apical extension, wild-type-like physical asymmetry can be achieved by shifting the cleavage furrow basally. Alternatively, excessive basal expansion, combined with an apically shifted cleavage furrow, should result in inverted physical asymmetry (Figure 4M). To test this model, we measured apical and basal expansions as well as the cleavage furrow shift and found a good correlation with the final sibling cell size ratio (Figure 4N).

Taken together, we conclude that to establish physical asymmetry, shifting the cleavage furrow can compensate for the lack of biased cortical extension.

Discussion

Sibling cell size asymmetry occurs in multiple cell types and organisms, but the underlying mechanisms are diverse and incompletely understood (Roubinet and Cabernard, 2014, Cabernard, 2017). Here, we characterized the biophysical forces underlying the formation of unequal sibling cell size in asymmetrically dividing fly neuroblasts. We used AFM to map dynamic changes in cellular stiffness throughout asymmetric cell division. These measurements revealed a characteristic stiffness asymmetry, marking the position of the prospective cleavage furrow already in early anaphase. This finding is consistent with our previous measurements, which revealed an accumulation of the centralspindlin component Tumbelweed in the prospective furrow region as well as an increase in actomyosin accumulation before measurable furrowing (Roubinet et al., 2017). Consistent with human cells (Stewart et al., 2011) we found that neuroblast stiffness increased during mitosis, peaking shortly after anaphase onset. The global increase in cell stiffness is predominantly attributed to an increase in intracellular pressure and only partially to local accumulation of Myosin. However, correlations between cellular stiffness and Myosin localization can be found at specific time points and cellular locations such as the cleavage furrow region in anaphase.

Here, we also report the interplay between Myosin relocalization, biased neuroblast cortex expansion, and changes in hydrostatic pressure, resulting in an intuitive model that can explain the establishment of sibling cell size asymmetry. Relieving the apical cell cortex from actomyosin contractile tension in early anaphase allows for pressure-driven biased cortical expansion. Subsequently, the drop in hydrostatic pressure—presumably due to an increase in cell volume—is compensated by an assembly of actomyosin at the cleavage furrow, which enables the continuation of apical extension and the onset of basal membrane extension based on constriction-driven displacement of cytoplasmic material (Figure 4O). This biased cortical expansion is coordinated by actomyosin contractile tension, which underlies precise spatiotemporal control (Connell et al., 2011). For instance, apical Myosin relocalization dynamics is controlled by the apical polarity protein Pins through biased localization of Rok and Pkn (Cabernard et al., 2010, Tsankova et al., 2017) and basal Myosin relocalization is controlled by the spindle-dependent pathway (Roth et al., 2015, Roubinet et al., 2017). Both apical and basal Myosin relocalization occurs through cortical Myosin flow (Roubinet et al., 2017). Apical Myosin flow onset starts shortly after anaphase onset, at the peak of hydrostatic pressure. However, on the basal cell cortex, Myosin relocalization occurs with ∼1-min delay (Roubinet et al., 2017), suggesting that the relaxing apical cell cortex permits initial pressure-driven apical expansion, but due to the delay of basal Myosin relocalization, reduced hydrostatic pressure is insufficient to overcome basal actomyosin contractile tension.

Biased cortical expansion is important to establish physical asymmetry. However, we discovered that neuroblasts utilize a backup mechanism to compensate for the lack of asymmetric polar expansion. For instance, modulating either hydrostatic pressure or Myosin distribution created situations in which both poles expand simultaneously. However, due to a shift in furrow positioning, or a late basal furrow positioning mechanism, these neuroblasts can still establish near wild-type-like physical asymmetry. Although we have not further investigated the mechanisms underlying final furrow positioning, previous results indicate that this is indirectly attributed to spindle-dependent cues (Cabernard et al., 2010, Roth et al., 2015, Roubinet et al., 2017). Spindle positioning, spindle geometry, or a combination thereof could influence the spatiotemporal establishment of a Myosin gradient. In wild-type neuroblasts, this gradient can be detected with our stiffness measurements and is already positioned early in anaphase. Modifications in spindle geometry and positioning could influence final furrow positioning by modulating Myosin flows. In sum, we propose that pressure-driven expansion, spindle geometry, and spindle positioning contribute toward the establishment of sibling cell size asymmetry. Under normal conditions, the primary determinant is biased cortical expansion, but if cortical expansion is compromised (either by reducing hydrostatic pressure or manipulating Myosin relocalization), a shifting furrow—most likely due to spindle geometry and/or positioning—can compensate.

Previously it was proposed that local modulations in cortical tension could allow cells to alter their shape (Stewart et al., 2011). Our study provides experimental evidence for this model under physiological conditions and could be potentially relevant to other invertebrate and vertebrate cells alike (Shin et al., 2013). In the future, it will be interesting to learn whether biased membrane extension is accompanied by asymmetric membrane addition or an unfolding of membrane stores. Similarly, the mechanisms regulating hydrostatic pressure during the cell cycle remain to be defined.

Limitations of the Study

The AFM data presented in this study are obtained from isolated neuroblasts. Our stiffness measurements thus neglect the contribution of neighboring cells such as cortex glia and GMCs. We also cannot exclude the possibility that the EIPA affects physiological processes other than hydrostatic pressure.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Acknowledgments

We thank members of the Cabernard laboratory for helpful discussions and Nicole Horsley for proofreading the manuscript. This work was supported by the Swiss National Science Foundation (SNSF; PP00P3_159318 to C.C. and 310030B_160255 to D.J.M.), the National Institutes of Health (NIH; 1R01GM126029-01, C.C.), and start-up funds from the University of Washington. T.T.P. was supported with a Systems X Transition Postdoc Fellowship (TPdF: SXFSIO_141991). Stocks obtained from the Bloomington Drosophila Stock Center (NIH P40OD018537) were used in this study.

Author Contributions

This study was conceived by T.T.P. and C.C. T.T.P. performed all the experiments with help from A.M., E.L., N.L., and J.H. A.M. generated the CAAX:vhhGFP4 and PhyB:mcherry:CAAX constructs. Training and access to AFM microscopy was provided by J.H. and D.J.M. T.T.P. and C.C. wrote the paper.

Declaration of Interests

The authors declare no competing financial interests.

Published: March 29, 2019

Footnotes

Supplemental Information includes Transparent Methods, three figures, and one data and can be found with this article online at https://doi.org/10.1016/j.isci.2019.02.002.

Supplemental Information

Document S1. Transparent Methods and Figures S1–S3
mmc1.pdf (4.3MB, pdf)
Data S1. Codes to Determine Statistical Averages for Cortical Stiffness, Hydrostatic Pressure, Myosin Intensity, and Expansion Dynamics, Related to Figures 1–4 and S1–S3
mmc2.zip (53.4KB, zip)

References

  1. Albertson R., Doe C.Q. Dlg, Scrib and Lgl regulate neuroblast cell size and mitotic spindle asymmetry. Nat. Cell Biol. 2003;5:166–170. doi: 10.1038/ncb922. [DOI] [PubMed] [Google Scholar]
  2. Berger C., Harzer H., Burkard T.R., Steinmann J., van der Horst S., Laurenson A.S., Novatchkova M., Reichert H., Knoblich J.A. FACS purification and transcriptome analysis of Drosophila neural stem cells reveals a role for Klumpfuss in self-renewal. Cell Rep. 2012;2:407–418. doi: 10.1016/j.celrep.2012.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cabernard C. Sibling cell size matters. Elife. 2017;6 doi: 10.7554/eLife.24038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cabernard C., Doe C.Q. Apical/basal spindle orientation is required for neuroblast homeostasis and neuronal differentiation in Drosophila. Dev. Cell. 2009;17:134–141. doi: 10.1016/j.devcel.2009.06.009. [DOI] [PubMed] [Google Scholar]
  5. Cabernard C., Prehoda K.E., Doe C.Q. A spindle-independent cleavage furrow positioning pathway. Nature. 2010;467:91–94. doi: 10.1038/nature09334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cai Y., Yu F., Lin S., Chia W., Yang X. Apical complex genes control mitotic spindle geometry and relative size of daughter cells in Drosophila neuroblast and pI asymmetric divisions. Cell. 2003;112:51–62. doi: 10.1016/s0092-8674(02)01170-4. [DOI] [PubMed] [Google Scholar]
  7. Chen C., Inaba M., Venkei Z.G., Yamashita Y.M. Klp10A, a stem cell centrosome-enriched kinesin, balances asymmetries in Drosophila male germline stem cell division. Elife. 2016;5 doi: 10.7554/eLife.20977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Clark A.G., Wartlick O., Salbreux G., Paluch E.K. Stresses at the cell surface during animal cell morphogenesis. Curr. Biol. 2015;24:R484–R494. doi: 10.1016/j.cub.2014.03.059. [DOI] [PubMed] [Google Scholar]
  9. Connell M., Cabernard C., Ricketson D., Doe C.Q., Prehoda K.E. Asymmetric cortical extension shifts cleavage furrow position in Drosophila neuroblasts. Mol. Biol. Cell. 2011;22:4220–4226. doi: 10.1091/mbc.E11-02-0173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Costache V., Hebras C., Pruliere G., Besnardeau L., Failla M., Copley R.R., Burgess D., Chenevert J., McDougall A. Kif2 localizes to a subdomain of cortical endoplasmic reticulum that drives asymmetric spindle position. Nat. Commun. 2017;8:917. doi: 10.1038/s41467-017-01048-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. D'Avino P.P., Giansanti M.G., Petronczki M. Cytokinesis in animal cells. Cold Spring Harb. Perspect. Biol. 2015;7:a015834. doi: 10.1101/cshperspect.a015834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Derivery E., Seum C., Daeden A., Loubéry S., Holtzer L., Jülicher F., Gonzalez-Gaitan M. Polarized endosome dynamics by spindle asymmetry during asymmetric cell division. Nature. 2015;528:280–285. doi: 10.1038/nature16443. [DOI] [PubMed] [Google Scholar]
  13. Gallaud E., Pham T., Cabernard C. Drosophila melanogaster neuroblasts: a model for asymmetric stem cell divisions. Results Probl. Cell Differ. 2017;61:183–210. doi: 10.1007/978-3-319-53150-2_8. [DOI] [PubMed] [Google Scholar]
  14. Glotzer M. Cytokinesis in metazoa and fungi. Cold Spring Harb. Perspect. Biol. 2017;9:a022343. doi: 10.1101/cshperspect.a022343. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Green R.A., Paluch E., Oegema K. Cytokinesis in animal cells. Annu. Rev. Cell Dev. Biol. 2011;28:a015834. doi: 10.1146/annurev-cellbio-101011-155718. [DOI] [PubMed] [Google Scholar]
  16. Homem C.C.F., Knoblich J.A. Drosophila neuroblasts: a model for stem cell biology. Development. 2012;139:4297–4310. doi: 10.1242/dev.080515. [DOI] [PubMed] [Google Scholar]
  17. Kiyomitsu T., Cheeseman I.M. Cortical dynein and asymmetric membrane elongation coordinately position the spindle in anaphase. Cell. 2013;154:391–402. doi: 10.1016/j.cell.2013.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Krieg M., Fläschner G., Alsteens D., Gaub B.M., Roos W.H., Wuite G.J.L., Gaub H.E., Gerber C., Dufrêne Y.F., Muller D.J. Atomic force microscopy-based mechanobiology. Nat. Rev. Phys. 2018;475:1. [Google Scholar]
  19. Ou G., Stuurman N., D'Ambrosio M., Vale R.D. Polarized myosin produces unequal-size daughters during asymmetric cell division. Science. 2010;330:677–680. doi: 10.1126/science.1196112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Rappaport R. Establishment of the mechanism of cytokinesis in animal cells. Int. Rev. Cytol. 1986;105:245–281. doi: 10.1016/s0074-7696(08)61065-7. [DOI] [PubMed] [Google Scholar]
  21. Roth M., Roubinet C., Iffländer N., Ferrand A., Cabernard C. Asymmetrically dividing Drosophila neuroblasts utilize two spatially and temporally independent cytokinesis pathways. Nat. Commun. 2015;6:6551. doi: 10.1038/ncomms7551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Roubinet C., Cabernard C. Control of asymmetric cell division. Curr. Opin. Cell Biol. 2014;31:84–91. doi: 10.1016/j.ceb.2014.09.005. [DOI] [PubMed] [Google Scholar]
  23. Roubinet C., Tsankova A., Pham T.T., Monnard A., Caussinus E., Affolter M., Cabernard C. Spatio-temporally separated cortical flows and spindle geometry establish physical asymmetry in fly neural stem cells. Nat. Commun. 2017;8:1383. doi: 10.1038/s41467-017-01391-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Royou A., Sullivan W., Karess R. Cortical recruitment of nonmuscle myosin II in early syncytial Drosophila embryos: its role in nuclear axial expansion and its regulation by Cdc2 activity. J. Cell Biol. 2002;158:127–137. doi: 10.1083/jcb.200203148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Saerens D., Pellis M., Loris R., Pardon E., Dumoulin M., Matagne A., Wyns L., Muyldermans S., Conrath K. Identification of a universal VHH framework to graft non-canonical antigen-binding loops of camel single-domain antibodies. J. Mol. Biol. 2005;352:597–607. doi: 10.1016/j.jmb.2005.07.038. [DOI] [PubMed] [Google Scholar]
  26. Shin J.-W., Buxboim A., Spinler K.R., Swift J., Christian D.A., Hunter C.A., Léon C., Gachet C., Dingal P.C., Ivanovska I.L. Contractile forces sustain and polarize hematopoiesis from stem and progenitor cells. Cell Stem Cell. 2013;14:81–93. doi: 10.1016/j.stem.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Stewart M.P., Helenius J., Toyoda Y., Ramanathan S.P., Muller D.J., Hyman A.A. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469:226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
  28. Tan C.H., Gasic I., Huber-Reggi S.P., Dudka D., Barisic M., Maiato H., Meraldi P. The equatorial position of the metaphase plate ensures symmetric cell divisions. Elife. 2015;4 doi: 10.7554/eLife.05124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Tsankova A., Pham T.T., Garcia D.S., Otte F., Cabernard C. Cell polarity regulates biased myosin activity and dynamics during asymmetric cell division via Drosophila rho kinase and protein kinase N. Dev. Cell. 2017;42:143–155.e5. doi: 10.1016/j.devcel.2017.06.012. [DOI] [PubMed] [Google Scholar]
  30. White E.A., Glotzer M. Centralspindlin: at the heart of cytokinesis. In: Robinson D.N., editor. Vol. 69. Hoboken; 2012. pp. 882–892. (Cytoskeleton). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Yoneda M. Tension at the highly stretched surface of sea-urchin eggs*. Dev. Growth Differ. 1980;22:39–47. doi: 10.1111/j.1440-169X.1980.00039.x. [DOI] [PubMed] [Google Scholar]
  32. Yoneda M. Tension at the surface of sea-urchin egg: a critical examination of Cole's experiment. J. Exp. Biol. 1964;41:893–906. doi: 10.1242/jeb.41.4.893. [DOI] [PubMed] [Google Scholar]
  33. Zhang J., Megraw T.L. Proper recruitment of -tubulin and D-TACC/Msps to embryonic drosophila centrosomes requires centrosomin motif 1. Mol. Biol. Cell. 2007;18:4037–4049. doi: 10.1091/mbc.E07-05-0474. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Transparent Methods and Figures S1–S3
mmc1.pdf (4.3MB, pdf)
Data S1. Codes to Determine Statistical Averages for Cortical Stiffness, Hydrostatic Pressure, Myosin Intensity, and Expansion Dynamics, Related to Figures 1–4 and S1–S3
mmc2.zip (53.4KB, zip)

Articles from iScience are provided here courtesy of Elsevier

RESOURCES