Threading of Unconcatenated Ring Polymers at High Concentrations: Double-Folded vs Time-Equilibrated Structures

Abstract

Unconcatenated ring polymers in concentrated solutions and melt are remarkably well described as double-folded conformations on randomly branched primitive trees. This picture though contrasts recent evidence for extensive intermingling between close-by rings in the form of long-lived topological constraints or threadings. Here, we employ the concept of ring minimal surface to quantify the extent of threadings in polymer solutions of the double-folded rings vs rings in equilibrated molecular dynamics computer simulations. Our results show that the double-folded ring polymers are significantly less threaded compared to their counterparts at equilibrium. Second, threadings form through a slow process whose characteristic time-scale is of the same order of magnitude as that of the diffusion of the rings in solution. These findings are robust, being based on universal (model-independent) observables as the average fraction of threaded length or the total penetrations between close-by rings and the corresponding distribution functions.

Concentrated solutions and melts of unconcatenated and unknotted ring polymers have stimulated intensive theoretical¹⁻²⁰ and experimental²¹⁻²⁷ work in the past years.

Under high concentrations rings challenge most of the peculiarities characterizing the more familiar case of solutions of linear chains. First, spatial constraints arising from global topological invariance and the consequential departure⁴ from the Flory-like mechanism²⁸⁻³⁰ for compensation of excluded volume effects imply that the average ring size or gyration radius, R_g, scales in the limit of large polymer mass or contour length, L_c, like^11,12R_g ∼ L_c^1/3, while for linear chains²⁸⁻³⁰R_g ∼ L_c. Second, the absence of free ends implies that rings do not relax via common reptation which is, instead, the dominating mechanism for linear chains.²⁸⁻³⁰ Consequently, stress relaxation in ring solutions decays as a power-law²¹ with no sign of the rubber-like plateau of linear melts.^29,30

Substantial theoretical progress was made back in the ‘80s, when Khokhlov and Nechaev¹ and Rubinstein³¹ mapped the problem of rings in entangled solutions to the one of a single ring in an array of fixed obstacles to which it is not topologically linked. In the latter conditions, rings should adopt double-folded conformations on randomly branching primitive trees.^1,31 Recently,¹¹ explicit numerical mapping of ring polymers in solution to randomly branched structures has demonstrated that relevant properties such as the polymer gyration radius or contact frequencies can be accurately reproduced. Further theoretical and numerical investigations^12,15,18,32 also support the “rings/branched polymers” analogy.

This successful picture is challenged in recent works³³ showing that mutually exposed surfaces between neighbor rings form long-lived topological constraints, commonly known as threadings.^17,20,34,35 Absent in systems of linear chains, threadings are responsible for the observed glassy behavior of ring solutions under pinning perturbations.^17,20,36 Conversely, being relaxed only up to the entanglement scale (Section IA in SI), ring polymers folding into branched structures display little interpenetration with close-by neighbors.

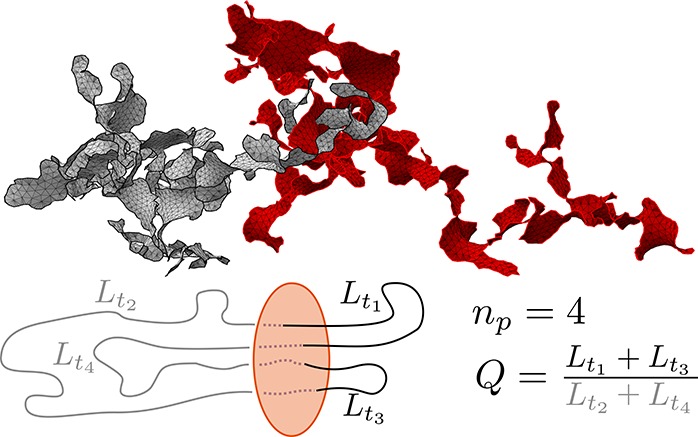
To shed light on this apparent conflict, in this Letter we quantify the extent of threadings between distinct pairs of unconcatenated rings in solution and melt by employing the concept of ring minimal surface (Figure 1(A), top), which was recently^10,33 applied to detect threadings in melts of rings. Specifically, a ring is defined as “threaded” by another ring if its minimal surface is crossed by the other ring (Figure 1(A), bottom). Here we investigate only two-ring threadings; therefore, self-threadings are ignored. Numerical construction of minimal surfaces has been performed in turn for: (1) double-folded ring polymers on interacting randomly branched primitive trees¹¹ (IBP model) (for details, see Sec. IA in Supporting Information (SI)) and (2) rings in solutions equilibrated through large-scale, brute-force molecular dynamics (MD) computer simulations. As for the latter, two microscopic, distinct polymer models have been chosen (Sec. IB in SI): (a) the classical Kremer–Grest (KG) polymer model (hereafter, EQ MD 1) from ref (7) at melt conditions and (b) the generalized KG polymer model (hereafter, EQ MD 2) from refs (11 and 37) with larger stiffness at semidilute conditions. The initial ring conformations adopted in this second case come from the IBP model, and thus we will use the full MD trajectories to characterize the time progression of the threading statistics. To analyze results from the two different polymer models on equal footing, observables will be given as functions of the total number of entanglements Z ≡  L_c/L_e,^38,39 where L_c is the ring contour length and L_e is the entanglement length.²⁹ The largest rings which can be equilibrated in reasonable computational time are for Z ≈ 100 for both setups (see Table S1 in SI for details on the systems and corresponding statistics used). To speed up the equilibration of the longest rings of EQ MD 1, we used a novel anisotropic doubling scheme (see Sec. IB in SI).

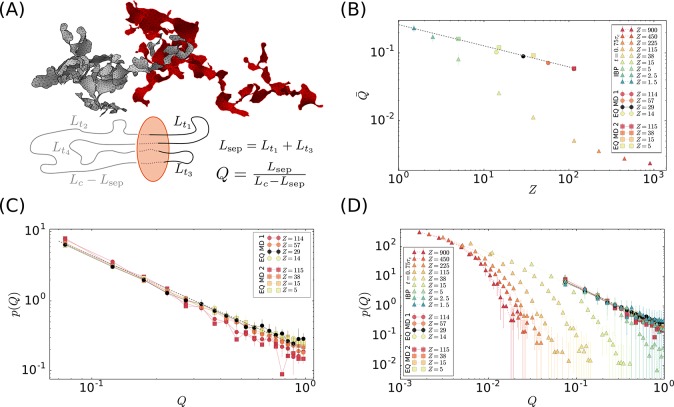
Figure 1.

Threading statistics in terms of relative contour length fraction Q. (A) Top: Minimal surfaces of a pair of close-by rings modeled as double-folded polymers on interacting branched primitive trees (IBP model). Bottom: Schematic representation of one ring (black and gray) penetrating the minimal surface of another ring (orange) of total contour length L_c. L_ti is the contour length of subchain i penetrating the second ring. In this example, four surface penetrations (n_p = 4) split the penetrating ring into the segment pairs (L_t1,L_t3) and (L_t2,L_t4) which are on opposite sides of the surface: this defines the separation length, L_sep, and its complementary, L_c – L_sep. Adapted with permission from ref (33). (B) Mean relative contour length fraction, Q̅, of one ring threading another ring as a function of ring mass, Z. The dashed line is the best fit to the data for MD-equilibrated rings, Q̅ ≈ 0.26Z^–0.31. (C) Probability distribution functions, p(Q) (log–log scale). Results for MD-equilibrated rings from polymer models EQ MD 1 and EQ MD 2. The dashed gray line p(Q) ∼ Q^–1.35 is the best fit to the distributions tail. (D) Comparison between p(Q)’s for the IBP model and MD-equilibrated rings. In panels (C) and (D), the bin size is Q_max/20 with Q_max being the largest value of Q in the given data set.

Threadings statistics: Minimal surfaces spanned on the ring polymers are obtained by a slightly modified version of the minimization algorithm from ref (33) (see Sec. IC in SI). The algorithm is based on successive iterations of triangulations evolving under surface tension by moving the free vertices. Typically, each ring penetrates the minimal surfaces of more of its neighbors, and this number grows with Z (see Sec. IE in SI for details). Then, following ref (33) we introduce the separation length

1

where L_ti is the (threading) length between the i-th and the (i + 1)-th penetrations of the surface (Figure 1(A), bottom). L_sep characterizes how much material of the penetrating ring is on one side of the penetrated ring (the contour length on the other side being L_c – L_sep, of course). Accordingly, the quantity 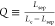accounts for the relative extent of contour length on one side with respect to the other, Q = 1, meaning the penetrating ring is half split by the penetrated surface.

The mean value Q̅ = Q̅(Z), obtained by averaging Q over 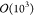up to 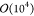interpenetrating rings pairs (see Table S1 in SI), is plotted in Figure 1(B). Remarkably, data for MD-equilibrated rings collapse on the same (universal) curve characterized by simple power-law decay Q̅ = (0.26 ± 0.09)Z^{–0.31±0.09} (dashed line). As the two polymer models EQ MD 1 and 2 have different monomer densities and entanglement lengths (Sec. IB in SI), this is a nontrivial result, which pinpoints Q̅ as a suitable “order parameter” for characterizing the total extent of threading between close-by rings. In fact, double-folded rings display smaller values for Q̅ suggesting a lesser extent of threadings between close-by rings. Figure 1(C) shows the complete distribution functions, p(Q), for MD-equilibrated rings at different Z’s. Mirroring corresponding averages in Figure 1(B), p(Q)’s from the two different polymer models agree well, and the observed power-law behavior p(Q) ∼ Q^–1.35 for 0.1 ≲ Q ≲ 1 agrees with the reported³³ decay for distribution functions, p(L_sep), of separation length. In turn, expecting that the minimal size of penetrating length is 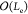, the average value Q̅ ≈ ∫_1/Z¹Q^–0.35 dQ/∫_1/ZQ^–1.35 dQ ≈ 0.54 Z^–0.35 is consistent with the power-law behavior reported in Figure 1(B). Small, systematic differences toward Q → 1 between p(Q)’s for rings with Z = 114 and Z = 115 should be attributed to incomplete equilibration of the corresponding data sets (see discussion in Sec. IB in SI). As explained in the following, such deviations from the equilibrium distribution emerge also for smaller Z’s whenever polymer chains are not fully equilibrated. In sharp contrast with the results for equilibrated rings, p(Q) distributions for rings constructed according to the IBP model decay very differently (Figure 1(D)). This is particularly evident for very large rings, whose p(Q)’s feature an exponential cutoff toward Q → 1. As the fine structure of the IBP rings is, by construction, relaxed only up to spatial scales of the order of Z ≈ 1 (Sec. IA in SI), we suspect threadings between large rings have not yet relaxed. Consistent with that, very short IBP rings (Z = 1.5) are instead fully relaxed, as the corresponding p(Q) exhibits the same universal equilibrium form from Figure 1(C).

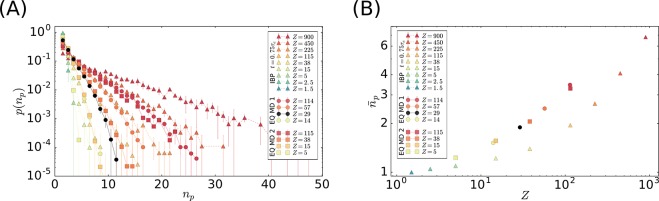
We complete the discussion by focusing on how many times (n_p) any ring penetrates the minimal surface of any other single ring. In order to dismiss any fine scale detail related to the employed polymer model, a given threading segment contributes to n_p only if its contour length exceeds the entanglement length L_e.³⁸ We notice, though, that with this constraint n_p is not necessarily an even number as in the original work.³³Figure 2(A) shows that distribution functions p(n_p)’s display exponential tails for both MD-equilibrated rings (in agreement with ref (33)) and IBP-model rings. Instead, corresponding mean values n̅_p ≡ ∫ n_pp(n_p)dn_p as functions of ring mass Z behave differently for MD-equilibrated vs IBP rings (Figure 2(B)). As for Q̅(Z), n̅_p(Z) from different MD simulations nicely collapses on a single curve. However, at odds with Q̅(Z) (Figure 1(B)), n̅_p(Z) is laying at the threshold of a (slow) crossover, and consequently, our attempt to fit the data for Z ≥ 29 to a single power-law behavior gave poor results. Obviously, the lower values for n̅_p(Z) from nonequilibrated rings reflect, as for Q̅(Z), how these chains systematically “underthread” their spatially close neighbors. Due to the exponential character of the p(n_p) distributions and the fact that each ring threads its neighbors (see Sec. IE in SI), the mean value n̅_p is a good indicator of the typical number of penetrations made by a single ring.

Figure 2.

Threading statistics in terms of number of penetrations. (A) Probability distribution functions, p(n_p), of the number of penetrations, n_p, for the different polymer models and ring masses Z (linear-log scale). (B) Corresponding mean number of penetrations, n̅_p, as a function of the ring mass, Z (log–log scale).

Threadings dynamics: We are now going to discuss how almost unthreaded rings constructed according to the IBP model progressively thread each other. These rings reproduce several properties of equilibrated ring conformations like the gyration radius and contact probabilities.¹¹ On the other hand (Figures 1 and 2), they fail in reproducing threading statistics. Therefore, we track how threading statistics is changing as ring conformations are relaxing over time. In the following, time is always expressed in units of the entanglement time τ_e,²⁹ corresponding to the characteristic time scale above which entanglements start slowing down chain dynamics.

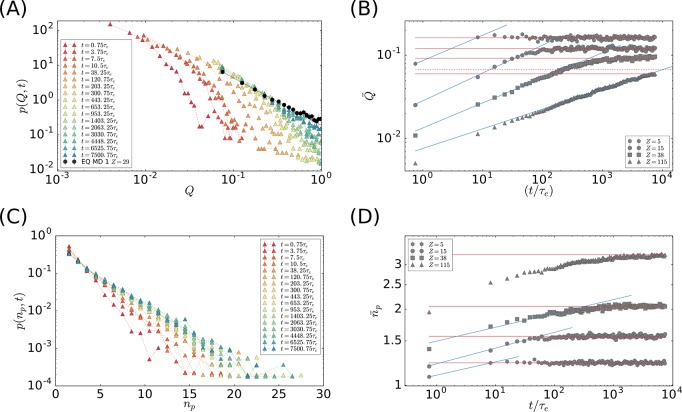
Figure 3(A) shows the evolution of the distribution function p(Q,t) for Z = 115 (similar plots are obtained for Z = 5, 15, and 38, not shown) at different times. For short times, the distribution p(Q,t) is a power-law for Q → 0 and has an exponential cutoff at larger Q → 1, as in Figure 1(D). As time increases, the exponential cutoff is progressively shifting to larger Q values as longer threadings occur. Then, we consider how the mean value, Q̅(t) ≡ ∫ Q p(Q,t)dQ, changes with time (Figure 3(B)). Interestingly, Q̅(t) grows at early times according to the simple power-law:

2

For Z = 5, 15, and 38 this regime is followed by a plateau, implying that equilibrium has been reached. Best fits of eq 2 to the data before the plateau (blue lines in Figure 3(B)) give effective exponents α_Q ≈ 0.3 (for specific values, see Table S2 in SI). The heights of the different plateaus correspond (solid horizontal lines) to the equilibrium values for Q̅(Z) (symbols “□” in Figure 1(B)). For Z = 115 instead, due to the incomplete equilibration, threadings are still evolving. In this case, the height of the corresponding plateau (dashed horizontal line) is extrapolated from the reported (Figure 1(B)) power-law behavior Q̅(Z) ≈ 0.26Z^–0.31. The intercept between the fitted power-law and the plateau defines the threading relaxation time, τ_rel,Q^th(Z) (for specific values, see Table S2 in SI). Interestingly, τ_rel,Q(Z) is of the same order of the relaxation times, τ_rel^diff(Z), associated with ring thermal diffusion (Table S2 in SI) and defined (see Sec. IB in SI) at the intercept between the time mean-square displacement of the ring center of mass, ⟨g₃(t)⟩ ≡ ⟨(r⃗_cm(t) – r⃗_cm(0))²⟩, and the time-dependent mean-square gyration radius, ⟨R_g(t)⟩. On the other hand, τ_rel^diff is expected⁸ to be significantly larger than the time scale associated with internal ring motion,⁸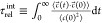, where c⃗(t) = d⃗₁(t) × d⃗₂(t) and d⃗₁(t) and d⃗₂(t) are any arbitrarily chosen pair of spanning ring diameters whose tails are separated by the contour length Z/4. Accurate numerical evaluation of τ_rel (see Sec. IB in SI) confirms that τ_rel^int < τ_rel at any given Z (Table S2 in SI). Threadings constitute then the dominant degrees of freedom governing ring relaxation.

Figure 3.

Time evolution of threading statistics. (A) Time-dependent distribution functions, p(Q,t), of the relative contour length fraction, Q, of one ring threading another ring (log–log scale). Results for solutions of rings with Z = 115 prepared according to the IBP model. Similar curves are found also for other Z’s (not shown). Black circles represent the equilibrium distribution p(Q) calculated for rings with Z = 29 (Figure 1(C)). (B) Corresponding mean values, Q̅(t) (symbols), as functions of time (log–log scale) and power-law fits to the data (eq 2, blue lines) in the initial stage of the equilibration. Solid horizontal lines for Z = 5, 15, and 38 denote corresponding equilibrium values Q̅(Z). For Z = 115, the solid line is for the value measured at the end of the trajectory, and the dashed line is for the extrapolated equilibrium value. (C) Time-dependent distribution functions, p(n_p,t), of the number of penetrations, n_p (linear-log scale). Similar curves are found also for other Z’s (not shown). (D) Corresponding mean number of penetrations, n̅_p(t) (symbols), as functions of time (log–log scale) and power-law fits to the data (eq 3, blue lines) in the initial stage of the equilibration. Horizontal lines are for asymptotic values n̅_p(Z).

We complete our analysis by considering the time evolution of the distribution function of the number of penetrations, p(n_p,t), as the rings progressively thread (Figure 3(C)) as well as the corresponding average value, n̅_p(t) ≡ ∫ n_pp(n_p,t)dn_p (Figure 3(D)). Data appear slightly noisier than the ones for Q̅(t) (Figure 3(B)), yet n̅_p(t) is also clearly exhibiting an initial power-law regime

3

followed by given plateaus for Z = 5, 15, and 38 whose heights (solid horizontal lines) correspond to the equilibrium values n̅_p(Z) (symbols “□” in Figure 2(B)). In those cases, the effective exponents α_np are close to ≈0.06, while the crossover times τ_rel,np^th(Z) match well the corresponding τ_rel,Q(Z)’s (Table S2 in SI). As for Z = 115, arguably because of incomplete equilibration, the initial crossover to equilibrium resembles less a single power-law compared to the other cases with smaller Z. Since the evaluation of the asymptotic behavior at large t is also problematic (see discussion on threading statistics), corresponding α_np and τ_rel,np^th cannot be reliably estimated.

Conclusions: Theoretical considerations^1,3,31 corroborated by recent numerical work¹¹ led to the conclusion that topologically constrained ring polymers like rings in a gel³⁶ or rings in concentrated solutions and melt^7,8,11,12 should resemble double-folded conformations with randomly branched structures.

In this Letter, we have shown that this picture is not complete as it tends to underestimate the correct extent of threadings^17,20,34,35 between close-by rings at equilibrium. Following refs (10 and 33) our analysis relies upon the concept of ring minimal surface, and our results are independent from model details: in particular we report that both the relative contour length penetrating the minimal surface of a given ring (Q and its distribution p(Q), Figure 1) and the absolute number of penetrations (n_p and its distribution p(n_p), Figure 2) display universal features. At the same time, we have demonstrated that threading relaxation to equilibrium (functions Q̅(t) and n̅_p(t), Figure 3) is power-law and that the associated time scales match ring diffusion in melt while remaining significantly larger than the time scales associated with ring internal relaxation. Based on that, we predict that threadings dominate ring relaxation in entangled solutions. At the same time, two of our results also hint on the reason why double-folded models work well:¹¹ (1) the observed relation Q̅(Z)⁻¹ = (Z – Z_sep)/Z_sep ∼ Z^0.31 implying that the separation length Z_sep ≡ L_sep/L_e increases only sublinearly in the ring mass Z and (2) the small (Figure 2(B)) mean number of threadings. The static properties could then be well governed by the larger unthreaded contour length L_c – L_sep, in agreement with the tree picture. Yet, the smaller L_sep could affect the dynamics.

We speculate that the exponent α_Q ≈ 0.3 governing threading relaxation could be (related to) the exponent 1/3 of the late-stage phase-ordering kinetics with a conserved order parameter.⁴⁰⁻⁴² If the number of branches of the ring conformation is conserved during the relaxation from the IBP state, the curvilinear diffusion of the branches could be viewed as switching the branches from a nonthreading to a threading state. To find out if the correspondence does exist, we would need to connect our threading analysis with an algorithm to detect branches such as the one in ref (18).

A limitation of the present analysis is that while concentrating primarily on pairwise threadings it neglects higher-order ones whose contribution to ring dynamics in melts appears to be not negligible.³⁵ In the future, a potential noninvasive method to detect the complex threadings could help to clarify their microscopic origin and effect.

In light of these results, the question related to how to construct “by first-principles” equilibrated solutions of ring polymers not based on double-folded conformations¹¹ is still open: whether the answer will require us to rethink double-folded conformations or a completely different approach, in both cases it remains a promising research line for the future.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsmacrolett.8b00828.

• Additional details on: preparation of initial melts of ring conformations, molecular dynamics computer simulations, and the algorithm to compute minimal surfaces (PDF)

The authors declare no competing financial interest.