Abstract
The Achilles is the thickest tendon in the body and is the primary elastic energy-storing component during running. The form and function of the human Achilles is complex: twisted structure, intratendinous interactions, and differential motor control from the triceps surae muscles make Achilles behavior difficult to intuit. Recent in vivo imaging of the Achilles has revealed nonuniform displacement patterns that are not fully understood and may result from complex architecture and musculotendon interactions. In order to understand which features of the Achilles tendon give rise to the nonuniform deformations observed in vivo, we used computational modeling to predict the mechanical contributions from different features of the tendon. The aims of this study are to: (i) build a novel computational model of the Achilles tendon based on ultrashort echo time MRI, (ii) compare simulated displacements with published in vivo ultrasound measures of displacement, and (iii) use the model to elucidate the effects of tendon twisting, intratendon sliding, retrocalcaneal insertion, and differential muscle forces on tendon deformation. Intratendon sliding and differential muscle forces were found to be the largest factors contributing to displacement nonuniformity between tendon regions. Elimination of intratendon sliding or muscle forces reduced displacement nonuniformity by 96% and 85%, respectively, while elimination of tendon twist and the retrocalcaneal insertion reduced displacement nonuniformity by only 35% and 3%. These results suggest that changes in the complex internal structure of the tendon alter the interaction between muscle forces and tendon behavior and therefore may have important implications on muscle function during movement.
Keywords: finite element, computational model, MRI, soft tissue, connective tissue
INTRODUCTION
Tendons are vital for human movement as they transmit forces from muscles to bones. In addition to this fundamental role, tendons are important for the dynamics of coordinated movement as they serve to store and release elastic energy during cyclic movements (Alexander and Bennet-Clark, 1977; Alexander, 1991; Ishikawa et al., 2005; Sasaki and Neptune, 2006), protect muscle fibers from damage due to stretch (Griffiths, 1991), allow muscles to work at favorable power outputs (Cronin et al., 2013; Lichtwark and Wilson, 2006), and enhance muscle performance by enabling muscle-tendon-unit performance that exceeds the capabilities of muscles alone (Roberts, 2002). As the largest and strongest tendon in the human body (Järvinen et al., 2005), the Achilles tendon is important for walking and running, sustaining loads many times body weight during these tasks (Giddings et al., 2000).
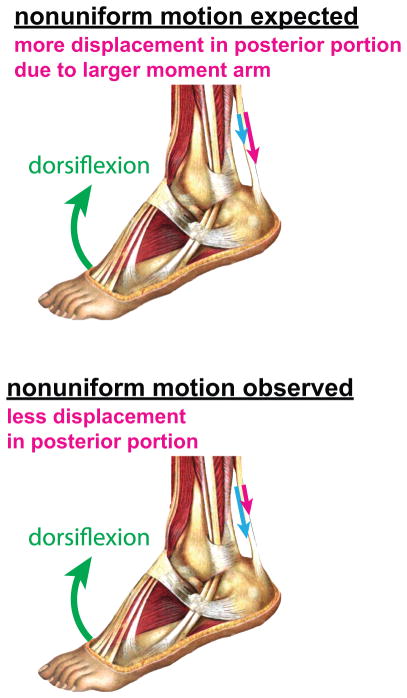
Recent research has demonstrated the complexity of in vivo behavior of the Achilles tendon. Using dynamic ultrasound imaging, Arndt et al. (2012) showed nonuniform tissue displacements within the Achilles tendon during cyclic passive ankle dorsiflexion. In that study, tissue displacements were greater in the anterior portion of the tendon as compared to the displacements in the posterior portion of the tendon, an interesting result considering that the moment arm is greater for the posterior portion (Fig. 1). Slane and Thelen (2014) observed similar nonuniformity in both passive and eccentric loading conditions, with less extreme nonuniformity during eccentric trials. Bojsen-Møller et al. (2004) showed nonuniform displacements between the soleus distal aponeurosis and the gastrocnemius distal aponeurosis (proximal to the Achilles tendon) during isometric ankle plantarflexion. Finally, Franz et al. (2015) observed nonuniform displacements of the Achilles tendon in healthy subjects during normal treadmill walking.
Figure 1.
Illustration of tissue displacements in Achilles tendon. Kinematics alone suggests greater displacements in the posterior tendon during ankle dorsiflexion. In multiple experimental observations, greater displacement was seen in the anterior tendon (Arndt et al., 2012; Franz et al., 2015; Slane and Thelen, 2015, 2014). Figure adapted from Sobotta (1909).
What gives rise to these observations of nonuniform displacements? Structurally, the tendon is composed of three subtendons1 (Handsfield et al., 2016), each of which is controlled by a different muscle belly in the triceps surae (Bojsen-Møller and Magnusson, 2015; Edama et al., 2014; Sarrafian, 1993; Szaro et al., 2009). These subtendons twist about one another in an internal direction (Bojsen-Møller and Magnusson, 2015; Edama et al., 2014; van Gils et al., 1996; White, 1943), but the functional significance of this twist is not well understood. Additionally, recent work has suggested that sliding of tendon substructures may occur in healthy and young, but not older, animals (Thorpe et al., 2013). Interestingly, Slane and Thelen (2015) observed reduced regional nonuniformity in middle-aged subjects, as compared to young subjects.
As an explanation for the nonuniformity observed in the Achilles, Arndt et al. (2012) and Bojsen-Møller et al. (2004) have proposed differential force contributions from the triceps surae muscles. Due to the complexity of Achilles behavior and structure such as twisted subtendons, intra-tendon sliding, and an osseous insertion behind the calcaneus (retrocalcaneal), it is difficult to intuit how these and other features of the tendon contribute to patterns of deformation. While a useful tool for dynamic musculoskeletal imaging, ultrasound studies are generally limited to a small imaging region within some portion of the tendon, making it difficult to appreciate the behavior of the entire tendon. Taken together, there are questions that cannot be answered from imaging studies alone: i) do differential muscle forces give rise to the tissue displacements observed experimentally? ii) what role does inter-subtendon sliding have in creating tissue displacement profiles? iii) what are the mechanical contributions of various features of the Achilles tendon such as twisting and a retrocalcaneal insertion?
The overall goal of this work was to create a finite element model of the Achilles tendon to investigate the contributions of Achilles tendon geometry, twisting tendon morphology, and differential muscle forces on tendon displacement profiles. The model geometry was constructed from images obtained using a customized ultrashort echo time (UTE) MRI sequence. The specific goals were to use the model to replicate tissue displacements observed in the literature; estimate muscle force contributions; and use the model to understand the interactions of muscle forces, subtendon twisting and sliding, and a retrocalcaneal insertion on tendon displacements and strains.
METHODS
Ultrashort echo time magnetic resonance imaging
A healthy 27 year-old female volunteer (height: 1.63m, mass: 52 kg) provided informed consent to the following protocol, which was approved by the University of Virginia Institutional Review Board for Human Subjects Research. We scanned the volunteer using a 3T Siemens (Erlangen, Germany) Trio MRI scanner with a combination ultrashort echo time (UTE) and short echo time (shTE) dual-echo pulse sequence utilizing a spoke-radial 3D k-space trajectory which was originally developed for imaging cortical bone and is fully described elsewhere (Miller et al., 2015). We placed a flex coil around the subject’s right ankle which was manually positioned to 25° of plantarflexion. We used the following sequence parameters optimized for tendon imaging- TE1(UTE)/TE2(shTE)/TR/α: 0.08ms/2.54ms/6ms/10°. Field of view was 192×192×192 mm3 and spatial resolution was 0.8mm isotropic. The 3D radial k-space trajectory consisted of 91,088 individual spokes, corresponding to 50% undersampling at this field of view and resolution. The shTE magnitude images were subtracted pixel-by-pixel from inherently co-registered UTE magnitude images to maximize tendon contrast. To reduce noise, we averaged and resampled images at a slice thickness of 2.4mm in the axial plane using Osirix imaging software (Rosset et al., 2004).
Model geometry
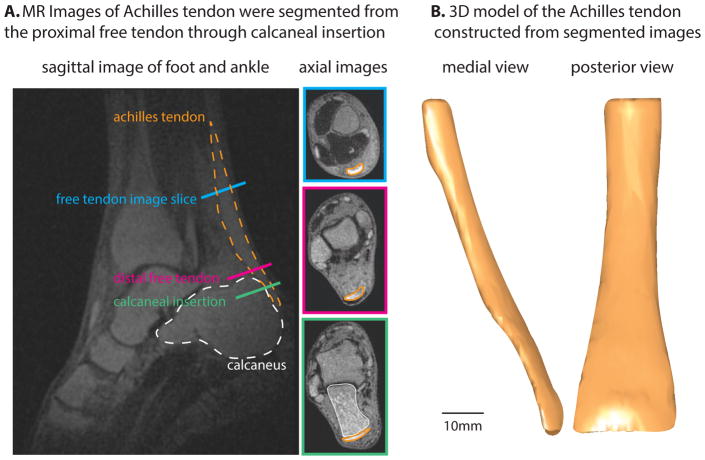
We manually outlined the Achilles tendon in MR images from the soleus muscle-tendon junction to the extent of tendon insertion on the calcaneus (Fig. 2) using in-house segmentation software written in Matlab (The Mathworks, Natick, MA). The control points that defined the tendon external geometry were exported to Autodesk Inventor Professional (Autodesk Inc, San Rafael, CA). To reconstruct axial cross-sections of tendon, we interpolated control points with closed cubic splines. 3D tendon geometry was constructed by lofting over all axial cross-sections.
Figure 2.
Summary of imaging and segmentation of external tendon geometry. A: Sagittal and axial slices from 3D UTE-shTE images illustrate the location of the Achilles tendon and its segmentation in axial slices. B: 3D reconstruction of the segmented images reveals whole tendon shape from soleus myotendinous junction to retrocalcaneal insertion.
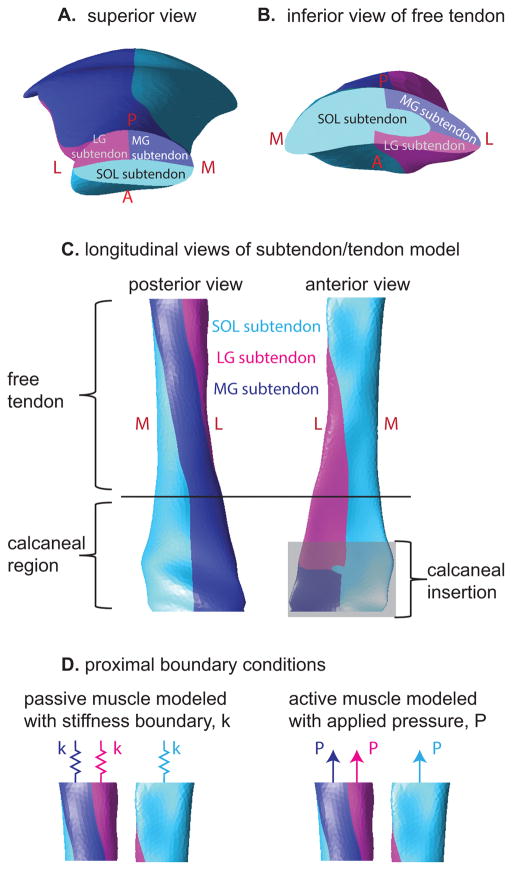
In order to model the Achilles sub-structure, we defined 2D surfaces in Autodesk Inventor that subdivided the 3D tendon geometry into three subtendons. Each of the three subtendons corresponded to one of the three muscles of the triceps surae (Fig. 3) (Bojsen-Møller and Magnusson, 2015; Edama et al., 2014; Sarrafian, 1993; Szaro et al., 2009). At the proximal aspect of the tendon, we defined the anterior portion as the subtendon extending from the soleus (hereafter referred to as SOL subtendon), the posterior medial portion as the subtendon extending from the medial gastrocnemius (MG subtendon), and the posterior lateral portion as the subtendon extending from the lateral gastrocnemius (LG subtendon), as these are the relative locations of the triceps surae muscles informed by MRI (Handsfield et al., 2014). At the distal aspect of the free tendon, we defined the location of each subtendon according to literature reports of dissection studies that separated the three portions of the Achilles tendon by peeling away the portions of the tendon from the proximal end of the tendon where the muscles’ distal aponeuroses are separate and distinguishable (Bojsen-Møller and Magnusson, 2015; Edama et al., 2014; Sarrafian, 1993; Szaro et al., 2009). This positioning resulted in an internal twisting of the Achilles subtendons, which is consistent with literature (Bojsen-Møller and Magnusson, 2015; Edama et al., 2014; van Gils et al., 1996; White, 1943).
Figure 3.
Illustration of the subtendons defined in the finite element model. A: Proximal view of model displays subtendons associated with the soleus, medial gastrocnemius, and lateral gastrocnemius muscles. B: distal view of the free tendon displays the location of the three subtendons at this level, which are rotated relative to the locations in A. C: Longitudinal views of the tendon reveal the twisted orientation of the subtendons. D: Passive and active muscle forces were modeled as stiffness and pressure boundary conditions, respectively. Passive simulations consisted of stiffness boundaries only while eccentric simulations consisted of both stiffness and pressure boundaries.
The morphology of the Achilles subtendons in the calcaneal region is not well defined in the literature; therefore, in the present model, the cross-sectional morphology at the end of the free tendon was maintained through the tendon’s insertion on the calcaneus. This morphology is consistent with sagittal imaging studies depicting collagen fibers with a longitudinal orientation in the insertional region (Milz et al., 2002) as well as photographs of the posterior collagen fiber directions of the Achilles tendon (Dalmau-Pastor et al., 2014). The model geometry was transferred to AMPSolid (AMPS Technologies, Pittsburgh, PA) and meshed into tetrahedral solid elements.
Constitutive model
Each subtendon was modeled as an incompressible Neo-Hookean solid with strain energy density function, W, given by Equation 1:
| (Equation 1) |
where C is a material constant and I1 is the first invariant of the right Cauchy-Green deformation tensor. The first invariant, I1, is defined as the sum of squares of the principal stretches, λ1 λ2 & λ3, according to Equation 2:
| (Equation 2) |
The material parameter C was set to a value of 45 MPa for all three subtendons. This parameter corresponds to a Young’s modulus of approximately 270 MPa which is consistent with previously reported Young’s moduli for the human Achilles tendon in vivo (Kubo et al., 2002).
Model boundary conditions
A frictionless contact interface was defined between the three subtendons. This interface was chosen to simulate subtendon sliding, a property demonstrated in fascicles of healthy energy-storing equine tendons (Thorpe et al., 2013) that may be relevant for human Achilles subtendons. While the mechanics of the interfascicular matrix have been explored previously (Thorpe et al., 2015), the mechanics of the human Achilles intersubtendon matrix are not known. A frictionless boundary condition was used here to be computationally simple; in conjunction with a nonsliding boundary condition (see Variation of model morphology section below) these conditions represent the extreme examples of the sliding that may occur between Achilles subtendons. The proximal aspect of the Achilles was constrained to only move in the proximal-distal direction. The anterior-distal aspect of the calcaneal insertion was assigned to rotate 25° to simulate the rotation of the ankle during the dorsiflexion portion of the loading conditions described by Slane and Thelen (2014). The center of rotation was defined as the center of the line joining the subject’s medial and lateral malleoli determined from MR images. The axis of rotation was perpendicular to the sagittal imaging plane and passed through the center of rotation.
To simulate the forces applied to the tendon by the three triceps surae muscles during both passive and active eccentric ankle dorsiflexion, nodal stiffness and pressure boundaries were applied to the proximal surface of each subtendon (Fig. 3D). Linear nodal stiffness boundary conditions were used to simulate the passive forces in muscle, which increase with increasing stretch (Herzog et al., 1991). The stiffness parameters were tuned based on comparison with in vivo data of passive dorsiflexion, which is described below. Linearly ramped pressure boundaries were used to simulate the active component of muscle forces on the ascending limb of the muscle force-length curve (Maganaris, 2003); for eccentric simulations, both passive and active properties of muscle were modeled.
Comparison with in vivo data and muscle force determination
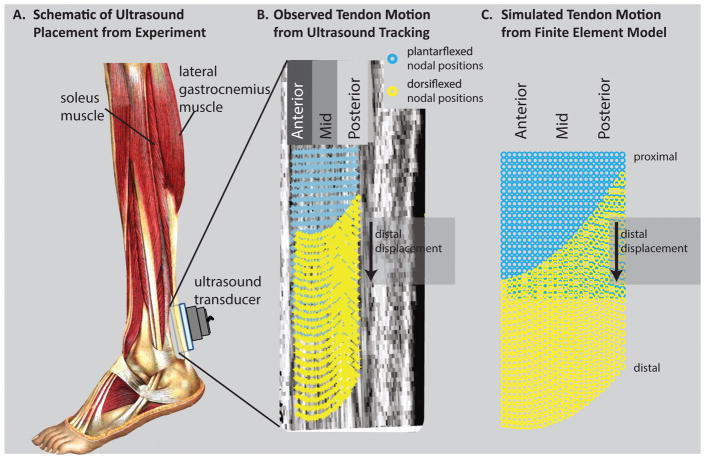
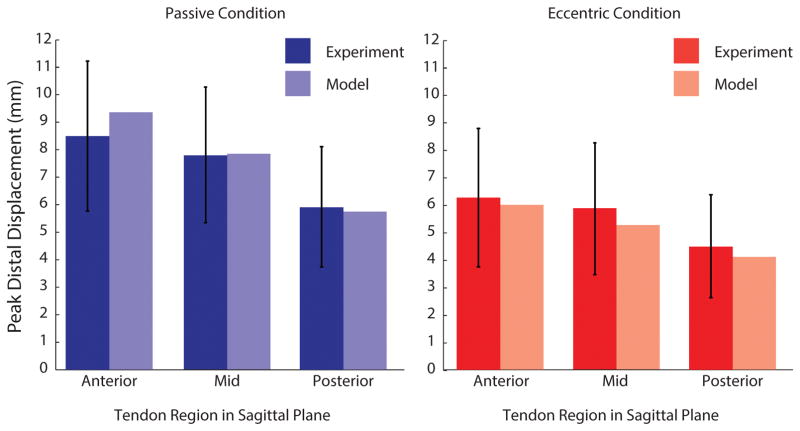
To compare the present modeling results with the tissue displacements from Slane and Thelen (2014), we defined a region of interest within the model that was consistent with the region of interest from their imaging study (Fig. 4). We projected 3D nodal displacements from the region of interest into the sagittal plane to obtain sagittal displacement profiles. Sagittal displacement profiles were smoothed with a quadratic surface fit as was done to ultrasound data from Slane and Thelen (2014). Nodes were binned into Anterior, Middle, and Posterior regions of the tendon (Fig. 4B and 4C) and displacements were averaged within these bins.
Figure 4.
Qualitative comparison of displacement profiles between experiment and finite element model. A: In Slane and Thelen (2014), the Achilles tendon was imaged with ultrasound while subjects went through cyclic ankle dorsiflexion (adapted from Sobotta (1909)). B: With dorsiflexion, ultrasound imaging reveals nonuniform displacements—anterior tissue displaced more than posterior tissue. (adapted from Slane and Thelen (2014)) C: In the FE model, nodal displacements in the anterior region were greater than those in the posterior region.
To approximate the muscle forces relevant during passive and eccentric ankle dorsiflexion, we first tuned the stiffness coefficients corresponding to the proximal boundary conditions according to the displacement profiles from passive trials reported in (Slane and Thelen, 2014). The stiffness boundary conditions in the passive model were varied until the nodal displacements in the Anterior, Middle, and Posterior regions were within one standard deviation of experimental values. After stiffness boundaries had been set, we tuned pressure boundaries using data from eccentric trials reported in (Slane and Thelen, 2014) following the same protocol. Stiffness coefficients and pressure magnitudes for the LG subtendon were each set as one-half the coefficients and magnitudes used for the MG subtendon. This proportion reflects the relative PCSAs of these two muscles (Handsfield et al., 2014). In addition to the passive and eccentric tuned models, we ran an additional simulation with no force boundary conditions on the subtendons. These no muscle force models were used in order to observe the isolated effects of ankle kinematics on Achilles displacements, in the absence of any muscle force contribution.
Variation of model morphology
In order to explore the contributions of different geometric and functional features of the Achilles tendon, we created additional models that systematically eliminated various features. The first model variation—no insertion—was identical to the full model in the free tendon region, but did not include the calcaneal region of the tendon. The second model variation—no insertion no twist— similarly did not include the calcaneal region, but also lacked any twisting of the subtendons. The third model variation—no sliding— included the full tendon morphology but did not allow sliding between subtendons. External model geometry and all proximal and distal boundary conditions were maintained across the model variations.
RESULTS
Muscle force determination and comparison with experimental results
The model generated sagittal plane displacement profiles similar to those reported in Slane and Thelen (2014), and reproduced the result (Fig. 1) that distal displacements were greater in the anterior region of the free tendon than in the middle and posterior regions (Fig. 4)(Arndt et al., 2012; Franz et al., 2015; Slane and Thelen, 2015, 2014). Displacement magnitudes in the simulations were within one-third of one standard deviation of the mean from experimental ultrasound data (Fig. 5) and the profile of the displacements shows the same qualitative trend as the data in Slane and Thelen for both passive and eccentric cases. The maximum simulated muscle forces are given in Table 1. Passive muscle forces in the soleus represented 34% of the total passive forces in the triceps surae, passive forces in the medial gastrocnemius represented 39% of the total, and passive forces in the lateral gastrocnemius represented 27% of the total (Table 1). In eccentric simulations, forces in the soleus represented 63% of the total triceps surae force, medial gastrocnemius force represented 23% of the total, and lateral gastrocnemius force represented 14% of the total (Table 1).
Figure 5.
Quantitative comparison of regional displacements between experiment and finite element model. The peak distal displacements occurring in the anterior, middle, and posterior regions are shown for ultrasound experiments (Slane and Thelen, 2014) and for the present finite element model. For both passive and eccentric cases, finite element simulations predicted regional displacements within one standard deviation of experimental results.
Table 1.
Maximum muscle forces on Achilles subtendon in FE model
| Condition | Maximum Forces During Simulation (Passive Forces) [% of total] | ||
|---|---|---|---|
| Soleus Subtendon | MG Subtendon | LG Subtendon | |
| Passive | (189 N) [34%] | (217 N) [39%] | (149 N) [27%] |
| Eccentric | 1157 N (111 N) [63%] | 423 N (132 N) [23%] | 263 N (118 N) [14%] |
Maximum muscle forces in the passive and eccentric models are tabulated. Total force in each subtendon are given in Newtons, passive force in parentheses; percent of total Achilles force is given in brackets.
Strains, displacements, and forces in tendon
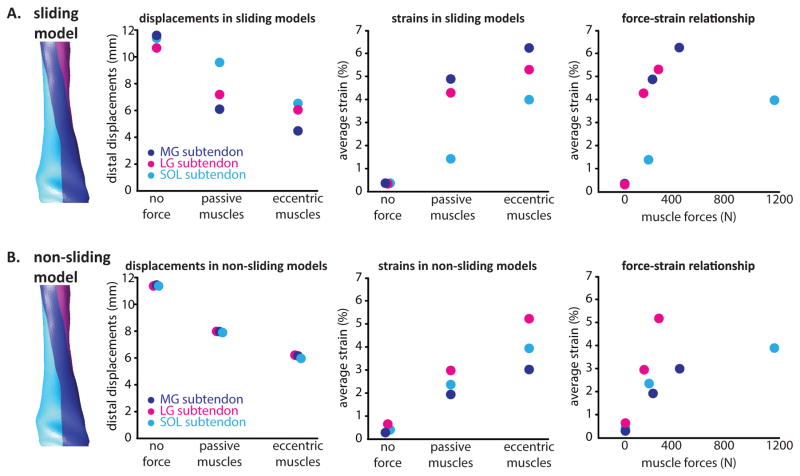
Simulation of increased muscle force conditions resulted in an overall decrease in tissue displacements and increase in average strains in the free Achilles tendon (Fig. 6). In spite of a uniform stress-strain relationship in all subtendons, the force-strain relationships differed across subtendons and between sliding and no sliding models (Fig. 6) as a result of differences in geometry between the subtendons and differences in overall loading related to sliding vs. no sliding models. Displacement nonuniformity between subtendons was greatest for the passive force sliding models (Fig. 6A). For both the passive and eccentric simulations in the sliding model, strains were highest in the MG subtendon followed by the LG subtendon and SOL subtendon (Fig. 6A). Non-zero strains were observed in the no muscle force condition as a result of boundary conditions such as the constrained path of the proximal free tendon and contact between subtendons, which caused small strains in the subtendons. Differential strains were highest between the SOL and MG subtendons in the passive muscle force condition. Strains in the SOL subtendon were consistently the lowest, even when simulated soleus muscle forces were greater than either gastrocnemius muscle (Fig. 6A). For the non-sliding models at all force conditions, displacement nonuniformity was negligible (Fig. 6B).
Figure 6.
Relationships between simulated muscle forces, tissue displacements, and strains in FE models. A: In the sliding model, distal displacements in the proximal free tendon decreased with increasing muscle forces and equivalent strains increased with muscle force. Force-strain relationships were similar between the gastrocnemius subtendons but differed in the soleus subtendon. B: In the absence of sliding subtendons, differential displacements were negligible and force-strain relationships were altered for all three subtendons.
Displacement nonuniformity: contribution of muscle forces, insertion, twist, and sliding
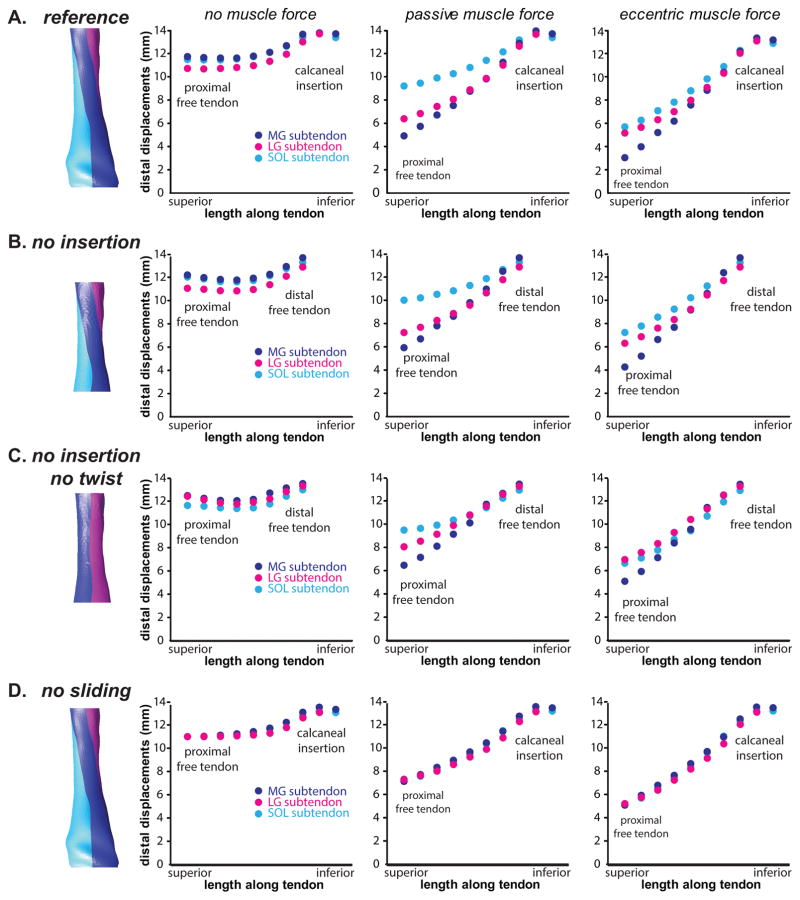
Displacement nonuniformity in the Achilles tendon varied throughout the length of the tendon, was greatest near the proximal aspect of the free tendon, and diminished toward the calcaneal insertion (Fig. 7A). When no forces were applied to the subtendons, displacement nonuniformity was negligible. In the sliding models, displacement nonuniformity between subtendons was non-negligible when any muscle forces (passive or eccentric) were applied, and were the greatest in the passive force condition (Fig. 7A). In the absence of the retrocalcaneal tendon insertion (i.e. free tendon only), displacements increased throughout the length of the free tendon but displacement nonuniformity between the subtendons did not differ greatly compared to the model containing an insertion region (Fig. 7). In the absence of both the retrocalcaneal tendon insertion and the twisting subtendons, displacements decreased in the SOL subtendon but increased in the LG and MG subtendons, resulting in an overall decrease in displacement nonuniformity (Fig. 7). For all of the sliding models, variations in the force boundary conditions had a greater effect on displacement nonuniformity than any of the morphological variations. Displacement nonuniformity was negligible through the length of the tendon for the non-sliding models, especially between MG and SOL subtendons (Fig. 7D).
Figure 7.
Displacement profiles across morphological variations of the Achilles tendon. A:The reference Achilles model includes twisted subtendons, inter-subtendon sliding, and a retrocalcaneal insertion. B: Without this insertion, the model displays nonuniform displacements. C: Without twisted subtendons, the differential displacements in the free tendon are slightly reduced. D: In the absence of sliding, differential displacements between subtendons are negligible.
DISCUSSION
Nonuniform displacements within the tendon resulted primarily from different applied muscle forces between subtendons. The highest nonuniformity occurred during passive muscle force simulations when the MG muscle contributed the most (39%) to total Achilles tendon force, followed by the soleus (34%) and the LG muscle (27%). In the eccentric condition, displacements were more uniform and the soleus contributed the most force (63%), followed by the MG (23%) and the LG (14%). Thus, differences in relative force contribution from the muscles may explain differences between passive and eccentric trials. There are known architectural and functional differences between the soleus and gastrocnemius muscles which could explain this phenomenon (Arndt et al., 1998; Cronin et al., 2013a). The higher passive force contribution from the medial gastrocnemius compared to the soleus implies that these muscles may differ in passive force curves or slack lengths relative to ankle position. In the present model, the stiffness boundary condition used to simulate medial gastrocnemius passive force was nearly two-and-a-half times the stiffness that simulated soleus passive force. The hypothesized greater passive stiffness in the medial gastrocnemius subtendon may promote higher stretching and elastic storage of energy in the posterior aspect of the Achilles tendon, a potentiality which warrants further study.
Elimination of intra-tendon sliding altered displacement nonuniformity more than variations in muscle force or tendon morphology. Sliding was a necessary condition in order to recapitulate the displacement profiles from the literature. Elimination of sliding severely reduced displacement nonuniformity in the tendon. In contrast to the nonsliding models, models with no retrocalcaneal insertion and no subtendon twist diminished displacement nonuniformity only slightly. This suggests that sliding is a much more important contributor to nonuniformity than twisting or insertion location. Taken together, sliding and non-zero muscle forces were both necessary to induce noticeable nonuniform displacements within the tendon model. Interestingly, sliding appears to be a phenomenon present in healthy young, but is diminished in older, horse fascicles (Thorpe et al., 2013) and human tendons (Slane and Thelen, 2015). In the present work, we lacked values or estimates of the material stiffness of the matrix between Achilles subtendons; therefore, we used frictionless sliding and nonsliding as bounds for the sliding that likely occurs between subtendons. In a previous work, Thorpe et al. investigated the mechanics of the matrix between tendon fascicles (Thorpe et al., 2015); a similar study of the matrix between human Achilles subtendons would enable a deeper understanding of the behavior of these structures.
In this study, we estimated triceps surae muscle forces by tuning force boundary condition magnitudes to displacement profiles observed in (Slane and Thelen, 2014). Peak soleus forces simulated in this study are on the order of 200N passive and 1000N active. Peak gastrocnemius forces simulated in this study are about 350N passive and 450N active. Slane & Thelen (2014) reported net eccentric plantarflexion moments in excess of 30Nm, implying plantarflexion forces around 600N. The forces in the current model exceeded these net force estimates from Slane & Thelen (2014) but were physiologically reasonable and consistent with several in vivo literature reports (Arndt et al., 1998; Finni and Komi, 1998; Mian et al., 2007; Rubenson et al., 2012). It should be noted that our boundary conditions ignored any resistive forces from fluid and connective tissue within the ankle.
Subject-specific material properties were not available in this study. The material parameters chosen to model subtendons were based on literature reports of in vivo Achilles tendon material properties (Kubo et al., 2002). The Neo-Hookean model used was within the range of tendon material response previously observed (Kubo et al., 2002; Lichtwark and Wilson, 2005; Stenroth et al., 2012). Our material model was less stiff than the average for young women observed by Stenroth et al. (2012), but it was within the broad range of previously reported tendon material responses (Kubo et al., 2002; Lichtwark and Wilson, 2005; Maganaris and Paul, 2002; Stenroth et al., 2012; Zajac, 1989). Because we tuned our forces to observed displacements, our result of high subtendon stretch, especially in the MG subtendon, is not sensitive to the specific material stiffness chosen in this study. Future incorporation of a transversely isotropic (Weiss et al., 1996) or biphasic (Yin and Elliott, 2004) material model may be used to model Achilles behavior in finer detail. We used an assumption that the ankle axis of rotation was perpendicular to the sagittal plane, which simplifies the kinematics of ankle motion that have been demonstrated previously (Lundberg et al., 1989). Incorporation of more sophisticated ankle kinematics, potentially also including inversion and eversion, may reveal more specific subtendon deformation patterns, especially increased displacements in the MG subtendon. In this study, we defined a region within the Achilles tendon model to be consistent with the region that was imaged using ultrasound in Slane and Thelen (2014). In light of the 3D structure of the Achilles tendon, it is likely that variations in ultrasound probe placement on the posterior ankle and morphological variations of subtendons across subjects may alter the tendon deformation patterns observed with ultrasound. In previous works, nonuniform deformations have been consistently observed (Arndt et al., 2012; Franz et al., 2015; Slane and Thelen, 2014) in spite of potential inter-subject variations and probe placement variations, implying that these variations may not contribute much to variations in deformation. In the future, the 3D computational models presented here could be used to explore the effect of anatomical variation and probe placement variation on the observed deformation of the Achilles tendon.
We used UTE MRI and literature information about subtendon morphology to develop an image-based model of the Achilles tendon. The imaging sequence used here is a 3D radial UTE sequence that was tuned to promote high contrast between tendon, cortical bone, fat, bursa, and muscle. UTE sequences may be used to image tissues with short T2* times. The sequence used here worked well to distinguish the Achilles tendon from its neighboring structures. Finite element models of the Achilles tendon have been used previously to understand tendon loading (Shim et al., 2014) and the effects of surgery on the tendon (Von Forell and Bowden, 2014). This is the first work to our knowledge to use UTE MRI to inform Achilles model geometry. The UTE MR images did not have enough resolution to distinguish the separate Achilles subtendons, which necessitated our use of literature information to model these sub-structures. Future imaging and modeling approaches incorporating the meso- and micro-scale structures of tendon may reveal additional insights into the importance of these substructures.
This study may have implications to the aging tendon. Aging is reportedly related to a reduction in length of the retrocalcaneal insertion of the Achilles (Kim et al., 2011), possibly due to progressive ossification of the most distal regions of the insertion or calcaneal growth that alters the relative location of tendon insertion. Aging also may reduce intra-tendon sliding due to collagen cross-linking (Thorpe et al., 2013). Changes such as these would be expected to reduce displacement nonuniformity between subtendons. Age-related muscle weakening (Doherty, 2003) and changes to tendon stiffness (Narici et al., 2008; Stenroth et al., 2012) would also affect the degree of nonuniformity in subtendon displacements. Future work may suggest if and how subtendon sliding is related to tendon aging and may indicate if tendon health is related to the ability for sliding between subtendons.
The current work provides a foundation for how intra-tendon sliding, muscle forces, twisting subtendons, and insertional morphology may influence the extent of displacement nonuniformity within the Achilles tendon. Future modeling and experimental work are needed to further explore these and other morphological features of the tendon and to contextualize the mechanisms of differential muscle forces and intratendon sliding as contributors to nonuniform Achilles deformation.
Acknowledgments
We wish to acknowledge Kelley Virgilio for her assistance with this project. Funding was provided by NIH Grant R01AR056201, NSF CMMI grant #1235244, and NIH Grant F31AG043216.
Footnotes
Previous authors have used different terminology to describe the portions of the Achilles arising from the distinct muscular heads of the triceps surae. Here, we use the term “subtendon” for this structure. For a brief review and comparison of different terminologies used, see Handsfield et al. (2016).
CONFLICTS OF INTEREST
The authors have no conflicts of interest to disclose.
References
- Alexander RM. Energy-saving mechanisms in walking and running. J Exp Biol. 1991;160:55–69. doi: 10.1242/jeb.160.1.55. [DOI] [PubMed] [Google Scholar]
- Alexander RM, Bennet-Clark HC. Storage of elastic strain energy in muscle and other tissues. Nature. 1977;265:114–117. doi: 10.1038/265114a0. [DOI] [PubMed] [Google Scholar]
- Arndt A, Bengtsson AS, Peolsson M, Thorstensson A, Movin T. Non-uniform displacement within the Achilles tendon during passive ankle joint motion. Knee Surgery, Sport Traumatol Arthrosc. 2012;20:1868–1874. doi: 10.1007/s00167-011-1801-9. [DOI] [PubMed] [Google Scholar]
- Arndt AN, Kom PV, Briiggemann G, Lukkariniem J. Individual muscle contributions to the in vivo achilles tendon force. Clin Biomech. 1998;13:532–541. doi: 10.1016/s0268-0033(98)00032-1. [DOI] [PubMed] [Google Scholar]
- Bojsen-Møller J, Hansen P, Aagaard P, Svantesson U, Kjaer M, Magnusson SP. Differential displacement of the human soleus and medial gastrocnemius aponeuroses during isometric plantar flexor contractions in vivo. J Appl Physiol. 2004;97:1908–14. doi: 10.1152/japplphysiol.00084.2004. [DOI] [PubMed] [Google Scholar]
- Bojsen-Møller J, Magnusson SP. Heterogeneous Loading of the Human Achilles Tendon In Vivo. Exerc Sport Sci Rev. 2015;43:190–197. doi: 10.1249/JES.0000000000000062. [DOI] [PubMed] [Google Scholar]
- Cronin NJ, Avela J, Finni T, Peltonen J. Differences in contractile behaviour between the soleus and medial gastrocnemius muscles during human walking. J Exp Biol. 2013a;216:909–14. doi: 10.1242/jeb.078196. [DOI] [PubMed] [Google Scholar]
- Cronin NJ, Prilutsky BI, Lichtwark GA, Maas H. Does ankle joint power reflect type of muscle action of soleus and gastrocnemius during walking in cats and humans? J Biomech. 2013b;46:1383–1386. doi: 10.1016/j.jbiomech.2013.02.023. [DOI] [PubMed] [Google Scholar]
- Dalmau-Pastor M, Fargues-Polo B, Casanova-Martínez D, Vega J, Golanó P. Anatomy of the Triceps Surae: A Pictorial Essay. Foot Ankle Clin. 2014;19:603–635. doi: 10.1016/j.fcl.2014.08.002. [DOI] [PubMed] [Google Scholar]
- Doherty TJ. Invited review: Aging and sarcopenia. J Appl Physiol (Bethesda, Md 1985) 2003;95:1717–1727. doi: 10.1152/japplphysiol.00347.2003. [DOI] [PubMed] [Google Scholar]
- Edama M, Kubo M, Onishi H, Takabayashi T, Inai T, Yokoyama E, Hiroshi W, Satoshi N, Kageyama I. The twisted structure of the human Achilles tendon. Scand J Med Sci Sports. 2014:1–7. doi: 10.1111/sms.12342. [DOI] [PubMed] [Google Scholar]
- Finni T, Komi PV. Achilles tendon loading during walking: application of a novel optic fiber technique. Eur J Appl Physiol. 1998;77:289–291. doi: 10.1007/s004210050335. [DOI] [PubMed] [Google Scholar]
- Franz JR, Slane LC, Rasske K, Thelen DG. Non-uniform in vivo deformations of the human Achilles tendon during walking. Gait Posture. 2015;41:192–197. doi: 10.1016/j.gaitpost.2014.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giddings VL, Beaupré GS, Whalen RT, Carter DR. Calcaneal loading during walking and running. Med Sci Sports Exerc. 2000;32:627–634. doi: 10.1097/00005768-200003000-00012. [DOI] [PubMed] [Google Scholar]
- Griffiths RI. Shortening of Muscle Fiberes During Stretch of the Active Cat Medial Gastrocnemius Muscle: The Role of Tendon Compliance. J Physiol. 1991;436:219–236. doi: 10.1113/jphysiol.1991.sp018547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handsfield GG, Meyer CH, Hart JM, Abel MF, Blemker SS. Relationships of 35 lower limb muscles to height and body mass quantified using MRI. J Biomech. 2014;47:631–8. doi: 10.1016/j.jbiomech.2013.12.002. [DOI] [PubMed] [Google Scholar]
- Handsfield GG, Slane LC, Screen HRC. Nomenclature of the Tendon Hierarchy: An Overview of Inconsistent Terminology and a Proposed Size-Based Naming Scheme with Terminology for Multi-Muscle Tendons. J Biomech. 2016 doi: 10.1016/j.jbiomech.2016.06.028. [DOI] [PubMed] [Google Scholar]
- Herzog W, Read LJ, Ter Keurs HE. Experimental determination of force-length relations of intact human gastrocnemius muscles. Clin Biomech (Bristol, Avon) 1991;6:230–8. doi: 10.1016/0268-0033(91)90051-Q. [DOI] [PubMed] [Google Scholar]
- Ishikawa M, Komi PV, Grey MJ, Lepola V, Bruggemann GP. Muscle-tendon interaction and elastic energy usage in human walking. J Appl Physiol. 2005;99:603–8. doi: 10.1152/japplphysiol.00189.2005. [DOI] [PubMed] [Google Scholar]
- Järvinen TAH, Kannus P, Maffulli N, Khan KM. Achilles tendon disorders: Etiology and epidemiology. Foot Ankle Clin. 2005;10:255–266. doi: 10.1016/j.fcl.2005.01.013. [DOI] [PubMed] [Google Scholar]
- Kim PJ, Martin E, Ballehr L, Richey JM, Steinberg JS. Variability of insertion of the Achilles tendon on the calcaneus: an MRI study of younger subjects. J Foot Ankle Surg. 2011;50:41–3. doi: 10.1053/j.jfas.2010.10.007. [DOI] [PubMed] [Google Scholar]
- Kubo K, Kawakami Y, Kanehisa H, Fukunaga T. Measurement of viscoelastic properties of tendon structures in vivo. Scand J Med Sci Sport. 2002;12:3–8. doi: 10.1034/j.1600-0838.2002.120102.x. [DOI] [PubMed] [Google Scholar]
- Lichtwark Ga, Wilson aM. Interactions between the human gastrocnemius muscle and the Achilles tendon during incline, level and decline locomotion. J Exp Biol. 2006;209:4379–4388. doi: 10.1242/jeb.02434. [DOI] [PubMed] [Google Scholar]
- Lichtwark Ga, Wilson aM. In vivo mechanical properties of the human Achilles tendon during one-legged hopping. J Exp Biol. 2005;208:4715–25. doi: 10.1242/jeb.01950. [DOI] [PubMed] [Google Scholar]
- Lundberg A, Svensson OK, Nemeth G, Selvik G. The axis of rotation of the ankle joint. J Bone Jt Surg. 1989;71:94–99. doi: 10.1302/0301-620X.71B1.2915016. [DOI] [PubMed] [Google Scholar]
- Maganaris CN. Force-length characteristics of the in vivo human gastrocnemius muscle. Clin Anat. 2003;16:215–23. doi: 10.1002/ca.10064. [DOI] [PubMed] [Google Scholar]
- Maganaris CN, Paul JP. Tensile properties of the in vivo human gastrocnemius tendon. J Biomech. 2002;35:1639–1646. doi: 10.1016/S0021-9290(02)00240-3. [DOI] [PubMed] [Google Scholar]
- Mian OS, Thom JM, Ardigò LP, Minetti aE, Narici MV. Gastrocnemius muscle-tendon behaviour during walking in young and older adults. Acta Physiol (Oxf) 2007;189:57–65. doi: 10.1111/j.1748-1716.2006.01634.x. [DOI] [PubMed] [Google Scholar]
- Miller GW, Eames M, Snell J, Aubry JF. Ultrashort echo-time MRI versus CT for skull aberration correction in MR-guided transcranial focused ultrasound: In vitro comparison on human calvaria. Med Phys. 2015;42:2223–2233. doi: 10.1118/1.4916656. [DOI] [PubMed] [Google Scholar]
- Milz S, Rufai a, Buettner a, Putz R, Ralphs JR, Benjamin M. Three-dimensional reconstructions of the Achilles tendon insertion in man. J Anat. 2002;200:145–152. doi: 10.1046/j.0021-8782.2001.00016.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narici MV, Maffulli N, Maganaris CN. Ageing of human muscles and tendons. Disabil Rehabil. 2008;30:1548–54. doi: 10.1080/09638280701831058. [DOI] [PubMed] [Google Scholar]
- Roberts TJ. The integrated function of muscles and tendons during locomotion. Comp Biochem Physiol. 2002;133:1087–1099. doi: 10.1016/s1095-6433(02)00244-1. [DOI] [PubMed] [Google Scholar]
- Rosset A, Spadola L, Ratib O. OsiriX: an open-source software for navigating in multidimensional DICOM images. J Digit Imaging. 2004;17:205–16. doi: 10.1007/s10278-004-1014-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubenson J, Pires NJ, Loi HO, Pinniger GJ, Shannon DG. On the ascent: the soleus operating length is conserved to the ascending limb of the force-length curve across gait mechanics in humans. J Exp Biol. 2012;215:3539–51. doi: 10.1242/jeb.070466. [DOI] [PubMed] [Google Scholar]
- Sarrafian SK. Anatomy of the Foot and Ankle: Descriptive Topographic Functional. J.B. Lippincott Company; Philadelphia: 1993. Calcaneal (achilles) tendon; pp. 280–282. [Google Scholar]
- Sasaki K, Neptune RR. Muscle mechanical work and elastic energy utilization during walking and running near the preferred gait transition speed. Gait Posture. 2006;23:383–90. doi: 10.1016/j.gaitpost.2005.05.002. [DOI] [PubMed] [Google Scholar]
- Shim VB, Fernandez JW, Gamage PB, Regnery C, Smith DW, Gardiner BS, Lloyd DG, Besier TF. Subject-specific finite element analysis to characterize the influence of geometry and material properties in Achilles tendon rupture. J Biomech. 2014;47:3598–3604. doi: 10.1016/j.jbiomech.2014.10.001. [DOI] [PubMed] [Google Scholar]
- Slane LC, Thelen DG. Achilles tendon displacement patterns during passive stretch and eccentric loading are altered in middle-aged adults. Med Eng Phys. 2015;37:712–716. doi: 10.1016/j.medengphy.2015.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slane LC, Thelen DG. Non-uniform displacements within the Achilles tendon observed during passive and eccentric loading. J Biomech. 2014;47:2831–5. doi: 10.1016/j.jbiomech.2014.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobotta J. Atlas and Text-Book of Human Anatomy. W.B. Saunders and Co; Philadelphia: 1909. [Google Scholar]
- Stenroth L, Peltonen J, Cronin NJ, Sipilä S, Finni T. Age-related differences in Achilles tendon properties and triceps surae muscle architecture in vivo. J Appl Physiol. 2012;113:1537–44. doi: 10.1152/japplphysiol.00782.2012. [DOI] [PubMed] [Google Scholar]
- Szaro P, Witkowski G, Smigielski R, Krajewski P, Ciszek B. Fascicles of the adult human Achilles tendon - an anatomical study. Ann Anat. 2009;191:586–593. doi: 10.1016/j.aanat.2009.07.006. [DOI] [PubMed] [Google Scholar]
- Thorpe CT, Godinho MSC, Riley GP, Birch HL, Clegg PD, Screen HRC. The interfascicular matrix enables fascicle sliding and recovery in tendon, and behaves more elastically in energy storing tendons. J Mech Behav Biomed Mater. 2015;52:85–94. doi: 10.1016/j.jmbbm.2015.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorpe CT, Udeze CP, Birch HL, Clegg PD, Screen HR. Capacity for sliding between tendon fascicles decreases with ageing in injury prone equine tendons: a possible mechanism for age-related tendinopathy? Eur Cell Mater. 2013;25:48–60. doi: 10.22203/ecm.v025a04. [DOI] [PubMed] [Google Scholar]
- van Gils CC, Steed RH, Page JC. Torsion of the human Achilles tendon. J Foot Ankle Surg. 1996;35:41–48. doi: 10.1016/S1067-2516(96)80011-1. [DOI] [PubMed] [Google Scholar]
- Von Forell Ga, Bowden AE. A damage model for the percutaneous triple hemisection technique for tendo-achilles lengthening. J Biomech. 2014;47:3354–60. doi: 10.1016/j.jbiomech.2014.08.006. [DOI] [PubMed] [Google Scholar]
- Weiss JA, Maker BN, Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput Methods Appl Mech Eng. 1996;135:107–128. [Google Scholar]
- White JW. Torsion of the Achilles tendon: its surgical significance. Arch Surg. 1943;46:784. [Google Scholar]
- Yin L, Elliott DM. A biphasic and transversely isotropic mechanical model for tendon: Application to mouse tail fascicles in uniaxial tension. J Biomech. 2004;37:907–916. doi: 10.1016/j.jbiomech.2003.10.007. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17:359–411. [PubMed] [Google Scholar]