Design of Polyphosphate Inhibitors: a Molecular Dynamics Investigation on Polyethylene glycol-linked Cationic Binding Groups

Abstract

Inorganic polyphosphate (polyP) released by human platelets has recently been shown to activate blood clotting and identified as a potential target for the development of novel antithrombotics. Recent studies have shown that polymers with cationic binding groups (CBGs) inhibit polyP and attenuate thrombosis. However, a good molecular-level understanding of the binding mechanism is lacking for further drug development. While molecular dynamics (MD) simulation can provide molecule-level information, the time scale required to simulate these large biomacromolecules makes classical MD simulation impractical. To overcome this challenge, we employed metadynamics simulations with both all-atom and coarse-grained force fields. The force field parameters for polyethylene glycol (PEG) conjugated CBGs and polyP were developed to carry out coarse-grained MD simulations, which enabled simulations of these large biomacromolecules in a reasonable time scale. We found that the length of the PEG tail does not impact the interaction between the (PEG)_n-CBG and polyP. As expected, increasing the number of the charged tertiary amine groups in the head group strengthens its binding to polyP. Our simulation shows that (PEG)_n-CBG initially form aggregates, mostly with the PEG in the core and the hydrophilic CBG groups pointing toward water, then the aggregates approach the polyP and sandwich the polyP to form a complex. We found that the binding of (PEG)_n-CBG remains intact against various lengths of polyP. Binding thermodynamics for two of the (PEG)_n-CBG/polyP systems simulated were measured by isothermal titration calorimetry to confirm the key finding of the simulations that the length PEG tail does not influence ligand binding to polyP.

Graphical Abstract

Introduction

Thrombosis, the formation of clots within the blood vessels, blocks blood flow and can cause serious health complications. It can be fatal if clot forms within or to a crucial part of the circulatory system, such as the heart, brain or the lungs.¹ Recently it has been identified that highly-anionic polyphosphates (polyP), ranging from a few to hundreds of orthophosphate units (Figure 1a), activate blood coagulation via multiple pathways^2–6. The process is not fully understood, but it has been proposed that polyP may accelerate the activation of factor V by factor XIa⁷, sensitize resistive fibrin clot structures to fibrinolysis⁸, promote activation of factor XI by thrombin⁹, and trigger the activation of the contact pathway of blood clotting^{3, 10}. Therefore, polyP has been proposed as a therapeutic target to inhibit thrombosis.

Figure 1.

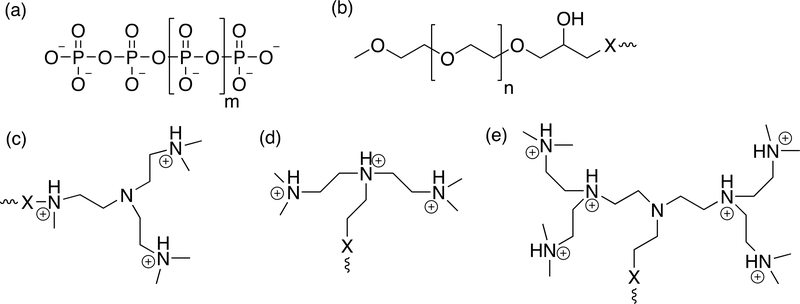
The molecular structure of polyP (a), PEG-based chain (b), and different CBGs: R₁ (c), R₂ (d), and R₃ (e). ‘X’ denotes the attachment location of PEG-based chain and the head group in (c), (d), and (e).

Electrostatic attraction between cationic macromolecules and negatively-charged polyP has been used to design antithrombotic agents that counteract the prothrombotic activity of polyP. Two cationic polymers, polyethylenimine (PEI) and polyamidoamine (PAMAM), have been investigated as inhibitors of polyP^11–12 Previous studies have shown that these two molecules bind to negatively-charged DNA and form compact complexes.^13–14 Both PEI and PAMAM bind to polyP with high affinity and consequently attenuate blood clotting.^11–12 Despite the effectiveness of these polycations, a major limitation is that they are not biocompatible. The PEI and PAMAM carry a large number of unshielded positive charges at the physiological pH as a result of the protonation of the amine groups. An undesirable effect of such a highly-charged state is that these polymers also bind to other proteins and cell membrane, leading to toxicity.^15–17 Recently a new class of dendritic polymers has been synthesized to address the challenges associated with introducing unshielded polycations into the vasculature¹⁸. These molecules are comprised of a hyperbranched polyglycerol (HPG) core displaying a chosen number of cationic ligands, with a soft brush of PEG chains then presented on the functionalized HPG surface to inhibit the interaction of the charged ligands with non-target anionic species. We have shown one molecule based on this design that displays a tertiary amine as the cationic ligand, called Universal Heparin Reversal Agent (UHRA), binds all clinically relevant forms of heparin tightly and specifically to completely neutralize heparin’s anticoagulant activity. The HPG core, including the specific chemistry and density of ligands within it, provides for that neutralization activity, while the protective PEG layer provides excellent biocompatibility and further enhances selectivity.^19–21 The basic chemistry used to synthesize these molecules is highly flexible, offering the ability to change molecule size, ligand type and density, and PEG length and grafting density. While the cationic ligands, with their spacing and the properties of the PEG brush layer used within UHRA, make it highly effective in binding and neutralizing the polyanion heparin²¹, they are not designed to specifically bind polyP, as both the rigidity and charge spacing of the polyP polyanion differ from those of heparin. Changes to both the ligand used and the grafted PEG chain length employed are required to strengthen the binding and specificity to polyP. Here, molecular dynamics (MD) are used to establish a molecular-level understanding of the binding mechanism and its sensitivity to the cationic binding group (CBG) structure and PEG chain length within linear model compounds comprised of a candidate CBG (Figure 1c-e) and PEG length (Figure 1b). The model compounds selected are intended to show how CBG structure, charge density, and PEG length affect polyP binding at the molecular level.

Molecular dynamics (MD) simulation, which has been increasingly used to assist drug discovery during the past several years^22–24, has significantly increased the pace of drug development by providing atomic-level information and high-throughput initial screening. A great challenge in carrying out MD simulations for large pharmaceutical molecules is the limited time scale accessible by current computer capacity. Limited simulation time prevents complete sampling of the conformational phase space, usually because a system’s metastable states are separated by high energy barriers. Overcoming energy-barriers larger than the thermal energy rarely happens in a time period of nanosecond or even microsecond. To overcome the insufficient sampling of the phase space, several enhanced sampling methods have been applied.^25–29 In these methods, one or a few relevant collective variables (CVs), describing the system in reduced dimensions, are biased, encouraging exploration of large regions of the phase space.^26–29 Among the enhanced sampling methods, metadynamics²⁸ (MetaD) and its variant forms^30–32 have been successfully applied to study the mechanism of drug binding to bio-macromolecules.³³ In this study, the parallel tempering metadynamics³¹ (PTMetaD) is employed to study the interaction between the (PEG)_n-R_i and the polyP. PTMetaD takes advantages of the enhanced sampling at different temperatures in accord with the replica exchange molecular dynamics²⁷ (REMD) while an optimal number of CVs are actively biased by implementing the well-tempered MetaD³⁰ during the simulation. Hence, the choice of CVs, which is a common difficulty, associated with the MetaD, no longer affects the final results. To increase the overall efficiency, PTMetaD is sometimes employed in the well-tempered ensemble^34–35 (WTE), where the energy overlap and the exchange acceptance probability are increased by enlarging the potential energy fluctuations through using the potential energy as a system CV. This study implements PTMetaD-WTE to expedite the transition of the binding between polyP and (PEG)_n-R_i from one metastable state to another.

Besides the enhanced sampling methods, another way to accelerate the MD simulation is to exploit coarse-grained (CG) MD simulations, in which lumping groups of atoms into several CG beads reduces the number of degrees of freedom. Subsequently, applying softer potentials and larger time steps lifts the time scale limitation and extends the simulation to a larger length scale. For these reasons, CG-MD simulation has become a necessary tool to study many large biomolecular systems.^36–38 The MARTINI force field³⁹ is one of the most well-known CG force fields, with which a variety of biomolecules, such as peptides/proteins^40–42, lipids^43–46, carbohydrates^47–48, and polymers^49–52, have been parameterized to study a wide range of applications.³⁹ Based on the MARTINI force field³⁹, every three or four heavy atoms along with their H atoms are mapped to CG beads. Then, the beads in terms of the chemical nature are categorized into four major types of interaction sites: polar, non-polar, apolar, and charged. To represent an accurate chemical nature of the underlying atomic structure, each particle type is divided into subtypes according to their hydrogen-bonding capability and degree of polarity. To the best of our knowledge, neither polyP nor (PEG)_n-R_i has been parameterized in accord with the MARTINI force field. In this study, we will develop the required parameters to study the interaction between (PEG)_n-R_i and polyP.

In this paper, we use MD simulations to find the possible routes of improving the design of PEG-CBGs for polyP inhibition. The effects of the PEG chain length, the charge densities of the CBG, and the polyP chain length are investigated to obtain a PEG-CBG molecule that could serve as the basic repeat structure within a dendritic hyperbranched polyglycerol that specifically binds polyP to inhibit its pro-coagulant activity. We found that within the simple model compounds the PEG length did not impact on the interaction between the PEG-CBG and polyP, suggesting that while PEG presented as a soft brush on the surface of a functionalized HPG nanoparticle (e.g. UHRA) can influence binding, a PEG chain simply appended onto the end of a polycationic ligand does not. However, increasing the charge density on the CBGs strengthens the PEG-CBG avidity of binding to polyP, indicating that the coulombic interaction is the main driving force for complexation with polyP. Finally, we found that the binding of PEG-CBGs to polyP was not affected by the chain length of the polyP over the range of 28 to 133 phosphate monomers.

Materials and Methods

All-atom MD simulations.

Studies on the interaction between (PEG)_n-R_i and polyP in aqueous solutions with NaCl concentration of 0.1 M were carried out using the GROMACS-5.1.4 software package^53–54. The force field parameters describing the behaviors of PolyP, (PEG)_n-R_i, and NaCl were originated from the Generalized Amber force field (GAFF)⁵⁵. All bonded and non-bonded interaction parameterizations for (PEG)_n-R_i and polyP except the partial charges were carried out using the ACPYPE⁵⁶. To assign the partial charges for the polyP and (PEG)_n-R_i atoms, quantum mechanical calculations with the Hartree-Fock (HF) method using the 6–31G(d) basis set were used to obtain the optimized geometry and energy. All required calculations were done using the Gaussian 09 program⁵⁷. The restrained electrostatic potential (RESP)⁵⁸ approach was used to assign the electrostatic point charges for the polyP and (PEG)_n-R_i using antechamber-14⁵⁹. The obtained partial charges are presented in Table S1–5 in the Supporting Information. The TIP3P⁶⁰ model was used to describe the behaviors of water molecules. The details of the studied systems are shown in Table 1. In the all-atom MD simulations, we studied the interaction between one polyP with 28 phosphate monomers and the corresponding number of (PEG)_n-R_i, which satisfies the total charge ratio of 1:1. To set up the initial configuration, the (PEG)_n-R_i along with the polyP were randomly placed into the simulation box. Before starting the MD simulations, 10000 steps of the steep-descent energy minimization were performed to correct the position of each atom.

Table 1.

The configurations of different (PEG)_n-R_i and polyP simulations.

System	Ligand	NPEGa	Ndrugb	Qdrugc	NNaCld	Nwatere	Box size (nm3)
I	R1	24	10	+3	21	11000	7 × 7 × 7
II	R1	12	10	+3	11	6000	4.5 × 6 × 7
III	R1	8	10	+3	11	6000	4.5 × 6 × 7
IV	R2	12	10	+3	11	6000	4.5 × 6 × 7
V	R3	12	5	+6	11	6000	4.5 × 6 × 7

^a)the total length of PEG-based chain

^b)number of (PEG)_n-R in the simulations

^c)the total charge for each molecule of (PEG)_n-R_i

^d)the number NaCl corresponding to 0.1 M

^e)the approximate number of water molecules in the simulation box

After setting up the initial configuration, a 2-ns MD simulation in the canonical ensemble (NVT) was performed while the positions of the heavy atoms in polyP and (PEG)_n-R_i were fixed to relax the water molecules. Then, a 10-ns MD simulation in the NVT ensemble without any position restraints was performed to equilibrate the system. The temperature of the polyP/(PEG)_n-R_i/ions and water molecules was maintained at 310 K separately using a stochastic global thermostat⁶¹ with a coupling constant of 0.1 ps. The OH-bonds of water were constrained by the SETTLE algorithm⁶². The rest of the bonds were constrained using the P-LINCS algorithm⁶³ with a LINCS order of 4. A simulation time step of 2 fs was used to integrate the equations of motion. The Lennard-Jones cutoff radius was 1.0 nm, where the interaction was smoothly shifted to 0 after 0.9 nm. Periodic boundary conditions were applied to all three directions. The particle mesh Ewald (PME) algorithm with a real cutoff radius of 1.0 nm and a grid spacing of 0.16 nm were used to calculate the long-range coulombic interactions.⁶⁴ To prepare the system for the PTMetaD-WTE simulations, a 4-ns MD simulation was performed isothermally and isobarically (NPT) at 1 bar with water compressibility of 4.48×10⁻⁵ bar⁻¹ to relax the box volume. The pressure was maintained at 1 bar using the Parrinello-Rahman barostat⁶⁵ with a pressure constant of 2.0 ps. Subsequently, by fixing the box volume, the PTMetaD-WTE simulations were carried out in the NVT ensemble.

To start the PTMetaD-WTE simulation, the last trajectory of the NPT simulation was chosen as the initial atomic coordinates of replicas at different temperatures, which were distributed exponentially⁶⁶ in the range of 310 ‒ 460 K to achieve an efficient exchange rate between the replicas. A 4-ns NVT-MD simulation was performed so that each replica reached the specified temperature with some relaxation of the polymer structures. Except system I where 12 identical replicas were used, 8 identical replicas were simulated for all other systems (shown in Table 1). Afterwards, a 15-ns WTE simulation was carried out^34–35, allowing us to achieve an optimum exchange rate of 30–35% between the replicas. The theoretical background of how the metadynamics simulation is implemented has been thoroughly reviewed elsewhere.⁶⁷

Here we briefly represent the parameters for our PTMetaD-WTE simulations. The bias factor of 50 was used for all systems except for system I, where a bias factor of 40 was used. The bias was deposited with a Gaussian width of 250 kJ/mol, an initial Gaussian amplitude of 4.18 kJ/mol, and a deposition period of 0.5 ps. The well-tempered metadynamics simulations were implemented using the PLUMED 2⁶⁸. In a typical PTMetaD-WTE simulation, the bias potential acts statically on the potential energy of different replicas, allowing biasing other CVs during the production run. However, the obtained static bias potential during the initial setup has to be smooth, or it may affect the final result. To overcome this problem, Sprenger and Pfaendtner have suggested a new protocol in which potential energy and CVs are biased on two separate bias potentials in the same time during the production run.⁶⁹ The bias potential from the initial step is carried over, and the frequency of Gaussian depositions is significantly reduced to one hill every 60 ps. The driving force of interaction between the polyP and the (PEG)_n-R_i is dominated by the electrostatic attraction, therefore the Debye-Huckel energy⁷⁰ between the polyP and the (PEG)_n-R_i (R) was actively biased during the production run using a NaCl ionic strength of 0.1 M with the following functional form:

$$DH=\frac{1}{k_{B}T{\epsilon }_w}\sum _{i\in polyP}\sum _{j\in R}{q}_i{q}_j\frac{e^{-\kappa \left|r_{ij}\right|}}{\left|r_{ij}\right|}$$ (1)

where k_B is the Boltzmann constant, ε_w is the water dielectric constant, q_i is the electrostatic point charge of atom i, r_ij is the distance from the center of mass of the coarse-grained site i on the polyP to the center of mass of the coarse-grained site j on the cationic headgroup (R), which are defined in Figure S6. $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\kappa $}\right.$ is the screening length, which is a function of the ionic strength.⁷⁰ In addition, the (PEG)_n-R_i binding stoichiometry (S) number around polyP is one of the main factors determining the efficiency of binding, and it was estimated by the following switching function:

$$S=\sum _{i\in polyP}\sum _{j\in R}\left(\frac{1-{\left(\frac{r_{ij}}{r_0}\right)}^n}{1-{\left(\frac{r_{ij}}{r_0}\right)}^m}\right)$$ (2)

where S varies between 0 to N_drug (shown in Table 1). For instance, when all head groups of (PEG)₁₂-R₁ are associated with the polyP, S is 10. n, m, and r₀ are the tuning parameters which were adjusted using 200 ns simulation run of system I in the NVT ensemble so that a smooth switching curve for each drug molecule was obtained. The parameters n, m, and r₀ are 12, 24, and 1.5 nm, respectively. The same values were used for all systems. r_ij is the distance from the center of mass of the CBG (R_i) to the center of mass of the polyP. The S number was monitored for all the systems shown in Table 1 except for the system I where it was biased alongside the Debye-Huckel energy. The bias factor for the all systems was 20. The Gaussian bias was deposited every 0.4 ps with an initial amplitude of 2 kJ/mol and a width of 0.2 kJ/mol. All PTMetaD-WTE simulations were performed for ~150 ns using the PLUMED 2⁶⁸. The change in the free energy is negligible for the last ~10 ns of the simulations, indicating the convergence was attained.

At the end of each simulation, the reweighting⁷¹ algorithm developed by Tiwary and Parrinello was used to find the unbiased probability distributions of any desirable properties, such as the binding free energies from the production runs. In the last step, we recorded the trajectory corresponding to the minimum free energy as a function of the Debye-Huckle (DH) energy for system I-V, and then equilibrated for 15 ns using classical MD simulation in the NPT ensemble with the details described in the above all-atom MD simulations section. We used the last 10 ns for the analysis presented in the current study.

CG-MD.

To study the binding of (PEG)₂₄-R₁ on polyP with various chain length, the force field parameters based on the MARTINI³⁹ CG force field were developed for both the polyP and (PEG)₂₄-R₁ (details given in the Supplementary Information). The details of the studied systems including 1 molecule of polyP are presented in Table 2. The MARTINI polarizable water model (PW)⁷² was used to describe the water behaviors. Before initiating the dynamics, the positions of the beads were corrected by performing the steep-descent energy minimization for 30,000 steps. Simulations were performed using the GROMACS 5.1.4 GPU computation algorithm^{53–54, 73} in the NPT ensemble. The input options implemented in the simulations were mainly adapted from the “martini_v2.x_new.mdp”⁷⁴ with slight modifications: the neighbor list was updated every 40 steps to compute with the GPUs more efficiently. The temperature of the polyP/(PEG)_n-R_i/ions and water was maintained at 310 K separately using the V-rescale thermostat with a temperature constant of 0.3 ps.³² The isotropic pressure coupling using the Parrinello-Rahman barostat⁶⁵ with a pressure constant of 12.0 ps was used to maintain the system pressure at 1 bar with a compressibility of 3.0×10⁻⁴ bar^-1. The Lennard-Jones interactions were truncated at a cutoff radius of 1.1 nm. However, to better conserve energy, the potentials were modified by the potential-shift-Verlet. Periodic boundary conditions were applied to all three directions. The electrostatic interactions were treated by the reaction-field approach with a cutoff radius of 1.1 nm. The MARTINI polarizable water bonds were constrained using the P-LINCS algorithm⁶³ with a LINCS order of 4. A 4-ns NPT simulation with a time step of 2 fs was executed to relax the particles in the system. Subsequently, a NPT simulation of 1 μs was carried out for each system in Table 2 with a time step of 8 fs to study the interaction between the polyP and the (PEG)₂₄-R₁.

Table 2.

Configurations of the (PEG)₂₄-R₁ and the numbers of polyP monomers used for CG-MD simulations.

System	npolyPa	Ndrugb	Qdrugc	QpolyPd	NNaCl	Nwatere	Box (nm3)
1	28	10	+30	−30	21	2600	7 × 7 × 7
2	61	21	+63	−63	60	7600	10 × 10 × 10
3	115	39	+117	−117	165	21000	14 × 14 × 14
4	133	45	+135	−135	203	26000	15 × 15 × 15

^anumber of polyP beads

^bnumber of (PEG)₂₄-R₁ in the simulations

^cthe total charge for each molecule of (PEG)₂₄-R₁

^dthe total charge of 1 polyP molecule with 28 phosphate monomers

^ethe approximate number of the MARTINI polarizable water in the simulation box

Synthesis and Characterization of (PEG)_n-R_i compounds.

All the materials were purchased from Sigma-Aldrich unless otherwise stated. All deuterated solvents (DMSO-d6, CDCl₃ and D₂O) were purchased from Cambridge Isotope Laboratories, Inc. The dry reactions were run under argon using Schlenk line techniques. ¹H and ¹³C NMR spectra were recorded on a Bruker Avance 300 MHz spectrometer at room temperature using CDCl₃, D₂O, or DMSO-d6 as solvent.

Synthesis of m-PEG epoxides (350 (n = 7), 550 (n = 12)).

Synthesis of m-PEG epoxide-350²¹ and 550²¹ was followed as reported in literature.²¹ See supporting information for NMR spectra (Figures S23 to S26).

m-PEG epoxide₅₅₀.

¹H NMR (300 MHz, CDCl₃): δ (ppm) 2.53 (dd, J = 2.74, 2.74 Hz, 1H, -CH₂OCH), 2.72 (t, J = 4.12 Hz, 1H, -CH₂OCH), 3.10 (m, 1H, -CH₂OCH), 3.31 (s, 1H, -OCH₃), 3.37 (dd, J = 5.94, 5.94 Hz, 1H, -CHCH₂O), 3.48−3.75 (m, 51H, -CH₂O). ¹³C NMR (75 MHz, CDCl₃): δ (ppm) 44.89 (CH₂OCH), 51.57 (-CH₂OCH, −CCH₂O), 58.21 (−OCH₃), 69.74, 71.16, 71.52 (-CH₂O−).

m-PEG epoxide₃₅₀.

¹H NMR (300 MHz, D₂O): δ (ppm) 2.80 (m, 1H, -CH₂OCH), 2.98 (m, 1H, CH₂OCH), 3.40 (br, 5H, CH₂OCH,-CH₂O, -OCH₃), 3.65−3.95 (m, 36H, CH₂O). ¹³C NMR (75 MHz, D₂O): δ (ppm) 44.89 (CH₂OCH), 51.56 (CH₂OCH), 58.18 (−CCH₂O and −OCH₃), 69.71, 71.13, 71.49 (CH₂O−).

Synthesis of model compounds II and III.

The synthesis was followed as reported in literature.¹⁸ Briefly, to the solution of m-PEG epoxide (500 mg, 0.824 mmol) in MeOH (60 mL), TREN was added (133 mg, 0.906 mmol) and refluxed for 20 h. The polymer was precipitated twice from DCM and cold pentane. The recovered precipitate was dissolved in water (25 mL), and an excess of formaldehyde (1.5 mL) and formic acid (0.75 mL) was added successively at 0° C. After refluxing (120 °C) the reaction mixture for 24 h, the solution pH was increased to pH = 11, and the sample was concentrated on a rotary evaporator. The precipitate was dialyzed for 8 h against water using a regenerated cellulose (RC) membrane (200–500 MWCO). The final polymer solution was freeze dried, and the functionalized polymer structure was confirmed by NMR spectroscopy (see Supporting Information).

Compound II. Yield-55%. ¹H NMR (D₂O, 300 MHz): δ ppm 2.14 (s, -NCH₃), 2.21 (s, -NCH₃), 2.41–2.55 (br, -NCH₂), 3.31 (s, -OCH₃), 3.35–4.00 (-OCH₂CH₂O), ¹³C NMR (DMSO, 75 MHz): 42.40 (-NCH₃), 44.38 (-NCH₂), 50.92 (-NCH₂), 51.34 (-NCH₂), 54.02 (-NCH₂), 55.14 (-NCH₂), 58.18 (-NCH₂), 59.57 (-OMe), 67.53 (-COH), 69.88 (-CH₂O-), 71.10 (-CH₂O-), 73.61 (-CH₂O-).

Compound III. Yield-40%. ¹H NMR (D₂O, 300 MHz): δ ppm 2.13 (s, -NCH₃), 2.20 (s, -NCH₃), 2.42–2.70 (-NCH₂), 3.30 (-OCH₃), 3.35–3.85 (-OCH₂CH₂O) ¹³C NMR (DMSO, 75 MHz): 42.40 (-NCH₃), 44.37 (-NCH₂), 50.84 (-NCH₂), 51.27 (-NCH₂), 53.99 (-NCH₂), 55.12 (-NCH₂), 58.17 (-NCH₂), 59.54 (-OMe), 67.47 (-COH), 69.63 (-CH₂O-), 71.05 (-CH₂O-), 73.56 (-CH₂O-).

Isothermal titration calorimetry (ITC).

All ITC experiments were performed in phosphate buffered saline (PBS) pH 7.40 (± 0.2). All solutions were degassed with stirring at room temperature before loading in the ITC cell. ITC experiments were performed using a MicroCal iTC200 (Malvern Instruments). Experiments were performed by injecting consecutive 2 μL aliquots of polymer solution (10 or 20 mM) into the ITC cell (volume = 200 μL) containing 100 μM (estimated polymer concentration based on average polymer size of 75 phosphates) polyphosphate (polyP₇₅). The heats of dilution from titrations of polymer solution into buffer only (without polyP₇₅) were subtracted from the heats obtained from titrations of polymer solution into polyP₇₅ solution to obtain net binding heats. All the experiments were carried out in duplicate. Raw ITC data of polymer binding to polyP₇₅ were analyzed with Origin software from Microcal, Inc. (Northampton, MA). A one-site binding model was used to fit the isotherms by a nonlinear least- squares analysis.

Results and Discussion

PEG length effect.

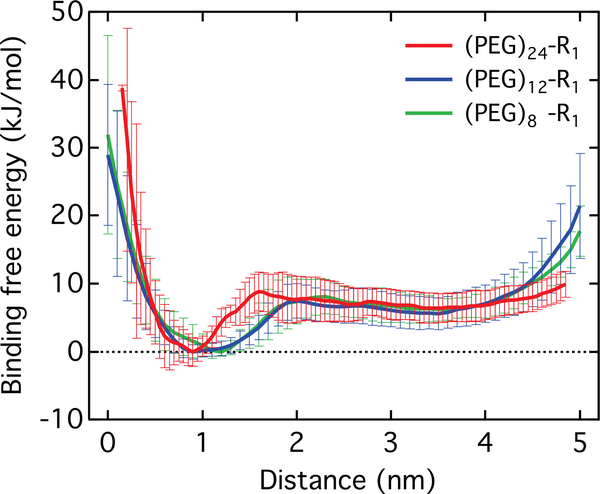
Our simulations show that the length of the PEG chain has little impact on the interaction between the (PEG)_n-R_i and the polyP. To investigate the effect of the PEG length on the binding efficacy, the binding free energy along with the S number (Eq. 2) were calculated with various PEG tail length. Figure 2 shows the binding free energy reaches its minimum at a distance of around 1 nm, measured from the center of mass of the polyP to the center of mass of the (PEG)_n-R₁ head group. There are no significant differences in the binding free energy for (PEG)_n-R₁ with n = 8 – 24. In all cases, the binding free energy between (PEG)_n-R₁ and polyP is ~ −7 kJ/mol.

Figure 2.

Computed binding free energy between (PEG)_n-R₁and polyp using the AA force field. The distance is defined between the center of mass of polyP and the center of mass of the (PEG)_n-R₁ head group. The binding free energy profile was obtained by calculating the averaged binding free energy of all (PEG)_n-CBG molecules in the system. The error bar indicates the standard deviation.

The binding free energy as a function of the S number was calculated from the PTMetaD-WTE simulations. The S number at the minimum free energy indicates how many (PEG)_n-R_i molecules participate in inhibiting the polyP. The results are summarized in System I - III in Table 3. The energy profiles of the (PEG)_n-R₁ with various PEG lengths are presented in Figure S8 in the Supporting Information. The S number for the (PEG)_n-R₁ remains in the range of 7 to 8 with n = 8, 12, and 24, suggesting that the PEG tail length has little effect on the value of S.

Table 3.

Extracted S number of (PEG)_n-R_i around polyP corresponding to the minimum free energy.

System	Candidates	S
I	(PEG)24-R1	~7 out of 10
II	(PEG)12-R1	~8 out of 10
III	(PEG)8-R1	~7 out of 10
IV	(PEG)12-R2	~8 out of 10
V	(PEG)12-R3	~4 out of 5

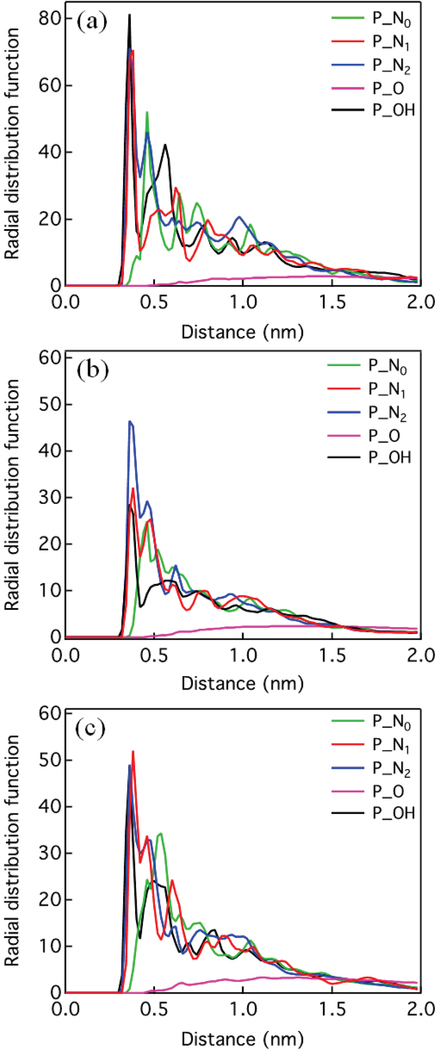
Further analysis of the simulation results confirms that the electrostatic attraction is the main driving force that inhibits the polyP activity. Figure 3a-c illustrates the radial distribution function between the P atoms of polyP and the unprotonated amine N atoms (N₀), the protonated connective amine N atoms (N₁), the protonated terminal amine N atoms (N₂), the O atoms of PEG-based chain, and the only O atom of hydroxide group (OH) in the PEG-based chain. It is clear that the electrostatic attraction induces a layered structure of the N₁ and N₂ atoms near the P atoms (red and blue curves in Figure 3a-3c) but N₀ does not interact directly with the polyP and mostly resides in the second layer.

Figure 3.

Radial distribution functions of the unprotonated amine N atoms (N₀), the protonated connective amine N atom (N₁), the protonated terminal amine N atom (N₂), O atoms of PEG-based chain, and the only O atom of hydroxyl group (OH) with respect to the P atoms of polyP. (a) (PEG)₈-R₁, (b) (PEG)₁₂-R₁, (c) (PEG)₂₄-R₁. The radial distribution functions were obtained from 10 ns of classical MD simulations in the NPT ensemble using the AA force field. P atoms were used as the reference point of the radial distribution function.

The hydrogen bonding between the H atoms on the protonated amine groups and the O atoms on the phosphate groups also promotes the binding interaction between the (PEG)_n-R₁ and the polyP. Interestingly, the polyP has no significant interaction with the O atoms in PEG-based chain as no layered structure of O atoms formed around the polyP (magenta curve), suggesting that this hydrophilic interaction is not strong enough to promote the association of the (PEG)_n-R₁ to the polyP. However, the hydroxyl O atom (OH) strongly interact with the polyP as they can be easily found in the first solvating shell of the P atoms. The strong interaction between the P atoms and the hydroxyl O atom of the (PEG)_n-R₁ mainly stems from the hydrogen bonding between hydroxyl H atoms and the O atoms of the phosphate groups in the polyP. Therefore, hydrogen bonding may facilitate thwarting of the prothrombotic activity of polyP.

Head group effect.

Our simulations indicate that increasing the number of the charged tertiary amine groups in the head group strengthens the binding to polyP. Figure 4 shows the binding free energies of (PEG)₁₂-R_i with three different head groups R₁, R₂, and R₃, as shown in Figure 1c, 1d, and 1e, respectively. Both R₁ and R₂ have a net charge of +3 but the unprotonated amine group is removed from R₂. Therefore, R₂ has slightly higher charge density than R₁. On the other hand, R₃ has a net charge of +6. Figure 4 shows that the binding free energy is almost the same (~ −7 kJ/mol) for (PEG)₁₂-R₁ and (PEG)₁₂-R₂. (PEG)₁₂-R₂ has a slightly greater binding affinity to the polyP because of its higher charge density in the head group. On the other hand, R₃ has a much higher affinity to the polyP (~−50 kJ/mol) because of its significantly higher net charge. The equilibrium S number presented in Table 3 shows that there is no meaningful difference between (PEG)₁₂-R₁ and (PEG)₁₂-R₂ as both S numbers are around 8. Although the ratio of the number of (PEG)₁₂-R_i participating in the polyP inhibition to the total number of (PEG)₁₂-R_i in the system is around 0.8, the higher binding affinity of (PEG)₁₂-R₃ results in a higher residence time and stability in the (PEG)_n-R₃/polyP complex; therefore it is more effective for inhibiting the polyP.

Figure 4.

Computed Binding free energy between the (PEG)₁₂-R_i and the polyp using AA force field. The distance is defined between the center of mass of the polyP and the center of mass of (PEG)₁₂-R_i head groups. The binding free energy profile was obtained by calculating the averaged binding free energy of (PEG)₁₂-R_i molecules in the system. Error bars indicate the standard deviation.

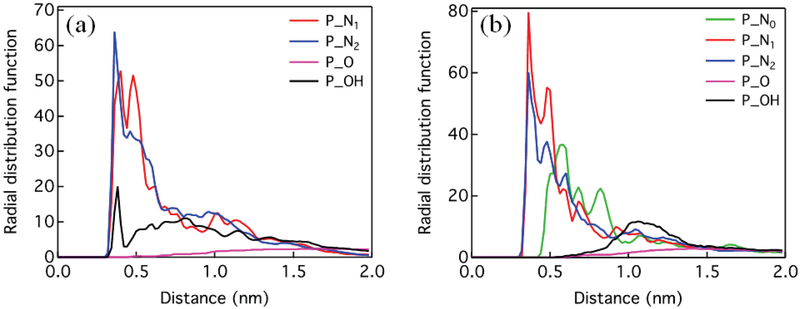
The simulations also show that a higher charge density in the head group leads to a more dominating coulombic attraction over the hydrogen bonding and hydrophilic interactions. Figure 5a and 5b show the radial distribution functions of N₀, N₁, N₂, O, and the O atom of OH for (PEG)₁₂-R₂ and (PEG)₁₂-R₃ with respect to the P atoms of polyP. Similar to previous cases, while N₁ and N₂ atoms form layered structure around the P atoms because of the electrostatic affinity, N₀ atoms on the (PEG)₁₂-R₃ (Figure 5b, green band) are not directly involved in the interaction with the polyP as it mostly settles in the second solvation shell. In contrast to the previous cases in Figure 3, the higher charge density in the head groups of (PEG)₁₂-R₃ disturbs the hydrogen bond formations between the OH group and the P atoms as less number of hydroxyl H atoms approach to the P atoms (black curve in Figure 5 a-b). The radial distribution function also indicates that a change in the ligand charge density does not promote the hydrophilic interaction between O atoms of PEG-based chain and the P atoms, confirming that the PEG tail length play a relatively small in inhibiting the polyP. The key role of the PEG tail is likely to reduce the drug toxicity rather than inhibiting the polyP.

Figure 5.

Radial distribution functions of the unprotonated amine N atoms (N₀), the protonated connective amine N atom (N₁), the protonated terminal amine N atom (N₂), O atoms of PEG-based chain, and the only O atom of hydroxide group (OH) with respect to the P atoms of polyP. (a) (PEG)₁₂-R₂, (b) (PEG)₁₂-R₃. The radial distribution function was obtained from 10 ns of classical MD simulations in the NPT ensemble using the AA force field. The P atom is the reference point of the radial distribution functions.

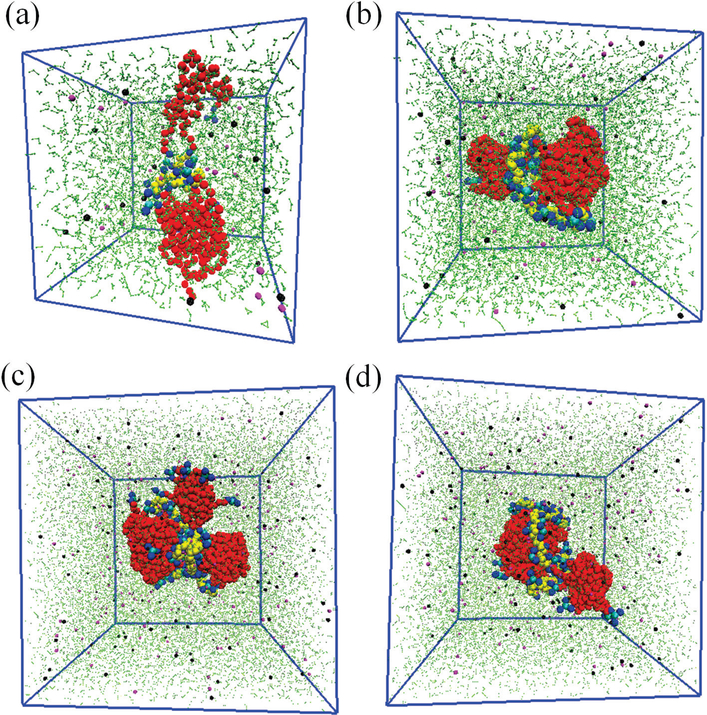
We have also carried out microsecond-scale CG-MD simulations to show the process of the polyP inhibition for the systems listed in Table 2. Initially the (PEG)₂₄-R₁ form aggregates mostly with the PEG in the core and the hydrophilic R₁ groups pointing toward water. Then the aggregates approach the polyP and sandwich the polyP to form a complex, as shown in Figure 6. In this complex, the PEG tails are in the outer layer, which may provide a shield preventing the complex from binding to other proteins or membranes as PEG is known for its antifouling properties. Therefore, the PEG tails most likely make the drug more hemocompatible.

Figure 6.

Final snapshot of a microsecond CGMD simulation for polyPs with 28 (a), 61 (b), 115 (c), and 133 (d) phosphate monomers. Details of the system are listed in Table 2. Color codes for the beads: MARTINI polarizable water (green), PEG monomer (red), protonated connective and terminal amine groups (dark blue), unprotonated amine group (light blue), phosphate group (BP) (yellow), Na⁺ (magenta), and Cl^- (black). The visualization was made by VMD⁷⁵.

Effect of PolyP chain length.

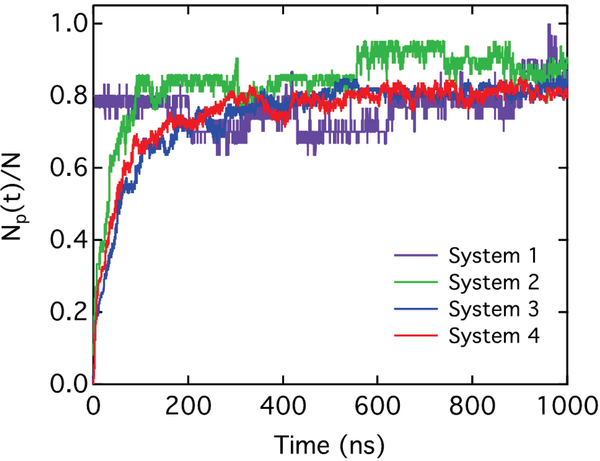
Our simulations indicate that, over the size range tested, the chain length of polyP does not significantly affect the binding efficiency. To test if the chain length of the polyP affects the efficiency of the (PEG)_n-R_i, we calculated the number of protonated amine groups approaching the polyP to form the complex. We assumed that the CG protonated amine form complexes with the CG phosphate, if the amine beads reside within a cutoff distance from phosphate beads. The cutoff distance for each system was determined by the first minimum of the radial distribution function (Figure S22a and S22c). Figure 7 shows the fraction of protonated amine groups coupled to the polyP with various chain lengths as a function of time. For all cases, the portion of (PEG)₂₄-R₁ involved in inactivating the polyP is around 0.8. It indicates that the polyP chain length does not affect the (PEG)_n-R_i binding efficiency. In addition, further analysis of the radial distribution function (Figure S22) of phosphate particles with unprotonated amine and PEG beads of (PEG)₂₄-R₁ confirms that the length of polyP chain does not alter the nature of interactions between the (PEG)_n-R_i and polyP over the range of 28 to 133 phosphate monomers.

Figure 7.

Calculated fraction of protonated amine beads involved in the complex formation with polyPs with 28 (a), 61 (b), 115 (c), and 133 (d) phosphate monomers using the CG force field. The details of the systems are described in Table 2. N_p(t) is the calculated number of protonated amine beads interacting with the phosphate beads. N is the total number of protonated amine beads in each system.

Experimental Validation.

To validate the key finding in the simulation studies that binding affinity was not influenced by the length of the PEG chain, we synthesized two of the cationic PEG-based molecules studied by simulation. m-PEG epoxides-350 and 550 were synthesized as reported in the literature²¹ Those epoxides were independently refluxed with tris(2-aminoethyl)amine (TREN) and purified by precipitation from DCM and cold pentane. The aminated m-PEGs were methylated by Eschweiler–Clarke reaction (Scheme 1) to generate compounds II (PEG₈-R₁ (studied in simulation system 3)) and III (PEG₁₂-R₁ (simulation system 2)), and the purity of the compounds was confirmed by ¹H NMR.

Scheme 1.

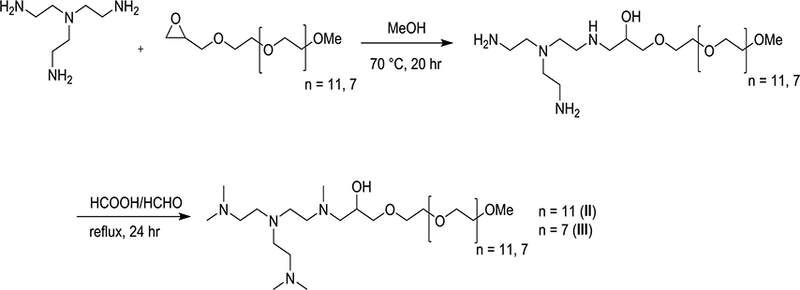
Synthesis of model compounds II (PEG_x-R₁) and III (PEG_y-R₁).

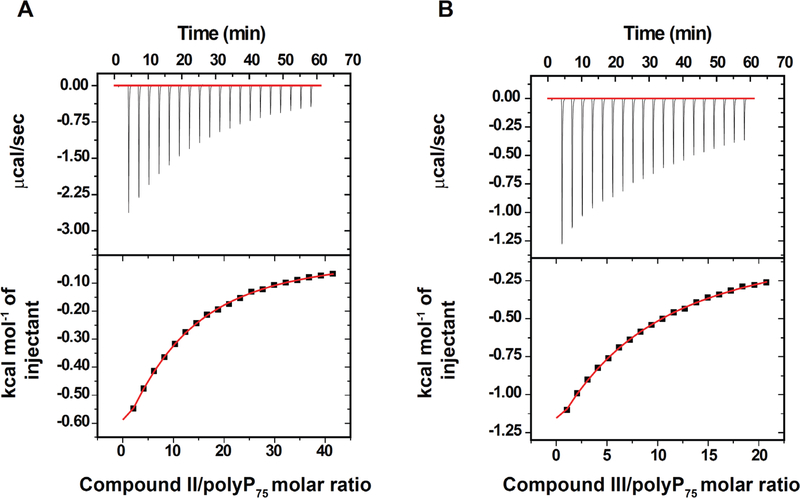
Isothermal titration calorimetry (ITC) data for binding of compounds II or III to polyP₇₅ (a polyP preparation with median polymer length of ~75 phosphate units) are shown in Figure 8. Compounds II and III both exhibit binding affinities in the millimolar range (1.4 and 1.7 mM, respectively). No statistically significant difference in binding affinity and free energy of binding (ΔG) among these two candidates (~16 KJ/mol) was observed, consistent with the key simulation results that the length of the PEG chain did not influence binding affinity. It does, however, affect the binding stoichiometry (N). N = 6.6 for binding of compound II to polyP₇₅, compared to only 3.4 molecules of compound III binding on average to polyP₇₅, in accordance with the larger size of compound III.

Figure 8:

ITC thermograms for PEG-linked cationic ligands binding to polyP_75. In each thermogram, the top panel shows the raw heat signal and the bottom panel shows the differential binding curve showing both experimental data and the nonlinear least square fit. Titrations were performed in PBS at pH 7.4 (± 0.2) and 298 K. (A) ITC thermogram obtained for compound II binding to polyP₇₅; (B) ITC thermogram obtained for compound III binding to polyP₇₅.

Conclusions

To provide a molecular-level understanding on the design of cationic inhibitor for polyP, we used MD simulations to investigate the interaction between polyP and (PEG)_n-R_i, a model compound containing a PEG-based tail attached to various cationic headgroups. The binding free energy analysis indicated that PEG length does not have any impact on the interaction between the (PEG)_n-R₁ and polyP. Similarly, CG-MD simulations revealed that the binding efficiency of the (PEG)₂₄-R₁ remained intact against the various chain lengths of polyP. However, higher charge density on the headgroup strengthens the (PEG)₁₂-R_i avidity of polyP binding, suggesting that the coulombic interaction is the main driving force for polyP inhibition. ITC experiments confirmed the lack of influence of the length of the PEG chain on binding affinity to polyP.

Table 4:

Thermodynamic parameters for interaction of polymers with polyP₇₅ determined by isothermal titration calorimetry^a

Compound	Nb	Kd (M)b	ΔG (kJ/mol)c
II	6.6 (± 0.82)	1.4 (± 0.08) × 10−3	−16.1 (± 0.12)
III	3.4 (± 0.64)	1.7 (± 0.15) × 10−3	−15.7 (± 0.21)

^aAll data were collected in PBS at pH 7.4 (± 0.2) and 298 K. Values given represent an average from two independent titrations and standard deviations are indicated in parentheses. N: number of moles of polymer binding per mole of polyP₇₅; K_d: dissociation constant; ΔG: free energy change.

^bObtained from isothermal titration calorimetry experiments.

^cCalculated from the equation ΔG = −RTlnK_a.