Effect of age on stiffness modulation during postural maintenance of the arm

Abstract

The ability to modify the mechanical impedance of our limbs allows us to perform a variety of motor control tasks while interacting with the environment in a stable manner. Prior work has shown that young, healthy people are capable of modulating arm stiffness via selective muscle co-contraction to account for external disturbances in various directions. Increased age detrimentally affects control of movement and stability, although the neural mechanisms underlying these deficits are not entirely understood. In this study, younger and older subjects performed a static postural maintenance task with two types of directional force perturbations. Older individuals showed significantly less stiffness modification between the two perturbation conditions compared to the younger individuals, indicating less optimal modulation of arm impedance. This impairment should be considered during motor control evaluation in older populations, whether it be activities of daily living or skill assessment.

I. Introduction

When performing daily activities, we make a variety of movements that enable us to manipulate objects and interact with our environment. Due to the unpredictable nature of our surroundings [1], [2] and noise in our motor system [3], the ability to modulate the mechanical impedance our limbs is important to ensure stability during postural and movement control. Limb impedance may also be altered to meet various task requirements, conditions, or constraints [4], [5]. Co-contraction of an agonist-antagonist muscle pair can be used to increase joint stiffness, effectively regulating limb impedance [6] However, there is a tradeoff between stability and metabolic efficiency, as co-contraction is energetically costly.

Previous studies have shown that people can control both the general magnitude and geometry of their hand (endpoint) stiffness by tuning co-contraction of specific muscle pairs in the arm. By selectively modulating muscle co-contraction, the human motor system can balance stability with metabolic cost. When perturbed during reaching movements [7], [8] and static postural maintenance tasks [9] – [11], people have been shown to optimally tune the endpoint stiffness of their arm towards the direction of destabilizing forces. Such modulation of the hand stiffness geometry, however, is significantly greater during movement compared to a postural task, even after training over multiple days in the static condition.

We are particularly interested in studying impedance modulation in older adults, as this population is known to experience increased impairments in motor control and stability [12] – [14]. A better fundamental understanding of the aging nervous system can help us develop strategies to help older individuals cope with movement deficiencies. Additionally, knowledge of the age-related effects on human motor control can be important for occupations such as surgery, which demand dexterous manipulation of generally older individuals [15] In this study, we ask the question: Does age affect the ability to optimally tune arm stiffness with respect to instabilities in the environment? To address this question, we tested younger and older people in a postural maintenance task with directional force perturbations at the arm.

II. Materials and Methods

A. Stiffness Representation

Planar movement of the human arm can be modeled by

$$f=M\ddot{x}+B\dot{x}+K\left(x-x_0\right),$$ (1)

where f is the Cartesian force vector at the hand, x, ẋ, and ẍ are the position displacement, velocity, and acceleration, and M, B, and K are the mass, damping, and stiffness matrices at the equilibrium position x₀ in hand space [16].

The hand stiffness matrix K

$$K=\left[\begin{array}{cc}{K}_{xx}& K_{xy}\\ K_{yx}& K_{yy}\end{array}\right]$$ (2)

characterizes the elastic behavior of the hand. This matrix can be visualized as an ellipse [17], where the major axis indicates the direction of the largest restoring forces to a displacement (Fig. 1). Similarly, the mass M and damping B matrices can be represented as ellipses.

Figure 1.

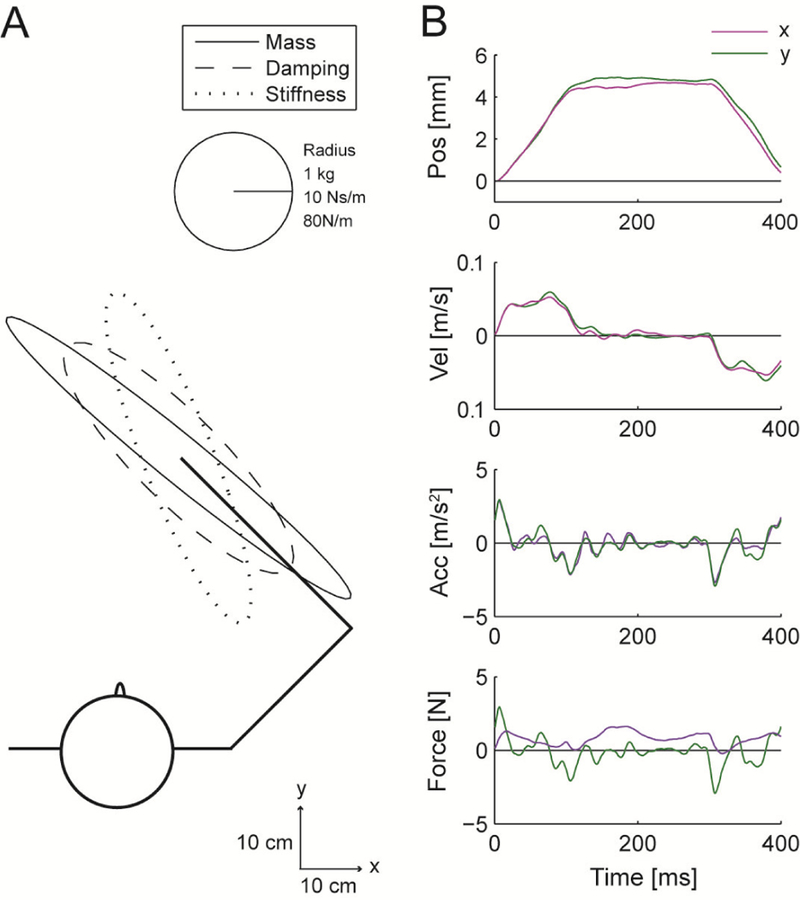
Arm impedance measurements. (A) Impedance ellipses of the human arm estimated from (B) measured kinematics and forces during step displacements.

To relate endpoint (hand) stiffness to joint stiffness, the equivalent stiffness in joint space R, can be calculated by

$$R=J^{T}KJ,$$ (3)

where J is the Jacobian matrix at the equilibrium arm configuration. The joint stiffness matrix relates joint torques to joint displacements

$$R=\left[\begin{array}{cc}{R}_{ss}& R_{se}\\ R_{es}& R_{ee}\end{array}\right]=\left[\begin{array}{cc}{k}_s+\frac{r_1}{r_2}{k}_d& k_d\\ k_d& k_e+\frac{r_2}{r_1}{k}_d\end{array}\right],$$ (4)

where R_ss relates shoulder torque and shoulder displacement, R_se relates shoulder torque and elbow displacement, R_es relates elbow torque and shoulder displacement, and R_ee relates elbow torque and elbow displacement. These parameters are affected by the single-joint shoulder muscle stiffness k_s, single-joint elbow muscle stiffness k_e, and biarticular (double-joint) muscle stiffness k_d, where r₁ and r₂ are the moment arms of the biarticular muscles at the shoulder and elbow, respectively [18]. Stiffness of the joints can be altered through co-contraction of the muscle pairs.

B. Impedance Estimation

Experiments were performed with the KINARM Exoskeleton Lab (BKIN Technologies, Kingston, Ontario) (Fig. 2A), a robotic device that allows planar movement of the shoulder and elbow. The subject’s arm is placed in the upper arm and forearm trays, which are adjusted to match his arm parameters, thus coupling the limb to the robot. The shoulder and elbow joints are driven through timing belts by two motors, with a peak torque pulse of 12 Nm (approximately 35 N at the hand) and encoder resolution of 0.0045° (approximately 30 micron at the hand). Kinematics and applied joint torques are recorded at a rate of 1 kHz.

Figure 2.

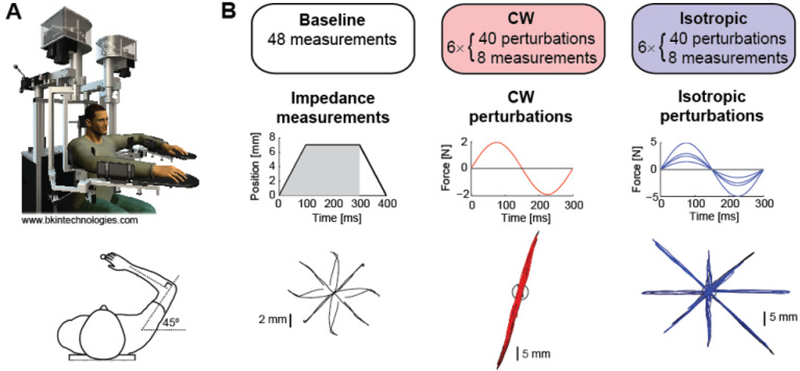
Experiment protocol. (A) Subjects used a planar exoskeleton robot with their arm positioned at shoulder and elbow angles of 45° and 90°, respectively. (B) In the Baseline session, subjects relaxed their arm while an estimate of arm impedance was computed using positional displacements in eight directions. Recorded kinematics and forces from the first 300 ms were used. In the CW session, arm impedance was measured as subjects tried to maintain an arm posture while resisting force perturbations along one axis. In the Isotropic session, perturbations of various magnitude occurred in eight directions. Hand trajectories from a representative subject are shown.

The robot’s intrinsic compliance limits the ability to generate quick, accurate position displacements required for direct stiffness measurements [19]. Thus, we used a modified version of the estimation technique presented in [16] to simultaneously estimate M, B, and K in (1).

Position displacements of 7 mm were applied in eight different directions (0°, ±45°, ±90°, ±135°, 180°) (Fig. 2B). The servo-controlled (PD controller gains: K_p = 3000 N/m, K_d = 40 Ns/m) position displacements consisted of a 100 ms ramp up, 200 ms hold, and 100 ms ramp down. Average position, velocity (zero-phase, low-pass filtered), acceleration (numerical differentiation of the velocity), and force traces for each direction were used in a linear regression of (1). Only the first 300 ms of data was used, to avoid including voluntary responses to the displacements, while still using a sufficient amount of data for fitting. Since the arm was positioned in the same configuration throughout the experiment, the M matrix was held constant for each subject, as determined from the baseline impedance measurement (see Section II.C).

We validated this method by implementing virtual springs in Cartesian and joint space and measuring the subsequent changes in stiffness.

C. Experiment Protocol

Eleven subjects (4 male, 7 female) under the age of 40 (27 ± 5 years) were in the “Younger” group. Eleven subjects (7 male, 4 female) over the age of 40 (58 ± 12 years) were in the “Older” group. The experiment protocol was approved by the Johns Hopkins University School of Medicine Institutional Review Board, and all subjects signed a consent form prior to participating.

Subjects were seated with their dominant arm positioned in the robot arm trays (Fig. 2A). The visual display system showed a cursor at the tip of the index finger (radius 0.75 cm) and a virtual target (radius 1 cm) overlaid on a plane above the arm, while view of the actual arm was concealed.

Subjects first completed a Baseline session (Fig. 2B) during which their passive arm impedance was measured. They were instructed to position their hand cursor at the target, then relax their arm as much as possible. The target was placed where the shoulder and elbow joints were 45° and 90°, respectively. The cursor position was frozen during the position displacements (used for the impedance measurement) to further minimize voluntary responses. Subjects were also told to avoid reacting to the position displacements. A baseline stiffness ellipse was generated for each subject.

During the six blocks of the Clockwise (CW) Perturbation session, subjects were instructed to actively resist the large force perturbations in order to stay within the target. Subjects were told to maintain a constant (tonic) level of moderate tenseness (muscle activity) in their arm, while avoiding excessive muscle contraction to avoid fatigue. There were 40 force perturbations and eight impedance measurements (pseudo-randomly presented) in each block. The target turned green when the hand cursor was completely within the target, and red otherwise. The robot only applied forces when the subject’s hand cursor was stationary within the target. Perturbations were applied along an axis 45° clockwise of the major axis of each subject’s baseline stiffness ellipse (Fig. 2B). The sinusoidal force perturbations were of magnitude 2 N and period 300 ms. In each trial, subjects’ hand movements were constrained to the axis along which perturbations were applied via a force channel (P controller gain: K_p = 2500 N/m). Subjects received a score reflecting the amount of time their hand was outside the target for each perturbation trial (100: cursor never left the target, 0: outside for longer than 800 ms). The timer started upon onset of the perturbation, stopping when the hand returned to the target and remained inside for 1 s. At the end of each block, the total score was displayed. Using the impedance measurements taken over the course of the six blocks, a stiffness ellipse was estimated for the CW session for each subject.

Subjects were given the same instructions for the Isotropic Perturbation session. During the six blocks, perturbations were applied in eight directions, along the 0°, 45°, 90°, and 135° axes (Fig. 2B). To ensure approximately equal displacement along these axes, the magnitude of the perturbations differed by direction (2.5, 1.5, 3, and 5 N, respectively) to account for the anisotropy of the arm’s impedance. Similar to the CW session, a single stiffness ellipse was generated for each subject from the Isotropic session.

III. Results

A. Impedance Measurements

The 48 impedance measurements in each of the Baseline, CW, and Isotropic sessions were used to compute a single impedance estimate for each condition. To validate the estimation, the actual forces were correlated against the force reconstructed from the computed M, B, and K values (in addition to the measured kinematics). The correlation coefficients for the Younger and Older groups were 0.79 ± 0.07 and 0.83 ± 0.06, respectively.

Through visual inspection, the impedance estimates were also deemed reasonable. The mass ellipse was generally aligned in the direction of the forearm, and the baseline stiffness ellipse was roughly oriented along the line connecting the hand and the shoulder (Fig. 1), as has been previously reported [20]. Different researchers have reported quite a large range of stiffness values for the passive human arm, which has been shown to depend on the amplitude of the measurement perturbations [21]. Our stiffness estimates are of similar magnitude to those of [20].

B. Task Performance

Subjects’ performance in the postural maintenance task was quantified by the length of time their hand was displaced from the target following a force perturbation (Fig. 3A). The timer began upon onset of the perturbation, and stopped once the hand cursor was completely within the target and remained there for 1 s. Overshooting or oscillatory movements around the target contributed to the increase of this time-out metric. To better capture the steady state performance, rather than the learning effects, the time-out metric was calculated for the last 20 perturbations in each block (data collapsed across perturbation direction).

Figure 3.

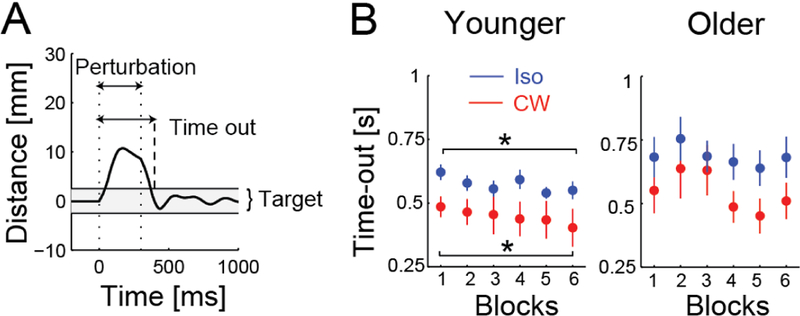
Postural maintenance performance. (A) The time the hand spent outside of the target was measured from the start of the perturbation (applied between dotted lines) to when it re-entered the target (dashed line) and stayed there for 1 s. (B) Younger subjects improved over the six blocks for both perturbation sessions (*p < 0.05), but older subjects did not.

Both the Younger and Older subjects were better at maintaining the given arm posture during the CW perturbations compared to the Isotropic perturbations (Fig. 3B). This was expected since the CW perturbations were applied in fewer directions, and therefore easier to predict and resist. Averaging the time-out metric across all six blocks, a two-way ANOVA showed a main effect of perturbation (CW vs. Isotropic, p = 0.0001), with subjects returning to the target faster in the CW condition, but showed no main effect of age (Younger vs. Older, p = 0.24) and no interaction (p = 0.29).

With more practice, the Younger subjects also improved at the postural maintenance task over the course of the six blocks. A paired t-test comparing the time-out metric in the first and last blocks showed a significant decrease for the CW (p = 0.003) and Isotropic conditions (p = 0.03). The Older subjects, however, did not show improvement over time (both p > 0.28), with their performance appearing more variable.

C. Stiffness Modulation

1). Hand Stiffness

For the CW session, the axis along which perturbations were applied was 71 ± 6° and 75 ± 4° for the Younger and Older subjects, respectively.

Example hand stiffness ellipses, estimated from the CW and Isotropic sessions, of a Younger and Older subject are shown in Fig. 4A. Note that the stiffness ellipses from the Isotropic session (blue) are rotated counter-clockwise from those of the CW session (red), much more so for the younger subject. The orientation of an ellipse (angle of the major axis or principal eigenvector) was determined by singular value decomposition of the hand stiffness matrix K. As a group, both the Younger and Older subjects show counter-clockwise rotation of their hand stiffness ellipse from the CW to Isotropic condition (Fig. 4B). Significant differences in stiffness ellipse orientation was verified by one-sided pairwise t-tests for the Younger (p < 0.001) and Older (p = 0.003) groups. A one-way ANOVA also showed that Younger subjects were able to produce larger changes in orientation of the stiffness ellipse than Older subjects (p = 0.04). Note that the stiffness ellipse of the CW condition was rotated towards the axis along which the perturbations were applied, yet it was far from aligning with this axis of instability. This limited change in rotation agrees with previous work that reported smaller changes in stiffness orientation for static tasks compared with movement tasks [9], [7].

Figure 4.

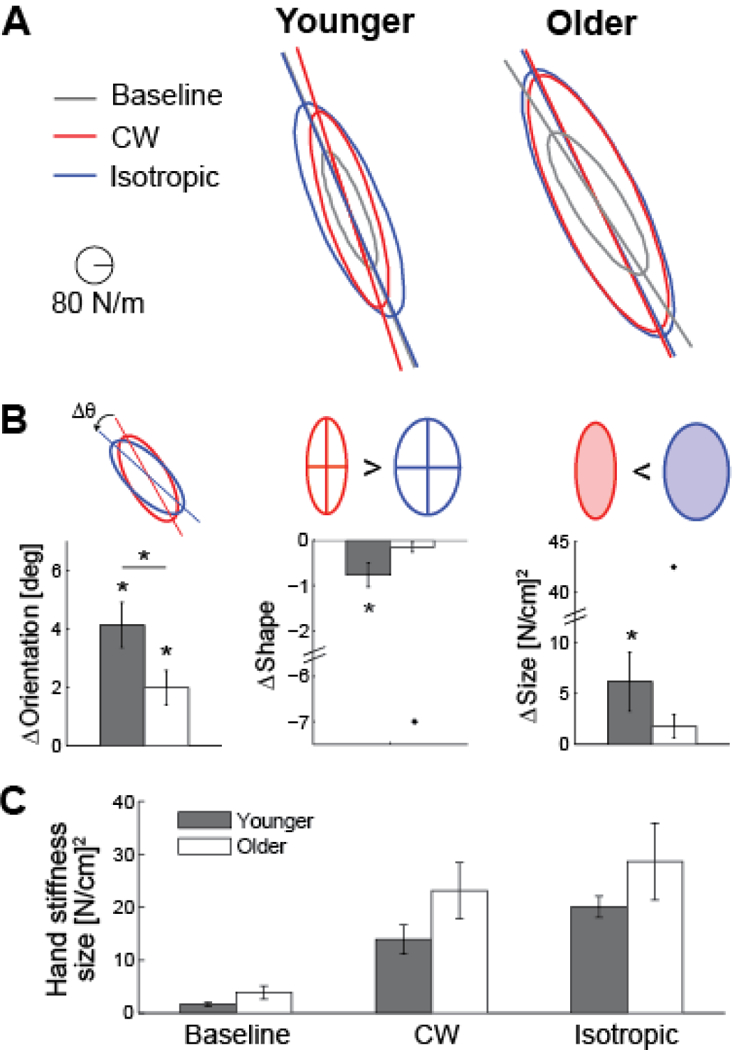
Modulation of the hand stiffness ellipse. (A) Estimated stiffness ellipse for the Baseline (grey), CW (red), and Isotropic (blue) perturbation sessions for a representative younger and older subject. Major axes have been extended to highlight changes in ellipse orientation. (B) Relative changes in the stiffness ellipse between the two perturbation sessions are quantified by difference in orientation, shape (ratio of the major to the minor axis), and size (area). Mean ± standard error, with outliers (> 2 standard deviations away from the overall mean) represented by dots. *p < 0.05. (C) All subjects increase the size of their hand stiffness ellipse in the CW and Isotropic sessions, compared to the baseline session.

The stiffness ellipse can also be characterized by its shape and size. The shape is described as the ratio of the lengths of the major axis and the minor axis, where a value of 1 denotes a circle and a value of 0 denotes a line. The size corresponds to the area of the ellipse. The shape of the Younger subjects’ hand stiffness ellipse decreases from the CW to Isotropic condition (one-sided pairwise t-test, p = 0.006), while the Older subjects showed no significant difference in ellipse shape (p = 0.12). Younger subjects altered their arm stiffness such that the geometrical shape of the endpoint stiffness was more circular in the Isotropic than the CW condition. This change in stiffness is appropriate because the Isotropic session required subjects to resist force perturbations that were applied in many different directions.

The Younger subjects also showed larger modifications to the size of their hand stiffness ellipse. A one-sided pairwise t-test showed that the stiffness ellipse was larger in the Isotropic than the CW condition for the Younger subjects (p = 0.02), but the Older subjects did not show a consistent change in ellipse size (p = 0.09). This result is consistent with [9], where subjects also showed greater overall stiffness in the condition with isotropic perturbations. The absolute sizes of the stiffness ellipses were not significantly different for the two groups for any particular session (Baseline, CW, or Isotropic) (Fig. 4C).

2). Joint Stiffness

The changes in the hand stiffness ellipse can also be related to changes in shoulder and elbow joint stiffness (3). For each subject, hand stiffness matrices K for the CW and Isotropic conditions were transformed into joint stiffness matrices R. Pairwise two-tailed t-tests showed that R_ss (p = 0.005) and R_se (p = 0.03) components increased from the CW to the Isotropic condition for the Younger subjects (Fig. 5A). Similarly, there was also an increase in the R_ss component in the Older group (p = 0.047). A ratio of the R_ss to R_ee term can also provide insight to the relative shoulder and elbow stiffness. Both groups experienced an increase in this ratio from the CW to Isotropic condition (Younger: p < 0.0001, Older: p = 0.02) (Fig. 5B).

Figure 5.

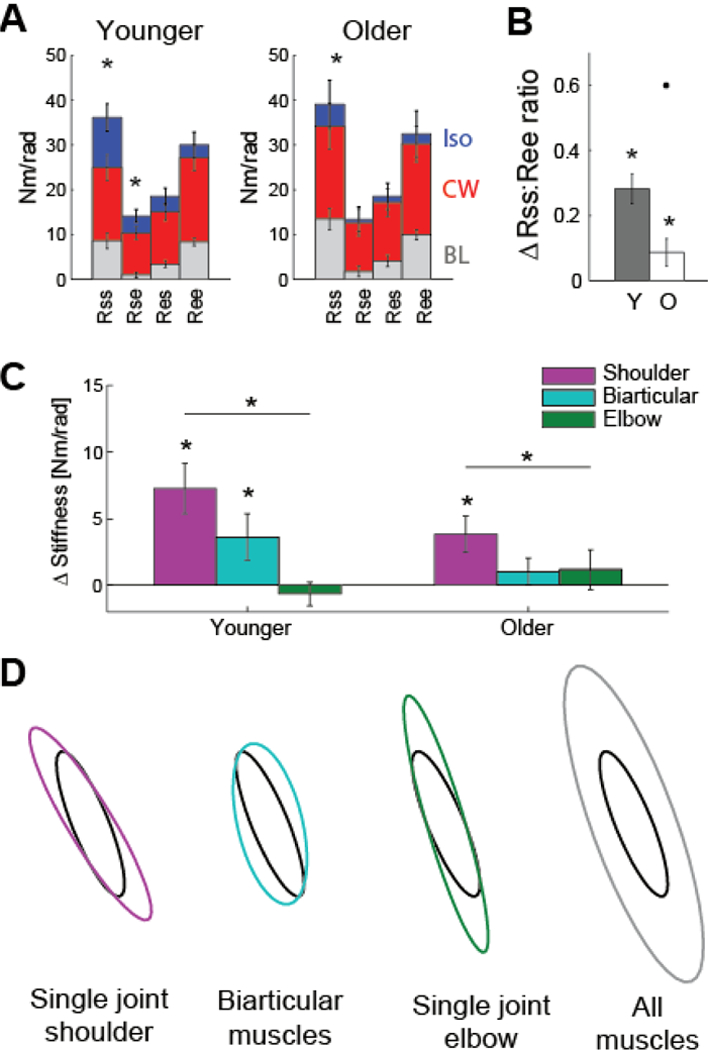
Modulation of joint stiffness. (A) Comparison of the components of the joint stiffness matrices for the Baseline, CW, and Isotropic conditions (mean ± standard error). Subjects increase stiffness at the shoulder joint from the CW to Isotropic condition. *p < 0.05. (B) The change in relative contribution of the shoulder and elbow joint stiffness (ratio of Rss and Ree components) between the two perturbation conditions. An outlier is represented as a dot. (C) Changes in co-contraction of single-joint shoulder, biarticular, and single-joint elbow muscles are estimated from the CW and Isotropic joint stiffness matrices. (D) Simulated results show the effect of co-contraction of specific muscle pairs on the hand stiffness ellipse. The black ellipse is passive stiffness in the baseline condition.

The difference in the CW and Isotropic perturbations can explain this increase in shoulder stiffness. The CW session resulted in more displacement at the elbow. Alternatively, the Isotropic perturbations produced movement at both joints, causing subjects to increase stiffness of the shoulder joint in order to maintain their arm posture.

Co-contraction of antagonist muscle pairs about the shoulder and elbow joints contributes to the observed changes in joint stiffness. However, the relationship between joint stiffness and muscle co-contraction is not straightforward, as the biarticular muscles can contribute differently to the four terms of the joint stiffness matrix, depending on their moment arms. To approximate the involvement of the different muscles in altering the joint stiffness, a linear regression of (4) was performed using the difference in the four matrix components between the CW and Isotropic conditions. The moment arms of the biarticular muscles were assumed to be equal (r₁ = r₂). Changes in stiffness of the three different muscle groups (single-joint shoulder muscles, biarticular muscles, and single-joint elbow muscles) can be interpreted as changes in co-contraction, as shown in Fig. 5C. Both the Younger (p = 0.001) and Older groups (p = 0.023) showed significantly increased co-contraction at the single-joint shoulder muscles in the Isotropic condition compared to the CW condition. Single-joint shoulder muscle co-contraction was also greater than co-contraction of the single-joint elbow muscles (Younger: p < 0.0001; Older: p = 0.036). Younger controls also showed a significant increase in biarticular muscle co-contraction (p = 0.045).

The changes in muscle co-contraction and joint stiffness can explain the modifications to hand stiffness. Similar to [8], simulations were performed to determine the effect of co-contraction of the different muscle groups on the hand stiffness ellipse. The baseline stiffness ellipse of one subject is shown as the black ellipses in Fig. 5D. The hand stiffness matrix was then converted to the joint stiffness matrix and increases in co-contraction of individual muscle groups were simulated from (4), equivalent to increases in stiffness of 10 Nm/rad. Co-contraction of any muscle group always results in an increase in size of the hand stiffness ellipse. Co-contraction of the single-joint shoulder muscles results in counter-clockwise rotation. Co-contraction of the biarticular muscles and the single-joint elbow muscles both produced clockwise rotation, although with different changes in shape. Generalized co-contraction (simultaneous co-contraction of the three muscle groups) resulted in a large change in size of the hand stiffness ellipse, and only a small change in orientation. Thus, the differences in stiffness seen between the CW and Isotropic conditions in this experiment can be primarily explained by an increase in single-joint shoulder muscle co-activation.

IV. Discussion and Conclusion

Both Younger and Older subjects increased arm stiffness to maintain an arm posture while being disturbed by force perturbations. Younger subjects showed greater modification to the geometry of their hand stiffness ellipse – orientation, shape, and size – that was specific to the perturbations. This ability was limited in the Older subjects. The changes in the hand stiffness ellipse from the CW to Isotropic condition were mainly due to increased shoulder stiffness, as a result of increased co-contraction of the single-joint shoulder muscles. Similar changes in joint stiffness and muscle co-contraction were seen in the Older subjects, though to a lesser extent.

To our knowledge, the effect of age on modulation of arm stiffness has not been previously studied. Prior work showing stiffness modulation during static tasks [9], [10] involved only young subjects between the ages of 19 and 30. The deficit observed in older individuals cannot be attributed to an inability to increase arm stiffness. The size of the Older subjects’ hand stiffness ellipses, indicating general stiffness, was no smaller than those of the Younger subjects (Fig. 4C). If anything, Older subjects may have been slightly stiffer than Younger subjects, although there was no statistical difference.

Prior research shows that older individuals use increased muscle co-contraction during a variety of tasks. Increased co-contraction has been observed in whole body postural control during standing and in response to perturbations [14], [22], activities of daily living such as descending stairs [23], arm movements [13], [12], and contrived tasks such as measurement of maximum voluntary contractions [24]. In addition to greater co-contraction, we have shown that older individuals are also impaired at modulating co-contraction compared to younger individuals. This reliance on more generalized co-contraction may be the result of a neurological deficit due to aging. Alternatively, it may be a voluntary strategy to help cope with other sensorimotor impairments due to aging, such as increased movement variability, decreased muscle strength, or deterioration of sensory input and processing [14], [23]. Excessive co-contraction, which requires greater effort, could potentially lead to further movement deficiencies due to premature muscle fatigue.

Although our Younger subjects showed consistent modulation of arm stiffness, specific to the perturbation condition, rotation of the hand stiffness ellipse was smaller than previously reported values. Greater stiffness ellipse rotation was observed when subjects voluntarily modified co-contraction of different arm muscles [25] and stiffness ellipse orientation [26] with visual feedback of the respectively controlled variables. In [9], subjects performed a postural task similar to ours, but each subject group only experienced one perturbation condition; our subjects experienced both the CW and Isotropic perturbations. Thus, the close proximity of the two perturbation sessions in time may have prevented subjects from learning a new stiffness pattern in the second Isotropic condition [10].

For future work, it would be interesting to see if older individuals can learn to better modulate their arm stiffness over time. Perhaps by using multiple days of training or more cognitive control with the addition of EMG biofeedback, older adults may be able to learn selective co-contraction of different muscle pairs. EMG recordings could also verify modified co-contraction patterns or reveal different strategies used to resist the perturbations, such as compensating for the disturbances by applying an opposing force. Additional studies could also be performed with older adults who routinely perform dexterous tasks (e.g., surgery) to see if their stiffness control is more refined than their age-matched counterparts.