Abstract
An image-balsed skeletal dosimetry model for internal electron sources was created for the ICRP-defined reference adult female. Many previous skeletal dosimetry models, which are still employed in commonly used internal dosimetry software, do not properly account for electron escape from trabecular spongiosa, electron cross-fire from cortical bone, and the impact of marrow cellularity on active marrow self-irradiation. Furthermore, these existing models do not employ the current ICRP definition of a 50-μm bone endosteum (or shallow marrow). Each of these limitations was addressed in the present study. Electron transport was completed to determine specific absorbed fractions to both active and shallow marrow of the skeletal regions of the University of Florida reference adult female. The skeletal macrostructure and microstructure were modeled separately. The bone macrostructure was based on the whole-body hybrid computational phantom of the UF series of reference models, while the bone microstructure was derived from microCT images of skeletal region samples taken from a 45-year-old female cadaver. The active and shallow marrow are typically adopted as surrogate tissue regions for the hematopoietic stem cells and osteoprogenitor cells, respectively. Source tissues included active marrow, inactive marrow, trabecular bone volume, trabecular bone surfaces, cortical bone volume, and cortical bone surfaces. Marrow cellularity was varied from 10 to 100 percent for active marrow self-irradiation. All other sources were run at the defined ICRP Publication 70 cellularity for each bone site. A total of 33 discrete electron energies, ranging from 1 keV to, 10 MeV, were either simulated or analytically modeled. The method of combining skeletal macrostructure and microstructure absorbed fractions assessed using MCNPX electron transport was found to yield results similar to those determined with the PIRT model applied to the UF adult male skeletal dosimetry model. Calculated skeletal averaged absorbed fractions for each source-target combination were found to follow similar trends of more recent dosimetry models (image-based models) but did not follow results from skeletal models based upon assumptions of an infinite expanse of trabecular spongiosa.
Keywords: skeletal dosimetry, bone dosimetry, hematopoietic stem cells, osteoprogenitor cells, reference adult female, electron transport
1. Introduction
The skeletal regions of the body are difficult to model for dosimetric purposes due to their complex 3D geometry in the regions that comprise bone trabeculae and bone marrow cavities. The irradiation of the hematopoietically active (or red) bone marrow has been linked to the induction of radiogenic leukemia (ICRP, 2015). Similarly, the irradiation of the osteoprogenitor cells that line the trabecular bone surfaces, or the inner surfaces of the long bone shafts, has been linked to radiogenic bone cancer (ICRP, 2015). In skeletal dosimetry studies, active marrow (AM) is used as a surrogate tissue region for the hematopoietically active marrow stem cells, while shallow marrow, TM50 (also called bone endosteum), is applied as the surrogate tissue region for the osteoprogenitor cells that reside along the bone surfaces (ICRP, 2009).
In its Publication 110 (ICRP, 2009), the International Commission on Radiological Protection (ICRP) retained its original definition of the target tissue for leukemia induction as active (or red) bone marrow localized to the non-fatty regions of trabecular spongiosa of the adult skeleton. However, a major change was made in the target tissue definition for bone cancer induction. The previous ICRP model of Publication 30 (ICRP, 1980) defined bone surfaces as a 10-μm tissue layer running along the surfaces of the bone trabeculae (in spongiosa regions of the skeleton) and along the surfaces of the Haversian canals (in cortical bone regions of the skeleton). In the present ICRP model, the target tissue for bone cancer induction (endosteum in ICRP terminology and shallow marrow in the University of Florida (UF) series of models) is defined as a 50-μm tissue layers along the surfaces of the bone trabeculae, as well as the inner surfaces of the shafts of all long bones.
Consequently, there no longer exists a skeletal target tissue in cortical bone. These definitions are reflected in the model presented here.
Currently, there are two main classes of computational models for skeletal dosimetry: pathlength-based models and image-based models. The foundation of pathlength-based models originated from the work of Frederick Spiers and the Bone Dosimetry Research Unit at the University of Leeds. Their work completed studies on a 44-year-old adult male cadaver in which 7 bone sites were imaged using contact radiographs. The acquired pathlength distributions from this individual formed the underpinning for the majority of the skeletal dosimetry models that followed, including those in MIRD Pamphlet No. 11 (Snyder et al., 1975), ICRP Publication 30 (ICRP, 1980), and Stabin and Siegel (2003).
Currently, the three forms of image-based models are Voxel-Based Infinite Spongiosa Transport (VBIST), Voxel-Based Restricted Spongiosa Transport (VBRST), and Paired- Image Radiation Transport (PIRT) (Shah et al., 2005b). Each of these bone dosimetry models utilize nuclear magnetic resonance (NMR) or microCT images of the cored samples of trabecular spongiosa, providing a three-dimensional model for particle transport through marrow cavities and bone trabeculae. These methods differ, however, in the way the skeletal macrostructure is defined. In the VBIST method, no model is provided for the bone macrostructure and thus radiation transport is considered through an infinite expanse of spongiosa. In contrast, a stylized model of the cortical bone cortex is used to represent the bone macrostructure in the VBRST model. The PIRT model uses ex-vivo CT images of bone macrostructure. In PIRT simulations, the bone macrostructure and microstructure are considered simultaneously, allowing for electron escape into cortical bone (Shah et al., 2005a).
A study conducted by Hough et al. (2011) used the PIRT method to create a skeletal dosimetry model for the ICRP-defined reference adult male (ICRP, 2002, 2009). The bone macrostructure was derived through an ex-vivo whole body CT scan, at 1 mm resolution, of a 40-year-old male cadaver. For the geometry of the bone microstructure, ex-vivo microCT images were taken of spongiosa samples from 38 bone sites, at an isotropic resolution of 30 μm.
Four main areas of potential improvement can be identified given limitations in previous models. These include consideration of (1) electron cross-fire from cortical bone, (2) electron escape from trabecular spongiosa, (3) the influence of varying cellularity on active marrow self-irradiation, and (4) revisions to the ICRP definition of the surrogate tissue region for the osteoprogenitor cells (ICRP, 2009). Each limitation was accounted for in the present dosimetry model in the development of a new skeletal electron dosimetry model of the ICRP-defined reference adult female. As with the previous adult male model of Hough et al. (2011), electron sources are considered in active marrow, inactive marrow, trabecular bone surfaces, trabecular bone volumes, and cortical bone. As the explicit microstructure of the Haversian canals are not considered in the present model (cortical bone is treated as a homogeneous tissue region), computations of cortical bone electron sources are applied equally for cortical bone volume and surface sources.
2. Materials and Methods
2.1. Bone Site Image Acquisition
A 45 year-old female cadaver was acquired for the present study under an IRB- approved protocol. The skeletal macrostructure was derived from a whole-body in-vivo CT image as well as various ex-vivo CT images following bone harvest. CT imaging was performed on a 64-slice Toshiba CT scanner in the Department of Radiology at UF Health Shands Hospital at the University of Florida (UF). For ex-vivo CT imaging, the following skeletal sites were excised: cranium, mandible, clavicles, scapulae, sternum, vertebrae (cervical, thoracic, and lumbar), ribs (upper, middle, and lower), os coxae, sacrum, patellae, and the proximal and distal ends of the humeri, radii, ulnae, femora, tibiae, and fibulae. For each skeletal site, both bone-filtered and soft tissue-filtered ex-vivo scans were completed at a 1-mm slice thickness. These separate images were acquired to optimize the visualization of the boundary between cortical bone and trabecular spongiosa. From these images, and from total body reference bone masses given for the ICRP reference adult female (ICRP, 2002), targeted values of cortical bone volume and spongiosa volume were assigned for each skeletal site.
Through inspection of the ex-vivo images, a region of interest was chosen for spongiosa coring at each skeletal site. The spongiosa cores were imaged under microCT as performed by SCANCO, Inc. (Brüttisellen, Switzerland) at an isotropic resolution of 30 μm. These images were converted to a 50-μm isotropic resolution. For ease in labeling, the voxels comprising the first voxel layer within the marrow spaces were defined as the target region shallow marrow. Multiple steps were necessary to convert the microCT images into a useful form for radiation transport. First, a region of interest had to be determined for each image, removing cortical bone from the selected ROI. Next, in order to increase the signal-to-noise of each image, a median filter was applied. An example of an image from a single slice of the third cervical vertebrae after application of the median filter is given in Figure 1A. Next, a threshold value for the gray level was determined that optimized the appearance of the interface between trabecular bone and the adjacent marrow cavities. Finally, using this determined threshold value, the images were segmented into binary images (Hough et al., 2011). This segmentation was performed using an ITK-based user program based upon algorithms reported by Rajon et al (2006). Figure 1B shows a postsegmented image slice of the third cervical vertebrae, for which the threshold value was 172. The increased ability to delineate the boundaries between the bone trabeculae and marrow cavity is clear from the comparison of the pre- and post-segmented images of the third cervical vertebrae.
Figure 1.

MicroCT image conversion process as illustrated with the third cervical vertebra. (A) Pre-segmented, post-filtered image, (B) post-segmented, post-filtered image (using a threshold value of 172), (C) ICRP 70 cellularity applied, and (D) shallow marrow layer labeled in blue.
2.2. Modeling of the Skeletal Macrostructure
Thirty-four bone sites constitute the modeled macrostructure of the adult female: the cranium, mandible, vertebrae (cervical, thoracic, lumbar), sternum, ribs, scapulae, clavicles, os coxae, sacrum, humeri, radii, ulnae, wrists and hands, femora, tibiae, fibulae, patellae and ankles and feet. Each bone site was isolated from the UF hybrid adult female (UFHADF) computational phantom (Hurtado et al., 2012) and was voxelized for geometrical input to the MCNPX v2.7 radiation transport code (Pelowitz, 2011). The long bones were divided into their proximal end, shaft, and distal end. The shafts of the femora and humeri were further divided into the upper and lower shaft regions, due to the presence of active marrow within their upper and not lower halves as per ICRP Publication 70 (ICRP, 1995).
For the appendicular skeleton, only one body side (right) was modeled, with the exception of the os coxae.
The approximate height, width, and depth of the bone macrostructure sites from the UFHADF computational phantom were measured in Rhinoceros™ (McNeel North America, Seattle, WA) in order to determine an isotropic voxel resolution (Wayson, 2012):
| (1) |
where risotropic is the isotropic voxel resolution, X is the measured height (in cm), Y is the measured width (in cm), Z is the measured depth (in cm), and N is the target voxel matrix size. The targeted matrix size was 5.42 × 107, as previously determined by Wayson (Wayson, 2012) to be the total number of voxel elements that can be efficiently modeled within MCNPX, given existing computational resources in our laboratory. Voxel resolutions ranged from 149 to 670 μm, values which corresponded to the proximal radii and to the ribs, respectively.
2.2.1. Modeling of the Vertebrae.
MicroCT images were obtained from multiple vertebral samples, including L1-L5, T1, T3, T6, T9, T12, C3 and C6. Consequently, the vertebral column of the UFHADF reference phantom was partitioned into these individual vertebrae. Vertebral partitioning was accomplished with various Rhinoceros™ commands, primarily cutting planes and control point deletions and manipulations. The separated lumbar vertebrae were voxelized at a resolution of 0.18 mm and the separated cervical and thoracic vertebrae at a resolution of 0.20 mm. Figure 2 shows an example of the separated C3 vertebra.
Figure 2.

Separated C3 vertebra macrostructure (left), microCT image of cored spongiosa (center), and 3D microstructure rendering in voxel format with bounding box (right).
2.2.2. Modeling of the Shafts of the Long Bones.
The long bone shafts were modeled in MCNPX using cylinders. The effective radius of the medullary cavity was determined as follows (Pafundi, 2009):
| (2) |
where is the effective radius of the medullary cavity (in cm), is the volume of the medullary marrow in both the left and right shafts for that skeletal site (in cm3), with h being the length of the shaft (in cm). Medullary cavity radii and volumes were determined in Rhinoceros™ within the ex-vivo CT images of the humeri (upper and lower shafts), radii, ulnae, femora (upper and lower shafts), tibiae, and fibulae. The cortical bone surrounding the long bone shafts was further modeled as a cylindrical shell within MCNPX.
Shallow marrow was modeled as a 50-μm thick cylindrical shell just within the cylindrical volume of the medullary cavity. Therefore, the outer radius of the medullary cavity and the outer radius of the shallow marrow shell are coincident. The outer radii of the medullary cavities, inner radius of the shallow marrow shell, outer radius of the cortical bone shell, and the heights of the shafts are provided in Table 1 for all six long bones.
Table 1.
Dimensions used for the long bone shaft cylindrical models of the UFHADF.
| Skeletal Site | Measured Medullary Cavity Volume (cm3) | Measured Medullary Cavity Height (cm) | Calculated Medullary Cavity Radius (cm) | Calculated Medullary Cavity Surface (cm2) | Calculated Outer Cortical Bone Radius (cm) | Calculated Medullary Endosteum Radius (cm) |
|---|---|---|---|---|---|---|
| Humerii, Upper Shaft | 23.33 | 9.76 | 0.617 | 37.82 | 0.861 | 0.612 |
| Humerii, Lower Shaft | 20.62 | 10.00 | 0.573 | 35.98 | 0.798 | 0.568 |
| Radii, Shaft | 15.74 | 17.53 | 0.378 | 41.64 | 0.540 | 0.373 |
| Ulnae, Shaft | 18.51 | 17.44 | 0.411 | 45.04 | 0.590 | 0.406 |
| Femora, Upper Shaft | 64.69 | 14.64 | 0.839 | 77.15 | 1.157 | 0.834 |
| Femora, Lower Shaft | 73.97 | 14.11 | 0.914 | 80.98 | 1.264 | 0.909 |
| Tibiae, Shaft | 78.85 | 23.74 | 0.727 | 108.46 | 0.783 | 0.722 |
| Fibulae, Shaft | 7.76 | 23.76 | 0.228 | 34.04 | 0.349 | 0.223 |
The same procedure was completed for the long bone shafts of the UF adult male phantom (UFHADM). In the Hough et al (2011) study, the bone surfaces were modeled as a thin volume with a 1 μm thickness on each side of the bone and medullary cavity interface. In this current study, the adult male shafts have been rerun with the surface source being modeled as infinitely thin. Corrected dosimetry data are reported later in this study.
2.3. Modeling of the Skeletal Microstructure
The following 37 skeletal sites were cored and imaged, therefore constituting the skeletal microstructure of the UF reference adult female: C3, C6, L1-L5, T1, T3, T6, T9, T12, clavicle, craniofacial bones (frontal, parietal, occipital), mandible, os coxae, patella, sacrum, scapula, sternum, femur (distal, proximal head, proximal neck), and the proximal and distal ends of the fibula, humerus, radius, tibia, and ulna. The skeletal microstructure was not available for the wrists and hands and ankles and feet; consequently, their marrow volume and mineral bone volume fractions were used as free variables in order to match total skeletal tissue masses as defined for the ICRP reference adult female.
Each microCT image was converted (from the 30-μm imaging resolution) to have an isotropic voxel resolution of 50 μm. This resolution was chosen to match the definition of shallow marrow so that the first layer of marrow voxels surrounding the bone trabeculae could be interpreted as that target region. The inactive marrow and active marrow portions of shallow marrow have different tag numbers for energy deposition tallying purposes within MCNPX. This process was followed so that total active marrow could also be defined as a target region. Resultantly, the portion of active marrow within the shallow marrow target needed to be accounted for in the calculation of absorbed fractions to both target tissues. Figure 3 shows an example of a 3D rendering of the skeletal macrostructure and microstructure (derived from microCT images, one of which is shown) for the sternum. Source regions within the bone microstructure include active marrow (AM), inactive marrow (IM), trabecular bone surfaces (TBS), and trabecular bone volumes (TBV). The source regions of cortical bone surfaces (CBS) and cortical volumes (CBV) are considered only in the bone macrostructural models (Section 2.2).
Figure 3.
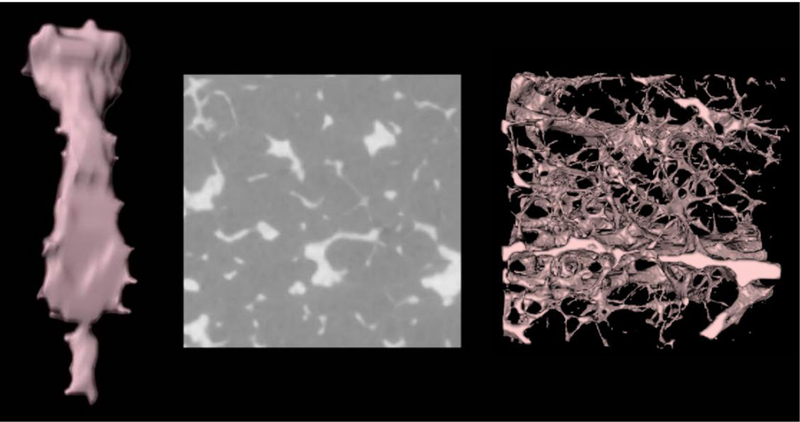
The bone macrostructure (left), microCT image slice (center), and bone microstructure (right) for the adult female sternum.
2.3.1. Cellularity.
Marrow cellularity is defined as the fraction of marrow space that is hematopoietically active (Hough et al., 2011). As inactive (or yellow) marrow is primarily composed of adipocytes, the marrow cellularity defined in this study is equivalent to one minus the marrow fat fraction. ICRP Publication 70 provides reference values for the cellularity of each skeletal site for the adult female (ICRP, 1995). For the humeri and femora, ICRP Publication 70 reports a reference cellularity factor of 0.25 (or 25%) for the “upper half” of these long bones but does not specify its distribution among the proximal ends (head and neck) and upper medullary cavity (ICRP, 1995). In the present study, the proximal ends were assigned a cellularity factor of 0.35 while the upper halves of the medullary cavities were assigned a cellularity factor of 0.15, resulting in a linear average of 0.25 over the entire upper halves of the humeri and femora.
As individual patients may have marrow cellularities that differ from ICRP reference values, versions of each microstructure were created in which the cellularity was incremented from a minimum of 10% to a maximum of 100% (at which point the marrow cavity is comprised entirely of active marrow). A version of each microstructure was also created at its ICRP Publication 70 reference cellularity. An example of a microstructure image after imposing a reference marrow cellularity of 70% can be seen in Figure 1C for the third cervical vertebra.
2.3.2. Defining the Shallow Marrow.
Special considerations were taken when identifying voxels assigned as the shallow marrow target. Due to the use of a voxelized geometry, shallow marrow voxels might interface adjacent bone trabeculae voxels at either their edges or corners. These geometrical cases imply that the transected distance traveled through the voxel by the transported particle could exceed the specified target thickness of 50 μm. For clarification on what is meant by edge and corner voxels, the reader is referred to Figure 4. If one were to only label the voxels whose faces interface with the bone voxels, an underestimation of shallow marrow volume would occur. Likewise, when using the whole volume of a corner or edge voxel, one would overestimate the volume of the shallow marrow. To properly account for the shallow marrow volume occupying such voxels, geometric weighting factors were derived. These weighting factors are simply the volume that would be occupied by shallow marrow over the total voxel volume. For voxels denoted as edge voxels, the energy-deposition weighting factor is π/4, while the corresponding weighting factor for corner voxels is π/6. Edge and corner voxels were labeled separately with their own tag numbers for dose tallying purposes to allow for proper weighting of energy deposition following particle transport. Figure 1D illustrates a microstructure image with the shallow marrow layer labeled.
Figure 4.
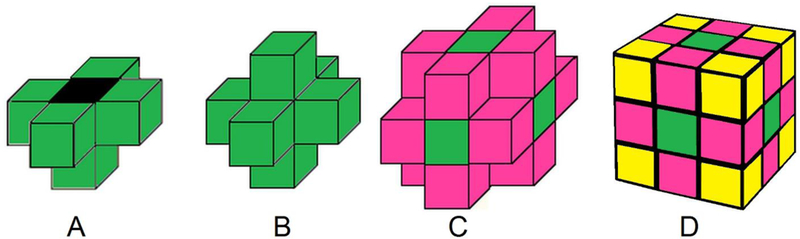
(A) Exposed mineral bone voxel (black). (B) Face Voxels (green). (C) Edge Voxels (magenta). (D) Corner Voxels (yellow).
2.4. Radiation Transport
Twenty-five mono-energetic electron energies were run for each bone macro- and microstructure, ranging from 10 keV to 1 MeV. Limiting values of the absorbed fraction were assigned at 1 keV, with values between 1 and 10 keV assigned via log-log interpolation. The elemental compositions and densities used for the material definitions in MCNPX for the macro- and microstructure of each skeletal site are given in Tables 2 and 3, respectively. As will be discussed in Section 3.2, absorbed fractions assessed during microstructural transport runs (infinite spongiosa) are later corrected for electron escape based upon absorbed fractions assessed during macrostructural transport runs. This method thus differs from prior PIRT model simulations, where both geometries are considered simultaneously (Shah et al., 2005b).
Table 2.
Elemental compositions and densities used for the material definitions for each skeletal site macrostructure.
| Skeletal Site | Element | Density | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Spongiosa / Medullary Cavity) | H | C | N | O | Na | Mg | P | S | Cl | K | Ca | Fe | (g/cm) |
| Craniofacial Bones | 5.96 | 26.74 | 3.47 | 42.31 | 0.23 | 0.16 | 6.42 | 0.25 | 0.02 | 0.00 | 0.01 | 14.42 | 1.600 |
| Mandible | 9.95 | 46.78 | 2.21 | 36.03 | 0.13 | 0.09 | 1.48 | 0.17 | 0.02 | 0.00 | 0.01 | 3.09 | 1.131 |
| Scapulae | 9.20 | 44.81 | 2.39 | 35.30 | 0.15 | 0.11 | 2.47 | 0.18 | 0.01 | 0.01 | 5.35 | 0.03 | 1.047 |
| Clavicles | 9.69 | 46.12 | 2.20 | 35.71 | 0.14 | 0.09 | 1.86 | 0.17 | 0.02 | 0.00 | 0.01 | 3.96 | 1.067 |
| Sternum | 9.83 | 38.69 | 2.91 | 44.13 | 0.12 | 0.13 | 1.28 | 0.19 | 0.04 | 0.00 | 0.03 | 2.59 | 1.086 |
| Ribs | 9.46 | 38.67 | 2.96 | 42.80 | 0.13 | 0.14 | 1.79 | 0.20 | 0.03 | 0.00 | 0.02 | 3.74 | 1.093 |
| Cervical Vertebrae | 8.88 | 35.53 | 3.10 | 43.95 | 0.15 | 0.14 | 2.51 | 0.21 | 0.04 | 0.00 | 0.02 | 5.42 | 1.170 |
| Thoracic Vertebrae | 9.68 | 39.34 | 2.92 | 42.90 | 0.13 | 0.13 | 1.50 | 0.19 | 0.03 | 0.00 | 0.02 | 3.08 | 1.114 |
| Lumbar Vertebrae | 9.57 | 39.47 | 2.93 | 42.36 | 0.13 | 0.14 | 1.66 | 0.19 | 0.03 | 0.00 | 0.02 | 3.44 | 1.126 |
| Sacrum | 9.44 | 38.41 | 2.97 | 43.00 | 0.14 | 0.14 | 1.81 | 0.20 | 0.03 | 0.00 | 0.02 | 3.79 | 1.138 |
| Os coxae | 9.77 | 43.18 | 2.49 | 39.15 | 0.13 | 0.10 | 1.58 | 0.18 | 0.03 | 0.00 | 0.02 | 3.31 | 1.046 |
| Humeri, Proximal | 9.96 | 48.99 | 1.95 | 33.70 | 0.13 | 0.07 | 1.60 | 0.16 | 0.02 | 0.00 | 0.01 | 3.38 | 1.080 |
| Humeri, Upper Shaft (MC) | 11.17 | 55.37 | 1.52 | 31.46 | 0.10 | 0.05 | 0.12 | 0.13 | 0.02 | 0.00 | 0.01 | 0.00 | 0.989 |
| Humeri, Lower Shaft (MC) | 11.47 | 63.26 | 0.76 | 24.19 | 0.10 | 0.00 | 0.10 | 0.10 | 0.01 | 0.00 | 0.00 | 0.00 | 0.981 |
| Humeri, Distal | 9.49 | 50.91 | 1.64 | 29.87 | 0.15 | 0.05 | 2.42 | 0.15 | 0.01 | 0.00 | 0.01 | 5.30 | 1.135 |
| Radii, Proximal | 10.25 | 55.61 | 1.30 | 27.72 | 0.13 | 0.03 | 1.53 | 0.13 | 0.01 | 0.00 | 0.01 | 3.28 | 1.089 |
| Radii, Shaft (MC) | 11.48 | 63.67 | 0.74 | 23.80 | 0.10 | 0.00 | 0.10 | 0.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.981 |
| Radii, Distal | 9.91 | 53.57 | 1.45 | 28.62 | 0.14 | 0.04 | 1.93 | 0.14 | 0.01 | 0.00 | 0.01 | 4.19 | 1.101 |
| Ulnae, Proximal | 9.38 | 50.25 | 1.69 | 30.16 | 0.15 | 0.05 | 2.55 | 0.15 | 0.01 | 0.00 | 0.01 | 5.60 | 1.223 |
| Ulnae, Shaft (MC) | 11.48 | 63.65 | 0.74 | 23.83 | 0.10 | 0.00 | 0.10 | 0.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.981 |
| Ulnae, Distal | 9.63 | 51.81 | 1.57 | 29.45 | 0.15 | 0.05 | 2.25 | 0.15 | 0.01 | 0.00 | 0.01 | 4.92 | 1.016 |
| Wrists and Hands | 9.49 | 50.94 | 1.64 | 29.84 | 0.15 | 0.05 | 2.42 | 0.15 | 0.01 | 0.00 | 0.01 | 5.30 | 1.062 |
| Femora, Proximal | 9.38 | 45.14 | 2.19 | 35.58 | 0.15 | 0.08 | 2.29 | 0.17 | 0.02 | 0.00 | 0.01 | 4.96 | 1.199 |
| Femora, Upper Shaft (MC) | 11.14 | 54.02 | 1.58 | 32.77 | 0.10 | 0.05 | 0.12 | 0.13 | 0.03 | 0.00 | 0.02 | 0.00 | 0.989 |
| Femora, Lower Shaft (MC) | 11.47 | 63.32 | 0.75 | 24.14 | 0.10 | 0.00 | 0.10 | 0.10 | 0.01 | 0.00 | 0.00 | 0.00 | 0.981 |
| Femora, Distal | 9.55 | 51.19 | 1.62 | 29.80 | 0.15 | 0.05 | 2.34 | 0.15 | 0.01 | 0.00 | 0.01 | 5.13 | 1.164 |
| Patellae | 9.55 | 51.04 | 1.62 | 29.96 | 0.15 | 0.05 | 2.34 | 0.15 | 0.01 | 0.00 | 0.01 | 5.11 | 1.149 |
| Tibiae, Proximal | 9.91 | 53.52 | 1.45 | 28.69 | 0.14 | 0.04 | 1.92 | 0.14 | 0.01 | 0.00 | 0.01 | 4.17 | 1.123 |
| Tibiae, Shaft (MC) | 11.46 | 62.82 | 0.78 | 24.62 | 0.10 | 0.00 | 0.10 | 0.10 | 0.01 | 0.00 | 0.01 | 0.00 | 0.981 |
| Tibiae, Distal | 9.80 | 52.83 | 1.50 | 28.99 | 0.14 | 0.04 | 2.06 | 0.14 | 0.01 | 0.00 | 0.01 | 4.48 | 1.135 |
| Fibulae, Proximal | 10.38 | 56.46 | 1.24 | 27.33 | 0.13 | 0.03 | 1.37 | 0.13 | 0.01 | 0.00 | 0.01 | 2.91 | 1.091 |
| Fibulae, Shaft (MC) | 11.47 | 63.15 | 0.76 | 24.30 | 0.10 | 0.00 | 0.10 | 0.10 | 0.01 | 0.00 | 0.00 | 0.00 | 0.981 |
| Fibulae, Distal | 9.54 | 51.12 | 1.62 | 29.83 | 0.15 | 0.05 | 2.36 | 0.15 | 0.01 | 0.00 | 0.01 | 5.16 | 1.144 |
| Ankles and Feet | 9.55 | 51.14 | 1.62 | 29.86 | 0.15 | 0.05 | 2.34 | 0.15 | 0.01 | 0.00 | 0.01 | 5.13 | 1.063 |
| (All Cortical Bone) | 3.57 | 15.95 | 4.19 | 44.82 | 0.30 | 0.20 | 9.40 | 0.30 | 0.00 | 0.00 | 0.00 | 21.27 | 1.90 |
Table 3.
Elemental compositions and densities used for the material definitions for each skeletal site microstructure.
| Element | Density | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Skeletal Tissue | H | C | N | O | Na | Mg | P | S | Cl | K | Ca | Fe | (g/cm3) |
| Active Marrow | 10.50 | 41.40 | 3.40 | 43.90 | 0.10 | 0.20 | 0.20 | 0.20 | 0.00 | 0.00 | 0.00 | 0.10 | 1.03 |
| Inactive Marrow | 11.50 | 64.40 | 0.70 | 23.10 | 0.10 | 0.00 | 0.10 | 0.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.98 |
| Mineral Bone | 3.50 | 16.00 | 4.20 | 44.50 | 0.30 | 0.20 | 9.50 | 0.30 | 0.00 | 0.00 | 21.50 | 0.00 | 1.90 |
Data from ICRP Publication 89
2.4.1. Macrostructure Runs.
Electron transport using MCNPX v2.7 was completed for all 34 bone sites, as well as the separated lumbar vertebrae. For each skeletal site, two transport runs were completed (at each given energy): one with the electron source defined within the cortical bone volume (CBV), and one with the electron source defined as the spongiosa volume. This approach allowed us to account for both electron escape from spongiosa, as well as electron cross-fire from cortical bone to spongiosa targets. It is important to note that because microstructure of cortical bone is not considered in this study (ICRP no longer considers cortical bone to house relevant target cells), electron sources on the inner surfaces of the Haversian canals are considered to be properly represented by a CBV source. For each macrostructure source, the target region was the spongiosa. A *F8 tally was used to score the deposited energy (in MeV) in the defined target region. Statistical tally errors were within 1%; however, most tally errors were well below 1%.
2.4.2. Long Bone Shafts.
For the shafts of the long bones, the cortical bone volume, medullary marrow, and boney interface between these two regions were each run separately as defined electron source regions. The 50-μm shallow marrow shell was the only target for all the shafts, with the exception of the upper femora and humeri, which in our model also contains active marrow as an additional target region. The cortical bone surface source was defined as an infinitely thin surface at the interface of the cortical bone shell and medullary marrow. Statistical tally errors were within 1%.
2.4.3. Microstructure Runs.
All 37 skeletal microstructures were modeled in MCNPX v2.7 for electron transport. The defined target regions, and therefore regions in which energy deposition was tallied, were active marrow and shallow marrow. Source regions included: active marrow, inactive marrow, trabecular bone volume, trabecular bone surfaces, cortical bone volume, and cortical bone surfaces. Again, energy deposition with secondary electron transport (in MeV) was scored in both defined target regions. In order to model the microstructure as infinite in spatial extent, reflective surfaces were employed in MCNPX. Resultantly, when a particle reached the boundaries of the entire voxel model, it was reflected back, without energy loss or interaction. An illustration of this bounding box is shown in Figure 2 in which the box surrounds the 3D microstructure of the third cervical vertebra. Each microstructure was run at marrow cellularities of 10%, 20%, 40%, 60%, 80%, 100%, as well as at the ICRP reference cellularity for that skeletal site. Active marrow, inactive marrow, and trabecular bone were run separately as sources. Statistical tally errors were below 1%, with the majority well below 1%.
2.4.4. Physics Considerations.
Integrated Tiger Series (ITS) indexing was used, rather than the default MCNPX electron energy bin indexing, as it is a more accurate algorithm for energy binning through the use of the nearest-bin electron energy rather than a bin- centered value (Wayson, 2012). The effect on tally means was investigated by varying the input parameter estep in the material card; in particular, the effect was assessed on the shallow marrow layer as this was the thinnest target region considered, and therefore the region that would be maximally impacted. The number of electron substeps per electron energy step is equivalent to the estep of that material. When comparing the tallies resulting from using the suggested number of electron substeps to that of the default value, the difference observed was less than 1%.
3. Results
3.1. Skeletal Tissue Model for the UF Reference Adult Female
Two sets of image-based volume fractions were determined to establish the skeletal tissue distribution model for the reference adult female. Ex-vivo CT images of each excised bone site were segmented into regions of cortical bone, spongiosa, and for the long bones, the medullary cavities. Their corresponding volume fractions (CBVF, SVF, and MCVF), along with the homogenous bone volumes to which they apply, are shown in columns 3–5 of Table 4. MicroCT images of cored spongiosa were similarly used to establish volume fractions for trabecular bone (TBVF), total marrow (MVF), and shallow marrow (SMVF), shown in columns 6–8 of Table 4. Shallow marrow, as a fraction of marrow space, is further given, along with the marrow cellularity, in the final two columns of Table 4.
Table 4.
Macroscopic and microscopic volume fractions within the skeleton of the UF adult female hybrid phantom (UFHADF).
| Homogeneous | Homogeneous Bone Volume Fractions |
Spongiosa Volume Fractions |
TM50 | ICRP 70 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Skeletal Site | Bone Volume (cm3) |
Cortical Bone | Spongiosa | Med Cavity | Trab Bone | Marrow | Shallow Marrow | (% MV) | Cellularity |
| Craniofacial Bones | 579.0 | 0.589 | 0.411 | 0.679 | 0.321 | 0.186 | 58.0% | 38% | |
| Mandible | 48.4 | 0.502 | 0.498 | 0.150 | 0.851 | 0.099 | 11.7% | 38% | |
| Scapulae | 306.2 | 0.389 | 0.611 | 0.054 | 0.947 | 0.122 | 12.9% | 38% | |
| Clavicles | 51.2 | 0.435 | 0.565 | 0.078 | 0.923 | 0.094 | 10.2% | 33% | |
| Sternum | 38.9 | 0.261 | 0.739 | 0.082 | 0.918 | 0.096 | 10.5% | 70% | |
| Ribs | 309.2 | 0.429 | 0.571 | 0.091 | 0.909 | 0.112 | 12.3% | 70% | |
| Cervical Vertebrae | 80.2 | 0.358 | 0.642 | 0.178 | 0.822 | 0.209 | 25.5% | 70% | |
| Thoracic Vertebrae | 229.8 | 0.211 | 0.789 | 0.114 | 0.886 | 0.155 | 17.4% | 70% | |
| Lumbar Vertebrae | 271.5 | 0.151 | 0.849 | 0.126 | 0.874 | 0.150 | 17.1% | 70% | |
| Sacrum | 194.5 | 0.258 | 0.742 | 0.150 | 0.850 | 0.169 | 19.8% | 48% | |
| Os coxae | 639.7 | 0.230 | 0.770 | 0.046 | 0.954 | 0.083 | 8.7% | 48% | |
| Humeri, Proximal | 127.1 | 0.119 | 0.881 | 0.092 | 0.909 | 0.140 | 15.4% | 35% | |
| Humeri, Upper Shaft | 67.4 | 0.647 | 0.353 | 0.000 | 1.000 | 0.015 | 1.5% | 15% | |
| Humeri, Lower Shaft | 59.4 | 0.649 | 0.351 | 0.000 | 1.000 | 0.019 | 1.9% | 0% | |
| Humeri, Distal | 80.9 | 0.236 | 0.764 | 0.169 | 0.831 | 0.197 | 23.7% | 0% | |
| Radii, Proximal | 12.6 | 0.255 | 0.745 | 0.118 | 0.882 | 0.142 | 16.1% | 0% | |
| Radii, Shaft | 46.9 | 0.661 | 0.339 | 0.000 | 1.000 | 0.028 | 2.8% | 0% | |
| Radii, Distal | 22.8 | 0.174 | 0.826 | 0.131 | 0.869 | 0.166 | 19.1% | 0% | |
| Ulnae, Proximal | 42.8 | 0.188 | 0.812 | 0.265 | 0.735 | 0.238 | 32.4% | 0% | |
| Ulnae, Shaft | 55.6 | 0.661 | 0.339 | 0.000 | 1.000 | 0.022 | 2.2% | 0% | |
| Ulnae, Distal | 8.0 | 0.182 | 0.818 | 0.073 | 0.927 | 0.141 | 15.3% | 0% | |
| Wrists and Hands | 115.3 | 0.647 | 0.353 | 0.046 | 0.954 | 0.197 | 20.7% | 0% | |
| Femora, Proximal | 181.9 | 0.099 | 0.901 | 0.225 | 0.775 | 0.185 | 23.9% | 35% | |
| Femora, Upper Shaft | 125.2 | 0.475 | 0.525 | 0.000 | 1.000 | 0.012 | 1.2% | 15% | |
| Femora, Lower Shaft | 142.9 | 0.477 | 0.523 | 0.000 | 1.000 | 0.011 | 1.1% | 0% | |
| Femora, Distal | 237.2 | 0.144 | 0.856 | 0.182 | 0.818 | 0.189 | 23.1% | 0% | |
| Patellae | 25.5 | 0.141 | 0.859 | 0.185 | 0.815 | 0.213 | 26.2% | 0% | |
| Tibiae, Proximal | 188.1 | 0.117 | 0.883 | 0.157 | 0.843 | 0.208 | 24.7% | 0% | |
| Tibiae, Shaft | 167.5 | 0.528 | 0.472 | 0.000 | 1.000 | 0.014 | 1.4% | 0% | |
| Tibiae, Distal | 69.1 | 0.148 | 0.852 | 0.170 | 0.830 | 0.195 | 23.6% | 0% | |
| Fibulae, Proximal | 15.8 | 0.166 | 0.834 | 0.121 | 0.880 | 0.161 | 18.4% | 0% | |
| Fibulae, Shaft | 25.4 | 0.686 | 0.314 | 0.000 | 1.000 | 0.041 | 4.1% | 0% | |
| Fibulae, Distal | 15.5 | 0.257 | 0.743 | 0.179 | 0.821 | 0.182 | 22.2% | 0% | |
| Ankles and Feet | 368.7 | 0.315 | 0.685 | 0.046 | 0.954 | 0.189 | 19.8% | 0% | |
| Total Skeleton (cm3) | 4950.0 | ||||||||
| Total Skeletal Mass (g) | 6877.4 | ||||||||
| ICRP 89 Mass (g) | 6860.0 | Note - ICRP value for total skeletal mass excludes cartilage and teeth. | |||||||
| Ratio | 1.00 | ||||||||
| Ave Skel Density (g/cm3) | 1.39 | ||||||||
The distribution of mineral bone in each skeletal site into its cortical and trabecular form are provided in Table 5. The results of the present study are compared with values reported by Johnson (1964) and by Spiers and Beddoe (1983). Notable differences are seen in the craniofacial bones and vertebrae. For the former, the percentage of cortical bone in the present study is significantly lower than reported in the Johnson study - 68% versus 95%. For the vertebral series, Johnson reported that mineral bone is more predominate in its trabecular form, while the opposite was found in the CT/microCT image analysis of the present study. We report the percentage of cortical bone to be 76%, 70%, and 59% of mineral bone in the cervical, thoracic, and lumbar vertebrae of the adult female.
Table 5.
Distribution of mineral bone in the present model for the adult female, compared to the mineral bone distributions computed in a study by Johnson (1964) and a study by Spiers and Beddoe (1983) for the adult male.
| Distribution of mineral bone | ||||||||
|---|---|---|---|---|---|---|---|---|
| Skeletal Site |
Present Model |
Johnson (1964) |
Spiers & Beddoe (1983) |
|||||
| %CB | %TB | %CB | %TB | %CB | %TB | |||
| Craniofacial Bones | 68 | 32 | 95 | 5 | ||||
| Mandible | 87 | 13 | 95 | 5 | ||||
| Scapulae | 92 | 8 | 94 | 6 | ||||
| Clavicles | 91 | 9 | 94 | 6 | ||||
| Sternum | 81 | 19 | 94 | 6 | ||||
| Ribs | 89 | 11 | 94 | 6 | ||||
| Cervical Vertebrae | 76 | 24 | 25 | 75 | ||||
| Thoracic Vertebrae | 70 | 30 | 25 | 75 | ||||
| Lumbar Vertebrae | 59 | 41 | 34 | 66 | ||||
| Sacrum | 70 | 30 | 75 | 25 | ||||
| Os coxae | 87 | 13 | 90 | 10 | ||||
| Humeri | 81 | 19 | 80 | 20 | 90 | 10 | ||
| Radii | 79 | 21 | 84 | 16 | 87 | 13 | ||
| Ulnae | 74 | 26 | 87 | 13 | 87 | 13 | ||
| Wrist and Hands | 98 | 2 | 95 | 5 | ||||
| Femora | 70 | 30 | 67 | 33 | 77 | 23 | ||
| Patellae | 53 | 47 | ||||||
| Tibiae | 65 | 35 | 74 | 26 | 83 | 17 | ||
| Fibulae | 76 | 24 | 76 | 24 | 89 | 11 | ||
| Ankles and Feet | 91 | 9 | 95 | 5 | ||||
Table 6 presents the finalized estimates of bone-specific skeletal tissue masses for the reference adult female, to include active marrow, inactive marrow, trabecular bone, and cortical bone. For each of these tissues, two masses are given - one excluding and one including miscellaneous skeletal tissues (MST), which comprise a total mass of 160 g in the adult female (ICRP, 2002). Excluding their MST components, active and inactive marrow are shown to match ICRP Publication 89 values to within 0.24% and 0.38%, respectively. Estimates of trabecular and cortical bone masses are within 8.5% and 1.4%, respectively, of ICRP 89 reference values. The total skeletal tissue mass of the UF reference adult female is shown to be within only 0.25% of the ICRP reference value of 6860 g (less cartilage and teeth) (bottom of Table 4).
Table 6.
Skeletal tissue masses and their fractional distribution within the skeleton of the UF adult female hybrid phantom.
| Tissue Masses exclusive of MST (g) | Tissue Masses inclusive of MST (g) | Surface Areas (m2) | Fractional Tissue Weights | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Skeletal Site | AM | IM | TBV | CBV | AM | IM | TM50 | TBV | CBV | TBS | CBSHC | CBSMC | fAM | fIM | fTBV | fTBS | fCBV | fCBS-HC | fCBS-MC |
| Craniofacial Bones | 29.1 | 45.0 | 303.0 | 635.3 | 30.0 | 46.6 | 44.4 | 308.2 | 646.3 | 2.870 | 1.003 | 0.0322 | 0.0251 | 0.3491 | 0.3491 | 0.2014 | 0.1995 | ||
| Mandible | 7.7 | 12.0 | 6.7 | 45.5 | 8.0 | 12.4 | 2.4 | 6.8 | 46.3 | 0.064 | 0.072 | 0.0086 | 0.0067 | 0.0077 | 0.0077 | 0.0144 | 0.0143 | ||
| Scapulae | 66.8 | 103.6 | 18.6 | 224.1 | 69.0 | 107.1 | 22.7 | 18.9 | 228.0 | 0.176 | 0.354 | 0.0741 | 0.0578 | 0.0214 | 0.0214 | 0.0710 | 0.0704 | ||
| Clavicles | 8.8 | 16.9 | 4.2 | 41.7 | 9.1 | 17.5 | 2.7 | 4.3 | 42.4 | 0.040 | 0.066 | 0.0097 | 0.0094 | 0.0048 | 0.0048 | 0.0132 | 0.0131 | ||
| Sternum | 18.4 | 7.5 | 4.4 | 19.0 | 19.0 | 7.7 | 2.8 | 4.5 | 19.3 | 0.042 | 0.030 | 0.0204 | 0.0042 | 0.0051 | 0.0051 | 0.0060 | 0.0060 | ||
| Ribs | 112.1 | 45.6 | 29.8 | 248.0 | 115.7 | 47.2 | 20.0 | 30.3 | 252.3 | 0.283 | 0.392 | 0.1242 | 0.0254 | 0.0344 | 0.0344 | 0.0786 | 0.0779 | ||
| Cervical Vertebrae | 29.5 | 12.0 | 17.1 | 53.7 | 30.5 | 12.4 | 10.9 | 17.4 | 54.6 | 0.162 | 0.085 | 0.0327 | 0.0067 | 0.0197 | 0.0197 | 0.0170 | 0.0169 | ||
| Thoracic Vertebrae | 112.2 | 45.7 | 38.5 | 90.6 | 115.9 | 47.2 | 28.4 | 39.2 | 92.1 | 0.365 | 0.143 | 0.1244 | 0.0255 | 0.0444 | 0.0444 | 0.0287 | 0.0285 | ||
| Lumbar Vertebrae | 140.7 | 57.3 | 54.2 | 76.7 | 145.2 | 59.2 | 35.1 | 55.1 | 78.0 | 0.513 | 0.121 | 0.1559 | 0.0319 | 0.0624 | 0.0624 | 0.0243 | 0.0241 | ||
| Sacrum | 58.8 | 60.5 | 40.5 | 93.6 | 60.7 | 62.5 | 24.4 | 41.2 | 95.3 | 0.384 | 0.148 | 0.0651 | 0.0337 | 0.0466 | 0.0466 | 0.0297 | 0.0294 | ||
| Os coxae | 224.9 | 231.5 | 42.5 | 275.0 | 232.2 | 239.3 | 40.8 | 43.2 | 279.7 | 0.403 | 0.434 | 0.2493 | 0.1291 | 0.0490 | 0.0490 | 0.0872 | 0.0864 | ||
| Humeri, Proximal | 35.5 | 62.7 | 19.1 | 28.2 | 36.7 | 64.8 | 15.7 | 19.5 | 28.7 | 0.181 | 0.045 | 0.0394 | 0.0349 | 0.0220 | 0.0220 | 0.0089 | 0.0089 | ||
| Humeri, Upper Shaft | 3.5 | 18.8 | 0.0 | 82.2 | 3.6 | 19.5 | 0.3 | 0 | 83.6 | 0 | 0.130 | 0.004 | 0.0039 | 0.0105 | 0.0000 | 0.0000 | 0.0261 | 0.0258 | 0.0008 |
| Humeri, Lower Shaft | 0 | 19.5 | 0.0 | 72.4 | 0 | 20.2 | 0.4 | 0 | 73.7 | 0 | 0.114 | 0.004 | 0.0000 | 0.0109 | 0.0000 | 0.0000 | 0.0230 | 0.0228 | 0.0007 |
| Humeri, Distal | 0 | 48.7 | 19.5 | 35.6 | 0 | 50.4 | 12.0 | 19.9 | 36.2 | 0.185 | 0.056 | 0.0000 | 0.0272 | 0.0225 | 0.0225 | 0.0113 | 0.0112 | ||
| Radii, Proximal | 0 | 7.8 | 2.1 | 6.0 | 0 | 8.1 | 1.3 | 2.1 | 6.1 | 0.020 | 0.009 | 0.0000 | 0.0044 | 0.0024 | 0.0024 | 0.0019 | 0.0019 | ||
| Radii, Shaft | 0 | 14.9 | 0.0 | 58.2 | 0 | 15.4 | 0.4 | 0 | 59.2 | 0 | 0.092 | 0.004 | 0.0000 | 0.0083 | 0.0000 | 0.0000 | 0.0184 | 0.0183 | 0.0008 |
| Radii, Distal | 0 | 15.5 | 4.6 | 7.4 | 0 | 16.0 | 3.1 | 4.7 | 7.6 | 0.044 | 0.012 | 0.0000 | 0.0086 | 0.0053 | 0.0053 | 0.0024 | 0.0023 | ||
| Ulnae, Proximal | 0 | 24.2 | 17.2 | 15.0 | 0 | 25.0 | 8.1 | 17.5 | 15.3 | 0.163 | 0.024 | 0.0000 | 0.0135 | 0.0198 | 0.0198 | 0.0048 | 0.0047 | ||
| Ulnae, Shaft | 0 | 17.6 | 0.0 | 69.2 | 0 | 18.2 | 0.4 | 0 | 70.4 | 0 | 0.109 | 0.005 | 0.0000 | 0.0098 | 0.0000 | 0.0000 | 0.0219 | 0.0217 | 0.0009 |
| Ulnae, Distal | 0 | 5.7 | 0.9 | 2.7 | 0 | 5.9 | 0.9 | 0.9 | 2.7 | 0.008 | 0.004 | 0.0000 | 0.0032 | 0.0010 | 0.0010 | 0.0009 | 0.0008 | ||
| Wrists and Hands | 0 | 36.3 | 3.5 | 140.3 | 0 | 37.5 | 7.8 | 3.5 | 142.7 | 0.033 | 0.222 | 0.0000 | 0.0202 | 0.0040 | 0.0040 | 0.0445 | 0.0441 | ||
| Femora, Proximal | 44.4 | 78.2 | 68.8 | 33.7 | 45.8 | 80.9 | 30.1 | 70.0 | 34.3 | 0.652 | 0.053 | 0.0492 | 0.0436 | 0.0793 | 0.0793 | 0.0107 | 0.0106 | ||
| Femora, Upper Shaft | 9.8 | 52.7 | 0.0 | 111.5 | 10.1 | 54.5 | 0.8 | 0 | 113.5 | 0 | 0.176 | 0.008 | 0.0109 | 0.0294 | 0.0000 | 0.0000 | 0.0354 | 0.0350 | 0.0015 |
| Femora, Lower Shaft | 0 | 70.8 | 0.0 | 127.3 | 0 | 73.2 | 0.8 | 0 | 129.5 | 0 | 0.201 | 0.008 | 0.0000 | 0.0395 | 0.0000 | 0.0000 | 0.0404 | 0.0400 | 0.0016 |
| Femora, Distal | 0 | 157.3 | 69.1 | 63.9 | 0 | 162.6 | 37.5 | 70.3 | 65.0 | 0.655 | 0.101 | 0.0000 | 0.0877 | 0.0797 | 0.0797 | 0.0203 | 0.0201 | ||
| Patellae | 0 | 16.9 | 7.6 | 6.7 | 0 | 17.5 | 4.6 | 7.7 | 6.8 | 0.072 | 0.011 | 0.0000 | 0.0094 | 0.0087 | 0.0087 | 0.0021 | 0.0021 | ||
| Tibiae, Proximal | 0 | 132.7 | 48.7 | 41.1 | 0 | 137.2 | 33.8 | 49.5 | 41.8 | 0.461 | 0.065 | 0.0000 | 0.0740 | 0.0561 | 0.0561 | 0.0130 | 0.0129 | ||
| Tibiae, Shaft | 0 | 74.7 | 0.0 | 165.5 | 0 | 77.3 | 1.1 | 0 | 168.4 | 0 | 0.261 | 0.011 | 0.0000 | 0.0417 | 0.0000 | 0.0000 | 0.0525 | 0.0520 | 0.0022 |
| Tibiae, Distal | 0 | 46.3 | 18.7 | 19.3 | 0 | 47.8 | 11.3 | 19.0 | 19.6 | 0.177 | 0.030 | 0.0000 | 0.0258 | 0.0216 | 0.0215 | 0.0061 | 0.0060 | ||
| Fibulae, Proximal | 0 | 11.0 | 3.0 | 4.9 | 0 | 11.4 | 2.1 | 3.0 | 5.0 | 0.028 | 0.008 | 0.0000 | 0.0061 | 0.0034 | 0.0034 | 0.0015 | 0.0015 | ||
| Fibulae, Shaft | 0 | 7.4 | 0.0 | 33.0 | 0 | 7.6 | 0.3 | 0 | 33.6 | 0 | 0.052 | 0.003 | 0.0000 | 0.0041 | 0.0000 | 0.0000 | 0.0105 | 0.0104 | 0.0007 |
| Fibulae, Distal | 0 | 8.9 | 3.8 | 7.4 | 0 | 9.2 | 2.0 | 3.9 | 7.6 | 0.036 | 0.012 | 0.0000 | 0.0050 | 0.0044 | 0.0044 | 0.0024 | 0.0023 | ||
| Ankles and Feet | 0 | 227.0 | 21.7 | 219.6 | 0 | 234.8 | 46.5 | 22.0 | 223.3 | 0.205 | 0.347 | 0.0000 | 0.1266 | 0.0250 | 0.0250 | 0.0696 | 0.0690 | ||
| Totals | 902 | 1793 | 868 | 3154 | 931 | 1854 | 456 | 883 | 3209 | 8.22 | 4.98 | 0.05 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9908 | 0.0092 |
| Total MST Mass | 160 | ||||||||||||||||||
| ICRP 89 Values | 900 | 1800 | 800 | 3200 | ICRP 89 Value | 160 | |||||||||||||
| Ratio | 1.00 | 1.00 | 1.08 | 0.99 | Ratio | 1.00 | |||||||||||||
Estimates of the skeletal distribution of shallow marrow (TM50) is provided in column 8 of Table 6, and is based upon the shallow marrow volume fractions given in Table 4. These estimates include the application of geometric scaling factors as described earlier in Section 2.3.2. Total shallow marrow in the reference adult female is estimated to be 456 g. Table 6 additionally provides estimates of trabecular and cortical surface areas, calculated as the product of their corresponding bone volumes and ICRP Publication 89 reference surface-to-volume ratios (ICRP, 1995). The total trabecular surface area is estimated to be 8.22 m2 in the adult female. The total cortical surface area is 5.03 m2 which is dominated by the internal surfaces of the Harversian canals. Less than 1% of cortical surfaces are associated with the medullary cavities of the long bones.
Fractional tissue weights are given in the final set of columns of Table 6, and are based upon skeletal masses inclusive of MST. These values are subsequently used in the computation of skeletal averaged absorbed fractions. The largest reserves of active marrow are found in the os coxae (25%), lumbar vertebrae (16%), thoracic vertebrae (12%), and ribs (12%). Corresponding gender-neutral values given in ICRP Publication 70, based upon early estimates by Cristy (1981), are 17.5%, 12.3%, 16%, and 16%, respectively. Cristy had estimated that for the reference adult, a total of 7.6% of total active marrow lies within the cranium. Our microCT/ex-vivo CT studies of the adult male (40- year) (Hough et al., 2011) and adult female (45-year) (present study) indicate a much smaller percentage - 5% and 3%, respectively.
3.2. Absorbed Fractions and Specific Absorbed Fractions
Absorbed fractions (AF) were determined for two target regions rT - active marrow and shallow marrow - for various source tissues in either spongiosa (AM, IM, TBS, and TBV) or cortical bone (CBS and CBV). Absorbed fractions for spongiosa or medullary marrow sources rS for electron energy Ei were computed as:
| (3) |
where is the AF based upon transport in the skeletal microstructure, and is the corresponding AF based upon transport in the skeletal macrostructure. When the electron source is in cortical bone, the following expression, adapted from Wayson (2012), was applied:
| (4) |
with CF as the ICRP reference cellularity, and TBVF as the trabecular bone volume fraction.
The mathematical combination of radiation transport results for both the skeletal macrostructure and microstructure was found to yield AFs very similar to those of the UF adult male skeletal model of Hough et al. (2011) which were determined using the PIRT method. An example of this AF comparison is shown in Figure 5, with the skeletal site being the sternum and the source/target combination being AM to AM.
Figure 5.
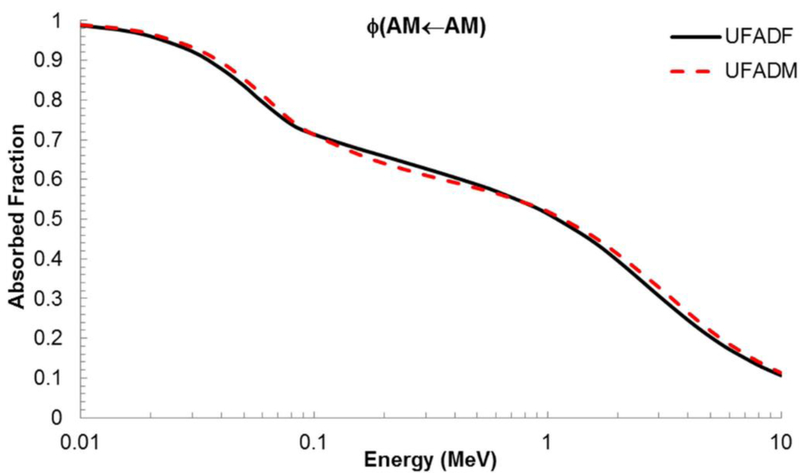
Absorbed fractions for active marrow irradiating active marrow for the sternum of the UF adult female and the UF adult male at ICRP 70 reference cellularity.
Annex A contains numerical data of electron specific absorbed fractions (SAFs) to AM and TM50 targets (ratio of AF and target mass). The skeletal site-specific AFs to AM and TM50 targets are further shown graphically in Annexes B and C, respectively. Updated values of for the UF adultmale reference model are given in Annex D.
4. Discussion
Examining Bone Sample Contributions
Craniofacial bones.
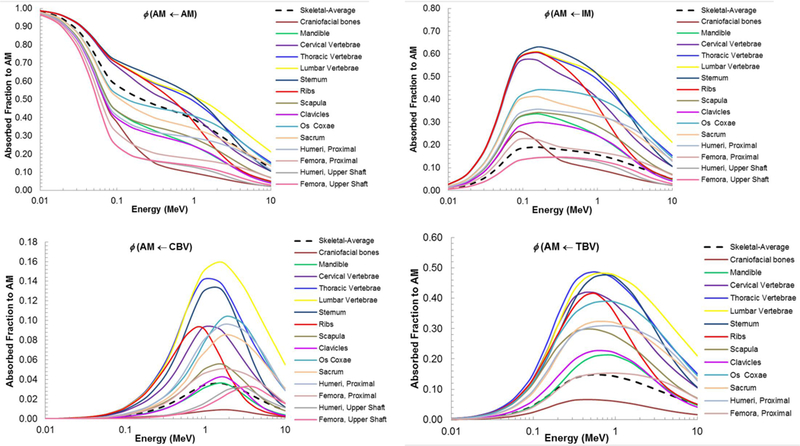
The contributions from multiple microstructure samples to a single skeletal site averaged absorbed fraction were examined. The AFs for AM self-irradiation for the frontal bone, occipital bone, and parietal bone were compared to the average AF computed for the craniofacial bones as shown in Figure 6A. At low energies (below 70 keV), the AFs are approximately equal. They begin to diverge above 70 keV, with the frontal bone being the greatest and parietal being the lowest. This is to be expected as the MVF is the highest for the frontal bone and the lowest for the parietal bone. This trend of divergence at approximately 70 keV is also seen in Figures 6B and 6C, which show the AF to AM by IM and TBV electron sources, respectively. The AFs for the frontal bone are again the highest for each source and the AFs for the parietal the lowest. This trend of the frontal bone AFs being the greatest and parietal bone AFs being the lowest is reversed when examining the AFs to TM50 for an AM source at low energies (up to approximately 200 keV), as shown in Figure 6D. At higher electron energies, these AFs begin to converge and then decrease, due to the increased initial electron energy allowing the particles to completely traverse the shallow marrow layer.
Figure 6.
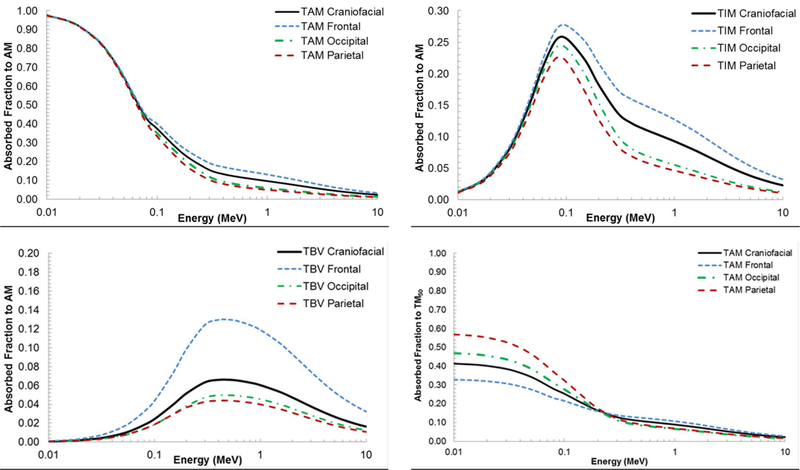
Contributions of frontal, occipital, and parietal bone sample absorbed fractions to the craniofacial absorbed fractions at ICRP 70 reference cellularity (A) AM self-irradiation. (B) AM irradiated by IM. (C) AM irradiated by TBV. (D) TM50 irradiated by AM.
Separated Lumbar Vertebrae.
An additional question explored was the impact of vertebra-to-vertebra crossfire for electron sources. This would be anticipated only at higher energies when particles traverse the intervertebral discs, allowing energy to be deposited in the spongiosa of adjacent vertebrae. Results from this comparison - single vertebrae versus vertebral column as the bone macrostructure - are shown in Figure 7 for the lumbar series. Figure 7A compares AFs for AM self-irradiation for each individual lumbar vertebra (dashed lines) to those for the entire vertebral column (solid lines). A clear divergence at high energies is noted. The same divergence is seen for AFs to AM by IM, TBV, and CBV sources (data not shown). The highest divergence in the two models is seen for the L1 vertebrae with an AF ratio up to 1.35. The divergence decreases with each lumbar vertebra (L2-L5) due to the increase in vertebral size, therefore leading to less electron escape and to less vertebra-to-vertebra cross-fire. Similar trends can be seen in Figure 7B for the shallow marrow target TM50.
Figure 7.
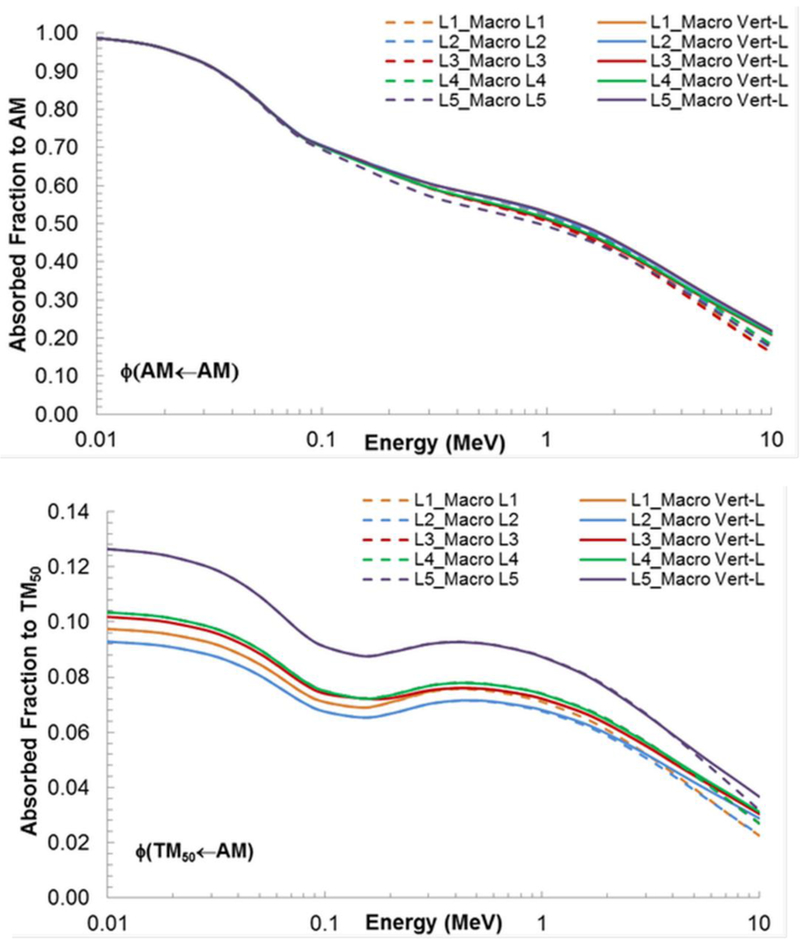
Comparison of absorbed fraction to (A) active marrow and (B) shallow marrow for an active marrow source in the lumbar vertebra (L1-L5) when the separated vertebra were used as the microstructure and when the entire lumbar vertebral column was used as the macrostructure.
4.2. Skeletal Average Quantities
4.2.1. Computations for the adult female model.
The skeletal-averaged absorbed fractions and specific absorbed fractions for the reference adult female, as a function of election energy Ei, were computed using the following expressions from Appendix B of Pafundi (2010):
| (5) |
and
| (6) |
where and are the corresponding AF and SAF for skeletal site x, fx,S and fx,T are the fractional masses of the source and target tissues (as given in Table 6), and mskel,T is the total skeletal mass of the target tissue - either 931 g for total active marrow or 456 g for total shallow marrow - both at ICRP reference cellularities and inclusive of their miscellaneous skeletal tissues. Energy-dependent skeletal-averaged absorbed fractions for internal electron sources within the reference adult female are given in Table 7, with corresponding specific absorbed fractions shown in Table 8.
Table 7.
Skeletal-averaged absorbed fractions for active marrow and shallow marrow targets in the adult female.
| Energy (MeV) |
Φ(AM←AM) | Φ(AM←IM) | Φ(AM←TBS) | Φ(AM←TBV) | Φ(AM←CBS) | Φ(AM←CBV) | Φ(TM50←AM) | Φ(TM50←IM) | Φ(TM50←TBS) | Φ(TM50←TBV) | Φ(TM50←CBS) | Φ(TM50←CBV) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 9.82E–01 | 8.27E–03 | 1.76E–01 | 1.13E–03 | 4.19E–04 | 5.63E–05 | 1.56E–01 | 1.52E–01 | 5.37E–01 | 3.85E–03 | 9.04E–03 | 5.98E–05 |
| 0.015 | 9.64E–01 | 1.66E–02 | 1.79E–01 | 2.23E–03 | 4.78E–04 | 1.12E–04 | 1.54E–01 | 1.51E–01 | 5.45E–01 | 7.58E–03 | 9.19E–03 | 1.17E–04 |
| 0.02 | 9.41E–01 | 2.75E–02 | 1.78E–01 | 3.71E–03 | 5.53E–04 | 1.89E–04 | 1.52E–01 | 1.49E–01 | 5.42E–01 | 1.26E–02 | 9.23E–03 | 1.95E–04 |
| 0.03 | 8.86E–01 | 5.32E–02 | 1.78E–01 | 7.35E–03 | 7.42E–04 | 3.82E–04 | 1.47E–01 | 1.44E–01 | 5.39E–01 | 2.49E–02 | 9.38E–03 | 3.90E–04 |
| 0.04 | 8.21E–01 | 8.33E–02 | 1.77E–01 | 1.20E–02 | 9.91E–04 | 6.37E–04 | 1.41E–01 | 1.37E–01 | 5.28E–01 | 4.04E–02 | 9.52E–03 | 6.39E–04 |
| 0.05 | 7.57E–01 | 1.12E–01 | 1.75E–01 | 1.71E–02 | 1.28E–03 | 9.29E–04 | 1.35E–01 | 1.31E–01 | 5.17E–01 | 5.70E–02 | 9.66E–03 | 9.30E–04 |
| 0.06 | 6.96E–01 | 1.40E–01 | 1.74E–01 | 2.26E–02 | 1.60E–03 | 1.27E–03 | 1.28E–01 | 1.24E–01 | 5.06E–01 | 7.48E–02 | 9.77E–03 | 1.26E–03 |
| 0.08 | 6.13E–01 | 1.75E–01 | 1.73E–01 | 3.47E–02 | 2.38E–03 | 2.06E–03 | 1.17E–01 | 1.14E–01 | 4.56E–01 | 1.09E–01 | 8.85E–03 | 1.90E–03 |
| 0.1 | 5.77E–01 | 1.86E–01 | 1.75E–01 | 4.67E–02 | 3.23E–03 | 2.92E–03 | 1.11E–01 | 1.08E–01 | 4.00E–01 | 1.32E–01 | 7.82E–03 | 2.46E–03 |
| 0.15 | 5.32E–01 | 1.91E–01 | 1.86E–01 | 7.82E–02 | 5.58E–03 | 5.31E–03 | 1.06E–01 | 1.03E–01 | 2.93E–01 | 1.58E–01 | 6.71E–03 | 3.63E–03 |
| 0.2 | 5.06E–01 | 1.88E–01 | 1.98E–01 | 1.04E–01 | 7.98E–03 | 7.75E–03 | 1.06E–01 | 1.03E–01 | 2.39E–01 | 1.58E–01 | 6.69E–03 | 4.66E–03 |
| 0.3 | 4.74E–01 | 1.81E–01 | 2.11E–01 | 1.34E–01 | 1.27E–02 | 1.26E–02 | 1.08E–01 | 1.05E–01 | 1.89E–01 | 1.46E–01 | 7.76E–03 | 6.60E–03 |
| 0.4 | 4.55E–01 | 1.77E–01 | 2.15E–01 | 1.44E–01 | 1.72E–02 | 1.71E–02 | 1.08E–01 | 1.05E–01 | 1.70E–01 | 1.39E–01 | 9.33E–03 | 8.45E–03 |
| 0.5 | 4.42E–01 | 1.73E–01 | 2.14E–01 | 1.48E–01 | 2.15E–02 | 2.15E–02 | 1.07E–01 | 1.04E–01 | 1.60E–01 | 1.34E–01 | 1.11E–02 | 1.02E–02 |
| 0.6 | 4.30E–01 | 1.70E–01 | 2.12E–01 | 1.48E–01 | 2.53E–02 | 2.53E–02 | 1.05E–01 | 1.03E–01 | 1.53E–01 | 1.31E–01 | 1.27E–02 | 1.17E–02 |
| 0.8 | 4.09E–01 | 1.63E–01 | 2.06E–01 | 1.46E–01 | 3.10E–02 | 3.12E–02 | 1.02E–01 | 1.01E–01 | 1.42E–01 | 1.24E–01 | 1.54E–02 | 1.41E–02 |
| 1 | 3.89E–01 | 1.57E–01 | 1.99E–01 | 1.42E–01 | 3.42E–02 | 3.45E–02 | 9.81E–02 | 9.80E–02 | 1.35E–01 | 1.19E–01 | 1.71E–02 | 1.56E–02 |
| 1.5 | 3.48E–01 | 1.43E–01 | 1.81E–01 | 1.30E–01 | 3.58E–02 | 3.62E–02 | 8.90E–02 | 9.15E–02 | 1.21E–01 | 1.07E–01 | 1.83E–02 | 1.68E–02 |
| 2 | 3.14E–01 | 1.31E–01 | 1.65E–01 | 1.19E–01 | 3.38E–02 | 3.41E–02 | 8.11E–02 | 8.52E–02 | 1.10E–01 | 9.78E–02 | 1.76E–02 | 1.62E–02 |
| 3 | 2.63E–01 | 1.11E–01 | 1.40E–01 | 1.01E–01 | 2.81E–02 | 2.84E–02 | 6.86E–02 | 7.44E–02 | 9.41E–02 | 8.31E–02 | 1.48E–02 | 1.36E–02 |
| 4 | 2.27E–01 | 9.58E–02 | 1.21E–01 | 8.79E–02 | 2.30E–02 | 2.32E–02 | 5.94E–02 | 6.55E–02 | 8.19E–02 | 7.21E–02 | 1.21E–02 | 1.12E–02 |
| 5 | 1.99E–01 | 8.42E–02 | 1.07E–01 | 7.78E–02 | 1.89E–02 | 1.91E–02 | 5.25E–02 | 5.80E–02 | 7.23E–02 | 6.35E–02 | 9.95E–03 | 9.23E–03 |
| 6 | 1.78E–01 | 7.50E–02 | 9.62E–02 | 6.99E–02 | 1.58E–02 | 1.59E–02 | 4.71E–02 | 5.19E–02 | 6.46E–02 | 5.67E–02 | 8.24E–03 | 7.70E–03 |
| 8 | 1.47E–01 | 6.13E–02 | 7.97E–02 | 5.80E–02 | 1.13E–02 | 1.14E–02 | 3.90E–02 | 4.23E–02 | 5.28E–02 | 4.63E–02 | 5.82E–03 | 5.53E–03 |
| 10 | 1.25E–01 | 5.15E–02 | 6.76E–02 | 4.92E–02 | 8.47E–03 | 8.53E–03 | 3.30E–02 | 3.52E–02 | 4.41E–02 | 3.88E–02 | 4.25E–03 | 4.10E–03 |
Table 8.
Skeletal-averaged specific absorbed fractions (g-1) for active marrow and shallow marrow targets in the adult female.
| Energy (MeV) |
Φ(AM←AM) | Φ(AM←IM) | Φ(AM←TBS) | Φ(AM←TBV) | Φ(AM←CBS) | Φ(AM←CBV) | Φ(TM50←AM) | Φ(TM50←IM) | Φ(TM50←TBS) | Φ(TM50←TBV) | Φ(TM50←CBS) | Φ(TM50←CBV) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 1.09E-03 | 9.17E-06 | 1.95E-04 | 1.25E-06 | 4.65E-07 | 6.24E-08 | 3.42E-04 | 3.34E-04 | 1.18E-03 | 8.45E-06 | 1.98E-05 | 1.28E-07 |
| 0.015 | 1.07E-03 | 1.84E-05 | 1.98E-04 | 2.47E-06 | 5.30E-07 | 1.25E-07 | 3.39E-04 | 3.31E-04 | 1.20E-03 | 1.66E-05 | 2.02E-05 | 2.51E-07 |
| 0.02 | 1.04E-03 | 3.05E-05 | 1.97E-04 | 4.12E-06 | 6.13E-07 | 2.10E-07 | 3.34E-04 | 3.26E-04 | 1.19E-03 | 2.77E-05 | 2.02E-05 | 4.17E-07 |
| 0.03 | 9.82E-04 | 5.90E-05 | 1.98E-04 | 8.15E-06 | 8.24E-07 | 4.24E-07 | 3.23E-04 | 3.15E-04 | 1.18E-03 | 5.45E-05 | 2.06E-05 | 8.35E-07 |
| 0.04 | 9.10E-04 | 9.24E-05 | 1.96E-04 | 1.33E-05 | 1.10E-06 | 7.08E-07 | 3.09E-04 | 3.02E-04 | 1.16E-03 | 8.86E-05 | 2.08E-05 | 1.37E-06 |
| 0.05 | 8.39E-04 | 1.25E-04 | 1.94E-04 | 1.89E-05 | 1.42E-06 | 1.03E-06 | 2.95E-04 | 2.87E-04 | 1.13E-03 | 1.25E-04 | 2.11E-05 | 1.99E-06 |
| 0.06 | 7.72E-04 | 1.55E-04 | 1.93E-04 | 2.51E-05 | 1.79E-06 | 1.41E-06 | 2.80E-04 | 2.73E-04 | 1.11E-03 | 1.64E-04 | 2.14E-05 | 2.70E-06 |
| 0.08 | 6.79E-04 | 1.94E-04 | 1.91E-04 | 3.84E-05 | 2.66E-06 | 2.30E-06 | 2.57E-04 | 2.49E-04 | 1.00E-03 | 2.38E-04 | 1.93E-05 | 4.08E-06 |
| 0.1 | 6.40E-04 | 2.06E-04 | 1.94E-04 | 5.18E-05 | 3.62E-06 | 3.28E-06 | 2.44E-04 | 2.37E-04 | 8.78E-04 | 2.90E-04 | 1.71E-05 | 5.29E-06 |
| 0.15 | 5.90E-04 | 2.11E-04 | 2.07E-04 | 8.67E-05 | 6.32E-06 | 6.02E-06 | 2.33E-04 | 2.25E-04 | 6.43E-04 | 3.47E-04 | 1.45E-05 | 7.78E-06 |
| 0.2 | 5.60E-04 | 2.08E-04 | 2.20E-04 | 1.15E-04 | 9.14E-06 | 8.90E-06 | 2.33E-04 | 2.26E-04 | 5.25E-04 | 3.47E-04 | 1.45E-05 | 1.00E-05 |
| 0.3 | 5.25E-04 | 2.01E-04 | 2.34E-04 | 1.48E-04 | 1.49E-05 | 1.48E-05 | 2.37E-04 | 2.30E-04 | 4.15E-04 | 3.21E-04 | 1.68E-05 | 1.43E-05 |
| 0.4 | 5.05E-04 | 1.96E-04 | 2.38E-04 | 1.60E-04 | 2.07E-05 | 2.07E-05 | 2.37E-04 | 2.30E-04 | 3.73E-04 | 3.05E-04 | 2.05E-05 | 1.85E-05 |
| 0.5 | 4.90E-04 | 1.92E-04 | 2.37E-04 | 1.64E-04 | 2.66E-05 | 2.66E-05 | 2.35E-04 | 2.28E-04 | 3.50E-04 | 2.95E-04 | 2.47E-05 | 2.26E-05 |
| 0.6 | 4.77E-04 | 1.88E-04 | 2.35E-04 | 1.65E-04 | 3.20E-05 | 3.22E-05 | 2.31E-04 | 2.26E-04 | 3.35E-04 | 2.86E-04 | 2.89E-05 | 2.65E-05 |
| 0.8 | 4.53E-04 | 1.81E-04 | 2.28E-04 | 1.62E-04 | 4.14E-05 | 4.17E-05 | 2.24E-04 | 2.21E-04 | 3.12E-04 | 2.72E-04 | 3.65E-05 | 3.35E-05 |
| 1 | 4.32E-04 | 1.74E-04 | 2.20E-04 | 1.58E-04 | 4.79E-05 | 4.84E-05 | 2.15E-04 | 2.15E-04 | 2.96E-04 | 2.60E-04 | 4.22E-05 | 3.87E-05 |
| 1.5 | 3.86E-04 | 1.58E-04 | 2.00E-04 | 1.44E-04 | 5.57E-05 | 5.63E-05 | 1.95E-04 | 2.01E-04 | 2.66E-04 | 2.35E-04 | 5.03E-05 | 4.62E-05 |
| 2 | 3.48E-04 | 1.45E-04 | 1.83E-04 | 1.32E-04 | 5.71E-05 | 5.78E-05 | 1.78E-04 | 1.87E-04 | 2.42E-04 | 2.15E-04 | 5.30E-05 | 4.88E-05 |
| 3 | 2.92E-04 | 1.23E-04 | 1.55E-04 | 1.12E-04 | 5.47E-05 | 5.54E-05 | 1.50E-04 | 1.63E-04 | 2.06E-04 | 1.82E-04 | 5.23E-05 | 4.82E-05 |
| 4 | 2.51E-04 | 1.06E-04 | 1.34E-04 | 9.75E-05 | 5.04E-05 | 5.11E-05 | 1.30E-04 | 1.44E-04 | 1.80E-04 | 1.58E-04 | 4.89E-05 | 4.51E-05 |
| 5 | 2.21E-04 | 9.33E-05 | 1.19E-04 | 8.63E-05 | 4.62E-05 | 4.69E-05 | 1.15E-04 | 1.27E-04 | 1.59E-04 | 1.39E-04 | 4.52E-05 | 4.17E-05 |
| 6 | 1.98E-04 | 8.32E-05 | 1.07E-04 | 7.75E-05 | 4.25E-05 | 4.31E-05 | 1.03E-04 | 1.14E-04 | 1.42E-04 | 1.24E-04 | 4.17E-05 | 3.86E-05 |
| 8 | 1.63E-04 | 6.79E-05 | 8.84E-05 | 6.42E-05 | 3.65E-05 | 3.70E-05 | 8.55E-05 | 9.28E-05 | 1.16E-04 | 1.02E-04 | 3.56E-05 | 3.32E-05 |
| 10 | 1.38E-04 | 5.71E-05 | 7.49E-05 | 5.45E-05 | 3.17E-05 | 3.21E-05 | 7.25E-05 | 7.73E-05 | 9.68E-05 | 8.51E-05 | 3.07E-05 | 2.88E-05 |
Skeletal-averaged values of the absorbed fractions to active marrow are shown graphically in Figure 8 for each of the five primary skeletal sources of internal electrons. It is further noted that the data for CBV sources is further used to represent CBS sources as the macrostructural models of cortical bone in this study do not explicitly define the Harversian canals. For active marrow self-irradiation, Figure 9A shows the bone-specific variations in ɸ(AM←AM) about its skeletal-averaged values. At high electron energies (1 MeV and above), values of ɸ(AM←AM) are greatest for the lumbar vertebrae. For energies below 300 keV, the upper shafts of the femora have the lowest values of ɸ(AM←AM). Above 300 keV, the craniofacial bones exhibit the lowest ɸ(AM←AM). At low electron energies, the AF is proportional to the marrow cellularity with the highest cellularity sites (vertebrae, sternum and ribs at CF=70%) having the highest AFs, while the lowest cellularity sites (long bone shafts at CF=15%), exhibit the lowest AFs. At high electron energies, the AF is dominated by electron escape from the macrostructure.
Figure 8.
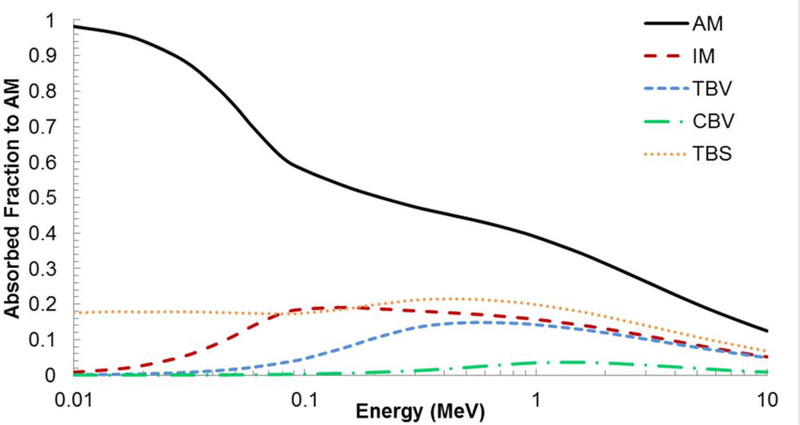
Skeletal-averaged absorbed fractions to active marrow in the adult female by active marrow, inactive marrow, trabecular bone volume, trabecular bone surfaces, and cortical bone volume sources.
Figure 9.
Comparison of absorbed fractions for active marrow irradiation by (A) AM, (B) IM, (C) CBV, and (D) TBV for each bone site that contains active marrow at each skeletal site’s ICRP 70 reference cellularity and the resulting skeletal-average value.
The bone-specific absorbed fractions to active marrow targets are shown in Figures 9B, 9C, and 9D for electron sources within inactive marrow, cortical bone, and trabecular bone, respectively. The skeletal-averaged values are also presented (dashed lines). For IM sources, the skeletal-averaged values are lower than the majority of the displayed bone- specific values, due in part to the large percent of inactive marrow localized in skeletal regions that do not contain active marrow (resulting in AF=0 values included in the source- mass weighted average). Values of ɸ(AM←IM), ɸ(AM←CBV), and ɸ(AM←TBV) at electron energies above 300 keV are lowest in the craniofacial bones. For electron energies above 1 MeV, the lumbar vertebrae has the greatest values of ɸ(AM←IM), ɸ(AM←CBV), and ɸ(AM←TBV). Between electron energies of 70 to 900 keV, the absorbed fractions to AM with an IM source are greatest for the sternum. These figures clearly demonstrate the existence of strong bone-site dependences of the active marrow dose from internal electron sources, values of which are not well predicated by use of a single skeletal- averaged absorbed fraction.
4.2.2. Comparisons with Previous Dosimetry Models.
The skeletal-averaged AFs of the present study were compared to values given in previous skeletal dosimetry models. These included the University of Florida 15-year-old female (UFH15F) (Pafundi, 2009), UF reference adult male (Hough et al., 2011), the Stabin and Siegel adult male (ADM) (Stabin and Siegel, 2003), and the ICRP Publication 110 reference adult female (ADF). The values for the latter were derived using the bone-specific absorbed fractions of this study and the fractional tissues masses of the ICRP 110 reference adult female as reported in Table 10 of Hough et al. (2011). Figure 10A shows the skeletal-averaged AFs for active marrow selfirradiation. Each model follows a similar trend, with the exception of the Stabin and Siegel model at high electron energies where the skeletal-averaged AF plateaus at energies above ~40–50 keV. This model applies infinite spongiosa transport with no allowance for electron escape.
Table 10.
Mean pathlengths through marrow cavities and bone trabeculae of the 45-year female cadaver of this study, 40-year male cadaver of the Hough et al (2011) study and those for the 44-year male cadaver of Beddoe et al (1976).
| Skeletal Site | Mean Pathlengths (μm) |
|||||
|---|---|---|---|---|---|---|
| Present Model | Hough et al | Beddoe et al | ||||
| Cavity | Trabeculae | Cavity | Trabeculae | Cavity | Trabeculae | |
| Craniofacial bones | ||||||
| Frontal | 385 | 327 | 500 | 392 | ||
| Parietal | 257 | 526 | 516 | 326 | 389 | 511 |
| Occipital | 215 | 449 | 154 | 746 | ||
| Mandible | 1079 | 340 | 1430 | 205 | ||
| Scapulae | 1190 | 139 | 1162 | 253 | ||
| Clavicles | 1679 | 230 | 1162 | 268 | ||
| Sternum | 1360 | 255 | 1551 | 164 | ||
| Ribs | 1706 | 265 | ||||
| Upper | 671 | 159 | 1344 | 192 | ||
| Lower | 638 | 218 | 1146 | 247 | ||
| Cervical Vertebrae | ||||||
| C3 | 833 | 240 | 864 | 189 | ||
| C6 | 1037 | 223 | 913 | 254 | ||
| Thoracic Vertebrae | ||||||
| T1 | 876 | 192 | ||||
| T3 | 1154 | 235 | 1232 | 221 | ||
| T6 | 1222 | 203 | 1913 | 154 | ||
| T9 | 966 | 219 | ||||
| T12 | 1489 | 182 | ||||
| Lumbar Vertebrae | ||||||
| L1 | 1604 | 218 | ||||
| L2 | 861 | 236 | 861 | 214 | 1172 | 235 |
| L3 | 1406 | 262 | ||||
| L4 | 1370 | 247 | 1714 | 192 | ||
| L5 | 1137 | 238 | ||||
| Sacrum | 1028 | 246 | 1458 | 227 | ||
| Os Coxae | 1423 | 170 | 1381 | 187 | 907 | 253 |
| Humeri | ||||||
| Proximal | 1347 | 191 | 1660 | 231 | ||
| Distal | 988 | 222 | 1170 | 226 | ||
| Radii | ||||||
| Proximal | 1136 | 220 | 1172 | 281 | ||
| Distal | 1295 | 219 | 1344 | 198 | ||
| Ulnae | ||||||
| Proximal | 688 | 283 | 1253 | 263 | ||
| Distal | 1402 | 160 | 1032 | 193 | ||
| Femora | 1418 | 267 | ||||
| Proximal Head | 669 | 334 | 910 | 283 | ||
| Proximal Neck | 952 | 218 | 1509 | 192 | ||
| Distal | 928 | 260 | 1171 | 216 | ||
| Patellae | 838 | 232 | 1171 | 216 | ||
| Tibiae | ||||||
| Proximal | 969 | 209 | 1409 | 198 | ||
| Distal | 1074 | 237 | 1344 | 215 | ||
| Fibulae | ||||||
| Proximal | 1067 | 212 | 1699 | 187 | ||
| Distal | 1073 | 255 | 1118 | 219 | ||
Figure 10.
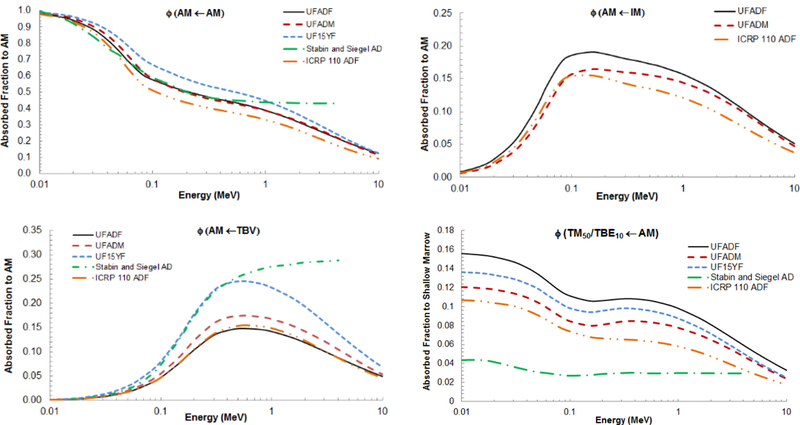
Comparison of skeletal-averaged absorbed fractions to (A) AM by AM source, (B) AM by IM, (C) AM by TBV, and (D) TM50 by AM of the UFHADF from this study to the UFHADM, UFH15F (when available), Stabin and Siegel AD (when available), and ICRP 110 ADF models.
Figure 10B shows the skeletal-averaged absorbed fractions to AM for internal IM electron sources for all models that consider this unique source region. Each model follows a similar trend, with the absorbed fractions increasing until just above 100 keV with subsequent decreases. Values from the present study are shown to exceed those of the other two models.
In Figure 10C, the five previous models are compared with respect to AM irradiation by electron sources in the TBV. A similar trend is observed between the models, with the AFs increasing until ~500 keV with subsequent declines at higher energies. Again, the one exception is the Stabin and Siegel model. The skeletal-average AFs to AM for TBV electron sources are fairly close for the remaining three adult skeletal models.
The substantial impact of the change in the definition of target tissue for the osteoprogenitor cells - 10 to 50 μm from bone surfaces - can be seen in Figure 10D. Of the five models compared, the Stabin and Siegel model is the only one to use the previous 10 μm definition, resulting in skeletal-averaged absorbed fractions significantly lower than given by other models. Of the remaining four models, values of ɸ(TM50 ← AM) are greatest for the present adult female model. This is directly attributable to the shallow marrow masses being higher due to the new method of shallow marrow definition. The inclusion of the partial volumes of both edge and corner voxels in the microstructure models results in a larger volume for energy deposition scoring.
4.3. Effects of Varying Cellularity
The absorbed fraction and specific absorbed fraction for AM self-irradiation are highly dependent on marrow cellularity. This is clearly seen in Figures 11A and 11B which display values for AF and SAF, respectively, for AM self-irradiation in the female sternum of the present model. The AF to AM is greatest for a cellularity of 100% and decreases at lower cellularities. The SAF is greatest for 10% cellularity and decreases with increasing cellularity, due to increases in target mass. The difference in SAFs at low energies is greatest between the smaller cellularities and decreases with increasing cellularity.
Figure 11.
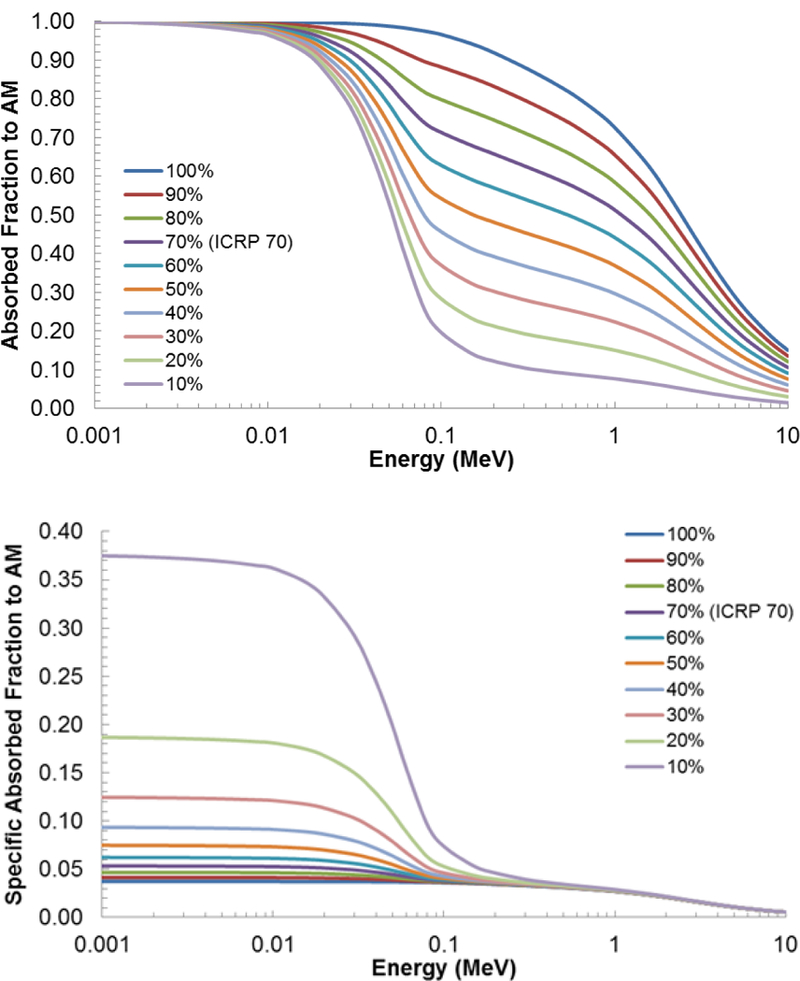
The effect of varying cellularity on (A) absorbed fractions and (B) specific absorbed fractions for active marrow self-irradiation in the sternum.
The other source and target combinations do not display this cellularity dependence. For this reason, other source/target combinations had been run at the ICRP 70 reference cellularity for each skeletal site, as previously mentioned. An example of this independence of marrow cellularity can be seen in Figure 12 which shows the AF to shallow marrow for AM sources at varying cellularities. Values of the AF at different cellularities cannot be visualized on the linear y-axis scale provided.
Figure 12.
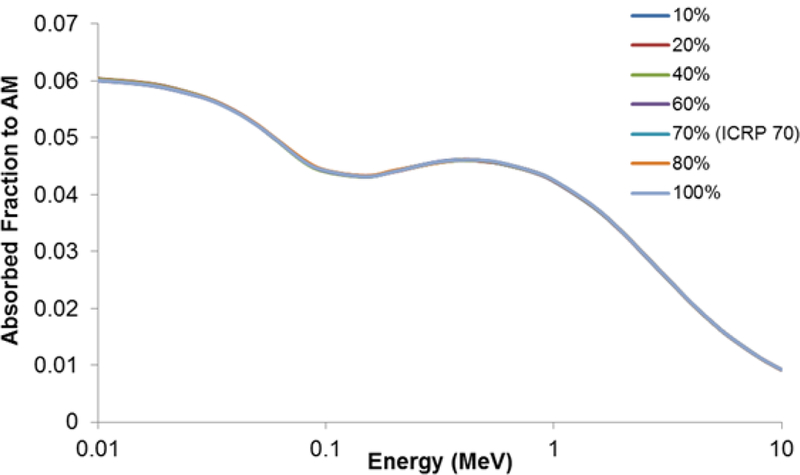
The lack of effect of varying cellularity on absorbed fractions for shallow marrow when active marrow is the source, for the sternum.
4.4. Skeletal Radionuclide S-values
S values were computed using an in-house MATLAB™ script for each skeletal source and target combination for the UF reference adult female of the present study, and for the following beta-emitting radionuclides: 90Sr, 89Sr, 90Y, 45Ca, 32P, 33P, and 166Ho. For comparison, an additional set was generated for the UF reference adult male using reported skeletal-average absorbed fractions in Hough et al (2011). For both computations, the full beta-spectra were utilized as given in ICRP Publication 107 (ICRP, 2008). A third set of radionuclide S values was also generated for the reference adult female as reported by the OLINDA code (Stabin et al., 2005). These results are shown in Table 9, where there is equivalency in the source/target combinations for active marrow targets, but not for those defining the target tissue for the osteoprogenitor cells: 50-μm shallow marrow in the UF models, and either 10-μm trabecular bone endosteum (TBE) or 10-mm cortical bone endosteum (CBE) for the OLINDA code.
Table 9.
S-values (in units of mGy MBq−1 s−1) for Sr-90, Sr-89, Y-90, P-32, P-33, Ca-45, and Ho-166 calculated for various skeletal source–target regions in the skeleton of the ICRP reference adult female based upon skeletal-averaged specific absorbed fractions from the present study, the UF adult male odel of Hough et al (2011), and the adult female model from OLINDA (Stabin et al., 2005). Both mean and maximum beta-particle energies are listed in parentheses.
| UF Models | OLINDA 2005 | Sr-90 (196 keV/546 keV) | Sr-89 (585 keV/1460 keV) | Y-90 (933 keV/2280 keV) | Ca-45 (77 keV/257 keV) | P-32 (695 keV/1710 keV) | P-33 (76 keV/249 keV) | Ho-166 (665 keV/1854 keV) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
S Value (mGy/MBq-s) |
S Value (mGy/MBq-s) |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
UF Adult Female |
UF Adult Male |
OLINDA Adult Female |
| Targets - Surrogate Tissues for the HSC | ||||||||||||||||||||||
| S (AM←AM) | S (AM←AM) | 1.74E–05 | 1.32E–05 | 1.26E–05 | 4.32E–05 | 3.31E–05 | 3.34E–05 | 6.23E–05 | 4.82E–05 | 5.23E–05 | 8.33E–06 | 6.46E–06 | 6.07E–06 | 5.01E–05 | 3.84E–05 | 3.94E–05 | 8.3E–06 | 6.4E–06 | 6.0E–06 | 4.8E–05 | 4.0E–05 | 4.0E–05 |
| S (AM←IM) | S (AM←IM) | 6.25E–06 | 2.47E–06 | NA | 1.70E–05 | 6.90E–06 | NA | 2.51E–05 | 1.04E–05 | NA | 2.29E–06 | 8.79E–07 | NA | 1.99E–05 | 8.10E–06 | NA | 2.3E–06 | 8.7E–07 | NA | 1.9E–05 | 8.0E–06 | NA |
| S (AM←TBS) | S (AM←TBS) | 7.09E–06 | 5.34E–06 | 6.74E–06 | 2.11E–05 | 1.62E–05 | 2.46E–05 | 3.15E–05 | 2.44E–05 | 4.01E–05 | 2.50E–06 | 1.85E–06 | 2.35E–06 | 2.48E–05 | 1.91E–05 | 2.95E–05 | 2.5E–06 | 1.8E–06 | 2.3E–06 | 2.4E–05 | 1.9E–05 | 2.9E–05 |
| S (AM←TBV) | S (AM←TBV) | 4.00E–06 | 3.75E–06 | 5.02E–06 | 1.46E–05 | 1.37E–05 | 2.29E–05 | 2.23E–05 | 2.10E–05 | 3.84E–05 | 7.68E–07 | 7.21E–07 | 5.62E–07 | 1.74E–05 | 1.63E–05 | 2.78E–05 | 7.4E–07 | 6.9E–07 | 5.5E–07 | 1.6E–05 | 1.6E–05 | 2.7E–05 |
| S (AM←CBS) | S (AM←CBS) | 4.03E–07 | 2.23E–07 | 0.00E+00 | 2.90E–06 | 1.95E–06 | 1.63E–10 | 5.34E–06 | 4.11E–06 | 0.00E+00 | 5.61E–08 | 2.70E–08 | 0.00E+00 | 3.66E–06 | 2.54E–06 | 0.00E+00 | 5.4E–08 | 2.6E–08 | 0.0E+00 | 3.5E–06 | 2.5E–06 | 5.6E–08 |
| S (AM←CBV) | S (AM←CBV) | 3.96E–07 | 2.59E–07 | 0.00E+00 | 2.91E–06 | 2.27E–06 | 1.63E–10 | 5.38E–06 | 4.79E–06 | 0.00E+00 | 5.21E–08 | 3.14E–08 | 0.00E+00 | 3.68E–06 | 2.95E–06 | 0.00E+00 | 5.0E–08 | 3.0E–08 | 0.0E+00 | 3.5E–06 | 2.9E–06 | 5.6E–08 |
| Targets – Surrogate Tissues for the OPC | ||||||||||||||||||||||
| S (TM50←AM) | S (TBE←AM) | 1.04E–05 | 5.92E–06 | 1.02E–05 | 2.90E–05 | 1.68E–05 | 3.10E–05 | 4.29E–05 | 2.50E–05 | 4.98E–05 | 4.37E–06 | 2.45E–06 | 3.96E–06 | 3.39E–05 | 1.97E–05 | 3.69E–05 | 4.3E–06 | 2.4E–06 | 3.9E–06 | 3.2E–05 | 2.0E–05 | 3.7E–05 |
| S (TM50←IM) | S (TBE←IM) | 1.01E–05 | 3.33E–06 | NA | 2.87E–05 | 9.65E–06 | NA | 4.34E–05 | 1.48E–05 | NA | 4.23E–06 | 1.40E–06 | NA | 3.37E–05 | 1.14E–05 | NA | 4.2E–06 | 1.4E–06 | NA | 3.2E–05 | 1.1E–05 | NA |
| S (TM50←TBS) | S (TBE←TBS) | 2.23E–05 | 1.09E–05 | 2.19E–05 | 4.35E–05 | 2.03E–05 | 3.75E–05 | 6.14E–05 | 2.81E–05 | 5.50E–05 | 1.44E–05 | 7.61E–06 | 1.90E–05 | 4.97E–05 | 2.29E–05 | 4.32E–05 | 1.4E–05 | 7.6E–06 | 1.9E–05 | 4.8E–05 | 2.6E–05 | 5.2E–05 |
| S (TM50←TBV) | S (TBE←TBV) | 1.38E–05 | 7.23E–06 | 1.29E–05 | 3.59E–05 | 1.82E–05 | 3.14E–05 | 5.23E–05 | 2.66E–05 | 4.89E–05 | 4.61E–06 | 2.80E–06 | 5.44E–06 | 4.18E–05 | 2.11E–05 | 3.70E–05 | 4.5E–06 | 2.8E–06 | 5.4E–06 | 4.0E–05 | 2.1E–05 | 3.8E–05 |
| S (TM50←CBS) | S (CBE←CBS) | 7.77E–07 | 6.50E–06 | 1.65E–05 | 4.20E–06 | 8.29E–06 | 3.23E–05 | 7.88E–06 | 1.08E–05 | 4.82E–05 | 1.02E–07 | 5.49E–06 | 1.46E–06 | 5.28E–06 | 8.95E–06 | 3.75E–05 | 3.0E–07 | 5.5E–06 | 1.6E–05 | 4.9E–06 | 1.2E–05 | 4.6E–05 |
| S (TM50←CBV) | S (CBE←CBV) | 5.80E–07 | 3.64E–07 | 6.55E–06 | 3.77E–06 | 2.65E–06 | 2.21E–05 | 7.09E–06 | 5.61E–06 | 3.51E–05 | 2.97E–07 | 7.43E–08 | 1.57E–05 | 4.76E–06 | 3.43E–06 | 2.62E–50 | 9.9E–08 | 7.3E–08 | 1.4E–06 | 4.5E–06 | 3.4E–06 | 2.6E–05 |
In reviewing the data of Table 9 for active marrow targets, value of S(AM ← rs) are consistently higher for the UF adult female than for the UF adult male. Mean ratios of adult male to adult female values of S(AM ← rs) for AM, IM, TBS, TBV, CBS, and CBV sources are 0.78, 0.40, 0.76, 0.94, 0.62, and 0.74, respectively. Similarly, the mean ratio of the OLINDA reported value of S(AM ← AM) to that of the present study is 0.77. However, the values of S(AM ← TBS) and S(AM ← TBV) from OLINDA are factors of 1.10 and 1.32 times higher, respectively, than those of the present study. Again, OLINDA does not consider an inactive marrow source, nor does it model active marrow irradiation from electron sources in cortical bone - volume or surfaces.
4.5. Pathlength Distributions
Omni-directional pathlength distributions were further computed for both the marrow cavities and bone trabeculae within all 37 microCT measured bone microstructures of the adult female skeleton. These distributions are provided numerically within Annex E and were computed using the 3D ray-trace algorithm of Rajon and Bolch (2003). The mean pathlengths are shown in Table 10 and are compared to those of the 40- year adult male model of Hough et al (2011) and the 44-year adult male model of Beddoe et al (1976).
Considerable variation exists between the microCT-based pathlength distributions of the two UF adult cadaver studies. Ratios of mean marrow cavity pathlengths (male-to- female) vary from a low of 0.69 (clavicles) to a high of 2.00 (parietal bone) (average ratio is 1.26). Corresponding ratios of mean bone trabeculae pathlengths vary from a low of 0.60 (mandible) to a high of 1.81 (scapulae) (average ratio of 1.00). Mean pathlengths in the marrow cavities were 385, 257, and 215 μm within the frontal, parietal, and occipital bones of the 45-year female cadaver, with corresponding values of 500, 516, and 154 μm in the cranium of the 40-year male cadaver. The mean pathlength of the marrow cavities in the parietal bone of the 44-year Leeds male was 389 mm, a value closer to our value seen in the 45-year female subject. Mean pathlengths through the bone trabeculae are 327, 526, and 449 μm within the frontal, parietal, and occipital bones of the 45-year female, with corresponding male values of 392, 326, and 756 μm. It was reported that the microCT coring of occipital bone spongiosa of the 40-year male cadaver was problematic, and perhaps taken too far toward the cranial base to properly sample its trabecular spongiosa (Hough et al., 2011). The reported value for the mean pathlength across the trabeculae of the parietal bone of the Leeds 44-year male subject as 511 μm - again, a value close to that reported in the present study of the adult female.
4.6. Photon Dose to the Skeletal Tissues
The model presented here is restricted to electron sources internal to the skeleton, and thus the issue of photon dose to the skeletal tissues is not addressed. Photon dose to active and shallow bone marrow throughout the skeleton may be accomplished through the use of photon fluence to dose response functions as presented in Johnson et al (2011). These functions are based upon values of photon interaction cross-sections, skeletal tissue elemental compositions, and skeletal electron absorbed fractions as reported here. They may be applied during the transport of photons, including electron-generated bremsstrahlung x-rays, within whole-body computational phantoms with all skeletal regions available for energy deposition.
5. Conclusions
An image-based skeletal dosimetry model was created for the ICRP-defined reference adult female. The active marrow, inactive marrow, and total skeletal masses were to within 0.24%, 0.38%, and 0.25% of their ICRP 89 reference values. Absorbed fractions and specific absorbed fractions were determined for 34 skeletal sites for active marrow and shallow marrow targets over a discrete electron energy range from 1 keV to 10 MeV. Source regions included (as applicable): active marrow, inactive marrow, trabecular bone surfaces, trabecular bone volumes, and cortical bone volumes (serving as a surrogate for the cortical bone surfaces in regions other than the long bone shafts).
The method of combining macro- and microstructure absorbed fractions calculated using MCNPX electron transport was found to yield results similar to those determined with the PIRT model for the UF adult male skeletal model. Electron escape from spongiosa and cortical bone cross-fire were accounted for in each skeletal site. The ICRP change in the definition of the shallow marrow thickness from 10 to 50 μm was also taken into account. Absorbed fractions for each skeletal site, and their skeletal averaged values were found to follow expected trends for each electron source region. An absorbed fraction and specific absorbed fraction dependence on marrow cellularity for cases of active marrow self-irradiation was further demonstrated, indicating potential errors in individualized marrow dose for low-energy electron emitters that localize in bone marrow. The absence of such a dependence on the irradiation of the shallow marrow was also presented. Finally, it is clear that use of a single skeletal average AF is not representative of energy deposition to either active or shallow marrow within individual regions of the skeleton.
ACKNOWLEDGEMENTS
This research was supported in part by grants R01 CA116743 and R01 CA96441 with the National Cancer Institute, and by grant DE-FG07–06ID14773 with the US Department of Energy. The research of SEO (first author) was supported by the J. Crayton Pruitt Family Department of Biomedical Engineering and the University of Florida Graduate School.
References:
- Beddoe AH, Darley P J and Spiers F W 1976. Measurements of trabecular bone structure in man Phys. Med. Biol. 21 589–607 [DOI] [PubMed] [Google Scholar]
- Cristy M 1981. Active bone marrow distribution as a function of age in humans Phys Med Biol 26 389–400. [DOI] [PubMed] [Google Scholar]
- Hough M, Johnson P, Rajon D, Jokisch D, Lee C and Bolch W 2011. An image-based skeletal dosimetry model for the ICRP reference adult male-internal electron sources Phys Med Biol 56 2309–46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurtado J L, Lee C, Lodwick D, Goede T, Williams J L and Bolch W E 2012. Hybrid computational phantoms representing the reference adult male and adult female: construction and applications for retrospective dosimetry Health Phys 102 292–304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- ICRP 1980. ICRP Publication 30: Limits for intakes of radionuclides by workers. (Oxford, UK: International Commission on Radiological Protection; ) [PubMed] [Google Scholar]
- ICRP 1995. ICRP Publication 70: Basic anatomical and physiological data for use in radiological protection: the skeleton Ann ICRP 25 1–180 [PubMed] [Google Scholar]
- ICRP 2002. ICRP Publication 89: Basic anatomical and physiological data for use in radiological protection - reference values Ann ICRP 32 1–277 [PubMed] [Google Scholar]
- ICRP 2008. ICRP Publication 107: Nuclear decay data for dosimetric calculations Ann ICRP 38 1–26 [DOI] [PubMed] [Google Scholar]
- ICRP 2009. ICRP Publication 110: Adult reference computational phantoms Ann ICRP 39 1–165 [DOI] [PubMed] [Google Scholar]
- ICRP 2015. ICRP Publication 131 - Stem cell biology with respect to carcinogenesis aspects of radiological protection Ann ICRP 44 1–357 [DOI] [PubMed] [Google Scholar]
- Johnson L C 1964. Bone Biodynamics, ed Frost HM pp 543–654 [Google Scholar]
- Johnson P B, Bahadori A A, Eckerman K F, Lee C and Bolch W E 2011. Response functions for computing absorbed dose to skeletal tissues from photon irradiation--an update Phys Med Biol 56 2347–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pafundi D, Rajon D, Jokisch D, Lee C and Bolch W 2010. An image-based skeletal dosimetry model for the ICRP reference newborn--internal electron sources Phys Med Biol 55 1785–814 [DOI] [PubMed] [Google Scholar]
- Pafundi D H 2009. Image-based skeletal tissue and electron dosimetry models for the ICRP reference pediatric age series Biomedical Engineering, University of Florida, PhD Dissertation. [Google Scholar]
- Pelowitz D B 2011. MCNPX User’s Manual Version 2.7.0. (LANL: Los Alamos National Laboratory; ) [Google Scholar]
- Rajon D, Pichardo J, Brindle J, Kielar K, Jokisch D, Patton P and Bolch W 2006. Image segmentation of trabecular spongiosa by visual inspection of the gradient magnitude Phys Med Biol 51 4447–4467 [DOI] [PubMed] [Google Scholar]
- Rajon D A and Bolch W E 2003. Interactions within 3D isotropic and homogeneous radiation fields: A Monte Carlo simulation algorithm Comput Methods Programs Biomed 70 167–177 [DOI] [PubMed] [Google Scholar]
- Shah A, Jokisch D, Watchman C, Rajon D, Patton P and Bolch W 2005a. Chord-based versus voxel-based methods of electron transport in the skeletal tissues Med Phys 32 3151–3159 [DOI] [PubMed] [Google Scholar]
- Shah A, Rajon D, Patton P, Jokisch D and Bolch W 2005b. Accounting for beta-particle energy loss to cortical bone via Paired-Image Radiation Transport (PIRT) Med Phys 32 1354–1366 [DOI] [PubMed] [Google Scholar]
- Snyder W S, Ford M R, Warner G G and Watson S B 1975. MIRD Pamphlet No. 11: S, absorbed dose per unit cumulated activity for selected radionuclides and organs. (New York, NY: Society of Nuclear Medicine; ) [Google Scholar]
- Spiers F W and Beddoe A H 1983. Sites of incidence of osteosarcoma in the long bones of man and the beagle Health Phys 44 49–64 [DOI] [PubMed] [Google Scholar]
- Stabin M G and Siegel J A 2003. Physical models and dose factors for use in internal dose assessment Health Phys 85 294–310 [DOI] [PubMed] [Google Scholar]
- Stabin M G, Sparks R B and Crowe E 2005. OLINDA/EXM: the second-generation personal computer software for internal dose assessment in nuclear medicine J Nucl Med 46 1023–7 [PubMed] [Google Scholar]
- Wayson MB 2012. Computational internal dosimetry methods as applied to the University of Florida series of hybrid phantoms Biomedical Engineering, University of Florida, Dissertation. [Google Scholar]


