Susceptibility Mapping of the Dural Sinuses and Other Superficial Veins in the Brain

Abstract

Quantitative susceptibility mapping (QSM) is a means to obtain direct measurements of local tissue susceptibility distribution. Usually the focus is on imaging tissues in the brain, and the region of the brain studied is dictated by an eroded skull stripped mask. Producing the pristine local phase behavior for regions at the edge of the brain has been difficult in the past. For structures such as the superior sagittal sinus (SSS) that run alongside the surface of the brain and under the skull bones, a considerable part of the external phase from the dipole effect is lost due to the short T2* of the bones. In this paper, we propose a method that seeks to reconstruct the susceptibility distribution inside the dural sinuses by ensuring that the entire geometry of the dural sinuses is preserved with the help of an MR angiogram and venogram (MRAV). Having a geometrical model of the vessels makes it possible to estimate the missing phase outside the brain as well, by using the forward phase model and, hence, allowing a complete phase map to be reconstructed. Fifteen healthy volunteers were scanned using a susceptibility weighted imaging (SWI) sequence with interleaved rephaseddephased echoes. QSM results were compared between the conventional techniques and the proposed method of phase preservation outside the brain and inside the dural sinuses. This method demonstrates the reconstruction of the SSS, whereas conventional methods are either unable to preserve this structure or unable to provide complete phase information. The mean and standard deviation inside the SSS for all volunteers was 435 ± 5 ppb (this is the inter-subject error). To validate the proposed approach, the mean susceptibility inside the straight sinus showed good agreement between conventional approach and the proposed method. The results presented in this study indicate the potential of generating the susceptibility map for the whole brain, including the SSS (as well as potentially all the cortical veins).

INTRODUCTION

Quantitative susceptibility mapping (QSM) is a means to obtain direct measurements of local tissue susceptibility distribution [1]. The clinical value of QSM is currently being explored and holds great promise for vascular, inflammatory and neurodegenerative diseases of the brain [1–6]. In the advent of higher field strengths to allow higher resolution scanning and sophisticated methods to remove the unwanted background field, QSM data processing has become more clinically viable than ever and has become an important tool for quantifying iron, calcium and oxygen saturation in the brain [7–13]. Quantifying the susceptibility of the intracranial vascular structures, such as dural sinuses, can be potentially useful for many clinical applications such as measuring the oxygen extraction fraction and the behavior of the arachnoid granulations, which resorb fluid from the cerebral spinal fluid; and it is essential for studying many neurovascular conditions [14] such as stroke, Parkinson’s disease [15], headache [16,17] and idiopathic intracranial hypertension [18,19]. Any congenital lack of the dural system completely, as has may play a role in the development of the disease and/or increased iron deposition in the midbrain or basal ganglia [15]. Unfortunately, the QSM reconstruction pipeline, which addresses the unwanted phase changes from background fields at the air/tissue or bone/tissue interfaces, requires skull stripping and discarding noisy pixels outside the brain in the phase images. This often leads to eroding the superior sagittal sinus (SSS) and other cortical structures and a loss of the local phase behavior for veins and other dural sinuses at the edge of the brain.

In this paper, we propose a method that seeks to reconstruct the susceptibility distribution inside the SSS despite the issues mentioned above. One key feature is to ensure that the entire geometry of the dural sinuses is preserved, which is often not possible with current brain extraction procedures [20]. In order to overcome this issue, we used a special rephased/dephased sequence [21,22] to create arterial-venous (MRAV) data to preserve the geometry accurately and, hence, the internal phase for the SSS and transverse sinuses (TRS). The MRAV data and QSM results are generated from the same single susceptibility weighted imaging (SWI) sequence, which guarantees that no misregistration artifacts will be introduced. The other important feature is to estimate phase outside the brain by using the forward phase model from the geometries segmented from the MRAV data and, hence, allow a complete phase map associated with the dipole effect of the vein to be reconstructed [23–25]. Finally, we combine these steps to obtain an estimate of the venous oxygen saturation levels (Yv) inside the dural sinuses from the final QSM maps.

METHODS

Extracting the geometry of surface vessels

The MRAV data represents only vessels and rapidly flowing cerebrospinal fluid with completely suppressed stationary tissues [21,22,26]. This allows a straightforward extraction of vessel geometry using a simple intensity threshold. From this data, a vessel mask was generated using an intensity threshold of th>3σ, where σ is the standard deviation of the noise. The resultant binary mask contains both arteries and veins (M_AV). A brain stripped binary mask (M_Brain) was generated using the brain extraction tool (BET) [20]. Subsequently, the M_Brain mask was eroded during the SHARP (kernel radius = 6, regularization threshold = 0.05) [27] process to create the mask, M_SHARP. (The BET process often eliminates the dural sinuses and at best they are captured inconsistently.) Next, M_Brain was dilated in 2D (M_Brain-Dil) using a circle of diameter 4mm (approximately matching the radius of the SSS) which in this case is 6 pixels to preserve and segment the entire geometry of the dural sinuses. In order to keep only the vessels on the surface of the brain that were lost due to the background removal method, the difference mask of M_Brain-Dil − M_SHARP (or ${\text{M}}_{\text{Brain-Dil}}+\overline{{\text{M}}_{\text{SHARP}}}$ where $\overline{{\text{M}}_{\text{SHARP}}}$ is the complement of M_SHARP) was applied to the vessel mask (M_AV) to discard all the vessels inside the brain. An in-house code was written in MATLAB (Mathworks, USA) that determined the connectivity of these vessels and was used to separate out a mask of only the dural sinuses, including SSS and the transverse sinuses, (M_DS). As this mask will be used for forward field modeling of these vessels, it was essential to discard any other unwanted tissues included by the masking process.

Preservation of the internal SSS phase

Post processing of phase images of rephased long echo time (TE) data (φ_r) was performed in two steps: first, the internal phase of the dural sinuses was preserved by extending the background field. Initially, SHARP filtering was applied on the unwrapped phase (using a 3D best-path phase unwrapping algorithm), to remove the background phase and, consequently, providing the local phase information (φ_brain) within the eroded brain mask, M_SHARP. Taylor series expansion was then used to estimate the local phase outside the brain but within the M_Brain-Dil region [27–29]. This extended background phase was then subtracted from the original phase data, masked with M_Brain-Dil, to produce an extended local phase map, φ_ext. A local phase derivative variance map, or quality map (Q_MAP) as shown by Abdul-Rahman et al, of the φ_ext was then used to improve M_Brain and M_Brain-Dil by removing any region with rapid phase changes, representing the lack of signal outside the brain that may have been included in these masks due to the dilation step in the previous step [29,30]. The criterion to remove the rapid phase changes is defined by an empirically chosen threshold of th>1.8π (or 90% of 2π) in the Q_MAP. Due to the Q_MAP, the M_Brain-Dil mask will include only the brain tissue and veins; and exclude any noisy phase regions caused by the low signal in the tissues outside the brain such as the skull bones and air sinuses. Any islands created in the center of the brain were filled in using the flood-fill algorithm.

Estimation of the external SSS phase and susceptibility mapping

In the next step, the lost external phase for the dural sinuses was then simulated by applying the forward phase model approach on the M_DS [23–25]. Assuming that the susceptibility inside the SSS and TRS is uniform and consistent with the straight sinus (STS), Δχ_SSS = Δχ_STS was assigned to simulate the lost half of the external M_DS phase (φ_Ext,SSS). The updated phase data now holds information both inside and outside the brain (φ_whole). Susceptibility maps from φ_brain, φ_ext and φ_whole were generated using the inverse Green’s function kernel, using a method known as susceptibility weighted imaging and mapping (SWIM) [31], a QSM method. This step was followed by using the geometry constrained truncated k-space algorithm with a forced susceptibility value inside the structure-of-interest, also known as forced iterative SWIM (FIT-SWIM), to reduce the internal streaking [1,7,32]. The structure-of-interest encapsulates the dural sinuses as selected by M_DS as well as the all the other veins extracted by setting a threshold of 150ppb on the initial SWIM result.

Adaptive Simulation (AS) Method:

Although the forward modeled phase of M_DS provides a robust way to recreate phase information where no signal is available, there is the possibility that the initial assumption of Δχ_SSS = Δχ_STS may not be always true. We hypothesize that due to possession of original phase information both inside and partially outside the dural sinuses, regardless of the initial assumption for forward modeling step, it will help the inverse process drive towards the right answer, which we refer to as adaptive simulation-SWIM (AS-SWIM). Hence, after the first iteration, we record the mean Δχ inside the dural sinuses and use that as our new initial condition (Δχ_SSS = Δχ_fp, where Δχ_fp means first pass, or first iteration, mean susceptibility estimate). The above steps are illustrated in Figure 1. AS-SWIM results were compared with extended-SWIM, where φ_ext was utilized to perform the inverse process instead of φ_brain as well as conventional-SWIM, where φ_brain is utilized to perform the inverse process. However, unlike AS-SWIM, no adaptive feedback approach was used to improve the susceptibility reconstruction for extended- and conventional-SWIM.

Figure 1.

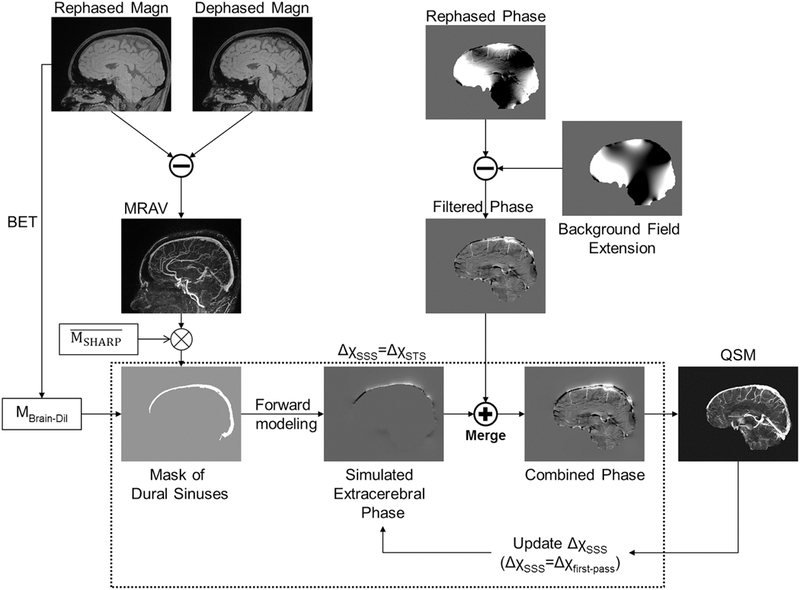
Illustration of the proposed adaptive simulations process using a rephaseddephased interleaved SWI sequence. The dotted-line box represents the main concept behind the AS method, which is to provide the best estimate of the missing phase outside the brain. The term ‘Merge’ represents merging the extended phase data with the external phase information of the dural sinuses, where the latter is produced by masking out all the phase information inside the mask, M_Brain-Dil. $\overline{{\text{M}}_{\text{SHARP}}}$ is a complement of M_SHARP, an eroded brain mask created after applying the SHARP algorithm on the unwrapped phase data.

Numerical simulations:

A 3D numerical brain model was used to simulate and study the AS approach. Different brain structures including the basal ganglia, veins and grey/white matter were assigned with an a priori susceptibility [32,33]. Veins were assigned a susceptibility of 0.45ppm (assuming venous oxygen saturation, Yv = 70%, hematocrit = 44% and Δχ_do = 0.27ppb in cgs units [34], where Δχ_do represents the susceptibility difference between deoxygenated and oxygenated blood. For the remainder of this paper, the same values of these constants will be used for computing Yv). The forward modeling process was used to generate the phase with the imaging parameters of: TE = 12.5ms, B0 = 3T, voxel resolution = 0.5mm isotropic and the matrix size of 512×512×512. The phase outside the brain, including the superior side of the external SSS phase, was forced to be zero. The background sources such as air sinuses and bones were not added to the simulation, as a controlled system was aimed for in this experiment, evaluating only the step of generating the susceptibility maps from the processed phase. The resultant masked phase was used to represent φ_ext, whereas a new brain mask eroded by a kernel with radius = 6pixels (mimicking the erosion due to SHARP) was used to represent φ_brain. Finally, in order to test the AS approach, the phase for the dural sinuses was simulated with different initial Δχ_SSS values from 0.1 to 0.8, with an interval of 0.1. The actual value used to create the data was 0.45ppm representing Yv = 70%. Only the external superior end of the SSS phase behavior was added back to the initial phase images to obtain φ_whole (internal as well as external inferior end of SSS phase is left unperturbed, and the extracerebral phase was zero). The simulated φ_brain, φ_ext and φ_whole were employed to generate the conventional-SWIM, extended-SWIM and ASSWIM, respectively. These results were then compared with the ground truth (i.e., the numerical 3D susceptibility model).

In vivo data acquisition:

In vivo human data were acquired at the Detroit Medical Center using a 3T Siemens VERIO scanner (Siemens Healthcare, Erlangen, Germany) with a product 32 channel head coil, after approval from the institutional review board of Wayne State University, Detroit, MI and performed in accordance with the ethical guidelines of the Declaration of Helsinki. Written informed consent was obtained in all fifteen healthy volunteers. All subjects were scanned with an interleaved SWI sequence comprised of two fully flow compensated, RF spoiled, 3D gradient echo sequences with interleaved rephaseddephased gradients [21,22]. This in-house sequence was comprised of two interleaved single-echo SWI sequences. The magnitude images of the interleaved rephaseddephased echoes were subtracted to generate MRAV maps. Table 1 lists the parameters used, including the longer TE (TE_L) that was utilized for both MRAV and QSM. The total number of datasets acquired was fifteen (transverse or axial=8, sagittal=7) with two subjects scanned more than once.

Table 1.

Imaging parameters for used for different healthy volunteers at 3T sorted based on the acquisition time (TA). TR = repetition time, FA = flip angle, BW = bandwidth, tra = transverse acquisition and sag = sagittal acquisition.

Data	Read (mm)	Phase (mm)	Partition (mm)	Orientation	TR (ms)	TEL (ms)	FA (deg)	BW (Hz/px)	# of slices	TA (min:sec)	# of coils
1	0.67	1.34	2	tra	20	12.5	12	240	64	3:59	32
2	0.67	1.34	2	tra	20	12.5	12	240	64	3:59	32
3	0.67	1.34	2	tra	20	12.5	12	240	64	3:59	32
4	0.67	1.34	2.7	tra	20	12.5	12	240	80	4:53	12
5	0.67	0.67	1.33	sag	25	17.5	12	210	64	5:34	32
6	0.67	0.67	1.4	sag	18.72	12.5	12	240	64	8:20	32
7	0.57	0.57	1.2	tra	18	12.3	15	310	104	12:04	32
8	0.67	0.67	1.33	tra	21	15	12	277	103	13:04	12
9	0.67	0.67	1.35	tra	19.04	12.5	10	240	128	14:12	12
10	0.67	0.67	1.35	tra	19.02	12.5	12	240	128	14:12	12
11	0.67	0.67	1.5	sag	18.72	12.5	12	240	112	14:50	12
12	0.67	0.67	1.5	sag	19	12.5	12	240	112	15:32	12
13	0.67	0.67	1.5	sag	19	12.5	12	240	112	15:32	12
14	0.67	0.67	1.5	sag	19	12.5	12	240	112	15:32	12
15	0.67	0.67	1.5	sag	19	12.5	12	240	112	15:32	12

Validation of the adaptive simulation method:

In order to validate the proposed method, we tested it on the straight sinus (STS), which is enclosed within the central region of the brain. A venous mask was generated from the conventional-SWIM result. SHARP processed phase or φ_brain was used for the regions inside the STS and the external phase of the STS was predicted using the forward model (assuming the initial Δχ = 0.45ppm). The mean and standard deviation of the susceptibility distribution as well as the computed Yv (assuming hematocrit = 44% and Δχ_do = 0.27ppb in cgs units) was obtained from the conventional SWIM and the proposed AS-SWIM, as explained above, for each volunteer.

RESULTS

Numerical Simulations:

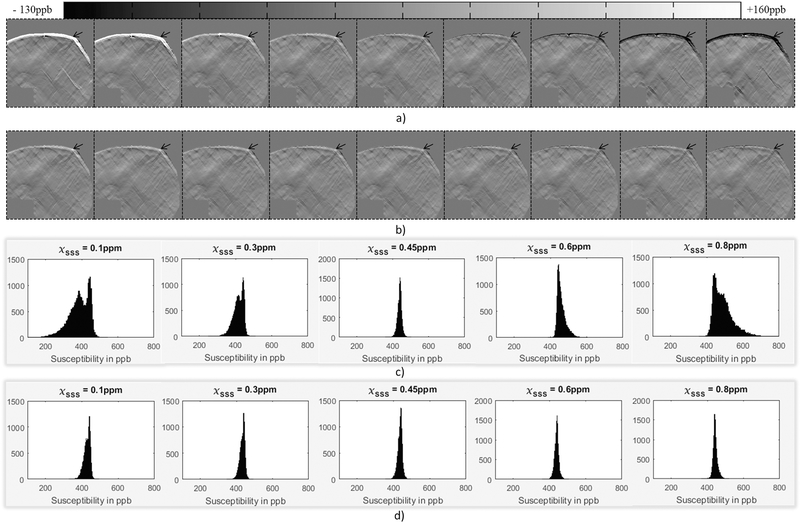
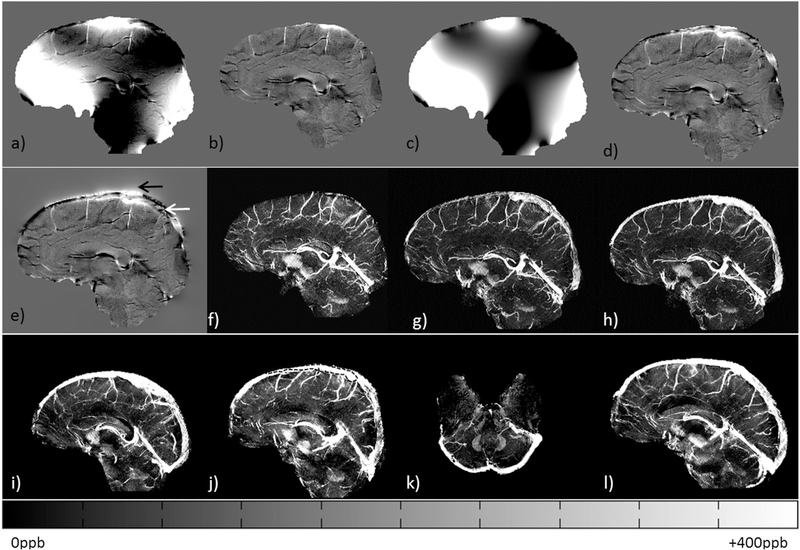
Results from the brain simulation (Figure 2) demonstrate the difference in susceptibility mapping capabilities of the conventional-SWIM (i.e., the spherical mean value (SMV) background removal with the eroded brain mask), extended-SWIM and the adaptive simulation or AS-SWIM described herein. The extended SWIM and AS-SWIM were both able to preserve the structures at the edge regions of the brain. However, the AS-SWIM approach provided a uniform distribution inside the dural sinuses (measured Δχ within SSS = 451±12ppb or Yv = 69.79%, which is in agreement with the initially assigned value for venous oxygenation in the numerical model) as opposed to the extended-SWIM results (measured Δχ within SSS = 291±67ppb or Yv = 80.51%, which inhabits an error of over 10% from the assigned Yv).

Figure 2.

A numerical 3D human brain model (a) was utilized to generate simulations for conventional SMV approach for background field removal (b), extension of brain boundary using Taylor series expansion of the field approach (c) and the AS approach of introducing phase outside the brain pertaining to SSS (φ_whole) (d). Due to the lack of the SSS in (b), the histogram (e) does not include the SWIM data of conventional-SWIM (as shown in f). The histogram compares: g) extended-SWIM and h) SWIM data from φ_whole after applying the AS method. The images (b-d and f-h) are zoomed based on the inset shown in (a). Please refer to Table 2 for more details.

The first pass results shown in Table 2 demonstrate that the measured mean value before AS-SWIM were not far from the true mean value (0.45ppm) assigned to the dural sinuses. For example, with the assigned initial value of Δχ_SSS = 0.6ppm, the mean value of the dural sinuses was measured to be 0.46ppm. The error in mean susceptibility was reduced from 0.15ppm, which was initially introduced by assigning a wrong susceptibility value to the SSS, down to 0.01ppm. After performing one iteration of the AS method, the initial guess that was assigned to the SSS model was replaced by the first pass mean susceptibility value. Due to this step of updating the initial guess, the final results are consistently within the error range of ±10ppb, regardless of the initial value. Figure 3 shows difference maps generated by subtracting the extended SWIM results as well as the results of AS-SWIM with and without correcting the initial Δχ_SSS (after performing one iteration of the AS method) from the ground truth. Subsequently, Figures 3c and 3d show that after the second iteration, the distributions inside the structure of interest were consistent and independent of the initial assumption.

Table 2.

The measured mean Δχ and standard deviation inside superior sagittal sinus using the FIT-SWIM on φ_whole: a) before and b) after AS-SWIM correction. Similarly, for the extended-SWIM using FIT-SWIM, Δχ = 383.9±75ppb.

Assigned Δχ (in ppb)
	100	200	300	400	450	500	600	700	800
Mean Δχ	384.7	399.8	414.9	430.0	437.5	445.1	460.2	475.3	490.4
Std Dev	57.7	42.7	28.1	15.4	11.7	12.6	23.6	37.8	52.8
a)
Assigned Δχ (in ppb)
	100	200	300	400	450	500	600	700	800
Mean Δχ	427.7	430.0	432.2	434.5	435.7	436.8	439.1	441.4	443.6
Std Dev	17.0	15.4	13.9	12.8	12.3	11.9	11.5	11.5	12.0
b)

Figure 3.

Difference maps from the ground truth produced by subtracting the FIT-SWIM results before (a) and after (b) applying AS-SWIM. From left to right, the images in (a) and (b) represent different initial assumptions for Δχ_SSS (in ppm) as: 0.1, 0.2, 0.3, 0.4, 0.45, 0.5, 0.6, 0.7 and 0.8. The actual value assigned to SSS in all cases was 0.45ppm. The error, identified by the region around the black arrows, is more substantial for the extended-SWIM result and for the FIT-SWIM process without any correction. These plots demonstrate that before correction (c), the variation in the Δχ distribution inside the dural sinuses was dependent on the initial value, whereas after the AS correction (c) the Δχ distribution was consistent independent of the initial

In vivo data:

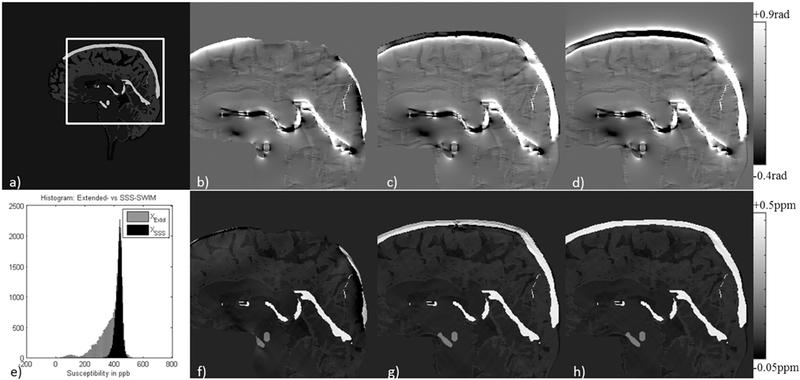
The resultant MRAVs (Figure 4a) show a strong, easily distinguishable signal inside the SSS, which was used to segment the geometry of the dural sinuses for forward modeling. The rest of the veins/arteries were masked out using the eroded SHARPbased brain mask. The internal phase of the SSS (white arrow on Figure 4f) and external phase of the SSS (black arrow on Figure 4f) are now clearly visible. The susceptibility mapping results were then compared between the conventionalSWIM(Figure 4g) and the QSM generated using the proposed method of phase preservation outside the brain (Figure 4h). This new method clearly shows the SSS, whereas the conventional-SWIMmethodology (Figure 4g) was unable to image this structure.

Figure 4.

Intermediate results of the AS-SWIM method for a healthy volunteer. a) Maximum intensity projection (MIP) of the MRAV data generated from the rephaseddephased interleaved SWI data, b) Original unwrapped phase, c) processed phase using SHARP, d) extrapolation of background field using the Taylor’s expansion method, (e) extended local phase generated by subtracting (‘d’ from ‘b’), (f) modified phase data containing internal (black arrow) and external (white arrow) phase for the SSS or φ_whole. MIP of susceptibility maps generated using conventional SMV decomposition method (g) and modified susceptibility maps generated from ‘f’ (h). ASSWIM data for four other volunteers are shown in (i-l), demonstrating the QSM reconstruction of whole brain, including the dural sinuses. In this case, the MIPs were projected over 16 slices or 24mm. The black dotted line in (h) represents an example of the manually selected region for QSM analysis.

The QSM results inside the SSS from 16 healthy volunteers are plotted in Figure 5. The region-of-interest (ROI) for evaluating the STS was chosen by manually drawing a contour of a homogeneous region in sagittal view of the brain. Similarly, for the SSS, a homogeneous region of the perpendicular section of the SSS was manually selected (please refer to the dotted black line in Figure 4h). The mean and inter-subject variability inside the SSS of all volunteers was 435.3±5.2ppb or Yv = 70.86%.

Figure 5.

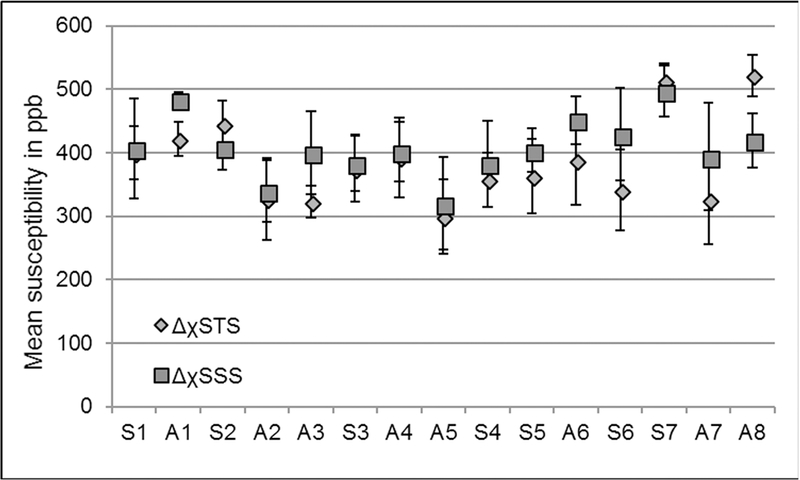
The plot of mean susceptibility values quantified from the dural sinuses from fifteen volunteers. Sn=sagittal and An=axial acquisition, where n is the volunteer number, i.e. n = 1, 2, 3…15. The mean ± σ_M inside the SSS of all volunteers was 435.3±5.2ppb, where σ_M represents the variation of the mean between subjects.

Furthermore, in order to validate the proposed approach, the mean susceptibility inside the STS was measured from one of the volunteers for conventional-SWIM was compared with the proposed method and were found to be in agreement (conventionalSWIM: 449±42ppb or Yv = 69.92% and proposed approach: 455±55ppb or Yv = 69.52%). In addition, the error between convention QSM and the proposed AS-SWIM QSM method for mean Δχ_STS was measured to be within the range of ±30ppb, showing good agreement in the reconstruction. Figure 6 demonstrates the validation of the ASSWIM method by utilizing the simulated external phase for major veins in the brain to generate a decent estimate of their susceptibility distributions; for two volunteers, one with sagittal acquisition (Figure 6a-6c) and the other with axial acquisition (Figure 6d-6f). The STS and other extracted major veins were almost completely suppressed on the difference maps of conventional-SWIM and the proposed approach. Maximum intensity projections were generated from the difference maps to highlight any mismatch. MIP of the difference maps (Figure 6c and 6f) indicate that the veins that were extracted (Figure 6b and 6e) have been suppressed. Other structures, such as the basal ganglia, as well as the veins with susceptibility smaller than the threshold were not extracted and, hence, they can still be seen on the difference MIPs.

Figure 6.

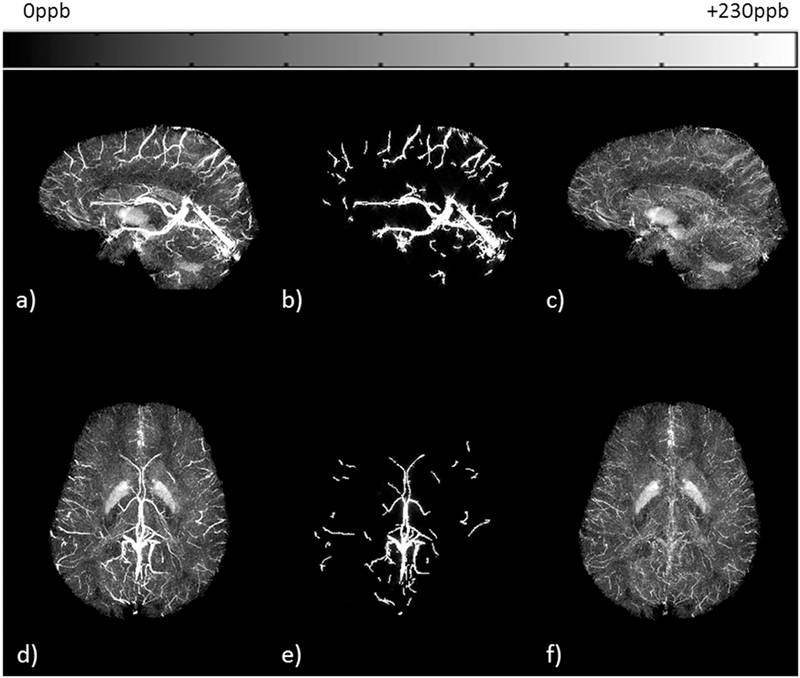
Original FIT-SWIM data (a, d) were used to generate a binary venous mask using an intensity-based threshold. The AS method was applied on this mask to produce an estimate of susceptibility reconstruction of the extracted veins (b, e). The QSM estimate from the AS method was subtracted from the original FIT-SWIM data. These difference maps are shown here in the form of: (c, f) MIP. MIP was performed over 32 slices or effective slice slab of 42.5mm. Sagittal acquisition: (a-c) and axial acquisition: (d-f).

DISCUSSION AND CONCLUSION

In this work, we have presented a method to generate the susceptibility distribution of the whole brain, including the SSS (as well as all the cortical veins) by utilizing MRAV along with the conventional SWI sequence. Simultaneous acquisition of the SWI and MRAV helps in reducing the processing steps by avoiding the need for image registration. However, the main goal here was to abet the QSM reconstruction even for the boundary structures, such as the dural sinuses, by adding an MRAV. Hence, we anticipate that the AS method is equally applicable when one possesses SWI data and a time-of-flight MRAV with the same whole brain coverage, followed by an additional step of registering the two datasets.

Considering the fact that, regardless of the approaches used for QSM reconstruction, the external phase for surface veins will always be unavailable for non ultra-short TE (<1ms at 3T) data. Therefore, it should also be noted that the proposed AS approach, which provides an estimate of external phase using the extracted M_DS masks, can be extended to other methods including the total field inversion (TFI) approach, that solve the inverse, field-to-susceptibility process [35–38].

We have evaluated this method using a brain model, for validation (Figure 2) as well as the comparison of mean susceptibility inside the STS with standard QSM, on in vivo data, for accuracy. The STS was chosen in this study for the comparison due to its similarity in size and the draining properties with the SSS. The forward modeling process allows us to obtain an estimate of the phase behavior for a given object which plays the key role when only a part of the phase data is available. The presence of the skull bone on the superior end of the SSS, for example, creates a partial loss of phase making it impossible to quantify the susceptibility of the SSS. As seen from Figures 2g and 2h, using the SSS information from the MRAV data to create phase in the missing regions provided a much better susceptibility map (Figure 2h). The susceptibility inside the dural sinuses was assumed to be the same as that of STS. The STS is situated near the center area of the brain, hence there is a complete set of phase data available to make a good estimate of its mean susceptibility value which can then be used as an educated guess for the initial condition. The estimated missing phase, generated by assuming that Δχ_SSS= Δχ_STS, acts as a good initial condition for the dural sinuses. However, this may be not always true especially for patients suffering from a neurological disease that causes an abnormal glymphatic clearance. This could create a strong susceptibility difference in the arachnoid granulations of the dural sinuses.

In order to address this, the resultant mean value of the SSS was used as the initial condition in the next iteration, instead of the mean susceptibility of STS. With the original internal phase as well as the inferior end of external phase is still available, we theorize that the inverse process will drive the Δχ distribution inside the SSS towards the correct values. After adding this feedback step, the improvement can be clearly seen in Figure 3b. Although the assumption for the SSS susceptibility value was chosen incorrectly, the final result converges towards the real assigned value, after only one iteration. This additional step constitutes the ‘adaptive’ part of the AS method. Hence, by simulating the external phase for the SSS, we can provide the missing part of the phase information to produce a more accurate measurement of the oxygen saturation. This approach will also allow reconstruction of the surface veins and cortical areas that can be essential for measuring the cerebral metabolic rate of oxygen in cortical grey matter. The method was shown to be reproducible through different imaging parameters tested for this work (see Table 1). The variation in measured mean susceptibility value seen in Figure 5 can be attributed to the ±10% difference in hematocrit levels [39] or the presence of caffeine in blood [7]. The main purpose here was to evaluate whether the AS-SWIM method provides an accurate susceptibility distribution with respect to the conventional-SWIM or extended-SWIM.

Susceptibility differences across the tissues can create an additional local gradient. These magnetic susceptibility-induced gradients are similar to the field gradients created near the air-tissue interfaces. Due to first order gradient moment nulling, the magnitude of phase accumulation due to the blood flow velocity (ν) depends only on the background gradients (G’) over time, t: φ_f = (YG'vt²)/2, where γ is the gyromagnetic ratio for protons (γ~ 42.58 MHz/T) [40,41]. However, the region near dural sinuses is almost spherical and situated far away from strong field perturbations. Although it has been shown recently that flow through magnetic field gradients in the frontal sinuses can cause the arteries to develop phase [42], flow in the veins is slow (ν≈7 ml/s) [43] and field variations by the dural sinuses are small; therefore, we do not expect this effect to produce significant phase variations in the veins. It is also important to note that this new method introduces the estimated lost external phase only pertaining to the veins.

In conclusion, we demonstrated that we can improve the susceptibility estimates of the SSS when complete three-dimensional phase information is not available and use this to obtain an improved estimate of the venous oxygen saturation levels inside the dural sinuses.