Observation of enhanced thermopower due to spin fluctuation in weak itinerant ferromagnet

Thermopower, which generates electricity from heat, can be greatly enhanced in weak ferromagnets even above room temperature.

Abstract

Increasing demand for higher energy efficiency calls for waste heat recovery technology. Thus, facilitating practical thermoelectric generation systems is strongly desired. One option is enhancing the thermoelectric power factor, S²/r, where S is the Seebeck coefficient and r is the electrical resistivity, although it is still challenging because of the trade-off between S and r. We demonstrate that enhanced S²/r can be achieved by incorporating magnetic interaction in ferromagnetic metals via the spin fluctuation arising from itinerant electrons. We show that electron-doped Heusler alloys exhibit weak ferromagnetism at T_C near room temperature with a small magnetic moment. A pronounced enhancement around T_C was observed, with a 20% improvement in the power factor from the case where spin fluctuation is suppressed by applying magnetic field. This result supports the merit of using spin fluctuation to further enhance thermoelectric properties and the potential to further probe correlations and synergy between magnetic and thermoelectric fields.

INTRODUCTION

Thermoelectric generation is a promising technology as it can convert waste heat to electric power. An urgent task is to further enhance the conversion efficiency. While the importance of calculation methods is rapidly increasing in this and other research fields, it is also vitally important to incorporate new principles that have not been considered in the current calculations of thermoelectric materials. Improvement in thermoelectric properties has been achieved, for example, by synergizing lattice distortion due to the Peierls transition (1), creating resonant electronic states (2), using anharmonic atomic vibrations (3) or critical fluctuation around polar structural transitions (4), etc. The use of magnetic interactions for power generation is also rapidly expanding, such as in spin Seebeck effect, anomalous Nernst effect, magnon-drag thermopower, etc. (5–10).

It should be noted that these magnon- or spin-related effects are based on thermally nonequilibrium spin currents. The relevant spins are effective only in the magnetically ordered state and are mainly due to spatially localized electrons. In the present work, by contrast, we focus on other spin-related dynamics, namely, spin fluctuations in itinerant electron systems, which are effective even in the paramagnetic state. This interaction has not been actively exploited for power generation applications up to now, despite the fact that it can be essentially important in terms of thermodynamic properties.

Spin fluctuations in itinerant electron systems give predominant effects on thermodynamic properties in weakly or nearly ferromagnetic metals (11, 12). The electronic specific heat is enhanced from that of a normal metal, indicating that the electronic entropy is increased due to spin fluctuations. Thermopower, which is roughly regarded as the entropy transferred by a charge carrier, is also expected to be enhanced through spin fluctuations in the vicinity of the magnetic ordering. Pronounced peak structure was observed in the temperature-dependent Seebeck coefficient of YCo₂ and LuCo₂ (13). Since these compounds are classified to be nearly ferromagnetic metals, the peaks in the Seebeck coefficients were attributed to the paramagnon drag effect, indicating the pronounced spin fluctuation contribution (13). The effect of spin fluctuation was also discussed for the filled skutterudites AFe₄Sb₁₂ (A = Ca, Sr, Ba), which are considered to be close to the ferromagnetic instability (14). The Seebeck coefficient of AFe₄Sb₁₂ shows a shoulder-like anomaly at 50 K, near which the magnetic susceptibility also exhibits a maximum. Theoretical study has predicted that spin fluctuations in nearly ferromagnetic metals can cause a peak in the Seebeck coefficient around the temperature characteristic to the spin fluctuation energy (15).

While the spin fluctuation effect in thermopower is intriguing from an academic point of view, it has not been considered useful for practical purposes. Seebeck coefficients of the RCo₂ compounds were too small to be applied for thermoelectric generation because of the metallic nature. In the case of AFe₄Sb₁₂ skutterudites, although filled skutterudites form a class of promising thermoelectric materials for high-temperature application, the effect of spin fluctuation was only observed at cryogenic temperatures. If those effects can occur in thermoelectric materials at their working temperatures, then introducing spin fluctuation can be a new guiding principle to enhance thermoelectric properties. Here, we demonstrate that the enhancement in the Seebeck coefficient indeed occurs even near room temperatures by showing experimental results of the Heusler compounds Fe₂V_1-xT_xAl_1-ySi_y, where T is a transition element.

The mother compound, Fe₂VAl, has been extensively investigated for thermoelectric applications (16, 17). Fe₂VAl shows a semiconductor-like electrical conductivity with a nonmagnetic ground state due to the presence of a pseudogap at the Fermi energy (18). By replacing constituents with other elements or introducing nonstoichiometry, carriers can be doped and thermoelectric properties can be greatly improved, with the highest power factor (PF) of 55 μW/K² cm obtained around room temperature for the chemical composition of Fe₂VAl_0.9Si_0.1 (19). In the course of our research on these Heusler-type thermoelectric materials, we obtained Cr-doped samples with chemical composition close to Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 and Fe-rich samples, Fe_2.2V_0.8Al_1-ySi_y. We observed weak ferromagnetic behavior in these samples. Furthermore, we discovered a pronounced enhancement in the Seebeck coefficient around the Curie temperature because of strong coupling with the spin fluctuation. One notable feature of our discovery is that, by intrinsic nature, the thermoelectric enhancement is not limited to temperatures below the magnetic ordering temperature but is effective at higher working temperatures. We observed large PFs up to 12 μW/K² cm in these compounds around room temperature and will show that a substantial portion of this can be attributed to the enhancement by spin fluctuations.

RESULTS

Magnetic and thermoelectric properties

First, we show the results of the Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 sample. As is shown in Materials and Methods, this sample includes unintentionally doped Cr (and a small amount of Ni) ions, which presumably are doped mainly in the V sites. Figure 1A shows the field-dependent magnetization M measured at fixed temperatures. The data show that ferromagnetic behavior develops at low temperatures. An interesting point is that the saturation magnetization M_S is only 0.4 μ_B per magnetic atom at 10 K. Here, only Fe and Cr atoms are assumed to be responsible for the magnetization. Figure 1B shows temperature dependence of the magnetization M and the inverse magnetic susceptibility H/M measured at H = 1 T. The rapid increase in M below about 200 K suggests a weak ferromagnetic transition. The Curie temperature T_C = 160 K was determined from the peak in the dM/dH curve measured at H = 0.1 T (see fig. S1). Above 200 K, H/M shows a T linear dependence, indicating a Curie-Weiss behavior, H/M = (T − θ)/C, where θ and C are the Weiss temperature and the Curie constant, respectively. Here, C = Np_eff²/3k_B, where N, p_eff, and k_B are the number of magnetic ions, the effective magnetic moment, and the Boltzmann constant, respectively. By fitting the data above 250 K with a linear function, θ = 167 K and C = 2.27 K emu/mol were obtained. The value of θ is in good agreement with T_C = 160 K, indicating that the small M_s is not due to ferrimagnetism or canted antiferromagnetism but to a pure ferromagnetism. Moreover, the C value yields an effective magnetic moment p_eff = 4.26 μ_B per magnetic ion. The value of p_eff is close to the theoretical value for an Fe²⁺ (S = 2 for the high-spin state) ion, p_eff = g{S(S + 1)}^1/2μ_B = 4.90μ_B with g = 2. These facts assure that the ferromagnetism is due to the bulk effect of the sample but not to a small amount of ferromagnetic impurity. These results indicate that this compound is a weak itinerant ferromagnet. This is more evident if we compare the data with other ferromagnetic materials on the well-known Rhodes-Wohlfarth plot (11, 20, 21), which is shown in fig. S2. In these weak ferromagnets, thermal fluctuation of the local spin density, which is referred to as spin fluctuation, is significant, as has been demonstrated for many intermetallic systems (11, 12).

Fig. 1. Magnetic and transport properties of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1.

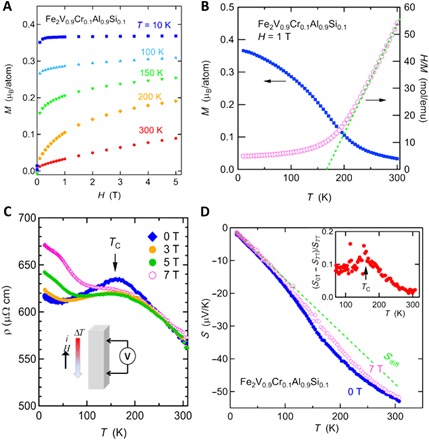
Measured under magnetic fields H as functions of temperature T. (A) The compound shows a ferromagnetic ordering with a small saturation magnetization of 0.4 μ_B per magnetic atom, indicating weak itinerant ferromagnetic state. (B) M versus T data show that ferromagnetic ordering occurs below T_C = 160 K. The inverse magnetic susceptibility H/M shows a T linear dependence above T_C, indicating a Curie-Weiss behavior H/M = (T − θ)/C, where θ is the Weiss temperature and C is the Curie constant (shown as a broken line). From the fitting, θ = 167 K and the effective magnetic moment p_eff = 4.26 μ_B per atom are obtained, where the magnetic atoms are Fe or Cr. (C) Electrical resistivity ρ shows a cusp-like anomaly at T_C. This behavior is suppressed by magnetic fields. Inset: The configuration for transport measurements in magnetic fields. (D) Seebeck coefficient S measured at 0 and 7 T. S exhibits a shoulder-like enhancement around T_C, and the enhancement is suppressed by magnetic field. At H = 7 T, S(T) becomes closer to the linear T behavior as is expected for a normal degenerate semiconductor. Inset: The difference of S between H = 0 and 7 T with respect to the values at 7 T, which exhibits a peak at T_C, indicating a strong effect of spin fluctuation.

While the mother compound Fe₂VAl has a nonmagnetic ground state, this compound is very close to ferromagnetic ordering, as has been demonstrated by many studies. Ferromagnetic behavior has been observed for Fe_2+xV_1-xAl with 0.1 ≤ x, and both ferromagnetic moment and T_C linearly increase with increasing x (18, 22). These magnetic properties have been interpreted within the framework of itinerant electron magnetism with strong spin fluctuation (23). The magnetic properties of Fe₂VAl_1-xSi_x have so far been investigated for lightly Si-doped samples with x ≤ 0.04 (24, 25), and it was reported that superparamagnetic contribution develops below 300 K in Fe₂VAl_1-xSi_x for x ≤ 0.02. Thus, it is reasonable that Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 shows a ferromagnetic transition with a small saturation magnetization of 0.4 μ_B and a relatively low T_C = 160 K. These values are close to those observed for Fe_2.25V_0.75Al, with T_C = 120 K and M_S = 0.4 μ_B (22). The small saturation magnetization reflects that the ferromagnetism is due to itinerant electrons and that their thermodynamic properties are strongly affected by spin fluctuations, of which amplitude is expected to develop with temperature (11).

In Fig. 1C, temperature-dependent electrical resistivity, ρ(T), is shown. ρ(T) measured under zero field exhibits a cusp at T_C = 160 K. ρ(T) shows a semiconductor-like increase for T > T_C, while it changes to a metallic behavior for T < T_C. A similar change in the ρ(T) slope at T_C has been reported for Fe_2+xV_1-xAl as well (18, 22). When magnetic field is applied, the peak is suppressed and turns into a broad maximum. The magnetoresistance (MR) is most significant at T_C = 160 K; ρ_7T/ρ_0T reaches −2.6%. The negative MR and the peak structure behavior are attributed to scattering of carrier electrons by spin fluctuations, the effect of which is suppressed by magnetic fields. On the other hand, positive MR is observed below 100 K. Here, the magnetic field is applied in the parallel direction with electric current, as shown in the inset of Fig. 1C; thereby, the conventional transverse MR is not responsible. At present, the origin of this positive MR is unclear and can be relevant to some change in the electronic state. Similar positive MR was reported for Fe_1-xCo_xSi (26), where a weakly ferromagnetic state is induced by doping Co into the nonmagnetic semiconductor FeSi. Figure 1D shows temperature dependence of the Seebeck coefficient S(T) measured under zero field and at 7 T. S(T) shows negative values, and the absolute values increase with temperature monotonically. This is consistent with the n-type doping since Cr and Si have one more valence electrons than V and Al, respectively. Notably, S(T) at zero field exhibits a broad shoulder-like hump between 150 and 200 K. At 7 T, the hump almost disappears and S(T) changes to show nearly T linear behavior like that of typical degenerate semiconductors. The shoulder-like enhancement of S(T) is most significant around T_C. It can be more evident in the inset of Fig. 1D, where the enhancement ratio, ΔS/S_7T = |S_0T − S_7T|/S_7T, is plotted. ΔS/S_7T exhibits a maximum at T_C = 160 K. Furthermore, the enhancement exists in a wide temperature range: Substantial enhancement of 5 to 10% is seen even above T_C up to about 200 K. This rules out the contribution of the magnon drag effect as a dominant mechanism for the enhancement (8–10), since that effect would be present only in the ferromagnetically ordered state.

Temperature dependence of the PF is shown in Fig. 2. In the inset, the enhancement ratio of PF due to magnetic field, ΔPF/PF_7T = (PF_0T − PF_7T)/PF_7T, is shown. The PF at H = 0 T is larger by more than 20% at around T_C than that at H = 7 T, where spin fluctuation is suppressed. Furthermore, the effect remains almost up to room temperatures. Temperature dependence of the thermal conductivity, κ(T), is shown in fig. S3. The κ(T) measured at H = 7 T agrees well with that at H = 0 T, indicating the minor effect of external fields on thermal conductivity.

Fig. 2. Thermoelectric PF of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1.

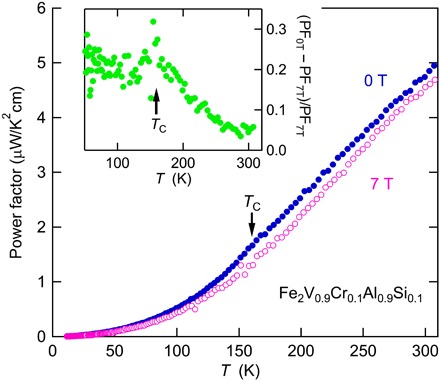
At zero field and 7 T. Inset: The difference of PF with respect to the values at 7 T, |PF_0T − PF_7T|/PF_7T as a function of T. The enhancement in PF is most significant at T_C = 160 K by a factor of ~20%, and the effect persists above T_C.

It is important to clarify in what temperature range the enhancement in Seebeck coefficient is significant and how the magnetic field can alter the properties. In Fig. 3A, values of |S/T| of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 are plotted in the T-H plane. At zero field, |S/T| exhibits a sharp peak at T_C. With increasing field, the peak becomes less sharp and turns into a broad maximum. This crossover can be understood by the suppression of spin fluctuations under external fields, which is schematically depicted in Fig. 3B. Spin fluctuation gives the most dominant effect around T_C and is important even above T_C, since the energy scale of spin fluctuation is usually one to two orders of magnitudes larger than T_C for itinerant electron ferromagnets (11, 12). This is in contrast to spin wave (magnon)–related phenomena, which exist only below T_C. When a magnetic field is applied, the net magnetic moment increases. In that case, spin fluctuation, i.e., thermal fluctuation of the local spin density, is suppressed concomitantly, as illustrated in Fig. 3C. Under H = 7 T, the broad peak still remains, indicating that the effect of spin fluctuation is not fully suppressed yet. One can see that the enhancement in |S/T| exists in a wide temperature range. It is therefore expected that enhanced thermoelectric properties in a more applicable temperature range will be achieved by using itinerant ferromagnetic materials with T_C close to room temperature.

Fig. 3. Enhanced thermopower by spin fluctuation.

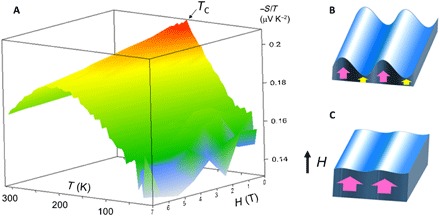
(A) Seebeck coefficient divided by temperature S/T of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1, plotted as functions of magnetic field and temperature. −S/T has a sharp peak at T_C under zero magnetic field and is remarkably suppressed with increasing H. This implies that the Seebeck coefficient at zero field is enhanced by spin fluctuation. (B) Spin fluctuation, i.e., thermal fluctuation of local spin density of itinerant electrons, is schematically illustrated. The fluctuation is most significant near T_C, although the static magnetic moment is small. (C) Under a strong magnetic field, while the net magnetic moment is stabilized, the fluctuation is suppressed accordingly.

To test the use of spin fluctuation enhancement toward applications, we examined thermoelectric properties in a Fe₂VAl-based material with higher T_C. Since the Fe_2+xV_1-xAl system exhibits ferromagnetic ordering with T_C near room temperatures (22), we selected Fe_2.2V_0.8Al_1-ySi_y. Magnetic properties of y = 0 (Fe_2.2V_0.8Al) and y = 1.0 (Fe_2.2V_0.8Si) were reported to show ferromagnetic ordering at around 80 and 200 K, respectively (27, 28). While p-type behavior was reported for y = 0, the y = 1.0 sample is known to be n type. The optimum carrier concentration can be expected to occur in the middle of the two compositions. In Fig. 4, the results for the y = 0.4 sample are displayed. In fig. S4, ρ-T and κ-T of y = 0.4 are also presented. Results for y = 0.6 and 0.8 are shown in figs. S5 and S6. We found that Fe_2.2V_0.8Al_0.6Si_0.4 exhibits weak ferromagnetism with T_C = 285 K and M_S = 0.55 μ_B/Fe. T-dependent Seebeck coefficients measured in zero field and at 9 T (shown in Fig. 4C) increase linearly with T up to 200 K and then turn to show nonlinear curves up to the highest temperature measured (400 K). The enhancement is slightly suppressed at H = 9 T. The relative difference of the Seebeck coefficients between H = 0 and 9 T, |S_0T − S_9T|/|S_9T|, shows a maximum value of about 14% at T_C and is constantly higher than 10% from 200 to 350 K. The relative enhancement in PF, |PF_0T − PF_9T|/PF_9T, is 20% at T_C, as shown in Fig. 4D, and is larger than 10% from 100 to 400 K.

Fig. 4. Magnetic and thermoelectric properties of Fe_2.2V_0.8Al_0.6Si_0.4.

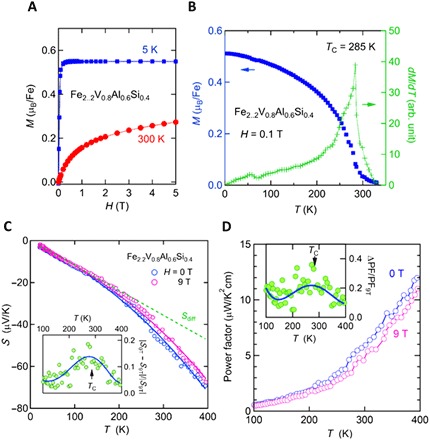
(A) Field dependence of the magnetization M of Fe_2.2V_0.8Al_0.6Si_0.4. The saturation magnetization at T = 5 K is as small as M_S = 0.55 μ_B per Fe. (B) T dependence of M measured at H = 0.1 T and its field derivative dM/dH. T_C = 285 K is determined by the peak of dM/dH. Above T_C, fitting yields the effective magnetic moment p_eff = 4.20 μ_B and the Weiss temperature θ = 292 K. (C) Seebeck coefficient measured at H = 0 and 9 T. Solid lines are the results of the fitting by the spin fluctuation model (Eq. 2), which is explained in the Discussion. Broken line is the linear extrapolation from the low-temperature data. Inset: The relative difference of Seebeck coefficients, |S_0T − S_9T|/|S_9T|. Solid line in the inset is a fit with a polynomial function. (D) T dependence of the PF. Inset: The relative difference of the PF, |PF_0T − PF_9T|/|PF_9T|. Solid line in the inset is a fit with a polynomial function.

As was shown for the Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 compound in Fig. 3A, the effect of spin fluctuation is not fully suppressed by magnetic fields of a few Tesla. The net enhancement is presumably much higher. If we assume that the diffusion part of the Seebeck coefficient without spin fluctuation effect is approximated by the linear extrapolation from the low-temperature data, which is shown as the green broken lines in Fig. 4C, noted as S_diff, then the enhancement in the Seebeck coefficient due to spin fluctuation can reach ~50% at 400 K. This indicates that the PF could have been approximately doubled by the effect of spin fluctuation at 400 K, as a result of which a high value of 12 μW/K² cm is achieved. Similar orders of enhancement are also observed for Fe_2.2V_0.8Al_1-ySi_y with y = 0.6 and 0.8 samples as well (see figs. S5 and S6, respectively), although S_diff was not able to be estimated for the two samples because of strong phonon drag effect. Electronic band structure calculations are desired to derive accurate values of S_diff, which allows exactly evaluating the contribution of spin fluctuation. Nevertheless, the present results unambiguously demonstrate that spin fluctuations in weak itinerant ferromagnets have an excellent potential to boost thermoelectric PF up to practically useful levels around the room temperature range. The possible effect due to electron-magnon drag will also be considered in the Discussion.

Magnetotransport property

To shed light on the correlation of carrier transport and magnetic moments, we measured the Hall resistivity of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 at various temperatures. The Hall resistivity is generally expressed as ρ_xy = R₀H + 4πR_sM, where the first term corresponds to the normal Hall contribution, with R₀ being the normal Hall coefficient, and the second term represents the contribution of the anomalous Hall effect (AHE), with R_s and M being the anomalous Hall coefficient and the magnetization, respectively. In Fig. 5, measured results are presented. The ρ_xy data exhibit strong nonlinear behavior over the whole temperature ranges, which is attributed to AHE. At T = 10 K, ρ_xy shows almost parallel behavior to the M(H) data at 10 K (Fig. 1A). From the comparison of ρ_xy and M(H), the AHE term is estimated to be as large as 11 μΩ cm. It was reported that the ferromagnetic semiconductor Fe_1-xCo_xSi shows a large AHE with ρ_xy = 1.4 μΩ cm, which is 150 times larger than that of Fe_1-xMn_xSi with similar magnetic properties (29). In this regard, the AHE of ρ_xy = 11 μΩ cm in our sample can be unusually large. We consider whether this may simply be attributed to the larger magnetic moment in Fe₂V_0.9Cr_0.1Al_0.9Si_0.1. The saturation magnetization for Fe_0.9Co_0.1Si was 4πM ≈ 370 G from (29), while 4πM ≈ 1900 G for Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 from Fig. 1. Therefore, we fit the ρ_xy data to obtain the values of R₀ and R_s using the M(H) data, as shown in fig. S7. As a result, the AHE coefficient at T = 10 K is obtained as R_s = 0.63 cm³ per C. This value is comparable to that of Fe_0.9Co_0.1Si, R_s ≈ 0.5 cm³ per C, indicating that the AHE of the present compound is also unusually large, comparable to the case of the Fe_0.9Co_0.1Si compound (29). Notably, R₀ of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 changes its sign between two temperatures. This may imply that there are two types of carriers with different effective mass and mobility. Although the origin of the large AHE is yet unclear, this unambiguously demonstrates strong coupling between magnetism and carrier conduction in these materials.

Fig. 5. Hall resistivity ρ_xy of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1.

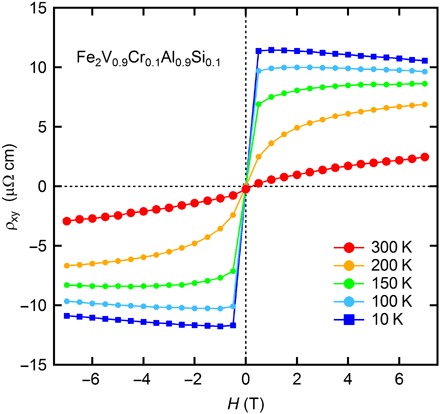
ρ_xy shows behavior that is well parallel to the M(H) data shown in Fig. 1A and is explained by ρ_xy = HR₀ + 4πMR_s, where R₀ and R_s are the normal and the anomalous Hall constants, respectively. The values of R₀ and R_s were obtained by fitting the data, which are shown in fig. S7.

DISCUSSION

In addition to spin fluctuations, the effect of magnon (spin wave) excitations may also need to be considered for the present compounds. The magnon drag thermopower was first suggested to occur in Fe (30). Comparison with the latest theoretical results (31, 32) and experimental data demonstrated that the Seebeck coefficients of Fe, Co, and Ni are well explained by the sum of the T linear diffusion thermopower S_diff and the magnon drag term S_mag (33). The latter is predicted to have a T^3/2 dependence under the assumption of a quadratic magnon dispersion (33). In the present case, estimation of S_diff is difficult because electronic energy band calculations are not available for Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 and Fe_2.2V_0.8Al_0.6Si_0.4. We hence approximate S_diff by a T linear extrapolation of the S(T) data from low-temperature values, as shown by the broken lines in Figs. 1D and 4C. In Fig. 6, ΔS = |S_0T − S_diff| of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 and Fe_2.2V_0.8Al_0.6Si_0.4 are plotted as functions of T in log-log scales. In the figures, the difference |S_0T − S_9T| is also plotted. For both compounds, temperature dependence of ΔS is weak below 0.5 T_C. For the middle temperature range (0.5 T_C < T < T_C), ΔS appears to obey a power law Tⁿ, with n = 2.5 for Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 and n = 4.7 for Fe_2.2V_0.8Al_0.6Si_0.4, both of which values are much larger than n = 3/2 predicted by the magnon drag theory. The difference |S_0T − S_9T| also shows a similar tendency. Hence, the magnon drag effect does not seem to be important in the present systems.

Fig. 6. Power law behavior in thermopower.

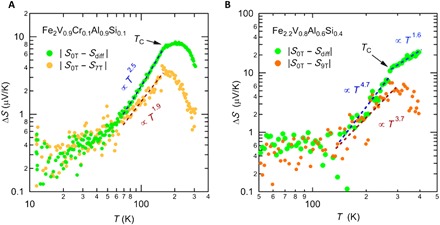
Difference of Seebeck coefficients at H = 0 T and the diffusion thermopower, |S_0T − S_diff|, of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 (A) and that of Fe_2.2V_0.8Al_0.6Si_0.4 (B). Here, S_diff was approximated by the linear extrapolation of the low-temperature data in Figs. 1D and 4C. Difference of S between 0 T and magnetic fields [7 T for (A) and 9 T for (B)] is also shown. Fitting results with a power law are shown by broken lines.

Possible reasons for the absence of the magnon drag effect are considered in the following. First, the spontaneous magnetic moments of the present compounds are very small compared to conventional ferromagnets such as Fe and Co. The heat flux carried by magnons would therefore be limited. In the case of weak ferromagnets, in particular, the magnon excitation is only well defined in a narrow q-ω range since the Stoner excitations dominate over wide q-ω space (11). Accordingly, the contribution of magnons to thermal properties can be small.

Second, the magnon drag thermopower may be weakened in the case of weak itinerant ferromagnets. From the theoretical study based on the spin-motive force, the magnon drag thermopower is described as

$${\mathit{S}}_{\text{mag}}\propto (\mathrm{\beta }-3\mathrm{\alpha }){\mathit{P}}_{\mathrm{s}}{\mathrm{\kappa }}_{\mathrm{m}}$$ (1)

where β, α, P_s, and κ_m indicate the spin-transfer torque parameter, the Gilbert damping parameter, the spin polarization of conduction electrons, and the thermal conductivity due to magnons, respectively (9, 10, 32). It was pointed out that the ratio β/α is equal to S_t/S_i, which is the ratio of the total magnetic moment (S_t) to the spin moment of itinerant electrons (S_i) (9, 34). While conventional ferromagnets such as Fe belong to itinerant electron systems, they are close to localized moment systems in the Rhodes-Wohlfarth plot (fig. S2). This implies that the condition S_t/S_i ≫ 1, i.e., β ≫ α, is valid. For the weak ferromagnet, however, S_t and S_i are in the same order; thereby, the prefactor (β − 3α) can be reduced significantly. Therefore, it is suggested that the enhanced thermoelectric properties in our study contain a new mechanism other than the magnon drag effect. One thing that we also note is that the exponent n = 3/2 of the power law in the magnon drag theory arises from the assumption of quadratic magnon dispersion, which is generally true for ferromagnets. In the case of antiferromagnets, n = 3 would be expected (35). Hence, the possibility that the large n values in Fig. 6 stem from a unique magnon band structure may not be completely excluded. It is desirable in the future to perform inelastic neutron scattering experiments to investigate the dispersion relation in the present Heusler compounds.

Next, let us consider whether the context of the magnon drag theory can be applied to describe the spin fluctuation enhancement. Since Eq. 1 includes the spin polarization P_s, it cannot explain the enhanced S(T) above T_C, where P_s should be zero. On the other hand, Watzman et al. (33) pointed out that another approach using a hydrodynamic theory can also explain the magnon drag thermopower. They treated magnons and electrons as two fluids, and only the interaction between the two fluids is considered. Thus, scatterings of electron-phonon or magnon-magnon are neglected. As a result, they suggested that S_mag is proportional to the magnon heat capacity, C_mag. Since this theory does not depend on a microscopic model, this can be straightforwardly extended to the spin fluctuation effect. If the spin fluctuations are regarded as a fluid and the interaction among them is neglected, then the thermopower due to spin fluctuation can roughly be related to specific heat due to spin fluctuations. It was shown that the spin fluctuation–related specific heat continues to increase with temperature monotonically beyond T_C and that the critical divergence at T_C does not occur for weak ferromagnets (11). This seems to be consistent with the observation of S(T) for Fe_2.2V_0.8Al_0.6Si_0.4 shown in Fig. 4C. Thus, the hydrodynamic approach for the magnon drag thermopower may give a qualitative explanation for the spin fluctuation enhancement. The assumption to neglect internal coupling may be valid at very low temperatures. At high temperatures, interaction among them (mode-mode coupling of spin fluctuations) should be essentially important, since those collective excitations dominate the low-energy excitations (11). Hence, analysis based on the spin fluctuation theory should be more appropriate.

As explained in the Introduction, S(T) of nearly ferromagnetic metals such as YCo₂ (13) and CaFe₄Sb₁₂ (14, 36) exhibits a peak around the temperatures where the magnetic susceptibility shows a maximum. The peak in S(T) for CaFe₄Sb₁₂ is completely suppressed by applying magnetic field (14). On the basis of these experimental results, Okabe (15) studied the effect of spin fluctuations by a two-band model. In this model, d electrons are responsible for the spin fluctuation, while transport properties are due to conduction electrons, which are dragged by spin fluctuations. According to (15), the Seebeck coefficient is described as

$${\mathit{S}}_{\text{SF}}=\mathit{A}\mathit{T}+\mathit{B}\mathit{T}{\left(\frac{\mathit{T}}{{\mathit{T}}_0}\right)}^2\text{ln}\frac{\mathrm{\delta }+{(\mathit{T}/{\mathit{T}}_0)}^2}{{(\mathit{T}/{\mathit{T}}_0)}^2}$$ (2)

where A, B, T₀, and δ are parameters. We have fit the data of Fe_2.2V_0.8Al_0.6Si_0.4 and plotted the results in Fig. 4C as solid lines, where δ = 4 was assumed (15) and the values of the parameters A and B were fixed against H. Equation 2 appears to explain the data over the measured temperature range. The characteristic temperatures were obtained to be T₀ = 931 and 1120 K for H = 0 and 9 T, respectively. The increased T₀ with H suggests that the low-energy spin fluctuation is more easily suppressed by the magnetic field.

So far, we have interpreted the enhanced Seebeck coefficient and the magnetism in terms of strong spin fluctuation. This was based on the assumption of a uniform distribution of ferromagnetic moments due to itinerant electrons. On the other hand, Lue et al. (37) suggested that the magnetism of Fe₂VAl-based alloys can be dominated by localized magnetic moments of Fe antisites. If this is the case, then our observation of the enhanced Seebeck coefficient and large AHE may be interpreted as due to the interaction of carriers with localized magnetic moments at Fe antisites or disorders. It should be noted that this interaction between localized moments and carriers can also lead to enhanced Seebeck coefficients, as observed in chalcopyrite-based magnetic semiconductors (38, 39). This may partially be the case. However, magnetic susceptibility (Fig. 1B, above T_C) shows a clear Curie-Weiss behavior with positive θ and reasonable value of effective magnetic moment, indicating that all the Fe sites contribute to the ferromagnetic behavior. Therefore, the uniform ferromagnetic moment due to itinerant electrons is the more probable explanation for the present case.

Notably, in the Fe_2.2V_0.8Al_1-ySi_y system, p-type behavior is reported for y = 0, where the Seebeck coefficient does not show any field variation up to H = 15 T, although the compound exhibits ferromagnetism below about 90 K (27). In our study, Si doping allowed for a change in the polarity of the sample to n type, and the remarkable field dependence occurs only in n-type samples. The precise mechanism of the spin fluctuation enhancement and the strong correlation between carrier transport and magnetism are yet to be clarified; thus, detailed theoretical study is necessary.

In summary, we identified weak ferromagnetism for the Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 and Fe_2.2V_0.8Al_0.6Si_0.4 samples below 160 and 285 K, respectively, which is understood in terms of weak itinerant ferromagnet. Thermoelectric property measurements revealed an unusual enhancement in the temperature-dependent Seebeck coefficient. The enhancement is most prominent around T_C but is observed for a wide temperature range from 100 K up to above room temperatures. When a magnetic field is applied, the enhancement is rapidly suppressed and a normal linear T behavior starts to be recovered. This remarkable feature should be attributed to the effect of spin fluctuation, which is significant for weakly or nearly ferromagnetic metals. As a result, the PFs of the samples are enhanced by more than 20% when compared to that when spin fluctuation is suppressed by a magnetic field. If we assume that the normal diffusion thermopower is approximated by the linear extrapolation of S-T data at low temperatures, then the enhancement in the Seebeck coefficient of Fe_2.2V_0.8Al_0.6Si_0.4 can reach 50% at 400 K, indicating that spin fluctuation brings a critically important contribution to the large PF (12 μW/K² cm at 400 K). Unlike the case of classical ferromagnets such as Fe and Co, Seebeck coefficients were not explained by the magnon drag effect. Instead, the calculated results based on the spin fluctuation theory appear to be consistent with the experimental data of Fe_2.2V_0.8Al_0.6Si_0.4. We observed an unusually large AHE in the present sample. All these findings demonstrate that the magnetic interaction is strongly coupled with the carrier transport to cause enhanced thermoelectric properties, which points to a new and effective strategy to obtain high output in thermoelectric generating devices. In this regard, our finding is quite unique and will add a new aspect of correlating magnetism to the power generation technologies.

MATERIALS AND METHODS

Sample preparation

Initially, polycrystalline samples of Fe₂VAl_0.9Si_0.1 were synthesized by mechanical alloying, followed by a spark plasma sintering (SPS) method with an attempt to synthesize samples with low thermal conductivity due to controlled nanostructures (40). Appropriate amounts of Fe (99.9%), V (99.9%), Fe-Al (99.9%), and Si (99.9%) powders were weighed to make Fe₂VAl_0.9Si_0.1 and were milled in a planetary ball mill with a Cr steel pot and balls. The pot was clamped and sealed with a rubber O-ring. Then, it was evacuated and filled with argon gas (99.9%) to prevent oxidation during the milling. The milling was performed at a revolution speed of 350 rpm for 7 hours with interval time taken every 5 min. The powder was loaded in a graphite die and was sintered by the SPS in a vacuum of 2 × 10⁻² Pa under pressure of 40 MPa at 1173 K for 30 min. Powder x-ray diffraction pattern (fig. S8) confirmed the single-phase sample with the cubic Heusler-type structure, and no secondary phase was detected. The chemical composition of the sample was checked by means of an electron probe microanalysis (EPMA) with wavelength-dispersive spectroscopy (WDS) using JEOL JXA-8500F. The results are shown in fig. S9. It has been revealed that Cr and a small amount of Ni are contaminated and are distributed almost uniformly over the sample, with the chemical composition of Fe_2.00V_0.94Cr_0.08Ni_0.02Al_0.86Si_0.10. This result is likely to suggest that 6% of the V site and 4% of the Al site are replaced by Cr and a small amount of Ni. The EPMA mapping showed that small particle–like regions have a chemical composition of about Fe_2.10V_0.85Cr_0.17Ni_0.05Al_0.74Si_0.09. This part presumably is also the Heusler-type phase but with less V and Al and with more Cr and Ni concentrations. Since the volume fraction of this Cr- and Ni-rich particle is very small, we describe this sample as Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 in the text for clarity.

Since an intriguing correlation between weak ferromagnetism and thermoelectric properties has been found in this composition, we then tried to synthesize other samples where part of the V site is replaced by transition metals. Fe_2.2V_0.8Al_1-ySi_y was chosen since Fe_2.2V_0.8Al and Fe_2.2V_0.8Si are reported to be ferromagnetic (27, 28). Appropriate amounts of Fe (99.98%), V (99.9%), Si (99.9999%), and Al (99.999%) were melted in an arc furnace under Ar. The weight loss of the samples during the melting was less than 1%; thereby, the chemical compositions are expected to be close to the nominal ones. The ingots were sealed in quartz tubes under Ar and were subjected to the heat treatment at 1237 K for 6 hours, followed by slow cooling down to 627 K in 48 hours, where the samples were further annealed for 12 hours and were rapidly cooled to room temperature. Powder x-ray diffraction (shown in fig. S10) confirmed that all these compounds crystallized in the L2₁-type structure.

Physical property measurements

Magnetization measurements were performed by a superconducting quantum interference device magnetometer from Quantum Design, MPMS (magnetic property measurement system). Electrical resistivity, Seebeck coefficient, and thermal conductivity were measured using a physical property measurement system (PPMS; Quantum Design) from 10 to 400 K under magnetic fields from 0 to 7 T for all the samples and up to 9 T for selected samples. Magnetic field, electric current, and temperature gradient were all in parallel, as indicated in the inset of Fig. 1C. Hall effect measurements of the Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 sample were carried out using a square-shaped sample (5 by 5 by 1 mm³) by the PPMS with a current of 10 mA under scanning magnetic field from −7 to 7 T.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/2/eaat5935/DC1

Fig. S1. Temperature dependence of the T derivative of the magnetization, dM/dT, of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 measured at H = 0.1 T.

Fig. S2. Rhodes-Wohlfarth plot of ferromagnetic compounds (20, 21) with the present data of the Heusler-type compounds.

Fig. S3. Thermal conductivity κ and the figure of merit Z of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1.

Fig. S4. Electrical resistivity ρ and thermal conductivity κ of Fe_2.2V_0.8Al_0.6Si_0.4 measured in H = 0 and 9 T.

Fig. S5. Magnetic and thermoelectric properties of Fe_2.2V_0.8Al_0.4Si_0.6.

Fig. S6. Magnetic and thermoelectric properties of Fe_2.2V_0.8Al_0.2Si_0.8.

Fig. S7. Hall resistivity ρ_xy (filled symbols) of Fe₂V_0.9Cr_0.1Al_0.9Si_0.1.

Fig. S8. Powder x-ray diffraction pattern of the Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 sample, which confirms the cubic L2₁-type structure with no secondary phase.

Fig. S9. Results of EPMA with the WDS for the Fe₂V_0.9Cr_0.1Al_0.9Si_0.1 sample.

Fig. S10. Powder x-ray diffraction patterns of the Fe_2.2V_0.8Al_1-ySi_y samples.